Harnessing Machine Learning and Data Fusion for Accurate Undocumented Well Identification in Satellite Images

Abstract

This study utilizes satellite data to detect undocumented oil and gas wells, which pose significant environmental concerns, including greenhouse gas emissions. Three key findings emerge from the study. Firstly, the problem of imbalanced data is addressed by recommending oversampling techniques like Rotation–GaussianBlur–Solarization data augmentation (RGS), the Synthetic Minority Over-Sampling Technique (SMOTE), or ADASYN (an extension of SMOTE) over undersampling techniques. The performance of borderline SMOTE is less effective than that of the rest of the oversampling techniques, as its performance relies heavily on the quality and distribution of data near the decision boundary. Secondly, incorporating pre-trained models trained on large-scale datasets enhances the models’ generalization ability, with models trained on one county’s dataset demonstrating high overall accuracy, recall, and F1 scores that can be extended to other areas. This transferability of models allows for wider application. Lastly, including persistent homology (PH) as an additional input improves performance for in-distribution testing but may affect the model’s generalization for out-of-distribution testing. A careful consideration of PH’s impact on overall performance and generalizability is recommended. Overall, this study provides a robust approach to identifying undocumented oil and gas wells, contributing to the acceleration of a net-zero economy and supporting environmental sustainability efforts.

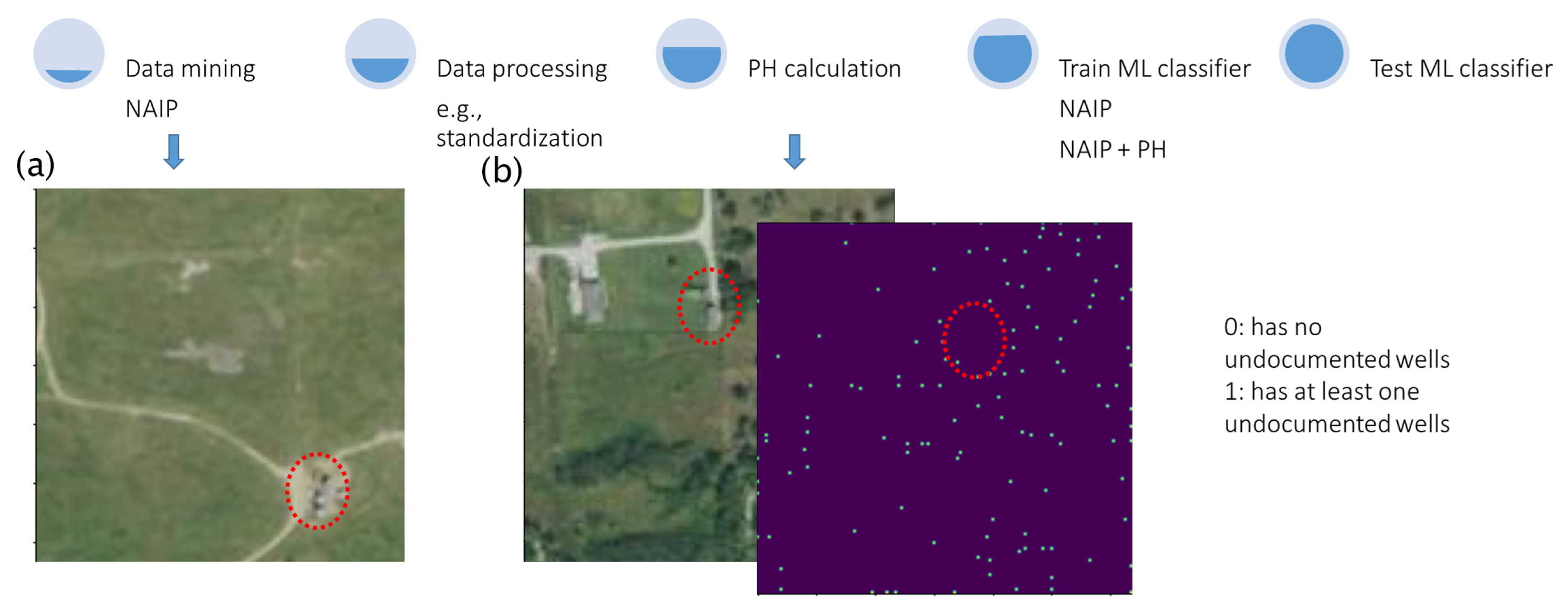
1. Introduction

Oil and gas (O&G) wells that are improperly abandoned or orphaned pose a significant environmental risk and potentially contribute to global methane emissions [1]. Unplugged or damaged wells introduce the risk of contaminates to the soil and groundwater [2,3,4,5,6] and greenhouse gasses to the atmosphere [1,7], meaning that each and every oil and gas well needs to be regularly assessed and maintained or properly plugged to isolate it from its surroundings.

There are currently over 120,000 documented orphaned wells [8], and the Department of Energy estimates hundreds of thousands of undocumented orphaned wells (UOWs) in the U.S. [9]. An orphaned O&G well is generally defined as an idle well for which the operator is unknown or insolvent. An undocumented well is defined as a well with an unknown location and missing information such as ownership and construction details [8]. Thus, an undocumented orphaned O&G well (UOW) is idle and lost from the records. Without knowing where these wells are, it is impossible to characterize them (e.g., their age, depth, condition, and risk associations), quantify their methane emissions, and execute mitigation measures [10]. Such an undertaking is daunting; however, developing automated techniques for identifying wells from high-resolution satellite imagery data is one of many approaches that hold promise for large-scale data analysis.

Machine learning (ML) is crucial in processing satellite data for various applications, including climate change mitigation [11]. Here, we focus on two aspects: image classification [12] and data fusion [13]. ML algorithms can be trained to classify satellite images into different categories, such as images that contain UOWs or ones that do not (Figure 1a). This enables the automated analysis of large volumes of satellite imagery, providing valuable information for identifying UOWs. Our ML problem here is a binary classification problem. Binary classification is an ML task that assigns input data points to one of two classes (0: no UOWs in the image; 1: at least one UOW in the image) or categories. The goal is to build a model to accurately predict the class label of new, unseen instances based on the patterns and relationships it learns from the training data.

Data fusion is an essential step in analyzing satellite data, which frequently originates from diverse sources and sensors, each offering distinct types of information. Through ML algorithms, data fusion enables the merging and integration of data from multiple satellites, resulting in a more comprehensive and precise representation within analysis systems. In this context, we combine two distinct data streams: satellite images presented in RGB format and the persistent homology (PH) of those images (Figure 1b). We hypothesize that, by incorporating additional input streams, we can enhance the ability of our ML models to learn meaningful patterns and consequently improve their accuracy in identifying UOWs.

PH, a tool from topological data analysis and computational topology, describes the connectivity structure of datasets [14,15,16]. PH can be applied to different data types, such as point clouds, digital images, and level sets of real-valued functions, to observe the change in homology, or “holes” of different dimensions, over a filtration of nested simplicial or cubical complexes placed on the data [17,18]. Since its development, PH has been applied in a multitude of fields, such as the identification of cancer cells in medical imagery, e.g., [19,20], characterizing porous material, e.g., [21,22], collective behavior in biology, e.g., [23], and comparing musical pieces [24]. More recently, researchers have also realized the use of PH as an automatic detection tool for geospatial objects in the geosciences, e.g., [25,26], the social sciences, e.g., [27,28,29], and transportation [30]. We hypothesized that the PH analysis of satellite imagery can draw attention to surface features related to O&G wells.

2. Materials and Methods

2.1. Machine Learning (ML) Models

Binary classification aims to classify instances into two classes or categories. These classes are typically represented as “positive” and “negative”, “1” and “0”, or “yes” and “no [31]”. The model is trained in binary classification using a labeled dataset in which each instance is associated with a class label [32]. The input features or variables are used to make predictions or decisions about the class membership of new, unseen instances. 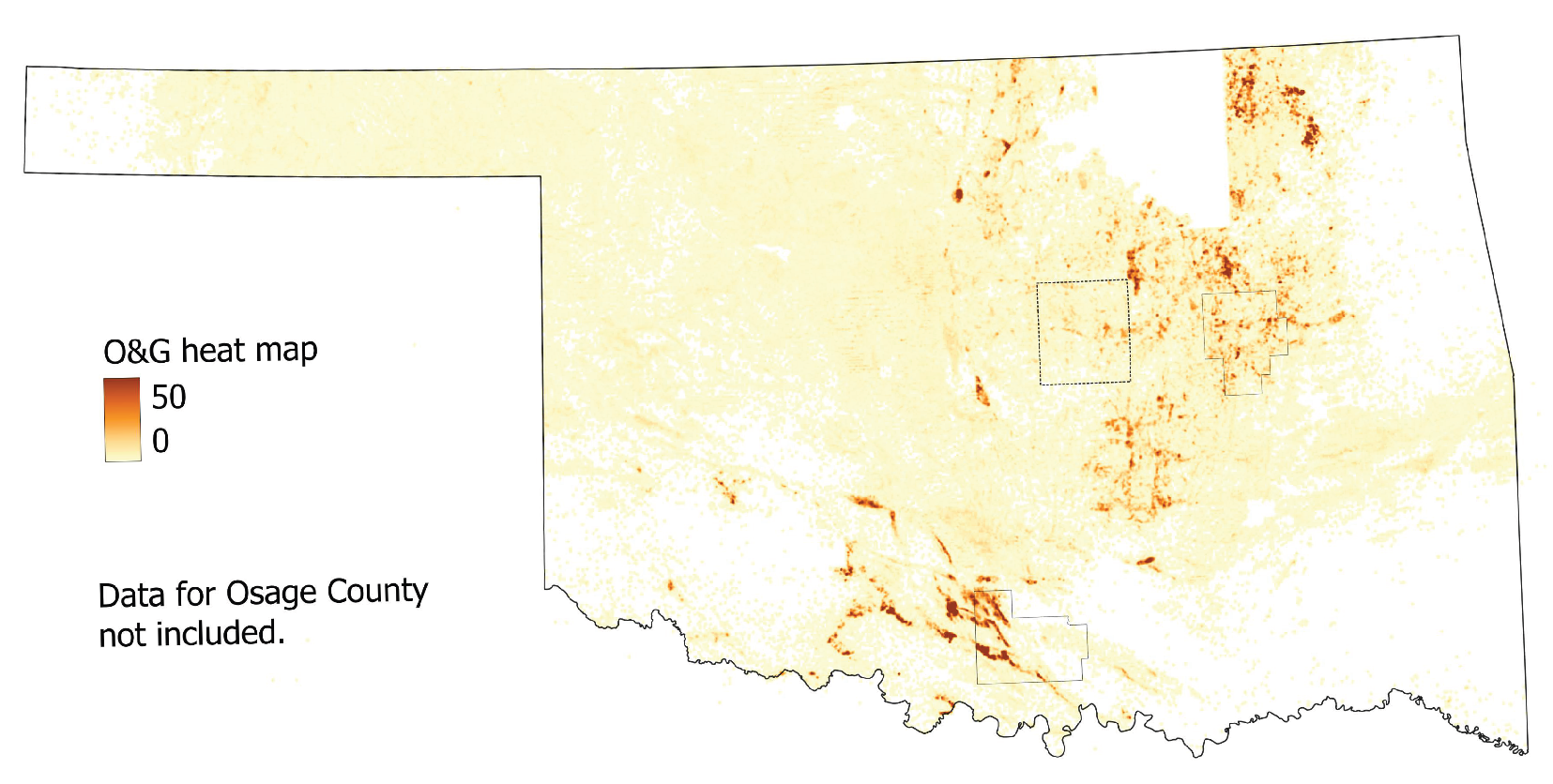Here, our inputs were the RGB imagery of three counties in Oklahoma from the National Agriculture Imagery Program [33] and Oklahoma Corporation Commission’s O&G well database with positive and negative examples of orphan wells [34], which served as our labeled data. This region was chosen for its high density of O&G wells (Figure 2) and public database of documented orphan wells (DOWs). Our outputs were “1” if at least one UOW existed in the image and “0” if no UOWs existed. Figure 3 highlights the different scenarios that the models faced.

We utilized five early deep convolutional neural network models—vanilla convolutional neural networks (CNN), ResNet-50, ResNet-101, RegNet-Y 400MF, and VGG-13 BN [35,36,37,38]—for this study. CNNs are effective for classification tasks, particularly in image recognition and capturing spatial patterns and hierarchical representations [39]. Our vanilla CNN consists of two convolutional layers and three linear layers, each with ReLU activation. ResNet-50 and ResNet-101 are variants of the Residual Network (ResNet) architecture with 50 and 101 layers, respectively. They address the vanishing gradient problem, allowing for the training of very deep networks [36]. RegNet-Y 400MF is a scalable and efficient model designed for various computer vision tasks [37], and it balances the model’s size, computational efficiency, and performance. VGG-13 BN is a 13-layer variant of the VGG architecture with batch normalization, and it is known for its depth and strong performance in image classification tasks [38,40]. While computationally intensive, it is suitable for scenarios with adequate resources.

We selected these models because all except vanilla CNN have pre-trained versions available in PyTorch, facilitating the application of transfer learning. (We used vanilla CNN as the simplest version of the ML classifier.) We leveraged pre-trained weights to accelerate the training process and compare the performance of each model when trained from scratch versus when using transfer learning. Furthermore, these models represent diverse architectures widely studied and validated in the literature, providing a robust basis for the comparative analysis of the impacts of different architectural features on our tasks’ performance while ensuring reproducibility and ease of implementation.

Furthermore, having pre-trained models allows us to compare the performance of each model when trained from scratch versus when using transfer learning. This comparison provides valuable insights into the benefits and limitations of transfer learning in our specific application context. By analyzing these two versions, we can better understand how pre-trained weights influence model convergence, generalization capabilities, and overall performance, informing future model selection and training strategies.

During the training phase, we utilized the ADAM optimizer— [41] with a learning rate of 0.0001 and a weight decay of $5\times {10}^{-3}$. The remaining parameters of the optimizer were left at their default values. Each model was trained for 50 epochs, employing a batch size of 128. 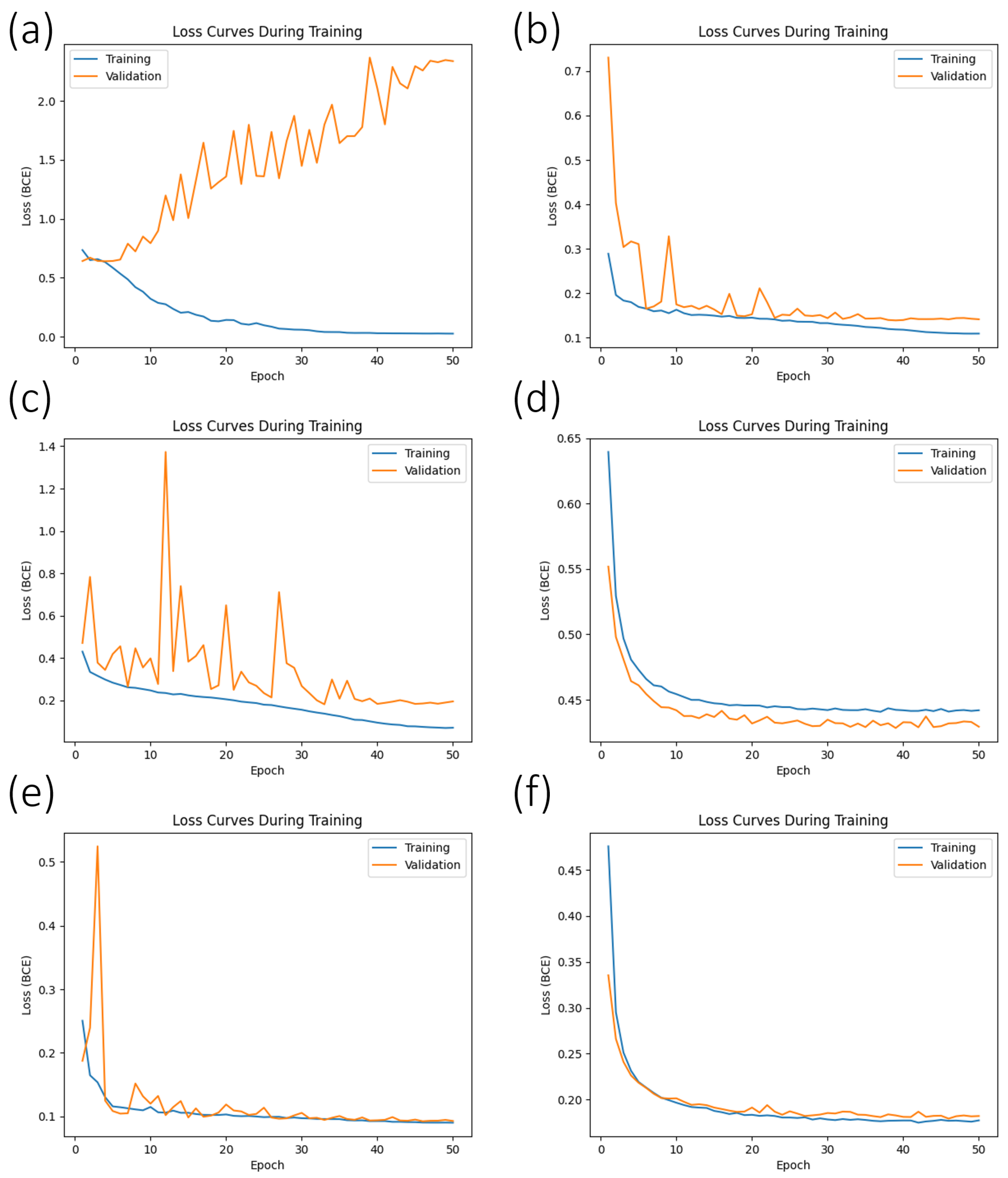We utilized the early stopping technique to mitigate overfitting during training, and we used generalized cross-validation criteria [42]. Rather than abruptly ending the training process, we adopted a strategy to save the set of trained weights and biases only when the current validation loss was lower than the lowest observed in all previous training cycles. This approach enabled us to identify the optimal model that minimized the validation loss and enhanced the model’s generalization performance. For instance, if the validation loss reached its lowest point at the 43rd epoch, see Figure 4a, we utilized the weights and biases obtained for the inference phase on the test set. On the other hand, if the lowest validation loss was at the 8th epoch, we utilized the weights and biases obtained at that epoch for the test set.

2.2. Data Imbalance

The dataset exhibited a data imbalance issue [43]. Due to the large number of O&G wells in our study area, there were significantly more samples representing orphan wells than those without. This can have various impacts on models [44] such as biased model performance, due to which the majority class is favored, the ability to learn patterns is reduced, data overfitting occurs in the training set, and feature representation is biased.

Two primary ways to deal with this data imbalance are (1) undersampling and (2) oversampling [45]. Undersampling involves reducing the number of samples from the majority class to create a more balanced dataset. By removing instances from the majority class, we can match the number of samples with the minority class, thereby reducing the class imbalance [46]. There are multiple ways to perform undersampling, such as random undersampling, cluster-based undersampling, Tomek-links undersampling, or edited nearest neighbors [47]. Our study, however, limited our scope only to random undersampling. Random undersampling involves randomly selecting a subset of samples from the majority class until the desired balance is achieved. This approach can lead to the loss of potentially valuable information present in the majority class.

Conversely, oversampling involves increasing the number of samples in the minority class to balance the dataset. By replicating or generating synthetic instances, the minority class representation is enhanced, allowing the model to learn its characteristics more effectively. We focused on Rotation–GaussianBlur–Solarization (RGS), the Synthetic Minority Over-Sampling Technique (SMOTE), borderline SMOTE, and Adaptive Synthetic (ADASYN) [48,49,50,51]. RGS applies a random rotation, Gaussian blur, and solarization to create variations in the minority-class samples. SMOTE generates synthetic samples by interpolating between neighboring instances, expanding the representation of the minority class [49]. As the name implies, borderline SMOTE targets borderline instances near the decision boundary, generating synthetic samples to improve classification accuracy in these challenging areas [50]. ADASYN focuses on difficult-to-learn instances by assigning higher weights during the generation process, adaptively balancing the class distribution [51]. The choice between SMOTE, borderline SMOTE, and ADASYN depends on the dataset’s characteristics and the problem being addressed. We used implementations provided in Scikit-learn [52] with a random seed of 42 for reproducibility. Additionally, we acknowledge the potential of generative AI, such as generative adversarial networks (GANs), for data augmentation, and we will investigate this approach in future studies.

Apart from undersampling or undersampling techniques, we pre-processed our input stream (satellite data and PH) using classical standardization or z-score normalization [53]. Standardization transforms the data with a mean of 0 and a standard deviation (std) of 1. The formula for standardization is standardized $x=(x-\mathrm{mean})/\mathrm{std}$, where x is the original value, the mean is the mean of the dataset, and std is the standard deviation of the dataset. By subtracting the mean and dividing it by the std, the data are centered around 0 and scaled based on the spread of the data.

2.3. Data Fusion with Persistent Homology (PH)

In addition to imagery data represented in RGB format (3 channels), we also explored the integration of PH as an additional input, introducing an extra channel (RGB + PH). PH extracts features from a topological space X based on a function defined within that space. In the context of remote sensing data, we can view the data as a two-dimensional, rough surface where the morphology is described using pixel values (referred to as height, denoted as $h(x,y)$, where x and y represent the column and row positions, respectively).

To perform PH on a rough surface, such as single-channel remote sensing data, we set a sequence of decreasing heights uniformly spaced between the images’ maximum and minimum pixel values. Conceptually, we can think of this process using the analogy from [54]: PH on a rough surface is akin to observing a landscape with islands of varying sizes as the sea level changes. No islands are visible when the sea level is high enough (h > maximum pixel value). This state corresponds to $X_0$. As the sea level drops, islands (0-dimensional homological or $H_0$ features) start to emerge, representing different levels of $X_i$ and gradually increasing in size ($X_i\subseteq X_{i+1}$). Islands can merge as the sea level reaches a saddle location, similar to two islands merging. The formation of isolated pools occurs when further sea level drops are 1-dimensional homological or $H_1$ features with their boundaries defined by the connected land surrounding them. The levels of pools correspond to the sea level, and eventually, they dry up. The birth and death of islands and pools define the topological structure of the land surface, and PH identifies and quantifies these features. By computing the difference between birth and death, often referred to as the lifetime, we can measure the persistence of these features. In the case of our data—natural-color imagery with a resolution of 1 m—RBG images were converted from RGB to grayscale using the Luminosity method ($grayscale=0.3R+0.59G+0.11\ast B$) to provide a single-channel surface for analysis. The lifespans of 0-dimensional homology reflect grayscale peaks; thus, PH analysis allowed us to detect and characterize surface features that produced a color contrast to their surroundings.

We utilized the Ripser PH package in Python [55,56] to compute PH and visualize persistence diagrams. Ripser PH employs the lower-star filtration method, which enables PH sublevel-set filtration on an image. This technique is particularly suitable for continuous data, treating the image as a continuous entity, rather than a collection of discrete Euclidean points, e.g., [57,58]. The lower-star filtration divides the image into segments, ranging from a minimum to a maximum limit, similar to a rising sea level. We inverted each image by scaling it by −1 to accommodate this filtration process. This adjustment allowed us to identify local maxima in the image as births and saddle points as deaths in $H_0$. It is important to note that, although PH can provide information on higher-order homology (such as $H_1$), the Python implementation of the lower star filtration method only returns $H_0$ results. We chose this because it allowed us to efficiently map the features’ locations regarding pixel indices. As explained in the following section, this limitation influenced the selection of the most suitable dataset for our purposes.

With the wide range of publicly available remote sensing information, each has pros and cons. In regions with ample vegetation, the presence of a well may be identifiable as clearings or a distinctive lack of vegetation. Magnetic surveys (0–50 m above ground level) are highly suitable for detecting the anomalous magnetic field intensity from well casing. We opted to perform PH on the imagery we were training and testing for binary classification to specifically test whether the images contained PH information that improved the model’s performance, see Figure 5 for an example of PH.

2.4. Evaluation Metrics

To assess the performance of our approach, we utilized appropriate evaluation metrics. Commonly used metrics for binary classification tasks include overall accuracy (herein referred to as accuracy), recall, and the F1 score. Accuracy measures the overall correctness of the predictions, while recall calculates the proportion of correctly predicted UOWs out of all actual wells. The F1 score is the harmonic mean of precision and recall, providing a balanced measure. We used the implementation provided in Scikit-learn [52].

We employed accuracy, recall, and the F1 score as evaluation metrics to assess the performance of our models [59]. These widely used metrics in ML and statistics offer valuable insights into various aspects of model performance, enabling us to evaluate their effectiveness. By considering accuracy, recall, and the F1 score, we comprehensively understand how well our models perform in classification tasks. The description and formulation of these metrics are listed below [59,60].

This study focused on key performance metrics such as Accuracy, Recall, and the F1 score, see

Table 1. Evaluation metrics for the classification models.

Metric	Description	Formula
Accuracy	Measures how often the model correctly predicts the target variable.	$\frac{\mathrm{Correct}\mathrm{Predictions}}{\mathrm{Total}\mathrm{Predictions}}$
Recall	A measure of the model’s ability to identify all positive instances correctly.	$\frac{\mathrm{True}\mathrm{Positives}}{\mathrm{True}\mathrm{Positives}+\mathrm{False}\mathrm{Negatives}}$
Precision	A measure of the model’s ability to identify only the relevant instances or positive cases correctly.	$\frac{\mathrm{True}\mathrm{Positives}}{\mathrm{True}\mathrm{Positives}+\mathrm{False}\mathrm{Positives}}$
F1 Score	The harmonic mean of precision and recall, providing a balance between the two.	$2\times \left(\frac{\mathrm{Precision}\times \mathrm{Recall}}{\mathrm{Precision}+\mathrm{Recall}}\right)$

. While Precision is an important metric in evaluating a model’s performance, we opted not to present it separately due to space constraints. It is important to note that Precision can be inferred from the provided metrics. Specifically, Precision can be derived using the F1 score and Recall, as it is integral to calculating the F1 score. The full list of performance metrics is in Appendix A.

3. Results

Trainable parameters are the weights and biases within the neural network that are updated during the training process. We defined all layers as models that do not employ transfer learning, meaning that these models were built from scratch without pre-trained models and only replaced the last layer with a fresh linear layer. When employing the transfer learning approach, where a pre-trained model is utilized, and only the last layer is replaced, the number of trainable parameters significantly decreases. This is because the pre-trained model has already learned useful features from a large dataset, and only the final layer needs to be fine-tuned to adapt to the specific task at hand.

Table 2. Summary of trainable parameters.

	Trainable Parameters
	without PH		with PH
Model	All Layers	Freeze (Train Only Last Layer)	All Layers	Freeze (Train Only Last Layer)
vanilla CNN	16,252,241	NA	16,252,391	NA
ResNet-50	23,510,081	11,457	23,513,217	14,593
ResNet-101	42,502,209	11,457	42,505,345	14,593
RegNet-Y 400MF	3,903,585	441	3,903,873	1593
VGG-13 BN	145,742,145	16,787,201	145,742,721	16,787,777

shows that the VGG-13 BN model possesses the highest number of trainable parameters, making it the most computationally expensive model. This implies that the VGG-13 BN architecture has a larger number of layers and more complex network connections, resulting in more parameters to be trained. On the other end of the spectrum, the RegNet-Y 400MF model has the least trainable parameters, making it the least computationally expensive model. This indicates that the RegNet-Y 400MF architecture has a simpler network structure with fewer layers and connections, resulting in fewer parameters that must be trained.

When we incorporated PH as an additional input feature, the number of trainable parameters slightly increased for both the transfer and non-transfer learning approaches. This was not surprising, as the PH feature requires additional weights and biases to be learned within the network, contributing to a marginal rise in the overall number of trainable parameters.

Data Augmentation

As stated before, data imbalance mitigation techniques are required with this particular dataset. Our original dataset consists of 48,400 samples, with 46,778 samples labeled 0 (no DOWs) and 1622 samples labeled 1 (with DOWs). We focused on having a significantly smaller number of samples with DOWs (labeled as 1 in 1622 samples) than those without (labeled as 0 in 46,778 samples). We randomly subsampled the label-0 samples from 46,778 to 3244 samples using a uniform distribution as prior. After the different oversampling techniques were applied, the ratio of samples with DOWs and those without DOWs ranged from 0.49 to 0.54 (

Table 3. Summary of data samples and their data augmentation.

	Augmentation	Total Images	Images with Orphan Wells	Ratio	Remark
Okmulgee	none	48,400	1622	0.03	Yse for training (0.7), validation (0.2), and testing (0.1)
	RGS	101,926	55,148	0.54
	SMOTE	93,556	46,778	0.50
	borderline SMOTE	93,556	46,778	0.50
	ADASYN	92,958	46,180	0.49
	RGS + SMOTE	93,556	46,778	0.50
Carter	none	NA	78	NA	Use for testing
Lincoln	none	NA	558	NA

).

To partition the total samples, we allocated 70% to training, 20% to validation, and 10% to testing. We tested the generalization capability of our model by evaluating it with out-of-distribution data. Specifically, we trained our model using satellite and well data from Okmulgee County, and we tested its performance using satellite and well data from Okmulgee (

Table 4. F1 model performance scores (mean and std) by ML model and data imbalance mitigation technique. Data trained on Okmulgee County data for predictions in Okmulgee County. * Image data with pre-trained weights and biases; $\widehat{*}$ image data with PH results. BL SMOTE = borderline SMOTE; RN50 = ResNet-50; RN100 = ResNet-100; RegNetY = RegNet-400MF; VGG = VGG-13-BN. The best results for each model and technique combination are highlighted in bold within the table. ^† True positives = 9493, false positives = 93, false negatives = 293, and true negatives = 310.

	Vanilla CNN	RN50	RN101	RegNetY	VGG
-	0.12 ± 0.07	0.00 ± 0	0.01 ± 0.02	0.00 ± 0	0.00 ± 0
RGS	0.94 ± 0.003	0.96 ± 0.002	0.92 ± 0.003	0.95 ± 0.001	0.96 ± 0.001
SMOTE	0.96 ± 0.005	0.92 ± 0.003	0.92 ± 0.001	0.93 ± 0.005	0.93 ± 0.002
BL SMOTE	0.96 ± 0.003	0.95 ± 0.001	0.95 ± 0.005	0.97 ± 0.001	0.95 ± 0.004
ADASYN	0.96 ± 0.006	0.92 ± 0.003	0.92 ± 0.007	0.94 ± 0.005	0.92 ± 0.003
RGS *		0.92 ± 0.002	0.94 ± 0.002	0.90 ± 0.001	0.93 ± 0.001
SMOTE *		0.84 ± 0.004	0.83 ± 0.002	0.78 ± 0.004	0.81 ± 0.003
ADASYN *		0.83 ± 0.006	0.82 ± 0.003	0.78 ± 0.003	0.81 ± 0.003
RGS+SMOTE	0.95 ± 0.002	0.96 ± 0.003	0.96 ± 0.003	0.95 ± 0.001	0.96 ± 0.002
SMOTE $\widehat{*}$	0.97 ± 0.002	0.97 ± 0.002	0.97 ± 0.001	0.98 ± 0.001	0.98 ± 0.002
RGS $\widehat{*}$	0.97 ± 0.001	0.98 ± 0.001	0.95 ± 0.041	0.98 ± 0.001  †	0.98 ± 0.006
RGS *$\widehat{*}$		0.96 ± 0.001	0.97 ± 0.001	0.94 ± 0.002	0.95 ± 0.001
SMOTE *$\widehat{*}$		0.94 ± 0.002	0.94 ± 0.003	0.94 ± 0.002	0.94 ± 0.004

), Carter (

Table 5. F1 model performance scores (mean and std) by ML model and data imbalance mitigation technique. Data trained on Okmulgee County data for predictions in Carter County. * Image data with pre-trained weights and biases; $\widehat{*}$ image data with PH results. BL SMOTE = borderline SMOTE; RN50 = ResNet-50; RN100 = ResNet-100; RegNetY = RegNet-400MF; VGG = VGG-13-BN. F1 scores over 0.5 are shown in bold. ^† True postivites = 46, false positives = 0, false negatives = 10, and true negatives = 22.

	Vanilla CNN	RN50	RN101	RegNetY	VGG
-	0.09 ± 0.07	0.00 ± 0	0.01 ± 0.01	0.00 ± 0	0.00 ± 0
RGS	0.15 ± 0.069	0.02 ± 0.106	0.24 ± 0.097	0.16 ± 0.051	0.18 ± 0.051
SMOTE	0.41 ± 0.108	0.30 ± 0.054	0.30 ± 0.046	0.29 ± 0.093	0.30 ± 0.054
BL SMOTE	0.34 ± 0.057	0.30 ± 0.054	0.30 ± 0.068	0.25 ± 0.043	0.31 ± 0.042
ADASYN	0.35 ± 0.04	0.31 ± 0.055	0.34 ± 0.074	0.34 ± 0.019	0.29 ± 0.07
RGS *		0.25 ± 0.038	0.32 ± 0.07	0.25 ± 0.031	0.07 ± 0.031
SMOTE *		0.79 ± 0.005	0.83 ± 0.026	0.90 ± 0.007  †	0.83 ± 0.023
ADASYN *		0.81 ± 0.03	0.81 ± 0.044	0.89 ± 0.012	0.80 ± 0.015
RGS+SMOTE	0.17 ± 0.104	0.17 ± 0.084	0.15 ± 0.049	0.13 ± 0.058	0.10 ± 0.066
RGS $\widehat{*}$	0.09 ± 0.078	0.09 ± 0.035	0.05 ± 0.046	0.09 ± 0.021	0.10 ± 0.037
SMOTE $\widehat{*}$	0.04 ± 0.014	0.02 ± 0.035	0.13 ± 0.229	0.05 ± 0.09	0.01 ± 0.011
RGS *$\widehat{*}$		0.15 ± 0.018	0.07 ± 0.011	0.26 ± 0.071	0.24 ± 0.017
SMOTE *$\widehat{*}$		0.11 ± 0.026	0.18 ± 0.052	0.19 ± 0.033	0.15 ± 0.012

), and Lincoln (

Table 6. F1 model performance scores (mean and std) by ML model and data imbalance mitigation technique. Data trained on Okmulgee County data for predictions in Lincoln County. * Image data with pre-trained weights and biases; $\widehat{*}$ image data with PH results. BL SMOTE= borderline SMOTE; RN50 = ResNet-50; RN100 = ResNet-100; RegNetY = RegNet-400MF; VGG = VGG-13-BN. F1 scores over 0.5 are shown in bold. ^† True positives = 129, false positives = 0, false negatives = 97, and true negatives = 332.

	Vanilla CNN	RN50	RN101	RegNetY	VGG
-	0.05 ± 0.02	0.01 ± 0.01	0.01 ± 0.01	0.00 ± 0.01	0.00 ± 0
RGS	0.62 ± 0.044	0.68 ± 0.047	0.69 ± 0.04	0.65 ± 0.035	0.63 ± 0.037
SMOTE	0.27 ± 0.061	0.25 ± 0.039	0.27 ± 0.045	0.24 ± 0.06	0.30 ± 0.048
BL SMOTE	0.19 ± 0.015	0.16 ± 0.014	0.17 ± 0.032	0.11 ± 0.037	0.19 ± 0.029
ADASYN	0.25 ± 0.033	0.26 ± 0.036	0.26 ± 0.036	0.26 ± 0.014	0.27 ± 0.031
RGS *		0.64 ± 0.02	0.63 ± 0.024	0.62 ± 0.009	0.61 ± 0.031
SMOTE *		0.61 ± 0.015	0.68 ± 0.013	0.71 ± 0.01	0.62 ± 0.019
ADASYN *		0.62 ± 0.019	0.67 ± 0.01	0.71 ± 0.024	0.59 ± 0.007
RGS+SMOTE	0.63 ± 0.067	0.63 ± 0.055	0.67 ± 0.052	0.63 ± 0.034	0.62 ± 0.044
RGS $\widehat{*}$	0.54 ± 0.061	0.73 ± 0.016	0.62 ± 0.127	0.73 ± 0.02 †	0.72 ± 0.027
SMOTE $\widehat{*}$	0.09 ± 0.024	0.02 ± 0.017	0.06 ± 0.039	0.01 ± 0.018	0.10 ± 0.008
RGS *$\widehat{*}$		0.57 ± 0.022	0.51 ± 0.031	0.47 ± 0.017	0.58 ± 0.02
SMOTE *$\widehat{*}$		0.14 ± 0.026	0.18 ± 0.026	0.18 ± 0.02	0.24 ± 0.019

) counties. We followed early stopping and generalized cross-validation criteria to prevent overfitting during training [42]. Rather than strictly stopping the training cycle, we only saved the set of trained weights and biases when the current validation loss was lower than the lowest from all previous training cycles. This approach helped us find the optimal model that minimized the validation loss and improved the generalization performance of our model. All the model performance results presented here are the mean and standard deviation (std) of five runs. Examples of training and validation losses using RegNet-Y 400 MF (Figure 6) were organized by data augmentation technique.

4. Discussion

4.1. Data Augmentation Tool Comparison

The employed models with no data augmentation approaches yielded near-zero F1 scores, regardless of whether the data were in distribution (Okmulgee) or out of distribution (Carter and Lincoln), which suggests that undersampling might not be the optimal solution for this classification task. While all the models benefited from data augmentation, we highlight the approaches that produced the most favorable results with out-of-distribution data, noting that Carter had far fewer samples with DOWs (78) than Lincoln (558).

RGS augmentation significantly improved the Lincoln models (F1 scores = 0.62–0.69) and, to a lesser degree, improved the Carter models (F1 scores = 0.02–0.24), suggesting a higher degree of similarity between Okmulgee and Lincoln counties (full metrics in

Table A2. Performance of models with RGS data augmentation (mean ± std)—oversampling.

Trained on Okmulgee	Model	Accuracy	Recall	F1
predict Okmulgee	vanilla CNN	0.94 ± 0.003	0.92 ± 0.007	0.94 ± 0.003
	ResNet-50	0.96 ± 0.002	0.93 ± 0.002	0.96 ± 0.002
	ResNet-101	0.92 ± 0.004	0.9 ± 0.028	0.92 ± 0.003
	RegNet-Y 400MF	0.95 ± 0.001	0.93 ± 0.004	0.95 ± 0.001
	VGG-13 BN	0.96 ± 0.001	0.93 ± 0.002	0.96 ± 0.001
predict Carter	vanilla CNN	0.08 ± 0.042	0.08 ± 0.042	0.15 ± 0.069
	ResNet-50	0.11 ± 0.065	0.11 ± 0.065	0.2 ± 0.106
	ResNet-101	0.14 ± 0.062	0.14 ± 0.062	0.24 ± 0.097
	RegNet-Y 400MF	0.09 ± 0.03	0.09 ± 0.03	0.16 ± 0.051
	VGG-13 BN	0.1 ± 0.032	0.1 ± 0.032	0.18 ± 0.051
predict Lincoln	vanilla CNN	0.45 ± 0.044	0.45 ± 0.044	0.62 ± 0.044
	ResNet-50	0.51 ± 0.053	0.51 ± 0.053	0.68 ± 0.047
	ResNet-101	0.53 ± 0.047	0.53 ± 0.047	0.69 ± 0.04
	RegNet-Y 400MF	0.48 ± 0.039	0.48 ± 0.039	0.65 ± 0.035
	VGG-13 BN	0.46 ± 0.039	0.46 ± 0.039	0.63 ± 0.037

). SMOTE augmentation improved the Carter models nearly 2× more than RGS augmentation in Carter (full metrics in

Table A3. Performance of models with SMOTE (mean ± std)—oversampling.

Trained on Okmulgee	Model	Accuracy	Recall	F1
predict Okmulgee	vanilla CNN	0.96 ± 0.005	0.97 ± 0.008	0.96 ± 0.005
	ResNet-50	0.92 ± 0.002	0.9 ± 0.012	0.92 ± 0.003
	ResNet-101	0.92 ± 0.001	0.91 ± 0.005	0.92 ± 0.001
	RegNet-Y 400MF	0.94 ± 0.005	0.92 ± 0.009	0.93 ± 0.005
	VGG-13 BN	0.93 ± 0.001	0.89 ± 0.011	0.93 ± 0.002
predict Carter	vanilla CNN	0.26 ± 0.084	0.26 ± 0.084	0.41 ± 0.108
	ResNet-50	0.18 ± 0.038	0.18 ± 0.038	0.3 ± 0.054
	ResNet-101	0.18 ± 0.031	0.18 ± 0.031	0.3 ± 0.046
	RegNet-Y 400MF	0.17 ± 0.064	0.17 ± 0.064	0.29 ± 0.093
	VGG-13 BN	0.18 ± 0.036	0.18 ± 0.036	0.3 ± 0.054
predict Lincoln	vanilla CNN	0.15 ± 0.04	0.15 ± 0.04	0.27 ± 0.061
	ResNet-50	0.14 ± 0.026	0.14 ± 0.026	0.25 ± 0.039
	ResNet-101	0.16 ± 0.03	0.16 ± 0.03	0.27 ± 0.045
	RegNet-Y 400MF	0.14 ± 0.04	0.14 ± 0.04	0.24 ± 0.06
	VGG-13 BN	0.18 ± 0.033	0.18 ± 0.033	0.3 ± 0.048

). We interpret this to mean that SMOTE synthesizes new samples from the minority class through interpolation between neighboring samples and enhancing the generalizability of the models. However, the overall out-of-distribution performance was poor (F1 score = 0.25–0.4) indicating that SMOTE augmentation may also remove the similarities between Okmulgee and Lincoln that contributed to significantly improved RGS performance. Borderline SMOTE (full metrics in

Table A4. Performance of models with borderline SMOTE (mean ± std)—oversampling.

Trained on Okmulgee	Model	Accuracy	Recall	F1
predict Okmulgee	vanilla CNN	0.96 ± 0.002	0.95 ± 0.004	0.96 ± 0.003
	ResNet-50	0.95 ± 0.001	0.94 ± 0.005	0.95 ± 0.001
	ResNet-101	0.95 ± 0.004	0.94 ± 0.011	0.95 ± 0.005
	RegNet-Y 400MF	0.97 ± 0.001	0.96 ± 0.004	0.97 ± 0.001
	VGG-13 BN	0.95 ± 0.003	0.93 ± 0.008	0.95 ± 0.004
predict Carter	vanilla CNN	0.21 ± 0.04	0.21 ± 0.04	0.34 ± 0.057
	ResNet-50	0.18 ± 0.037	0.18 ± 0.037	0.3 ± 0.054
	ResNet-101	0.18 ± 0.047	0.18 ± 0.047	0.3 ± 0.068
	RegNet-Y 400MF	0.14 ± 0.028	0.14 ± 0.028	0.25 ± 0.043
	VGG-13 BN	0.19 ± 0.03	0.19 ± 0.03	0.31 ± 0.042
predict Lincoln	vanilla CNN	0.1 ± 0.009	0.1 ± 0.009	0.19 ± 0.015
	ResNet-50	0.09 ± 0.008	0.09 ± 0.008	0.16 ± 0.014
	ResNet-101	0.1 ± 0.019	0.1 ± 0.019	0.17 ± 0.032
	RegNet-Y 400MF	0.06 ± 0.021	0.06 ± 0.021	0.11 ± 0.037
	VGG-13 BN	0.11 ± 0.018	0.11 ± 0.018	0.19 ± 0.029

) did not improve model performance beyond what SMOTE already accomplished. ADASYN performed slightly better in Carter and slightly worse in Lincoln (full metrics in

Table A5. Performance of models with ADASYN (mean ± std)—oversampling.

Trained on Okmulgee	Model	Accuracy	Recall	F1
predict Okmulgee	vanilla CNN	0.97 ± 0.006	0.96 ± 0.003	0.96 ± 0.006
	ResNet-50	0.92 ± 0.003	0.9 ± 0.006	0.92 ± 0.003
	ResNet-101	0.92 ± 0.007	0.9 ± 0.01	0.92 ± 0.007
	RegNet-Y 400MF	0.94 ± 0.006	0.92 ± 0.004	0.94 ± 0.005
	VGG-13 BN	0.93 ± 0.003	0.89 ± 0.005	0.92 ± 0.003
predict Carter	vanilla CNN	0.21 ± 0.03	0.21 ± 0.03	0.35 ± 0.04
	ResNet-50	0.19 ± 0.038	0.19 ± 0.038	0.31 ± 0.055
	ResNet-101	0.21 ± 0.055	0.21 ± 0.055	0.34 ± 0.074
	RegNet-Y 400MF	0.21 ± 0.014	0.21 ± 0.014	0.34 ± 0.019
	VGG-13 BN	0.17 ± 0.048	0.17 ± 0.048	0.29 ± 0.07
predict Lincoln	vanilla CNN	0.14 ± 0.021	0.14 ± 0.021	0.25 ± 0.033
	ResNet-50	0.15 ± 0.024	0.15 ± 0.024	0.26 ± 0.036
	ResNet-101	0.15 ± 0.023	0.15 ± 0.023	0.26 ± 0.036
	RegNet-Y 400MF	0.15 ± 0.01	0.15 ± 0.01	0.26 ± 0.014
	VGG-13 BN	0.16 ± 0.021	0.16 ± 0.021	0.27 ± 0.031

). SMOTE and ADASYN yielded better results than borderline SMOTE. All three data augmentation tools improved the models compared to those with no augmentation; however, RGS performed much better in Lincoln, likely due to similarities between the Okmulgee and Lincoln samples.

We considered a joint implementation of RGS and SMOTE to improve the SMOTE, borderline SMOTE, and ADASYN performance (full metrics in

Table A9. Performance of models with RGS data augmentation and SMOTE (mean ± std).

Trained on Okmulgee	Model	Accuracy	Recall	F1
predict Okmulgee	vanilla CNN	0.95 ± 0.003	0.92 ± 0.003	0.95 ± 0.002
	ResNet-50	0.95 ± 0.003	0.93 ± 0.005	0.96 ± 0.003
	ResNet-101	0.96 ± 0.003	0.93 ± 0.004	0.96 ± 0.003
	RegNet-Y 400MF	0.95 ± 0.001	0.92 ± 0.004	0.95 ± 0.001
	VGG-13 BN	0.96 ± 0.002	0.94 ± 0.004	0.96 ± 0.002
predict Carter	vanilla CNN	0.1 ± 0.061	0.1 ± 0.061	0.17 ± 0.104
	ResNet-50	0.09 ± 0.05	0.09 ± 0.05	0.17 ± 0.084
	ResNet-101	0.08 ± 0.03	0.08 ± 0.03	0.15 ± 0.049
	RegNet-Y 400MF	0.07 ± 0.033	0.07 ± 0.033	0.13 ± 0.058
	VGG-13 BN	0.05 ± 0.038	0.05 ± 0.038	0.1 ± 0.066
predict Lincoln	vanilla CNN	0.46 ± 0.072	0.46 ± 0.072	0.63 ± 0.067
	ResNet-50	0.46 ± 0.059	0.46 ± 0.059	0.63 ± 0.055
	ResNet-101	0.5 ± 0.059	0.5 ± 0.059	0.67 ± 0.052
	RegNet-Y 400MF	0.46 ± 0.036	0.46 ± 0.036	0.63 ± 0.034
	VGG-13 BN	0.45 ± 0.047	0.45 ± 0.047	0.62 ± 0.044

. This had no benefit in the Carter models, and in fact, the performance was worse than with SMOTE alone. The Lincoln models yielded similar F1 scores to RGS alone. These scores indicate that the influence of RGS augmentation on model performance outweighs that of SMOTE techniques.

4.2. Data Augmentation with Pre-Trained Layers

Training only the newly added layer allowed us to adapt the model to our target task while minimizing the risk of overfitting or losing valuable knowledge in the pre-trained layers. The pre-trained models used in this study were obtained from the PyTorch model zoo (https://pytorch.org/vision/stable/models.html accessed on 22 September 2022), and they came with pre-trained weights learned from large-scale image datasets like ImageNet.

The performance of the RGS, SMOTE, and ADASYN data augmentation techniques using a pre-trained model (full metrics in

Table A6. Performance of models with RGS data augmentation and pre-trained weights and biases (mean ± std).

Trained on Okmulgee	Model	Accuracy	Recall	F1
predict Okmulgee	ResNet-50	0.91±0.002	0.89±0.003	0.92±0.002
	ResNet-101	0.93 ± 0.002	0.91 ± 0.002	0.94 ± 0.002
	RegNet-Y 400MF	0.89 ± 0.001	0.85 ± 0.001	0.9 ± 0.001
	VGG-13 BN	0.93 ± 0.001	0.89 ± 0.003	0.93 ± 0.001
predict Carter	ResNet-50	0.15 ± 0.025	0.15 ± 0.025	0.25 ± 0.038
	ResNet-101	0.19 ± 0.05	0.19 ± 0.05	0.32 ± 0.07
	RegNet-Y 400MF	0.14 ± 0.02	0.14 ± 0.02	0.25 ± 0.031
	VGG-13 BN	0.04 ± 0.017	0.04 ± 0.017	0.07 ± 0.031
predict Lincoln	ResNet-50	0.47 ± 0.022	0.47 ± 0.022	0.64 ± 0.02
	ResNet-101	0.46 ± 0.025	0.46 ± 0.025	0.63 ± 0.024
	RegNet-Y 400MF	0.45 ± 0.009	0.45 ± 0.009	0.62 ± 0.009
	VGG-13 BN	0.44 ± 0.032	0.44 ± 0.032	0.61 ± 0.031

,

Table A7. Performance of models with SMOTE and pre-trained weights and biases (mean ± std).

Trained on Okmulgee	Model	Accuracy	Recall	F1
predict Okmulgee	ResNet-50	0.84 ± 0.004	0.8 ± 0.008	0.84 ± 0.004
	ResNet-101	0.84 ± 0.003	0.79 ± 0.006	0.83 ± 0.002
	RegNet-Y 400MF	0.79 ± 0.003	0.73 ± 0.006	0.78 ± 0.004
	VGG-13 BN	0.83 ± 0.002	0.74 ± 0.006	0.81 ± 0.003
predict Carter	ResNet-50	0.65 ± 0.007	0.65 ± 0.007	0.79 ± 0.005
	ResNet-101	0.72 ± 0.039	0.72 ± 0.039	0.83 ± 0.026
	RegNet-Y 400MF	0.81 ± 0.011	0.81 ± 0.011	0.9 ± 0.007
	VGG-13 BN	0.71 ± 0.035	0.71 ± 0.035	0.83 ± 0.023
predict Lincoln	ResNet-50	0.44 ± 0.016	0.44 ± 0.016	0.61 ± 0.015
	ResNet-101	0.52 ± 0.014	0.52 ± 0.014	0.68 ± 0.013
	RegNet-Y 400MF	0.55 ± 0.012	0.55 ± 0.012	0.71 ± 0.01
	VGG-13 BN	0.45 ± 0.02	0.45 ± 0.02	0.62 ± 0.019

, and

Table A8. Performance of models with ADASYN and pre-trained weights and biases (mean ± std).

Trained on Okmulgee	Model	Accuracy	Recall	F1
predict Okmulgee	ResNet-50	0.84 ± 0.004	0.8 ± 0.011	0.83 ± 0.006
	ResNet-101	0.83 ± 0.002	0.78 ± 0.009	0.82 ± 0.003
	RegNet-Y 400MF	0.79 ± 0.003	0.73 ± 0.014	0.78 ± 0.003
	VGG-13 BN	0.83 ± 0.002	0.74 ± 0.004	0.81 ± 0.003
predict Carter	ResNet-50	0.68 ± 0.042	0.68 ± 0.042	0.81 ± 0.03
	ResNet-101	0.68 ± 0.061	0.68 ± 0.061	0.81 ± 0.044
	RegNet-Y 400MF	0.81 ± 0.02	0.81 ± 0.02	0.89 ± 0.012
	VGG-13 BN	0.66 ± 0.021	0.66 ± 0.021	0.8 ± 0.015
predict Lincoln	ResNet-50	0.45 ± 0.021	0.45 ± 0.021	0.62 ± 0.019
	ResNet-101	0.51 ± 0.011	0.51 ± 0.011	0.67 ± 0.01
	RegNet-Y 400MF	0.55 ± 0.029	0.55 ± 0.029	0.71 ± 0.024
	VGG-13 BN	0.42 ± 0.007	0.42 ± 0.007	0.59 ± 0.007

, respectively) were compared against those same techniques without the use of a pre-trained model. RGS with a pre-trained model is only marginally different from RGS without a pre-trained model. One possible explanation for this minimal difference in RGS performance is that the RGS augmentation technique (which involves rotation, Gaussian blur, and solarization) does not closely resemble the data types to which the pre-trained models were exposed during their training. Pre-trained models are typically trained on large-scale datasets like ImageNet, consisting of natural images with diverse lighting, poses, and object appearance variations. Therefore, the features learned via pre-trained models might not align perfectly with the specific augmentations introduced in RGS.

The performance of SMOTE and ADASYN with a pre-trained model, on the other hand, showed significant improvement in out-of-distribution testing with the Carter models (F1 scores = 0.79–0.90), performing better than the Lincoln models (0.59–0.71). The higher scores obtained in out-of-distribution testing imply that the synthetic data generated via SMOTE augmentation captured important patterns and characteristics present in the training data, aligning more closely with the representations learned via the pre-trained models. As a result, the models became more adept at handling previously unseen data, demonstrating their improved ability to generalize beyond the training distribution.

4.3. Data Augmentation and Data Fusion

Recall that PH data were derived from satellite images and incorporated as a fourth channel. Grayscale images proved the most useful in performing PH to detect our features of interest. In grayscale images, the cleared area surrounding a well has a fairly constant pixel value, and the well structure is a ”bright spot” in the middle. Note that this brightness is a function of the pixel color; different RGB combinations can translate to the same grayscale value. A well is more easily recognized as an $H_0$ feature in lower-star filtration results (Figure 5, bottom). The filtration produced what this application considers false positives and true negatives even when we implemented a height cut-off. Nevertheless, the results add a layer of information for ML to consider. This was incorporated in the models with data augmentation and no pre-trained model, as well as data augmentation with a pre-trained model. Since borderline SMOTE showed inferior performance, and ADASYN exhibited such similar behavior to SMOTE, they are not discussed further.

There was a small enhancement when adding PH to RGS-augmented data (full metric in

Table A10. Performance of models with RGS data augmentation and PH (mean ± std).

Trained on Okmulgee	Model	Accuracy	Recall	F1
predict Okmulgee	vanilla CNN	0.97 ± 0.001	0.95 ± 0.003	0.97 ± 0.001
	ResNet-50	0.98 ± 0.001	0.96 ± 0.002	0.98 ± 0.001
	ResNet-101	0.95 ± 0.039	0.92 ± 0.073	0.95 ± 0.041
	RegNet-Y 400MF	0.97 ± 0.002	0.96 ± 0.003	0.98 ± 0.001
	VGG-13 BN	0.98 ± 0.006	0.96 ± 0.009	0.98 ± 0.006
predict Carter	vanilla CNN	0.05 ± 0.043	0.05 ± 0.043	0.09 ± 0.078
	ResNet-50	0.05 ± 0.019	0.05 ± 0.019	0.09 ± 0.035
	ResNet-101	0.03 ± 0.025	0.03 ± 0.025	0.05 ± 0.046
	RegNet-Y 400MF	0.05 ± 0.011	0.05 ± 0.011	0.09 ± 0.021
	VGG-13 BN	0.05 ± 0.02	0.05 ± 0.02	0.1 ± 0.037
predict Lincoln	vanilla CNN	0.38 ± 0.056	0.38 ± 0.056	0.54 ± 0.061
	ResNet-50	0.57 ± 0.019	0.57 ± 0.019	0.73 ± 0.016
	ResNet-101	0.46 ± 0.12	0.46 ± 0.12	0.62 ± 0.127
	RegNet-Y 400MF	0.57 ± 0.025	0.57 ± 0.025	0.73 ± 0.02
	VGG-13 BN	0.57 ± 0.032	0.57 ± 0.032	0.72 ± 0.027

) compared to RGS and no PH information. For the Lincoln models, the difference was not notable. For the Carter models, the performance was worse. As noted before, the far better performance in the Lincoln models suggests more similarities between the Okmulgee and Lincoln samples. The PH analysis of Lincoln imagery likely revealed similar patterns as those found in Okmulgee that were absent in Carter, thus making the addition of PH in the Carter models not beneficial. Utilizing a pre-trained model (full metric in

Table A12. Performance of models with RGS data augmentation, pre-trained weights and biases, and PH (mean ± std).

Trained on Okmulgee	Model	Accuracy	Recall	F1
predict Okmulgee	ResNet-50	0.96 ± 0.001	0.94 ± 0.003	0.96 ± 0.001
	ResNet-101	0.96 ± 0.001	0.95 ± 0.001	0.97 ± 0.001
	RegNet-Y 400MF	0.94 ± 0.002	0.92 ± 0.002	0.94 ± 0.002
	VGG-13 BN	0.95 ± 0.001	0.93 ± 0.003	0.95 ± 0.001
predict Carter	ResNet-50	0.08 ± 0.011	0.08 ± 0.011	0.15 ± 0.018
	ResNet-101	0.04 ± 0.006	0.04 ± 0.006	0.07 ± 0.011
	RegNet-Y 400MF	0.15 ± 0.046	0.15 ± 0.046	0.26 ± 0.071
	VGG-13 BN	0.14 ± 0.011	0.14 ± 0.011	0.24 ± 0.017
predict Lincoln	ResNet-50	0.4 ± 0.021	0.4 ± 0.021	0.57 ± 0.022
	ResNet-101	0.35 ± 0.028	0.35 ± 0.028	0.51 ± 0.031
	RegNet-Y 400MF	0.31 ± 0.014	0.31 ± 0.014	0.47 ± 0.017
	VGG-13 BN	0.41 ± 0.02	0.41 ± 0.02	0.58 ± 0.02

) resulted in a decline in performance.

The inclusion of PH in SMOTE-augmented data resulted in a decline in performance. Although utilizing a pre-trained model (full metrics in

Table A13. Performance of models with SMOTE, pre-trained weights and biases, and PH (mean ± std).

Trained on Okmulgee	Model	Accuracy	Recall	F1
predict Okmulgee	ResNet-50	0.95 ± 0.002	0.91 ± 0.004	0.94 ± 0.002
	ResNet-101	0.95 ± 0.003	0.91 ± 0.006	0.94 ± 0.003
	RegNet-Y 400MF	0.94 ± 0.001	0.91 ± 0.006	0.94 ± 0.002
	VGG-13 BN	0.95 ± 0.003	0.9 ± 0.007	0.94 ± 0.004
predict Carter	ResNet-50	0.06 ± 0.015	0.06 ± 0.015	0.11 ± 0.026
	ResNet-101	0.1 ± 0.031	0.1 ± 0.031	0.18 ± 0.052
	RegNet-Y 400MF	0.1 ± 0.02	0.1 ± 0.02	0.19 ± 0.033
	VGG-13 BN	0.08 ± 0.007	0.08 ± 0.007	0.15 ± 0.012
predict Lincoln	ResNet-50	0.08 ± 0.015	0.08 ± 0.015	0.14 ± 0.026
	ResNet-101	0.1 ± 0.016	0.1 ± 0.016	0.18 ± 0.026
	RegNet-Y 400MF	0.1 ± 0.012	0.1 ± 0.012	0.18 ± 0.02
	VGG-13 BN	0.14 ± 0.012	0.14 ± 0.012	0.24 ± 0.019

) resulted in better performance than without a pre-trained model (full metrics in

Table A11. Performance of models with SMOTE and PH (mean ± std).

Trained on Okmulgee	Model	Accuracy	Recall	F1
predict Okmulgee	vanilla CNN	0.97 ± 0.001	0.94 ± 0.004	0.97 ± 0.002
	ResNet-50	0.97 ± 0.002	0.95 ± 0.004	0.97 ± 0.002
	ResNet-101	0.97 ± 0.001	0.95 ± 0.003	0.97 ± 0.001
	RegNet-Y 400MF	0.98 ± 0.001	0.95 ± 0.003	0.98 ± 0.001
	VGG-13 BN	0.98 ± 0.002	0.95 ± 0.004	0.98 ± 0.002
predict Carter	vanilla CNN	0.02 ± 0.007	0.02 ± 0.007	0.04 ± 0.014
	ResNet-50	0.01 ± 0.018	0.01 ± 0.018	0.02 ± 0.035
	ResNet-101	0.08 ± 0.156	0.08 ± 0.156	0.13 ± 0.229
	RegNet-Y 400MF	0.03 ± 0.05	0.03 ± 0.05	0.05 ± 0.09
	VGG-13 BN	0 ± 0.006	0 ± 0.006	0.01 ± 0.011
predict Lincoln	vanilla CNN	0.05 ± 0.013	0.05 ± 0.013	0.09 ± 0.024
	ResNet-50	0.01 ± 0.009	0.01 ± 0.009	0.02 ± 0.017
	ResNet-101	0.03 ± 0.021	0.03 ± 0.021	0.06 ± 0.039
	RegNet-Y 400MF	0 ± 0.009	0 ± 0.009	0.01 ± 0.018
	VGG-13 BN	0 ± 0.004	0 ± 0.004	0.01 ± 0.008

), both results were very poor. We interpret this to indicate that the fourth (PH) channel has the potential to decrease the model’s generalization capabilities, which is an important consideration for overall performance across different testing scenarios.

Our analysis suggests that the RegNetY model delivers the most accurate results across different testing scenarios. For in-distribution testing, where the model was trained and tested with Okmulgee data, using RGS data augmentation with PH augmentation achieved an F1 score of 0.98, with 9493 true positives (TPs) and only 293 false negatives (FNs). In out-of-distribution testing, when the model was trained on Okmulgee data and tested on Carter data, using SMOTE data augmentation without PH augmentation resulted in an F1 score of 0.90, with 46 true positives and 10 false negatives. For testing with Lincoln data, using RGS data augmentation with PH augmentation produced an F1 score of 0.73, with 129 true positives and 97 false negatives. This demonstrates the model’s high performance and the effectiveness of different augmentation techniques under varying conditions.

It is worth noting that, for future studies, one can explore different strategies for freezing and retraining specific parts of the models. This includes freezing some intermediate layers while retraining others, providing more flexibility in leveraging pre-trained models. Such investigations could uncover additional insights into the transferability of features across different layers and their impact on a model’s performance.

5. Conclusions

This study leveraged satellite data to detect undocumented O&G wells in three counties in Oklahoma. Based on our findings, we conclude with three key points:

• To address the problem of imbalanced data, we recommend oversampling approaches such as Rotation–GaussianBlur–Solarization data augmentation (RGS), the Synthetic Minority Over-Sampling Technique (SMOTE), or ADASYN (an extension of SMOTE) over undersampling techniques. Borderline SMOTE may not substantially improve our specific problem, as its performance relies heavily on the quality and distribution of data near the decision boundary.
• Incorporating pre-trained models, which have been trained on large-scale datasets before being used for a specific task, can enhance the models’ generalization ability. We have observed that models with pre-trained parameters trained on one county’s dataset can be extended to others, achieving high F1 scores, such as 0.8. This transferability of models is beneficial, as it allows us to use models trained on one geographic region for another region.
• Adding PH as an additional input can improve performance for in-distribution testing while potentially compromising the model’s generalization ability for out-of-distribution testing. Therefore, the inclusion of PH should be carefully considered, considering its impact on the model’s overall performance and ability to generalize across different testing scenarios.