Predicting Winter Wheat Yield with Dual-Year Spectral Fusion, Bayesian Wisdom, and Cross-Environmental Validation
Abstract
1. Introduction
2. Materials and Methods
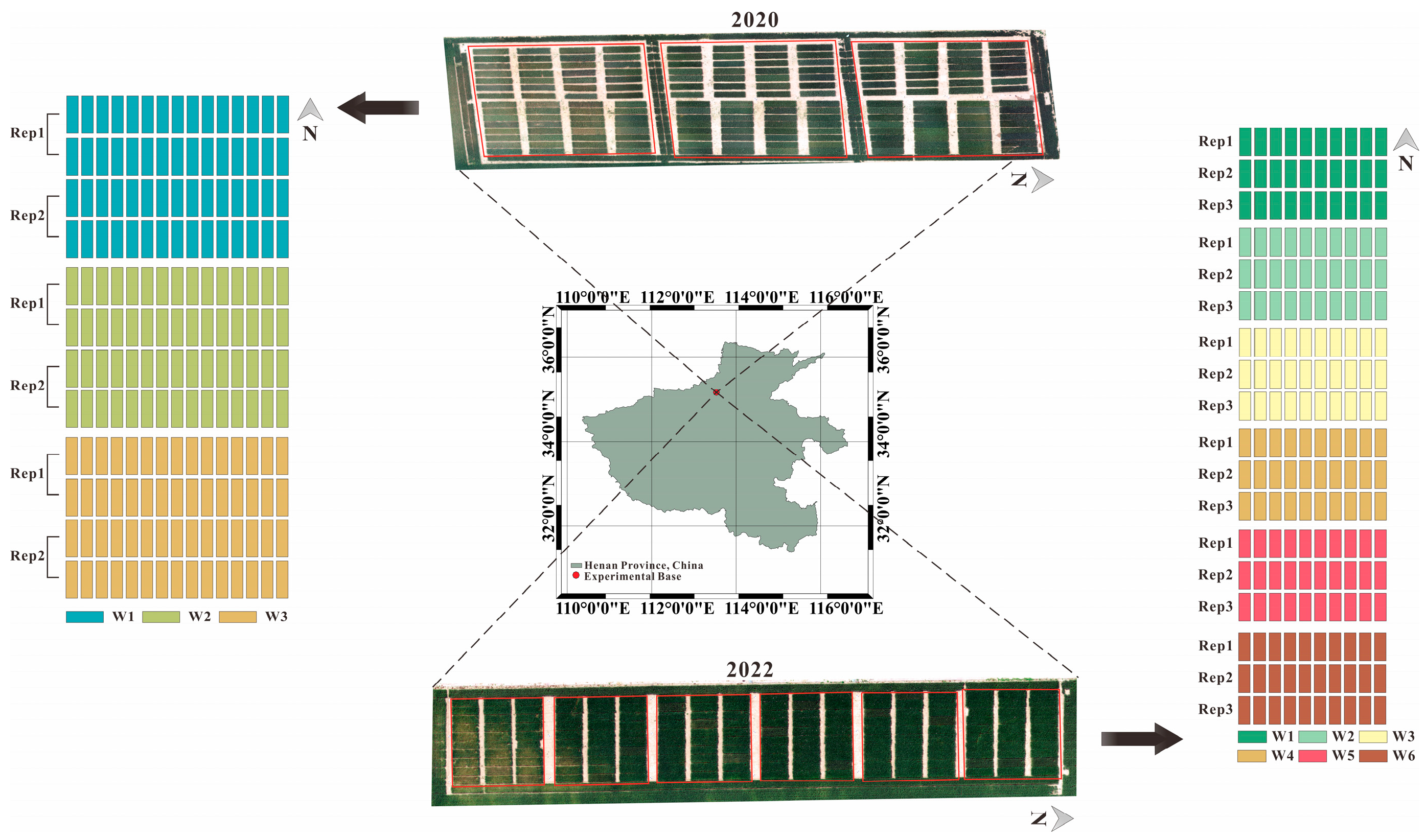
2.1. Experimental Area and Design
2.2. UAV Spectral Data Acquisition
2.3. Pre-Processing of UAV Images
2.4. Spectral Features
2.5. Model Framework
2.6. Parameters for Model Accuracy Evaluation
3. Results
3.1. Yield Distribution
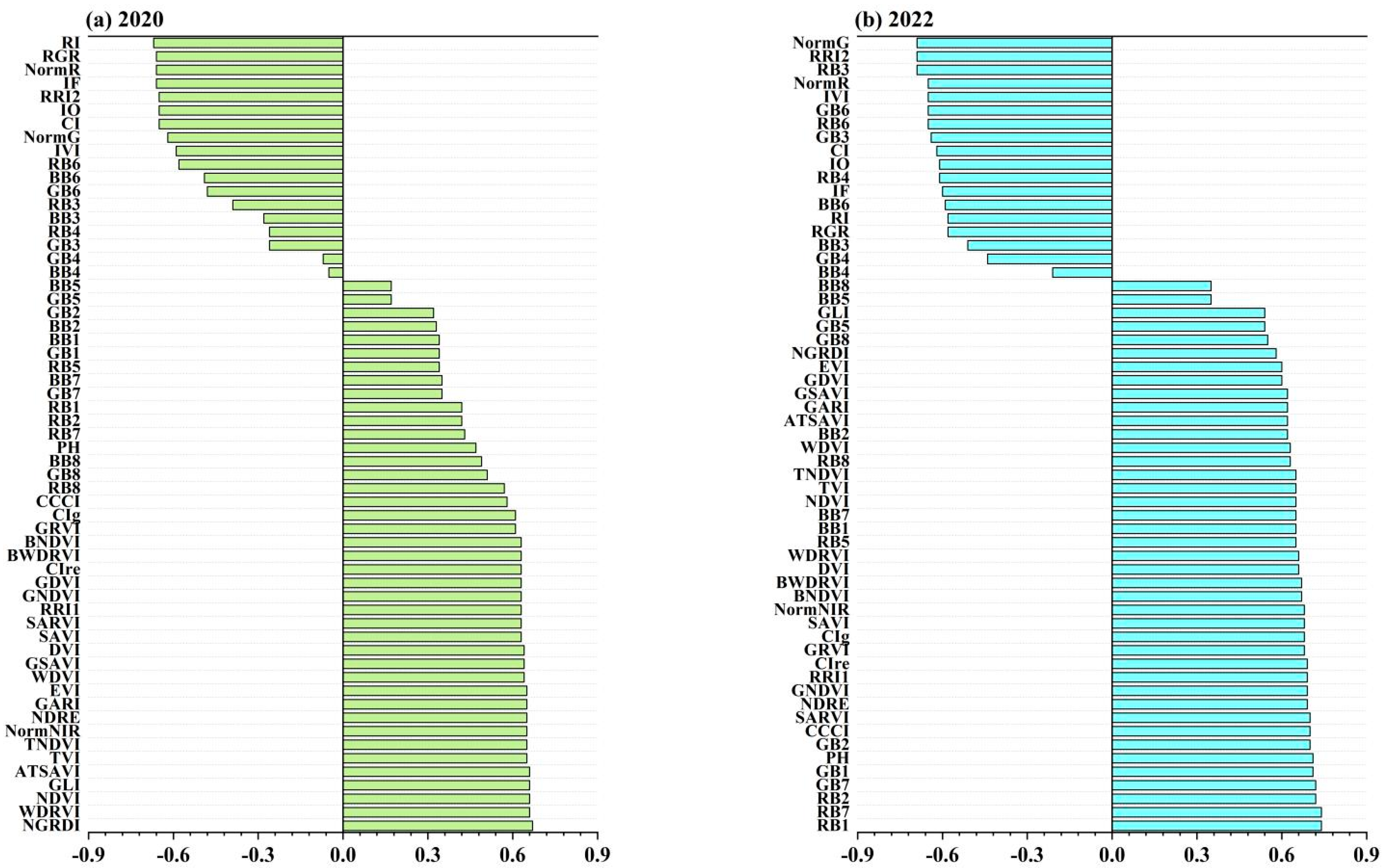
3.2. Spectral Feature Selection
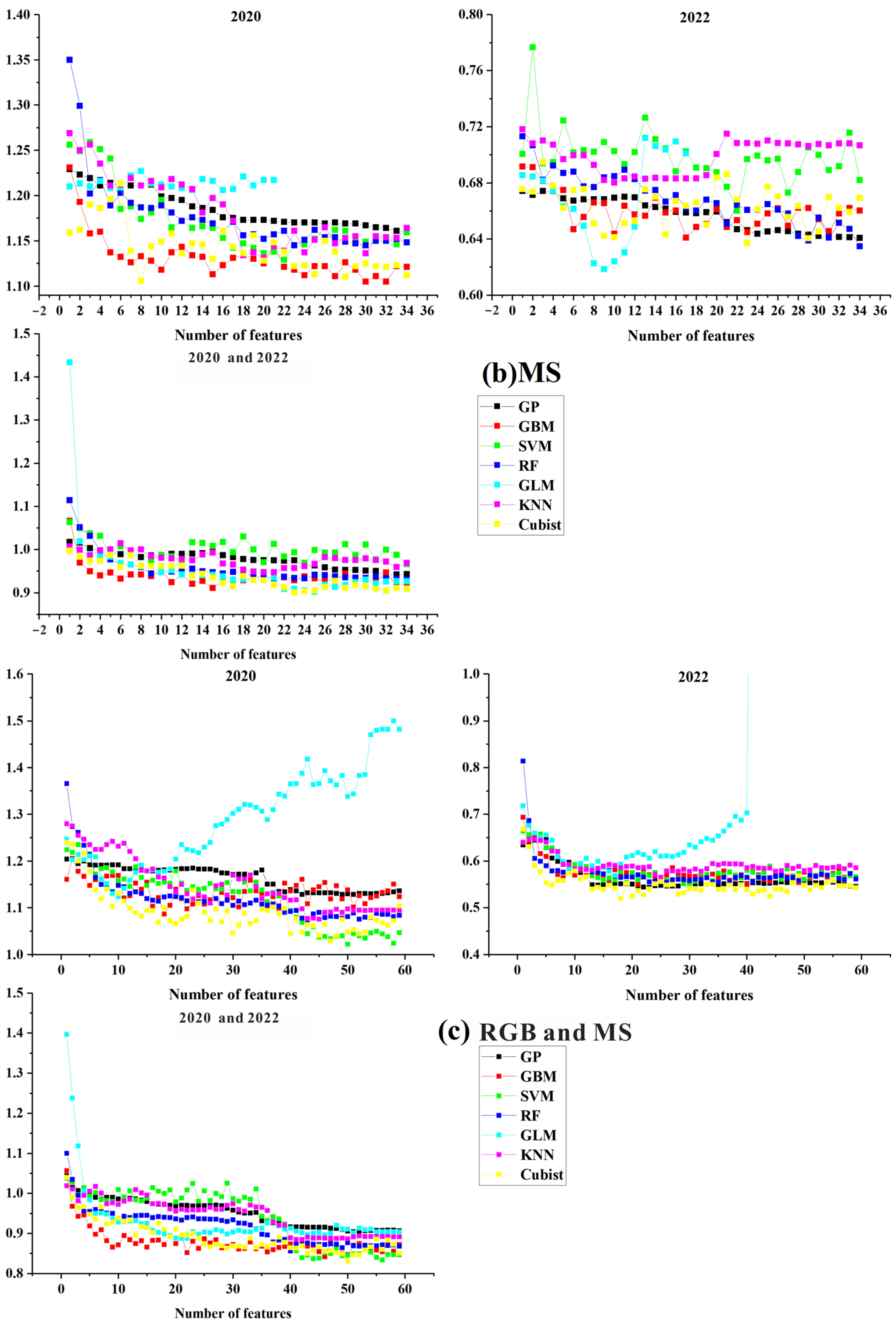
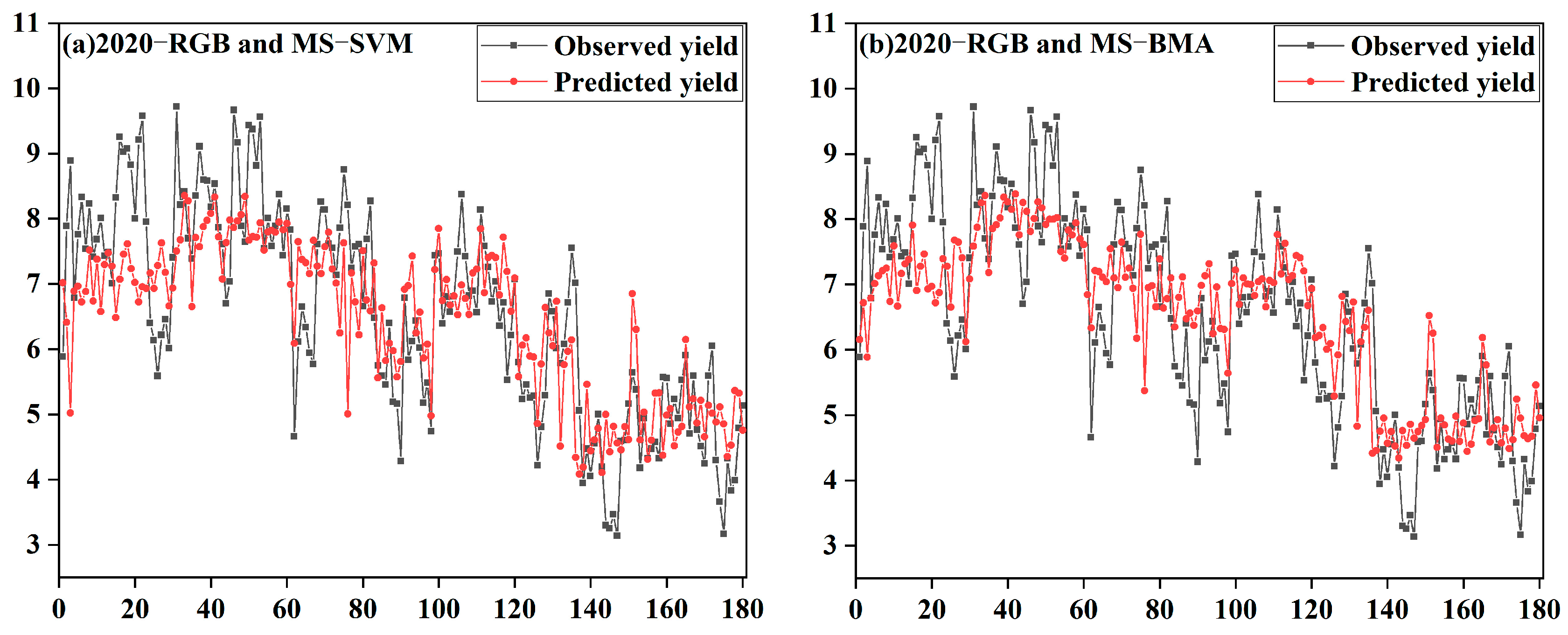
3.3. Analysis of the Model Accuracy
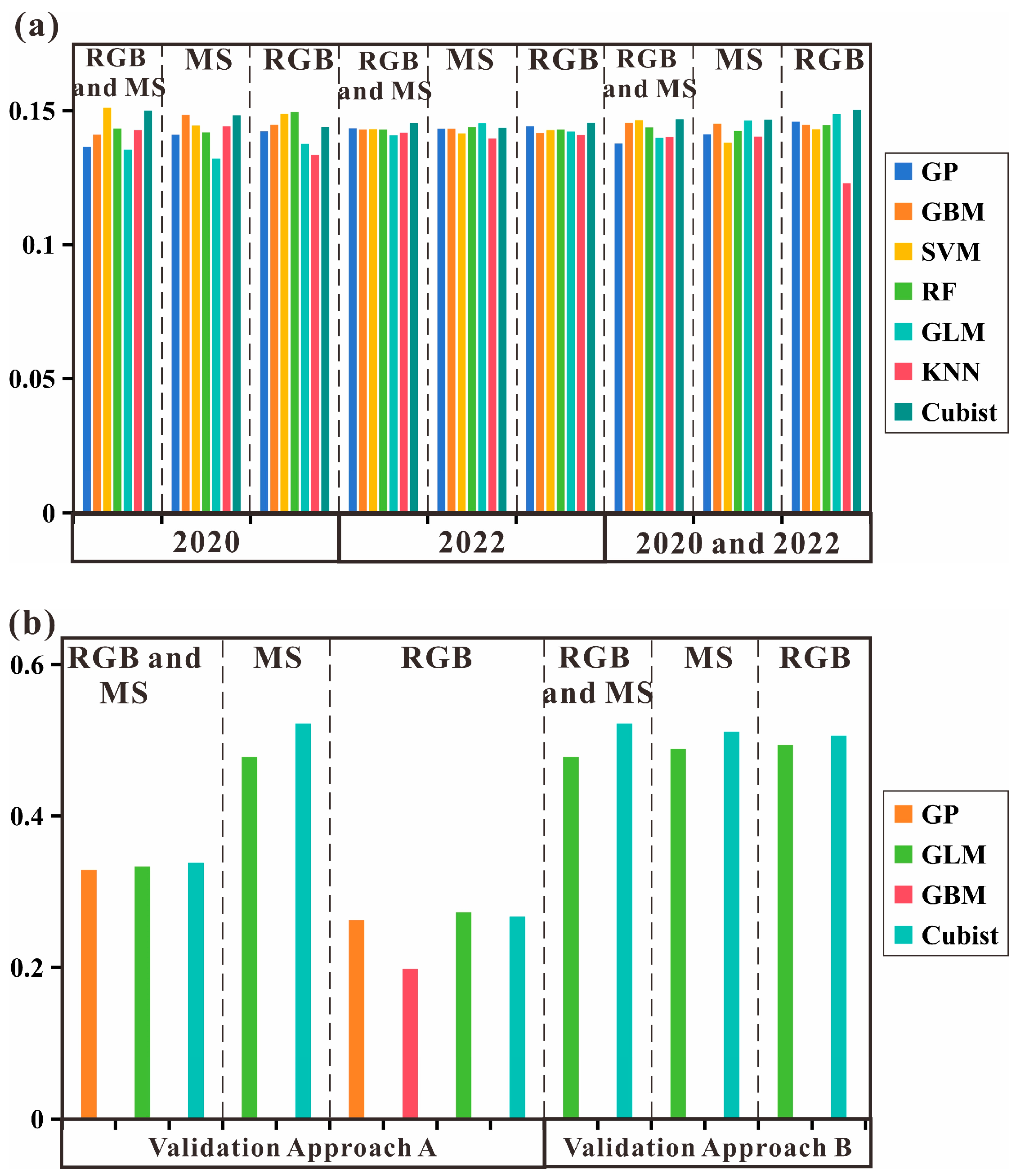
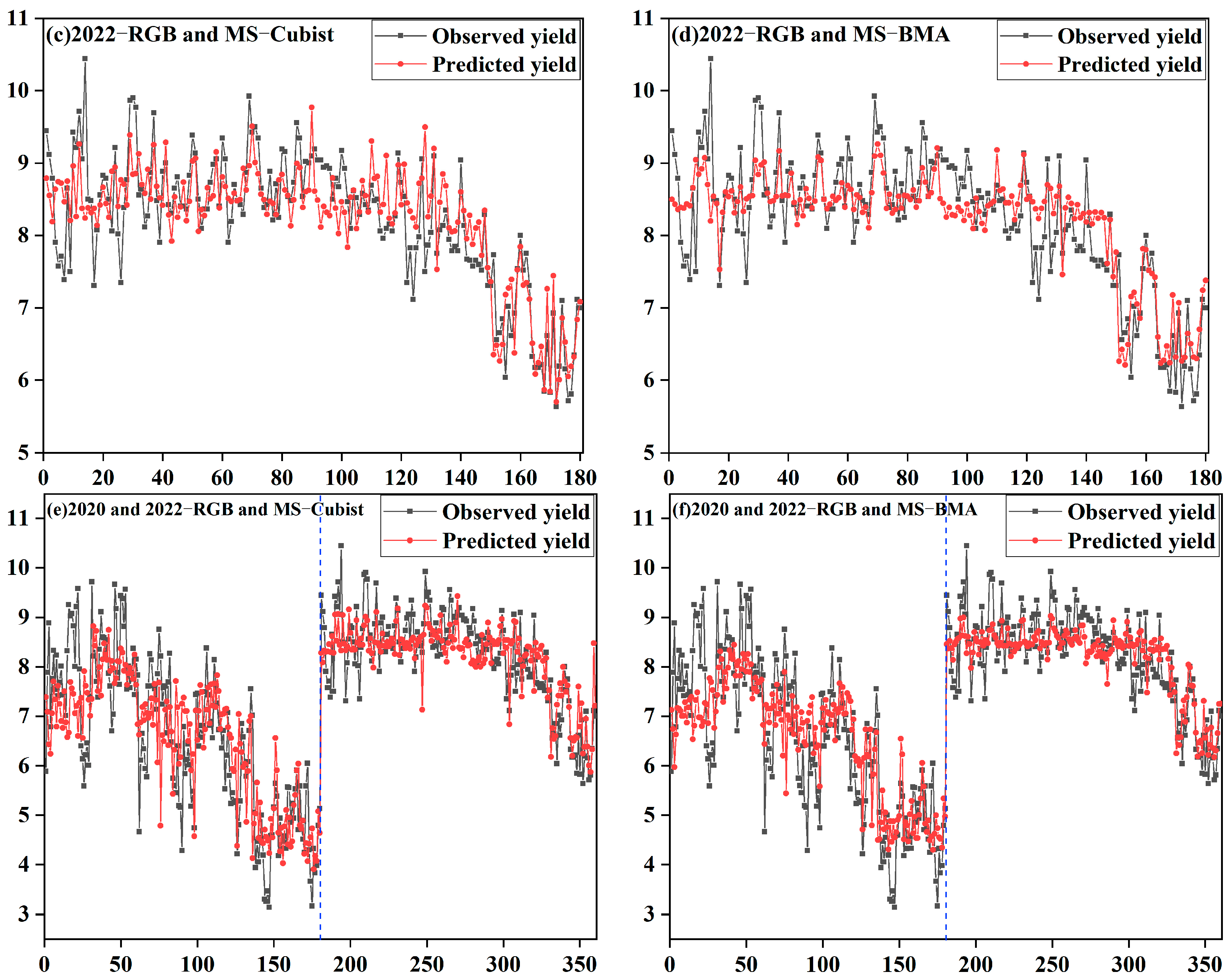
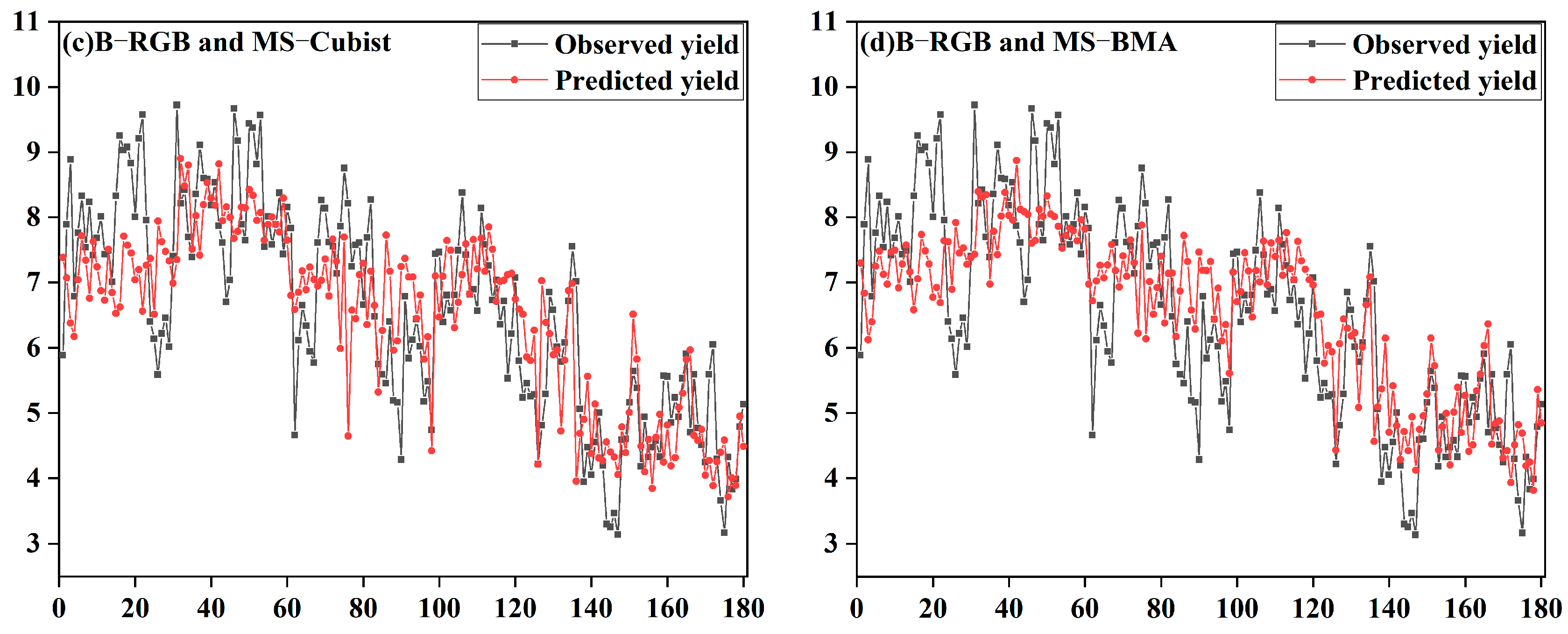
3.4. Model Generalizability Validation Analysis
4. Discussion
4.1. Multi-Sensor Features
4.2. Advantages of the RFE Approach Based on Multiple Individual Models
4.3. Advantages of Individual Machine Learning Models
4.4. Advantages of the BMA Model
4.5. Analysis of Model Generalization Capabilities
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fu, Z.; Jiang, J.; Gao, Y.; Krienke, B.; Wang, M.; Zhong, K.; Cao, Q.; Tian, Y.; Zhu, Y.; Cao, W.; et al. Wheat Growth Monitoring and Yield Estimation based on Multi-Rotor Unmanned Aerial Vehicle. Remote Sens. 2020, 12, 508. [Google Scholar] [CrossRef]
- Maes, W.H.; Steppe, K. Perspectives for Remote Sensing with Unmanned Aerial Vehicles in Precision Agriculture. Trends Plant Sci. 2019, 24, 152–164. [Google Scholar] [CrossRef] [PubMed]
- Diaz-Gonzalez, F.A.; Vuelvas, J.; Correa, C.A.; Vallejo, V.E.; Patino, D. Machine learning and remote sensing techniques applied to estimate soil indicators—Review. Ecol. Indic. 2022, 135, 108517. [Google Scholar] [CrossRef]
- Katsigiannis, P.; Galanis, G.; Dimitrakos, A.; Tsakiridis, N.; Kalopesas, C.; Alexandridis, T.; Chouzouri, A.; Patakas, A.; Zalidi, G. Fusion of Spatio-Temporal UAV and Proximal Sensing Data for an Agricultural Decision Support System. In Proceedings of the Fourth International Conference on Remote Sensing and Geoinformation of the Environment (RSCY2016), Paphos, Cyprus, 4–8 April 2016; Volume 1, p. 9688. [Google Scholar]
- Loots, M.; Grobbelaar, S.; van der Lingen, E. A review of remote-sensing unmanned aerial vehicles in the mining industry. J. S. Afr. Inst. Min. Metall. 2022, 122, 387–396. [Google Scholar] [CrossRef]
- Huang, W.; Lu, J.; Ye, H.; Kong, W.; Mortimer, A.H.; Shi, Y. Quantitative identification of crop disease and nitrogen-water stress in winter wheat using continuous wavelet analysis. Int. J. Agric. Biol. Eng. 2018, 11, 145–152. [Google Scholar] [CrossRef]
- Primicerio, J.; Di Gennaro, S.F.; Fiorillo, E.; Genesio, L.; Lugato, E.; Matese, A.; Vaccari, F.P. A flexible unmanned aerial vehicle for precision agriculture. Precis. Agric. 2012, 13, 517–523. [Google Scholar] [CrossRef]
- Nijland, W.; de Jong, R.; de Jong, S.M.; Wulder, M.A.; Bater, C.W.; Coops, N.C. Monitoring plant condition and phenology using infrared sensitive consumer grade digital cameras. Agric. For. Meteorol. 2014, 184, 98–106. [Google Scholar] [CrossRef]
- Zheng, H.; Cheng, T.; Li, D.; Zhou, X.; Yao, X.; Tian, Y.; Cao, W.; Zhu, Y. Evaluation of RGB, Color-Infrared and Multispectral Images Acquired from Unmanned Aerial Systems for the Estimation of Nitrogen Accumulation in Rice. Remote Sens. 2018, 10, 824. [Google Scholar] [CrossRef]
- Mahlein, A. Plant Disease Detection by Imaging Sensors—Parallels and Specific Demands for Precision Agriculture and Plant Phenotyping. Plant Dis. 2016, 100, 241–251. [Google Scholar] [CrossRef]
- Prashar, A.; Jones, H.G. Assessing Drought Responses Using Thermal Infrared Imaging. In Methods in Molecular Biology; Duque, P., Ed.; Springer Nature: Shanghai, China, 2016; Volume 1398, pp. 209–219. [Google Scholar]
- Prey, L.; Hanemann, A.; Ramgraber, L.; Seidl-Schulz, J.; Noack, P.O. UAV-Based Estimation of Grain Yield for Plant Breeding: Applied Strategies for Optimizing the Use of Sensors, Vegetation Indices, Growth Stages, and Machine Learning Algorithms. Remote Sens. 2022, 14, 6345. [Google Scholar] [CrossRef]
- Geipel, J.; Link, J.; Wirwahn, J.A.; Claupein, W. A Programmable Aerial Multispectral Camera System for In-Season Crop Biomass and Nitrogen Content Estimation. Agriculture 2016, 6, 4. [Google Scholar] [CrossRef]
- Honkavaara, E.; Saari, H.; Kaivosoja, J.; Polonen, I.; Hakala, T.; Litkey, P.; Makynen, J.; Pesonen, L. Processing and Assessment of Spectrometric, Stereoscopic Imagery Collected Using a Lightweight UAV Spectral Camera for Precision Agriculture. Remote Sens. 2013, 5, 5006–5039. [Google Scholar] [CrossRef]
- Lohmann, G. Analysis and synthesis of textures—A co-occurrence-based approach. Comput. Graph. 1995, 19, 29–36. [Google Scholar] [CrossRef]
- Yue, J.; Yang, G.; Tian, Q.; Feng, H.; Xu, K.; Zhou, C. Estimate of winter-wheat above-ground biomass based on UAV ultrahigh-ground-resolution image textures and vegetation indices. ISPRS J. Photogramm. Remote Sens. 2019, 150, 226–244. [Google Scholar] [CrossRef]
- Zheng, H.; Cheng, T.; Zhou, M.; Li, D.; Yao, X.; Tian, Y.; Cao, W.; Zhu, Y. Improved estimation of rice aboveground biomass combining textural and spectral analysis of UAV imagery. Precis. Agric. 2019, 20, 611–629. [Google Scholar] [CrossRef]
- Poley, L.G.; McDermid, G.J. A Systematic Review of the Factors Influencing the Estimation of Vegetation Aboveground Biomass Using Unmanned Aerial Systems. Remote Sens. 2020, 12, 1052. [Google Scholar] [CrossRef]
- Cao, J.; Leng, W.; Liu, K.; Liu, L.; He, Z.; Zhu, Y. Object-Based Mangrove Species Classification Using Unmanned Aerial Vehicle Hyperspectral Images and Digital Surface Models. Remote Sens. 2018, 10, 89. [Google Scholar] [CrossRef]
- Kotoku, J. An Introduction to Machine Learning. Igaku Butsuri Nihon Igaku Butsuri Gakkai Kikanshi Jpn. J. Med. Phys. 2016, 36, 18–22. [Google Scholar]
- Revill, A.; Florence, A.; MacArthur, A.; Hoad, S.; Rees, R.; Williams, M. Quantifying Uncertainty and Bridging the Scaling Gap in the Retrieval of Leaf Area Index by Coupling Sentinel-2 and UAV Observations. Remote Sens. 2020, 12, 1843. [Google Scholar] [CrossRef]
- Barzin, R.; Kamangir, H.; Bora, G.C. Comparison of machine learning methods for leaf nitrogen estimation in corn using multispectral uav images. Trans. ASABE 2021, 64, 2089–2101. [Google Scholar] [CrossRef]
- Proietti, T.; Luati, A. Generalized linear cepstral models for the spectrum of a time series. Stat. Sin. 2019, 29, 1561–1583. [Google Scholar]
- Li, Y. SVM-based Weed Identification Using Field Imaging Spectral Data. Remote Sens. Inf. 2014, 29, 40–43,50. [Google Scholar]
- Silva, E.B.; Giasson, E.; Dotto, A.C.; Ten Caten, A.; Melo Dematte, J.A.; Bacic, I.L.Z.; Da Veiga, M. A Regional Legacy Soil Dataset for Prediction of Sand and Clay Content with Vis-Nir-Swir, in Southern Brazil. Rev. Bras. Cienc. Solo 2019, 43, e0180174. [Google Scholar] [CrossRef]
- Cao, Q.; Xu, D.; Ju, H. Biomass estimation of five kinds of mangrove community with the KNN method based on the spectral information and textural features of TM images. For. Res. 2011, 24, 144–150. [Google Scholar]
- Yang, H.; Hu, Y.; Zheng, Z.; Qiao, Y.; Zhang, K.; Guo, T.; Chen, J. Estimation of Potato Chlorophyll Content from UAV Multispectral Images with Stacking Ensemble Algorithm. Agronomy 2022, 12, 2318. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Z.; Cheng, Q.; Duan, F.; Sui, R.; Huang, X.; Xu, H. UAV-Based Hyperspectral and Ensemble Machine Learning for Predicting Yield in Winter Wheat. Agronomy 2022, 12, 202. [Google Scholar] [CrossRef]
- Lin, X.; Chen, J.; Lou, P.; Yi, S.; Qin, Y.; You, H.; Han, X. Improving the estimation of alpine grassland fractional vegetation cover using optimized algorithms and multi-dimensional features. Plant Methods 2021, 17, 96. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Yi, Q.; Xie, L.; Yao, X.; Zheng, J.; Xu, T.; Li, J.; Chen, S. Non-destructive monitoring of amylose content in rice by UAV-based hyperspectral images. Front. Plant Sci. 2022, 13, 1035379. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.; Cheng, T.; Li, D.; Yao, X.; Tian, Y.; Cao, W.; Zhu, Y. Combining Unmanned Aerial Vehicle (UAV)-Based Multispectral Imagery and Ground-Based Hyperspectral Data for Plant Nitrogen Concentration Estimation in Rice. Front. Plant Sci. 2018, 9, 936. [Google Scholar] [CrossRef]
- Qiao, L.; Zhao, R.; Tang, W.; An, L.; Sun, H.; Li, M.; Wang, N.; Liu, Y.; Liu, G. Estimating maize LAI by exploring deep features of vegetation index map from UAV multispectral images. Field Crops Res. 2022, 289, 108739. [Google Scholar] [CrossRef]
- Liu, Z.; Merwade, V. Separation and prioritization of uncertainty sources in a raster based flood inundation model using hierarchical Bayesian model averaging. J. Hydrol. 2019, 578, 124100. [Google Scholar] [CrossRef]
- Ossandon, A.; Rajagopalan, B.; Lall, U.; Nanditha, J.S.; Mishra, V. A Bayesian Hierarchical Network Model for Daily Streamflow Ensemble Forecasting. Water Resour. Res. 2021, 57, e2021WR029920. [Google Scholar] [CrossRef]
- Mustafa, S.M.T.; Nossent, J.; Ghysels, G.; Huysmans, M. Estimation and Impact Assessment of Input and Parameter Uncertainty in Predicting Groundwater Flow with a Fully Distributed Model. Water Resour. Res. 2018, 54, 6585–6608. [Google Scholar] [CrossRef]
- Zhou, T.; Wen, X.; Feng, Q.; Yu, H.; Xi, H. Bayesian Model Averaging Ensemble Approach for Multi-Time-Ahead Groundwater Level Prediction Combining the GRACE, GLEAM, and GLDAS Data in Arid Areas. Remote Sens. 2023, 15, 188. [Google Scholar] [CrossRef]
- Huang, H.; Liang, Z.; Li, B.; Wang, D.; Hu, Y.; Li, Y. Combination of Multiple Data-Driven Models for Long-Term Monthly Runoff Predictions Based on Bayesian Model Averaging. Water Resour. Manag. 2019, 33, 3321–3338. [Google Scholar] [CrossRef]
- Li, Z.; Zhou, X.; Cheng, Q.; Fei, S.; Chen, Z. A Machine-Learning Model Based on the Fusion of Spectral and Textural Features from UAV Multi-Sensors to Analyse the Total Nitrogen Content in Winter Wheat. Remote Sens. 2023, 15, 2152. [Google Scholar] [CrossRef]
- Hancock, D.W.; Dougherty, C.T. Relationships between blue- and red-based vegetation indices and leaf area and yield of alfalfa. Crop Sci. 2007, 47, 2547–2556. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel algorithms for remote estimation of vegetation fraction. Remote Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef]
- Gamon, J.A.; Surfus, J.S. Assessing leaf pigment content and activity with a reflectometer. New Phytol. 1999, 143, 105–117. [Google Scholar] [CrossRef]
- Ehammer, A.; Fritsch, S.; Conrad, C.; Lamers, J.; Dech, S. Statistical derivation of fPAR and LAI for irrigated cotton and rice in arid Uzbekistan by combining multi-temporal RapidEye data and ground measurements. In Proceedings of the Remote Sensing for Agriculture, Ecosystems, and Hydrology XII, Toulouse, France, 20–22 September 2010; Volume 7824. [Google Scholar]
- Bastiaanssen, W.; Molden, D.J.; Makin, I.W. Remote sensing for irrigated agriculture: Examples from research and possible applications. Agric. Water Manag. 2000, 46, 137–155. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Hunt, E.R., Jr.; Daughtry, C.S.T.; Eitel, J.U.H.; Long, D.S. Remote Sensing Leaf Chlorophyll Content Using a Visible Band Index. Agron. J. 2011, 103, 1090–1099. [Google Scholar] [CrossRef]
- Wu, C.; Niu, Z.; Tang, Q.; Huang, W.; Rivard, B.; Feng, J. Remote estimation of gross primary production in wheat using chlorophyll-related vegetation indices. Agric. For. Meteorol. 2009, 149, 1015–1021. [Google Scholar] [CrossRef]
- Hewson, R.D.; Cudahy, T.J.; Huntington, J.F. Geologic and alteration mapping at Mt Fitton, South Australia, using ASTER satellite-borne data. In Proceedings of the IGARSS 2001: Scanning the Present and Resolving the Future, Proceedings, Sydney, NSW, Australia, 9–13 July 2001; Volumes 1–7, pp. 724–726. [Google Scholar]
- Tran, T.V.; Reef, R.; Zhu, X. A Review of Spectral Indices for Mangrove Remote Sensing. Remote Sens. 2022, 14, 4868. [Google Scholar] [CrossRef]
- Ahamed, T.; Tian, L.; Zhang, Y.; Ting, K.C. A review of remote sensing methods for biomass feedstock production. Biomass Bioenergy 2011, 35, 2455–2469. [Google Scholar] [CrossRef]
- LUO, Y.; XU, J.; YUE, W.; CHEN, W. A Comparative Study of Extracting Urban Vegetation Information by Vegetation Indices from Thematic Mapper Images. Remote Sens. Technol. Appl. 2006, 21, 212–219. [Google Scholar]
- Tucker, C.J.; Elgin, J.H., Jr.; McMurtrey, J.E.I.; Fan, C.J. Monitoring corn and soybean crop development with hand-held radiometer spectral data. Remote Sens. Environ. 1979, 8, 237–248. [Google Scholar] [CrossRef]
- Da Luz, A.G.; Bleninger, T.B.; Polli, B.A.; Lipski, B. Spatio-temporal variation of aquatic macrophyte cover in a reservoir using Landsat images and Google Earth Engine. RBRH-Revista Brasileira De Recursos Hidricos 2022, 27, e37. [Google Scholar] [CrossRef]
- Abdollahi, A.; Zakeri, N. Cospectrality of multipartite graphs. Ars Math. Contemp. 2022, 22, 1. [Google Scholar] [CrossRef]
- Del Portal, F.R.; Salazar, J.M. Shape index in metric spaces. Fundam. Math. 2003, 176, 47–62. [Google Scholar] [CrossRef][Green Version]
- Rajapakse, J.C.; Duan, K.B.; Yeo, W.K. Proteomic cancer classification with mass spectrometry data. Am. J. Pharmacogenom. 2005, 5, 281–292. [Google Scholar] [CrossRef] [PubMed]
- Ding, J.; Shi, J.; Wu, F. SVM-RFE based feature selection for tandem mass spectrum quality assessment. Int. J. Data Min. Bioinform. 2011, 5, 73–88. [Google Scholar] [CrossRef] [PubMed]
- Rehman, T.U.; Mahmud, M.S.; Chang, Y.K.; Jin, J.; Shin, J. Current and future applications of statistical machine learning algorithms for agricultural machine vision systems. Comput. Electron. Agric. 2019, 156, 585–605. [Google Scholar] [CrossRef]
- Payne, R.W. Developments from analysis of variance through to generalized linear models and beyond. Ann. Appl. Biol. 2014, 164, 11–17. [Google Scholar] [CrossRef]
- Fernandez-Delgado, M.; Sirsat, M.S.; Cernadas, E.; Alawadi, S.; Barro, S.; Febrero-Bande, M. An extensive experimental survey of regression methods. Neural Netw. 2019, 111, 11–34. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Wu, Z.; Xu, H.; Wang, H. Prediction and early warning method of inundation process at waterlogging points based on Bayesian model average and data-driven. J. Hydrol.-Reg. Stud. 2022, 44, 101248. [Google Scholar] [CrossRef]
- Garner, G.G.; Thompson, A.M. Ensemble statistical post-processing of the National Air Quality Forecast Capability: Enhancing ozone forecasts in Baltimore, Maryland. Atmos. Environ. 2013, 81, 517–522. [Google Scholar] [CrossRef]
- Vivone, G. Multispectral and hyperspectral image fusion in remote sensing: A survey. Inf. Fusion 2023, 89, 405–417. [Google Scholar] [CrossRef]
- Kim, J.; Chung, Y. A short review of RGB sensor applications for accessible high-throughput phenotyping. J. Crop Sci. Biotechnol. 2021, 24, 495–499. [Google Scholar] [CrossRef]
- Zhang, J. Multi-Source Remote Sensing Data Fusion: Status And Trends. Int. J. Image Data Fusion 2010, 1, 5–24. [Google Scholar] [CrossRef]
- Wu, D.; Li, R.; Zhang, F.; Liu, J. A review on drone-based harmful algae blooms monitoring. Environ. Monit. Assess. 2019, 191, 2114. [Google Scholar] [CrossRef] [PubMed]
- Yin, Y.; Jang-Jaccard, J.; Xu, W.; Singh, A.; Zhu, J.; Sabrina, F.; Kwak, J. IGRF-RFE: A hybrid feature selection method for MLP-based network intrusion detection on UNSW-NB15 dataset. J. Big Data 2023, 10, 15. [Google Scholar] [CrossRef]
- Zhou, R.; Yang, C.; Li, E.; Cai, X.; Yang, J.; Xia, Y. Object-Based Wetland Vegetation Classification Using Multi-Feature Selection of Unoccupied Aerial Vehicle RGB Imagery. Remote Sens. 2021, 13, 4910. [Google Scholar] [CrossRef]
- Jeon, H.; Oh, S. Hybrid-Recursive Feature Elimination for Efficient Feature Selection. Appl. Sci. 2020, 10, 3211. [Google Scholar] [CrossRef]
- Chen, X.; Jeong, J.C. Enhanced recursive feature elimination. In Proceedings of the ICMLA 2007: Sixth International Conference on Machine Learning and Applications, Proceedings, Cincinnati, OH, USA, 13–15 December 2007; pp. 429–435. [Google Scholar]
- Bastanlar, Y.; Ozuysal, M. Introduction to Machine Learning. In Methods in Molecular Biology; Yousef, M., Allmer, J., Eds.; Springer Nature: Shanghai, China, 2014; Volume 1107, pp. 105–128. [Google Scholar]
- Maimaitijiang, M.; Sagan, V.; Sidike, P.; Daloye, A.M.; Erkbol, H.; Fritschi, F.B. Crop Monitoring Using Satellite/UAV Data Fusion and Machine Learning. Remote Sens. 2020, 12, 1357. [Google Scholar] [CrossRef]
- Prodhan, F.A.; Zhang, J.; Hasan, S.S.; Sharma, T.P.P.; Mohana, H.P. A review of machine learning methods for drought hazard monitoring and forecasting: Current research trends, challenges, and future research directions. Environ. Model. Softw. 2022, 149, 105327. [Google Scholar] [CrossRef]
- Ishida, T.; Kurihara, J.; Angelico Viray, F.; Baes Namuco, S.; Paringit, E.C.; Jane Perez, G.; Takahashi, Y.; Joseph Marciano, J., Jr. A novel approach for vegetation classification using UAV-based hyperspectral imaging. Comput. Electron. Agric. 2018, 144, 80–85. [Google Scholar] [CrossRef]
- Qun’Ou, J.; Lidan, X.; Siyang, S.; Meilin, W.; Huijie, X. Retrieval Model For Total Nitrogen Concentration Based On Uav Hyper Spectral Remote Sensing Data And Machine Learning Algorithms—A Case Study In The Miyun Reservoir, China. Ecol. Indic. 2021, 124, 107356. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, J.; Guo, S.; Ye, Z.; Deng, H.; Hou, X.; Zhang, H. Urban Tree Classification Based on Object-Oriented Approach and Random Forest Algorithm Using Unmanned Aerial Vehicle (UAV) Multispectral Imagery. Remote Sens. 2022, 14, 3885. [Google Scholar] [CrossRef]
- Yin, J.; Medellin-Azuara, J.; Escriva-Bou, A.; Liu, Z. Bayesian machine learning ensemble approach to quantify model uncertainty in predicting groundwater storage change. Sci. Total Environ. 2021, 769, 144715. [Google Scholar] [CrossRef]
- Wang, F.; Yi, Q.; Hu, J.; Xie, L.; Yao, X.; Xu, T.; Zheng, J. Combining spectral and textural information in UAV hyperspectral images to estimate rice grain yield. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102397. [Google Scholar] [CrossRef]




| Data Type | Features | Formulas | References | Applications |
|---|---|---|---|---|
| MS | Normalized difference vegetation index | [38] | Agriculture. Vegetation | |
| Normalized difference red-edge | [38] | Vegetation | ||
| Blue NDVI | [38] | Vegetation | ||
| Green NDVI | [38] | Vegetation | ||
| Blue-wide dynamic range vegetation index | [39] | Vegetation | ||
| Canopy chlorophyll content index | [38] | Agriculture. Vegetation | ||
| Coloration index | [38] | Vegetation | ||
| Green ratio vegetation index | [40] | Vegetation | ||
| Red-green ratio | [41] | Vegetation | ||
| Red-edge ratio index 1 | [42] | Remote sensing | ||
| Red-edge ratio index 2 | [42] | Remote sensing | ||
| Soil and atmospherically resistant vegetation | [43] | Soil, Vegetation | ||
| Adjusted transformed soil-adjusted vegetation index | [44] | Soil, Vegetation | ||
| Chlorophyll index green | [45] | Vegetation | ||
| Chlorophyll index red-edge | [38] | Vegetation | ||
| Ideal vegetation index | [46] | Vegetation | ||
| Difference vegetation index | [38] | Vegetation | ||
| Iron oxide | [47] | Geology | ||
| Weighted difference Vegetation index | [42] | Vegetation | ||
| Transformed vegetation index | [48] | Vegetation | ||
| Wide dynamic range Vegetation index | [49] | Biomass, LAI | ||
| Transformed NDVI | [50] | Vegetation | ||
| Soil-adjusted vegetation index | [38] | Soil, Vegetation | ||
| Green difference vegetation index | [51] | Vegetation | ||
| Enhanced vegetation index | [48] | Vegetation | ||
| Green leaf index | [48] | Agriculture. Vegetation | ||
| Green atmospherically resistant vegetation index | [48] | Vegetation | ||
| Green soil adjusted vegetation index | [52] | Soil, Vegetation | ||
| Norm G | [53] | Vegetation | ||
| Norm NIR | [53] | Vegetation | ||
| Norm R | [53] | Vegetation | ||
| Normalized green-red difference index | [49] | Vegetation | ||
| Redness index | [48] | Agriculture | ||
| Shape index | [54] | Vegetation | ||
| RGB | Gray-level co-occurrence matrix | ME, HO, DI, EN, SE, VA, CO, COR | [38] | Vegetation |
| Plant height | / | Agriculture. Vegetation |
| Year | Sensor Type | GP | GBM | SVM | RF | GLM | KNN | Cubist |
|---|---|---|---|---|---|---|---|---|
| 2020 | RGB | 16 | 17 | 22 | 17 | 7 | 12 | 17 |
| MS | 30 | 32 | 22 | 30 | 16 | 20 | 8 | |
| RGB and MS | 42 | 18 | 50 | 43 | 10 | 45 | 47 | |
| 2022 | RGB | 25 | 6 | 12 | 13 | 13 | 23 | 22 |
| MS | 34 | 17 | 22 | 34 | 9 | 10 | 23 | |
| RGB and MS | 22 | 40 | 30 | 50 | 17 | 25 | 18 | |
| 2020 and 2022 | RGB | 25 | 14 | 18 | 16 | 15 | 9 | 23 |
| MS | 32 | 15 | 12 | 34 | 25 | 20 | 23 | |
| RGB and MS | 51 | 46 | 56 | 40 | 21 | 41 | 50 |
| 2020 | 2022 | 2020 and 2022 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RGB | MS | RGB and MS | RGB | MS | RGB and MS | RGB | MS | RGB and MS | ||
| GP | R2 | 0.505 | 0.493 | 0.509 | 0.660 | 0.532 | 0.663 | 0.626 | 0.631 | 0.657 |
| RMSE/(t·ha−1) | 1.141 | 1.150 | 1.116 | 0.541 | 0.641 | 0.544 | 0.942 | 0.941 | 0.905 | |
| MSE/(t·ha−1) | 1.302 | 1.323 | 1.247 | 0.293 | 0.411 | 0.296 | 0.887 | 0.885 | 0.819 | |
| GBM | R2 | 0.497 | 0.531 | 0.538 | 0.610 | 0.562 | 0.657 | 0.618 | 0.655 | 0.700 |
| RMSE/(t·ha−1) | 1.126 | 1.105 | 1.087 | 0.574 | 0.641 | 0.550 | 0.951 | 0.911 | 0.842 | |
| MSE/(t·ha−1) | 1.268 | 1.221 | 1.182 | 0.329 | 0.411 | 0.303 | 0.904 | 0.830 | 0.709 | |
| SVM | R2 | 0.532 | 0.512 | 0.597 | 0.643 | 0.517 | 0.658 | 0.616 | 0.612 | 0.707 |
| RMSE/(t·ha−1) | 1.101 | 1.129 | 1.022 | 0.560 | 0.660 | 0.549 | 0.963 | 0.965 | 0.834 | |
| MSE/(t·ha−1) | 1.212 | 1.275 | 1.044 | 0.314 | 0.436 | 0.301 | 0.927 | 0.931 | 0.696 | |
| RF | R2 | 0.537 | 0.505 | 0.554 | 0.641 | 0.530 | 0.661 | 0.620 | 0.642 | 0.695 |
| RMSE/(t·ha−1) | 1.097 | 1.145 | 1.072 | 0.558 | 0.635 | 0.550 | 0.952 | 0.931 | 0.857 | |
| MSE/(t·ha−1) | 1.203 | 1.311 | 1.149 | 0.311 | 0.403 | 0.303 | 0.906 | 0.867 | 0.734 | |
| GLM | R2 | 0.494 | 0.445 | 0.508 | 0.634 | 0.561 | 0.638 | 0.654 | 0.660 | 0.671 |
| RMSE/(t·ha−1) | 1.17 | 1.206 | 1.124 | 0.567 | 0.619 | 0.578 | 0.922 | 0.902 | 0.888 | |
| MSE/(t·ha−1) | 1.369 | 1.454 | 1.263 | 0.321 | 0.383 | 0.334 | 0.850 | 0.814 | 0.789 | |
| KNN | R2 | 0.446 | 0.531 | 0.566 | 0.612 | 0.495 | 0.647 | 0.492 | 0.627 | 0.673 |
| RMSE/(t·ha−1) | 1.196 | 1.131 | 1.076 | 0.582 | 0.680 | 0.565 | 1.109 | 0.947 | 0.885 | |
| MSE/(t·ha−1) | 1.430 | 1.279 | 1.158 | 0.339 | 0.462 | 0.319 | 1.230 | 0.897 | 0.783 | |
| Cubist | R2 | 0.498 | 0.516 | 0.595 | 0.683 | 0.571 | 0.703 | 0.649 | 0.663 | 0.715 |
| RMSE/(t·ha−1) | 1.132 | 1.106 | 1.029 | 0.524 | 0.637 | 0.520 | 0.910 | 0.900 | 0.831 | |
| MSE/(t·ha−1) | 1.281 | 1.223 | 1.059 | 0.275 | 0.406 | 0.270 | 0.828 | 0.810 | 0.691 | |
| BMA | R2 | 0.539 | 0.535 | 0.600 | 0.712 | 0.616 | 0.713 | 0.685 | 0.681 | 0.725 |
| RMSE/(t·ha−1) | 1.084 | 1.084 | 1.008 | 0.508 | 0.592 | 0.508 | 0.882 | 0.877 | 0.814 | |
| MSE/(t·ha−1) | 1.175 | 1.177 | 1.017 | 0.258 | 0.351 | 0.258 | 0.778 | 0.768 | 0.663 | |
| Feature | Feature Category | Metrics | GP | GBM | SVM | RF | Cubist | KNN | GLM | BMA |
|---|---|---|---|---|---|---|---|---|---|---|
| Validation Approach A | RGB and MS | R2 | 0.543 | 0.468 | 0.039 | 0.350 | 0.634 | 0.432 | 0.594 | 0.673 |
| RMSE/(t·ha−1) | 0.639 | 0.909 | 1.406 | 0.780 | 0.593 | 0.762 | 0.617 | 0.560 | ||
| MSE/(t·ha−1) | 0.408 | 0.390 | 1.978 | 0.608 | 0.352 | 0.580 | 0.381 | 0.313 | ||
| MS | R2 | 0.444 | 0.389 | 0.016 | 0.197 | 0.543 | 0.331 | 0.561 | 0.586 | |
| RMSE/(t·ha−1) | 0.700 | 0.811 | 1.763 | 0.964 | 0.678 | 0.935 | 0.642 | 0.640 | ||
| MSE/(t·ha−1) | 0.491 | 0.659 | 3.109 | 0.929 | 0.459 | 0.874 | 0.412 | 0.410 | ||
| RGB | R2 | 0.526 | 0.497 | 0.266 | 0.341 | 0.568 | 0.379 | 0.595 | 0.651 | |
| RMSE/(t·ha−1) | 0.681 | 1.013 | 1.391 | 0.950 | 0.654 | 1.462 | 0.620 | 0.594 | ||
| MSE/(t·ha−1) | 0.463 | 1.026 | 1.934 | 0.902 | 0.428 | 2.136 | 0.384 | 0.353 | ||
| Validation Approach B | RGB and MS | R2 | 0.478 | 0.306 | 0.005 | 0.235 | 0.567 | 0.342 | 0.499 | 0.569 |
| RMSE/(t·ha−1) | 1.149 | 1.404 | 1.932 | 1.470 | 1.056 | 1.389 | 1.137 | 1.044 | ||
| MSE/(t·ha−1) | 1.321 | 1.970 | 3.735 | 2.161 | 1.116 | 1.928 | 1.293 | 1.089 | ||
| MS | R2 | 0.463 | 0.162 | 0.003 | 0.003 | 0.512 | 1.156 | 0.489 | 0.525 | |
| RMSE/(t·ha−1) | 1.165 | 1.478 | 1.900 | 1.938 | 1.118 | 1.537 | 1.140 | 1.096 | ||
| MSE/(t·ha−1) | 1.358 | 2.183 | 3.609 | 3.755 | 1.250 | 2.363 | 1.300 | 1.202 | ||
| RGB | R2 | 0.451 | 0.355 | 0.154 | 0.375 | 0.498 | 0.313 | 0.488 | 0.510 | |
| RMSE/(t·ha−1) | 1.267 | 1.537 | 1.776 | 1.490 | 1.165 | 1.939 | 1.203 | 1.170 | ||
| MSE/(t·ha−1) | 1.605 | 2.361 | 3.156 | 2.220 | 1.358 | 3.760 | 1.448 | 1.368 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Cheng, Q.; Chen, L.; Zhang, B.; Guo, S.; Zhou, X.; Chen, Z. Predicting Winter Wheat Yield with Dual-Year Spectral Fusion, Bayesian Wisdom, and Cross-Environmental Validation. Remote Sens. 2024, 16, 2098. https://doi.org/10.3390/rs16122098
Li Z, Cheng Q, Chen L, Zhang B, Guo S, Zhou X, Chen Z. Predicting Winter Wheat Yield with Dual-Year Spectral Fusion, Bayesian Wisdom, and Cross-Environmental Validation. Remote Sensing. 2024; 16(12):2098. https://doi.org/10.3390/rs16122098
Chicago/Turabian StyleLi, Zongpeng, Qian Cheng, Li Chen, Bo Zhang, Shuzhe Guo, Xinguo Zhou, and Zhen Chen. 2024. "Predicting Winter Wheat Yield with Dual-Year Spectral Fusion, Bayesian Wisdom, and Cross-Environmental Validation" Remote Sensing 16, no. 12: 2098. https://doi.org/10.3390/rs16122098
APA StyleLi, Z., Cheng, Q., Chen, L., Zhang, B., Guo, S., Zhou, X., & Chen, Z. (2024). Predicting Winter Wheat Yield with Dual-Year Spectral Fusion, Bayesian Wisdom, and Cross-Environmental Validation. Remote Sensing, 16(12), 2098. https://doi.org/10.3390/rs16122098







