Spatial Downscaling of Satellite-Based Soil Moisture Products Using Machine Learning Techniques: A Review
Abstract
1. Introduction
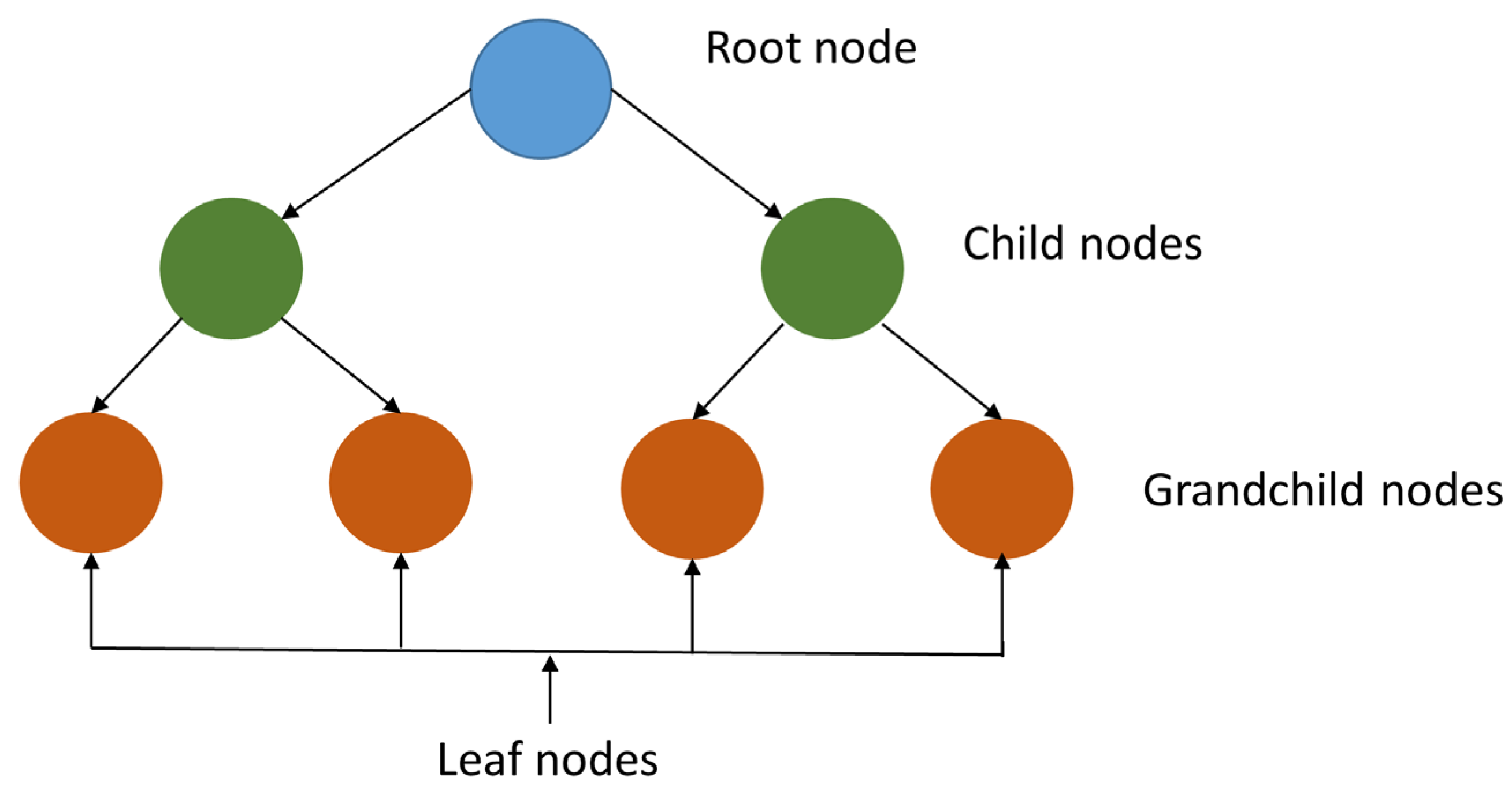
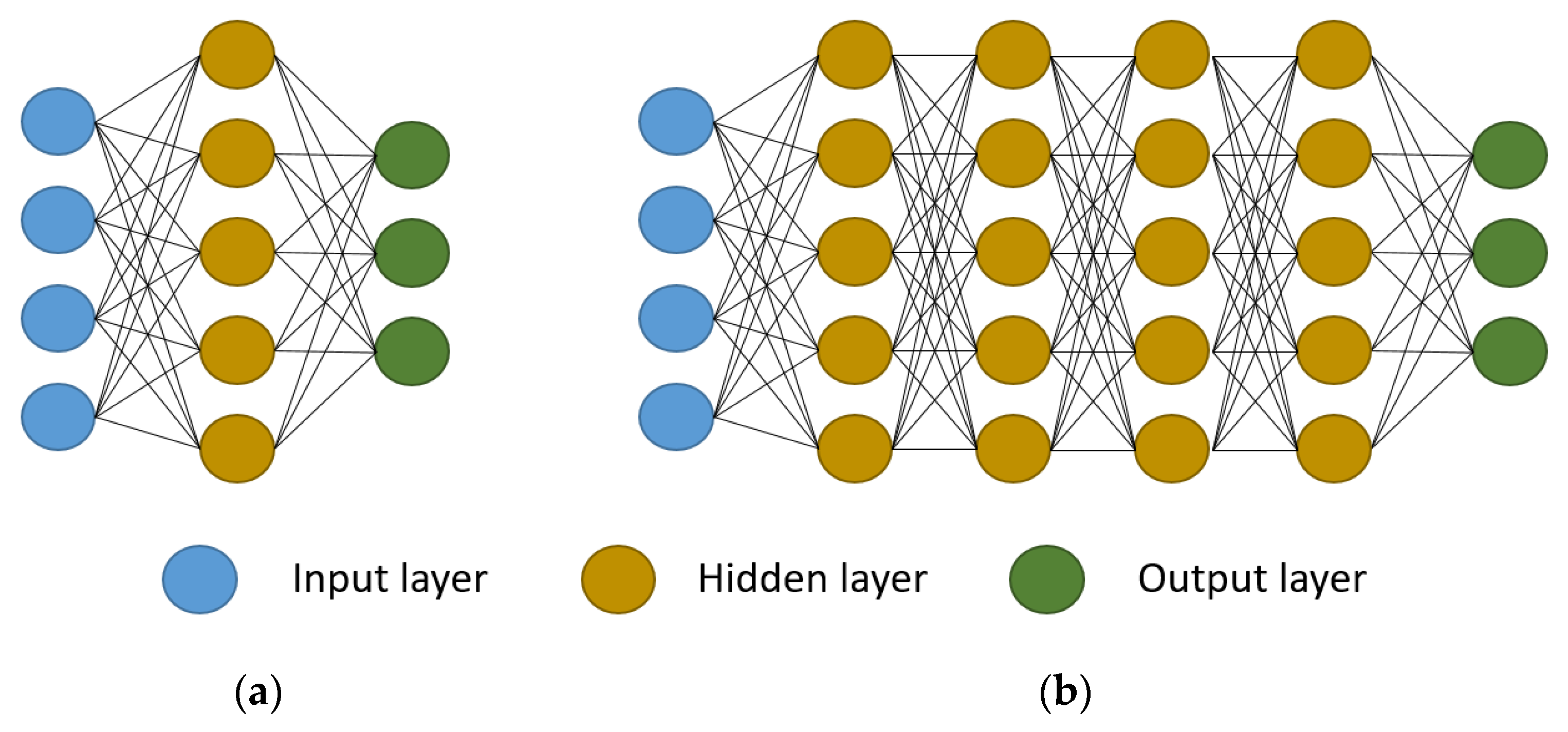
2. Review of ML Algorithms
3. ML-Based Downscaling Techniques for Microwave-Based SM Products
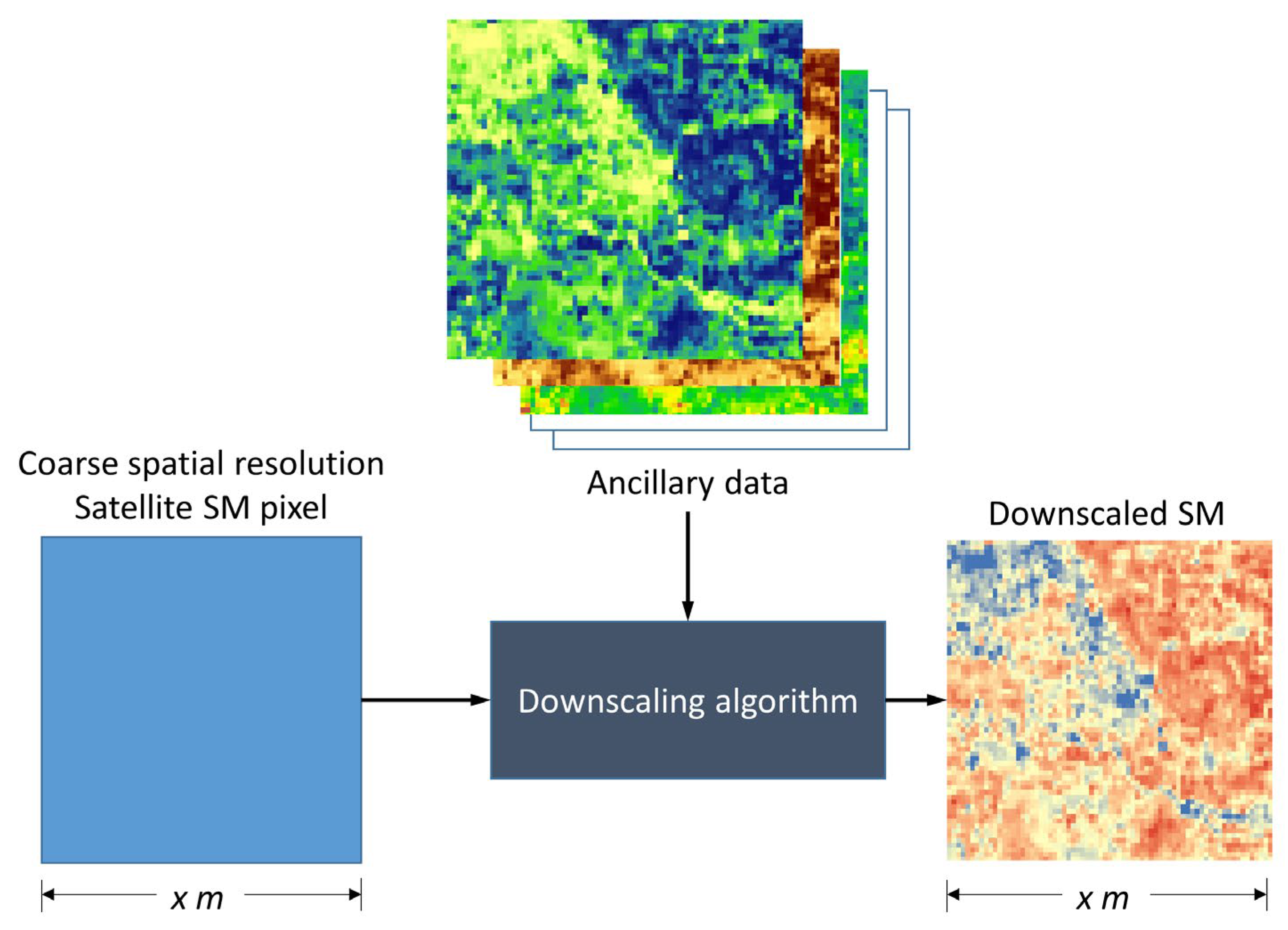
3.1. Methodological Framework of ML-Based Downscaling Approach
3.2. ML-Based Downscaling Methods
3.2.1. Classical-ML-Model-Based Downscaling Approaches
3.2.2. Ensemble-Method-Based Downscaling Approaches
3.2.3. Neural Nets and DL-Method-Based Downscaling Approaches
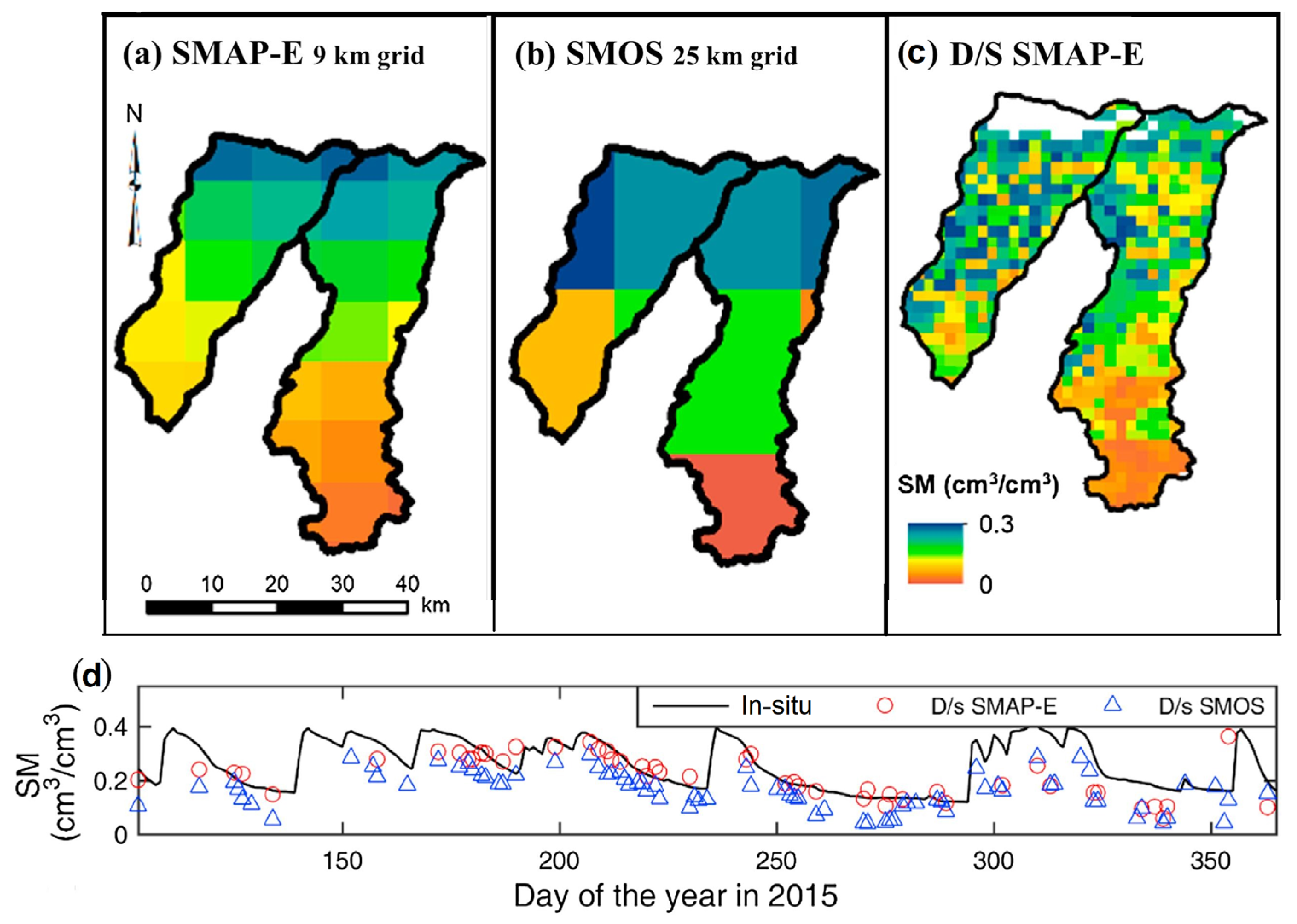
3.2.4. SM Downscaling Studies Which Used Comparative Analysis between Different ML Techniques
4. Significance of Ancillary Variables, Modifications Made to ML Techniques in Downscaling SM Products, and Validation Methods Used for Downscaled SM
4.1. ML-Based Insights: Key Geophysical and Remote-Sensing-Based Land Surface Variables in SM Downscaling
4.2. Improvements Made to ML-Based SM Downscaling
4.3. Validation Methods Used for Downscaled SM
4.4. Future Research
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AMSR2 | Advanced Microwave Scanning Radiometer 2 |
| AMSR-E | Advanced Microwave Scanning Radiometer Earth Observing System |
| ASCAT | Advanced Scatterometer |
| AWRA-L | Australian water resource assessment Landscape |
| BAYE | Bayesian |
| BPNN | Back propagation neural network |
| CART | Classification and regression tree |
| CLDAS | China meteorological administration land data assimilation system |
| CNN | Convolutional neural network |
| DBN | Deep belief network |
| DEM | Digital Elevation model |
| DisPATCH | Disaggregation based on physical and theoretical change |
| DL | Deep Learning |
| ERA | European Robotic Arm |
| ESA | European space agency |
| ESA-CCI | European Space Agency Climate Change Initiative |
| ET | Evapotranspiration |
| EVI | Enhanced vegetation index |
| FDR | Frequency domain reflectometers |
| FNN | Feedforward neural network |
| GBDT | Gradient boosting decision tree |
| GLDAS | Global land data assimilation system |
| GLM | Generalized linear model |
| GPR | Gaussian Process Regression |
| ISMN | International soil moisture network |
| KNN | K nearest neighbours |
| LAI | Leaf area index |
| LEE | Land evaporative efficiency |
| LSM | Land surface model |
| LST | Land surface temperature |
| LSTM | Long short-term memory |
| MATCH | hybrid downscaling method that integrates several approaches based on Bayesian three cornered hat merging |
| MAE | Mean absolute error |
| ML | Machine Learning |
| NAFE’05 | National airborne field experiment 2005 |
| NDVI | Normalized difference vegetation index |
| PCA | Principal Component Analysis |
| r | Correlation Coefficient |
| R2 | Coefficient of determination |
| ResNet | Residual Network |
| RF | Random Forest |
| RMSE | Root-mean-square error |
| RNN | Recurrent neural network |
| SAR | Synthetic aperture radar |
| SASMAS | Scaling and Assimilation of Soil Moisture and Streamflow |
| SM | Soil Moisture |
| SMAP | Soil moisture active passive |
| SMAP-E | SMAP Enhanced 9 km data |
| SMAPEx | Soil Moisture Active Passive Experiments |
| SMOS | Soil moisture and ocean salinity |
| SRTM | Shuttle radar topographic mission |
| SSR | Soil surface roughness |
| SVATARK | SVR and area-to-area kriging |
| SVM | Support vector machine |
| SVR | Support vector regression |
| SWI | Saga Wetness Index |
| TC | Triple Collocation |
| TDR | Time domain reflectometers |
| TWI | Topographic wetness Index |
| ubRMSE | Unbiased root-mean-square error |
| VI | Vegetation Index |
| XGB | Extreme gradient boost |
References
- Krueger, E.S.; Ochsner, T.E.; Quiring, S.M. Development and evaluation of soil moisture-based indices for agricultural drought monitoring. Agron. J. 2019, 111, 1392–1406. [Google Scholar] [CrossRef]
- Martínez-Fernández, J.; González-Zamora, A.; Sánchez, N.; Gumuzzio, A.; Herrero-Jiménez, C. Satellite soil moisture for agricultural drought monitoring: Assessment of the SMOS derived Soil Water Deficit Index. Remote Sens. Environ. 2016, 177, 277–286. [Google Scholar] [CrossRef]
- Baik, J.; Zohaib, M.; Kim, U.; Aadil, M.; Choi, M. Agricultural drought assessment based on multiple soil moisture products. J. Arid Environ. 2019, 167, 43–55. [Google Scholar] [CrossRef]
- Yeh, T.; Wetherald, R.T.; Manabe, S. The effect of soil moisture on the short-term climate and hydrology change—A numerical experiment. Mon. Weather Rev. 1984, 112, 474–490. [Google Scholar] [CrossRef]
- Schultz, R.C.; Hewlett, J.D. Soil moisture as part of the hydrologic cycle. In Proceedings of the Soil Moisture-Site Productivity Symposium Proceedings, Myrtle Beach, SC, USA, 1–3 November 1977; pp. 7–21. [Google Scholar]
- Brocca, L.; Melone, F.; Moramarco, T.; Morbidelli, R. Soil moisture temporal stability over experimental areas in Central Italy. Geoderma 2009, 148, 364–374. [Google Scholar] [CrossRef]
- Kochendorfer, J.P.; Ramírez, J.A. The impact of land–atmosphere interactions on the temporal variability of soil moisture at the regional scale. J. Hydrometeorol. 2005, 6, 53–67. [Google Scholar] [CrossRef][Green Version]
- Small, E.E.; Kurc, S.A. Tight coupling between soil moisture and the surface radiation budget in semiarid environments: Implications for land-atmosphere interactions. Water Resour. Res. 2003, 39, 1278. [Google Scholar] [CrossRef]
- Berg, A.; Lintner, B.R.; Findell, K.L.; Malyshev, S.; Loikith, P.C.; Gentine, P. Impact of soil moisture–atmosphere interactions on surface temperature distribution. J. Clim. 2014, 27, 7976–7993. [Google Scholar] [CrossRef]
- Berg, A.; Sheffield, J. Climate change and drought: The soil moisture perspective. Curr. Clim. Chang. Rep. 2018, 4, 180–191. [Google Scholar] [CrossRef]
- Huszar, T.; Mika, J.; Loczy, D.; Molnar, K.; Kertesz, A. Climate change and soil moisture: A case study. Phys. Chem. Earth Part A Solid Earth Geod. 1999, 24, 905–912. [Google Scholar] [CrossRef]
- Chiew, F.; Whetton, P.; McMahon, T.; Pittock, A. Simulation of the impacts of climate change on runoff and soil moisture in Australian catchments. J. Hydrol. 1995, 167, 121–147. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture–climate interactions in a changing climate: A review. Earth-Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Vreugdenhil, M.; Dorigo, W.A.; Wagner, W.; De Jeu, R.A.; Hahn, S.; Van Marle, M.J. Analyzing the vegetation parameterization in the TU-Wien ASCAT soil moisture retrieval. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3513–3531. [Google Scholar] [CrossRef]
- Entekhabi, D.; Rodriguez-Iturbe, I. Analytical framework for the characterization of the space-time variability of soil moisture. Adv. Water Resour. 1994, 17, 35–45. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; D’odorico, P.; Porporato, A.; Ridolfi, L. On the spatial and temporal links between vegetation, climate, and soil moisture. Water Resour. Res. 1999, 35, 3709–3722. [Google Scholar] [CrossRef]
- Engman, E.T. Applications of microwave remote sensing of soil moisture for water resources and agriculture. Remote Sens. Environ. 1991, 35, 213–226. [Google Scholar] [CrossRef]
- Jackson, T.; Schmugge, J.; Engman, E. Remote sensing applications to hydrology: Soil moisture. Hydrol. Sci. J. 1996, 41, 517–530. [Google Scholar] [CrossRef]
- Peng, J.; Loew, A.; Merlin, O.; Verhoest, N.E. A review of spatial downscaling of satellite remotely sensed soil moisture. Rev. Geophys. 2017, 55, 341–366. [Google Scholar] [CrossRef]
- Walker, J.P.; Willgoose, G.R.; Kalma, J.D. In situ measurement of soil moisture: A comparison of techniques. J. Hydrol. 2004, 293, 85–99. [Google Scholar] [CrossRef]
- Panciera, R.; Walker, J.P.; Jackson, T.J.; Gray, D.A.; Tanase, M.A.; Ryu, D.; Monerris, A.; Yardley, H.; Rüdiger, C.; Wu, X. The soil moisture active passive experiments (SMAPEx): Toward soil moisture retrieval from the SMAP mission. IEEE Trans. Geosci. Remote Sens. 2013, 52, 490–507. [Google Scholar] [CrossRef]
- Panciera, R.; Walker, J.P.; Kalma, J.D.; Kim, E.J.; Hacker, J.M.; Merlin, O.; Berger, M.; Skou, N. The NAFE’05/CoSMOS data set: Toward SMOS soil moisture retrieval, downscaling, and assimilation. IEEE Trans. Geosci. Remote Sens. 2008, 46, 736–745. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Hohensinn, R.; Hahn, S.; Paulik, C.; Xaver, A.; Gruber, A.; Drusch, M.; Mecklenburg, S.; Oevelen, P.v. The International Soil Moisture Network: A data hosting facility for global in situ soil moisture measurements. Hydrol. Earth Syst. Sci. 2011, 15, 1675–1698. [Google Scholar] [CrossRef]
- Fang, H.; Beaudoing, H.K.; Teng, W.L.; Vollmer, B.E. Global Land data assimilation system (GLDAS) products, services and application from NASA hydrology data and information services center (HDISC). In Proceedings of the ASPRS 2009 Annual Conference, Baltimore, MD, USA, 9–13 March 2009. [Google Scholar]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Pitman, A. Underlying uncertainty in the simulation of soil moisture and runoff from climate models. Australas. J. Water Resour. 2002, 5, 147–163. [Google Scholar] [CrossRef]
- Agutu, N.; Ndehedehe, C.; Awange, J.; Kirimi, F.; Mwaniki, M. Understanding uncertainty of model-reanalysis soil moisture within Greater Horn of Africa (1982–2014). J. Hydrol. 2021, 603, 127169. [Google Scholar] [CrossRef]
- Mohanty, B.P.; Cosh, M.H.; Lakshmi, V.; Montzka, C. Soil moisture remote sensing: State-of-the-science. Vadose Zone J. 2017, 16, 1–9. [Google Scholar] [CrossRef]
- Das, N.N.; Entekhabi, D.; Njoku, E.G.; Shi, J.J.; Johnson, J.T.; Colliander, A. Tests of the SMAP combined radar and radiometer algorithm using airborne field campaign observations and simulated data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2018–2028. [Google Scholar] [CrossRef]
- Entekhabi, D.; Yueh, S.; O’Neill, P.E.; Kellogg, K.H.; Allen, A.; Bindlish, R.; Brown, M.; Chan, S.; Colliander, A.; Crow, W.T. SMAP Handbook–Soil Moisture Active Passive: Mapping Soil Moisture and Freeze/Thaw From Space; National Aeronautics and Space Administration, Jet Propulsion Laboratory: Pasadena, CA, USA, 2014. [Google Scholar]
- Gruber, A.; De Lannoy, G.; Albergel, C.; Al-Yaari, A.; Brocca, L.; Calvet, J.-C.; Colliander, A.; Cosh, M.; Crow, W.; Dorigo, W. Validation practices for satellite soil moisture retrievals: What are (the) errors? Remote Sens. Environ. 2020, 244, 111806. [Google Scholar] [CrossRef]
- Xu, M.; Yao, N.; Yang, H.; Xu, J.; Hu, A.; de Goncalves, L.G.G.; Liu, G. Downscaling SMAP soil moisture using a wide & deep learning method over the Continental United States. J. Hydrol. 2022, 609, 127784. [Google Scholar]
- Chen, Q.; Miao, F.; Wang, H.; Xu, Z.X.; Tang, Z.; Yang, L.; Qi, S. Downscaling of satellite remote sensing soil moisture products over the Tibetan Plateau based on the random forest algorithm: Preliminary results. Earth Space Sci. 2020, 7, e2020EA001265. [Google Scholar] [CrossRef]
- Wei, Z.; Meng, Y.; Zhang, W.; Peng, J.; Meng, L. Downscaling SMAP soil moisture estimation with gradient boosting decision tree regression over the Tibetan Plateau. Remote Sens. Environ. 2019, 225, 30–44. [Google Scholar] [CrossRef]
- Colliander, A.; Jackson, T.J.; Chan, S.; O’Neill, P.; Bindlish, R.; Cosh, M.; Caldwell, T.; Walker, J.; Berg, A.; McNairn, H. An assessment of the differences between spatial resolution and grid size for the SMAP enhanced soil moisture product over homogeneous sites. Remote Sens. Environ. 2018, 207, 65–70. [Google Scholar] [CrossRef]
- Lakshmi, V. Remote sensing of soil moisture. ISRN Soil Sci. 2013, 2013, 424178. [Google Scholar] [CrossRef]
- Das, N.N.; Entekhabi, D.; Njoku, E.G. An algorithm for merging SMAP radiometer and radar data for high-resolution soil-moisture retrieval. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1504–1512. [Google Scholar] [CrossRef]
- Montzka, C.; Jagdhuber, T.; Horn, R.; Bogena, H.R.; Hajnsek, I.; Reigber, A.; Vereecken, H. Investigation of SMAP fusion algorithms with airborne active and passive L-band microwave remote sensing. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3878–3889. [Google Scholar] [CrossRef]
- Narayan, U.; Lakshmi, V.; Jackson, T.J. High-resolution change estimation of soil moisture using L-band radiometer and radar observations made during the SMEX02 experiments. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1545–1554. [Google Scholar] [CrossRef]
- Njoku, E.G.; Wilson, W.J.; Yueh, S.H.; Dinardo, S.J.; Li, F.K.; Jackson, T.J.; Lakshmi, V.; Bolten, J. Observations of soil moisture using a passive and active low-frequency microwave airborne sensor during SGP99. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2659–2673. [Google Scholar] [CrossRef]
- Fang, B.; Lakshmi, V. Soil moisture at watershed scale: Remote sensing techniques. J. Hydrol. 2014, 516, 258–272. [Google Scholar] [CrossRef]
- Piles, M.; Petropoulos, G.P.; Sánchez, N.; González-Zamora, Á.; Ireland, G. Towards improved spatio-temporal resolution soil moisture retrievals from the synergy of SMOS and MSG SEVIRI spaceborne observations. Remote Sens. Environ. 2016, 180, 403–417. [Google Scholar] [CrossRef]
- Merlin, O.; Rudiger, C.; Al Bitar, A.; Richaume, P.; Walker, J.P.; Kerr, Y.H. Disaggregation of SMOS soil moisture in Southeastern Australia. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1556–1571. [Google Scholar] [CrossRef]
- O’Neill, P.; Entekhabi, D.; Njoku, E.; Kellogg, K. The NASA soil moisture active passive (SMAP) mission: Overview. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 3236–3239. [Google Scholar]
- Merlin, O.; Walker, J.P.; Chehbouni, A.; Kerr, Y. Towards deterministic downscaling of SMOS soil moisture using MODIS derived soil evaporative efficiency. Remote Sens. Environ. 2008, 112, 3935–3946. [Google Scholar] [CrossRef]
- Neeck, S.P. The NASA earth science flight program: An update. In Proceedings of the Sensors, Systems, and Next-Generation Satellites XIX, Toulouse, France, 21–24 September 2015; p. 963907. [Google Scholar]
- Carlson, T. An overview of the “triangle method” for estimating surface evapotranspiration and soil moisture from satellite imagery. Sensors 2007, 7, 1612–1629. [Google Scholar] [CrossRef]
- Petropoulos, G.; Carlson, T.; Wooster, M.; Islam, S. A review of Ts/VI remote sensing based methods for the retrieval of land surface energy fluxes and soil surface moisture. Prog. Phys. Geogr. 2009, 33, 224–250. [Google Scholar] [CrossRef]
- Werbylo, K.L.; Niemann, J.D. Evaluation of sampling techniques to characterize topographically-dependent variability for soil moisture downscaling. J. Hydrol. 2014, 516, 304–316. [Google Scholar] [CrossRef]
- Busch, F.A.; Niemann, J.D.; Coleman, M. Evaluation of an empirical orthogonal function–based method to downscale soil moisture patterns based on topographical attributes. Hydrol. Process. 2012, 26, 2696–2709. [Google Scholar] [CrossRef]
- Coleman, M.L.; Niemann, J.D. Controls on topographic dependence and temporal instability in catchment-scale soil moisture patterns. Water Resour. Res. 2013, 49, 1625–1642. [Google Scholar] [CrossRef]
- Kaheil, Y.H.; Gill, M.K.; McKee, M.; Bastidas, L.A.; Rosero, E. Downscaling and assimilation of surface soil moisture using ground truth measurements. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1375–1384. [Google Scholar] [CrossRef]
- Kim, G.; Barros, A.P. Downscaling of remotely sensed soil moisture with a modified fractal interpolation method using contraction mapping and ancillary data. Remote Sens. Environ. 2002, 83, 400–413. [Google Scholar] [CrossRef]
- Bindlish, R.; Barros, A.P. Subpixel variability of remotely sensed soil moisture: An inter-comparison study of SAR and ESTAR. IEEE Trans. Geosci. Remote Sens. 2002, 40, 326–337. [Google Scholar] [CrossRef]
- Ines, A.V.; Mohanty, B.P.; Shin, Y. An unmixing algorithm for remotely sensed soil moisture. Water Resour. Res. 2013, 49, 408–425. [Google Scholar] [CrossRef]
- Shin, Y.; Mohanty, B.P. Development of a deterministic downscaling algorithm for remote sensing soil moisture footprint using soil and vegetation classifications. Water Resour. Res. 2013, 49, 6208–6228. [Google Scholar] [CrossRef]
- Sahoo, A.K.; De Lannoy, G.J.; Reichle, R.H.; Houser, P.R. Assimilation and downscaling of satellite observed soil moisture over the Little River Experimental Watershed in Georgia, USA. Adv. Water Resour. 2013, 52, 19–33. [Google Scholar] [CrossRef]
- Lievens, H.; De Lannoy, G.; Al Bitar, A.; Drusch, M.; Dumedah, G.; Franssen, H.-J.H.; Kerr, Y.; Tomer, S.K.; Martens, B.; Merlin, O. Assimilation of SMOS soil moisture and brightness temperature products into a land surface model. Remote Sens. Environ. 2016, 180, 292–304. [Google Scholar] [CrossRef]
- Nadeem, A.A.; Zha, Y.; Shi, L.; Ali, S.; Wang, X.; Zafar, Z.; Afzal, Z.; Tariq, M.A.U.R. Spatial downscaling and gap-filling of SMAP soil moisture to high resolution using MODIS surface variables and machine learning approaches over ShanDian River Basin, China. Remote Sens. 2023, 15, 812. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, S.; Liu, K.; Li, X.; Li, Z.; Zhang, X.; Liu, B. Downscaling of AMSR-E soil moisture over north China using random forest regression. ISPRS Int. J. Geo-Inf. 2022, 11, 101. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Y.; Chen, L.; Xu, S.; Sun, H. A machine learning-based approach for generating high-resolution soil moisture from SMAP products. Geocarto Int. 2022, 37, 16086–16107. [Google Scholar] [CrossRef]
- Hernández-Sánchez, J.C.; Monsivais-Huertero, A.; Judge, J.; Jiménez-Escalona, J.C. Downscaling smap soil moisture retrievals over an agricultural region in central Mexico using machine learning. In Proceedings of the IGARSS 2019–2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 7049–7052. [Google Scholar]
- Zappa, L.; Forkel, M.; Xaver, A.; Dorigo, W. Deriving field scale soil moisture from satellite observations and ground measurements in a hilly agricultural region. Remote Sens. 2019, 11, 2596. [Google Scholar] [CrossRef]
- Im, J.; Park, S.; Rhee, J.; Baik, J.; Choi, M. Downscaling of AMSR-E soil moisture with MODIS products using machine learning approaches. Environ. Earth Sci. 2016, 75, 1120. [Google Scholar] [CrossRef]
- Sun, H.; Cui, Y. Evaluating downscaling factors of microwave satellite soil moisture based on machine learning method. Remote Sens. 2021, 13, 133. [Google Scholar] [CrossRef]
- Sishah, S.; Abrahem, T.; Azene, G.; Dessalew, A.; Hundera, H. Downscaling and validating SMAP soil moisture using a machine learning algorithm over the Awash River basin, Ethiopia. PLoS ONE 2023, 18, e0279895. [Google Scholar] [CrossRef]
- Bai, J.; Cui, Q.; Zhang, W.; Meng, L. An approach for downscaling SMAP soil moisture by combining Sentinel-1 SAR and MODIS data. Remote Sens. 2019, 11, 2736. [Google Scholar] [CrossRef]
- Shi, J.; Wang, J.; Hsu, A.Y.; O’Neill, P.E.; Engman, E.T. Estimation of bare surface soil moisture and surface roughness parameter using L-band SAR image data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1254–1266. [Google Scholar]
- Hachani, A.; Ouessar, M.; Paloscia, S.; Santi, E.; Pettinato, S. Soil moisture retrieval from Sentinel-1 acquisitions in an arid environment in Tunisia: Application of Artificial Neural Networks techniques. Int. J. Remote Sens. 2019, 40, 9159–9180. [Google Scholar] [CrossRef]
- Couckuyt, A.; Seurinck, R.; Emmaneel, A.; Quintelier, K.; Novak, D.; Van Gassen, S.; Saeys, Y. Challenges in translational machine learning. Hum. Genet. 2022, 141, 1451–1466. [Google Scholar] [CrossRef] [PubMed]
- Torgo, L. Regression Trees. In Encyclopedia of Machine Learning; Sammut, C., Webb, G.I., Eds.; Springer: Boston, MA, USA, 2010; pp. 842–845. [Google Scholar]
- Steinberg, D.; Colla, P. CART: Classification and regression trees. In Top Ten Algorithms Data Min; Steinbach, M., Tan, P.-N., Eds.; Chapman and Hall/CRC: New York, NY, USA, 2009; Volume 9, p. 179. [Google Scholar]
- Awad, M.; Khanna, R. Support vector regression. In Efficient Learning Machiness: Theories, Concepts, and Applications for Engineers and System Designers; Awad, M., Khanna, R., Eds.; Apress: Berkeley, CA, USA, 2015; pp. 67–80. [Google Scholar]
- Zhang, F.; O’Donnell, L.J. Support vector regression. In Machine Learning; Elsevier: Amsterdam, The Netherlands, 2020; pp. 123–140. [Google Scholar]
- Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Their Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Steinwart, I.; Christmann, A. Support Vector Machines; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Myles, A.J.; Feudale, R.N.; Liu, Y.; Woody, N.A.; Brown, S.D. An introduction to decision tree modeling. J. Chemom. A J. Chemom. Soc. 2004, 18, 275–285. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Xia, Y.; Liu, C.; Li, Y.; Liu, N. A boosted decision tree approach using Bayesian hyper-parameter optimization for credit scoring. Expert Syst. Appl. 2017, 78, 225–241. [Google Scholar] [CrossRef]
- Liu, W.; Fan, H.; Xia, M. Credit scoring based on tree-enhanced gradient boosting decision trees. Expert Syst. Appl. 2022, 189, 116034. [Google Scholar] [CrossRef]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Zupan, J. Introduction to artificial neural network (ANN) methods: What they are and how to use them. Acta Chim. Slov. 1994, 41, 327. [Google Scholar]
- Kukreja, H.; Bharath, N.; Siddesh, C.; Kuldeep, S. An introduction to artificial neural network. Int. J. Adv. Res. Innov. Ideas. Educ. 2016, 1, 27–30. [Google Scholar]
- Peterson, L.E. K-nearest neighbor. Scholarpedia 2009, 4, 1883. [Google Scholar] [CrossRef]
- Steinbach, M.; Tan, P.-N. K-nearest neighbors. In Top Ten Algorithms Data Min; Steinbach, M., Tan, P.-N., Eds.; Chapman and Hall/CRC: New York, NY, USA, 2009; pp. 151–162. [Google Scholar]
- Kramer, O. K-nearest neighbors. In Dimensionality Reduction with Unsupervised Nearest Neighbors; Kramer, O., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 13–23. [Google Scholar]
- Wu, J. Introduction to convolutional neural networks. Natl. Key Lab Nov. Softw. Technol. Nanjing Univ. China 2017, 5, 495. [Google Scholar]
- Xue, Y.; Li, Y. A fast detection method via region-based fully convolutional neural networks for shield tunnel lining defects. Comput. Aided Civ. Infrastruct. Eng. 2018, 33, 638–654. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Mehrzadi, A.; Rezaee, E.; Gharaghani, S.; Fakhar, Z.; Mirhosseini, S.M. A Molecular Generative Model of COVID-19 Main Protease Inhibitors Using Long Short-Term Memory-Based Recurrent Neural Network. J. Comput. Biol. 2024, 31, 83–98. [Google Scholar] [CrossRef]
- Staudemeyer, R.C.; Morris, E.R. Understanding LSTM—A tutorial into long short-term memory recurrent neural networks. arXiv 2019, arXiv:1909.09586. [Google Scholar]
- Hinton, G.E. Deep belief networks. Scholarpedia 2009, 4, 5947. [Google Scholar] [CrossRef]
- He, X.; Xu, T.; Xia, Y.; Bateni, S.M.; Guo, Z.; Liu, S.; Mao, K.; Zhang, Y.; Feng, H.; Zhao, J. A Bayesian three-cornered hat (BTCH) method: Improving the terrestrial evapotranspiration estimation. Remote Sens. 2020, 12, 878. [Google Scholar] [CrossRef]
- Li, Z.; Yuan, Q.; Su, X. High-spatial-resolution surface soil moisture retrieval using the Deep Forest model in the cloud environment over the Tibetan Plateau. Geo-Spat. Inf. Sci. 2024, 1–20. [Google Scholar] [CrossRef]
- Mohseni, F.; Ahrari, A.; Haunert, J.-H.; Montzka, C. The synergies of SMAP enhanced and MODIS products in a random forest regression for estimating 1 km soil moisture over Africa using Google Earth Engine. Big Earth Data 2024, 8, 33–57. [Google Scholar] [CrossRef]
- Ning, J.; Yao, Y.; Tang, Q.; Li, Y.; Fisher, J.B.; Zhang, X.; Jia, K.; Xu, J.; Shang, K.; Yang, J. Soil moisture at 30 m from multiple satellite datasets fused by random forest. J. Hydrol. 2023, 625, 130010. [Google Scholar] [CrossRef]
- Yu, Y.; Renzullo, L.; Tian, S. Continental scale downscaling of AWRA-L analysed soil moisture using random forest regression. In Proceedings of the 24th International Congress on Modelling and Simulation, MODSIM2021, Sydney, NSW, Australia, 5–10 December 2021. [Google Scholar] [CrossRef]
- Abbaszadeh, P.; Moradkhani, H.; Zhan, X. Downscaling SMAP radiometer soil moisture over the CONUS using an ensemble learning method. Water Resour. Res. 2019, 55, 324–344. [Google Scholar] [CrossRef]
- Fang, Y.; Xu, L.; Chen, Y.; Zhou, W.; Wong, A.; Clausi, D.A. A Bayesian deep image prior downscaling approach for high-resolution soil moisture estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 4571–4582. [Google Scholar] [CrossRef]
- Lv, A.; Zhang, Z.; Zhu, H. A neural-network based spatial resolution downscaling method for soil moisture: Case study of qinghai province. Remote Sens. 2021, 13, 1583. [Google Scholar] [CrossRef]
- Alemohammad, S.H.; Kolassa, J.; Prigent, C.; Aires, F.; Gentine, P. Global downscaling of remotely sensed soil moisture using neural networks. Hydrol. Earth Syst. Sci. 2018, 22, 5341–5356. [Google Scholar] [CrossRef]
- Alemohammad, S.H.; Kolassa, J.; Prigent, C.; Aires, F.; Gentine, P. Statistical downscaling of remotely-sensed soil moisture. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 2511–2514. [Google Scholar]
- Shangguan, Y.; Min, X.; Shi, Z. Inter-comparison and integration of different soil moisture downscaling methods over the Qinghai-Tibet Plateau. J. Hydrol. 2023, 617, 129014. [Google Scholar] [CrossRef]
- Zhang, X.; Jiao, Z.; Zhao, C.; Qu, Y.; Liu, Q.; Zhang, H.; Tong, Y.; Wang, C.; Li, S.; Guo, J. Review of land surface albedo: Variance characteristics, climate effect and management strategy. Remote Sens. 2022, 14, 1382. [Google Scholar] [CrossRef]
- Jarecke, K.M.; Bladon, K.D.; Wondzell, S.M. The influence of local and nonlocal factors on soil water content in a steep forested catchment. Water Resour. Res. 2021, 57, e2020WR028343. [Google Scholar] [CrossRef]
- Winzeler, H.E.; Owens, P.R.; Read, Q.D.; Libohova, Z.; Ashworth, A.; Sauer, T. Topographic wetness index as a proxy for soil moisture in a hillslope catena: Flow algorithms and map generalization. Land 2022, 11, 2018. [Google Scholar] [CrossRef]
- Bretreger, D.; Yeo, I.-Y.; Melchers, R. LiDAR derived terrain wetness indices to infer soil moisture above underground pipelines. Int. J. Smart Sens. Intell. Syst. 2020, 13, 1–7. [Google Scholar] [CrossRef]
- Kim, D.; Moon, H.; Kim, H.; Im, J.; Choi, M. Intercomparison of downscaling techniques for satellite soil moisture products. Adv. Meteorol. 2018, 2018, 4832423. [Google Scholar] [CrossRef]
- Fang, B.; Lakshmi, V.; Bindlish, R.; Jackson, T.J.; Cosh, M.; Basara, J. Passive microwave soil moisture downscaling using vegetation index and skin surface temperature. Vadose Zone J. 2013, 12, 1–19. [Google Scholar] [CrossRef]
- Fang, B.; Lakshmi, V.; Bindlish, R.; Jackson, T.J. Downscaling of SMAP Soil Moisture Using Land Surface Temperature and Vegetation Data. Vadose Zone J. 2018, 17, 1–15. [Google Scholar] [CrossRef]
- Senanayake, I.; Yeo, I.-Y.; Tangdamrongsub, N.; Willgoose, G.; Hancock, G.; Wells, T.; Fang, B.; Lakshmi, V.; Walker, J. An in-situ data based model to downscale radiometric satellite soil moisture products in the Upper Hunter Region of NSW, Australia. J. Hydrol. 2019, 572, 820–838. [Google Scholar] [CrossRef]
- Senanayake, I.; Yeo, I.-Y.; Willgoose, G.; Hancock, G. Disaggregating satellite soil moisture products based on soil thermal inertia: A comparison of a downscaling model built at two spatial scales. J. Hydrol. 2021, 594, 125894. [Google Scholar] [CrossRef]
- Karimi, S.S.; Saintilan, N.; Wen, L.; Valavi, R. Application of machine learning to model wetland inundation patterns across a large semiarid floodplain. Water Resour. Res. 2019, 55, 8765–8778. [Google Scholar] [CrossRef]
- Wakigari, S.A.; Leconte, R. Enhancing Spatial Resolution of SMAP Soil Moisture Products through Spatial Downscaling over a Large Watershed: A Case Study for the Susquehanna River Basin in the Northeastern United States. Remote Sens. 2022, 14, 776. [Google Scholar] [CrossRef]
- Li, L.; Zhu, Q.; Lai, X.; Liao, K. Improved downscaling of microwave-based surface soil moisture over a typical subtropical monsoon region. J. Hydrol. 2023, 627, 130431. [Google Scholar] [CrossRef]
- Ghafari, E.; Walker, J.P.; Zhu, L.; Colliander, A.; Faridhosseini, A. Spatial downscaling of SMAP radiometer soil moisture using radar data: Application of machine learning to the SMAPEx and SMAPVEX campaigns. Sci. Remote Sens. 2024, 9, 100122. [Google Scholar] [CrossRef]
- Guevara, M.; Vargas, R. Downscaling satellite soil moisture using geomorphometry and machine learning. PLoS ONE 2019, 14, e0219639. [Google Scholar] [CrossRef]
- Warner, D.L.; Guevara, M.; Callahan, J.; Vargas, R. Downscaling satellite soil moisture for landscape applications: A case study in Delaware, USA. J. Hydrol. Reg. Stud. 2021, 38, 100946. [Google Scholar] [CrossRef]
- Xu, W.; Zhang, Z.; Long, Z.; Qin, Q. Downscaling SMAP soil moisture products with convolutional neural network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 4051–4062. [Google Scholar] [CrossRef]
- Ming, W.; Ji, X.; Zhang, M.; Li, Y.; Liu, C.; Wang, Y.; Li, J. A hybrid triple collocation-deep learning approach for improving soil moisture estimation from satellite and model-based data. Remote Sens. 2022, 14, 1744. [Google Scholar] [CrossRef]
- Llamas, R.M.; Valera, L.; Olaya, P.; Taufer, M.; Vargas, R. Downscaling Satellite Soil Moisture Using a Modular Spatial Inference Framework. Remote Sens. 2022, 14, 3137. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Y.; Jing, W.; Yue, X. Comparison of different machine learning approaches for monthly satellite-based soil moisture downscaling over Northeast China. Remote Sens. 2017, 10, 31. [Google Scholar] [CrossRef]
- Liu, Y.; Jing, W.; Wang, Q.; Xia, X. Generating high-resolution daily soil moisture by using spatial downscaling techniques: A comparison of six machine learning algorithms. Adv. Water Resour. 2020, 141, 103601. [Google Scholar] [CrossRef]
- Mohite, J.; Sawant, S.; Pandit, A.; Pappula, S. Spatial downscaling of SMAP soil moisture using the MODIS and SRTM observations. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, 43, 933–938. [Google Scholar] [CrossRef]
- Liu, Y.; Xia, X.; Yao, L.; Jing, W.; Zhou, C.; Huang, W.; Li, Y.; Yang, J. Downscaling satellite retrieved soil moisture using regression tree-based machine learning algorithms over Southwest France. Earth Space Sci. 2020, 7, e2020EA001267. [Google Scholar] [CrossRef]
- Senanayake, I.; Yeo, I.-Y.; Walker, J.; Willgoose, G. Estimating catchment scale soil moisture at a high spatial resolution: Integrating remote sensing and machine learning. Sci. Total Environ. 2021, 776, 145924. [Google Scholar] [CrossRef]
- Srivastava, P.K.; Han, D.; Ramirez, M.R.; Islam, T. Machine learning techniques for downscaling SMOS satellite soil moisture using MODIS land surface temperature for hydrological application. Water Resour. Manag. 2013, 27, 3127–3144. [Google Scholar] [CrossRef]
- Zhao, H.; Li, J.; Yuan, Q.; Lin, L.; Yue, L.; Xu, H. Downscaling of soil moisture products using deep learning: Comparison and analysis on Tibetan Plateau. J. Hydrol. 2022, 607, 127570. [Google Scholar] [CrossRef]
- Cai, Y.; Fan, P.; Lang, S.; Li, M.; Muhammad, Y.; Liu, A. Downscaling of SMAP soil moisture data by using a Deep Belief Network. Remote Sens. 2022, 14, 5681. [Google Scholar] [CrossRef]
- Imanpour, F.; Dehghani, M.; Yazdi, M. Improving SMAP soil moisture spatial resolution in different climatic conditions using remote sensing data. Environ. Monit. Assess. 2023, 195, 1476. [Google Scholar] [CrossRef]
- Sang, X.; Li, J.; Zhang, C.; Xing, J.; Liu, X.; Wang, H.; Zhang, C. Downscaling Microwave Soil Moisture Products with SM-RDNet for Semiarid Mining Areas. Water 2022, 14, 1792. [Google Scholar] [CrossRef]
- Shangguan, Y.; Min, X.; Wang, N.; Tong, C.; Shi, Z. A long-term, high-accuracy and seamless 1km soil moisture dataset over the Qinghai-Tibet Plateau during 2001–2020 based on a two-step downscaling method. GIScience Remote Sens. 2024, 61, 2290337. [Google Scholar] [CrossRef]
- Jin, Y.; Ge, Y.; Liu, Y.; Chen, Y.; Zhang, H.; Heuvelink, G.B. A machine learning-based geostatistical downscaling method for coarse-resolution soil moisture products. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 14, 1025–1037. [Google Scholar] [CrossRef]
- Karamouz, M.; Alipour, R.S.; Roohinia, M.; Fereshtehpour, M. A remote sensing driven soil moisture estimator: Uncertain downscaling with geostatistically based use of ancillary data. Water Resour. Res. 2022, 58, e2022WR031946. [Google Scholar] [CrossRef]
- Senanayake, I.P.; Yeo, I.Y.; Hancock, G.R.; Willgoose, G.R. A decadal record of soil moisture space–time variability over a south-east Australian catchment. Hydrol. Process. 2022, 36, e14770. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J.; Shen, W. A review of ensemble learning algorithms used in remote sensing applications. Applied Sciences. 2022, 12, 8654. [Google Scholar] [CrossRef]
- Karami, A.; Moradi, H.R.; Mousivand, A.; van Dijk, A.I.; Renzullo, L. Using ensemble learning to take advantage of high-resolution radar backscatter in conjunction with surface features to disaggregate SMAP soil moisture product. Int. J. Remote Sens. 2022, 43, 894–914. [Google Scholar] [CrossRef]
- Dorigo, W.; Himmelbauer, I.; Aberer, D.; Schremmer, L.; Petrakovic, I.; Zappa, L.; Preimesberger, W.; Xaver, A.; Annor, F.; Ardö, J. The International Soil Moisture Network: Serving Earth system science for over a decade. Hydrol. Earth Syst. Sci. Discuss. 2021, 25, 5749–5804. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 53. [Google Scholar] [CrossRef] [PubMed]
- Tavella, P.; Premoli, A. Estimating the instabilities of N clocks by measuring differences of their readings. Metrologia 1994, 30, 479. [Google Scholar] [CrossRef]
- Yang, K.; Wang, C.; Bao, H. Contribution of soil moisture variability to summer precipitation in the Northern Hemisphere. J. Geophys. Res. Atmos. 2016, 121, 108–112. [Google Scholar] [CrossRef]
- Cowley, G.S.; Niemann, J.D.; Green, T.R.; Seyfried, M.S.; Jones, A.S.; Grazaitis, P.J. Impacts of precipitation and potential evapotranspiration patterns on downscaling soil moisture in regions with large topographic relief. Water Resour. Res. 2017, 53, 1553–1574. [Google Scholar] [CrossRef]
- Kwon, M.; Kwon, H.-H.; Han, D. A spatial downscaling of soil moisture from rainfall, temperature, and AMSR2 using a Gaussian-mixture nonstationary hidden Markov model. J. Hydrol. 2018, 564, 1194–1207. [Google Scholar] [CrossRef]
- Gao, H.-B.; SHAO, M.-a. Effect of temperature on soil moisture parameters. Adv. Water Sci. 2011, 22, 484–494. [Google Scholar]
- Colliander, A.; Fisher, J.B.; Halverson, G.; Merlin, O.; Misra, S.; Bindlish, R.; Jackson, T.J.; Yueh, S. Spatial downscaling of SMAP soil moisture using MODIS land surface temperature and NDVI during SMAPVEX15. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2107–2111. [Google Scholar] [CrossRef]
- Davarzani, H.; Smits, K.; Tolene, R.M.; Illangasekare, T. Study of the effect of wind speed on evaporation from soil through integrated modeling of the atmospheric boundary layer and shallow subsurface. Water Resour. Res. 2014, 50, 661–680. [Google Scholar] [CrossRef] [PubMed]
- Akinyemi, O.D.; Mendes, N.; Jonsson, M.; Meissner, J.; De Linhares, S. Effects of psychrometrics conditions on the drying of a porous soil. J. Build. Phys. 2007, 31, 73–89. [Google Scholar] [CrossRef]
- MacDonald, M.K.; Pomeroy, J.W.; Essery, R.L. Water and energy fluxes over northern prairies as affected by chinook winds and winter precipitation. Agric. For. Meteorol. 2018, 248, 372–385. [Google Scholar] [CrossRef]
- Liu, M.; Bárdossy, A.; Li, J.; Jiang, Y. Physically-based modeling of topographic effects on spatial evapotranspiration and soil moisture patterns through radiation and wind. Hydrol. Earth Syst. Sci. 2012, 16, 357–373. [Google Scholar] [CrossRef]
- Young, A.; Sabburg, J. Cloud effects on evaporation at a sub-tropical site. In Proceedings of the Australian Institute of Physics (AIP) 17th National Congress 2006, Brisbane, Australia, 3–8 December 2006. Referreed Papers. [Google Scholar]
- Ranney, K.J.; Niemann, J.D.; Lehman, B.M.; Green, T.R.; Jones, A.S. A method to downscale soil moisture to fine resolutions using topographic, vegetation, and soil data. Adv. Water Resour. 2015, 76, 81–96. [Google Scholar] [CrossRef]
- Qiu, Z.; Pennock, A.; Giri, S.; Trnka, C.; Du, X.; Wang, H. Assessing soil moisture patterns using a soil topographic index in a humid region. Water Resour. Manag. 2017, 31, 2243–2255. [Google Scholar] [CrossRef]
- Rasheed, M.W.; Tang, J.; Sarwar, A.; Shah, S.; Saddique, N.; Khan, M.U.; Imran Khan, M.; Nawaz, S.; Shamshiri, R.R.; Aziz, M.; et al. Soil Moisture Measuring Techniques and Factors Affecting the Moisture Dynamics: A Comprehensive Review. Sustainability 2022, 14, 11538. [Google Scholar] [CrossRef]
- Ying, X. An Overview of Overfitting and its Solutions. J. Phys. Conf. Ser. 2019, 1168, 022022. [Google Scholar] [CrossRef]
- Aliferis, C.; Simon, G. (Eds.) Overfitting, Underfitting and General Model Overconfidence and Under-Performance Pitfalls and Best Practices in Machine Learning and AI. In Artificial Intelligence and Machine Learning in Health Care and Medical Sciences: Best Practices and Pitfalls; Springer International Publishing: Cham, Switzerland, 2024; pp. 477–524. [Google Scholar]
- Xu, T.; Liang, F. Machine learning for hydrologic sciences: An introductory overview. Wiley Interdiscip. Rev. Water 2021, 8, e1533. [Google Scholar] [CrossRef]
- Mosaffa, H.; Sadeghi, M.; Mallakpour, I.; Jahromi, M.N.; Pourghasemi, H.R. Application of machine learning algorithms in hydrology. In Computers in Earth and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2022; pp. 585–591. [Google Scholar]
- Stoffelen, A. Toward the true near-surface wind speed: Error modeling and calibration using triple collocation. J. Geophys. Res. Ocean. 1998, 103, 7755–7766. [Google Scholar] [CrossRef]
- Schneider, A.; Hommel, G.; Blettner, M. Linear regression analysis: Part 14 of a series on evaluation of scientific publications. Dtsch. Arztebl. Int. 2010, 107, 776–782. [Google Scholar] [CrossRef] [PubMed]
- Marill, K.A. Advanced Statistics: Linear Regression, Part II: Multiple Linear Regression. Acad. Emerg. Med. 2004, 11, 94–102. [Google Scholar] [CrossRef] [PubMed]
- Sperandei, S. Understanding logistic regression analysis. Biochem. Med. 2014, 24, 12–18. [Google Scholar] [CrossRef] [PubMed]
- Fang, J. Why logistic regression analyses are more reliable than multiple regression analyses. J. Bus. Econ. 2013, 4, 620–633. [Google Scholar]
- Ayer, T.; Chhatwal, J.; Alagoz, O.; Kahn, C.E., Jr.; Woods, R.W.; Burnside, E.S. Comparison of logistic regression and artificial neural network models in breast cancer risk estimation. Radiographics 2010, 30, 13–22. [Google Scholar] [CrossRef] [PubMed]
- Karamizadeh, S.; Abdullah, S.M.; Halimi, M.; Shayan, J.; Rajabi, M.j. Advantage and drawback of support vector machine functionality. In Proceedings of the 2014 International Conference on Computer, Communications, and Control Technology (I4CT), Langkawi, Malaysia, 2–4 September 2014; pp. 63–65. [Google Scholar]
- Kirchner, A.; Signorino, C.S. Using Support Vector Machines for Survey Research. Surv. Pract. 2018, 11, 1–14. [Google Scholar] [CrossRef][Green Version]
- Elngar, A.A.; Arafa, M.; Fathy, A.; Moustafa, B.; Mahmoud, O.; Shaban, M.; Fawzy, N. Image classification based on CNN: A survey. J. Cybersecur. Inf. Manag. 2021, 6, 18–50. [Google Scholar] [CrossRef]
- Kotu, V.; Deshpande, B. Chapter 4—Classification. In Data Science, 2nd ed.; Kotu, V., Deshpande, B., Eds.; Morgan Kaufmann: Burlington, MA, USA, 2019; pp. 65–163. [Google Scholar]
- Jadhav, S.D.; Channe, H. Comparative study of K-NN, naive Bayes and decision tree classification techniques. Int. J. Sci. Res. (IJSR) 2016, 5, 1842–1845. [Google Scholar]
- Gupta, B.; Rawat, A.; Jain, A.; Arora, A.; Dhami, N. Analysis of various decision tree algorithms for classification in data mining. Int. J. Comput. Appl. 2017, 163, 15–19. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Livingstone, D.J.; Manallack, D.T.; Tetko, I.V. Data modelling with neural networks: Advantages and limitations. J. Comput.—Aided Mol. Des. 1997, 11, 135–142. [Google Scholar] [CrossRef] [PubMed]
- Ali, J.; Khan, R.; Ahmad, N.; Maqsood, I. Random forests and decision trees. Int. J. Comput. Sci. Issues (IJCSI) 2012, 9, 272. [Google Scholar]
- Akkaya, B.; Çolakoğlu, N. Comparison of multi-class classification algorithms on early diagnosis of heart diseases. In Recent Advances in Data Science and Business Analytics, y-BIS Conference 2019, Istanbul, Turkey, 25–28 September 2019; pp. 162–172.
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Wu, J.; Li, Y.; Ma, Y. Comparison of XGBoost and the Neural Network model on the class-balanced datasets. In Proceedings of the 2021 IEEE 3rd International Conference on Frontiers Technology of Information and Computer (ICFTIC), Greenville, SC, USA, 12–14 November 2021; pp. 457–461. [Google Scholar]
- Tu, J.V. Advantages and disadvantages of using artificial neural networks versus logistic regression for predicting medical outcomes. J. Clin. Epidemiol. 1996, 49, 1225–1231. [Google Scholar] [CrossRef]
- Montesinos López, O.A.; Montesinos López, A.; Crossa, J. Convolutional Neural Networks. In Multivariate Statistical Machine Learning Methods for Genomic Prediction; Montesinos López, O.A., Montesinos López, A., Crossa, J., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 533–577. [Google Scholar]
- Yang, T.; Silver, D.L. The Disadvantage of CNN versus DBN Image Classification Under Adversarial Conditions. In Proceedings of the Canadian Conference on AI, Vancouver, Canada, 25–28 May 2021; pp. 1–6. [Google Scholar]
- Abdel-Nasser, S. Principle of Neural Network and Its Main Types: Review. J. Adv. Appl. Comput. Math. 2020, 7, 8–19. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) network. Phys. D. Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Al-Selwi, S.M.; Hassan, M.F.; Abdulkadir, S.J.; Muneer, A.; Sumiea, E.H.; Alqushaibi, A.; Ragab, M.G. RNN-LSTM: From applications to modeling techniques and beyond—Systematic review. J. King Saud Univ.—Comput. Inf. Sci. 2024, 36, 102068. [Google Scholar] [CrossRef]
- Xia, J.; Pan, S.; Zhu, M.; Cai, G.; Yan, M.; Su, Q.; Yan, J.; Ning, G. A Long Short-Term Memory Ensemble Approach for Improving the Outcome Prediction in Intensive Care Unit. Comput Math Methods Med 2019, 2019, 8152713. [Google Scholar] [CrossRef]
- Han, Q.; Zeng, Y.; Zhang, L.; Wang, C.; Prikaziuk, E.; Niu, Z.; Su, B. Global long term daily 1 km surface soil moisture dataset with physics informed machine learning. Sci. Data 2023, 10, 101. [Google Scholar] [CrossRef]
- Lakshmi, V.; Fang, B. SMAP-Derived 1-km Downscaled Surface Soil Moisture Product, Version 1; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2023. [Google Scholar] [CrossRef]
- Zheng, C.; Jia, L.; Zhao, T. A 21-year dataset (2000–2020) of gap-free global daily surface soil moisture at 1-km grid resolution. Sci. Data 2023, 10, 139. [Google Scholar] [CrossRef]
- Vergopolan, N.; Chaney, N.W.; Pan, M.; Sheffield, J.; Beck, H.E.; Ferguson, C.R.; Torres-Rojas, L.; Sadri, S.; Wood, E.F. SMAP-HydroBlocks, a 30-m satellite-based soil moisture dataset for the conterminous US. Sci. Data 2021, 8, 264. [Google Scholar] [CrossRef] [PubMed]
- Colliander, A.; Jackson, T.; Bindlish, R.; Chan, S.; Das, N.; Kim, S.; Cosh, M.; Dunbar, R.; Dang, L.; Pashaian, L. Validation of SMAP surface soil moisture products with core validation sites. Remote Sens. Environ. 2017, 191, 215–231. [Google Scholar] [CrossRef]
- Rüdiger, C.; Davidson, R.; Hemakumara, H.; Walker, J.; Kalma, J.; Willgoose, G.; Houser, P. Catchment monitoring for scaling and assimilation of soil moisture and streamflow. In Proceedings of the International Congress on Modelling and Simulation (MODSIM), Darwin, Australia, 9–14 July 2023; pp. 386–391. [Google Scholar]
- Smith, A.; Walker, J.; Western, A.; Young, R.; Ellett, K.; Pipunic, R.; Grayson, R.; Siriwardena, L.; Chiew, F.; Richter, H. The Murrumbidgee soil moisture monitoring network data set. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Ye, N.; Walker, J.; Wu, X.; Jackson, T.; Renzullo, L.; Merlin, O.; Rüdiger, C.; Entekhabi, D.; DeJeu, R.; Kim, E. Towards validation of SMAP: SMAPEX-4 &-5. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3469–3472. [Google Scholar]
- Merlin, O.; Walker, J.P.; Kalma, J.D.; Kim, E.J.; Hacker, J.; Panciera, R.; Young, R.; Summerell, G.; Hornbuckle, J.; Hafeez, M. The NAFE’06 data set: Towards soil moisture retrieval at intermediate resolution. Adv. Water Resour. 2008, 31, 1444–1455. [Google Scholar] [CrossRef]
- Boulet, G.; Walker, J.; Maisongrande, P.; Saleh, K.; Rüdiger, C.; Gruhier, C.; de Rosnay, P.; Panciera, R.; Merlin, O.; Kalma, J. Exploitation of the NAFE’05 campaign for cal/val activities of the SMOS mission. In Proceedings of the 3rd International Workshop on Catchment-scale Hydrologic Modeling and Data Assimilation, Melbourne, Australia, 9–11 January 2008. [Google Scholar]
- Entekhabi, D.; Reichle, R.H.; Koster, R.D.; Crow, W.T. Performance metrics for soil moisture retrievals and application requirements. J. Hydrometeorol. 2010, 11, 832–840. [Google Scholar] [CrossRef]
- Liu, K.; Zhang, H.; Bo, Y.; Li, D.; Li, L.; Li, H.; Wang, S.; Li, X. Downscaling satellite-derived soil moisture in the Three North region using ensemble machine learning and multiple-source knowledge integration. Hydrol. Earth Syst. Sci. Discuss. 2024; under review. [Google Scholar]
- Fang, B.; Lakshmi, V.; Zhang, R. Validation of downscaled 1-km SMOS and SMAP soil moisture data in 2010–2021. Vadose Zone J. 2024, 23, e20305. [Google Scholar] [CrossRef]
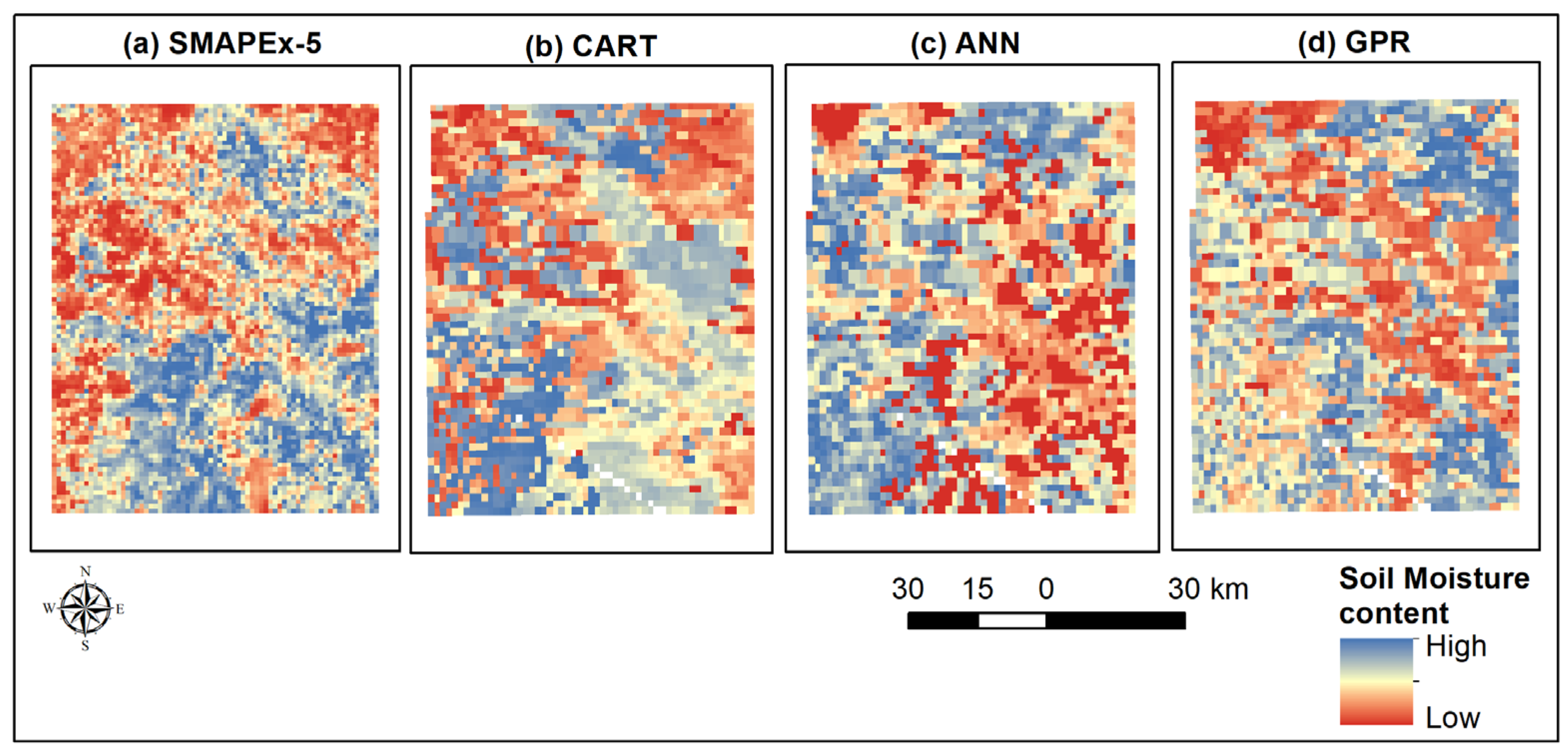
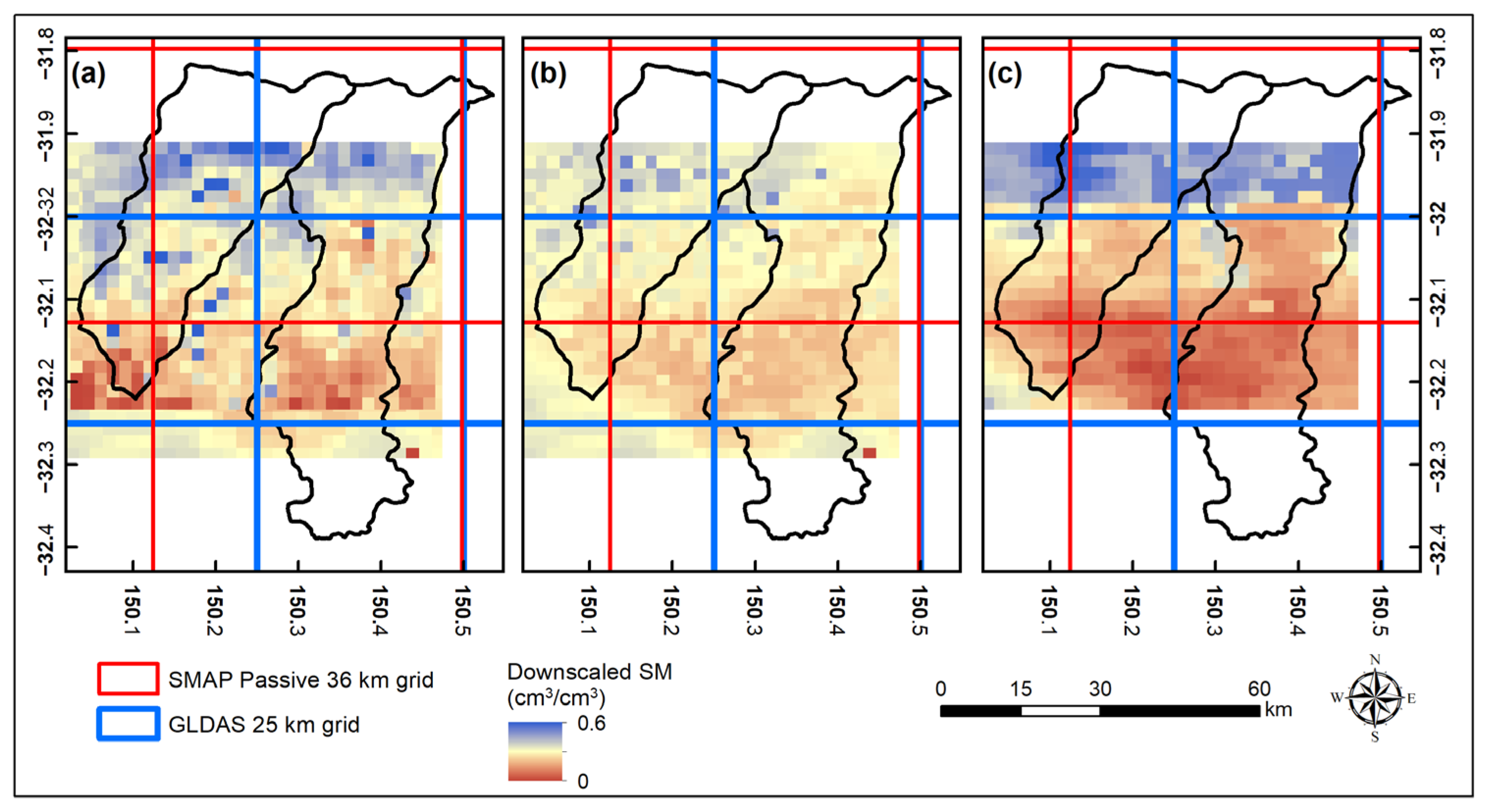
| Category | ML/DL Methods | References |
|---|---|---|
| Classical methods | SVR | [108] |
| Self-regularised Regressive models | [62] | |
| Regression/Regression Tree | [109,110,111,112] | |
| Ensemble methods | RF | [33,63,66,67,97,98,113,114,115,116] |
| GBDT | [34] | |
| Neural nets and deep learning methods | ANN | [100,101,102] |
| Kernel weighted KNN | [117,118] | |
| CNN | [119] | |
| Bayesian deep image prior algorithm combined with a fully convolutional neural network and a forward model | [99] | |
| LSTM | [120] | |
| Deep neural network with a generalized linear model (GLM) | [32] | |
| Comparisons of methods | Kernel-weighted KNN, RF | [121] |
| RF, ANN | [59] | |
| CART, KNN, Bayesian (BAYE), RF | [122] | |
| ANN, BAYE, CART, KNN, RF, SVM | [123] | |
| Multivariate linear regression, SVR, RF | [124] | |
| Multiple linear regression, RF, SVR | [60] | |
| GBDT, RF, ANN, RseNet, LSTM, CNN | [103] | |
| RF, CART, GBDT, and XGB | [125] | |
| regression tree, ANN, and Gaussian process regression (GPR) models | [126] | |
| ANN, SVM, Relevance Vector Machine, and linear regression | [127] | |
| DBN, neighbourhood constraint-based improved DBN, ResNet | [128] | |
| DBN, RF | [129] | |
| Regression, ANN | [130] | |
| CNN (SM-residual Dense Net), RF | [131] | |
| RF, boosted regression trees, Cubist | [64] | |
| RF, LSTM | [61] | |
| SVR, FNN | [65] | |
| CNN, ANN, XGB, LSTM and ResNet | [132] | |
| SVR, KNN | [133] | |
| ANN kriging | [134] |
| ML/DL Technique | Strengths | Weaknesses |
|---|---|---|
| Linear Regression [159,160] | Easy and simple implementation. Fast training capacity. Less complexity. Overfitting can be avoided by dimensionality reduction techniques. | Applicable for linear relationships. Sensitivity to outliers. Prone to multi collinearity. |
| Logistic Regression [161,162,163] | Easy and simple implementation. Easy updating. Fast training capacity. | Prone to model overfitting. Difficulty of capturing non-linear relationships. Necessity of large number of training samples. |
| SVM [164,165,166] | Works well with structured and semi-structured data. Scales well for high dimensional data. Capacity of generalization. | Long duration of training for large datasets. Complex to understand and interpret the final output. |
| Decision Tree [167,168,169] | Easy implementation. Ability to handle both numerical and categorical data. Preforms well with large datasets. | Trees are probe to non-robustness. Prone to overfitting. |
| PCA [170,171] | Remove correlated features. Reduce the possibility of over fitting. | Must perform data standardization before PCA. Prone to loss of information. |
| RF [78,172,173] | Avoid overfitting in decision trees and improve the accuracy. Can be used for both classification and regression. Data normalisation is not necessary as it uses a rule-based approach. | More complex than decision trees. Considerable time of training. |
| XGB [173,174,175] | Flexibility of the technique. Handles missing data. | Often ignores the overfitting. Increased complexity in classification. Long computational time. Sensitive to outliers. |
| ANN [163,166,171,176] | Less formal statistical training is required before developing. Detect complex and non-linear relationships between variables. Ability to detect all possible interactions between predictor variables. Multiple training algorithms can be used. | Limited opacity in identifying possible casual relationships—“black box”. Can be more difficult to use. Greater computational resources. Prone to overfitting. |
| CNN [166,177,178] | Computationally efficient. Parameter sharing. | Difficulty in classifying tilted or rotated images. Requires large number of training samples. |
| KNN [166,168,173] | Intuitive and simple. Responds quickly to real-time changes in the input data. Easy to implement for multi-class problems. Can be used for both classification and regression. | Sensitive to outliers. Not capable of dealing with missing value problems. Biased if the data are imbalanced. Necessity to choose optimal number of neighbours to be considered. Works well with smaller number of input variables. |
| RNN [179,180,181] | Processes inputs of any length. Excellent capacity in time series prediction. | Gradient vanishing and exploding issues. Complexity in training. |
| LSTM [180,181,182] | Avoids long-term dependency problem. Processes inputs of any length. Excellent capacity in time series prediction. | Complexity in training. Prone to overfitting. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Senanayake, I.P.; Pathira Arachchilage, K.R.L.; Yeo, I.-Y.; Khaki, M.; Han, S.-C.; Dahlhaus, P.G. Spatial Downscaling of Satellite-Based Soil Moisture Products Using Machine Learning Techniques: A Review. Remote Sens. 2024, 16, 2067. https://doi.org/10.3390/rs16122067
Senanayake IP, Pathira Arachchilage KRL, Yeo I-Y, Khaki M, Han S-C, Dahlhaus PG. Spatial Downscaling of Satellite-Based Soil Moisture Products Using Machine Learning Techniques: A Review. Remote Sensing. 2024; 16(12):2067. https://doi.org/10.3390/rs16122067
Chicago/Turabian StyleSenanayake, Indishe P., Kalani R. L. Pathira Arachchilage, In-Young Yeo, Mehdi Khaki, Shin-Chan Han, and Peter G. Dahlhaus. 2024. "Spatial Downscaling of Satellite-Based Soil Moisture Products Using Machine Learning Techniques: A Review" Remote Sensing 16, no. 12: 2067. https://doi.org/10.3390/rs16122067
APA StyleSenanayake, I. P., Pathira Arachchilage, K. R. L., Yeo, I.-Y., Khaki, M., Han, S.-C., & Dahlhaus, P. G. (2024). Spatial Downscaling of Satellite-Based Soil Moisture Products Using Machine Learning Techniques: A Review. Remote Sensing, 16(12), 2067. https://doi.org/10.3390/rs16122067








