Multi-Scale Object Detection in Remote Sensing Images Based on Feature Interaction and Gaussian Distribution
Abstract
1. Introduction
2. Related Work
2.1. Object Detection in Remote Sensing Images
2.2. Small Infrared Object Detection
2.3. Multi-Scale Object Detection
2.3.1. Multi-Scale Object Detection in Remote Sensing Images
2.3.2. Multi-Scale Features
2.3.3. Scale Invariance of Regression Loss
3. Materials and Methods
3.1. Overall Architecture
3.2. Multi-Scale Feature Interaction Network
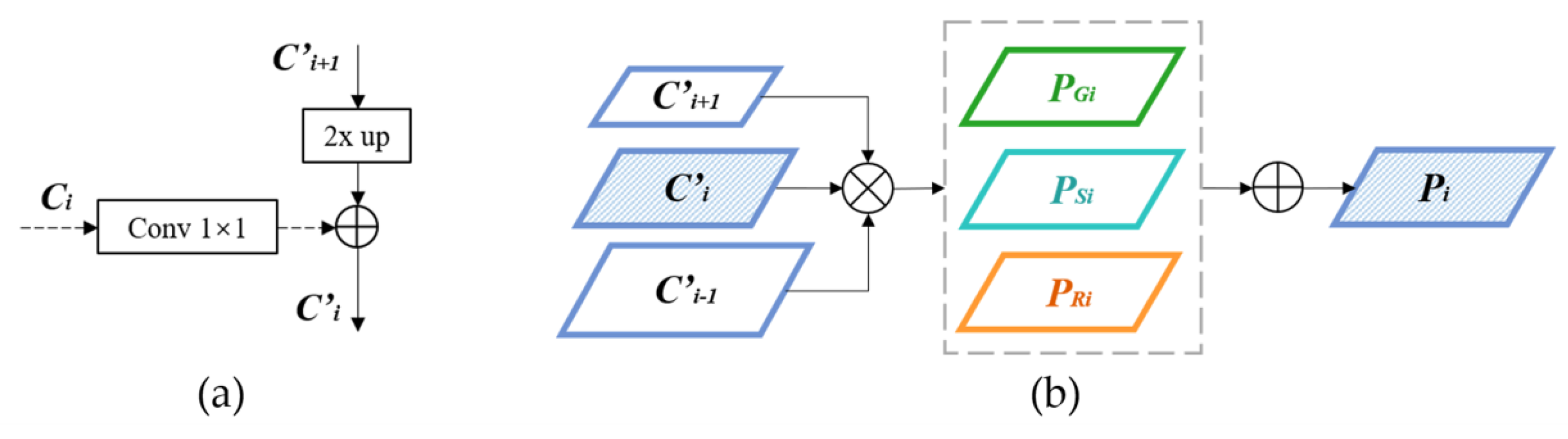
3.2.1. Cross-Level Feature Interaction Network
3.2.2. Spatial Feature Interaction Network
3.2.3. Multi-Scale Feature Interaction Network
3.3. Regression Loss Based on Gaussian Distribution
3.3.1. Oriented Bounding Box Representation based on Gaussian Distribution
3.3.2. Regression Loss of Normalized GJSD
3.3.3. Gaussian Angle Loss for the Problem of Angle Confusion
3.3.4. Regression Loss Based on Gaussian Distribution
4. Experiments and Results
4.1. Datasets
4.1.1. DOTA-v1.0
4.1.2. HRSC2016
4.2. Implementation Details
4.3. Results on the DOTA-v1.0 Dataset
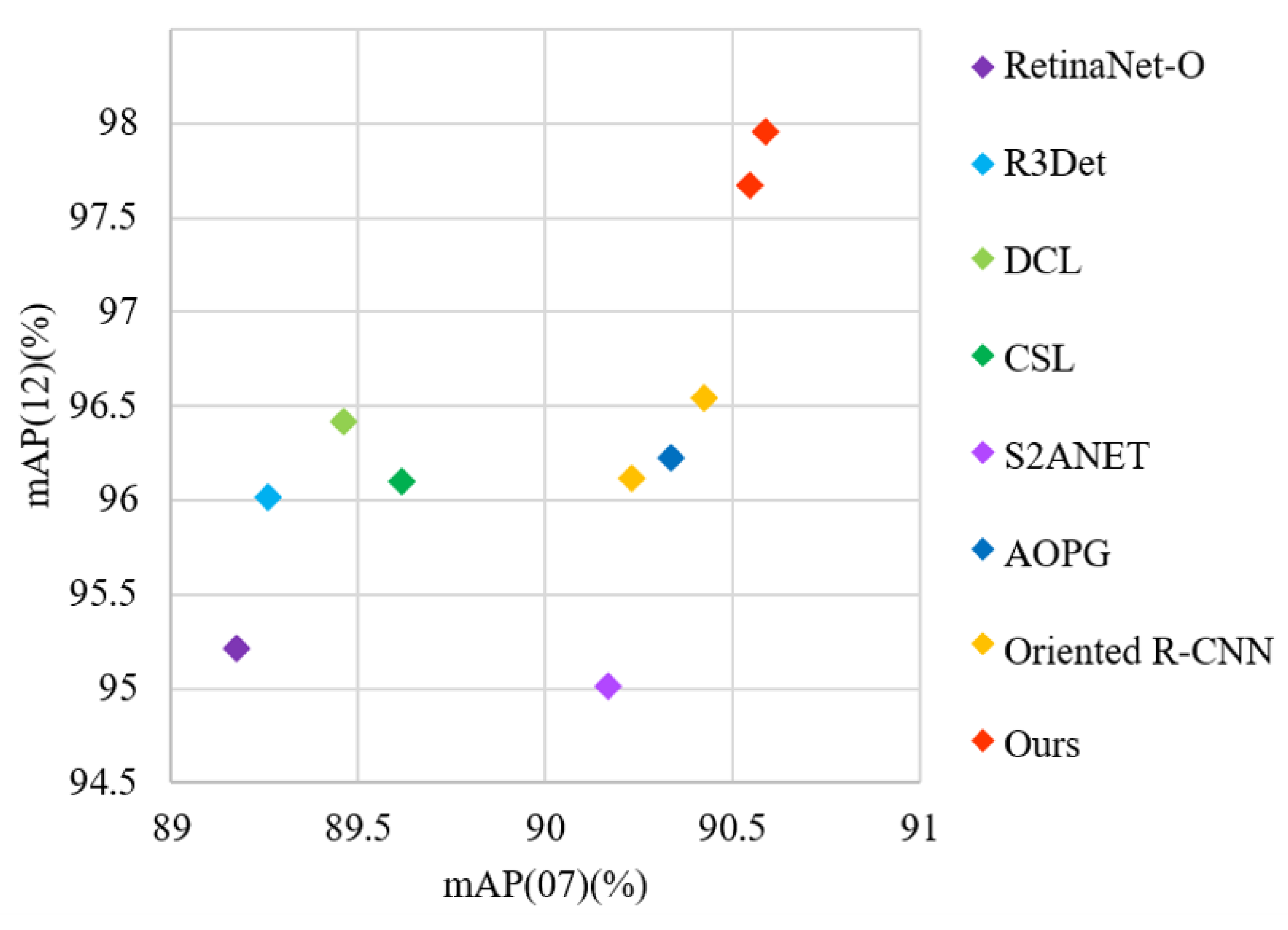
4.4. Results on the HRSC2016 Dataset
4.5. Visualization Results
5. Discussion
5.1. Ablation Study
5.2. Effect of the MSFI
5.3. Effect of the RLGD
5.4. Visualization Analysis
5.5. Limitations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Proof of Scale Invariance of GJSD
References
- Cheng, G.; Han, J. A survey on object detection in optical remote sensing images. Isprs J. Photogramm. Remote Sens. 2016, 117, 11–28. [Google Scholar] [CrossRef]
- Li, K.; Wan, G.; Cheng, G.; Meng, L.; Han, J. Object detection in optical remote sensing images: A survey and a new benchmark. ISPRS J. Photogramm. Remote Sens. 2020, 159, 296–307. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H.; Hu, C.; Luo, S.; Luo, Y.; Chen, C.W. Learning to aggregate multi-scale context for instance segmentation in remote sensing images. IEEE Trans. Neural Netw. Learn. Syst. 2024. early access. [Google Scholar] [CrossRef]
- Xia, G.S.; Bai, X.; Ding, J.; Zhu, Z.; Belongie, S.; Luo, J.; Datcu, M.; Pelillo, M.; Zhang, L. DOTA: A large-scale dataset for object detection in aerial images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3974–3983. [Google Scholar]
- Liao, Y.; Wang, H.; Lin, C.; Li, Y.; Fang, Y.; Ni, S. Research progress of deep learning-based object detection of optical remote sensing image. J. Commun. 2022, 43, 190–203. [Google Scholar]
- Yang, J.; Li, C.; Dai, X.; Gao, J. Focal modulation networks. Adv. Neural Inf. Process. Syst. 2022, 35, 4203–4217. [Google Scholar]
- Yang, X.; Yan, J.; Ming, Q.; Wang, W.; Zhang, X.; Tian, Q. Rethinking rotated object detection with gaussian wasserstein distance loss. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 11830–11841. [Google Scholar]
- Nielsen, F. On a generalization of the Jensen–Shannon divergence and the Jensen–Shannon centroid. Entropy 2020, 22, 221. [Google Scholar] [CrossRef]
- Yu, X.; Lu, J.; Lin, M.; Zhou, L.; Ou, L. MKIoU loss: Toward accurate oriented object detection in aerial images. J. Electron. Imaging 2023, 32, 033030. [Google Scholar] [CrossRef]
- Xie, X.; Cheng, G.; Wang, J.; Yao, X.; Han, J. Oriented R-CNN for object detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 3520–3529. [Google Scholar]
- Liu, Z.; Yuan, L.; Weng, L.; Yang, Y. A high resolution optical satellite image dataset for ship recognition and some new baselines. In Proceedings of the International Conference on Pattern Recognition Applications and Methods, Porto, Portugal, 24–26 February 2017; Volume 2, pp. 324–331. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. Adv. Neural Inf. Process. Syst. 2015, 28, 91–99. [Google Scholar] [CrossRef]
- Ding, J.; Xue, N.; Long, Y.; Xia, G.S.; Lu, Q. Learning RoI transformer for oriented object detection in aerial images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition 2019, Long Beach, CA, USA, 16–17 June 2019; pp. 2849–2858. [Google Scholar]
- Han, J.; Ding, J.; Xue, N.; Xia, G.S. Redet: A rotation-equivariant detector for aerial object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition 2021, Virtual, 19–25 June 2021; pp. 2786–2795. [Google Scholar]
- Xu, Y.; Fu, M.; Wang, Q.; Wang, Y.; Chen, K.; Xia, G.S.; Bai, X. Gliding vertex on the horizontal bounding box for multi-oriented object detection. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 1452–1459. [Google Scholar] [CrossRef]
- Han, J.; Ding, J.; Li, J.; Xia, G.S. Align deep features for oriented object detection. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–11. [Google Scholar] [CrossRef]
- Law, H.; Deng, J. Cornernet: Detecting objects as paired keypoints. In Proceedings of the European Conference on Computer Vision (ECCV) 2018, Munich, Germany, 8–14 September 2018; pp. 734–750. [Google Scholar]
- Wang, J.; Yang, W.; Li, H.C.; Zhang, H.; Xia, G.S. Learning center probability map for detecting objects in aerial images. IEEE Trans. Geosci. Remote Sens. 2020, 59, 4307–4323. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, D.; Krähenbühl, P. Objects as points. arXiv 2019, arXiv:1904.07850. [Google Scholar]
- Li, W.; Chen, Y.; Hu, K.; Zhu, J. Oriented reppoints for aerial object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition 2022, New Orleans, LA, USA, 18–24 June 2022; pp. 1829–1838. [Google Scholar]
- Pan, X.; Ren, Y.; Sheng, K.; Dong, W.; Yuan, H.; Guo, X.; Ma, C.; Xu, C. Dynamic refinement network for oriented and densely packed object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition 2020, Seattle, WA, USA, 13–19 June 2020; pp. 11207–11216. [Google Scholar]
- Qian, W.; Yang, X.; Peng, S.; Yan, J.; Guo, Y. Learning modulated loss for rotated object detection. In Proceedings of the AAAI Conference on Artificial Intelligence 2021, Vancouver, BC, Canada, 2–9 February 2021; Volume 35, pp. 2458–2466. [Google Scholar]
- Yang, X.; Yan, J.; Feng, Z.; He, T. R3det: Refined single-stage detector with feature refinement for rotating object. In Proceedings of the AAAI Conference on Artificial Intelligence 2021, Vancouver, BC, Canada, 2–9 February 2021; Volume 35, pp. 3163–3171. [Google Scholar]
- Cheng, G.; Wang, J.; Li, K.; Xie, X.; Lang, C.; Yao, Y.; Han, J. Anchor-free oriented proposal generator for object detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–11. [Google Scholar] [CrossRef]
- Li, Y.; Hou, Q.; Zheng, Z.; Cheng, M.M.; Yang, J.; Li, X. Large selective kernel network for remote sensing object detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision 2023, Paris, France, 4–6 October 2023; pp. 16794–16805. [Google Scholar]
- Pu, Y.; Wang, Y.; Xia, Z.; Han, Y.; Wang, Y.; Gan, W.; Wang, Z.; Song, S.; Huang, G. Adaptive rotated convolution for rotated object detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision 2023, Paris, France, 4–6 October; pp. 6589–6600.
- Ma, T.; Mao, M.; Zheng, H.; Gao, P.; Wang, X.; Han, S.; Ding, E.; Zhang, B.; Doermann, D. Oriented object detection with transformer. arXiv 2021, arXiv:2106.03146. [Google Scholar]
- Dai, L.; Liu, H.; Tang, H.; Wu, Z.; Song, P. Ao2-detr: Arbitrary-oriented object detection transformer. IEEE Trans. Circuits Syst. Video Technol. 2022, 33, 2342–2356. [Google Scholar] [CrossRef]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-end object detection with transformers. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 213–229. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Bello, I.; Zoph, B.; Vaswani, A.; Shlens, J.; Le, Q.V. Attention Augmented Convolutional Networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV) 2019, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision 2021, Montreal, QC, Canada, 10–17 October 2021; pp. 10012–10022. [Google Scholar]
- Zhang, M.; Zhang, R.; Yang, Y.; Bai, H.; Zhang, J.; Guo, J. ISNet: Shape matters for infrared small target detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 877–886. [Google Scholar]
- Zhang, M.; Bai, H.; Zhang, J.; Zhang, R.; Wang, C.; Guo, J.; Gao, X. Rkformer: Runge-kutta transformer with random-connection attention for infrared small target detection. In Proceedings of the 30th ACM International Conference on Multimedia, Lisbon, Portugal, 10–14 October 2022; pp. 1730–1738. [Google Scholar]
- Zhang, M.; Yue, K.; Zhang, J.; Li, Y.; Gao, X. Exploring feature compensation and cross-level correlation for infrared small target detection. In Proceedings of the 30th ACM International Conference on Multimedia, Lisbon, Portugal, 10–14 October 2022; pp. 1857–1865. [Google Scholar]
- Zhang, M.; Li, B.; Wang, T.; Bai, H.; Yue, K.; Li, Y. Chfnet: Curvature half-level fusion network for single-frame infrared small target detection. Remote Sens. 2023, 15, 1573. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, H.; Yue, K.; Zhang, X.; Zhu, Y.; Li, Y. Thermodynamics-Inspired Multi-Feature Network for Infrared Small Target Detection. Remote Sens. 2023, 15, 4716. [Google Scholar] [CrossRef]
- Ma, T.; Yang, Z.; Song, Y.F.; Liang, J.; Wang, H. DMEF-Net: Lightweight Infrared Dim Small Target Detection Network for Limited Samples. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–15. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, H.; Guo, J.; Li, Y.; Gao, X.; Zhang, J. IRPruneDet: Efficient Infrared Small Target Detection via Wavelet Structure-Regularized Soft Channel Pruning. In Proceedings of the AAAI Conference on Artificial Intelligence 2024, Vancouver, BC, Canada, 22–25 February 2024; Volume 38, pp. 7224–7232. [Google Scholar]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2017, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Li, Q.; Mou, L.; Liu, Q.; Wang, Y.; Zhu, X.X. HSF-Net: Multiscale deep feature embedding for ship detection in optical remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 7147–7161. [Google Scholar] [CrossRef]
- Liu, X.; Ma, S.; He, L.; Wang, C.; Chen, Z. Hybrid network model: TransConvNet for oriented object detection in remote sensing images. Remote Sens. 2022, 14, 2090. [Google Scholar] [CrossRef]
- Li, Q.; Chen, Y.; Zeng, Y. Transformer with transfer CNN for remote-sensing-image object detection. Remote Sens. 2022, 14, 984. [Google Scholar] [CrossRef]
- Yang, X.; Yang, X.; Yang, J.; Ming, Q.; Wang, W.; Tian, Q.; Yan, J. Learning high-precision bounding box for rotated object detection via kullback-leibler divergence. Adv. Neural Inf. Process. Syst. 2021, 34, 18381–18394. [Google Scholar]
- Zhu, X.; Lyu, S.; Wang, X.; Zhao, Q. TPH-YOLOv5: Improved YOLOv5 based on transformer prediction head for object detection on drone-captured scenarios. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 2778–2788. [Google Scholar]
- Xu, C.; Wang, J.; Yang, W.; Yu, L. Dot distance for tiny object detection in aerial images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition 2021, Nashville, TN, USA, 20–25 June 2021; pp. 1192–1201. [Google Scholar]
- Chalavadi, V.; Jeripothula, P.; Datla, R.; Ch, S.B.; Mohan, K.C. mSODANet: A network for multi-scale object detection in aerial images using hierarchical dilated convolutions. Pattern Recognit. 2022, 126, 108548. [Google Scholar] [CrossRef]
- Shi, Z.; Wu, C.; Li, C.; You, Z.; Wang, Q.; Ma, C. Object detection techniques based on deep learning for aerial remote sensing images: A survey. Chin. J. Image Graph. 2023, 28, 2616–2643. [Google Scholar]
- Liu, S.; Qi, L.; Qin, H.; Shi, J.; Jia, J. Path aggregation network for instance segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2018, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8759–8768. [Google Scholar]
- Zhang, D.; Zhang, H.; Tang, J.; Wang, M.; Hua, X.; Sun, Q. Feature pyramid transformer. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XXVIII 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 323–339. [Google Scholar]
- Zheng, Z.; Wang, P.; Liu, W.; Li, J.; Ye, R.; Ren, D. Distance-IoU loss: Faster and better learning for bounding box regression. In Proceedings of the AAAI Conference on Artificial Intelligence 2020, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 12993–13000. [Google Scholar]
- Rezatofighi, H.; Tsoi, N.; Gwak, J.; Sadeghian, A.; Reid, I.; Savarese, S. Generalized intersection over union: A metric and a loss for bounding box regression. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition 2019, Long Beach, CA, USA, 15–20 June 2019; pp. 658–666. [Google Scholar]
- Wang, X.; Girshick, R.; Gupta, A.; He, K. Non-local neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2018, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7794–7803. [Google Scholar]
- Khan, S.; Naseer, M.; Hayat, M.; Zamir, S.W.; Khan, F.S.; Shah, M. Transformers in vision: A survey. ACM Comput. Surv. (CSUR) 2022, 54, 1–41. [Google Scholar] [CrossRef]
- Hou, L.; Lu, K.; Yang, X.; Li, Y.; Xue, J. G-rep: Gaussian representation for arbitrary-oriented object detection. Remote Sens. 2023, 15, 757. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2016, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition 2009, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision 2017, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Hou, L.; Lu, K.; Xue, J.; Li, Y. Shape-adaptive selection and measurement for oriented object detection. In Proceedings of the AAAI Conference on Artificial Intelligence 2022, Virtual, 22 February–1 March 2022; Volume 36, pp. 923–932. [Google Scholar]
- Everingham, M.; Van Gool, L.; Williams, C.K.; Winn, J.; Zisserman, A. The pascal visual object classes (voc) challenge. Int. J. Comput. Vis. 2010, 88, 303–338. [Google Scholar] [CrossRef]
- Yang, X.; Hou, L.; Zhou, Y.; Wang, W.; Yan, J. Dense label encoding for boundary discontinuity free rotation detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 15819–15829. [Google Scholar]
- Yang, X.; Yan, J. Arbitrary-oriented object detection with circular smooth label. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part VIII 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 677–694. [Google Scholar]

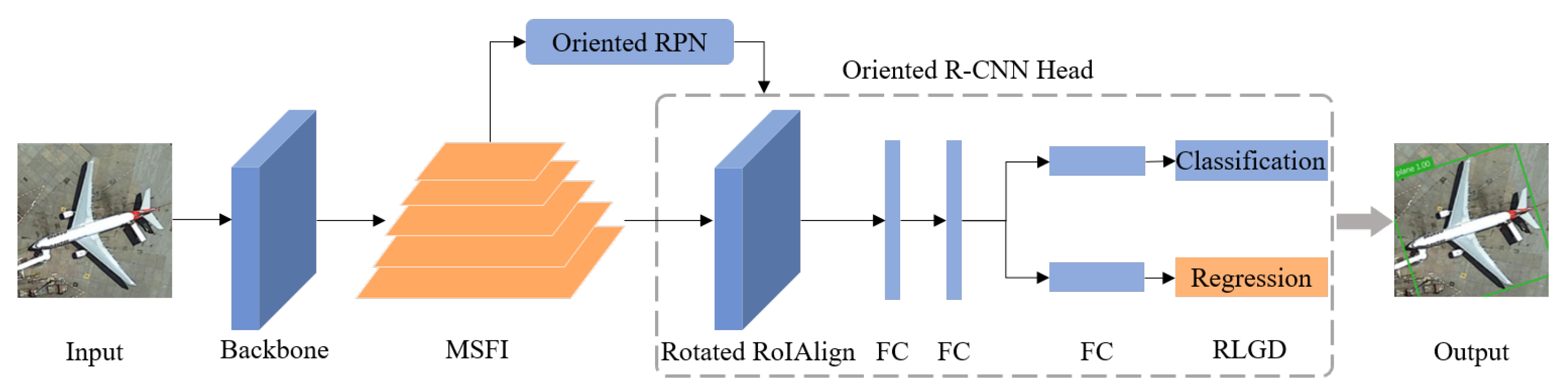
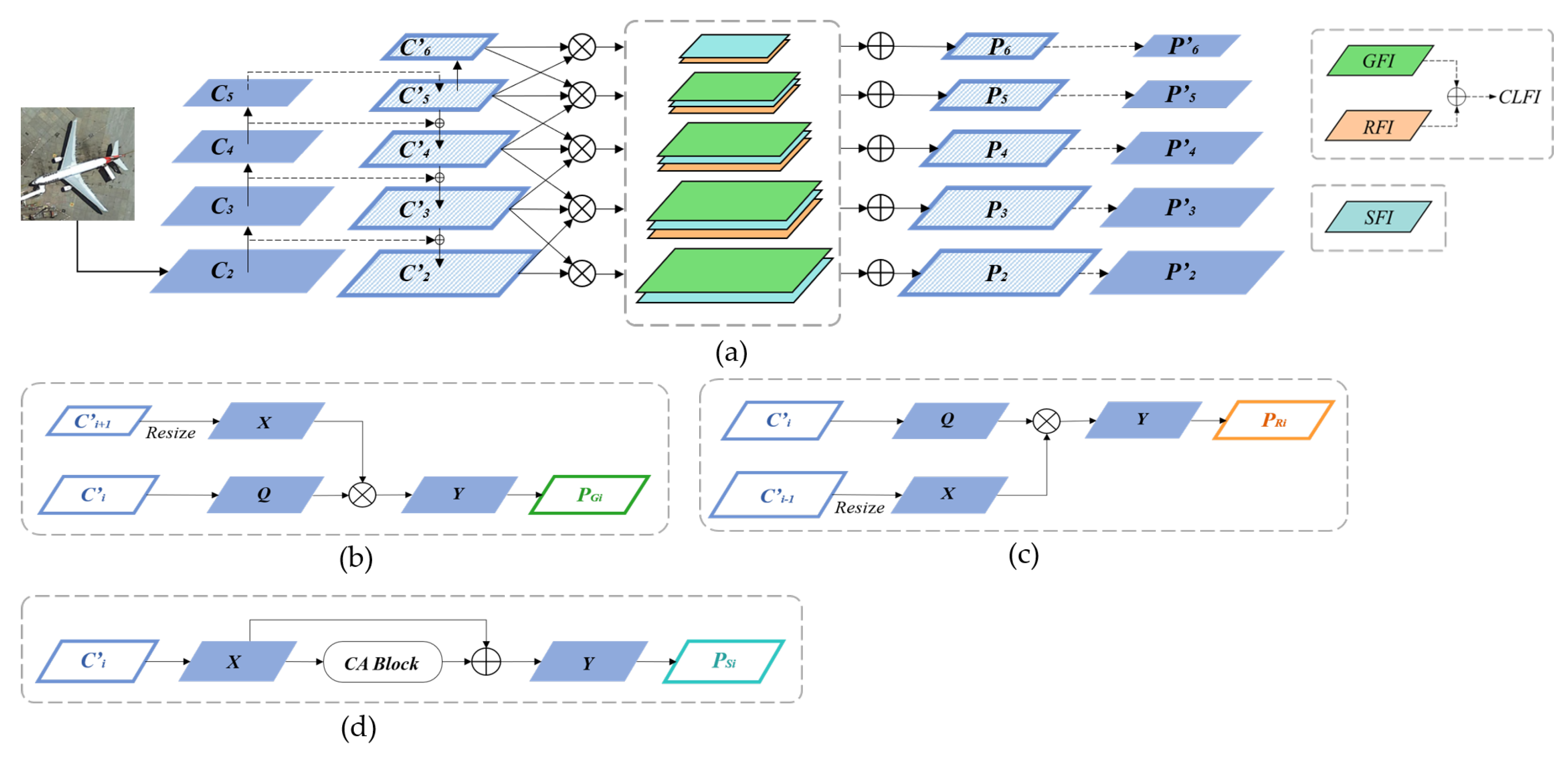
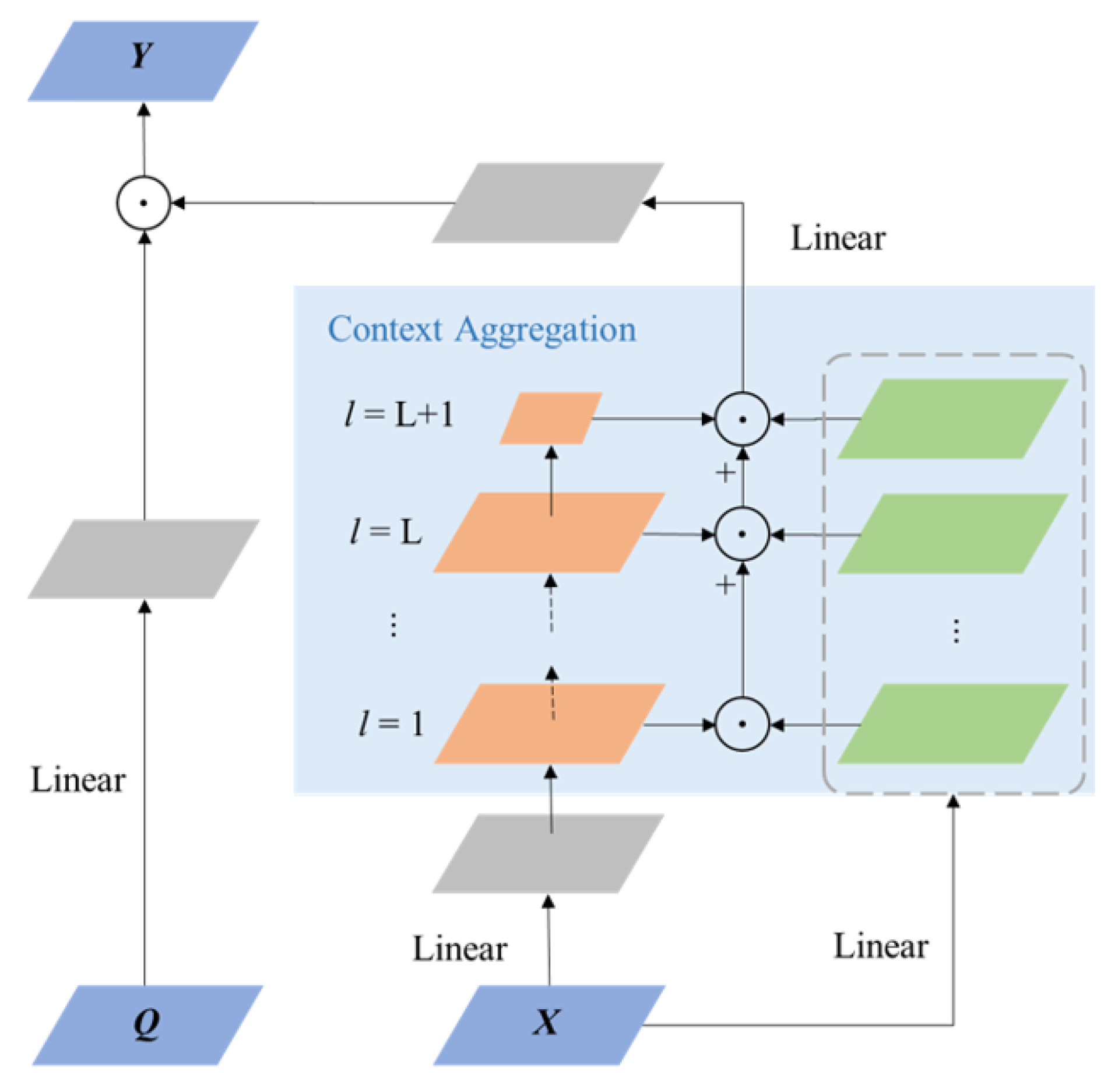
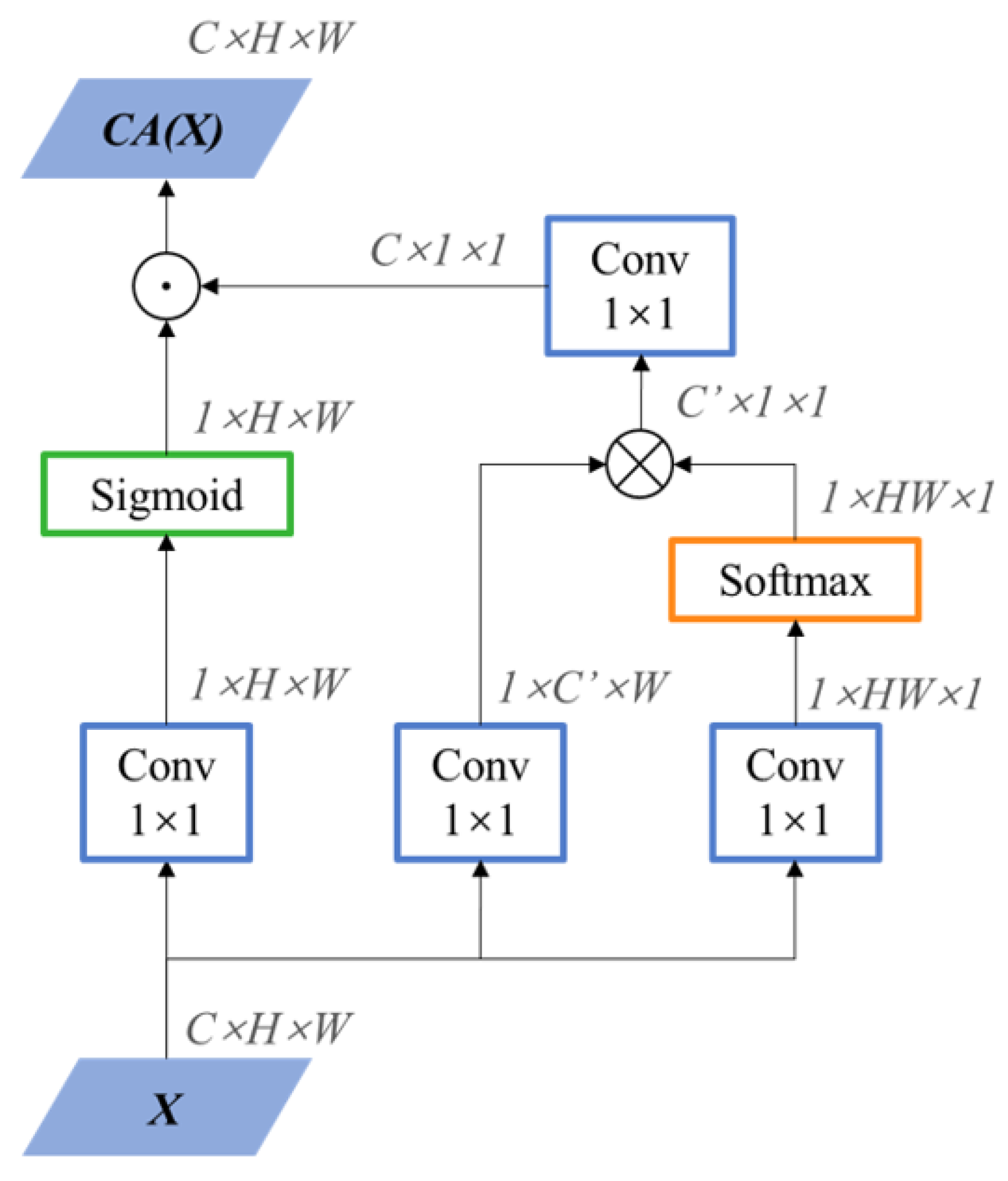

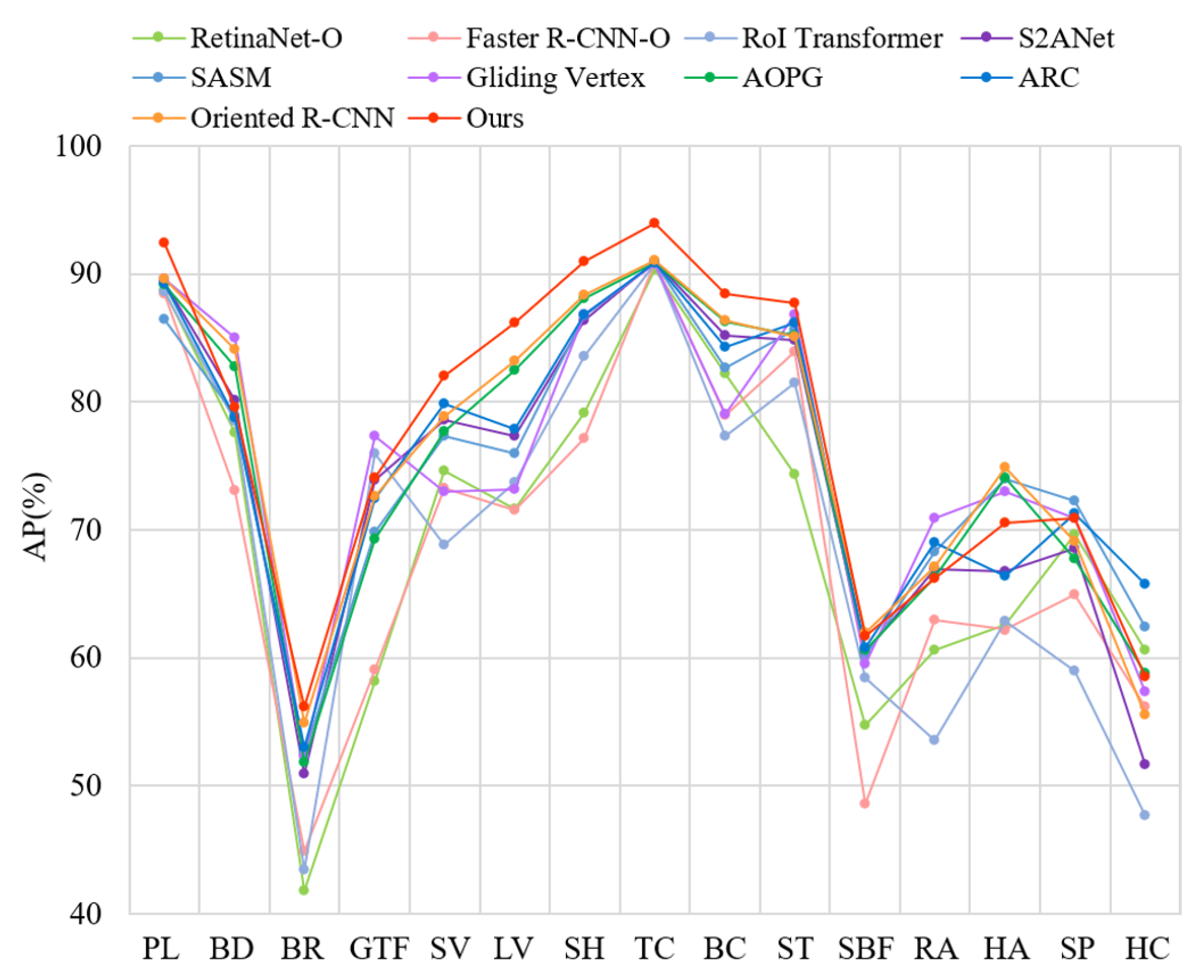

| Method | Backbone | PL | BD | BR | GTF | SV | LV | SH | TC | BC | ST | SBF | RA | HA | SP | HC | mAP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RetinaNet-O [58] | R-50 | 88.67 | 77.62 | 41.81 | 58.17 | 74.58 | 71.64 | 79.11 | 90.29 | 82.18 | 74.32 | 54.75 | 60.60 | 62.57 | 69.67 | 60.64 | 68.43 |
| Faster R-CNN-O [12] | R-50 | 88.44 | 73.06 | 44.86 | 59.09 | 73.25 | 71.49 | 77.11 | 90.84 | 78.94 | 83.90 | 48.59 | 62.95 | 62.18 | 64.91 | 56.18 | 69.05 |
| RoI Transformer [13] | R-101 | 88.64 | 78.52 | 43.44 | 75.92 | 68.81 | 73.68 | 83.59 | 90.74 | 77.27 | 81.46 | 58.39 | 53.54 | 62.83 | 58.93 | 47.67 | 69.56 |
| S2ANet [16] | R-50 | 89.30 | 80.11 | 50.97 | 73.91 | 78.59 | 77.34 | 86.38 | 90.91 | 85.14 | 84.84 | 60.45 | 66.94 | 66.78 | 68.55 | 51.65 | 74.13 |
| SASM [59] | R-50 | 86.42 | 78.97 | 52.47 | 69.84 | 77.30 | 75.99 | 86.72 | 90.89 | 82.63 | 85.66 | 60.13 | 68.25 | 73.98 | 72.22 | 62.37 | 74.92 |
| Gliding Vertex [15] | R-101 | 89.64 | 85.00 | 52.26 | 77.34 | 73.01 | 73.14 | 86.82 | 90.74 | 79.02 | 86.81 | 59.55 | 70.91 | 72.94 | 70.86 | 57.32 | 75.02 |
| AOPG [24] | R-101 | 89.14 | 82.74 | 51.87 | 69.28 | 77.65 | 82.42 | 88.08 | 90.89 | 86.26 | 85.13 | 60.60 | 66.30 | 74.05 | 67.76 | 58.77 | 75.39 |
| ARC [26] | R-50 | 89.28 | 78.77 | 53.00 | 72.44 | 79.81 | 77.84 | 86.81 | 90.88 | 84.27 | 86.20 | 60.74 | 68.97 | 66.35 | 71.25 | 65.77 | 75.49 |
| Oriented R-CNN [10] | Swin-T | 90.29 | 81.83 | 52.51 | 73.96 | 79.13 | 84.47 | 88.86 | 91.88 | 86.37 | 86.02 | 58.44 | 64.21 | 71.16 | 69.15 | 57.55 | 75.72 |
| Oriented R-CNN [10] | R-50 | 89.52 | 84.24 | 53.19 | 70.50 | 79.20 | 83.30 | 88.21 | 90.90 | 86.03 | 84.95 | 61.69 | 67.06 | 74.40 | 69.80 | 54.51 | 75.83 |
| Oriented R-CNN [10] | R-101 | 89.63 | 84.10 | 54.87 | 72.57 | 78.89 | 83.21 | 88.37 | 91.01 | 86.32 | 85.08 | 61.99 | 67.09 | 74.84 | 69.10 | 55.54 | 76.17 |
| Ours | Swin-T | 90.03 | 84.72 | 52.92 | 74.00 | 78.82 | 84.21 | 88.92 | 91.60 | 87.11 | 86.01 | 61.00 | 66.62 | 74.51 | 69.96 | 57.67 | 76.54 |
| Ours | R-50 | 91.43 | 85.62 | 55.05 | 72.24 | 80.52 | 84.94 | 90.06 | 92.85 | 87.79 | 86.94 | 62.29 | 66.80 | 74.47 | 70.26 | 53.41 | 76.98 |
| Ours | R-101 | 92.39 | 79.57 | 56.14 | 74.07 | 82.04 | 86.16 | 90.98 | 93.97 | 88.42 | 87.74 | 61.72 | 66.18 | 70.54 | 70.90 | 58.55 | 77.29 |
| Method | Backbone | mAP(07) | mAP(12) |
|---|---|---|---|
| RoI Transformer [13] | ResNet-101 | 86.20 | \ |
| Gliding Vertex [15] | ResNet-101 | 88.20 | \ |
| RetinaNet-O [58] | ResNet-101 | 89.18 | 95.21 |
| R3Det [23] | ResNet-101 | 89.26 | 96.01 |
| DCL [61] | ResNet-101 | 89.46 | 96.41 |
| CSL [62] | ResNet-101 | 89.62 | 96.10 |
| S2ANet [16] | ResNet-101 | 90.17 | 95.01 |
| SASM [59] | ResNet-101 | 90.27 | \ |
| AOPG [24] | ResNet-101 | 90.34 | 96.22 |
| ARC [26] | ResNet-50 | 90.41 | \ |
| Oriented R-CNN [10] | Swin-T | 89.70 | \ |
| Oriented R-CNN [10] | ResNet-50 | 90.23 | 96.11 |
| Oriented R-CNN [10] | ResNet-101 | 90.43 | 96.54 |
| Ours | Swin-T | 90.42 | \ |
| Ours | ResNet-50 | 90.55 | 97.67 |
| Ours | ResNet-101 | 90.59 | 97.95 |
| Method | MSFI | RLGD | mAP | mAP(07) | mAP(12) |
|---|---|---|---|---|---|
| Baseline | 75.83 | 90.23 | 96.11 | ||
| √ | 76.81 | 90.50 | 97.52 | ||
| √ | 76.70 | 90.35 | 96.62 | ||
| Ours | √ | √ | 76.98 | 90.55 | 97.67 |
| Method | GFI | RFI | SFI | mAP(%) | Params(M) | FLOPs(G) |
|---|---|---|---|---|---|---|
| Baseline | 75.83 | 41.14 | 211.43 | |||
| GFI | √ | 76.42 | 41.44 | 222.36 | ||
| RFI | √ | 76.07 | 41.44 | 217.81 | ||
| CLFI | √ | √ | 76.51 | 41.44 | 228.73 | |
| SFI | √ | 76.39 | 41.27 | 217.20 | ||
| MSFI | √ | √ | √ | 76.81 | 41.57 | 234.51 |
| Method | GD | GJSD | GA | mAP | mAP(07) | mAP(12) |
|---|---|---|---|---|---|---|
| Baseline | 75.83 | 90.23 | 96.11 | |||
| GWD | √ | 75.91 | 90.17 | 96.19 | ||
| GJSD | √ | √ | 76.12 | 90.30 | 96.58 | |
| RLGD | √ | √ | √ | 76.70 | 90.35 | 96.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, R.; Cai, H.; Zhang, B.; Feng, T. Multi-Scale Object Detection in Remote Sensing Images Based on Feature Interaction and Gaussian Distribution. Remote Sens. 2024, 16, 1988. https://doi.org/10.3390/rs16111988
Yu R, Cai H, Zhang B, Feng T. Multi-Scale Object Detection in Remote Sensing Images Based on Feature Interaction and Gaussian Distribution. Remote Sensing. 2024; 16(11):1988. https://doi.org/10.3390/rs16111988
Chicago/Turabian StyleYu, Ruixing, Haixing Cai, Boyu Zhang, and Tao Feng. 2024. "Multi-Scale Object Detection in Remote Sensing Images Based on Feature Interaction and Gaussian Distribution" Remote Sensing 16, no. 11: 1988. https://doi.org/10.3390/rs16111988
APA StyleYu, R., Cai, H., Zhang, B., & Feng, T. (2024). Multi-Scale Object Detection in Remote Sensing Images Based on Feature Interaction and Gaussian Distribution. Remote Sensing, 16(11), 1988. https://doi.org/10.3390/rs16111988








