Deep Multi-Order Spatial–Spectral Residual Feature Extractor for Weak Information Mining in Remote Sensing Imagery
Abstract
1. Introduction
2. Basic Methodology
2.1. High-Order Residual Quantization
2.2. Multi-Granularity Spectral Segmentation
2.3. Low-Rank Representation of RSIs
3. Datasets and Methods
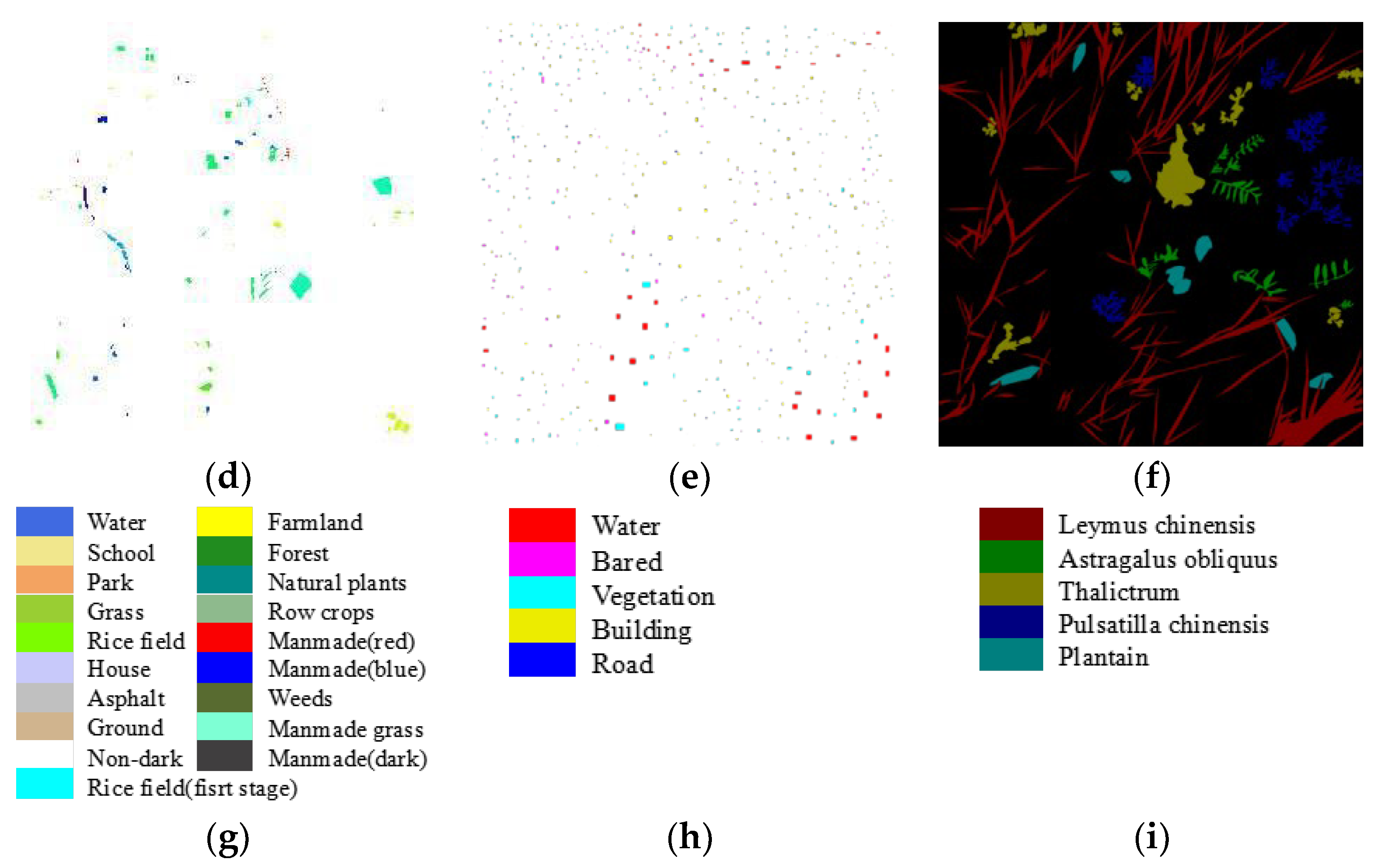
3.1. Datasets
3.2. Deep Multi-Order Spatial–Spectral Residual Feature Extraction
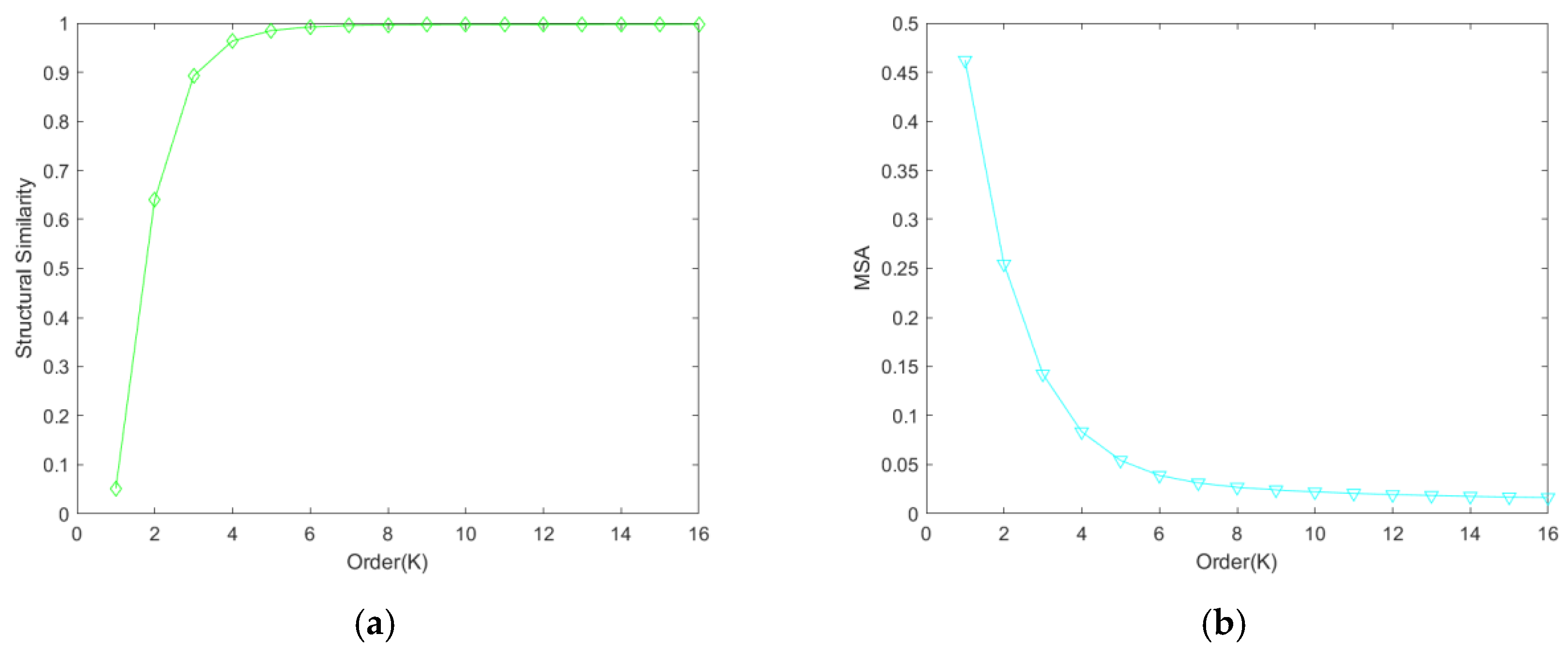
3.3. Evaluation Metrics
4. Results
4.1. Experimental Setting
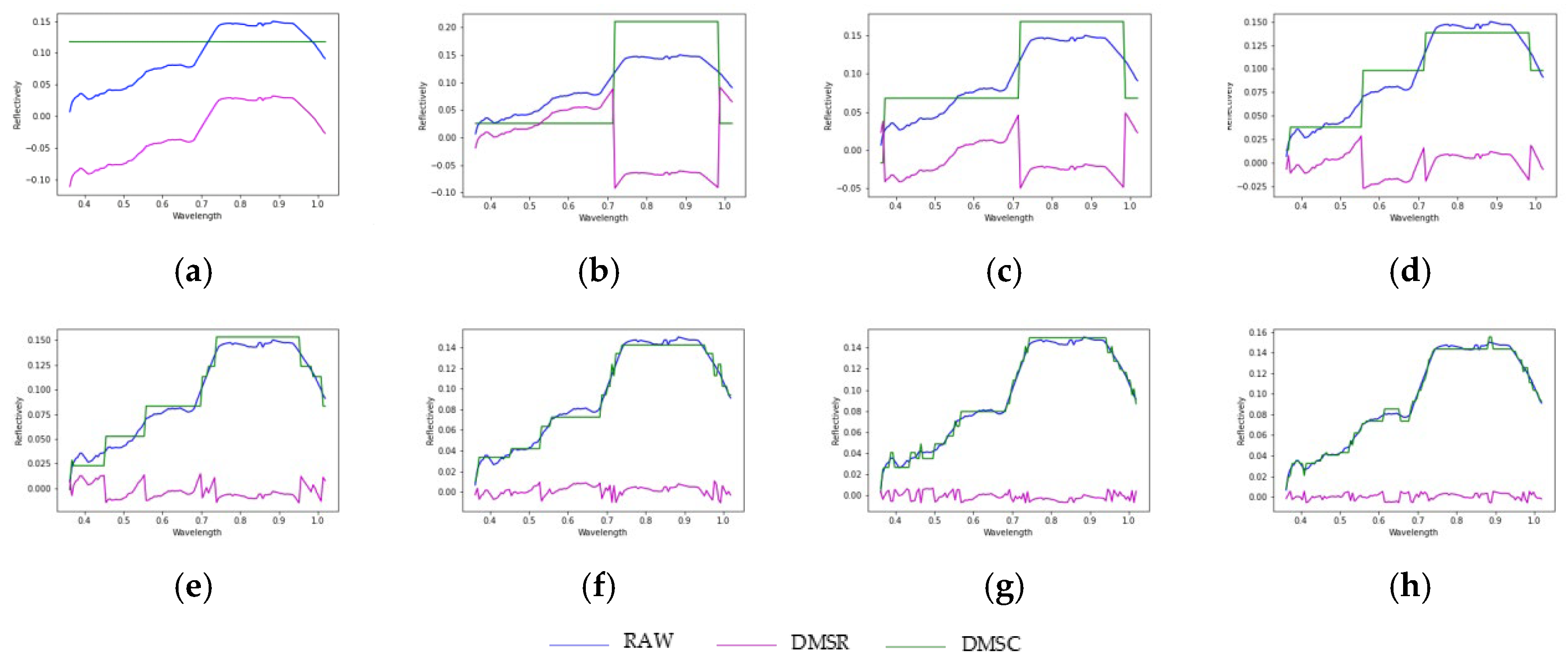
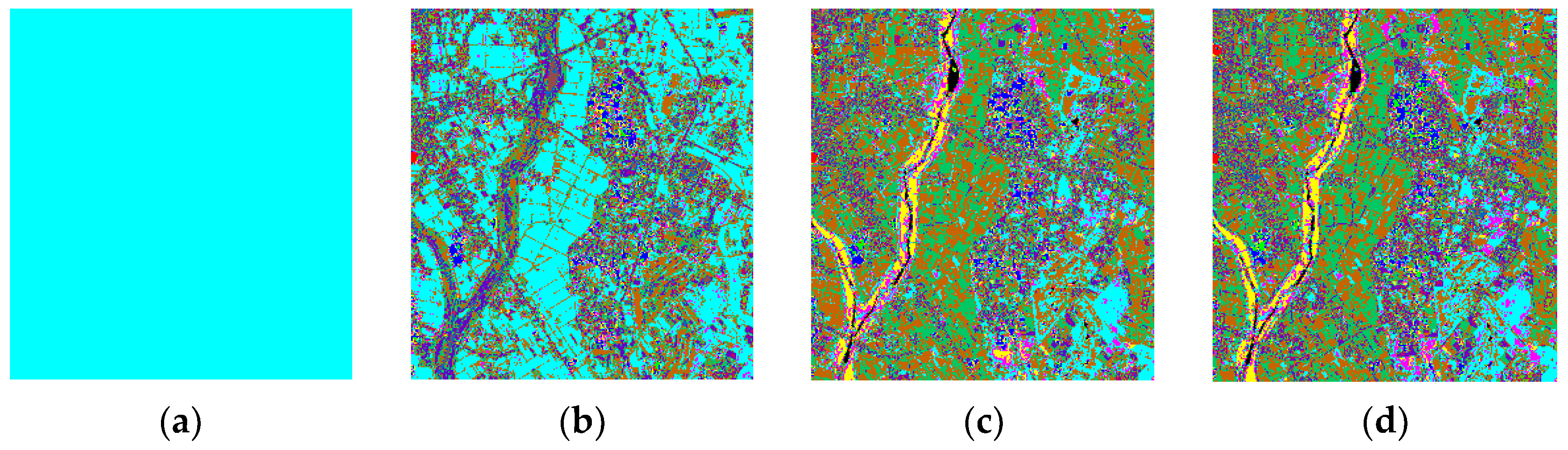
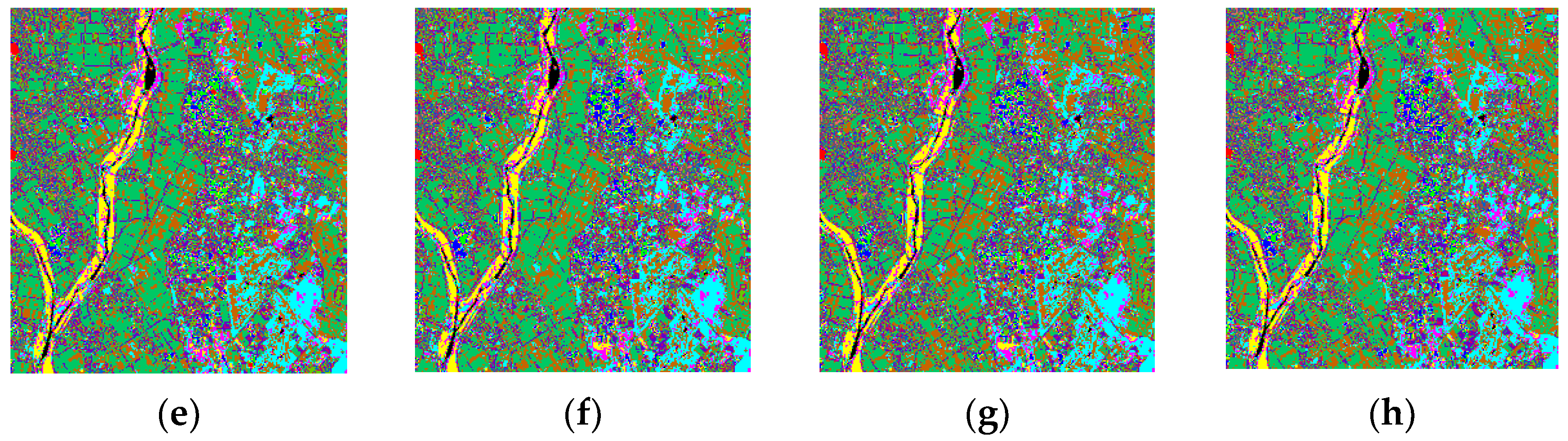
4.2. Spatial and Spectral Features of DMSR and DMSC
4.2.1. Spatial Features of DMSR and DMSC
4.2.2. Spectral Features of DMSR
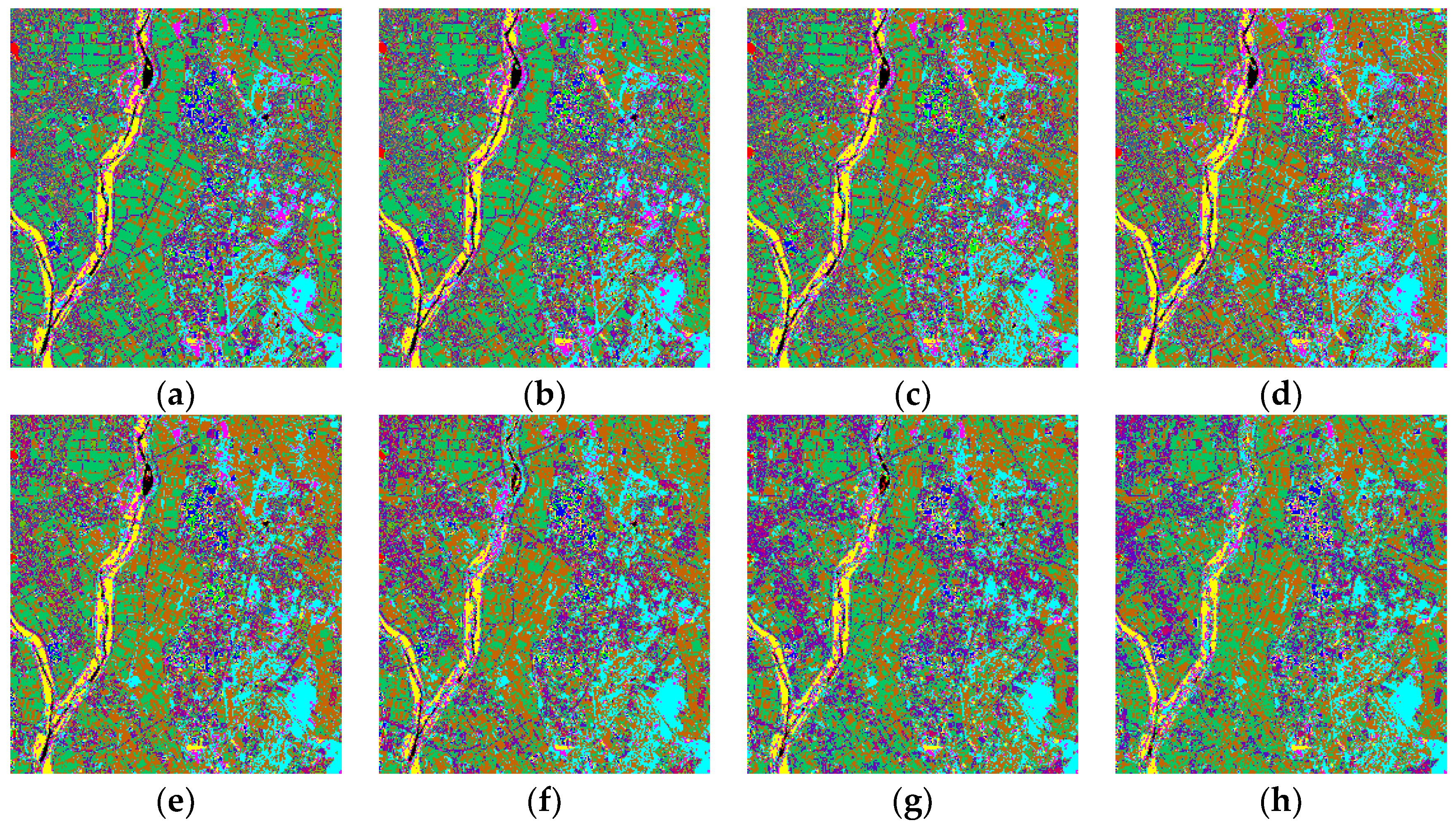
4.3. Classification Results Using DMSR and DMSC
5. Discussion
5.1. Research Contributions
5.2. Limitation and Potential Future Work
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shen, H.; Li, X.; Cheng, Q.; Zeng, C.; Yang, G.; Li, H.; Zhang, L. Missing Information Reconstruction of Remote Sensing Data: A Technical Review. IEEE Geosci. Remote Sens. Mag. 2015, 3, 61–85. [Google Scholar] [CrossRef]
- Qin, P.; Cai, Y.; Liu, J.; Fan, P.; Sun, M. Multilayer Feature Extraction Network for Military Ship Detection from High-Resolution Optical Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 11058–11069. [Google Scholar] [CrossRef]
- Shirmard, H.; Farahbakhsh, E.; Müller, R.D.; Chandra, R. A Review of Machine Learning in Processing Remote Sensing Data for Mineral Exploration. Remote Sens. Environ. 2022, 268, 112750. [Google Scholar] [CrossRef]
- Chen, H.; Qi, Z.; Shi, Z. Remote Sensing Image Change Detection with Transformers. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5607514. [Google Scholar] [CrossRef]
- Ozdogan, M.; Yang, Y.; Allez, G.; Cervantes, C. Remote Sensing of Irrigated Agriculture: Opportunities and Challenges. Remote Sens. 2010, 2, 2274–2304. [Google Scholar] [CrossRef]
- Yu, S.; De Backer, S.; Scheunders, P. Genetic Feature Selection Combined with Composite Fuzzy Nearest Neighbor Classifiers for High-Dimensional Remote Sensing Data. In Proceedings of the SMC 2000 International Conference on Systems, Man and Cybernetics. “Cybernetics Evolving to Systems, Humans, Organizations, and their Complex Interactions” (Cat. No.00CH37166), Nashville, TN, USA, 8–11 October 2000; Volume 3, pp. 1912–1916. [Google Scholar]
- Bhuvaneswari, K.; Dhamotharan, R.; Radhakrishnan, N. Information Extraction from Remote Sensing Image (RSI) for a Coastal Environment Along a Selected Coastline of Tamilnadu. IJCSET Board Memb. 2011, 95. [Google Scholar]
- Han, W.; Li, J.; Wang, S.; Wang, Y.; Yan, J.; Fan, R.; Zhang, X.; Wang, L. A Context-Scale-Aware Detector and a New Benchmark for Remote Sensing Small Weak Object Detection in Unmanned Aerial Vehicle Images. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102966. [Google Scholar] [CrossRef]
- Sun, Y.; Cai, W.; Shao, X. Chemometrics: An Excavator in Temperature-Dependent Near-Infrared Spectroscopy. Molecules 2022, 27, 452. [Google Scholar] [CrossRef]
- Fan, X.; Kang, X.; Gao, P.; Zhang, Z.; Wang, J.; Zhang, Q.; Zhang, M.; Ma, L.; Lv, X.; Zhang, L. Soil Salinity Estimation in Cotton Fields in Arid Regions Based on Multi-Granularity Spectral Segmentation (MGSS). Remote Sens. 2023, 15, 3358. [Google Scholar] [CrossRef]
- Wang, J.; Zhen, J.; Hu, W.; Chen, S.; Lizaga, I.; Zeraatpisheh, M.; Yang, X. Remote Sensing of Soil Degradation: Progress and Perspective. Int. Soil Water Conserv. Res. 2023, 11, 429–454. [Google Scholar] [CrossRef]
- Abdollahi, A.; Pradhan, B.; Shukla, N.; Chakraborty, S.; Alamri, A. Deep Learning Approaches Applied to Remote Sensing Datasets for Road Extraction: A State-Of-The-Art Review. Remote Sens. 2020, 12, 1444. [Google Scholar] [CrossRef]
- Rasti, B.; Hong, D.; Hang, R.; Ghamisi, P.; Kang, X.; Chanussot, J.; Benediktsson, J.A. Feature Extraction for Hyperspectral Imagery: The Evolution from Shallow to Deep: Overview and Toolbox. IEEE Geosci. Remote Sens. Mag. 2020, 8, 60–88. [Google Scholar] [CrossRef]
- Ebied, H.M. Feature Extraction Using PCA and Kernel-PCA for Face Recognition. In Proceedings of the 2012 8th International Conference on Informatics and Systems (INFOS), Giza, Egypt, 14–16 May 2012; p. MM-72. [Google Scholar]
- Aliyari Ghassabeh, Y.; Rudzicz, F.; Moghaddam, H.A. Fast Incremental LDA Feature Extraction. Pattern Recognit. 2015, 48, 1999–2012. [Google Scholar] [CrossRef]
- Prasad, S.; Bruce, L.M. Limitations of Principal Components Analysis for Hyperspectral Target Recognition. IEEE Geosci. Remote Sens. Lett. 2008, 5, 625–629. [Google Scholar] [CrossRef]
- Kumar, B.; Dikshit, O.; Gupta, A.; Singh, M.K. Feature Extraction for Hyperspectral Image Classification: A Review. Int. J. Remote Sens. 2020, 41, 6248–6287. [Google Scholar] [CrossRef]
- Ye, Z.; Bai, L.; He, M. Review of Spatial-Spectral Feature Extraction for Hyperspectral Image. J. Image Graph. 2021, 26, 1737–1763. [Google Scholar]
- Candès, E.J.; Li, X.; Ma, Y.; Wright, J. Robust Principal Component Analysis? J. ACM 2011, 58, 1–37. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T.; Tibshirani, R. Sparse Principal Component Analysis. J. Comput. Graph. Stat. 2006, 15, 265–286. [Google Scholar] [CrossRef]
- Yang, J.; Yang, J. Why Can LDA Be Performed in PCA Transformed Space? Pattern Recognit. 2003, 36, 563–566. [Google Scholar] [CrossRef]
- Bandos, T.V.; Bruzzone, L.; Camps-Valls, G. Classification of Hyperspectral Images with Regularized Linear Discriminant Analysis. IEEE Trans. Geosci. Remote Sens. 2009, 47, 862–873. [Google Scholar] [CrossRef]
- Du, Q. Modified Fisher’s Linear Discriminant Analysis for Hyperspectral Imagery. IEEE Geosci. Remote Sens. Lett. 2007, 4, 503–507. [Google Scholar] [CrossRef]
- Tipping, M.E.; Bishop, C.M. Probabilistic Principal Component Analysis. J. R. Stat. Soc. Ser. B Stat. Methodol. 1999, 61, 611–622. [Google Scholar] [CrossRef]
- Liang, Z.; Xia, S.; Zhou, Y. Normalized Discriminant Analysis for Dimensionality Reduction. Neurocomputing 2013, 110, 153–159. [Google Scholar] [CrossRef]
- He, X.; Niyogi, P. Locality Preserving Projections. Adv. Neural Inf. Process. Syst. 2003, 16. [Google Scholar]
- Cai, D.; He, X.; Wang, X.; Bao, H.; Han, J. Locality Preserving Nonnegative Matrix Factorization. In Proceedings of the Twenty-First International Joint Conference on Artificial Intelligence, Pasadena, CA, USA, 11–17 July 2009. [Google Scholar]
- Lee, D.D.; Seung, H.S. Learning the Parts of Objects by Non-Negative Matrix Factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef] [PubMed]
- Berge, A.; Solberg, A.S. Structured Gaussian Components for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3386–3396. [Google Scholar] [CrossRef]
- Bhagavathy, S.; Manjunath, B.S. Modeling and Detection of Geospatial Objects Using Texture Motifs. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3706–3715. [Google Scholar] [CrossRef]
- Pesaresi, M.; Benediktsson, J.A. A New Approach for the Morphological Segmentation of High-Resolution Satellite Imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 309–320. [Google Scholar] [CrossRef]
- Melgani, F.; Serpico, S.B. A Markov Random Field Approach to Spatio-Temporal Contextual Image Classification. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2478–2487. [Google Scholar] [CrossRef]
- Akcay, H.G.; Aksoy, S. Automatic Detection of Geospatial Objects Using Multiple Hierarchical Segmentations. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2097–2111. [Google Scholar] [CrossRef]
- Mallinis, G.; Koutsias, N.; Tsakiri-Strati, M.; Karteris, M. Object-Based Classification Using Quickbird Imagery for Delineating Forest Vegetation Polygons in a Mediterranean Test Site. ISPRS J. Photogramm. Remote Sens. 2008, 63, 237–250. [Google Scholar] [CrossRef]
- Fauvel, M.; Tarabalka, Y.; Benediktsson, J.A.; Chanussot, J.; Tilton, J.C. Advances in Spectral-Spatial Classification of Hyperspectral Images. Proc. IEEE 2012, 101, 652–675. [Google Scholar] [CrossRef]
- Benediktsson, J.A.; Palmason, J.A.; Sveinsson, J.R. Classification of Hyperspectral Data from Urban Areas Based on Extended Morphological Profiles. IEEE Trans. Geosci. Remote Sens. 2005, 43, 480–491. [Google Scholar] [CrossRef]
- Kang, X.; Li, S.; Benediktsson, J.A. Feature Extraction of Hyperspectral Images with Image Fusion and Recursive Filtering. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3742–3752. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, X.; Jia, X. Spectral–Spatial Classification of Hyperspectral Data Based on Deep Belief Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2381–2392. [Google Scholar] [CrossRef]
- Ma, X.; Wang, H.; Geng, J. Spectral–Spatial Classification of Hyperspectral Image Based on Deep Auto-Encoder. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4073–4085. [Google Scholar] [CrossRef]
- Kavitha, M.; Gayathri, R.; Polat, K.; Alhudhaif, A.; Alenezi, F. Performance Evaluation of Deep E-CNN with Integrated Spatial-Spectral Features in Hyperspectral Image Classification. Measurement 2022, 191, 110760. [Google Scholar] [CrossRef]
- Kang, X.; Zhang, A. A Novel Method for High-Order Residual Quantization-Based Spectral Binary Coding. Spectrosc. Spectr. Anal. 2019, 39, 3013–3020. [Google Scholar]
- Kang, X.; Zhang, A. Hyperspectral Remote Sensing Estimation of Pasture Crude Protein Content Based on Multi-Granularity Spectral Feature. Trans. Chin. Soc. Agric. Eng 2019, 35, 161–169. [Google Scholar]
- Kang, X.-Y.; Zhang, A.-W.; Pang, H.-Y. Estimation of Grassland Aboveground Biomass from UAV-Mounted Hyperspectral Image by Optimized Spectral Reconstruction. Spectrosc. Spectr. Anal. 2021, 41, 250–256. [Google Scholar]
- Pang, H.; Zhang, A.; Yin, S.; Zhang, J.; Dong, G.; He, N.; Qin, W.; Wei, D. Estimating Carbon, Nitrogen, and Phosphorus Contents of West–East Grassland Transect in Inner Mongolia Based on Sentinel-2 and Meteorological Data. Remote Sens. 2022, 14, 242. [Google Scholar] [CrossRef]
- Li, Z.; Ni, B.; Zhang, W.; Yang, X.; Gao, W. Performance Guaranteed Network Acceleration via High-Order Residual Quantization. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2603–2611. [Google Scholar]
- Rastegari, M.; Ordonez, V.; Redmon, J.; Farhadi, A. Xnor-Net: Imagenet Classification Using Binary Convolutional Neural Networks; Springer: Berlin/Heidelberg, Germany, 2016; pp. 525–542. [Google Scholar]
- Courbariaux, M.; Hubara, I.; Soudry, D.; El-Yaniv, R.; Bengio, Y. Binarized Neural Networks: Training Deep Neural Networks with Weights and Activations Constrained to +1 or −1. arXiv 2016, arXiv:1602.02830. [Google Scholar]
- Liu, G.; Lin, Z.; Yu, Y. Robust Subspace Segmentation by Low-Rank Representation. In Proceedings of the 27th international conference on machine learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 663–670. [Google Scholar]
- Yokoya, N.; Iwasaki, A. Airborne Hyperspectral Data over Chikusei; Technical Report SAL-2016-05-27; Space Application Laboratory, The University of Tokyo: Tokyo, Japan, 2016. [Google Scholar]
- Zhang, X.; Zhang, A.; Portelli, R.; Zhang, X.; Guan, H. ZY-1 02D Hyperspectral Imagery Super-Resolution via Endmember Matrix Constraint Unmixing. Remote Sens. 2022, 14, 4034. [Google Scholar] [CrossRef]
- Cao, C.; Yu, J.; Zhou, C.; Hu, K.; Xiao, F.; Gao, X. Hyperspectral Image Denoising via Subspace-Based Nonlocal Low-Rank and Sparse Factorization. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 973–988. [Google Scholar] [CrossRef]
- Sara, U.; Akter, M.; Uddin, M.S. Image Quality Assessment through FSIM, SSIM, MSE and PSNR—A Comparative Study. J. Comput. Commun. 2019, 7, 8–18. [Google Scholar] [CrossRef]
- Zhang, X.; Schaaf, C.B.; Friedl, M.A.; Strahler, A.H.; Gao, F.; Hodges, J.C.F. MODIS Tasseled Cap Transformation and Its Utility. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; Volume 2, pp. 1063–1065. [Google Scholar]
- Truong, V.T.; Hirayama, S.; Phan, D.C.; Hoang, T.T.; Tadono, T.; Nasahara, K.N. JAXA’s New High-Resolution Land Use Land Cover Map for Vietnam Using a Time-Feature Convolutional Neural Network. Sci. Rep. 2024, 14, 3926. [Google Scholar] [CrossRef]












| Class Name | Raw | First Order | Second Order | Third Order | Fourth Order | Fifth Order | Sixth Order | Seventh Order | Eighth Order |
|---|---|---|---|---|---|---|---|---|---|
| Water | 0.9939 | 0.9951 | 0.9916 | 0.9926 | 0.9939 | 0.9924 | 0.9754 | 0.9395 | 0.9402 |
| School | 0.9899 | 0.9850 | 0.9931 | 0.9855 | 0.9720 | 0.9483 | 0.9257 | 0.8300 | 0.7782 |
| Park | 0.7860 | 0.7146 | 0.8253 | 0.7566 | 0.5662 | 0.1176 | 0.5160 | 0.0000 | 0.0156 |
| Farmland | 0.9880 | 0.9826 | 0.9891 | 0.9847 | 0.9779 | 0.9630 | 0.9604 | 0.9446 | 0.9200 |
| Plants | 0.9935 | 0.9879 | 0.9895 | 0.9922 | 0.9893 | 0.9924 | 0.9849 | 0.9817 | 0.9834 |
| Weeds | 0.9704 | 0.9541 | 0.9530 | 0.9681 | 0.9626 | 0.9467 | 0.8929 | 0.9016 | 0.9045 |
| Forest | 0.9983 | 0.9962 | 0.9962 | 0.9951 | 0.9883 | 0.9857 | 0.9800 | 0.9742 | 0.9670 |
| Grass | 0.9953 | 0.9926 | 0.9957 | 0.9959 | 0.9948 | 0.9891 | 0.9772 | 0.9692 | 0.9611 |
| Rice field (grown) | 0.9987 | 0.9975 | 0.9978 | 0.9945 | 0.9847 | 0.9789 | 0.9739 | 0.9652 | 0.9539 |
| Rice field | 0.9951 | 0.9991 | 0.9973 | 0.9900 | 0.9913 | 0.9863 | 0.9842 | 0.9584 | 0.9689 |
| Row crops | 0.9971 | 0.9945 | 0.9936 | 0.9964 | 0.9947 | 0.9931 | 0.9846 | 0.9742 | 0.9570 |
| House | 0.9686 | 0.9794 | 0.9791 | 0.9687 | 0.9265 | 0.8136 | 0.7306 | 0.5956 | 0.5482 |
| Manmade | 0.9834 | 0.9834 | 0.9871 | 0.9680 | 0.9148 | 0.8597 | 0.8416 | 0.8203 | 0.8099 |
| Manmade (dark) | 0.9893 | 0.9942 | 0.9927 | 0.9928 | 0.9926 | 0.9885 | 0.9827 | 0.9723 | 0.9712 |
| Manmade (Red) | 1.0000 | 0.9935 | 0.9868 | 0.9987 | 0.9564 | 0.8688 | 0.7524 | 0.5589 | 0.2982 |
| Manmade (Blue) | 0.9950 | 0.9928 | 0.9700 | 0.9199 | 0.9258 | 0.8371 | 0.0741 | 0.0000 | 0.0000 |
| Manmade grass | 0.9879 | 0.9873 | 0.9914 | 0.9835 | 0.9756 | 0.9001 | 0.8633 | 0.6983 | 0.5340 |
| Asphalt | 0.8912 | 0.9599 | 0.9511 | 0.9456 | 0.9391 | 0.9151 | 0.8593 | 0.5614 | 0.4500 |
| Ground | 0.9339 | 0.9153 | 0.8279 | 0.8851 | 0.8185 | 0.8302 | 0.0876 | 0.0000 | 0.0000 |
| Overall accuracy | 0.9922 | 0.9913 | 0.9921 | 0.9902 | 0.9824 | 0.9708 | 0.9570 | 0.9324 | 0.9177 |
| Class Name | Raw | First Order | Second Order | Third Order | Fourth Order | Fifth Order | Sixth Order | Seventh Order | Eighth Order |
|---|---|---|---|---|---|---|---|---|---|
| Water | 0.9939 | 0.0000 | 0.0000 | 0.8549 | 0.8526 | 0.9711 | 0.9913 | 0.9920 | 0.9931 |
| School | 0.9899 | 0.0000 | 0.0000 | 0.9290 | 0.9826 | 0.9868 | 0.9905 | 0.9941 | 0.9920 |
| Park | 0.7860 | 0.0000 | 0.0000 | 0.0000 | 0.3573 | 0.6038 | 0.6798 | 0.6699 | 0.7229 |
| Farmland | 0.9880 | 0.0000 | 0.0000 | 0.9503 | 0.9620 | 0.9785 | 0.9787 | 0.9825 | 0.9833 |
| Plants | 0.9935 | 0.0000 | 0.8034 | 0.9634 | 0.9829 | 0.9896 | 0.9890 | 0.9941 | 0.9927 |
| Weeds | 0.9704 | 0.0000 | 0.0020 | 0.8749 | 0.9250 | 0.9456 | 0.9401 | 0.9590 | 0.9584 |
| Forest | 0.9983 | 0.4184 | 0.7992 | 0.9250 | 0.9688 | 0.9936 | 0.9942 | 0.9963 | 0.9968 |
| Grass | 0.9953 | 0.0000 | 0.7099 | 0.9819 | 0.9926 | 0.9944 | 0.9942 | 0.9964 | 0.9945 |
| Rice field (grown) | 0.9987 | 0.0000 | 0.7530 | 0.8947 | 0.9574 | 0.9930 | 0.9943 | 0.9962 | 0.9976 |
| Rice field | 0.9951 | 0.0000 | 0.0000 | 0.9885 | 0.9851 | 0.9965 | 0.9961 | 0.9965 | 0.9978 |
| Row crops | 0.9971 | 0.0000 | 0.3128 | 0.9617 | 0.9838 | 0.9919 | 0.9937 | 0.9928 | 0.9920 |
| House | 0.9686 | 0.0000 | 0.1283 | 0.8995 | 0.9691 | 0.9748 | 0.9782 | 0.9760 | 0.9836 |
| Manmade | 0.9834 | 0.0000 | 0.9656 | 0.9781 | 0.9819 | 0.9813 | 0.9858 | 0.9890 | 0.9843 |
| Manmade (dark) | 0.9893 | 0.0000 | 0.4234 | 0.9450 | 0.9485 | 0.9855 | 0.9920 | 0.9915 | 0.9931 |
| Manmade (Red) | 1.0000 | 0.0000 | 0.3644 | 0.9948 | 1.0000 | 1.0000 | 1.0000 | 0.9924 | 0.9963 |
| Manmade (Blue) | 0.9950 | 0.0000 | 0.8034 | 0.9624 | 1.0000 | 1.0000 | 0.9950 | 0.9926 | 0.9949 |
| Manmade grass | 0.9879 | 0.0000 | 0.1353 | 0.8688 | 0.9821 | 0.9877 | 0.9875 | 0.9846 | 0.9874 |
| Asphalt | 0.8912 | 0.0000 | 0.0000 | 0.6562 | 0.9253 | 0.9508 | 0.9297 | 0.9384 | 0.9488 |
| Ground | 0.9339 | 0.0000 | 0.0000 | 0.0000 | 0.5400 | 0.8787 | 0.7019 | 0.8664 | 0.7500 |
| Overall accuracy | 0.9922 | 0.2645 | 0.5839 | 0.6684 | 0.9625 | 0.9870 | 0.9890 | 0.9911 | 0.9917 |
| Class Name | Raw | First Order | Second Order | Third Order | Fourth Order | Fifth Order | Sixth Order | Seventh Order | Eighth Order |
|---|---|---|---|---|---|---|---|---|---|
| Water | 0.9546 | 0.9548 | 0.9567 | 0.9728 | 0.9756 | 0.9699 | 0.9367 | 0.8174 | 0.7897 |
| Building | 0.9672 | 0.968 | 0.9769 | 0.9852 | 0.994 | 0.966 | 0.9971 | 0.9969 | 0.9971 |
| Naked | 0.8373 | 0.8332 | 0.8005 | 0.6752 | 0.5353 | 0.3094 | 0.2881 | 0.1958 | 0.1892 |
| Vegetation | 0.9006 | 0.8998 | 0.8423 | 0.8164 | 0.9792 | 0.5321 | 0.4971 | 0.4434 | 0.4377 |
| Road | 0.8131 | 0.7992 | 0.7636 | 0.64 | 0.1454 | 0.5321 | 0.089 | 0.0346 | 0.0277 |
| Overall accuracy | 0.9207 | 0.9197 | 0.9016 | 0.8775 | 0.81081 | 0.73134 | 0.7096 | 0.645 | 0.6345 |
| Class Name | Raw | First Order | Second Order | Third Order | Fourth Order | Fifth Order | Sixth Order | Seventh Order | Eighth Order |
|---|---|---|---|---|---|---|---|---|---|
| Water | 0.9546 | 0.8261 | 0.9758 | 0.9764 | 0.9853 | 0.9709 | 0.9683 | 0.9616 | 0.9628 |
| Building | 0.9672 | 1 | 0.8559 | 0.9492 | 0.9629 | 0.9642 | 0.9683 | 0.9683 | 0.9666 |
| Naked | 0.8373 | 0 | 0.7779 | 0.8295 | 0.8334 | 0.8342 | 0.9339 | 0.8321 | 0.8359 |
| Vegetation | 0.9006 | 0 | 0.8081 | 0.8537 | 0.8777 | 0.8882 | 0.8975 | 0.9003 | 0.8961 |
| Road | 0.8131 | 0 | 0.2423 | 0.6855 | 0.7507 | 0.8002 | 0.8061 | 0.8101 | 0.8051 |
| Overall accuracy | 0.9207 | 0.5015 | 0.8514 | 0.9062 | 0.9204 | 0.9205 | 0.9232 | 0.9278 | 0.9213 |
| Class Name | Raw | First Order | Second Order | Third Order | Fourth Order | Fifth Order | Sixth Order | Seventh Order | Eighth Order |
|---|---|---|---|---|---|---|---|---|---|
| Leymus chinensis | 0.7684 | 0.7673 | 0.7651 | 0.7635 | 0.7617 | 0.7616 | 0.7607 | 0.7607 | 0.7594 |
| Astragalus obliquus | 0.2955 | 0.3189 | 0.2842 | 0.2727 | 0.2042 | 0.1915 | 0.1124 | 0.1180 | 0.0362 |
| Thalictrum | 0.1039 | 0.1385 | 0.1040 | 0.0994 | 0.0900 | 0.0980 | 0.0679 | 0.0741 | 0.0275 |
| Pulsatilla chinensis | 0.2866 | 0.2891 | 0.2485 | 0.2711 | 0.2269 | 0.2118 | 0.1879 | 0.1833 | 0.1584 |
| Plantain | 0.3249 | 0.3986 | 0.3508 | 0.3747 | 0.3440 | 0.3495 | 0.2896 | 0.2960 | 0.2160 |
| Overall accuracy | 0.6325 | 0.64 | 0.6243 | 0.6128 | 0.6114 | 0.6113 | 0.6118 | 0.6115 | 0.6112 |
| Class Name | Raw | First Order | Second Order | Third Order | Fourth Order | Fifth Order | Sixth Order | Seventh Order | Eighth Order |
|---|---|---|---|---|---|---|---|---|---|
| Leymus chinensis | 0.7684 | 0.7575 | 0.7571 | 0.7581 | 0.7599 | 0.7624 | 0.7633 | 0.7644 | 0.7661 |
| Astragalus obliquus | 0.2955 | 0 | 0.0764 | 0.0759 | 0.1808 | 0.2158 | 0.2985 | 0.2962 | 0.2992 |
| Thalictrum | 0.1039 | 0 | 0 | 0.0000 | 0.0020 | 0.0254 | 0.0850 | 0.1114 | 0.1000 |
| Pulsatilla chinensis | 0.2866 | 0 | 0 | 0.0560 | 0.1434 | 0.2036 | 0.2718 | 0.2709 | 0.2743 |
| Plantain | 0.3249 | 0 | 0 | 0.0000 | 0.0640 | 0.1910 | 0.3143 | 0.3303 | 0.3192 |
| Overall accuracy | 0.6325 | 0.6096 | 0.6097 | 0.6109 | 0.6173 | 0.6247 | 0.6321 | 0.6343 | 0.6360 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Zhang, A.; Sun, Y.; Wang, J.; Pang, H.; Peng, J.; Chen, Y.; Zhang, J.; Giannico, V.; Legesse, T.G.; et al. Deep Multi-Order Spatial–Spectral Residual Feature Extractor for Weak Information Mining in Remote Sensing Imagery. Remote Sens. 2024, 16, 1957. https://doi.org/10.3390/rs16111957
Zhang X, Zhang A, Sun Y, Wang J, Pang H, Peng J, Chen Y, Zhang J, Giannico V, Legesse TG, et al. Deep Multi-Order Spatial–Spectral Residual Feature Extractor for Weak Information Mining in Remote Sensing Imagery. Remote Sensing. 2024; 16(11):1957. https://doi.org/10.3390/rs16111957
Chicago/Turabian StyleZhang, Xizhen, Aiwu Zhang, Yuan Sun, Juan Wang, Haiyang Pang, Jinbang Peng, Yunsheng Chen, Jiaxin Zhang, Vincenzo Giannico, Tsegaye Gemechu Legesse, and et al. 2024. "Deep Multi-Order Spatial–Spectral Residual Feature Extractor for Weak Information Mining in Remote Sensing Imagery" Remote Sensing 16, no. 11: 1957. https://doi.org/10.3390/rs16111957
APA StyleZhang, X., Zhang, A., Sun, Y., Wang, J., Pang, H., Peng, J., Chen, Y., Zhang, J., Giannico, V., Legesse, T. G., Shao, C., & Xin, X. (2024). Deep Multi-Order Spatial–Spectral Residual Feature Extractor for Weak Information Mining in Remote Sensing Imagery. Remote Sensing, 16(11), 1957. https://doi.org/10.3390/rs16111957









