A New Trajectory Clustering Method for Mining Multiple Periodic Patterns from Complex Oceanic Trajectories
Abstract
1. Introduction
2. Definitions and Symbols
3. The Proposed Method
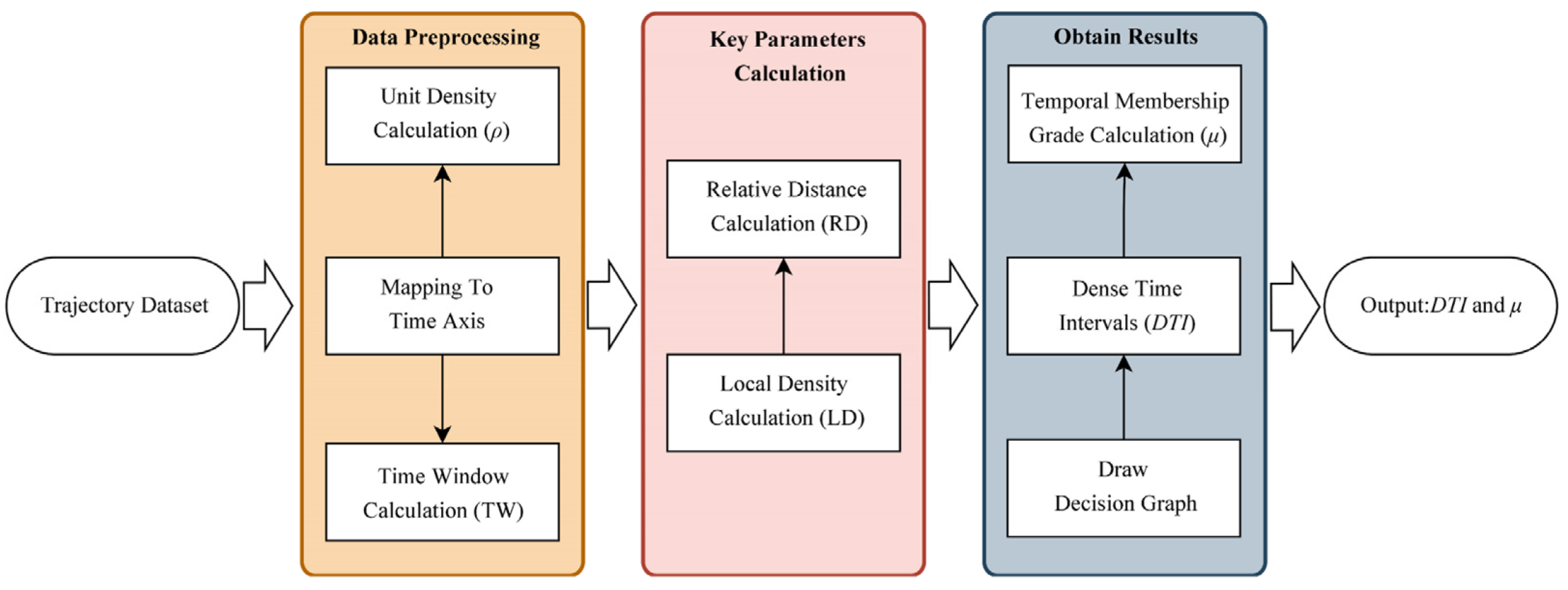
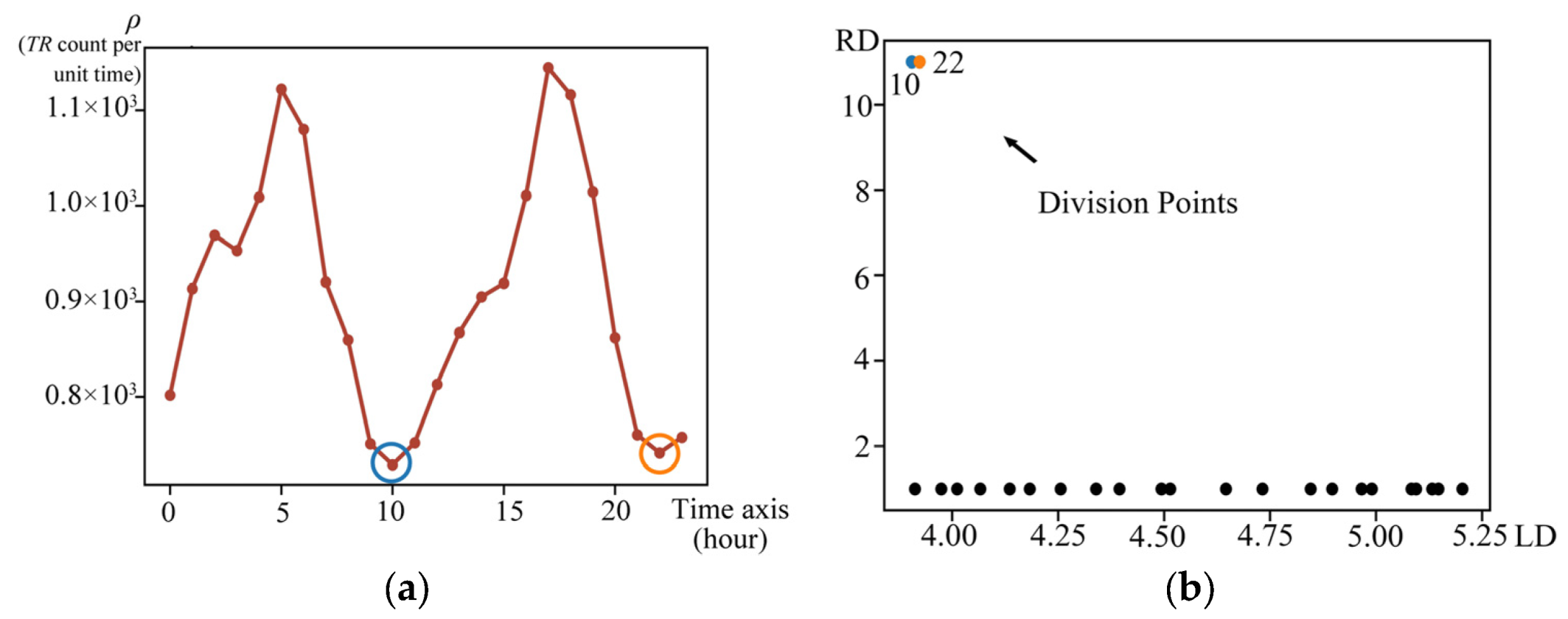
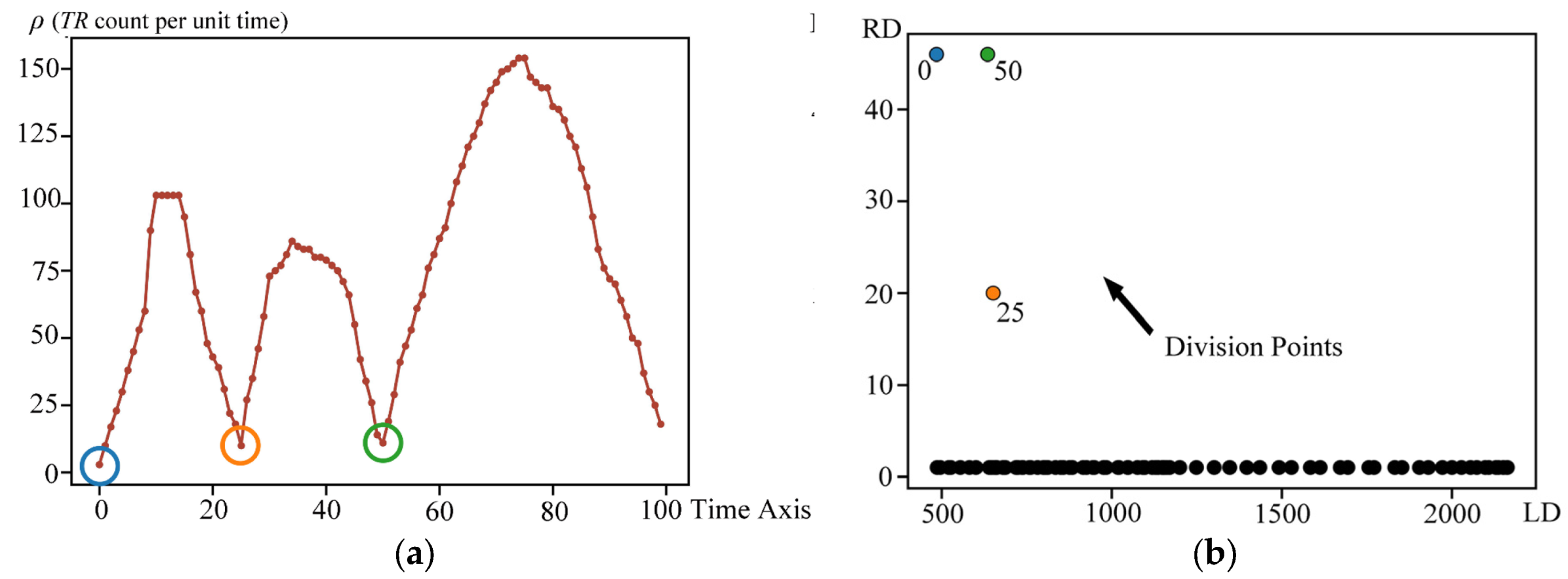
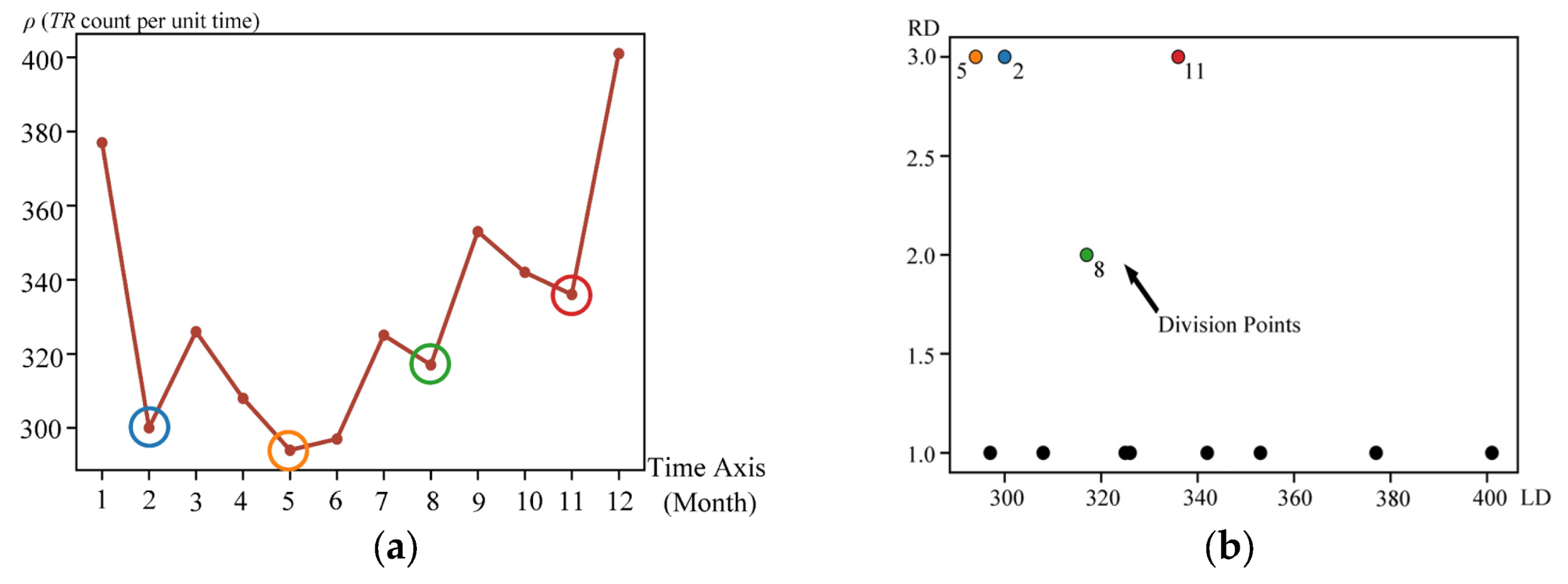
3.1. TR-Dense Time Interval Detection
3.2. Spectral Three-Way Fuzzy Clustering
| Algorithm 1: Dense time interval detection and spectral three-way fuzzy clustering (DTID-STFC) (Pseudocode for the DTID-STFC: /*** and ***/ represents explanatory content) | |
| Input: Trajectory dataset <, the time window size rate , the three-way threshold . | |
| /*** Dense time interval detection ***/ | |
| Initialization: (1) Construct the time axis based on trajectory data, including the length and units of the time axis. (2) Calculate the unit density of trajectories on the time axis. (3) Calculate the time window. | |
| 1: | For each time point on the time axis: |
| 2: | Calculate using Equation (1). |
| 3 | For each time point on the time axis: |
| 4: | Calculate using Equation (2). |
| 5: | Draw decision graph to determine the dense time intervals . |
| 6: | For each trajectory : |
| 7: | Calculate temporal membership grade using Equation (3). |
| /*** Spectral three-way fuzzy clustering ***/ | |
| 8: | For each dense : |
| 9: | /*** Determine the optimal value based on the quality of clustering results. ***/ |
| 10: | Construct the affinity matrix of trajectories occurring in using Equation (4). |
| 11: | Construct the degree matrix calculated by . |
| 12: | Initialize the three-way membership grade matrix using random floating-point numbers between 0 and 1. |
| 13: | ; // Equation (5). |
| 14: | Eigenvalues, eigenvectors = eigen decomposition (). |
| 15: | Sort(eigenvalues). |
| 16: | Select the eigenvectors corresponding to the smallest eigenvalue as the new coordinates in the spectral space, where the th row vector is defined as . |
| 17: | While not converged do |
| 18: | /*** Convergence experiment: ***/ |
| 19: | Calculate the centroids based on and using Equation (8). |
| 20: | Calculate cluster membership grade matrix using Equation (6). |
| 21: | Update three-way membership grade matrix based on using Equation (7). |
| 22: | /*** Convergence experiment: and ***/ |
| 23: | End while. |
| 24: | Output: the three-way membership grade matrix corresponding to . |
3.3. Computational Complexity Analysis
4. Experimental Results
4.1. Datasets
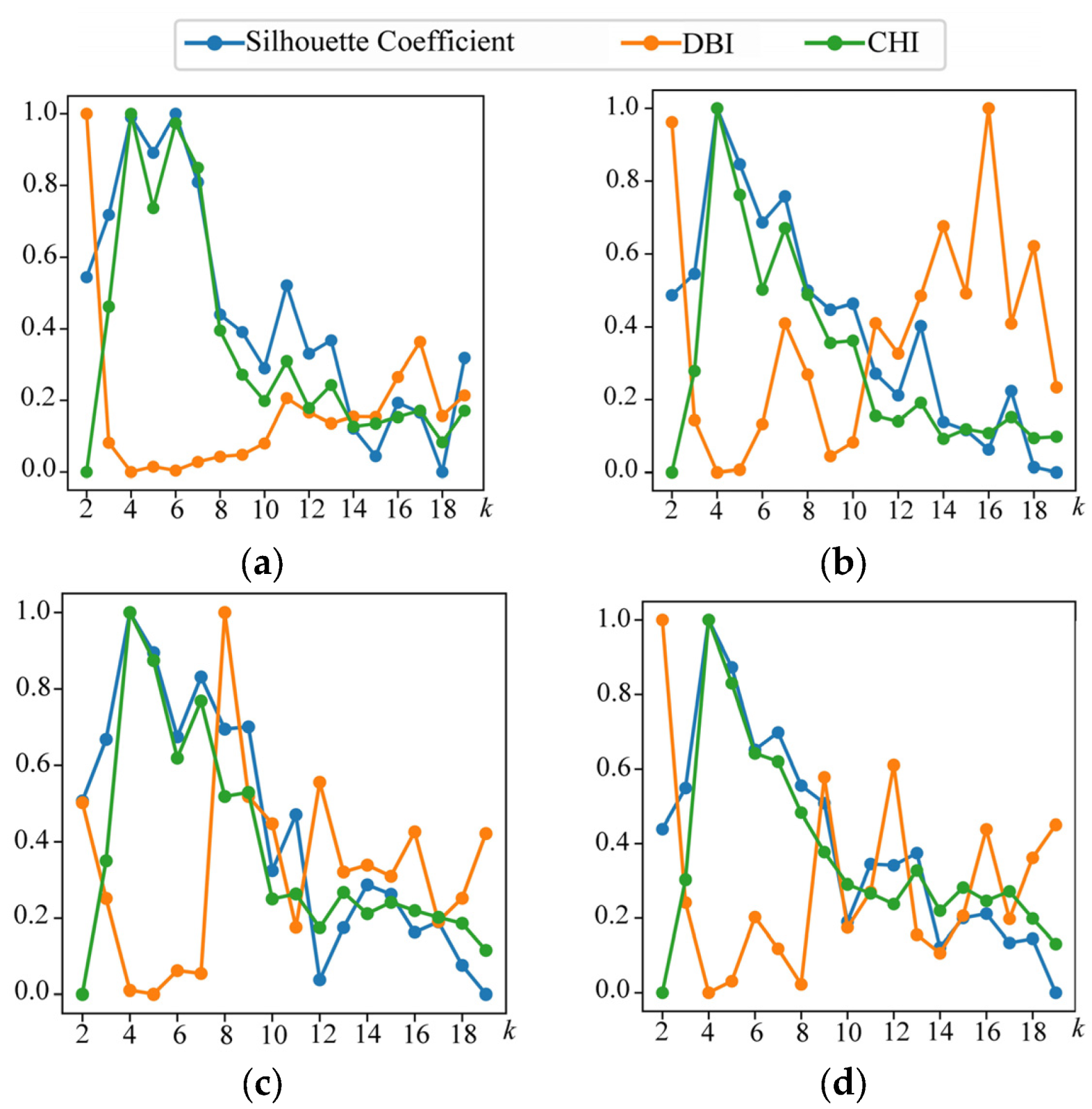
4.2. Evaluation Metrics
4.3. Experiment in Simulated Trajectory
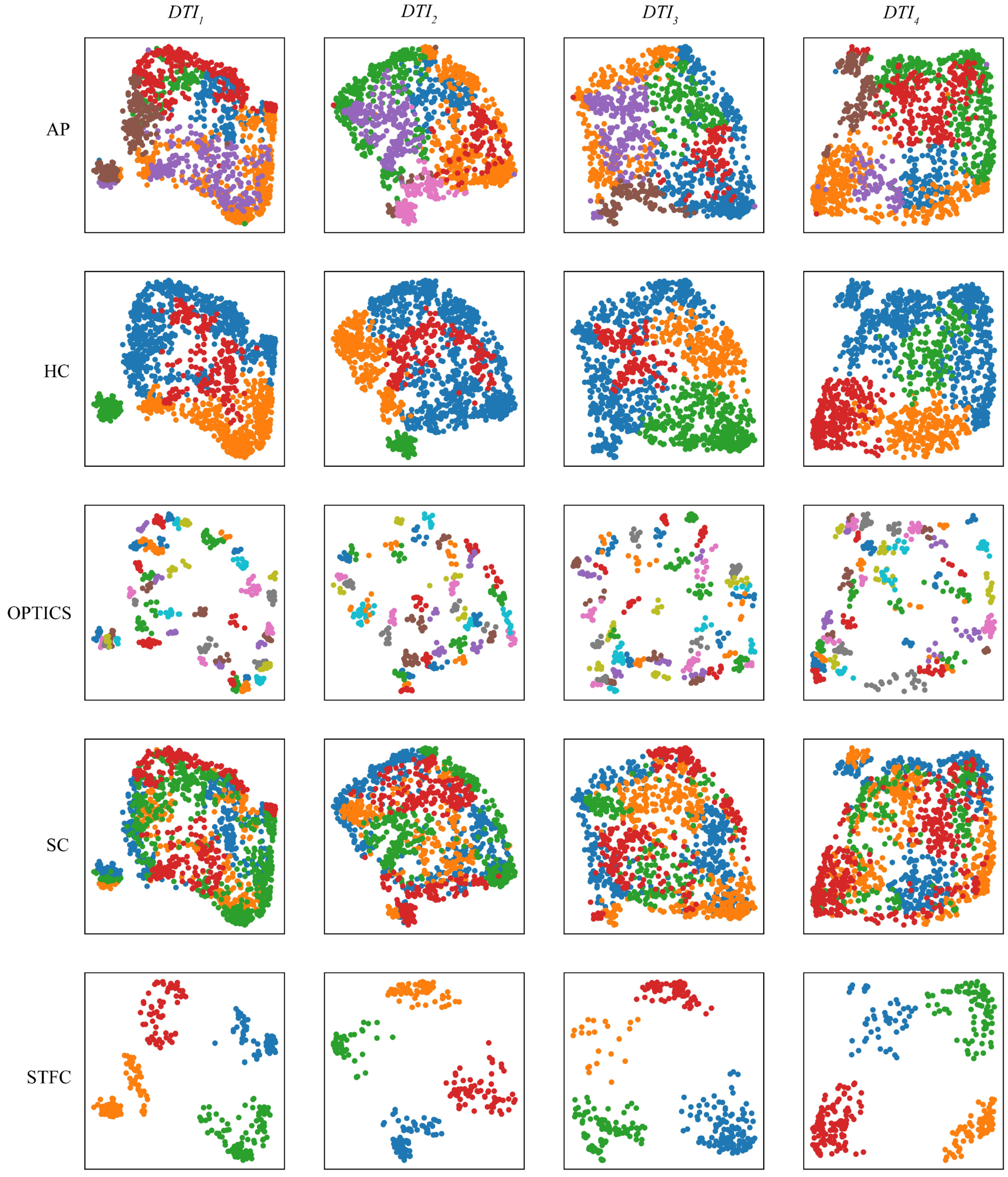
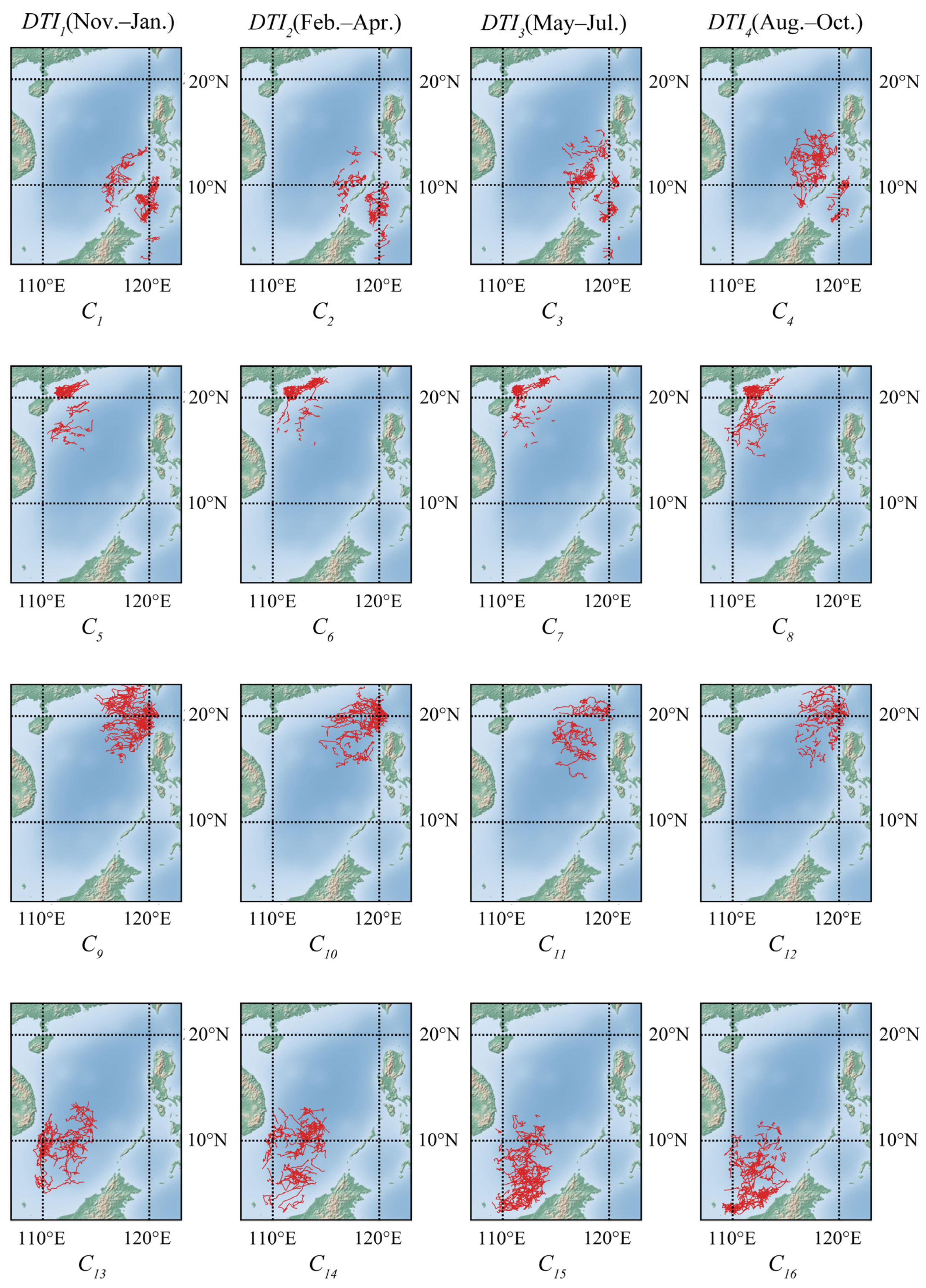
4.4. Experiment in Mesoscale Cyclonic Eddies Trajectory
4.5. Experiment in AIS Vessel Trajectory
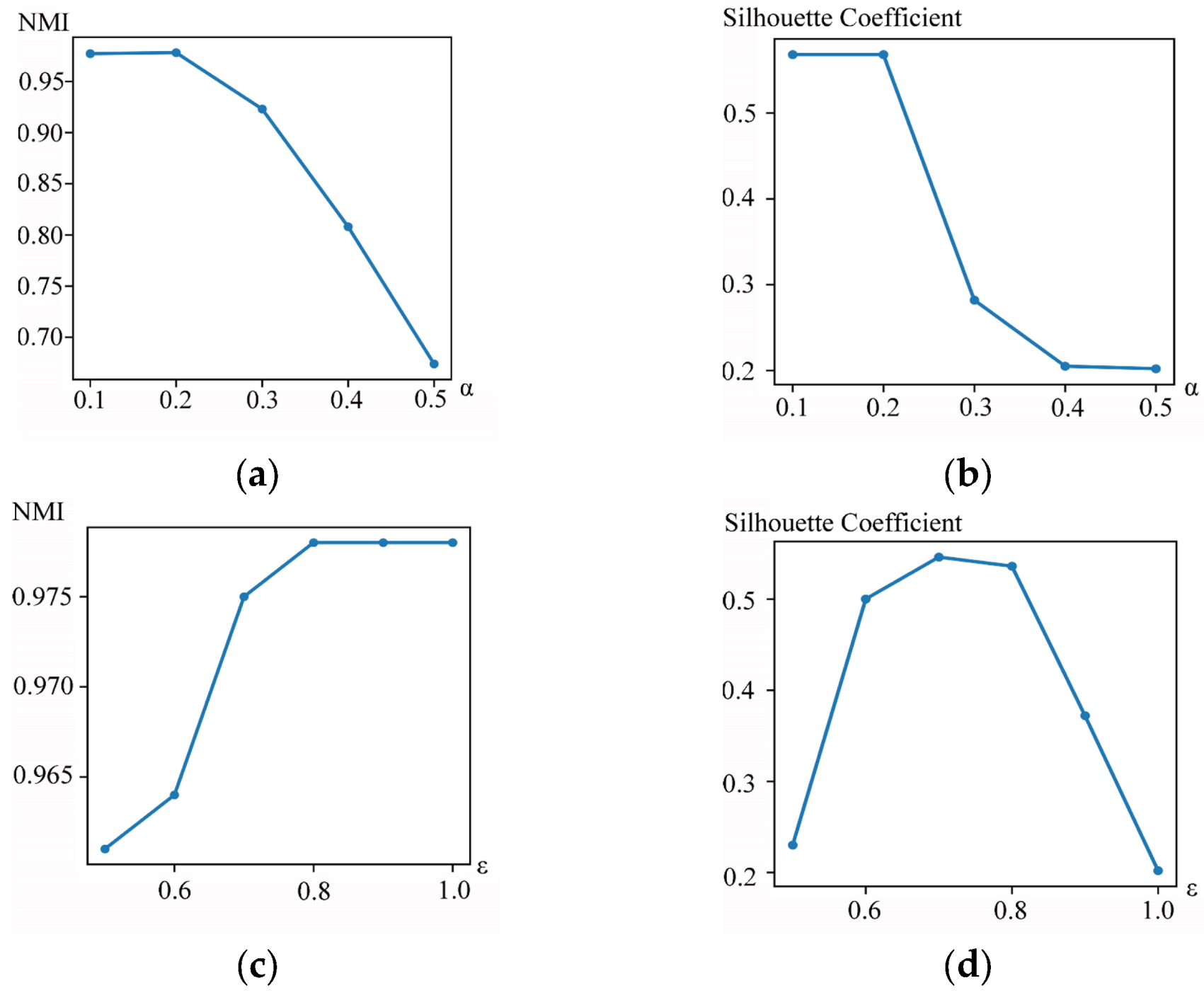
4.6. Parameter Analysis
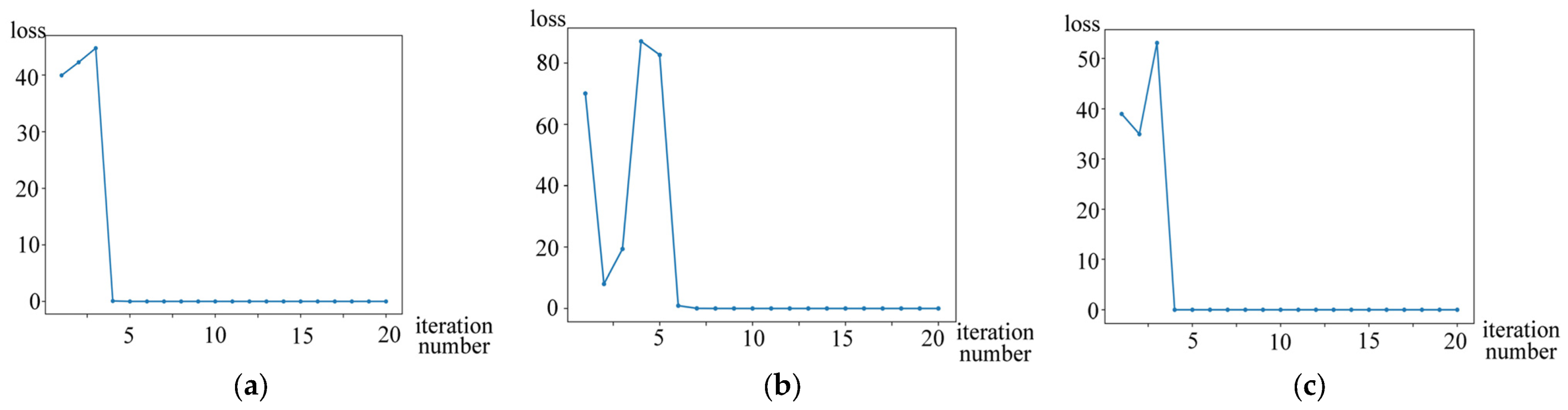
4.7. Convergence Experiments
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cuenca-Jara, J.; Terroso-Saenz, F.; Valdés-Vela, M.; Skarmeta, A.F. Classification of spatio-temporal trajectories from volunteer geographic information through fuzzy rules. Appl. Soft Comput. 2020, 86, 105916. [Google Scholar] [CrossRef]
- Liu, W.; Wang, B.; Yang, Y.; Mou, N.; Zheng, Y.; Zhang, L.; Yang, T. Cluster analysis of microscopic spatio-temporal patterns of tourists’ movement behaviors in mountainous scenic areas using open GPS-trajectory data. Tour. Manag. 2022, 93, 104614. [Google Scholar] [CrossRef]
- Niu, X.; Zhu, J.; Wu, C.Q.; Wang, S. On a clustering-based mining approach for spatially and temporally integrated traffic sub-area division. Eng. Appl. Artif. Intell. 2020, 96, 103932. [Google Scholar] [CrossRef]
- Li, Z.; Yu, W.; Li, T.; Murty, V.S.N.; Tangang, F. Bimodal character of cyclone climatology in the Bay of Bengal modulated by monsoon seasonal cycle. J. Clim. 2013, 26, 1033–1046. [Google Scholar] [CrossRef]
- Ottesen, E.A.; Young, C.R.; Gifford, S.M.; Eppley, J.M.; Marin, R., III; Schuster, S.C.; DeLong, E.F. Multispecies diel transcriptional oscillations in open ocean heterotrophic bacterial assemblages. Science 2014, 345, 207–212. [Google Scholar] [CrossRef] [PubMed]
- Shankar, D.; Vinayachandran, P.N.; Unnikrishnan, A.S. The monsoon currents in the north Indian Ocean. Prog. Oceanogr. 2002, 52, 63–120. [Google Scholar] [CrossRef]
- Liu, Q.; Hou, Z.; Yang, J. Detecting Spatial Communities in Vehicle Movements by Combining Multi-Level Merging and Consensus Clustering. Remote Sens. 2022, 14, 4144. [Google Scholar] [CrossRef]
- Wan, Y.; Fei, Y.; Wu, T.; Jin, R.; Xiao, T. A Novel Impervious Surface Extraction Method Integrating POI, Vehicle Trajectories, and Satellite Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8804–8814. [Google Scholar] [CrossRef]
- Yang, Y.; Cai, J.; Yang, H.; Zhang, J.; Zhao, X. TAD: A trajectory clustering algorithm based on spatial-temporal density analysis. Expert Syst. Appl. 2020, 139, 112846. [Google Scholar] [CrossRef]
- Li, F.; Shi, W.; Zhang, H. A Two-Phase Clustering Approach for Urban Hotspot Detection with Spatiotemporal and Network Constraints. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3695–3705. [Google Scholar] [CrossRef]
- Lee, J.G.; Han, J.; Whang, K.Y. Trajectory clustering: A partition-and-group framework. In Proceedings of the 2007 ACM SIGMOD International Conference on Management of Data, Beijing, China, 11–14 June 2007. [Google Scholar] [CrossRef]
- Tang, C.; Chen, M.; Zhao, J.; Liu, T.; Liu, K.; Yan, H.; Xiao, Y. A novel ship trajectory clustering method for Finding Overall and Local Features of Ship Trajectories. Ocean Eng. 2021, 241, 110108. [Google Scholar] [CrossRef]
- Qiao, D.; Yang, X.; Liang, Y.; Hao, X. Rapid trajectory clustering based on neighbor spatial analysis. Pattern Recognit. Lett. 2022, 156, 167–173. [Google Scholar] [CrossRef]
- Ansari, M.Y.; Ahmad, A.; Bhushan, G. Spatiotemporal trajectory clustering: A clustering algorithm for spatiotemporal data. Expert Syst. Appl. 2021, 178, 115048. [Google Scholar] [CrossRef]
- Bermingham, L.; Lee, I. A general methodology for n-dimensional trajectory clustering. Expert Syst. Appl. 2015, 42, 7573–7581. [Google Scholar] [CrossRef]
- Pan, X.; He, Y.; Wang, H.; Xiong, W.; Peng, X. Mining regular behaviors based on multidimensional trajectories. Expert Syst. Appl. 2016, 66, 106–113. [Google Scholar] [CrossRef]
- Hong, Z.; Chen, Y.; Mahmassani, H.S. Recognizing network trip patterns using a spatio-temporal vehicle trajectory clustering algorithm. IEEE Trans. Intell. Transp. Syst. 2017, 19, 2548–2557. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, D.; Wang, X.; Chen, B.; Ding, C.; Gao, S. Sensing Travel Source–Sink Spatiotemporal Ranges Using Dockless Bicycle Trajectory via Density-Based Adaptive Clustering. Remote Sens. 2023, 15, 3874. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, Y.; Zhang, C. Data mining approach for automatic ship-route design for coastal seas using AIS trajectory clustering analysis. Ocean Eng. 2021, 236, 109535. [Google Scholar] [CrossRef]
- Yang, J.; Liu, Y.; Ma, L.; Ji, C. Maritime traffic flow clustering analysis by density based trajectory clustering with noise. Ocean Eng. 2022, 249, 111001. [Google Scholar] [CrossRef]
- Birant, D.; Kut, A. ST-DBSCAN: An algorithm for clustering spatial–temporal data. Data Knowl. Eng. 2007, 60, 208–221. [Google Scholar] [CrossRef]
- Wang, L.; Chen, P.; Chen, L.; Mou, J. Ship AIS trajectory clustering: An HDBSCAN-based approach. J. Mar. Sci. Eng. 2021, 9, 566. [Google Scholar] [CrossRef]
- Von Luxburg, U. A tutorial on spectral clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The fuzzy c-means clustering algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Deng, C.; Choi, H.C.; Park, H.; Hwang, I. Trajectory pattern identification and classification for real-time air traffic applications in Area Navigation terminal airspace. Transp. Res. Part C Emerg. Technol. 2022, 142, 103765. [Google Scholar] [CrossRef]
- Liu, G.; Fan, Y.; Zhang, J.; Wen, P.; Lyu, Z.; Yuan, X. Deep flight track clustering based on spatial-temporal distance and denoising auto-encoding. Expert Syst. Appl. 2022, 198, 116733. [Google Scholar] [CrossRef]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef] [PubMed]
- Anonymized AIS Training Data, Distributed by Global Fishing Watch, May 2020. Available online: https://globalfishingwatch.org/data-download/datasets/public-training-data-v1 (accessed on 28 January 2024).
- Taylor, J.; Zhou, X.; Rouphail, N.M.; Porter, R.J. Method for investigating intradriver heterogeneity using vehicle trajectory data: A dynamic time warping approach. Transp. Res. Part B Methodol. 2015, 73, 59–80. [Google Scholar] [CrossRef]
- Li, H.; Lam, J.S.L.; Yang, Z.; Liu, J.; Liu, R.W.; Liang, M.; Li, Y. Unsupervised hierarchical methodology of maritime traffic pattern extraction for knowledge discovery. Transp. Res. Part C Emerg. Technol. 2022, 143, 103856. [Google Scholar] [CrossRef]
- Yao, Y. Three-way decisions with probabilistic rough sets. Inf. Sci. 2010, 180, 341–353. [Google Scholar] [CrossRef]
- Piciarelli, C.; Micheloni, C.; Foresti, G.L. Trajectory-based anomalous event detection. IEEE Trans. Circuits Syst. Video Technol. 2008, 18, 1544–1554. [Google Scholar] [CrossRef]
- Mesoscale Eddy Trajectory Atlas META3.2 Delayed-Time All Satellites: Version META3.2 DT Allsat; AVISO: Redwood City, CA, USA, 2022. [CrossRef]
- Strehl, A.; Ghosh, J. Cluster ensembles—A knowledge reuse framework for combining multiple partitions. J. Mach. Learn. Res. 2002, 3, 583–617. [Google Scholar]
- Chacón, J.E.; Rastrojo, A.I. Minimum adjusted Rand index for two clusterings of a given size. Adv. Data Anal. Classif. 2023, 17, 125–133. [Google Scholar] [CrossRef]
- Caliński, T.; Harabasz, J. A dendrite method for cluster analysis. Commun. Stat. Theory Methods 1974, 3, 1–27. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Davies, D.L.; Bouldin, D.W. A cluster separation measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, PAMI-1, 224–227. [Google Scholar] [CrossRef]
- Ankerst, M.; Breunig, M.M.; Kriegel, H.P.; Sander, J. OPTICS: Ordering points to identify the clustering structure. ACM Sigmod Rec. 1999, 28, 49–60. [Google Scholar] [CrossRef]
- Frey, B.J.; Dueck, D. Clustering by passing messages between data points. Science 2007, 315, 972–976. [Google Scholar] [CrossRef]
- Murtagh, F.; Legendre, P. Ward’s hierarchical agglomerative clustering method: Which algorithms implement Ward’s criterion? J. Classif. 2014, 31, 274–295. [Google Scholar] [CrossRef]
- Jiang, Q.; Yu, L.I.U.; Ziran DI, N.G.; Shun SU, N. Behavior pattern mining based on spatiotemporal trajectory multidimensional information fusion. Chin. J. Aeronaut. 2023, 36, 387–399. [Google Scholar] [CrossRef]
- Gulakaram, V.S.; Vissa, N.K.; Bhaskaran, P.K. Role of mesoscale eddies on atmospheric convection during summer monsoon season over the Bay of Bengal: A case study. J. Ocean Eng. Sci. 2018, 3, 343–354. [Google Scholar] [CrossRef]
- Li, H.; Wiesner, M.G.; Chen, J.; Ling, Z.; Zhang, J.; Ran, L. Long-term variation of mesopelagic biogenic flux in the central South China Sea: Impact of monsoonal seasonality and mesoscale eddy. Deep Sea Res. Part I Oceanogr. Res. Pap. 2017, 126, 62–72. [Google Scholar] [CrossRef]
- Du, Y.; Liu, Q.; Wang, L.; Xu, X.; Wei, Q.; Song, W. Multi-scale rotating anchor mechanism based automatic detection of ocean mesoscale eddy. J. Image Graph. 2022, 27, 3092–3101. [Google Scholar]
- Islam, M.M.; Sado, K. Time series analysis of SST for Java Sea and South China Sea using NOAA AVHRR data. In Proceedings of the 34th Conference of Remote Sensing Society of Japan, Tokyo, Japan, 1 November 2003. [Google Scholar]
- Tang, H.; Micheels, A.; Eronen, J.; Fortelius, M. Regional climate model experiments to investigate the Asian monsoon in the Late Miocene. Clim. Past 2011, 7, 847–868. [Google Scholar] [CrossRef]
- Van Der Maaten, L. Accelerating t-SNE using tree-based algorithms. J. Mach. Learn. Res. 2014, 15, 3221–3245. [Google Scholar]
- Pearson, K.V.I.I. Note on regression and inheritance in the case of two parents. Proc. R. Soc. Lond. 1895, 58, 240–242. [Google Scholar] [CrossRef]




| Symbol | Definition |
|---|---|
| The number of clusters utilized in the analysis, where denotes the number of clusters with respect to . | |
| The number of trajectories. | |
| The unit density at each time point on the time axis, where denotes the number of trajectories present at that specific time point . | |
| The temporal membership grade, where denotes the temporal membership grade of the with respect to . | |
| The cluster membership grade matrix, where denotes the membership grade of with respect to . | |
| The three-way membership grade matrix, where denotes the three-way membership grade of with respect to . | |
| The cluster center coordinates of . | |
| The coordinate of the point that maps to the lower-dimensional spectral space, i.e., the ith row vector of the eigenvectors corresponds to the smallest k eigenvalues resulting from the decomposition of the symmetric matrix L. |
| Class 1 | Class 2 | Class 3 | Class 4 | Class 5 | Noise | |||
|---|---|---|---|---|---|---|---|---|
| Label | 0 | 1 | 2 | 3 | 4 | 5 | 6 | −1 |
| Trajectory number | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 10 |
| Trajectory length | 15 | 15 | 20 | 10 | 20 | 30 | 25 | random |
| Average angle (°) | 60.30 | 213.00 | 129.46 | 126.45 | 93.38 | 176.69 | 77.60 | random |
| Average velocity | 0.124 | 0.124 | 0.095 | 0.175 | 0.077 | 0.056 | 0.065 | random |
| Scope of the time axis | 0–24 | 0–24 | 25–49 | 25–49 | 50–99 | 50–99 | 50–99 | random |
| NMI↑ 1 | ARI↑ | Silhouette Coefficient↑ | DBI↓ 2 | CHI↑ | |
|---|---|---|---|---|---|
| DTID-STFC | 0.978 | 0.985 | 0.798 | 0.423 | 635.920 |
| STFC | 0.926 | 0.905 | 0.627 | 0.769 | 383.367 |
| DTID-SFC | 0.957 | 0.959 | 0.623 | 0.591 | 436.107 |
| DTID-OPTICS | 0.944 | 0.933 | 0.601 | 0.594 | 389.058 |
| DTID-SC | 0.953 | 0.959 | 0.592 | 0.607 | 374.632 |
| DTID-AP | 0.893 | 0.824 | 0.414 | 1.175 | 190.523 |
| DTID-HC | 0.868 | 0.714 | 0.245 | 1.364 | 183.691 |
| NMI↑ 1 | ARI↑ | Silhouette Coefficient↑ | DBI↓ 2 | CHI↑ | Run Time (s) | |
|---|---|---|---|---|---|---|
| DTID-STFC | 0.978 | 0.985 | 0.798 | 0.423 | 635.920 | 126.400 |
| ST-DBSCAN | 0.496 | 0.258 | 0.023 | 1086.442 | 0.256 | 130.763 |
| MTCA | 0.883 | 0.816 | 0.501 | 0.904 | 240.946 | 961.127 |
| MIF-STKNNDC | 0.786 | 0.692 | 0.328 | 2.638 | 532.291 | 421.146 |
| ISCM | 0.897 | 0.767 | −0.238 | 619.892 | 0.201 | 136.923 |
| HDBSCAN-extended | 0.904 | 0.885 | 0.613 | 1.603 | 600.500 | 751.743 |
| Average Pearson Correlation | Time and Longitude | Time and Latitude | Longitude and Latitude | Average Pearson Correlation | Time and Longitude | Time and Latitude | Longitude and Latitude |
|---|---|---|---|---|---|---|---|
| −0.369 | −0.177 | 0.170 | −0.736 | 0.181 | −0.167 | ||
| −0.353 | −0.106 | 0.110 | −0.699 | 0.07 | −0.023 | ||
| −0.386 | −0.024 | −0.070 | −0.685 | 0.225 | −0.214 | ||
| −0.419 | 0.177 | 0.038 | −0.564 | 0.107 | −0.03 | ||
| −0.649 | −0.310 | 0.311 | −0.500 | 0.016 | 0.063 | ||
| −0.489 | −0.137 | 0.303 | −0.581 | 0.037 | 0.103 | ||
| −0.441 | −0.173 | 0.274 | −0.489 | −0.121 | 0.11 | ||
| −0.447 | −0.163 | 0.139 | −0.411 | −0.108 | 0.114 |
| Average Pearson Correlation | Time and Longitude | Time and Latitude | Longitude and Latitude | Average Pearson Correlation | Time and Longitude | Time and Latitude | Longitude and Latitude |
|---|---|---|---|---|---|---|---|
| 0.008 | −0.006 | 0.328 | −0.650 | −0.646 | 0.998 | ||
| 0.190 | 0.216 | −0.119 | −0.040 | 0.011 | 0.390 | ||
| 0.126 | −0.221 | −0.617 | −0.083 | −0.169 | −0.452 | ||
| 0.120 | −0.126 | 0.362 | −0.027 | −0.042 | −0.238 | ||
| 0.102 | 0.072 | 0.505 | −0.024 | −0.105 | 0.356 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, Y.; Chen, K.; Yi, G.; Yu, W.; Xian, Z.; Song, W. A New Trajectory Clustering Method for Mining Multiple Periodic Patterns from Complex Oceanic Trajectories. Remote Sens. 2024, 16, 1944. https://doi.org/10.3390/rs16111944
Du Y, Chen K, Yi G, Yu W, Xian Z, Song W. A New Trajectory Clustering Method for Mining Multiple Periodic Patterns from Complex Oceanic Trajectories. Remote Sensing. 2024; 16(11):1944. https://doi.org/10.3390/rs16111944
Chicago/Turabian StyleDu, Yanling, Keqi Chen, Guojie Yi, Wei Yu, Ziye Xian, and Wei Song. 2024. "A New Trajectory Clustering Method for Mining Multiple Periodic Patterns from Complex Oceanic Trajectories" Remote Sensing 16, no. 11: 1944. https://doi.org/10.3390/rs16111944
APA StyleDu, Y., Chen, K., Yi, G., Yu, W., Xian, Z., & Song, W. (2024). A New Trajectory Clustering Method for Mining Multiple Periodic Patterns from Complex Oceanic Trajectories. Remote Sensing, 16(11), 1944. https://doi.org/10.3390/rs16111944






