Modified ESRGAN with Uformer for Video Satellite Imagery Super-Resolution
Abstract
1. Introduction
- A lack of improvement in interpretational capabilities.
- The occurrence of spectral distortions.
- Color distortions.
- For pansharpening-based methods, it is necessary to have an identical high-resolution panchromatic image.
- The occurrence of artifacts in the case of video data where objects move quickly and the temporal resolution of the data is low.
- Correctness of operation only for specific types of data.
- A large number of images (frames), which increases the computational demands on processing units or prolongs the time required for data processing.
- Maintaining the estimation style of images for all images belonging to the sequence.
- The occurrence of noise and disturbances resulting from imperfect optical systems.
- Low temporal resolution due to limited computational power of the computers on board nanosatellites.
- An individual approach to each video frame enables the processing of video data of any temporal resolution;
- The frames are divided into smaller fragments (tiles), which allows the improvement of the spatial resolution of video data of unlimited dimensions;
- The use of a 10% overlap between tiles enables the achievement of the maximum quality of SR images while, at the same time, minimizing the amount of time required to improve the resolution of the video data (a higher overlap leads to a larger number of images to be processed);
- It is recommended to train the network using databases that consist of images of various spatial resolutions, as this allows for the model training to be made even more resistant to the vanishing gradients phenomenon (the probability of its occurrence for satellite data is much higher than in the case of images obtained from the surface of the Earth);
- Developing the GAN network model by layers of the Uformer model (the encoder–decoder network) allows for a significant improvement of the quality of the estimated SR images;
- The application of time windows to connect the tiles estimated by the GAN network generator enables the combination of them into one video data frame;
- The global quality assessment does not reflect the actual quality of the estimated SR images, but the application of the local assessment and image evaluation in the frequency domain enables a better assessment of SR images.
2. Related Works
3. Methodology
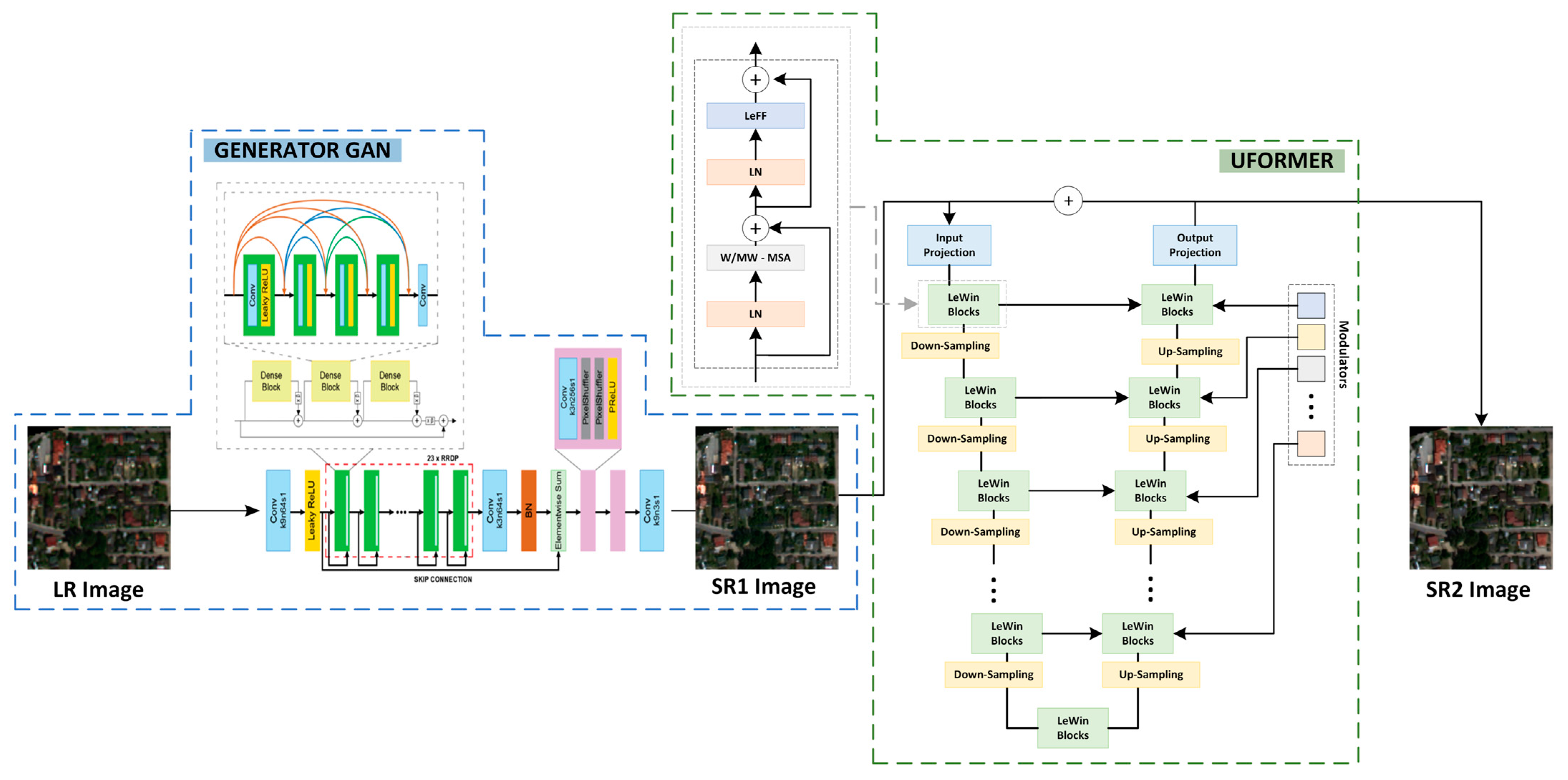
3.1. Proposed Methodology
3.1.1. MCWESRGAN
3.1.2. Uformer
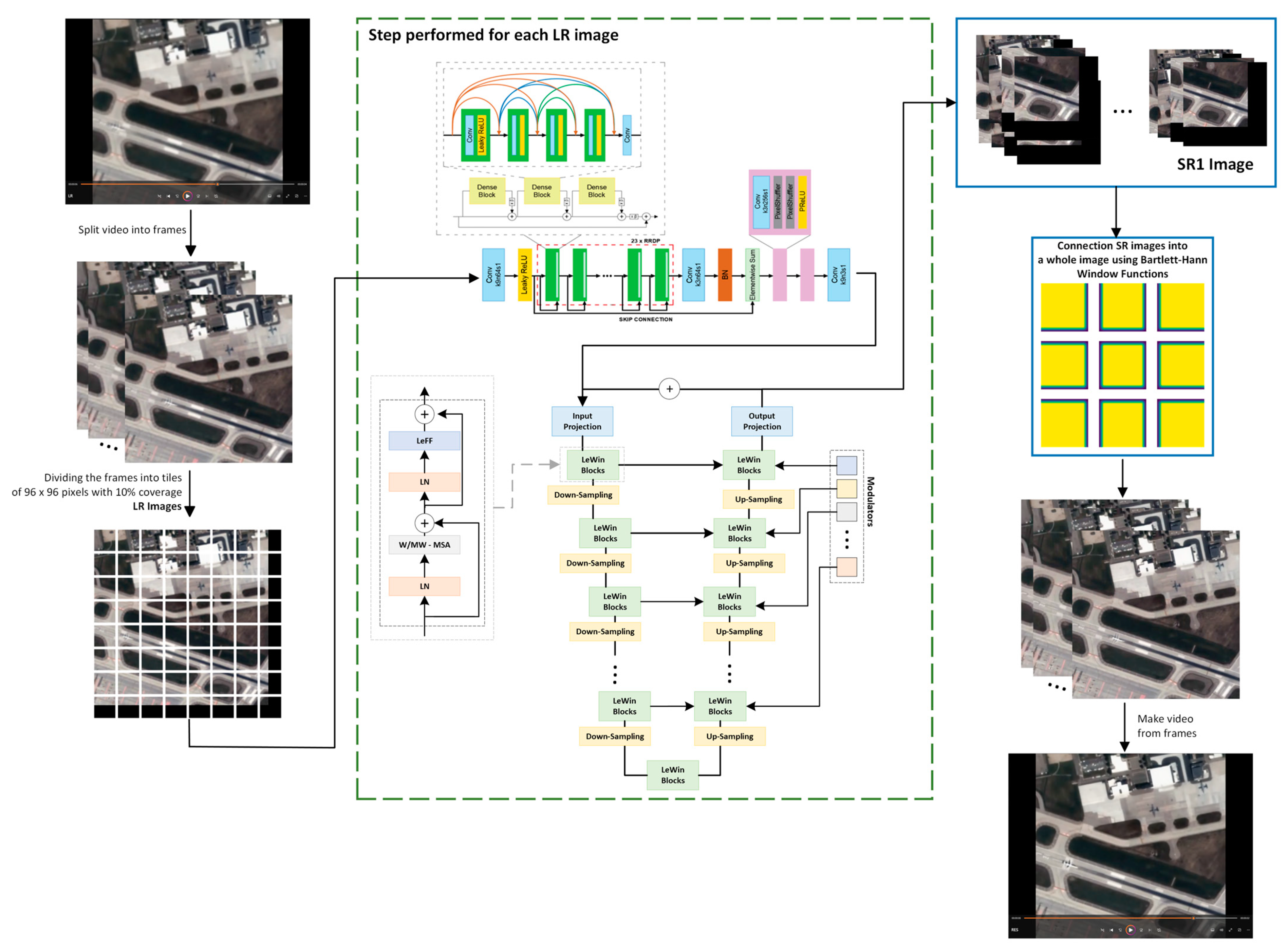
3.1.3. Bartlett–Hann Window Function
3.2. Evaluation Metrics
4. Experiments and Results
4.1. Datasets
- Beirut in Liban—collected on 06 October 2017, the resolution: 1.12 m, the frame size: 1920 × 1080 pixels, 25 frames per second (FPS), and video duration: 32 s.
- Florence in Italy—collected on 10th September 2018, the resolution: 0.9 m, frame size: 3840 × 2160 pixels, 10 FPS, and video duration: 31 s.
- Other materials added to the database were the video sequences collected by SkySat-1 from Las Vegas (25 March 2014), Burj Khalifa (9 April 2014), and Burj al-Arab (1 February 2019) [72].
4.2. Methodology of Processing Video Data
4.3. Implementation
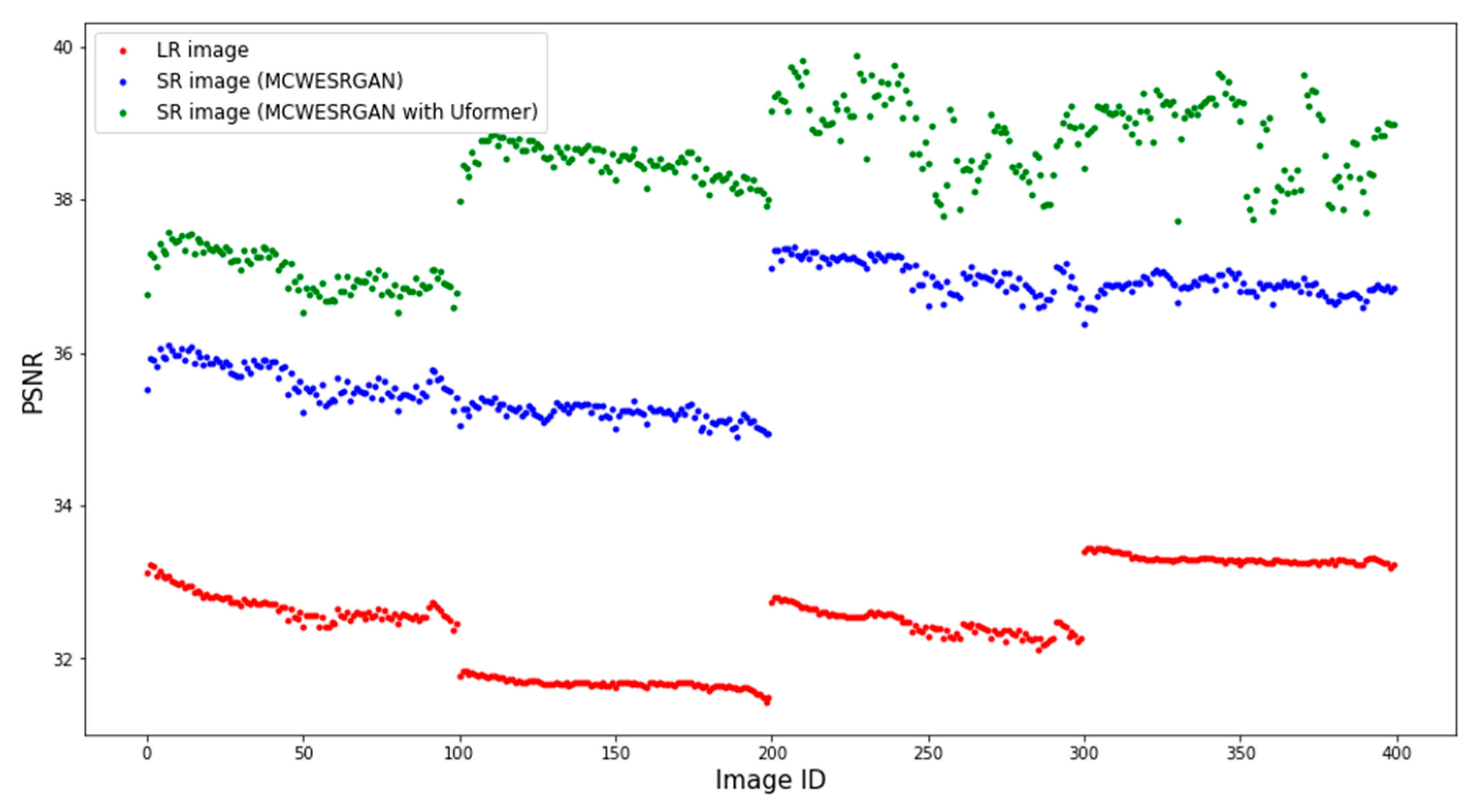
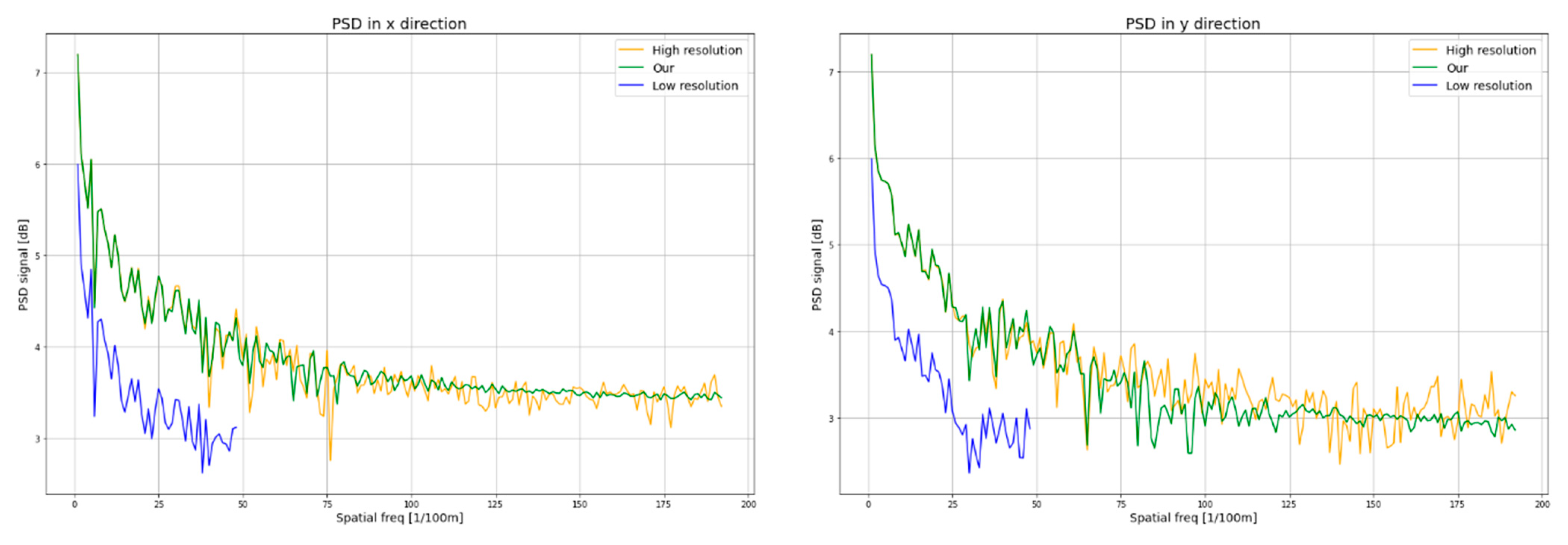
4.4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Image 1 | Image 2 | Image 3 | Image 4 | Image 5 | |
| LR |  |  |  |  |  |
| EDSR |  |  |  |  |  |
| EDSR * |  |  |  |  |  |
| ESPCN |  |  |  |  |  |
| ESPCN * |  |  |  |  |  |
| FSRCNN |  |  |  |  |  |
| FSRCNN * |  |  |  |  |  |
| RDN |  |  |  |  |  |
| RDN * |  |  |  |  |  |
| SRCNN |  |  |  |  |  |
| SRCNN * |  |  |  |  |  |
| SRDenseNet |  |  |  |  |  |
| SRDenseNet * |  |  |  |  |  |
| SRGAN |  |  |  |  |  |
| SRGAN * |  |  |  |  |  |
| ESRGAN |  |  |  |  |  |
| ESRGAN * |  |  |  |  |  |
| MCWESRGAN |  |  |  |  |  |
| MCWESRGAN * |  |  |  |  |  |
| Ground truth |  |  |  |  |  |
Appendix B
| Image 1 | ||||||||||||||||||
| Metric | EDSR | EDSR * | ESPCN | ESPCN * | FSRCNN | FSRCNN * | RDN | RDN * | SRCNN | SRCNN * | SRDenseNet | SRDenseNet * | SRGAN | SRGAN * | ESRGAN | ESRGAN * | MCWESRGAN | MCWESRGAN * |
| SSIM | 0.84 | 0.88 | 0.92 | 0.94 | 0.92 | 0.93 | 0.94 | 0.94 | 0.89 | 0.92 | 0.94 | 0.94 | 0.74 | 0.83 | 0.84 | 0.87 | 0.94 | 0.96 |
| PSNR | 26.36 | 27.2 | 31.26 | 27.16 | 30.88 | 32.37 | 32.99 | 32.79 | 29.0 | 30.65 | 32.88 | 32.64 | 22.56 | 24.57 | 26.96 | 28.15 | 33.02 | 34.08 |
| SAM | 0.09 | 0.08 | 0.05 | 0.08 | 0.05 | 0.04 | 0.04 | 0.04 | 0.06 | 0.05 | 0.04 | 0.04 | 0.13 | 0.11 | 0.08 | 0.07 | 0.04 | 0.03 |
| SCC | 0.34 | 0.43 | 0.42 | 0.25 | 0.32 | 0.41 | 0.44 | 0.43 | 0.32 | 0.43 | 0.40 | 0.42 | 0.11 | 0.28 | 0.26 | 0.38 | 0.45 | 0.46 |
| UQI | 0.99 | 0.99 | 1.0 | 0.97 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.98 | 0.99 | 0.99 | 1.00 | 1.00 | 1.00 |
| Image 2 | ||||||||||||||||||
| SSIM | 0.85 | 0.89 | 0.93 | 0.94 | 0.93 | 0.94 | 0.95 | 0.94 | 0.91 | 0.93 | 0.94 | 0.94 | 0.78 | 0.86 | 0.86 | 0.88 | 0.95 | 0.96 |
| PSNR | 25.26 | 25.77 | 29.78 | 30.01 | 29.93 | 31.08 | 31.34 | 31.41 | 27.85 | 29.15 | 30.91 | 31.12 | 22.8 | 24.57 | 26.02 | 27.36 | 31.68 | 32.46 |
| SAM | 0.10 | 0.09 | 0.06 | 0.06 | 0.06 | 0.05 | 0.05 | 0.05 | 0.07 | 0.06 | 0.05 | 0.05 | 0.13 | 0.10 | 0.09 | 0.07 | 0.05 | 0.04 |
| SCC | 0.25 | 0.31 | 0.30 | 0.31 | 0.22 | 0.29 | 0.30 | 0.30 | 0.23 | 0.29 | 0.27 | 0.29 | 0.09 | 0.21 | 0.19 | 0.25 | 0.31 | 0.32 |
| UQI | 0.99 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.98 | 0.99 | 0.99 | 0.99 | 1.00 | 1.00 |
| Image 3 | ||||||||||||||||||
| SSIM | 0.93 | 0.95 | 0.98 | 0.97 | 0.97 | 0.97 | 0.97 | 0.97 | 0.96 | 0.97 | 0.98 | 0.97 | 0.85 | 0.92 | 0.92 | 0.94 | 0.98 | 0.98 |
| PSNR | 32.26 | 33.9 | 38.35 | 37.57 | 35.93 | 37.2 | 37.01 | 37.01 | 34.34 | 36.37 | 38.35 | 37.36 | 23.86 | 25.4 | 30.88 | 31.79 | 37.67 | 37.41 |
| SAM | 0.06 | 0.05 | 0.03 | 0.03 | 0.04 | 0.04 | 0.04 | 0.04 | 0.05 | 0.04 | 0.03 | 0.03 | 0.15 | 0.12 | 0.07 | 0.07 | 0.03 | 0.03 |
| SCC | 0.17 | 0.22 | 0.20 | 0.20 | 0.13 | 0.19 | 0.18 | 0.18 | 0.14 | 0.21 | 0.17 | 0.19 | 0.05 | 0.16 | 0.11 | 0.16 | 0.19 | 0.20 |
| UQI | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.97 | 0.97 | 0.99 | 0.99 | 1.00 | 1.00 |
| Image 4 | ||||||||||||||||||
| SSIM | 0.92 | 0.95 | 0.98 | 0.98 | 0.96 | 0.97 | 0.97 | 0.98 | 0.96 | 0.97 | 0.98 | 0.98 | 0.87 | 0.93 | 0.91 | 0.94 | 0.98 | 0.98 |
| PSNR | 31.68 | 33.13 | 38.58 | 39.62 | 35.79 | 38.58 | 38.02 | 39.46 | 34.31 | 37.77 | 39.41 | 39.44 | 26.54 | 28.98 | 32.0 | 34.52 | 39.29 | 40.17 |
| SAM | 0.06 | 0.05 | 0.02 | 0.02 | 0.03 | 0.02 | 0.03 | 0.02 | 0.04 | 0.03 | 0.02 | 0.02 | 0.1 | 0.07 | 0.05 | 0.04 | 0.02 | 0.02 |
| SCC | 0.22 | 0.31 | 0.28 | 0.28 | 0.18 | 0.26 | 0.28 | 0.29 | 0.22 | 0.29 | 0.26 | 0.28 | 0.09 | 0.23 | 0.14 | 0.24 | 0.30 | 0.30 |
| UQI | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 |
| Image 5 | ||||||||||||||||||
| SSIM | 0.89 | 0.92 | 0.95 | 0.95 | 0.95 | 0.96 | 0.96 | 0.96 | 0.93 | 0.95 | 0.96 | 0.96 | 0.82 | 0.89 | 0.88 | 0.90 | 0.96 | 0.98 |
| PSNR | 28.99 | 29.89 | 34.23 | 34.59 | 33.62 | 35.14 | 35.65 | 35.46 | 31.87 | 33.25 | 35.67 | 35.25 | 24.77 | 26.96 | 29.73 | 30.89 | 35.87 | 36.94 |
| SAM | 0.09 | 0.08 | 0.05 | 0.05 | 0.05 | 0.04 | 0.04 | 0.04 | 0.06 | 0.05 | 0.04 | 0.04 | 0.14 | 0.11 | 0.08 | 0.07 | 0.04 | 0.03 |
| SCC | 0.26 | 0.34 | 0.31 | 0.33 | 0.25 | 0.32 | 0.34 | 0.33 | 0.26 | 0.33 | 0.31 | 0.32 | 0.09 | 0.24 | 0.18 | 0.28 | 0.34 | 0.36 |
| UQI | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 |
References
- Rujoiu-Mare, M.-R.; Mihai, B.-A. Mapping Land Cover Using Remote Sensing Data and GIS Techniques: A Case Study of Prahova Subcarpathians. Procedia Environ. Sci. 2016, 32, 244–255. [Google Scholar] [CrossRef]
- Hejmanowska, B.; Kramarczyk, P.; Głowienka, E.; Mikrut, S. Reliable Crops Classification Using Limited Number of Sentinel-2 and Sentinel-1 Images. Remote Sens. 2021, 13, 3176. [Google Scholar] [CrossRef]
- Han, P.; Huang, J.; Li, R.; Wang, L.; Hu, Y.; Wang, J.; Huang, W. Monitoring Trends in Light Pollution in China Based on Nighttime Satellite Imagery. Remote Sens. 2014, 6, 5541–5558. [Google Scholar] [CrossRef]
- Hall, O.; Hay, G.J. A Multiscale Object-Specific Approach to Digital Change Detection. Int. J. Appl. Earth Obs. Geoinf. 2003, 4, 311–327. [Google Scholar] [CrossRef]
- Nasiri, V.; Hawryło, P.; Janiec, P.; Socha, J. Comparing Object-Based and Pixel-Based Machine Learning Models for Tree-Cutting Detection with PlanetScope Satellite Images: Exploring Model Generalization. Int. J. Appl. Earth Obs. Geoinf. 2023, 125, 103555. [Google Scholar] [CrossRef]
- Li, W.; Zhou, J.; Li, X.; Cao, Y.; Jin, G. Few-Shot Object Detection on Aerial Imagery via Deep Metric Learning and Knowledge Inheritance. Int. J. Appl. Earth Obs. Geoinf. 2023, 122, 103s397. [Google Scholar] [CrossRef]
- Stateczny, A.; Kazimierski, W.; Gronska-Sledz, D.; Motyl, W. The Empirical Application of Automotive 3D Radar Sensor for Target Detection for an Autonomous Surface Vehicle’s Navigation. Remote Sens. 2019, 11, 1156. [Google Scholar] [CrossRef]
- de Moura, N.V.A.; de Carvalho, O.L.F.; Gomes, R.A.T.; Guimarães, R.F.; de Carvalho Júnior, O.A. Deep-Water Oil-Spill Monitoring and Recurrence Analysis in the Brazilian Territory Using Sentinel-1 Time Series and Deep Learning. Int. J. Appl. Earth Obs. Geoinf. 2022, 107, 102695. [Google Scholar] [CrossRef]
- Greidanus, H. Satellite Imaging for Maritime Surveillance of the European Seas. In Remote Sensing of the European Seas; Barale, V., Gade, M., Eds.; Springer: Dordrecht, The Netherlands, 2008; pp. 343–358. ISBN 978-1-4020-6772-3. [Google Scholar]
- Gavankar, N.L.; Ghosh, S.K. Automatic Building Footprint Extraction from High-Resolution Satellite Image Using Mathematical Morphology. Eur. J. Remote Sens. 2018, 51, 182–193. [Google Scholar] [CrossRef]
- Reda, K.; Kedzierski, M. Detection, Classification and Boundary Regularization of Buildings in Satellite Imagery Using Faster Edge Region Convolutional Neural Networks. Remote Sens. 2020, 12, 2240. [Google Scholar] [CrossRef]
- d’Angelo, P.; Máttyus, G.; Reinartz, P. Skybox Image and Video Product Evaluation. Int. J. Image Data Fusion 2016, 7, 3–18. [Google Scholar] [CrossRef]
- Yang, T.; Wang, X.; Yao, B.; Li, J.; Zhang, Y.; He, Z.; Duan, W. Small Moving Vehicle Detection in a Satellite Video of an Urban Area. Sensors 2016, 16, 1528. [Google Scholar] [CrossRef] [PubMed]
- Kawulok, M.; Tarasiewicz, T.; Nalepa, J.; Tyrna, D.; Kostrzewa, D. Deep Learning for Multiple-Image Super-Resolution of Sentinel-2 Data. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 3885–3888. [Google Scholar]
- Dong, H.; Supratak, A.; Mai, L.; Liu, F.; Oehmichen, A.; Yu, S.; Guo, Y. TensorLayer: A Versatile Library for Efficient Deep Learning Development. In Proceedings of the 25th ACM International Conference on Multimedia, Mountain View, CA, USA, 23–27 October 2017; pp. 1201–1204. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. arXiv 2014, arXiv:1406.2661. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate Image Super-Resolution Using Very Deep Convolutional Networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Fu, J.; Liu, Y.; Li, F. Single Frame Super Resolution with Convolutional Neural Network for Remote Sensing Imagery. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8014–8017. [Google Scholar]
- Lanaras, C.; Bioucas-Dias, J.; Galliani, S.; Baltsavias, E.; Schindler, K. Super-Resolution of Sentinel-2 Images: Learning a Globally Applicable Deep Neural Network. ISPRS J. Photogramm. Remote Sens. 2018, 146, 305–319. [Google Scholar] [CrossRef]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced Deep Residual Networks for Single Image Super-Resolution. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 1132–1140. [Google Scholar]
- Pouliot, D.; Latifovic, R.; Pasher, J.; Duffe, J. Landsat Super-Resolution Enhancement Using Convolution Neural Networks and Sentinel-2 for Training. Remote Sens. 2018, 10, 394. [Google Scholar] [CrossRef]
- Xiao, A.; Wang, Z.; Wang, L.; Ren, Y. Super-Resolution for “Jilin-1” Satellite Video Imagery via a Convolutional Network. Sensors 2018, 18, 1194. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Fevig, R.; Schultz, R.R. Super-Resolution Mosaicking of UAV Surveillance Video. In Proceedings of the 2008 15th IEEE International Conference on Image Processing, San Diego, CA, USA, 12–15 October 2008; pp. 345–348. [Google Scholar]
- Demirel, H.; Anbarjafari, G. IMAGE Resolution Enhancement by Using Discrete and Stationary Wavelet Decomposition. IEEE Trans. Image Process. 2011, 20, 1458–1460. [Google Scholar] [CrossRef] [PubMed]
- Dong, W.; Zhang, L.; Shi, G.; Wu, X. Nonlocal Back-Projection for Adaptive Image Enlargement. In Proceedings of the 2009 16th IEEE International Conference on Image Processing (ICIP), Cairo, Egypt, 7–10 November 2009; pp. 349–352. [Google Scholar]
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the Super-Resolution Convolutional Neural Network. In Computer Vision—ECCV 2016; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 391–407. [Google Scholar]
- Haris, M.; Shakhnarovich, G.; Ukita, N. Deep Back-Projection Networks for Super-Resolution. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1664–1673. [Google Scholar]
- Xiao, Y.; Yuan, Q.; He, J.; Zhang, Q.; Sun, J.; Su, X.; Wu, J.; Zhang, L. Space-Time Super-Resolution for Satellite Video: A Joint Framework Based on Multi-Scale Spatial-Temporal Transformer. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102731. [Google Scholar] [CrossRef]
- Choi, Y.-J.; Kim, B.-G. HiRN: Hierarchical Recurrent Neural Network for Video Super-Resolution (VSR) Using Two-Stage Feature Evolution. Appl. Soft Comput. 2023, 143, 110422. [Google Scholar] [CrossRef]
- Wang, P.; Sertel, E. Multi-Frame Super-Resolution of Remote Sensing Images Using Attention-Based GAN Models. Knowl. Based Syst. 2023, 266, 110387. [Google Scholar] [CrossRef]
- Jin, X.; He, J.; Xiao, Y.; Yuan, Q. Learning a Local-Global Alignment Network for Satellite Video Super-Resolution. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Liu, H.; Gu, Y.; Wang, T.; Li, S. Satellite Video Super-Resolution Based on Adaptively Spatiotemporal Neighbors and Nonlocal Similarity Regularization. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8372–8383. [Google Scholar] [CrossRef]
- He, Z.; Li, X.; Qu, R. Video Satellite Imagery Super-Resolution via Model-Based Deep Neural Networks. Remote Sens. 2022, 14, 749. [Google Scholar] [CrossRef]
- Li, S.; Sun, X.; Gu, Y.; Lv, Y.; Zhao, M.; Zhou, Z.; Guo, W.; Sun, Y.; Wang, H.; Yang, J. Recent Advances in Intelligent Processing of Satellite Video: Challenges, Methods, and Applications. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 6776–6798. [Google Scholar] [CrossRef]
- Yin, Q.; Hu, Q.; Liu, H.; Zhang, F.; Wang, Y.; Lin, Z.; An, W.; Guo, Y. Detecting and Tracking Small and Dense Moving Objects in Satellite Videos: A Benchmark. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–18. [Google Scholar] [CrossRef]
- Zhao, M.; Li, S.; Xuan, S.; Kou, L.; Gong, S.; Zhou, Z. SatSOT: A Benchmark Dataset for Satellite Video Single Object Tracking. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–11. [Google Scholar] [CrossRef]
- He, Q.; Sun, X.; Yan, Z.; Li, B.; Fu, K. Multi-Object Tracking in Satellite Videos With Graph-Based Multitask Modeling. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Xiao, Y.; Su, X.; Yuan, Q.; Liu, D.; Shen, H.; Zhang, L. Satellite Video Super-Resolution via Multiscale Deformable Convolution Alignment and Temporal Grouping Projection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–19. [Google Scholar] [CrossRef]
- Wang, X.; Sun, L.; Chehri, A.; Song, Y. A Review of GAN-Based Super-Resolution Reconstruction for Optical Remote Sensing Images. Remote Sens. 2023, 15, 5062. [Google Scholar] [CrossRef]
- Karwowska, K.; Wierzbicki, D. Using Super-Resolution Algorithms for Small Satellite Imagery: A Systematic Review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 3292–3312. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Y.; Zhang, H.; Fang, L. A Total Variation Model Based on Edge Adaptive Guiding Function for Remote Sensing Image De-Noising. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 89–95. [Google Scholar] [CrossRef]
- Irum, I.; Sharif, M.; Raza, M.; Mohsin, S. A Nonlinear Hybrid Filter for Salt & Pepper Noise Removal from Color Images. J. Appl. Res. Technology. JART 2015, 13, 79–85. [Google Scholar] [CrossRef]
- Wang, B.; Ma, Y.; Zhang, J.; Zhang, H.; Zhu, H.; Leng, Z.; Zhang, X.; Cui, A. A Noise Removal Algorithm Based on Adaptive Elevation Difference Thresholding for ICESat-2 Photon-Counting Data. Int. J. Appl. Earth Obs. Geoinf. 2023, 117, 103207. [Google Scholar] [CrossRef]
- Yang, H.; Su, X.; Wu, J.; Chen, S. Non-Blind Image Blur Removal Method Based on a Bayesian Hierarchical Model with Hyperparameter Priors. Optik 2020, 204, 164178. [Google Scholar] [CrossRef]
- Wang, Z.; Cun, X.; Bao, J.; Zhou, W.; Liu, J.; Li, H. Uformer: A General U-Shaped Transformer for Image Restoration. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 17662–17672. [Google Scholar]
- Shen, Z.; Wang, W.; Lu, X.; Shen, J.; Ling, H.; Xu, T.; Shao, L. Human-Aware Motion Deblurring. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 5571–5580. [Google Scholar]
- Rim, J.; Lee, H.; Won, J.; Cho, S. Real-World Blur Dataset for Learning and Benchmarking Deblurring Algorithms. In Computer Vision—ECCV 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.-M., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 184–201. [Google Scholar]
- Nah, S.; Kim, T.H.; Lee, K.M. Deep Multi-Scale Convolutional Neural Network for Dynamic Scene Deblurring. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 257–265. [Google Scholar]
- Kupyn, O.; Budzan, V.; Mykhailych, M.; Mishkin, D.; Matas, J. DeblurGAN: Blind Motion Deblurring Using Conditional Adversarial Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8183–8192. [Google Scholar]
- Xu, L.; Zheng, S.; Jia, J. Unnatural L0 Sparse Representation for Natural Image Deblurring. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 1107–1114. [Google Scholar]
- Kupyn, O.; Martyniuk, T.; Wu, J.; Wang, Z. DeblurGAN-v2: Deblurring (Orders-of-Magnitude) Faster and Better. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27–28 October 2019; pp. 8877–8886. [Google Scholar]
- Zhang, K.; Luo, W.; Zhong, Y.; Ma, L.; Stenger, B.; Liu, W.; Li, H. Deblurring by Realistic Blurring. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 2734–2743. [Google Scholar]
- Purohit, K.; Suin, M.; Rajagopalan, A.N.; Boddeti, V.N. Spatially-Adaptive Image Restoration Using Distortion-Guided Networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 2309–2319. [Google Scholar]
- Zhang, J.; Pan, J.; Ren, J.; Song, Y.; Bao, L.; Lau, R.W.H.; Yang, M.-H. Dynamic Scene Deblurring Using Spatially Variant Recurrent Neural Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2521–2529. [Google Scholar]
- Tao, X.; Gao, H.; Shen, X.; Wang, J.; Jia, J. Scale-Recurrent Network for Deep Image Deblurring. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8174–8182. [Google Scholar]
- Zhang, H.; Dai, Y.; Li, H.; Koniusz, P. Deep Stacked Hierarchical Multi-Patch Network for Image Deblurring. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5978–5986. [Google Scholar]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.-H.; Shao, L. Multi-Stage Progressive Image Restoration. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 14816–14826. [Google Scholar]
- Karwowska, K.; Wierzbicki, D. MCWESRGAN: Improving Enhanced Super-Resolution Generative Adversarial Network for Satellite Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 9459–9479. [Google Scholar] [CrossRef]
- Richardson, W.H. Bayesian-Based Iterative Method of Image Restoration. J. Opt. Soc. Am. 1972, 62, 55–59. [Google Scholar] [CrossRef]
- Orieux, F.; Giovannelli, J.-F.; Rodet, T. Bayesian Estimation of Regularization and PSF Parameters for Wiener-Hunt Deconvolution. J. Opt. Soc. Am. A 2010, 27, 1593–1607. [Google Scholar] [CrossRef] [PubMed]
- Karwowska, K.; Wierzbicki, D. Improving Spatial Resolution of Satellite Imagery Using Generative Adversarial Networks and Window Functions. Remote Sens. 2022, 14, 6285. [Google Scholar] [CrossRef]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Qiao, Y.; Loy, C.C. ESRGAN: Enhanced Super-Resolution Generative Adversarial Networks. In Computer Vision—ECCV 2018 Workshops; Leal-Taixé, L., Roth, S., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 63–79. [Google Scholar]
- Kantorovich, L.V.; Rubinshtein, S.G. On a Space of Totally Additive Functions. Vestn. St. Petersburg Univ. Math. 1958, 13, 52–59. [Google Scholar]
- Wang, D.; Liu, Q. Learning to Draw Samples: With Application to Amortized MLE for Generative Adversarial Learning. arXiv 2016, arXiv:1611.01722. [Google Scholar]
- Charbonnier, P.; Blanc-Feraud, L.; Aubert, G.; Barlaud, M. Two Deterministic Half-Quadratic Regularization Algorithms for Computed Imaging. In Proceedings of the 1st International Conference on Image Processing, Austin, TX, USA, 13–16 November 1994; Volume 2, pp. 168–172. [Google Scholar]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.-H.; Shao, L. Learning Enriched Features for Real Image Restoration and Enhancement. arXiv 2020, arXiv:1611.01722. [Google Scholar]
- Keelan, B. Handbook of Image Quality: Characterization and Prediction; CRC Press: Boca Raton, FL, USA, 2002; ISBN 978-0-429-22280-1. [Google Scholar]
- Wang, Z.; Bovik, A.C. A Universal Image Quality Index. IEEE Signal Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Goetz, A.; Boardman, W.; Yunas, R. Discrimination among Semi-Arid Landscape Endmembers Using the Spectral Angle Mapper (SAM) Algorithm. JPL, Summaries of the Third Annual JPL Airborne Geoscience Workshop. Volume 1: AVIRIS Workshop. 1992. Available online: https://ntrs.nasa.gov/search.jsp?R=19940012238 (accessed on 24 November 2023).
- Xia, G.-S.; Bai, X.; Ding, J.; Zhu, Z.; Belongie, S.; Luo, J.; Datcu, M.; Pelillo, M.; Zhang, L. DOTA: A Large-Scale Dataset for Object Detection in Aerial Images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3974–3983. [Google Scholar]
- Chang Guang Satellite Technology Co., Ltd. Available online: http://www.jl1.cn/EWeb/ (accessed on 24 November 2023).
- Planet|Homepage. Available online: https://www.planet.com/ (accessed on 24 November 2023).






| Peak signal-to-noise ratio (PSNR) [67] | |
| Universal Quality Measure (UQI) [68] | |
| Spectral Angle Mapper (SAM) [69] | |
| Structural Similarity Index (SSIM) [67] | |
| Root mean square error (RMSE) [67] | |
| Spatial Correlation Coefficient (SCC) [67] |
| Input size | 96 × 96 pixels |
| Learning rate | |
| Optimization | Adam (β_1 = 0.9, β_2 = 0.999, ε = 1 10−8) |
| Batch size | 4 |
| Epochs | 150 |
| Metrics | LR | MCWESRGAN | MCWESRGAN with Lucy–Richardson Algorithm | MCWESRGAN with Wiener Deconvolution | MCWESRGAN with Uformer |
|---|---|---|---|---|---|
| SSIM | 0.92 | 0.96 | 0.91 | 0.77 | 0.98 |
| PSNR | 31.37 | 36.21 | 23.83 | 15.18 | 38.32 |
| SAM | 0.07 | 0.03 | 0.08 | 0.10 | 0.02 |
| SCC | 0.15 | 0.26 | 0.08 | 0.08 | 0.27 |
| UQI | 0.991 | 0.993 | 0.966 | 0.818 | 0.996 |
| Metric | LR | EDSR | EDSR * | ESPCN | ESPCN * | FSRCNN | FSRCNN * | RDN | RDN * | SRCNN | SRCNN * | SRDenseNet | SRDenseNet * | SRGAN | SRGAN * | ESRGAN | ESRGAN * | MCWESRGAN | MCWESRGAN * |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SSIM | 0.92 | 0.87 | 0.90 | 0.95 | 0.94 | 0.90 | 0.93 | 0.94 | 0.94 | 0.93 | 0.94 | 0.94 | 0.94 | 0.62 | 0.67 | 0.78 | 0.83 | 0.96 | 0.98 |
| PSNR | 31.37 | 25.36 | 25.62 | 27.63 | 27.16 | 27.01 | 27.23 | 27.59 | 27.45 | 32.40 | 33.06 | 27.56 | 27.46 | 19.92 | 20.91 | 29.35 | 30.04 | 36.21 | 38.32 |
| SAM | 0.07 | 0.11 | 0.11 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.06 | 0.06 | 0.08 | 0.08 | 0.23 | 0.21 | 0.08 | 0.080 | 0.03 | 0.02 |
| SCC | 0.15 | 0.20 | 0.26 | 0.26 | 0.25 | 0.18 | 0.24 | 0.26 | 0.25 | 0.19 | 0.25 | 0.24 | 0.25 | 0.06 | 0.17 | 0.14 | 0.21 | 0.26 | 0.27 |
| UQI | 0.991 | 0.889 | 0.955 | 0.939 | 0.970 | 0.775 | 0.904 | 0.958 | 0.967 | 0.964 | 0.987 | 0.970 | 0.973 | 0.758 | 0.760 | 0.788 | 0.793 | 0.993 | 0.996 |
| LR | HR | EDSR | ESPCN |
 |  |  |  |
| FSRCNN | RDN | SRCNN | SRDenseNet |
 |  |  |  |
| SRGAN | ESRGAN | MCWESRGAN | MCWESRGAN with Uformer |
 |  |  |  |
| STAGE | Time [s] (*—per Frame) | |||
|---|---|---|---|---|
| Intel Xeon Silver 4216 with TITAN RTX 24 GB | Intel Xeon Silver 4216 | Intel Corei5-1235 | Intel Corei3-7100U | |
| Preparation of data | 0.004 0.00004 * | 0.04 0.0004 * | 0.2 0.002 * | 0.4 0.004 * |
| Resolution enhancement | 76.80 (0.19 per tile) | 988 (2.47 per tile) | 4316 (10.79 per tile) | 8861 (22.15 per tile) |
| Combining into video data | 0.07 0.0007 * | 0.9 0.009 * | 4 0.04 * | 8 0.08 * |
| Total time required to enhance the spatial resolution of one video | 76.87 (~1 min 17 s) 0.77 s * | 988.94 (~16 min 29 s) 9.9 s * | 4320.2 (~72 min) 43.2 s * | 8869.4 (~147 min 49 s) 88.7 s * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karwowska, K.; Wierzbicki, D. Modified ESRGAN with Uformer for Video Satellite Imagery Super-Resolution. Remote Sens. 2024, 16, 1926. https://doi.org/10.3390/rs16111926
Karwowska K, Wierzbicki D. Modified ESRGAN with Uformer for Video Satellite Imagery Super-Resolution. Remote Sensing. 2024; 16(11):1926. https://doi.org/10.3390/rs16111926
Chicago/Turabian StyleKarwowska, Kinga, and Damian Wierzbicki. 2024. "Modified ESRGAN with Uformer for Video Satellite Imagery Super-Resolution" Remote Sensing 16, no. 11: 1926. https://doi.org/10.3390/rs16111926
APA StyleKarwowska, K., & Wierzbicki, D. (2024). Modified ESRGAN with Uformer for Video Satellite Imagery Super-Resolution. Remote Sensing, 16(11), 1926. https://doi.org/10.3390/rs16111926








