Abstract
In this paper, to track maneuvering unmanned surface vehicles (USVs) in scenarios with clutter, we propose a novel method based on the probabilistic data association (PDA) algorithm and Rao-Blackwellized particle filter (RBPF) algorithm, and we further improve the tracking performance by Max-Q criterion-based waveform selection. This work develops a maneuvering target model in the context of clutter, integrating linear and nonlinear states as well as observations with false alarms. In order to jointly tackle the mixed-state tracking problem, the PDA algorithm is integrated into the RBPF framework. This allows it to be used with the complex nonlinear and linear hybrid system and helps to minimize the state dimensions of conventional particle filtering (PF). Additionally, by utilizing Q-learning principles, we provide a Max-Q-based criterion to select the waveform parameters, which guarantees low measurement errors and efficiently handles measurement uncertainties. Our simulation results show that the PDA-RBPF algorithm, which has a more appropriate tracking mechanism, produces results that are more accurate than those of the EKF or PF algorithms alone. Furthermore, the RMSE derived by the Max-Q-based criterion is smaller and more robust than that of other selection methods, as well as yielding a fixed waveform. Our proposed mechanism, which combines the concepts of PDA-RBPF and Max-Q waveform selection, performs well in target tracking tasks and exhibits relatively good performance over some existing ones.
1. Introduction
Currently, in the tracking of maneuvering USVs, traditional radar with single waveforms cannot adapt well to the complex and dynamic marine scenario. As discussed in [1,2,3], modern radar has focused on designing agile waveforms to enhance the tracking performance, where the tracking error is typically represented by the state estimation error covariance matrix and also depends on the transmitting waveform. Generally, by predefining a waveform library, the criterion for waveform selection is to optimize the cost function of different parameters at each time instant [2,3], where the goal is to select the waveform with the lowest cost value as the optimal transmitting waveform. Therein, such criteria include the minimum mean square error criterion (Min-MSE) [4], the maximum mutual information criterion (Max-MI) [5,6] and the minimum gate criterion (Min-Gate) [7]. A series of simulations and results show that these criteria-based optimization methods have high tracking accuracy and simple calculation principles, but with relatively high time costs [8]. Reference [9] proposed a new method using the particle swarm optimization (PSO) algorithm based on adaptive Kalman filtering to optimize the radar waveform parameters. The proposed method can reduce the velocity error and range error by 50% and 60%, respectively. The authors in [10] proposed an adaptive waveform selection algorithm based on indirect reinforcement learning, addressing uncertainties in the target-state space. Simulation results show that the algorithm has better computational efficiency and fewer state estimation errors, which improve the tracking accuracy. The authors in [11] also proposed a universal reinforcement learning waveform selection strategy to solve a broad class of waveform-agile tracking problems, while making minimal assumptions about the environment’s behavior. Therefore, their strategy is more general, and it provides better performance. Moreover, the authors in [8,12] utilized supervised learning and reinforcement learning for waveform selection, where these adaptive waveform selection methods further reduce the state estimation error and improve the tracking accuracy with much less processing time compared to the criteria-based optimization methods.
In general, most studies have focused on the cost function and choosing the criterion and learning mechanism, and they have ignored the effect of the target model on the receiver’s estimation filter. For a simple scenario (especially with a linear observation model), the effective Kalman filtering method has been proven to be the best [13]. Meanwhile, for complex marine scenarios with nonlinear non-Gaussian models, the traditional Kalman filter seems to be insufficient. Here, most marine USV tracking scenarios can be formulated as nonlinear and non-Gaussian or more sophisticated models. The estimation methods for such nonlinear models include the extended Kalman filter (EKF), particle filter (PF) and so on [14,15,16]. The limitation of the EKF is that it is only suitable for local linearization, aimed at models with a low degree of nonlinearity. Moreover, too many particles in the PF leads to higher computational complexity [17,18]. The question of how to balance the linear and nonlinear models is a problem that deserves careful consideration. In order to solve the uncertainty of the maneuvering model, authors usually turn to interacting multiple model (IMM) algorithms [7,19]. These algorithms result in remarkable improvements in the state estimation accuracy but greatly increase the computational workload [20]. To address this urgent issue, the Rao-Blackwellized particle filter (RBPF) algorithm can divide the state space into two subspaces [21,22], where one subspace is updated using a PF and the other employs other filters [23]. Due to the separation of the state space, the RBPF algorithm reduces the dimensionality of nonlinear states by the PF to ensure the accuracy of nonlinear filtering. Compared with traditional PF algorithms, given the same number of particles, the RBPF reduces the computational complexity and exhibits superior performance [24].
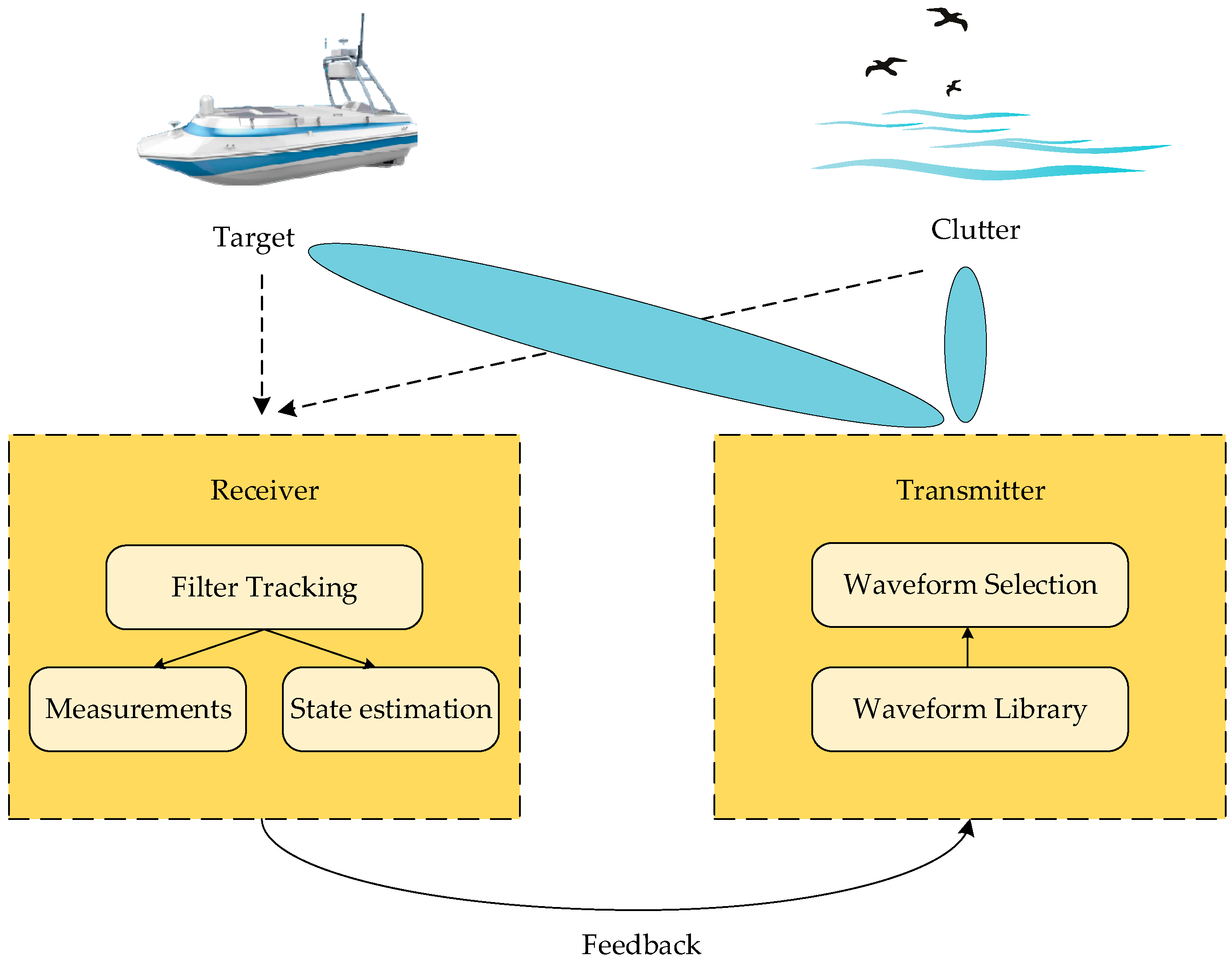
Based on the RBPF’s traits, in this paper, we further improve the tracking performance by utilizing the probabilistic data association (PDA) algorithm, Rao-Blackwellized particle filter (RBPF) algorithm and Max-Q-based adaptive waveform selection principle. We establish a hybrid system incorporating both nonlinear and linear components, considering some false alarms and clutter data. The PDA and RBPF algorithms are combined to address clutter interference and estimate the target’s state. Moreover, by leveraging the mechanism of Q-learning, we adaptively select the optimal waveform candidates from the waveform library in order to minimize the estimation errors and improve the tracking accuracy. Figure 1 shows the radar system for maneuvering target tracking in clutter scenario.
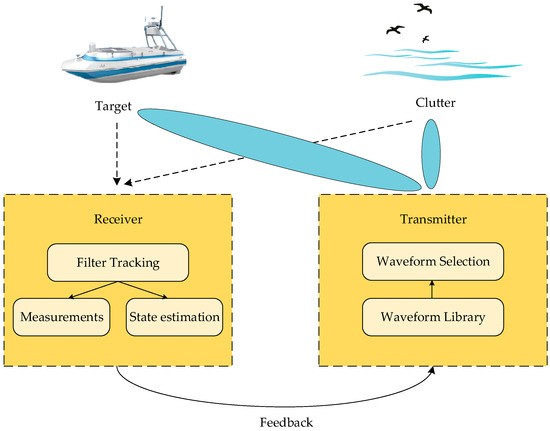
Figure 1.
Radar system for maneuvering target tracking in clutter scenario.
2. System Overview and Problem Formulation
In this section, we consider a radar system consisting of a transmitter located at and a receiver located at . Differing from the discussion in [8], the receiver in our work uses a novel PDA-RBPF algorithm to obtain local tracking trajectories. Thus, the dynamic hybrid model of the maneuvering target can be defined as
where and denote the nonlinear subsection and linear subsection of the target state vector at time instant , respectively. represents the transition function of the nonlinear state. represents the linear state transition matrix. and are the nonlinear and linear Gaussian process noise at time instant , respectively. is the state measurement value at time instant . denotes the nonlinear function of the observation process. Finally, is the measurement noise.
Generally, the target state vector at time instant can be denoted as , incorporating the position part and velocity part . Assuming that the target is located at with velocity , and the time delay and Doppler shift measurements are available for the receiver, then the radial range and range rate measurements can be calculated as
where and , respectively, represent the x and y positions of the transmitter.
By assembling (2) and (3) together, the measurement vector has
The range rate measurement error covariance matrix has
where is the transition matrix. As discussed in [1,25], is the Cramér–Rao Lower Bound (CRLB) matrix with a time delay and Doppler shift depending on SNR , as well as the transmitted waveform parameters. Although is also dependent on SNR , here, we simply treat it as a function of waveform parameter vector and focus on the adaptive waveform selection. Furthermore, the CRLB for the measurement error covariance of the Gaussian frequency-modulated waveform can be obtained by
It can be observed that the measurement error covariance is related to both the pulse duration and the linear frequency modulation rate. Therefore, by adjusting the waveform parameters according to certain metrics, the measurement error covariance can be further reduced, effectively improving the tracking accuracy.
3. Target Tracking Model and Its Algorithm Framework
In practical scenarios, the most crucial issue is how to handle the uncertainty in originating radar echoes and further accurately extract the target information [26]. The most common approach to addressing the problem of maneuverable target tracking with clutter interference is the probabilistic data association (PDA) algorithm. The PDA algorithm assumes that as long as there is a valid echo (within the gate) that may come from the target, each measurement would have a different probability of originating from this target [25]. Then, the PDA algorithm calculates the weighted coefficients for each probability. Finally, the updated target state can be obtained by using the resulting weighted measurements.
It is known that PF is computationally intensive and inefficient when sampling in a high-dimensional state space [27]. High-dimensional state spaces can be classified with different subspace processing methods using different filtering methods. For instance, the linear component can undergo Kalman filtering to derive a conditional posterior distribution, while the nonlinear component can be processed via PF. This hybrid approach yields a mixed filter, effectively reducing the dimensionality of the particle filtering sampling space. In the system model, the state model is represented by , and the observation model is described by . To track a target using RBPF, the specific steps involve the separate application of the PF and KF algorithms for measurement updates and target state prediction updates. This process aims to obtain the state estimation to generate the target trajectory and the covariance matrix of estimation errors for waveform selection.
Combining PDA and RBPF together could further address the tracking problem of mixed state targets in the presence of clutter interference. By marginalizing the linear state vector, particles only need to be present in the low-dimensional nonlinear state space, resolving the high computational complexity of the traditional PF. Meanwhile, KF with the optimal linear filtering method can enhance the tracking accuracy.
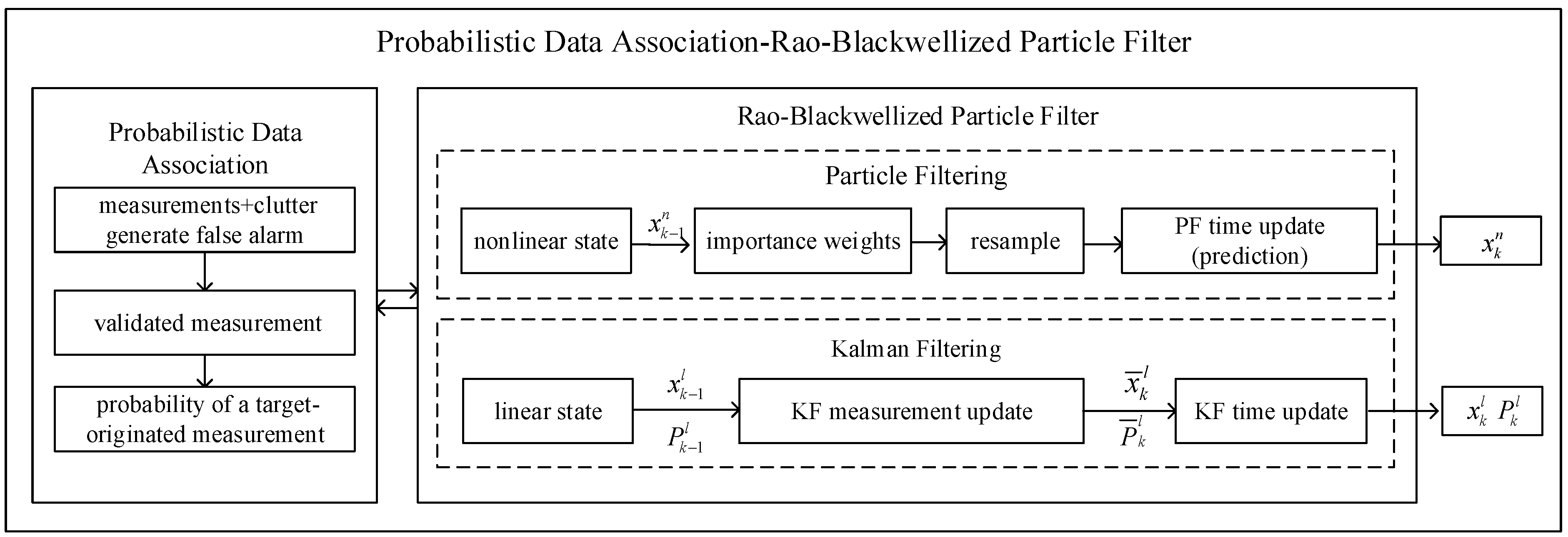
The algorithm framework is illustrated in Figure 2, with the detailed steps as follows.
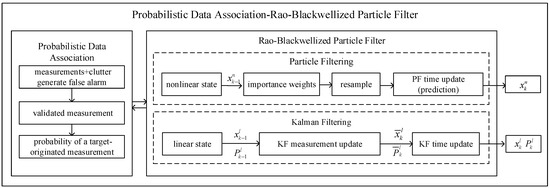
Figure 2.
Block diagram of novel PDA-RBPF tracking algorithm.
- Initializing particles and parameters
First, set the number N of particles required for PF and then initialize these particles‘ values and other relevant parameters.
- Kalman measurement updating for the linear state
Given the state estimate and its covariance at time instant , the predicted state estimate and covariance at time instant k can be computed by
- Calculating the predictive measurement
Nonlinear predicted state and linear predicted state form the target predicted state . The predictive measurement is
- Determining whether a measurement falls within the validation region
The region around the predictive measurement is defined as a validation region at time instant . The measurement derived from the target falls within this region with probability , which usually refers to the gating probability. The condition for a point to be in the validation region would be satisfied if
where is a threshold related to the gating probability . Here, is the residual covariance matrix.
- The probability of a validated measurement from the target and its association measurement
Suppose that there are m validated measurements; the probability of the j-th validated measurement has
The probability of having no measurement from the target falling within the validation region is
where is given by
where is the residual for the j-th validated measurement ,
The false alarms are assumed to be uniformly spatially distributed over the measurement space and independent over time. A Poisson distribution is used to model the number of false alarms [1], so is computed as
where is the clutter density. The detection probability of the target at time instant is given by , and is the probability of a false alarm.
Therefore, the association measurement can be computed by
- Normalizing the importance weights
Assuming that the importance distribution is only related to the state and measurement values at the previous moment, we can calculate the importance weights by
- Calculating the number of effective particles
The number of effective particles is calculated to quantify the degree of particle weight degeneracy and determine whether resampling is needed.
In the above equation, the smaller the effective number of particles—i.e., the larger the variance of the weights, indicating a greater disparity between particles with large and small weights—the more severe the weight degeneracy. In practical calculations, the effective number of particles can be approximated by
Based on (20), we set a threshold value . If the effective number of particles is less than this threshold, , it indicates severe degeneracy. The resampling mechanism should be applied to control the particles’ situation.
- Particle filter state updating for the nonlinear state
The particle distribution is approximated by
- Kalman state updating
In this way, the proposed PDA-RBPF algorithm can be used to calculate the probability of valid measurements and the importance weight of each particle and then estimate the mixed nonlinear and linear states at each time instant.
4. Adaptive Waveform Selection Mechanism and Discussion
As the measurement error covariance matrix is a function of (waveform parameter vector at time instant ), then the error covariance matrix and the residual covariance matrix are also dependent on , as demonstrated in Section 3. Next, we discuss several criterion-based optimization methods.
4.1. Criterion-Based Optimization Methods
4.1.1. Minimum Mean Square Error Criterion
The minimum mean square error method selects waveform parameters based on the mean square error (MSE) of target state estimation at each time instant. A smaller MSE indicates a closer estimation to the true value, resulting in more accurate tracking. For this case, the problem of adaptive waveform selection can be described as minimizing the trace of the error covariance matrix:
where denotes the waveform library in the transmitter.
4.1.2. Maximum Mutual Information Criterion
The mutual information between the predicted value and the measurement value can represent the certainty degree of one-step prediction for target state estimation [6]. According to the maximum mutual information criterion, the problem of the optimal waveform parameters is formulated as
By using this criterion, the selection of transmitted waveforms can be achieved by minimizing the determinant of the estimated error covariance matrix.
4.1.3. Minimum Gate Criterion
Considering radar measurements in clutter environments, the gating criterion function controls the size of the range gate to reduce false measurements in high-density clutter or measurement errors in high-noise situations, thereby improving the tracking performance. Since the gate volume is proportional to the determinant of the residual covariance matrix, the selection of the optimal waveform parameter can be expressed as
4.2. The Proposed Max-Q-Based Criterion
Q-learning is a model-free method that updates the Q-table by calculating the reward at each step and selecting the optimal path to complete the specified task [8]. The Q-value in the Q-table represents the cumulative discounted reward, indicating the expected return when taking action in state at a specific moment. The environment provides feedback in terms of rewards based on the agent’s actions. The main idea of this algorithm is to construct a Q-table that stores the Q-values for each state action and then select actions to maximize the expected return based on these Q-values.
where represents the agent state, represents the action, is the learning rate, and is the discount factor.
Therein, the current Q-value remains a proportion of old values, along with the reward obtained from the current action (waveform parameter), representing both the real-time reward of the action and the potential future rewards. By using these principles of Q-learning, we can design a waveform parameter selection mechanism to choose the optimal parameters. Here, we refer to the waveform selection idea as the Max-Q-based criterion.
First, we calculate the entropy state based on the estimated error covariance at time instant . This serves as an evaluation criterion for the radar tracking performance, measuring the overall uncertainty in the estimation of the target’s state.
By comparing the entropy state between time instants and , we further provide a real-time reward for the waveform parameters, where the real-time reward function is denoted as
Generally, a decrease in entropy indicates that the waveform factor can reduce the estimation uncertainty and result in a positive reward. Conversely, an increase in entropy implies an increase in uncertainty, leading to a negative reward or a penalty. After obtaining the real-time reward, we update based on Formula (30). Finally, we select the waveform parameters corresponding to the maximum Q-value as the optimal decision, which yields the optimal waveform selection strategy for time instant . Therefore, the adaptive waveform selection problem can be described as
where denotes the waveform library, containing different waveform categories or parameters.
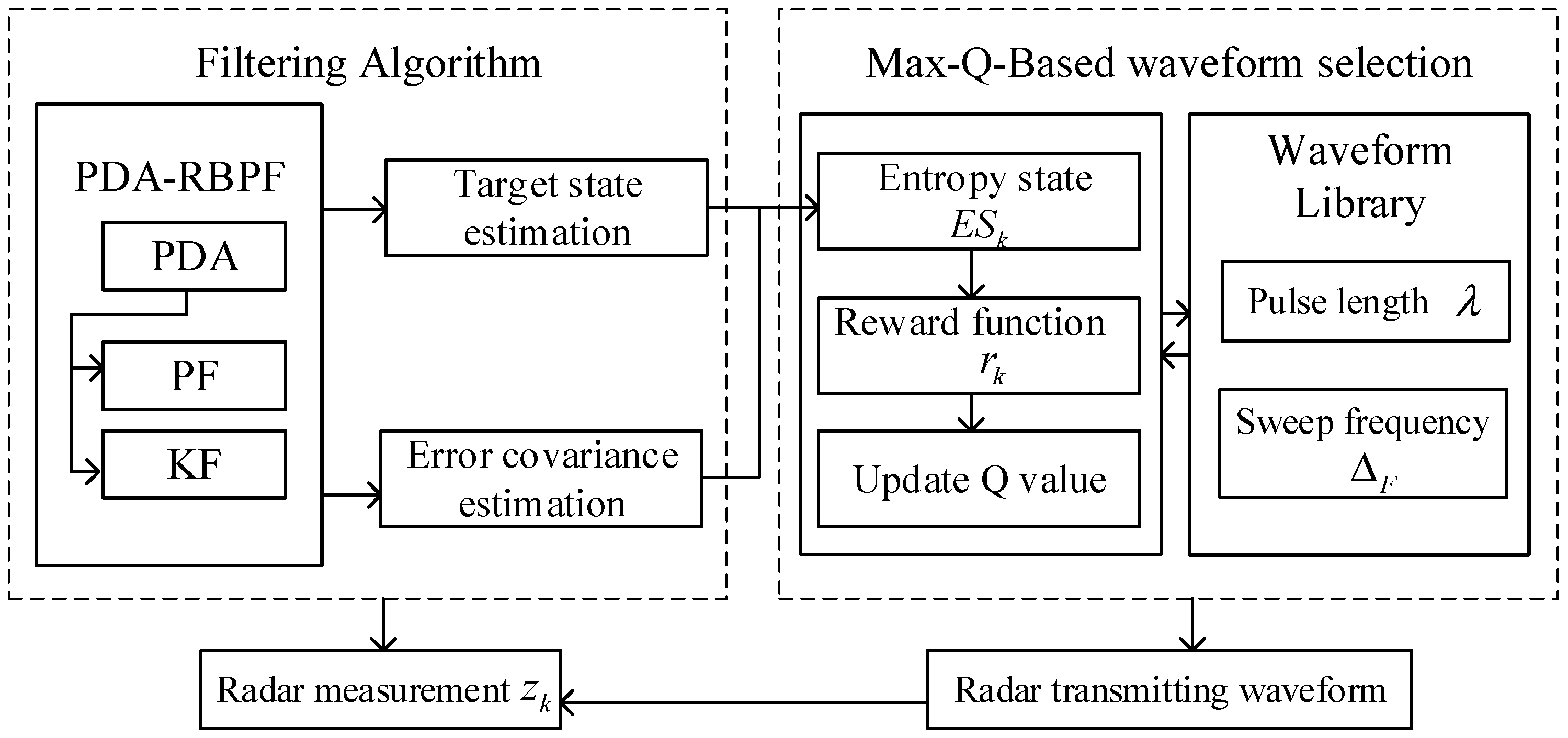
The block diagram in Figure 3 demonstrates the Max-Q-based waveform selection mechanism. After the filtering tracking, the obtained target state estimation and error covariance matrix are fed back to the transmitter. By traversing the waveform library, the next prediction error covariance matrix is calculated, alongside acquiring the entropy state and reward function. Consequently, the cumulative discounted reward Q-value for each waveform is obtained to update the Q-table. The waveform parameters corresponding to the largest Q-value in the Q-table are selected as the best transmitted waveform, which will be transmitted in the next step.
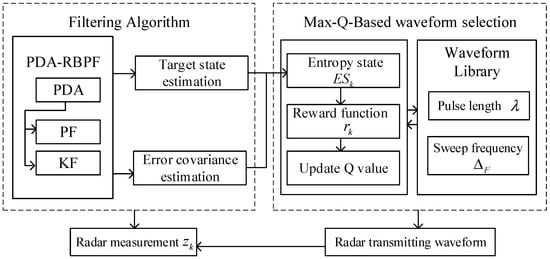
Figure 3.
Block diagram of Max-Q-based waveform selection mechanism.
5. Simulations and Analysis
In this section, we consider a tracking scenario in which the radar is located at the origin (0, 0) m. The target’s state information includes the two-dimensional position and velocity, i.e.,
The initial position of the target is located at (3000, 3000) m, and the initial velocity magnitude is (2, 2) m/s. It obeys a dynamic hybrid model of a discrete-time system. In this context, the updating of the x-axis position refers to a nonlinear model, while the y-axis position and velocities adhere to a linear model. Therefore, the state space is divided into two parts, and nonlinear filtering (particle filtering) and linear filtering (Kalman filtering) are performed separately for each part. The measurement vector for the target state can be denoted as , and the measurement function is denoted as , as follows:
where p and v represent the measured values for the distance and velocity, respectively. Moreover, represents the position of the receiver.
The initial state of the target has
The initial error covariance matrix is
The measurement error covariance matrix is
In this simulation, the radar transmitter emits Gaussian LFM pulses, which are given by
where is the Gaussian pulse length parameter and is the frequency modulation rate. is the sweep frequency. is the effective pulse duration, which is approximated by . The transmission frequency is set to , the pulse repetition interval to , and the signal propagation speed to [28].
Here, we assume that the waveform library is composed of Gaussian LFM pulses with different pulse lengths and sweep frequencies, where the pulse length ranges within and the sweep frequency ranges within . Random variables falling within the validation region are seen as clutter and added to the predicted measurement (namely, false alarms), where the number of false alarms obeys a Poisson distribution. The gating probability is , the threshold corresponding to the gate probability is , the probability of false alarms is , and the clutter density is [1,29].
To analyze the performance of different waveform selection criteria and filtering algorithms, the following performance metrics have been defined, i.e.,
where , , , and represent the true state values of the target model. Additionally, the average value of the RMSE (ARMSE) according to the position variable is
The ARMSEs for other state components are calculated in the same way.
We first consider the tracking problem with clutter data by using the PDA algorithm and then proceed to compare the RBPF algorithm with other nonlinear tracking algorithms.
In this section, the nonlinear target’s x-axis position is represented by the inverse tangent function and is also affected by the x-axis velocity, i.e.,
The y-axis position and velocities adhering to a linear model are
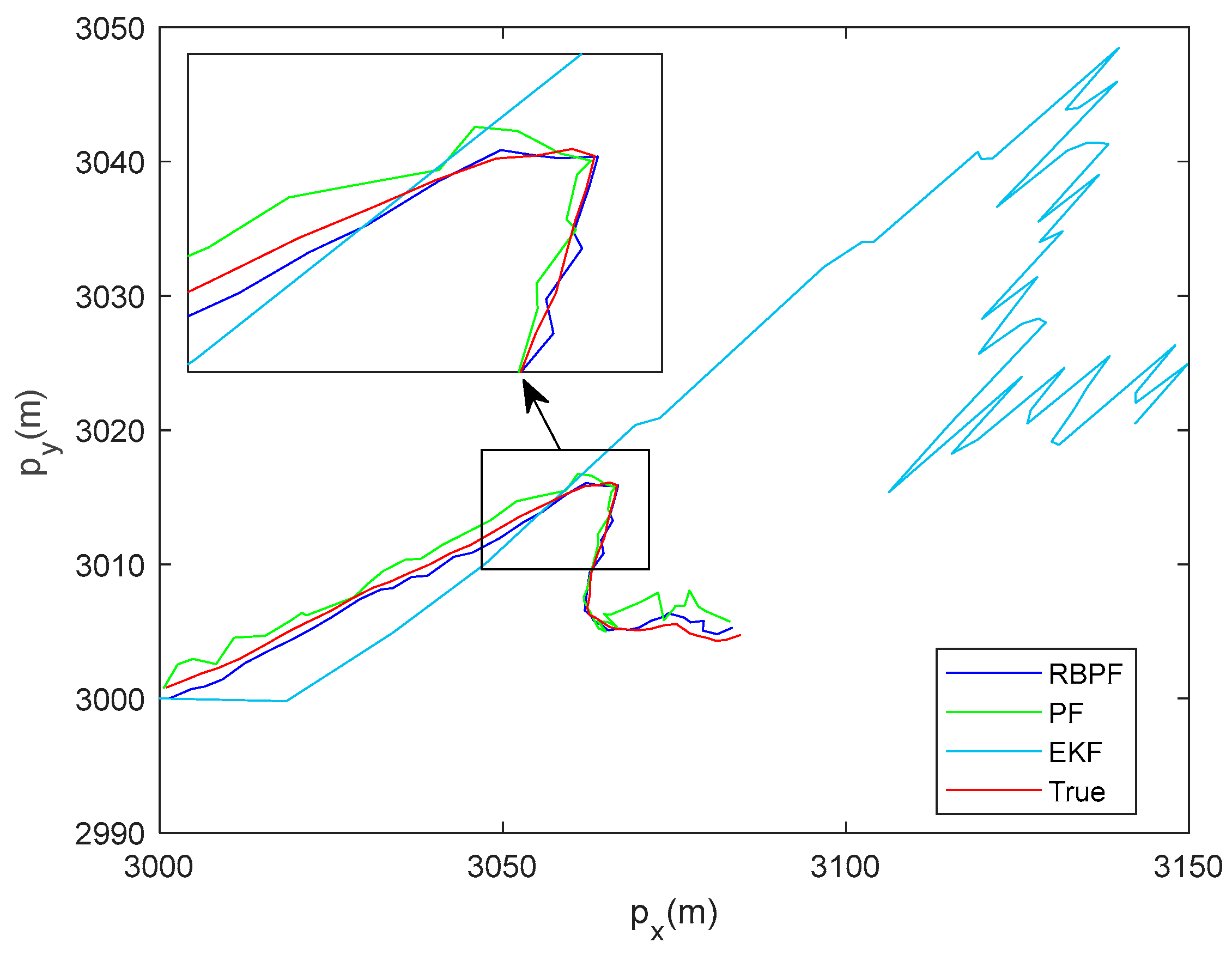
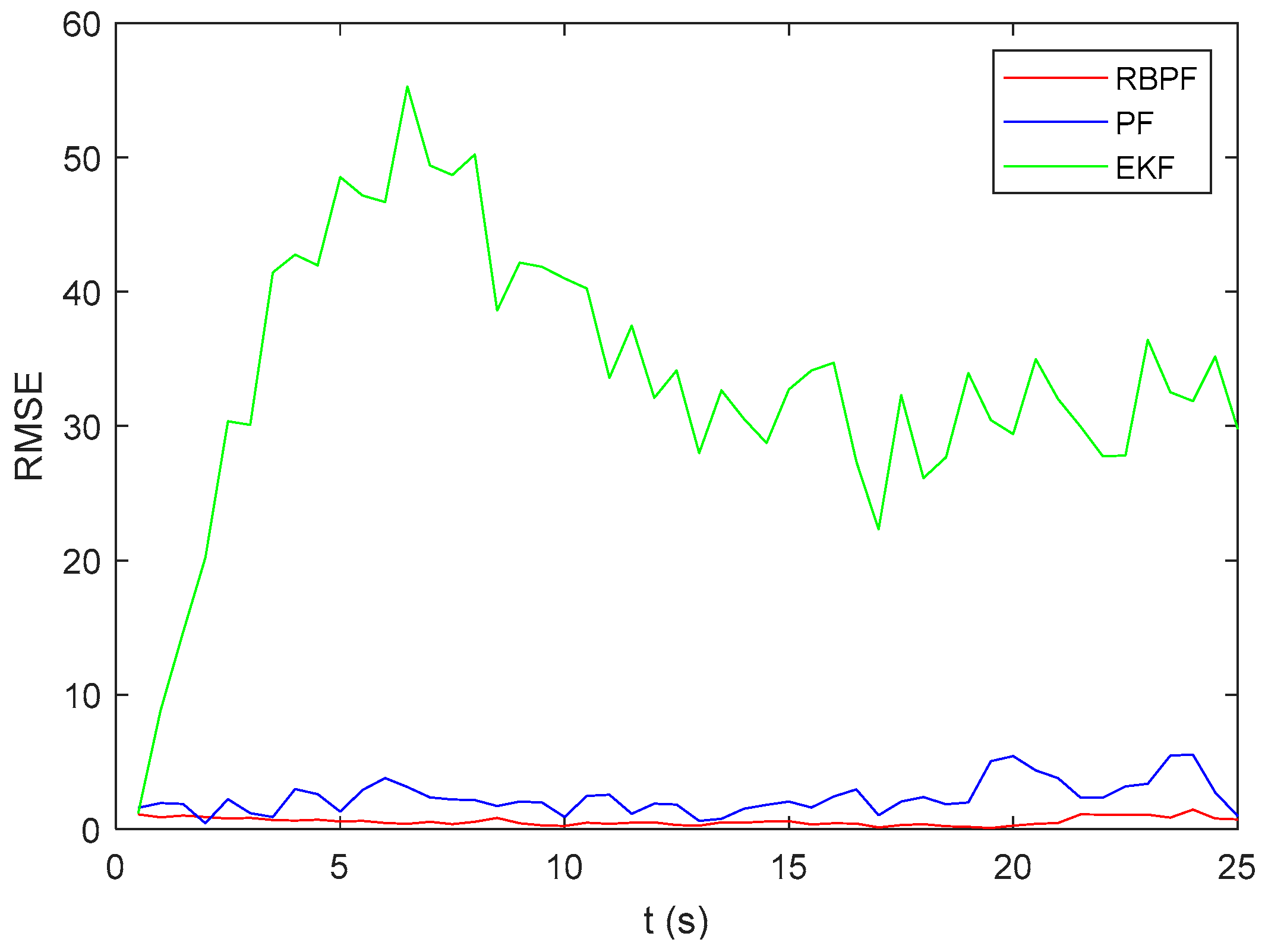
As shown in Figure 4 and Figure 5, the RMSE of the EKF algorithm is significantly greater than that of the other two algorithms. The RMSE of the PF algorithm is below 5, while the RMSE of the RBPF algorithm can reach about 1. It can be observed that the RBPF algorithm results in a smaller RMSE compared to the EKF or PF algorithm alone, indicating a more accurate result. The reason is that KF in the RBPF framework is the optimal estimation algorithm for the linear state updating model, while PF provides a more accurate estimation for the complex nonlinear part. The combination of the two parts can improve the accuracy of target tracking.
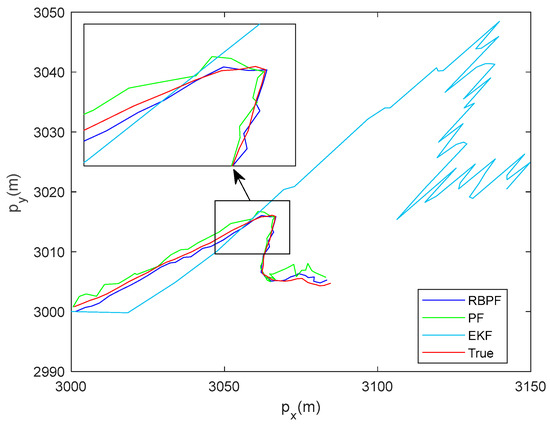
Figure 4.
Comparison of tracking algorithms in clutter scenario.
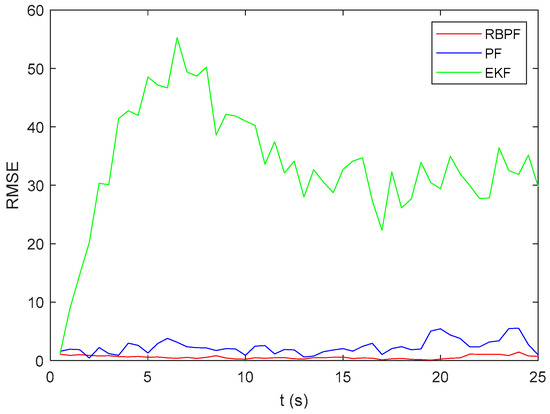
Figure 5.
RMSE comparison of different tracking algorithms.
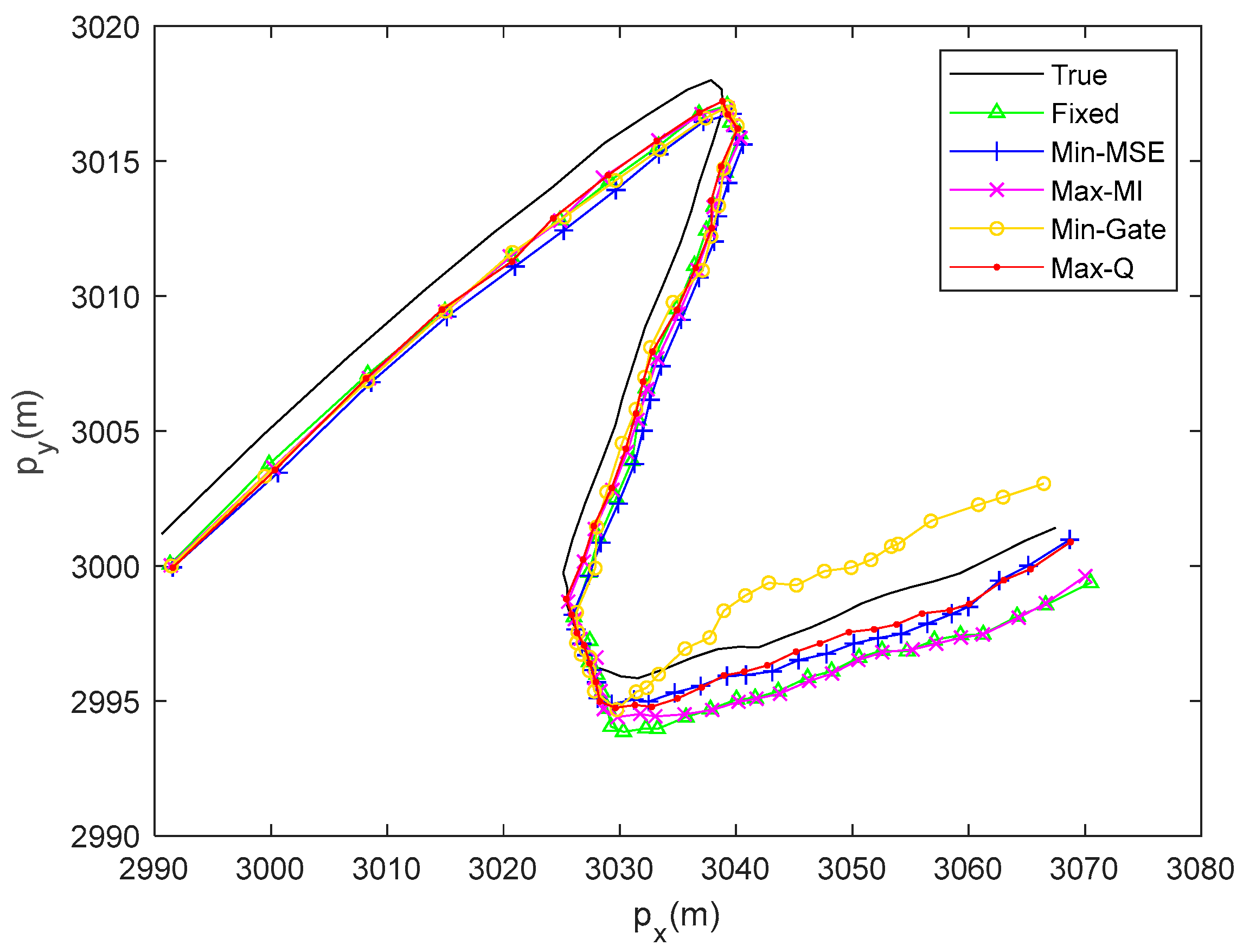
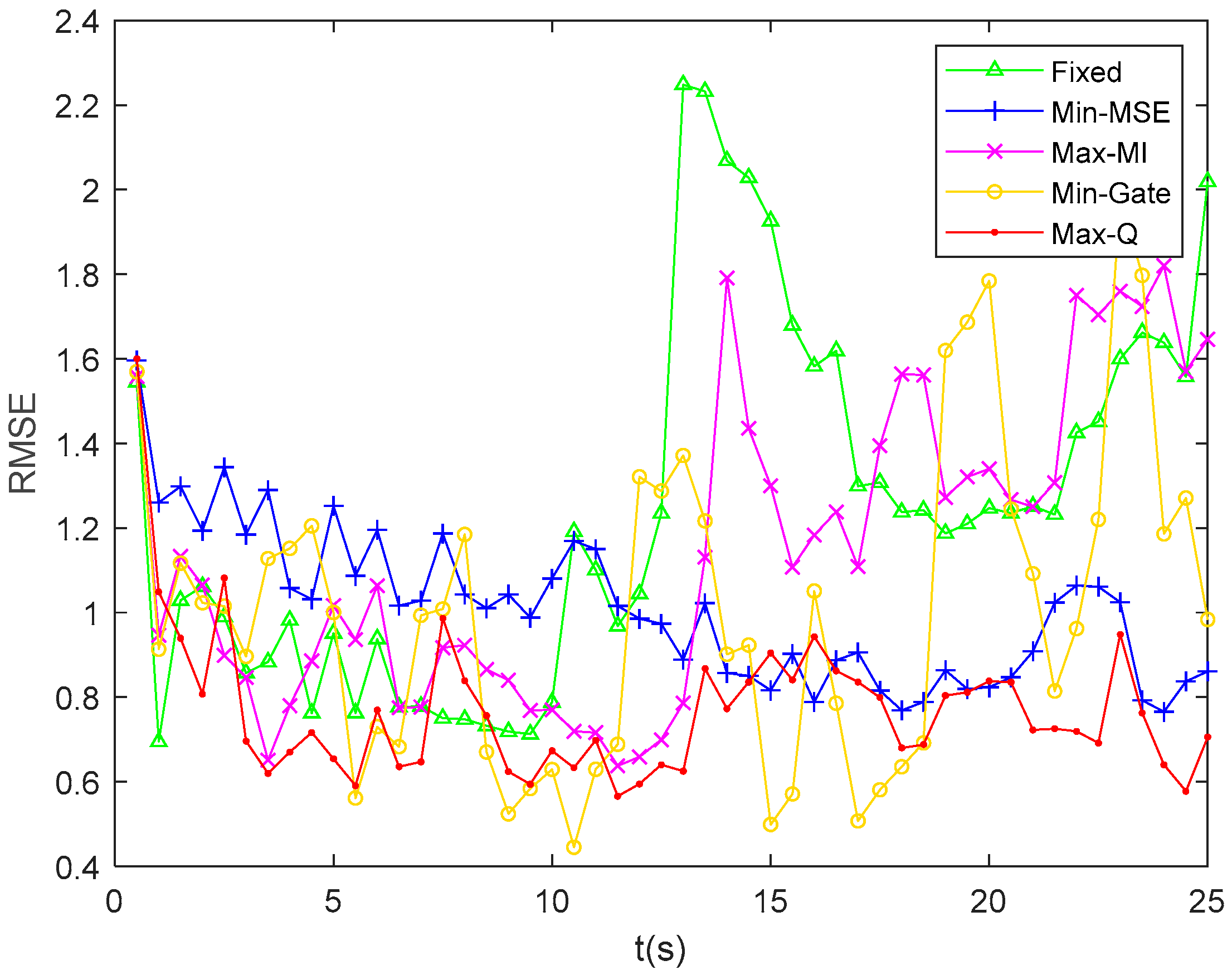
Next, the PDA-RBPF algorithm and Max-Q-based criterion are used to estimate the target trajectory and select waveform parameters. We set the number of particles N = 100. In Figure 6 and Figure 7 and Table 1, we demonstrate a series of comparisons using different waveform selection schemes. Based on the PDA-RBPF algorithm for target tracking, the waveform parameters are selected using the Max-Q-based criterion proposed in this paper and compared with fixed waveform parameters and other criterion-based optimization methods. The RMSE and ARMSE of target state estimation are listed.
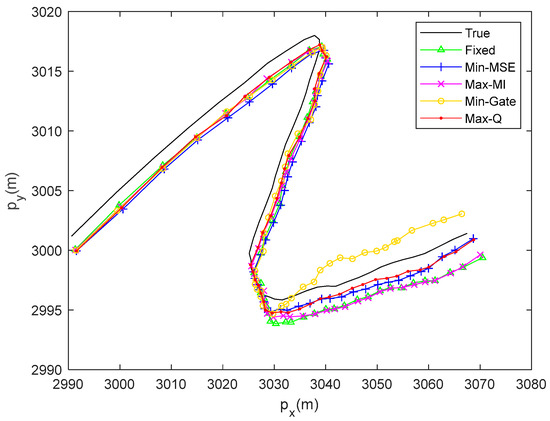
Figure 6.
Tracking results of PDA-RBPF using different waveform selection mechanisms.
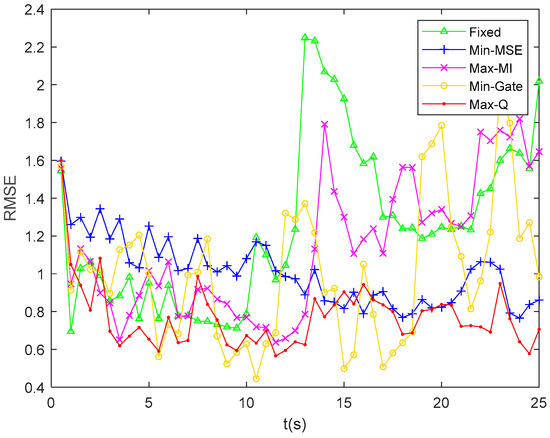
Figure 7.
RMSE comparison using different waveform selection mechanisms in PDA-RBPF.

Table 1.
ARMSE comparison using different waveform selection mechanisms in PDA-RBPF.
In Figure 6, it is evident that the target undergoes maneuvering motion, where the first obvious turn occurs around and the second large turn occurs around . During turning, the direction of the x-axis or y-axis velocity often changes. Correspondingly, the RMSEs in these turning instances exhibit varying tendencies, as shown in Figure 7. In particular, the increase in the RMSE is particularly noticeable during the large turn of the target’s movement around . It is noted that the utilization of the PDA-RBPF algorithm and the Max-Q criterion can maintain the RMSE at each time instant within 2 or even blow 1. The ARMSEs for the position and velocity estimations are around 1 m and 0.5 m/s, respectively. Compared with other waveform selection methods, the RMSE obtained by the Max-Q-based criterion is smaller and more stable. Our proposed algorithm demonstrates excellent tracking performance.
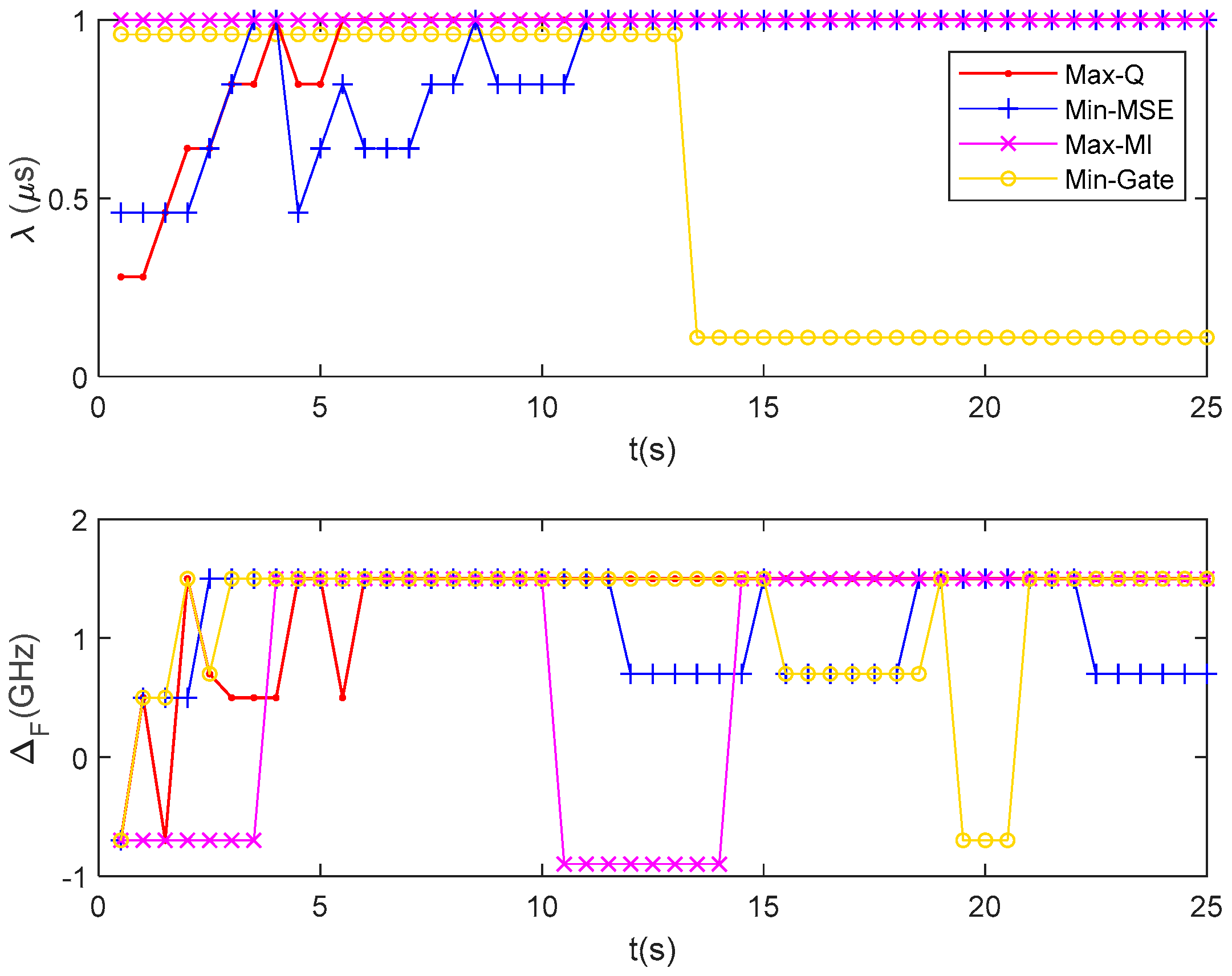
Additionally, the optimal waveform parameters , for the transmitting waveform at each time instant are adaptively selected according to different methods, as shown in Figure 8.
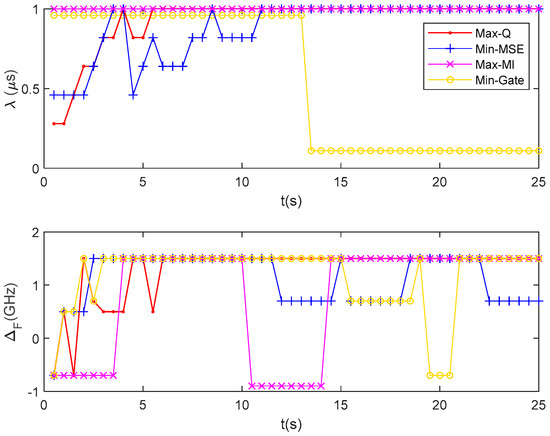
Figure 8.
Waveform parameters selected by different methods at each time instant.
In Figure 8, we can find that the waveform parameter selection process also fluctuates with the target’s maneuvering state. This phenomenon means that different waveform selection schemes often choose different waveform parameters due to the use of their own criteria and produce different tracking results. Obviously, our proposed Max-Q method can adapt to the maneuvering state and adjust to reduce the tracking ARMSE, as shown in Table 1.
6. Conclusions
In this paper, we propose a novel waveform selection mechanism based on the Max-Q criterion using PDA-RBPF for maneuvering target tracking in clutter. Therein, the PDA-RBPF algorithm separates the linear and nonlinear states from the complex mixed system and employs Kalman filtering and particle filtering to estimate the target’s states, including the position and velocity. This algorithm is not only suitable for complex hybrid systems but also reduces the computational complexity and improves the tracking accuracy through appropriate filtering methods. By maximizing the Q-value of the Max-Q-based criterion, we can adaptively select the waveform parameters to effectively reduce the tracking errors and improve the tracking precision. The simulation results demonstrate that the proposed algorithm can adjust the transmitting waveform parameters, resulting in a lower and more stable RMSE compared with a fixed waveform or other selection methods. Moreover, it performs better in tracking a maneuvering target with clutter than other tracking algorithms, equipped with some adaptability and robustness.
Author Contributions
Conceptualization, X.F. and Z.Z. (Zhiquan Zhou); methodology, P.S.; software, X.W.; validation, X.F., Z.Z. (Zhanfeng Zhao) and Z.Z. (Zhiquan Zhou); formal analysis, P.S.; investigation, X.F. and M.L.; resources, Z.Z. (Zhanfeng Zhao); data curation, P.S.; writing—original draft preparation, P.S.; writing—review and editing, X.F.; visualization, P.S.; supervision, X.F.; project administration, Z.Z. (Zhiquan Zhou) and Z.Z. (Zhanfeng Zhao); funding acquisition, Z.Z. (Zhiquan Zhou). All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by the major scientific and technological innovation projects of Shandong Province of China (Grant No. 2021ZLGX05 and 2022ZLGX04).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Nguyen, N.H.; Dogancay, K. Signal Processing for Multistatic Radar Systems, 1st ed.; Academic Press: Cambridge, MA, USA, 2019; pp. 11–61. [Google Scholar]
- Shi, C.; Wang, Y.; Salous, S.; Zhou, J.; Yan, J. Joint Transmit Resource Management and Waveform Selection Strategy for Target Tracking in Distributed Phased Array Radar Network. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 2762–2778. [Google Scholar] [CrossRef]
- Zhang, H.; Xie, J.; Shi, J.; Fei, T.; Ge, J.; Zhang, Z. Joint beam and waveform selection for the MIMO radar target tracking. Signal Process. 2019, 156, 31–40. [Google Scholar] [CrossRef]
- Yang, Y.; Blum, R.S. MIMO radar waveform design based on mutual information and minimum mean-square error estimation. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 330–343. [Google Scholar] [CrossRef]
- Yao, Y.; Miao, P.; Chen, Z. Cognitive Waveform Optimization for Phase-Modulation-Based Joint Radar-Communications System. IEEE Access 2020, 8, 33276–33288. [Google Scholar] [CrossRef]
- Sen, S.; Nehorai, A. OFDM MIMO Radar With Mutual-Information Waveform Design for Low-Grazing Angle Tracking. IEEE Trans. Signal Process. 2010, 58, 3152–3162. [Google Scholar] [CrossRef]
- Kershaw, D.; Evans, R. Optimal waveform selection for tracking systems. IEEE Trans. Inf. Theory 1994, 40, 1536–1550. [Google Scholar] [CrossRef]
- Zhu, P.; Liang, J.; Luo, Z.; Shen, X. Cognitive Radar Target Tracking Using Intelligent Waveforms Based on Reinforcement Learning. IEEE Trans. Geosci. Remote. Sens. 2023, 61, 5107315. [Google Scholar] [CrossRef]
- Song, D.; Zhao, B.; Wang, C. Waveform selection method for cognitive radar target tracking. Electron. Des. Eng. 2017, 25, 46–49. [Google Scholar] [CrossRef]
- Cao, X.; Zheng, Z.; An, D. Adaptive Waveform Selection Algorithm based on Reinforcement Learning for Cognitive Radar. In Proceedings of the 2019 IEEE 2nd International Conference on Automation, Electronics and Electrical Engineering (AUTEEE), Shenyang, China, 22–24 November 2019; pp. 208–213. [Google Scholar] [CrossRef]
- Thornton, C.E.; Buehrer, R.M.; Dhillon, H.S.; Martone, A.F. Universal Learning Waveform Selection Strategies for Adaptive Target Tracking. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 5798–5814. [Google Scholar] [CrossRef]
- Hu, J.; Wei, Z.; Li, Y.; Li, H.; Wu, J. Designing Unimodular Waveform(s) for MIMO Radar by Deep Learning Method. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 1184–1196. [Google Scholar] [CrossRef]
- Yunita, M.; Suryana, J.; Izzuddin, A. Error Performance Analysis of IMM-Kalman Filter for Maneuvering Target Tracking Application. In Proceedings of the 2020 6th International Conference on Wireless and Telematics (ICWT), Yogyakarta, Indonesia, 3–4 September 2020; pp. 1–6. [Google Scholar]
- Cao, J.; Zhang, X.; Hao, H.; Shi, X. Noncircular Signal Tracking with Distributed Passive Arrays: Combining Data Fusion and Extended Kalman Filter. IEEE Sens. J. 2024, 24, 757–768. [Google Scholar] [CrossRef]
- Vaishnav, P.; Santra, A. Continuous Human Activity Classification with Unscented Kalman Filter Tracking Using FMCW Radar. IEEE Sens. Lett. 2020, 4, 7001704. [Google Scholar] [CrossRef]
- Bao, Z.; Jiang, Q.; Liu, F. Multiple model efficient particle filter based track-before-detect for maneuvering weak targets. J. Syst. Eng. Electron. 2020, 31, 647–656. [Google Scholar]
- Rohal, P.; Ochodnicky, J. Target Tracking Based on Particle and Kalman Filter Combined with Neural Network. In Proceedings of the 2019 Communication and Information Technologies (KIT), Vysoke Tatry, Slovakia, 9–11 October 2019; pp. 1–6. [Google Scholar]
- Li, Y.; Bian, C.; Chen, H. Object Tracking in Satellite Videos: Correlation Particle Filter Tracking Method with Motion Estimation by Kalman Filter. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5630112. [Google Scholar] [CrossRef]
- Zhang, L.; Jiang, M. Cognitive Radar Target Tracking Algorithm based on Waveform Selection. In Proceedings of the 2021 IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 March 2021; pp. 1506–1510. [Google Scholar] [CrossRef]
- Youn, W.; Myung, H. Robust Interacting Multiple Model with Modeling Uncertainties for Maneuvering Target Tracking. IEEE Access 2019, 7, 65427–65443. [Google Scholar] [CrossRef]
- Cheng, C.; Tourneret, J.-Y.; Lu, X. A Rao-Blackwellized Particle Filter with Variational Inference for State Estimation With Measurement Model Uncertainties. IEEE Access 2020, 8, 55665–55675. [Google Scholar] [CrossRef]
- Schon, T.; Gustafsson, F.; Nordlund, P.J. Marginalized particle filters for mixed linear/nonlinear state-space models. IEEE Trans. Signal Process. 2005, 53, 2279–2289. [Google Scholar] [CrossRef]
- Hu, J.; Chen, H.; Li, Y.; Li, H.; Xie, J. Moving target parameter estimation for MIMO radar based on the improved particle filter. Multidimens. Syst. Signal Process. 2018, 29, 1–17. [Google Scholar] [CrossRef]
- Shen, M.; Sun, J.; Peng, H.; Zhao, D. Improving Localization Accuracy in Connected Vehicle Networks Using Rao–Blackwellized Particle Filters: Theory, Simulations, and Experiments. IEEE Trans. Intell. Transp. Syst. 2019, 20, 2255–2266. [Google Scholar] [CrossRef]
- Nguyen, N.H.; Dogancay, K.; Davis, L.M. Adaptive waveform selection for multistatic target tracking. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 688–701. [Google Scholar] [CrossRef]
- He, S.; Shin, H.-S.; Tsourdos, A. Distributed Joint Probabilistic Data Association Filter with Hybrid Fusion Strategy. IEEE Trans. Instrum. Meas. 2020, 69, 286–300. [Google Scholar] [CrossRef]
- Murphy, K.; Russell, S. Rao-Blackwellised Particle Filtering for Dynamic Bayesian Networks. In Sequential Monte Carlo Methods in Practice. Statistics for Engineering and Information Science; Doucet, A., de Freitas, N., Gordon, N., Eds.; Springer: New York, NY, USA, 2001. [Google Scholar] [CrossRef]
- Zedong, N.; Shengli, W. A maneuvering target tracking algorithm based on amplitude characteristics in sea clutter. In Proceedings of the 2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, China, 12–14 June 2020; pp. 1528–1533. [Google Scholar] [CrossRef]
- Vivone, G.; Braca, P. Joint Probabilistic Data Association Tracker for Extended Target Tracking Applied to X-Band Marine Radar Data. IEEE J. Ocean. Eng. 2016, 41, 1007–1019. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).