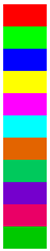Abstract
In hyperspectral image classification (HSIC), every pixel of the HSI is assigned to a land cover category. While convolutional neural network (CNN)-based methods for HSIC have significantly enhanced performance, they encounter challenges in learning the relevance of deep semantic features and grappling with escalating computational costs as network depth increases. In contrast, the transformer framework is adept at capturing the relevance of high-level semantic features, presenting an effective solution to address the limitations encountered by CNN-based approaches. This article introduces a novel adaptive learnable spectral–spatial fusion transformer (ALSST) to enhance HSI classification. The model incorporates a dual-branch adaptive spectral–spatial fusion gating mechanism (ASSF), which captures spectral–spatial fusion features effectively from images. The ASSF comprises two key components: the point depthwise attention module (PDWA) for spectral feature extraction and the asymmetric depthwise attention module (ADWA) for spatial feature extraction. The model efficiently obtains spectral–spatial fusion features by multiplying the outputs of these two branches. Furthermore, we integrate the layer scale and DropKey into the traditional transformer encoder and multi-head self-attention (MHSA) to form a new transformer with a layer scale and DropKey (LD-Former). This innovation enhances data dynamics and mitigates performance degradation in deeper encoder layers. The experiments detailed in this article are executed on four renowned datasets: Trento (TR), MUUFL (MU), Augsburg (AU), and the University of Pavia (UP). The findings demonstrate that the ALSST model secures optimal performance, surpassing some existing models. The overall accuracy (OA) is 99.70%, 89.72%, 97.84%, and 99.78% on four famous datasets: Trento (TR), MUUFL (MU), Augsburg (AU), and University of Pavia (UP), respectively.
1. Introduction
The advent of advanced imaging technologies has garnered increased attention for various remote sensing modalities, with hyperspectral remote sensing technology emerging as a vital domain. Distinguished from grayscale and RGB imagery, hyperspectral images (HSIs) are the three-dimensional (3D) data encapsulated across hundreds of contiguous spectral bands, offering an abundance of spectral information alongside intricate spatial texture information [1]. HSIs have found extensive applications across diverse sectors, including plant disease diagnosis [2], military reconnaissance [3], ecosystem assessment [4], urban planning [5], and target detection [6], among others [7,8,9]. Therefore, substantial research efforts have been channeled into HSI-related works, spanning classification [10], band selection [11], and anomaly detection tasks [12]. Notably, hyperspectral image classification (HSIC) has a critical status within this spectrum of applications, which aims to distinguish land covers precisely at the pixel level [13].
Primitively, the assessment of the similarity in spectral information was evaluated by statistical algorithms, which then served as a basis for distinguishing hyperspectral pixels [14,15]. Nonetheless, this approach encounters limitations due to the potential variability of spectral characteristics within identical land objects and the occurrence of similar spectral features across different land types. In the past, HSIC predominantly leveraged traditional machine learning models. Given that the spectral bands in HSIs typically exceed 100, whereas the actual categories of land objects are usually fewer than 30, this causes a notable redundancy in spectral information. To address this, machine learning algorithms often employ techniques, such as principal component analysis (PCA) [16], independent component analysis (ICA) [17], and linear discriminant analysis (LDA) [18], to mitigate spectral redundancy. Subsequently, classifiers like decision trees [19], support vector machines (SVMs) [20], and K-nearest neighbors (KNNs) [21] were applied to the refined features for classification. Although machine learning methods have marked a substantial advancement over earlier statistical approaches to performance, they largely depend on manually crafted feature extraction, which may not effectively extract the more intricate information embedded within hyperspectral data. This limitation underscores the need for more advanced methodologies capable of autonomously adapting the complex patterns inherent in HSIs [22].
The rapid evolution of deep learning [23,24,25,26] has rendered it a more potent tool than traditional machine learning for extracting abstract information through multi-layer neural networks, significantly improving classification performance [27]. Deep learning techniques are the forefront methods of HSIC. Chen et al. [28] first introduced deep learning to HSIC, utilizing stacked autoencoders to extract spatial–spectral features and achieve notable classification outcomes. Since then, a plethora of deep learning architectures have been applied to HSIC, including deep belief networks (DBNs) [29], convolutional neural networks (CNNs) [30], graph convolutional networks (GCNs) [31], vision transformers [32], and other models [33,34]. Notably, CNNs and vision transformers have emerged as a leading approach in HSIC, attributed to the exceptional ability of CNNs to capture intricate spatial and spectral patterns and of vision transformers to capture long-range information, thereby setting a benchmark in the methodological advancement.
Roy et al. [35] combined the strengths of three-dimensional and two-dimensional convolutional neural networks (3DCNNs and 2DCNNs, respectively) to create a hybrid spectral CNN that excels in spatial–spectral feature representation, enhancing spatial feature delineation. Sun et al. [36] introduced a novel classification model featuring heterogeneous spectral–spatial attention convolutional blocks, which supports plug-and-play functionality and adeptly extracts 3D features of HSIs. CNNs demonstrate formidable performance due to their intrinsic network architecture, but their effectiveness is somewhat constrained when processing the lengthy spectral feature sequences inherent to HSIs. Acknowledging the transformative potential of vision transformers, Hong et al. [37] developed a spectral transformer tailored for extracting discriminative spectral features from block frequency bands. Sun et al. [38] introduced a spectral–spatial feature tokenization transformer that adeptly captures sequential relationships and high-level semantic features. Although vision transformers have shown proficiency in handling spectral sequence features, their exploitation of local spatial information remains suboptimal. To address this gap, Wang et al. [39] proposed a novel spectral–spatial kernel that integrates with an enhanced visual transformation method, facilitating comprehensive extraction of spatial–spectral features. Huang et al. [40] introduced the 3D Swin Transformer (3DSwinT) model, specifically designed to embrace the 3D nature of HSI and to exploit the rich spatial–spectral information they contain. Fang et al. [41] developed the MAR-LWFormer, which joins the attention mechanism with a lightweight transformer to facilitate multi-channel feature representation. The MAR-LWFormer capitalizes on the multispectral and multiscale spatial–spectral information intrinsic to HSI data, showing remarkable effectiveness even at exceedingly low sampling rates. Despite the above application of deep learning methods widespread in HSI classification, several challenges persist in the field. In these methods, the CNN layers employ a fixed approach to feature extraction without the dynamic fusion of spectral–spatial information. Moreover, during the deep information extraction phase by the transformer, dynamic feature updates are not conducted, limiting the adaptability and potential effectiveness of the model in capturing intricate data patterns.
To fully extract the spectral–spatial fusion features in HSIs and increase classification performance, a novel adaptive learnable spectral–spatial fusion transformer (ALSST) is designed. The dual-branch adaptive spectral–spatial fusion gating mechanism (ASSF) is engineered to concurrently extract spectral–spatial fusion features from HSIs. Additionally, the learnable transition matrix layer scale is incorporated into the original vision transformer encoder to enhance training dynamics. Furthermore, the DropKey technique is implemented in the multi-head self-attention (MHSA) to mitigate the risk of overfitting. This approach enhances the model’s generalization capabilities, ensuring more robust and reliable performance across diverse hyperspectral datasets. The key contributions of the ALSST are as follows:
- In this study, a dual-branch fusion model named ALSST is designed to extract the spectral–spatial fusion features of HSIs. This model synergistically combines the prowess of CNNs in extracting local features with the capacity of a vision transformer to discern long-range dependencies. Through this integrated approach, the ALSST aims to provide a comprehensive learning mechanism for the spectral–spatial fusion features of HSIs, optimizing the ability of the model to interpret and classify complex hyperspectral data effectively.
- A dual-branch fusion feature extraction module known as ASSF is developed in the study. The module contains the point depthwise attention module (PDWA) and the asymmetric depthwise attention module (ADWA). The PDWA primarily focuses on extracting spectral features from HSIs, whereas the ADWA is tailored to capture spatial information. The innovative design of ASSF enables the exclusion of linear layers, thereby accentuating local continuity while maintaining the richness of feature complexity.
- The new transformer with a layer scale and DropKey (LD-Former) is proposed to increase the data dynamics and prevent performance degradation as the transformer deepens. The layer scale was added to the output of each residual block, and different output channels were multiplied by different values to make the features more refined. At the same time, the DropKey is adopted into self-attention (SA) to obtain DropKey self-attention (DSA). The combination of these two techniques overcomes the risk of overfitting and can train deeper transformers.
The remainder of this article is structured as follows: Section 2 delves into the underlying theory behind the proposed ALSST method. Section 3 introduces the four prominent HSI datasets, the experimental settings, and experiments conducted on datasets. Section 4 discusses the ablation analysis, the ratio of DropKey, and the impact of varying training samples. Section 5 provides a conclusion, summarizing the main findings and contributions of the article.
2. Methodology
2.1. Overall Architecture
The ALSST proposed in this article is shown in Figure 1. The ASSF with the PDWA and the ADWA is designed to enhance the spectral–spatial fusion feature extraction. The novel LD-Former is proposed to increase the data dynamics and prevent performance degradation as the transformer deepens.
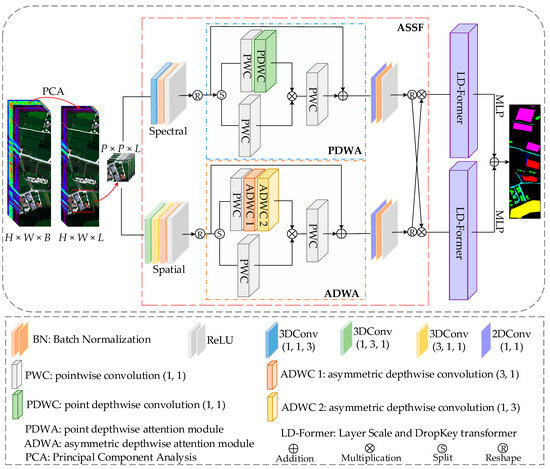
Figure 1.
Structure for proposed ALSST model. (The ASSF is proposed to exclude the fully connected layers and capture local continuity while considering complexity. The multiplication is used to fusion the spectral–spatial features. The LD-Former is designed to increase the data dynamics and prevent performance degradation as the transformer deepens. In this figure, is the size of the original HSI, is the size of HSI after PCA, and is the patches size).
From Figure 1, the original input data of the ALSST could be represented as , where height is , width is , and spectra are . HSIs feature extensive spectral bands that offer valuable information but concurrently elevate computational costs. The PCA is applied to reduce the spectral dimensions of the HSI, optimizing the balance between information retention and computational efficiency. The data after PCA would be reshaped to , of which is the amounts of bands after PCA.
is sent to dual-branch ASSF to extract spectral–spatial fusion features and . is firstly sent to the convolution kernel in the spectral branch to extract the spectral features , and then is reshaped to the to make the feature dimension match the subsequent PDWA. We put into the PDWA to focus on extracting spectral features. The outputs of the PDWA are sent to the convolution kernel for reducing the feature channels. Then, the new outputs are reshaped to the one-dimensional (1D) vectors. is synchronously sent to the convolution kernel and in the spatial branch to extract the spatial features , and then is reshaped to the to make the feature dimension match the subsequent ADWA. We put into the ADWA to focus on extracting spatial features. The outputs of the PDWA are also sent to the convolution kernel for reducing the feature channels. Then, the new outputs are also reshaped to the1D vectors. The and are multiplied to obtain the spectral–spatial fusion features for the subsequent LD-Former to extract the in-depth dynamic features information. The LD-Former may loop times. Then, the outputs and are put into the multi-layer perceptron (MLP) [42] separately for the final classification. The cross-entropy loss (CE) function is used to measure the degree of inconsistency between the predicted labels and the true labels .
2.2. Feature Extraction via ASSF
While transformer networks adeptly model global interactions between token embeddings via SA, they exhibit limitations in extracting fine-grained local feature patterns [42]. Given the proven effectiveness of CNNs in modeling spatial context features, particularly in HSI classification tasks, we integrate a CNN for feature extraction from input data. We draw inspiration from the GSAU [43] to devise the ASSF module for further refined feature representation. Central to ASSF are the PDWA and the ADWA, which bypass the linear layer and capture local continuity while managing complexity effectively.
The PDWA, deployed for extracting spectral features from HSIs, is depicted on the left of Figure 2. It comprises several key components: pointwise convolution (PWC), point depthwise convolution (PDWC), the multiplication operation, and the residual connection. These elements collaboratively function to enhance the feature extraction process. The input of the module is divided into and . is sent to the PWC layer to obtain . We feed into PDWC with convolution kernel to yield the output . Groups in the PDWC layer are equal to the channels of . Given that the convolution kernel size is and the number of groups equals the input channels, this configuration effectively concentrates on the channel information, enabling a focused analysis and processing of the spectral or feature channels in the data. This approach ensures that the convolution operation emphasizes inter-channel relationships, enhancing the ability to capture and exploit channel-specific features of the model. also obtains by a PWC. To keep a portion of the original information intact, no transformations or operations are applied to . This ensures the preservation of essential raw data characteristics within the analytical framework. The data obtained by multiplying and are sent to a new PWC and obtain the output . We set a random parameter matrix of size (1, 1, channels) and set it to be backpropagated and updated with training. The result of multiplying and is connected with by residual connection to obtain the output . By the matrix G, the adaptive update of the output of this module is achieved. The PWC employs a convolution kernel designed to modify the data dimensions, which is crucial for aligning the dimensions across different layers. The main process of the PDWA is as follows:
here, and represent the characteristic data of the two branches in the PDWA, respectively. and represent PDWC and multiplication.
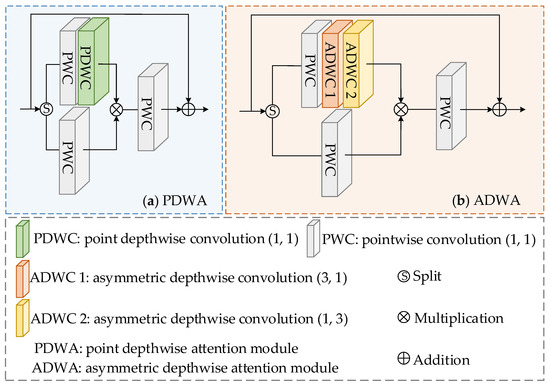
Figure 2.
Structure for proposed ASSF. PDWA is used to extract the spectral features of HSI, and ADWA is used to extract the spatial features of HSI.
The ADWA is primarily utilized to extract spatial features from HSIs, with its structure illustrated on the right of Figure 2. The ADWA framework encompasses several key components: the PWC, two layers of asymmetric depthwise convolution (ADWC), the multiplication operation, and the residual connection. These elements collectively enhance the capacity to capture and integrate spatial features of the model effectively, thereby enriching the overall feature representation. In this module, the PDWC within the PDWA is replaced by two ADWC layers with and convolution kernels, respectively, while all other operations remain consistent. This modification allows for a more nuanced extraction of spatial features by capturing variations along different dimensions, thereby enhancing the ability to discern spatial features within the data. The main processes of the ADWA are as follows:
where and represent the features of the two branches in the ADWA. and represent two ADWCs.
2.3. LD-Former Encoder
Figure 3 delineates the structure of the proposed LD-Former. The LD-Former encoders are adept at modeling deep semantic interrelations among feature tokens, transforming the input of LD-Former into a sequence of vectors. A class token is integrated at the beginning of this vector sequence to encapsulate the overall sequence information. Subsequently, positional encodings are embedded into the sequence to generate multiple tokens, with encoding similarity reflecting proximity in information. These tokens are then processed through the transformer encoder. The output from the multi-head DropKey self-attention (MHDSA) undergoes classification via an MLP, comprising one layer norm (LN) and two fully connected layers (FC), with a Gaussian error linear unit (GELU) [44] activation function employed for classification. The operations are iteratively applied times. In deeper models, attention maps of subsequent blocks tend to be more similar, suggesting limited benefits from excessively increasing depth.
Figure 3.
Structure for proposed LD-Former. In this paper, MHDSA is the DropKey multi-head self-attention, ADD is the residual connection, MLP is the multi-layer perceptron, and NORM is the layer norm. N is the times of the encoder loops.
To address potential limitations of deep transformers, a learnable matrix (layer scale), inspired by CaiT models [45], is integrated into the transformer encoder. This layer scale introduces a learnable diagonal matrix to each residual block’s output, initialized near zero, enabling differentiated scaling across SA or MLP output channels, thereby refining feature representation and supporting the training of deeper models. The formulas are as follows:
here, LN is the layer norm and MLP is the feed-forward network in the LD-Former. and are learnable weights for the outputs of MHDSA and MLP. The diagonal values are all initialized to the fixed small value . When the depth is within 18, , when the depth is within 24, , and is adopted to the deeper networks.
Figure 4 delineates the structure of the proposed MHDSA. To elucidate the interrelations among feature tokens, the learnable weights denoted , , and are established for the SA mechanism. These weights are utilized to multiply with the feature tokens, subsequently linearly aggregating them into three distinct matrices representing queries (Q), keys (K), and values (V). The is then applied to the resultant scores, transforming them into weight probabilities, thereby facilitating the SA computation, as delineated below.
where represents the dimension of .
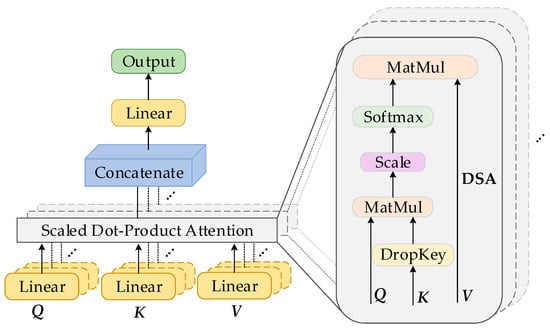
Figure 4.
Structure for proposed MHDSA. Q, K, and V are query, key, and value matrices.
At the same time, DropKey [46] is an innovative regularization technique designed for MHSA. It is an effective tool to combat overfitting, particularly in scenarios characterized by a scarcity of samples. DropKey prevents the model from relying too heavily on specific feature interactions by selectively dropping keys in the attention mechanism. It promotes a more generalized learning process that enhances the performance of the model on unseen data. The DSA computation is delineated below.
here, n is the number of feature tokens. is the ratio of DropKey. A structure analogous to MHSA named MHDSA is implemented in the approach, utilizing multiple sets of weights. MHDSA comprises several DSA units, where the scores from each DSA are aggregated. This method allows for a diversified and comprehensive analysis of the input features, capturing various aspects of the data through different attention perspectives. The formulation of this process is detailed in the following expression.
here, is the attention heads number and is the parameter matrix.
2.4. Final Classifier
The overarching algorithm of the ALSST for HSIC is detailed in Algorithm 1. The features and extracted from the LD-Former encoders are fed into MLP layers for the terminal classification stage. Each MLP has two linear layers and a GELU operation. The size of the output layer in MLP is customized to match the total class count, enabling the normalization of the activations of output units to sum to one.
This normalization makes the output embody a probability distribution of the class labels. Aggregating the final two output probability vectors yields the ultimate probability vector, with the maximum probability value designating the label of a pixel. Subsequently, the CE function is employed to calculate the loss value to enhance the precision of the classification results.
| Algorithm 1 Adaptive Learnable Spectral–spatial Fusion Transformer for Hyperspectral Image Classification. | |
| Input: HSI: , Labels: , Patches = 11 × 11, PCA = 30. | |
| Output: Prediction: | |
| 1 | Initialize: batch size = 64, epochs = 100, the initial learning rate of the optimizer Adam depends on datasets. |
| 2 | PCA: . |
| 3 | Patches: Accomplish the slicing process for HSI to acquire the small patches . |
| 4 | Split and into training sets and test sets ( has the class labels, and has not the class labels). |
| 5 | Training ALSST (begin) |
| 6 | for epoch in range(epochs): |
| 7 | for i, (,) in enumerate (): |
| 8 | Generate the spectral–spatial fusion features using the ASSF. |
| 9 | Perform the LD-Former encoder: |
| 10 | The learnable class tokens are added to the first locations of the 1D spectral–spatial fusion feature vectors derived from ASSF, while the positional embedding is carried out to the total feature vectors, to form the semantic tokens. The semantic tokens learned by Equations (3)–(7). |
| 11 | Input the spectral–spatial class tokens from LD-Former into the MLP. |
| 12 | |
| 13 | |
| 14 | Training ALSST (end) and test ALSST |
| 15 | |
3. Experimental Results
3.1. Data Description
The performance of the proposed ALSST method in this article is evaluated on four public multi-modal datasets: Trento (TR), MUUFL (MU) [47,48], Augsburg (AU), and University of Pavia (UP). Details of all datasets are described as follows.
- TR dataset
The TR dataset covers a rural area surrounding the city of Trento, Italy. It includes 600 × 166 pixels and six categories. The HSI has 63 bands in the wavelength range from 420.89 to 989.09 nm. The spectral resolution is 9.2 nm, and the spatial resolution is 1 m. The pseudo-color image of HSIs and the ground-truth image are in Figure 5. The color, class name, training samples, and test samples for the TR dataset are in Table 1.

Figure 5.
TR dataset. (a) Pseudo-color image; (b) Ground-truth image.

Table 1.
Details on TR dataset.
- 2.
- MU dataset
The MU dataset covers the University of Southern Mississippi Gulf Park Campus, Long Beach, Mississippi, USA. The dataset was acquired in November 2010 with a spatial resolution of 1 m per pixel. The original dataset is 325 × 337 pixels with 72 bands, and the imaging spectral range is between 380 nm and 1050 nm. Due to the influence of imaging noise, the first 4 and the last 4 bands were removed, and finally, 64 bands were used. The invalid area on the right of the original image is removed, and the 325 × 220 pixels is retained. Objects in the imaging scene were placed into eleven categories. The pseudo-color image of the HSI and the ground-truth image are in Figure 6. The details of MU dataset are in Table 2.
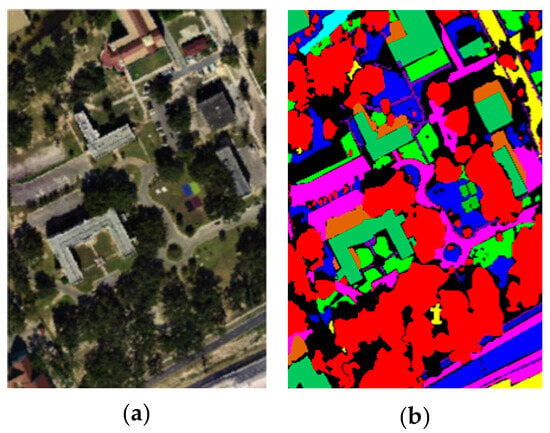
Figure 6.
MU dataset. (a) Pseudo-color image; (b) Ground-truth image.

Table 2.
Details on MU dataset.
- 3.
- AU dataset
The AU dataset was captured over the city of Augsburg, Germany. The spatial resolutions were down sampled to a resolution of 30 m. The HSI has 180 bands from 0.4 to 2.5 μm. The pixels size of AU is 332 × 485, and it depicts seven different land cover classes. The pseudo-color image of the HSI and the ground-truth image are in Figure 7. Details on the AU dataset are provided in Table 3.

Figure 7.
AU dataset. (a) Pseudo-color image; (b) Ground-truth image.

Table 3.
Details on AU dataset.
- 4.
- UP dataset
The UP hyperspectral dataset, captured in 2003, focuses on the urban area around the University of Pavia in Northern Italy. The dataset comprises 610 × 340 pixels, encompassing nine distinct categories of ground objects. It includes 115 consecutive spectral bands ranging from 0.43 to 0.86 μm, offering a spatial resolution of 1.3 m. Due to noise, 12 bands were discarded, leaving 103 bands for analysis. The pseudo-color image of the HSI, and the ground-truth image are in the Figure 8. Table 4 displays the image cube, ground-truth image, class names, training samples, and test samples for the UP dataset.

Figure 8.
UP dataset. (a) Pseudo-color image; (b) Ground-truth image.

Table 4.
Details on UP dataset.
3.2. Experimental Setting
The experiments presented in this article are executed on Windows 11 and an RTX 3090Ti. The programming is conducted in Python 3.8, utilizing PyTorch 1.12.0. The input image size is 11 × 11, with a batch size of 64 and 100 epochs. The PCA method is employed to reduce the dimensionality of HSIs to 30. To enhance the robustness of the experimental outcomes, training and test samples for the TR, MU, AU, and UP are selected randomly. Table 2, Table 3, Table 4 and Table 5 detail the number of training and testing samples for these four datasets, and the selection of training samples for each class depends on its distribution and total number. The experiments are repeated five times to ensure consistency, with the final classification results representing the average of these iterations. The evaluation metrics of overall accuracy (OA), average accuracy (AA), and the statistical Kappa coefficient (K) are the primary indicators of performance in these classification experiments.
It is imperative to compare experimental outcomes across different parameter settings to achieve optimal accuracy. In this article, variables such as the initial learning rate of the Adam optimizer, the number of attention heads, the depth of encoders, and the depth of the LD-Former are rigorously tested across all datasets. A controlled variable method is employed in these experiments, ensuring consistency in input size, number of epochs, experiment iterations, and the quantity of training and testing samples.
3.2.1. Initial Learning Rate
Table 5 illustrates the impact of various initial learning rates for the Adam optimizer on the experimental outcomes. The initial learning rates of 0.001, 0.0005, and 0.0001 are evaluated in the experiments. The findings indicate that the optimal accuracy is achieved when the initial learning rates for the TR, MU, and UP datasets are 0.001 and for the AU dataset is 0.0005.

Table 5.
OA (%) of different initial learning rate on all datasets (Bold represents the best accuracy).
Table 5.
OA (%) of different initial learning rate on all datasets (Bold represents the best accuracy).
| Datasets | Initial Learning Rate | ||
|---|---|---|---|
| 0.001 | 0.0005 | 0.0001 | |
| TR | 99.70 ± 0.03 | 99.68 ± 0.04 | 99.59 ± 0.01 |
| MU | 89.72 ± 0.36 | 88.67 ± 0.47 | 87.76 ± 0.69 |
| AU | 97.82 ± 0.11 | 97.84 ± 0.09 | 97.39 ± 0.04 |
| UP | 99.78 ± 0.03 | 99.56 ± 0.05 | 99.54 ± 0.06 |
3.2.2. Depth and Heads
Figure 9 presents the combined influence of the number of attention heads, encoder depths, and the depth of the LD-Former on the performance of the ALSST. In this work, we evaluate the LD-Former with four distinct configurations (i.e., 4 + 2, 4 + 1, 8 + 2, and 8 + 1) for the number of attention heads and the depth of the encoder. The findings indicate that the optimal configuration for the TR, MU, and UP datasets involves setting the attention heads and LD-Former depth to 8 and 1, respectively, while a different optimal setting is 4 and 1 for the AU dataset.
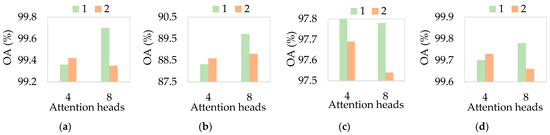
Figure 9.
Combined effect of the heads for attention, and the depth for encoders on four datasets. (a) TR dataset (8 + 1); (b) MU dataset (8 + 1); (c) AU dataset (4 + 1); (d) UP dataset (8 + 1). The horizontal axis represents the attention heads, while the vertical axis denotes the OA (%). The green represents one encoder depth and fusion block depth, and the orange represents two encoder depths and fusion block depths.
3.3. Performance Comparison
In this section, we evaluate the performance of the proposed ALSST against various methods, including LiEtAl [49], SSRN [50], HyBridSN [35], DMCN [10], SpectralFormer [37], SSFTT [38], morpFormer [51], and 3D-ConvSST [52], to validate its classification effectiveness. The initial learning rates for all methods are aligned with those used for the ALSST to ensure a fair comparison, facilitating optimal performance evaluation. The classification outcomes and maps for each method across all datasets are detailed in Section 3.3.1. Subsequently, Section 3.3.2 provides a comparative analysis of resource consumption and computational complexity for all the methods.
3.3.1. Experimental Results
The classification outcomes for the proposed ALSST model and all compared methods are detailed in Table 6, Table 7, Table 8 and Table 9. The ALSST model consistently outperforms others across various evaluation metrics, with an OA of 99.70%, 89.72%, 97.84%, and 99.78%; AA of 99.53%, 92.39%, 90.30%, and 99.57%; and K × 100 of 99.60%, 86.59%, 96.91%, and 99.71% on the TR, MU, AU, and UP datasets. To provide a visual comparison of classification performance, Figure 10, Figures 12, 14 and 16 display the classification maps generated by all the considered methods, and Figures 11, 13, 15 and 17 display the T-SNE visualization by all the considered methods, further illustrating the superior performance of the ALSST model.
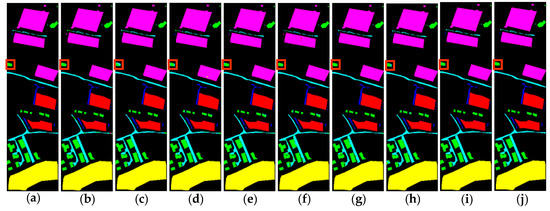
Figure 10.
Classification images of different methods on TR dataset. (a) Ground-truth Image; (b) LiEtAl (98.10%); (c) SSRN (98.91%); (d) HyBridSN (98.57%); (e) DMCN (99.35%); (f) SpectralFormer (97.99%); (g) SSFTT (98.18%); (h) morpFormer (99.02%); (i) 3D-ConvSST (99.58%); (j) ALSST (99.70%).
- TR dataset
Table 6 indicates that SpectralFormer yields the most favorable classification outcomes among the compared methods. This inferior performance is attributed to its approach of directly flattening image blocks into vectors, a process that disrupts the intrinsic structural information of the image. Following SpectralFormer, LiEtAl ranks as the second-least-effective, primarily due to its simplistic structure, which limits its feature extraction capabilities. The proposed ALSST improves OA by 1.60%, 0.79%, 1.13%, 0.35%, 1.71%, 0.52%, 0.68%, and 0.12% compared to LiEtAl, SSRN, HyBridSN, DMCN, SpectralFormer, SSFTT, morpFormer, and 3D-ConvSST. At the same time, the proposed ALSST improves K × 100 by 2.80%, 1.17%, 1.57%, 0.66%, 2.99%, 0.83%, 1.04%, and 0.14% on AA, and improves 2.14%, 1.06%, 1.51%, 0.47%, 2.29%, 0.70%, 0.91%, and 0.16%, respectively. In addition, it could be found that the accuracy of category 3, 4 and 5 of the proposed ALSST reached 100%. The simplicity of the sample distribution facilitates the effective learning of feature information.

Table 6.
OA, AA, K and per-class accuracy for TR dataset (Bold represents the best accuracy).
Table 6.
OA, AA, K and per-class accuracy for TR dataset (Bold represents the best accuracy).
| Class | LiEtAl | SSRN | HyBridSN | DMCN | SpectralFormer | SSFTT | Morp- Former | 3D-ConvSST | ALSST |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 99.39 ± 0.42 | 99.68 ± 0.23 | 99.23 ± 0.62 | 99.65 ± 0.35 | 99.10 ± 0.72 | 98.84 ± 0.61 | 97.89 ± 0.75 | 98.94± 0.39 | 99.56 ± 0.05 |
| 2 | 92.61 ± 1.47 | 94.31 ± 6.20 | 95.18 ± 2.08 | 99.74 ± 0.49 | 94.49 ± 0.39 | 98.01 ± 0.50 | 96.49 ± 2.57 | 99.06 ± 0.64 | 99.48 ± 0.25 |
| 3 | 97.75 ± 0.37 | 99.68 ± 0.64 | 99.89 ± 0.21 | 99.44 ± 0.56 | 97.54 ± 0.58 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 |
| 4 | 99.88 ± 0.12 | 99.99 ± 0.01 | 100 ± 0.00 | 99.99 ± 0.01 | 99.92 ± 0.08 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 |
| 5 | 99.62 ± 0.40 | 99.42 ± 1.07 | 99.24 ± 0.48 | 99.97 ± 0.03 | 99.65 ± 0.23 | 99.99 ± 0.01 | 99.97 ± 0.02 | 99.95 ± 0.05 | 100 ± 0.00 |
| 6 | 91.16 ± 2.99 | 97.06 ± 1.66 | 94.18 ± 1.58 | 96.42 ± 1.12 | 88.51 ± 5.55 | 95.38 ± 2.23 | 96.58 ± 2.84 | 98.39 ± 0.51 | 98.17 ± 0.23 |
| OA (%) | 98.10 ± 0.24 | 98.91 ± 0.55 | 98.57 ± 0.22 | 99.35 ± 0.17 | 97.99 ± 0.64 | 99.18 ± 0.12 | 99.02 ± 0.28 | 99.58 ± 0.08 | 99.70 ± 0.03 |
| AA (%) | 96.73 ± 0.41 | 98.36 ± 0.82 | 97.96 ± 0.26 | 98.87 ± 0.35 | 96.54 ± 0.51 | 98.70 ± 0.22 | 98.49 ± 0.42 | 99.39 ± 0.11 | 99.53 ± 0.05 |
| K × 100 | 97.46 ± 0.26 | 98.54 ± 0.74 | 98.09 ± 0.29 | 99.13 ± 0.58 | 97.31 ± 0.49 | 98.90 ± 0.17 | 98.69 ± 0.38 | 99.44 ± 0.11 | 99.60 ± 0.04 |
As depicted in Figure 10, the ALSST model exhibits the least amount of salt-and-pepper noise in its classification maps compared to other methods, demonstrating its superior ability to produce cleaner and more accurate classification results. The category in the red box is represented by green, and only the proposed method can achieve all green, while other comparison methods are mixed with blue. It can also be seen from Figure 11 that the clustering effect of the model with higher precision is better, and the clustering effect of the ALSST is the best. Taking categories 2 and 8 as examples, the ALSST can separate them to a greater extent.
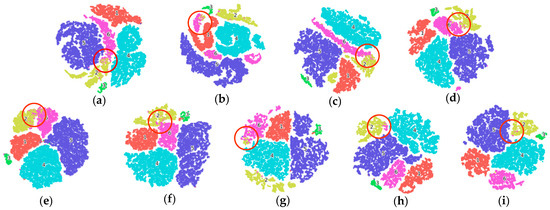
Figure 11.
T-SNE visualization on the TR dataset with different methods. (a) LiEtAl (98.10%); (b) SSRN (98.91%); (c) HyBridSN (98.57%); (d) DMCN (99.35%); (e) SpectralFormer (97.99%); (f) SSFTT (98.18%); (g) morpFormer (99.02%); (h) 3D-ConvSST (99.58%); (i) ALSST (99.70%).
- 2.
- MU dataset
Table 7 shows that LiEtAl has the worst classification results, and MFT_PT has the second worst because it only carries out ordinary convolutional feature extraction on HSIs. The OA of the proposed ALSST rises by 6.84%, 2.78%, 4.50%, 2.33%,2.64%, 2.66%, 4.76%, and 3.51% compared to LiEtAl, SSRN, HyBridSN, DMCN, SpectralFormer, SSFTT, morpFormer, and 3D-ConvSST. Meanwhile, the AA rises by 7.26%, 2.05%, 3.10%, 2.30%, 3.09%, 3.21%, 4.82%, and 4.22%, and the K × 100 rises by 8.73%, 3.54%, 5.62%, 2.99%, 3.45%, 3.40%, 5.98%, and 4.47%. The uneven and intricate sample distribution of the MU dataset causes considerable challenges in improving classification accuracy. The ALSST model leverages dynamic spectral–spatial fusion feature information to obtain a superior classification performance relative to other algorithms.

Table 7.
OA, AA, K and per-class accuracy for MU dataset (Bold represents the best accuracy).
Table 7.
OA, AA, K and per-class accuracy for MU dataset (Bold represents the best accuracy).
| Class | LiEtAl | SSRN | HyBridSN | DMCN | SpectralFormer | SSFTT | Morp- Former | 3D-ConvSST | ALSST |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 85.06 ± 2.01 | 87.51 ± 1.37 | 84.03 ± 3.53 | 87.76 ± 2.37 | 88.62 ± 0.36 | 88.16 ± 0.57 | 85.14 ± 2.26 | 87.46 ± 0.89 | 89.65 ± 1.03 |
| 2 | 77.97 ± 3.56 | 83.77 ± 4.79 | 83.28 ± 2.45 | 84.85 ± 6.81 | 78.01 ± 9.75 | 84.27 ± 9.82 | 79.49 ± 6.40 | 81.75 ± 2.38 | 88.06 ± 1.17 |
| 3 | 74.57 ± 5.76 | 81.63 ± 3.24 | 79.96 ± 2.46 | 78.90 ± 3.35 | 81.75 ± 8.58 | 79.53 ± 3.86 | 81.83 ± 2.22 | 77.71 ± 4.43 | 86.21 ± 1.12 |
| 4 | 89.03 ± 4.60 | 95.27 ± 0.70 | 97.15 ± 1.16 | 96.42 ± 1.54 | 94.88 ± 2.49 | 93.89 ± 7.73 | 96.30 ± 0.65 | 94.62 ± 1.23 | 94.18 ± 1.85 |
| 5 | 81.11 ± 3.52 | 84.43 ± 1.04 | 82.14 ± 1.69 | 88.05 ± 3.91 | 88.62 ± 0.36 | 84.34 ± 3.17 | 79.83 ± 5.17 | 85.35 ± 2.31 | 87.77 ± 2.57 |
| 6 | 99.49 ± 0.51 | 100 ± 0.00 | 99.81 ± 0.25 | 99.84 ± 0.16 | 99.43 ± 0.57 | 99.68 ± 0.32 | 99.56 ± 0.38 | 99.24 ± 1.01 | 100 ± 0.00 |
| 7 | 87.48 ± 1.81 | 94.07 ± 0.95 | 90.06 ± 2.08 | 92.44 ± 3.04 | 91.38 ± 2.04 | 94.30 ± 2.57 | 90.16 ± 2.72 | 87.83 ± 2.07 | 95.59 ± 0.88 |
| 8 | 88.90 ± 4.96 | 91.64 ± 2.12 | 95.86 ± 1.27 | 94.56 ± 2.32 | 92.28 ± 0.85 | 93.03 ± 1.47 | 92.82 ± 2.00 | 93.76 ± 1.21 | 94.38 ± 0.55 |
| 9 | 64.96 ± 1.89 | 77.67 ± 2.34 | 76.99 ± 1.71 | 75.45 ± 3.57 | 76.79 ± 0.93 | 78.93 ± 1.39 | 76.16 ± 6.12 | 72.74 ± 1.40 | 83.45 ± 2.50 |
| 10 | 92.75 ± 4.21 | 99.39 ± 1.21 | 93.94 ± 3.31 | 94.24 ± 5.76 | 93.94 ± 6.06 | 86.68 ± 10.92 | 83.03 ± 10.43 | 90.30 ± 3.53 | 98.18 ± 1.48 |
| 11 | 97.14 ± 1.34 | 98.32 ± 0.92 | 98.99 ± 0.34 | 99.24 ± 0.76 | 99.50 ± 0.52 | 98.32 ± 1.68 | 98.99 ± 0.34 | 99.16 ± 0.03 | 98.82 ± 0.67 |
| OA (%) | 82.88 ± 2.30 | 86.94 ± 0.87 | 85.22 ± 1.47 | 87.39 ± 1.12 | 87.08 ± 1.24 | 87.06 ± 0.85 | 84.96 ± 1.10 | 86.21 ± 0.70 | 89.72 ± 0.36 |
| AA (%) | 85.13 ± 1.20 | 90.34 ± 0.49 | 89.29 ± 0.62 | 90.09 ± 0.99 | 89.30 ± 1.12 | 89.18 ± 1.64 | 87.57 ± 0.80 | 88.17 ± 0.53 | 92.39 ± 0.51 |
| K × 100 | 77.86 ± 0.93 | 83.05 ± 1.08 | 80.97 ± 1.75 | 83.60 ± 0.21 | 83.14 ± 1.64 | 83.19 ± 0.43 | 80.61 ± 1.31 | 82.12 ± 0.87 | 86.59 ± 0.46 |
As can be seen from the area inside the blue box in Figure 12, the classification image produced by the ALSST aligns most closely with the ground-truth image. As can be seen from the area inside the red circle of the T-SNE visualization in Figure 13, the ALSST has the best clustering effect.
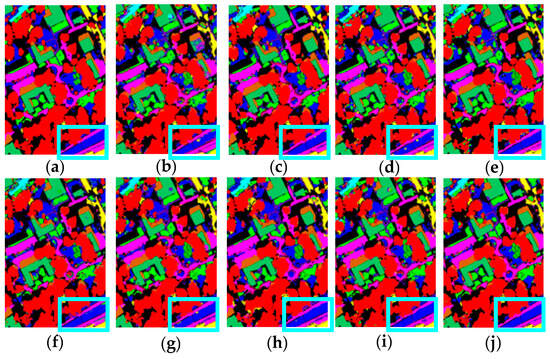
Figure 12.
Classification images of different methods on MU dataset. (a) Ground-truth Image; (b) LiEtAl (82.88%); (c) SSRN (86.94%); (d) HyBridSN (85.22%); (e) DMCN (87.39%); (f) SpectralFormer (87.08%); (g) SSFTT (87.06%); (h) morpFormer (84.96%); (i) 3D-ConvSST (86.21%); (j) ALSST (89.72%).
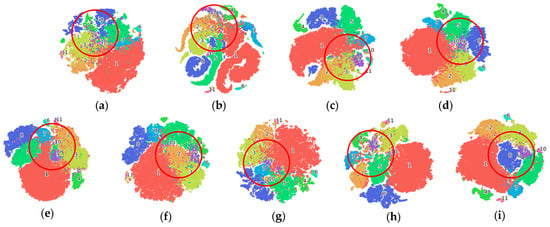
Figure 13.
T-SNE visualization on the MU dataset with different methods. (a) LiEtAl (82.88%); (b) SSRN (86.94%); (c) HyBridSN (85.22%); (d) DMCN (87.39%); (e) SpectralFormer (87.08%); (f) SSFTT (87.06%); (g) morpFormer (84.96%); (h) 3D-ConvSST (86.21%); (i) ALSST (89.72%).
- 3.
- AU dataset
As Table 8 shows, SpectralFormer has the worst classification results, and LiEtAl has the second worst. The OA of the ALSST increased by 3.00%, 0.43%, 1.34%, 1.60%, 3.95%, 0.76%, 0.99%, and 0.70% compared to LiEtAl, SSRN, HyBridSN, DMCN, SpectralFormer, SSFTT, morpFormer, and 3D-ConvSST. Simultaneously, the AA of the proposed method increased by 18.64%, 2.56%, 5.86%, 9.27%, 18.64%, 4.18%, 2.27%, and 3.55%, and the K×100 increased by 4.33%, 0.62%, 1.93%, 2.31%, 5.69%, 1.10%, 1.43%, and 1.01%.
The red boxed area in Figure 14 indicates that the ALSST model generates classification maps with minimal salt-and-pepper noise compared to alternative methods, showcasing its capability to yield more precise classification outcomes. Furthermore, Figure 15 reveals that the higher the accuracy, the better the clustering effects, and the ALSST can distinguish categories 3 and 6 to the greatest extent.
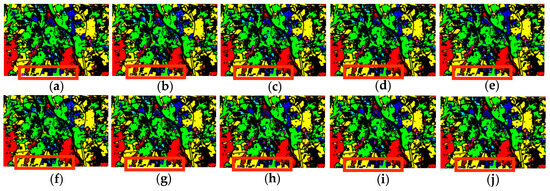
Figure 14.
Classification images of different methods on AU dataset. (a) Ground-truth Image; (b) LiEtAl (94.84%); (c) SSRN (97.41%); (d) HyBridSN (96.50%); (e) DMCN (96.24%); (f) SpectralFormer (93.89%); (g) SSFTT (97.08%); (h) morpFormer (96.85%); (i) 3D-ConvSST (97.14%); (j) ALSST (97.84%).
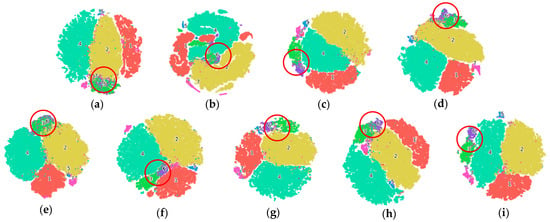
Figure 15.
T-SNE visualization on the AU dataset with different methods. (a) LiEtAl (94.84%); (b) SSRN (97.41%); (c) HyBridSN (96.50%); (d) DMCN (96.24%); (e) SpectralFormer (93.89%); (f) SSFTT (97.08%); (g) morpFormer (96.85%); (h) 3D-ConvSST (97.14%); (i) ALSST (97.84%).

Table 8.
OA, AA, K and per-class accuracy for AU dataset (Bold represents the best accuracy).
Table 8.
OA, AA, K and per-class accuracy for AU dataset (Bold represents the best accuracy).
| Class | LiEtAl | SSRN | HyBridSN | DMCN | SpectralFormer | SSFTT | Morp- Former | 3D-ConvSST | ALSST |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 98.25 ± 0.43 | 98.94 ± 0.22 | 99.12 ± 0.26 | 98.59 ± 0.56 | 86.10 ± 0.44 | 98.82 ± 0.08 | 97.71 ± 0.21 | 99.09 ± 0.32 | 98.67 ± 0.25 |
| 2 | 77.97 ± 3.56 | 99.23 ± 0.25 | 99.16 ± 0.36 | 98.52 ± 0.44 | 96.10 ± 1.44 | 99.02 ± 0.33 | 98.54 ± 0.25 | 98.58 ± 0.25 | 99.06 ± 0.09 |
| 3 | 97.54 ± 0.48 | 89.29 ± 1.18 | 95.61 ± 1.00 | 87.64 ± 1.51 | 75.99 ± 8.92 | 90.13 ± 1.39 | 89.69 ± 1.46 | 93.33 ± 1.53 | 95.96 ± 0.39 |
| 4 | 98.54 ± 0.22 | 99.12 ± 0.22 | 98.95 ± 0.21 | 99.02 ± 0.58 | 98.66 ± 0.34 | 98.77 ± 0.34 | 98.53 ± 0.11 | 98.86 ± 0.18 | 99.13 ± 0.14 |
| 5 | 64.97 ± 5.04 | 85.01 ± 5.23 | 84.64 ± 9.87 | 71.08 ± 3.99 | 48.88 ± 7.61 | 79.09 ± 5.60 | 84.88 ± 3.06 | 81.02 ± 2.98 | 87.39 ± 4.08 |
| 6 | 46.60 ± 2.01 | 69.67 ± 4.19 | 72.04 ± 3.59 | 47.82 ± 5.15 | 27.56 ± 9.54 | 70.12 ± 3.37 | 75.45 ± 3.58 | 64.48 ± 2.90 | 78.80 ± 1.73 |
| 7 | 58.39 ± 3.58 | 72.93 ± 2.74 | 72.67 ± 1.95 | 64.51 ± 1.86 | 55.50 ± 4.95 | 66.88 ± 1.20 | 71.36 ± 3.58 | 71.90 ± 2.29 | 73.08 ± 0.60 |
| OA (%) | 94.84 ± 0.39 | 97.41 ± 0.24 | 96.50 ± 0.08 | 96.24 ± 1.36 | 93.89 ± 0.27 | 97.08 ± 0.18 | 96.85 ± 0.07 | 97.14 ± 0.18 | 97.84 ± 0.09 |
| AA (%) | 71.66 ± 0.85 | 87.74 ± 1.59 | 84.44 ± 0.58 | 81.03 ± 2.30 | 71.66 ± 2.58 | 86.12 ± 1.93 | 88.03 ± 1.21 | 86.75 ± 1.02 | 90.30 ± 0.71 |
| K × 100 | 92.58 ± 0.79 | 96.29 ± 0.34 | 94.98 ± 0.11 | 94.60 ± 0.42 | 91.22 ± 0.43 | 95.81 ± 0.25 | 95.48 ± 0.10 | 95.90 ± 0.26 | 96.91 ± 0.13 |
- 4.
- UP dataset
According to Table 9, LiEtAl exhibits the lowest classification performance, with SpectralFormer exhibiting the second lowest. The ALSST model demonstrates significant improvements in the OA of 1.92%, 0.22%, 1.29%, 0.58%, 1.77%, 0.32%, 0.52%, and 0.26% when compared to LiEtAl, SSRN, HyBridSN, DMCN, SpectralFormer, SSFTT, morpFormer, and 3D-ConvSST, respectively. Similarly, the AA values enhance by 3.30%, 0.37%, 1.81%, 0.98%, 2.97%, 0.50%, 0.96%, and 0.57%, while the K × 100 increases by 2.55%, 0.29%, 1.72%, 0.77%, 2.35%, 0.42%, 0.69%, and 0.35%.

Table 9.
OA, AA, K and per-class accuracy for UP dataset (Bold represents the best accuracy).
Table 9.
OA, AA, K and per-class accuracy for UP dataset (Bold represents the best accuracy).
| Class | LiEtAl | SSRN | HyBridSN | DMCN | SpectralFormer | SSFTT | Morp- Former | 3D-ConvSST | ALSST |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 99.06 ± 0.4 | 99.8 ± 0.08 | 98.22 ± 0.31 | 99.70 ± 0.14 | 97.54 ± 0.18 | 99.73 ± 0.29 | 99.65 ± 0.10 | 99.81 ± 0.17 | 99.99 ± 0.01 |
| 2 | 99.76 ± 0.10 | 99.99 ± 0.03 | 99.95 ± 0.04 | 99.95 ± 0.05 | 99.89 ± 0.09 | 99.97± 0.02 | 99.97 ± 0.03 | 99.97 ± 0.02 | 99.99 ± 0.01 |
| 3 | 86.53 ± 1.52 | 97.07 ± 1.93 | 93.24 ± 1.30 | 94.78 ± 2.55 | 85.79 ± 2.05 | 97.39 ± 0.87 | 98.06 ± 1.38 | 97.55 ± 1.04 | 99.91 ± 0.11 |
| 4 | 95.49 ± 0.54 | 99.31 ± 0.41 | 98.43 ± 0.38 | 97.20 ± 1.20 | 97.45 ± 0.74 | 97.95 ± 0.64 | 98.34 ± 0.39 | 97.98 ± 0.47 | 98.17 ± 0.35 |
| 5 | 100 ± 0.00 | 99.95 ± 0.09 | 100 ± 0.00 | 100 ± 0.00 | 99.98 ± 0.03 | 99.94 ± 0.09 | 99.55 ± 0.27 | 100 ± 0.00 | 99.97 ± 0.04 |
| 6 | 97.56 ± 0.65 | 100 ± 0.00 | 97.70 ± 0.29 | 99.89 ± 0.15 | 99.31 ± 0.47 | 99.75 ± 0.29 | 99.99 ± 0.02 | 100 ± 0.00 | 99.98 ± 0.04 |
| 7 | 98.86 ± 1.18 | 98.53 ± 0.55 | 99.41 ± 0.4 | 99.49 ± 0.38 | 99.43 ± 0.24 | 99.90 ± 0.19 | 99.79 ± 0.14 | 99.95 ± 0.06 | 100 ± 0.00 |
| 8 | 94.60 ± 1.03 | 98.07 ± 0.43 | 94.90 ± 1.00 | 97.40 ± 1.00 | 94.36 ± 1.28 | 98.30 ± 0.72 | 95.91 ± 0.91 | 98.75 ± 0.31 | 99.50 ± 0.23 |
| 9 | 94.58 ± 3.34 | 100 ± 0.00 | 97.98 ± 0.73 | 98.89 ± 1.22 | 95.62 ± 2.01 | 98.71 ± 0.51 | 96.24 ± 0.60 | 96.98 ± 0.57 | 98.62 ± 0.45 |
| OA (%) | 97.86 ± 0.39 | 99.56 ± 0.09 | 98.49 ± 0.16 | 99.20 ± 0.13 | 98.01 ± 0.11 | 99.46 ± 0.15 | 99.26 ± 0.05 | 99.52 ± 0.06 | 99.78 ± 0.03 |
| AA (%) | 96.27 ± 0.74 | 99.20 ± 0.19 | 97.76 ± 0.32 | 98.59 ± 0.24 | 96.60 ± 0.24 | 99.07 ± 0.25 | 98.61 ± 0.15 | 99.00 ± 0.13 | 99.57 ± 0.08 |
| K × 100 | 97.16 ± 0.52 | 99.42 ± 0.12 | 97.99 ± 0.21 | 98.94 ± 0.17 | 97.36 ± 0.15 | 99.29 ± 0.20 | 99.02 ± 0.07 | 99.36 ± 0.08 | 99.71 ± 0.04 |
The blue box area in Figure 16 underscores that higher accuracy correlates with reduced salt-and-pepper noise, affirming the precision of the ALSST model. Additionally, the red circle area of the T-SNE visualization in Figure 17 illustrates that the ALSST achieves the most effective clustering among the compared methods. These observations collectively indicate that the ALSST substantially enhances classification performance.
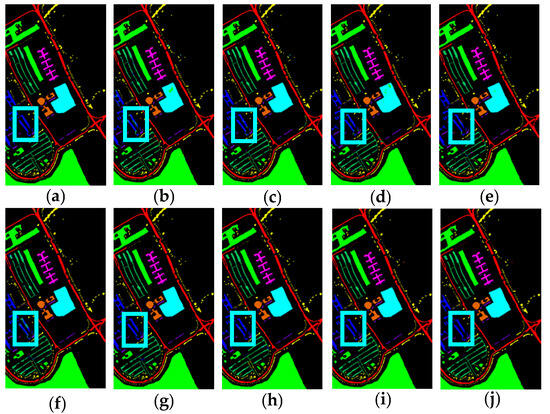
Figure 16.
Classification images of different methods on UP dataset. (a) Ground-truth Image; (b) LiEtAl (97.86%); (c) SSRN (99.56%); (d) HyBridSN (98.49%); (e) DMCN (99.20%); (f) SpectralFormer (98.01%); (g) SSFTT (99.46%); (h) morpFormer (99.26%); (i) 3D-ConvSST (99.52%); (j) ALSST (99.78%).
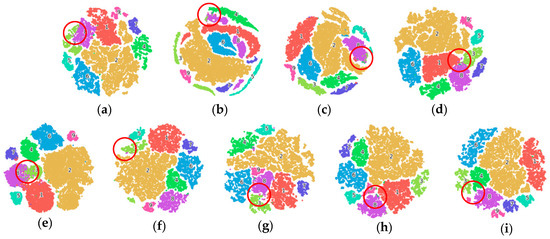
Figure 17.
T-SNE visualization on the UP dataset. (a) LiEtAl (97.86%); (b) SSRN (99.56%); (c) HyBridSN (98.49%); (d) DMCN (99.20%); (e) SpectralFormer (98.01%); (f) SSFTT (99.46%); (g) morpFormer (99.26%); (h) 3D-ConvSST (99.52%); (i) ALSST (99.78%).
3.3.2. Consumption and Computational Complexity
In this section, we conduct a thorough comparative analysis of the proposed ALSST against benchmark methods to evaluate classification performance. Main metrics, such as total parameters (TPs), training time (Tr), testing time (Te), and floating-point operations (Flops), are evaluated for each method. The detailed results are presented in Table 10. It is important to note that the padding in the convolution layers of the ALSST increases the number of parameters and the complexity of the model. However, the padding also introduces additional learnable features, which can contribute to enhancing classification accuracy.

Table 10.
Total parameters, training time, testing time, and Flops of all methods on different datasets (Bold represents the best accuracy).
The experimental configurations are consistent with those previously described. The 3D-ConvSST has the most Flops. The ALSST model demonstrates a reduction in total parameters compared to HyBridSN and DMCN and a decrease in Flops compared to DMCN. When analyzing the MU, AU, and UP datasets, the ALSST exhibits fewer Flops than SSRN, although it shows an increase in Flops for the TR dataset. The ALSST has a shorter testing duration, more total parameters, more Flops, and longer training time than the morpFormer on the TR dataset. Conversely, for the MU, AU, and UP datasets, the ALSST has shorter training times than morpFormer. The ALSST tends to have more total parameters and Flops compared to other methods across these datasets. Despite these aspects, the ALSST stands out by delivering superior classification performance, highlighting its effectiveness in handling diverse datasets.
4. Discussion
4.1. Ablation Analysis
This section takes the UP dataset as an example to assess the impact of various components on performance. The first and second columns in Table 11 are the convolutional fusion feature extraction module, ASSF, shown in Figure 1. The third column of Table 11 is the multiplication for the fusion of spectral–spatial features in the ASSF. The fourth column of Table 11 is the ordinary vision transformer encoder. According to the results, the ALSST model proposed in this study achieves the highest classification accuracy, indicating that each component positively enhances the classification performance.

Table 11.
Effect of different combinations on ALSST (Rows represent different combinations, √ indicates that the component exists, ⊗ represents the multiplication of spectral–spatial features, and the bold represents the best accuracy).
Table 12 illustrates the impact of employing the asymmetric convolution kernel within the ALSST. A 3D convolution kernel can be decomposed into multiple 2D convolution kernels. When a 2D kernel possesses a rank of 1, it effectively functions as a sequence of 1D convolutions and reinforces the core structure of CNNs. Therefore, the classification accuracy of the proposed model is improved.

Table 12.
The effect of asymmetric convolution for ALSST (Bold represents the best accuracy).
4.2. Ratio of DropKey
DropKey is an innovative regularizer applied within MHSA to effectively address the issue of overfitting, particularly in scenarios where samples are limited. In this section, we investigate the influence of varying DropKey ratios, ranging from 0.1 to 0.9, on the classification accuracy across four distinct datasets. The experimental results, including OA, AA, and K × 100, are showcased in Figure 18, indicating dataset-specific optimal DropKey ratios. Specifically, optimal performance for the TR and UP datasets is achieved with a DropKey ratio of 0.3, while the MU dataset peaks at 0.7 and the AU dataset at 0.8. Accordingly, the DropKey ratios are set to 0.3, 0.7, 0.8, and 0.3 for the TR, MU, AU, and UP datasets to optimize classification outcomes.
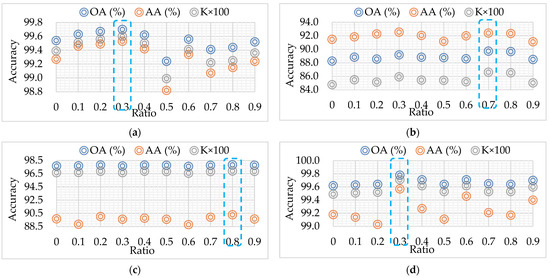
Figure 18.
OA (%), AA (%), and K×100 on different ratio of DropKey. (a) TR dataset; (b) MU dataset; (c) AU dataset; (d) UP dataset. In the blue dashed box is the ratio corresponding to the best accuracy.
4.3. Training Percentage
In this section, we conducted experiments to evaluate the performance of the proposed ALSST model across various training set sizes. The experimental configurations were consistent with the previously described settings.
The outcomes of these experiments are presented in Figure 19, illustrating the performance of the models under different training percentages. For TR, AU, and UP datasets, we designated 2%, 4%, 6%, and 8% of the total samples as the training samples. However, due to the notably uneven sample distribution of the MU dataset, 5%, 10%, 15%, and 20% of the total samples are selected for training. Our experiments demonstrated a significant improvement in the accuracies of all methods as the size of the training set increased. The ALSST model displayed superior performance across all scenarios, especially showing a marked increase in accuracy on the MU dataset. This enhancement is attributed to the capacity to leverage rich learnable features of the ALSST, which allows for more effective adaptation to uneven distributions and thus improves accuracy. Furthermore, the effectiveness of the ALSST across all datasets underscores its broad applicability in tasks that involve spectral–spatial feature fusion and classification.
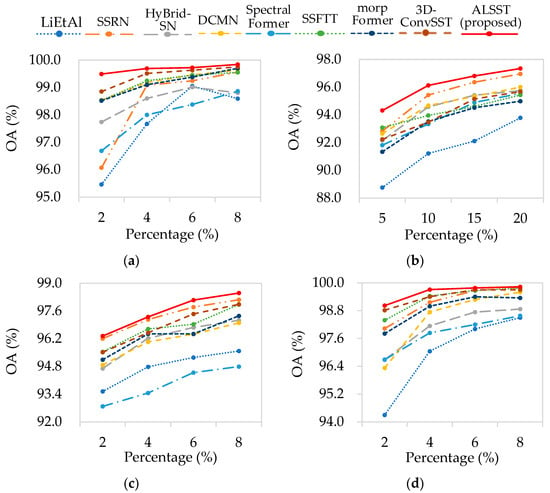
Figure 19.
OA (%) of different training percentage on all methods. (a) TR dataset; (b) MU dataset; (c) AU dataset; (d) UP dataset. The accuracies of all evaluated methods demonstrated significant improvement as the number of training samples increased. Notably, the ALSST model consistently outperformed the other methods in every scenario, showcasing its superior effectiveness.
5. Conclusions
In this article, an adaptive learning spectral–spatial fusion model named ALSST is proposed. Firstly, a dual-branch ASSF is to extract spectral–spatial fusion features, which mainly includes the PDWA and the ADWA. The PDWA could extract the spectral information of HSIs. The ADWA could extract the spatial information of HSIs. Moreover, a transformer model that amalgamates MHSA and MLP is utilized to thoroughly leverage the correlations and heterogeneities among spectral–spatial features. Then, by adding a layer scale and DropKey to the primary transformer encoder and SA, the data dynamics are improved, and the influence of transformer depth on model classification performance is alleviated. Numerous experiments were executed across four HSI datasets to evaluate the performance of the ALSST in comparison with existing classification methods, aiming to validate its effectiveness and componential contributions. The outcomes of these experiments affirm the method’s effectiveness and its superior performance, underscoring the advantages of the ALSST in HSIC tasks. The inclusion of data padding in ASSF results an increase in model complexity and parameters. Consequently, a future direction for research is to focus on the development of a model that is both precise and lightweight, balancing the need for detailed feature extraction with the imperative for computational efficiency.
Author Contributions
Conceptualization, M.W., Y.S. and J.X.; methodology, software, validation, writing–original draft, M.W., Y.S. and R.S.; writing—review and editing, M.W., Y.S. and Y.Z.; supervision, J.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Fundamental Research Funds for the Central Universities, grant number 3072022CF0801, the National Key R&D Program of China, grant number 2018YFE0206500, and the National Key Laboratory of Communication Anti Jamming Technology, grant number 614210202030217.
Data Availability Statement
The University of Pavia dataset used in this study is available at https://www.ehu.eus/ccwintco/index.php?title=Hyperspectral_Remote_Sensing_Scenes, the MUUFL dataset is available at https://github.com/GatorSense/MUUFLGulfport/, and the Trento and Augsburg datasets are available at https://github.com/AnkurDeria/MFT?tab=readme-ov-file. All the websites can be accessed on 15 March 2024.
Acknowledgments
The authors gratefully thank the peer researchers for their source codes and all the public HSI datasets.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Czaja, W.; Kavalerov, I.; Li, W. Exploring the High Dimensional Geometry of HSI Features. In Proceedings of the 2021 11th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Amsterdam, The Netherlands, 24–26 March 2021; pp. 1–5. [Google Scholar]
- Mahlein, A.; Oerke, E.; Steiner, U.; Dehne, H. Recent Advances in Sensing Plant Diseases for Precision Crop Protection. Eur. J. Plant Pathol. 2012, 133, 197–209. [Google Scholar] [CrossRef]
- Shimoni, M.; Haelterman, R.; Perneel, C. Hyperspectral imaging for military and security applications: Combining myriad processing and sensing techniques. IEEE Geosci. Remote Sens. Mag. 2019, 7, 101–117. [Google Scholar] [CrossRef]
- Hestir, E.; Brando, V.; Bresciani, M.; Giardino, C.; Matta, E.; Villa, P.; Dekker, A. Measuring Freshwater Aquatic Ecosystems: The Need for a Hyperspectral Global Mapping Satellite Mission. Remote Sens. Environ. 2015, 167, 181–195. [Google Scholar] [CrossRef]
- Xu, Y.; Du, B.; Zhang, F.; Zhang, L. Hyperspectral Image Classification Via a Random Patches Network. ISPRS J. Photogramm. Remote Sens. 2018, 142, 344–357. [Google Scholar] [CrossRef]
- Wu, X.; Hong, D.; Chanussot, J. UIU-Net: U-Net in U-Net for infrared small object detection. IEEE Trans. Image Process. 2023, 32, 364–376. [Google Scholar] [CrossRef] [PubMed]
- Vaishnavi, B.B.S.; Pamidighantam, A.; Hema, A.; Syam, V.R. Hyperspectral Image Classification for Agricultural Applications. In Proceedings of the IEEE 2022 International Conference on Electronics and Renewable Systems (ICEARS), Tuticorin, India, 16–18 March 2022; pp. 1–7. [Google Scholar]
- Schimleck, L.; Ma, T.; Inagaki, T.; Tsuchikawa, S. Review of Near Infrared Hyperspectral Imaging Applications Related to Wood and Wood Products. Appl. Spectrosc. Rev. 2022, 57, 2098759. [Google Scholar] [CrossRef]
- Liao, X.; Liao, G.; Xiao, L. Rapeseed Storage Quality Detection Using Hyperspectral Image Technology–An Application for Future Smart Cities. J. Test. Eval. 2022, 51, JTE20220073. [Google Scholar] [CrossRef]
- Xiang, J.H.; Wei, C.; Wang, M.H.; Teng, L. End-to-End Multilevel Hybrid Attention Framework for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Let. 2022, 19, 5511305. [Google Scholar] [CrossRef]
- Feng, J.; Bai, G.; Li, D.; Zhang, X.G.; Shang, R.H.; Jiao, L.C. MR-Selection: A Meta-Reinforcement Learning Approach for Zero-Shot Hyperspectral Band Selection. IEEE Trans. Geosci. Remote Sens. 2022, 61, 5500320. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, X.; Tang, X.; Zhou, H.; Jiao, L. Hyperspectral Anomaly Detection Based on Low-Rank Representation with DataDriven Projection and Dictionary Construction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2226–2239. [Google Scholar] [CrossRef]
- Hong, D.; Wu, X.; Ghamisi, P.; Chanussot, J.; Yokoya, N.; Zhu, X.X. Invariant attribute profiles: A Spatial-Frequency Joint Feature Extractor for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3791–3808. [Google Scholar] [CrossRef]
- Bruzzone, L.; Roli, F.; Serpico, S.B. An Extension of the Ieffreys–Matusita Distance to Multiclasscases for Feature Selection. IEEE Tran. Geosci. Remote Sens. 1995, 33, 1318–1321. [Google Scholar] [CrossRef]
- Keshava, N. Distance Metrics and Band Selection in Hyperspectral Processing with Applications to Material Identification and Spectral Libraries. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1552–1565. [Google Scholar] [CrossRef]
- Prasad, S.; Bruce, L.M. Limitations of Principal Components Analysis for Hyperspectral Target Recognition. IEEE Geosci. Remote Sens. Let. 2008, 5, 625–629. [Google Scholar] [CrossRef]
- Villa, A.; Benediktsson, J.A.; Chanussot, J. Hyperspectral Image Classification with Independent Component Discriminant Analysis. IEEE Geosci. Remote Sens. 2011, 49, 4865–4876. [Google Scholar] [CrossRef]
- Bandos, T.V.; Bruzzone, L.; Camps–Valls, G. Classification of Hyperspectral Images with Regularized Linear Discriminant Analysis. IEEE Geosci. Remote Sens. 2009, 47, 862–873. [Google Scholar] [CrossRef]
- Friedl, M.A.; Brodley, C.E. Decision Tree Classification of Land Cover from Remotely Sensed Data. Remote Sens. Environ. 1997, 61, 399–409. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of Hyperspectral Remote Sensing Images with Support Vector Machines. IEEE Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Blanzieri, E.; Melgani, F. Nearest Neighbor Classification of Remote Sensing Images with the Maximal Margin Principle. IEEE Geosci. Remote Sens. 2008, 46, 1804–1811. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, L.; Shi, Y. Classification of Hyperspectral Image with Small-Sized Samples Based on Spatial–Spectral Feature Enhancement. J. Harbin Eng. Univ. 2022, 43, 436–443. [Google Scholar]
- Zhang, R.; Xu, L.; Yu, Z.; Shi, Y.; Mu, C.; Xu, M. Deep-IRTarget: An automatic target detector in infrared imagery using dual-domain feature extraction and allocation. IEEE Trans. Multimed. 2022, 24, 1735–1749. [Google Scholar] [CrossRef]
- Zhang, R.; Cao, Z.; Yang, S.; Si, L.; Sun, H.; Xu, L.; Sun, F. Cognition-Driven Structural Prior for Instance-Dependent Label Transition Matrix Estimation. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 38190682. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Tan, J.; Cao, Z.; Xu, L.; Liu, Y.; Si, L.; Sun, F. Part-Aware Correlation Networks for Few-shot Learning. IEEE Trans. Multimedia. 2024, 1–13. [Google Scholar] [CrossRef]
- Zhang, R.; Yang, S.; Zhang, Q.; Xu, L.; He, Y.; Zhang, F. Graph-based few-shot learning with transformed feature propagation and optimal class allocation. Neuro Comput. 2022, 470, 247–256. [Google Scholar] [CrossRef]
- Hong, Q.Q.; Zhong, X.Y.; Chen, W.T.; Zhang, Z.G.; Li, B. SATNet: A Spatial Attention Based Network for Hyperspectral Image Classification. Remote Sens. 2022, 14, 5902. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep Learning-Based Classification of Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, X.; Jia, X. Spectral–Spatial Classification of Hyperspectral Data Based on Deep Belief Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2381–2392. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Hong, D.; Gao, L.; Yao, J.; Zhang, B.; Plaza, A.; Chanussot, J. Graph Convolutional Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5966–5978. [Google Scholar] [CrossRef]
- He, X.; Chen, Y.; Li, Q. Two-Branch Pure Transformer for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6015005. [Google Scholar] [CrossRef]
- Zhu, K.; Chen, Y.; Ghamisi, P.; Jia, X.; Benediktsson, J.A. Deep Convolutional Capsule Network for Hyperspectral Image Spectral and Spectral-Spatial Classification. Remote Sens. 2019, 11, 223. [Google Scholar] [CrossRef]
- Feng, J.; Yu, H.; Wang, L.; Cao, X.; Zhang, X.; Jiao, L. Classification of Hyperspectral Images Based on Multiclass Spatial–Spectral Generative Adversarial Networks. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5329–5343. [Google Scholar] [CrossRef]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN feature hierarchy for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2020, 17, 277–281. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, M.; Wei, C.; Zhong, Y.; Xiang, J. Heterogeneous spectral-spatial network with 3D attention and MLP for hyperspectral image classification using limited training samples. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 8702–8720. [Google Scholar] [CrossRef]
- Hong, D.; Han, Z.; Yao, J. SpectralFormer: Rethinking hyperspectral image classification with transformers. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5518615. [Google Scholar] [CrossRef]
- Sun, L.; Zhao, G.; Zheng, Y.; Wu, Z. Spectral–spatial feature tokenization transformer for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Wang, A.; Xing, S.; Zhao, Y.; Wu, H.; Iwahori, Y. A hyperspectral image classification method based on adaptive spectral spatial kernel combined with improved vision transformer. Remote Sens. 2022, 14, 3705. [Google Scholar] [CrossRef]
- Huang, X.; Dong, M.; Li, J.; Guo, X. A 3-d-swin transformer-based hierarchical contrastive learning method for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5411415. [Google Scholar] [CrossRef]
- Fang, Y.; Ye, Q.; Sun, L.; Zheng, Y.; Wu, Z. Multi-attention joint convolution feature representation with lightweight transformer for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5513814. [Google Scholar] [CrossRef]
- Gulati, A.; Qin, J.; Chiu, C.C. Conformer: Convolution-augmented transformer for speech recognition. arXiv 2020, arXiv:2005.08100. [Google Scholar]
- Wang, Y.; Li, Y.; Wang, G.; Liu, X. Multi-scale attention network for single image super-resolution. arXiv 2022, arXiv:2209.14145. [Google Scholar]
- Hendrycks, D.; Gimpel, K. Gaussian Error Linear Units (gelus). arXiv 2016, arXiv:1606.08415. [Google Scholar]
- Touvron, H.; Cord, M.; Sablayrolles, A. Going deeper with image transformers. arXiv 2021, arXiv:2103.17239v2. [Google Scholar]
- Li, B.; Hu, Y.; Nie, X.; Han, C.; Jiang, X.; Guo, T.; Liu, L. DropKey. arXiv 2023, arXiv:2208.02646v4. [Google Scholar]
- Gader, P.; Zare, A.; Close, R.; Aitken, J.; Tuell, G. Muufl Gulfport Hyperspectral and LiDAR Airborne Data Set; Technical Report REP-2013–570; University of Florida: Gainesville, FL, USA, 2013. [Google Scholar]
- Du, X.; Zare, A. Scene Label Ground T ruth Map for Muufl Gulfport Data Set; Technical Report 20170417; University of Florida: Gainesville, FL, USA, 2017. [Google Scholar]
- Li, Y.; Zhang, H.K.; Shen, Q. Spectral–Spatial Classification of Hyperspectral Imagery with 3D Convolutional Neural Network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–Spatial Residual Network for Hyperspectral Image Classification: A 3-D Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Swalpa, K.R.; Ankur, D.; Shah, C. Spectral–spatial morphological attention transformer for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 61, 5503615. [Google Scholar]
- Shyam, V.; Aryaman, S.; Shiv, R.D.; Satish, K.S. 3D-Convolution Guided Spectral-Spatial Transformer for Hyperspectral Image Classification. arXiv 2024, arXiv:2404.13252. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).