Abstract
Accurately estimating forest aboveground biomass (AGB) is imperative for comprehending carbon cycling, calculating carbon budgets, and formulating sustainable forest management plans. Currently, random forest (RF) and other machine learning models are widely used to estimate forest AGB, as they can effectively handle nonlinear relationships. However, by constructing a global model using all the samples collected from a study area, these models fail to account for the spatial heterogeneity in the AGB and cannot correct the prediction biases, thereby constraining the estimation accuracy. To overcome these limitations, we proposed a novel approach termed geographical random forest and empirical Bayesian kriging (GRFEBK). This hybrid model combines the localized modeling capability of geographical random forest (GRF) with the bias correction strength of empirical Bayesian kriging (EBK). GRF adapts RF to account for the spatial heterogeneity of the AGB, while EBK utilizes the spatial autocorrelation of residuals to correct the prediction deviations. This study was conducted in Hainan Island, utilizing spectral bands, vegetation indices, tasseled cap components derived from Landsat-8 imagery, backscattering coefficients from ALOS-2 synthetic aperture radar, topographic features, and the forest canopy height as the explanatory variables. A total of 195 forest aboveground biomass (AGB) samples were collected for modeling and assessing the predictive accuracy. The results demonstrate that, among the tested models, including GRFEBK, RF, support vector machine (SVM), k-nearest neighbor (KNN), geographically weighted regression (GWR), GRF, and EBK, GRFEBK attains the highest (0.78) and the lowest RMSE (36.04 Mg/ha) and RRMSE (22.87%), significantly outperforming the conventional models and using GRF or EBK alone. These results demonstrate that by accounting for local non-stationarity in AGB and correcting prediction biases, GRFEBK achieves significantly higher accuracy than conventional RF and other models. While the results are promising, the computational cost of GRFEBK and its performance under varying geographical conditions warrant further investigation at larger scales to assess its broader applicability. Nevertheless, GRFEBK provides an innovative and more reliable approach for accurate forest AGB estimation with great potential to support global forest resource monitoring.
1. Introduction
Forests, as integral components of terrestrial ecosystems, play a paramount regulatory role in the global carbon cycling process due to their substantial carbon storage capacity and carbon sequestration functions [1,2,3,4]. Forest aboveground biomass (AGB) serves as a pivotal indicator of forest productivity, forming the foundational basis for comprehending the structure and functionality of forest ecosystems, as well as serving as a significant parameter for assessing the carbon balance within forests [5,6]. Consequently, the accurate estimation of forest biomass not only facilitates the formulation of sustainable forest management plans but also provides essential data support for evaluating forest carbon fluxes and discerning their role within the global carbon cycle [7,8,9].
The current methods commonly used for forest AGB estimation include traditional ground surveys and remote sensing (RS)-based methods. The former involves directly measuring parameters such as the tree height and diameter at breast height (DBH), from which the AGB of individual trees is computed using allometric equations [10,11]. However, this approach is susceptible to geographical and meteorological conditions, and it is associated with high time and labor costs, rendering it suitable only for application in small-scale areas [6,12]. By contrast, RS-based methods, with their advantages of efficiency, cost-effectiveness, timeliness, and minimal impact on tree integrity, have become the primary method for regional and larger-scale forest AGB estimation [11,13,14].
In the context of forest AGB estimation using RS-based methods, empirical models are frequently employed for the estimation process. This procedure revolves around utilizing the AGB data collected from sample plots as the response variable and multiple AGB-related features derived from RS data as explanatory variables. An empirical model is then developed for the purpose of AGB estimation [2]. Empirical models can be divided into two categories: traditional statistical regression methods and emerging machine learning (ML) algorithms [11,15]. Statistical regression methods feature predefined model structures that are straightforward and computationally efficient but fall short in capturing the intricate nonlinear relationships between AGB and RS features [11]. In contrast, ML determines the model structure in a data-driven manner, which better leverages the large volumes of RS data. Compared to statistical regressions, ML is more capable of capturing intricate nonlinear relationships between AGB and diverse predicting variables, resulting in heightened predictive accuracy [12,14,16,17]. Consequently, ML algorithms find broader applications in studies focused on predicting forest AGB.
Notably, complex ecological and anthropogenic factors across different geographical regions can lead to spatial heterogeneity in forest AGB [18]. However, traditional ML models, such as random forest (RF), decision trees, and support vector machine (SVM), typically regard the study area as a whole by utilizing all the samples collected within the region to train a global estimation model, thereby failing to account for variations among the data from different geographical regions. To address this issue, Georganos et al. [19] proposed the geographical random forest (GRF) model. This model employs a local modeling strategy by dividing the study area into smaller sub-areas and constructing independent regression models within each area to adapt to the data distribution and spatial characteristics of the different regions. The existing research has shown that under proper spatial scales, GRF outperforms RF in solving problems requiring consideration of geographical location effects on spatial data prediction [20,21].
Although GRF can account for local relationships between the target variable and explanatory variables to better fit the deterministic component (trend) of the target variable, it falls short in modeling the stochastic component (residuals) of the target variable [22]. However, modeling the residuals is imperative when predicting AGB. On the one hand, residuals encompass random errors in the data that were not captured during trend modeling [23]. On the other hand, models typically provide an approximate rather than an exact depiction of the data generation process. The residuals within the model represent the biases between simulated values and actual data. Consequently, modeling prediction residuals is instrumental in rectifying both systematic and random errors in predictive models, thereby enhancing the fit to actual data and improving prediction accuracy [22,24].
Considering the presence of spatial autocorrelation in residuals [25], employing kriging interpolation emerges as an effective method for residual modeling [24]. By examining the spatial correlations among known observation points, kriging interpolation can infer the residuals at unknown locations based on the residual values at these observation points. Among the various kriging interpolation algorithms, empirical Bayesian kriging (EBK) typically outperforms other approaches [26,27]. Considering the uncertainty introduced by utilizing a single semivariogram function for interpolation in classical kriging, EBK simulates multiple semivariogram functions during prediction, with each signifying a potential spatial correlation structure. By synthesizing these diverse semivariogram functions, EBK achieves greater robustness and precision in its interpolation outcomes [28].
In addition to traditional ML algorithms, deep learning (DL) methods, such as a convolutional neural network and recurrent neural network, have been increasingly applied to RS-based estimation of various forest attributes in recent years [29]. DL models are capable of automatically extracting complex features from data without requiring extensive expertise and manual intervention. The multilayer structure of DL models enables the construction of increasingly sophisticated data representations layer by layer. These advantages generally allow DL models to achieve ideal results [30]. However, DL models typically require substantial amounts of labeled data and computational resources to train [31,32].
In this study, we focus on the impact of spatial heterogeneity in RS data on AGB estimation. Given the computational efficiency and explicit consideration of geographical location factors, we have opted for the GRF model as the primary method. Moreover, considering the limitations of traditional ML models used for estimating AGB, the hybridization of GRF and EBK has the potential to achieve higher accuracy by accounting for both the spatial heterogeneity of AGB through localized modeling as well as correcting prediction biases via residual interpolation. However, to the best of our knowledge, there has been no prior research utilizing GRFEBK for AGB prediction. In this research, we focus on Hainan Island in China and utilize spectral bands, vegetation indices, tasseled cap components from Landsat-8 multispectral imagery, backscatter coefficients from ALOS-2 synthetic aperture radar, topographic features, and the forest canopy height as the explanatory variables, with field-measured AGB as the response variable. This research aims to (1) predict forest AGB using the GRFEBK method; (2) test whether GRFEBK outperforms traditional methods, including RF, SVM, k-nearest neighbors (KNN), and geographically weighted regression (GWR), as well as standalone GRF and EBK models; (3) evaluate the strengths and weaknesses of the GRFEBK method; and (4) generate a 30 forest AGB map for the study area, providing data support for forest management, carbon stock estimation, and ecological research in the region.
2. Study Area and Data
2.1. Study Area
This research was conducted on Hainan Island, located in the southern part of China (Figure 1). The island is situated between 18°10′N and 20°10′N latitude and 108°37′E and 111°03′E longitude, covering a total area of 33,920 km2. The topography of Hainan Island primarily consists of mountains, hills, and plains. The central and southern regions are characterized by mountainous terrain, with Wuzhi Mountain being the highest peak. The northern and eastern parts, on the other hand, comprise hills and plains. The climate of Hainan Island falls within the tropical monsoon climate category, characterized by warm and humid conditions throughout the year. The average annual temperature ranges from 23 to 26 °C, and the annual precipitation generally varies between 1000 and 2400 mm [33]. Such climatic conditions contribute to the abundance of forest resources on Hainan Island, with forest coverage of 60% [34], making it one of the regions in China with the highest forest coverage. The forests on the island are predominantly tropical rainforest and seasonal rainforest, with the tropical rainforest being the northernmost geographical location worldwide.
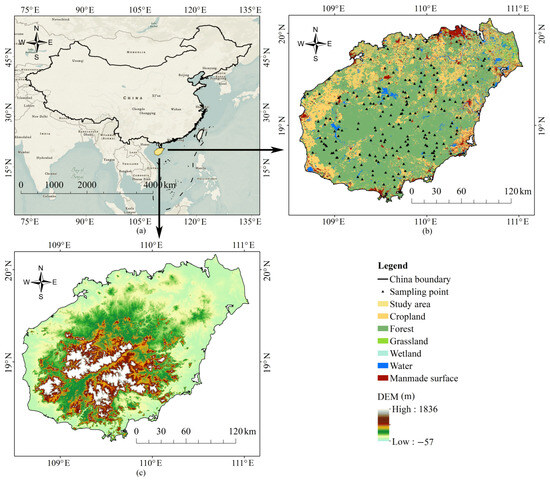
Figure 1.
Overview of the study area: (a) location of Hainan Island in China, (b) land use map of Hainan Island (30 m) [34], and (c) topography of Hainan Island (30 m) [35].
2.2. Data Acquisition and Preprocessing
In this study, a total of 26 features related to forest AGB [14,36,37] were gathered from RS imagery and published research, serving as explanatory variables for AGB estimation. Among these, six spectral bands, eleven vegetation indices, and three components of brightness, greenness, and wetness obtained through the tasseled cap transformation (TCT) were extracted from Landsat-8 (L8) images. Additionally, three terrain features and two backscatter coefficients were derived from the Shuttle Radar Topography Mission (SRTM) and ALOS-2 datasets, respectively. The forest canopy height data were obtained from the dataset published by Potapov et al. [38]. The subsequent sections will provide detailed descriptions of the data preprocessing and feature extraction processes for each category.
2.2.1. Landsat-8-Based Data
For this research, we utilized the RS cloud platform Google Earth Engine (GEE) to collect and mosaic the L8 Operational Land Imager (OLI) images covering the study area for the year 2020. The L8 OLI imagery comprises nine spectral bands, with a spatial resolution of 15 for the panchromatic band and 30 for the remaining bands. We employed GEE to perform cloud removal on the collected images and then used the median composite to obtain cloud-free images for the entire year in the study area. The bands used in this research were bands 2–7 of the L8 images, namely, blue, green, red, near-infrared, and two shortwave infrared bands. In addition to the multispectral bands, we derived 11 vegetation indices (VIs) as the explanatory variables for estimating the AGB. These indices include the Normalized Difference Vegetation Index (NDVI), Ratio Vegetation Index (RVI), Enhanced Vegetation Index (EVI), Difference Vegetation Index (DVI), Soil Adjust Vegetation Index (SAVI), Green Chlorophyll Vegetation Index (GCVI), Green Leaf Index (GLI), Chlorophyll Vegetation Index (CVI), Mid-infrared Vegetation Index (MVI), Nonlinear Vegetation Index (NVI), and Specific Leaf Area Vegetation Index (SLAVI).
Additionally, we derived the brightness, greenness, and wetness feature components from the Landsat-8 imagery using the tasseled cap transformation (TCT). TCT is an RS data processing technique that transforms the raw multispectral bands into feature components with ecological significance [39]. These feature components are capable of characterizing the soil and vegetation conditions on the ground surface [37,40], thereby providing supplementary land surface information for forest biomass estimation.
2.2.2. ALOS-2-Based Data
Considering that the L-band of synthetic aperture radar (SAR) is more accurate in estimating AGB than the X and C bands [16], we chose the ALOS-2 PALSAR-2 ScanSAR Level 2.2 imagery with a spatial resolution of 25 as the SAR data for this experiment. This dataset includes HH and HV polarization modes and has undergone ortho-rectification and is radiometrically terrain-corrected. Using GEE, we sequentially completed the collection of ScanSAR images for the entire year in the study area, speckle noise removal based on the Refined Lee algorithm, conversion of the DN values to gamma naught values, and median composite. Subsequently, the backscatter coefficients of the two polarizations of ScanSAR were extracted as the explanatory variables.
2.2.3. Forest Canopy Height Data
Given the strong correlation between forest canopy height (FCH) and forest AGB [16], we utilized the 30 resolution FCH data published by Potapov et al. in 2021 [38] as an explanatory variable. This dataset provides global coverage of the FCH data for the year 2019, obtained through spatial extrapolation of discrete FCH data acquired by the Global Ecosystem Dynamics Investigation (GEDI) using Landsat analysis-ready data and regression tree algorithms. The accuracy of this dataset was validated with a coefficient of determination () of 0.62, indicating the reliability of the FCH map results.
2.2.4. Topographic Data
The SRTM dataset provides a digital elevation model (DEM) for over 80% of the Earth’s land. The SRTM DEM comes in multiple spatial resolutions, with the SRTM V3 dataset of 30 resolution being utilized in this study [35]. The GEE platform was used to mosaic the SRTM DEM tiles for Hainan Island. The slope and aspect were then extracted from this DEM mosaic and incorporated alongside the elevation as the topographic features for modeling the AGB.
2.2.5. Land Cover/Use Data
To exclude land cover/use (LC/U) categories other than forests from the imagery, we utilized the GlobeLand30 2020 Global LC/U dataset [34]. This dataset was derived from Landsat, HJ-1, and GF-1 imagery, with a spatial resolution of 30 . Based on the validation results from ground samples, the overall accuracy is 86%, with a Kappa coefficient of 0.82. The LC/U dataset comprises a total of ten categories, including forests. After obtaining the LC/U data for Hainan Island (Figure 1b), a mask was applied to exclude non-forest regions from the imagery, preserving solely the forested areas for the subsequent experiments.
2.2.6. Field Measurement Data
The field survey in this study was conducted from July to September 2020, during which the data from 195 sample plots were collected. These data were randomly divided into training, validation, and test sets at a ratio of 5:2.5:2.5. To maintain consistency with the resolution of the Landsat images, each plot was set to a size of 30 × 30 , and the location of the center point of each plot was recorded using a GPS device. Within each plot, the DBH D (cm) and tree height H (m) of each tree with a DBH > 5 cm were measured using a diameter tape and a laser height meter. Subsequently, the individual tree AGB was calculated based on these data using the allometric equations for Chinese tree species [41]. The AGB of each field plot was calculated by summing the AGB of individual trees with a DBH > 5 cm within the plot. For tree species lacking specific allometric equations, the general allometric equation for Chinese tree species was applied for AGB estimation [41]. The calculated AGB of the field plots ranged from 51 to 383 Mg/ha, with a mean of 155 Mg/ha and a standard deviation of 77 Mg/ha. The specific allometric equations used for this research are presented in Table 1.

Table 1.
Allometric equations for AGB estimation at field plots.
3. Methods
In this study, the 26 image features (Table 2) extracted as described in Section 2.2 were utilized as the explanatory variables, with the field-measured AGB as the response variable. A hybrid approach utilizing GRF and EBK was proposed to estimate the AGB. The methodology comprised four key steps. Firstly, the training set was used to train the GRF model. Secondly, the GRF model was employed to estimate the AGB for the validation set, and the residuals from the predictions were computed. Thirdly, the residuals were spatially interpolated using the EBK algorithm and added to the predictions obtained from the GRF model. Lastly, the accuracy of the GRFEBK-estimated AGB results was evaluated using the test set. The flowchart of this research is shown in Figure 2. Additionally, to compare the performance of our approach, we also employed the GWR, RF, SVM, KNN, GRF, and EBK models to predict the forest AGB across Hainan Island using the training set, and their prediction accuracies were assessed using the test set.
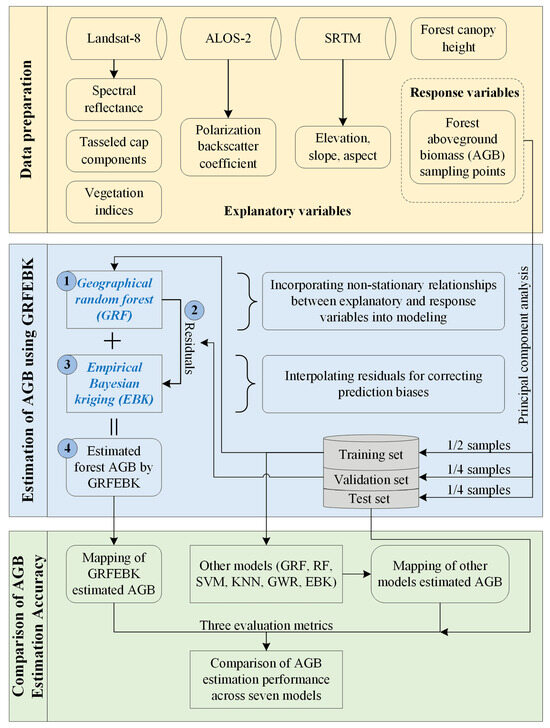
Figure 2.
Flowchart of the methodology for data collection, analysis, and validation in this study.
3.1. Feature Dimension Reduction and Hyperparameter Optimization
For this research, the 26 extracted explanatory variables were first standardized. Then, a principal component analysis (PCA) was applied to the extracted RS features, with the cumulative explained variance threshold set to 95%. This approach aimed to retain as much information from the original data as possible while reducing the dimensionality and effectively mitigating the multicollinearity issue among the original explanatory variables. For the hyperparameters in the regression models, 5-fold cross-validation (CV) [42] based on the training set was utilized for optimization to enhance the model accuracy and reduce the computational resource consumption.

Table 2.
Explanatory variables used in this research. B, G, R, NIR, and SWIR represent the blue, green, red, near-infrared, and short-wave infrared bands of L8, respectively.
Table 2.
Explanatory variables used in this research. B, G, R, NIR, and SWIR represent the blue, green, red, near-infrared, and short-wave infrared bands of L8, respectively.
| Type | Variable | Description | Reference |
|---|---|---|---|
| Spectral reflectance | B, G, R, NIR, SWIR1, SWIR2 | L8 2-7 bands | [43] |
| VIs | NDVI | (Band 5 − Band 4)/(Band 5 + Band 4) | [44] |
| RVI | Band 5/Band 4 | [44] | |
| EVI | (2.5 × (Band 5 − Band 4))/(Band 5 + 6 × Band 4 − 7.5 × Band 2 + 1) | [44] | |
| DVI | 2.4 × Band 5 − Band 4 | [45] | |
| SAVI | ((1 + L) × (Band 5 − Band 4))/(Band 5 + Band 4 + L); L = 0.5 | [44] | |
| CIgreen | (Band 5/Band 3) − 1 | [46] | |
| GLI | (2 × Band 3 − Band 4 − Band 2)/(2 × Band 3 + Band 4 + Band 2) | [47] | |
| CVI | Band 5 × (Band 4/) | [47] | |
| MVI | Band 5/Band 6 | [48] | |
| NVI | ( − Band 4)/( + Band 4) | [49] | |
| SLAVI | Band 5/(Band 4 + Band 7) | [50] | |
| TCT components | Brightness, greenness, wetness | First three components of tassel cap transformation | [39] |
| Terrain features | Elevation, slope, aspect | Elevation, slope, and aspect of ground | [35] |
| Backscatter coefficients | HV, HH | Backscatter coefficient values of HV and HH polarization | [51] |
| Forest canopy height | FCH | Vertical distance from forest canopy top to ground | [38] |
3.2. Geographical Random Forest
RF is an ensemble learning algorithm that makes predictions by constructing multiple decision tree models [17]. It forms multiple sub-sample sets through random sampling and builds decision trees on each sub-sample set, increasing model diversity by randomly selecting features. In the prediction phase, RF averages the prediction results from each decision tree to obtain the final results [14]. RF has high robustness, the ability to handle high-dimensional data and missing values, and a relatively fast computational speed, thus being widely applied across many domains. However, RF assumes all samples share the same variable relationships when modeling. As a result, RF focuses on the overall relationship of the target variable and fails to capture spatial variations adequately when applied to interpret spatial processes [52]. GRF proposed by [19] is a spatial extension of RF, with the core idea of decomposing the global RF model into multiple local sub-models. During prediction, GRF constructs a local sub-model using only the samples within a neighborhood radius of the prediction point, where this radius is defined as the distance between the prediction point and its farthest neighbor. Compared to RF, GRF is capable of capturing spatial heterogeneity in geographical data as each of its sub-models is built by learning the specific variable relationships within its respective sub-region. The GRF model has three essential hyperparameters, namely, n_estimators, max_feature, and neighbors, determining the number of decision trees, maximum tree depth, and number of nearby samples, respectively. The three parameters were determined via 5-fold CV.
3.3. Empirical Bayesian kriging
EBK is a statistical spatial interpolation method that extends conventional kriging by accounting for errors introduced during the estimation of the semivariogram. The process begins by estimating a semivariogram from the data and utilizing this function to simulate new values at the locations of each sample point. Subsequently, new semivariograms are derived based on the simulated data. This iterative process is repeated multiple times to generate multiple semivariograms. The Bayesian rule is then utilized to compute the weights for each semivariogram, facilitating kriging interpolation [28]. By simulating multiple sets of semivariograms, EBK mitigates the uncertainties associated with using only one semivariogram in conventional kriging, resulting in more accurate and reliable interpolation estimates [27].
In the present study, the residuals of the GRF-predicted AGB results were calculated using the samples from the validation set. Subsequently, these residuals were used to generate a seamless map of the GRF prediction residuals through the EBK tool in ArcGIS software (v10.6), which automatically selected the default power function for the semivariogram model. Finally, the interpolated residual values were summed with GRF predictions to produce the final AGB estimations. Notably, as EBK evolved from the kriging interpolation algorithm, it is crucial to conduct normality testing on the data used for interpolation. This step ensures that the fundamental assumptions of kriging are satisfied before performing EBK interpolation [24].
3.4. Other Comparative Models
To compare with the estimation results of the proposed GRFEBK in this work, the RF, GRF, SVM, KNN, GWR, and EBK models were trained and evaluated using the training and test set, respectively. SVM regression aims to find an optimal hyperplane that fits the data in the feature space while maximizing the margin. In contrast to conventional linear regression methods, the SVM regressor demonstrates superior capability in handling high-dimensional data and nonlinear relationships and has shown good predictive performance in many practical applications [2]. KNN regression is an ML algorithm that predicts the output for a data point by averaging the outputs of its k-nearest neighbors. Unlike parameterized models, KNN regression relies on instance-based learning, thus performing well on complex data relationships and nonlinear patterns [2]. GWR is a spatial regression analysis method for dealing with spatial non-stationarity in geographic data. Unlike global regression models, GWR allows for the localized calibration of regression coefficients by weighting neighboring sample points based on both value and spatial location [14], thereby providing more accurate spatial prediction.
The seven prediction models were constructed using the Python third-party packages Scikit-learn, SPRF, and MGWR as well as the ArcGIS software. The primary hyperparameters of RF, GRF, SVM, KNN, and GWR were optimized via the 5-fold CV algorithm.
3.5. Accuracy Assessment
We assessed the accuracy of the AGB estimation methods using the following three metrics: the root mean squared error (RMSE), relative RMSE (RRMSE), and . The RMSE quantifies the average deviation between the predicted and true values. The RRMSE represents the RMSE expressed as a percentage of the mean of the true values, constituting a dimensionless method for evaluating prediction error. ranges from 0 to 1, with larger values indicating a more substantial explanatory power of regression model regarding the target variable. The formulas for these metrics are shown below:
where and represent the true value and the predicted value for the i-th sample, respectively; indicates the mean of the true values, and n is the number of samples.
4. Results
4.1. Feature Dimension Reduction and Hyperparameter Tuning
Prior to prediction, a PCA was conducted on the 26 extracted explanatory variables. Based on the results (Figure 3), it was found that the cumulative explained variance by the first eight principal components exceeded 95% (95.69%). Considering that these eight components effectively reduce the data dimensionality while adequately retaining data information, they were selected for the subsequent data analysis and modeling. The tuning key hyperparameters of the RF, GRF, KNN, SVM, and GWR models resulting from the 5-fold CV are presented in Table 3.
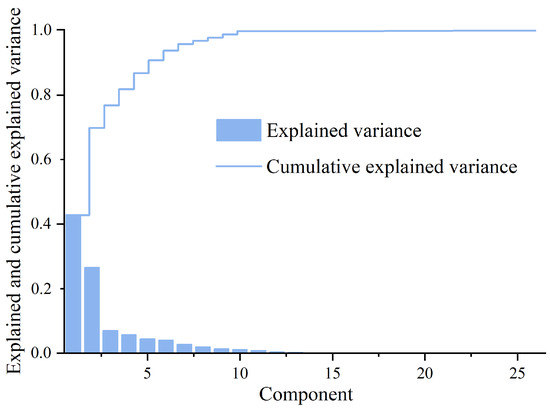
Figure 3.
Plot of individual and cumulative explained variance for 26 new components after principal component transformation.

Table 3.
Hyperparameter tuning results for RF, GRF, KNN, SVM, and GWR.
4.2. EBK Interpolation of Residuals from GRF AGB Estimation
To correct the bias in the GRF estimation results, the trained GRF model was first utilized to predict the validation set. The estimation residuals were then calculated and subjected to the Anderson–Darling normality test. The test statistic of 0.47 was less than the critical value of 0.74 at a 5% significance level, indicating that the residuals follow a normal distribution suitable for EBK interpolation. After spatially interpolating these residuals using EBK, a seamless residual map of the GRF-estimated AGB across the study area was produced. The non-forest areas were then masked out, and the forest area was used for the subsequent analysis.
As shown in Figure 4, the residuals of the GRF estimations exhibited pronounced spatial distribution patterns. The highest residual values appeared in the southeast of Hainan Island, and overall, a diffusing trend from this region to other directions was observed, with the residuals decreasing gradually from 16 Mg/ha to −20 Mg/ha. The lowest values occurred in the northeast. Overall, the northwest, southwest, and southeast regions of Hainan Island were predominantly characterized by positive residuals (with the GRF predictions lower than the true values), and the negative residuals were also relatively high, with most falling between −6 and 0 Mg/ha. By contrast, all the residuals in the northeast were negative, with more than half below −12 Mg/ha. These observations suggest that GRF overestimated the forest AGB in the northeastern part of Hainan Island while underestimating it in other regions.
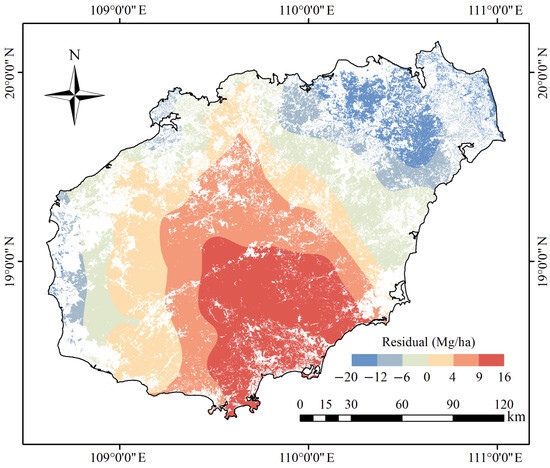
Figure 4.
EBK interpolation map of residuals from GRF-estimated forest AGB based on the validation dataset.
4.3. Comparison of Forest AGB Estimation Accuracy Among Models
The scatterplots of the estimations from the seven models versus the test set, along with the results of the three evaluation metrics, are presented in Figure 5. Among the seven models, GRFEBK attained the highest of 0.78, indicating the strongest linear correlation with the validation data. Furthermore, GRFEBK also achieved the lowest RRMSE and RMSE, at 22.87% and 36.04 Mg/ha, respectively, signifying its superior predictive accuracy and minimized error dispersion among the seven models. In contrast, GRF demonstrated slightly inferior predictive accuracy compared to GRFEBK, with an of 0.74. Among the remaining five conventional models, RF exhibited the best performance with an of 0.69. GWR and SVM showed comparable performances, inferior to RF but superior to KNN. The poorest performance was observed in EBK, with an of less than 0.4. From the scatterplot, the fitting line for GRFEBK most closely approximates the 1:1 reference line, indicative of its minimal overall bias in predictions. The closeness of the fitting lines to the 1:1 reference line for the other models was consistent with the rankings from the three evaluation metrics. However, EBK had the narrowest 95% confidence interval band, reflecting the best prediction stability of EBK, while GRFEBK had the second narrowest.
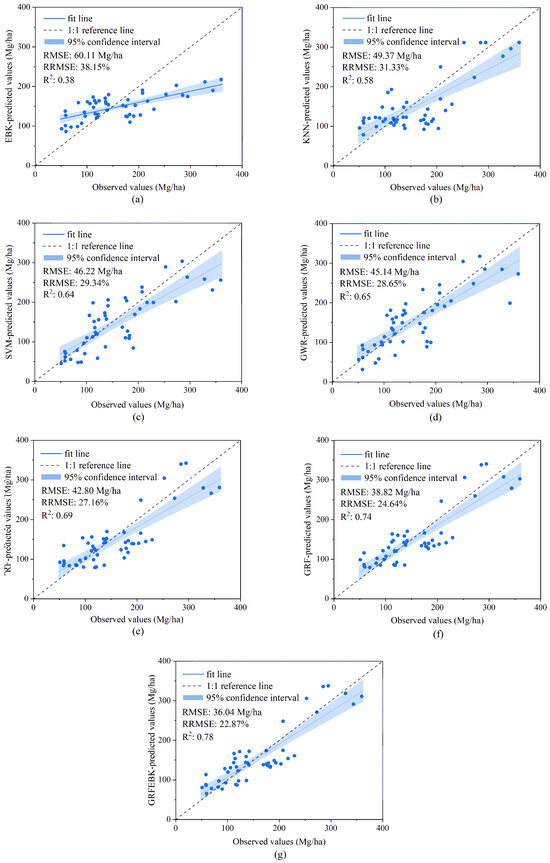
Figure 5.
Scatterplots of true AGB values versus AGB predicted by the seven models based on the test set (n = 49): (a) EBK, (b) KNN, (c) SVM, (d) GWR, (e) RF, (f) GRF, and (g) GRFEBK.
To further compare the performance of the seven models, we calculated four statistical statistics (mean, minimum, maximum, and standard deviation) of their predictions versus the truth values (test set). As Figure 6 illustrates, the mean values of the predictions from all seven models closely align with those of the truth values. For the standard deviation, only EBK displayed a significant deviation from the truth values, while the remaining six models are in proximity, with GRFEBK being the closest. In terms of the minimum and maximum values, substantial differences are observed among the seven models. EBK and GWR exhibit predictions with minimum values significantly diverging from truth values, with KNN, RF, and GRF markedly higher than the truth values. Only SVM and GRFEBK closely approximate the truth values, with SVM being slightly lower and GRFEBK slightly higher. For the maximum values, EBK was far below the truth values. Although KNN, GWR, and SVM were noticeably better than EBK, they still exhibited apparent differences from the truth values. RF and GRF had similar maximums, both being the closest to the truth values along with GRFEBK, but the former two were lower while the latter was higher. Taking all the aforementioned analysis results into account, GRFEBK demonstrates the overall best performance in terms of the prediction accuracy, stability, and goodness of fit. GRF and RF also exhibit strong predictive abilities. The performances of KNN, GWR, and SVM were mediocre, while EBK noticeably underperformed compared to the other six models.
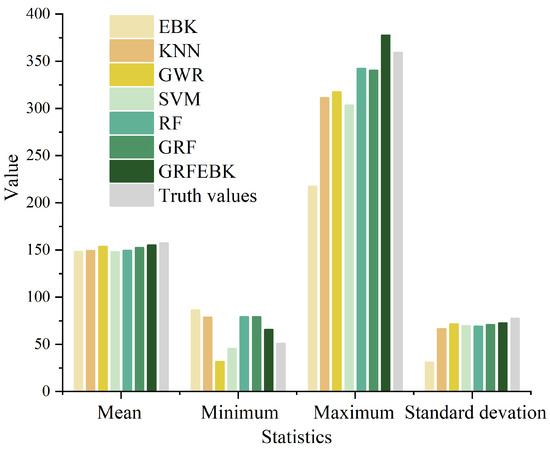
Figure 6.
Comparison of four statistical metrics for the predictions of seven models versus truth values (test set).
4.4. Mapping of Forest AGB Estimated with GRFEBK
Considering GRFEBK achieved the highest prediction accuracy, its predicted results were used to generate a 30 m resolution forest AGB map across the study area in 2020 (Figure 7). As shown in the figure, the overall distribution of forest AGB in Hainan Island ranges from 45 to 375 Mg/ha. High AGB values are predominantly concentrated in the southwestern part of the island, where the AGB generally exceeds 190 Mg/ha. In contrast, other regions exhibit lower AGB values, typically ranging between 45 and 140 Mg/ha. Examining the DEM of Hainan Island (Figure 1c), a distinct correlation between the AGB and elevation is evident. In the mountainous southwestern region at elevations above 900 , the forest AGB is mostly over 245 Mg/ha, with the highest AGB values in Hainan Island occurring in this zone. Conversely, in other regions, the AGB tends to decrease with decreasing elevation.
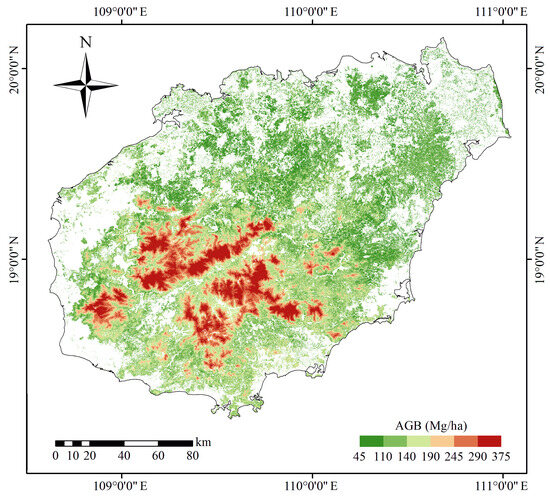
Figure 7.
Estimation of forest AGB on Hainan Island in 2020 based on GRFEBK and multisource RS data.
5. Discussion
5.1. Evaluating Current and Potential Explanatory Variables for AGB Modeling
For this research, we derived numerous highly correlated features with forest AGB from RS data, including multispectral bands, vegetation indices, terrain characteristics, SAR backscatter coefficients, three components from TCT, and the FCH. These features were utilized as explanatory variables for estimating forest AGB after dimensionality reduction via PCA. The variables used were identified in previous studies to be strongly correlated with forest AGB [14,36,37], and the favorable estimation results achieved in this study further validate the appropriateness and effectiveness of these selected explanatory variables. Furthermore, these variables were derived from open-access RS data, facilitating the application of this method to other areas.
However, apart from these variables, the inclusion of additional information during modeling may potentially enhance AGB prediction accuracy. Firstly, studies have indicated that different tree species exhibit varying growth rates and tree structures, resulting in differences in biomass accumulation [8,53]. Therefore, the inclusion of categorical information regarding the tree species in the study area as an explanatory variable into the model holds promise for enhancing predictive accuracy. Furthermore, the amount of precipitation and soil nutrients can affect tree growth and are related to biomass [54]. Hence, integrating them as explanatory variables may also benefit AGB estimation. However, complete tree species data for Hainan Island are currently unavailable. Additionally, the spatial resolution of the accessible soil nutrient and precipitation datasets is generally low, rendering the differences in these features across different regions less distinct. Consequently, the aforementioned three explanatory variables were not incorporated into the analysis.
Additionally, because the principal components obtained through the PCA are linear combinations of original variables, each component lacks a clear physical or ecological significance, making them difficult to interpret intuitively [55]. Furthermore, PCA does not provide a ranking or weight scoring of the original explanatory variables with respect to their importance in predicting the target variable (AGB) [55], preventing researchers from directly understanding the significance of each variable. Given these limitations of a PCA in terms of variable interpretability and importance assessment, we plan to explore other feature selection methods, such as Recursive Feature Elimination, in future research. This approach will be combined with the GRFEBK AGB estimation method proposed in our current study, aiming to enhance the assessment capabilities of variable importance while maintaining the desired estimation accuracy.
5.2. Performance of GRFEBK in Estimating Forest AGB
ML models can capture complex nonlinear relationships between AGB and explanatory variables through flexible model structures [2,12,17]. Therefore, compared to statistical models, ML predictions are often more accurate, leading to their wide application in forest AGB estimation research [7,14,56]. However, traditional ML algorithms such as RF, KNN, SVM, etc., currently suffer from two significant shortcomings affecting their performance in AGB estimation. Firstly, these algorithms are intrinsically unable to effectively account for the spatial heterogeneity of forest AGB in the modeling process [19]. Due to the influence of geography, climate, and anthropogenic activities, forest AGB exhibits pronounced spatial heterogeneity [18]. Nevertheless, ML algorithms typically perform global modeling using all samples collected within the study area, capturing only feature interactions at the global scale rather than localized relationships across locations [15]. To overcome this issue, we adopt the GRF model developed by Georganos et al. [19] in this research, expecting to achieve higher accuracy over conventional ML methods by virtue of its inherent capability of localized instead of global modeling. The final prediction results (Figure 5 and Figure 6) demonstrate that among the six models, EBK, KNN, GWR, SVM, RF, and GRF, RF achieved the second highest prediction accuracy after GRF owing to its ensemble learning modeling strategy. GRF attained higher prediction accuracy than RF by additionally incorporating local spatial features based on RF. Among the other models, although GWR employs localized modeling similar to GRF, it exhibited significantly lower predictive performance. One potential reason is that as a linear regression method, GWR is confined by linear assumptions and struggles to capture intricate nonlinear spatial relationships, like RF [22,57]. Additionally, unlike ensemble learning, GWR cannot establish multiple localized models to obtain more robust and accurate predictions. Therefore, the prediction accuracy of GWR is inferior to those of RF and GRF. In conclusion, by incorporating considerations of spatial heterogeneity into the robust RF model, GRF demonstrates higher accuracy in estimating forest AGB compared to traditional ML models.
Another major limitation of conventional ML approaches in predicting AGB is that these models, including the aforementioned GRF, are devised to fit the trend (deterministic) component of the target variable as accurately as possible through their sophisticated mechanisms [19]. However, in geostatistics, the target variable comprises both trend and residual (stochastic) components, and the inability to model residuals compromises prediction performance [22,25]. Considering that residuals exhibit spatial autocorrelation [15,18], in this study, we employed the kriging interpolation algorithm to model the residuals of the GRF predictions. Subsequently, the interpolation results were added to the trend components predicted by GRF. This approach allows for a more comprehensive utilization of spatial information in RS data, with the aim of achieving a more complete spatial estimation of the target variable and further enhancing the precision of the predictive outcomes. Our results confirm this hypothesis. Compared to standalone GRF, GRFEBK in our study attained an elevated of 0.04, alongside an RMSE and RRMSE reduced by 2.78 m and 1.77%, indicating that by hybridizing GRF and EBK, which are capable of accurately modeling trend and stochastic components, respectively, superior prediction of forest AGB can be achieved over merely modeling the trend.
5.3. Uncertainties in This Study
The forest AGB estimation method proposed in this study exhibits three sources of uncertainty. The first is the uncertainty in the quality of the measured AGB data. When collecting field-measured forest AGB data, we measured the DBH and H for all the individual trees with a DBH > 5 cm within the sample plots. Subsequently, we computed the AGB for each sample plot using species-specific allometric equations given in published studies [41]. For species without available allometric equations, general equations for Chinese broadleaf or coniferous trees were used. However, due to the structural and growth characteristic variations among the different species [8,37], using general equations may introduce uncertainties in estimating individual tree AGB, consequently contributing to uncertainties in subsequent estimations. Future efforts to acquire more species-specific allometric equations could reduce the uncertainty linked to AGB estimation within sample plots.
The second source of uncertainty arises from temporal differences in the collection of multisource data. In this research, the multispectral and SAR data used were the yearly median composites of 2020 Landsat-8 and ALOS-2 imagery, respectively; the FCH data represented the average forest height in the study area from April 2019 to April 2020 [38]; and the terrain data depicted the topographical features in the area from the year 2000 [35]. However, the field measurements of the AGB were conducted between July and September 2020. It is evident that the acquisition times of most explanatory variables do not closely match the timing of the field-based AGB measurements, introducing uncertainty into the estimated results. However, eliminating explanatory variables that do not align with the field measurement timing could result in an insufficient number of available explanatory variables, potentially affecting the estimation accuracy of the GRFEBK model. Given that temporal disparity is a common challenge in RS studies [8,16] and difficult to completely avoid, it is worthwhile to develop a correction model that accounts for the temporal effects of different variables. This model could involve back-propagation or forward-propagation to a unified target time, allowing for temporal standardization to mitigate the influence of temporal differences.
The uncertainties arising from RS signal saturation also need to be considered. Signal saturation can affect the accuracy of AGB estimation in areas with high forest canopy closure. Studies have shown that in forest areas with AGB exceeding 150 Mg/ha, multispectral and backscatter signals begin to saturate [8,58,59], resulting in lower model estimations for these regions. To mitigate the uncertainty caused by saturation effects to some extent, we incorporated multiple RS features such as terrain characteristics, FCH, components obtained from the TCT, and others as the explanatory variables, which expanded the dynamic range of the signals. However, this cannot completely eliminate the saturation effect [8]. In the estimations using the GRFEBK model (Figure 5g), the number of underestimated samples continued to increase when the AGB > 150 Mg/ha. In the future, identifying saturated signal pixels and modeling them separately may further alleviate the impact of this phenomenon.
In addition to the three uncertainties mentioned above, the feasibility and efficiency of the GRFEBK model in estimating AGB at larger geographical scales also merit discussion. In our experiments, the modeling time for GRF alone was several times that of regular RF, and the EBK modeling also required substantial computational resources. The high computational costs could pose challenges when handling large-scale datasets. Consequently, we plan to explore the feasibility of deploying the GRFEBK model on the GEE platform, leveraging the high computational power of the cloud to potentially enable its application at national or even global scales. Moreover, although promising results were obtained in the natural environment of Hainan Island, considering the impact of varying ecological conditions on model estimates of AGB [54], we intend to apply the model in a broader geographical context in future research. This will test its robustness, reveal potential limitations, and necessitate adjustments, thereby more comprehensively assessing the applicability of the GRFEBK model.
6. Conclusions
To overcome the limitations of conventional ML models in forest AGB estimation, this study proposed a novel hybrid approach that combines GRF and EBK. The study demonstrated that GRFEBK excels in AGB estimation within the research area, yielding the highest (0.78) and the lowest RMSE (36.04 Mg/ha) and RRMSE (22.87%) values, considerably outperforming other traditional models, including RF and GWR, as well as standalone GRF and EBK. These results unequivocally confirm that GRFEBK can achieve higher estimation accuracy compared to conventional global trend modeling methods by retaining the capability of RF in handling nonlinear problems, accounting for spatial heterogeneity in forest AGB via local modeling, and correcting prediction bias by modeling residuals. Thus, it provides a more robust and accurate method for forest AGB estimation based on RS data. The 30 distribution map generated by GRFEBK delineates the spatial pattern of the forest AGB in Hainan Island, which holds great significance for forest management, carbon stock assessment, and ecological research across this region. In future research, employing a feature selection method that allows for the evaluation of importance could provide a clearer understanding of the role of each feature in AGB estimation. This approach, coupled with using more accurate allometric equations, incorporating additional explanatory variables like tree species, and alleviating signal saturation, would be promising to further improve the prediction performance of GRFEBK for AGB estimation. Additionally, testing the GRFEBK model on larger geographic scales is essential, not only for validating its stability and adaptability across ecological and geographical settings but also for assessing its efficiency and practicality in handling large-scale datasets.
Author Contributions
Conceptualization, Z.W. and J.Z; methodology, Z.W.; software, H.L.; validation, Z.W., H.L., and J.Z.; formal analysis, Z.W.; investigation, Z.W. and J.Z.; resources, F.Y. and J.Z.; data curation, Z.W., F.Y., and J.Z.; writing—original draft preparation, Z.W.; writing—review and editing, Z.W. and J.Z.; visualization, H.L.; supervision, J.Z.; project administration, F.Y. and J.Z.; funding acquisition, F.Y. and J.Z. All authors have read and agreed to the published version of this manuscript.
Funding
This work was supported by the Finance Science and Technology Project of Hainan Province (No. ZDYF2021SHFZ063), the National Key Research and Development Program of China (No. 2023YFF1303600), and the Special Educating Project of the Talent for Carbon Peak and Carbon Neutrality of University of Chinese of Academy of Science.
Data Availability Statement
The data are available on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Narine, L.L.; Popescu, S.; Neuenschwander, A.; Zhou, T.; Srinivasan, S.; Harbeck, K. Estimating aboveground biomass and forest canopy cover with simulated ICESat-2 data. Remote Sens. Environ. 2019, 224, 1–11. [Google Scholar] [CrossRef]
- Wu, C.; Shen, H.; Shen, A.; Deng, J.; Gan, M.; Zhu, J.; Xu, H.; Wang, K. Comparison of machine-learning methods for above-ground biomass estimation based on Landsat imagery. J. Appl. Remote Sens. 2016, 10, 035010. [Google Scholar] [CrossRef]
- Li, X.; Du, H.; Mao, F.; Zhou, G.; Chen, L.; Xing, L.; Fan, W.; Xu, X.; Liu, Y.; Cui, L.; et al. Estimating bamboo forest aboveground biomass using EnKF-assimilated MODIS LAI spatiotemporal data and machine learning algorithms. Agric. For. Meteorol. 2018, 256, 445–457. [Google Scholar] [CrossRef]
- Mitchard, E.T. The tropical forest carbon cycle and climate change. Nature 2018, 559, 527–534. [Google Scholar] [CrossRef]
- Li, L.; Zhou, B.; Liu, Y.; Wu, Y.; Tang, J.; Xu, W.; Wang, L.; Ou, G. Reduction in Uncertainty in Forest Aboveground Biomass Estimation Using Sentinel-2 Images: A Case Study of Pinus densata Forests in Shangri-La City, China. Remote Sens. 2023, 15, 559. [Google Scholar] [CrossRef]
- Shen, W.; Li, M.; Huang, C.; Tao, X.; Wei, A. Annual forest aboveground biomass changes mapped using ICESat/GLAS measurements, historical inventory data, and time-series optical and radar imagery for Guangdong province, China. Agric. For. Meteorol. 2018, 259, 23–38. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Y.; Ren, C.; Zhang, B.; Wang, Z. Assessment of multi-wavelength SAR and multispectral instrument data for forest aboveground biomass mapping using random forest kriging. For. Ecol. Manag. 2019, 447, 12–25. [Google Scholar] [CrossRef]
- Zhang, R.; Zhou, X.; Ouyang, Z.; Avitabile, V.; Qi, J.; Chen, J.; Giannico, V. Estimating aboveground biomass in subtropical forests of China by integrating multisource remote sensing and ground data. Remote Sens. Environ. 2019, 232, 111341. [Google Scholar] [CrossRef]
- Liu, Y. Estimation of Forest Above-Ground Biomass and Net Primary Productivity Using Multi-Source Remote Sensing Data. Ph.D. Thesis, Wuhan University, Wuhan, China, 2019. [Google Scholar]
- Yang, M.; Zhou, X.; Peng, C.; Li, T.; Chen, K.; Liu, Z.; Li, P.; Zhang, C.; Tang, J.; Zou, Z. Developing allometric equations to estimate forest biomass for tree species categories based on phylogenetic relationships. For. Ecosyst. 2023, 10, 100130. [Google Scholar] [CrossRef]
- Mohd Zaki, N.A.; Abd Latif, Z. Carbon sinks and tropical forest biomass estimation: A review on role of remote sensing in aboveground-biomass modelling. Geocarto Int. 2017, 32, 701–716. [Google Scholar] [CrossRef]
- Lu, J.; Wang, H.; Qin, S.; Cao, L.; Pu, R.; Li, G.; Sun, J. Estimation of aboveground biomass of Robinia pseudoacacia forest in the Yellow River Delta based on UAV and Backpack LiDAR point clouds. Int. J. Appl. Earth Obs. Geoinf. 2020, 86, 102014. [Google Scholar] [CrossRef]
- Salazar Villegas, M.H.; Qasim, M.; Csaplovics, E.; González-Martinez, R.; Rodriguez-Buritica, S.; Ramos Abril, L.N.; Salazar Villegas, B. Examining the Potential of Sentinel Imagery and Ensemble Algorithms for Estimating Aboveground Biomass in a Tropical Dry Forest. Remote Sens. 2023, 15, 5086. [Google Scholar] [CrossRef]
- Forkuor, G.; Zoungrana, J.B.B.; Dimobe, K.; Ouattara, B.; Vadrevu, K.P.; Tondoh, J.E. Above-ground biomass mapping in West African dryland forest using Sentinel-1 and 2 datasets-A case study. Remote Sens. Environ. 2020, 236, 111496. [Google Scholar] [CrossRef]
- Izadi, S.; Sohrabi, H.; Khaledi, M.J. Estimation of coppice forest characteristics using spatial and non-spatial models and Landsat data. J. Spat. Sci. 2022, 67, 143–156. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A survey of remote sensing-based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Ghosh, S.M.; Behera, M.D. Aboveground biomass estimation using multi-sensor data synergy and machine learning algorithms in a dense tropical forest. Appl. Geogr. 2018, 96, 29–40. [Google Scholar] [CrossRef]
- Propastin, P. Modifying geographically weighted regression for estimating aboveground biomass in tropical rainforests by multispectral remote sensing data. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 82–90. [Google Scholar] [CrossRef]
- Georganos, S.; Grippa, T.; Niang Gadiaga, A.; Linard, C.; Lennert, M.; Vanhuysse, S.; Mboga, N.; Wolff, E.; Kalogirou, S. Geographical random forests: A spatial extension of the random forest algorithm to address spatial heterogeneity in remote sensing and population modelling. Geocarto Int. 2021, 36, 121–136. [Google Scholar] [CrossRef]
- Wang, H.; Seaborn, T.; Wang, Z.; Caudill, C.C.; Link, T.E. Modeling tree canopy height using machine learning over mixed vegetation landscapes. Int. J. Appl. Earth Obs. Geoinf. 2021, 101, 102353. [Google Scholar] [CrossRef]
- Grekousis, G.; Feng, Z.; Marakakis, I.; Lu, Y.; Wang, R. Ranking the importance of demographic, socioeconomic, and underlying health factors on US COVID-19 deaths: A geographical random forest approach. Health Place 2022, 74, 102744. [Google Scholar] [CrossRef]
- Ye, H.; Huang, W.; Huang, S.; Huang, Y.; Zhang, S.; Dong, Y.; Chen, P. Effects of different sampling densities on geographically weighted regression kriging for predicting soil organic carbon. Spat. Stat. 2017, 20, 76–91. [Google Scholar] [CrossRef]
- Imran, M.; Stein, A.; Zurita-Milla, R. Using geographically weighted regression kriging for crop yield mapping in West Africa. Int. J. Geogr. Inf. Sci. 2015, 29, 234–257. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, C.; Li, W. Comparison of geographically weighted regression and regression kriging for estimating the spatial distribution of soil organic matter. Giscience Remote Sens. 2012, 49, 915–932. [Google Scholar] [CrossRef]
- Kumar, S.; Lal, R.; Liu, D. A geographically weighted regression kriging approach for mapping soil organic carbon stock. Geoderma 2012, 189, 627–634. [Google Scholar] [CrossRef]
- Gribov, A.; Krivoruchko, K. Empirical Bayesian kriging implementation and usage. Sci. Total Environ. 2020, 722, 137290. [Google Scholar] [CrossRef] [PubMed]
- Krivoruchko, K.; Gribov, A. Evaluation of empirical Bayesian kriging. Spat. Stat. 2019, 32, 100368. [Google Scholar] [CrossRef]
- Krivoruchko, K. Empirical bayesian kriging. ArcUser Fall 2012, 6, 1145. [Google Scholar]
- Astola, H.; Seitsonen, L.; Halme, E.; Molinier, M.; Lönnqvist, A. Deep neural networks with transfer learning for forest variable estimation using sentinel-2 imagery in boreal forest. Remote Sens. 2021, 13, 2392. [Google Scholar] [CrossRef]
- Shaheen, F.; Verma, B.; Asafuddoula, M. Impact of automatic feature extraction in deep learning architecture. In Proceedings of the 2016 International Conference on Digital Image Computing: Techniques and Applications (DICTA), IEEE, Gold Coast, QLD, Australia, 30 November–2 December 2016; pp. 1–8. [Google Scholar]
- Qin, Y.; Wu, B.; Lei, X.; Feng, L. Prediction of tree crown width in natural mixed forests using deep learning algorithm. For. Ecosyst. 2023, 10, 100109. [Google Scholar] [CrossRef]
- Diez, Y.; Kentsch, S.; Fukuda, M.; Caceres, M.L.L.; Moritake, K.; Cabezas, M. Deep learning in forestry using uav-acquired rgb data: A practical review. Remote Sens. 2021, 13, 2837. [Google Scholar] [CrossRef]
- Wu, S.; Xing, C.; Zhu, J. Analysis of climate characteristics in Hainan Island. J. Trop. Biol. 2022, 13, 315–323. [Google Scholar]
- Chen, J.; Chen, J.; Liao, A.; Cao, X.; Chen, L.; Chen, X.; He, C.; Han, G.; Peng, S.; Lu, M.; et al. Global land cover mapping at 30 m resolution: A POK-based operational approach. ISPRS J. Photogramm. Remote Sens. 2015, 103, 7–27. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45, 21–24. [Google Scholar] [CrossRef]
- Hernández-Stefanoni, J.L.; Castillo-Santiago, M.Á.; Mas, J.F.; Wheeler, C.E.; Andres-Mauricio, J.; Tun-Dzul, F.; George-Chacón, S.P.; Reyes-Palomeque, G.; Castellanos-Basto, B.; Vaca, R.; et al. Improving aboveground biomass maps of tropical dry forests by integrating LiDAR, ALOS PALSAR, climate and field data. Carbon Balance Manag. 2020, 15, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Niu, C.; Liu, X.; Feng, Y.; Ma, Q.; Wang, X.; Tang, H.; Guo, Q. Mapping high-resolution forest aboveground biomass of China using multisource remote sensing data. GIScience Remote Sens. 2023, 60, 2203303. [Google Scholar] [CrossRef]
- Potapov, P.; Li, X.; Hernandez-Serna, A.; Tyukavina, A.; Hansen, M.C.; Kommareddy, A.; Pickens, A.; Turubanova, S.; Tang, H.; Silva, C.E.; et al. Mapping global forest canopy height through integration of GEDI and Landsat data. Remote Sens. Environ. 2021, 253, 112165. [Google Scholar] [CrossRef]
- Baig, M.H.A.; Zhang, L.; Shuai, T.; Tong, Q. Derivation of a tasselled cap transformation based on Landsat 8 at-satellite reflectance. Remote Sens. Lett. 2014, 5, 423–431. [Google Scholar] [CrossRef]
- Carreiras, J.M.; Pereira, J.M.; Pereira, J.S. Estimation of tree canopy cover in evergreen oak woodlands using remote sensing. For. Ecol. Manag. 2006, 223, 45–53. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, X.; Lu, F. Comprehensive Database of Biomass Regressions for China’s Tree Species; China Forestry Publishing House: Beijing, China, 2015. [Google Scholar]
- Rodriguez, J.D.; Perez, A.; Lozano, J.A. Sensitivity analysis of k-fold cross validation in prediction error estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 32, 569–575. [Google Scholar] [CrossRef]
- Roy, D.P.; Wulder, M.A.; Loveland, T.R.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Helder, D.; Irons, J.R.; Johnson, D.M.; Kennedy, R.; et al. Landsat-8: Science and product vision for terrestrial global change research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef]
- Ahamed, T.; Tian, L.; Zhang, Y.; Ting, K. A review of remote sensing methods for biomass feedstock production. Biomass Bioenergy 2011, 35, 2455–2469. [Google Scholar] [CrossRef]
- Bannari, A.; Morin, D.; Bonn, F.; Huete, A. A review of vegetation indices. Remote Sens. Rev. 1995, 13, 95–120. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Viña, A.; Arkebauer, T.J.; Rundquist, D.C.; Keydan, G.; Leavitt, B. Remote estimation of leaf area index and green leaf biomass in maize canopies. Geophys. Res. Lett. 2003, 30, 1248. [Google Scholar] [CrossRef]
- Hunt, E.R., Jr.; Daughtry, C.; Eitel, J.U.; Long, D.S. Remote sensing leaf chlorophyll content using a visible band index. Agron. J. 2011, 103, 1090–1099. [Google Scholar] [CrossRef]
- Schlerf, M.; Atzberger, C.; Hill, J. Remote sensing of forest biophysical variables using HyMap imaging spectrometer data. Remote Sens. Environ. 2005, 95, 177–194. [Google Scholar] [CrossRef]
- Pu, R.; Gong, P.; Yu, Q. Comparative analysis of EO-1 ALI and Hyperion, and Landsat ETM+ data for mapping forest crown closure and leaf area index. Sensors 2008, 8, 3744–3766. [Google Scholar] [CrossRef] [PubMed]
- Lymburner, L.; Beggs, P.J.; Jacobson, C.R. Estimation of canopy-average surface-specific leaf area using Landsat TM data. Photogramm. Eng. Remote Sens. 2000, 66, 183–192. [Google Scholar]
- Rosenqvist, A.; Shimada, M.; Suzuki, S.; Ohgushi, F.; Tadono, T.; Watanabe, M.; Tsuzuku, K.; Watanabe, T.; Kamijo, S.; Aoki, E. Operational performance of the ALOS global systematic acquisition strategy and observation plans for ALOS-2 PALSAR-2. Remote Sens. Environ. 2014, 155, 3–12. [Google Scholar] [CrossRef]
- Aguirre-Gutiérrez, J.; Rifai, S.; Shenkin, A.; Oliveras, I.; Bentley, L.P.; Svátek, M.; Girardin, C.A.; Both, S.; Riutta, T.; Berenguer, E.; et al. Pantropical modelling of canopy functional traits using Sentinel-2 remote sensing data. Remote Sens. Environ. 2021, 252, 112122. [Google Scholar] [CrossRef]
- Zhao, P.; Lu, D.; Wang, G.; Liu, L.; Li, D.; Zhu, J.; Yu, S. Forest aboveground biomass estimation in Zhejiang Province using the integration of Landsat TM and ALOS PALSAR data. Int. J. Appl. Earth Obs. Geoinf. 2016, 53, 1–15. [Google Scholar] [CrossRef]
- Ali, A.; Lin, S.L.; He, J.K.; Kong, F.M.; Yu, J.H.; Jiang, H.S. Climate and soils determine aboveground biomass indirectly via species diversity and stand structural complexity in tropical forests. For. Ecol. Manag. 2019, 432, 823–831. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Pham, T.D.; Le, N.N.; Ha, N.T.; Nguyen, L.V.; Xia, J.; Yokoya, N.; To, T.T.; Trinh, H.X.; Kieu, L.Q.; Takeuchi, W. Estimating mangrove above-ground biomass using extreme gradient boosting decision trees algorithm with fused sentinel-2 and ALOS-2 PALSAR-2 data in can Gio biosphere reserve, Vietnam. Remote Sens. 2020, 12, 777. [Google Scholar] [CrossRef]
- Du, Z.; Wang, Z.; Wu, S.; Zhang, F.; Liu, R. Geographically neural network weighted regression for the accurate estimation of spatial non-stationarity. Int. J. Geogr. Inf. Sci. 2020, 34, 1353–1377. [Google Scholar] [CrossRef]
- Lu, X. Estimation of Mountain Forest Aboveground Biomass by Inteerating ICEsat and Landsat Data. Ph.D. Thesis, Chinese Academy of Sciences, Beijing, China, 2017. [Google Scholar]
- Wu, D. Forest Canopy Height and Aboveground Biomass Estimation Based on GLAS and MISR Data. Ph.D. Thesis, Northeast Forestry University, Harbin, China, 2015. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).