Impact of Satellite Wind on Improving Simulation of the Upper Ocean Response to Tropical Cyclones
Abstract
1. Introduction
2. Dataset and Methodology
2.1. Dataset
2.1.1. Multiple-Satellite Remote Sensing Data
- International Best Track Archive for Climate Stewardship (IBTrACS)
- b.
- Sea Surface Temperature (SST)
- c.
- Ocean Surface Winds
2.1.2. In Situ Observation Data
- Vertical Temperature
- b.
- Surface Current Velocities
2.2. Numerical Model Setup
3. Results and Discussion
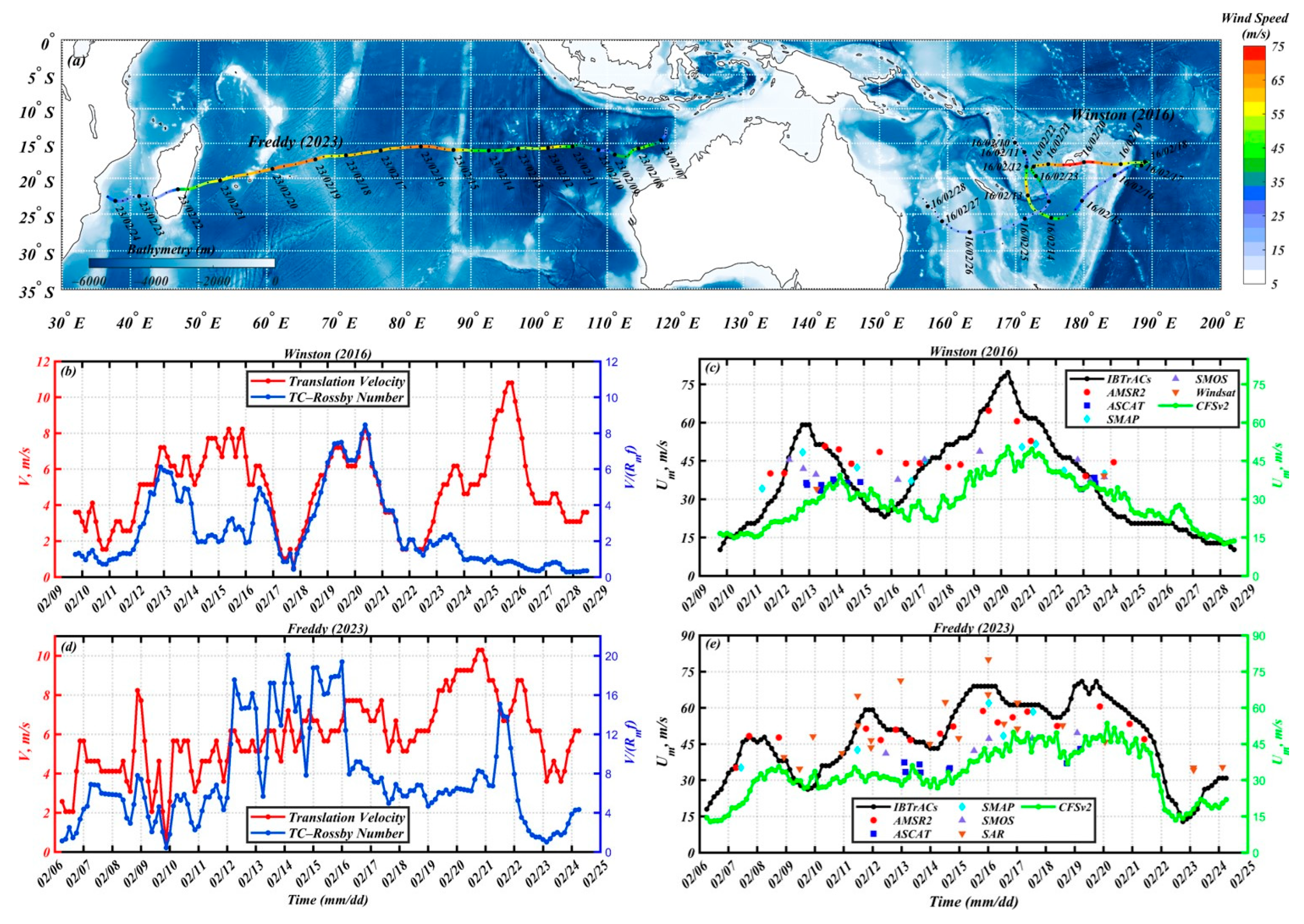
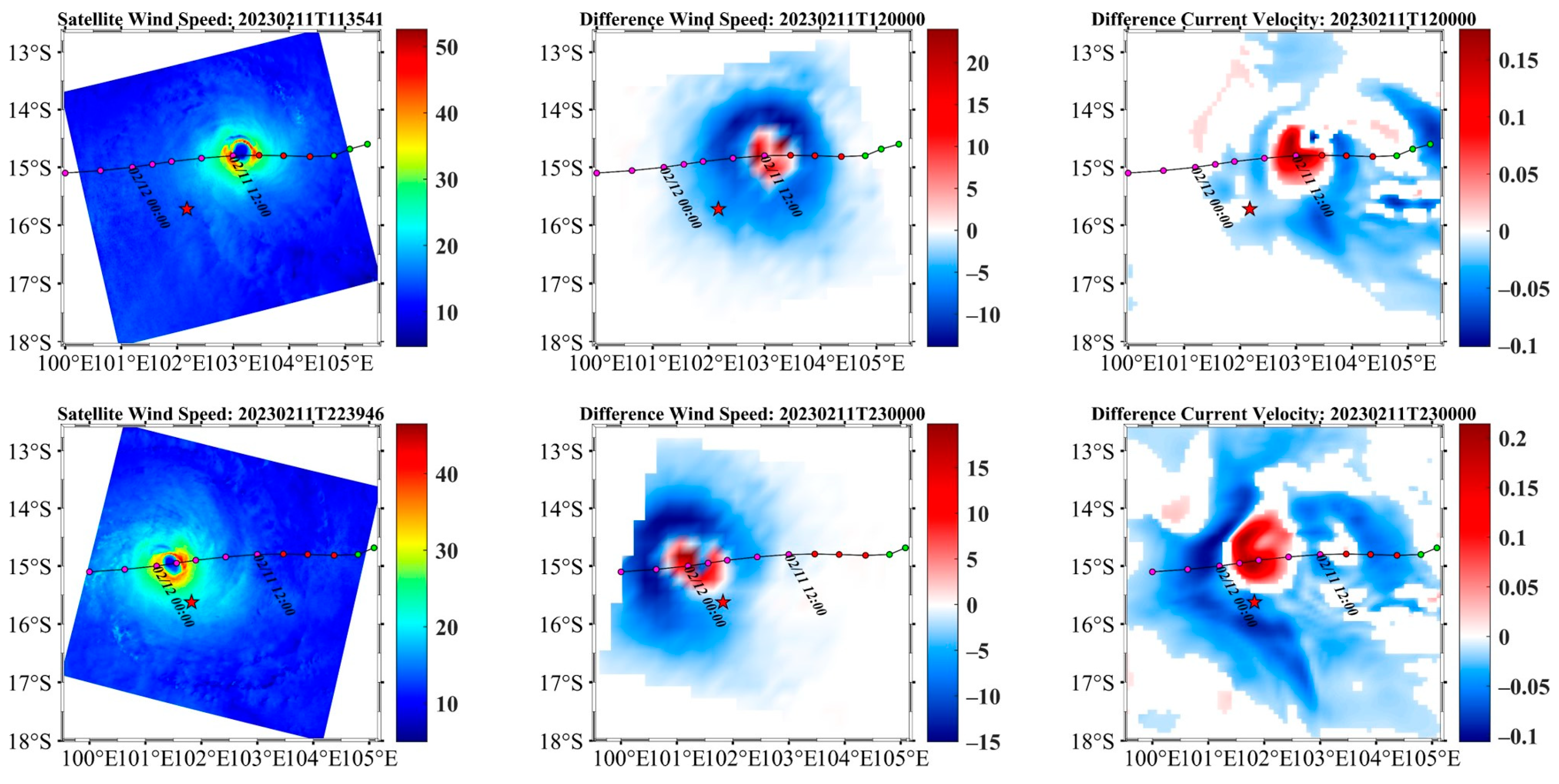
3.1. Brief Description of the Two TCs (Winston and Freddy)
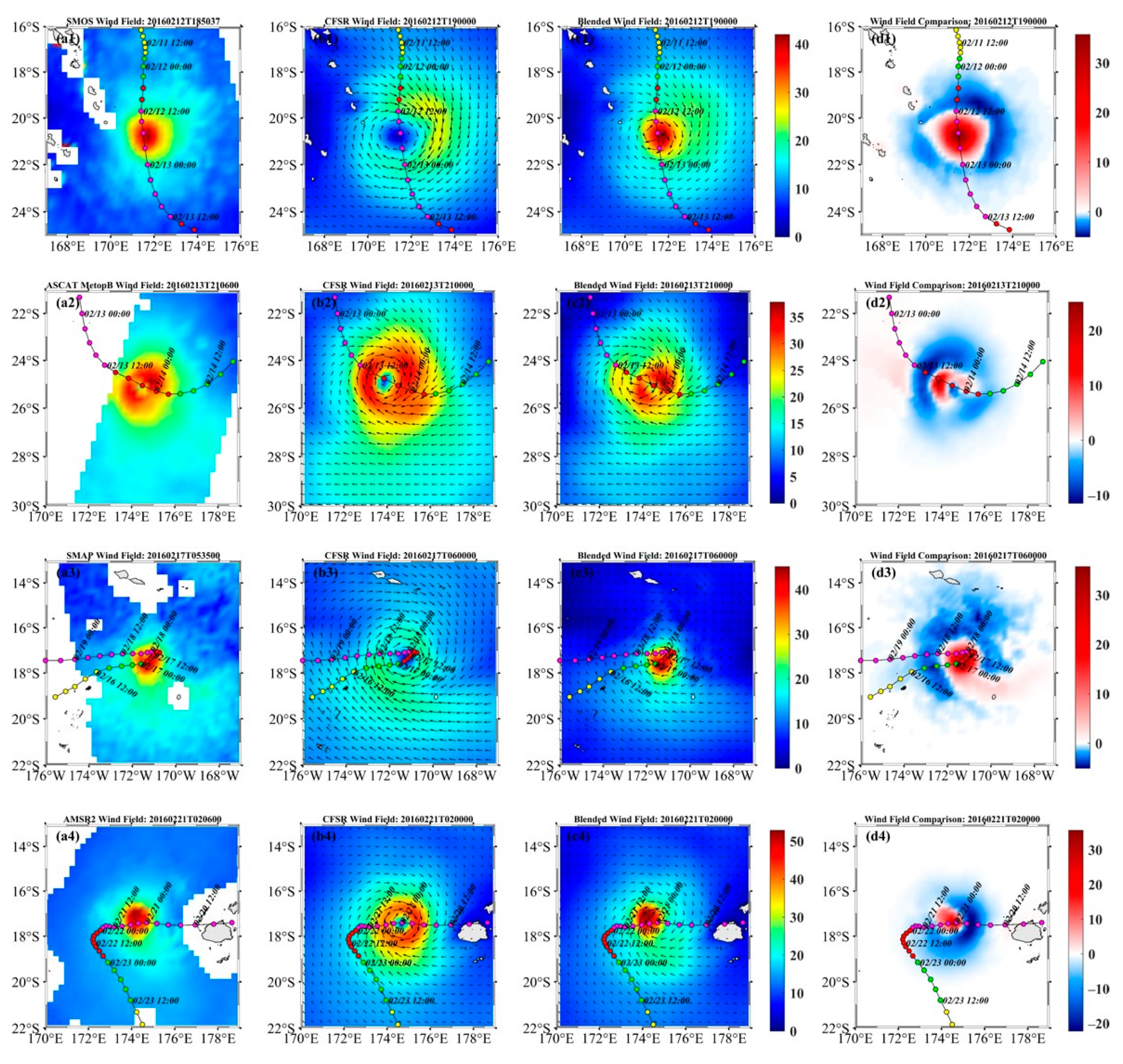
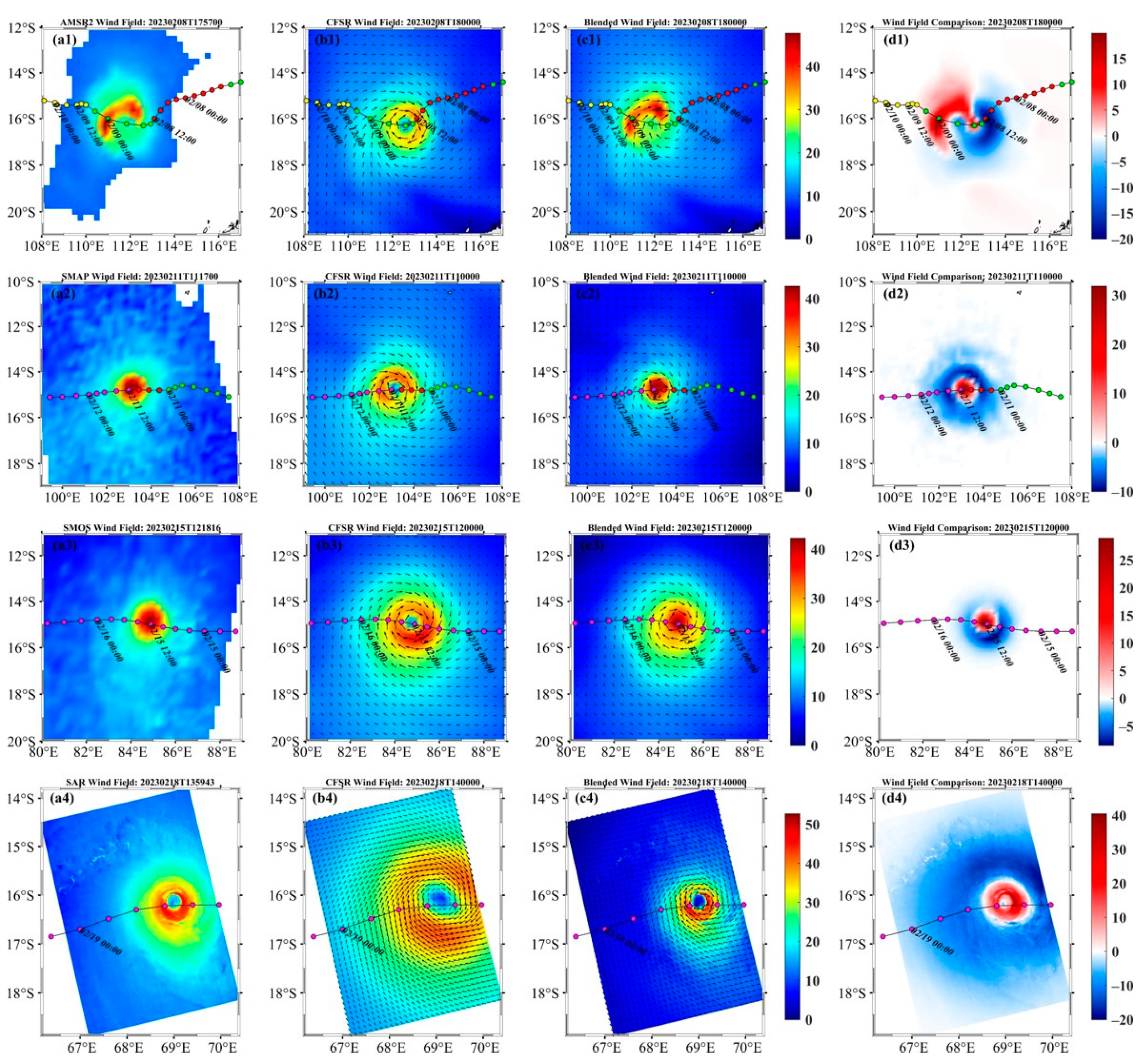
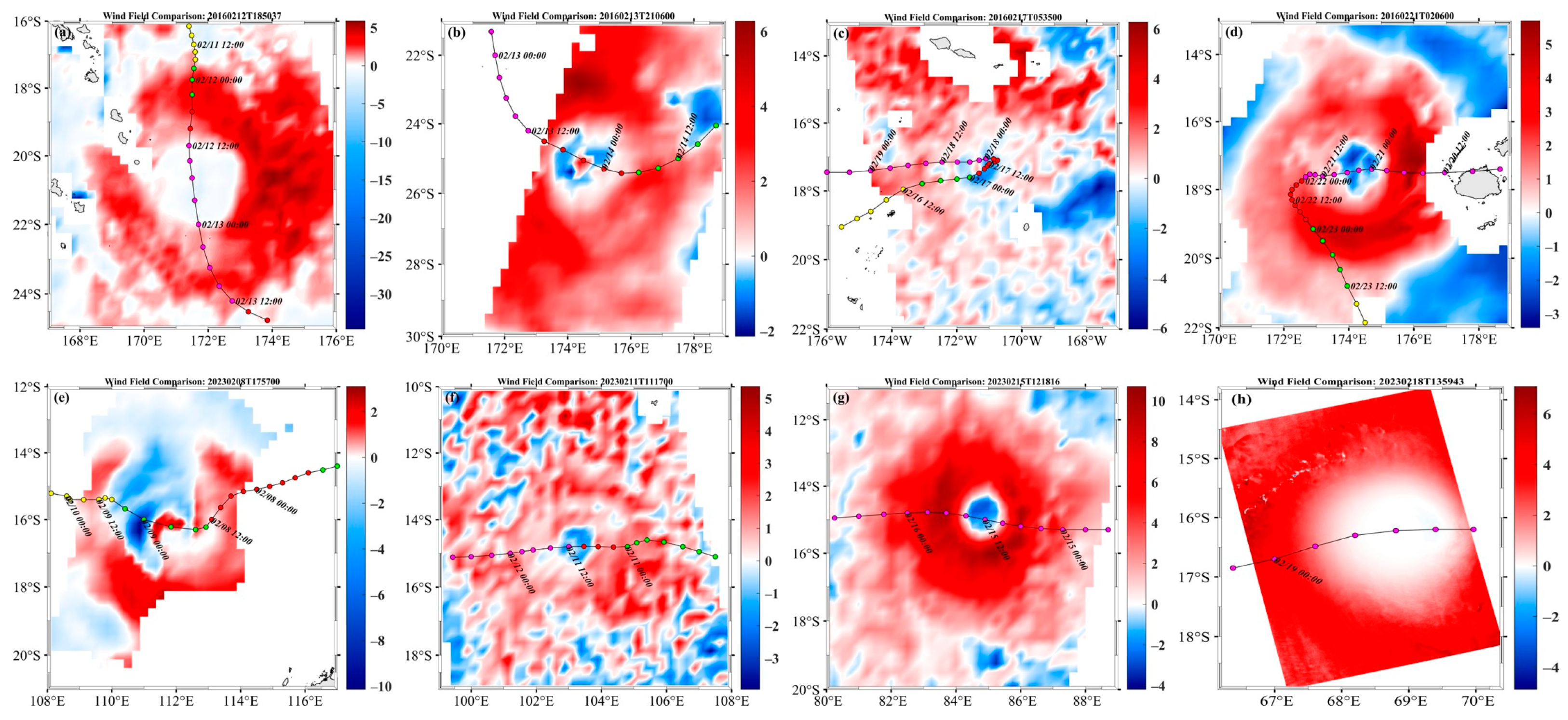
3.2. TC-Dedicated Blended Wind Fields
3.3. Oceanic Temperature Response
3.3.1. Sea Surface Cooling
3.3.2. Subsurface Response
3.4. Near Surface Current Velocity Response
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Price, J.F. Upper Ocean Response to a Hurricane. J. Phys. Oceanogr. 1981, 11, 153–175. [Google Scholar] [CrossRef]
- Bender, M.A.; Ginis, I.; Kurihara, Y. Numerical simulations of tropical cyclone-ocean interaction with a high-resolution coupled model. J. Geophys. Res. Atmos. 1993, 98, 23245–23263. [Google Scholar] [CrossRef]
- Bender, M.A.; Ginis, I. Real-Case Simulations of Hurricane–Ocean Interaction Using a High-Resolution Coupled Model: Effects on Hurricane Intensity. Mon. Weather Rev. 2000, 128, 917–946. [Google Scholar] [CrossRef]
- Sanford, T.B.; Price, J.F.; Girton, J.B.; Webb, D.C. Highly resolved observations and simulations of the ocean response to a hurricane. Geophys. Res. Lett. 2007, 34, L13604. [Google Scholar] [CrossRef]
- Halliwell, G.R.; Shay, L.K.; Jacob, S.D.; Smedstad, O.M.; Uhlhorn, E.W. Improving Ocean Model Initialization for Coupled Tropical Cyclone Forecast Models Using GODAE Nowcasts. Mon. Weather Rev. 2008, 136, 2576–2591. [Google Scholar] [CrossRef]
- Halliwell, G.R.; Shay, L.K.; Brewster, J.K.; Teague, W.J. Evaluation and Sensitivity Analysis of an Ocean Model Response to Hurricane Ivan. Mon. Weather Rev. 2011, 139, 921–945. [Google Scholar] [CrossRef]
- Morey, S.L.; Bourassa, M.A.; Davis, X.J.; O’Brien, J.J.; Zavala-Hidalgo, J. Remotely sensed winds for episodic forcing of ocean models. J. Geophys. Res. Ocean. 2005, 110, C10024. [Google Scholar] [CrossRef]
- Prasad, T.G.; Hogan, P.J. Upper-ocean response to Hurricane Ivan in a 1/25° nested Gulf of Mexico HYCOM. J. Geophys. Res. 2007, 112, C04013. [Google Scholar] [CrossRef]
- Seroka, G.; Miles, T.; Xu, Y.; Kohut, J.; Schofield, O.; Glenn, S. Rapid shelf-wide cooling response of a stratified coastal ocean to hurricanes. J. Geophys. Res. Ocean. 2017, 122, 4845–4867. [Google Scholar] [CrossRef]
- Kistler, R.; Kalnay, E.; Collins, W.; Saha, S.; White, G.; Woollen, J.; Chelliah, M.; Ebisuzaki, W.; Kanamitsu, M.; Kousky, V.; et al. The NCEP-NCAR 50-Year Reanalysis: Monthly Means CD-ROM and Documentation. Bull. Am. Meteorol. Soc. 2001, 82, 247–267. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Pan, H.L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D.; et al. The NCEP Climate Forecast System Reanalysis. Bull. Am. Meteorol. Soc. 2010, 91, 1015–1058. [Google Scholar] [CrossRef]
- Uppala, S.M.; KÅllberg, P.W.; Simmons, A.J.; Andrae, U.; Bechtold, V.D.C.; Fiorino, M.; Gibson, J.K.; Haseler, J.; Hernandez, A.; Kelly, G.A.; et al. The ERA-40 re-analysis. Q. J. R. Meteorol. Soc. 2005, 131, 2961–3012. [Google Scholar] [CrossRef]
- Kiss, P.; Jánosi, I.M. Comprehensive empirical analysis of ERA-40 surface wind speed distribution over Europe. Energy Convers. Manag. 2008, 49, 2142–2151. [Google Scholar] [CrossRef]
- Schenkel, B.A.; Lin, N.; Chavas, D.; Oppenheimer, M.; Brammer, A. Evaluating Outer Tropical Cyclone Size in Reanalysis Datasets Using QuikSCAT Data. J. Clim. 2017, 30, 8745–8762. [Google Scholar] [CrossRef]
- Signell, R.P.; Carniel, S.; Cavaleri, L.; Chiggiato, J.; Doyle, J.D.; Pullen, J.; Sclavo, M. Assessment of Wind Quality for Oceanographic Modelling in Semi-Enclosed Basins. J. Mar. Syst. 2005, 53, 217–233. [Google Scholar] [CrossRef]
- Wakelin, S.; Proctor, R. The impact of meteorology on modelling storm surges in the Adriatic Sea. Glob. Planet. Chang. 2002, 34, 97–119. [Google Scholar] [CrossRef]
- Hodur, R.M. The Naval Research Laboratory’s Coupled Ocean/Atmosphere Mesoscale Prediction System (COAMPS). Mon. Weather Rev. 1997, 125, 1414–1430. [Google Scholar] [CrossRef]
- Powell, M.D.; Houston, S.H.; Amat, L.R.; Morisseau-Leroy, N. The HRD real-time hurricane wind analysis system. J. Wind Eng. Ind. Aerodyn. 1998, 77–78, 53–64. [Google Scholar] [CrossRef]
- Price, J.F.; Sanford, T.B.; Forristall, G.Z. Forced Stage Response to a Moving Hurricane. J. Phys. Oceanogr. 1994, 24, 233–260. [Google Scholar] [CrossRef]
- Holland, G.J. An Analytic Model of the Wind and Pressure Profiles in Hurricanes. Mon. Weather Rev. 1980, 108, 1212–1218. [Google Scholar] [CrossRef]
- Holland, G. A Revised Hurricane Pressure-Wind Model. Mon. Weather Rev. 2008, 136, 3432–3445. [Google Scholar] [CrossRef]
- Holland, G.J.; Belanger, J.I.; Fritz, A. A Revised Model for Radial Profiles of Hurricane Winds. Mon. Weather Rev. 2010, 138, 4393–4401. [Google Scholar] [CrossRef]
- Uhlhorn, E.W.; Klotz, B.W.; Vukicevic, T.; Reasor, P.D.; Rogers, R.F. Observed Hurricane Wind Speed Asymmetries and Relationships to Motion and Environmental Shear. Mon. Weather Rev. 2014, 142, 1290–1311. [Google Scholar] [CrossRef]
- Olfateh, M.; Callaghan, D.P.; Nielsen, P.; Baldock, T.E. Tropical cyclone wind field asymmetry-Development and evaluation of a new parametric model. J. Geophys. Res. Ocean. 2017, 122, 458–469. [Google Scholar] [CrossRef]
- Willoughby, H.E.; Rahn, M.E. Parametric Representation of the Primary Hurricane Vortex. Part I: Observations and Evaluation of the Holland (1980) Model. Mon. Weather Rev. 2004, 132, 3033–3048. [Google Scholar] [CrossRef]
- Landsea, C.W.; Franklin, J.L. Atlantic Hurricane Database Uncertainty and Presentation of a New Database Format. Mon. Weather Rev. 2013, 141, 3576–3592. [Google Scholar] [CrossRef]
- Murty, P.L.N.; Bhaskaran, P.K.; Gayathri, R.; Sahoo, B.; Kumar, T.S.; SubbaReddy, B. Numerical study of coastal hydrodynamics using a coupled model for Hudhud cyclone in the Bay of Bengal. Estuar. Coast. Shelf Sci. 2016, 183, 13–27. [Google Scholar] [CrossRef]
- Murty, P.L.N.; Srinivas, K.S.; Rao, E.P.R.; Bhaskaran, P.K.; Shenoi, S.S.C.; Padmanabham, J. Improved cyclonic wind fields over the Bay of Bengal and their application in storm surge and wave computations. Appl. Ocean Res. 2020, 95, 102048. [Google Scholar] [CrossRef]
- Shao, Z.; Liang, B.; Li, H.; Wu, G.; Wu, Z. Blended wind fields for wave modeling of tropical cyclones in the South China Sea and East China Sea. Appl. Ocean Res. 2018, 71, 20–33. [Google Scholar] [CrossRef]
- Pan, Y.; Chen, Y.; Li, J.; Ding, X. Improvement of wind field hindcasts for tropical cyclones. Water Sci. Eng. 2016, 9, 58–66. [Google Scholar] [CrossRef]
- McConochie, J.D.; Hardy, T.A.; Mason, L.B. Modelling tropical cyclone over-water wind and pressure fields. Ocean Eng. 2004, 31, 1757–1782. [Google Scholar] [CrossRef]
- Rayson, M.D.; Ivey, G.N.; Jones, N.L.; Lowe, R.J.; Wake, G.W.; McConochie, J.D. Near-inertial ocean response to tropical cyclone forcing on the Australian North-West Shelf. J. Geophys. Res. Ocean. 2015, 120, 7722–7751. [Google Scholar] [CrossRef]
- Wei, J.; Liu, X.; Wang, D.X. Dynamic and thermal responses of the Kuroshio to typhoon Megi (2004). Geophys. Res. Lett. 2014, 41, 8495–8502. [Google Scholar] [CrossRef]
- Yin, X.; Wang, Z.; Liu, Y.; Xu, Y. Ocean response to Typhoon Ketsana traveling over the northwest Pacific and a numerical model spproach. Geophys. Res. Lett. 2007, 34, L21606. [Google Scholar] [CrossRef]
- Brennan, M.J.; Hennon, C.C.; Knabb, R.D. The Operational Use of QuikSCAT Ocean Surface Vector Winds at the National Hurricane Center. Weather Forecast. 2009, 24, 621–645. [Google Scholar] [CrossRef]
- Draper, D.W.; Long, D.G. Evaluating the effect of rain on SeaWinds scatterometer measurements. J. Geophys. Res. Ocean. 2004, 109, C02005. [Google Scholar] [CrossRef]
- Reul, N.; Tenerelli, J.; Chapron, B.; Vandemark, D.; Quilfen, Y.; Kerr, Y. SMOS satellite L-band radiometer: A new capability for ocean surface remote sensing in hurricanes. J. Geophys. Res. Ocean. 2012, 117, C02006. [Google Scholar] [CrossRef]
- Yueh, S.H.; Fore, A.G.; Tang, W.; Hayashi, A.; Stiles, B.; Reul, N.; Weng, Y.; Zhang, F. SMAP L-Band Passive Microwave Observations of Ocean Surface Wind During Severe Storms. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7339–7350. [Google Scholar] [CrossRef]
- Meissner, T.; Ricciardulli, L.; Wentz, F.J. Capability of the SMAP Mission to Measure Ocean Surface Winds in Storms. Bull. Am. Meteorol. Soc. 2017, 98, 1660–1677. [Google Scholar] [CrossRef]
- Knapp, K.R.; Kruk, M.C.; Levinson, D.H.; Diamond, H.J.; Neumann, C.J. The International Best Track Archive for Climate Stewardship (IBTrACS): Unifying Tropical Cyclone Data. Bull. Am. Meteorol. Soc. 2010, 91, 363–376. [Google Scholar] [CrossRef]
- GHRSST Project Office; Helen, B.; Ioanna, K.; Sandra, C. Sea Surface Temperature: An introduction to Users on the Set of GHRSST Products (1/2023); Zenodo: Geneva, Switzerland, 2023. [Google Scholar] [CrossRef]
- Gaiser, P.W.; St Germain, K.M.; Twarog, E.M.; Poe, G.A.; Purdy, W.; Richardson, D.; Grossman, W.; Jones, W.L.; Spencer, D.; Golba, G.; et al. The WindSat spaceborne polarimetric microwave radiometer: Sensor description and early orbit performance. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2347–2361. [Google Scholar] [CrossRef]
- Meissner, T.; Ricciardulli, L.; Manaster, A. Tropical Cyclone Wind Speeds from WindSat, AMSR and SMAP: Algorithm Development and Testing. Remote Sens. 2021, 13, 1641. [Google Scholar] [CrossRef]
- Ricciardulli, L.; Manaster, A. Intercalibration of ASCAT Scatterometer Winds from MetOp-A, -B, and -C, for a Stable Climate Data Record. Remote Sens. 2021, 13, 3678. [Google Scholar] [CrossRef]
- Entekhabi, D.; Yueh, S.; O’Neill, P.E.; Kellogg, K.H.; Allen, A.; Bindlish, R.; Brown, M.; Chan, S.; Colliander, A.; Crow, W.; et al. SMAP Handbook. National Aeronautics and Space Administration. 2014; p. 192. Available online: https://smap.jpl.nasa.gov/mission/description/ (accessed on 4 December 2023).
- Fernandez, D.E.; Carswell, J.R.; Frasier, S.; Chang, P.S.; Black, P.G.; Marks, F.D. Dual-polarized C- and Ku-band ocean backscatter response to hurricane-force winds. J. Geophys. Res. Oceans 2006, 111, C08013. [Google Scholar] [CrossRef]
- Sapp, J.W.; Alsweiss, S.O.; Jelenak, Z.; Chang, P.S.; Frasier, S.J.; Carswell, J. Airborne Co-polarization and Cross-Polarization Observations of the Ocean-Surface NRCS at C-Band. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5975–5992. [Google Scholar] [CrossRef]
- Mouche, A.A.; Chapron, B.; Zhang, B.; Husson, R. Combined Co- and Cross-Polarized SAR Measurements Under Extreme Wind Conditions. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6746–6755. [Google Scholar] [CrossRef]
- Chandra, A.; Kumar, S. Sea Surface Temperature and Ocean Heat Content during Tropical Cyclones Pam (2015) and Winston (2016) in the Southwest Pacific Region. Mon. Weather Rev. 2021, 149, 1173–1187. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Q.; Ma, Y. Upper Ocean Response to Typhoon Megi (2010). IOP Conf. Ser. Earth Environ. Sci. 2017, 52, 012063. [Google Scholar] [CrossRef]
- Elipot, S.; Lumpkin, R.; Perez, R.C.; Lilly, J.M.; Early, J.J.; Sykulski, A.M. A global surface drifter data set at hourly resolution. J. Geophys. Res. Ocean. 2016, 121, 2937–2966. [Google Scholar] [CrossRef]
- Lumpkin, R.; Pazos, M. Measuring surface currents with Surface Velocity Program drifters: The instrument, its data, and some recent results. In Lagrangian Analysis and Prediction of Coastal and Ocean Dynamics; Cambridge University Press: Cambridge, UK, 2007; pp. 39–67. [Google Scholar]
- Shchepetkin, A.F.; McWilliams, J.C. The regional oceanic modeling system (ROMS): A split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Model. 2005, 9, 347–404. [Google Scholar] [CrossRef]
- Fairall, C.W.; Bradley, E.F.; Hare, J.E.; Grachev, A.A.; Edson, J.B. Bulk Parameterization of Air–Sea Fluxes: Updates and Verification for the COARE Algorithm. J. Clim. 2003, 16, 571–591. [Google Scholar] [CrossRef]
- Umlauf, L.; Burchard, H. A generic length-scale equation for geophysical turbulence models. J. Mar. Res. 2003, 61, 235–265. [Google Scholar] [CrossRef]
- Umlauf, L.; Burchard, H.; Hutter, K. Extending the k − ω turbulence model towards oceanic applications. Ocean Model. 2003, 5, 195–218. [Google Scholar] [CrossRef]
- Robertson, R.; Hartlipp, P. Surface wind mixing in the Regional Ocean Modeling System (ROMS). Geosci. Lett. 2017, 4, 24. [Google Scholar] [CrossRef] [PubMed]
- Chassignet, E.P.; Hurlburt, H.E.; Smedstad, O.M.; Halliwell, G.R.; Hogan, P.J.; Wallcraft, A.J.; Baraille, R.; Bleck, R. The HYCOM (Hybrid Coordinate Ocean Model) data assimilative system. J. Mar. Syst. 2007, 65, 60–83. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Monzikova, A.; Combot, C.; Chapron, B.; Reul, N.; Quilfen, Y. A Simplified Model for the Baroclinic and Barotropic Ocean Response to Moving Tropical Cyclones: 1. Satellite Observations. J. Geophys. Res. Ocean. 2019, 124, 3446–3461. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Monzikova, A.; Combot, C.; Chapron, B.; Reul, N. A Simplified Model for the Baroclinic and Barotropic Ocean Response to Moving Tropical Cyclones: 2. Model and Simulations. J. Geophys. Res. Ocean. 2019, 124, 3462–3485. [Google Scholar] [CrossRef]
- Mei, W.; Pasquero, C.; Primeau, F. The effect of translation speed upon the intensity of tropical cyclones over the tropical ocean. Geophys. Res. Lett. 2012, 39, L07801. [Google Scholar] [CrossRef]
- Peng, S.; Li, Y. A parabolic model of drag coefficient for storm surge simulation in the South China Sea. Sci. Rep. 2015, 5, 15496. [Google Scholar] [CrossRef]
- Kara, A.B.; Rochford, P.A.; Hurlburt, H.E. An optimal definition for ocean mixed layer depth. J. Geophys. Res. Ocean. 2000, 105, 16803–16821. [Google Scholar] [CrossRef]
- Lim Kam Sian, K.T.; Dong, C.; Liu, H.; Wu, R.; Zhang, H. Effects of Model Coupling on Typhoon Kalmaegi (2014) Simulation in the South China Sea. Atmosphere 2020, 11, 432. [Google Scholar] [CrossRef]
- McWilliams, J.C.; Restrepo, J.M. The Wave-Driven Ocean Circulation. J. Phys. Oceanogr. 1999, 29, 2523–2540. [Google Scholar] [CrossRef]
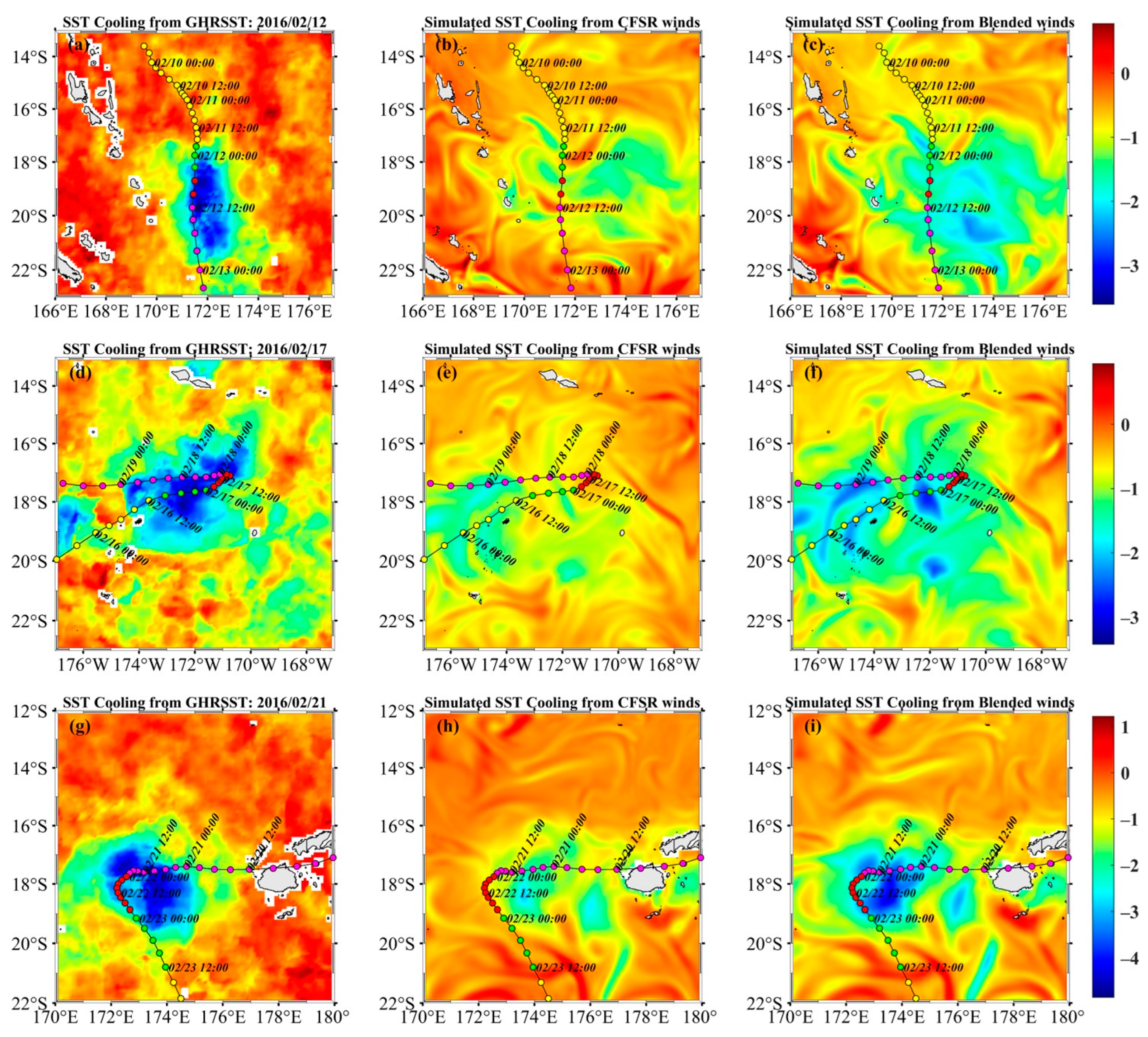

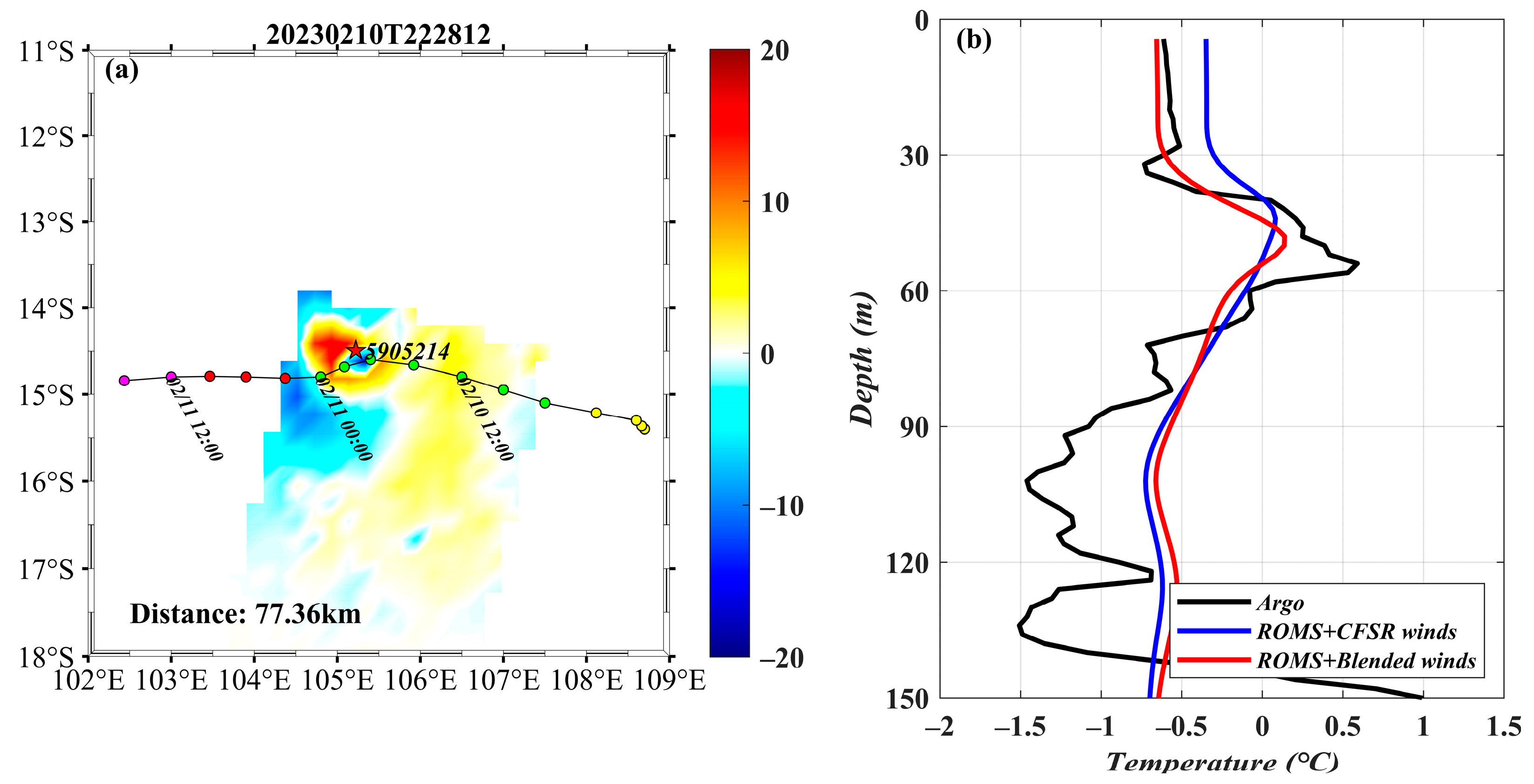
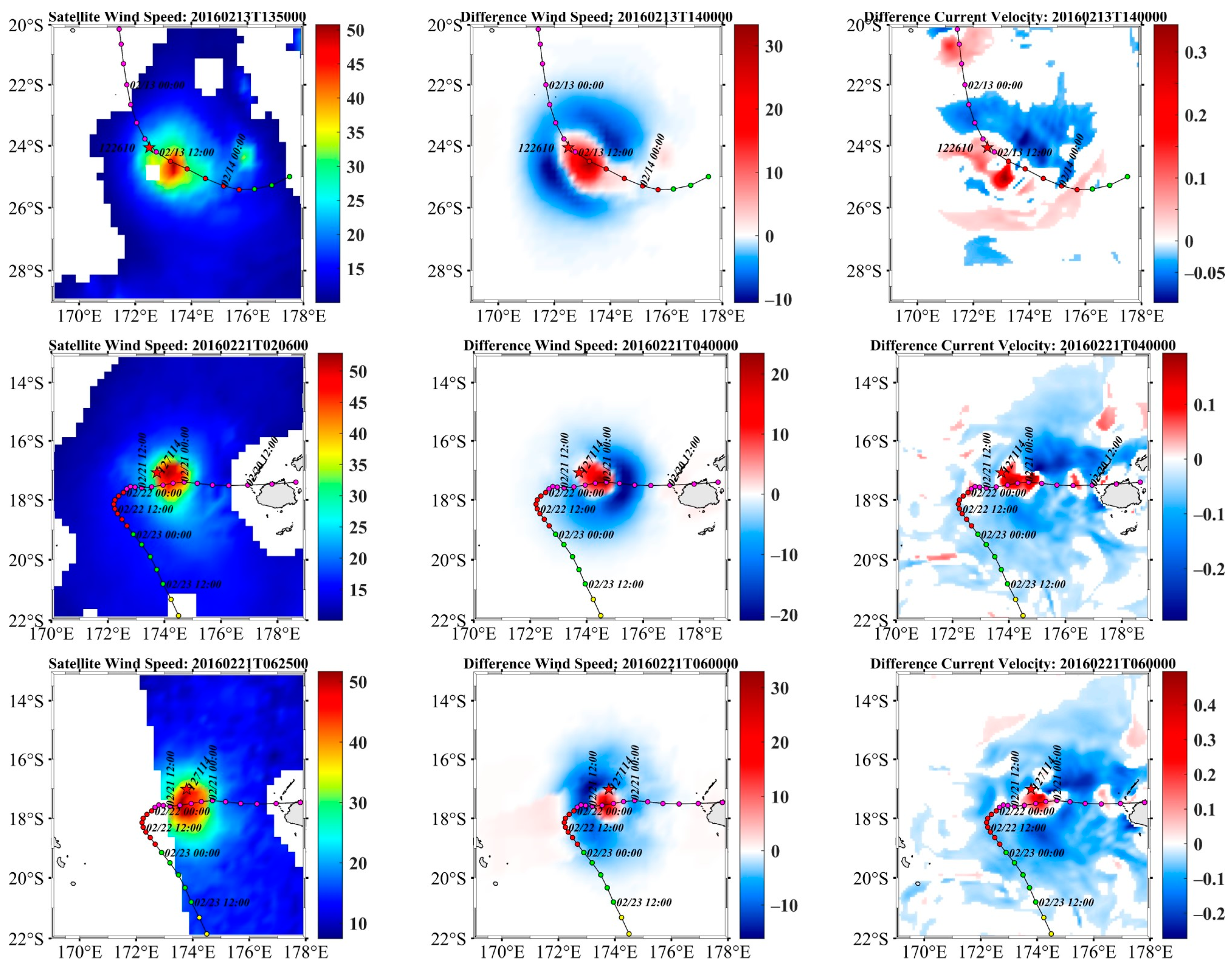
| Argo ID | ||||||
|---|---|---|---|---|---|---|
| R5902145 | 1.385 | 0.554 | 0.997 | 0.998 | 1.832 | 0.002 |
| R5904145 | 1.379 | 0.972 | 0.594 | 0.987 | 1.785 | 0.016 |
| R5900953 | 3.334 | 0.937 | 0.888 | 0.962 | 3.446 | 0.026 |
| R5905214 | 2.459 | 0.992 | 0.750 | 0.997 | 2.709 | 0.006 |
| UTC Time | |||||
|---|---|---|---|---|---|
| 2016-02-13 14:00 | 19.55 | 26.41 | 1.40 | 0.54 | 0.62 |
| 2016-02-21 03:00 | 39.21 | 45.85 | 1.00 | 0.71 | 0.81 |
| 2016-02-21 06:00 | 37.07 | 44.99 | 1.15 | 0.64 | 0.75 |
| 2023-02-11 12:00 | 22.22 | 17.21 | 0.52 | 0.23 | 0.18 |
| 2023-02-12 00:00 | 25.61 | 28.34 | 0.91 | 0.56 | 0.64 |
| UTC Time | |||||
|---|---|---|---|---|---|
| 2016-02-13 14:00 | 1.40 | 0.58 | 0.71 | 0.03 | 0.09 |
| 2016-02-21 03:00 | 1.00 | 1.03 | 1.27 | 0.31 | 0.46 |
| 2016-02-21 06:00 | 1.15 | 0.91 | 1.19 | 0.27 | 0.44 |
| 2023-02-11 12:00 | 0.52 | 0.33 | 0.22 | 0.10 | 0.04 |
| 2023-02-12 00:00 | 0.91 | 0.71 | 0.84 | 0.15 | 0.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, X.; Zhang, B. Impact of Satellite Wind on Improving Simulation of the Upper Ocean Response to Tropical Cyclones. Remote Sens. 2024, 16, 1832. https://doi.org/10.3390/rs16111832
Yue X, Zhang B. Impact of Satellite Wind on Improving Simulation of the Upper Ocean Response to Tropical Cyclones. Remote Sensing. 2024; 16(11):1832. https://doi.org/10.3390/rs16111832
Chicago/Turabian StyleYue, Xinxin, and Biao Zhang. 2024. "Impact of Satellite Wind on Improving Simulation of the Upper Ocean Response to Tropical Cyclones" Remote Sensing 16, no. 11: 1832. https://doi.org/10.3390/rs16111832
APA StyleYue, X., & Zhang, B. (2024). Impact of Satellite Wind on Improving Simulation of the Upper Ocean Response to Tropical Cyclones. Remote Sensing, 16(11), 1832. https://doi.org/10.3390/rs16111832







