Abstract
Precise and prompt predictions of crop yields are crucial for optimising farm management, post-harvest operations, and marketing strategies within the agricultural sector. While various machine learning approaches have been employed to forecast crop yield, their application to grain quality, particularly head rice yield (HRY), is less explored. This research collated crop-level HRY data across four seasons (2017/18–2020/21) from Australia’s rice-growing region. Models were developed using the XGBoost algorithm trained at varying time steps up to 16 weeks pre-harvest. The study compared the accuracy of models trained on datasets with climate data alone or paired with vegetative indices using two- and four-week aggregations. The results suggest that model accuracy increases as the harvest date approaches. The dataset combining climate and vegetative indices aggregated over two weeks surpassed industry benchmarks early in the season, achieving the highest accuracy two weeks before harvest (LCCC = 0.65; RMSE = 6.43). The analysis revealed that HRY correlates strongly with agroclimatic conditions nearer harvest, with the significance of vegetative indices-based features increasing as the season progresses. These features, indicative of crop and grain maturity, could aid growers in determining optimal harvest timing. This investigation offers valuable insights into grain quality forecasting, presenting a model adaptable to other regions with accessible climate and satellite data, consequently enhancing farm- and industry-level decision-making.
1. Introduction
In the agricultural sector, accurate and timely crop yield forecasts are crucial for stakeholders ranging from farmers to policymakers. These forecasts enable growers to refine management practices, such as variety selection and fertilisation, to maximise profits based on expected productivity [1,2]. Similarly, businesses in agricultural supply chains rely on these predictions for budgeting and planning, while at the government level, they may inform food security policy decisions [3,4].
Traditionally, crop productivity forecasting has relied heavily on field and farmer surveys, a method widespread across various countries and crop types but burdened with significant time and labour costs [5,6]. The need to address these limitations has led to a shift towards crop simulation and empirical models, offering a more efficient and accurate approach to forecasting [7]. Process-based crop models, such as the Agricultural Production Systems sIMulator (APSIM) [8], are foundational in agricultural science, built on the intricate interplay between crops, their environment, and management practices [9]. These models are invaluable for understanding crop behaviour under various conditions but hinge on extensive field data for calibration and validation. Despite their utility, the application of these models is often constrained by the assumptions they make about crop-environment–management relationships, which may not hold in new contexts [10].
In contrast, empirical models adopt a data-driven approach, relying on historical data and machine learning algorithms to forecast crop yields [6]. These models diverge from process-based counterparts by allowing the data to reveal underlying patterns and relationships independent of predefined theoretical frameworks [11]. This methodology capitalises on the vast amounts of data collected by agribusinesses for various purposes and aligns well with the growing availability of detailed agricultural data. This surge in data availability is propelled by advances in Internet of Things (IoT) technologies, sensor networks, climate data interpolation techniques, and the expanding capabilities of remote sensing platforms [12]. With their capacity to process and learn from large datasets, empirical models offer a flexible and powerful tool for predicting crop yields, adapting readily to the dynamic nature of agricultural environments and data landscapes.
Forecasting systems in agriculture, encompassing crop simulation and empirical models, have made significant strides in estimating crop yields. Yet, the focus on crop quality metrics, particularly for staple grains like rice, remains underexplored. Rice is a critical global commodity, serving as a vital calorie source and a primary income for farmers [13]. In the rice supply chain, assessing head rice yield (HRY) before storage poses a significant challenge. HRY, an essential metric in milling quality, measures the proportionate weight of intact rice grains after processing from harvested paddy rice samples [14]. The preference for white rice and the premium on unbroken grains in traditional markets underscore the economic importance of HRY, as broken grains receive only 60% of the market value of whole grains [15].
In the Australian context, HRY is pivotal for rice growers’ and millers’ revenue. Yet its measurement is hindered by the high moisture content of rice at delivery, delaying HRY assessments until post-harvest drying. While ensuring an accurate HRY measurement, this process imposes substantial costs on the industry, including sample transport, storage, and milling tests [16]. While the ability to predict HRY at the delivery stand has been reported by Clarke et al. [17], the potential for pre-harvest HRY forecasting and its implications for harvest timing remain unexamined. Such forecasts could significantly benefit the Australian rice sector by enhancing grower and industry decision-making, particularly for SunRice™, the industry’s primary player. The capacity to forecast HRY during the growing season and at the point of delivery unlocks opportunities for SunRice to enhance post-harvest management to maximise milling revenue. By categorising delivered rice into defined HRY grades, the milling process can be aligned with the forecasted milling potential. These processes include the storage drying temperatures [18], the rotational speed and pressure of abrasive rollers during milling [19], or the incorporation of a tempering phase during milling [20]. Additionally, the allocation of rice to brown rice markets can be improved, where crops with a lower forecasted HRY may be better suited to these markets, as brown rice milling bypasses the bran removal stage, thereby reducing the likelihood of grain breakage during milling.
In its 2022 Annual Report, SunRice highlighted a notable increase in revenue attributed to the improved availability of Australian rice following a prolonged drought period [21]. Despite this positive development, the company faced challenges in achieving its potential milling revenue. This shortfall was primarily due to an unexpectedly high HRY, which resulted in a surplus of whole grains and a deficit in the forecasted quantity of broken rice for flour production. To meet the obligations of existing sales contracts for broken rice, SunRice re-milled whole grains further, breaking the grain in the process. This process diminished the value of these grains and escalated milling costs due to the extended processing time required. The scenario underscores the critical need for accurate in-season forecasting capabilities, enabling rice milling companies to manage the balance between whole and broken rice in their sales contracts.
This study embarks on developing a sophisticated model to forecast HRY within the Australian rice industry, a critical factor influencing milling revenue and market value. By compiling training datasets that integrate crop-level records with an array of variables derived from climate data, satellite imagery, and soil characteristics collected over various pre-harvest time intervals, this research seeks to harness the predictive power of machine learning for HRY estimation. The objectives outlined for this investigation include the following:
- Develop machine learning models for forecasting HRY at time intervals before harvest.
- Quantify the difference in prediction accuracy based on model development using a climate-only and a climate with vegetative indices-based dataset.
- Quantify the relative importance of pre-harvest time intervals and individual predictor variables in determining HRY.
- Identify potential predictor variables that may inform grower decisions to improve HRY management.
Through data mining techniques, this study intends to bridge the gap between empirical predictions and the underlying biological mechanisms that influence HRY, translating these findings into actionable insights for growers. By achieving this, the research aspires to empower rice producers with knowledge and tools to improve HRY percentages.
2. Materials and Methods
2.1. Study Area
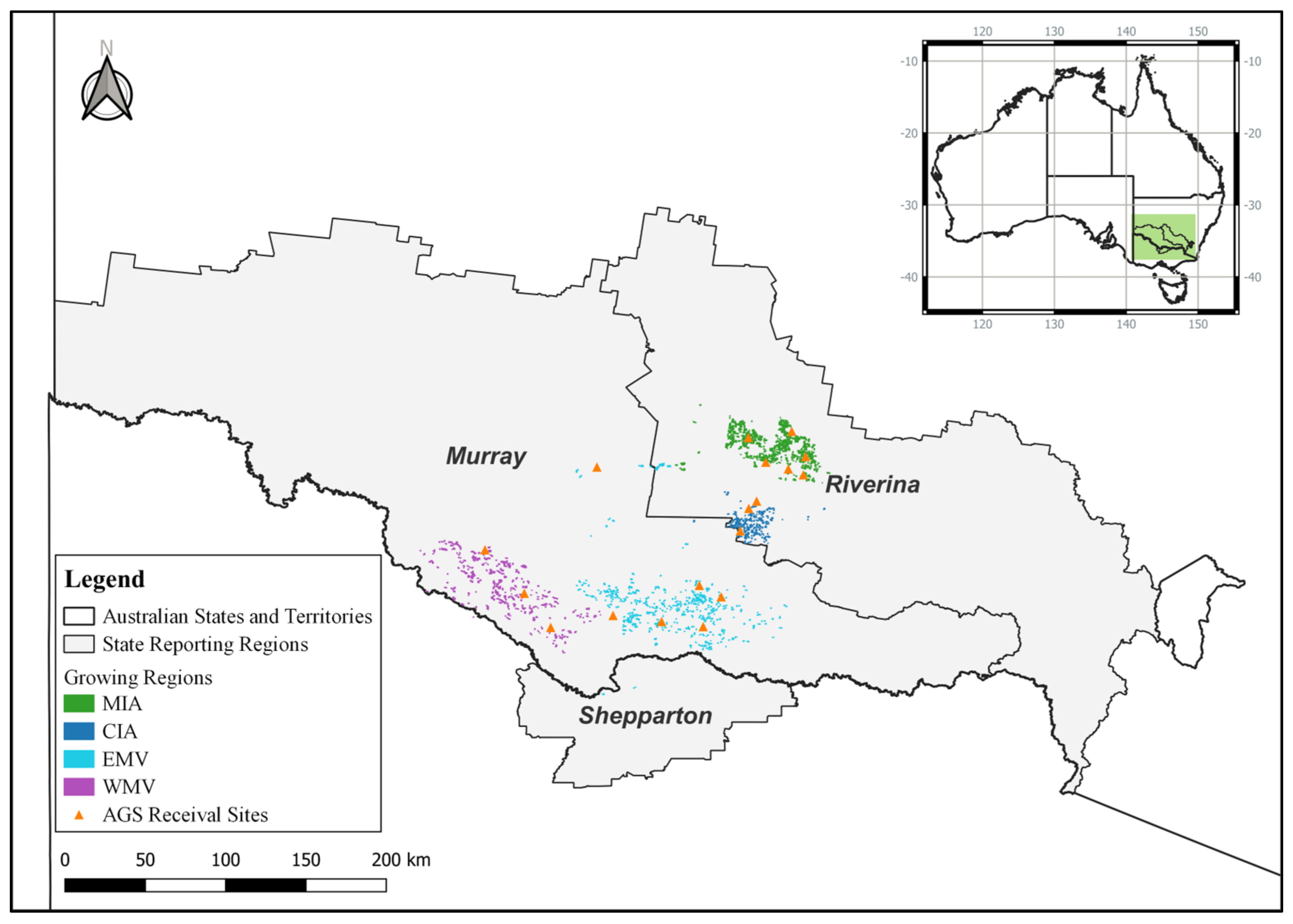
Rice cultivation in Australia is predominantly concentrated in the Murrumbidgee, Coleambally, and Murray irrigation districts of southern New South Wales [22] (Figure 1). This localisation is attributed to the availability of irrigation infrastructure, coupled with the region’s temperate summer climate, extensive flat landscapes, and the prevalence of heavy clay soils conducive to rice farming [23].
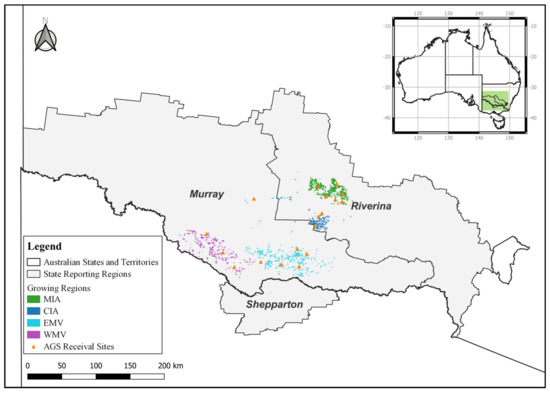
Figure 1.
Location of the rice growing regions where crop records were collated in this study. The field boundaries included in this study are coloured to highlight the rice-growing regions of the industry: MIA—Murrumbidgee Irrigation Area; CIA—Coleambally Irrigation Area; EMV—Eastern Murray Valley; WMV—Western Murray Valley. Australian Grain Storage (AGS) receival site locations are shown in orange. State reporting regions were taken from the Australian Bureau of Statistics—Statistical Areas Level 4 (SA4). Datum GDA2020 (print in colour.)
2.2. Datasets and Pre-Processing
The datasets curated for this investigation adhered to the TOPSAW framework delineated by Filippi et al. [24], designed to summarise the principal determinants of crop yield. Given the constraints of data accessibility, this study concentrated on the agronomy/management, weather, soil, and plant measurements outlined within the TOPSAW framework.
2.2.1. Agronomy
The Australian Rice Industry operates through a vertically integrated model. Growers procure seed from SunRice and, in turn, sell and transport their harvested rice to SunRice via its subsidiary, Australian Grain Storage (AGS), for processing, packaging, and marketing. SunRice supplied farm-level crop production records, detailing the irrigation valley, nearest AGS site, rice variety, sowing and harvest dates, harvest moisture levels, and the achieved HRY for each cultivated crop. These primary records served as the ‘baseline’ dataset, to which all subsequent data were integrated.
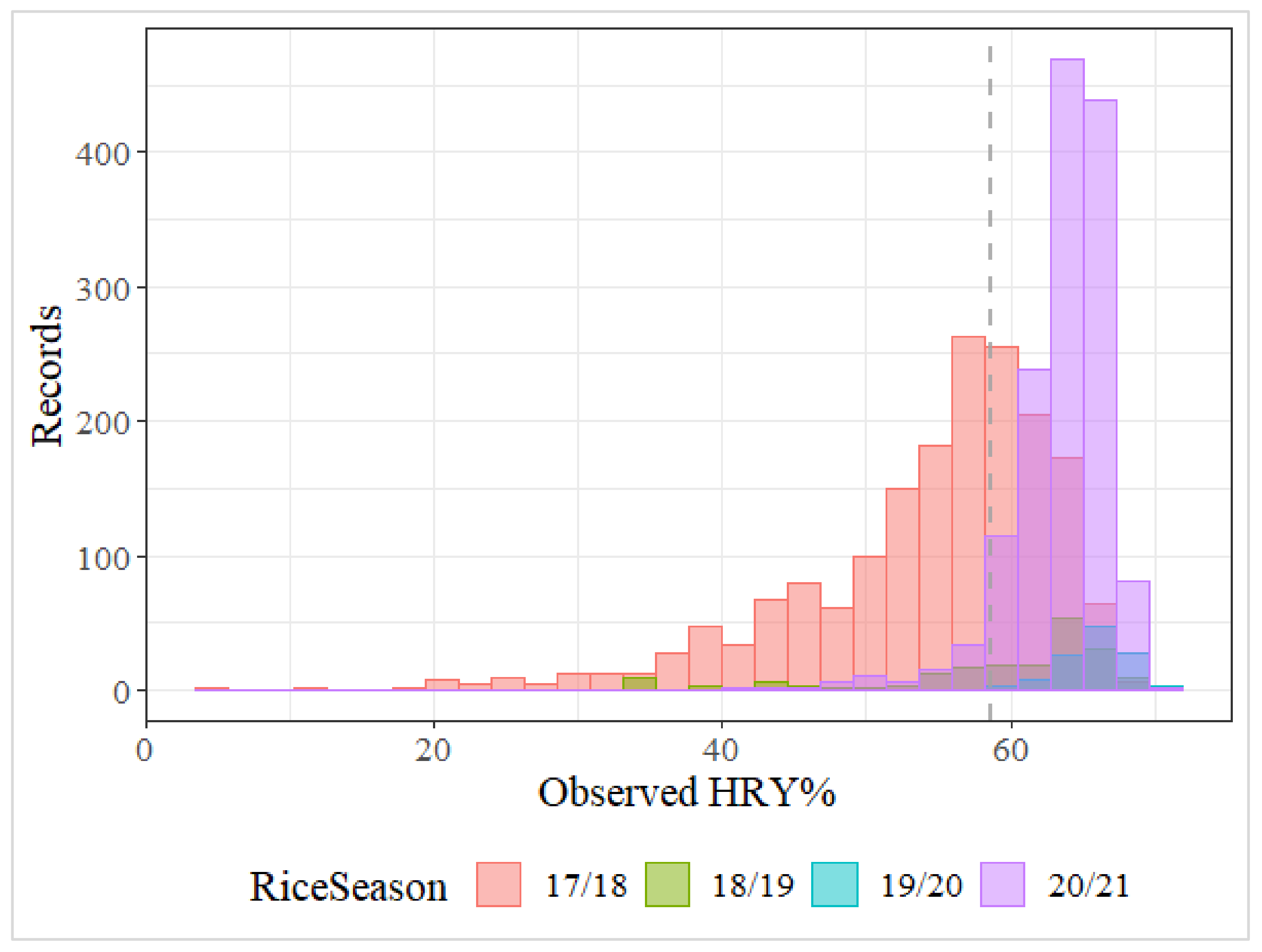
The analysis focused on a four-year dataset of the medium grain rice cultivar, Reiziq, where field shapefiles for the sown areas were accessible. The selected subset encompassed around 3500 crop production records from the 2017/18 to 2020/21 seasons. During this timeframe, the extent of land cultivated under rice production varied significantly, from a low of 2800 hectares in 2019/20 to nearly 35,000 hectares in 2020/21. Concurrently, the seasonal average HRY ranged from 65.4% in the 2019/20 season to 54.3% in the 2017/18 season, while across the four seasons, the crop level HRY ranged from 4.8% to 71%, with an average HRY of 58.7% (Figure 2).
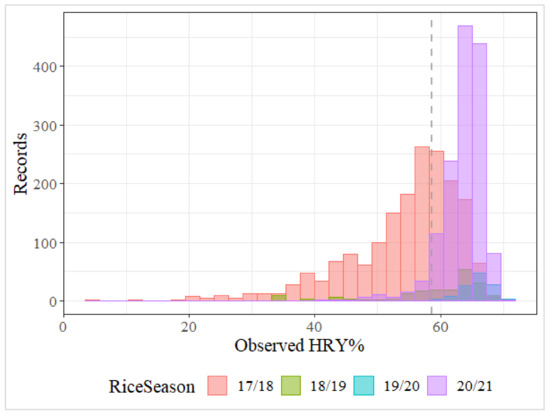
Figure 2.
HRY distribution across four rice growing seasons in the Riverina region of Australia. The histograms represent the frequency of HRY records, with each colour corresponding to a different season, as indicated. The dataset average HRY (58.7%) is displayed as the dashed vertical line.
2.2.2. Weather
Weather variations, including temperature, relative humidity, and evaporation, exert significant effects on the physiological development of rice grains and their propensity for fissure development, all of which are key factors affecting HRY [25,26]. To account for this influence, daily climate data were obtained from the Scientific Information for Land Owners (SILO) point database [27] (available at https://www.longpaddock.qld.gov.au/silo/, accessed on 5 March 2023). Weather data were matched to crop records based on the nearest AGS site (Figure 1).
2.2.3. Soil
Soil-type variables were chosen based on their impact on crop evaporative demand, thereby affecting the grain dry-down rate, which is a significant factor influencing HRY [28]. Soil properties were obtained from the ‘Digital soil maps for key soil properties over New South Wales’ (DSM-NSW), which provides a comprehensive dataset of modelled soil attributes at the 100 m pixel level [29]. Zonal statistics were calculated using the grower record field boundaries to produce records of the average clay content, cation exchange capacity (CEC), and electrical conductivity (EC) at two depths (0–30 cm, 30–100 cm) (Table 1).

Table 1.
List of features included in each dataset, including the crop production records and the feature-engineered climate, satellite, and soil variables calculated by each aggregation stage. Calculated meteorological features are shown in italics.
2.2.4. Plant Measurements
In-season vegetative indices (VI) were calculated through images captured by the Landsat satellite missions. Landsat was selected for its availability in the 2017/18 season when field boundaries were first made available to SunRice. The two Landsat sensors provide a 16-day repeat cycle, meaning passes occur on an 8-day repetition when combined due to the offset passes [30]. Landsat bands were used to calculate the normalized difference vegetation index (NDVI) and the enhanced vegetation index (EVI). The selection of NDVI and EVI variables considered their complementary nature, with NDVI being sensitive to chlorophyll level variation and EVI being linked to canopy structure [24]. While irrigation water is known to affect the value of the selected VIs, previous studies indicate that this impact occurs primarily during the early vegetative stage of the crop, i.e., before the rice canopy achieves complete closure [31,32,33]. In this study, aggregated features extend to 16 weeks before harvest, meaning that the crop canopy cover minimises the impact of ponded water on optical Vis; this trend persists throughout the season, even as VI levels decrease leading up to harvest. The selected VIs were aggregated to field-scale values from the Google Earth Engine (GEE) platform.
2.3. Crop Records Feature Engineering
The methodology for aggregation of environmental data in this research was adapted from the approach outlined by Clarke et al. [17], which involved condensing daily environmental data into discrete intervals extending back 16 weeks before harvest. While the climate-only dataset achieved the highest accuracy using a two-week segmentation, the Landsat revisit cycle constrained the training dataset’s size due to the necessity for at least one cloud-free image per two-week segment. To address this limitation, a four-week aggregation approach, which demonstrated comparable accuracy within the climate-only dataset, was employed for comparative analysis alongside the two-week framework. Adopting this four-week aggregation significantly increased the number of crop records containing a cloud-free image for each interval.
The two-week (2 W) interval method produced eight in-season aggregation stages, whereas the four-week (4 W) method produced four (Figure 3). To each of these methods, an extra stage was incorporated by differentiating predictions at the harvest date from those at the delivery stand, the latter including grain moisture measurements. Recognising the significant impact of grain moisture at harvest on HRY [34,35,36], this separation was designed to clarify the influence of late-season factors on HRY, independent of the dominant effect of harvest moisture.
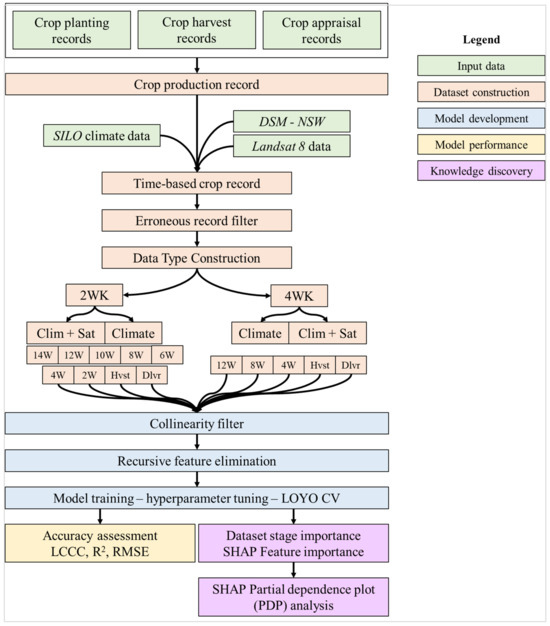
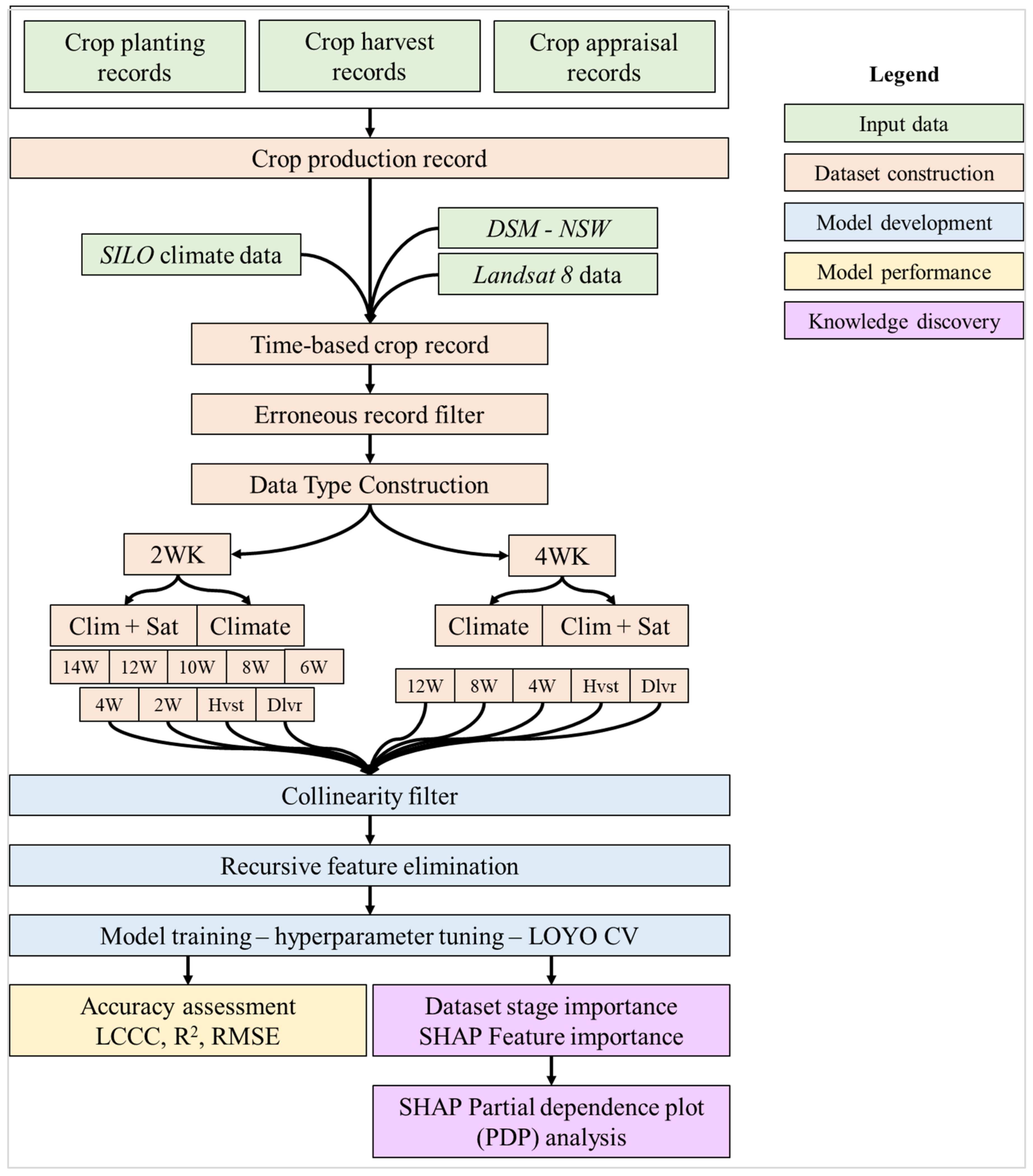
Figure 3.
Methods workflow diagram illustrating the replicated data processing and model development steps for the two-week (2 WK) and four-week (4 WK) dataset construction methods.
2.3.1. Environmental Feature Engineering
Meteorological data obtained from the SILO database were compiled for each growth stage within the predefined two-week (2 W) and four-week (4 W) intervals. For each weather variable, the mean value, alongside the three-day and seven-day rolling average mean, maximum and minimum, were calculated. Precipitation data were analysed to determine both the frequency of rain days (precipitation ≥ 1 mm) and the cumulative precipitation (Table 1). The aggregation of Landsat-derived EVI and NDVI included the calculation of first and last values, the maximum, mean, minimum, and slope within the specified interval (Table 1).
2.3.2. Erroneous Record Filter
Erroneous records were removed based on a filter of the average NDVI in the 8–12 weeks pre-harvest stage (4 W dataset), and the 10–12 weeks pre-harvest stage (2 W dataset). Outliers were defined using the interquartile range, where average NDVI was 1.5 times the interquartile range more than the third quartile (Q3) or 1.5 times the interquartile range less than the first quartile (Q1). This procedure was implemented to eliminate crop records where growers supplied an incorrect field shapefile to SunRice. Previous work has indicated that at 12 weeks pre-harvest, rice crops should be nearing peak NDVI, while fallow areas with bare soil will show lower NDVI values [37].
2.4. Model Development
Model development for each dataset aggregation was conducted using the XGBoost algorithm. The subsequent sections detail model construction, performance evaluation, and insight extraction processes (Figure 3).
2.4.1. Feature Selection
Feature selection was executed in two phases, following the methodology outlined by Ruan et al. [38]. The initial phase involved a collinearity filter using Pearson’s correlation coefficient to mitigate multi-collinearity issues among independent variables, which can diminish their statistical relevance and affect the performance of machine learning algorithms [39]. This is particularly relevant in agricultural datasets encompassing soil, climatic, and management variables [40]. Based on results from Clarke et al. [17], a correlation threshold of 0.95 was used for the filter.
The subsequent step involved recursive feature elimination (RFE) to refine the model by isolating the most influential variables. This technique iteratively discarded the least impactful variables during model training [41], utilising the XGBoost algorithm set with conservative hyperparameters (tree depth limit of three and a minimum child weight threshold of 50). The RFE procedure trained models on progressively larger feature subsets, ranging from 5 to 50 features in increments of 5. It also evaluated the top 100 features and the entire feature set for a comprehensive comparison. The selection of the optimal feature subset was based on achieving the lowest RMSE within a 5% margin of the best-performing model, thereby ensuring a balance between the relevance of variables and model complexity. Additionally, models constructed with the twenty, fifteen, and ten best features identified through RFE were compared.
2.4.2. Machine Learning Algorithm—XGBoost
In this study, the XGBoost (eXtreme Gradient Boosting) algorithm was employed for model training due to its prominence in recent crop yield prediction research [1,11,42,43]. XGBoost is renowned for its capacity to enhance model interpretability and identify key influencing factors. It constructs models through the sequential development of decision trees, each improving upon its predecessors, thereby creating a robust ensemble from individually weak predictors [11]. This aggregation of simple decision trees enables the model to delineate complex interactions within the data while minimising susceptibility to outliers [42,44].
2.4.3. Experiment Design
The four feature subsets derived in feature selection for each aggregation interval, data type, and forecast stage resulted in 20 and 32 distinct feature subsets for the 4 W and 2 W aggregation methods. This study replicated the model training process across all feature subset variations, following the methodology outlined by Vannoppen and Gobin [2]. Each dataset and feature subset combination was trained and validated using the XGBoost algorithm, with hyperparameter tuning conducted through leave-one-year-out cross-validation (LOYO-CV), as per Filippi et al. [24]. Hyperparameter tuning was performed manually, exploring tree depths of 2, 3, 4, and 5 in conjunction with minimum child weights of 1, 10, 30, 50, and 100, leading to 20 distinct training scenarios for each of the 52 feature subset configurations.
2.5. Model Performance
Model performance was quantified using Lin’s concordance correlation coefficient (LCCC) [45] and root mean square Error (RMSE). To contextualise these accuracy metrics within the industry framework, the RMSE values were benchmarked against the existing forecasting method used by SunRice for predicting HRY. This standard industry forecast employs a variety-specific, rolling 5-year average HRY calculated across the industry.
2.6. Knowledge Discovery
Shapley additive explanations (SHAP) were applied to identify key time intervals and data types within the highest-performing predictive models at the key forecast stages. Originating from game theory, SHAP analyses a model’s predictions to determine the impact of individual features, offering insights at both the instance and dataset levels [46]. To visualise how changes in certain explanatory variables affect the model’s predicted outcomes, SHAP partial dependence plots (PDP) were used, directly correlating with SHAP values. These plots expand the breadth of knowledge discovered using feature importance by displaying the function between a feature and the predictor variable [47].
3. Results
3.1. Model Accuracy
3.1.1. Crop Level Forecast
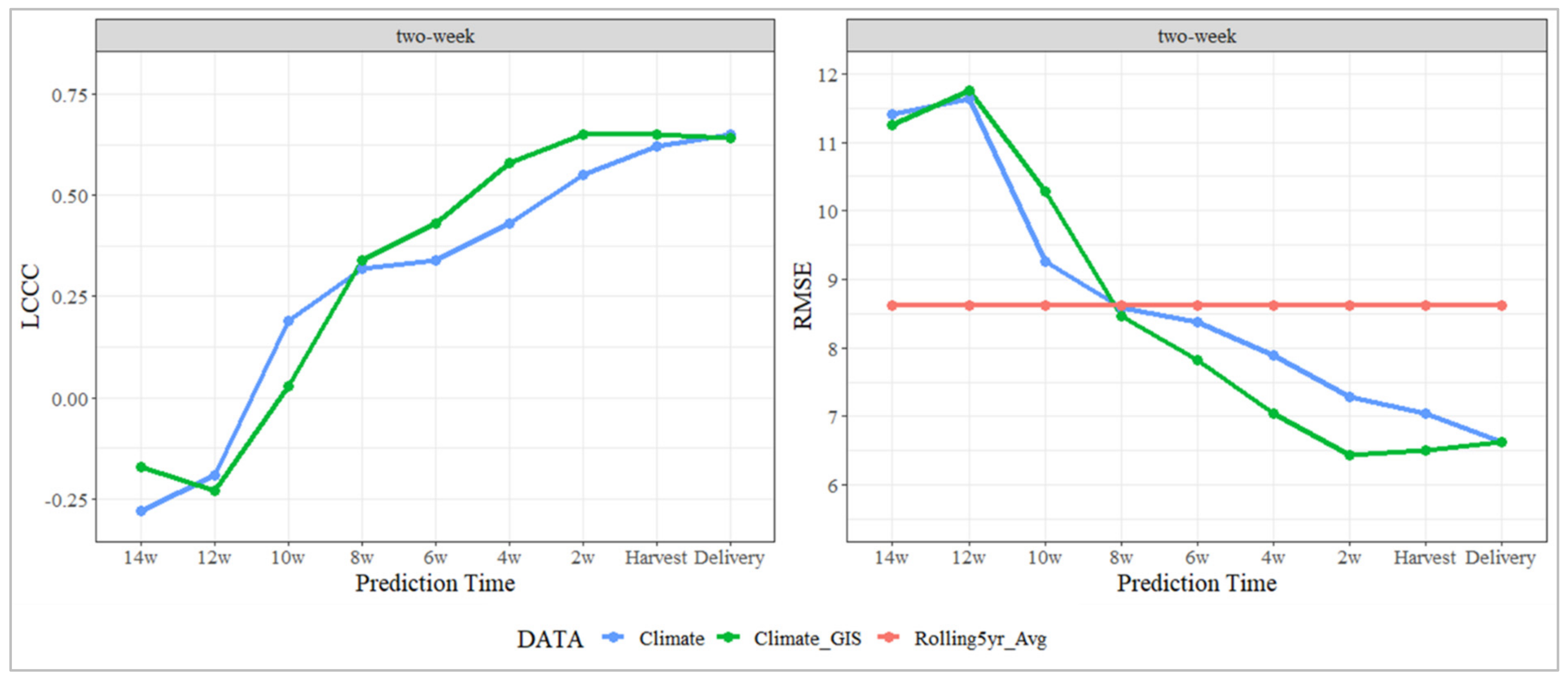
In the 2 W interval models, HRY% prediction accuracy was poor at the 16–14 wPH stage (Figure 4). The addition of data from the 14–12 wPH interval initially led to decreased prediction accuracy across both datasets, as evidenced by increased RMSE and lowered LCCC values. However, in both climate-only and climate and VI datasets, significant improvement in model performance was observed with the inclusion of subsequent stages towards harvest. Notably, the climate-only model outperformed the climate and VI datasets until the 10–8 wPH interval. However, beyond this point, including VI features consistently resulted in more accurate forecasts. However, the gap in prediction accuracy was reduced at the date of harvest prediction. In the delivery stage prediction, the addition of the harvest grain moisture resulted in comparable accuracy between data type models. The climate model achieved an LCCC of 0.65 and an RMSE of 6.62, while the climate and VI model achieved an LCCC of 0.64 and an RMSE of 6.63.
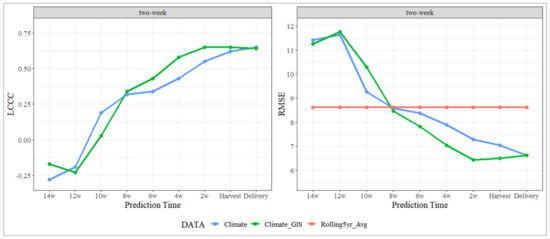
Figure 4.
Comparison of predictive model accuracies for HRY over two-week intervals leading up to harvest delivery. Model performance is evaluated using LCCC and RMSE, with intervals spanning from 14 weeks before harvest to the point of delivery.
Compared with the industry benchmark HRY forecast, average RMSE of 8.6%, both models surpassed their prediction accuracy from the 8 wPH stage onwards. The most notable improvement was observed in the climate and VI model, particularly at the 2 wPH stage model accuracy at this prediction interval; an LCCC of 0.65 and an RMSE of 6.43 highlight a substantial benefit of incorporating VI-based features into the precision of HRY forecasts.
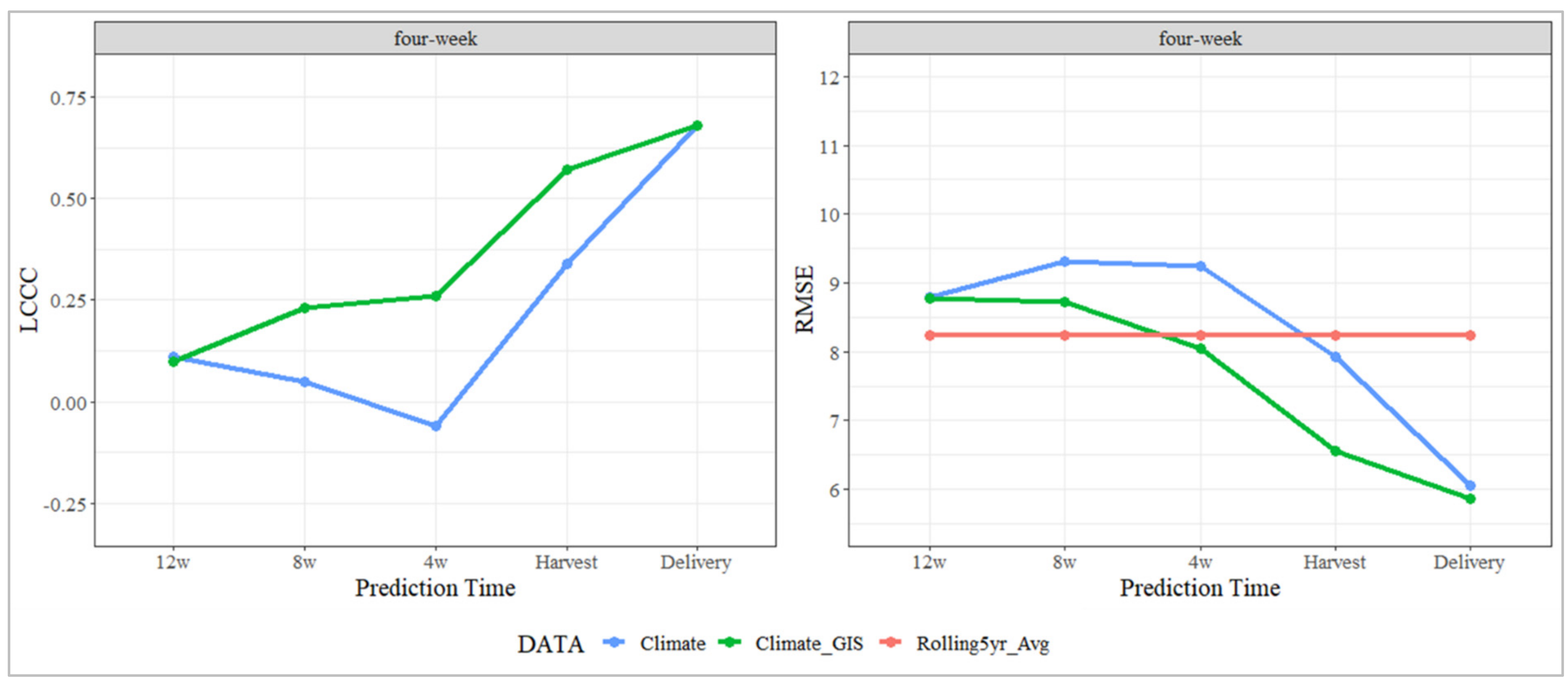
The 4 W interval models for both climate and climate and VI datasets demonstrated a similar trend in prediction accuracy, with poor results at earlier pre-harvest predictions compared to those closer to the harvest date (Figure 5). For the climate and VI 4W models, a steady enhancement in prediction accuracy was observed with the sequential inclusion of data from the 12–8 wPH and 8–4 wPH intervals. The most significant leap in model performance occurred with the addition of features from the final 4 wPH to the harvest stage. However, the highest accuracy was achieved at the delivery stand, with an LCCC of 0.68 and an RMSE of 5.86.
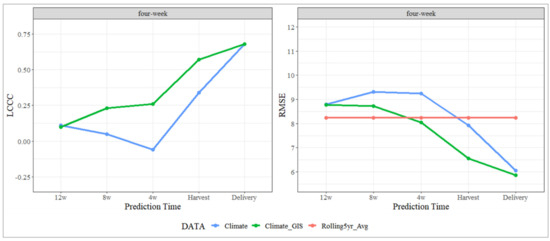
Figure 5.
Comparison of predictive model accuracies for HRY over four-week intervals leading up to harvest delivery. Model performance is evaluated using LCCC and RMSE, with intervals spanning from 12 weeks before harvest to the point of delivery.
Consistent with the later stages of the 2 W models, the 4 W climate-only models were outperformed by the climate and VI models. However, the climate-only model accuracy increased considerably after incorporating data from the 4 wPH to harvest stage. This late-season improvement continued to the delivery stand prediction, which achieved an LCCC of 0.68 and an RMSE of 6.06. Despite the high early-season RMSE of the 4 W climate models compared with the climate and VI models, its accuracy was superior to the early-season climate and climate and VI models from the 2W dataset iterations.
However, despite the higher accuracy at the delivery stand, the 4W models exhibited a notable limitation in their capacity to forecast HRY with sufficient lead time before harvest. The 4 W climate and VI model did not significantly improve over the industry benchmark (RMSE = 8.24) until just four weeks before harvest, indicating a four-week delay in its practical application relative to the 2 W models. Similarly, the 4 W climate-only model did not surpass the industry benchmark until the harvest date, underscoring a limitation for in-season crop-level forecasting. This delayed applicability highlights a trade-off between increased model accuracy at the delivery stand and the timely provision of actionable forecasts in the critical pre-harvest period.
3.1.2. Season Level Forecast
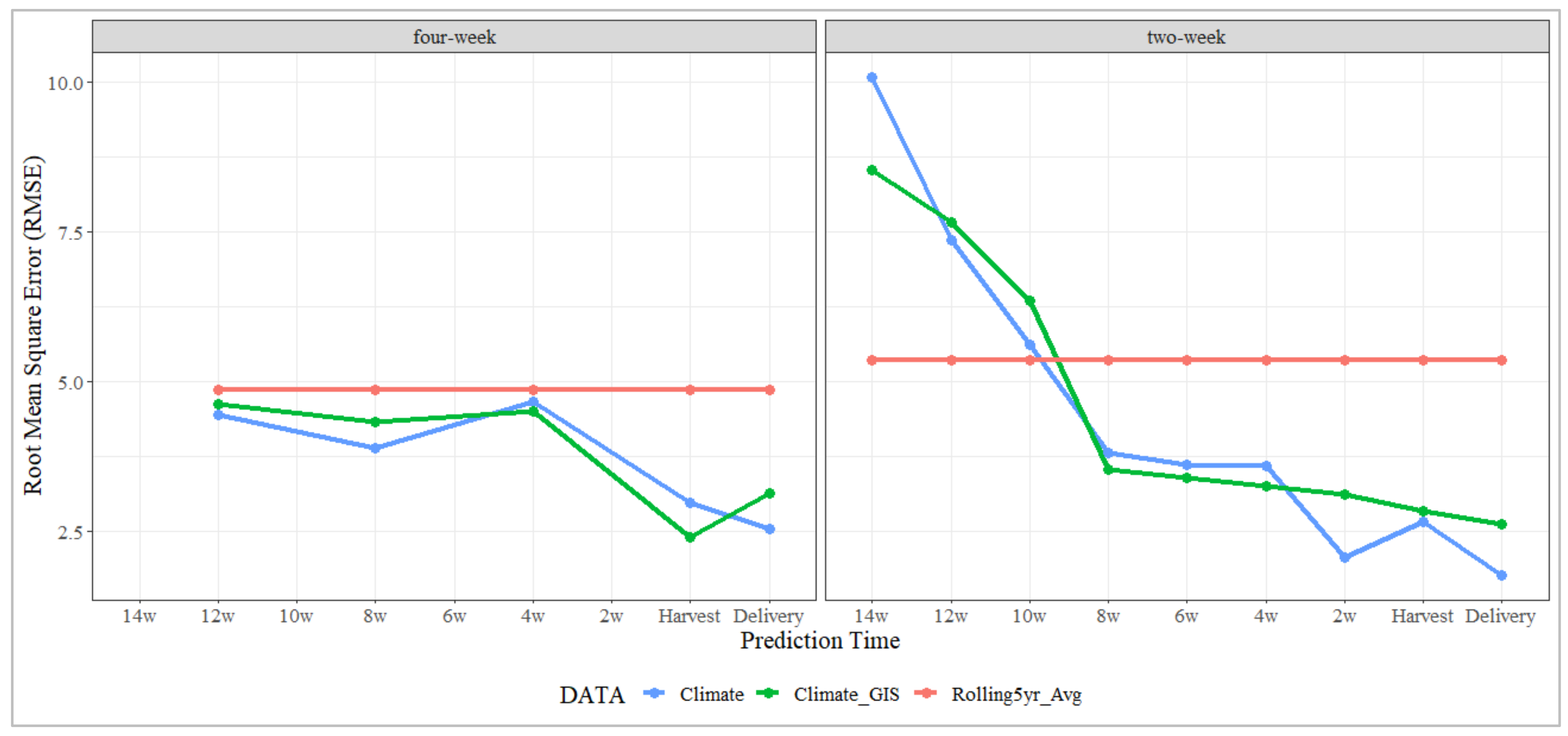
The industry forecast system utilised by SunRice is designed for an industry-wide application rather than a crop-level forecast. To facilitate a more relevant comparison, model RMSEs were contrasted against the industry benchmark at the season-by-industry level. The season-by-industry level provides a lower benchmark RMSE than at the crop-level, with an RMSE of 4.86 in the 4 W aggregation and 5.35 for the 2 W aggregation datasets. However, across both data types, the 2 W and 4 W interval models demonstrated superior performance over the industry standard.
The 4 W interval models exhibited a consistently lower RMSE across all predictive intervals compared with the industry benchmark (Figure 6). In contrast, the 2 W interval models initially lagged behind the industry benchmark, failing to improve on the level until the 10 wPH stage. However, a significant improvement in model accuracy was observed following this stage, where both the climate and climate and VI models outperformed the industry benchmark and the 4 W models at the eight and 4 wPH stages.
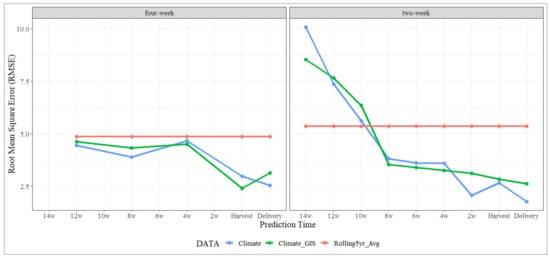
Figure 6.
Comparison of season-by-industry level prediction RMSE (HRY%) in the four-week and two-week data aggregation methods.
The improvement in predictive accuracy demonstrated by the 2 W models during the critical 8-, 6-, and 4-week intervals before harvest underscores the significant advantages of the climate and VI dataset using this aggregation. This enhancement in early-season prediction capability highlights the potential of the 2 W interval models, particularly those incorporating VI data, in providing valuable pre-harvest foresight into HRY outcomes, facilitating informed decision-making in the lead-up to harvest.
3.2. Feature Importance
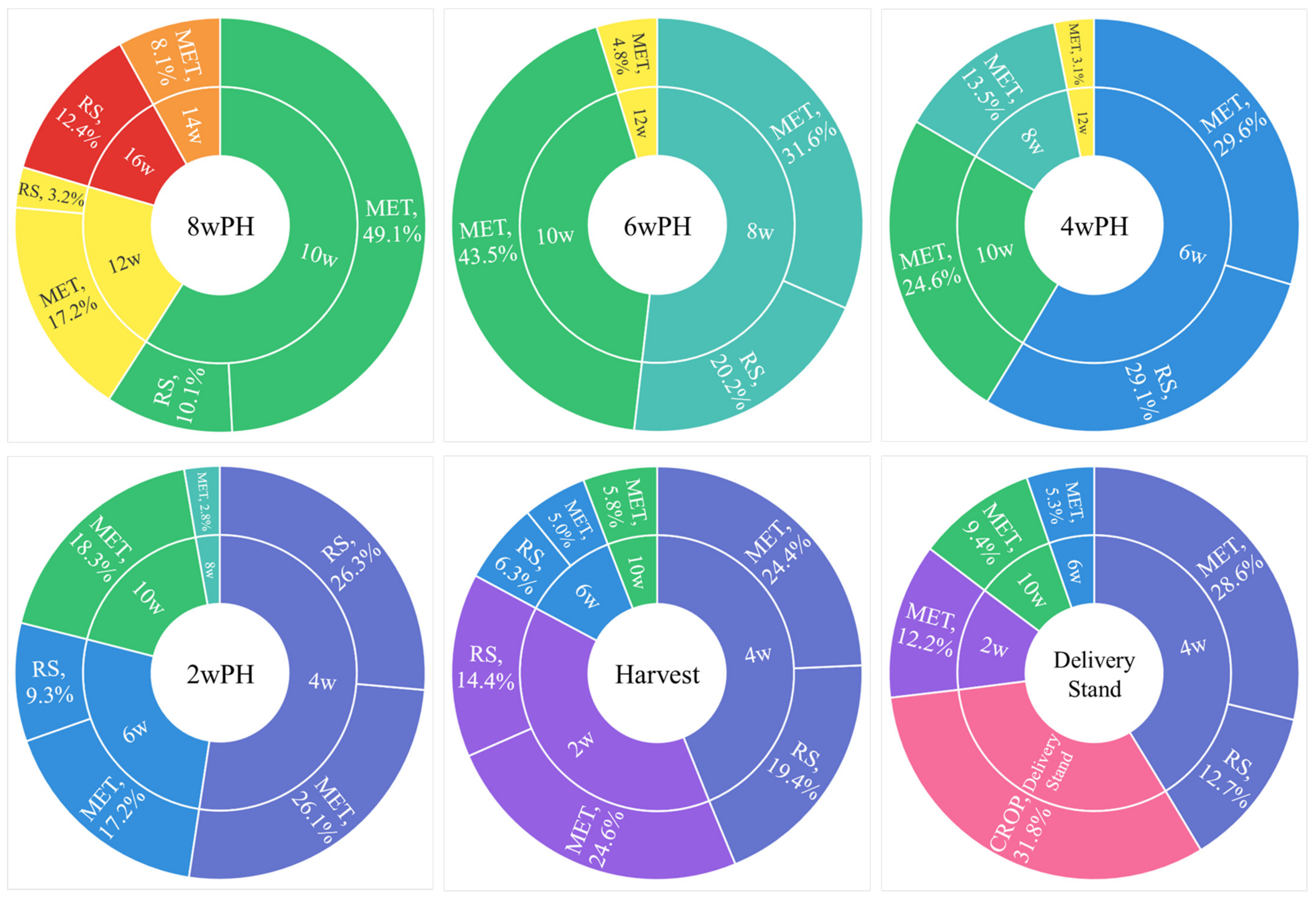
The 2 W climate and VI model, found to be most appropriate for industry application, was subjected to feature importance analysis. The study focused on prediction stages from 8 wPH onwards, where models were shown to surpass the current industry forecast. The mean SHAP value for each variable was calculated and categorised according to its respective 2 W interval and data type to dissect the influence of specific time stages and features. The SHAP values reflect the total contribution of all features included in the selected models.
In the 8, 6, 4, and 2 wPH prediction stages, the time interval immediately preceding the prediction emerged as the most influential, accounting for the highest aggregated SHAP value. For example, in the 8 wPH model, the interval between 8 and 10 wPH registered the largest contribution, with 59.2% to the total SHAP value (Figure 7). This pattern, where the preceding stage contributed over 50% of the total SHAP value, was observed across 8, 6, 4, and 2 wPH prediction models. In contrast, the highest accumulated SHAP values in the harvest date and delivery stand models came from the 2–4 wPH interval, at 43.8% and 41.3%, respectively. While the harvest date model saw a comparable contribution from the preceding 0–2 wPH stage (39%), the delivery stand model highlighted the importance of the 2–4 wPH interval, with the closest contribution arising from the grain moisture at harvest (31.8%).
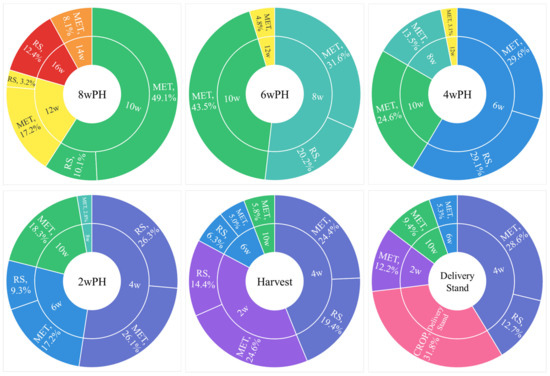
Figure 7.
Nested donut charts categorise the total mean SHAP of each model at the first level by the two-week time interval and delivery stand (categories shown in colour) and, secondly, by the type of data the stage-dependent features were calculated from. MET = meteorological data; RS = remote sensing; CROP = crop management.
A notable trend observed in the analysis was the progressive increase in the contribution of VI-based features to the total SHAP as the prediction intervals approached the harvest date. This trend was evident from the 6 wPH prediction, where VI-based SHAP values constituted 20.2% of the total, gradually ascending to 40.1% by the harvest date prediction. Consistent with the importance of the preceding stages, VI-based features were most influential in the interval immediately before the prediction. However, during the harvest date prediction, VI features in the 2–4 wPH interval contributed more (19.4%) to the total SHAP value than those in the 0–2 wPH stage (14.4%). Additionally, the delivery stand prediction had the lowest accumulated SHAP derived from VI-based features (12.7), coming solely from the 2–4 wPH stage. This change indicates that the grain moisture at harvest may account for much of the HRY variability previously explained by the late-season VI-based features.
Notably, the 8–10 wPH stage appeared across the final six prediction timings, primarily through meteorological features. Despite a gradual decrease in its SHAP contribution over time, its inclusion in the delivery stand model highlights the enduring impact of early meteorological conditions on HRY.
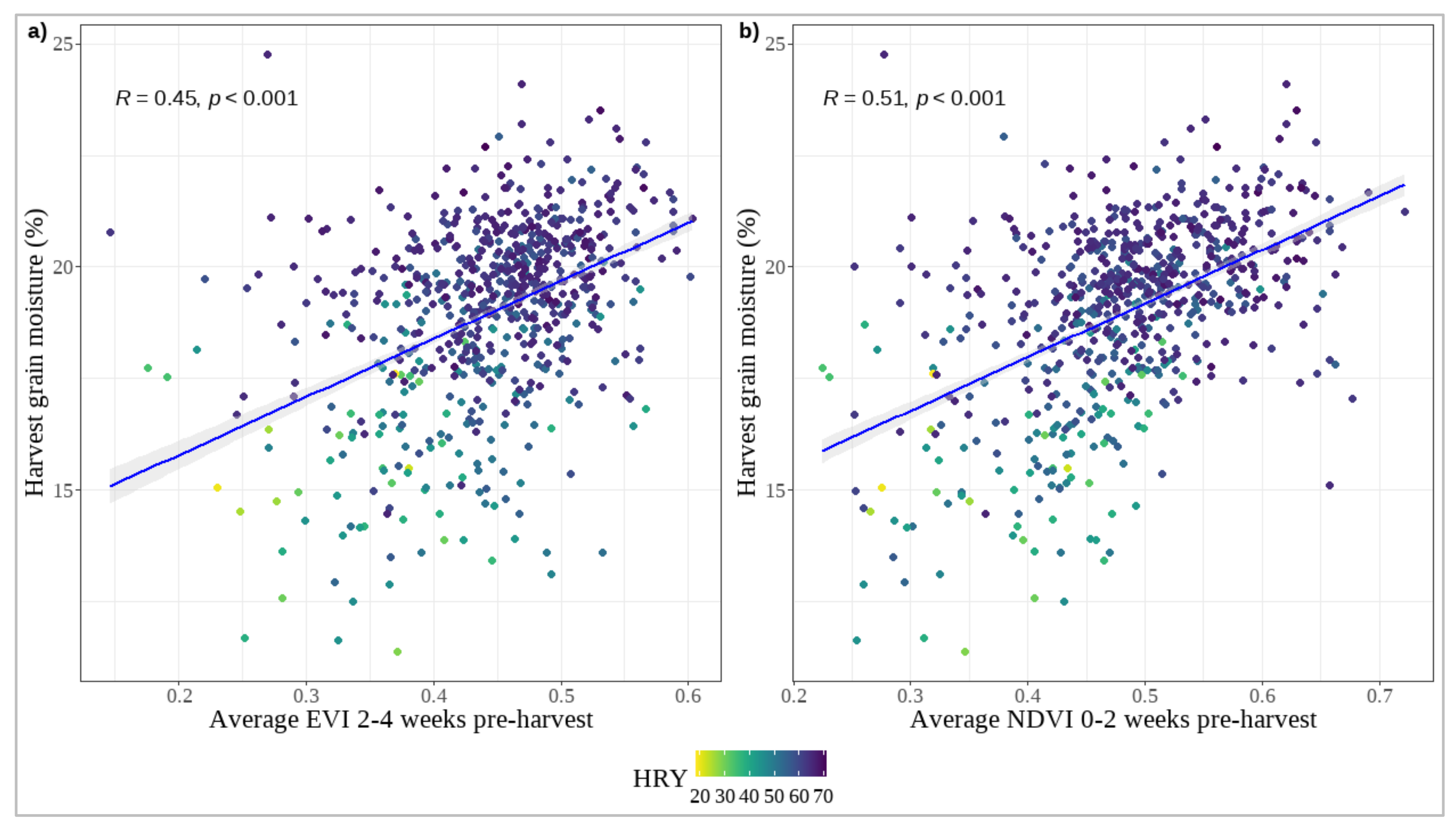
Among the VI-based features included in the late-season models, the crop average EVI during the 2–4 wPH interval was most frequently featured and recorded the highest total SHAP value. It was also the sole VI feature considered in the delivery stand model. Conversely, the average NDVI in the 0–2 wPH stage exhibited a higher mean SHAP value than the 2–4 wPH EVI in the harvest date model. The exclusion of grain moisture in the harvest date model implies a potential for late-season VI features to improve HRY forecasts before the delivery stand measurement is taken. Pearson correlation (R) analysis revealed a significant correlation between harvest grain moisture and average EVI in the 2–4 wPH stage (R = 0.45) and average NDVI in the 0–2 wPH stage (R = 0.51) (p < 0.001) (Figure 8).
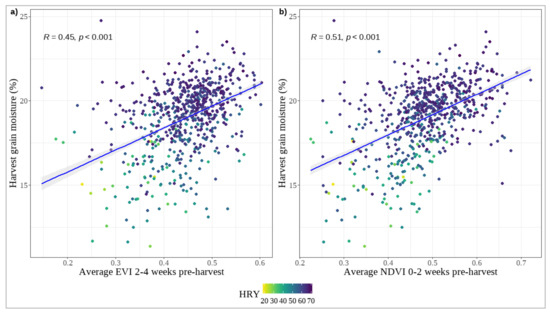
Figure 8.
Correlation between satellite-derived vegetation indices and harvest grain moisture percentage, stratified by HRY percentage. (a) Correlation between average EVI 2–4 weeks pre-harvest and harvest grain moisture percentage, (b) Correlation between average NDVI 0–2 weeks pre-harvest and harvest grain moisture percentage. Data points are colour-coded according to HRY ranging from lower (green/yellow) to higher (purple/blue) yields. The linear fit lines indicate the trend and strength of the relationship between these vegetation indices and the grain moisture content at harvest.
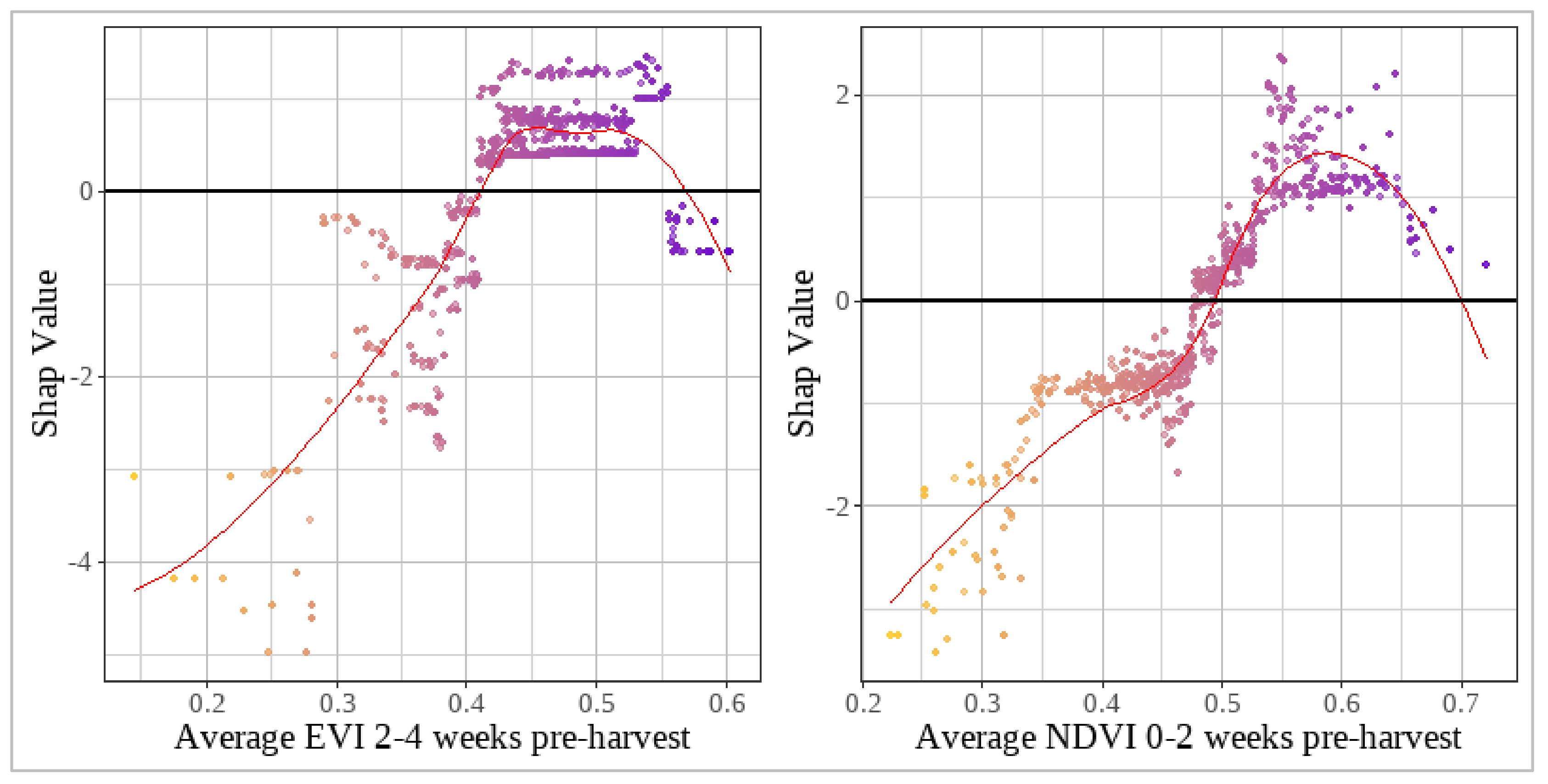
SHAP PDPs were analysed to interpret the impact of average EVI and NDVI on HRY. The average EVI during the 2–4 wPH stage positively correlated with HRY (Figure 9). However, EVI values above 0.55 resulted in a slight negative SHAP. The optimal range for a positive influence on HRY was identified between EVI levels of 0.4 and 0.55, corresponding to a SHAP value increase of about 1.5, with the largest negative impact, approximately −5% HRY, occurring at EVI levels below 0.3.
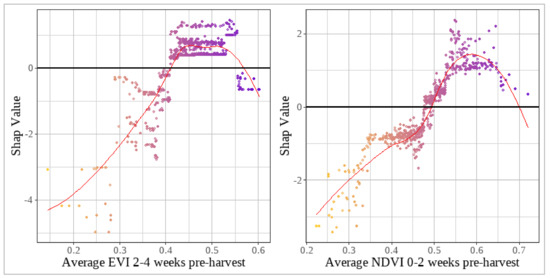
Figure 9.
SHAP value partial dependence plots of 2–4 wPH average EVI and 0–2 wPH average NDVI and HRY. The points represent each instance in the dataset, while the point colour indicates the feature value from low (yellow) to high (purple). The red lines in the plots indicate the smoothed LOESS relationship between the explanatory variables (on the x-axis) and their respective SHAP values (on the y-axis) (print in colour).
A similar pattern emerged for average NDVI in the 0–2 wPH stage, where lower NDVI levels contributed negatively to HRY, albeit to a lesser extent (around −3.5 percentage points HRY) (Figure 9). The peak positive SHAP impact occurred at NDVI levels ranging from 0.53 to 0.65, potentially increasing HRY by more than two percentage points. Like EVI, the higher range of NDVI levels did not increase HRY; however, unlike EVI, the reduced effect on HRY remained at a slight positive SHAP contribution.
4. Discussion
4.1. Model Performance
The improvement of all HRY forecast models as the prediction timeline approaches harvest aligns with existing research on crop yield forecasts in Australia [7], Canada [5] and China [9], highlighting the importance of late-season data. Additional features introduced at each stage were found to enhance model training, with predictions made closer to harvest resulting in the highest prediction accuracy. However, on a forecast basis, the practical value of harvest and delivery predictions is limited for rice storage and milling companies like SunRice. Instead, earlier-season forecasts may provide operational planning and marketing insights. The two-week aggregation method, offering comparable accuracy at harvest, offers superior early-season performance, showing an advantage for in-season forecasting. The effectiveness of this method agrees with previous work by Clarke et al. [48], identifying that the two-week aggregation produces the highest model accuracy for HRY prediction based on a climate-only dataset. However, the slightly enhanced harvest and delivery stand performances of the 4W climate, and VI models suggest that the 4W aggregation interval better suits Landsat-derived VI feature processing. The observed variation in prediction accuracy across prediction intervals, data aggregation, and data type availability highlight the need to design dataset construction based on the industry needs and data availability.
4.2. Feature Importance
The improved accuracy of the 2W climate and VI model at later prediction stages correlated with increased SHAP contribution from features in the stage immediately preceding the prediction interval. This trend indicates that agroclimatic conditions occurring later in the season better explain the HRY variation, consistent with the results of traditional field-based trials in Australia [28] and the US [34,49,50]. While early-season climatic conditions can influence HRY through the development of chalk [51,52,53], the effect of pre-harvest conditions on the grain moisture drying rate and fissure development is more pronounced. The impact of pre-harvest conditions on grain quality likely contributes to the higher error rates in the HRY prediction made earlier in the season. While the early-season models exhibit the potential to explain some of the observed variations, without knowledge of the critical late-season conditions, the model error is detrimentally impacted.
In the 2 W climate and VI model, the EVI and NDVI-based features, associated with crop vigour [10,54], were found to have greater impact later in the season. The mean total SHAP attributed to VI-based features increased steadily in the final six prediction stages, contributing 40.1% of total SHAP in the harvest date model. In contrast, many crop yield forecast models report the decreasing importance of VI-based features closer to harvest [55,56,57]. In these studies, features such as the peak NDVI, calculated near the middle of the growing season, contribute the most value to crop yield prediction [10,24,53].
Like climate-based features, the importance of late-season VI-based features is likely related to crop maturity and grain moisture. However, it is expected that the climate-based features cause the variation, while the VI-based features signal the response of the crop to the climatic conditions [58]. This discovery highlights the benefits of incorporating VI-based features when available, particularly in the case of missing fertiliser information and accurate soil characteristics data, known to affect the rate of crop maturation in rice [59].
The significant reduction in VI-based SHAP contribution in the delivery stand model reinforced the association between late-season VI-based features and grain moisture. Given the minimal difference in the model accuracy observed between the harvest and delivery stand models, this change underscores the ability of the grain moisture feature to effectively explain the similar aspects of HRY variation previously defined by the late-season VI-based features. This assumption is supported by the high levels of correlation observed between the two most important VI-based features, 2–4 wPH average EVI and 0–2 wPH average NDVI and grain moisture at harvest (Figure 8).
SHAP PDPs were constructed to build on the feature importance and correlation with grain moisture and explore the relationships between HRY and the average EVI and NDVI in the 2–4 wPH and 0–2 wPH stages. Average EVI in the 2–4 wPH stages suggested that higher EVI, within the optimal range, improves HRY. Given that EVI relates to crop vigour and grain moisture, crops within the optimal range may better withstand late-season detrimental conditions. However, as with values lower than the optimal range, crops above the optimal range also resulted in a negative SHAP value. These crops, displaying higher moisture in the 2–4 wPH stage, have likely faced excessive grain drying rates for the harvest to occur within two weeks. High rates of grain dry-down are related to fissure development [28], increasing the likelihood of grain cracking and subsequent breakage during milling.
The SHAP PDP for average NDVI in the 0–2 wPH stage also revealed a bell curve relationship where HRY could be maximised between 0.53 and 0.65, with lower SHAP values on either side. Given the strength in correlation and replacement by grain moisture in the delivery stand model, the positive SHAP contribution of NDVI is likely related to the crop being harvested at the correct grain moisture. In contrast, the negative impact of values exceeding the optimal NDVI range is expected to be related to crops harvested too early with an increased incidence of immature grains. These immature grains have reduced structural integrity and increased susceptibility to breakage during milling [36,60,61].
The significant positive correlations observed between the EVI and NDVI during the 2–4 wPH and 0–2 weeks 0–2 wPH stages, respectively, present a notable advancement, with implications for enhancing harvest decision-making among rice growers. This relationship suggests that tracking the crop EVI and NDVI levels could be reliable indicators for optimal harvest timing and crop drainage decisions. Furthermore, the use of NDVI field maps, provided they are of sufficient resolution, could enable precise identification of field zones ready for immediate harvest versus those where harvest could be postponed, thereby optimising the timing and sequence of harvesting operations. Such strategic use of VI data holds promise for improvement in the number of crops that experience optimal grain drying and can be harvested at ideal moisture levels, thereby increasing HRY outcomes.
4.3. Industry Applications
4.3.1. Grower Management
Implementation of a harvest moisture decision support tool (DST), underpinned by the HRY forecast models presented in this study, could enhance harvest timing decisions for rice growers. This DST would be particularly beneficial for crops subjected to adverse early-season conditions or undergoing rapid grain drying. While these conditions are likely to reduce the potential HRY, guidance on the optimal harvest moisture levels may mitigate the impact of these conditions. However, for real-time decision-making, this DST would benefit from integrating available weather forecasts with long-term average climate and VI conditions to fill the temporal gap between the prediction and the harvest date. Furthermore, the incorporation of long-term climatic averages could facilitate scenario analysis. The tool’s predictive accuracy and utility can be refined by enabling growers and agronomists to tailor the DST inputs based on historical seasons that mirror current conditions or specific weather patterns, such as El Niño or La Niña events.
4.3.2. Optimisation of Contracts of Milling Fractions
Optimisation of rice milling contracts via precise early-season HRY predictions could markedly influence the sales strategies of milling companies. In the 2020/21 season, SunRice’s contractual agreements for whole and broken grains were predicated on a five-season rolling average HRY of 58.9%. The actual season average, however, was 63.3%, leading to a shortfall in the anticipated broken grains and necessitating the conversion of whole grains to fulfil orders. Enhancing the HRY forecasting system could improve the accuracy of contractual terms based on expected whole and broken grain ratios.
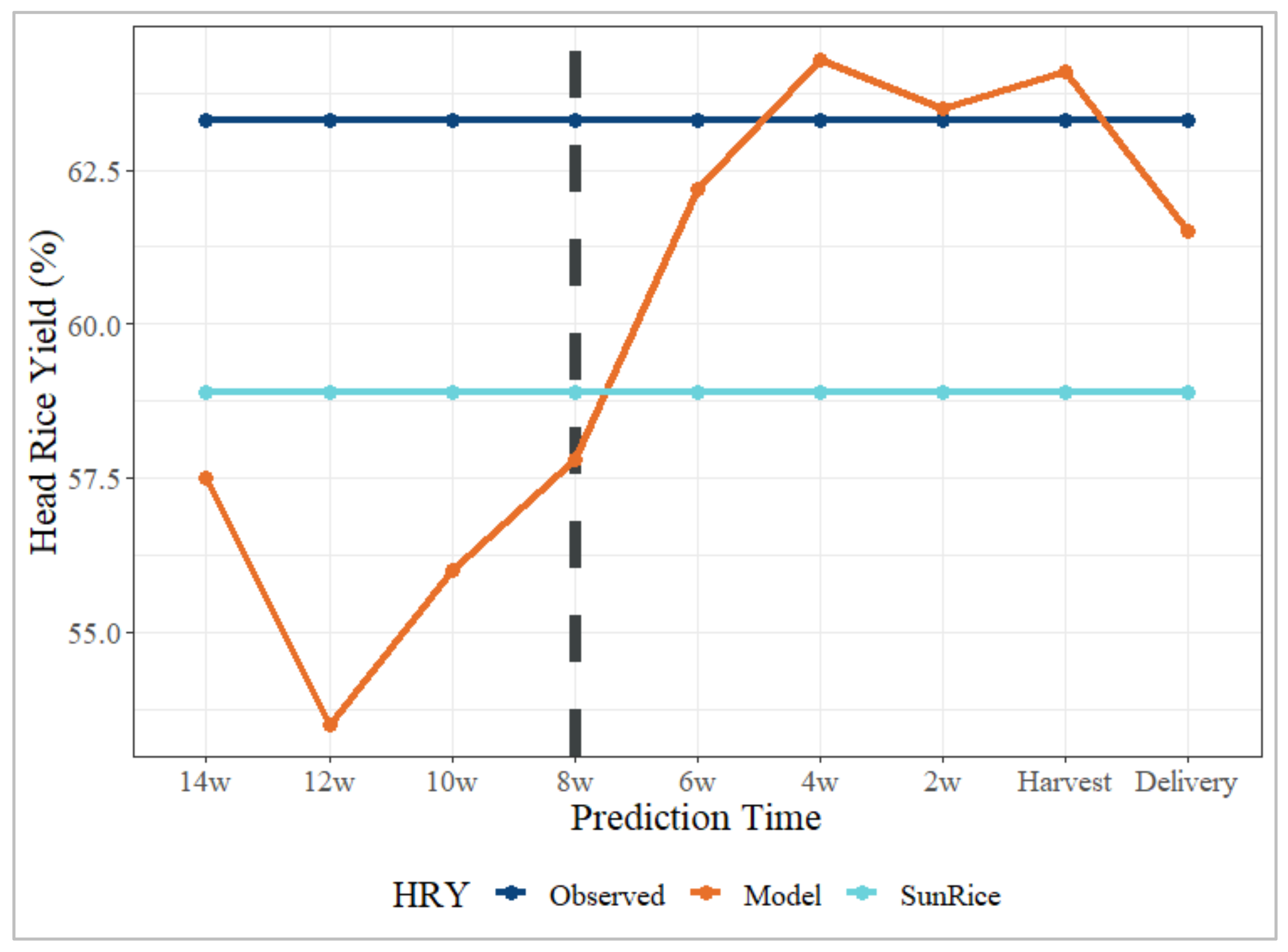
This study’s 2 W climate and VI model demonstrated superior accuracy relative to the industry benchmark up to eight weeks before harvest. Employing such an in-season predictive model could have potentially elevated SunRice’s milling revenue in the 20/2021 season. For instance, the 2020/21 model, trained on 2017/18 to 2019/20 data, provided predictions markedly closer to the actual HRY from 6 wPH (Figure 10). Utilising this approach at the 6 wPH stage could have minimised the need for re-milling and retained more whole grains to be sold at premium prices. Despite overestimations at 4- and 2-wPH, the model’s predictions remained closer to the actual HRY than the industry baseline, suggesting a more efficient allocation of whole grains to meet contractual demands. Even when accounting for potential purchases of whole grains to fulfil contracts, this approach would likely result in minimised costs while maximising the sale of Australian-grown whole grains at premium prices.
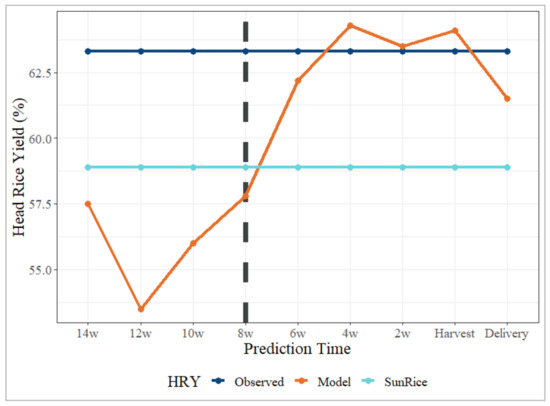
Figure 10.
Temporal comparison of the two-week climate + GIS model prediction in the CY21 season compared with the observed industry benchmark provided by SunRice. Prediction time points are shown on the x-axis, from 14 weeks before harvest to the grain elevator (delivery). The vertical dashed black line indicates the period from which the model was more accurate than the industry benchmark.
4.4. Limitations
A notable constraint in this study was the reliance on known harvest dates to determine the preceding stages for model development. While this approach was expected to enhance model accuracy, such specific harvest information would not be readily available in a real-time forecasting scenario. Consequently, future research should explore methodologies to predict the harvest date, potentially through surveys conducted with growers and agronomists or by analysing crop vigour trends via satellite-derived VI. These methods have demonstrated considerable success in estimating rice phenology and harvest timing in Australia [62,63] and internationally [32,64]. Adoption of VI-based phenological estimates could also refine the aggregation of environmental variables, improving the static time intervals employed in this research [1,5]. Additionally, advancements in satellite imagery technology, such as those provided by Sentinel and Planet Labs, marked by increased capture frequency and improved resolution, offer promising avenues for improving crop prediction models. These technological enhancements facilitate a more granular and frequent analysis of crop conditions, thereby enabling more accurate and timely evaluations of crop development, health, and potential yield. Incorporating Sentinel 2 data in this study would have enhanced the frequency of satellite imagery [30], potentially benefiting the two-week clustering method. However, Sentinel data became available in Australia only in December 2018 [65], precluding the utilisation of crop production data from the 2017/18 and 2018/19 seasons. The absence of these data years would have considerably diminished the dataset available for model development.
While the forecast models achieved commendable accuracy, integration of a broader array of grower management data could substantially enhance the predictions and their practical utility for growers and agronomists. Specifically, the application of SHAP analysis can reveal key relationships and inform growers about optimal management practices. The inclusion of detailed information on practices such as fertilisation and irrigation management is anticipated to be particularly beneficial, as has been demonstrated in recent studies predicting wheat yield in Australia [7,10] and India [66]. Furthermore, identifying management variables significantly impacting HRY could enhance the formulation of additional decision support tools (DST) for rice farmers.
5. Conclusions
Construction of datasets with two- and four-week and monthly aggregations of meteorological and remotely sensed data facilitated the development of models to predict HRY. Model accuracy improved progressively as the forecast period approached harvest, with the two-week aggregation of climate and vegetative indices data demonstrating superior accuracy, surpassing industry standards eight weeks before harvest. Shapley additive explanations (SHAP) revealed that features proximal to the forecast date significantly influenced HRY predictions. In the two-week climate and VI model, the importance of VI-based features escalated near harvest but reduced sharply after incorporating grain moisture data in the delivery stand prediction. This trend suggests the relevance of late-season VI-based features in reflecting crop maturity and grain moisture, offering decision support for optimal harvest commencement and prioritisation within fields. This model’s capability to exceed current industry benchmarks suggests potential benefits for the Australian rice industry in optimising rice storage and milling strategies to maximise HRY. Moreover, these insights could inform marketing strategies based on anticipated whole and broken grain ratios. Enhanced predictions of crop phenology and harvest timing are expected to yield more precise data aggregations. Concurrent satellite imagery and farm management data advancements will further refine HRY forecasting capabilities. This research provides crucial insights for grain quality forecasting, with methodologies that can be adapted to various regions, thereby improving decisions at both the crop and industry levels.
Author Contributions
Conceptualization, A.C., C.B., R.F. and M.Z.I.; methodology, A.C. and M.Z.I.; software, A.C.; validation, A.C. and M.Z.I.; formal analysis, A.C.; investigation, A.C.; resources, C.B. and M.Z.I.; data curation, A.C. and R.P.W.; writing—original draft preparation, A.C.; writing—review and editing, A.C.; visualization, A.C.; supervision, C.B., M.Z.I., D.Y., R.F. and S.-U.R.; project administration, C.B.; funding acquisition, C.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Food Agility Cooperative Research Centre (CRC) (RM102858), funded under the Australian Commonwealth Government Co-operative Research Centre program, and in part by Charles Sturt University, AgriFutures Australia, and Ricegrowers Ltd.
Data Availability Statement
The datasets constructed in this study are not openly available due to reasons of commercial sensitivity for Ricegrowers Ltd. However, a subset of these data and all relevant code may be available from the corresponding author upon reasonable request.
Conflicts of Interest
Author Allister Clarke and Robert Paul Walsh was employed by the company Ricegrowers Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Srivastava, A.K.; Safaei, N.; Khaki, S.; Lopez, G.; Zeng, W.; Ewert, F.; Gaiser, T.; Rahimi, J. Winter wheat yield prediction using convolutional neural networks from environmental and phenological data. Sci. Rep. 2022, 12, 3215. [Google Scholar] [CrossRef] [PubMed]
- Vannoppen, A.; Gobin, A. Estimating farm wheat yields from NDVI and meteorological data. Agronomy 2021, 11, 946. [Google Scholar] [CrossRef]
- Donohue, R.J.; Lawes, R.A.; Mata, G.; Gobbett, D.; Ouzman, J. Towards a national, remote-sensing-based model for predicting field-scale crop yield. Field Crops Res. 2018, 227, 79–90. [Google Scholar] [CrossRef]
- Wu, B.; Gommes, R.; Zhang, M.; Zeng, H.; Yan, N.; Zou, W.; Zheng, Y.; Zhang, N.; Chang, S.; Xing, Q. Global crop monitoring: A satellite-based hierarchical approach. Remote Sens. 2015, 7, 3907–3933. [Google Scholar] [CrossRef]
- Chipanshi, A.; Zhang, Y.; Kouadio, L.; Newlands, N.; Davidson, A.; Hill, H.; Warren, R.; Qian, B.; Daneshfar, B.; Bedard, F.; et al. Evaluation of the Integrated Canadian Crop Yield Forecaster (ICCYF) model for in-season prediction of crop yield across the Canadian agricultural landscape. Agric. For. Meteorol. 2015, 206, 137–150. [Google Scholar] [CrossRef]
- Yang, J.; Ouyang, C.; Dik, G.; Corry, P.; ter Hofstede, A.H. Crop Harvest Forecast via Agronomy-Informed Process Modelling and Predictive Monitoring. In Proceedings of the International Conference on Advanced Information Systems Engineering, Leuven, Belgium, 6–10 June 2022; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Feng, P.; Wang, B.; Liu, D.L.; Waters, C.; Xiao, D.; Shi, L.; Yu, Q. Dynamic wheat yield forecasts are improved by a hybrid approach using a biophysical model and machine learning technique. Agric. For. Meteorol. 2020, 285, 107922. [Google Scholar] [CrossRef]
- Keating, B.A.; Carberry, P.S.; Hammer, G.L.; Probert, M.E.; Robertson, M.J.; Holzworth, D.; Huth, N.I.; Hargreaves, J.N.; Meinke, H.; Hochman, Z. An overview of APSIM, a model designed for farming systems simulation. Eur. J. Agron. 2003, 18, 267–288. [Google Scholar] [CrossRef]
- Li, L.; Wang, B.; Feng, P.; Wang, H.; He, Q.; Wang, Y.; Liu, D.L.; Li, Y.; He, J.; Feng, H. Crop yield forecasting and associated optimum lead time analysis based on multi-source environmental data across China. Agric. For. Meteorol. 2021, 308, 108558. [Google Scholar] [CrossRef]
- Filippi, P.; Jones, E.J.; Wimalathunge, N.S.; Somarathna, P.D.; Pozza, L.E.; Ugbaje, S.U.; Jephcott, T.G.; Paterson, S.E.; Whelan, B.M.; Bishop, T.F. An approach to forecast grain crop yield using multi-layered, multi-farm data sets and machine learning. Precis. Agric. 2019, 20, 1015–1029. [Google Scholar] [CrossRef]
- Dhaliwal, J.K.; Panday, D.; Saha, D.; Lee, J.; Jagadamma, S.; Schaeffer, S.; Mengistu, A. Predicting and interpreting cotton yield and its determinants under long-term conservation management practices using machine learning. Comput. Electron. Agric. 2022, 199, 107107. [Google Scholar] [CrossRef]
- Delerce, S.; Dorado, H.; Grillon, A.; Rebolledo, M.C.; Prager, S.D.; Patiño, V.H.; Garcés Varón, G.; Jiménez, D. Assessing weather-yield relationships in rice at local scale using data mining approaches. PLoS ONE 2016, 11, e0161620. [Google Scholar] [CrossRef] [PubMed]
- Bautista, R.C.P.A. Counce. An overview of rice and rice quality. Cereal Foods World 2020, 65, 52. [Google Scholar]
- Lyman, N.B.; Jagadish, K.S.; Nalley, L.L.; Dixon, B.L.; Siebenmorgen, T. Neglecting rice milling yield and quality underestimates economic losses from high-temperature stress. PLoS ONE 2013, 8, e72157. [Google Scholar] [CrossRef]
- Mohan, V.; Ruchi, V.; Gayathri, R.; Ramya Bai, M.; Shobana, S.; Anjana, R.; Unnikrishnan, R.; Sudha, V. Hurdles in brown rice consumption. In Brown Rice; Springer: Berlin/Heidelberg, Germany, 2017; pp. 255–269. [Google Scholar]
- Kealey, L.M.; Clampett, W.S. Production of Quality Rice in South Eastern Australia; New South Wales Department of Agriculture: Orange, Australia, 2000. [Google Scholar]
- Clarke, A.; Yates, D.; Blanchard, C.; Islam, M.Z.; Ford, R.; Rehman, S.-U.; Walsh, R. The effect of dataset construction and data pre-processing on the eXtreme Gradient Boosting algorithm applied to head rice yield prediction in Australia. Comput. Electron. Agric. 2024, 219, 108716. [Google Scholar] [CrossRef]
- Pearce, M.D.; Marks, B.P.; Meullenet, J.F. Effects of Postharvest Parameters on Functional Changes During Rough Rice Storage. Cereal Chem. 2001, 78, 354–357. [Google Scholar] [CrossRef]
- Lee, S.B.; Chung, C.J.; Noh, S.H. Study on the Improvement of Milling Recovery and Performance (V)-Experimental Study on Rice Whitening Performance of Jet-air Abrasive-Type Whitener. J. Biosyst. Eng. 1983, 8, 17–29. [Google Scholar]
- Lapis, J.R.; Cuevas, R.P.O.; Sreenivasulu, N.; Molina, L. Measuring Head Rice Recovery in Rice. In Rice Grain Quality: Methods and Protocols; Springer: New York, NY, USA, 2019; pp. 89–98. [Google Scholar]
- SunRice. Annual Report 2022. 2022. Available online: https://www.sunrice.com.au/book/Annual_Report_2022.pdf (accessed on 5 February 2022).
- Ricegrowers Association of Australia. Submission to the Review of the Rice Vesting Proclamation. 2021. Available online: https://www.rga.org.au/common/Uploaded%20files/2021%20RGA%20-%20Submission%20to%20the%20review%20of%20the%20rice%20vesting%20proclomation%20140821%20Final.pdf (accessed on 5 February 2022).
- Ashton, D.; Oliver, M.; Norrie, D. Rice farms in the Murray–Darling Basin. In ABARES Research Report 16.2; Australian Bureau of Agricultural and Resource Economics and Sciences (ABARES): Canberra, Australia, 2016. [Google Scholar]
- Filippi, P.; Whelan, B.M.; Vervoort, R.W.; Bishop, T.F. Mid-season empirical cotton yield forecasts at fine resolutions using large yield mapping datasets and diverse spatial covariates. Agric. Syst. 2020, 184, 102894. [Google Scholar] [CrossRef]
- Lanning, S.; Siebenmorgen, T.; Counce, P.; Ambardekar, A.; Mauromoustakos, A. Extreme nighttime air temperatures in 2010 impact rice chalkiness and milling quality. Field Crops Res. 2011, 124, 132–136. [Google Scholar] [CrossRef]
- Zhao, X.; Fitzgerald, M. Climate change: Implications for the yield of edible rice. PLoS ONE 2013, 8, e66218. [Google Scholar] [CrossRef]
- Jeffrey, S.J.; Carter, J.O.; Moodie, K.B.; Beswick, A.R. Using spatial interpolation to construct a comprehensive archive of Australian climate data. Environ. Model. Softw. 2001, 16, 309–330. [Google Scholar] [CrossRef]
- Clampett, W.S.; Williams, R.L.; Lacy, J.M. Improvement of Rice Grain Quality. 2004. Available online: https://www.agrifutures.com.au/wp-content/uploads/publications/04-005.pdf (accessed on 10 March 2021).
- NSW Department of Planning and Environment. Digital Soil Maps for Key Soil Properties over New South Wales, Version 2.0. 2022. Available online: https://datasets.seed.nsw.gov.au/dataset/digital-soil-maps-for-key-soil-properties-over-new-south-wales-version-2-0 (accessed on 10 June 2023).
- Li, J.; Chen, B. Global revisit interval analysis of Landsat-8-9 and Sentinel-2a-2b data for terrestrial monitoring. Sensors 2020, 20, 6631. [Google Scholar] [CrossRef]
- Brinkhoff, J. Early-Season Industry-Wide Rice Maps Using Sentinel-2 Time Series. In Proceedings of the IGARSS 2022-2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 5854–5857. [Google Scholar]
- Wang, H.; Ghosh, A.; Linquist, B.; Hijmans, R. Satellite-based observations reveal effects of weather variation on rice phenology. Remote Sens. 2020, 12, 1522. [Google Scholar] [CrossRef]
- Madigan, E.; Guo, Y.; Pickering, M.; Held, A.; Jia, X. Quantitative monitoring of complete rice growing seasons using Sentinel 2 time series images. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 7699–7702. [Google Scholar]
- Bautista, R.; Siebenmorgen, T.; Mauromoustakos, A. The role of rice individual kernel moisture content distributions at harvest on milling quality. Trans. ASABE 2009, 52, 1611–1620. [Google Scholar] [CrossRef]
- Siebenmorgen, T.; Bautista, R.; Counce, P. Optimal harvest moisture contents for maximizing milling quality of long-and medium-grain rice cultivars. Appl. Eng. Agric. 2007, 23, 517–527. [Google Scholar] [CrossRef]
- Nalley, L.; Dixon, B.; Tack, J.; Barkley, A.; Jagadish, K. Optimal Harvest Moisture Content for Maximizing Mid-South Rice Milling Yields and Returns. Agron. J. 2016, 108, 701–712. [Google Scholar] [CrossRef]
- Mzid, N.; Pignatti, S.; Huang, W.; Casa, R. An Analysis of Bare Soil Occurrence in Arable Croplands for Remote Sensing Topsoil Applications. Remote Sens. 2021, 13, 474. [Google Scholar] [CrossRef]
- Ruan, G.; Li, X.; Yuan, F.; Cammarano, D.; Ata-UI-Karim, S.T.; Liu, X.; Tian, Y.; Zhu, Y.; Cao, W.; Cao, Q. Improving wheat yield prediction integrating proximal sensing and weather data with machine learning. Comput. Electron. Agric. 2022, 195, 106852. [Google Scholar] [CrossRef]
- Allen, M.P. Understanding Regression Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2004; pp. 176–180. [Google Scholar]
- Bocca, F.F.L.H.A. Rodrigues. The effect of tuning, feature engineering, and feature selection in data mining applied to rainfed sugarcane yield modelling. Comput. Electron. Agric. 2016, 128, 67–76. [Google Scholar] [CrossRef]
- Whitmire, C.D.; Vance, J.M.; Rasheed, H.K.; Missaoui, A.; Rasheed, K.M.; Maier, F.W. Using machine learning and feature selection for alfalfa yield prediction. AI 2021, 2, 71–88. [Google Scholar] [CrossRef]
- Ghafarian, F.; Wieland, R.; Lüttschwager, D.; Nendel, C. Application of extreme gradient boosting and Shapley Additive explanations to predict temperature regimes inside forests from standard open-field meteorological data. Environ. Model. Softw. 2022, 156, 105466. [Google Scholar] [CrossRef]
- Obsie, E.Y.; Qu, H.; Drummond, F. Wild blueberry yield prediction using a combination of computer simulation and machine learning algorithms. Comput. Electron. Agric. 2020, 178, 105778. [Google Scholar] [CrossRef]
- Chen, T.C. Guestrin, XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: San Francisco, CA, USA; pp. 785–794. [Google Scholar]
- Lin, L.I.-K. A Concordance Correlation Coefficient to Evaluate Reproducibility. Biometrics 1989, 45, 255–268. [Google Scholar] [CrossRef]
- Jones, E.J.; Bishop, T.F.; Malone, B.P.; Hulme, P.J.; Whelan, B.M.; Filippi, P. Identifying causes of crop yield variability with interpretive machine learning. Comput. Electron. Agric. 2022, 192, 106632. [Google Scholar] [CrossRef]
- Molnar, C. Interpretable Machine Learning. 2023. Available online: https://christophm.github.io/interpretable-ml-book/ (accessed on 1 November 2023).
- Clarke, A.; Yates, D.; Blanchard, C.; Islam, M.Z.; Ford, R.; Rehman, S.-U.; Walsh, R. Combining satellite, soil and climate data to predict Head Rice Yield in Australia using machine learning approaches. Artif. Intell. Agric. 2024; manuscript submitted for publication—awaiting first response. [Google Scholar]
- Counce, P.A.; Siebenmorgen, T.J.; Vories, E.D.; Pitts, D.J. Time of draining and harvest effects on rice grain yield and quality. J. Prod. Agric. 1990, 3, 436–445. [Google Scholar] [CrossRef]
- Kunze, O.R.; Peralta, E.; Turner, F.T. Fissured Rice Related to Grain Moisture, Weather and Fertilization Rates; American Society of Agricultural Engineers: St. Joseph, MI, USA, 1988. [Google Scholar]
- Abayawickrama, A.; Reinke, R.F.; Fitzgerald, M.A.; Harper, J.D.; Burrows, G.E. Influence of high daytime temperature during the grain filling stage on fissure formation in rice. J. Cereal Sci. 2017, 74, 256–262. [Google Scholar] [CrossRef]
- Ahmed, N.; Tetlow, I.J.; Nawaz, S.; Iqbal, A.; Mubin, M.; Nawaz ul Rehman, M.S.; Butt, A.; Lightfoot, D.A.; Maekawa, M. Effect of high temperature on grain filling period, yield, amylose content and activity of starch biosynthesis enzymes in endosperm of basmati rice. J. Sci. Food Agric. 2015, 95, 2237–2243. [Google Scholar] [CrossRef] [PubMed]
- Ali, F.; Waters, D.L.; Ovenden, B.; Bundock, P.; Raymond, C.A.; Rose, T.J. Heat stress during grain fill reduces head rice yield through genotype dependant increased husk biomass and grain breakage. J. Cereal Sci. 2019, 90, 102820. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Meroni, M.; Waldner, F.; Seguini, L.; Kerdiles, H.; Rembold, F. Yield forecasting with machine learning and small data: What gains for grains? Agric. For. Meteorol. 2021, 308, 108555. [Google Scholar] [CrossRef]
- Chen, Y.; Tao, F. Potential of remote sensing data-crop model assimilation and seasonal weather forecasts for early-season crop yield forecasting over a large area. Field Crops Res. 2022, 276, 108398. [Google Scholar] [CrossRef]
- Li, Y.; Zeng, H.; Zhang, M.; Wu, B.; Zhao, Y.; Yao, X.; Cheng, T.; Qin, X.; Wu, F. A county-level soybean yield prediction framework coupled with XGBoost and multidimensional feature engineering. Int. J. Appl. Earth Obs. Geoinf. 2023, 118, 103269. [Google Scholar] [CrossRef]
- Cai, Y.; Guan, K.; Lobell, D.; Potgieter, A.B.; Wang, S.; Peng, J.; Xu, T.; Asseng, S.; Zhang, Y.; You, L. Integrating satellite and climate data to predict wheat yield in Australia using machine learning approaches. Agric. For. Meteorol. 2019, 274, 144–159. [Google Scholar] [CrossRef]
- Alcantara, J.M.; Cassman, K.G.; Consuelo, M.; Bienvenido, O.; Samuel, P. Effects of late nitrogen fertilizer application on head rice yield, protein content, and grain quality of rice. Cereal Chem. 1996, 73, 556–560. [Google Scholar]
- Bautista, R.C.; Siebenmorgen, T.J. Rice kernel properties affecting milling quality at harvest. Res. Ser. Ark. Agric. Exp. Stn. 2000, 485, 238–243. [Google Scholar]
- Siebenmorgen, T.; Bautista, R.; Meullenet, J.F. Predicting rice physicochemical properties using thickness fraction properties. Cereal Chem. 2006, 83, 275–283. [Google Scholar] [CrossRef]
- Brinkhoff, J.; McGavin, S.L.; Dunn, T.; Dunn, B.W. Predicting rice phenology and optimal sowing dates in temperate regions using machine learning. Agron. J. 2023, 116, 871–885. [Google Scholar] [CrossRef]
- Brinkhoff, J.; Clarke, A.; Dunn, B.W.; Groat, M. Analysis and forecasting of Australian rice yield using phenology-based aggregation of satellite and weather data. Agric. For. Meteorol. 2024, 353, 110055. [Google Scholar] [CrossRef]
- Boschetti, M.; Stroppiana, D.; Brivio, P.; Bocchi, S. Multi-year monitoring of rice crop phenology through time series analysis of MODIS images. Int. J. Remote Sens. 2009, 30, 4643–4662. [Google Scholar] [CrossRef]
- Brinkhoff, J.; Houborg, R.; Dunn, B.W. Rice ponding date detection in Australia using Sentinel-2 and Planet Fusion imagery. Agric. Water Manag. 2022, 273, 107907. [Google Scholar] [CrossRef]
- Nayak, H.S.; Silva, J.V.; Parihar, C.M.; Krupnik, T.J.; Sena, D.R.; Kakraliya, S.K.; Jat, H.S.; Sidhu, H.S.; Sharma, P.C.; Jat, M.L.; et al. Interpretable machine learning methods to explain on-farm yield variability of high productivity wheat in Northwest India. Field Crops Res. 2022, 287, 108640. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).