A Daily High-Resolution Sea Surface Temperature Reconstruction Using an I-DINCAE and DNN Model Based on FY-3C Thermal Infrared Data
Abstract
1. Introduction
2. Study Area and Data
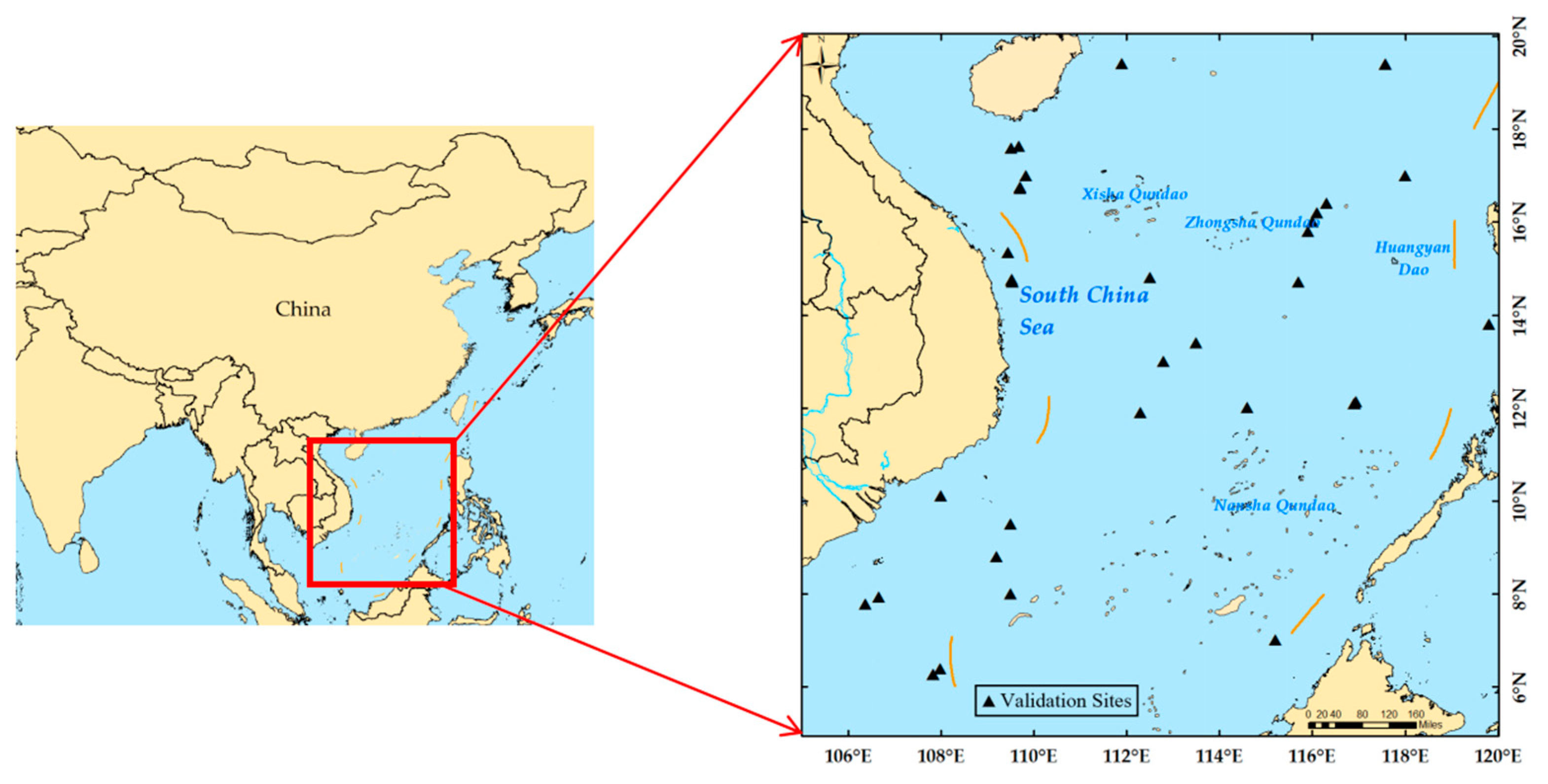
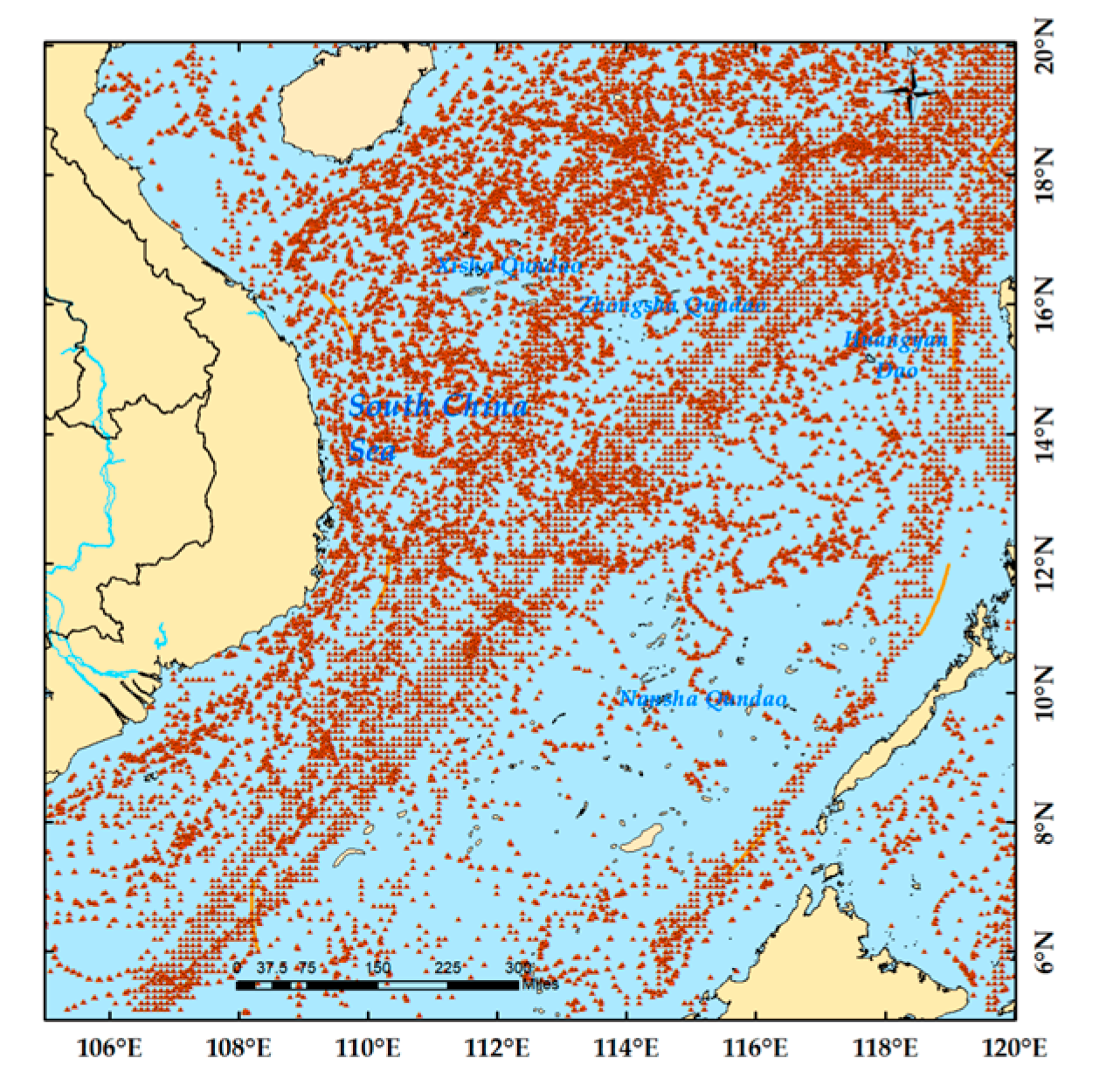
2.1. Study Area
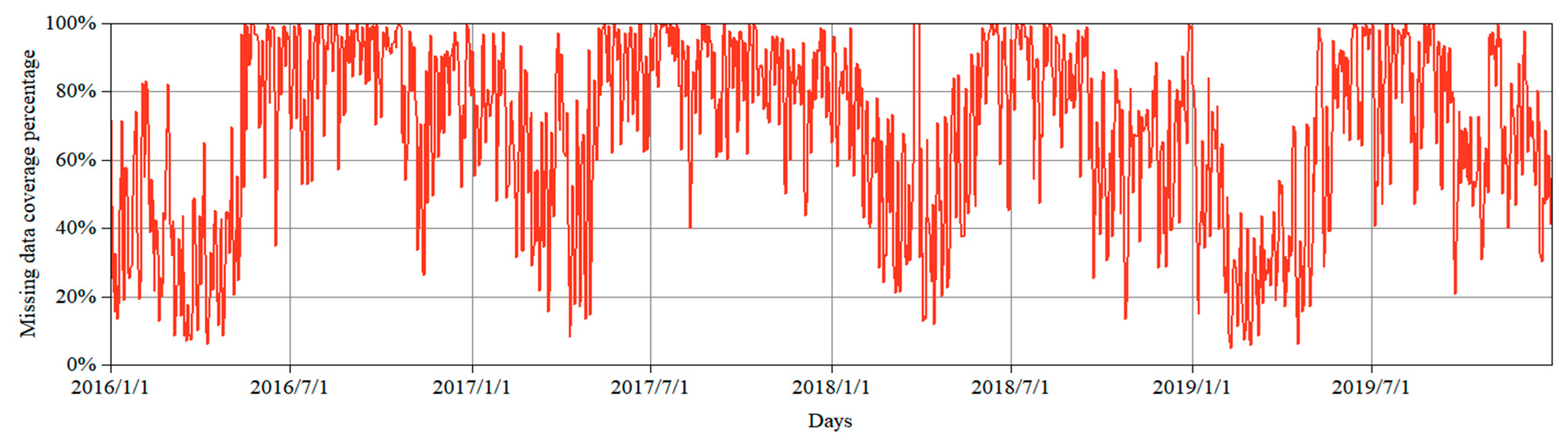
2.2. Satellite and In situ Data
3. Methods
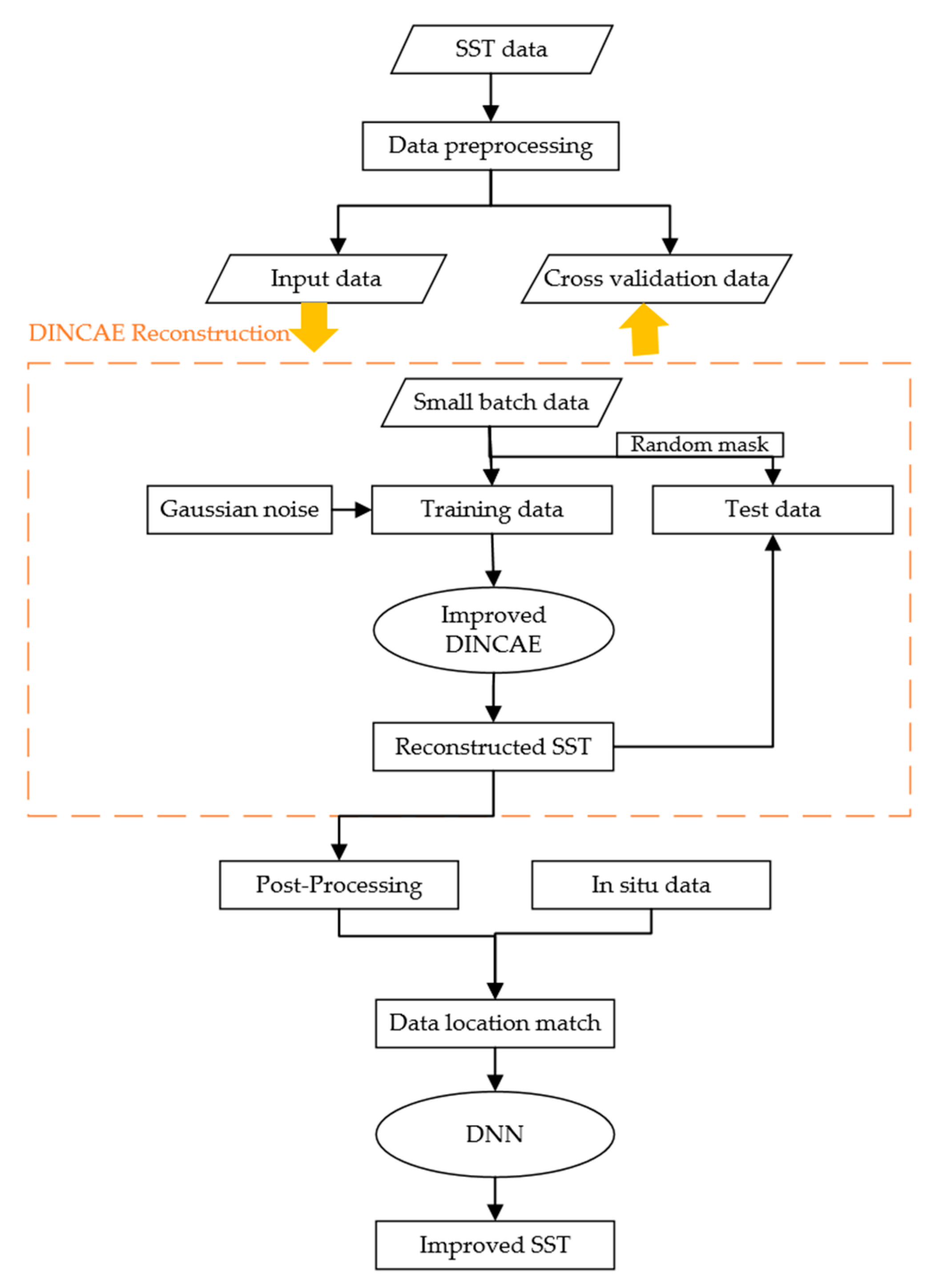
3.1. Reconstruction of SST Based on I-DINCAE
3.1.1. Satellite Data Preprocessing
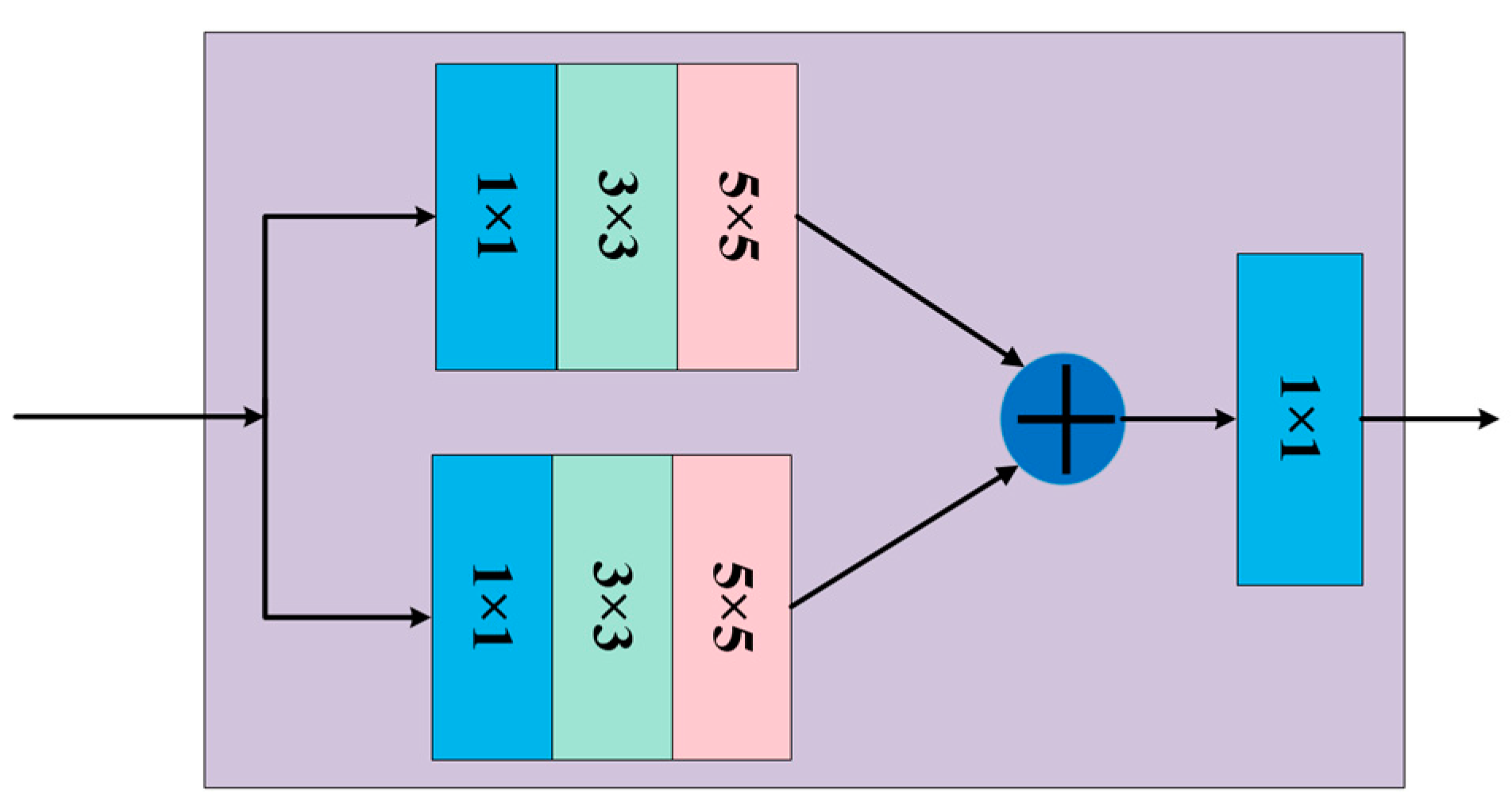
3.1.2. I-DINCAE Network Structure
3.2. Improvement for Reconstructed SST Data
3.2.1. Data Matching
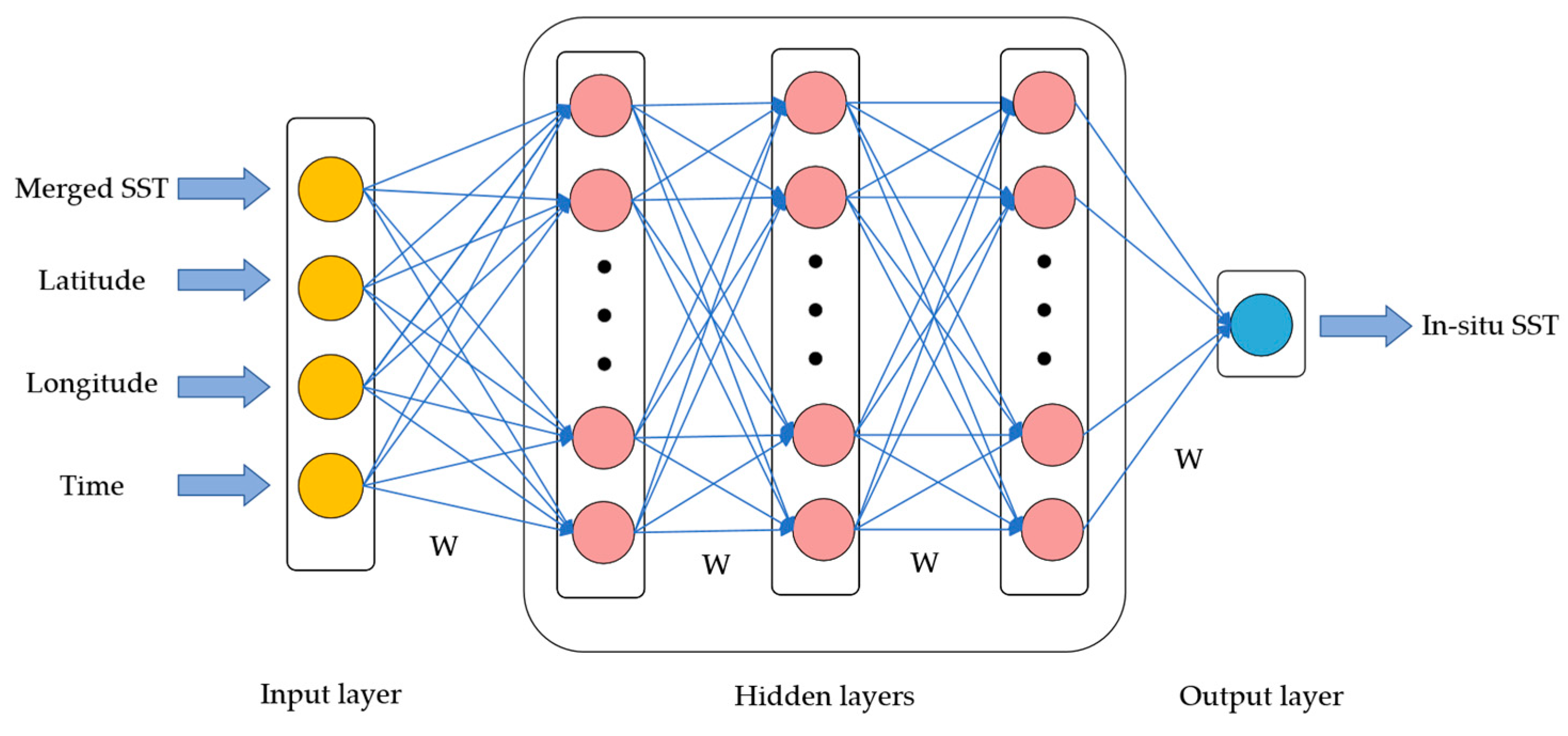
3.2.2. Deep Neural Network
4. Results and Discussion
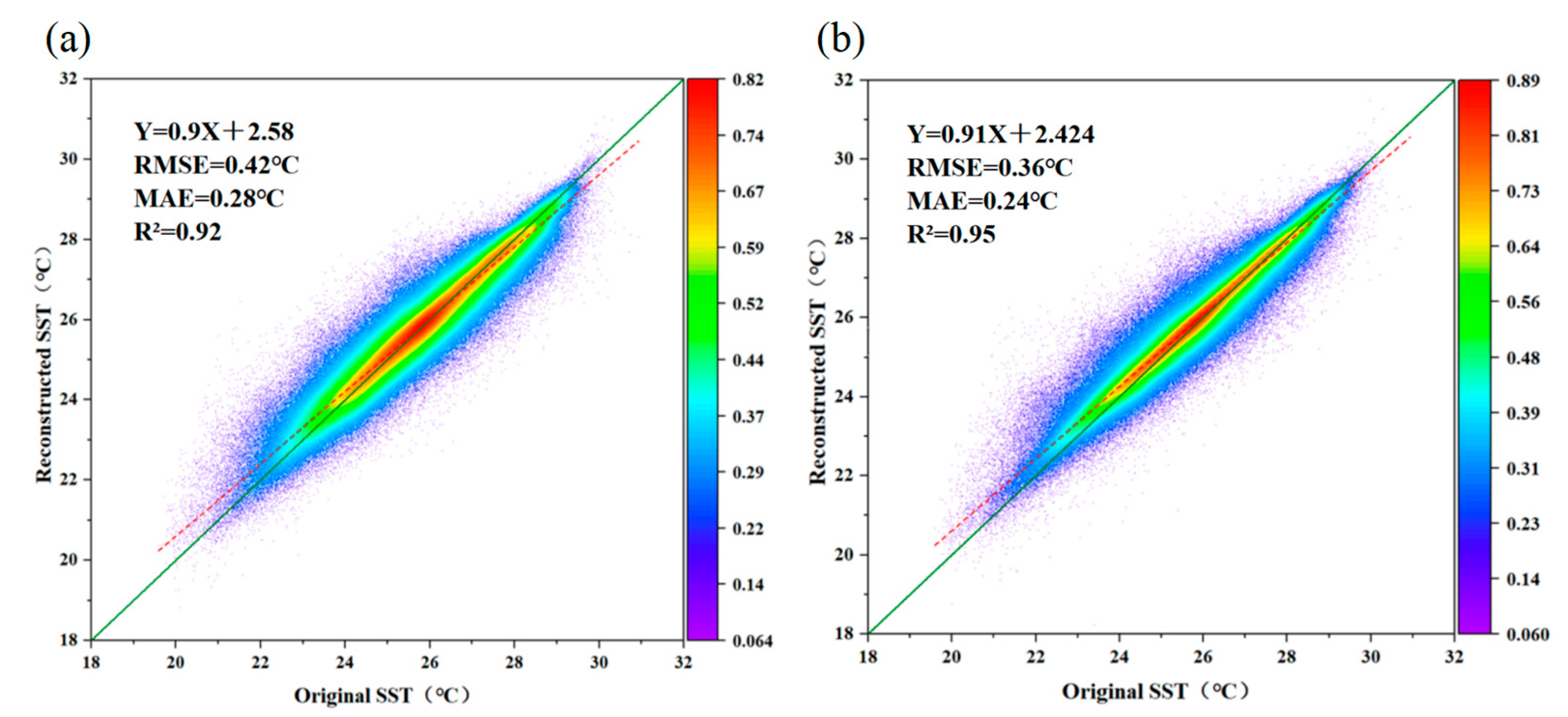
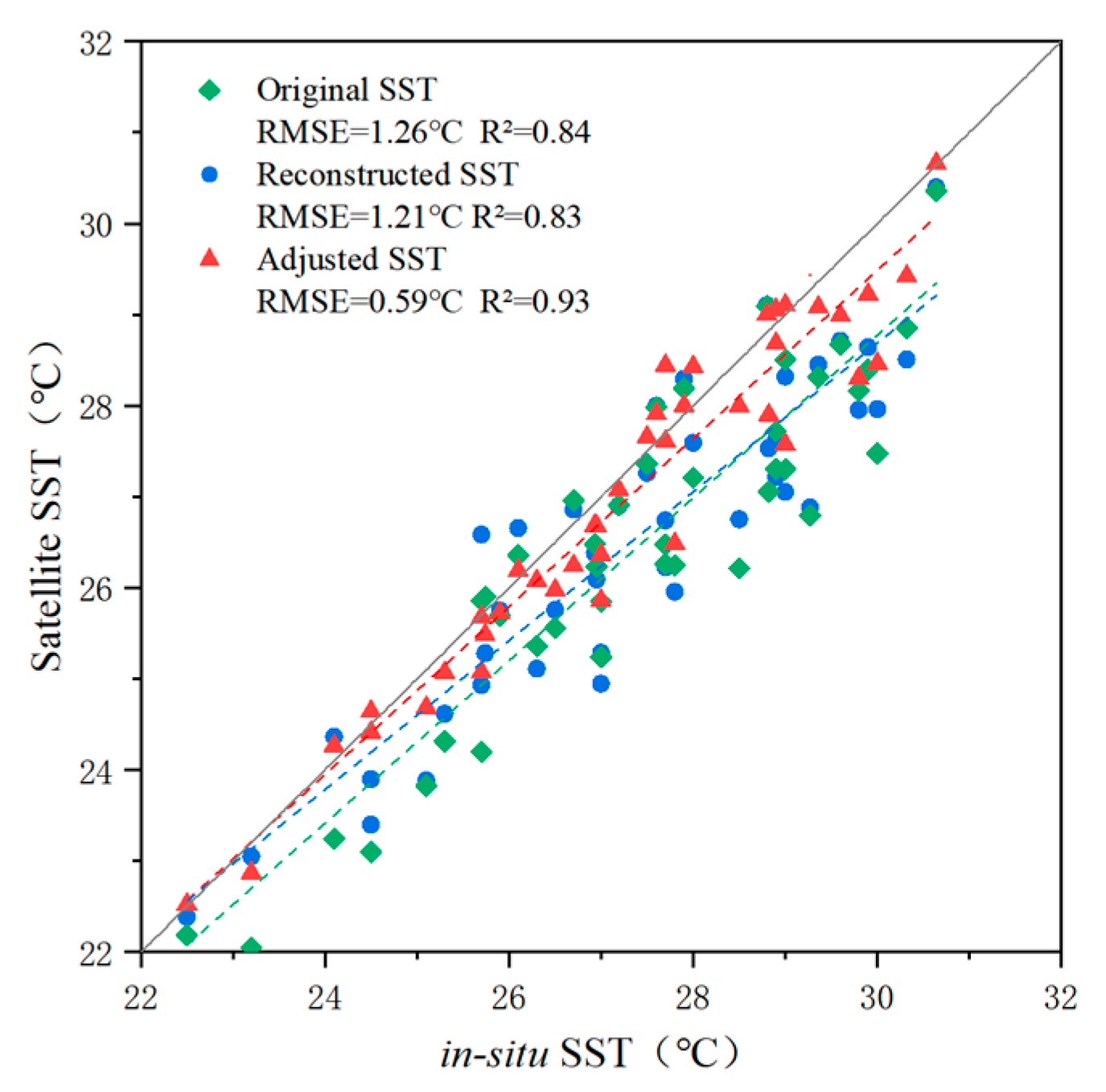
4.1. Validation of Reconstructed SST
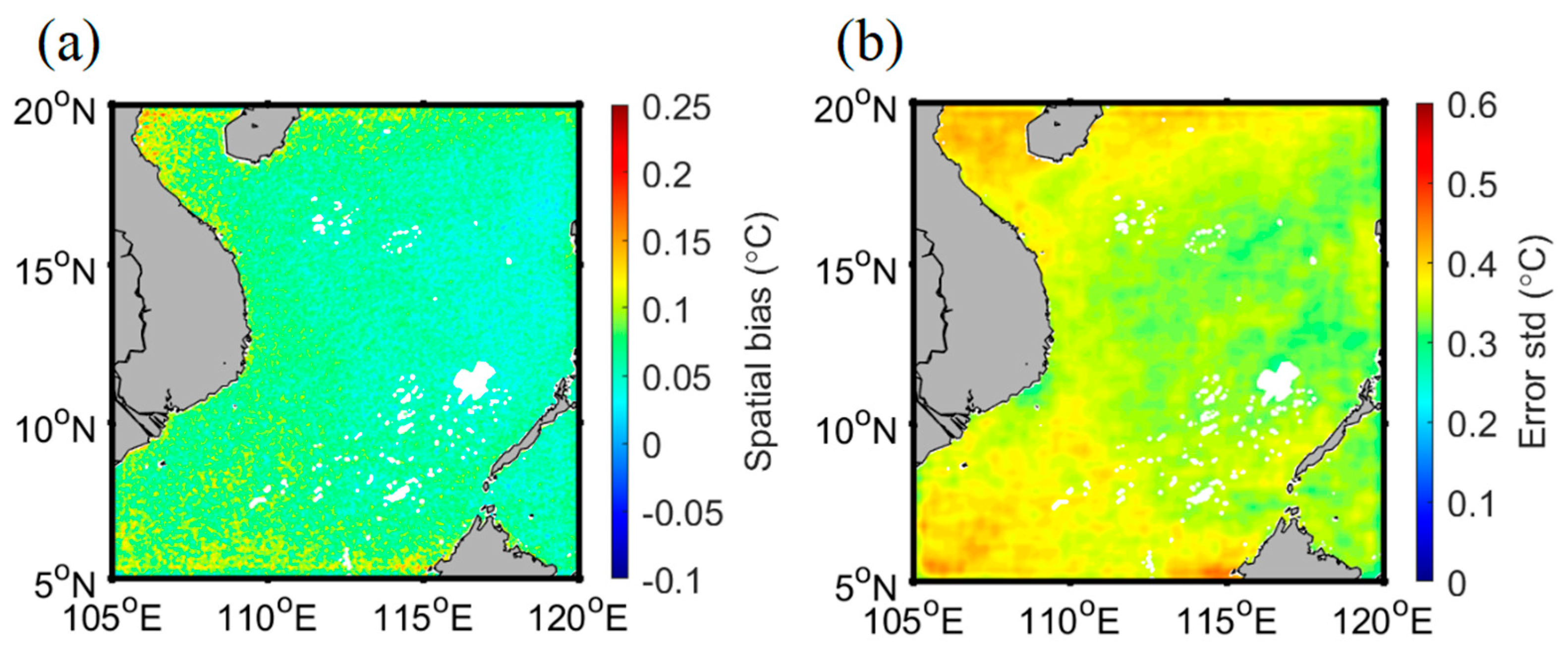
4.2. Adjustment of the Reconstructed SST
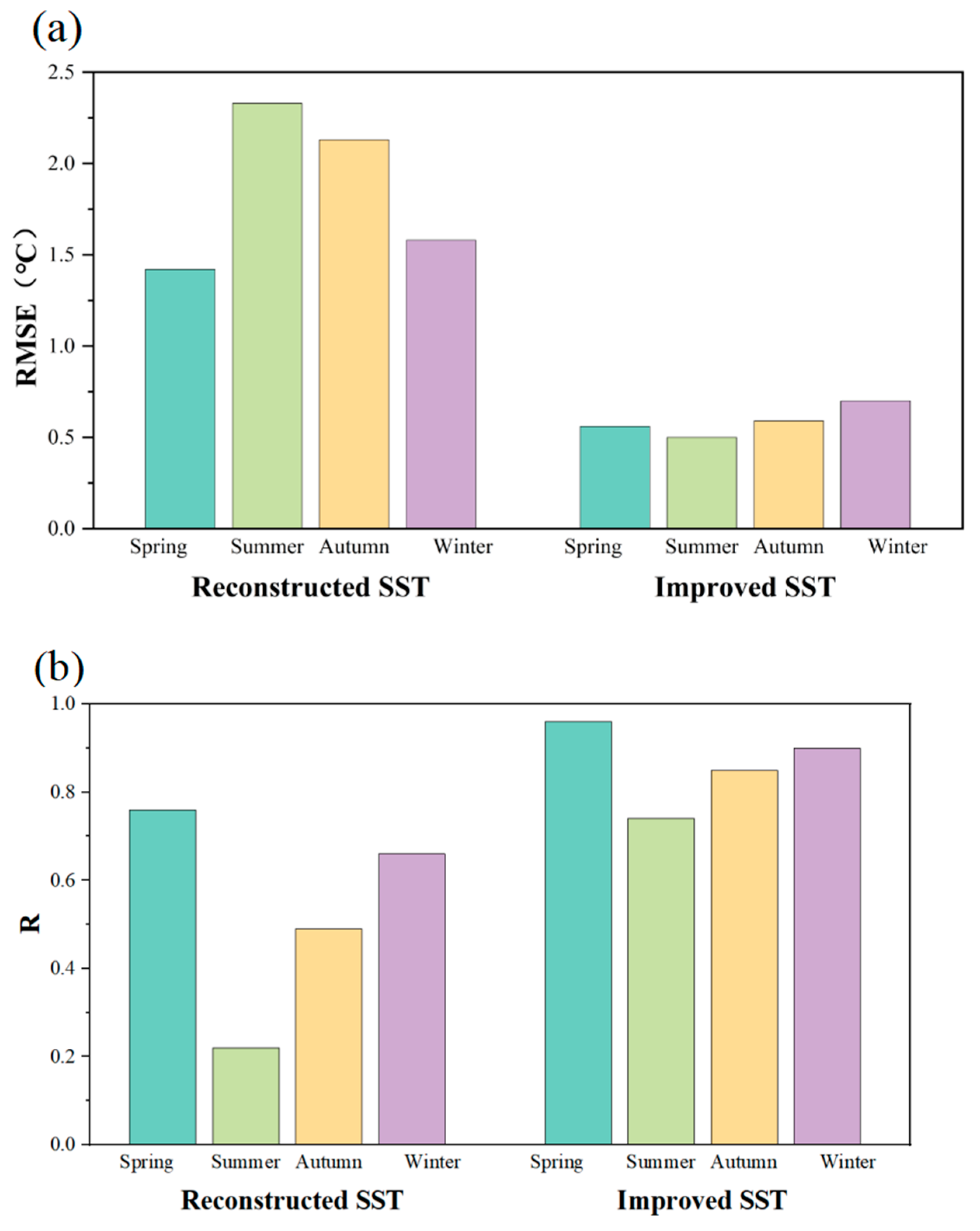
4.3. Seasonal Analysis on Improved Reconstructed SST
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, B.; Yu, J.; Zhang, L.; Shi, C.; Zhou, Z. Research progress on global sea surface temperature fusion. Prog. Meteorol. Technol. 2018, 8, 164–170. [Google Scholar]
- Park, S.; Deser, C.; Alexander, M.A. Estimation of the Surface Heat Flux Response to Sea Surface Temperature Anomalies over the Global Oceans. J. Clim. 2005, 18, 4582–4599. [Google Scholar] [CrossRef]
- Dunstan, P.K.; Foster, S.D.; King, E.; Risbey, J.; O’Kane, T.J.; Monselesan, D.; Hobday, A.J.; Hartog, J.R.; Thompson, P.A. Global Patterns of Change and Variation in Sea Surface Temperature and Chlorophyll a. Sci. Rep. 2018, 8, 14624. [Google Scholar] [CrossRef] [PubMed]
- Song, W.; Zhang, P.; Sun, L. Research on the Sea Surface Temperature Reconstruction Method of Fengyun Polar Orbit Meteorological Satellite Based on DINEOF. J. Oceanogr. Res. 2022, 40, 10. [Google Scholar]
- Shesu, R.V.; Bhaskar, T.V.S.U.; Rao, E.P.R.; Ravichandran, M.; Rao, B.V. An Improved Method for Quality Control of in Situ Data from Argo Floats Using α Convex Hulls. MethodsX 2021, 8, 101337. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z. Research on Sea Surface Temperature Prediction Based on Non-stationary Time Series; Shanghai Ocean University: Shanghai, China, 2021. [Google Scholar]
- Cao, M.; Mao, K.; Yan, Y.; Shi, J.; Wang, H.; Xu, T.; Fang, S.; Yuan, Z. A New Global Gridded Sea Surface Temperature Data Product Based on Multisource Data. Earth Syst. Sci. Data 2021, 13, 2111–2134. [Google Scholar] [CrossRef]
- Everson, R.; Cornillon, P.; Sirovich, L.; Webber, A. An Empirical Eigenfunction Analysis of Sea Surface Temperatures in the Western North Atlantic. J. Phys. Oceanogr. 1997, 27, 468–479. [Google Scholar] [CrossRef]
- Huang, X.-Y. Variational Analysis Using Spatial Filters. Mon. Weather. Rev. 2000, 128, 2588–2600. [Google Scholar] [CrossRef]
- Reynolds, R.W.; Smith, T.M. Improved Global Sea Surface Temperature Analyses Using Optimum Interpolation. J. Clim. 1994, 7, 929–948. [Google Scholar] [CrossRef]
- Müller, D. Estimation of Algae Concentration in Cloud Covered Scenes Using Geostatistical Methods. In Proceedings of the ENVISAT Symposium, Montreux, Switzerland, 23–27 April 2007. [Google Scholar]
- Feng, Y.; Lei, X.; Lu, Y. Applying spatial statistics theory to interpret the missing areas of remote sensing image information. J. Remote Sens. 2004, 8, 317–322. [Google Scholar]
- Yu, X.; Ma, A. A study on remote sensing missing data of sea surface chlorophyll based on Kriging spatial interpolation. Surv. Mapp. Bull. 2013, 12, 47–50. [Google Scholar]
- Beckers, J.M.; Rixen, M. EOF Calculations and Data Filling from Incomplete Oceanographic Datasets. J. Atmos. Ocean. Technol. 2003, 20, 1839–1856. [Google Scholar] [CrossRef]
- Zhou, F.; Tang, S.; Han, X.; Song, X.; Cao, G. Research on the reconstruction method of surface temperature using cloud based remote sensing. Remote Sens. Land Resour. 2021, 33, 78–85. [Google Scholar]
- Li, Y.; Sun, W.; Zhang, J.; Meng, J.; Zhao, Y. Reconstruction of Arctic SST Data and Generation of Multi-Source Satellite Fusion Products with High Temporal and Spatial Resolutions. Remote Sens. Lett. 2021, 12, 695–703. [Google Scholar] [CrossRef]
- Ćatipović, L.; Matić, F.; Kalinić, H. Reconstruction Methods in Oceanographic Satellite Data Observation—A Survey. J. Mar. Sci. Eng. 2023, 11, 340. [Google Scholar] [CrossRef]
- He, H.; Li, Y.; Wang, Y.; Song, X.; Liu, X. Reconstruction of chlorophyll-a concentration field in the East China Sea using empirical orthogonal function data interpolation method. Oceanogr. Res. 2013, 31, 10–15. [Google Scholar]
- Guo, J.; Song, J. Research on the Reconstruction Method of Remote Sensing Chlorophyll Data in the East China Sea. Remote Sens. Technol. Appl. 2016, 31, 939–949. [Google Scholar]
- Alvera-Azcárate, A.; Barth, A.; Parard, G.; Beckers, J.-M. Analysis of SMOS Sea Surface Salinity Data Using DINEOF. Remote Sens. Environ. 2016, 180, 137–145. [Google Scholar] [CrossRef]
- Sheng, Z.; Shi, H.; Ding, Y. Reconstruct missing satellite remote sensing sea surface temperature data using the DINEOF method. Prog. Mar. Sci. 2009, 27, 243–249. [Google Scholar]
- Jouini, M.; Lévy, M.; Crépon, M.; Thiria, S. Reconstruction of Satellite Chlorophyll Images under Heavy Cloud Coverage Using a Neural Classification Method. Remote Sens. Environ. 2013, 131, 232–246. [Google Scholar] [CrossRef]
- Park, J.; Kim, H.-C.; Bae, D.; Jo, Y.-H. Data Reconstruction for Remotely Sensed Chlorophyll-a Concentration in the Ross Sea Using Ensemble-Based Machine Learning. Remote Sens. 2020, 12, 1898. [Google Scholar] [CrossRef]
- Barth, A.; Alvera-Azcárate, A.; Licer, M.; Beckers, J.-M. DINCAE 1.0: A Convolutional Neural Network with Error Estimates to Reconstruct Sea Surface Temperature Satellite Observations. Geosci. Model Dev. 2020, 13, 1609–1622. [Google Scholar] [CrossRef]
- Krasnopolsky, V.; Nadiga, S.; Mehra, A.; Bayler, E.; Behringer, D. Neural Networks Technique for Filling Gaps in Satellite Measurements: Application to Ocean Color Observations. Comput. Intell. Neurosci. 2015, 2016, e6156513. [Google Scholar] [CrossRef]
- Li, J.; Sun, W.; Zhang, J. Reconstruct Infrared Sea Surface Temperature Data Based on an Improved DINCAE Method. In Proceedings of the IGARSS 2023—2023 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 16–21 July 2023; pp. 4120–4123. [Google Scholar]
- Xiong, Y. Deep Learning Based Data Reconstruction of Chlorophyll a and Its Spatiotemporal Variation Characteristics. Master’s Thesis, Guilin University of Technology, Guilin, China, 2023. [Google Scholar]
- Ye, H.; Tang, S.; Yang, C.; Chen, C. Reconstruction of Daily MODIS/Aqua Chlorophyll-a Concentration in Turbid Estuarine Waters Based on Attention U-NET. Remote Sens. 2023, 15, 546. [Google Scholar] [CrossRef]
- Jung, S.; Yoo, C.; Im, J. High-Resolution Seamless Daily Sea Surface Temperature Based on Satellite Data Fusion and Machine Learning over Kuroshio Extension. Remote Sens. 2022, 14, 575. [Google Scholar] [CrossRef]
- Ai, B.; Wen, Z.; Jiang, Y.; Gao, S.; Lv, G. Sea Surface Temperature Inversion Model for Infrared Remote Sensing Images Based on Deep Neural Network. Infrared Phys. Technol. 2019, 99, 231–239. [Google Scholar] [CrossRef]
- Sun, G.; Guan, D.; Zhao, D.; Wang, X.; Wang, X. Evaluation of the Applicability of TMI Sea Surface Temperature Data in the South China Sea. J. Mar. Environ. Sci. 2014, 33, 311–317. [Google Scholar]
- Ni, J. Information Extraction and Change Driving Force Analysis of Jiangsu Coastal mudflat Based on Satellite Images; Nan-jing University of Information Engineering: Nanjing, China, 2023. [Google Scholar]
- Morak-Bozzo, S.; Merchant, C.J.; Kent, E.C.; Berry, D.I.; Carella, G. Climatological Diurnal Variability in Sea Surface Temperature Characterized from Drifting Buoy Data. Geosci. Data J. 2016, 3, 20–28. [Google Scholar] [CrossRef]
- Zhang, C.; Li, S.; Liu, H.; Li, B.; Song, J. Inspection of Sea Surface Temperature Products for the Fengyun 3 Satellite Microwave Imager. J. Equip. Environ. Eng. 2021, 18, 115–123. [Google Scholar]
- Zhang, M.; Wang, S.; Qin, D.; Qiu, H.; Tang, S. Algorithm and accuracy testing of the FY-3C microwave imager sea surface temperature product. J. Remote Sens. 2018, 22, 713–722. [Google Scholar]
- Wang, S.; Cui, P.; Zhang, P.; Yang, Z.; Rao, M.; Hu, X.; Lu, F.; Liu, J. Development of FY-3 satellite VIRR sea surface temperature products. J. Shanghai Aero-Space 2017, 34, 79–84. [Google Scholar]
- Han, Z.; He, Y.; Liu, G.; Perrie, W. Application of DINCAE to Reconstruct the Gaps in Chlorophyll-a Satellite Observations in the South China Sea and West Philippine Sea. Remote Sens. 2020, 12, 480. [Google Scholar] [CrossRef]
- Xu, F.; Ignatov, A. In Situ SST Quality Monitor (iQuam). J. Atmos. Ocean. Technol. 2014, 31, 164–180. [Google Scholar] [CrossRef]
- Luo, X. Research on the Algorithm for Reconstructing Chlorophyll a Data from Yellow Sea and Bohai Sea Satellite Remote Sensing; Dalian Ocean University: Dalian, China, 2022. [Google Scholar]
- Yan, X.; Gao, Z.; Jiang, Y.; He, J.; Yin, J.; Wu, J. Application of Synthetic DINCAE–BME Spatiotemporal Interpolation Framework to Reconstruct Chlorophyll–a from Satellite Observations in the Arabian Sea. J. Mar. Sci. Eng. 2023, 11, 743. [Google Scholar] [CrossRef]
- Gao, M.; Huang, X.; Wang, F.; Zhang, H.; Zhao, H.; Gao, X. Inversion of sea surface salinity based on deep neural networks. J. Prog. Mar. Sci. 2022, 40, 496–504. [Google Scholar]
- Zhang, D. Research on the Reconstruction of Marine Chlorophyll a Concentration Data Based on Deep Learning; China University of Petroleum (East China): Shandong, China, 2020. [Google Scholar]




| Variables | |
|---|---|
| Input parameters | SST anomalies are scaled by the inverse of the error variance (the scaled anomaly is zero when data are absent) |
| The inverse of the error variance (zero when data are absent) | |
| Scaled SST anomalies of the previous day | |
| Inverse error variance of the previous day | |
| Scaled SST anomalies of the next day | |
| Inverse error variance of the next day | |
| Longitude (scaled linearly between −1 and 1) | |
| Latitude (scaled linearly between −1 and 1) | |
| Cosine of the day of the year divided by 365.25 | |
| Sine of the day of the year divided by 365.25 | |
| Output parameters | SST scaled by the inverse of the expected error variance |
| logarithm of the inverse of the expected error variance |
| Data | RMSE (°C) | MAE (°C) |
|---|---|---|
| Reconstructed SST | 1.826 | 1.415 |
| Improved SST | 0.466 | 0.296 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Wei, D.; Zhang, X.; Gao, Y.; Zhang, D. A Daily High-Resolution Sea Surface Temperature Reconstruction Using an I-DINCAE and DNN Model Based on FY-3C Thermal Infrared Data. Remote Sens. 2024, 16, 1745. https://doi.org/10.3390/rs16101745
Li Z, Wei D, Zhang X, Gao Y, Zhang D. A Daily High-Resolution Sea Surface Temperature Reconstruction Using an I-DINCAE and DNN Model Based on FY-3C Thermal Infrared Data. Remote Sensing. 2024; 16(10):1745. https://doi.org/10.3390/rs16101745
Chicago/Turabian StyleLi, Zukun, Daoming Wei, Xuefeng Zhang, Yaoting Gao, and Dianjun Zhang. 2024. "A Daily High-Resolution Sea Surface Temperature Reconstruction Using an I-DINCAE and DNN Model Based on FY-3C Thermal Infrared Data" Remote Sensing 16, no. 10: 1745. https://doi.org/10.3390/rs16101745
APA StyleLi, Z., Wei, D., Zhang, X., Gao, Y., & Zhang, D. (2024). A Daily High-Resolution Sea Surface Temperature Reconstruction Using an I-DINCAE and DNN Model Based on FY-3C Thermal Infrared Data. Remote Sensing, 16(10), 1745. https://doi.org/10.3390/rs16101745





