A Deep Learning Classification Scheme for PolSAR Image Based on Polarimetric Features

Abstract

Polarimetric features extracted from polarimetric synthetic aperture radar (PolSAR) images contain abundant back-scattering information about objects. Utilizing this information for PolSAR image classification can improve accuracy and enhance object monitoring. In this paper, a deep learning classification method based on polarimetric channel power features for PolSAR is proposed. The distinctive characteristic of this method is that the polarimetric features input into the deep learning network are the power values of polarimetric channels and contain complete polarimetric information. The other two input data schemes are designed to compare the proposed method. The neural network can utilize the extracted polarimetric features to classify images, and the classification accuracy analysis is employed to compare the strengths and weaknesses of the power-based scheme. It is worth mentioning that the polarized characteristics of the data input scheme mentioned in this article have been derived through rigorous mathematical deduction, and each polarimetric feature has a clear physical meaning. By testing different data input schemes on the Gaofen-3 (GF-3) PolSAR image, the experimental results show that the method proposed in this article outperforms existing methods and can improve the accuracy of classification to a certain extent, validating the effectiveness of this method in large-scale area classification.

1. Introduction

Polarimetric synthetic aperture radar (PolSAR) is able to acquire comprehensive polarization information of land targets, and it can actively detect targets in all-weather and all-day conditions. Compared to single- and dual-polarized images, PolSAR images contain a significant amount of back-scattering information about the objects [1]. Currently, PolSAR classification methods mainly include polarization feature-based approaches, statistical distribution characteristics of PolSAR data, and deep learning classification methods [2,3,4,5,6,7].

A large number of scholars have conducted in-depth research on PolSAR classification and achieved good results. The method mainly adopts polarization decomposition to extract the polarization scattering information of the targets and further classify them based on these features. Cloude et al. have undertaken a lot of work on PolSAR classification [8,9]. C. Lardeux et al. [10] used a support vector machine (SVM) classifier to extract polarization features from PolSAR images of different frequencies and perform classification using these features. Dickinson et al. [11] classified targets in multiple scenarios using polarization decomposition. Yin et al. [12] addressed the issue of insufficient information extraction for temporal polarization spatial features in existing models by using the Vision Transformer 3D attention module to classify multi-temporal PolSAR images, effectively addressing the aforementioned issues. Similarly, Wang et al. [13] also used ViT networks to achieve effective classification of PolSAR images. Hua et al. [14] proposed using a 3D residual module to extract information from PolSAR images. These methods also combine the extracted polarization features with deep learning to achieve the classification of PolSAR images.

The classification method based on statistical features of PolSAR images mainly utilizes the difference in statistical characteristics of target objects to classify different targets in the images. Lee et al. [15] used polarization decomposition and unsupervised classification based on a complex Wishart classifier to classify PolSAR images. Silva et al. [16] used the minimum random distance and Wishart distribution to segment the targets in PolSAR images. Chen et al. [17] used the method of polarimetric similarity and maximum–minimum scattering features to improve the accuracy of classification. Wu et al. [18] used a domain-based Wishart MRF method to classify PolSAR images and produced good results compared with other methods. Dong et al. [19]. proposed the copula-based joint statistical model to extract polarization features and use it for PolSAR image classification. Statistical methods can analyze land features in the data dimension and achieve image classification, but many parameters still need to be manually determined in advance, which brings a significant workload to research.

Although the above methods have achieved good results, they are all based on pixel-level classification, ignoring the relationship between the classified pixels and their neighborhoods. Liu et al. [20] used the information from the center pixel as well as the surrounding neighborhood pixels, combined them into superpixels, and used them as the smallest classification unit to classify PolSAR images, resulting in better classification outcomes.

Many researchers have studied the polarization decomposition method, and some famous algorithms include Pauli decomposition [8], SDH decomposition [21], Freeman decomposition [22], Yamaguchi decomposition [23], and reflection symmetrical decomposition (RSD) [24]. Van Zyl decomposition [25], H/A/Alpha decomposition [9], Huynen decomposition [26], Cameron decomposition [27], and Krogager decomposition [21] are also commonly used. These polarization decomposition algorithms have been applied to PolSAR land cover classification by relevant researchers. Nie et al. [28] utilized 12 polarization features obtained from Freeman–Durden decomposition, Van Zyl decomposition, and H/A/Alpha decomposition and achieved good classification results on limited samples using an enhanced learning framework. Wang et al. [2] applied the Freeman–Durden decomposition method and used a feature fusion strategy to classify PolSAR images of the Flevoland region. Ren et al. [29] utilized polarization scattering features obtained from T-matrix, Pauli decomposition, H/A/Alpha decomposition, and Freeman decomposition. Zhang et al. [30] applied the RSD method to extract polarimetric features from Gaofen3 images and obtained good results. Quan [31] proposed two polarimetric features—scattering contribution combiner (SCC) and scattering contribution angle (SCA)—for unified scattering characterization of manmade targets. The method achieved the physical optimization of scattering modeling. He also proposed a fine polarimetric decomposition method and derived several products to finely simulate the scattering mechanisms of urban buildings, which can also fulfill its use for effective surveillance [32].

Deep learning methods extract information about land targets through a certain number of network layers and utilize deep-level features extracted from the targets to classify objects in the image. Compared to traditional classification methods or machine learning, deep learning can more fully exploit the scattering characteristics inherent in land targets. In PolSAR data analysis, deep belief networks [33], stacked autoencoders [34], generative adversarial networks [35], convolutional neural networks [36,37], and deep stacked networks have achieved tremendous success [38,39,40]. Deep learning is a hierarchical learning method, and features extracted through this method are more discriminative [41]. Therefore, it demonstrates excellent performance in PolSAR image classification and target detection [42,43,44,45,46,47,48,49]. It has also led scholars to use various convolutional neural networks for the classification and information extraction of PolSAR images [50,51,52,53,54]. Liu et al. [55] proposed the active complex value convolutional wavelet neural network, and the Markov random fields method was proposed to classify PolSAR images, extracting information from multiple perspectives and achieving high-precision image classification. Yang et al. [56]. proposed a polarization direction angle composite sequence network, which extracts phase information from nondiagonal elements through real and complex convolutional long short-term memory networks. The network performance is better than that of existing convolutional neural networks based on real or complex numbers. Chu et al. [57] proposed a two-layer multi-objective superpixel segmentation network, with one layer used to optimize network parameters and the other layer used to refine segmentation results can achieve excellent segmentation results without obtaining prior information. These studies all demonstrate that the application of deep learning in the field of PolSAR is very successful. Considering the advantages of deep learning in extracting deep features from images and automatically learning parameters, drives us to use convolutional neural networks in this paper.

The PolSAR image contains multiple polarimetric characteristics and raw information about objects. Adopting an appropriate polarimetric decomposition method could extract features that represent objects, which benefits subsequent neural networks in classifying those features. Through existing research, it has been found that the most commonly used data input scheme is the 6-parameter data input scheme [58,59,60]. This method uses the total power of polarization, the two main diagonal elements of the polarimetric coherence matrix (T-matrix), and the correlation coefficient between the non-main diagonal elements of the matrix. Although this data input scheme has achieved good classification of objects using improved neural networks, some parameters do not have clear physical meanings at the polarimetric feature level, and from the perspective of polarimetric information content, it is not complete. This prompts us to seek a data input scheme that can have physical interpretability and a more complete utilization of polarimetric information at the polarimetric feature level.

This article presents a PolSAR deep learning classification method based on the power values of polarimetric channels. It mainly utilizes horizontal, vertical, left-handed, and right-handed polarization, as well as other equivalent power values of different polarimetric channels, as input schemes for the neural network. This data input scheme is essentially a combination of polarimetric powers. The channels are equivalent to each other and represent power values under different polarization observations, and their addition and subtraction operations have clear physical meanings. Three polarimetric data input schemes were used, and then these polarimetric features were input into the neural network model to classify objects.

The main goals of this study were, therefore, (1) to provide a method for PolSAR image classification based on polarimetric features through deep learning neural networks; (2) to examine the power of classical CNNs for the classification of back-scattering similar ground objects; (3) to investigate the generalization capacity of existing CNNs for the classification of different satellite imagery; (4) to explore polarimetric features which are helpful for wetland classification and provide comparisons with different data input schemes; (5) to compare the performance and efficiency of other two schemes. Thus, this study contributes to the CNN classification tools for complex land cover mapping using polarimetric data based on polarimetric features.

2. Method

A deep learning classification scheme for PolSAR images based on polarimetric features, which mainly includes data preprocessing, polarization decomposition, polarization feature normalization, a data input scheme, and neural network classification.

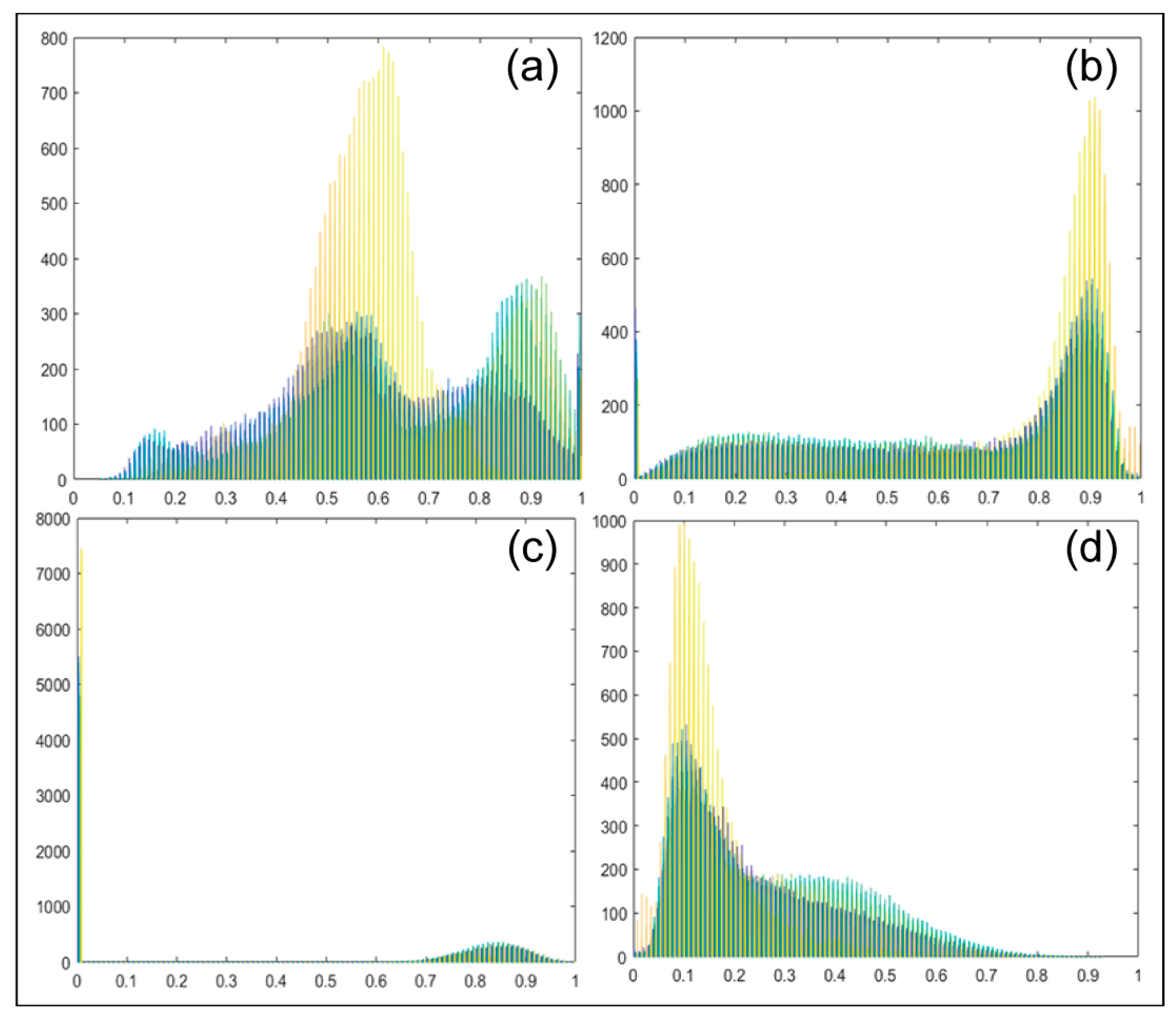
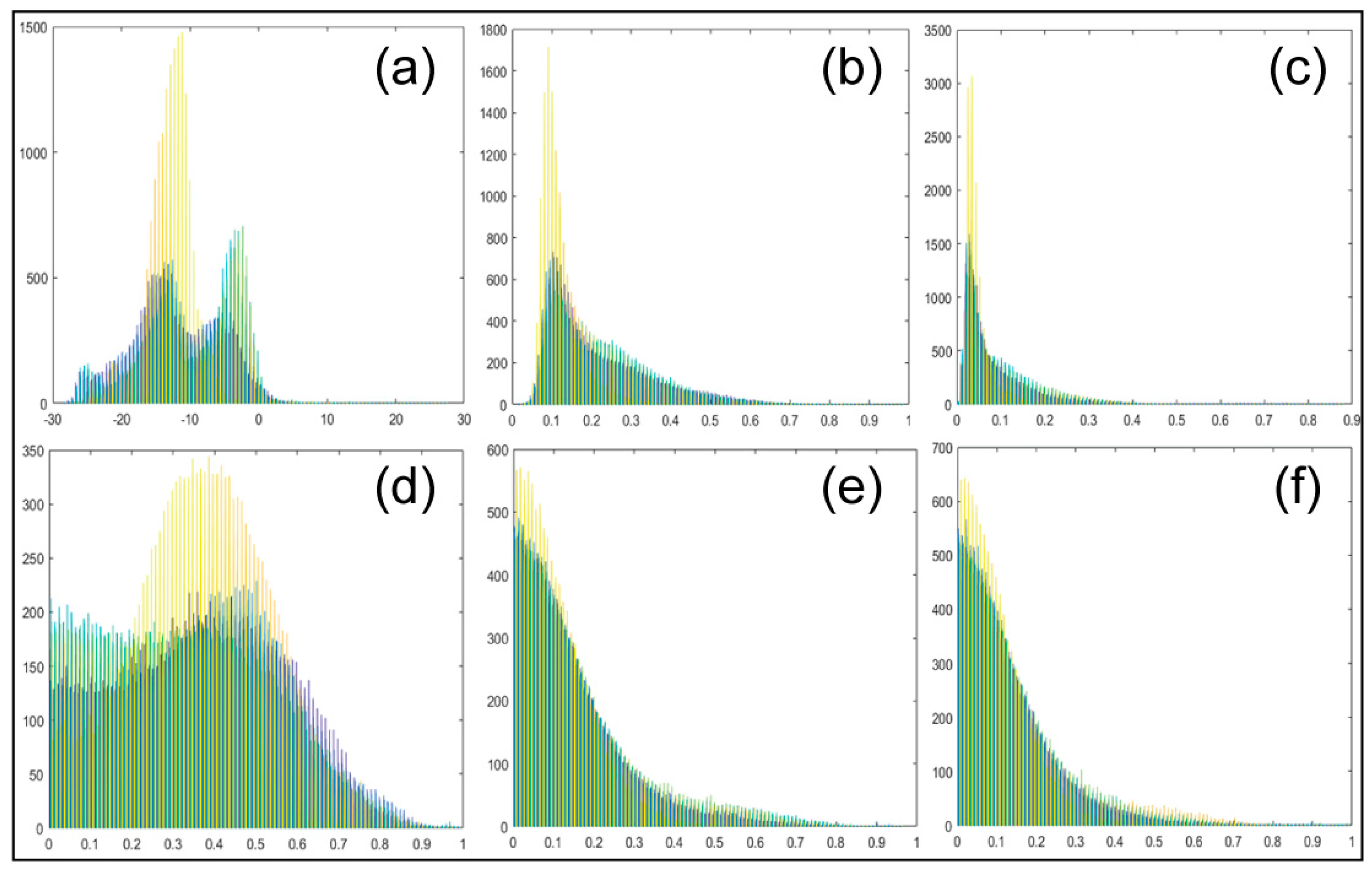
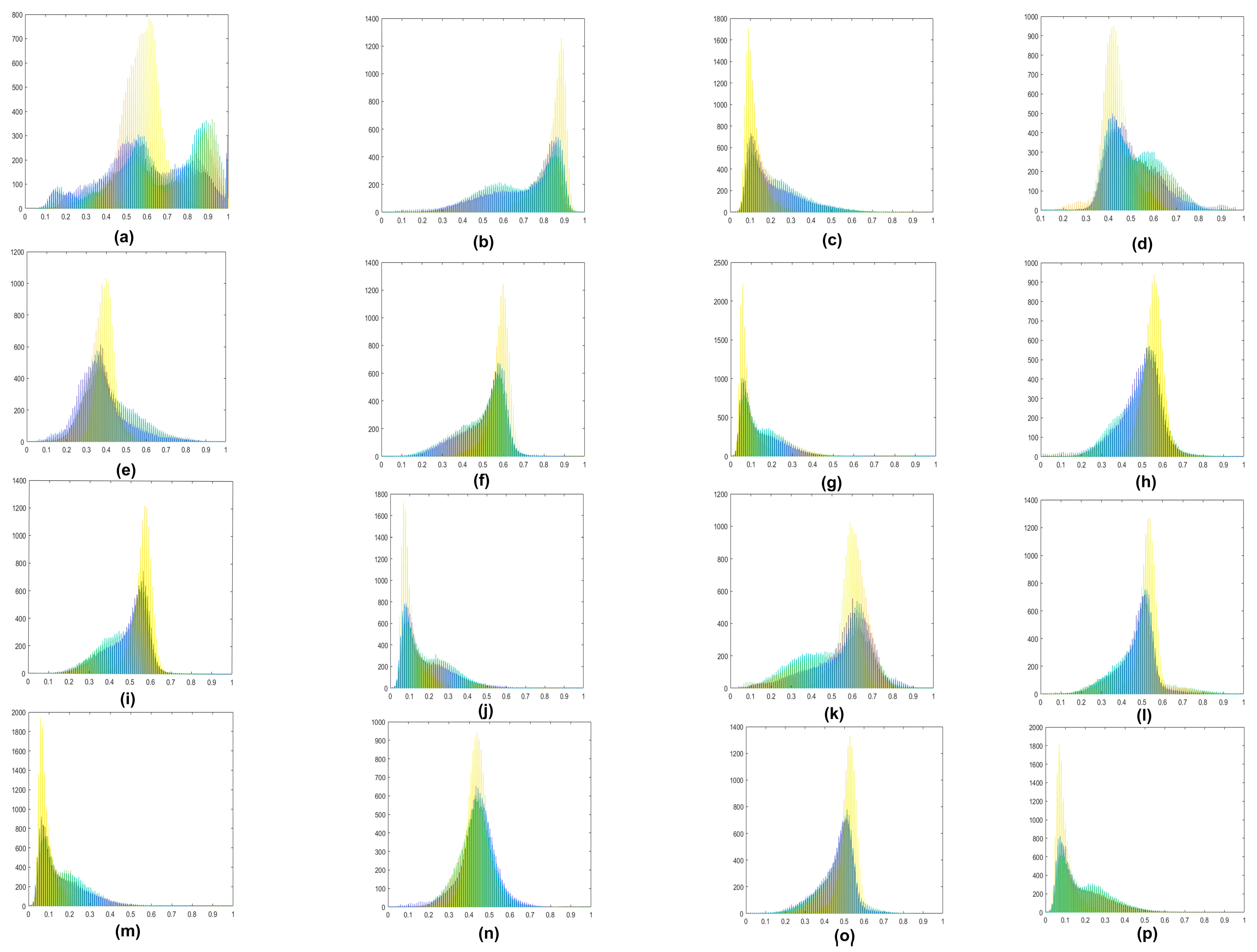
2.1. Polarization Decomposition Method Based on Polarimetric Scattering Features

Target decomposition is a primary approach in polarimetric SAR data processing, which essentially represents pixels as weighted sums of several scattering mechanisms. In 1998, scholars Anthony Freeman and Stephen L. Durden proposed the first model-based, non-coherent polarimetric decomposition algorithm [22], hereinafter referred to as the Freeman decomposition. The initial purpose of the Freeman decomposition was to facilitate viewers of multi-view SAR images in intuitively distinguishing the major scattering mechanisms of objects.

The Freeman decomposition is entirely based on the back-scattering data observed by radar, and its decomposed components have corresponding physical meanings. Therefore, it later became known as the first model-based, non-coherent polarimetric decomposition algorithm. The introduction of the Freeman decomposition was pioneering at that time. After the proposal of the Freeman decomposition, as scholars extensively utilized and further researched it, they found three main issues with the decomposition method: the overestimation of volume scattering components; the presence of negative power components in the results; and the loss of polarization information. Through research, it was discovered that these three problems are not completely independent. For example, the overestimation of volume scattering components is one of the reasons for the existence of negative power values in subsequent surface scattering and double bounce components, and the loss of polarization information is also one of the reasons for the inappropriate estimation of power values of the volume scattering component.

In 2005, Yamaguchi et al. proposed the second model-based, non-coherent polarimetric decomposition algorithm [23]. This algorithm includes four scattering components, hereinafter referred to as the Yamaguchi algorithm. The Yamaguchi decomposition introduced helical scattering as the fourth scattering component, breaking the reflection symmetry assumption of the Freeman decomposition. This expansion made the algorithm applicable to a wider range of scenarios and achieved better experimental results in urban area analysis. The improved volume scattering model proposed by Yamaguchi opened up the research direction in enhancing the performance of model-based, non-coherent polarimetric decomposition algorithms through improving the scattering model. Both of the above points were pioneering work. However, the Yamaguchi algorithm did not provide a theoretical basis for selecting helical scattering as the fourth component, and according to their paper, the selection of helical scattering was based more on the comparison and preference of multiple basic scattering objects. The main innovative aspect of the Yamaguchi decomposition focused on the scattering model itself, while no improvements were made to the decomposition algorithm itself. It still followed the processing method of the Freeman decomposition. Although the algorithm showed better experimental results, issues such as the overestimation of volume scattering, negative power components, and the loss of polarization information still persisted [24].

Compared to classical polarization decomposition methods such as Freeman decomposition and Yamaguchi decomposition, the reflection symmetric decomposition [24,61] has the advantage of obtaining polarization components with non-negative power values; the decomposed results can completely reconstruct the original polarimetric coherent matrix, and the decomposition aligns strictly with the theoretical models of volume scattering, surface scattering, and double scattering. Therefore, in this paper, we chose this method to extract the polarization features of targets from PolSAR images. The reflection symmetric decomposition (RSD) is a model-based incoherent polarization decomposition method that decomposes the polarimetric coherent matrix (T) into polarization features such as the power of the surface scattering component (PV), the power of the double scattering component (P_S), and the power of the volume scattering component (P_D). The value range of these three components is [0, +∞).

2.2. Vertical, Horizontal, Left-Handed Circular, Right-Handed Circular Polarization Methods

Currently, radar antennas primarily use two types of polarization bases: linear polarization and circular polarization. Typical linear polarization methods include horizontal polarization (H) and vertical polarization (V), and circular polarization methods include left-handed circular polarization (L) and right-handed circular polarization (R).

When a polarimetric radar uses linear polarization bases, this method first transmits horizontally polarized electromagnetic waves and uses horizontal and vertical antennas for reception. It then transmits vertically polarized electromagnetic waves and uses horizontal and vertical antennas for reception again. In the case of a single-station radar, the back-scattering alignment convention (BSA) is usually used, and the transmitting and receiving antennas use the same coordinate system. In this coordinate system, the Z-axis points towards the target, the X-axis is horizontal to the ground, and the Y-axis, along with the X-Z plane, forms a right-handed coordinate system pointing towards the sky. This coordinate system corresponds well to the horizontal (H) and vertical (V) polarization bases. In this case, the Sinclair scattering matrix can be abbreviated as:

$$\mathit{S}=\left[\begin{array}{cc}{S}_{\mathrm{HH}}& S_{\mathrm{HV}}\\ S_{\mathrm{VH}}& S_{\mathrm{VV}}\end{array}\right]$$

(1)

Upon satisfying the reciprocity theorem, the polarization coherency matrix T is derived post multi-look processing, eliminating coherent speckle noise:

$$\mathit{T}=〈\mathit{k}{\mathit{k}}^{\mathrm{H}}〉=\left[\begin{array}{ccc}{\mathit{T}}_{11}& {\mathit{T}}_{12}& {\mathit{T}}_{13}\\ {{\mathit{T}}^{\ast }}_{12}& {\mathit{T}}_{22}& {\mathit{T}}_{23}\\ {{\mathit{T}}^{\ast }}_{13}& {{\mathit{T}}^{\ast }}_{23}& {\mathit{T}}_{33}\end{array}\right]$$

(2)

Among them,

$$\mathit{k}=\frac{1}{\sqrt{2}}\left[\begin{array}{c}{S}_{\mathrm{HH}}+S_{\mathrm{VV}}\\ S_{\mathrm{HH}}-S_{\mathrm{VV}}\\ S_{\mathrm{HV}}-S_{\mathrm{VH}}\end{array}\right]$$

(3)

where k represents the scattering vector of the back-scattering S-matrix in the Pauli basis, and the superscript H denotes the Hermitian transpose. <•> represents an ensemble average. The T-matrix is a positive semi-definite Hermitian matrix, which can be represented as a 9-dimensional real vector [T₁₁, T₂₂, T₃₃, Re(T₁₂), Re(T₁₃), Re(T₂₃), Im(T₁₂), Im(T₁₃), Im(T₂₃)]. Tij represents the element in the i-th row and j-th column of the T-matrix. Re(T_ij) and Im(T_ij) represent the real and imaginary parts of the T_ij element, respectively.

The Sinclair matrix can be vectorized using the Pauli basis ${\psi }_{\mathrm{P}}$, which can be expressed as follows:

$${\psi }_{\mathrm{P}}=\left\{\sqrt{2}\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right], \sqrt{2}\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right], \sqrt{2}\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right], \sqrt{2}\left[\begin{array}{cc}0& -j\\ j& 0\end{array}\right]\right\}$$

(4)

The scattering vector ${\psi }_{\mathrm{P}}$ under the Sinclair matrix is:

$${\mathit{K}}_{4\mathrm{P}}=\frac{1}{\sqrt{2}}{\left[\begin{array}{cccc}{S}_{\mathrm{HH}}+S_{\mathrm{VV}}& S_{\mathrm{HH}}-S_{\mathrm{VV}}& S_{\mathrm{HV}}+S_{\mathrm{VH}}& j\left(S_{\mathrm{HV}}-S_{\mathrm{VH}}\right)\end{array}\right]}^{\mathrm{T}}$$

(5)

For single-polarization radar, under the condition of satisfying the reciprocity theorem, the above equation becomes:

$${\mathit{K}}_{\mathrm{P}}=\frac{1}{\sqrt{2}}{\left[\begin{array}{ccc}{S}_{\mathrm{HH}}+S_{\mathrm{VV}}& S_{\mathrm{HH}}-S_{\mathrm{VV}}& 2S_{\mathrm{HV}}\end{array}\right]}^{\mathrm{T}}$$

(6)

Therefore, in single-channel single-polarization SAR data, the polarimetric scattering characteristics of the target in the Pauli basis are represented by the polarimetric coherence matrix as follows:

$${\mathit{T}}_{3\times 3}=〈K_{\mathrm{P}}{K}_{\mathrm{P}}^{\ast T}〉=\frac{1}{2}\left[\begin{array}{ccc}〈{\left|S_{\mathrm{HH}}+S_{\mathrm{VV}}\right|}^2〉& 〈\left(S_{\mathrm{HH}}+S_{\mathrm{VV}}\right){\left(S_{\mathrm{HH}}-S_{\mathrm{VV}}\right)}^{\ast }〉& 〈2\left(S_{\mathrm{HH}}+S_{\mathrm{VV}}\right)S_{\mathrm{HV}}^{\ast }〉\\ 〈\left(S_{\mathrm{HH}}-S_{\mathrm{VV}}\right){\left(S_{\mathrm{HH}}+S_{\mathrm{VV}}\right)}^{\ast }〉& 〈{\left|S_{\mathrm{HH}}-S_{\mathrm{VV}}\right|}^2〉& 〈2\left(S_{\mathrm{HH}}-S_{\mathrm{VV}}\right)S_{\mathrm{HV}}^{\ast }〉\\ 〈2S_{\mathrm{HV}}{\left(S_{\mathrm{HH}}+S_{\mathrm{VV}}\right)}^{\ast }〉& 〈2S_{\mathrm{HV}}{\left(S_{\mathrm{HH}}-S_{\mathrm{VV}}\right)}^{\ast }〉& 〈4{\left|S_{\mathrm{HV}}\right|}^2〉\end{array}\right]$$

(7)

In the equation, * denotes conjugation, T represents transpose, <·> represents ensemble averaging. Thus,

$$\frac{\left(T_{11}+T_{22}\right)}{2}+\mathrm{Re}\left(T_{12}\right)={\left|S_{\mathrm{HH}}\right|}^2=H\left(T_{12}\right)$$

(8)

$$\frac{\left(T_{11}+T_{22}\right)}{2}-\mathrm{Re}\left(T_{12}\right)={\left|S_{\mathrm{VV}}\right|}^2=V\left(T_{12}\right)$$

(9)

In other words, the real part of the T₁₂ element information can be represented by the power values of the horizontal and vertical polarization channels. In the equation above, H(.) and V(.) are channel representation methods used in this paper. Similarly, for T₁₃, T₂₁, and T₂₃, the following four channel representation methods can be obtained.

$$\frac{\left(T_{11}+T_{33}\right)}{2}+\mathrm{Re}\left(T_{13}\right)=H\left(T_{13}\right)$$

(10)

$$\frac{\left(T_{11}+T_{33}\right)}{2}-\mathrm{Re}\left(T_{13}\right)=V\left(T_{13}\right)$$

(11)

$$\frac{\left(T_{22}+T_{33}\right)}{2}+\mathrm{Re}\left(T_{23}\right)=H\left(T_{23}\right)$$

(12)

$$\frac{\left(T_{22}+T_{33}\right)}{2}-\mathrm{Re}\left(T_{23}\right)=V\left(T_{23}\right)$$

(13)

Therefore, through equation substitution, we equivalently replace the elements in the T matrix. This can, to some extent, be represented by the horizontal and vertical polarization power components to represent the real part elements in the T-matrix. Similarly, we are also looking for a polarization power method that can represent the imaginary elements in the T-matrix. Under a circular polarization basis, the scattering matrix under the same method can be defined as follows:

$$\left[\begin{array}{c}{E}_{\mathrm{LS}}\\ E_{\mathrm{RS}}\end{array}\right]=\left[\begin{array}{cc}{S}_{\mathrm{LL}}& S_{\mathrm{LR}}\\ S_{\mathrm{RL}}& S_{\mathrm{RR}}\end{array}\right]\left[\begin{array}{c}{E}_{\mathrm{LI}}\\ E_{\mathrm{RI}}\end{array}\right]$$

(14)

For a single-station radar, under the condition of satisfying the reciprocity theorem (S_LR = S_RL), electromagnetic waves can be converted between a linear polarization basis and a circular polarization basis [62]. This enables the conversion of the scattering matrix between the linear polarization basis and circular polarization basis as well. The specific derivation process can be found in [63], and here only the results are given as follows:

$$\left[\begin{array}{c}{S}_{\mathrm{LL}}\\ \sqrt{2}{S}_{\mathrm{LR}}\\ S_{\mathrm{RR}}\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{2}& \frac{j}{\sqrt{2}}& -\frac{1}{2}\\ \frac{1}{\sqrt{2}}& 0& \frac{1}{\sqrt{2}}\\ \frac{1}{2}& -\frac{j}{\sqrt{2}}& -\frac{1}{2}\end{array}\right]\left[\begin{array}{c}{S}_{\mathrm{HH}}\\ \sqrt{2}{S}_{\mathrm{HV}}\\ S_{\mathrm{VV}}\end{array}\right]$$

(15)

Based on Formulas (6) and (14), the corresponding transformation formula between circular polarization basis and Pauli vector is as follows:

$$\left[\begin{array}{c}{S}_{\mathrm{LL}}\\ \sqrt{2}{S}_{\mathrm{LR}}\\ S_{\mathrm{RR}}\end{array}\right]=\left[\begin{array}{ccc}0& \frac{1}{\sqrt{2}}& \frac{j}{\sqrt{2}}\\ 1& 0& 0\\ 0& \frac{1}{\sqrt{2}}& -\frac{j}{\sqrt{2}}\end{array}\right]{{\rm K}}_{\mathrm{P}}$$

(16)

Then,

$$\left[\begin{array}{c}{S}_{\mathrm{LL}}\\ S_{\mathrm{RR}}\end{array}\right]=\frac{1}{2}\left[\begin{array}{c}{S}_{\mathrm{HH}}-S_{\mathrm{VV}}+j2S_{\mathrm{HV}}\\ S_{\mathrm{HH}}-S_{\mathrm{VV}}-j2S_{\mathrm{HV}}\end{array}\right]$$

(17)

By changing the two Equations (16) and (17), we can obtain the following form:

$$\left[\begin{array}{cc}{S}_{\mathrm{HH}}& S_{\mathrm{HV}}\\ S_{\mathrm{VH}}& S_{\mathrm{VV}}\end{array}\right]=S_{\mathrm{LR}}\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]+\frac{S_{\mathrm{RR}}}{2}\left[\begin{array}{cc}1& j\\ j& -1\end{array}\right]+\frac{S_{\mathrm{LL}}}{2}\left[\begin{array}{cc}1& -j\\ -j& -1\end{array}\right]$$

(18)

$$K_{\mathrm{P}}=S_{\mathrm{LR}}\left[\begin{array}{c}\sqrt{2}\\ 0\\ 0\end{array}\right]+\frac{S_{\mathrm{RR}}}{\sqrt{2}}\left[\begin{array}{c}0\\ 1\\ j\end{array}\right]+\frac{S_{\mathrm{LL}}}{\sqrt{2}}\left[\begin{array}{c}0\\ 1\\ -j\end{array}\right]$$

(19)

From the above equation, it can be inferred that the transformation from horizontal and vertical polarization to circular polarization can also be considered as a process of decomposing the scattering matrix into certain correlation terms. This means that the Sinclair matrix could be decomposed into components such as plane waves, left-handed helices, and right-handed helices, and S_LR, S_RR, S_LL correspond to the phase and power levels of each constituent.

Therefore, it can be inferred the following equations:

$$\frac{\left(T_{11}+T_{22}\right)}{2}+\mathrm{I}\mathrm{m}\left(T_{12}\right)={\left|S_{\mathrm{LL}}\right|}^2=L\left(T_{12}\right)$$

(20)

$$\frac{\left(T_{11}+T_{22}\right)}{2}-\mathrm{I}\mathrm{m}\left(T_{12}\right)={\left|S_{\mathrm{RR}}\right|}^2=R\left(T_{12}\right)$$

(21)

Thus, the imaginary part of the T₁₂ element information can be represented by the power values of the left-hand and right-hand polarization channels, where L(.) and R(.) are also the channel representation methods used in this article. Similarly, for T₁₃, T₂₃, four channel representation methods can be obtained as follows:

$$\frac{\left(T_{11}+T_{33}\right)}{2}+I\mathrm{m}\left(T_{13}\right)=L\left(T_{13}\right)$$

(22)

$$\frac{\left(T_{11}+T_{33}\right)}{2}-I\mathrm{m}\left(T_{13}\right)=R\left(T_{13}\right)$$

(23)

$$\frac{\left(T_{22}+T_{33}\right)}{2}+I\mathrm{m}\left(T_{23}\right)=L\left(T_{23}\right)$$

(24)

$$\frac{\left(T_{22}+T_{33}\right)}{2}-I\mathrm{m}\left(T_{23}\right)=R\left(T_{23}\right)$$

(25)

Therefore, through equation substitution, we equivalently replace the elements in the T matrix. This can, to some extent, be represented by the left-hand and right-hand polarization power components to represent the imaginary part elements in the T-matrix.

From the above derivation process, it can be seen that the new classification scheme first uses the power values of the horizontal, vertical, left-hand, and right-hand polarization channels. The other channels following also essentially represent power values of a certain polarization channel; that is to say, the elements in the T matrix are equivalently represented using polarization power features, and the input elements have actual physical meanings. Moreover, the combination of the mentioned channels can fully invert all elements of the T-matrix, making it comprehensive from the perspective of polarization information.

2.3. Input Feature Normalization and Design of Three Schemes

Before inputting these polarizing features into the neural network, it is necessary to normalize these physical quantities to meet the requirements of the network input. In the T-matrix, the total polarized power is converted into a physical quantity in units of dB. For polarized power parameters T₁₁, T₂₂, T₃₃, P_S, P_D, P_V, they are all divided by Span to achieve normalization.

Based on the existing literature and corresponding polarized power values, this paper designs three deep learning polarization data input schemes. First, the decomposed P_S, P_D, P_V with reflection symmetry, and the normalized P₀ (10log₁₀Span) were used as the data input Scheme 1. The elements in Scheme 1 were all based on the characteristics of polarization power and contained the main polarization information of the terrain objects. Therefore, this input scheme was used as the basic one. Then, according to references [58,59,60], the correlation coefficients between channels T₁₂, T₂₃, T₂₃, as well as the non-normalized P₀ (NonP₀) of the T matrix, were used as the research Scheme 2, where the correlation coefficients between channels are defined by Formulas (26)–(28).

$$coe{T}_{12}=\left|{\mathrm{T}}_{12}\right|/\sqrt{{\mathrm{T}}_{11}\cdot {\mathrm{T}}_{22}}$$

(26)

$$coe{T}_{13}=\left|{\mathrm{T}}_{13}\right|/\sqrt{{\mathrm{T}}_{11}\cdot {\mathrm{T}}_{33}}$$

(27)

$$coe{T}_{23}=\left|{\mathrm{T}}_{23}\right|/\sqrt{{\mathrm{T}}_{33}\cdot {\mathrm{T}}_{22}}$$

(28)

In this data input scheme, except for NonP₀, the value range of the other five parameters is between 0 and 1. Finally, a total of 16 parameters, including P₀, T₁₂, T₂₃, T₂₃, H(T₁₂), H(T₁₃), H(T₂₃), L(T₁₂), L(T₁₃), L(T₂₃), V(T₁₂), V(T₁₃), V(T₂₃), R(T₁₂), R(T₁₃), R(T₂₃), were used as data input Scheme 3, where P₀ had been normalized. The other channels were normalized by dividing them by P₀, as they represent the power values of specific polarization channels. The three data input schemes are shown in

Table 1. List of three polarization data input schemes.

Scheme	Parameters	Polarization Features
1	4	P0, PS, PD, PV
2	6	NonP0, T22, T33, coeT12, coeT13, coeT23
3	16	P0, T12, T23, T23, H(T12), H(T13), H(T23), L(T12), L(T13), L(T23), V(T12), V(T13), V(T23), R(T12), R(T13), R(T23)

.

At the same time, the data distribution of the three research schemes was also statistically analyzed. Except for the NonP₀ polarization feature of Scheme 2, the polarization characteristics of the other schemes were distributed in the range [0, 1]. In order to have a visual understanding of the polarization feature distribution of each data input scheme, we conducted a histogram analysis of the polarization feature distribution, as shown in Figure 1, Figure 2 and Figure 3.

Through the experiment, we obtained the distribution histogram of P₀ and classified features of four experimental images. We discovered that P₀ was distributed at [−30 dB, 0 dB]. We obtained the distribution histogram of ground objects and discovered that it was also distributed at [−30 dB, 0 dB]. Therefore, the selected value range distribution was appropriate, and no new categories were introduced.

2.4. Experiment and Pre-Processing

After obtaining the high-resolution Gaofen-3 Level 1A QPSI data, additional data were required for radiometric calibration. The method for radiometric calibration can be found in the Gaofen-3 user manual [64]. Due to inherent speckle noise in the data, an appropriate filtering method was necessary to remove the speckle, reducing its impact on subsequent classification. Compared to traditional filtering methods, the non-local means filtering method [65] considers the influence of neighboring pixels, making it more effective. Therefore, this paper selected this method to denoise the PolSAR images. The polarization coherence matrix data and all polarization characteristic parameters of the reflection symmetry decomposition were obtained by processing the data using the polarization decomposition production algorithm mentioned in reference [24,62].

2.5. Classification Process of Polarization Scattering Characteristics Using Deep Learning

In this paper, based on the scattering mechanism, the polarization characteristics were classified into three different input schemes. Then, these three research schemes were inputted into a network model to extract the features of the objects. Finally, a Softmax classifier was used to obtain the classification results at the end of the network. The Figure 4 is a flowchart of the entire experimental process, in which different colored CNN architectures represent the extracted polarization features of different schemes. After the experiments, it was found that when the network window size was 64 × 64, various research schemes could achieve the best classification results. Therefore, this experiment selected samples of this size for experimentation. The sample dimension sizes input into the neural network were 64 × 64 × 4, 64 × 64 × 6, and 64 × 64 × 16, respectively.

The entire process of this algorithm is shown as follows (Algorithm 1).

Algorithm 1: A deep learning classification scheme for PolSAR image based on polarimetric features

Input: GF-3 PolSAR images. Output: Predict label Ytest {y1, y2, …, ym} 1: Processing GF-3 PolSAR images. 2: Polarimetric decomposition. 3: Extract polarimetric features. 4: Feature normalization. 5: Three schemes are proposed based on the previous studies and scattering mechanisms. 6: Randomly select a certain proportion of training samples (Patch_Xtrain: {Patch_x1, Patch_x2, …, Patch_xn}, the remaining labeled samples are used as validation samples 7: Inputting Patch_xi into CNN. for i < N do the train one time. If good fitting, then Save model, and break. else if over-fitting or under-fitting, then Adjust parameters include, i.e., learning rate, bias. End 8: Predict Label: Y = Softmax (Patch_Xtrain) 9: Test images are input to the model and predict the patches of all pixels. 10: Do method evaluation, i.e., Statistic OA, AA, and Kappa coefficient.

3. Experimental and Result Analysis

In this section, high-resolution PolSAR images of the Yellow River Delta area, which have undergone field surveys, were used to verify the effectiveness of the proposed approach. All experiments were conducted on an i7-10700 CPU (Intel, Santa Clara, CA, USA)and RTX 3060 Ti GPU (NVIDIA, Santa Clara, CA, USA).

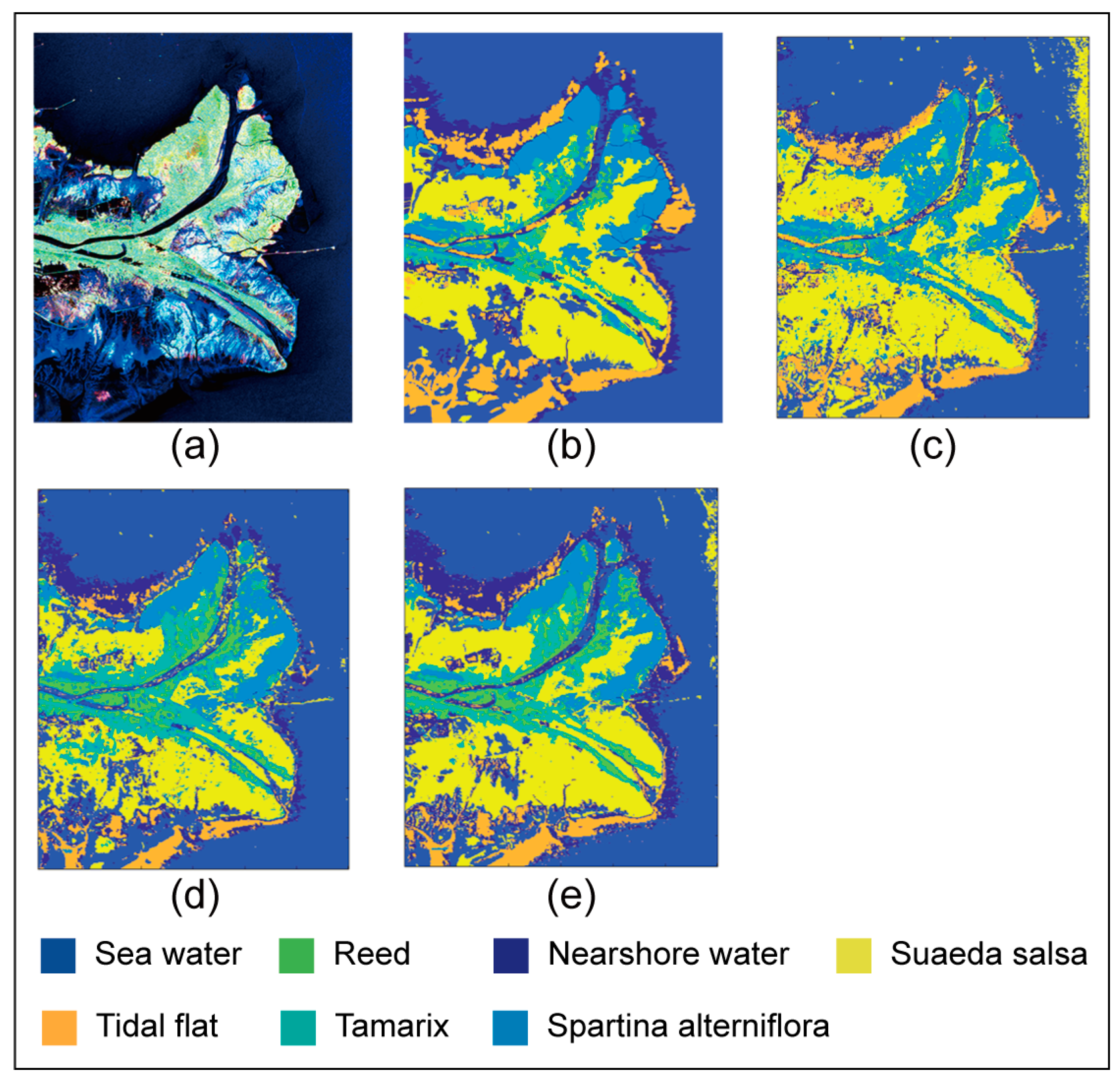
3.1. Study Area and Dataset

GF-3 has a quad-polarized instrument with different modes. In this article, we used high-resolution QPSI imaging mode PolSAR images (spatial resolution is 8m) of the Yellow River Delta area (Shandong, China) for the experiment (displayed in Figure 5). There are several classical types in this area, such as nearshore water, seawater, spartina alterniflora, tamarix, reed, tidal flat, and suaeda salsa. Restricted by historical resources, we chose four images of this area. The training and validation sets were selected from three different images taken during the same quarter in this region, specifically on 14 September 2021 and 13 October 2021. The test image was taken on 12 October 2017. We used unmanned aerial vehicle (UAV) images (displayed in Figure 6), which were shot in September 2021, combined with empirical knowledge, for marking targets to guarantee the accuracy of the labeled training datasets.

In this study, we classified seven species according to the survey results: nearshore water; seawater; spartina alterniflora; tamarix; reed; tidal flat; and suaeda salsa. We labeled these targets from numbers 1 to 7, respectively. We randomly selected 800 samples of each category for training and 200 for validation. The details are shown in

Table 2. Samples distribution.

Images	Nearshore Water	Seawater	Spartina Alterniflora	Tamarix	Reed	Tidal Flat	Suaeda Salsa
20210914_1	500	400	1000	500	500	500	500
20210914_2	500	200	0	0	0	500	0
20211013	0	400	0	500	500	0	500
Total	1000	1000	1000	1000	1000	1000	1000

.

3.2. Classification Results of the Yellow River Delta on AlexNet

In order to quantitatively evaluate the accuracy of the three data input schemes for classification and to avoid random results, in this paper, five independent experiments were conducted on AlexNet for each data input scheme. The overall accuracy of each classification was calculated for each experiment (the results were arranged in descending order, with the highest overall accuracy being the maximum value), as well as the average accuracy of the overall classification for the five experiments and the Kappa coefficient to evaluate the classification results. Both the accuracy of individual land cover classes and the Kappa coefficient were calculated based on the results with the highest overall accuracy.

From the classification results, obviously, it can be seen that when using Scheme 3 for polarized data input, both the highest overall accuracy and average overall accuracy were higher compared to the other two schemes, with values of 86.11% and 78.08%, respectively. We believe this is because Scheme 3 contains more polarization information than the other two schemes. The overall accuracy and Kappa coefficient of five independent experiments stayed at a relatively high level, showing the stronger robustness of Scheme 3.

It is worth noting that for the tidal flat, Scheme 2 and Scheme 3 performed poorly, with accuracies of 49.3% and 44.6%, respectively. This indicates that these two schemes did not contain polarization parameters that effectively represent the scattering characteristics of the tidal flat, resulting in low classification accuracy for this land cover. We also guess that tidal flats are unique ecosystems because the water cover changes intermittently with the tidal phase, which may also lead to low accuracy. It can also be seen from the table that the accuracy of the tamarix in Scheme 1 was lower than the other two schemes, only 40.1%, while the recognition accuracy of Scheme 2 and Scheme 3 reached 100%. This indicates that our proposed method can extract more information from PolSAR images, which is beneficial for improving the overall land use classification accuracy.

For Scheme 2, both the tidal flat and suaeda salsa had low classification accuracies of 49.3% and 50.8%, respectively. For Scheme 1, the classification accuracies for each land cover were lower than the other two schemes due to the limited number of polarization features. This indicates that neither of these two schemes effectively contained polarization information of classified features beyond a certain extent, which means that the polarization characteristics of these two schemes in terms of data input were incomplete.

In Scheme 3, the polarized features inputted into the deep learning network were the power values of the polarization channels. These channels were equivalent and contained all the polarization information using equivalent polarization power values. Apart from intertidal zones, high classification values were achieved for the other six land cover types. This indicates that using equivalent polarization power values can effectively distinguish most land cover types. However, strictly speaking, the polarization information in this scheme still cannot effectively differentiate classified land cover types, and overall classification accuracy needs further improvement. The classification accuracy and overall accuracy of land features for various schemes are shown in

Table 3. The classification accuracy of their polarization input schemes on AlexNet.

Classification Accuracy Input Scheme	Scheme 1	Scheme 2	Scheme 3
Nearshore water	83.4	96.8	100
Seawater	98.7	96.9	99.60
Spartina alterniflora	87.0	96.8	93.3
Tamarix	40.1	100	100
Reed	50.4	94.5	68.50
Tidal flat	61.8	49.3	44.6
Suaeda salsa	98.2	50.8	96.8
Indepent experiments Overall Accuracy	74.23	83.59	86.11
	71.36	81.41	81.53
	70.41	77.83	77.04
	68	73.66	73.73
	67.84	68.87	71.99
Average Overall Accuracy	70.368	77.072	78.08
Kappa coefficient	0.6993	0.8085	0.8380

.

We also classified the entire test image, and it is easy to see that the classification result of Scheme 3 was better than the other two schemes. From the overall classification effect, Scheme 3 was also better than the other two schemes in terms of the number of classified objects and the classification effect between different categories.

From the classification maps, we can see that spartina alterniflora, tamarix, and reed were easily classified in Scheme 3. In the other two schemes, there were some misclassification phenomena, which indicates that compared to Scheme 3, the polarization information carried cannot distinguish these wetland vegetation types very well.

The classification results of the entire image are shown in Figure 7.

3.3. Classification Results of the Yellow River Delta on VGG16

To further verify the above conclusion, we also conducted comparative experiments on three schemes through VGG16. Similar to the testing results on AlexNet, when using VGG16 to test three data input schemes, there were still situations where the classification accuracy of certain land objects was low. In Scheme 1, the reed classification accuracy was 26.1%, and the tamarix accuracy was 40.2%. In Scheme 2, the tidal flat accuracy was only 28.5%, while in Scheme 3, the reed accuracy was 44.7%, and the tidal Flat accuracy was 58.3%. This indicates that none of these three schemes could fully classify the selected features beyond a certain extent, but in terms of overall classification accuracy and Kappa coefficient, Scheme 3 was still better than the other two schemes, and it was relatively complete in carrying polarization features.

Overall, Scheme 3 showed better classification performance than the other two schemes. Except for reeds and tidal flats, the classification accuracy of the other five land cover types remained consistently high. The classification accuracy of Tamarix reached 100%, and the classification accuracy of other land features was also above 94.1%. At the same time, the highest overall classification accuracy and average overall classification accuracy were also superior to the other two schemes, indicating that Scheme 3 had relatively more complete polarization information prior to inputting it into the network model.

Scheme 2 slightly underperformed Scheme 3 in the classification accuracy of suaeda salsa, with an accuracy of only 66.2%. Particularly, Scheme 2 struggled to classify tidal flats well, with a classification accuracy of only 28.5%. The polarization information contained in Scheme 2 cannot effectively characterize these two types of ground objects, resulting in relatively low classification accuracy. Instead, Scheme 1, which included surface scattering and volume scattering components, effectively characterized the scattering characteristics of tidal flat and suaeda salsa. Therefore, the effect of Scheme 1 was better than that of Scheme 2.

For Scheme 1, the overall land cover classification accuracy was lower compared to the other two schemes, mainly due to the limited number of polarimetric feature parameters, which failed to effectively represent the classified area in the input network model. The specific classification accuracies are shown in

Table 4. The classification accuracy of their polarization input schemes on VGG16.

Classification Accuracy Input Scheme	Scheme 1	Scheme 2	Scheme 3
Nearshore water	89.3	95.7	95.6
Seawater	99.4	97.7	99.7
Spartina alterniflora	87.6	96.6	95.9
Tamarix	40.2	98.5	100
Reed	26.1	93.8	44.7
Tidal flat	73.2	28.5	58.3
Suaeda salsa	100	66.2	94.1
Indepent experiments overall accuracy	73.69	82.43	84.04
	72.8	82.21	83.57
	69.7	81.44	82.07
	68.66	79.44	81.54
	67.6	77.53	80.11
Average overall accuracy	70.49	80.61	82.266
Kappa coefficient	0.6930	0.7950	0.8138

.

Similarly, we also displayed the classification results of the entire image. The results of the three data input schemes on VGG16 are shown in Figure 8. From Figure 8, it can be observed that the classification results of Scheme 3 were still the best among the three schemes.

When using VGG16 for classification, the classification results of each scheme were clearer overall than when using AlexNet, and the clustering effect of each feature was better.

4. Conclusions

In this paper, a deep learning-based classification scheme for PolSAR images using polarimetric scattering features was proposed through rigorous mathematical derivation. This scheme utilized a combination of polarimetric power features, ensuring that each channel represented power values and was equivalent to other channels. Each channel possessed practical physical meanings and clear mathematical significance. Experimental results demonstrated that compared to the 6-parameter and 4-parameter data input schemes, the proposed scheme had more comprehensive information and achieved higher classification accuracy. The proposed scheme was validated on the GF-3 dataset and showed performance improvement. However, for the classification of certain land objects, this approach lacked sufficient accuracy, and there were situations where the information was not comprehensive enough.

In future work, more comprehensive data input schemes will be explored.