Abstract
To address the issue of estimating soil moisture at a hyper-resolution scale, a methodology referred to as Precision Irrigation Soil Moisture Mapper (PrISMM), that includes three key components, is developed: high-resolution remotely sensed optical and thermal data, surface energy balance modeling, and site-specific soil analysis. An Unmanned Aerial Vehicle/System (UAV or UAS) collects high-resolution multispectral imagery in the Dallas–Fort Worth metropolitan study area. Orthomosaics are converted to thermal inertia estimates in a spatially distributed format using the remotely sensed data combined with a set of surface energy balance modeling equations. Using thermal and physical properties of soil gained from site-specific soil analysis, thermal inertia estimates were further converted from thermal inertia to daily volumetric soil water content (VSWC) with a horizonal resolution of 8.6 cm. A ground truthing dataset of measured VSWC values taken from a Time Domain Reflectometer was compared with model results, producing a reasonable correlation with an average coefficient of determination of (R2) = 0.79, an average root mean square error (RMSE) = 0.0408, and mean absolute error (MAE) = 0.0308. This study highlights a practical approach of estimating VSWC for irrigation purposes while providing superior spatio-temporal coverage over in situ methods. The authors envision that PrISMM can be implemented in water usage management by relating VSWC with weather forecasts and evapotranspiration rates to develop time-based spatially distributed irrigation management plans.
1. Introduction
Currently, half of the world’s population resides in urban areas, and by 2050, that number is expected to rise to two-thirds [1]. The strain on water supplies has increased due to rapid urbanization and population expansion [2,3]. In dry and semi-arid areas like north central Texas, where water is scarce and in high demand, these pressures are increased. Strategies for managing water conservation are crucial in these areas since irrigation is the primary usage of freshwater for both urban and rural consumers. The water use survey report by Texas Water Development Board (TWDB) showed that in 2015, industrial water systems and public irrigation contributed to almost 51% of water use in the state, that accounts to around 5.22 million megaliters (ML) [4]. Irrigated agriculture is the most dominant categorical user of water in Texas which is then followed by urban–municipal uses with landscape irrigation as its largest sub-user. Urban–municipal landscaping areas, particularly in golf courses, parks, athletic fields, residential, institutional, and commercial lawns, are covered with turfgrass. In 2010, it was approximated that golf courses covered 465 sq·km in Texas using 0.449 ML water annually. Low-end estimates for landscapes, incorporating these golf courses, add up to 46.6% of the total urban–municipal water use, reaching 12.6% of the total annual demand for all activities in Texas [5].
More efficient irrigation delivery systems can be the key to considerable water and cost savings considering the massive use of freshwater in urban landscaping. Methods like potential evapotranspiration-based irrigation scheduling and in situ soil moisture (SM) sensing for time-based irrigation control have been proposed to improve efficiency [6,7]. With traditional methods, the spatial variability of SM cannot be represented, since in situ sensors are fixed and limited in location. To tackle this obstacle, many remote sensing approaches to SM estimation have been proposed and applied in many studies [8,9,10,11,12]. Among them, thermal sensing offers a special edge because longwave radiation that is reflected as heat is made up of thermal energy that extends to different depths and several layers below the surface. Through the processes of solar radiation and heat transport, temperature disparities naturally occur in accordance with the physical characteristics of the soil strata. Knowing soil composition, vegetation type, and temporal meteorological circumstances, it is possible to derive reliable estimations of soil moisture (SM) content. This is because soil and water have significant variations in thermal characteristics.
Current limitations on the primary methods for estimating SM fall into three main categories: microwave, optical, and thermal. Microwave estimation challenges are characterized by low spatial resolutions and are often impaired by vegetation and surface roughness [12,13,14,15,16]. Optical SM estimation can be reflectance-based, which is disadvantaged by a lack of surface penetration, poor SM correlation with dense vegetation, an inability to penetrate clouds, and inapplicability at night; vegetation indices have the same challenges in addition to significant lag times between water stress and vegetation response [17,18]. Traditional thermal methods fall into the sub-categories of temperature index and thermal inertia methods. Temperature index methods may have poor SM correlation with dense vegetation, an inability to penetrate cloud cover, and are empirically based [19,20,21,22]. Thermal inertia methods, while physically based, have similar limitations in addition to a sensitivity to atmospheric conditions [11,23,24,25,26,27,28,29].
Using a thermal inertial approach to estimate SM has been applied in many theoretical research studies [26,27,30,31,32]. The approach solves the SM value from physical relationships linking surface soil water content to soil thermal properties [33]; however, there is little direct applicability to field studies. Coppola et al. [34] used visible (VIS), near infrared (NIR), and thermal infrared (TIR) sensors mounted on a SkyArrow 650 light aircraft to retrieve high-resolution soil moisture data. Minacapilli et al. [28] used an 11-band passive remote sensor attached to a low-flying airplane to derive thermal inertia estimates of 4 m resolution. Using similar sensors as Minacapilli et al. [28], Maltese et al. [29] achieved a standard error of ∼0.01 by using a three-temperature approach phase correction to thermal inertia (3 m resolution) for the top soil layer. The authors also showed that, for landscapes with light vegetation, SM can be directly related to surface temperature and ground heat flux. Using an airborne thermal camera to study relationships between SM, mechanical resistance, and thermal inertia (0.6 m resolution) for a vineyard with grass-covered soil and a standing grape canopy, Soliman et al. [35] showed significant correlations between SM, the mechanical resistance of the vegetation, and thermal inertia, despite its complex heating and cooling patterns.
The existing literature suggests a need for a practical and affordable method with a clear physical meaning for remotely estimating SM on a daily basis, despite cloud cover. Therefore, the authors aim to develop and evaluate a remote sensing platform that can be used for safe and rapid deployment for the collection of high-resolution SM estimates that non-experts can adopt for improving water management strategies at a local scale. Unmanned Aerial Vehicles (UAVs) can operate in most visual meteorological situations and obtain great data density and continuity when compared to low-flying aircraft. Over the past decade, Unmanned Aerial Vehicles (UAVs) have enabled the collection of extremely high-resolution remote sensing data, that would have been prohibitively expensive and time-consuming to obtain through conventional means. In addition to providing centimeter-level positioning and accuracy, technological advancements have led to equipment size and cost reductions in equipment like Global Positioning Systems (GPSs), Inertial Measurement Units (IMUs), Inertial Navigation Systems (INSs), and Real-Time Kinematics (RTK) [36].
Limited studies using UAVs for the estimation of SM have been conducted until now and many of them derive SM using the machine learning approach [37,38], while a soil physics-based thermal inertia approach for the estimation of SM has never been attempted with UAVs. In order to reduce overwatering and prevent underwatering by precision irrigation, the authors are therefore inspired to create a fresh approach to estimate high-resolution, contiguous VSWC which is validated with in situ measurements using remote sensing techniques. In Data and Methodology, the study area is introduced, followed by a description of the UAS platform and its sensors with the detailed procedure for data collection. The daily volumetric soil water content (VSWC) maps are assessed with the ground truthing data in Results and Discussion. The paper concludes with the key findings, limitations and weaknesses, and suggestions for future studies and practical usage.
2. Data and Methodology
2.1. Study Area
The study area is selected as a city (City of Arlington)-owned golf course (Meadowbrook Park), in north central Texas, United States of America. The golf course is bounded in the northwest at East Abram Street and Willis Avenue (32.735271°, −97.092930°), the northeast at the intersection of East Abram Street and Overhill Drive (32.735452°, −97.089384°), the southeast at the intersection of Meadowbrook Drive and Coke Drive (32.727548°, −97.090065°), and the southwest at the intersection of McKay Street and Coke Drive (32.729162°, −97.092533°). The project area is approximately 0.1 km2 and elongated green spaces and narrow fairways are dotted with low trees as land features (Figure 1). The geography of Meadowbrook is moderately sloping, and it borders Johnson Creek on its western side. The City of Arlington (City) owns and runs the golf course. The location was chosen because of the City’s ongoing dedication to water-conservation measures and because there has not been much land modification for several decades, leaving the soil profile mostly intact. Meadowbrook consumes approximately 45,000 to 57,000 cubic meters of water annually. In 2013, the city began the installation of a water well that taps the Paluxy aquifer to eliminate the reliance on Arlington municipal water for irrigation. A pumping station draws water from the earth and stores it in a holding pond, which is then used to irrigate the course with the help of 162 sprinkler heads.
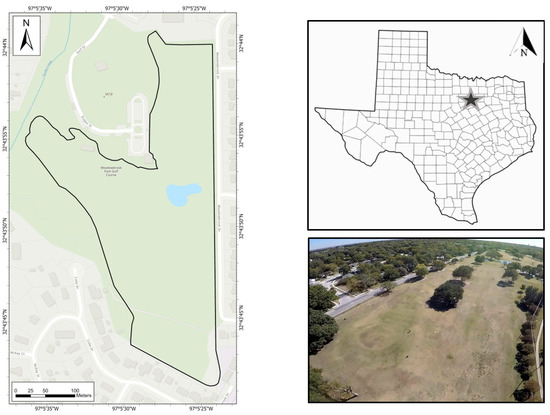
Figure 1.
Study area in north central Texas with location map and aerial of the golf course.
Figure 2 shows the soil analysis from SSURGO, followed by the soil classifications determined by field surveys. The study site was delineated into four soil groups, including (a) loamy sand, (b) sand, (c) sandy loam, and (d) silty clay loam. The majority soil type, loamy sand, is found all throughout the site. Sandy loam is located close to the golf course’s perimeter and is far less common. Throughout the course, elevated spots contained silty clay loam, which may hint that it was locally excavated and re-spread to match the course’s topography. Sand with a high porosity and infiltration rate is used to build putting greens and tee boxes. The model calibration based on spatial distribution was adjusted using these soil classifications.
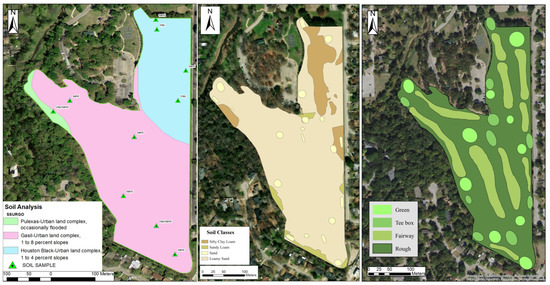
Figure 2.
Study area, delineation by soil analysis, soil class, and golf course topography.
2.2. UAV Platform
MavAir One, the custom-built UAV platform based on the DJI Matrice 600 Pro model (DJI, Shenzhen, China) that was used in this research, has eight rotors providing a maximum takeoff weight of eleven kilograms and can fit several multispectral sensors onboard (Figure 3). A Micasense RedEdgeTM camera (RedEdgeTM) (Micasense, Seattle, WA, USA) with an image array of 1280 × 960 pixels provides spectral data on five different narrow bands: blue (ρ1), green (ρ2), red (ρ3), red edge (ρ4), and NIR (ρ5) (Micasense 2015). For the development of vegetation indices like the NDVI, derived multi-band orthomosaics are employed. RedEdgeTM reflectance measurements are radiometrically calibrated utilizing two instruments, a down-welling light sensor (DLS) and a calibrated reflectance panel (CRP), with Version 1 manufactured by Micasense, to account for variations in ambient light that occur both during flight and on a daily basis. An image of the CRP is taken on each of the five RedEdgeTM bands, where the target’s albedo is known, both before and after each flight. Located at the top of the octocopter, the DLS is oriented upwards. Solar irradiance (W⋅m−2) is immediately captured for every camera-triggering event and is contained in each band’s metadata. Subsequently, in post-processing, both the CRP and DLS are employed to correct for variations in illuminations during flight (Micasense 2015), taking into account solar irradiance and sensor characteristics (gain/bias settings for every band).

Figure 3.
UAS platform seen collecting data over the study area (Arlington, TX, USA).
A FLIR Vue Pro R (FLIR) (Teledyne FLIR LLC, Wilsonville, OR, USA) derives the temperature for each pixel from the non-contact, calibrated, radiometric measurements. The thermal imager is an uncooled vanadium oxide microbolometer that detects longwave infrared energy in the 7.5–13.0 µm thermal spectral range with an image array of 640 × 512 pixels (FLIR 2016). A fixed emissivity is used to automatically calculate surface temperatures. Grayscale bands are used to record raw sensor data, which are then saved in an uncompressed 14-bit TIFF format.
There is a major research gap in procedures for validating and calibrating very-high-resolution (VHF) remotely sensed thermal imagery in the literature. The authors were thus motivated to devise a ground truthing procedure for use in this study. For both morning and afternoon flights, assuming a linear relationship between thermal brightness and land surface temperature, a thermal infrared gun was utilized to calibrate and confirm the aerial TIR images. A handheld Fluke ST2 IR gun (Fluke Cor., Everett, WA, USA) measured the surface temperature, with an accuracy of ±1%. At a one-meter distance, the gun was aimed at a 45° angle to the surface, leaving about a 0.25 m2 ground footprint. The surface temperatures of various objects were recorded with the IR gun for each flying day. These objects were selected from previously collected aerial TIR images from earlier flights not included in subsequent analyses. The authors identified large and conspicuous objects of various temperatures that were resolved by the thermal image array at mission altitude. Objects such as standing bodies of water, motor vehicles, boulders, pavement, gravel, concrete, and several patches of grass throughout the golf course were included in the daily collection for use in calibration and validation. With an average of twenty IR gun point measurements per dataset, an R2 of 0.94 was achieved with the aerial TIR imagery.
During pre-processing, the effects of vignetting, which is characteristic of thermal images, were eliminated. The program Pix4D Mapper Pro version 4.0 was used to import images and convert the raw thermal information to absolute temperature. Table 1 displays the specifications of the MavAir One sensor suite.

Table 1.
UAS sensor specifications.
2.3. Data Collection
Twice a day over six days (events) during the fall of 2017 (between 12 October and 30 October), remote sensing data were collected. Each dataset consists of data pairs from a morning flight and afternoon flight. Morning flights were initiated shortly before sunrise when surface heat fluxes were minimal. This acts as a starting point for optical and thermal imagery collected in the afternoon flight later the same day (within 1 h of solar noon). The meteorological data that guided the UAV flight and used to further solve the energy balance model were provided by the National Weather Service (NWS), collected at a local field office (Fort Worth). Table 2 summarizes the UAV flights and atmospheric conditions with the incoming shortwave radiation for each day provided in the Supplementary Materials. To eliminate variations in coverage and altitude, all flights had the same flight plan for every mission utilizing automated waypoint navigation. At 70 m above ground level (AGL), the mission’s forward speed was seven meters per second. There was an 80% vertical and horizontal photo overlap. The RedEdgeTM and FLIR’s ground sampling resolutions were 4.6 cm and 8.6 cm, respectively.

Table 2.
Meteorological conditions recorded at solar noon per collection date.
A detailed soil characterization of the study area is required by the thermal inertia approach used in this study. To determine the physical soil properties of the site like soil type, texture, mineral composition, bulk density, and thermal properties, a series of in situ and laboratory experiments was therefore conducted. The sand-cone method was used to determine the volume and bulk density of the soil samples (ASTM 2007 [39]). Textural analysis was also performed using the sieve and hydrometer method [40]. The texture of the surface soil horizon, as per USDA classification, is composed of loamy sand with a mass fraction of sand, silt, and clay of 0.85, 0.05, and 0.10 g·g−1, respectively. A KD2 Pro thermal (Water Sensor, Inc., Montreal, QC, Canada) conductivity probe equipped with a TR-1 thermal sensor determined the mean values for saturated and dry thermal conductivity for sandy loam and silty clay loam. An SH-1 dual-needle thermal diffusivity and specific heat sensor measured the mean value of specific heat for the corresponding soils. The soil parameters were then used to conduct the calculations in Step 3 of the PrISMM methodology as shown in Figure 4.
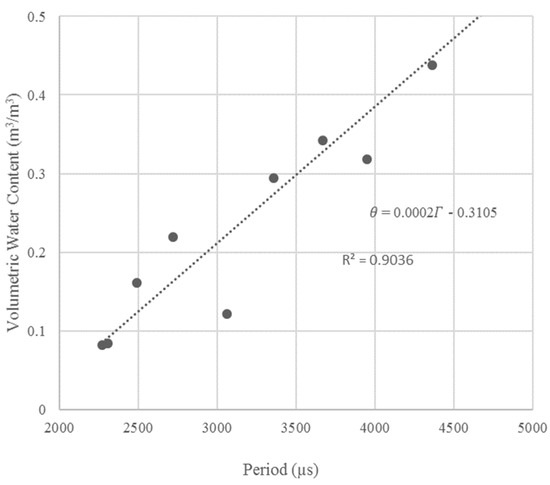
Figure 4.
TDR sensor’s period measurements (Γ) versus VSWC (θ).
The site-specific calibration was performed on the ground truthing instrument used in this study, a Time Domain Reflectometer (TDR). Calibration was then performed to develop a relation between the TDR sensor’s period measurements () and true VSWC () using a soil moisture meter (FieldScout model TDR 300, Spectrum Technologies, Inc., Plainfield, IL, USA) in gravimetric sampling as shown in the Figure 4. It should be noted that only ten core samples were extracted for analysis at the request of the property owner. The sample locations were systematically wetted to provide a full range of soil water contents. A soil column was extracted using a 25 cm long core sampler and inner sleeve diameter of 15 cm. The Create Random Points command was used in ArcMap version 10.7 to select core extraction locations within the study area boundaries. The calibrated results are further used for the validation of the UAS-remote sensing VSWC data by comparing the TDR-derived VSWC point measurements with the UAS-derived VSWC rasters as discussed in greater detail in Section 4.
Within 1 h of completing each afternoon flight, the TDR soil moisture meter carried out extensive ground truthing over the coverage area. The TDR contains a data logger and GPS which records geo-referenced period measurements in the logger’s storage file system. The authors used the shortest stainless steel guide rods of 7.6 cm with 3.3 cm spacing, fully inserted into the soil to best correspond with the rooting depth of the turfgrass. The difference in sample volumes should be noted between the TDR (6.5 × 10−5 m3) and core extraction (4.4 × 10−3 m3). This should be treated as a potential source of error due to the difference in volume and assumed differences in wetting depths. This depth most closely corresponds with the topmost layer reflected in the visible and near infrared spectrums (penetration depth ≈ 1 mm [41]) when compared to the longer rods. Implications regarding the accuracy with respect to the two different sampling depths between techniques are considered in Section 4. The ground truthing data were imported into ArcGIS as point features in six sets for PrISMM model validation.
The following section discusses the detailed steps in generating the spatially distributed VSWC using the thermal inertia approach with the UAV-collected data.
2.4. Model Description
Similar to the method proposed by Minacapilli et al. [28], thermal inertia is solved for twice using two distinct methods and datasets and then using a VSWC () retrieval process. Detailed equations are presented in Table 3 below.

Table 3.
Computational steps in PrISMM methodology.
Using remotely sensed imagery and surface energy balance modeling (Equations (1)–(13) detailed in Section 2.4.1), the first set of thermal inertia values are stored in GIS (Geographic Information System) raster format in ArcGIS. We refer to the remotely sensed (thus spatially distributed) estimation of thermal inertia as Prs.
For the second solution, thermal inertia is provided by solving Equations (14)–(18) (detailed in Section 2.4.2) for incremental values of using real soil physical parameters obtained from soil samples. We refer to this thermal inertia parameter as P. The incremental values of —as the independent variables in the solution of P—are stored in matrix format by soil group.
Finally, the spatially distributed map of is gained by matching thermal inertia between the raster and matrix (Prs and P, respectively). The corresponding values are retrieved from the matrix for every raster pixel of Prs. It should be noted that this process is often referred to as thermal inertia retrieval. We herein refer to the remotely sensed estimations of VSWC as to distinguish from VSWC measured with a TDR soil moisture sensor (). Figure 5 describes the general workflow of the PrISMM methodology. The following sections explain the details of each parameter.
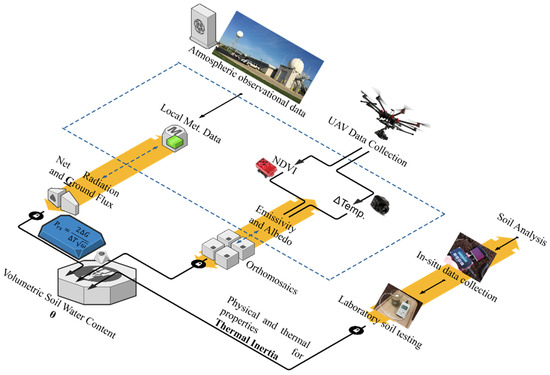
Figure 5.
Precision Irrigation Soil Moisture Mapper (PrISMM) workflow.
2.4.1. Remote Sensing Method and Surface Energy Balance Modeling
As proposed by Idso et al. [44] and Menenti [45], remote sensing methods can be used to derive thermal inertia estimates from surface heat flux and surface temperature variation using the following relationship:
where (K) is the difference between the minimum and maximum daily surface temperature, ω (rad s−1) is the angular velocity of the Earth’s rotation assuming a 24 h period (i.e., 2π/86,400 s), and ∆G (W·m−2) is the amplitude of the sinusoidally varying ground heat flux during this period.
The early morning values of G are approximately 0 W·m−2 and can be neglected, so ΔG is equivalent to the magnitude of G at solar noon. There are many empirical equations available for the estimation of G. Several equations were tried in this study [46,47,48,49] with the best results obtained from Santanello and Friedl [50], based on diurnal patterns from SHAW simulations:
where t (s) is the time of data capture relative to solar noon. A (-) represents the maximum value of G/Rn while B (s) is used to adjust the diurnal phase amplitude of G/Rn, defined as by Hoffmann et al., respectively [51]:
For simplicity, the calculation of net radiation was based on the methods used by Minacapilli et al. [28] which proved to yield good results. Summing both incoming and outgoing short (solar)- and long (thermal)-wave radiation at the surface gives the full equation for Rn [52]:
where incoming shortwave radiation is denoted by (W·m−2), combined soil and vegetation albedo is denoted by , the surface emissivity is , absorbed incoming longwave radiation is denoted by (W·m−2), and outgoing longwave radiation is denoted by . Albedo can be approximated as follows [53]:
where absolute reflectance for narrow bands in the visible spectrum is denoted by and the weighting factors are denoted by determined from the following equation [45]:
where solar irradiance for each narrow band, determined at the time of flight, is indicated by . In both Equations (6) and (7), n refers to the number of narrow bands included in the analysis and correspond with sensors of the Micasense RedEdgeTM camera, 1 = blue, 2 = green, 3 = red, 4 = red edge, and 5 = near infrared. Even though the calculated albedo does not represent the entire shortwave spectrum, for the turfgrass, calculated albedo values were found to be reasonable (0.26–0.28), which closely approximates the grass albedo values (0.24–0.26) reported by Campbell and Norman [54].
The above section solves the Prs by the remote sensing methods from Equations (1)–(7) as Step 1, and Step 2 is used to solve the surface energy balance modeling for Equation (5). The National Weather Service (NWS) of Fort Worth provided the values, with the weather station located approximately 22 km from the golf course. and are estimated as follows:
where atmospheric emissivity ε assumes an exponential atmospheric profile for temperature, pressure, and humidity; (5.67 × 10−8 W·m−2·K−4) is the Stefan–Boltzmann constant; and the near-surface air temperature is (K). and can be calculated by Brutsaert [55] and Bastiaanssen et al. [46], respectively:
where (°C) is the temperature at dew point and the actual vapor pressure (mb) is given by Chow et al. [56]:
The Normalized Difference Vegetation Index (NDVI) is given as the difference of reflectance values between the NIR and red bands, divided by the summation of NIR and red:
where a digital number (DN) between 0 and 255 represents reflectance.
Finally, by solving equations from (1) through (13), the remotely sensed (thus spatially distributed) estimation of thermal inertia as Prs is generated.
2.4.2. Soil Parameters Analysis
Thermal inertia can be defined for the physical properties of soil by Carslaw and Jaeger [57]:
where the thermal inertia is denoted by P (J·m−2·K−1·s−1/2), λ (W·m−1·K−1) denotes the soil thermal conductivity, the actual soil bulk density (including water) is (kg·m−3), and C (J·kg−1·K−1) is the soil heat capacity expressed as by de Vries [58]:
where the dry bulk density of soil is (kg·m−3), (~998 kg·m−3) represents the density of water at room temperature, and the heat capacities of the solid and liquid phases are (975 J·kg−1·K−1) and (4184 J·kg−1·K−1), respectively. And (m3·m−3) is the volumetric soil water content.
Accurate predictions of λ for a wide range of soils are provided by Johansen [59] introducing the concept of a normalized thermal conductivity, referred to as the Kersten number (). The empirical model is given by the following:
where the thermal conductivities of saturated and air-dry soils are represented by and (W·m−1·K−1), respectively. The Kersten number is an empirical parameter which is a function of saturation, Sr. Lu et al. [60] found very good agreement between measured and estimated λ values using the following expression for :
where shape parameter δ = 1.33 and Sr denotes the ratio between the actual volumetric soil water content, , and the saturated soil water content, .
γ = 0.96 is soil-texture dependent parameter, and it is determined by the sand fraction () as given by Lu et al. [60]:
A summary of the VSWC computation sets and equations is given in Table 3.
3. Results
Soil Moisture Results
Spatially distributed raster datasets of land surface temperature change (ΔTs), normalized difference vegetation index (NDVI), albedo (grass and soil combined) (α), surface emissivity (εs), net radiation (Rn), ground heat flux (G), thermal inertia (Prs), and volumetric soil water content () are processed and attained for each flying day with resolutions of 8.6 cm (Figure 6) in ArcGIS. With the essential application potential to provide guidance in irrigation requirements, all non-soil/grass features such as vegetation over 10 cm in height, asphalt, concrete, water bodies, and drainage structures are removed by the user in GIS. This can be accomplished by tracing the unwanted features to create a shapefile polygon for raster clipping. This procedure, while labor-intensive, only needs to be performed once and not all raster files require clipping. Because the study was performed in mid-fall, even during solar noon, the solar elevation angle was just under 50 degrees, leading to persistent shadows throughout the modeling domain. The regions of turfgrass that were covered in these persistent shadows were displayed in the model as false wet zones, which were further removed in pre-processing to prevent systematic bias. In this way, averages for spatially distributed calculated parameters exclusively represent the intended feature—turfgrass, as shown in Table 4. For this study, approximately 20% of the total area was removed.
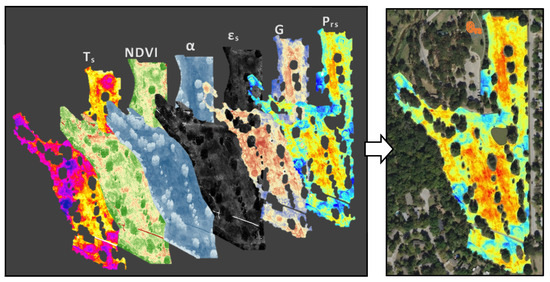
Figure 6.
Raster layers generated using PrISMM methodology for 25 October 2017: Ts, NDVI, α, εs, G, Prs, and (from left to right).

Table 4.
Average spatially distributed calculated parameters for six events.
As mentioned before, a calibrated TDR soil moisture meter was used for ground truthing. Immediately following every afternoon flight, georeferenced period measurements were taken; each dataset contained between 55 and 518 measurements, for a total of 1300 measurements. TDR measurements were evenly distributed during the initial survey on 12 October, with measurements collected with an average spacing of approximately ten meters. For the remaining five surveys, the authors collected TDR measurements in clusters of three to twelve over 3 × 3 m plots, as shown in Figure 7. The authors changed the sampling method so that stronger patterns of VSWC variability might emerge so that anomalies or outliers within these groupings could be easily identified. Uncertainties associated with the sampling method are discussed in Section 4. Summary statistics for the TDR readings by date are provided in Table 5. Due to irrigation sprinkler system flaws, there were over- and under-watered areas in each dataset. During the calibration of the PrISMM model, these areas were used as boundary conditions, representing saturated and dry conditions, respectively.
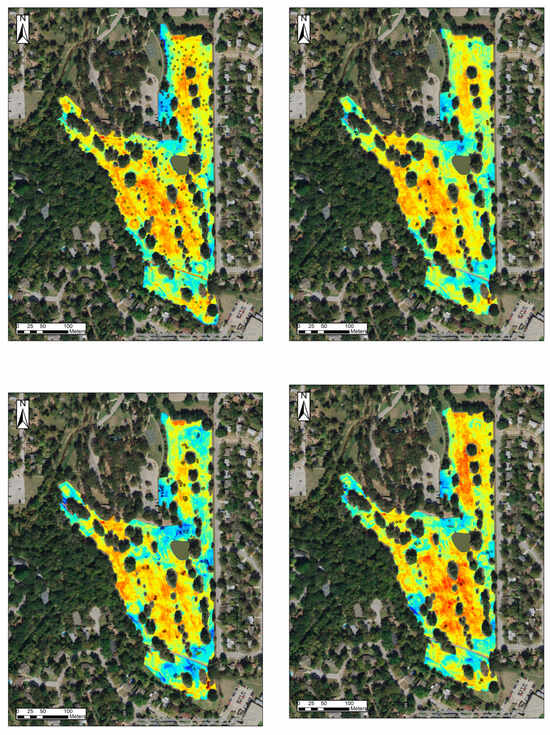
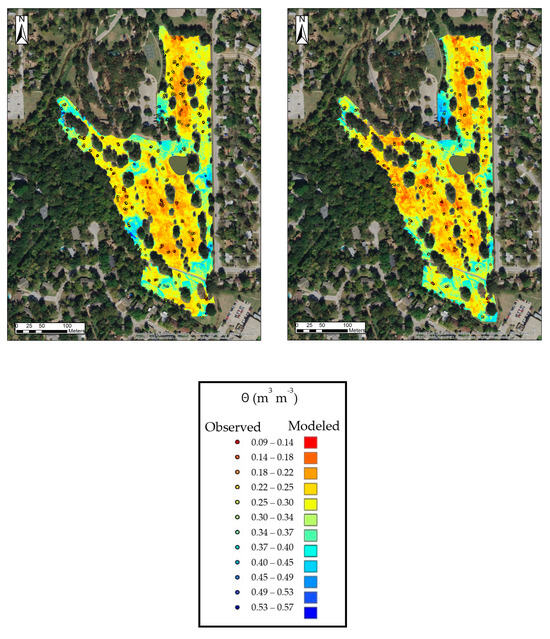
Figure 7.
PrISMM volumetric soil water content (VSWC) map results for six events (from top to right: 1st to 6th).

Table 5.
Summary statistics for TDR measurements for six events.
By using a radio-transfer model integrated into the FLIR, atmospheric corrections to the TIR imagery were completed before calculating ΔTs. The significant uniformity of surface temperatures across the golf course prevented the image processing software from mosaicking the early morning TIR images, as noted by Hoffman et al. [51]. Pix4D attempts to stitch overlapping photos together in the photogrammetry workflow by first finding prominent shared pixels (or key points) within an image batch. During triangulation, a line from the camera is projected by the software to key points using the camera’s location, orientation, and attributes like resolution and focal length. This process is repeated for each overlapping photo in the batch. The relative uniformity of the temperature field in the early morning makes it impractical to produce a sufficient key point density for TIR mosaicking, since key points are made up of temperature estimations as pixels.
As with Hoffman et al. [51], the starting surface temperature was determined from individual TIR photos taken at an elevation of 70 m using the mean temperature of the turfgrass. The afternoon TIR imagery was mosaicked normally using a standard 2D photogrammetry workflow. TIR orthomosaics were calibrated using temperature readings from the Fluke in ArcGIS. The final ΔTs orthomosaics were taken as the difference of the calibrated afternoon TIR orthomosaics and the average morning temperature of the turfgrass. During the period of study, ΔTs varied from 5.1 to 21.6 °C. Ponded water was linked to the smallest changes in temperature, while dry soils had the largest changes.
The golf course’s management regulations require mowing every three to six days, depending on the stage of the growth season which keeps the grass between 3 and 10 mm long. All turfgrass, such as the fairways, roughs, and tee boxes, was cut to the same length. It was expected that the distribution and density of grass would be uniform for the purposes of this investigation. Because of this supposition, mechanical resistance might be modeled in relation to the soil’s surface temperature by using a constant attenuation factor. The soil type was then assumed to be the primary driving factor for variations in thermal inertia.
PrISMM soil moisture maps are displayed against measured VSWC () in Figure 7 with wet zones in blue and dry zones in red. It can be concluded that the PrISMM keeps a constant overall performance over the study area, considering the similar meteorological conditions for each flying day. The system is also able to pick up the relative wet/dry spots over the study area, such as the wet spots adjacent to the parking lot and the pond. This is useful in identifying deficiencies in the irrigation system to prevent further under- and over-watering.
The degree of the relationship between the observed and modeled values of VSWC including the coefficient of correlation (r), coefficient of determination (R2), root mean square error (RMSE), and mean absolute error (MAE) was assessed using goodness-of-fit statistics, which are described in Table 6. In terms of R2 values, the best and the worst performances occurred on 18 October (0.83) and 30 October (0.67), respectively. Across the six events, the average R2 value was 0.79. On 29 October and 18 October, the minimum (0.04) and maximum (0.06) RMSE values were determined, respectively. Across the six dates, the average RMSE was 0.04. On 29 October and 18 October, the minimum (0.03) and maximum (0.04) MAE values were found, respectively. For each of the six dates, the mean MAE was 0.03. Figure 8 shows a scatter plot of the modeled versus observed VSWC values for all six dates combined. All things considered, the findings show that the PrISMM model can estimate VSWC fairly well. The performance of the model is covered in more detail below, along with suggestions for practical use.

Table 6.
Statistical summary of PrISMM model performance for six events.
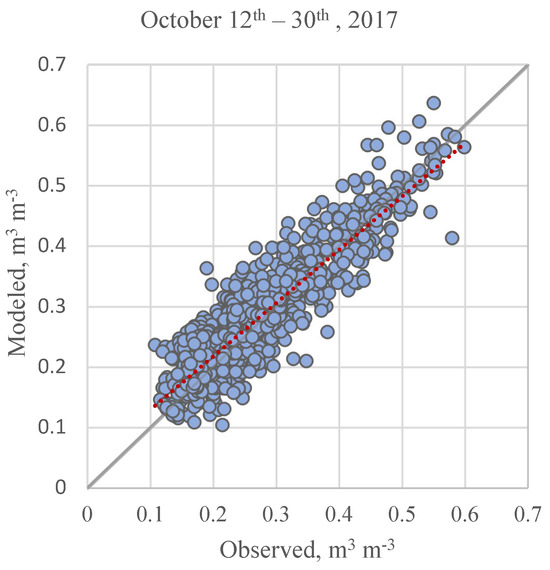
Figure 8.
Modeled versus observed VSWC for combined events (Red line indicates the linear regression line).
4. Discussion
First, the scatter plots of the modeled versus observed VSWC values for each flying day are provided in Figure 9. By changing the sampling method for TDR measurements after the first dataset, the coefficient of the results of modeled versus observed VSWC increased in the subsequent datasets. The scatters are evenly distributed along the one-to-one regression line. Table 7 shows the goodness-of-fit statistics separated by soil groups for comparison. The highest R2 value was associated with sandy loam (0.86), followed by silty clay loam (0.81), followed by loamy sand (0.77), and finally sand (0.57). An increased variability in SM distribution as observed during TDR measurements could be the reason behind the markedly reduced performance in predicting VSWC for sand. It should be noted that site-specific soil analysis was not conducted on putting greens which accounts for most of the sandy regions. The soil analysis is destructive in that it requires core extraction, and out of respect for the golf course, the putting greens were not disturbed. The literature was used instead to estimate the physical and thermal properties of the sand associated with the putting greens. The authors, however, hypothesize that the accuracy of VSWC estimation could be increased by performing this soil analysis for the sands.
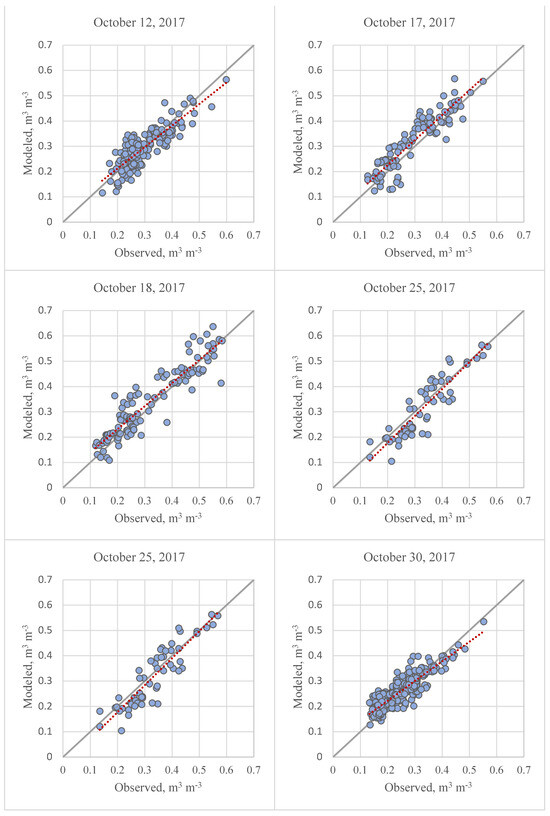
Figure 9.
Observed versus modeled VSWC values for six events (Red line indicates the linear regression line).

Table 7.
Statistics of observed versus modeled VSWC based on soil type.
An additional concern for the ground truthing dataset with implications on accuracy stems from differences in sampling depths. For TDR measurements, the sampling depth corresponds to 7.6 cm when fully inserted into the soil. It has been demonstrated that the penetration depth for visible and near-infrared (VIS-NIR) light rarely exceeds 1 mm from the surface as it relates to most soils [41]. Input parameters for the PrISMM model affected by VIS-NIR include surface emissivity, ground heat flux, and NDVI. Future studies will consider how these parameters are affected by various sampling depths. However, thermal infrared radiation, detected using remote sensors similar to those used in this study, have demonstrated a strong correlation between remotely sensed surface soil temperatures (SSTs) and subsoil temperatures of 10 cm depth or more [61]. The authors are thus motivated to relate the moisture content of soils at varying depths to evaluate the effectiveness of PrISMM under various conditions.
Figure 10 displays the scatter plots of the modeled versus observed VSWC for all six events (the residuals’ histograms are included in the Supplementary Materials). There are no discernible systematic errors in the combined residuals, which are centered around the origin. When the observed VSWC (m3 m−3) value is more than 0.17, the residuals for the combined events follow a normal distribution; when the observed value is less than 0.17, the PrISMM model tends to overstate the VSWC value.
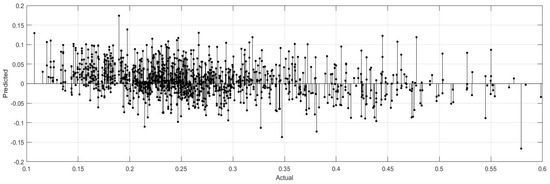
Figure 10.
Residuals of observed versus modeled VSWC (m3 m−3).
Computation of the ground heat flux (G) is a key component to the PrISMM methodology. Many empirical relations have been formulated for estimating G for vegetated surfaces. A review of the literature suggests that user experience is critical for selecting an equation. During this study, the authors compare the PrISMM results using various equations including the SHAW equation based on diurnal patterns [62], those proposed by Bastiaanssen [46], Allen et al. [47], Cuenca et al. [48], Singh et al. [49], and Santanello and Friedl [50]. Reference daily G values were published by the Texas AgriLife Extension Service for the study region. By comparing these, the authors found that the PrISMM model produced the most reasonable estimates when using SHAW while the other methods were found with discrepancies by an order of magnitude or greater without any calibration. These differing results are not well understood and will be the subject of future study.
Previous research has shown that calculating thermal inertia for low moisture concentrations can be challenging [28,37,38]. For example, Minacapilli et al. [28] showed more scattered VSWC projections at or below 0.15 m3 m−3. This phenomenon is explained by the link implied in Equations (6)–(9) between the volumetric soil water content (θ) and soil thermal conductivity (λ). Lower moisture contents cause water molecules to bond to soil particles more firmly; while θ rises in the dry domain, the water film on the particle surface keeps growing, and λ rises much less rapidly [37]. The water creates a bridge between soil particles as the film thickens, and λ starts to rise quickly. In this study, the values of moisture content around 0.17–0.50 m3 m−3 are considered to have a linear λ(θ) relationship. The λ(θ) relationship, however, tends to resemble an s-curve as the soil gets closer to saturation because it depends more and more on the air that is replaced by water, where θ increases along with a corresponding rise in thermal conductivity.
Table 8 presents a summary of residual statistics, including the total number of TDR measurements for every collection event. Since both negative and non-negative values of the mean residuals are around zero, there are no significant cases of model bias revealed by the analysis. The lowest residual (m3 m−3) for all six events was −0.17, while the largest residual (m3 m−3) was 0.17, both of which happened on October 18. The initial theory suggested that the overall range of residuals would grow as the sample population of TDR measurements rose, which would imply that on 29 October there should have been a maximum spread of residuals from the 529 measurements. The dataset presented here indicates, at least, no direct correlation between the number of TDR measurements and model errors, implying that to validate the PrISMM model for the research region, about 100 TDR measurements scattered or clustered (3 × 3 m) prove to be sufficient. This is roughly equal to 1000 TDR measurements per square kilometer. It should be noted, however, that the gridded sampling procedure on 12 October produced the second-lowest R2 of 0.686. Future work will be devoted to optimizing sample patterns and systematic bias to address this uncertainty.

Table 8.
Summary statistics for model residuals.
The average (%) values for each irrigation management zone are depicted in bar charts by date in Figure 11. For zones in which irrigation is conducted within the previous 12 h, the bars are marked as either irrigated by sprinkler head or watered by hand (hand watering is usually performed during daylight hours by visually identifying dry areas). Due to the high infiltration rates of the greens and tee boxes (sand + organics) and higher standards for playability and vigor, the frequency of irrigation is significantly higher than for other surfaces. One observable response includes the slight decrease in VWC (%) of the greens from 29–30 October where VWC remains relatively constant for the other surfaces. This is likely due to the lower intensity and precision (hence less water) of hand watering. For all four playing surfaces, VWC increases from 17–18 October which is consistent with the irrigation pattern. Tee boxes are slightly higher in moisture content than greens despite the green’s more frequent irrigation. This is likely due to the smaller sand fraction in the tee boxes which is by design. The roughs are also slightly higher in VWC than the fairways of which both surfaces are irrigated simultaneously. This is likely due to the tendency of ponded water to collect in the roughs. It is expected that as the number of consecutive data sets increase, and with more irrigation variability, stronger correlations between the response of to rainfall and irrigation patterns will emerge. The difficulty in determining (m3 m−3) for extreme values is not thought to be relevant in terms of the PrISMM model operability. The criteria for ≤ 0.17 and > 0.50 are properly detected by the PrISMM model, which classifies these pixels as too dry or wet, respectively. Decisions about precision irrigation management are made for the domain within 20% of field capacity, or between 0.17 and 0.54 (m3 m−3), as will be covered subsequently.
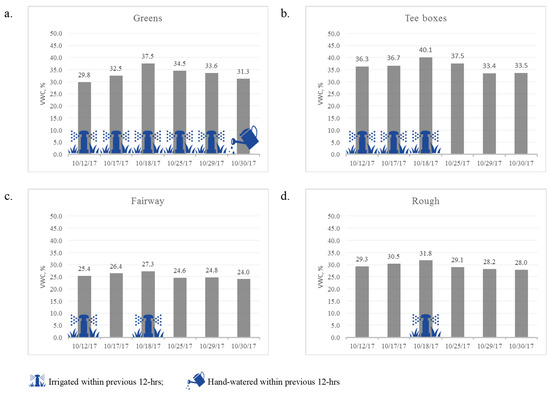
Figure 11.
Mean volumetric water content (m3 m−3) by grass type and date: (a) greens, (b) tee boxes, (c) fairway, and (d) rough.
The irrigation of turfgrass is designed to maintain the plant-available water level, which is the difference between field capacity and permanent wilting point, at or above 50% for the longest duration with minimal loss from runoff or drainage. Irrigation management zones’ delineation by soil texture and rooting depth must be performed for the PrISMM model to drive a time-based irrigation system. The percentage of plant-available water (in/ft) at the time of the afternoon flight is determined from VSWC maps. The plant-available water is related to daily evapotranspiration rates by introducing the carrying capacity of the soil, defined as the time required by the turf to deplete 50% of the plant-available water, using the following equation [63]:
As previously stated, thresholds for ≤ 0.17 are reliably detected by the PrISMM model. After these pixels are marked, irrigation is planned for a complete time interval every day until the values drop to within 20% of the field’s capacity. Similar to this, the PrISMM model flags pixels for ≥ 0.50, which are not scheduled for irrigation again until the values return back within 20% of the field capacity. Values are converted to percent plant-accessible water in accordance with the matching soil texture for values that are less than 20% of the field capacity. The carrying capacity is calculated using the rooting depth (6.6 cm) and the daily evapotranspiration rate (TexasET Network). The irrigation is then scheduled so that it replenishes plant-accessible water to a level that will ensure that until the next irrigation and/or rainfall event, it does not go below 50%.
The implications of PrISMM model results in relation to water usage management suggest that the development of spatially distributed irrigation systems based on VSWC will help guard against chronic under- and over-watering using threshold values as decision variables. PrISMM, while shown to be reasonably accurate within the context of this study, may lack the precision required by some water users. Because PrISMM is limited to, at best, daily estimates of VWSC, the application of the system requires accurate weather forecasting and evapotranspiration rates for planning purposes. In parts of the world where high-quality weather products are limited, daily VWSC estimates may be insufficient for precision irrigation.
The PrISMM model prevails over traditional methods for irrigation water management decisions due to the following reasons:
- It gives timely, accurate, spatially distributed soil moisture estimates;
- It has a wide range of operating conditions with easy and flexible use;
- It is a model with a clear physics meaning;
- By detecting chronic wet and dry spots, it can identify deficiencies in the irrigation system;
- It provides continuous, high-resolution estimates which are simply impossible to obtain using in situ sensors;
- The density and continuity of data are superior, which covers around 0.1 km2 in 30 min compared to 1.5 h for 100 TDR measurements in the same area;
- It allows for the operation of independent sprinkler heads with specified durations and frequencies.
Among numerous advantages, one of the advantages of PrISMM is that it exploits empirical relationships with clear physical meanings as opposed to machine learning. Ge et al. [64] utilized UAV-based hyperspectral imagery for farmland using an extreme gradient boost algorithm which provided an R2 of 0.921. Bertalan et al. [65] applied four machine learning regression algorithms to UAV-based thermal and multispectral imagery to estimate soil water content (SWC). They found that a Random Forest algorithm provided the best results (R2 = 0.97) and that multispectral imagery was a better predictor variable than thermal imagery. Their models indicated that the relationship between SWC and thermal data was best described by an exponential decay function which proved difficult to ingest into the machine learning algorithms with linear variables. They point out that SWC is dependent on physical soil properties such as thermal conductivity, diffusivity, and heat capacity. Araya et al. [66] have demonstrated the utility of machine learning models for soil moisture estimation using UAVs and high-resolution multispectral imagery that does not require a detailed soil or subsoil survey and analysis. The authors utilized predictor variables including rainfall, potential evapotranspiration, multispectral reflectance, and terrain variables derived from a digital elevation model (DEM) to estimate volumetric water content (VWC) for a small grassland catchment in Grassland Reserve, California. Using five different machine learning algorithms, they determined that a boosted regression tree algorithm provided the best accuracy with a MAE of 3.8% of VWC. They indicate that the four most important variables are precipitation, reflectance in the red band, evapotranspiration, and topographic position index (TPI). Here, the findings are similar to PrISMM in that their negative TPI values correspond to topographic low points such as valleys, which tend to have higher VWC, and positive TPI values correspond to topographic high points such as ridges, which have lower VWC.
One weakness of the model is that heterogeneity or thermographic anomalies in subsoils cannot be accounted for using the current methodology. As others have shown, thermal energy in the form of longwave radiation can extend to different depths and several layers below the surface. Temperature disparities can occur in accordance with the physical characteristics of the vertical strata. For instance, groundwater or underlying rock may increase thermal inertia beyond what may be indicated through site-specific soil analysis of the uppermost layer, introducing errors into thermal inertia retrieval. One of the potential solutions is to couple it with the surface–subsurface interaction to properly address certain levels of uncertainties [67]. The performance of PrISMM in cloudy or overcast conditions is currently unknown. Since the surface energy balance model assumes a cloudless sky, the model performance will be evaluated in a wider range of atmospheric conditions by installing a four-component net radiometer on site. The performance of the PrISMM model can also be affected during winter when days are shorter, and the effective root zone is deeper. Though it is not critical to irrigation management, further investigation on the impact of frost and the dormancy of grass in the system is required.
Another uncertainty on how PrISMM may perform in other urban environments stems from the vegetation cover. In this study, frequent mowing schedules limited the length of the grass to 3–10 mm. The authors theorized that the presence of grass creates mechanical resistance in relation to the soil’s surface temperature and may be modeled using a constant attenuation factor. For this study, the authors assumed that soil type was the primary driving factor for variations in thermal inertia; however, as the height or density of vegetation increases, the temperature of the vegetation will dominate and the established relationship between thermal inertia and SM will collapse. Additionally, while a good correlation (R2 < 0.90) is found between period measurements and VSWC, the authors acknowledge the need of including more samples to achieve a better statistical significance. A future study is needed to involve additional soil samples, different vegetation types, and growing seasons.
The primary limitation of the PrISMM method is the need for high-resolution and rigorously calibrated remote sensing data. In this study, a UAS platform was used to collect the data which requires basic operator skills, special certifications, and an observance of airspace restrictions. The remote sensing datasets are typically quite large and can be computationally expensive. Pre-processing for initial calibration and validation is intensive and may be a significant barrier for many urban water users. Additionally, soil heterogeneity may render the PrISMM methodology impractical if there are many soil classes present in the study area. The initial setup requires detailed site-specific analysis in order to achieve high accuracy estimates for the entire modeling domain. PrISMM is therefore better suited for irrigation applications with bare or sparsely vegetated soil and homogenous layers, such as croplands.
Aside from the challenges encountered, there are a few ways to further improve the capacities of PrISMM. First, ground heat flux, which is implicit in the solution of thermal inertia, could be more directly measured by introducing a shortwave infrared (SWIR) sensor to the UAV platform as opposed to methods introduced by Santanello and Friedl [50]. Incorporating weather forecasts and evapotranspiration rates into PrISMM could also enhance the applicability of the method by providing time-varied spatially distributed irrigation maps. For the present, still, all findings indicate that the spatial and temporal resolutions offered by PrISMM are better when compared to in situ methods and may be implemented to precisely irrigate urban landscapes, thus providing the potential to save millions of gallons of water annually if properly implemented.
5. Conclusions
To determine how much watering an urban landscape needs, this study demonstrated the use of the PrISMM method to assess soil moisture. In order to show the feasibility of considering precision irrigation based on spatially distributed VSWC estimates as the main decision variable, PrISMM was put into practice at the Arlington, Texas, golf course. The primary elements of a thermal inertia approach to the calculation of VSWC are site-specific soil analysis, surface energy balance modeling, and high-resolution, multispectral imaging obtained with a UAV. The estimations of thermal inertia are obtained by relating ground heat flux to the fluctuations in daily temperature that are recorded using a thermal camera. Then, using estimations of thermal inertia that were remotely detected and based on actual soil physical properties at an 8.6 cm resolution, VSWC retrieval was performed. TDR soil moisture sensor ground truthing data were used to measure PrISMM’s accuracy. Good model accuracy is indicated by the average best-of-fit statistics of the observed versus modeled VSWC (r: 0.89, R2: 0.79, RMSE: 0.04, and MAE: 0.03). The PrISMM technique, when coupled with weather forecasts and daily evapotranspiration rates, has been shown to have a great deal of promise for supporting irrigation decision-making. It involves predicting the frequency and length of irrigation requirements depending on the various management zones of the vegetation species.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs16101660/s1.
Author Contributions
Conceptualization, K.J.W. and Z.N.F.; Methodology, K.J.W., D.L. and Z.N.F.; Validation, K.J.W. and D.L.; Formal analysis, K.J.W. and D.L.; Investigation, K.J.W. and D.L.; Resources, Z.N.F.; Writing—original draft, K.J.W. and D.L.; Writing—review and editing, D.L. and Z.N.F.; Visualization, K.J.W. and D.L.; Supervision, D.L. and Z.N.F.; Project administration, D.L. and Z.N.F.; Funding acquisition, Z.N.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science Foundation, grant numbers 1832065 and 1940163.
Data Availability Statement
The data supporting the findings of this study are not publicly available due to the extensive storage requirements needed to host the data. However, subsets of the data or specific analyses may be made available upon reasonable request to the corresponding author.
Acknowledgments
We would especially like to thank Meadowbrook Park Golf Course staff and the City of Arlington for their participation in this study. We would also like to thank Xinbao Yu at the University of Texas at Arlington for his suggestions and input for the study. A special appreciation goes out to the West Gulf River Forecast Center and the National Weather Service for providing the meteorological data used in this study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- United Nations. Department of Economic and Social Affairs, Population Division; United Nations: New York, NY, USA, 2014. [Google Scholar]
- McDonald, R.I.; Green, P.; Balk, D.; Fekete, B.M.; Revenga, C.; Todd, M.; Montgomery, M. Urban Growth, Climate Change, and Freshwater Availability. Proc. Natl. Acad. Sci. USA 2011, 108, 6312–6317. [Google Scholar] [CrossRef] [PubMed]
- He, C.; Liu, Z.; Wu, J.; Pan, X.; Fang, Z.; Li, J.; Bryan, B.A. Future Global Urban Water Scarcity and Potential Solutions. Nat. Commun. 2021, 12, 4667. [Google Scholar] [CrossRef] [PubMed]
- Texas Water Development Board. 2017 Sate Water Plan, Water for Texas. Available online: https://www.twdb.texas.gov/waterplanning/swp/2017/doc/SWP17-Water-for-Texas.pdf (accessed on 1 April 2024).
- Cabrera, R.I.; Wagner, K.L.; Wherley, B. An Evaluation of Urban Landscape Water Use in Texas. Tex. Water J. 2013, 4, 14–27. [Google Scholar] [CrossRef]
- Bogena, H.; Huisman, J.; Oberdörster, C.; Vereecken, H. Evaluation of a Low-Cost Soil Water Content Sensor for Wireless Network Applications. J. Hydrol. 2007, 344, 32–42. [Google Scholar] [CrossRef]
- Hilaire, R.; Arnold, M.A.; Wilkerson, D.C.; Devitt, D.A.; Hurd, B.H.; Lesikar, B.J.; Lohr, V.I.; Martin, C.A.; McDonald, G.V.; Morris, R.L.; et al. Efficient Water Use in Residential Urban Landscapes. HortScience 2008, 43, 2081–2092. [Google Scholar] [CrossRef]
- Santi, E.; Paloscia, S.; Pettinato, S.; Notarnicola, C.; Pasolli, L.; Pistocchi, A. Comparison between SAR Soil Moisture Estimates and Hydrological Model Simulations over the Scrivia Test Site. Remote Sens. 2013, 5, 4961–4976. [Google Scholar] [CrossRef]
- Cho, E.; Choi, M.; Wagner, W. An Assessment of Remotely-Sensed Surface and Root Zone Soil Moisture through Active and Passive Sensors in Northeast Asia. Remote Sens. Environ. 2015, 160, 166–179. [Google Scholar] [CrossRef]
- Jonard, F.; Weiher Sadeghi, L.; Schwank, M.; Jadoon, K.Z.; Vereecken, H.; Lambot, S. Estimation of Hydraulic Properties of a Sandy Soil Using Ground-Based Active and Passive Microwave Remote Sensing. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3095–3109. [Google Scholar] [CrossRef]
- Fabre, S.; Briottet, X.; Lesaignoux, A. Estimation of Soil Moisture Content from the Spectral Reflectance of Bare Soils in the 0.4–2.5 Μm Domain. Sensors 2015, 15, 3262–3281. [Google Scholar] [CrossRef] [PubMed]
- Vereecken, H.; Huisman, J.; Pachepsky, Y.; Montzka, C.; Kruk, J.V.D.; Bogena, H.; Weihermüller, L.; Herbst, M.; Martinez, G.; Vanderborght, J. On the Spatio-Temporal Dynamics of Soil Moisture at the Field Scale. J. Hydrol. 2014, 516, 76–96. [Google Scholar] [CrossRef]
- Choudhury, B.J.; Schmugge, T.J.; Chang, A.; Newton, R.W. Effect of Surface Roughness on the Microwave Emission from Soils. J. Geophys. Res. Ocean. 1979, 84, 5699–5706. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing: Active and Passive, from Theory to Applications: 3; Artech House: Norwood, MA, USA, 1986; ISBN 978-0-89006-192-3. [Google Scholar]
- Schmugge, T.; Jackson, T. Passive Microwave Remote Sensing of Soil Moisture. In The Land Surface Processes in Hydrology; Sorooshian, S., Gupta, H.V., Rodda, J.C., Eds.; Springer: Berlin/Heidelberg, Germany, 1997; pp. 239–262. [Google Scholar]
- Al-Yaari, A.; Wigneron, J.-P.; Ducharne, A.; Kerr, Y.H.; Wagner, W.; De Lannoy, G.; Reichle, R.; Al Bitar, A.; Dorigo, W.; Richaume, P.; et al. Global-Scale Comparison of Passive (SMOS) and Active (ASCAT) Satellite Based Microwave Soil Moisture Retrievals with Soil Moisture Simulations (MERRA-Land). Remote Sens. Environ. 2014, 152, 614–626. [Google Scholar] [CrossRef]
- Muller, E.; Décamps, H. Modeling Soil Moisture–Reflectance. Remote Sens. Environ. 2001, 76, 173–180. [Google Scholar] [CrossRef]
- Zeng, Y.; Feng, Z.; Xiang, N. Assessment of Soil Moisture Using Landsat ETM+ Temperature/Vegetation Index in Semiarid Environment. In Proceedings of the IGARSS 2004. In Proceedings of the 2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; Volume 6, pp. 4306–4309. [Google Scholar]
- Idso, S.B.; Jackson, R.D.; Pinter, P.J.; Reginato, R.J.; Hatfield, J.L. Normalizing the Stress-Degree-Day Parameter for Environmental Variability. Agric. Meteorol. 1981, 24, 45–55. [Google Scholar] [CrossRef]
- Kogan, F.N. Droughts of the Late 1980s in the United States as Derived from NOAA Polar-Orbiting Satellite Data. Bull. Am. Meteorol. Soc. 1995, 76, 655–668. [Google Scholar] [CrossRef]
- Alderfasi, A.; Nielsen, D.C. Use of Crop Water Stress Index for Monitoring Water Status and Scheduling Irrigation in Wheat. Agric. Water Manag. 2001, 47, 69–75. [Google Scholar] [CrossRef]
- McVicar, T.R.; Van Niel, T.G.; Lingtao, L.; King, E.A.; Donohue, R.J. Deriving Moisture Availability from Time Series Remote Sensing for Ecohydrological Applications: Development of a Prototype near Real-Time Operational System. CSIRO Land Water Sci. Rep. 2007, 37, 144. [Google Scholar]
- Pohn, H.A.; Offield, T.W.; Watson, K. Thermal Inertia Mapping from Satellite—Discrimination of Geologic Units in Oman. J. Res. U.S. Geol. Surv. 1974, 2, 147–158. [Google Scholar]
- Kahle, A.B.; Gillespie, A.R.; Goetz, A.F.H. Thermal Inertia Imaging: A New Geologic Mapping Tool. Geophys. Res. Lett. 1976, 3, 26–28. [Google Scholar] [CrossRef]
- Price, J.C. Thermal Inertia Mapping: A New View of the Earth. J. Geophys. Res. 1977, 82, 2582–2590. [Google Scholar] [CrossRef]
- Carlson, T.N.; Dodd, J.K.; Benjamin, S.G.; Cooper, J.N. Satellite Estimation of the Surface Energy Balance, Moisture Availability and Thermal Inertia. J. Appl. Meteorol. Climatol. 1981, 20, 67–87. [Google Scholar] [CrossRef]
- Watson, K. Regional Thermal-inertia Mapping from an Experimental Satellite. Geophysics 1982, 47, 1681–1687. [Google Scholar] [CrossRef]
- Minacapilli, M.; Iovino, M.; Blanda, F. High Resolution Remote Estimation of Soil Surface Water Content by a Thermal Inertia Approach. J. Hydrol. 2009, 379, 229–238. [Google Scholar] [CrossRef]
- Maltese, A.; Bates, P.D.; Capodici, F.; Cannarozzo, M.; Ciraolo, G.; La Loggia, G. Critical Analysis of Thermal Inertia Approaches for Surface Soil Water Content Retrieval. Hydrol. Sci. J. 2013, 58, 1144–1161. [Google Scholar] [CrossRef]
- Carlson, T.N. Regional-scale Estimates of Surface Moisture Availability and Thermal Inertia Using Remote Thermal Measurements. Remote Sens. Rev. 1986, 1, 197–247. [Google Scholar] [CrossRef]
- Kahle, A.B. A Simple Thermal Model of the Earths Surface for Geologic Mapping by Remote Sensing. J. Geophys. Res. 1977, 82, 1673–1680. [Google Scholar] [CrossRef]
- Ghilain, N.; Arboleda, A.; Batelaan, O.; Ardö, J.; Trigo, I.; Barrios, J.-M.; Gellens-Meulenberghs, F. A New Retrieval Algorithm for Soil Moisture Index from Thermal Infrared Sensor On-Board Geostationary Satellites over Europe and Africa and Its Validation. Remote Sens. 2019, 11, 1968. [Google Scholar] [CrossRef]
- van de Griend, A.A.; Owe, M. On the Relationship between Thermal Emissivity and the Normalized Difference Vegetation Index for Natural Surfaces. Int. J. Remote Sens. 1993, 14, 1119–1131. [Google Scholar] [CrossRef]
- Coppola, A.; Basile, A.; Menenti, M.; Buonannno, M.; Colin, J.; Mascellis, R.D.; Esposito, M.; Lazzaro, U.; Magliulo, V.; Manna, P. Spatial distribution and structure of remotely sensed surface water content estimated by a thermal inertia approach. In Remote Sensing for Environmental Monitoring and Change Detection; Owe, M., Neale, C., Eds.; IAHS Publisher: Wallingford, UK, 2007; Volume 316, pp. 1–12. [Google Scholar]
- Soliman, A.; Heck, R.; Brenning, A.; Brown, R.; Miller, S. Remote Sensing of Soil Moisture in Vineyards Using Airborne and Ground-Based Thermal Inertia Data. Remote Sens. 2013, 5, 3729–3748. [Google Scholar] [CrossRef]
- Agüera-Vega, F.; Carvajal-Ramírez, F.; Martínez-Carricondo, P. Accuracy of Digital Surface Models and Orthophotos Derived from Unmanned Aerial Vehicle Photogrammetry. J. Surv. Eng. 2017, 143, 04016025. [Google Scholar] [CrossRef]
- Seo, M.-G.; Shin, H.-S.; Tsourdos, A. Soil Moisture Retrieval from Airborne Multispectral and Infrared Images Using Convolutional Neural Network. IFAC-PapersOnLine 2020, 53, 15852–15857. [Google Scholar] [CrossRef]
- Zhuang, R.; Manfreda, S.; Zeng, Y.; Su, Z.; Ben Dor, E.; Petropoulos, G.P. Soil Moisture Monitoring Using Unmanned Aerial System. In Unmanned Aerial Systems for Monitoring Soil, Vegetation, and Riverine Environments; Elsevier: Amsterdam, The Netherlands, 2023; pp. 179–200. ISBN 978-0-323-85283-8. [Google Scholar]
- ASTM DD1556/D1556M-15; Standard Test Method for Density and Unit Weight of Soil in Place by Sand-Cone Method. ASTM International: West Conshohocken, PA, USA, 2007. Available online: https://webstore.ansi.org/standards/astm/astmd1556d1556m15 (accessed on 6 January 2018).
- Klute, A.; Gee, G.W.; Bauder, J.W. Particle-Size Analysis. In SSSA Book Series: Methods of Soil Analysis: Part 1—Physical and Mineralogical Methods; ASA: Madison, WI, USA, 1986; pp. 383–411. [Google Scholar]
- Norouzi, S.; Sadeghi, M.; Liaghat, A.; Tuller, M.; Jones, S.B.; Ebrahimian, H. Information Depth of NIR/SWIR Soil Reflectance Spectroscopy. Remote Sens. Environ. 2021, 256, 112315. [Google Scholar] [CrossRef]
- ASTM D2419-14; Standard Test Method for Sand Equivalent Value of Soils and Fine Aggregate. ASTM International: West Conshohocken, PA, USA, 2014. Available online: https://webstore.ansi.org/standards/astm/astmd241914 (accessed on 6 January 2018).
- ASTM D2216-19; Standard Test Methods for Laboratory Determination of Water (Moisture) Content of Soil and Rock by Mass. ASTM International: West Conshohocken, PA, USA, 2019. Available online: https://www.astm.org/d2216-19.html (accessed on 6 January 2024).
- Idso, S.B.; Jackson, R.D.; Reginato, R.J. Compensating for Environmental Variability in the Thermal Inertia Approach to Remote Sensing of Soil Moisture. J. Appl. Meteorol. 1976, 15, 811–817. [Google Scholar] [CrossRef]
- Menenti, M. Physical Aspects and Determination of Evaporation in Deserts Applying Remote Sensing Techniques; EV: Wageningen, The Netherlands, 1984. [Google Scholar]
- Bastiaanssen, W. SEBAL-Based Sensible and Latent Heat Fluxes in the Irrigated Gediz Basin, Turkey. J. Hydrol. 2000, 229, 87–100. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)—Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Cuenca, R.; Ciotti, S.; Hagimoto, Y. Application of Landsat to Evaluate Effects of Irrigation Forbearance. Remote Sens. 2013, 5, 3776–3802. [Google Scholar] [CrossRef]
- Singh, R.K.; Irmak, A.; Irmak, S.; Martin, D.L. Application of SEBAL Model for Mapping Evapotranspiration and Estimating Surface Energy Fluxes in South-Central Nebraska. J. Irrig. Drain. Eng. 2008, 134, 273–285. [Google Scholar] [CrossRef]
- Santanello, J.A.; Friedl, M.A. Diurnal Covariation in Soil Heat Flux and Net Radiation. J. Appl. Meteorol. 2003, 42, 851–862. [Google Scholar] [CrossRef]
- Hoffmann, H.; Nieto, H.; Jensen, R.; Guzinski, R.; Zarco-Tejada, P.; Friborg, T. Estimating Evaporation with Thermal UAV Data and Two-Source Energy Balance Models. Hydrol. Earth Syst. Sci. 2016, 20, 697–713. [Google Scholar] [CrossRef]
- Melesse, A.M. Spatiotemporal Dynamics of Land Surface Parameters in the Red River of the North Basin. Phys. Chem. Earth Parts A/B/C 2004, 29, 795–810. [Google Scholar] [CrossRef]
- Liang, S. Quantitative Remote Sensing of Land Surfaces; Wiley-Interscience: Hoboken, NJ, USA, 2004. [Google Scholar]
- Campbell, G.S.; Norman, J.M. Introduction to Environmental Biophysics; Springer: New York, NY, USA, 1998. [Google Scholar]
- Brutsaert, W. On a Derivable Formula for Long-wave Radiation from Clear Skies. Water Resour. Res. 1975, 11, 742–744. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill Professional: New York, NY, USA, 2013. [Google Scholar]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Oxford University Press: London, UK, 1959. [Google Scholar]
- Vries, D.A. Thermal Properties of Soils. In Physics of Plant Environment; US Army Corps of Engineers, Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1963; pp. 210–235. [Google Scholar]
- Johansen, O. Thermal Conductivity of Soils. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 1975. [Google Scholar]
- Lu, S.; Ren, T.; Gong, Y.; Horton, R. An Improved Model for Predicting Soil Thermal Conductivity from Water Content at Room Temperature. Soil Sci. Soc. Am. J. 2007, 71, 8. [Google Scholar] [CrossRef]
- Frodella, W.; Lazzeri, G.; Moretti, S.; Keizer, J.; Verheijen, F.G.A. Applying Infrared Thermography to Soil Surface Temperature Monitoring: Case Study of a High-Resolution 48 h Survey in a Vineyard (Anadia, Portugal). Sensors 2020, 20, 2444. [Google Scholar] [CrossRef]
- Flerchinger, G.N.; Kustas, W.P.; Weltz, M.A. Simulating Surface Energy Fluxes and Radiometric Surface Temperatures for Two Arid Vegetation Communities Using the SHAW Model. J. Appl. Meteorol. Climatol. 1998, 37, 449–460. [Google Scholar] [CrossRef]
- Murphy, J.A. Best Management Practices for Irrigating Golf Course Turf. In Best Management Practices for Irrigating Golf Course Turf, Rutgers Cooperative Extension; Rutgers NJAES Cooperative Extension: New Brunswick, NJ, USA, 2002. [Google Scholar]
- Ge, X.; Ding, J.; Jin, X.; Wang, J.; Chen, X.; Li, X.; Liu, J.; Xie, B. Estimating Agricultural Soil Moisture Content through UAV-Based Hyperspectral Images in the Arid Region. Remote Sens. 2021, 13, 1562. [Google Scholar] [CrossRef]
- Bertalan, L.; Holb, I.; Pataki, A.; Négyesi, G.; Szabó, G.; Kupásné Szalóki, A.; Szabó, S. UAV-Based Multispectral and Thermal Cameras to Predict Soil Water Content—A Machine Learning Approach. Comput. Electron. Agric. 2022, 200, 107262. [Google Scholar] [CrossRef]
- Araya, S.N.; Fryjoff-Hung, A.; Anderson, A.; Viers, J.H.; Ghezzehei, T.A. Advances in Soil Moisture Retrieval from Multispectral Remote Sensing Using Unoccupied Aircraft Systems and Machine Learning Techniques. Hydrol. Earth Syst. Sci. 2021, 25, 2739–2758. [Google Scholar] [CrossRef]
- Lv, M.; Yang, Z.; Xu, Z.; Dan, L.; Lv, M.; Zheng, H. A Soil Moisture-Dependent Model to Simulate Water Table Depth and Proportions of Surface and Subsurface Runoff and Its Validation at the Basin Scale. JGR Atmos. 2021, 126, 2020JD033661. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).