Abstract
Accurate and timely precipitation forecasts are critical in modern society, influencing both economic activity and daily life. While deep learning methods leveraging remotely sensed radar data have become prevalent for precipitation nowcasting, longer-term forecasting remains challenging. This is due to accumulated errors in deep learning models and insufficient information about precipitation systems over longer time horizons. To address these challenges, we introduce the Short-Term Precipitation Forecast Network (STPF-Net), a recurrent neural network designed for longer-term precipitation prediction. STPF-Net uses a multi-tier structure with varying temporal resolutions to mitigate the accumulated errors during longer forecasts. Additionally, its transformer-based module incorporates larger spatial contexts, providing more complete information about precipitation systems. We evaluated STPF-Net on radar data from southeastern China, training separate models for 6 and 12 h forecasts. Quantitative results demonstrate STPF-Net achieved superior accuracy and lower errors compared to benchmark deep learning and numerical weather prediction models. Visualized case studies indicate reasonably coherent 6 h predictions from STPF-Net versus other methods. For 12 h forecasts, while STPF-Net outperformed other models, it still struggled with storm initiation over longer forecasting time.
1. Introduction
Weather forecasting influences many aspects of modern society, including energy, agriculture, and transportation. Precipitation forecasting is a crucial element of weather forecasting that directly affects daily life and activities. Moreover, extreme rainfall events over short time periods have led to severe damage and threats to people’s lives recently, such as the extreme rainstorm occurred in Zhengzhou, China on 21 July 2021. Therefore, more accurate short-term precipitation forecasts are urgently needed.
Recent improvements in short-term precipitation forecasting can be largely attributed to advances in numerical weather prediction (NWP). As a physics-based approach, NWP treats weather forecasting as an initial value problem in mathematical physics. Given boundary conditions, the future state of the weather can be predicted by integrating governing partial differential equations from initial values [1]. The NWP methods have been the primary approach for making weather forecasts over the past few decades. Progress in NWP has resulted from three key advancements: improved representation of physical processes, advances in computing technology, and assimilation of meteorological observations from global sensor networks [1]. Representation of physical processes has been enhanced through better parameterization schemes that model phenomena like deep convection and cloud microphysics [2,3]. Furthermore, extensive observations from sources like ground stations, satellites, and radar have been collected and incorporated into NWP models via data assimilation, providing accurate initial conditions [4,5,6]. These advances have continuously improved the ability of NWP models to predict future atmospheric states, such as precipitation, on both global and regional scales [7,8]. However, significant challenges remain for NWP in providing sufficiently accurate and timely precipitation forecasts, especially for short-term precipitation forecasting and nowcasting. For instance, understanding of atmospheric physics such as moist physics remains incomplete, limiting the representation of these processes even in state-of-the-art NWP models. Additionally, increasing model resolution to represent localized extreme rainfall comes at a steep computational cost. High-resolution precipitation forecasting thus requires substantially more time and computing resources compared to coarser resolution forecasting. Some extrapolation methods utilizing radar observations have thus been developed, including Tracking Radar Echo by Correlation (TREC) [9,10], Storm Cell Identification and Tracking [11,12], and Optical Flow methods [13]. Nonetheless, these conventional methods struggle to extract nonlinear relationships from large datasets.
In contrast to physics-based methods, data-driven deep learning approaches have recently achieved great success. Increased computing power, large datasets, and rapid progress in neural network architectures have enabled deep learning in many areas, including precipitation forecasting [14,15,16,17]. Deep learning holds the potential to address shortcomings of traditional NWP. Whereas NWP relies on mathematical representations of physical processes, deep learning methods can directly learn the complex spatiotemporal relationships between input and output variables from data alone. In this case, the precipitation forecasting task can be formulated as a spatiotemporal prediction problem, where both the model inputs and outputs are spatiotemporal sequences. A variety of deep learning approaches have been proposed for precipitation forecasting, including those based on convolutional neural networks (CNN) [18], recurrent neural networks (RNN) [19], generative adversarial networks (GAN) [20], and transformer-based networks [21].
CNN-based models have been used to predict precipitation. Agrawal et al. [22] introduced a CNN-based U-Net model to predict precipitation for 1 h. The U-Net model treated forecasting as an image-to-image problem and outperformed the optical flow and numerical weather prediction models. Ayzel et al. [23] proposed RainNet, a U-Net model for 5 min precipitation forecasting from radar images and recursively predicted 1 h precipitation. Han et al. [24] transformed the precipitation nowcasting into a classification task, using CNNs for 30 min forecasts. Another U-Net architecture is proposed to predict convective precipitation, showing comparative results with RNN models [25]. Trebing et al. [26] developed SmaAt-UNet, a convolutional neural network based on U-Net architecture equipped with attention modules. SmaAt-UNet can effectively reduce the model parameter size while maintaining a comparable performance in predicting precipitation in 30 min. Kaparakis et al. [27] integrated precipitation and wind speed variables into a 3D UNet core-model for 3 h precipitation nowcasting over western Europe. Chen et al. [28] proposed a 3D CNN to predict daily total precipitation for next several days. Overall, previous studies demonstrate the strong potential of CNN-based deep learning for precipitation forecasting across different spatial and temporal scales.
Besides CNN, a common approach for precipitation forecast is RNN, designed to model evolving states over time. Shi et al. [29] proposed the Convolutional LSTM (ConvLSTM) to predict 90 min radar echoes by combining convolutional operations to retain spatial structure with LSTM recurrent connections to capture temporal relations. To further model evolving atmospheric motions, Shi et al. [30] introduced Trajectory GRU (TrajGRU) which outperformed CNNs and ConvGRUs for 2 h precipitation nowcasting. Wang et al. [31] presented a predictive recurrent neural network (PredRNN), adding a new Spatiotemporal LSTM (ST-LSTM) unit that can zigzag across the RNN layers and within a single RNN layer. Furthermore, Wang et al. [32] proposed PredRNN++, adding Gradient Highway Unit to capture the short-term and long-term dependencies. Results show that PredRNN++ outperforms PredRNN and other baseline models. To tackle the problem of long-term prediction, Jing et al. [33] used a hierarchical prediction strategy and a recurrent coarse-to-fine mechanism in HPRNN to limit error accumulation. Google [34] proposed MetNet to predict precipitation up to 8 h, making a probabilistic precipitation forecast with the output of categorical distribution. MetNet-2 [35] was further developed to extend the forecast time to 12 h. Results show that both models outperform the High-Resolution Rapid Refresh (HRRR) system. To effectively handle complex and high non-stationary evolution of radar echoes, FDNet [36] is proposed to model the motion flow and shape change in two parallel cross pathways and achieves state-of-the-art prediction results for up to 2 h. RN-Net [37] provided high-resolution 2 h forecasts over large areas from multiple data sources. Klocek et al. [38] predicted future radar reflectivity at lead times up to 6 h with an encoder-forecaster convolutional LSTM model. A large input context is divided into several small input neighborhoods, which are treated as features in the model. Experiments show that the proposed model outperforms HRRR and optical flow. Liu et al. [39] proposed a spatiotemporal prediction model, named ST-LSTM-SA, based on the self-attentive mechanism for the next 3 h predictions. Zhang et al. [40] developed Pixel-CRN for convective storm nowcasting, which input 3-D radar and model reanalysis data and provided 30 min and 60 min predictions. Overall, RNN architectures have shown strong value for spatiotemporal precipitation forecasting.
In addition to CNNs and RNNs, other deep learning approaches have emerged for precipitation forecasting. Ravuri et al. [41] used a deep generative model to produce probabilistic 90 min nowcasts, outperforming baselines. A conditional generative adversarial network was also proposed to predict rainfall from 10 min to 4 h with weather radar observations, showing the capacity for short-term prediction [42]. Zhang et al. [43] incorporated physical schemes into NowcastNet, achieving state-of-the-art extreme precipitation nowcasting. Transformer-based architectures have gained traction, with Rainformer providing efficient precipitation nowcasting using a simple yet efficient Transformer-based architecture [44]. Gao et al. [45] designed the Earthformer using a space-time Transformer for earth system forecasting. Hu et al. [46] combined Swin Transformers and variational RNNs for 5-day ensemble forecasts. These studies demonstrate the potential of generative and Transformer models to complement CNNs and RNNs for skillful precipitation prediction across timescales from minutes to days ahead.
However, prior research focused only on precipitation nowcasting. Given the complexity of atmospheric processes that can last hours, there is a need to provide more accurate longer-term forecasts beyond nowcasting. Recurrent neural networks have been mainly applied for precipitation forecasting, as they can learn temporal dynamics with each prediction based on previous ones. However, this introduces accumulation of errors, especially for longer forecast horizons. Furthermore, longer-time predictions also require incorporating larger spatial contexts as weather systems move rapidly. Thus, extracting local information cannot provide sufficient spatial context for longer-time prediction. Overcoming these problems is thus key to enabling more accurate longer-term precipitation prediction with deep learning methods. Therefore, this paper proposes STPF-Net, a novel recurrent neural network model for short-term precipitation forecasting. STPF-Net incorporates multi-tier temporal modeling, with both high and low temporal resolution modules, to capture dynamics across different timescales and limit accumulated prediction errors. For temporal modeling, RNNs are utilized to learn temporal dependencies at each timescale. Furthermore, the Swin Transformer extracts global spatial context to provide sufficient information for short-term prediction. We evaluate STPF-Net on a 2-year radar dataset and surface rainfall observations from southeast China. Results demonstrate that STPF-Net outperforms deep learning and traditional NWP models on short-term precipitation forecasting.
The rest of this article is organized as follows: Section 2 introduces the data used in this study. Section 3 describes the proposed model architecture in detail. Section 4 describes the experiments implementation and evaluation configurations. The results and discussion are presented in Section 5. Finally, Section 6 summarizes the main conclusions of this work.
2. Data
The radar reflectivity data used to evaluate the proposed model covers the southeastern region of China, spanning latitudes from 21°N to 36°N and longitudes from 112°E to 125.9°E. The radar reflectivity data are preprocessed with quality control to remove non-precipitation echoes, including isolating noise echo filtering and anomalous propagation (AP) echo suppression. The former uses bi-directional searching and echo feature filtering. The latter adopts the fuzzy logic method [47]. The preprocessed radar reflectivity data are converted into resolution images with a 6 min temporal interval. The dataset is collected from the summer monsoon season of China (May to September) in 2017 and 2018. This paper aims to predict rainfall intensity through the Z-R relationship between radar reflectivity and rainfall intensity [48], which is defined as
Z is the radar reflectivity intensity in dBZ, and R is the rainfall intensity in mm/h. There are two constants, a = 58.53 and b = 1.56 [29,30,37]. Figure 1 shows the radar reflectivity and corresponding rainfall intensity at 2300 UTC on 1 July 2017 as an example. In addition, the precipitation data of regional automatic weather stations (AWSs) in eastern China with a time interval of 10 min is used as the ground truth to compare the proposed model with traditional NWP.
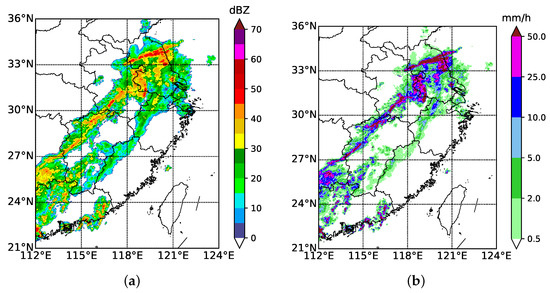
Figure 1.
(a) Radar reflectivity (dBZ) and corresponding (b) rainfall intensity (mm/h) at 2300 UTC 1 July 2017.
3. Model
To address the challenging problem of short-term precipitation forecasting, we propose STPF-Net, a recurrent encoder-forecaster network architecture (Figure 2). The input of our model is a sequence of T images, , which is transformed from radar reflectivity. The output is a predicted sequence of K future images, . The multi-tier forecasting approach interacts information between different tiers, providing higher temporal resolution predictions while limiting error accumulation. To capture evolutionary dynamics, temporal relations are encoded via a recurrent neural network (RNN) within each tier. Spatial patterns are extracted through a Swin Transformer, as in [49,50], to leverage sufficient spatial context for longer-term predictions. Details of the architecture are provided in the following subsections.
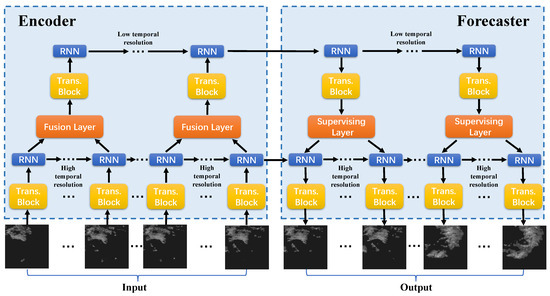
Figure 2.
The overall architecture of STPF-Net. The input sequence are first encoded hierarchically by the Encoder part and the predicted sequence are generated by the Forecaster part.
3.1. Temporal Encoding and Prediction with Multi-Tier Structure
To limit error accumulation over longer forecasts and capture temporal dynamics, STPF-Net adopts a multi-tier architecture. The prediction is decomposed into high- and low-resolution. The input sequence with high-resolution from original radar data are first encoded in the lower level of STPF-Net. High-resolution data contains more continuous temporal information. However, for a fixed forecast time, higher resolution leads to more forecast steps. For example, 60 steps are needed for 6 h prediction with a 6 min resolution, while 6 steps are needed for 6 h prediction with 1 h resolution. Since RNN is utilized to model temporal dynamics, in which prediction is based on the previous one. The errors will continue to accumulate as the forecast step increases. To mitigate this, the low-resolution tier operates at a coarser time step (e.g., 1 h resolution), resulting in fewer steps and less cumulative error. The multi-tier structure balances temporal modeling with different resolution and limit overall error growth.
The Encoder hierarchically encodes temporal information at different timescales. First, high-resolution temporal data are encoded in the lower tier RNN. The Fusion Layer then fuses these high-resolution outputs, concatenating them in the temporal dimension and using a CNN to extract relevant information. This condensed high-resolution encoding is passed as input to the top tier, encoding lower resolution temporal patterns. In the Forecaster part, the propagating order is reversed compared with the Encoder. The low-resolution states from the top tier are predicted first. A Supervising Layer conveys information between tiers, using a convolution operation to model temporal patterns from the low-resolution RNN outputs. After that, the outputs are separated and fed as the inputs to the lower tier. In this way, the top tier provides coarse-scale temporal context, while the bottom tier generates high-resolution forecasts guided by the top tier supervision. The hierarchical multi-tier interaction enables the model to leverage multi-scale temporal patterns and limits accumulated errors for long-range forecasting.
3.2. Spatiotemporal Information Extraction
The spatiotemporal information is extracted hierarchically to represent features at different levels. As mentioned, a weather system could last several hours and move fast in its life cycle. Traditional CNNs focus on local receptive fields, while modeling longer-range weather system evolution requires broader spatial context. Though convolution is usually coupled with pooling in a hierarchical structure (like pyramids), it is still challenging to model global and long-range information. Inspired by Liu [49,50], a Swin Transformer-based module is introduced in STPF-Net to capture both local patterns and global, long-range spatial dependencies within the radar data with great computational efficiency. The architecture of the Swin Transformer module is illustrated in Figure 3. Assuming that the resolution of the feature map is , in which C is the channel, H is the height, and W is the width. First, The Swin Transformer takes radar images as input and divides them into embedded patches, as (patch size of 3), with each patch token representing a local region. A linear embedding layer is applied to this feature to project it to an arbitrary dimension (denoted as ). Then, Swin Transformer block is applied to these patch tokens, as is shown in Figure 3a. Self-attention is first applied within local windows to model relationships between nearby patches (W-MSA). The shifted window-based multi-head self-attention module (SW-MSA) is built to connect patterns across the whole spatial area. This combination of local and global modeling allows efficient learning of both fine-grained and long-range spatial dependencies.
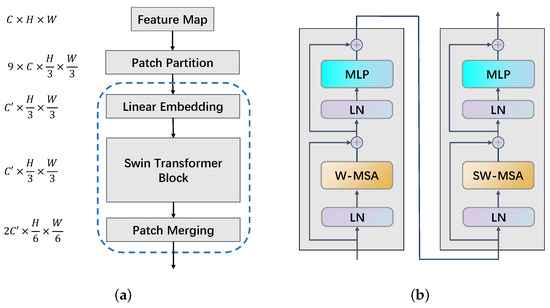
Figure 3.
(a) The architecture of Swin Transformer, which is composed of Patch Partion, Linear Embedding, Swin Transformer blocks and Patch Merging; (b) The details in Swin Transformer Blocks with multi-head self attention (W-MSA) and shifted window multi-head self attention (SW-MSA).
Additionally, a LayerNorm (LN) layer is applied before the MSA and MLP module, and a residual connection is applied after each module. The Swin Transformer employs a hierarchical structure, with Patch Merging layers that produce higher-level representations by reducing the number of tokens. The extracted feature maps are then taken as the input of the RNN, which leverage these localized and global spatial patterns to model multi-tier temporal dynamics. Overall, the Swin Transformer provides an effective backbone for extracting hierarchical spatiotemporal features from radar data. By combining multi-scale spatial modeling with multi-tier temporal encoding, STPF-Net can capture comprehensive environmental context and evolutionary dynamics for accurate precipitation nowcasting.
4. Experiments
4.1. Implementation Details
The proposed STPF-Net comprises two hierarchical layers to model high and low temporal resolution dynamics, respectively. The Swin Transformer encoder blocks have feature dimensions of 72 and 144, using a patch size of 3. The number of attention heads is set to 3 and 12, with a window size of 5 and shift of 2 patches between windows. Patch merging layers in the encoder downsample spatial resolution by while doubling the feature dimension. Conversely, patch expanding layers are used in the forecaster to upsample resolution and halve the feature depth. For the recurrent components, ConvLSTM modules with 144 and 288 channels are utilized to model the temporal dynamics at each layer.
To comprehensively evaluate the performance of STPF-Net, several widely used deep learning models are selected as baselines: U-Net, ConvLSTM, PredRNN, TrajGRU and HPRNN. The main architectures of the deep learning baselines follow the same as Ayzel et al. [23], Shi et al. [30], Wang et al. [31], and Jing et al. [33]. In addition, the Global/Regional Assimilation Prediction System (GRAPES) is included as a traditional NWP benchmark. GRAPES is the numerical prediction system developed by the China Meteorological Administration (CMA), which is one of the primary reference sources for province-level daily weather forecasting [51,52,53]. GRAPES provides high-resolution (0.03°, 1 h) mesoscale forecasts up to 36 h [54]. More details about the GRAPES can be found in [55].
The models are evaluated on a 2-year Doppler radar dataset covering 25.632°N to 35.624°N, 112°E to 123.115°E cropped into images. The dataset consists of 293 days in total. The training, validation, and testing dataset are drawn from non-overlapping time ranges, with 187 days for training, 46 days for validation and 60 days for testing. The input sequence length is the past 2 h, with 12 min time steps. All the deep learning models are implemented in Pytorch [56] and trained end-to-end using the Adam optimizer with an initial learning rate of . To improve prediction quality and handle imbalanced rainfall levels, the loss function combines weighted mean square error (MSE), mean absolute error (MAE), and structural similarity index (SSIM) terms (Equation (2) [57]). The weights for different rainfall levels are set to 1, 2, 3, 5, and 10, corresponding to 0.5, 2, 5, 10, and 30 mm/h from the rainfall intensity of ground truth. The constants a, b, and c are set to 1, 1, and 2500, respectively.
where x is the ground truth, y is the predicted value, is the average of x, is the average of y, is the variance of x, is the variance of y, and is the covariance of x and y. and are constants.
4.2. Evaluation Metrics
To evaluate the short-term quantitative precipitation forecasting performance of STPF-Net, several complementary metrics are utilized: Critical Success Index (CSI) score, probability of detection (POD), false-alarm ratio (FAR), bias score (BIAS), Heidke Skill Score (HSS), balanced MSE (BMSE), and balanced MAE (BMAE). These metrics are computed on the predicted and observed rainfall rates, providing a comprehensive assessment of different aspects of forecast quality. The detailed definitions are as follows.
where is the ground truth and is the prediction. TP is the true positive, TN is the true negative, FP is the false positive, and FN is the false negative. N is the total number of frames, W and H are the width and height of images, and is the weight for different rainfall levels. The weights are set to 1, 2, 3, 5, and 10, corresponding to the rainfall intensity of 0.5, 2, 5, 10, and 30 mm/h.
5. Results and Discussion
To comprehensively evaluate the performance of STPF-Net, precipitation forecasting experiments are conducted for 6 and 12 h prediction horizons. The 6 h forecasts demonstrate the short-term precipitation prediction skill. Considering that some precipitation events can last for a longer time, the 12 h forecasts further investigate generalization ability for longer-range prediction of sustained precipitation events. We compare STPF-Net to both deep learning and traditional NWP (GRAPES) models.
5.1. Performance on 6 h Predictions
The 6 h precipitation forecast skill of STPF-Net is first assessed against the baseline models. Table 1 shows the average 6 h prediction results across multiple quantitative metrics. Higher CSI, HSS and POD indicate greater forecast skill. Lower FAR, BMSE and BMAE represent better performance. BIAS indicates the deviation of predictions, in which the predictions are stronger than the ground truth when BIAS > 1, and predictions are weaker when BIAS < 1. CSI, HSS, POD, FAR and BIAS are averaged on 0.5, 1.0, 2.0 and 5.0 mm/h thresholds, showing the general performance of different rainfall intensities. In addition, all metrics are averaged on the whole forecasting sequence. For CSI, obviously U-Net exhibits the lowest score, indicating poorer skill of CNN-based model in predicting rainfall intensity over 6 h compared to the RNN-based models. In contrast, the proposed STPF-Net achieves the highest CSI, quantitative precipitation forecasting skill among all deep learning baselines for 6 h. Apart from STPF-Net, HPRNN yields a relatively higher CSI score than other baselines. Since HPRNN is also designed for long-range predictions, it proves the improvements on 6 h predictions than previous methods. The comparison between STPF-Net and HPRNN highlights the effectiveness of STPF-Net’s architecture for long-range prediction. HSS and POD results are similar to CSI scores. STPF-Net attains the highest scores and U-Net gets the lowest scores. For FAR and BIAS, it is found that STPF-Net obtains higher FAR as well as BIAS that is more than 1. It indicates that the proposed STPF-Net tends to predict stronger and wider coverage of precipitation, leading to more false alarms at the same time. In comparison, PredRNN obtains the lowest FAR and U-Net has the lowest BIAS that is less than 1, demonstrating PredRNN and U-Net usually predicts less and weaker precipitation. For BMSE and BMAE, the balanced errors reflect the forecast quality on both light and heavy rainfall. Among the deep learning-based models, STPF-Net also exhibits the lowest balanced errors. In summary, the proposed STPF-Net architecture demonstrates state-of-the-art quantitative precipitation forecasting performance at the 6 h timescale, outperforming all the deep learning baselines on most metrics. The results highlight the strengths of STPF-Net on short-term precipitation forecasting task.

Table 1.
The quantitative evaluation results of 6 h prediction.
To further analyze STPF-Net’s performance, we discuss the CSI and POD evolution over forecast time for different thresholds. Figure 4 compares CSI for all the deep learning-based models. Generally, CSI declines for all models as time increases, indicating forecast quality strongly depends on lead time, with errors accumulating over time. For CSI at 0.5 mm/h (Figure 4a, U-Net has the lowest scores throughout, evidencing the weakest prediction capability of CNN-based models. Other deep learning models have comparable 0.5 mm/h performance. At 1 mm/h (Figure 4b), differences of CSI become more pronounced. Initially, STPF-Net, HPRNN and PredRNN achieve relatively higher scores, while U-Net remains lowest. As forecast time increases, other baselines begin to degrade, while STPF-Net maintains higher CSI, aligning with superior quantitative results in Table 1. This trend continues at 2.0 mm/h (Figure 4c) and 5.0 mm/h (Figure 4d). The improvement of STPF-Net over other deep learning methods becomes more prominent at higher thresholds. Among other models, PredRNN performs better initially, but degrades over time, while HPRNN scores higher at longer leads, evidencing advantages for longer predictions. Figure 5 shows the POD changing curves along with different times at different thresholds. Generally, STPF-Net shows more significant improvements over other baselines than CSI. It is found that POD also declines as the threshold increases, indicating degraded skill for stronger precipitation across all models. For 0.5 mm/h, STPF-Net obtains the highest score over the whole forecasting period. For 1.0 and 0.5 mm/h, though other baselines outperform STPF-Net at the first several forecasting steps, the improvement of STPF-Net becomes obvious as time leads. This shows the performance of STPF-Net on longer-range forecasting. Similarly, U-Net almost gets the lowest POD for all thresholds. Overall, proposed STPF-Net outperforms deep learning baselines in predicting rainfall intensity for the next 6 h, especially at increased thresholds and lead times where its architecture provides benefits.
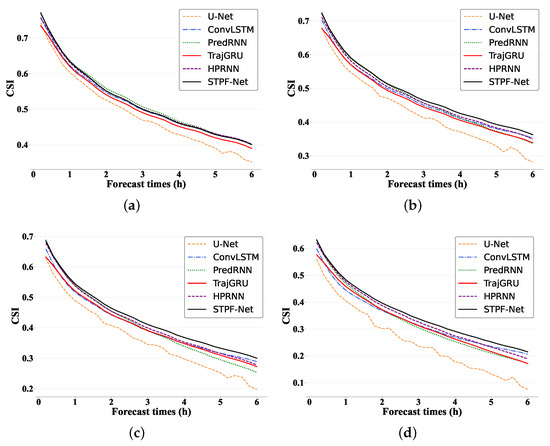
Figure 4.
The CSI scores evolution over forecast times for 6 h prediction on different thresholds. (a) 0.5 mm/h. (b) 1 mm/h. (c) 2 mm/h. (d) 5 mm/h.
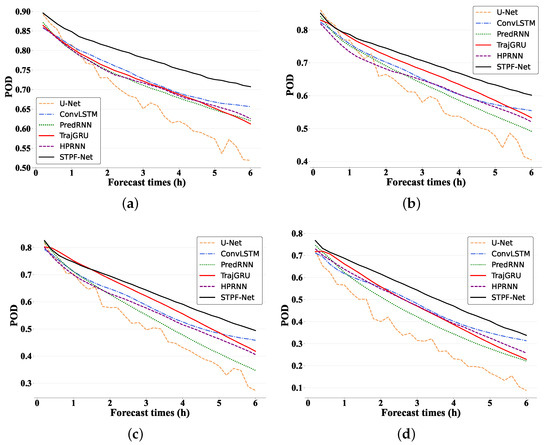
Figure 5.
The POD scores evolution over forecast times for 6 h prediction on different thresholds. (a) 0.5 mm/h. (b) 1 mm/h. (c) 2 mm/h. (d) 5 mm/h.
The previous results compare the proposed STPF-Net to other widely-used deep learning models. To assess performance against traditional NWP methods, its difference from GRAPES is analyzed. Since NWP directly predicts rainfall instead of radar reflectivity, it is inappropriate to compare STPF-Net with NWP on the radar dataset. Thus, we use the surface rainfall observations (AWSs) as the ground truth. Figure 6 displays the CSI scores at different thresholds over forecast lead time. All green bars show NWP results, while red bars indicate STPF-Net improvement over NWP. The proposed STPF-Net outperforms NWP at all the thresholds for the 6 h prediction. Especially early on, substantial improvements highlight NWP’s weaker initial prediction capacity versus deep learning. As time increases, both models degrade and the gap between them narrows. However, STPF-Net still demonstrates advantages. In summary, for next 6 h rainfall intensity prediction, STPF-Net surpasses the traditional NWP model GRAPES. This aligns with prior work comparing deep learning and NWP models, which found similar conclusions on MetNet-2 skill over NWP [35].
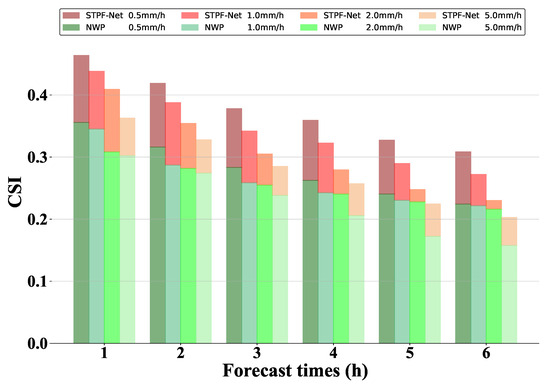
Figure 6.
The CSI scores of 6 h prediction at different thresholds from STPF-Net and NWP.
5.2. Extending Forecast Time to 12 h
The results have demonstrated that STPF-Net improves 6 h precipitation intensity forecasting. To further assess performance at longer timescales, we conduct 12 h prediction experiments by retraining all models. This longer-range experiment helps evaluate the scope of the models’ capabilities and determine whether they can generate reasonable longer-term forecasts of precipitation systems.
Table 2 shows the overall evaluation results for 12 h. As with the 6 h forecasts, CSI, HSS, POD, FAR and BIAS are averaged on different thresholds. When extending forecast time to 12 h, STPF-Net still yields the highest CSI, HSS and POD scores. Moreover, the improvements of STPF-Net over other baselines are more significant compared to 6 h results. Thus, it demonstrate the ability of STPF-Net to mitigate accumulated errors, especially over longer forecasting time. PredRNN obtains the lowest CSI, HSS and POD for 12 h predictions, since PredRNN is designed for precipitation nowcasting with poor performance for longer-range prediction. Apart from STPF-Net, HPRNN obtains the second highest scores, showing better performance for 12 h prediction. The improvement of STPF-Net over HPRNN also prove the effectiveness of Swin Transformer to provide sufficient spatial context. For FAR, STPF-Net still yields higher values since it tends to predict wider spatial coverage of precipitation. ConvLSTM has the lowest FAR score, showing less false predictions. For BIAS, only STPF-Net has a BIAS more than 1, indicating higher precipitation intensities than the ground truth, which is consistent with FAR scores. All other baselines predicts weaker precipitation than the ground truth (BIAS < 1). For BMSE and BMAE, the proposed STPF-Net achieves the lowest errors among all baselines. In summary, the proposed STPF-Net clearly outperforms the deep learning baselines quantitatively for 12 h precipitation forecasting.

Table 2.
The quantitative evaluation results of 12 h prediction.
Figure 7 and Figure 8 show the CSI and POD evolution over the 12 h prediction for different thresholds. For CSI at 0.5 mm/h, all models have close CSI initially, but STPF-Net gradually attains higher scores after 4 h. For heavier precipitation (Figure 7b–d), STPF-Net’s advantages emerge earlier, e.g., at 2.0 mm/h (Figure 7c), and it outperforms from 1 h onward while others remain similar. Thus, STPF-Net’s improvements manifest earlier for heavier versus lighter precipitation intensity forecasts. Among other models, U-Net and PredRNN achieve the lowest scores at longer leads. While PredRNN excels at short-term under 4 h forecasting, its performance quickly declines for longer time, indicating poor ability for long-range forecasting. For POD, STPF-Net almost maintains the highest POD score for all thresholds over the whole forecasting time. Apart from STPF-Net, ConvLSTM obtains relatively higher scores at 0.5 mm/h. As thresholds increase, HPRNN gets better POD except for STPF-Net. In contrast, PredRNN shows lower POD, especially at longer time. In summary, the proposed STPF-Net makes the best 12 h predictions, corroborated by the averaged results in Table 2.
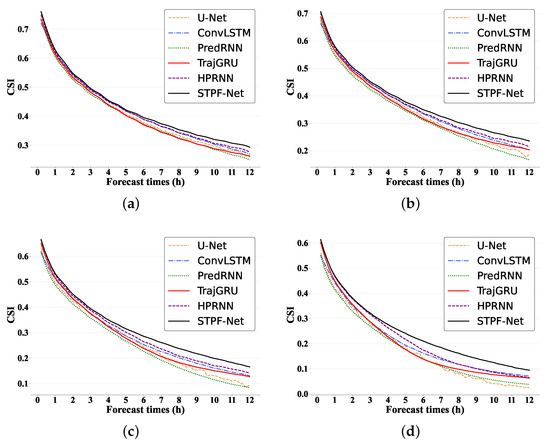
Figure 7.
The CSI scores evolution over forecast times for 12 h prediction at different thresholds. (a) 0.5 mm/h. (b) 1.0 mm/h. (c) 2.0 mm/h. (d) 5.0 mm/h.
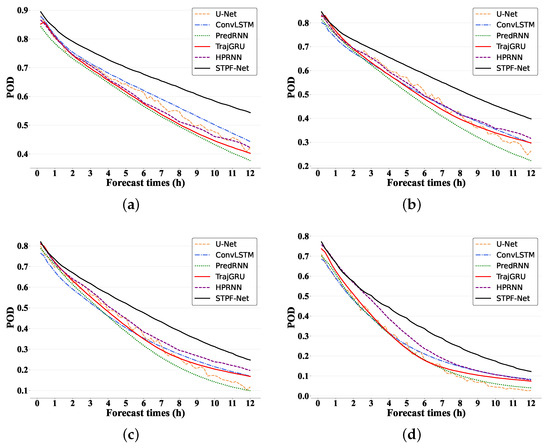
Figure 8.
The POD scores evolution over forecast times for 12 h prediction at different thresholds. (a) 0.5 mm/h. (b) 1.0 mm/h. (c) 2.0 mm/h. (d) 5.0 mm/h.
Similarly, Figure 9 compares 12 h prediction performance between STPF-Net and the NWP model using AWSs as the ground truth. Clear advantages can be found in STPF-Net across all thresholds versus NWP. NWP exhibits poor early-stage skill, while the deep learning model shows significant early improvements. Although the performance of STPF-Net degrades with time leading, it still exhibits better performance than NWP. The difference between deep learning and NWP models becomes more subtle over time. Especially for heavier 5.0 mm/h precipitation, both STPF-Net and NWP have poor prediction ability, with a weak advantage of STPF-Net over NWP. Overall, quantitative evaluation results demonstrate that STPF-Net outperforms deep learning and NWP models on short-term predictions for both 6 h and 12 h experiments. This indicates that the STPF-Net can mitigate the accumulated errors of recurrent-based neural networks and provide better precipitation prediction for the next few hours.
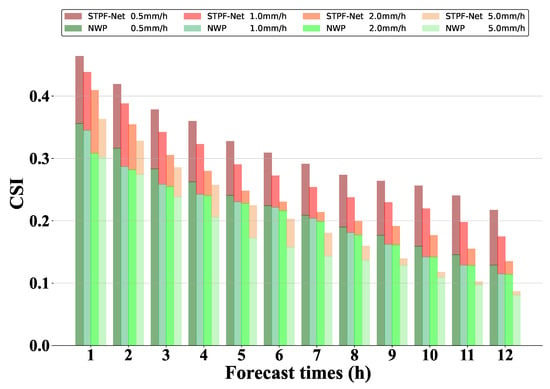
Figure 9.
The CSI scores of 12 h prediction at different thresholds from STPF-Net and NWP.
5.3. Case Study and Visual Assessment
To investigate the spatial and temporal performance of the proposed model, we visualize precipitation intensity distributions at different forecast times. Figure 10 illustrates the visualization results for a case study on 24 June 2017. The input sequence consists of the historical 2 h observations from June 23 at 22:00 UTC to June 24 at 00:00 UTC. The output sequence includes 12 h forecasts initialized at 00:00 UTC on 24 June 2017. Average CSI scores for each prediction time are labeled below each image.
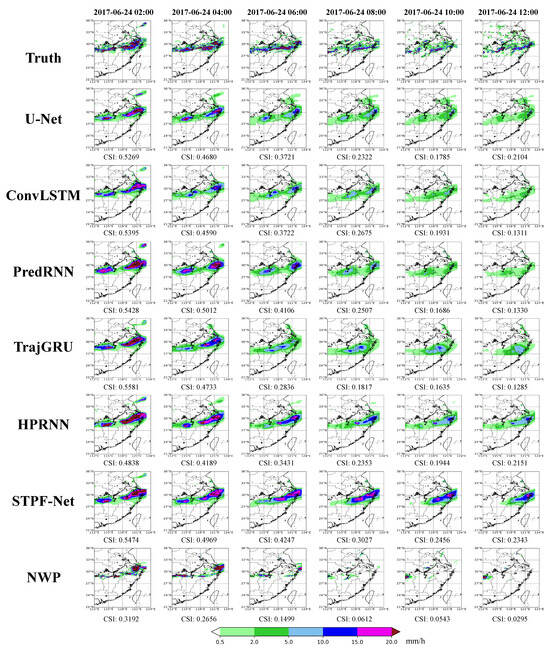
Figure 10.
A case study of precipitation intensity from ground truth (the top row) and predictions from different models. The prediction is initialed at 0000 UTC 24 June 2017. The CSI score of each prediction is averaged by five thresholds, which are 0.5, 2, 5, 10 and 30 mm/h.
The top row in Figure 10 shows the ground truth of a heavy rainfall event across eastern China, spanning Anhui, Hunan, Jiangxi, and Zhejiang provinces. The rainfall lasted over 12 h, with the main rainstorm moving west to east and decaying as time increased. Meanwhile, some new cells developed around the main event. At 02:00 UTC, nearly all models accurately predict the central location of the two heavy rainfall events. TrajGRU obtains the highest average CSI of 0.5581, exhibiting the best early forecast performance in location and structure. STPF-Net achieves a close CSI of 0.5474. Among deep learning models, U-Net has lower CSI than others. Compared to deep learning models, NWP performs the worst for 02:00 UTC, reasonably predicting the primary rainstorm but with weaker intensity and area versus ground truth. As the forecast time leads, all deep learning models degrade. U-Net, ConvLSTM, PredRNN, and TrajGRU gradually lose the ability to predict heavy precipitation intensity after 6 h (0600 UTC). Due to accumulated errors, baseline models only predict maximum intensities of 15 mm/h, below the ground truth. HPRNN performs relatively better than other baselines, with a maximum prediction intensity of 20 mm/h. In contrast, STPF-Net still performs well in heavy rainfall at 6 h, capturing the main precipitation with an intensity of 20 mm/h. Quantitatively, STPF-Net has the highest average CSI of 0.4247, demonstrating that the accumulated errors can be well mitigated in STPF-Net. The prediction of NWP degrades as forecast time increases, which is still far worse than the performance of STPF-Net.
When extending the prediction to 12 h, NWP fails to predict heavy rainfall along the east coast. Although NWP shows a precipitation center in the West and a few small-scale cells, the location and intensity are inconsistent with ground truth. Thus, NWP still obtains the lowest CSI score. In comparison, deep learning models can capture the evolution of the main precipitation along the eastern coast. However, U-Net, PredRNN, and TrajGRU underestimate the intensity, with predictions of only about 2 or 5 mm/h, clearly below the heavy rainfall ground truth. While HPRNN reaches intensities up to 10 mm/h, this still falls short of the ground truth. In comparison, STPF-Net can still predict the heavy precipitation center along the coast. Quantitatively, STPF-Net achieves the best performance on the 12 h predictions. A limitation for all deep learning models is the weak ability to predict newly developed precipitation cells in the West.
Overall, the case study visualizes the performance of all models on precipitation forecasting. For early 6 h predictions, baseline deep learning models suffer from accumulated errors, losing heavy rainfall skill over longer timescales. STPF-Net effectively mitigates these errors and captures heavy rainfall at 6 h. When extending the forecast to 12 h, all deep learning methods adeptly predict evolving and decaying precipitation, yet struggle with predicting new cells. Although achieving the best performance, STPF-Net still falters at 12 h storm initiation. In contrast, NWP can predict new cells due to physical constraints, but with less accuracy than deep learning baselines. Thus, deep learning and NWP models possess distinct complementary strengths.
6. Conclusions
In this paper, we propose a short-term precipitation forecast model (STPF-Net) to address the challenges of accumulated prediction errors and insufficient spatial context for longer-range forecasts.To mitigate these issues, STPF-Net utilizes a multi-tier prediction approach, decomposing the forecast into high and low temporal resolution components. The interaction between tiers helps reduce accumulated errors at extended prediction times. Furthermore, a transformer-based module extracts global information to provide sufficient spatial context for longer forecasts. Quantitative results demonstrate STPF-Net outperforms other deep learning and NWP models at both 6 and 12 h timescales, especially improving longer-range precipitation prediction almost after the first 2 h. Additionally, a case study visualizes STPF-Net’s ability to capture heavy rainfall at 6 h, which other baselines gradually lose over time. At 12 h, although STPF-Net surpasses other models, storm initiation prediction remains challenging. Comparisons with NWP models highlight the strengths of DL-based approaches for short-term precipitation forecasting.
This study demonstrates that well-trained recurrent neural networks can extend precipitation prediction to longer time ranges. However, challenges remain in representing smaller-scale features and predicting newly developed cells. Moreover, the proposed model tends to predict stronger and wider spatial coverage of precipitation causing false alarms. For future work, we will continue advancing weather prediction with neural networks to improve accuracy. For example, incorporating physical constraints into networks could combine the strengths of NWP and deep learning models. Furthermore, this study only leverages radar reflectivity observations. With multiple meteorological data sources available today, future work will fully utilize these multi-source observations to provide enhanced precipitation forecasts.
Author Contributions
Conceptualization, J.W., J.G. and X.W.; methodology, J.W. and F.Z.; software, J.W.; validation, T.C. and L.Z.; investigation, J.W. and J.G.; data curation, J.G. and F.Z.; writing—original draft preparation, J.W.; writing—review and editing, J.G., X.W. and T.C.; supervision, L.Z.; funding acquisition, L.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China grant number 41975066.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to their containing information that could compromise the privacy of research participants.
Acknowledgments
The authors would like to thank the anonymous reviewers for providing professional and insightful comments about this manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bauer, P.; Thorpe, A.; Brunet, G. The quiet revolution of numerical weather prediction. Nature 2015, 525, 47–55. [Google Scholar] [CrossRef] [PubMed]
- Hong, S.Y.; Pan, H.L. Convective trigger function for a mass-flux cumulus parameterization scheme. Mon. Weather Rev. 1998, 126, 2599–2620. [Google Scholar] [CrossRef]
- Bechtold, P.; Semane, N.; Lopez, P.; Chaboureau, J.P.; Bormann, N. Representing equilibrium and nonequilibrium convection in large-scale models. J. Atmos. Sci. 2014, 71, 734–753. [Google Scholar] [CrossRef]
- Bannister, R.N. A review of operational methods of variational and ensemble-variational data assimilation. Q. J. R. Meteorol. Soc. 2017, 143, 607–633. [Google Scholar] [CrossRef]
- Barker, D.M.; Huang, W.; Guo, Y.R.; Bourgeois, A.J.; Xiao, Q.N. A three-dimensional variational data assimilation system for MM5: Implementation and initial results. Mon. Weather Rev. 2004, 132, 897–914. [Google Scholar] [CrossRef]
- Lorenc, A.C. The potential of the ensemble kalman filter for nwp—A comparison with 4D-Var. Q. J. R. Meteorol. Soc. 2010, 129, 3183–3203. [Google Scholar] [CrossRef]
- Short-range quantitative precipitation forecasting in Hong Kong. J. Hydrol. 2004, 288, 189–209. [CrossRef]
- Done, C.A.D.J.; Weisman, M. The next generation of NWP: Explicit forecastsof convection using the weather research andforecasting (WRF) model. Atmos. Sci. Lett. 2004, 5, 110–117. [Google Scholar] [CrossRef]
- Mecklenburg, S.; Joss, J.; Schmid, W. Improving the nowcasting of precipitation in an alpine region with an enhanced radar echo tracking algorithm. J. Hydrol. 2000, 239, 46–68. [Google Scholar] [CrossRef]
- Li, L.; Schmid, W.; Joss, J. Nowcasting of motion and growth of precipitation with radar over a complex orography. J. Appl. Meteorol. 1995, 34, 1286–1300. [Google Scholar] [CrossRef]
- Han, L.; Fu, S.-X.; Zhao, L.-F.; Zheng, Y.; Wang, H.-Q.; Lin, Y. 3d convective storm identification, tracking, and forecasting—An enhanced titan algorithm. J. Atmos. Ocean. Technol. 2009, 26, 719–732. [Google Scholar] [CrossRef]
- Hou, J.; Wang, P. Storm tracking via tree structure representation of radar data. J. Atmos. Ocean. Technol. 2017, 34, 729–747. [Google Scholar] [CrossRef]
- Bowler, N.E.; Pierce, C.; Seed, A.W. Development of a precipitation nowcasting algorithm based upon optical flow techniques. J. Hydrol. 2004, 288, 74–91. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat. Deep learning and process understanding for data-driven earth system science. Nature 2019, 566, 195. [Google Scholar] [CrossRef] [PubMed]
- Schultz, M.G.; Betancourt, C.; Gong, B.; Kleinert, F.; Stadtler, S. Can deep learning beat numerical weather prediction? Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2021, 379, 20200097. [Google Scholar] [CrossRef] [PubMed]
- Prudden, R.; Adams, S.; Kangin, D.; Robinson, N.; Ravuri, S.; Mohamed, S.; Arribas, A. A review of radar-based nowcasting of precipitation and applicable machine learning techniques. arXiv 2020, arXiv:2005.04988. [Google Scholar]
- Shi, X.; Yeung, D.Y. Machine learning for spatiotemporal sequence forecasting: A survey. arXiv 2018, arXiv:1808.06865. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Cho, K.; Merrienboer, B.V.; Gulcehre, C.; BaHdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.C.; Bengio, Y. Generative adversarial nets. arXiv 2014, arXiv:1406.2661. [Google Scholar]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. In Proceedings of the 30th Conference on Neural Information Processing Systems (NIPS 2016), Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Agrawal, S.; Barrington, L.; Bromberg, C.; Burge, J.; Gazen, C.; Hickey, J. Machine learning for precipitation nowcasting from radar images. arXiv 2019, arXiv:1912.12132. [Google Scholar]
- Ayzel, G.; Scheffer, T.; Heistermann, M. Rainnet v1.0: A convolutional neural network for radar-based precipitation nowcasting. Geosci. Model Dev. 2020, 13, 2631–2644. [Google Scholar] [CrossRef]
- Han, L.; Sun, J.; Zhang, W. Convolutional neural network for convective storm nowcasting using 3D doppler weather radar data. IEEE Trans. Geosci. Remote Sens. 2019, 58, 1487–1495. [Google Scholar] [CrossRef]
- Han, L.; Liang, H.; Chen, H.; Zhang, W.; Ge, Y. Convective precipitation nowcasting using U-Net model. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4103508. [Google Scholar] [CrossRef]
- Trebing, K.; Staǹczyk, T.; Mehrkanoon, S. SmaAt-UNet: Precipitation nowcasting using a small attention-UNet architecture. Pattern Recognit. Lett. 2021, 145, 178–186. [Google Scholar] [CrossRef]
- Kaparakis, C.; Mehrkanoon, S. Wf-unet: Weather fusion unet for precipitation nowcasting. arXiv 2023, arXiv:2302.04102. [Google Scholar]
- Chen, G.; Wang, W. Short-term precipitation prediction for contiguous united states using deep learning. Geophys. Res. Lett. 2022, 49, e2022GL097904. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.-k.; Woo, W.-c. Convolutional lstm network: A machine learning approach for precipitation nowcasting. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Shi, X.; Gao, Z.; Lausen, L.; Wang, H.; Yeung, D.-Y.; Wong, W.-k.; Woo, W.-c. Deep learning for precipitation nowcasting: A benchmark and a new model. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Wang, Y.; Long, M.; Wang, J.; Gao, Z.; Yu, P.S. PredRNN: Recurrent neural networks for predictive learning using spatiotemporal LSTMs. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; pp. 879–888. [Google Scholar]
- Wang, Y.; Gao, z.; Long, M.; Wang, J.; Yu, P.S. PredRNN++: Towards a resolution of the deep-in-time dilemma in spatiotemporal predictive learning. arXiv 2018, arXiv:1804.06300. [Google Scholar]
- Jing, J.; Li, Q.; Peng, X.; Ma, Q.; Tang, S. HPRNN: A hierarchical sequence prediction model for long-term weather radar echo extrapolation. In Proceedings of the ICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020. [Google Scholar]
- Snderby, C.K.; Espeholt, L.; Heek, J.; Dehghani, M.; Oliver, A.; Salimans, T.; Agrawal, S.; Hickey, J.; Kalchbrenner, N. MetNet: A neural weather model for precipitation forecasting. arXiv 2020, arXiv:2003.12140. [Google Scholar]
- Espeholt, L.; Agrawal, S.; Sønderby, C.; Kumar, M.; Heek, J.; Bromberg, C.; Gazen, C.; Hickey, J.; Bell, A.; Kalchbrenner, N. Skillful twelve hour precipitation forecasts using large context neural networks. arXiv 2021, arXiv:2111.07470. [Google Scholar]
- Yan, B.Y.; Yang, C.; Chen, F.; Takeda, K.; Wang, C. FDNet: A deep learning approach with two parallel cross encoding pathways for precipitation nowcasting. arXiv 2021, arXiv:2105.02585. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, X.; Guan, J.; Wu, M.; Guo, L. RN-Net: A deep learning approach to 0–2 h rainfall nowcasting based on radar and automatic weather station data. Sensors 2021, 21, 1981. [Google Scholar] [CrossRef] [PubMed]
- Klocek, S.; Dong, H.; Dixon, M.; Kanengoni, P.; Kazmi, N.; Luferenko, P.; Lv, Z.; Sharma, S.; Weyn, J.; Xiang, S. MS-nowcasting: Operational precipitation nowcasting with convolutional lstms at microsoft weather. arXiv 2021, arXiv:2111.09954. [Google Scholar]
- Liu, J.; Xu, L.; Chen, N. A spatiotemporal deep learning model ST-LSTM-SA for hourly rainfall forecasting using radar echo images. J. Hydrol. 2022, 609, 127748. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, H.; Han, L.; Zhang, R.; Ge, Y. Pixel-CRN: A new machine learning approach for convective storm nowcasting. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4102212. [Google Scholar] [CrossRef]
- Ravuri, S.; Lenc, K.; Willson, M.; Kangin, D.; Lam, R.; Mirowski, P.; Fitzsimons, M.; Athanassiadou, M.; Kashem, S.; Madge, S. Skillful precipitation nowcasting using deep generative models of radar. Nature 2021, 597, 672–677. [Google Scholar] [CrossRef]
- Kim, Y.; Hong, S. Very short-term rainfall prediction using ground radar observations and conditional generative adversarial networks. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4104308. [Google Scholar] [CrossRef]
- Zhang, Y.; Long, M.; Chen, K.; Xing, L.; Jin, R.; Jordan, M.I.; Wang, J. Skilful nowcasting of extreme precipitation with NowcastNet. Nature 2023, 619, 526–532. [Google Scholar] [CrossRef]
- Bai, C.; Sun, F.; Zhang, J.; Song, Y.; Chen, S. Rainformer: Features extraction balanced network for radar-based precipitation nowcasting. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4023305. [Google Scholar] [CrossRef]
- Gao, Z.; Shi, X.; Wang, H.; Zhu, Y.; Wang, Y.B.; Li, M.; Yeung, D.-Y. Earthformer: Exploring space-time transformers for earth system forecasting. Adv. Neural Inf. Process. Syst. 2022, 35, 390–403. [Google Scholar]
- Hu, Y.; Chen, L.; Wang, Z.; Li, H. Swinvrnn: A data-driven ensemble forecasting model via learned distribution perturbation. J. Adv. Model. Earth Syst. 2022, 15, e2022MS003211. [Google Scholar] [CrossRef]
- Wu, T.; Wan, Y.; Weifeng, W.; Leng, L. Design and application of radar reflectivity quality control algorithm in SWAN. Meteorol. Sci. Technol. 2013, 41, 809–817. [Google Scholar]
- Li, P.W.; Wong, W.-K.; Chan, K.Y.; Lai, E.S.T. Swirls—An Evolving Nowcasting System; Hong Kong Special Administrative Region Government: Hong Kong, China, 2000.
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. arXiv 2021, arXiv:2103.14030. [Google Scholar]
- Bojesomo, A.; Al-Marzouqi, H.; Liatsis, P. A novel transformer network with shifted window cross-attention for spatiotemporal weather forecasting. arXiv 2022, arXiv:2208.01252. [Google Scholar] [CrossRef]
- Zhang, R.H.; Shen, X.S. On the development of the GRAPES—A new generation of the national operational NWP system in China. Sci. Bull. 2008, 53, 3429–3432. [Google Scholar] [CrossRef]
- Chen, D. Recent progress on GRAPES research and application. J. Appl. Meteorol. Sci. 2006, 6, 1001–7313. [Google Scholar]
- Chen, D.H.; Xue, J.S.; Yang, X.S.; Zhang, H.L.; Shen, X.S.; Jianglin, H.U.; Wang, Y.; Amp, L.R. New generation of multi-scale NWP system (GRAPES):general scientific design. Chin. Sci. Bull. 2008, 53, 3433–3445. [Google Scholar] [CrossRef]
- Liu, D.; Jie, F.; Li, J.; Wang, J. The impacts of time-step size and spatial resolution on the prediction skill of the GRAPES-meso forecast system. Chin. J. Atmos. Sci. 2015, 42, 1146–1156. [Google Scholar]
- Zhang, X.; Tang, W.; Zheng, Y.; Sheng, J.; Zhu, W. Comprehensive evaluations of GRAPES_3km numerical model in forecasting convective storms using various verification methods. Meteorol. Mon. 2020, 46, 14. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. arXiv 2019, arXiv:1912.01703. [Google Scholar]
- Zhang, F.; Wang, X.; Guan, J. A novel multi-input multi-output recurrent neural network based on multimodal fusion and spatiotemporal prediction for 0–4 h precipitation nowcasting. Atmosphere 2021, 12, 1596. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).