Uncertainty Analysis and Data Fusion of Multi-Source Land Evapotranspiration Products Based on the TCH Method
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.1.1. The Land Section of the Fifth-Generation ECMWF Re-Analysis (ERA5-Land) ET
2.1.2. Global Land Data Assimilation System (GLDAS) ET
2.1.3. The Second Modern-Era Retrospective Analysis for Research and Applications (MERRA-2) ET
2.1.4. Eddy Covariance (EC) ET
2.2. Methods
2.2.1. Uncertainty Analysis Based on the TCH Method
2.2.2. Fusion Method
2.2.3. The Verification Method of the Fused Product
3. Results and Discussion
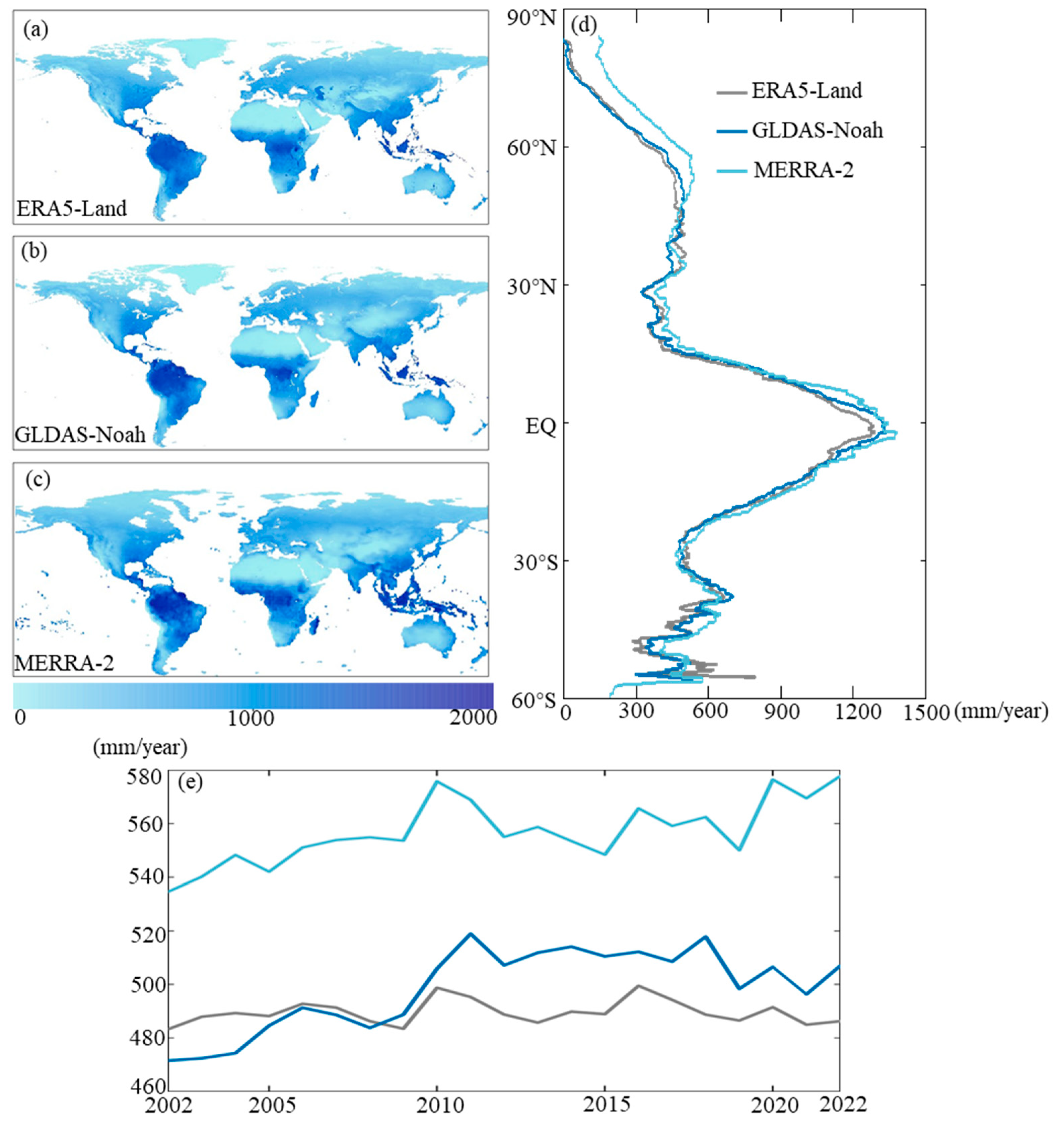
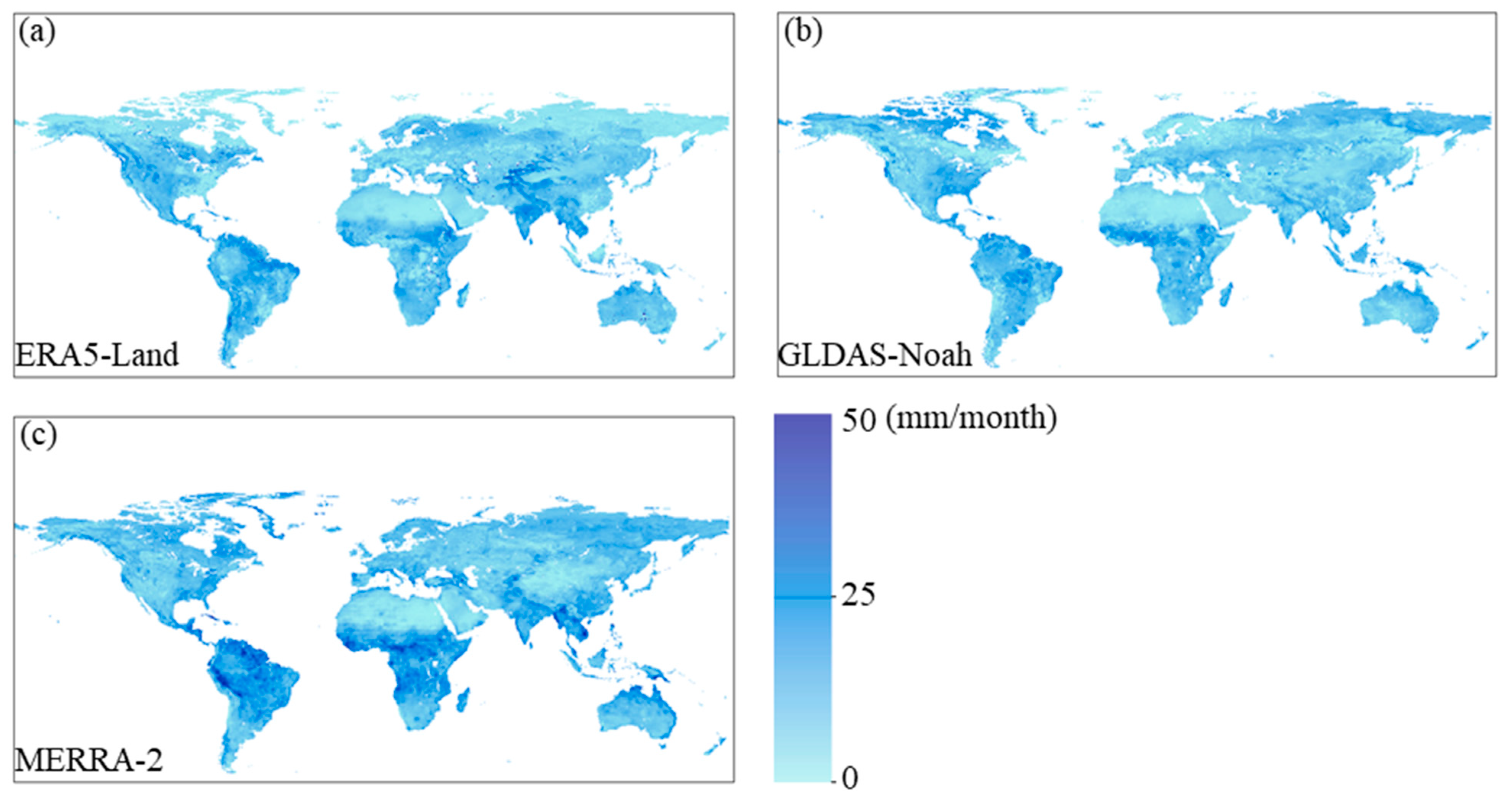
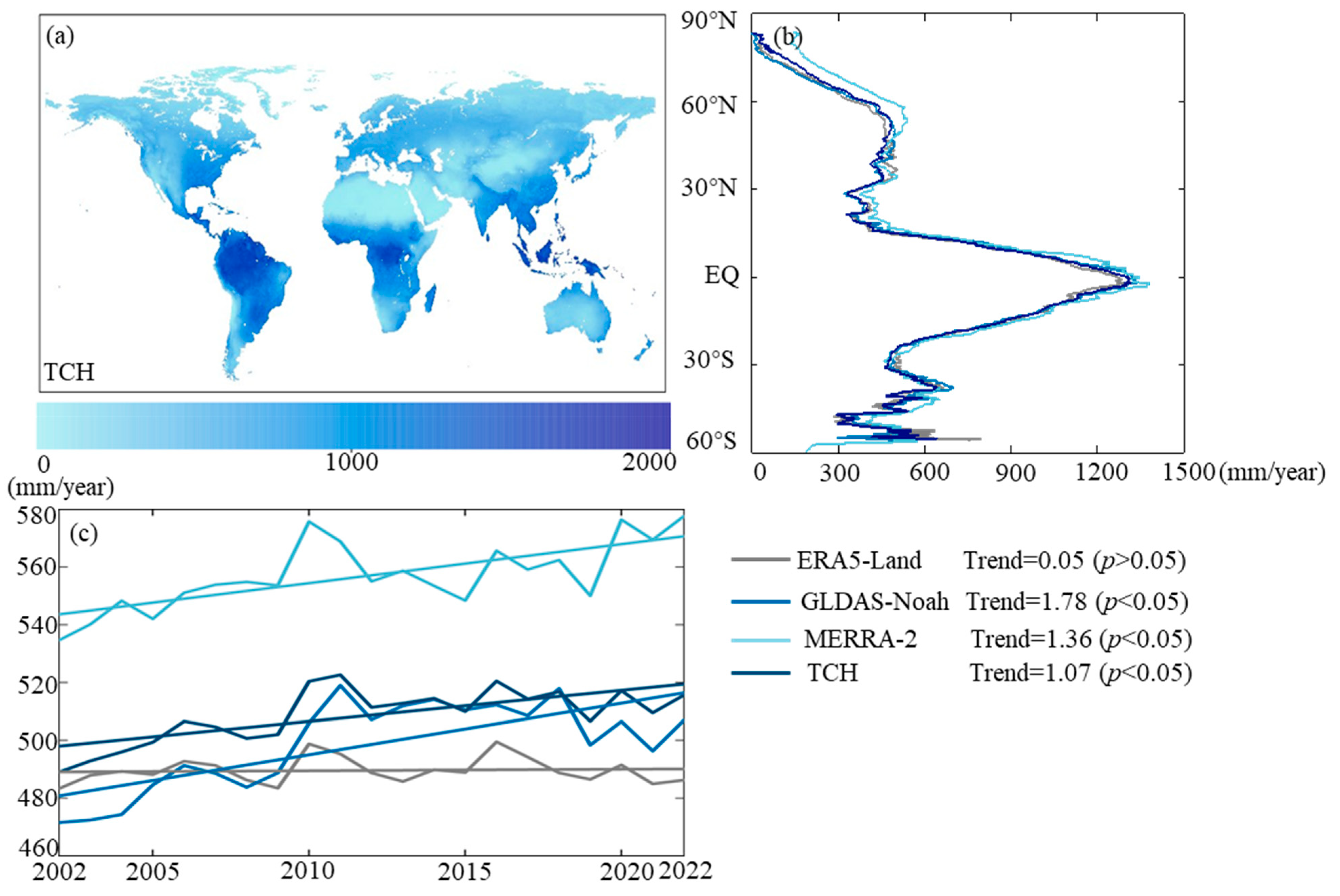
3.1. Spatial and Temporal Distribution of the Three ET Products
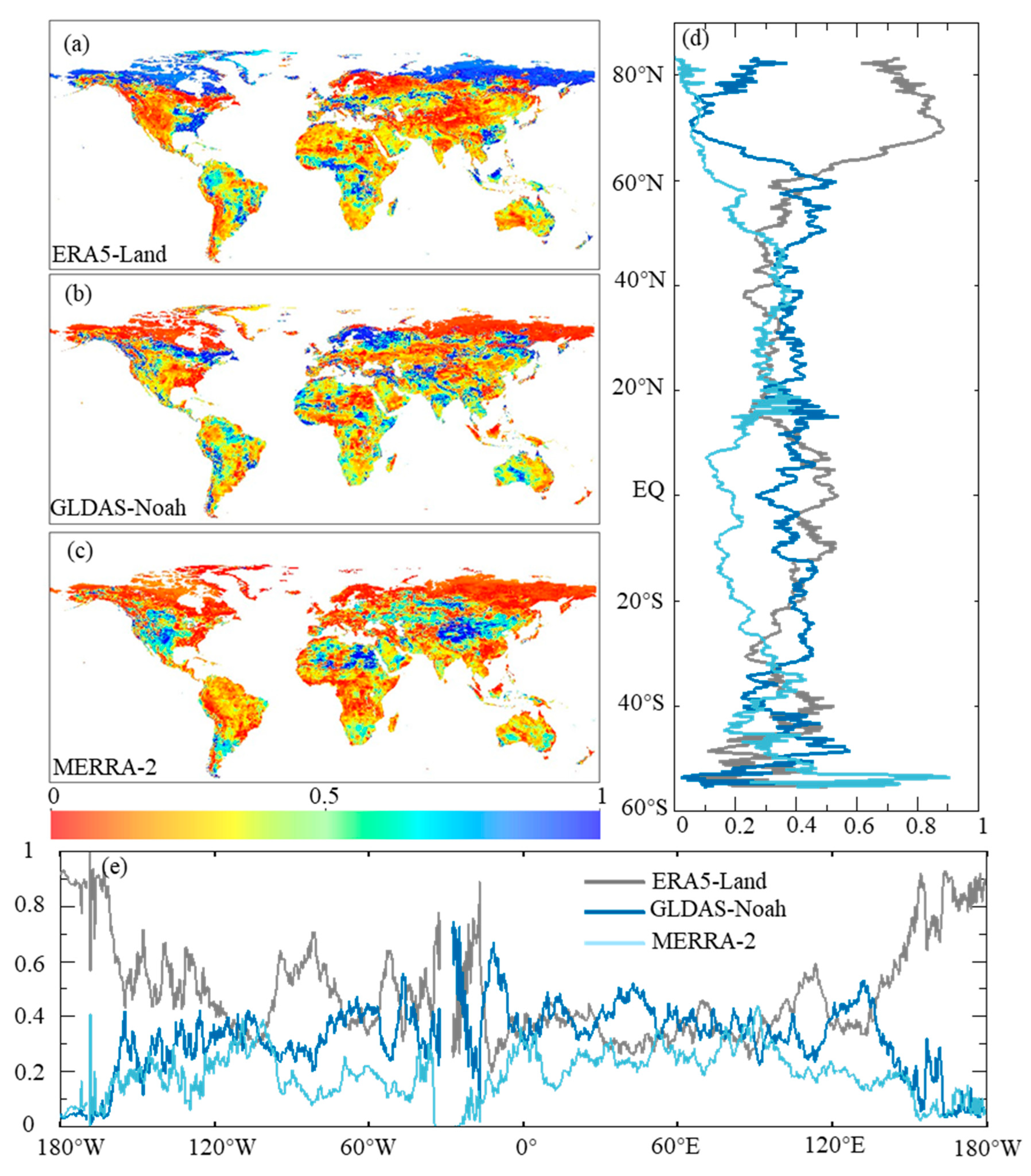
3.2. The Uncertainty of the Three Products
3.3. The Weight of the Three Products
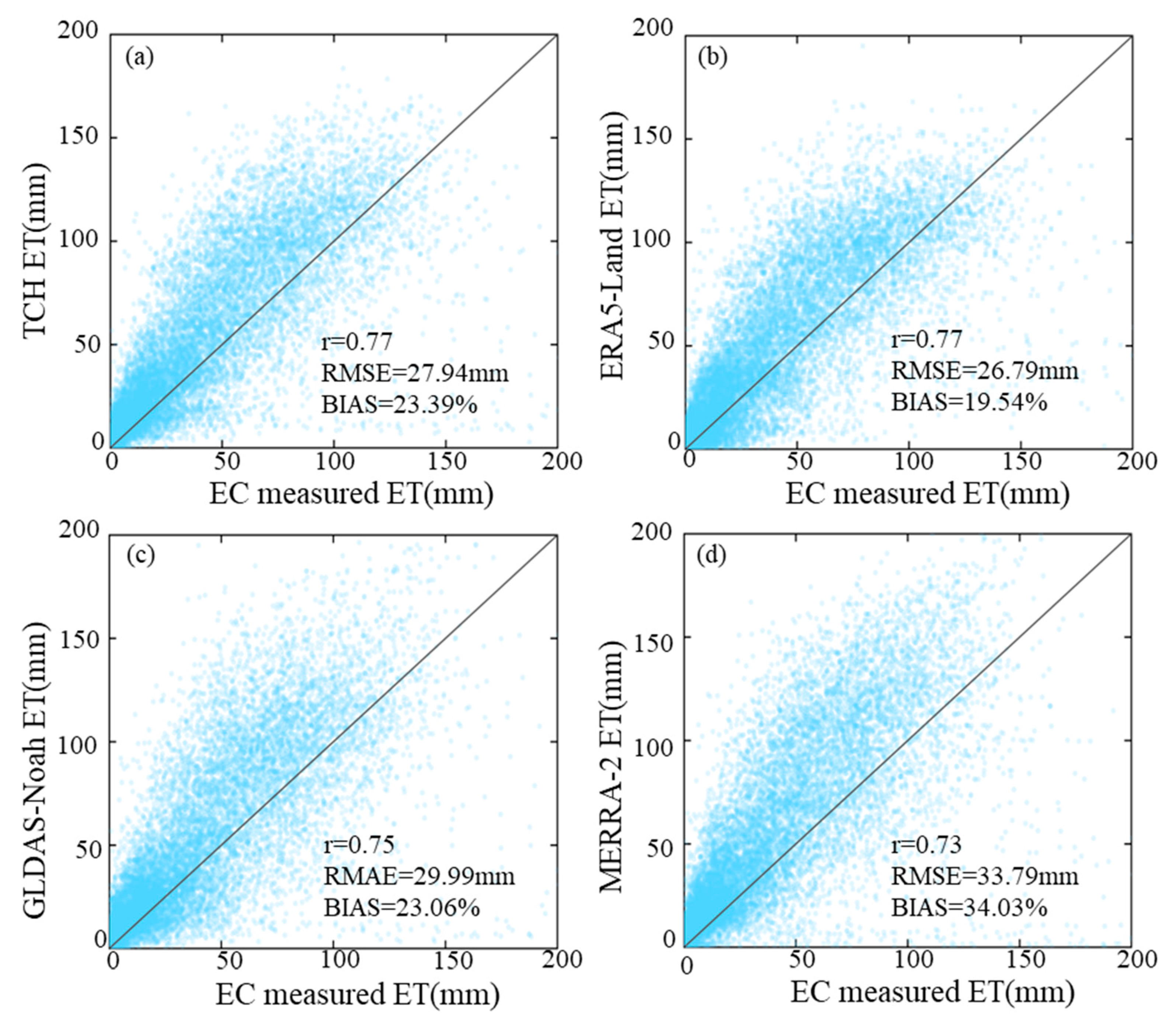
3.4. Evaluation of Products after Fusion
3.5. Spatial and Temporal Distributions of the Fusion Product
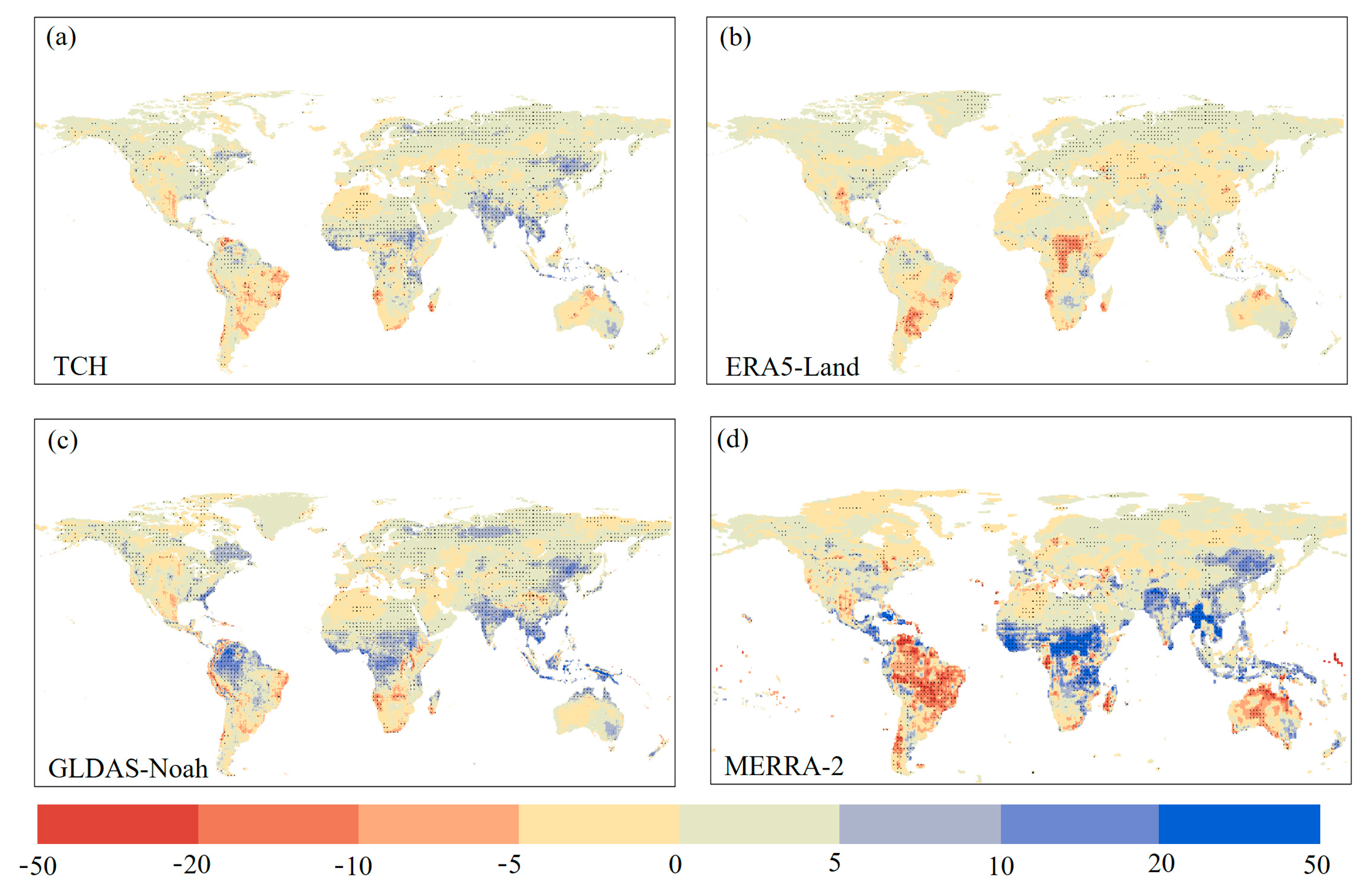
3.6. Spatial Distribution of the Linear Trend of Four ET Products
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, K.C.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev. Geophys. 2012, 50, RG2005. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Fasullo, J.T.; Kiehl, J. Earth’s global energy budget. Bull. Am. Meteorol. Soc. 2009, 90, 311–323. [Google Scholar] [CrossRef]
- Sun, S.L.; Chen, H.S.; Ju, W.M.; Wang, G.J.; Sun, G.; Huang, J.; Ma, H.D.; Hua, W.J.; Yan, G.X. On the coupling between precipitation and potential evapotranspiration: Contributions to decadal drought anomalies in the Southwest China. Clim. Dyn. 2017, 48, 3779–3797. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F.; Roderick, M.L. Little change in global drought over the past 60 years. Nature 2012, 491, 435–438. [Google Scholar] [CrossRef] [PubMed]
- Majozi, N.P.; Mannaerts, C.M.; Ramoelo, A.; Mathieu, R.; Mudau, A.E.; Verhoef, W. An intercomparison of satellite-based daily evapotranspiration estimates under different eco-climatic regions in South Africa. Remote Sens. 2017, 9, 307. [Google Scholar] [CrossRef]
- Lu, J.; Wang, G.J.; Chen, T.X.; Li, S.J.; Hagan, D.F.T.; Kattel, G.; Peng, J.; Jiang, T.; Su, B.D. A harmonized global land evaporation dataset from model-based products covering 1980–2017. Earth Syst. Sci. Data 2021, 13, 5879–5898. [Google Scholar] [CrossRef]
- Reichle, R.H.; Draper, C.S.; Liu, Q.; Girotto, M.; Mahanama, S.P.P.; Koster, R.D.; De Lannoy, G.J.M. Assessment of MERRA-2 land surface hydrology estimates. J. Clim. 2017, 30, 2937–2960. [Google Scholar] [CrossRef]
- Miralles, D.G.; De Jeu, R.A.M.; Gash, J.H.; Holmes, T.R.H.; Dolman, A.J. Magnitude and variability of land evaporation and its components at the global scale. Hydrol. Earth Syst. Sci. 2011, 15, 967–981. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Jung, M.; Koirala, S.; Weber, U.; Ichii, K.; Gans, F.; Camps-Valls, G.; Papale, D.; Schwalm, C.; Tramontana, G.; Reichstein, M. The FLUXCOM ensemble of global land-atmosphere energy fluxes. Sci. Data 2019, 6, 74. [Google Scholar] [CrossRef]
- Gentine, P.; Pritchard, M.; Rasp, S.; Reinaudi, G.; Yacalis, G. Could machine learning break the convection parameterization deadlock? Geophys. Res. Lett. 2018, 45, 5742–5751. [Google Scholar] [CrossRef]
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J.; et al. Deep learning in environmental remote sensing: Achievements and challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
- Cai, X.; Yang, Z.L.; David, C.H.; Niu, G.Y.; Rodell, M. Hydrological evaluation of the Noah-MP land surface model for the Mississippi River Basin. J. Geophys. Res. Atmos. 2014, 119, 23–38. [Google Scholar] [CrossRef]
- Bechtold, M.; De Lannoy, G.J.M.; Koster, R.D.; Reichle, R.H.; Mahanama, S.P.; Bleuten, W.; Bourgault, M.A.; Brümmer, C.; Burdun, I.; Desai, A.R.; et al. PEAT-CLSM: A specific treatment of peatland hydrology in the NASA Catchment Land Surface Model. J. Adv. Model 2019, 11, 2130–2162. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.; Jia, L. Estimation of evapotranspiration of “soil-vegetation” system with a scheme combining a dual-source model and satellite data assimilation. J. Hydrol. 2021, 603, 12745. [Google Scholar] [CrossRef]
- Jang, K.; Kang, S.; Lim, Y.; Jeong, S.; Kim, J.; Kimball, J.S.; Hong, S.Y. Monitoring daily evapotranspiration in Northeast Asia using MODIS and a regional land data assimilation system. J. Geophys. Res. Atmos. 2013, 118, 12927–12940. [Google Scholar] [CrossRef]
- Li, Z.L.; Tang, R.; Wan, Z.; Bi, Y.; Zhou, C.; Tang, B.; Yan, G.; Zhang, X. A review of current methodologies for regional evapotranspiration estimation from remotely sensed data. Sensors 2009, 9, 3801–3853. [Google Scholar] [CrossRef] [PubMed]
- Tang, R.; Li, Z.L.; Tang, B. An application of the Ts-VI triangle method with enhanced edges determination for evapotranspiration estimation from MODIS data in arid and semi-arid regions: Implementation and validation. Remote Sens. Environ. 2010, 114, 540–551. [Google Scholar] [CrossRef]
- Wenbin, Z.; Shengrong, T.; Jiaxing, W.; Shaofeng, J.; Zikun, S. Multi-scale evaluation of global evapotranspiration products derived from remote sensing images: Accuracy and uncertainty. J. Hydrol. 2022, 611, 127982. [Google Scholar]
- Jiménez, C.; Martens, B.; Miralles, D.M.; Fisher, J.B.; Beck, H.E.; Fernández-Prieto, D. Exploring the merging of the global land evaporation WACMOS-ET products based on local tower measurements. Hydrol. Earth Syst. Sci. 2018, 22, 4513–4533. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.; De Jeu, R.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef] [PubMed]
- Mueller, B.; Hirschi, M.; Jimenez, C.; Ciais, P.; Dirmeyer, P.A.; Dolman, A.J.; Fisher, J.B.; Jung, M.; Ludwig, F.; Maignan, F.; et al. Benchmark products for land evapotranspiration: LandFlux-EVAL multi-data set synthesis. Hydrol. Earth Syst. Sci. 2013, 17, 3707–3720. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Li, X.; Hong, Y.; Fisher, J.; Zhang, N.; Chen, J.; Cheng, J.; Zhao, S.; Zhang, X.; et al. Bayesian multimodel estimation of global terrestrial latent heat flux from eddy covariance, meteorological, and satellite observations. J. Geophys. Res. Atmos. 2014, 119, 4521–4545. [Google Scholar] [CrossRef]
- Yilmaz, M.T.; Crow, W.T.; Anderson, M.C.; Hain, C. An objective methodology for merging satellite-and model-based soil moisture products. Water Resour. Res. 2012, 48, W11502. [Google Scholar] [CrossRef]
- Kim, S.; Parinussa, R.M.; Liu, Y.Y.; Johnson, F.M.; Sharma, A. A framework for combining multiple soil moisture retrievals based on maximizing temporal correlation. Geophys. Res. Lett. 2015, 42, 6662–6670. [Google Scholar] [CrossRef]
- Kim, H.; Parinussa, R.; Konings, A.G.; Wagner, W.; Cosh, M.H.; Lakshmi, V.; Zohaib, M.; Choi, M. Global-scale assessment and combination of SMAP with ASCAT (active) and AMSR2 (passive) soil moisture products. Remote Sens. Environ. 2018, 204, 260–275. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Li, X.; Zhang, Y.; Chen, J.; Jia, K.; Zhang, X.; Fisher, J.; Wang, X.; Zhang, L.; et al. Estimation of high-resolution terrestrial evapotranspiration from Landsat data using a simple Taylor skill fusion method. J. Hydrol. 2017, 553, 508–526. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, Q.; Yang, Y.; Hao, X.; Zhang, H. Evaluation of evapotranspiration models over semi-arid and semi-humid areas of China. Hydrol. Process. 2016, 30, 4292–4313. [Google Scholar] [CrossRef]
- Premoli, A.; Tavella, P. A revisited three-cornered hat method for estimating frequency standard instability. IEEE Trans. Instrum. Meas. 1993, 42, 7–13. [Google Scholar] [CrossRef]
- Zhang, Y.; Ye, A. Uncertainty analysis of multiple terrestrial gross primary productivity products. Glob. Ecol. Biogeogr. 2022, 31, 2204–2218. [Google Scholar] [CrossRef]
- Muñoz Sabater, J. ERA5-Land Hourly Data from 1950 to Present. Copernicus Climate Change Service (C3S) Climate Data Store (CDS). 2019. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-land?tab=overview (accessed on 1 September 2023).
- Sheffield, J.; Wood, E.F. Characteristics of global and regional drought, 1950–2000: Analysis of soil moisture data from off-line simulation of the terrestrial hydrologic cycle. J. Geophys. Res. 2007, 112, D17115. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The modern-era retrospective analysis for research and applications, version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Park, J.; Baik, J.; Choi, M. Triple collocation-based multi-source evaporation and transpiration merging. Agric. For. Meteorol. 2023, 331, 109353. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Randle, C.A.; da Silva, A.M.; Buchard, V.; Colarco, P.R.; Darmenov, A.; Govindaraju, R.; Smirnov, A.; Holben, B.; Ferrare, R.; Hair, J.; et al. The MERRA-2 Aerosol Reanalysis, 1980 Onward. Part I: System Description and Data Assimilation Evaluation. J. Clim. 2017, 30, 6823–6850. [Google Scholar] [CrossRef]
- Koster, R.D.; Suarez, M.J.; Ducharne, A.; Stieglitz, M.; Kumar, P. A catchment-based approach to modeling land surface processes in a general circulation model: 1. Model structure. J. Geophys. Res. Atmos. 2000, 105, 24809–24822. [Google Scholar] [CrossRef]
- Bosilovich, M.G.; Chen, J.Y.; Robertson, F.R.; Adler, R.F. Evaluation of global precipitation in reanalysis. J. Appl. Meteorol. Climatol. 2008, 47, 2279–2299. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Steven, W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Awange, J.L.; Ferreira, V.G.; Forootan, E.; Khandu; Andam-Akorful, S.A.; Agutua, N.O.; He, X.F. Uncertainties in remotely sensed precipitation data over Africa. Int. J. Climatol. 2016, 1, 303–323. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Wang, A.H.; Zeng, X.B. Evaluation of multireanalysis products with in situ observations over the Tibetan Plateau. J. Geophys. Res. Atmos. 2012, 117, D05102. [Google Scholar] [CrossRef]
- Feng, T.; Su, T.; Ji, F.; Zhi, R.; Han, Z. Temporal characteristics of actual evapotranspiration over China under global warming. J. Geophys. Res. Atmos. 2018, 123, 5845–5858. [Google Scholar] [CrossRef]
- Wang, F.; Wang, L.; Koike, T.; Zhou, H.; Yang, K.; Wang, A.; Li, W. Evaluation and application of a fine resolution global data set in a semiarid mesoscale river basin with a distributed biosphere hydrological model. J. Geophys. Res. Atmos. 2011, 116, D21108. [Google Scholar] [CrossRef]
- Baik, J.; Liaqat, U.W.; Choi, M. Assessment of satellite- and reanalysis-based evapotranspiration products with two blending approaches over the complex landscapes and climates of Australia. Agric. For. Meteorol. 2018, 263, 388–398. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Khan, M.S.; Liaqat, U.W.; Baik, J.; Choi, M. Stand-alone uncertainty characterization of GLEAM, GLDAS and MOD16 evapotranspiration products using an extended triple collocation approach. Agric. For. Meteorol. 2018, 252, 256–268. [Google Scholar] [CrossRef]
- Gomis-Cebolla, J.; Jimenez, J.C.; Sobrino, J.A.; Corbari, C.; Mancini, M. Intercomparison of remote-sensing based evapotranspiration algorithms over amazonian forests. Int. J. Appl. Earth Obs. Geoinf. 2019, 80, 280–294. [Google Scholar] [CrossRef]
- Miralles, D.G.; Jiménez, C.; Jung, M.; Michel, D.; Ershadi, A.; McCabe, M.F.; Hirschi, M.; Martens, B.; Dolman, A.J.; Fisher, J.B.; et al. The WACMOS-ET project–Part 2: Evaluation of global terrestrial evaporation data sets. Hydrol. Earth Syst. Sci. 2016, 20, 823–842. [Google Scholar] [CrossRef]
- Kim, H.W.; Hwang, K.; Mu, Q.; Lee, S.O.; Choi, M. Validation of MODIS 16 global terrestrial evapotranspiration products in various climates and land cover types in Asia. KSCE J. Civ. Eng. 2012, 16, 229–238. [Google Scholar] [CrossRef]
- Ershadi, A.; McCabe, M.; Evans, J.; Chaney, N.; Wood, E. Multi-site evaluation of terrestrial evaporation models using FLUXNET data. Agric. For. Meteorol. 2014, 187, 46–61. [Google Scholar] [CrossRef]
- Burnett, M.W.; Quetin, G.R.; Konings, A.G. Data-driven estimates of evapotranspiration and its controls in the Congo Basin. Hydrol. Earth Syst. Sci. 2020, 24, 4189–4211. [Google Scholar] [CrossRef]
- Crowhurst, D.; Dadson, S.; Peng, J.; Washington, R. Contrasting controls on Congo Basin evaporation at the two rainfall peaks. Clim. Dyn. 2020, 56, 1609–1624. [Google Scholar] [CrossRef]
- Dong, B.; Dai, A. The uncertainties and causes of the recent changes in global evapotranspiration from 1982 to 2010. Clim. Dyn. 2016, 49, 279–296. [Google Scholar] [CrossRef]
- Fisher, J.B.; Melton, F.; Middleton, E.; Hain, C.; Anderson, M.; Allen, R.; McCabe, M.; Hook, S.; Baldocchi, D.; Townsend, P.A.; et al. The Future of Evapotranspiration: Global requirements for ecosystem functioning, carbon and climate feedbacks, agricultural management, and water resources. Water Resour. Res. 2017, 53, 2618–2626. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. Evapotranspiration information reporting: I. Factors governing measurement accuracy. Agric. Water Manag. 2011, 98, 899–920. [Google Scholar] [CrossRef]
- Foken, T. The energy balance closure problem: An overview. Ecol. Appl. 2008, 18, 1351–1367. [Google Scholar] [CrossRef]
- Wang, S.; Pan, M.; Mu, Q.; Shi, X.; Mao, J.; Brümmer, C.; Jassal, R.S.; Krishnan, P.; Li, J.; Black, T.A. Comparing evapotranspiration from eddy covariance measurements, water budgets, remote sensing, and land surface models over Canada. J. Hydrometeorol. 2015, 16, 1540–1560. [Google Scholar] [CrossRef]


| Dataset | Spatial Resolution (°) | Temporal Resolution | Time Span | Citation |
|---|---|---|---|---|
| ERA5-Land | 0.1 × 0.1 | 1 h | 2002–2022 | [31] |
| GLDAS2.1 | 0.25 × 0.25 | 3 h | 2002–2022 | [32] |
| MERRA-2 | 0.625 × 0.5 | 1 h | 2002–2022 | [33] |
| Vegetation Classifications | TCH | ERA5-Land | GLDAS-Noah | MERRA-2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| r | RMSE | BIAS | r | RMSE | BIAS | r | RMSE | BIAS | r | RMSE | BIAS | |
| CRO | 0.66 | 34.45 | 20.26 | 0.70 | 32.02 | 20.59 | 0.70 | 36.48 | 26.21 | 0.60 | 37.84 | 19.64 |
| DBF | 0.82 | 29.40 | 41.27 | 0.82 | 28.79 | 41.24 | 0.82 | 30.70 | 42.01 | 0.76 | 33.39 | 43.61 |
| EBF | 0.76 | 29.44 | 16.98 | 0.79 | 25.45 | 16.06 | 0.71 | 32.30 | 15.21 | 0.73 | 40.36 | 23.27 |
| ENF | 0.80 | 24.56 | 24.54 | 0.77 | 23.49 | 15.49 | 0.78 | 27.30 | 26.36 | 0.75 | 33.25 | 47.71 |
| GRA | 0.90 | 18.82 | 23.47 | 0.84 | 20.64 | 13.77 | 0.83 | 22.22 | 17.05 | 0.88 | 23.67 | 33.64 |
| MF | 0.83 | 30.24 | 52.70 | 0.84 | 27.47 | 46.48 | 0.75 | 32.78 | 43.31 | 0.87 | 36.00 | 72.88 |
| OSH | 0.81 | 19.08 | 36.25 | 0.69 | 21.99 | 31.74 | 0.80 | 20.66 | 43.90 | 0.77 | 23.13 | 44.70 |
| SAV | 0.86 | 20.71 | 6.06 | 0.81 | 22.10 | −2.87 | 0.85 | 21.70 | 6.56 | 0.85 | 27.80 | 15.37 |
| WET | 0.46 | 46.69 | −2.02 | 0.53 | 42.79 | −3.98 | 0.47 | 47.01 | −1.29 | 0.41 | 49.74 | 4.53 |
| ASA | 0.84 | 21.92 | −6.41 | 0.83 | 22.75 | 7.55 | 0.83 | 22.84 | −7.69 | 0.79 | 31.41 | 10.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Z.; Zhang, Y.; Wang, A.; Wu, J.; Li, C. Uncertainty Analysis and Data Fusion of Multi-Source Land Evapotranspiration Products Based on the TCH Method. Remote Sens. 2024, 16, 28. https://doi.org/10.3390/rs16010028
Cui Z, Zhang Y, Wang A, Wu J, Li C. Uncertainty Analysis and Data Fusion of Multi-Source Land Evapotranspiration Products Based on the TCH Method. Remote Sensing. 2024; 16(1):28. https://doi.org/10.3390/rs16010028
Chicago/Turabian StyleCui, Zilong, Yuan Zhang, Anzhi Wang, Jiabing Wu, and Chunbo Li. 2024. "Uncertainty Analysis and Data Fusion of Multi-Source Land Evapotranspiration Products Based on the TCH Method" Remote Sensing 16, no. 1: 28. https://doi.org/10.3390/rs16010028
APA StyleCui, Z., Zhang, Y., Wang, A., Wu, J., & Li, C. (2024). Uncertainty Analysis and Data Fusion of Multi-Source Land Evapotranspiration Products Based on the TCH Method. Remote Sensing, 16(1), 28. https://doi.org/10.3390/rs16010028









