Detection of Rubber Tree Powdery Mildew from Leaf Level Hyperspectral Data Using Continuous Wavelet Transform and Machine Learning
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Acquisition
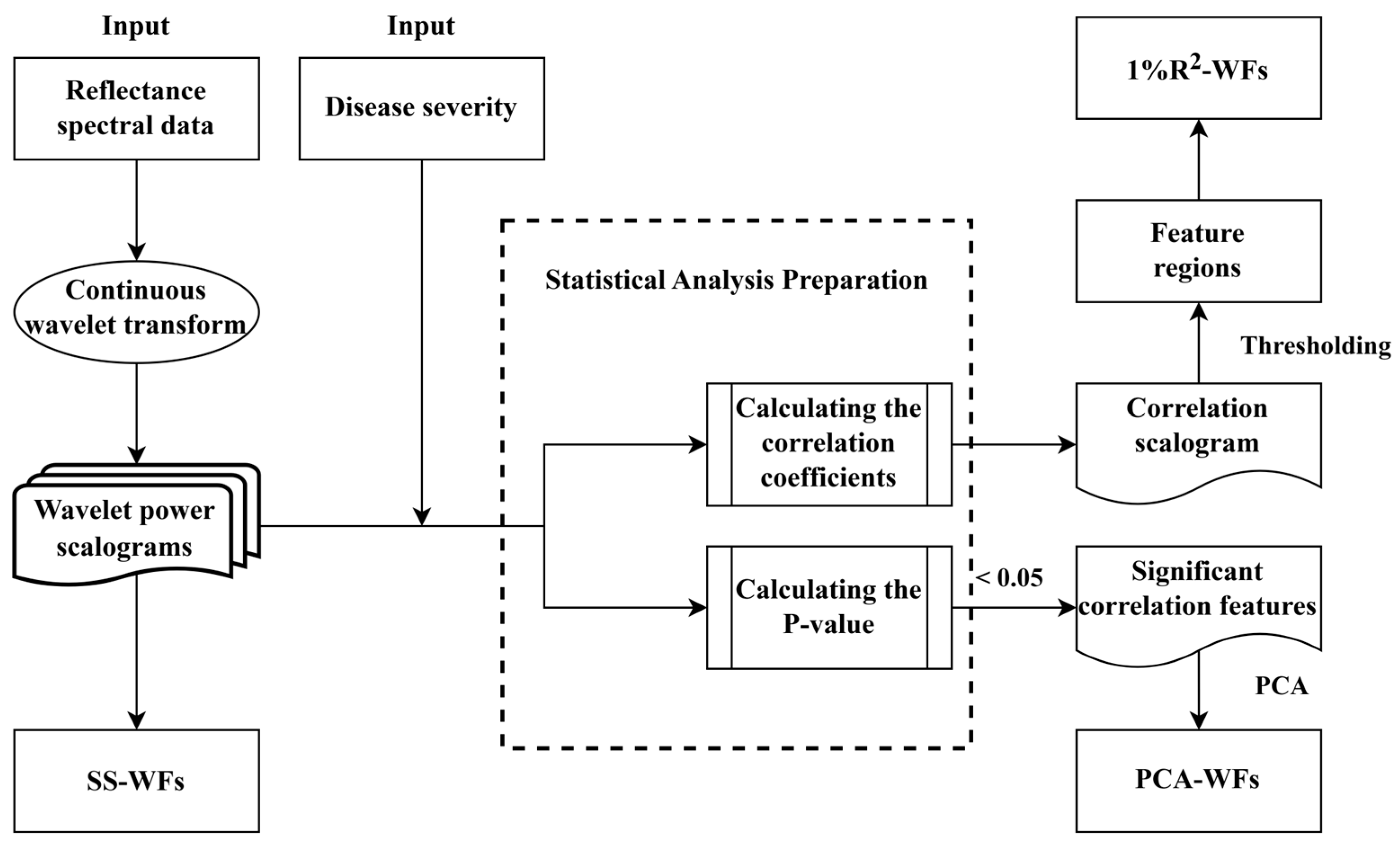
2.3. Feature Extraction and Analysis
2.3.1. Traditional Spectral Features
2.3.2. Continuous Wavelet Transform and Features Extraction
2.4. Model Construction
2.5. Accuracy Assessment
3. Results
3.1. Spectral Responses of Rubber Tree Powdery Mildew
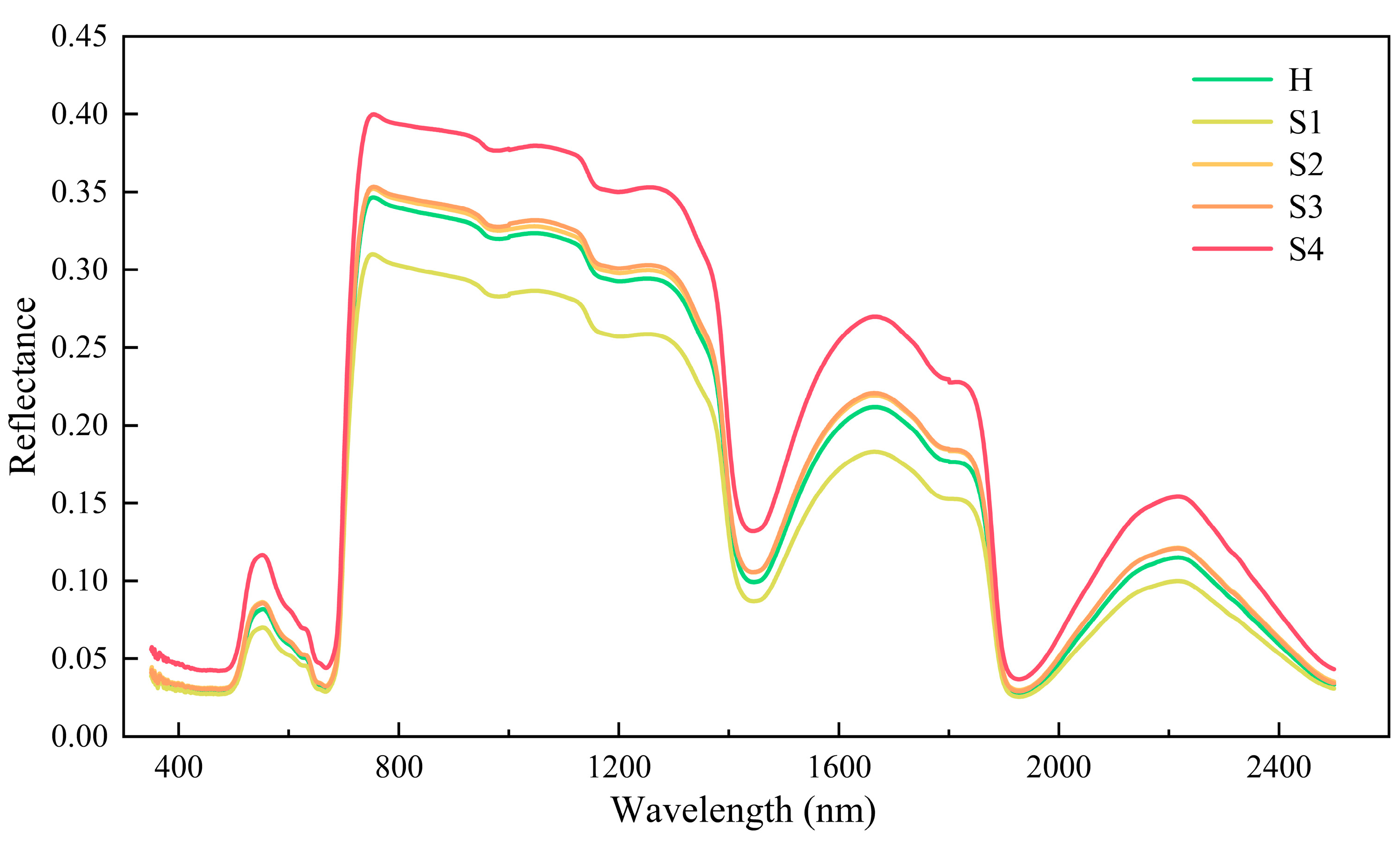
3.1.1. Spectral Responses in Leaves under Powdery Mildew Infection
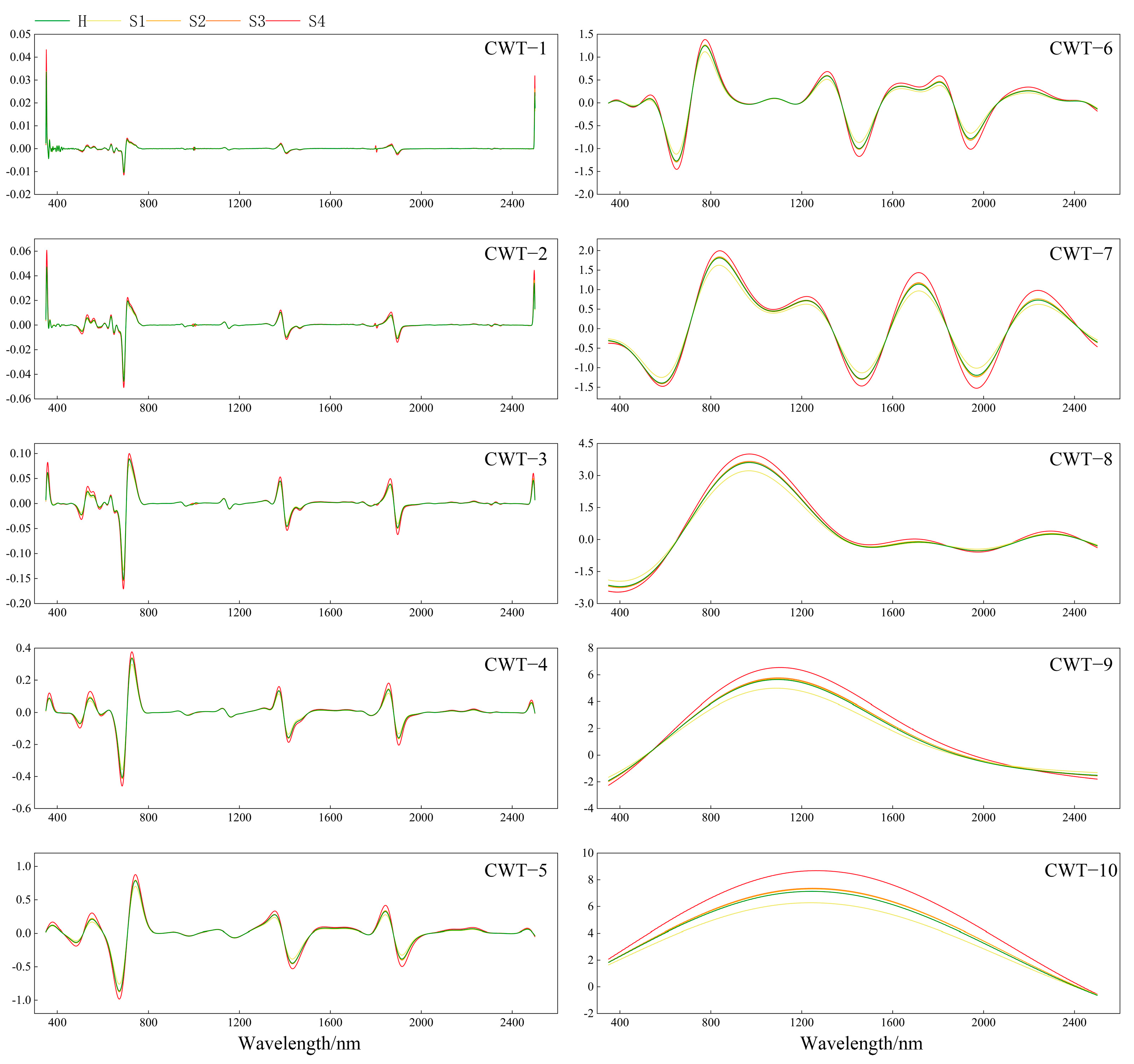
3.1.2. Wavelet Coefficient Responses under Powdery Mildew Infection
3.2. Optimal Feature Extraction Results for Rubber Tree Powdery Mildew
3.2.1. Traditional Spectral Features
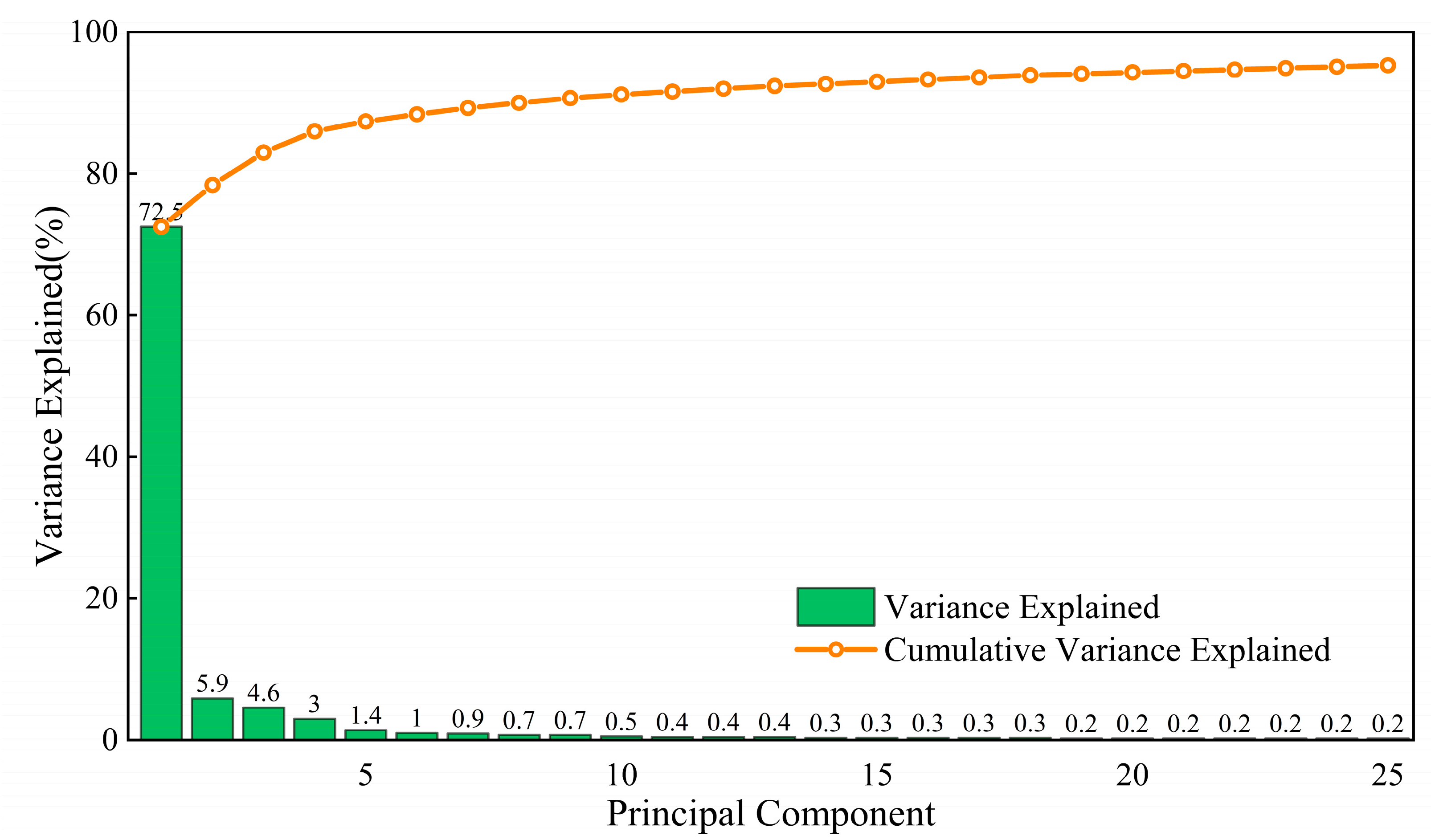
3.2.2. Wavelet features
3.3. Evaluation of Rubber Tree Powdery Mildew Detection Models
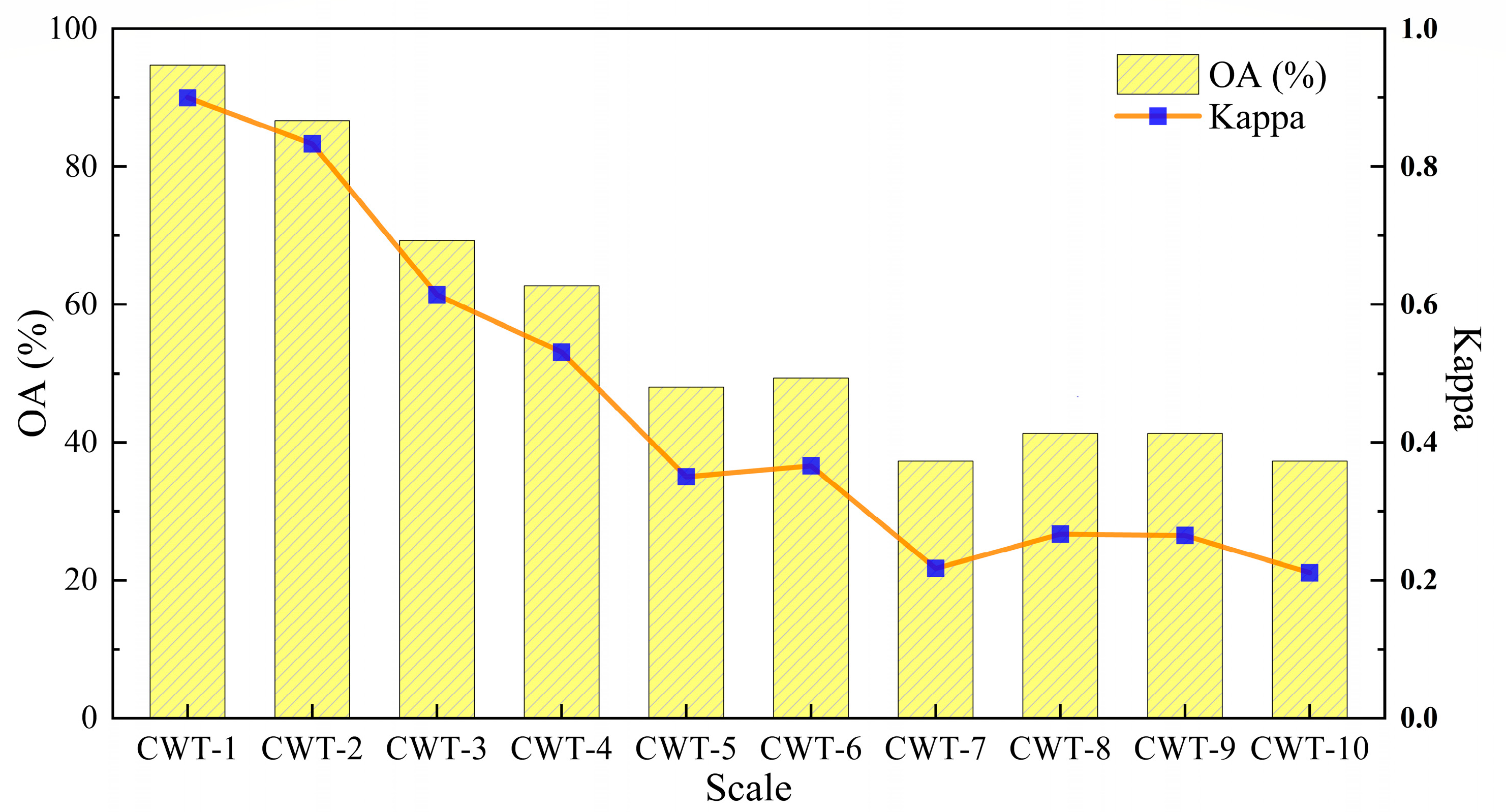
3.3.1. Comparison of Disease Detection Models Based on Different Wavelet Features
3.3.2. Comparison of Disease Detection Models Based on Optimal Wavelet Features and Traditional Spectral Features
4. Discussion
5. Conclusions
- (1)
- The overall magnitude of the spectral curves of rubber tree leaves increases in the visible and near-infrared wavelength ranges as the disease severity progresses.
- (2)
- All three selected WFs can effectively detect the severity of rubber tree powdery mildew. The models constructed based on PCA-WFs exhibited relatively high accuracy and exceptional stability. The models based on WFs all outperform those based on SFs. For example, the OA based on the RF classification method exhibits prominent improvements of 46.7%, 49.4%, and 42.7%, respectively. For models based on the same WF type, those constructed with the RF classification method achieve the highest OA and kappa coefficient. In particular, compared with the BPNN and SVM methods, the model’s OA improves by more than 5% and 8%, respectively.
- (3)
- The model combining PCA-WFs with RF demonstrates the best performance among all models, achieving an OA of 92.0% and a kappa coefficient of 0.90. This demonstrates the feasibility of CWT in the detection of rubber tree powdery mildew.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Van Beilen, J.B.; Poirier, Y. Establishment of New Crops for the Production of Natural Rubber. TRENDS Biotechnol. 2007, 25, 522–529. [Google Scholar] [CrossRef] [PubMed]
- Liyanage, K.K.; Khan, S.; Mortimer, P.E.; Hyde, K.D.; Xu, J.; Brooks, S.; Ming, Z. Powdery Mildew Disease of Rubber Tree. For. Pathol. 2016, 46, 90–103. [Google Scholar] [CrossRef]
- Limkaisang, S.; Kom-un, S.; Takamatsu, S.; Furtado, E.L.; Liew, K.W.; Salleh, B.; Sato, Y. Molecular Phylogenetic and Morphological Analyses of Oidium Heveae, a Powdery Mildew of Rubber Tree. Mycoscience 2005, 46, 220–226. [Google Scholar] [CrossRef]
- De, A.; Liyanage, S.; JACOB, C.K. Diseases of Economic Importance in Rubber. In Developments in Crop Science; Elsevier: Amsterdam, The Netherlands, 1992; Volume 23, pp. 324–359. [Google Scholar] [CrossRef]
- Thomas, S.; Kuska, M.T.; Bohnenkamp, D.; Brugger, A.; Alisaac, E.; Wahabzada, M.; Behmann, J.; Mahlein, A.-K. Benefits of Hyperspectral Imaging for Plant Disease Detection and Plant Protection: A Technical Perspective. J. Plant Dis. Prot. 2018, 125, 5–20. [Google Scholar] [CrossRef]
- Gowen, A.A.; O’Donnell, C.P.; Cullen, P.J.; Downey, G.; Frias, J.M. Hyperspectral Imaging—An Emerging Process Analytical Tool for Food Quality and Safety Control. Trends Food Sci. Technol. 2007, 18, 590–598. [Google Scholar] [CrossRef]
- Zhang, J.C.; Pu, R.; Wang, J.; Huang, W.; Yuan, L.; Luo, J. Detecting Powdery Mildew of Winter Wheat Using Leaf Level Hyperspectral Measurements. Comput. Electron. Agric. 2012, 85, 13–23. [Google Scholar] [CrossRef]
- Feng, W.; Shen, W.; He, L.; Duan, J.; Guo, B.; Li, Y.; Wang, C.; Guo, T. Improved Remote Sensing Detection of Wheat Powdery Mildew Using Dual-Green Vegetation Indices. Precis. Agric. 2016, 17, 608–627. [Google Scholar] [CrossRef]
- Huang, L.; Wu, Z.; Huang, W.; Ma, H.; Zhao, J. Identification of Fusarium Head Blight in Winter Wheat Ears Based on Fisher’s Linear Discriminant Analysis and a Support Vector Machine. Appl. Sci. 2019, 9, 3894. [Google Scholar] [CrossRef]
- Zhang, J.; Pu, R.; Loraamm, R.W.; Yang, G.; Wang, J. Comparison between Wavelet Spectral Features and Conventional Spectral Features in Detecting Yellow Rust for Winter Wheat. Comput. Electron. Agric. 2014, 100, 79–87. [Google Scholar] [CrossRef]
- Tian, L.; Xue, B.; Wang, Z.; Li, D.; Yao, X.; Cao, Q.; Zhu, Y.; Cao, W.; Cheng, T. Spectroscopic Detection of Rice Leaf Blast Infection from Asymptomatic to Mild Stages with Integrated Machine Learning and Feature Selection. Remote Sens. Environ. 2021, 257, 112350. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, Y.; Wang, J.; Huang, W.; Chen, L.; Zhang, D. Spectroscopic Leaf Level Detection of Powdery Mildew for Winter Wheat Using Continuous Wavelet Analysis. J. Integr. Agric. 2012, 11, 1474–1484. [Google Scholar] [CrossRef]
- Luo, J.; Huang, W.; Yuan, L.; Zhao, C.; Du, S.; Zhang, J.; Zhao, J. Evaluation of Spectral Indices and Continuous Wavelet Analysis to Quantify Aphid Infestation in Wheat. Precis. Agric. 2013, 14, 151–161. [Google Scholar] [CrossRef]
- Shi, Y.; Huang, W.; González-Moreno, P.; Luke, B.; Dong, Y.; Zheng, Q.; Ma, H.; Liu, L. Wavelet-Based Rust Spectral Feature Set (WRSFs): A Novel Spectral Feature Set Based on Continuous Wavelet Transformation for Tracking Progressive Host–Pathogen Interaction of Yellow Rust on Wheat. Remote Sens. 2018, 10, 525. [Google Scholar] [CrossRef]
- Ma, H.; Huang, W.; Jing, Y.; Pignatti, S.; Laneve, G.; Dong, Y.; Ye, H.; Liu, L.; Guo, A.; Jiang, J. Identification of Fusarium Head Blight in Winter Wheat Ears Using Continuous Wavelet Analysis. Sensors 2019, 20, 20. [Google Scholar] [CrossRef] [PubMed]
- Cheng, T.; Rivard, B.; Sánchez-Azofeifa, G.A.; Feng, J.; Calvo-Polanco, M. Continuous Wavelet Analysis for the Detection of Green Attack Damage Due to Mountain Pine Beetle Infestation. Remote Sens. Environ. 2010, 114, 899–910. [Google Scholar] [CrossRef]
- Rodriguez, J.; Lizarazo, I.; Prieto, F.; Angulo-Morales, V. Assessment of Potato Late Blight from UAV-Based Multispectral Imagery. Comput. Electron. Agric. 2021, 184, 106061. [Google Scholar] [CrossRef]
- Duarte-Carvajalino, J.M.; Alzate, D.F.; Ramirez, A.A.; Santa-Sepulveda, J.D.; Fajardo-Rojas, A.E.; Soto-Suárez, M. Evaluating Late Blight Severity in Potato Crops Using Unmanned Aerial Vehicles and Machine Learning Algorithms. Remote Sens. 2018, 10, 1513. [Google Scholar] [CrossRef]
- Zhang, T.; Cai, Y.; Zhuang, P.; Li, J. Remotely Sensed Crop Disease Monitoring by Machine Learning Algorithms: A Review. Un. Sys. 2023, 1–11. [Google Scholar] [CrossRef]
- Su, J.; Liu, C.; Coombes, M.; Hu, X.; Wang, C.; Xu, X.; Li, Q.; Guo, L.; Chen, W.-H. Wheat Yellow Rust Monitoring by Learning from Multispectral UAV Aerial Imagery. Comput. Electron. Agric. 2018, 155, 157–166. [Google Scholar] [CrossRef]
- Wang, H.; Qin, F.; Ruan, L.; Wang, R.; Liu, Q.; Ma, Z.; Li, X.; Cheng, P.; Wang, H. Identification and Severity Determination of Wheat Stripe Rust and Wheat Leaf Rust Based on Hyperspectral Data Acquired Using a Black-Paper-Based Measuring Method. PLoS ONE 2016, 11, e0154648. [Google Scholar] [CrossRef]
- Bohnenkamp, D.; Behmann, J.; Mahlein, A.-K. In-Field Detection of Yellow Rust in Wheat on the Ground Canopy and UAV Scale. Remote Sens. 2019, 11, 2495. [Google Scholar] [CrossRef]
- Lan, Y.; Huang, Z.; Deng, X.; Zhu, Z.; Huang, H.; Zheng, Z.; Lian, B.; Zeng, G.; Tong, Z. Comparison of Machine Learning Methods for Citrus Greening Detection on UAV Multispectral Images. Comput. Electron. Agric. 2020, 171, 105234. [Google Scholar] [CrossRef]
- Xishuangbanna Dai Autonomous Prefecture People’s Government Official Website. Available online: https://www.xsbn.gov.cn/index.dhtml (accessed on 9 December 2023).
- Milton, E.J.; Schaepman, M.E.; Anderson, K.; Kneubühler, M.; Fox, N. Progress in Field Spectroscopy. Remote Sens. Environ. 2009, 113, S92–S109. [Google Scholar] [CrossRef]
- ASD Portable Spectrometers & Spectroradiometers | Malvern Panalytical. Available online: https://www.malvernpanalytical.com/en/products/product-range/asd-range (accessed on 9 December 2023).
- Thenkabail, P.S.; Smith, R.B.; De Pauw, E. Hyperspectral Vegetation Indices and Their Relationships with Agricultural Crop Characteristics. Remote Sens. Environ. 2000, 71, 158–182. [Google Scholar] [CrossRef]
- Gamon, J.A.; Penuelas, J.; Field, C.B. A Narrow-Waveband Spectral Index That Tracks Diurnal Changes in Photosynthetic Efficiency. Remote Sens. Environ. 1992, 41, 35–44. [Google Scholar] [CrossRef]
- Kim, M.S.; Daughtry, C.S.T.; Chappelle, E.W.; McMurtrey, J.E.; Walthall, C.L. The Use of High Spectral Resolution Bands for Estimating Absorbed Photosynthetically Active Radiation (A Par). In Proceedings of the 6th International Symposium on Physical Measurements and Signatures in Remote Sensing, Val D’Isere France, 17–21 January 1994. [Google Scholar]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated Narrow-Band Vegetation Indices for Prediction of Crop Chlorophyll Content for Application to Precision Agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Daughtry, C.S.; Walthall, C.L.; Kim, M.S.; De Colstoun, E.B.; McMurtrey Iii, J.E. Estimating Corn Leaf Chlorophyll Concentration from Leaf and Canopy Reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Merton, R.; Huntington, J. Early Simulation Results of the ARIES-1 Satellite Sensor for Multi-Temporal Vegetation Research Derived from AVIRIS. In Proceedings of the Eighth Annual JPL Airborne Earth Science Workshop, Pasadena, CA, USA, 9–11 February 1999; Citeseer: State College, PA, USA, 1999; pp. 9–11. [Google Scholar]
- Merzlyak, M.N.; Gitelson, A.A.; Chivkunova, O.B.; Rakitin, V.Y. Non-destructive Optical Detection of Pigment Changes during Leaf Senescence and Fruit Ripening. Physiol. Plant. 1999, 106, 135–141. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N.; Chivkunova, O.B. Optical Properties and Nondestructive Estimation of Anthocyanin Content in Plant Leaves. Photochem. Photobiol. 2007, 74, 38–45. [Google Scholar] [CrossRef]
- Filella, I.; Serrano, L.; Serra, J.; Peñuelas, J. Evaluating Wheat Nitrogen Status with Canopy Reflectance Indices and Discriminant Analysis. Crop Sci. 1995, 35, 1400–1405. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing Prediction Power and Stability of Broadband and Hyperspectral Vegetation Indices for Estimation of Green Leaf Area Index and Canopy Chlorophyll Density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Gong, P.; Pu, R.; Heald, R.C. Analysis of in Situ Hyperspectral Data for Nutrient Estimation of Giant Sequoia. Int. J. Remote Sens. 2002, 23, 1827–1850. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar] [CrossRef]
- Mallat, S. Zero-Crossings of a Wavelet Transform. IEEE Trans. Inf. Theory 1991, 37, 1019–1033. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Cheng, T.; Rivard, B.; Sanchez-Azofeifa, A. Spectroscopic Determination of Leaf Water Content Using Continuous Wavelet Analysis. Remote Sens. Environ. 2011, 115, 659–670. [Google Scholar] [CrossRef]
- Lin, C.; Peng, F.; Wang, B.-H.; Sun, W.-F.; Kong, X.-J. Research on PCA and KPCA Self-Fusion Based MSTAR SAR Automatic Target Recognition Algorithm. J. Electron. Sci. Technol. 2012, 10, 352–357. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999. [Google Scholar] [CrossRef]
- Karatzoglou, A.; Meyer, D.; Hornik, K. Support Vector Machines in R. J. Stat. Softw. 2006, 15, 1–28. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A Tutorial on Support Vector Regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Panda, S.S.; Ames, D.P.; Panigrahi, S. Application of Vegetation Indices for Agricultural Crop Yield Prediction Using Neural Network Techniques. Remote Sens. 2010, 2, 673–696. [Google Scholar] [CrossRef]
- Allouche, O.; Tsoar, A.; Kadmon, R. Assessing the Accuracy of Species Distribution Models: Prevalence, Kappa and the True Skill Statistic (TSS). J. Appl. Ecol. 2006, 43, 1223–1232. [Google Scholar] [CrossRef]
- Foody, G.M. Explaining the Unsuitability of the Kappa Coefficient in the Assessment and Comparison of the Accuracy of Thematic Maps Obtained by Image Classification. Remote Sens. Environ. 2020, 239, 111630. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Heeren, T.; D’Agostino, R. Robustness of the Two Independent Samples t -test When Applied to Ordinal Scaled Data. Stat. Med. 1987, 6, 79–90. [Google Scholar] [CrossRef] [PubMed]
- Bai, R.; Wang, J.; Li, N. Climate Change Increases the Suitable Area and Suitability Degree of Rubber Tree Powdery Mildew in China. Ind. Crops Prod. 2022, 189, 115888. [Google Scholar] [CrossRef]
- Sarker, I.H. Machine Learning: Algorithms, Real-World Applications and Research Directions. SN Comput. Sci. 2021, 2, 160. [Google Scholar] [CrossRef]
- Boulent, J.; Foucher, S.; Théau, J.; St-Charles, P.-L. Convolutional Neural Networks for the Automatic Identification of Plant Diseases. Front. Plant Sci. 2019, 10, 941. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Kovacs, J.M. The Application of Small Unmanned Aerial Systems for Precision Agriculture: A Review. Precision Agric. 2012, 13, 693–712. [Google Scholar] [CrossRef]
- Guo, A.; Huang, W.; Dong, Y.; Ye, H.; Ma, H.; Liu, B.; Wu, W.; Ren, Y.; Ruan, C.; Geng, Y. Wheat Yellow Rust Detection Using UAV-Based Hyperspectral Technology. Remote Sens. 2021, 13, 123. [Google Scholar] [CrossRef]
- Su, J.; Liu, C.; Hu, X.; Xu, X.; Guo, L.; Chen, W.-H. Spatio-Temporal Monitoring of Wheat Yellow Rust Using UAV Multispectral Imagery. Comput. Electron. Agric. 2019, 167, 105035. [Google Scholar] [CrossRef]


| Level | Healthy | Severity 1 | Severity 2 | Severity 3 | Severity 4 |
|---|---|---|---|---|---|
| Leaf spot area | 0 | 0~12.5% | 12.5~25% | 25~50% | 50~75% |
| Canopy appearance characteristics | No disease lesion infestation. | Leaves are covered with a layer of white powdery substance, with disease lesions occupying one-eighth of the total leaf area. | Disease lesions occupy one-quarter of the total leaf area, or leaves are mildly wrinkled due to the disease. | Disease lesions occupy half of the total leaf area, or leaves are moderately wrinkled due to the disease. | Disease lesions occupy three-fourths of the total leaf area, or leaves are severely wrinkled due to the disease. |
| Category | Index/Spectral Feature | Definition | Description or Formula | Reference |
|---|---|---|---|---|
| Vegetation indices | NBNDVI | Narrow-band normalized Difference vegetation index | (R850 − R680)/(R850 + R680) | [27] |
| PRI | Photochemical/physiological reflectance index | (R531 − R570)/(R531 + R570) | [28] | |
| PHRI | Physiological reflectance index | (R550 − R531)/(R531 + R550) | [28] | |
| CARI | Chlorophyll absorption ratio index | (|(a × 670 + R670 + b)|/(a2 + 1)1/2) × (R700/R670) a = (R700 − R550)/150, b = R550 − (a × 550) | [29] | |
| TCARI | Transformed chlorophyll absorption and reflectance index | 3 × [(R700 − R670) − 0.2 × (R700 − R500)]/(R700/R670) | [30] | |
| MCARI | Modified chlorophyll absorption ratio index | [(R701 − R671) − 0.2 × (R701 − R549)]/(R700/R670) | [31] | |
| RVSI | Red-edge vegetation stress Index | [(R712 + R752)/2] − R732 | [32] | |
| PSRI | Plant senescence reflectance Index | (R680 − R500)/R750 | [33] | |
| ARI | Anthocyanin reflectance index | (R550)−1 − (R700)−1 | [34] | |
| NRI | Nitrogen reflectance index | (R570 − R670)/(R570 + R670) | [35] | |
| TVI | Triangular vegetation index | 0.5 × [120(R750 − R550) − 200(R670 − R550)] | [36] | |
| Differential spectral features | Db | First-order maximal derivative inside blue edge | Blue edge covers 490–530 nm. Db is the maximum value of the first-order derivatives within the blue edge of 41 bands | [37] |
| SDb | Summation of first-order derivatives inside blue edge | Defined by the sum of the first-order derivative values of 41 bands within the blue edge | [37] | |
| λb | Wavelength at Db | λb is the wavelength at Db | [37] | |
| Dy | First-order maximal derivative inside yellow edge | Yellow edge covers 550–582 nm. Dy is the maximum value of the first-order derivatives within the yellow edge of 33 bands | [37] | |
| SDy | Summation of first-order derivatives inside yellow edge | Defined by the sum of the first-order derivative values of 33 bands within the yellow edge | [37] | |
| λy | Wavelength at Dy | λy is the wavelength at Dy | [37] | |
| Dr | First-order maximal derivative inside red edge | Red edge covers 670–737 nm. Dr is the maximum value of the first-order derivatives within the red edge of 68 bands | [37] | |
| SDr | Summation of first-order derivatives inside red edge | Defined by the sum of the first-order derivative values of 68 bands within the red edge | [37] | |
| λr | Wavelength at Dr | λr is the wavelength at Dr | [37] | |
| SDr/SDb | Ratio of SDr and SDb | SDr/SDb | [37] | |
| (SDr − SDb)/(SDr + SDb) | Normalized value of SDr and SDb | (SDr − SDb)/(SDr + SDb) | [37] | |
| (SDr − SDy)/(SDr + SDy) | Normalized value of the SDr and SDy | (SDr − SDy)/(SDr + SDy) | [37] |
| Spectral Parameter | |||
|---|---|---|---|
| Feature | Coefficient of Correlation (R) | Feature | Coefficient of Correlation (R) |
| MCARI | 0.420908 ** | PhRI | 0.050046 ** |
| TCARI | 0.411013 ** | λr | 0.030369 ** |
| Db | 0.344213 ** | Dy | −0.006288 |
| SDb | 0.342047 ** | λy | −0.076195 ** |
| (SDr − SDy)/(SDr + SDy) | 0.326514 ** | NBNDVI | −0.126625 ** |
| TVI | 0.311946 ** | PSRI | −0.163091 ** |
| SDr | 0.295594 ** | RVSI | −0.238656 ** |
| Dr | 0.284244 ** | SDr/SDb | −0.26991 ** |
| PRI | 0.194551 ** | ARI | −0.279479 ** |
| CARI | 0.175568 ** | (SDr − SDb)/(SDr + SDb) | −0.326462 ** |
| NRI | 0.09784 ** | SDy | −0.340163 ** |
| λb | 0.078608 ** | ||
| Algorithm | PCA-WFs | 1%R2-WFs | SS-WFs | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H | S1 | S2 | S3 | S4 | OA(%) | Kappa | H | S1 | S2 | S3 | S4 | OA(%) | Kappa | H | S1 | S2 | S3 | S4 | OA(%) | Kappa | ||
| RF | H | 18 | 0 | 0 | 0 | 0 | 92.0 | 0.90 | 17 | 0 | 0 | 1 | 0 | 88.0 | 0.85 | 18 | 0 | 0 | 0 | 0 | 94.7 | 0.93 |
| S1 | 0 | 13 | 2 | 0 | 0 | 2 | 13 | 0 | 0 | 0 | 0 | 15 | 0 | 0 | 0 | |||||||
| S2 | 0 | 1 | 13 | 0 | 0 | 2 | 2 | 10 | 0 | 0 | 0 | 0 | 13 | 0 | 0 | |||||||
| S3 | 0 | 1 | 0 | 11 | 1 | 0 | 0 | 0 | 13 | 0 | 0 | 0 | 0 | 12 | 1 | |||||||
| S4 | 0 | 0 | 0 | 1 | 14 | 0 | 0 | 0 | 2 | 13 | 0 | 0 | 0 | 1 | 13 | |||||||
| SVM | H | 18 | 0 | 0 | 0 | 0 | 86.7 | 0.83 | 13 | 0 | 1 | 2 | 0 | 58.7 | 0.48 | 11 | 0 | 1 | 0 | 0 | 53.3 | 0.42 |
| S1 | 0 | 13 | 2 | 0 | 0 | 3 | 10 | 2 | 0 | 0 | 4 | 5 | 5 | 1 | 0 | |||||||
| S2 | 1 | 2 | 11 | 0 | 0 | 1 | 1 | 11 | 0 | 0 | 1 | 2 | 7 | 2 | 2 | |||||||
| S3 | 0 | 1 | 0 | 11 | 1 | 0 | 1 | 0 | 11 | 2 | 3 | 3 | 6 | 6 | 2 | |||||||
| S4 | 0 | 1 | 0 | 2 | 12 | 2 | 0 | 0 | 1 | 14 | 0 | 0 | 1 | 2 | 11 | |||||||
| BPNN | H | 11 | 1 | 0 | 0 | 0 | 84.0 | 0.80 | 4 | 8 | 3 | 0 | 0 | 70.7 | 0.64 | 10 | 1 | 1 | 0 | 0 | 70.7 | 0.64 |
| S1 | 0 | 12 | 3 | 0 | 0 | 0 | 12 | 3 | 0 | 0 | 1 | 10 | 4 | 0 | 0 | |||||||
| S2 | 0 | 2 | 12 | 0 | 0 | 4 | 2 | 5 | 0 | 0 | 0 | 2 | 11 | 0 | 0 | |||||||
| S3 | 0 | 1 | 2 | 14 | 3 | 0 | 1 | 4 | 8 | 8 | 2 | 1 | 1 | 8 | 8 | |||||||
| S4 | 0 | 0 | 0 | 0 | 14 | 1 | 0 | 0 | 0 | 14 | 0 | 0 | 0 | 0 | 14 | |||||||
| Algorithm | PCA-WFs | SFs | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H | S1 | S2 | S3 | S4 | OA(%) | Kappa | H | S1 | S2 | S3 | S4 | OA(%) | Kappa | ||
| RF | H | 18 | 0 | 0 | 0 | 0 | 92.0 | 0.90 | 8 | 2 | 1 | 1 | 0 | 45.3 | 0.32 |
| S1 | 0 | 13 | 2 | 0 | 0 | 8 | 5 | 1 | 1 | 0 | |||||
| S2 | 0 | 1 | 13 | 0 | 0 | 5 | 2 | 3 | 1 | 3 | |||||
| S3 | 0 | 1 | 0 | 11 | 1 | 3 | 3 | 5 | 7 | 2 | |||||
| S4 | 0 | 0 | 0 | 1 | 14 | 0 | 0 | 1 | 2 | 11 | |||||
| SVM | H | 18 | 0 | 0 | 0 | 0 | 86.7 | 0.83 | 3 | 4 | 1 | 6 | 2 | 41.3 | 0.26 |
| S1 | 0 | 13 | 2 | 0 | 0 | 3 | 8 | 0 | 4 | 0 | |||||
| S2 | 1 | 2 | 11 | 0 | 0 | 5 | 5 | 0 | 1 | 2 | |||||
| S3 | 0 | 1 | 0 | 11 | 1 | 2 | 3 | 1 | 5 | 3 | |||||
| S4 | 0 | 1 | 0 | 2 | 12 | 1 | 0 | 0 | 1 | 15 | |||||
| BPNN | H | 11 | 1 | 0 | 0 | 0 | 84.0 | 0.80 | 4 | 1 | 6 | 4 | 1 | 44.0 | 0.30 |
| S1 | 0 | 12 | 3 | 0 | 0 | 2 | 6 | 3 | 4 | 0 | |||||
| S2 | 0 | 2 | 12 | 0 | 0 | 4 | 2 | 3 | 4 | 0 | |||||
| S3 | 0 | 1 | 2 | 14 | 3 | 1 | 3 | 1 | 7 | 2 | |||||
| S4 | 0 | 0 | 0 | 0 | 14 | 1 | 0 | 2 | 1 | 13 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, X.; Feng, Y.; Guo, A.; Huang, W.; Cai, Z.; Dong, Y.; Guo, J.; Qian, B.; Hao, Z.; Chen, G.; et al. Detection of Rubber Tree Powdery Mildew from Leaf Level Hyperspectral Data Using Continuous Wavelet Transform and Machine Learning. Remote Sens. 2024, 16, 105. https://doi.org/10.3390/rs16010105
Cheng X, Feng Y, Guo A, Huang W, Cai Z, Dong Y, Guo J, Qian B, Hao Z, Chen G, et al. Detection of Rubber Tree Powdery Mildew from Leaf Level Hyperspectral Data Using Continuous Wavelet Transform and Machine Learning. Remote Sensing. 2024; 16(1):105. https://doi.org/10.3390/rs16010105
Chicago/Turabian StyleCheng, Xiangzhe, Yuyun Feng, Anting Guo, Wenjiang Huang, Zhiying Cai, Yingying Dong, Jing Guo, Binxiang Qian, Zhuoqing Hao, Guiliang Chen, and et al. 2024. "Detection of Rubber Tree Powdery Mildew from Leaf Level Hyperspectral Data Using Continuous Wavelet Transform and Machine Learning" Remote Sensing 16, no. 1: 105. https://doi.org/10.3390/rs16010105
APA StyleCheng, X., Feng, Y., Guo, A., Huang, W., Cai, Z., Dong, Y., Guo, J., Qian, B., Hao, Z., Chen, G., & Liu, Y. (2024). Detection of Rubber Tree Powdery Mildew from Leaf Level Hyperspectral Data Using Continuous Wavelet Transform and Machine Learning. Remote Sensing, 16(1), 105. https://doi.org/10.3390/rs16010105









