Sea Surface Moving Target Detection Using a Modified Keystone Transform on Wideband Radar Data
Abstract
1. Introduction
2. Problem Formulation
2.1. Received Signal Model of Moving RSTs
2.2. Clutter Model
3. Proposed Approach
3.1. RCM Correction Based on Modified KT
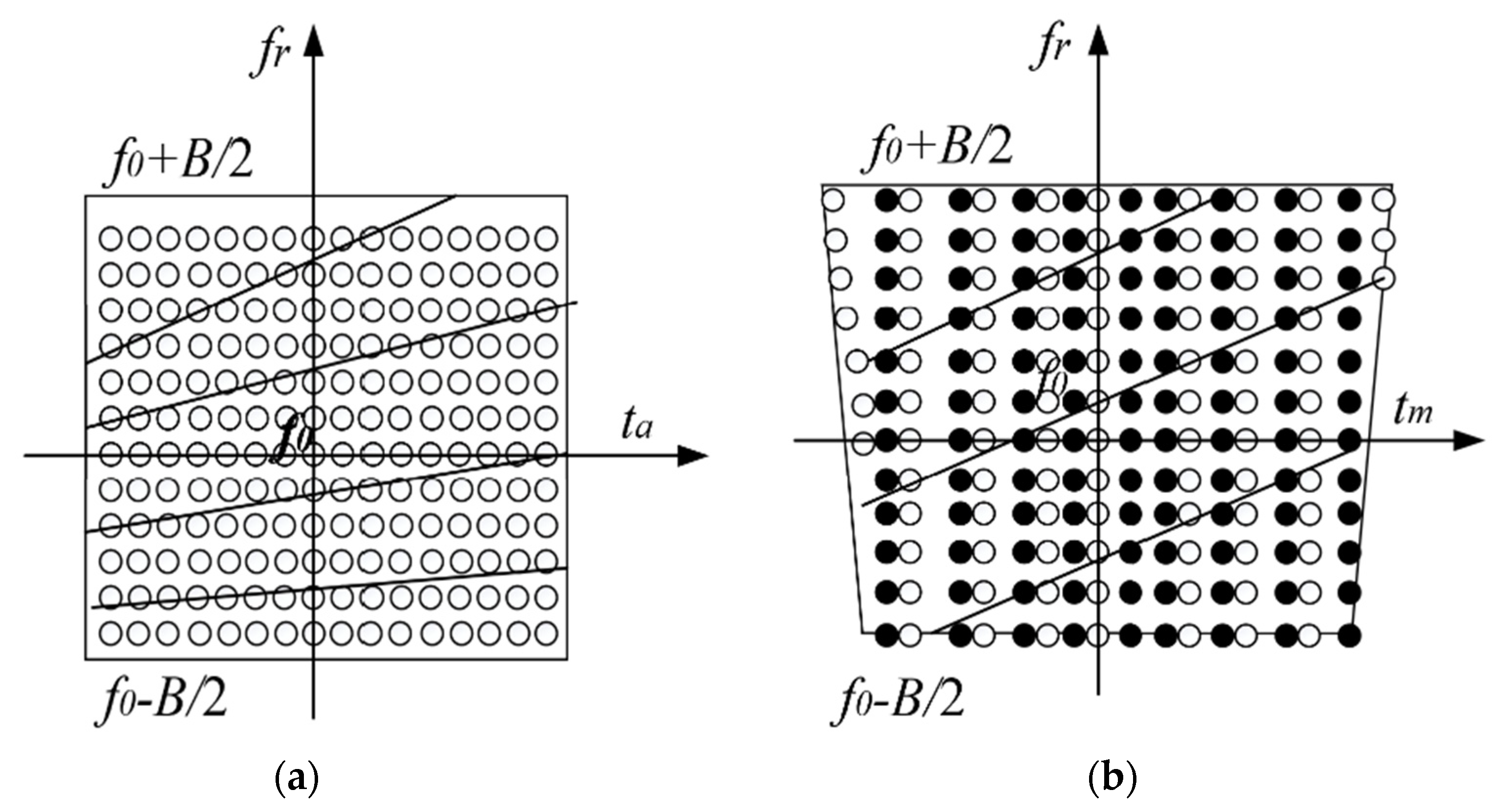
3.1.1. Review of the Traditional KT Algorithm
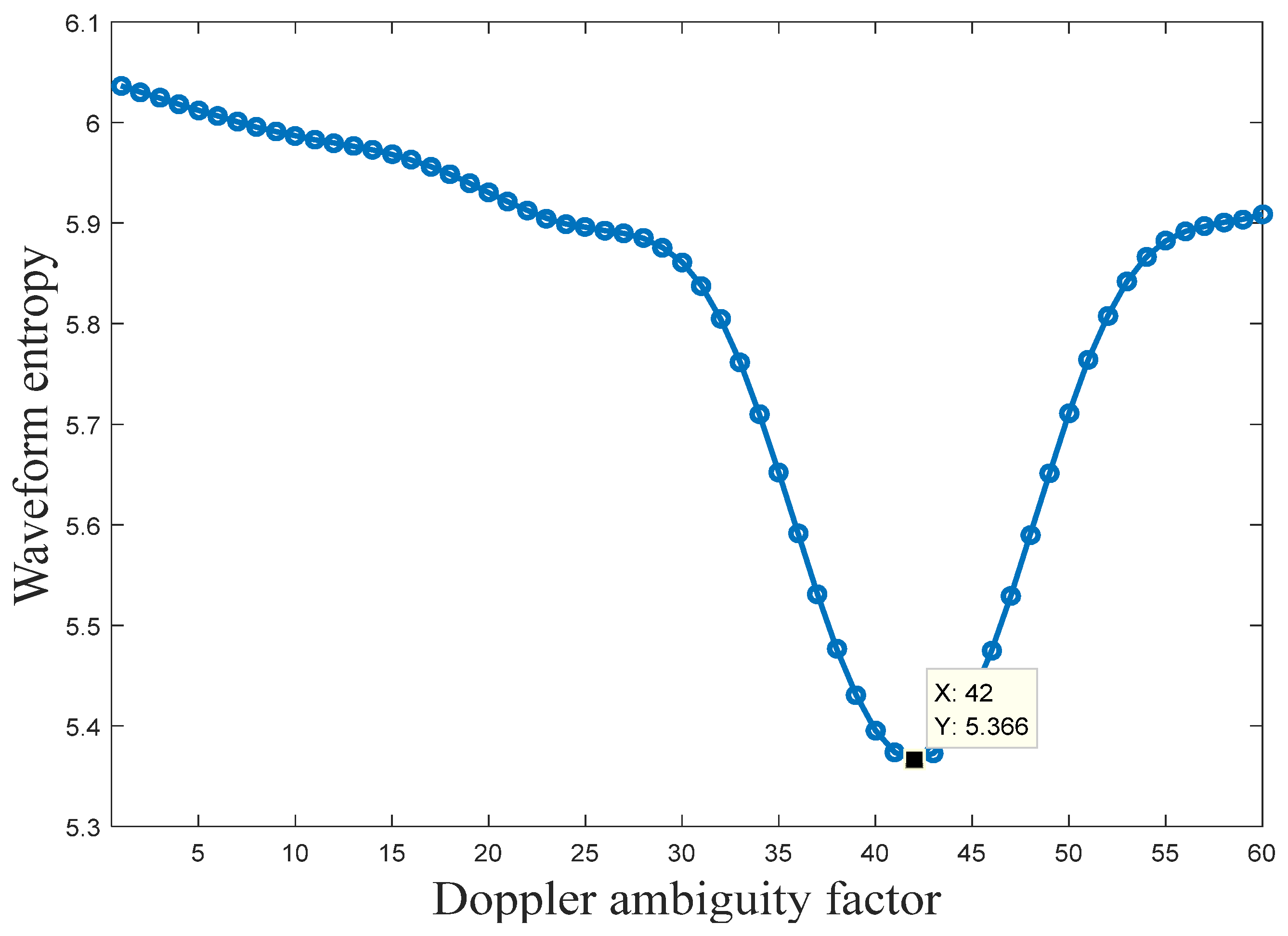
3.1.2. KT Algorithm Based on Waveform Entropy Minimization
3.1.3. MKT Algorithm
- Fitness Function
- 2.
- HPO Algorithm
- Step 1: Randomly initialize the population in the HPO, which can be expressed as:
- Step 2: Perform the search mechanism, which consists of two random steps:
- Step 3: Determine the hunter and prey, which are evaluated based on a random process written as follows:
3.2. Detection Method
3.2.1. Traditional EI Method
3.2.2. IEI Method
- 3.
- Optimized Test Statistic
- 4.
- Adaptive Threshold
- 5.
- Adaptive Detection Window
- Step 1: For a certain type of target, set the sliding window length area and sliding step value on the assumption that the target size range is known, which does not require obtaining the precise target size.
- Step 2: Calculate the test statistics in all sliding windows, make the sliding window corresponding to the maximum test statistic the detection window, perform the adaptive threshold processing, and then save the maximum test statistic as the threshold and the corresponding detection window length .
- Step 3: Make a decision. Under the hypothesis (with different SCR cases), if the test statistic (the detection window length corresponding to the test statistic should be close to or equal to that of the threshold ), then the target is absent. It is noted that the detection statistic and the threshold are obtained in the same way, the only difference is that the echoes of the threshold do not contain the target signal but are pure clutter.
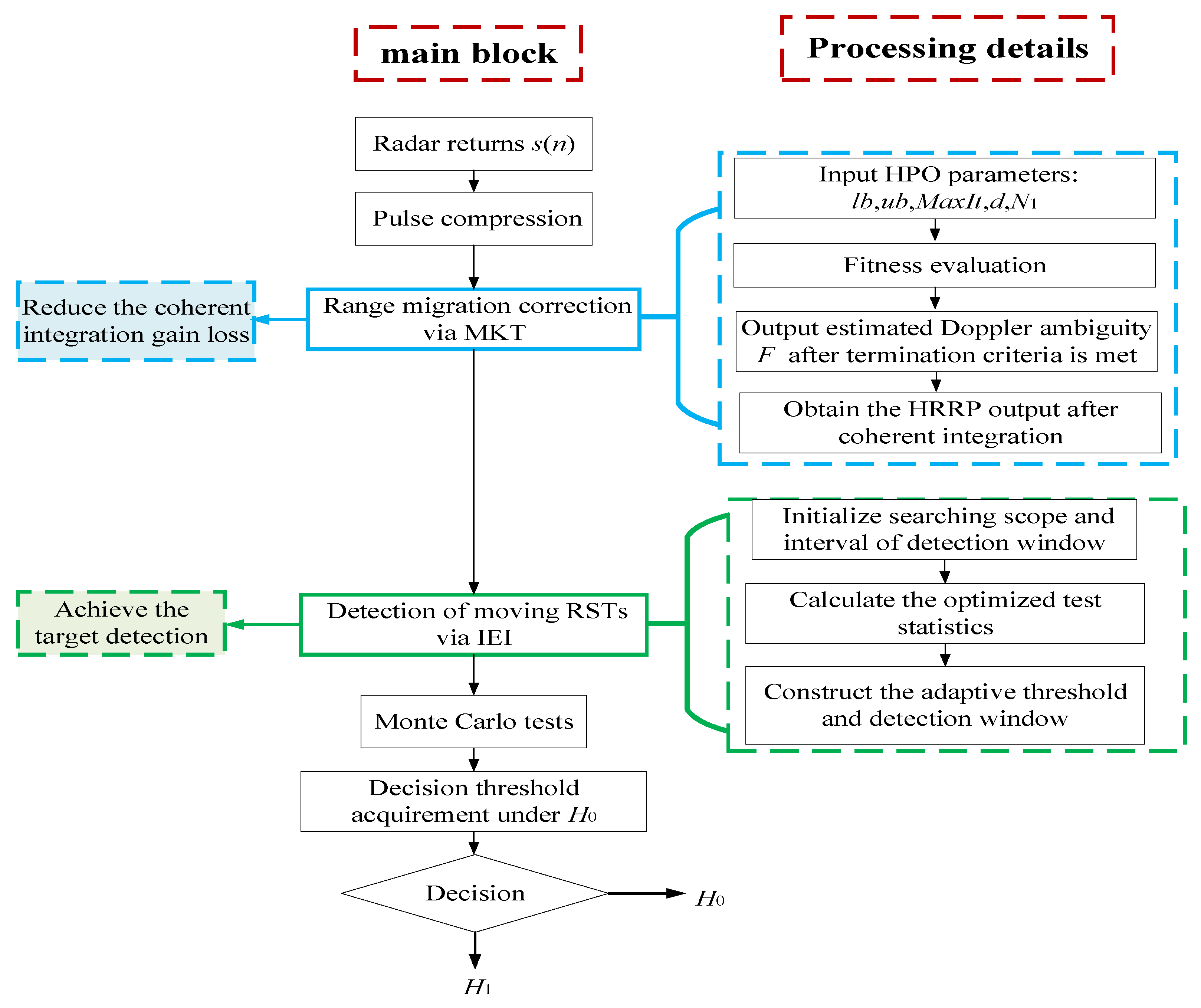
3.3. Detailed Procedure of the Proposed Method
4. Experiments and Discussions
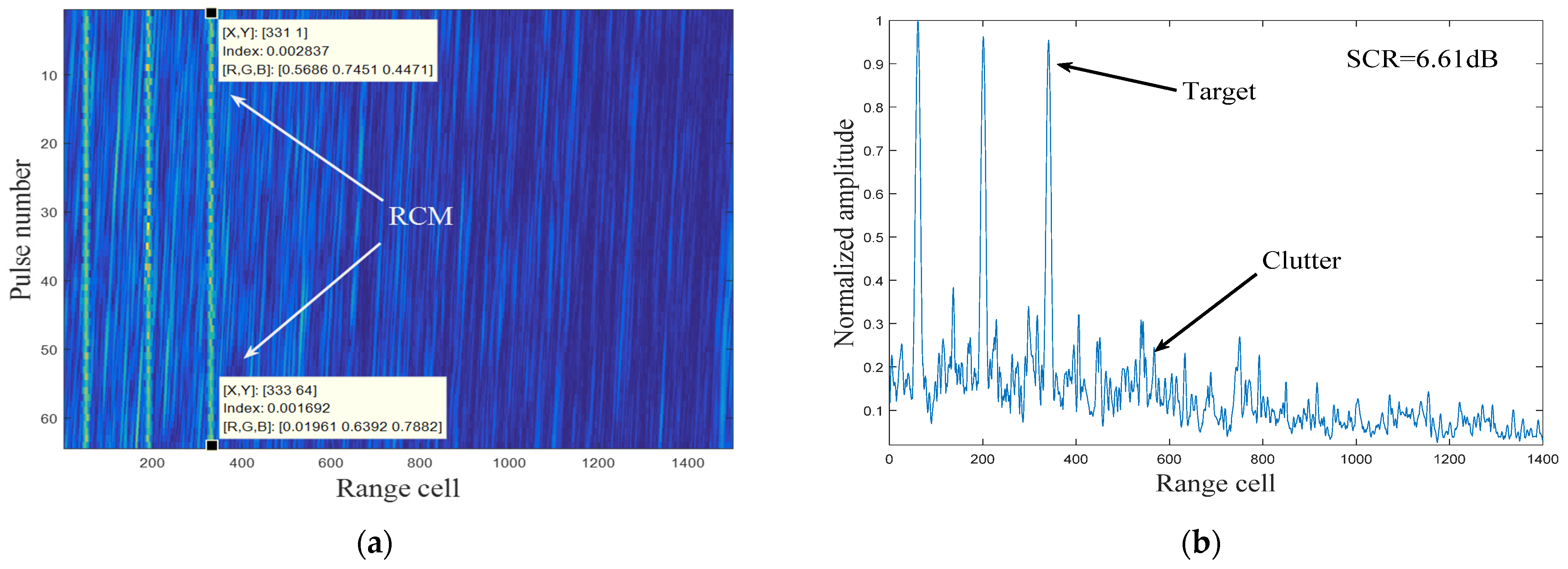
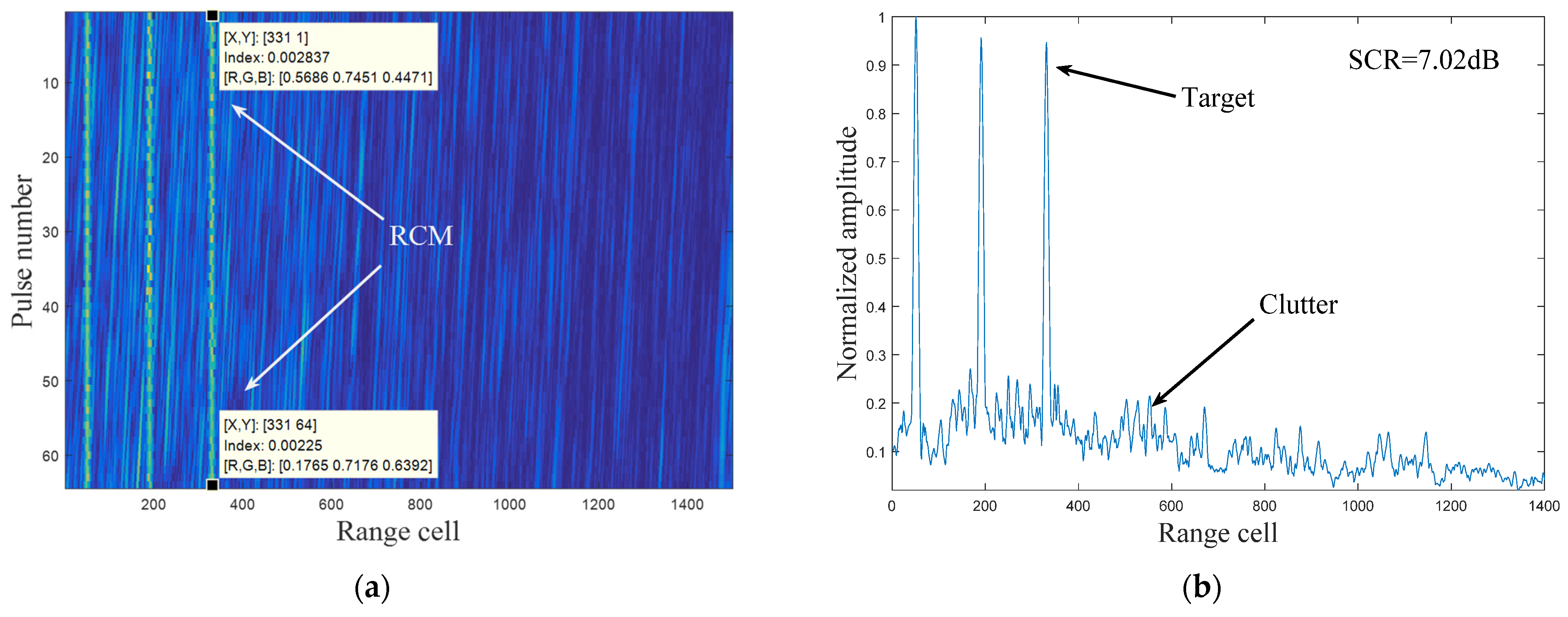
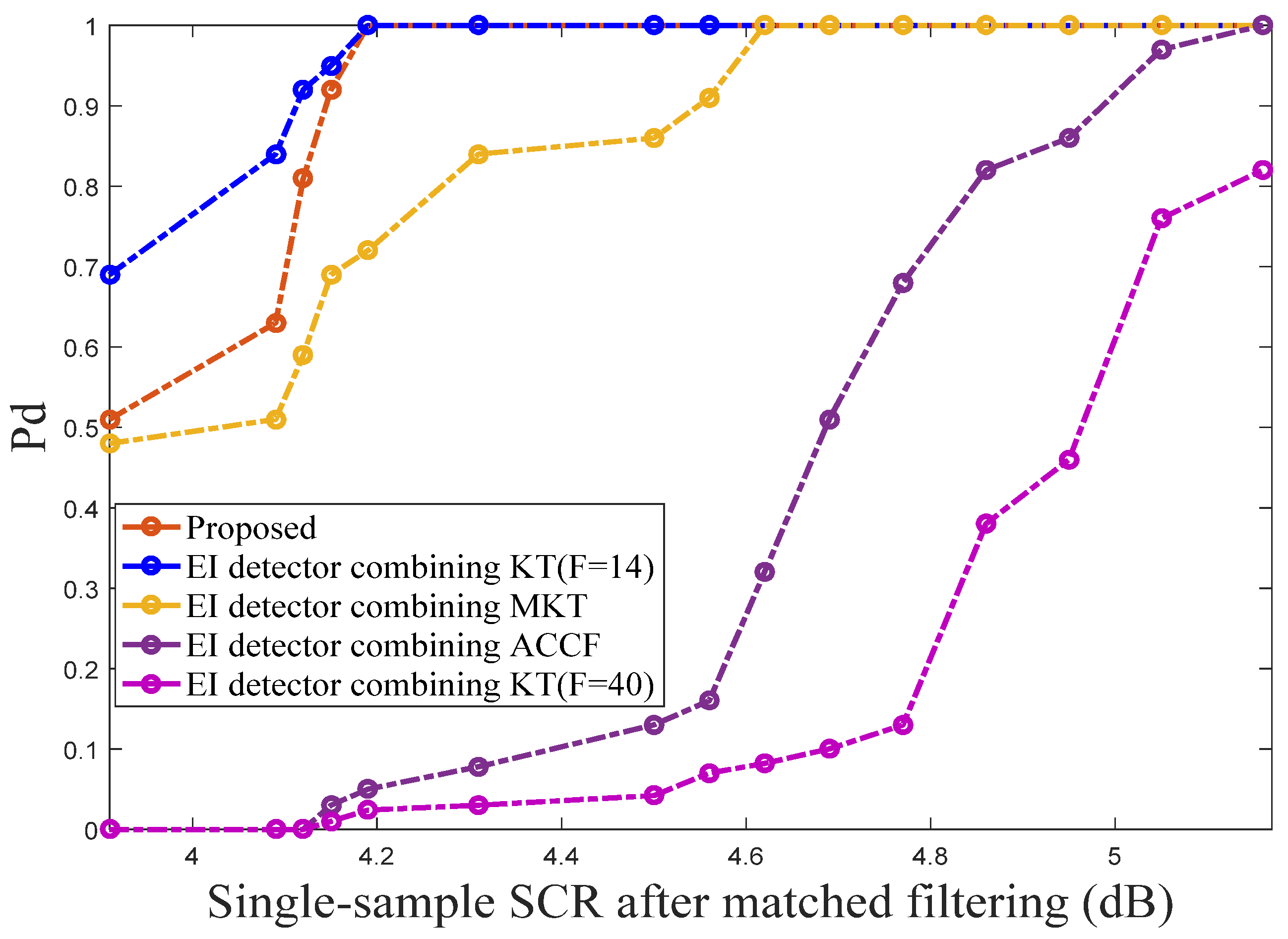
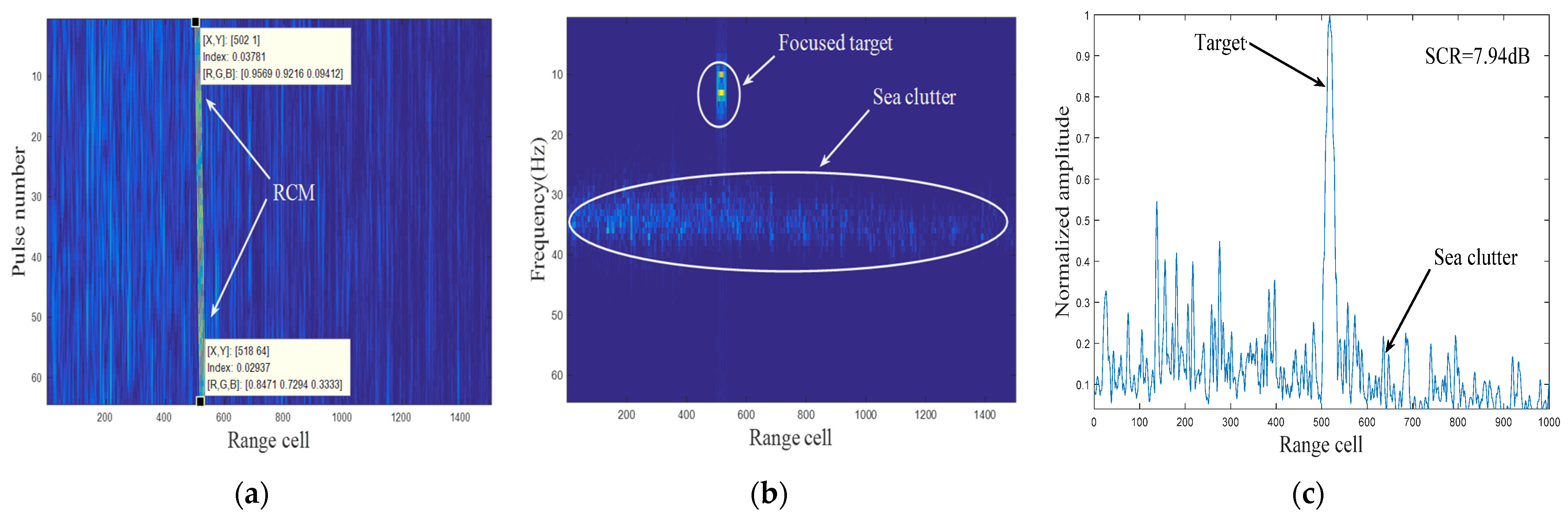
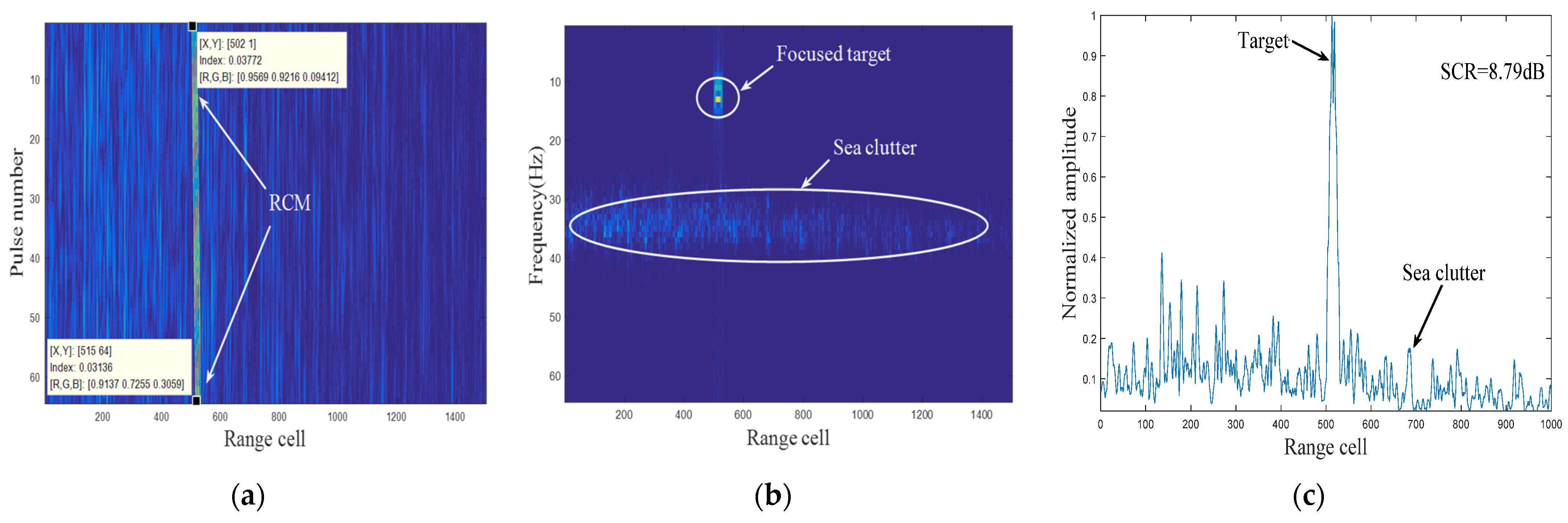
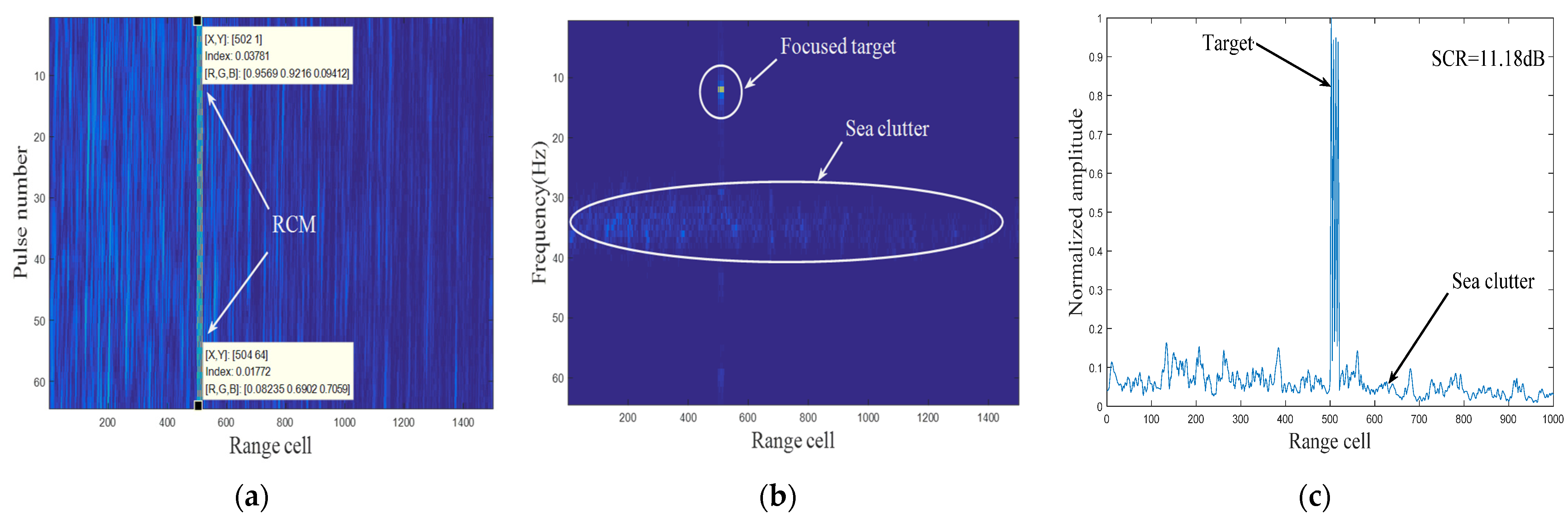
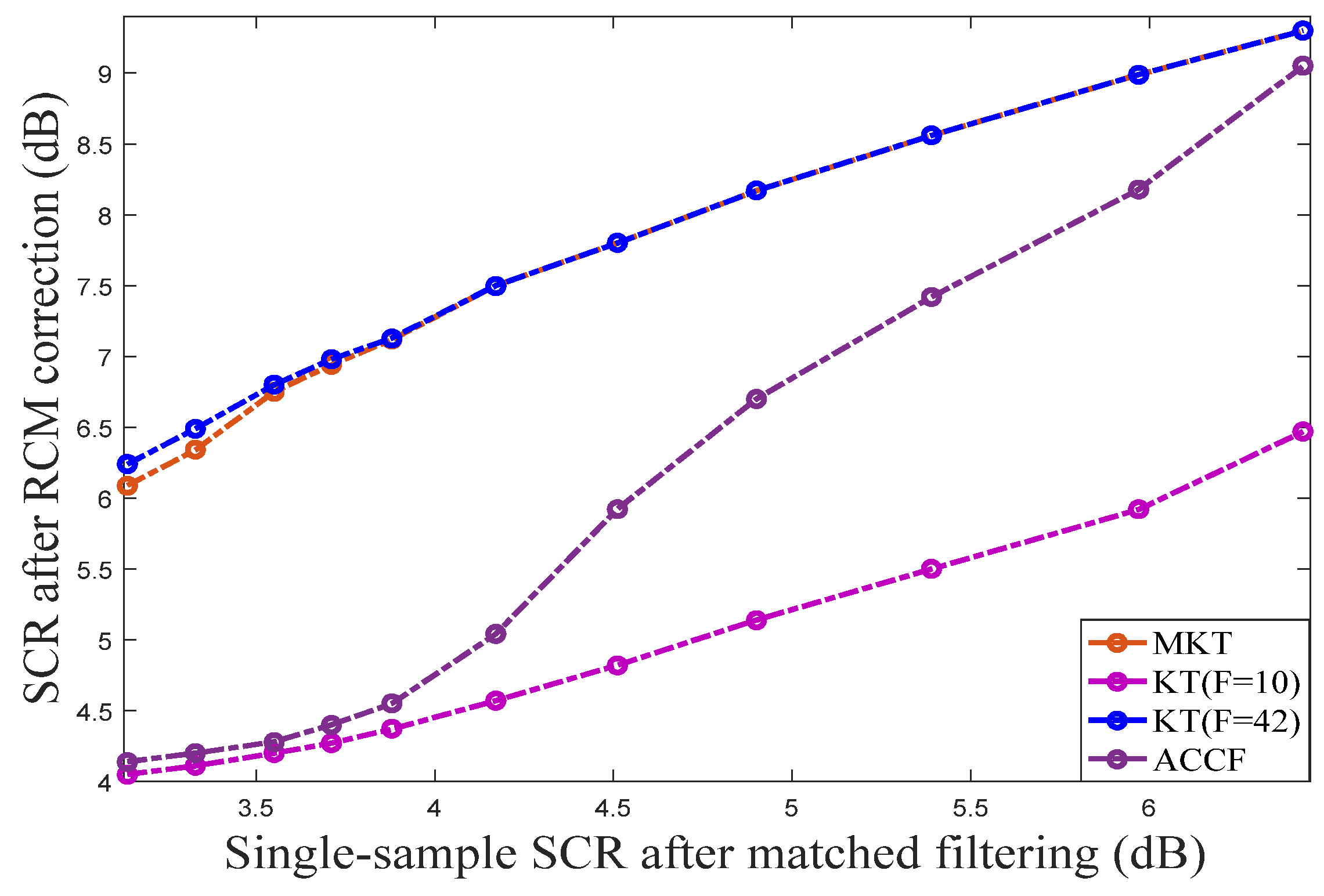
4.1. Experiment Analysis Based on Simulated Sea Clutter
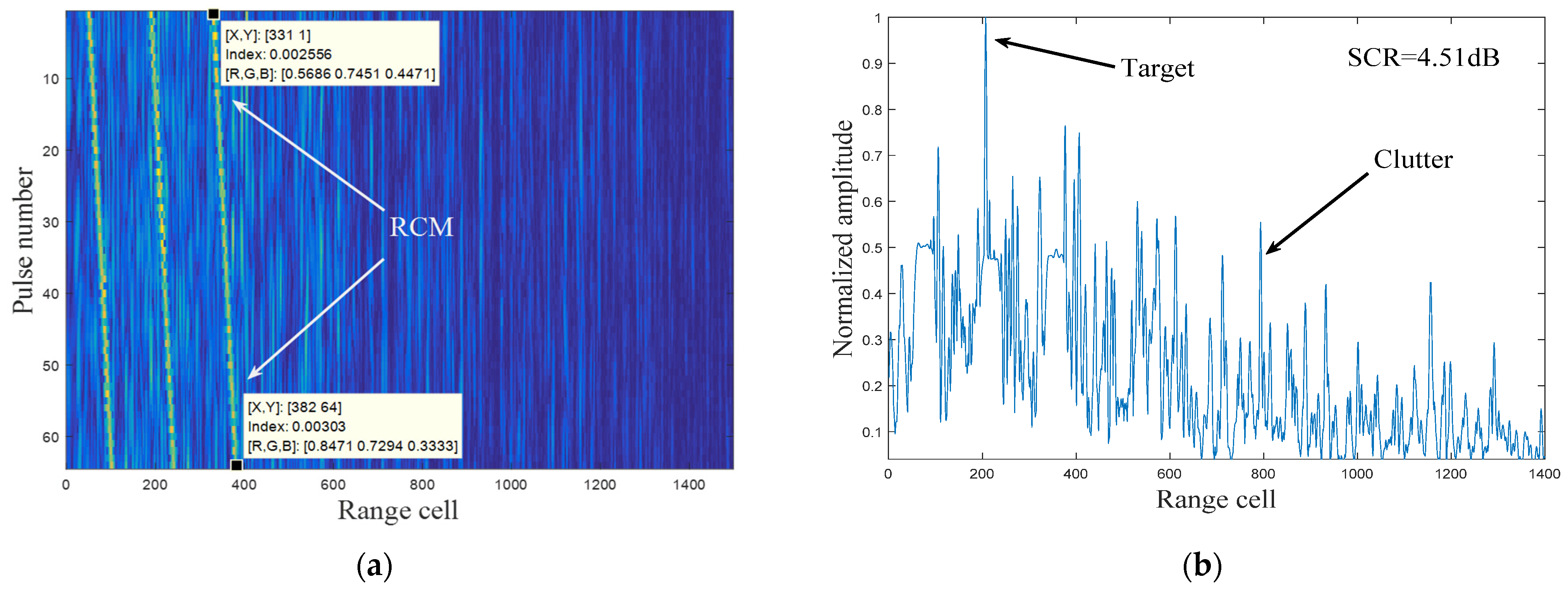
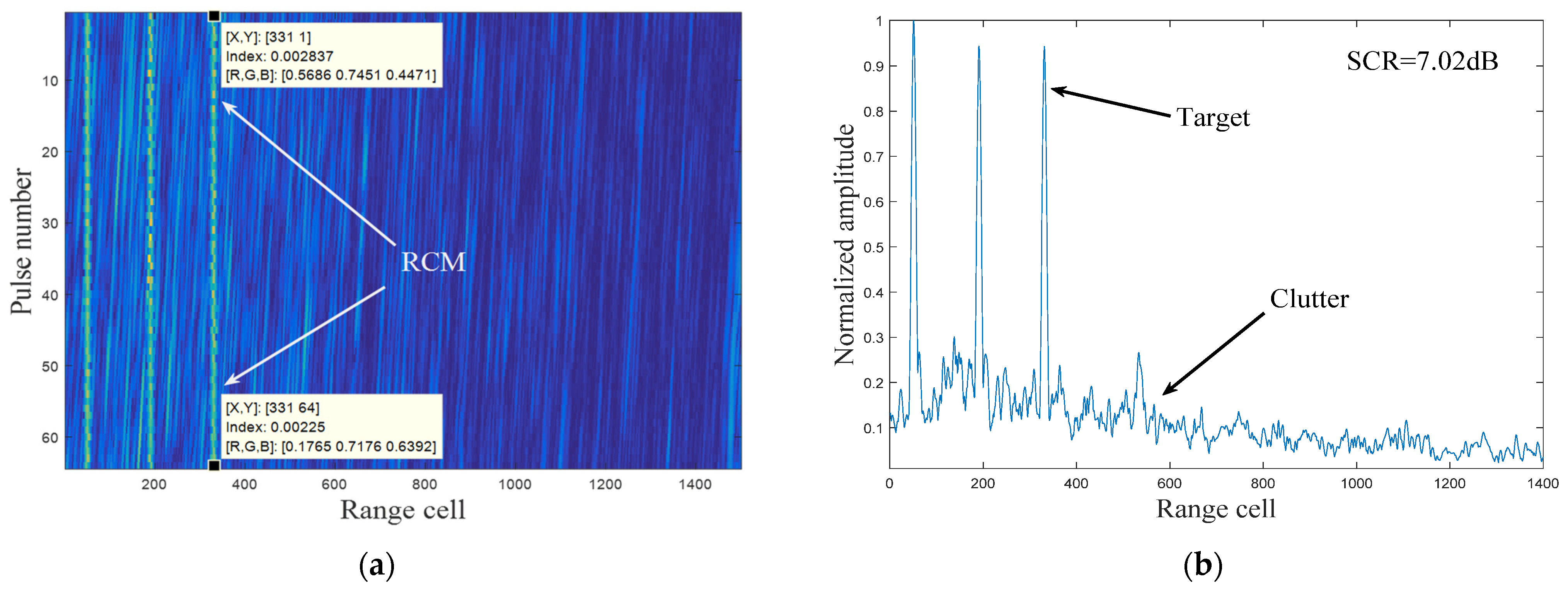
4.2. Experiment Analysis Based on Real Measured Clutter
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhen, D.; Zhang, Z.; Yu, W. An adaptive OFDM detection strategy for range and Doppler spread targets in non-Gaussian clutter. IEEE Access 2018, 6, 61223–61231. [Google Scholar]
- Yu, X.; Chen, X.; Huang, Y.; Zhang, L.; Guan, J.; He, Y. Radar moving target detection in clutter background via adaptive dual-threshold sparse Fourier transform. IEEE Access 2019, 7, 58200–58211. [Google Scholar] [CrossRef]
- Bao, M.; Jia, B.; Li, Y.; Guo, L.; Xing, M. Coherent integration for maneuvering target detection at low SNR based on Radon-general linear chirplet transform. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4027505. [Google Scholar] [CrossRef]
- Ma, J.; Huang, P.; Yu, J.; Liang, G.; Liao, G. An efficient coherent integration method for maneuvering target detection with nonuniform pulse sampling based on filterbank framework. IEEE Geosci. Remote Sens. Lett. 2020, 17, 2045–2049. [Google Scholar] [CrossRef]
- Carlson, B.; Evans, E.; Wilson, S. Search radar detection and track with the Hough transform. III. Detection performance with binary integration. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 116–125. [Google Scholar] [CrossRef]
- Ehlers, F.; Ricci, G.; Orlando, D. Batch tracking algorithm for multi-static sonars. IET Radar Sonar Navigat. 2012, 6, 746–752. [Google Scholar] [CrossRef]
- Sharif, M.; Abeysekera, S. Efficient wideband signal parameter estimation using a Radon-ambiguity transform slice. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 673–688. [Google Scholar] [CrossRef]
- Xu, J.; Yan, L.; Zhou, X.; Long, T. Adaptive radon–Fourier transform for weak radar target detection. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1641–1662. [Google Scholar] [CrossRef]
- Li, X.; Cui, G.; Kong, L.; Yi, W. Fast non-searching method for maneuvering target detection and motion parameters estimation. IEEE Trans. Signal Process. 2016, 64, 2232–2244. [Google Scholar] [CrossRef]
- Zheng, J.; Su, T.; Zhu, W.; He, X.; Liu, Q. Radar high-speed target detection based on the scaled inverse Fourier transform. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 1108–1119. [Google Scholar] [CrossRef]
- Li, X.; Cui, G.; Yi, W.; Kong, L. Sequence-reversing transform based coherent integration for high-speed target detection. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1573–1580. [Google Scholar] [CrossRef]
- Li, X.; Cui, G.; Yi, W.; Kong, L. Radar maneuvering target detection and motion parameter estimation based on TRT-SGRFT. Signal Process. 2017, 133, 107–116. [Google Scholar] [CrossRef]
- Li, X.; Cui, G.; Yi, W.; Kong, L. Fast coherent integration for maneuvering target with high-order range migration via TRT-SKT-LVD. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2803–2814. [Google Scholar] [CrossRef]
- Li, G.; Xia, X.; Peng, Y. Doppler keystone transform: An approach suitable for parallel implementation of SAR moving target imaging. IEEE Geosci. Remote Sens. Lett. 2008, 5, 573–577. [Google Scholar] [CrossRef]
- Perry, R.; Dipietro, R.; Fante, R. SAR imaging of moving targets. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 188–200. [Google Scholar] [CrossRef]
- Bai, B.; Ding, Y.; Li, X.; Liu, Y. A radar detection method of plasma-sheath-covered target based on the improved keystone algorithm. Remote Sens. 2022, 14, 4869. [Google Scholar] [CrossRef]
- Dai, Z.; Zhang, X.; Fang, H.; Bai, Y. High accuracy velocity measurement based on keystone transform using entropy minimization. Chin. J. Electron. 2016, 25, 774–778. [Google Scholar] [CrossRef]
- Sun, G.; Xing, M.; Xia, X.; Wu, Y. Robust ground moving-target imaging using deramp–keystone processing. IEEE Trans. Geosci. Remote Sens. 2013, 51, 966–982. [Google Scholar] [CrossRef]
- Yu, X.; Chen, X.; Guan, J.; Huang, Y. Radar marine maneuvering target detection via high resolution sparse fractional ambiguity function. J. Commun. 2019, 40, 72–84. [Google Scholar]
- Chen, X.; Guan, J.; Wang, G.; Ding, H.; Huang, Y. Fast and refined processing of radar maneuvering target based on hierarchical detection via sparse fractional representation. IEEE Access 2019, 7, 149878–149889. [Google Scholar] [CrossRef]
- Li, X.; Sun, Z.; Yi, W.; Cui, G.; Kong, L. Radar detection and parameter estimation of high-speed target based on MART-LVT. IEEE Sens. J. 2019, 19, 1478–1486. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, J.; Chen, H.; Yang, W. Adaptive robust radar target detector based on gradient test. Remote Sens. 2022, 14, 5236. [Google Scholar] [CrossRef]
- Liu, J.; Gao, M.; Zheng, J. Model-based wald test for adaptive range-spread target detection. IEEE Access 2020, 8, 73259–73266. [Google Scholar] [CrossRef]
- Huges, P.K. A high-resolution radar detection strategy. IEEE Trans. Aerosp. Electron. Syst. 1983, 19, 663–667. [Google Scholar] [CrossRef]
- Gerlach, K.; Steiner, M.; Lin, F.C. Detection of a spatially distributed target in white noise. IEEE Signal Process. Lett. 1997, 4, 198–200. [Google Scholar] [CrossRef]
- Wang, Z.; He, Z.; He, Q.; Cheng, Z. Persymmetric range-spread targets detection in compound Gaussian sea clutter with inverse Gaussian texture. IEEE Geosci. Remote Sens. Lett. 2022, 19, 8018305. [Google Scholar] [CrossRef]
- Ollila, E.; Tyler, D.E.; Koivunen, V.; Poor, H.V. Compound-Gaussian clutter modeling with an inverse Gaussian texture distribution. IEEE Signal Process. Lett. 2012, 19, 876–879. [Google Scholar] [CrossRef]
- Ciuonzo, D.; Maio, A.D.; Orlando, D. A unifying framework for adaptive radar detection in homogeneous plus structured interference—Part I: On the maximal invariant statistic. IEEE Trans. Signal Process. 2016, 64, 2894–2906. [Google Scholar] [CrossRef]
- Ciuonzo, D.; Maio, A.D.; Orlando, D. A unifying framework for adaptive radar detection in homogeneous plus structured interference—Part II: Detectors design. IEEE Trans. Signal Process. 2016, 64, 2907–2919. [Google Scholar] [CrossRef]
- Tang, M.; Rong, Y.; Maio, A.D.; Chen, C.; Zhou, J. Adaptive radar detection in Gaussian disturbance with structured covariance matrix via invariance theory. IEEE Trans. Signal Process. 2019, 67, 5671–5685. [Google Scholar] [CrossRef]
- Tang, M.; Rong, Y.; Li, X.; Zhou, J. Invariance theory for adaptive detection in non-Gaussian clutter. IEEE Trans. Signal Process. 2020, 68, 2045–2060. [Google Scholar] [CrossRef]
- Huang, B.; Jian, J.; Basit, A.; Gui, R.; Wang, W. Adaptive distributed target detection for FDA-MIMO radar in Gaussian clutter without training data. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 2961–2971. [Google Scholar] [CrossRef]
- Chen, X.; Chen, B.; Guan, J.; Huang, Y.; He, Y. Space-range-doppler focus-based low-observable moving target detection using frequency diverse array MIMO radar. IEEE Access 2018, 6, 43892–43904. [Google Scholar] [CrossRef]
- Gui, R.; Wang, W.; Zheng, Z. Low-complexity GLRT for FDA radar without training data. Digit. Signal Process. 2020, 107, 102861. [Google Scholar] [CrossRef]
- Huang, B.; Basit, A.; Wang, W.; Zhang, S. Adaptive detection with Bayesian framework for FDA-MIMO radar. IEEE Geosci. Remote Sens. Lett. 2022, 19, 3509505. [Google Scholar] [CrossRef]
- Huang, P.; Xia, X.; Liao, G.; Yang, Z.; Zhou, J.; Liu, X. Ground moving target refocusing in SAR imagery using scaled GHAF. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1030–1045. [Google Scholar] [CrossRef]
- Sun, Z.; Li, X.; Cui, G. A fast approach for detection and parameter estimation of maneuvering target with complex motions in coherent radar system. IEEE Trans. Veh. Technol. 2021, 70, 10278–10290. [Google Scholar] [CrossRef]
- Du, L.; Liu, H.; Bao, Z.; Xing, M. Radar HRRP target recognition based on higher order spectra. IEEE Trans. Signal Process. 2005, 53, 2359–2368. [Google Scholar]
- Li, D.; Zhan, M.; Liu, H.; Liao, Y. A robust translational motion compensation method for ISAR imaging based on keystone transform and fractional Fourier transform under low snr environment. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2140–2156. [Google Scholar] [CrossRef]
- Husam, A.R.; Baseem, K.; Ahmed, A.Z.D. Accurate parameters estimation of three diode model of photovoltaic modules using hunter–prey and wild horse optimizers. IEEE Access 2022, 10, 87435–87453. [Google Scholar]





| SCR/dB | KT Based on Entropy Minimization | MKT |
|---|---|---|
| 4.77 | 403.4 s | 221.6 s |
| 5.19 | 392.6 s | 224.9 s |
| 5.74 | 373.7 s | 223.7 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, J.; Fu, X.; Zhao, C.; Feng, C. Sea Surface Moving Target Detection Using a Modified Keystone Transform on Wideband Radar Data. Remote Sens. 2023, 15, 2284. https://doi.org/10.3390/rs15092284
Chang J, Fu X, Zhao C, Feng C. Sea Surface Moving Target Detection Using a Modified Keystone Transform on Wideband Radar Data. Remote Sensing. 2023; 15(9):2284. https://doi.org/10.3390/rs15092284
Chicago/Turabian StyleChang, Jiayun, Xiongjun Fu, Congxia Zhao, and Cheng Feng. 2023. "Sea Surface Moving Target Detection Using a Modified Keystone Transform on Wideband Radar Data" Remote Sensing 15, no. 9: 2284. https://doi.org/10.3390/rs15092284
APA StyleChang, J., Fu, X., Zhao, C., & Feng, C. (2023). Sea Surface Moving Target Detection Using a Modified Keystone Transform on Wideband Radar Data. Remote Sensing, 15(9), 2284. https://doi.org/10.3390/rs15092284







