GRACE Downscaler: A Framework to Develop and Evaluate Downscaling Models for GRACE
Abstract
1. Introduction
2. Materials and Methods
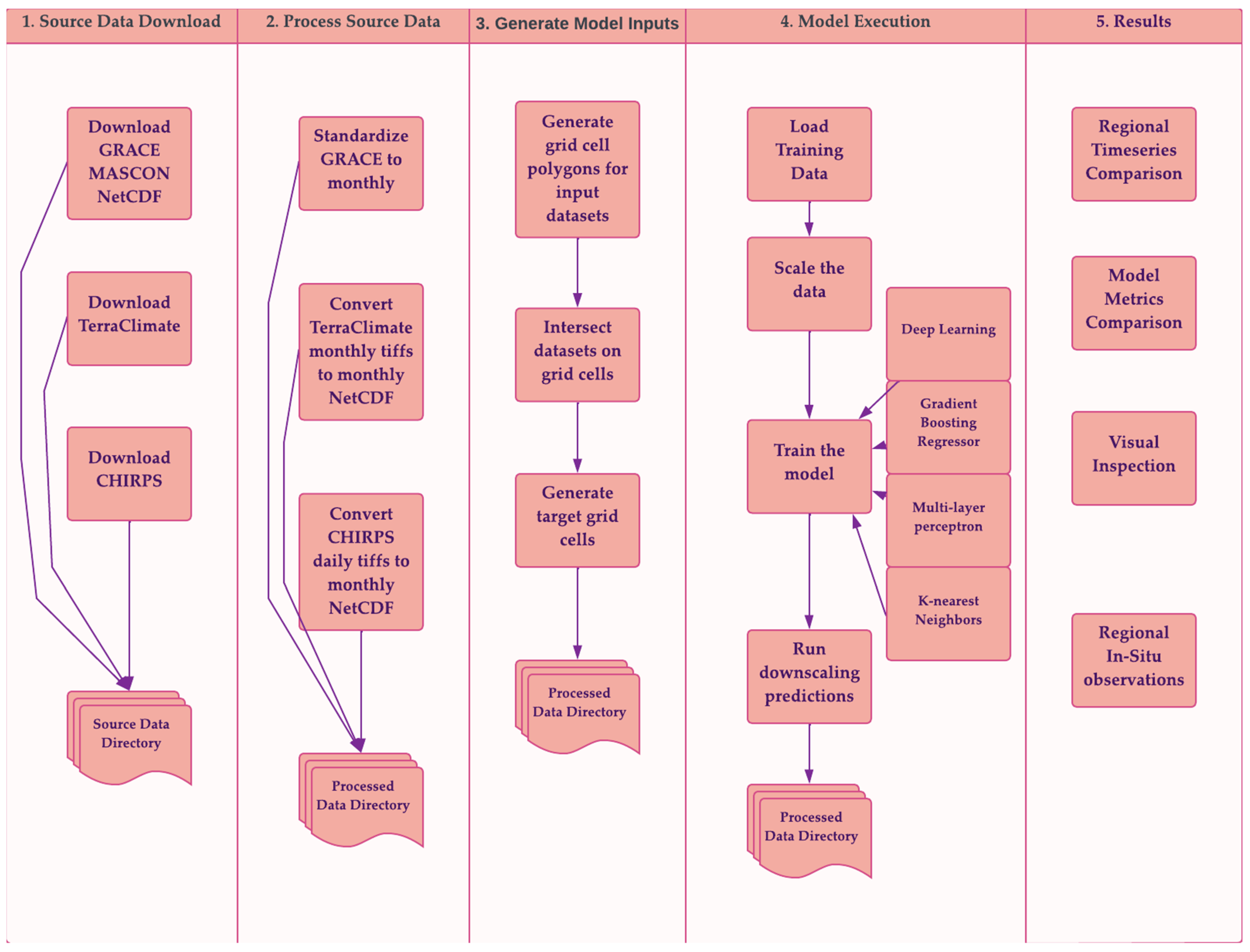
2.1. Project Template
2.2. Datasets
2.2.1. GRACE Data
2.2.2. Climate Hazards Group Infrared Precipitation with Stations (CHIRPS)
2.2.3. TerraClimate
2.2.4. Rationale of Data Source Selection
2.3. Data Processing
2.3.1. Download Source Data
2.3.2. Process Source Data
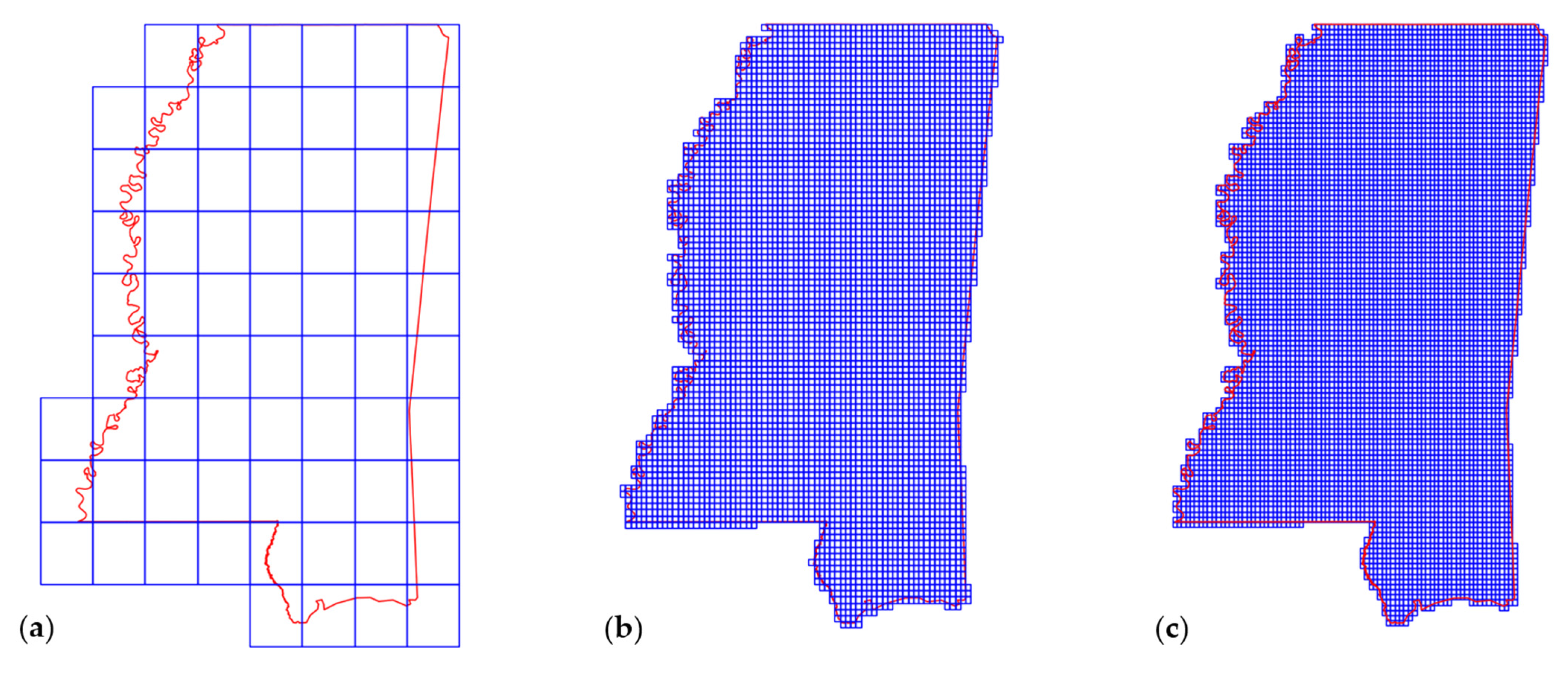
2.3.3. Generate Model Inputs
2.4. Models
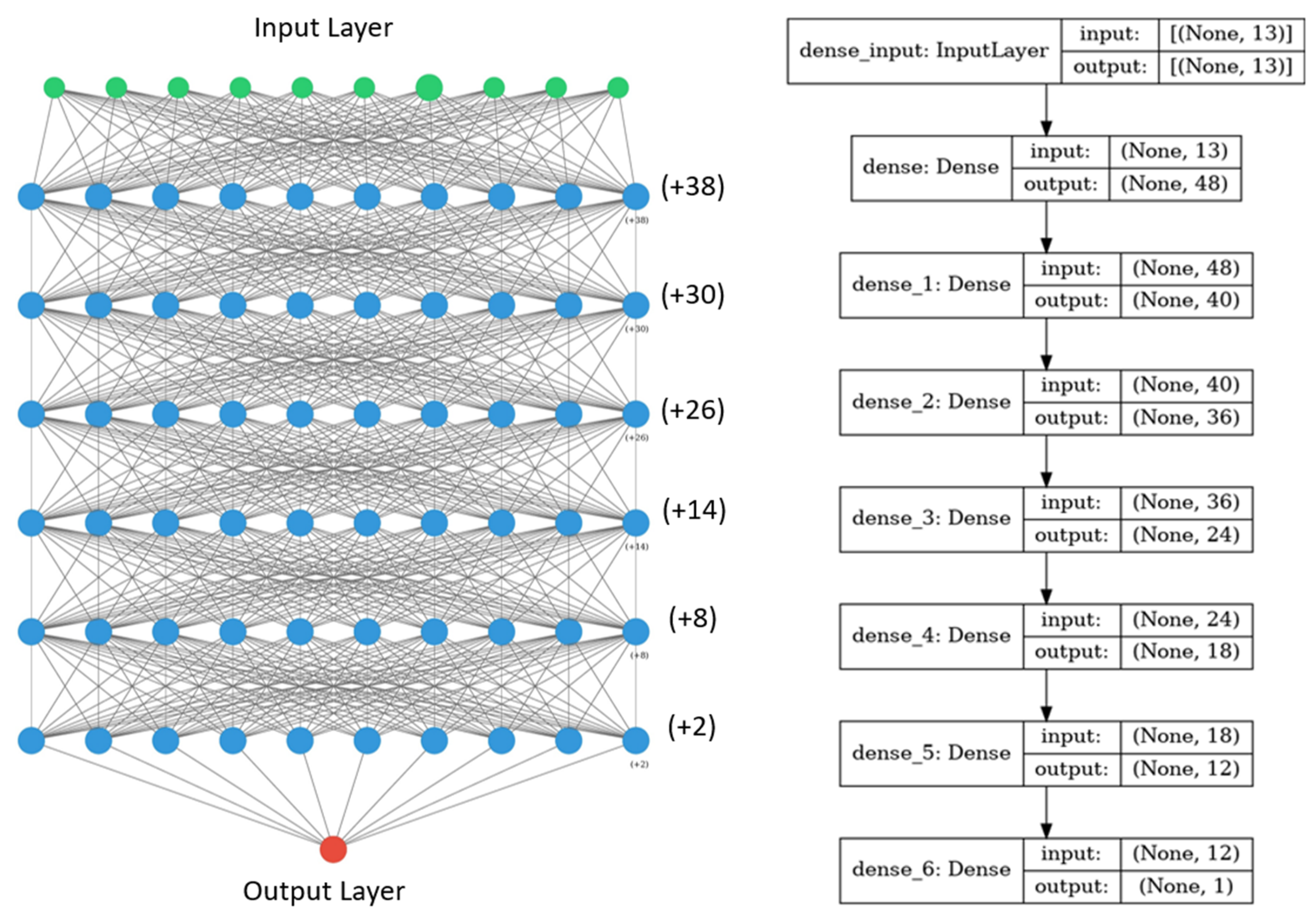
2.4.1. Deep Learning Model
2.4.2. Gradient Boosting Regressor Model
2.4.3. Multi-Layer Perceptron Regressor Model
2.4.4. K-Nearest Neighbors Regressor Model
3. Results
3.1. Model Metrics
3.2. Model Validation
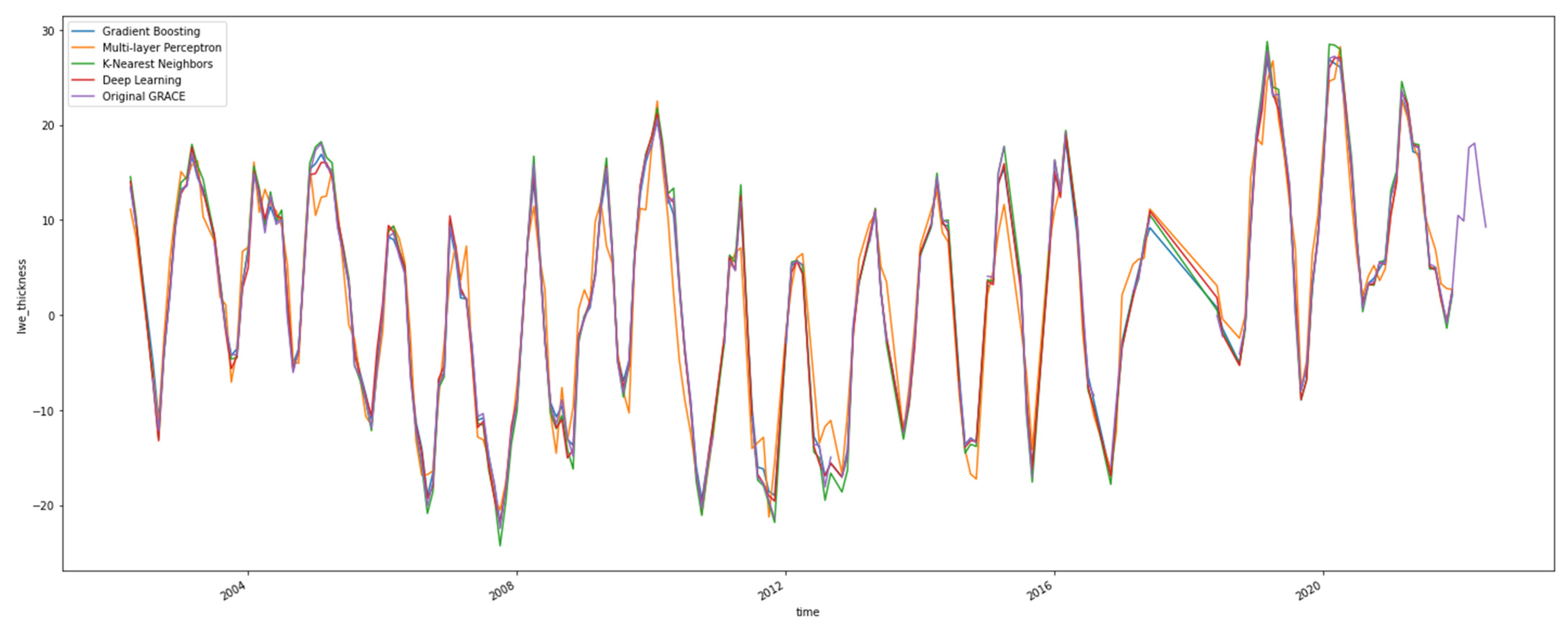
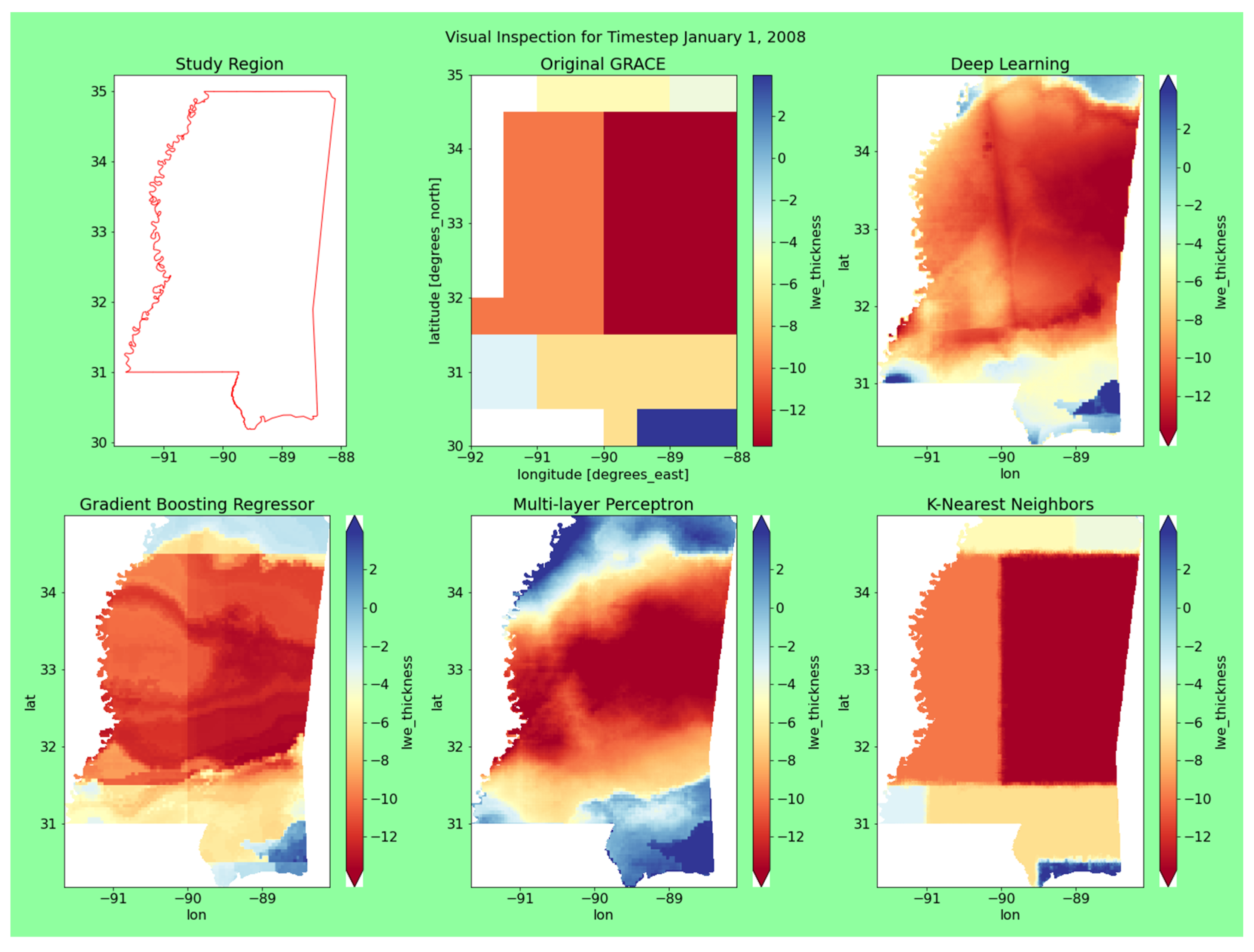
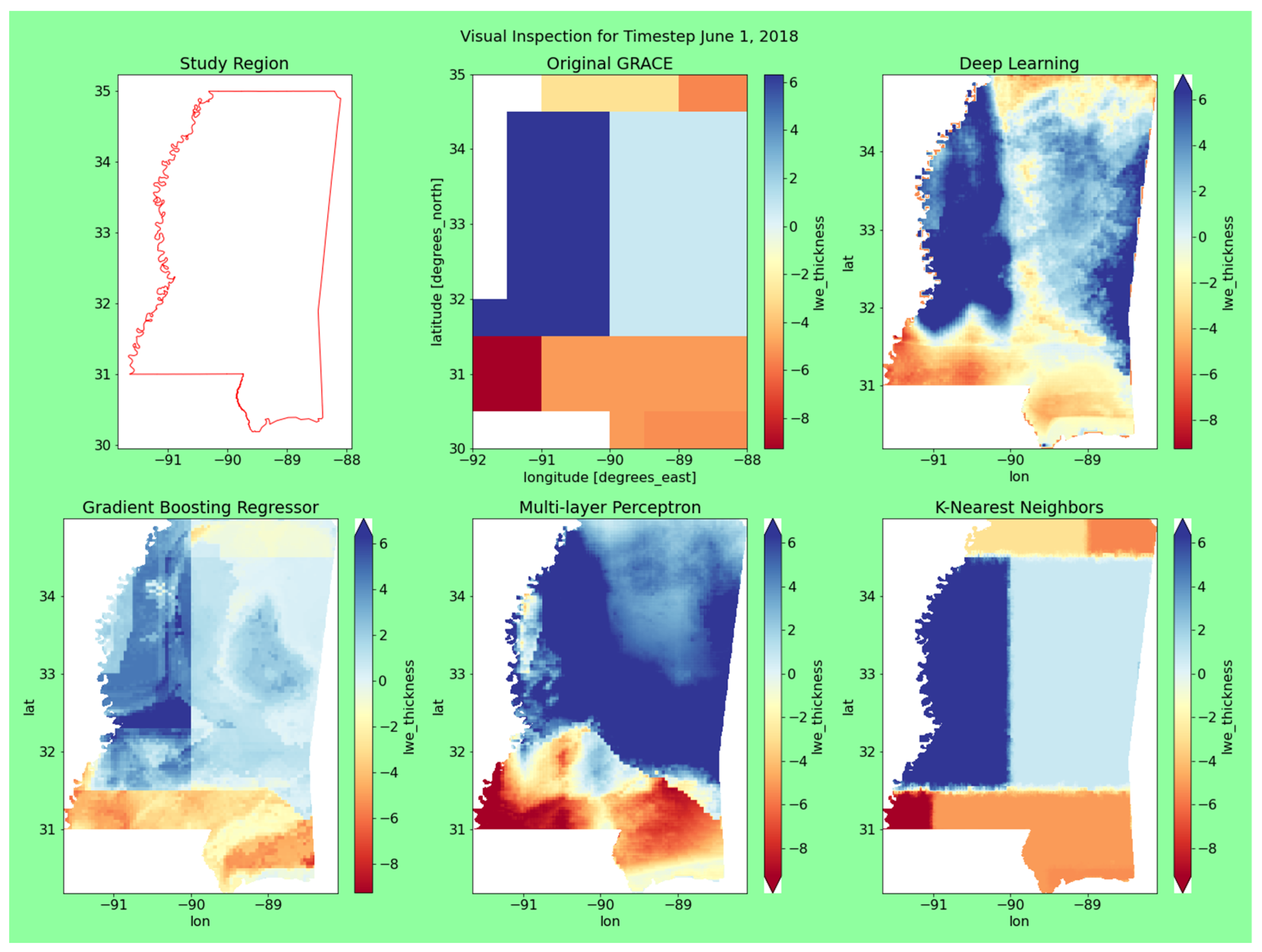
3.3. Visual Inspection
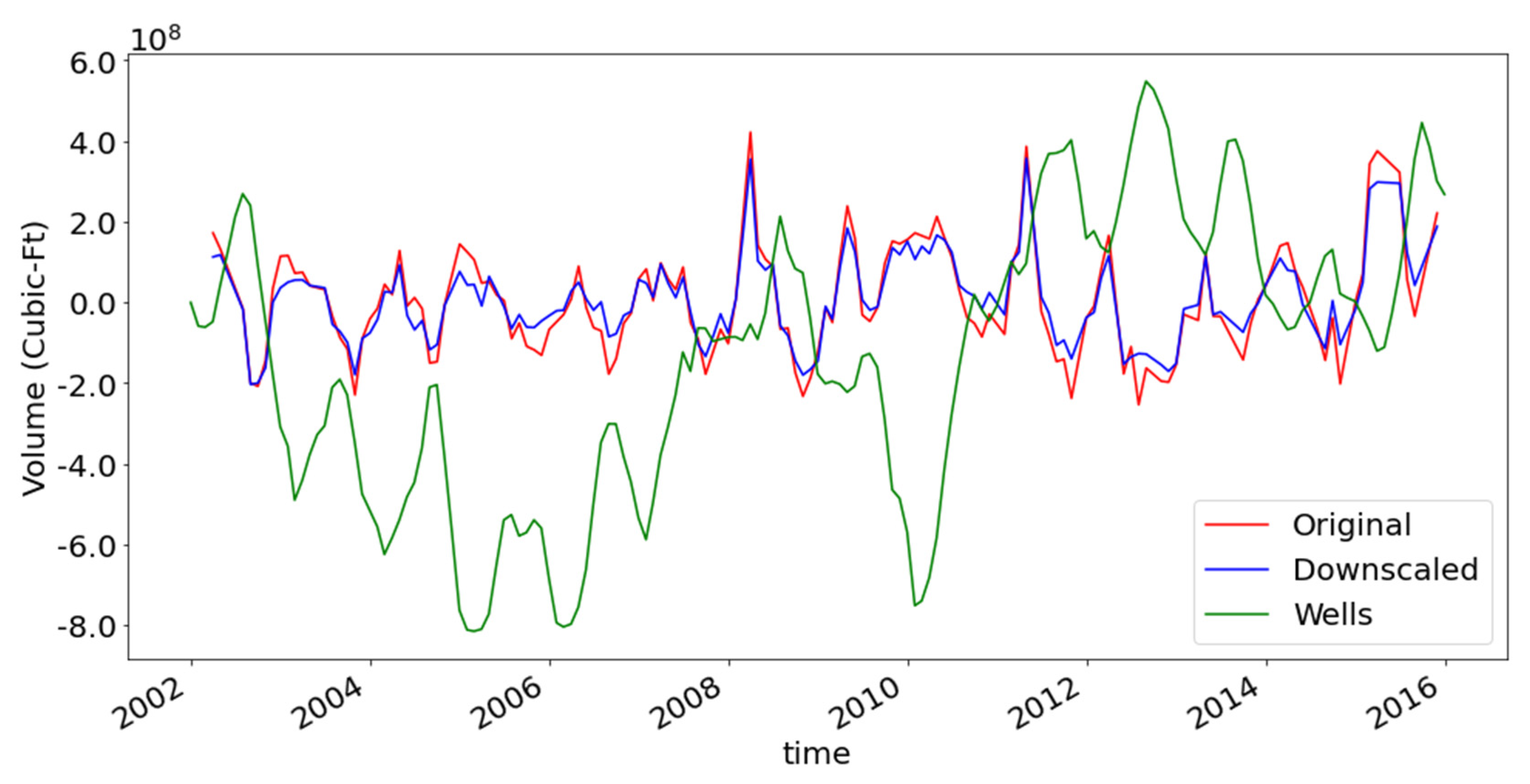
3.4. Case Study
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Miro, M.E.; Famiglietti, J.S. Downscaling GRACE Remote Sensing Datasets to High-Resolution Groundwater Storage Change Maps of California’s Central Valley. Remote Sens. 2018, 10, 143. [Google Scholar] [CrossRef]
- Pascal, C.; Ferrant, S.; Selles, A.; Maréchal, J.-C.; Paswan, A.; Merlin, O. Evaluating Downscaling Methods of GRACE (Gravity Recovery and Climate Experiment) Data: A Case Study over a Fractured Crystalline Aquifer in Southern India. Hydrol. Earth Syst. Sci. 2022, 26, 4169–4186. [Google Scholar] [CrossRef]
- Milewski, A.M.; Thomas, M.B.; Seyoum, W.M.; Rasmussen, T.C. Spatial Downscaling of GRACE TWSA Data to Identify Spatiotemporal Groundwater Level Trends in the Upper Floridan Aquifer, Georgia, USA. Remote Sens. 2019, 11, 2756. [Google Scholar] [CrossRef]
- Seyoum, W.M.; Kwon, D.; Milewski, A.M. Downscaling GRACE TWSA Data into High-Resolution Groundwater Level Anomaly Using Machine Learning-Based Models in a Glacial Aquifer System. Remote Sens. 2019, 11, 824. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, K.; Wang, M. Downscaling Groundwater Storage Data in China to a 1-Km Resolution Using Machine Learning Methods. Remote Sens. 2021, 13, 523. [Google Scholar] [CrossRef]
- Yin, W.; Zhang, G.; Liu, F.; Zhang, D.; Zhang, X.; Chen, S. Improving the Spatial Resolution of GRACE-Based Groundwater Storage Estimates Using a Machine Learning Algorithm and Hydrological Model. Hydrogeol. J. 2022, 30, 947–963. [Google Scholar] [CrossRef]
- Vishwakarma, B.D.; Zhang, J.; Sneeuw, N. Downscaling GRACE Total Water Storage Change Using Partial Least Squares Regression. Sci. Data 2021, 8, 95. [Google Scholar] [CrossRef]
- Ali, S.; Khorrami, B.; Jehanzaib, M.; Tariq, A.; Ajmal, M.; Arshad, A.; Shafeeque, M.; Dilawar, A.; Basit, I.; Zhang, L.; et al. Spatial Downscaling of GRACE Data Based on XGBoost Model for Improved Understanding of Hydrological Droughts in the Indus Basin Irrigation System (IBIS). Remote Sens. 2023, 15, 873. [Google Scholar] [CrossRef]
- Chen, L.; He, Q.; Liu, K.; Li, J.; Jing, C. Downscaling of GRACE-Derived Groundwater Storage Based on the Random Forest Model. Remote Sens. 2019, 11, 2979. [Google Scholar] [CrossRef]
- Foroumandi, E.; Nourani, V.; Jeanne Huang, J.; Moradkhani, H. Drought Monitoring by Downscaling GRACE-Derived Terrestrial Water Storage Anomalies: A Deep Learning Approach. J. Hydrol. 2023, 616, 128838. [Google Scholar] [CrossRef]
- Gorugantula, S.S.; Kambhammettu, B.P. Sequential Downscaling of GRACE Products to Map Groundwater Level Changes in Krishna River Basin. Hydrol. Sci. J. 2022, 67, 1846–1859. [Google Scholar] [CrossRef]
- Zhang, G.; Zheng, W.; Yin, W.; Lei, W. Improving the Resolution and Accuracy of Groundwater Level Anomalies Using the Machine Learning-Based Fusion Model in the North China Plain. Sensors 2020, 21, 46. [Google Scholar] [CrossRef]
- Arshad, A.; Mirchi, A.; Samimi, M.; Ahmad, B. Combining Downscaled-GRACE Data with SWAT to Improve the Estimation of Groundwater Storage and Depletion Variations in the Irrigated Indus Basin (IIB). Sci. Total Environ. 2022, 838, 156044. [Google Scholar] [CrossRef]
- Wang, H.; Zang, F.; Zhao, C.; Liu, C. A GWR Downscaling Method to Reconstruct High-Resolution Precipitation Dataset Based on GSMaP-Gauge Data: A Case Study in the Qilian Mountains, Northwest China. Sci. Total Environ. 2022, 810, 152066. [Google Scholar] [CrossRef]
- Agarwal, V.; Akyilmaz, O.; Shum, C.K.; Feng, W.; Yang, T.-Y.; Forootan, E.; Syed, T.H.; Haritashya, U.K.; Uz, M. Machine Learning Based Downscaling of GRACE-Estimated Groundwater in Central Valley, California. Sci. Total Environ. 2023, 865, 161138. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Save, H.; Wiese, D.N.; Landerer, F.W.; Long, D.; Longuevergne, L.; Chen, J. Global Evaluation of New GRACE Mascon Products for Hydrologic Applications. Water Resour. Res. 2016, 52, 9412–9429. [Google Scholar] [CrossRef]
- Gemitzi, A.; Koutsias, N.; Lakshmi, V. A Spatial Downscaling Methodology for GRACE Total Water Storage Anomalies Using GPM IMERG Precipitation Estimates. Remote Sens. 2021, 13, 5149. [Google Scholar] [CrossRef]
- Delman, A.; Landerer, F. Downscaling Satellite-Based Estimates of Ocean Bottom Pressure for Tracking Deep Ocean Mass Transport. Remote Sens. 2022, 14, 1764. [Google Scholar] [CrossRef]
- Seyoum, W. GRACE TWSA Downscale in R 2022. Available online: https://github.com/wondy30/GRACE-TWSA-downscaling-ml (accessed on 3 March 2022).
- Cookiecutter Data Science. Available online: https://github.com/drivendata/cookiecutter-data-science (accessed on 3 March 2022).
- Kluyver, T.; Ragan-Kelley, B.; Rez, F.; Granger, B.; Bussonnier, M.; Frederic, J.; Kelley, K.; Hamrick, J.; Grout, J.; Corlay, S.; et al. Jupyter Notebooks—A publishing format for reproducible computational workflows. In Positioning and Power in Academic Publishing: Players, Agents and Agendas; IOS Press: Amsterdam, The Netherlands, 2016; pp. 87–90. [Google Scholar] [CrossRef]
- Wiese, D.N.; Yuan, D.-N.; Boening, C.; Landerer, F.W.; Watkins, M.M. JPL GRACE Mascon Ocean, Ice, and Hydrology Equivalent Water Height Release 06 Coastal Resolution Improvement (CRI) Filtered Version 1.0. Available online: https://podaac.jpl.nasa.gov/dataset/TELLUS_GRACE_MASCON_CRI_GRID_RL06_V1 (accessed on 25 September 2022).
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The Climate Hazards Infrared Precipitation with Stations—A New Environmental Record for Monitoring Extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef]
- Abatzoglou, J.T.; Dobrowski, S.Z.; Parks, S.A.; Hegewisch, K.C. TerraClimate, a High-Resolution Global Dataset of Monthly Climate and Climatic Water Balance from 1958–2015. Sci. Data 2018, 5, 170191. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Reedy, R.C.; Pool, D.R.; Save, H.; Long, D.; Chen, J.; Wolock, D.M.; Conway, B.D.; Winester, D. Hydrologic Implications of GRACE Satellite Data in the Colorado River Basin. Water Resour. Res. 2015, 51, 9891–9903. [Google Scholar] [CrossRef]
- Zhao, X.; Xia, H.; Pan, L.; Song, H.; Niu, W.; Wang, R.; Li, R.; Bian, X.; Guo, Y.; Qin, Y. Drought Monitoring over Yellow River Basin from 2003–2019 Using Reconstructed MODIS Land Surface Temperature in Google Earth Engine. Remote Sens. 2021, 13, 3748. [Google Scholar] [CrossRef]
- Wang, J.; Liu, G.; Zhu, C. Evaluating Precipitation Products for Hydrologic Modeling over a Large River Basin in the Midwestern USA. Hydrol. Sci. J. 2020, 65, 1221–1238. [Google Scholar] [CrossRef]
- de Andrade, J.M.; Ribeiro Neto, A.; Bezerra, U.A.; Moraes, A.C.C.; Montenegro, S.M.G.L. A Comprehensive Assessment of Precipitation Products: Temporal and Spatial Analyses over Terrestrial Biomes in Northeastern Brazil. Remote Sens. Appl. Soc. Environ. 2022, 28, 100842. [Google Scholar] [CrossRef]
- Wu, Q. Geemap: A Python Package for Interactive Mapping with Google Earth Engine. J. Open Source Softw. 2020, 5, 2305. [Google Scholar] [CrossRef]
- ESRI. ESRI Shapefile Technical Description; White Paper J-7855; ESRI: Redlands, CA, USA, 1998; p. 28. [Google Scholar]
- Butler, H.; Daly, M.; Doyle, A.; Gillies, S.; Schaub, T.; Hagen, S. The GeoJSON Format; Internet Engineering Task Force: Berlin, Germany, 2016; Available online: http://www.rfc-editor.org/info/rfc7946 (accessed on 7 September 2022).
- OPeNDAP. Available online: https://www.opendap.org/ (accessed on 7 September 2022).
- May, R.; Arms, S.; Leeman, J.; Chastang, J. Siphon: A Collection of Python Utilities for Accessing Remote Atmospheric and Oceanic Datasets 2022. Available online: https://unidata.github.io/siphon/latest/ (accessed on 11 March 2023).
- University of Idaho TerraClimate: Monthly Climate and Climatic Water Balance for Global Terrestrial Surfaces, Earth Engine Data Catalog. Available online: https://developers.google.com/earth-engine/datasets/catalog/IDAHO_EPSCOR_TERRACLIMATE (accessed on 10 October 2022).
- ClimateSERV. Available online: https://climateserv.servirglobal.net/ (accessed on 7 September 2022).
- UNIDATA NetCDF. Available online: https://www.unidata.ucar.edu/software/netcdf/ (accessed on 7 September 2022).
- Hoyer, S.; Joseph, H. Xarray: N-D Labeled Arrays and Datasets in Python. J. Open Res. Softw. 2017, 5, 10. [Google Scholar] [CrossRef]
- Rasterio Software 2022. Available online: https://github.com/rasterio/rasterio (accessed on 11 March 2023).
- Gudivada, V.; Apon, A.; Ding, J. Data Quality Considerations for Big Data and Machine Learning: Going Beyond Data Cleaning and Transformations. Int. J. Adv. Softw. 2017, 10, 1–20. [Google Scholar]
- Schwarzwald, K. Xagg 2022. Available online: https://xagg.readthedocs.io/en/latest/index.html (accessed on 11 March 2023).
- Levi, O.; Richards, M.; Fleischmann, M. GeoPandas. 2022. Available online: https://github.com/geopandas/geopandas (accessed on 7 September 2022).
- Apache Parquet Apache Parquet. Available online: https://parquet.apache.org/ (accessed on 12 September 2022).
- Bursztein, E.; Chollet, F.; Rasskin, G.; Jin, H.; Watson, M.; Zhu, Q.S. Keras: Deep Learning for Humans 2022. Available online: https://github.com/keras-team/keras (accessed on 7 September 2022).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Müller, A.; Nothman, J.; Louppe, G.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2012, 12, 2825–2830. [Google Scholar] [CrossRef]
- Ahmed, K.; Shahid, S.; Haroon, S.B.; Xiao-jun, W. Multilayer Perceptron Neural Network for Downscaling Rainfall in Arid Region: A Case Study of Baluchistan, Pakistan. J. Earth Syst. Sci. 2015, 124, 1325–1341. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic Gradient Boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Roberts, W.; Williams, G.P.; Jackson, E.; Nelson, E.J.; Ames, D.P. Hydrostats: A Python Package for Characterizing Errors between Observed and Predicted Time Series. Hydrology 2018, 5, 66. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Spearman, C. The Proof and Measurement of Association between Two Things. Am. J. Psychol. 1987, 100, 441–471. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient. In Noise Reduction in Speech Processing; Cohen, I., Huang, Y., Chen, J., Benesty, J., Eds.; Springer Topics in Signal Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. ISBN 978-3-642-00296-0. [Google Scholar]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Barbosa, S.A.; Pulla, S.T.; Williams, G.P.; Jones, N.L.; Mamane, B.; Sanchez, J.L. Evaluating Groundwater Storage Change and Recharge Using GRACE Data: A Case Study of Aquifers in Niger, West Africa. Remote Sens. 2022, 14, 1532. [Google Scholar] [CrossRef]
- McStraw, T.C.; Pulla, S.T.; Jones, N.L.; Williams, G.P.; David, C.H.; Nelson, J.E.; Ames, D.P. An Open-Source Web Application for Regional Analysis of GRACE Groundwater Data and Engaging Stakeholders in Groundwater Management. JAWRA J. Am. Water Resour. Assoc. 2022, 58, 1002–1016. [Google Scholar] [CrossRef]
- Evans, S.W.; Jones, N.L.; Williams, G.P.; Ames, D.P.; Nelson, E.J. Groundwater Level Mapping Tool: An Open Source Web Application for Assessing Groundwater Sustainability. Environ. Model. Softw. 2020, 131, 104782. [Google Scholar] [CrossRef]
- Evans, S.; Williams, G.P.; Jones, N.L.; Ames, D.P.; Nelson, E.J. Exploiting Earth Observation Data to Impute Groundwater Level Measurements with an Extreme Learning Machine. Remote Sens. 2020, 12, 2044. [Google Scholar] [CrossRef]
- Brookfield, A.E.; Hill, M.C.; Rodell, M.; Loomis, B.D.; Stotler, R.L.; Porter, M.E.; Bohling, G.C. In Situ and GRACE-Based Groundwater Observations: Similarities, Discrepancies, and Evaluation in the High Plains Aquifer in Kansas. Water Resour. Res. 2018, 54, 8034–8044. [Google Scholar] [CrossRef]
- Long, D.; Longuevergne, L.; Scanlon, B.R. Uncertainty in Evapotranspiration from Land Surface Modeling, Remote Sensing, and GRACE Satellites. Water Resour. Res. 2014, 50, 1131–1151. [Google Scholar] [CrossRef]
- Yeh, P.J.-F.; Swenson, S.C.; Famiglietti, J.S.; Rodell, M. Remote Sensing of Groundwater Storage Changes in Illinois Using the Gravity Recovery and Climate Experiment (GRACE). Water Resour. Res. 2006, 42, W12203. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Li, J.; Zhang, Z. Reducing Leakage Error in GRACE-Observed Long-Term Ice Mass Change: A Case Study in West Antarctica. J. Geod. 2015, 89, 925–940. [Google Scholar] [CrossRef]
- Huang, Z.; Jiao, J.J.; Luo, X.; Pan, Y.; Zhang, C. Sensitivity Analysis of Leakage Correction of GRACE Data in Southwest China Using A-Priori Model Simulations: Inter-Comparison of Spherical Harmonics, Mass Concentration and In Situ Observations. Sensors 2019, 19, 3149. [Google Scholar] [CrossRef] [PubMed]
- Mu, D.; Yan, H.; Feng, W.; Peng, P. GRACE Leakage Error Correction with Regularization Technique: Case Studies in Greenland and Antarctica. Geophys. J. Int. 2017, 208, 1775–1786. [Google Scholar] [CrossRef]


| Attribute/Band | Units | Description | Justification |
|---|---|---|---|
| aet | mm | Actual evapotranspiration, derived using a one-dimensional soil water balance model | One of the leading indicators of drought; Affects the groundwater recharge |
| def | mm | Climate water deficit, derived using a one-dimensional soil water balance model | Hydrologic variable that influences the sur-face water storage |
| pdsi | - | Palmer Drought Severity Index | Indicator of long-term drought conditions; Helps capture groundwater depletion |
| pet | mm | Reference evapotranspiration (ASCE Penman-Montieth) | A hydrologic variable that influences groundwater and surface water storage |
| pr | mm | Precipitation accumulation | Hydrologic variable influencing the surface water storage and groundwater recharge |
| ro | mm | Runoff, derived using a one-dimensional soil water balance model | Hydrologic variable influencing all the TWS components |
| srad | W·m−2 | Downward surface shortwave radiation | Hydrologic variable influencing drought |
| soil | mm | Soil moisture, derived using a one-dimensional soil water balance model | Influences soil moisture component of TWS |
| swe | mm | Snow water equivalent, derived using a one-dimensional soil water balance model | Influences the snow water equivalent com-ponent of TWS |
| Model | R-Squared | Mean Absolute Error | Mean Squared Error | Root Mean Squared Error |
|---|---|---|---|---|
| Deep learning | 0.961 | 1.911 | 6.948 | 2.635 |
| Gradient boosting | 0.964 | 1.752 | 6.381 | 2.526 |
| Multi-layer perceptron | 0.836 | 4.209 | 29.455 | 5.427 |
| K-nearest neighbors | 0.996 | 0.158 | 0.599 | 0.774 |
| Metric | Deep Learning | Gradient Boosting Regressor | Multi-Layer Perceptron | K-Nearest Neighbors |
|---|---|---|---|---|
| Pearson correlation coefficient | 0.997551 | 0.998527 | 0.969011 | 0.999333 |
| Nash–Sutcliffe efficiency | 0.995073 | 0.996227 | 0.938837 | 0.996128 |
| Modified Nash–Sutcliffe | 0.934946 | 0.943833 | 0.775171 | 0.939307 |
| Spearman correlation coefficient | 0.997703 | 0.998340 | 0.968447 | 0.999118 |
| R-squared | 0.995108 | 0.997056 | 0.938982 | 0.998667 |
| Mean | 0.984076 | 0.986797 | 0.918090 | 0.986511 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pulla, S.T.; Yasarer, H.; Yarbrough, L.D. GRACE Downscaler: A Framework to Develop and Evaluate Downscaling Models for GRACE. Remote Sens. 2023, 15, 2247. https://doi.org/10.3390/rs15092247
Pulla ST, Yasarer H, Yarbrough LD. GRACE Downscaler: A Framework to Develop and Evaluate Downscaling Models for GRACE. Remote Sensing. 2023; 15(9):2247. https://doi.org/10.3390/rs15092247
Chicago/Turabian StylePulla, Sarva T., Hakan Yasarer, and Lance D. Yarbrough. 2023. "GRACE Downscaler: A Framework to Develop and Evaluate Downscaling Models for GRACE" Remote Sensing 15, no. 9: 2247. https://doi.org/10.3390/rs15092247
APA StylePulla, S. T., Yasarer, H., & Yarbrough, L. D. (2023). GRACE Downscaler: A Framework to Develop and Evaluate Downscaling Models for GRACE. Remote Sensing, 15(9), 2247. https://doi.org/10.3390/rs15092247






