Multispectral Remote Sensing Monitoring of Soil Particle-Size Distribution in Arid and Semi-Arid Mining Areas in the Middle and Upper Reaches of the Yellow River Basin: A Case Study of Wuhai City, Inner Mongolia Autonomous Region
Abstract
1. Introduction
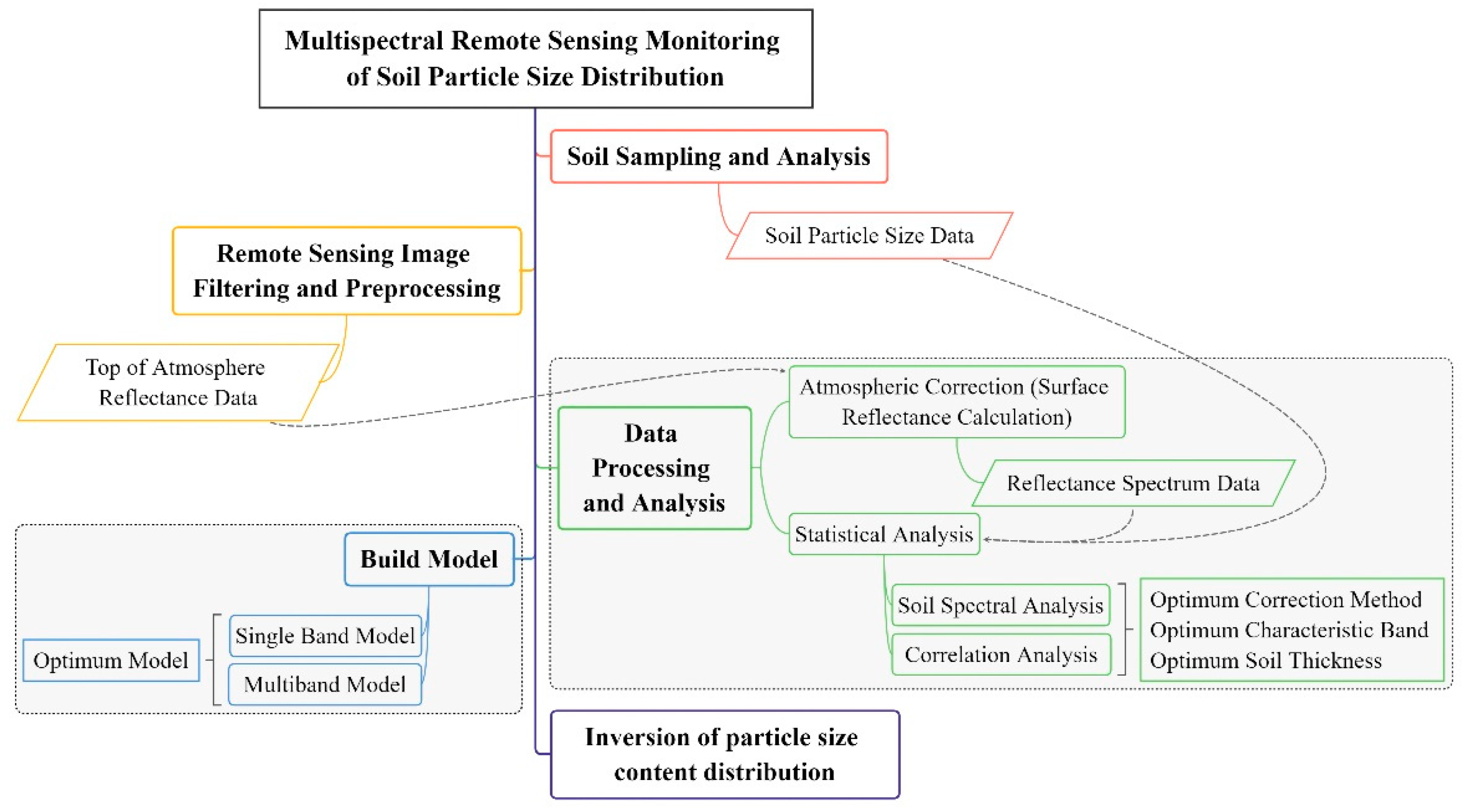
2. Data and Methods
2.1. Experimental Scheme
2.2. Overview of the Study Area
2.3. Soil Sampling and Analysis
2.4. Remote Sensing Image Data Selection, Processing and Analysis
2.4.1. Image Selection and Preprocessing
2.4.2. Calculation of Surface Reflectivity
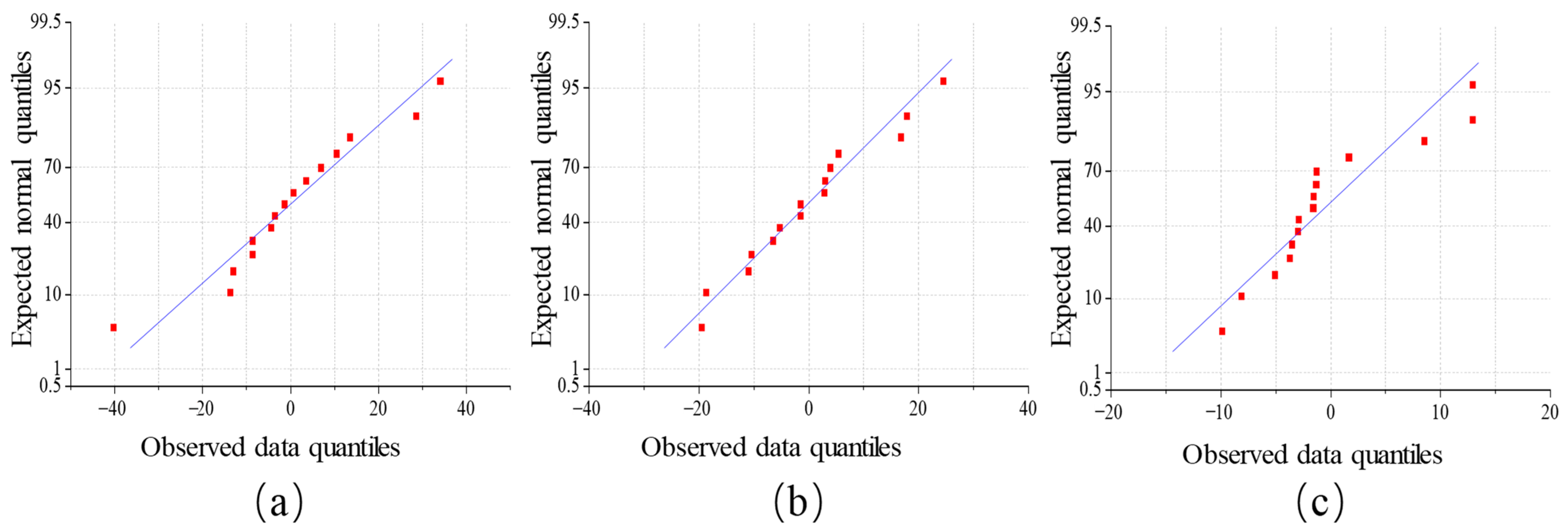
2.4.3. Statistical Analysis
2.5. Modeling Process
- For the single-band model, we define the independent variable as a single characteristic band’s surface reflectance data, while the dependent variable is the particle-size content of the three different soil types. The single-band optimum fitting model of the different particle sizes was established using Origin2018 software;
- For the multi-band model, we define the independent variable as all the surface reflectance data of Bands 1–7, while dependent variable is the content of the three different soil particle size types. The regression equation between and was established using the MLR and PLSR methods as follows:
2.6. Modeling Evaluation
3. Results and Analysis
3.1. Analysis of Surface Soil Reflection Spectra at Sampling Points
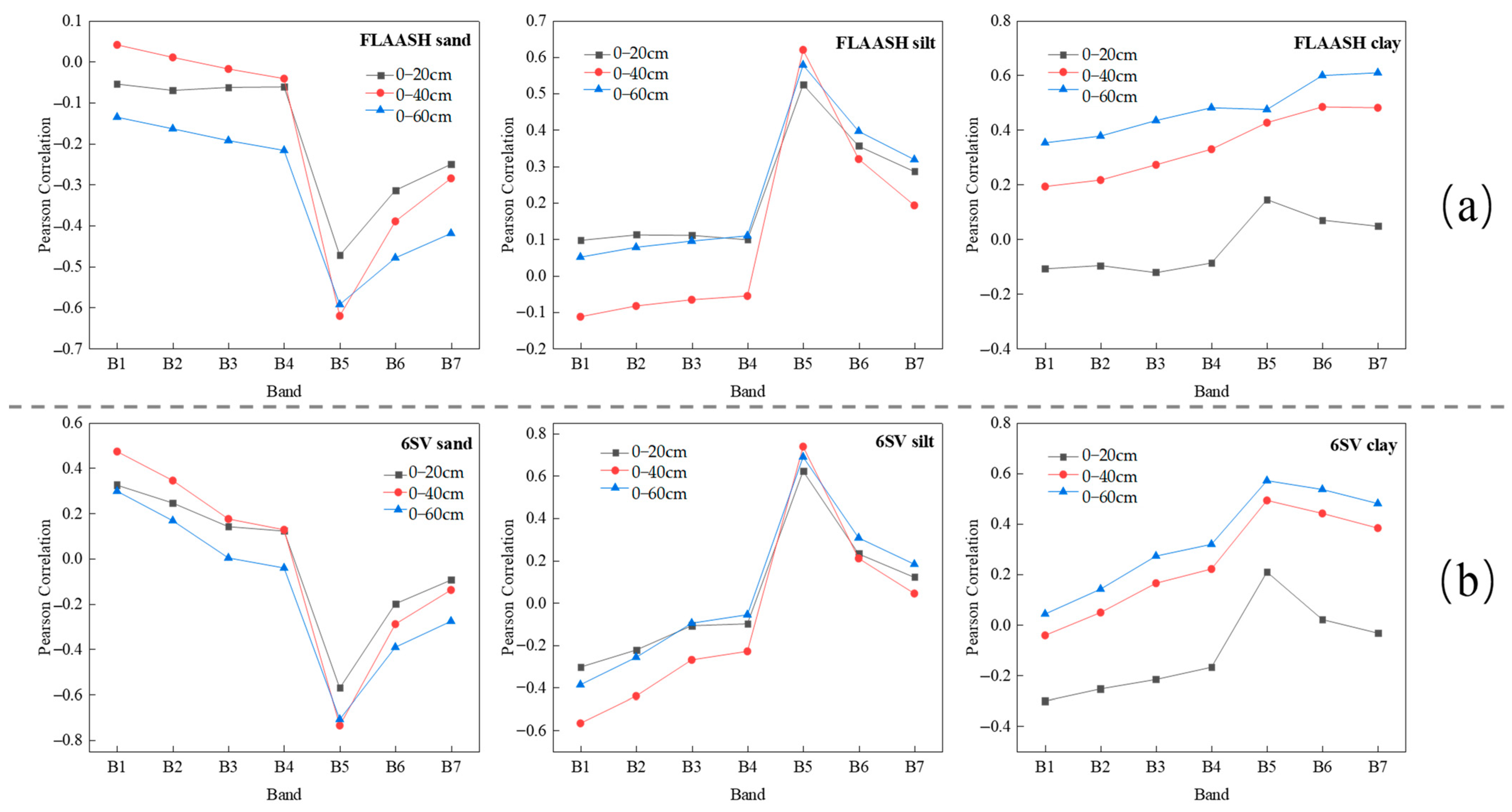
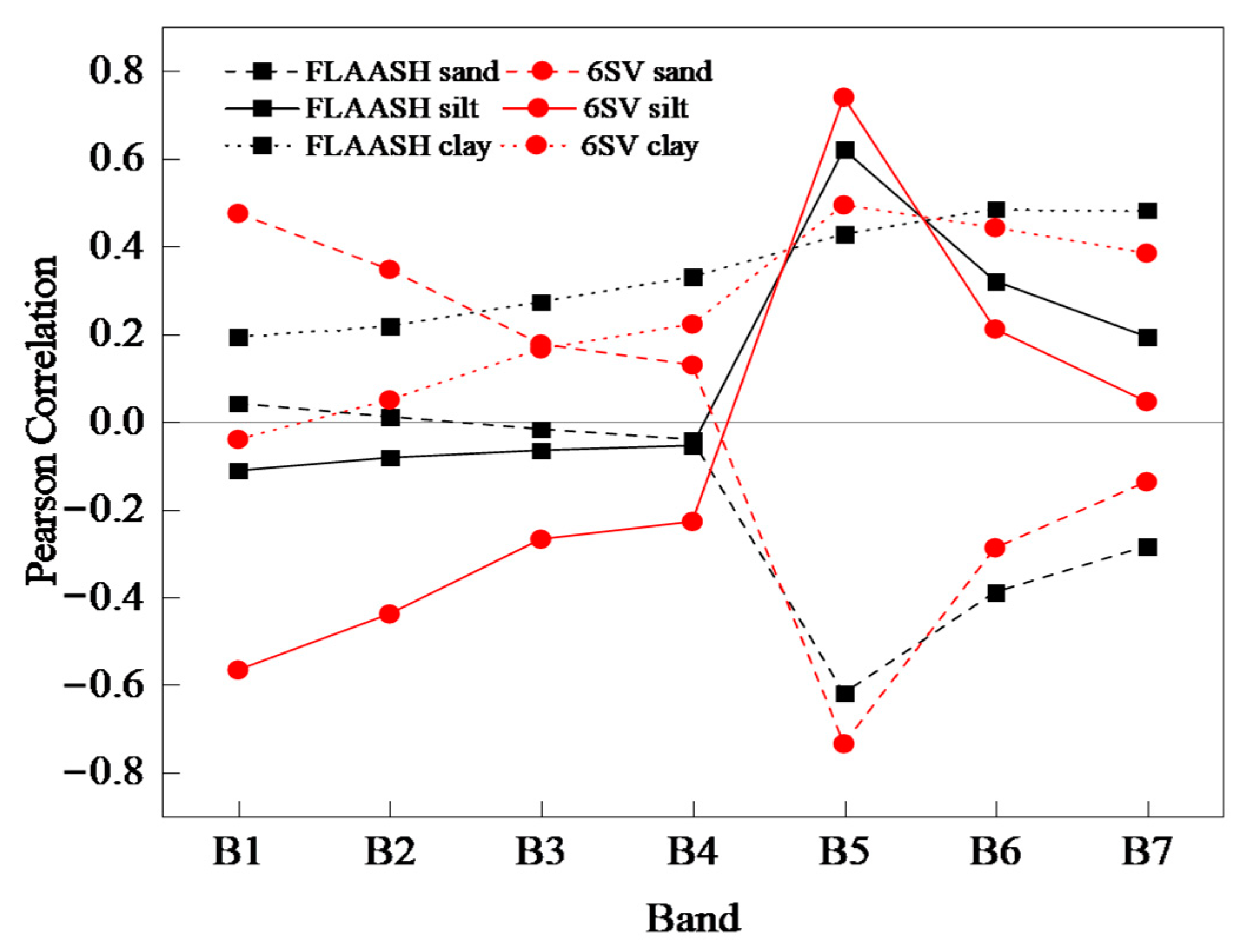
3.2. Correlation Analysis between Soil Grain Size and Surface Reflectance
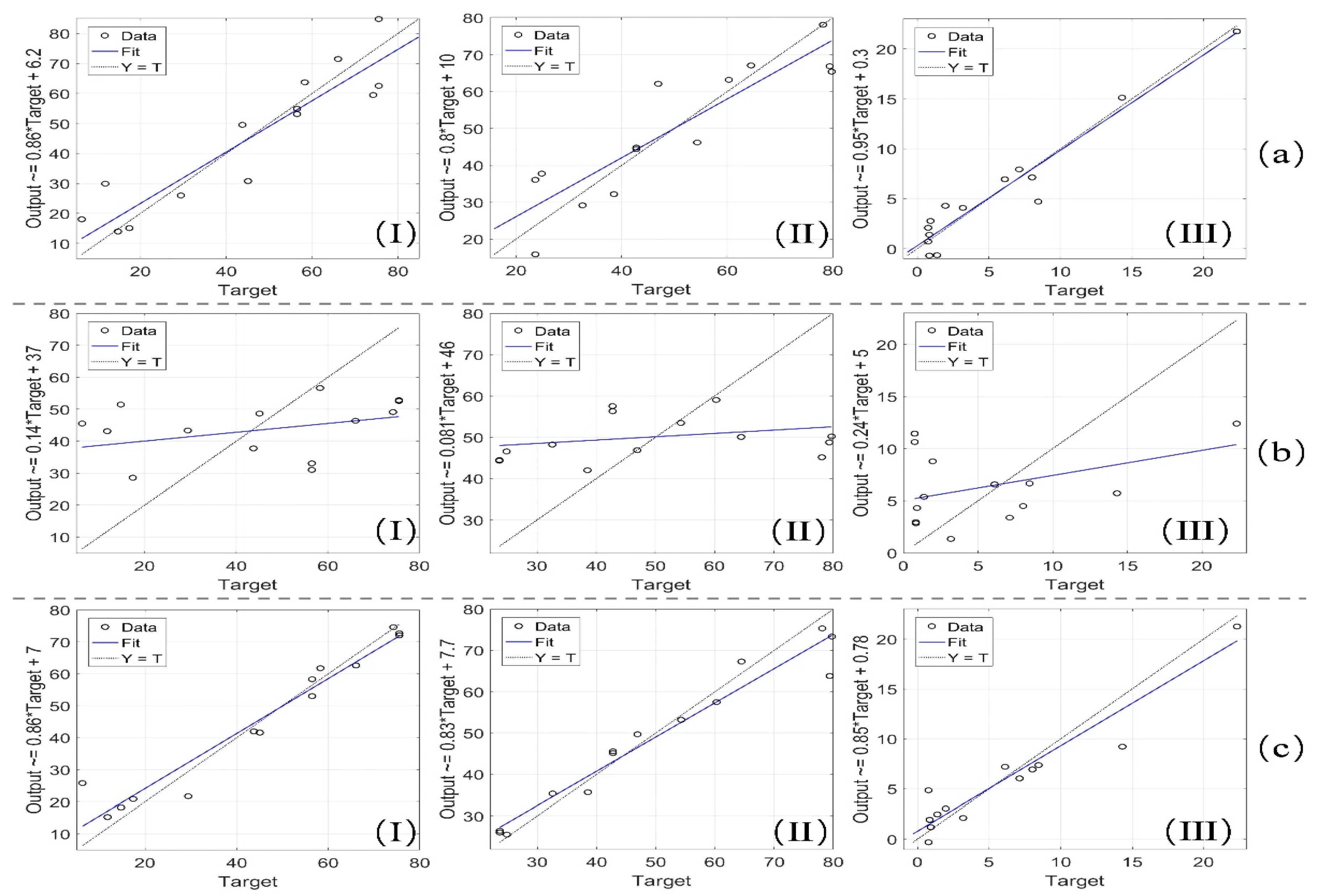
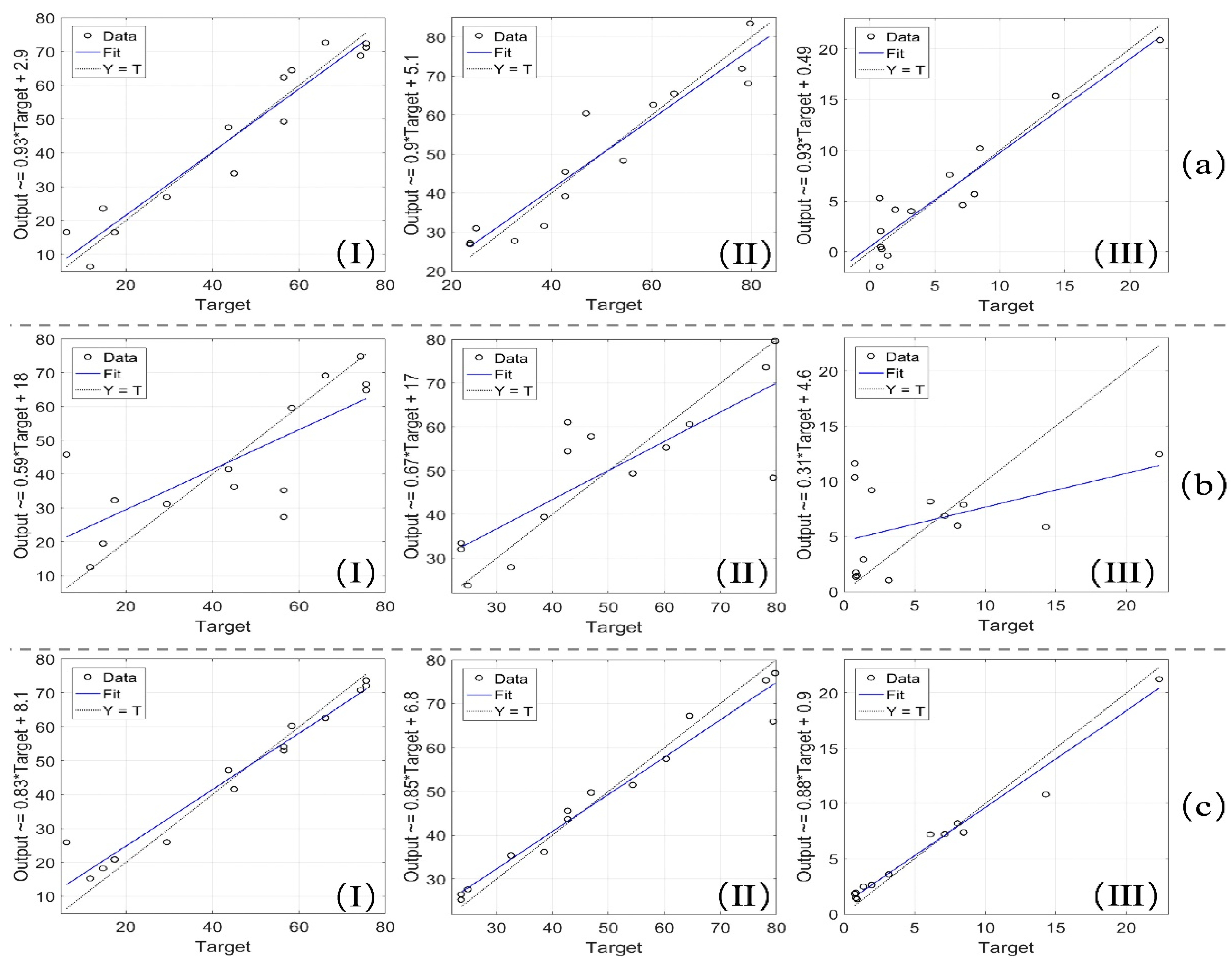
3.3. Model Establishment and Verification
3.3.1. Single-Band Model Analysis
3.3.2. Multi-Band Model Analysis
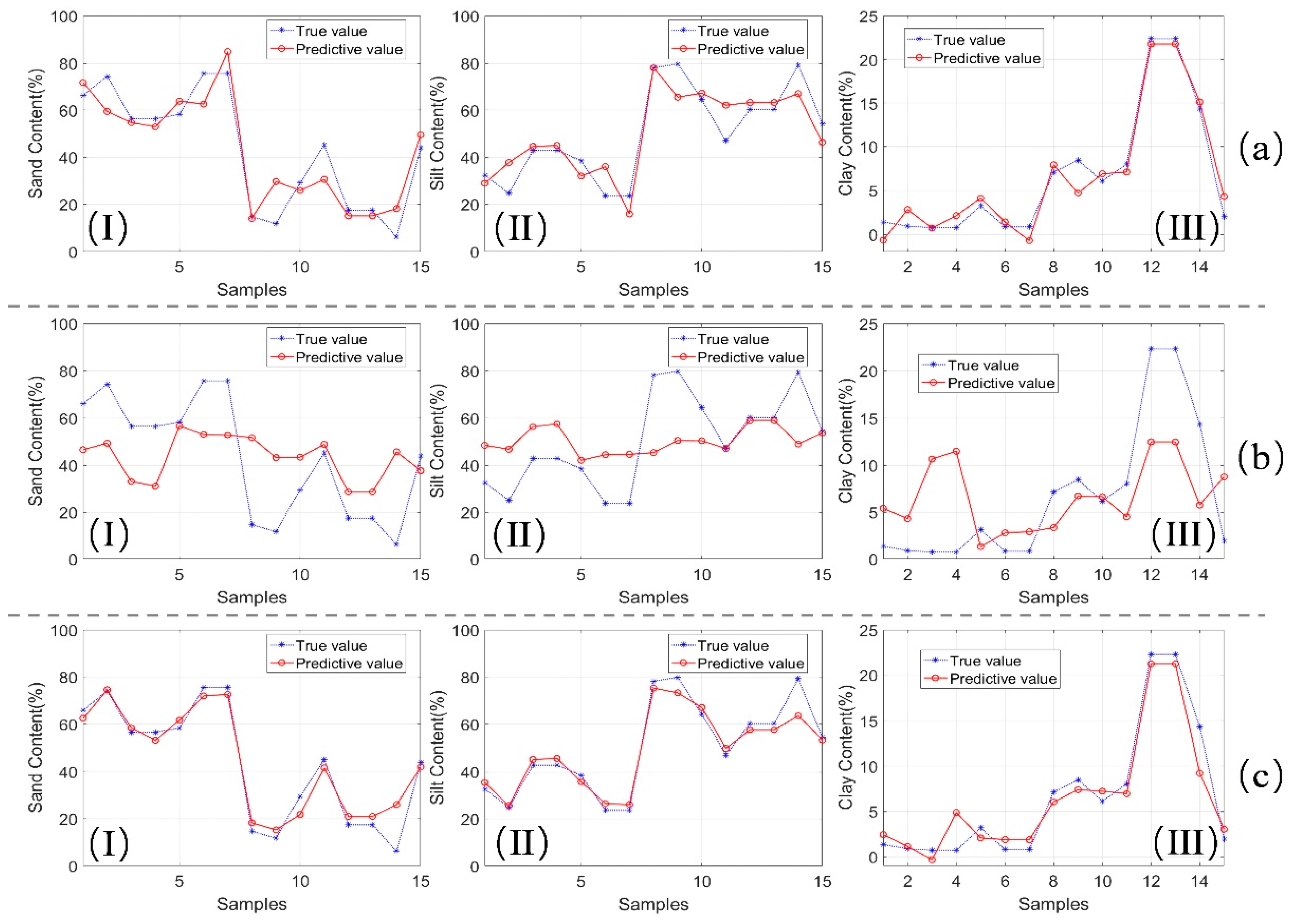
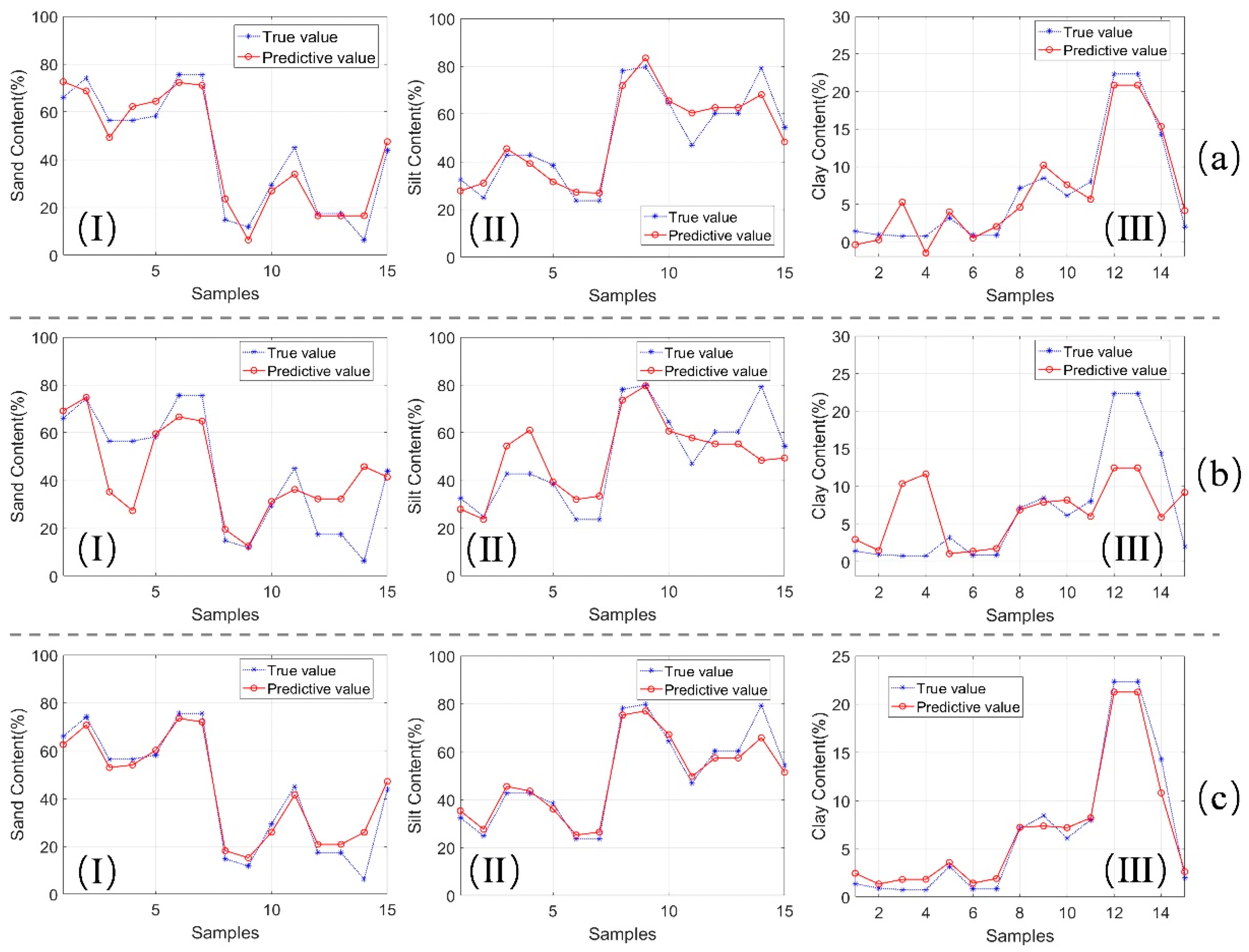
3.4. Inversion Results of Prediction Model
4. Discussion
4.1. Effectiveness of Surface Spectral Reflectance Data in Predicting Soil Particle-Size Distribution
4.2. Evaluation of Advantages and Disadvantages of Different Models
4.3. Applicability and Limitations
5. Conclusions
- (1)
- Compared with the FLAASH atmospheric correction model, the calculated surface reflectance data for modeling and analyzing the soil particle-size contents have higher accuracy and can more truly reflect its surface reflectance characteristics when using the 6SV atmospheric correction model in arid and semi-arid areas with undulating terrain;
- (2)
- Among the particle size content data of 3 kinds of soil with different thicknesses (0–20 cm, 0–40 cm, and 0–60 cm), the sand and silt contents of the soil with a thickness of 0–40 cm have the strongest correlation with the reflectance data of multiple bands, which is the optimum soil thickness for modeling and predicting the particle size content in this study;
- (3)
- The order of the single-band prediction model’s accuracy is silt > sand > clay. The adjusted values of the silt and sand content prediction models are 0.518 and 0.451, respectively, and the clay content model does not have significant prediction ability;
- (4)
- The order of the multi-band prediction model’s accuracy is SVM > MLR > PLSR. Among them, the 6SV-SVM model has the highest accuracy in predicting the particle size content of the soil with a thickness of 0–40 cm, and the prediction accuracy of the 3 particle sizes’ contents is above 0.95;
- (5)
- The 6SV-SVM model based on Landsat8 OLI images established in this study can calculate the soil particle size content distribution in arid and semi-arid areas with undulating terrain. It is suitable for arid and semi-arid mines in western China and other areas with complex terrain. It provides effective data support for the change monitoring of mine-reclaimed soil texture. It has broad application prospects in mastering the law of soil particle-size change and optimizing regional ecological environment governance monitoring.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Azizi, K.; Garosi, Y.; Ayoubi, S.; Tajik, S. Integration of Sentinel-1/2 and topographic attributes to predict the spatial distribution of soil texture fractions in some agricultural soils of western Iran. Soil Tillage Res. 2023, 229, 105681. [Google Scholar] [CrossRef]
- Bi, Y.L.; Peng, S.P.; Du, S.Z. Technological difficulties and future directions of ecological reconstruction in open pit coal mine of the arid and semi-arid areas of Western China. J. China Coal Soc. 2021, 46, 1355–1364. [Google Scholar] [CrossRef]
- Han, J.Z.; Hu, Z.Q.; Wang, P.J.; Yan, Z.G.; Li, G.S.; Zhang, Y.H.; Zhou, T. Spatio-temporal evolution and optimization analysis of ecosystem service value-A case study of coal resource-based city group in Shandong, China. J. Clean Prod. 2022, 363, 12. [Google Scholar] [CrossRef]
- Hu, Z.Q.; Zhao, Y.L. Main problems in ecological restoration of mines and their solutions. China Coal 2021, 47, 2–7. [Google Scholar] [CrossRef]
- Hu, Z.Q.; Zhao, Y.L. Principle and technology of coordinated control of eco-environment of mining areas and river sediments in Yellow River watershed. J. China Coal Soc. 2022, 47, 438–448. [Google Scholar] [CrossRef]
- Xi, J.P. Speech at the symposium on ecological protection and high-quality development in the Yellow River basin. Water Conserv. Constr. Manag. 2019, 39, 1–3+6. [Google Scholar] [CrossRef]
- Bao, N.; Liu, S.; Zhou, Y. Predicting particle-size distribution using thermal infrared spectroscopy from reclaimed mine land in the semi-arid grassland of North China. Catena 2019, 183, 104190. [Google Scholar] [CrossRef]
- Domínguez-Haydar, Y.; Velásquez, E.; Carmona, J.; Lavelle, P.; Chavez, L.F.; Jiménez, J.J. Evaluation of reclamation success in an open-pit coal mine using integrated soil physical, chemical and biological quality indicators. Ecol. Indic. 2019, 103, 182–193. [Google Scholar] [CrossRef]
- Clark, R.N.; Roush, T.L. Reflectance spectroscopy: Quantitative analysis techniques for remote sensing applications. J. Geophys. Res. Solid Earth 1984, 89, 6329–6340. [Google Scholar] [CrossRef]
- Xiao, J.; Shen, Y.; Tateishi, R.; Bayaer, W. Development of topsoil grain size index for monitoring desertification in arid land using remote sensing. Int. J. Remote Sens. 2007, 27, 2411–2422. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Chabrillat, S.; Demattê, J.A.M.; Taylor, G.R.; Hill, J.; Whiting, M.L.; Sommer, S. Using Imaging Spectroscopy to study soil properties. Remote Sens. Environ. 2009, 113, S38–S55. [Google Scholar] [CrossRef]
- Fongaro, C.T.; Demattê, J.A.M.; Rizzo, R.; Lucas Safanelli, J.; Mendes, W.D.; Dotto, A.C.; Vicente, L.E.; Franceschini, M.H.D.; Ustin, S.L. Improvement of Clay and Sand Quantification Based on a Novel Approach with a Focus on Multispectral Satellite Images. Remote Sens. 2018, 10, 1555. [Google Scholar] [CrossRef]
- Shi, P.; Six, J.; Sila, A.; Vanlauwe, B.; Van Oost, K. Towards spatially continuous mapping of soil organic carbon in croplands using multitemporal Sentinel-2 remote sensing. ISPRS J. Photogramm. Remote Sens. 2022, 193, 187–199. [Google Scholar] [CrossRef]
- Wang, S.; Guan, K.; Zhang, C.; Lee, D.; Margenot, A.J.; Ge, Y.; Peng, J.; Zhou, W.; Zhou, Q.; Huang, Y. Using soil library hyperspectral reflectance and machine learning to predict soil organic carbon: Assessing potential of airborne and spaceborne optical soil sensing. Remote Sens. Environ. 2022, 271, 112914. [Google Scholar] [CrossRef]
- McCarty, G.W.; Reeves, J.B.; Reeves, V.B.; Follett, R.F.; Kimble, J.M. Mid-infrared and near-infrared diffuse reflectance spectroscopy for soil carbon measurement. Soil Sci. Soc. Am. J. 2002, 66, 640–646. [Google Scholar] [CrossRef]
- Chen, F.; Kissel, D.E.; West, L.T.; Adkins, W.; Rickman, D.; Luvall, J.C. Mapping soil organic carbon concentration for multiple fields with image similarity analysis. Soil Sci. Soc. Am. J. 2008, 72, 186–193. [Google Scholar] [CrossRef]
- D’Acqui, L.P.; Pucci, A.; Janik, L.J. Soil properties prediction of western Mediterranean islands with similar climatic environments by means of mid-infrared diffuse reflectance spectroscopy. Eur. J. Soil Sci. 2010, 61, 865–876. [Google Scholar] [CrossRef]
- Levi, N.; Karnieli, A.; Paz-Kagan, T. Airborne imaging spectroscopy for assessing land-use effect on soil quality in drylands. ISPRS J. Photogramm. Remote Sens. 2022, 186, 34–54. [Google Scholar] [CrossRef]
- Shoshany, M.; Roitberg, E.; Goldshleger, N.; Kizel, F. Universal quadratic soil spectral reflectance line and its deviation patterns’ relationships with chemical and textural properties: A global data base analysis. Remote Sens. Environ. 2022, 280, 113182. [Google Scholar] [CrossRef]
- Zolfaghari, A.A.; Toularoud, A.A.S.; Baghi, F.; Mirzaee, S. Spatial prediction of soil particle size distribution in arid agricultural lands in central Iran. Arab. J. Geosci. 2022, 15, 1574. [Google Scholar] [CrossRef]
- Shirazi, M.P.; Abtahi, S.A.; Nejad, M.B.; Moosavi, A.A.; Navidi, M.N. Improving Soil Texture Digital Mapping Using Landsat 8 Satellite Imageries in Calcareous Soils of Southern Iran. J. Agric. Sci. Technol. 2023, 25, 485–502. [Google Scholar]
- Zhao, X.; Xu, Z.J.; Yin, J.P.; Bi, R.T.; Feng, J.F.; Liu, P. Retrieval of Soil Organic Carbon in Cinnamon Mining Belt Subsidence Area Based on OLI and 6SV. Spectrosc. Spect. Anal. 2019, 39, 886–893. [Google Scholar]
- Madari, B.E.; Reeves, J.B.; Machado, P.; Guimaraes, C.M.; Torres, E.; McCarty, G.W. Mid- and near-infrared spectroscopic assessment of soil compositional parameters and structural indices in two Ferralsols. Geoderma 2006, 136, 245–259. [Google Scholar] [CrossRef]
- Liao, K.; Xu, S.; Wu, J.; Zhu, Q. Spatial estimation of surface soil texture using remote sensing data. Soil Sci. Plant Nutr. 2013, 59, 488–500. [Google Scholar] [CrossRef]
- Pereira, G.E.; Sequinatto, L.; Almeida, J.A.d.; ten Caten, A.; Mota, J.M. VIS-NIR spectral reflectance for discretization of soils with high sand content. Semin. Ciências Agrárias 2019, 40, 99–112. [Google Scholar] [CrossRef]
- Rosero-Vlasova, O.A.; Vlassova, L.; Pérez-Cabello, F.; Montorio, R.; Nadal-Romero, E. Soil organic matter and texture estimation from visible–near infrared–shortwave infrared spectra in areas of land cover changes using correlated component regression. Land Degrad. Dev. 2019, 30, 544–560. [Google Scholar] [CrossRef]
- Cooley, T.; Anderson, G.P.; Felde, G.W.; Hoke, M.L.; Ratkowski, A.J.; Chetwynd, J.H.; Gardner, J.A.; Adler-Golden, S.M.; Matthew, M.W.; Berk, A.; et al. FLAASH, a MODTRAN4-based atmospheric correction algorithm, its application and validation. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; pp. 1414–1418. [Google Scholar]
- Houborg, R.; McCabe, M.F. Impacts of dust aerosol and adjacency effects on the accuracy of Landsat 8 and RapidEye surface reflectances. Remote Sens. Environ. 2017, 194, 127–145. [Google Scholar] [CrossRef]
- Escribano, P.; Schmid, T.; Chabrillat, S.; Rodríguez-Caballero, E.; García, M. Chapter 4—Optical Remote Sensing for Soil Mapping and Monitoring. In Soil Mapping and Process Modeling for Sustainable Land Use Management; Pereira, P., Brevik, E.C., Muñoz-Rojas, M., Miller, B.A., Eds.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 87–125. [Google Scholar]
- Janik, L.J.; Forrester, S.T.; Rawson, A. The prediction of soil chemical and physical properties from mid-infrared spectroscopy and combined partial least-squares regression and neural networks (PLS-NN) analysis. Chemom. Intell. Lab. Syst. 2009, 97, 179–188. [Google Scholar] [CrossRef]
- Rossel, R.A.V.; Behrens, T. Using data mining to model and interpret soil diffuse reflectance spectra. Geoderma 2010, 158, 46–54. [Google Scholar] [CrossRef]
- Vereecken, H.; Schnepf, A.; Hopmans, J.W.; Javaux, M.; Or, D.; Roose, T.; Vanderborght, J.; Young, M.H.; Amelung, W.; Aitkenhead, M.; et al. Modeling Soil Processes: Review, Key Challenges, and New Perspectives. Vadose Zone J. 2016, 15, 1–57. [Google Scholar] [CrossRef]
- Zhang, F.; Hu, Z.Q.; Fu, Y.K.; Yang, K.; Wu, Q.Y.; Feng, Z.W. A New Identification Method for Surface Cracks from UAV Images Based on Machine Learning in Coal Mining Areas. Remote Sens. 2020, 12, 1571. [Google Scholar] [CrossRef]
- Zheng, G.; Ryu, D.; Jiao, C.; Xie, X.; Cui, X.; Shang, G. Visible and Near-Infrared Reflectance Spectroscopy Analysis of a Coastal Soil Chronosequence. Remote Sens. 2019, 11, 2336. [Google Scholar] [CrossRef]
- Tavakoli, H.; Correa, J.; Sabetizade, M.; Vogel, S. Predicting key soil properties from Vis-NIR spectra by applying dual-wavelength indices transformations and stacking machine learning approaches. Soil Tillage Res. 2023, 229, 105684. [Google Scholar] [CrossRef]
- Chursin, V.V.; Kuzhevskaia, I.; Merzliakov, O.E.; Valevich, T.; Ruchkina, K. Design of satellite sensing data classification algorithm based on machine learning using the example of granulometric composition of soils in agricultural landscapes of Western Siberia. Sovrem. Probl. Distantsionnogo Zondirovaniya Zemli Kosm. 2021, 18, 39–50. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, L. Machine Learning Theory and Algorithms; Science Press: Beijing, China, 2012. [Google Scholar]
- Stevens, A.; van Wesemael, B.; Bartholomeus, H.; Rosillon, D.; Tychon, B.; Ben-Dor, E. Laboratory, field and airborne spectroscopy for monitoring organic carbon content in agricultural soils. Geoderma 2008, 144, 395–404. [Google Scholar] [CrossRef]
- Ishiyama, T.; Tsuchiya, K.; Sugihara, S. Ground surface features of the Taklimakan Desert. Adv. Space Res. 1996, 17, 41–48. [Google Scholar] [CrossRef]
- Lagacherie, P.; Baret, F.; Feret, J.B.; Netto, J.M.; Robbez-Masson, J.M. Estimation of soil clay and calcium carbonate using laboratory, field and airborne hyperspectral measurements. Remote Sens. Environ. 2008, 112, 825–835. [Google Scholar] [CrossRef]
- Seidel, M.; Vohland, M.; Greenberg, I.; Ludwig, B.; Ortner, M.; Thiele-Bruhn, S.; Hutengs, C. Soil moisture effects on predictive VNIR and MIR modeling of soil organic carbon and clay content. Geoderma 2022, 427, 116103. [Google Scholar] [CrossRef]
- Li, P.F.; Li, B.G. Study on some characteristics of evaporation of sand dune and evapotranspiration of grassland in Mu Us desert. J. Hydraul. Eng. 2000, 3, 25–30. [Google Scholar]
- Zhang, L. Research on Reservoir Water Depth Inversion and Water Area Extraction Based on Multi-Band Remote Sensing. Master’s Thesis, Inner Mongolia Agricultural University, Huhhot, China, 2018. [Google Scholar]
- Xiong, Y.; Li, Q.K. China Soil, 2nd ed.; Science Press: Beijing, China, 1986. [Google Scholar]
- USGS. Available online: https://earthexplorer.usgs.gov/ (accessed on 5 May 2022).
- Li, M.; Han, D.; Wang, X. Spectral Analysis Techniques and Their Applications; Science Press: Beijing, China, 2006. [Google Scholar]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. NASA Spec. Publ. 1974, 351, 309. [Google Scholar]
- Tanre, D.; Deuze, J.L.; Herman, M.; Santer, R.; Vermote, E. Second Simulation of the Satellite Signal in the Solar Spectrum, 6S: An overview. IEEE Trans. Geosci. Remote Sens. 2002, 35, 675–686. [Google Scholar]
- Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary analysis of the performance of the Landsat 8/OLI land surface reflectance product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef]
- CSDN. Available online: https://blog.csdn.net/gordon3000/article/details/102911626 (accessed on 5 November 2022).
- Dalal, R.C.; Henry, R.J. Simultaneous Determination of Moisture, Organic Carbon, and Total Nitrogen by Near Infrared Reflectance Spectrophotometry. Soil Sci. Soc. Am. J. 1986, 50, 120–123. [Google Scholar] [CrossRef]
- Wold, S. The multivariate calibration problem in chemistry solved by the PLS method. In Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
- Hapke, B. Theory of Reflectance and Emittance Spectroscopy; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Clark, R.N. Spectroscopy of rocks and minerals and principles of spectroscopy. Man. Remote Sens. 1999, 3, 3–58. [Google Scholar]


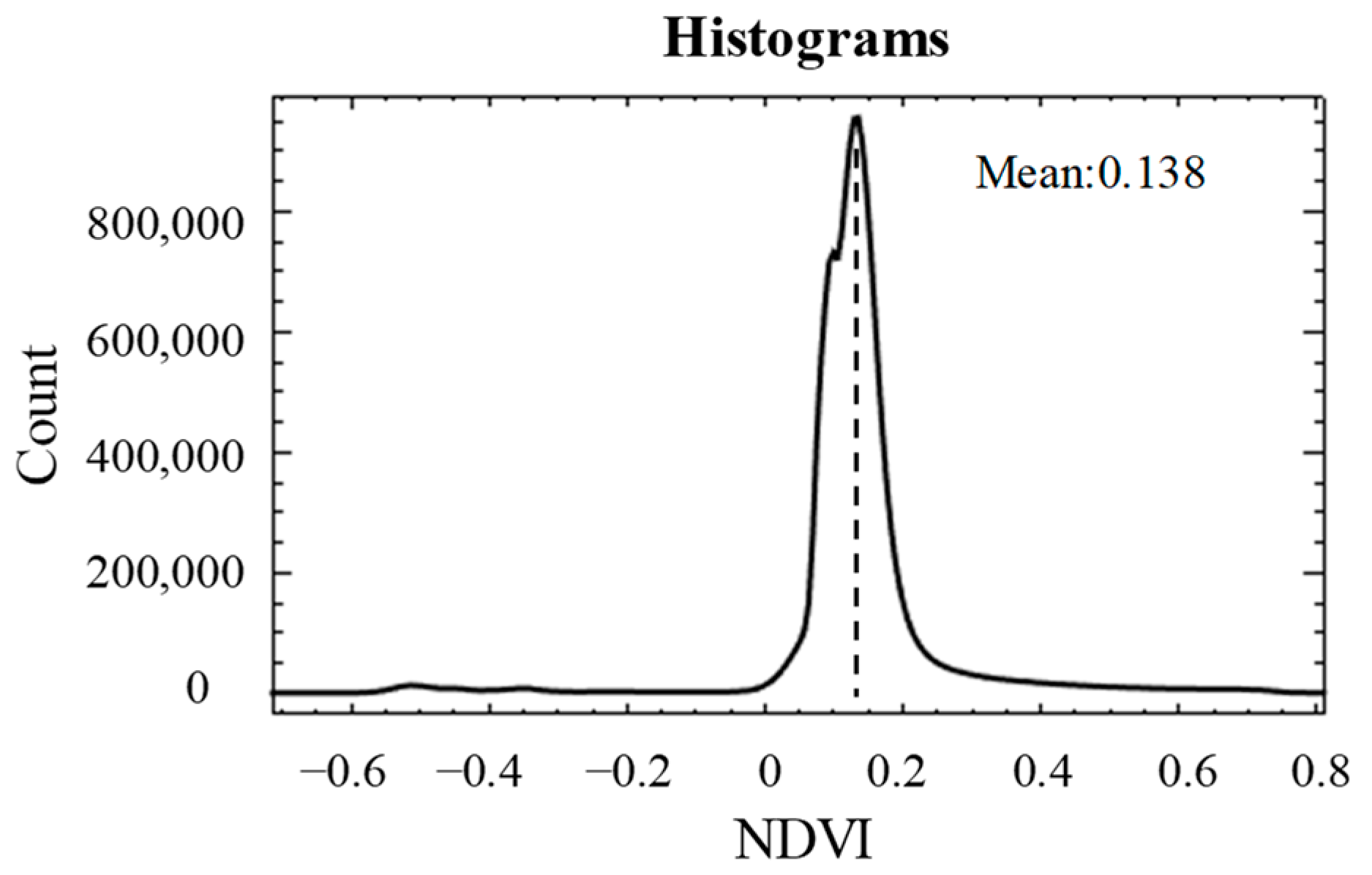
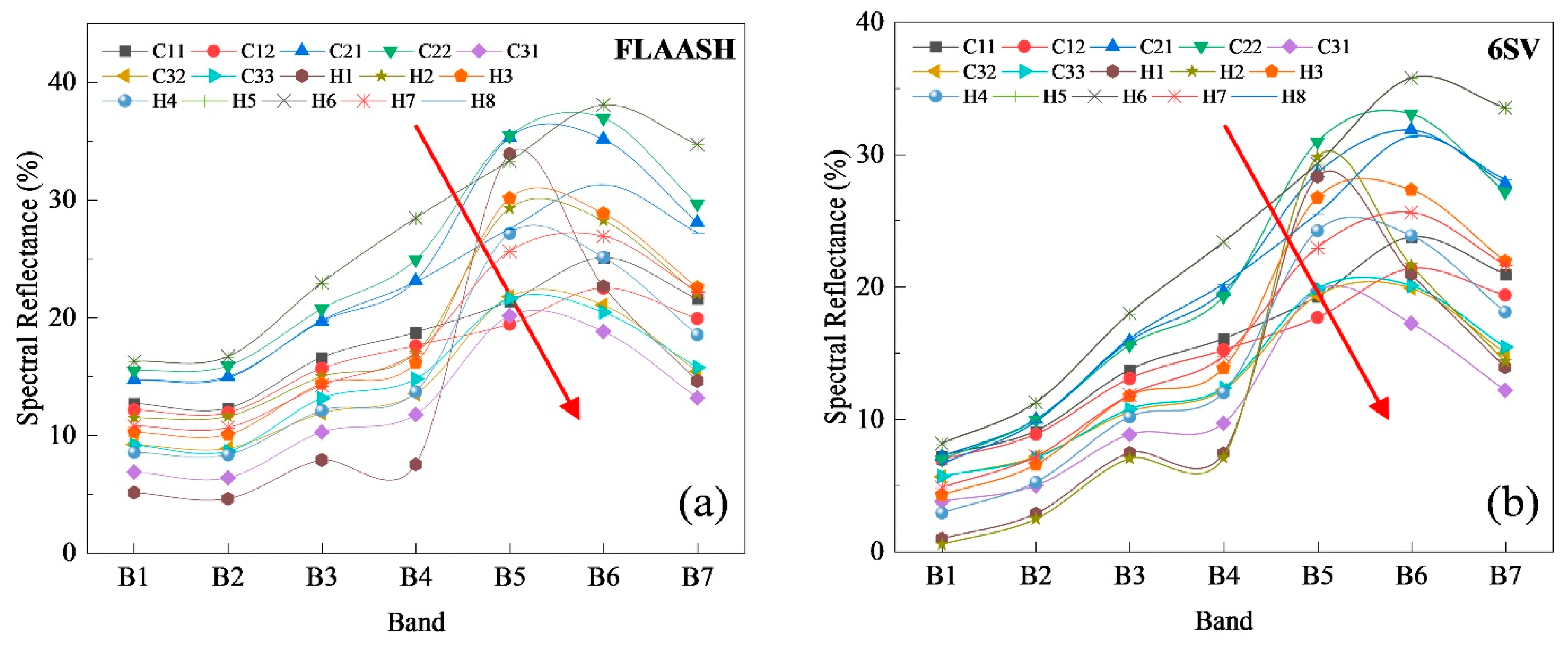
| Sampling Point | Soil Thickness (cm) | Average Content (%) | ||
|---|---|---|---|---|
| Sand | Silt | Clay | ||
| C | 0–20 | 61.954 | 36.800 | 1.246 |
| 0–40 | 66.114 | 32.467 | 1.419 | |
| 0–60 | 66.339 | 32.185 | 1.476 | |
| H | 0–20 | 31.798 | 60.226 | 7.976 |
| 0–40 | 24.071 | 66.167 | 9.763 | |
| 0–60 | 26.361 | 63.917 | 9.723 | |
| Band | Wavelength Range/μm | Signal-to-Noise Ratio | Spatial Resolution/m |
|---|---|---|---|
| 1—COASTAL/AEROSOL | 0.43–0.45 | 130 | 30 |
| 2—Blue | 0.45–0.51 | 130 | 30 |
| 3—Green | 0.53–0.59 | 100 | 30 |
| 4—Red | 0.64–0.67 | 90 | 30 |
| 5—NIR | 0.85–0.88 | 90 | 30 |
| 6—SWIR1 | 1.57–1.65 | 100 | 30 |
| 7—SWIR2 | 2.11–2.29 | 100 | 30 |
| 8—PAN | 0.50–0.68 | 80 | 15 |
| 9—Cirrus | 1.36–1.38 | 50 | 30 |
| Soil Properties | Optimum Model Function | R2 | F | P |
|---|---|---|---|---|
| Sand content | Exp2PMod2 | 0.451 | 46.705 | 1.199 × 10−5 * |
| Silt content | Langevin | 0.518 | 71.415 | 2.168 × 10−7 * |
| Clay content | Exp1p2Md | 0.172 | 17.024 | 1 |
| Model | (Particle Size Content) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| MLR | (sand) | −61.51 | −3.07 | 0.84 | 36.91 | −7.91 | −1.65 | 9.26 | −19.92 |
| (silt) | 111.97 | −6.80 | 9.59 | −20.32 | −1.54 | 0.45 | −4.96 | 13.82 | |
| (clay) | 49.54 | 9.87 | −10.43 | −16.59 | 9.45 | 1.20 | −4.30 | 6.10 | |
| PLSR | (sand) | 111.00 | 3.11 | 1.70 | 0.36 | 0.07 | −2.61 | −0.96 | −0.61 |
| (silt) | 2.19 | −2.79 | −1.59 | −0.43 | −0.14 | 2.16 | 0.74 | 0.45 | |
| (clay) | −13.20 | −0.32 | −0.11 | 0.07 | 0.08 | 0.45 | 0.22 | 0.16 |
| Atmospheric Correction Model | Model | Evaluation Index | Soil Properties | ||
|---|---|---|---|---|---|
| Sand Content | Silt Content | Clay Content | |||
| FLAASH | MLR | R2 | 0.856 | 0.798 | 0.955 |
| F | 5.948 | 3.943 | 21.102 | ||
| PLSR | R2 | 0.138 | 0.081 | 0.240 | |
| SVM | R2 | 0.946 | 0.953 | 0.936 | |
| MSE | 0.008 | 0.008 | 0.008 | ||
| 6SV | MLR | R2 | 0.934 | 0.899 | 0.926 |
| F | 14.129 | 8.873 | 12.435 | ||
| PLSR | R2 | 0.591 | 0.667 | 0.307 | |
| SVM | R2 | 0.958 | 0.965 | 0.983 | |
| MSE | 0.007 | 0.006 | 0.003 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Hu, Z.; Zhang, F.; Song, D.; Liang, Y.; Yu, Y. Multispectral Remote Sensing Monitoring of Soil Particle-Size Distribution in Arid and Semi-Arid Mining Areas in the Middle and Upper Reaches of the Yellow River Basin: A Case Study of Wuhai City, Inner Mongolia Autonomous Region. Remote Sens. 2023, 15, 2137. https://doi.org/10.3390/rs15082137
Li Q, Hu Z, Zhang F, Song D, Liang Y, Yu Y. Multispectral Remote Sensing Monitoring of Soil Particle-Size Distribution in Arid and Semi-Arid Mining Areas in the Middle and Upper Reaches of the Yellow River Basin: A Case Study of Wuhai City, Inner Mongolia Autonomous Region. Remote Sensing. 2023; 15(8):2137. https://doi.org/10.3390/rs15082137
Chicago/Turabian StyleLi, Quanzhi, Zhenqi Hu, Fan Zhang, Deyun Song, Yusheng Liang, and Yi Yu. 2023. "Multispectral Remote Sensing Monitoring of Soil Particle-Size Distribution in Arid and Semi-Arid Mining Areas in the Middle and Upper Reaches of the Yellow River Basin: A Case Study of Wuhai City, Inner Mongolia Autonomous Region" Remote Sensing 15, no. 8: 2137. https://doi.org/10.3390/rs15082137
APA StyleLi, Q., Hu, Z., Zhang, F., Song, D., Liang, Y., & Yu, Y. (2023). Multispectral Remote Sensing Monitoring of Soil Particle-Size Distribution in Arid and Semi-Arid Mining Areas in the Middle and Upper Reaches of the Yellow River Basin: A Case Study of Wuhai City, Inner Mongolia Autonomous Region. Remote Sensing, 15(8), 2137. https://doi.org/10.3390/rs15082137





