Shoreline Detection from PRISMA Hyperspectral Remotely-Sensed Images
Abstract
1. Introduction
2. Materials and Methods
2.1. PRISMA Mission and Products, HSI and PAN
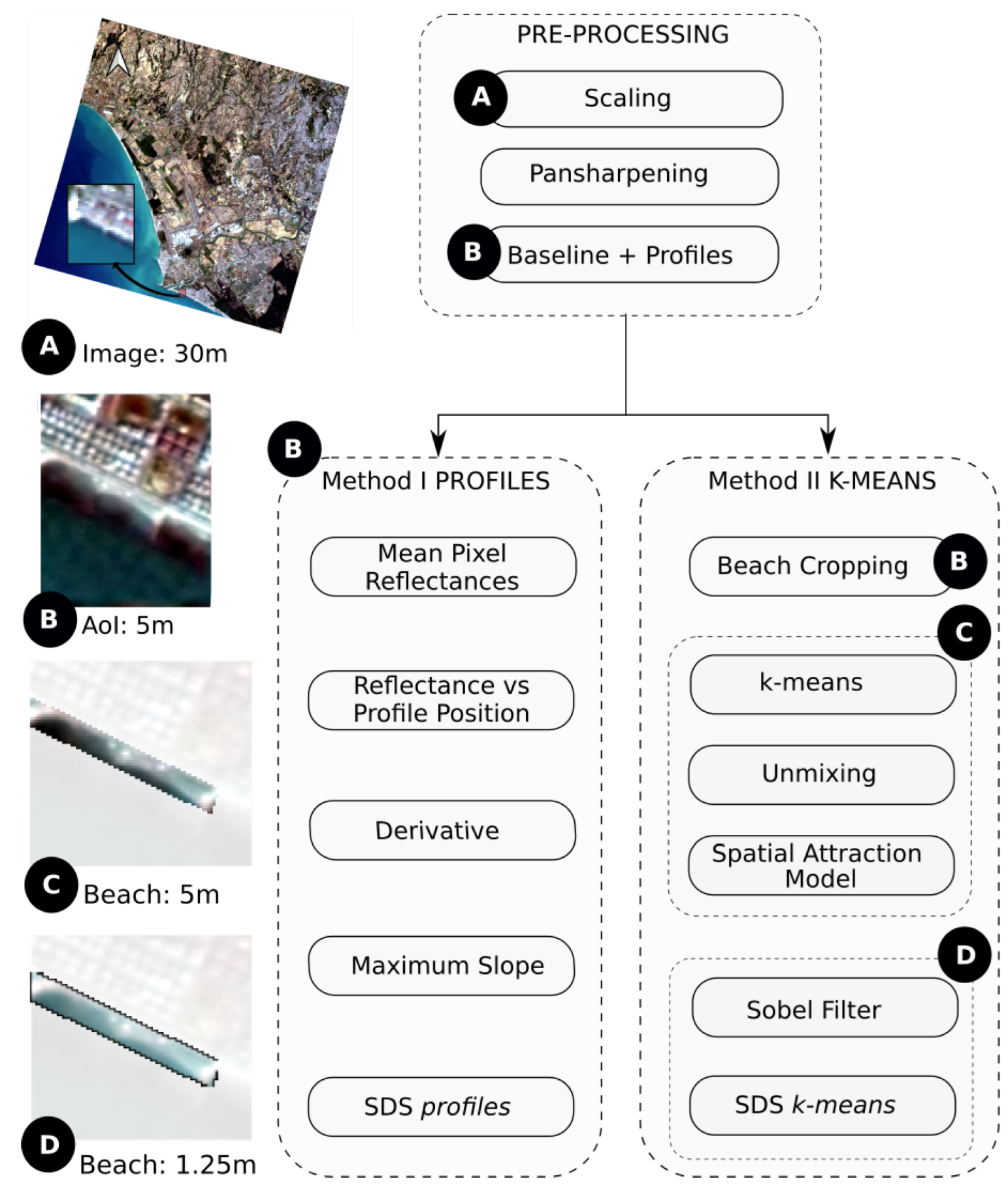
2.2. Shoreline Extraction Algorithms
- Reflectance. The (at-surface) reflectance values (for VNIR, SWIR and PAN) are obtained from the respective “digital numbers” (n, unsigned 16-bit integers, which are provided by PRISMA) via linear transformation [33].where and are the minimum and maximum scaling factor values which are specified inside the image file. Provided that , the reflectance values range from to .
- Pansharpening methods use a multispectral image and a panchromatic band to obtain a new multispectral image with the spatial resolution of the panchromatic band [35]. Among the existing algorithms, the Gram–Schmidt adaptive method [35,36] is chosen since its low computational complexity reduces the spectral distortion produced by other algorithms while maintaining spatial information. Still, pansharpening is the most time-consuming step in the preprocessing, its computational cost increasing linearly with the size of the area.
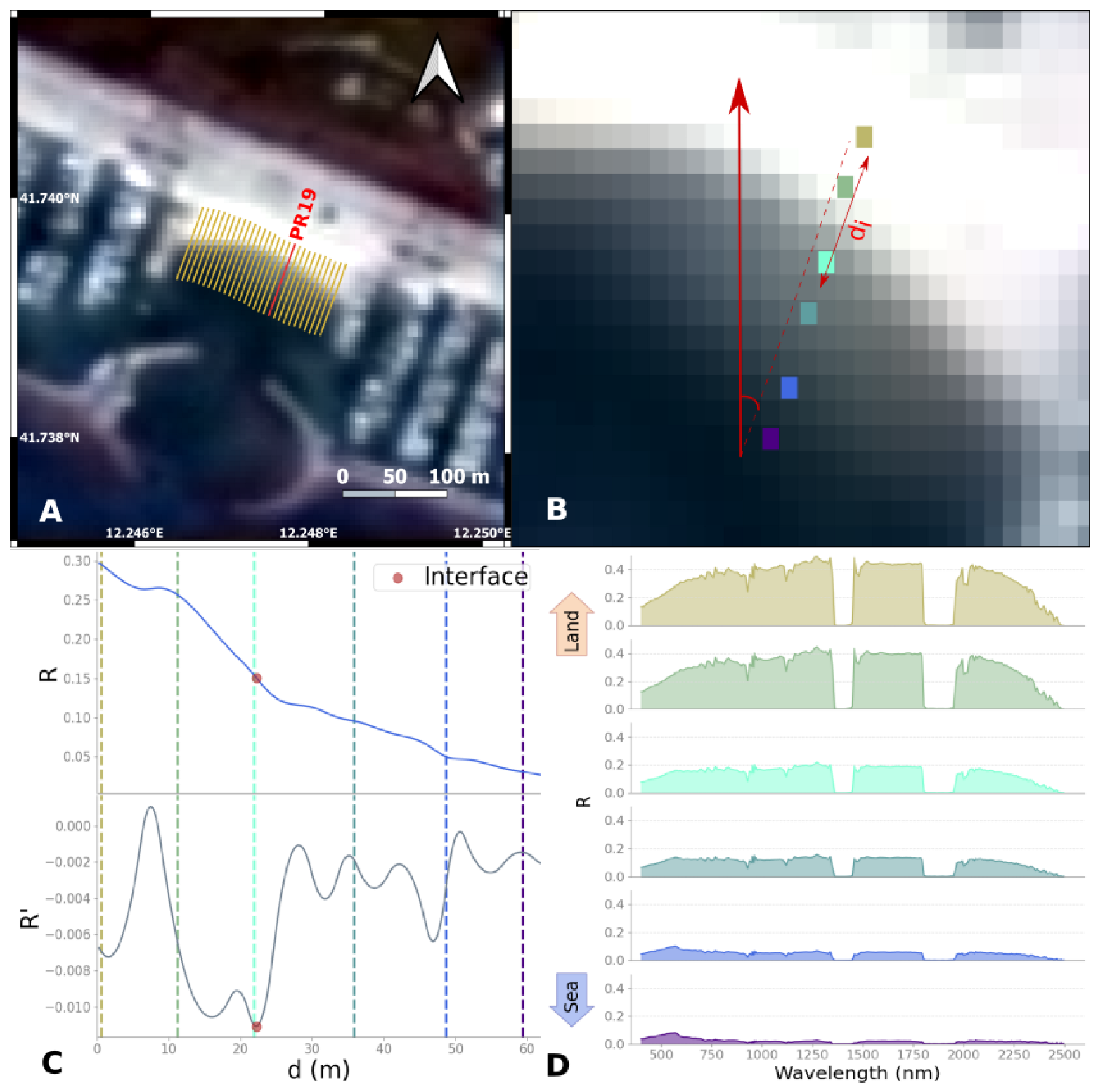
- Baseline and profiles. The baseline, i.e., the line delimiting the beach at its land part, is manually digitised from the pan-sharpened images of 5 m spatial resolution Area of Interest (AoI, Figure 1, insight B) and is then interpolated every 4.5 m to have at least one baseline point per pixel. Then, one profile per point is generated perpendicular to the baseline average direction (so that all the profiles are parallel).
2.2.1. Method I: Profile Approach
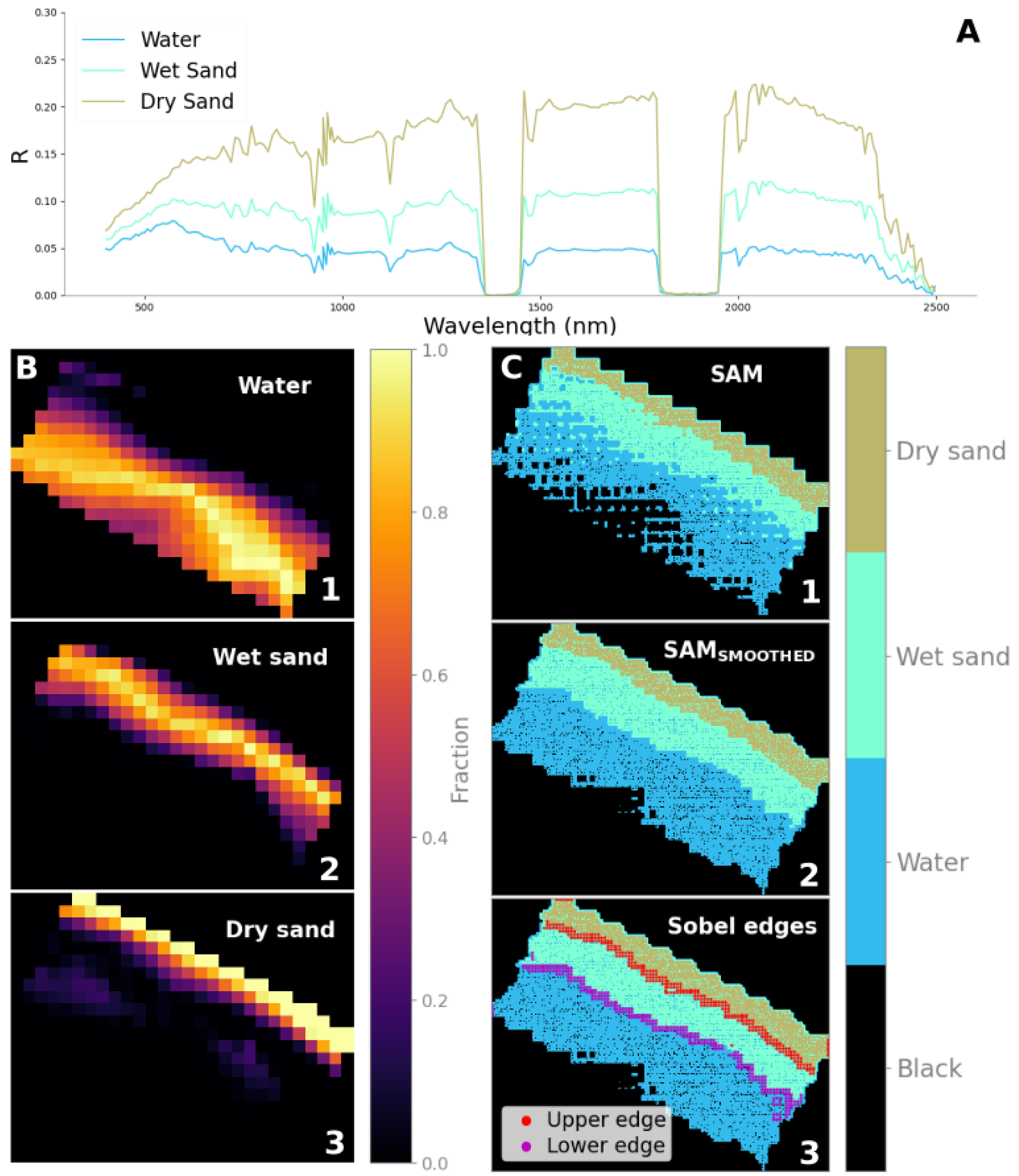
2.2.2. Method II: k-Means Approach
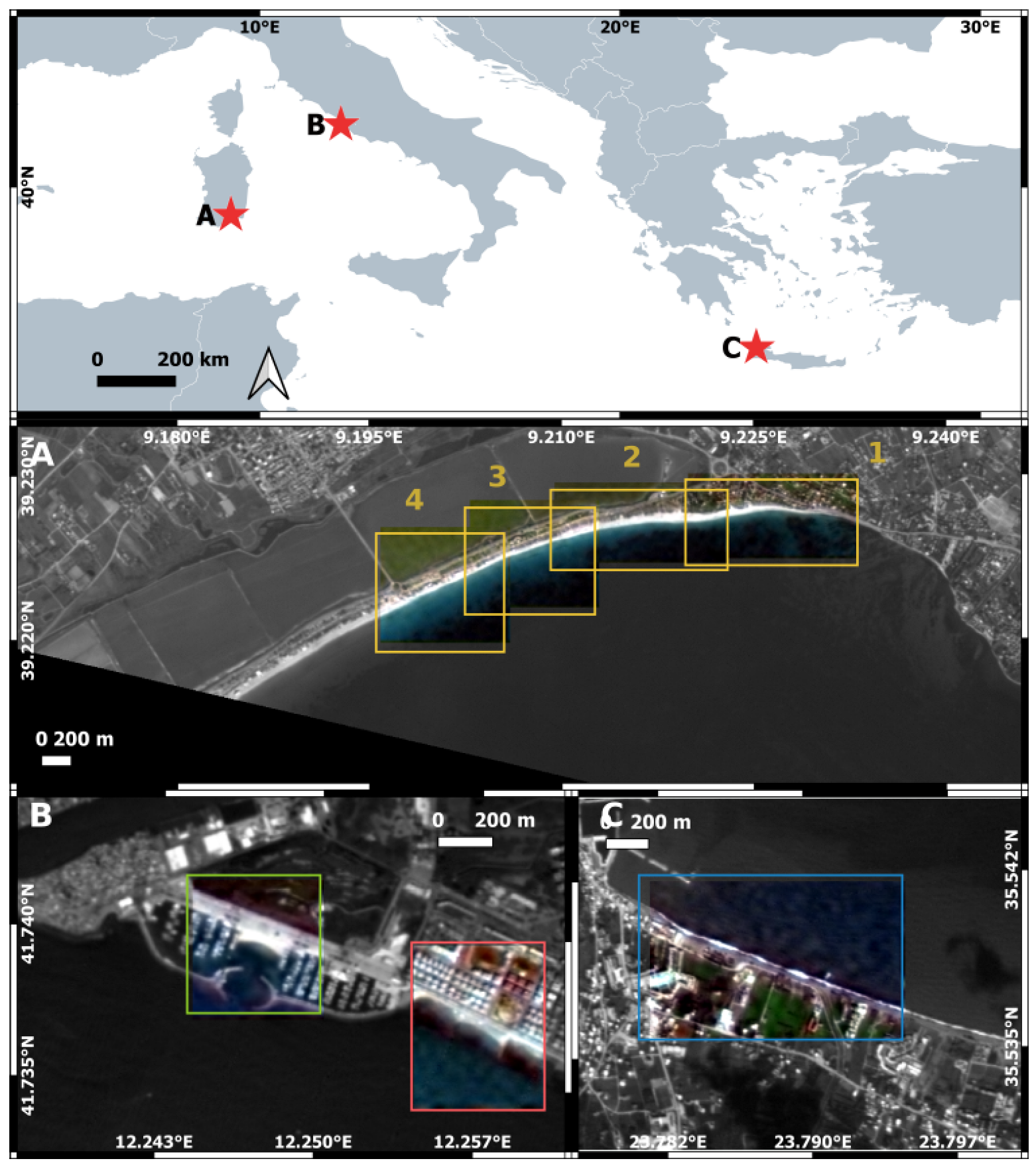
2.3. Study Areas
2.4. PRISMA Dataset and Ground Truthing
2.5. Georeferecing Accuracy and Co-Registration
3. Results
3.1. Ground Truth Error Assessment
3.1.1. Co-Registration Error
3.1.2. Manual Digitization Error
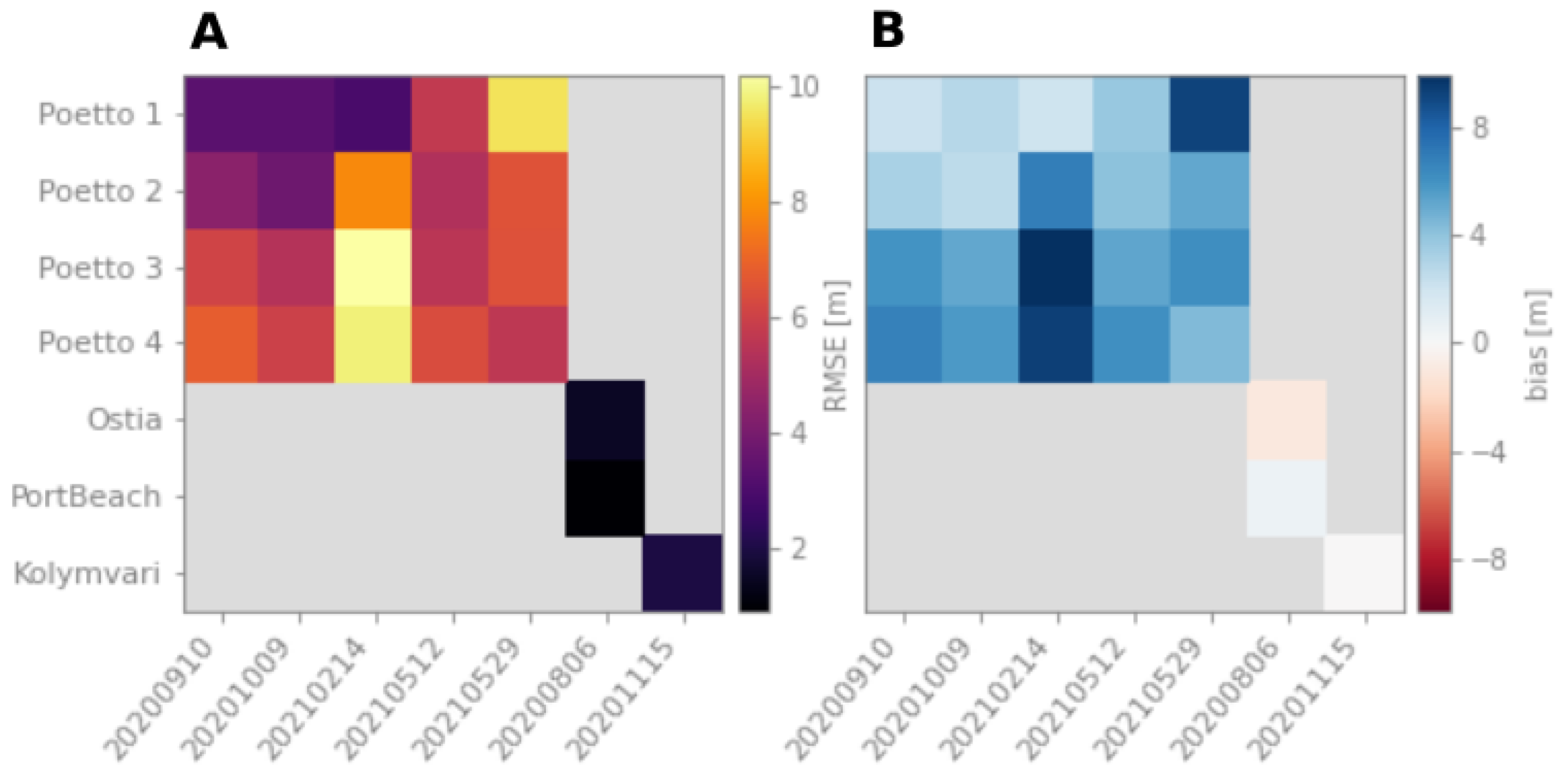
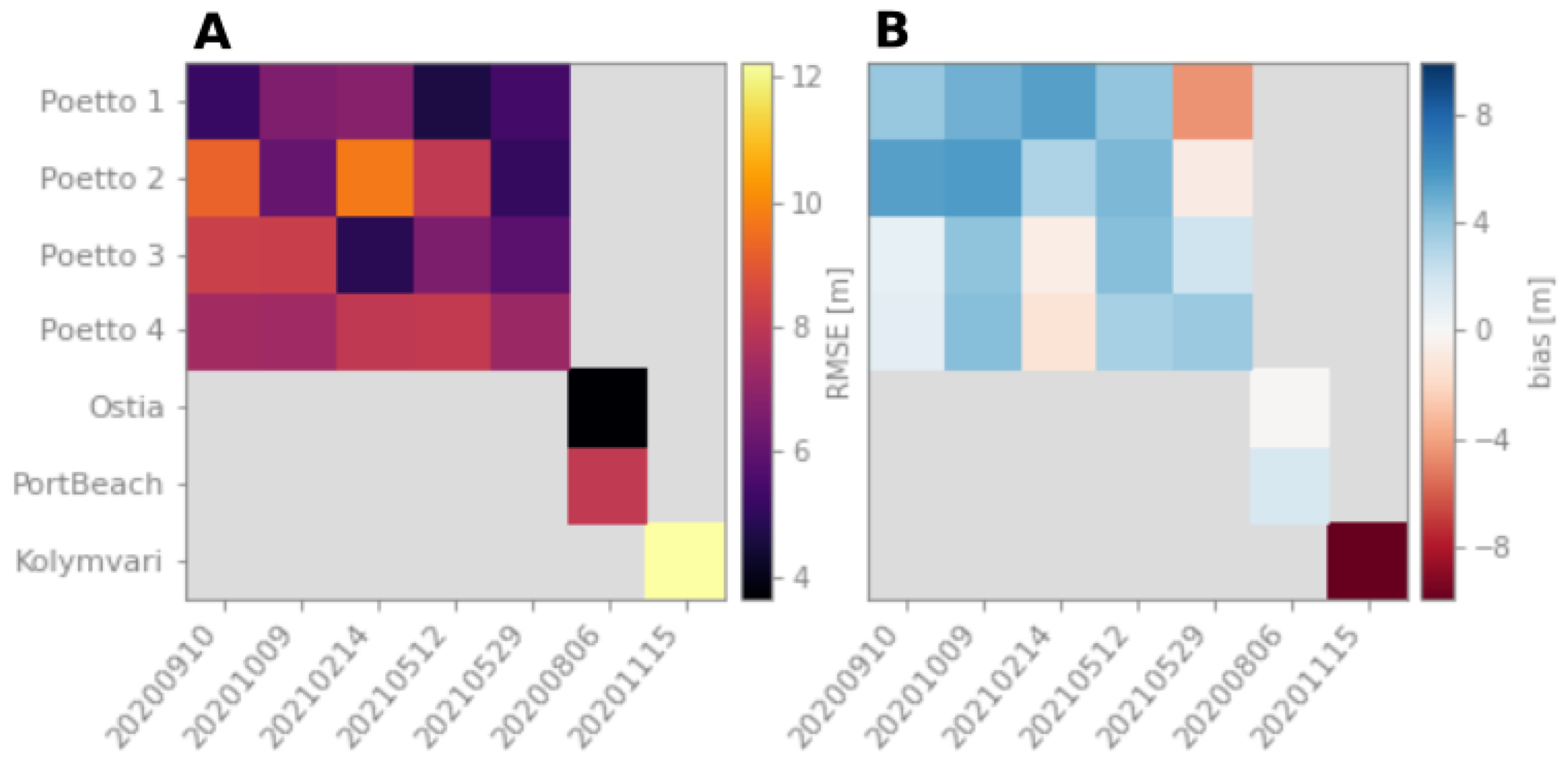
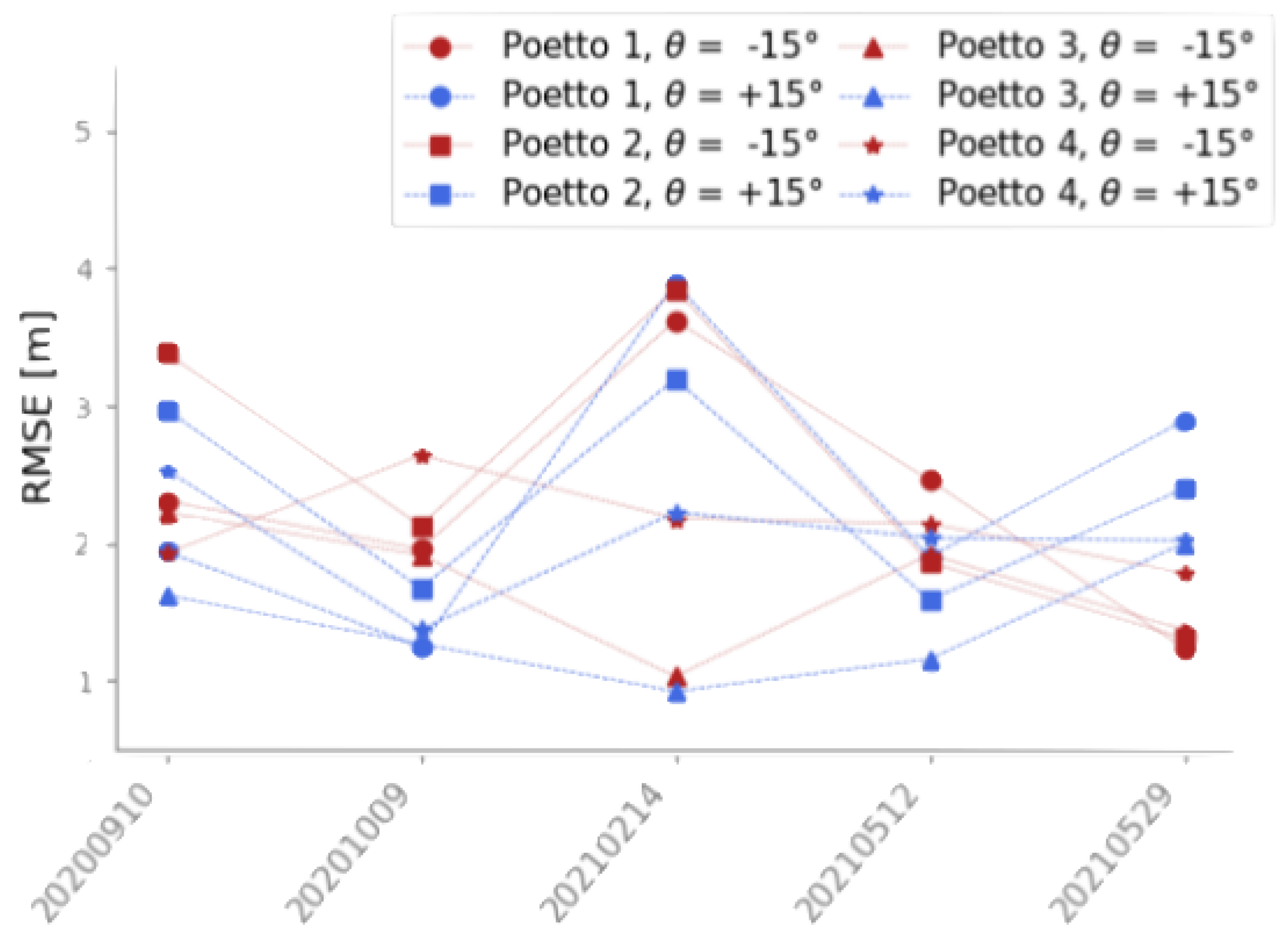
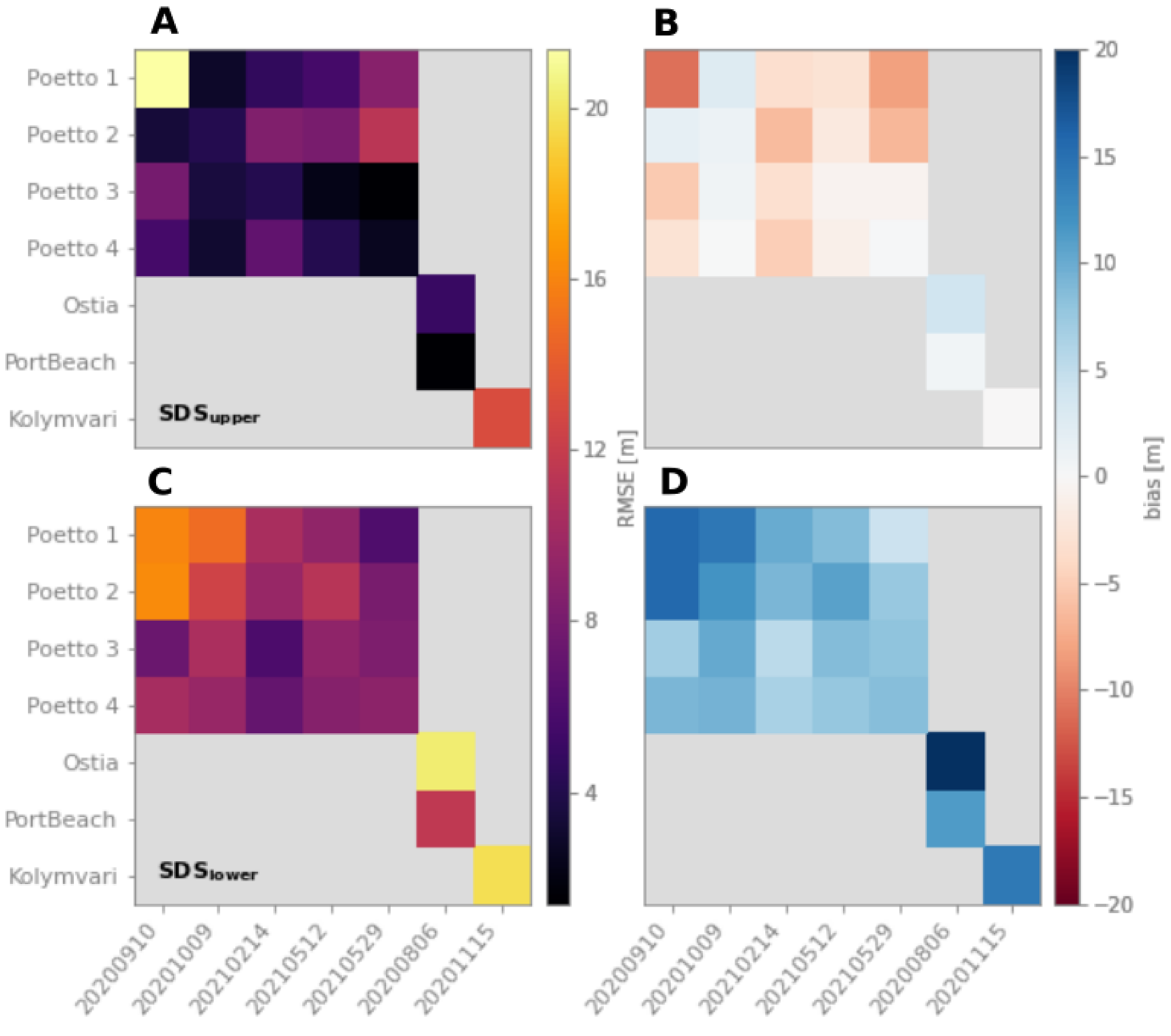
3.2. Method I: Profiles Approach Performance
3.3. Method 2: k-Means Approach Performance
4. Discussion
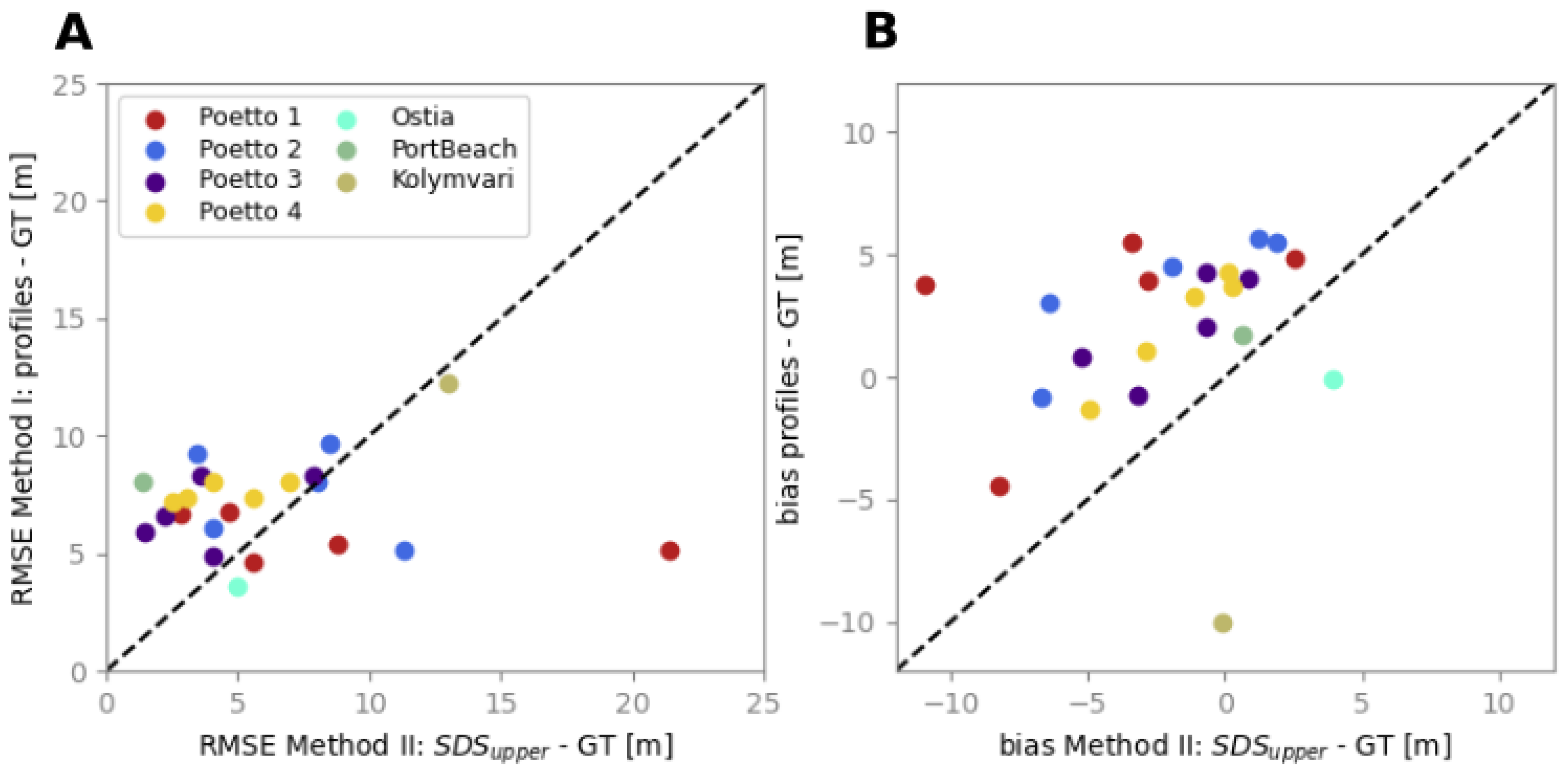
4.1. Profiles vs. k-Means Approaches
4.2. Comparison with other SDS Mapping Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AoI | Area of Interest |
| ECFAS | A proof of concept for the implementation of a European |
| Copernicus coastal flood awareness system | |
| FCLS | Fully Constrained Least-Squares Based Linear Unmixing |
| GCP | Ground Control Poin |
| GT | Ground Truth |
| HDF5 | Hierarchical Data Format Release 5 |
| HSI | hyperspectral imaging |
| MNDWI | Modified Normalized Difference Water Index |
| MSI | Multispectral imaging |
| NDWI | Normalized Difference Water Index |
| PAN | Panchromatic |
| PRISMA | PRecursore IperSpettrale della Missione Applicativa |
| RMSE | Root Mean Square Error |
| SAM | Spatial Attraction Model |
| SDS | Satellite-Derived Shorelines |
| SWIR | Shortwave infrared |
| VNIR | Visible near-infrared |
References
- Committee, F.G.D. Revised Proposal for a National Shoreline Data Standard. 1998. Available online: https://www.fgdc.gov/standards/projects/metadata/shoreline-metadata/proposal (accessed on 14 January 2023).
- Luijendijk, A.; Hagenaars, G.; Ranasinghe, R.; Baart, F.; Donchyts, G.; Aarninkhof, S. The state of the world’s beaches. Sci. Rep. 2018, 8, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Hinkel, J.; Nicholls, R.J.; Tol, R.S.; Wang, Z.B.; Hamilton, J.M.; Boot, G.; Vafeidis, A.T.; McFadden, L.; Ganopolski, A.; Klein, R.J. A global analysis of erosion of sandy beaches and sea-level rise: An application of DIVA. Glob. Planet. Chang. 2013, 111, 150–158. [Google Scholar] [CrossRef]
- McGranahan, G.; Balk, D.; Anderson, B. The rising tide: Assessing the risks of climate change and human settlements in low elevation coastal zones. Environ. Urban. 2007, 19, 17–37. [Google Scholar] [CrossRef]
- Cham, D.D.; Son, N.T.; Minh, N.Q.; Thanh, N.T.; Dung, T.T. An analysis of shoreline changes using combined multitemporal remote sensing and digital evaluation model. Civ. Eng. J. 2020, 6, 1–10. [Google Scholar] [CrossRef]
- Charlier, R.H.; De Meyer, C.P. Beach nourishment as efficient coastal protection. Environ. Manag. Health 1995, 6, 26–34. [Google Scholar] [CrossRef]
- Sunder, S.; Ramsankaran, R.; Ramakrishnan, B. Inter-comparison of remote sensing sensing-based shoreline mapping techniques at different coastal stretches of India. Environ. Monit. Assess. 2017, 189, 290. [Google Scholar] [CrossRef]
- Gens, R. Remote sensing of coastlines: Detection, extraction and monitoring. Int. J. Remote Sens. 2010, 31, 1819–1836. [Google Scholar] [CrossRef]
- Goward, S.; Arvidson, T.; Williams, D.; Faundeen, J.; Irons, J.; Franks, S. Historical record of Landsat global coverage. Photogramm. Eng. Remote Sens. 2006, 72, 1155–1169. [Google Scholar] [CrossRef]
- Bergsma, E.W.; Almar, R. Coastal coverage of ESA’Sentinel 2 mission. Adv. Space Res. 2020, 65, 2636–2644. [Google Scholar] [CrossRef]
- Dellepiane, S.; De Laurentiis, R.; Giordano, F. Coastline extraction from SAR images and a method for the evaluation of the coastline precision. Pattern Recognit. Lett. 2004, 25, 1461–1470. [Google Scholar] [CrossRef]
- Toure, S.; Diop, O.; Kpalma, K.; Maiga, A.S. Shoreline detection using optical remote sensing: A review. ISPRS Int. J.-Geo-Inf. 2019, 8, 75. [Google Scholar] [CrossRef]
- Zulkifle, F.A.; Hassan, R.; Kasim, S.; Othman, R.M. A review on shoreline detection framework using remote sensing satellite image. Int. J. Innov. Comput. 2017, 7, 40–51. [Google Scholar]
- Sun, W.; Du, Q. Hyperspectral band selection: A review. IEEE Geosci. Remote Sens. Mag. 2019, 7, 118–139. [Google Scholar] [CrossRef]
- Sukcharoenpong, A.; Yilmaz, A.; Li, R. An integrated active contour approach to shoreline mapping using HSI and DEM. IEEE Trans. Geosci. Remote Sens. 2015, 54, 1586–1597. [Google Scholar] [CrossRef]
- Elaksher, A.F. Fusion of hyperspectral images and lidar-based dems for coastal mapping. Opt. Lasers Eng. 2008, 46, 493–498. [Google Scholar] [CrossRef]
- Yousefi Lalimi, F.; Silvestri, S.; Moore, L.; Marani, M. Coupled topographic and vegetation patterns in coastal dunes: Remote sensing observations and ecomorphodynamic implications. J. Geophys. Res. Biogeosci. 2017, 122, 119–130. [Google Scholar] [CrossRef]
- Valentini, E.; Taramelli, A.; Cappucci, S.; Filipponi, F.; Nguyen Xuan, A. Exploring the dunes: The correlations between vegetation cover pattern and morphology for sediment retention assessment using airborne multisensor acquisition. Remote Sens. 2020, 12, 1229. [Google Scholar] [CrossRef]
- Taramelli, A.; Cappucci, S.; Valentini, E.; Rossi, L.; Lisi, I. Nearshore sandbar classification of Sabaudia (Italy) with LiDAR Data: The FHyL approach. Remote Sens. 2020, 12, 1053. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, L.; Sun, W.; Xu, W.; Tian, B.; Zhou, Y.; Yang, G.; Chen, C. A New Adaptive Remote Sensing Extraction Algorithm for Complex Muddy Coast Waterline. Remote Sens. 2022, 14, 861. [Google Scholar] [CrossRef]
- Arslan, O.; Akyürek, Ö.; Kaya, Ş.; Şeker, D.Z. Dimension reduction methods applied to coastline extraction on hyperspectral imagery. Geocarto Int. 2020, 35, 376–390. [Google Scholar] [CrossRef]
- Hong, Z.; Li, X.; Han, Y.; Zhang, Y.; Wang, J.; Zhou, R.; Hu, K. Automatic sub-pixel coastline extraction based on spectral mixture analysis using EO-1 Hyperion data. Front. Earth Sci. 2019, 13, 478–494. [Google Scholar] [CrossRef]
- Boardmann, J.; Kruse, F.; Green, R. Mapping target signatures via partial unmixing of AVIRIS data. In Proceedings of the Summaries of the 5th Annual JPL Airborne Geoscience Workshop, Pasadena, CA, USA, 23–26 January 1995; Volume 1. [Google Scholar]
- Mertens, K.C.; De Baets, B.; Verbeke, L.P.; De Wulf, R.R. A sub-pixel mapping algorithm based on sub-pixel/pixel spatial attraction models. Int. J. Remote. Sens. 2006, 27, 3293–3310. [Google Scholar] [CrossRef]
- Cogliati, S.; Sarti, F.; Chiarantini, L.; Cosi, M.; Lorusso, R.; Lopinto, E.; Miglietta, F.; Genesio, L.; Guanter, L.; Damm, A.; et al. The PRISMA imaging spectroscopy mission: Overview and first performance analysis. Remote. Sens. Environ. 2021, 262, 112499. [Google Scholar] [CrossRef]
- Taramelli, A.; Tornato, A.; Magliozzi, M.L.; Mariani, S.; Valentini, E.; Zavagli, M.; Costantini, M.; Nieke, J.; Adams, J.; Rast, M. An interaction methodology to collect and assess user-driven requirements to define potential opportunities of future hyperspectral imaging sentinel mission. Remote Sens. 2020, 12, 1286. [Google Scholar] [CrossRef]
- Giardino, C.; Bresciani, M.; Braga, F.; Fabbretto, A.; Ghirardi, N.; Pepe, M.; Gianinetto, M.; Colombo, R.; Cogliati, S.; Ghebrehiwot, S.; et al. First Evaluation of PRISMA Level 1 Data for Water Applications. Sensors 2020, 20, 4553. [Google Scholar] [CrossRef] [PubMed]
- Niroumand-Jadidi, M.; Bovolo, F.; Bruzzone, L. Water Quality Retrieval from PRISMA Hyperspectral Images: First Experience in a Turbid Lake and Comparison with Sentinel-2. Remote Sens. 2020, 12, 3984. [Google Scholar] [CrossRef]
- Vangi, E.; D’Amico, G.; Francini, S.; Giannetti, F.; Lasserre, B.; Marchetti, M.; Chirici, G. The new hyperspectral satellite PRISMA: Imagery for forest types discrimination. Sensors 2021, 21, 1182. [Google Scholar] [CrossRef] [PubMed]
- Pepe, M.; Pompilio, L.; Gioli, B.; Busetto, L.; Boschetti, M. Detection and Classification of Non-Photosynthetic Vegetation from PRISMA Hyperspectral Data in Croplands. Remote Sens. 2020, 12, 3903. [Google Scholar] [CrossRef]
- Amici, S.; Piscini, A. Exploring PRISMA Scene for Fire Detection: Case Study of 2019 Bushfires in Ben Halls Gap National Park, NSW, Australia. Remote Sens. 2021, 13, 1410. [Google Scholar] [CrossRef]
- Palomar-Vázquez, J.; Almonacid-Caballer, J.; Cabezas-Rabadán, C.; Pardo-Pascual, J.E. SAET: A new tool for automatic shoreline extraction with subpixel accuracy for characterising shoreline changes linked to coastal storms. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 23–27 May 2022. [Google Scholar]
- PRISMA. PRISMA Products Specifications. Available online: http://prisma.asi.it/missionselect/docs/PRISMA%20Product%20Specifications_Is2_3.pdf (accessed on 14 January 2023).
- Guarini, R.; Loizzo, R.; Facchinetti, C.; Longo, F.; Ponticelli, B.; Faraci, M.; Dami, M.; Cosi, M.; Amoruso, L.; De Pasquale, V.; et al. PRISMA hyperspectral mission products. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 179–182. [Google Scholar]
- Aiazzi, B.; Baronti, S.; Selva, M. Improving component substitution pansharpening through multivariate regression of MS + Pan data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3230–3239. [Google Scholar] [CrossRef]
- Loncan, L.; De Almeida, L.B.; Bioucas-Dias, J.M.; Briottet, X.; Chanussot, J.; Dobigeon, N.; Fabre, S.; Liao, W.; Licciardi, G.A.; Simoes, M.; et al. Hyperspectral pansharpening: A review. IEEE Geosci. Remote. Sens. Mag. 2015, 3, 27–46. [Google Scholar] [CrossRef]
- Armaroli, C.; Balouin, Y.; Ciavola, P.; Gardelli, M. Bar changes due to storm events using ARGUS: Lido di Dante, Italy. In Coastal Dynamics 2005: State of the Practice; ASCE: New York, NY, USA, 2006; pp. 1–14. [Google Scholar]
- Braga, F.; Tosi, L.; Prati, C.; Alberotanza, L. Shoreline detection: Capability of COSMO-SkyMed and high-resolution multispectral images. Eur. J. Remote Sens. 2013, 46, 837–853. [Google Scholar] [CrossRef]
- Prades, J.; Safont, G.; Salazar, A.; Vergara, L. Estimation of the number of endmembers in hyperspectral images using agglomerative clustering. Remote Sens. 2020, 12, 3585. [Google Scholar] [CrossRef]
- Biondo, M.; Buosi, C.; Trogu, D.; Mansfield, H.; Vacchi, M.; Ibba, A.; Porta, M.; Ruju, A.; De Muro, S. Natural vs. Anthropic Influence on the Multidecadal Shoreline Changes of Mediterranean Urban Beaches: Lessons from the Gulf of Cagliari (Sardinia). Water 2020, 12, 3578. [Google Scholar] [CrossRef]
- Brambilla, W.; Van Rooijen, A.; Simeone, S.; Ibba, A.; DeMuro, S. Field observations, video monitoring and numerical modeling at poetto beach, Italy. J. Coast. Res. 2016, 75, 825–829. [Google Scholar] [CrossRef]
- Porta, M.; Buosi, C.; Trogu, D.; Ibba, A.; De Muro, S. An integrated sea-land approach for analyzing forms, processes, deposits and the evolution of the urban coastal belt of Cagliari. J. Maps 2021, 17, 65–74. [Google Scholar] [CrossRef]
- Cenci, L.; Pampanoni, V.; Laneve, G.; Santella, C.; Boccia, V. Evaluating the Potentialities of Copernicus Very High Resolution (VHR) Optical Datasets for Assessing the Shoreline Erosion Hazard in Microtidal Environments. AIT Ser. Trends Earth Obs. 2021, 2, 81–84. [Google Scholar]
- Lisco, S.N.; Acquafredda, P.; Gallicchio, S.; Sabato, L.; Bonifazi, A.; Cardone, F.; Corriero, G.; Gravina, M.F.; Pierri, C.; Moretti, M. The sedimentary dynamics of Sabellaria alveolata bioconstructions (Ostia, Tyrrhenian Sea, central Italy). J. Palaeogeogr. 2020, 9, 1–18. [Google Scholar] [CrossRef]
- Synolakis, C.E.; Kalligeris, N.; Foteinis, S.; Voukouvalas, E. The plight of the beaches of Crete. In Proceedings of the Solutions to Coastal Disasters 2008 Conference, Oahu, HI, USA, 13–16 April 2008; pp. 495–506. [Google Scholar]
- Velegrakis, A.; Trygonis, V.; Chatzipavlis, A.; Karambas, T.; Vousdoukas, M.; Ghionis, G.; Monioudi, I.; Hasiotis, T.; Andreadis, O.; Psarros, F. Shoreline variability of an urban beach fronted by a beachrock reef from video imagery. Nat. Hazards 2016, 83, 201–222. [Google Scholar] [CrossRef]
- Hagenaars, G.; de Vries, S.; Luijendijk, A.P.; de Boer, W.P.; Reniers, A.J. On the accuracy of automated shoreline detection derived from satellite imagery: A case study of the sand motor mega-scale nourishment. Coast. Eng. 2018, 133, 113–125. [Google Scholar] [CrossRef]
- Sánchez-García, E.; Palomar-Vázquez, J.; Pardo-Pascual, J.E.; Almonacid-Caballer, J.; Cabezas-Rabadán, C.; Gómez-Pujol, L. An efficient protocol for accurate and massive shoreline definition from mid-resolution satellite imagery. Coast. Eng. 2020, 160, 103732. [Google Scholar] [CrossRef]
- Giacomo, C.; Ettore, L.; Rino, L.; Rosa, L.; Rocchina, G.; Girolamo, D.M.; Patrizia, S. The hyperspectral prisma mission in operations. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 3282–3285. [Google Scholar]
- Lopinto, E.; Fasano, L.; Longo, F.; Varacalli, G.; Sacco, P.; Chiarantini, L.; Sarti, F.; Agrimano, L.; Santoro, F.; Cogliati, S.; et al. Current Status and Future Perspectives of the PRISMA Mission at the Turn of One Year in Operational Usage. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1380–1383. [Google Scholar]
- Marshall, M.; Belgiu, M.; Boschetti, M.; Pepe, M.; Stein, A.; Nelson, A. Field-level crop yield estimation with PRISMA and Sentinel-2. ISPRS J. Photogramm. Remote Sens. 2022, 187, 191–210. [Google Scholar] [CrossRef]
- Wulder, M.A.; Loveland, T.R.; Roy, D.P.; Crawford, C.J.; Masek, J.G.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Belward, A.S.; Cohen, W.B.; et al. Current status of Landsat program, science, and applications. Remote Sens. Environ. 2019, 225, 127–147. [Google Scholar] [CrossRef]
- Ye, Y.; Yang, C.; Zhu, B.; Zhou, L.; He, Y.; Jia, H. Improving Co-Registration for Sentinel-1 SAR and Sentinel-2 Optical Images. Remote Sens. 2021, 13, 928. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: New York, NY, USA, 2003. [Google Scholar]
- Boak, E.H.; Turner, I.L. Shoreline definition and detection: A review. J. Coast. Res. 2005, 21, 688–703. [Google Scholar] [CrossRef]
- Fabbri, S.; Grottoli, E.; Armaroli, C.; Ciavola, P. Using high-spatial resolution UAV-derived data to evaluate vegetation and geomorphological changes on a dune field involved in a restoration endeavour. Remote Sens. 2021, 13, 1987. [Google Scholar] [CrossRef]
- Del Río, L.; Gracia, F.J. Error determination in the photogrammetric assessment of shoreline changes. Nat. Hazards 2013, 65, 2385–2397. [Google Scholar] [CrossRef]
- Ribas, F.; Simarro, G.; Arriaga, J.; Luque, P. Automatic shoreline detection from video images by combining information from different methods. Remote Sens. 2020, 12, 3717. [Google Scholar] [CrossRef]
- Short, A.; Jackson, D. Beach morphodynamics. Treatise Geomorphol. 2013, 106–129. [Google Scholar]
- Castelle, B.; Masselink, G.; Scott, T.; Stokes, C.; Konstantinou, A.; Marieu, V.; Bujan, S. Satellite-derived shoreline detection at a high-energy meso-macrotidal beach. Geomorphology 2021, 383, 107707. [Google Scholar] [CrossRef]
- Vos, K.; Splinter, K.D.; Harley, M.D.; Simmons, J.A.; Turner, I.L. CoastSat: A Google Earth Engine-enabled Python toolkit to extract shorelines from publicly available satellite imagery. Environ. Model. Softw. 2019, 122, 104528. [Google Scholar] [CrossRef]
- Dolan, R.; Hayden, B.; Heywood, J. A new photogrammetric method for determining shoreline erosion. Coast. Eng. 1978, 2, 21–39. [Google Scholar] [CrossRef]
- Armaroli, C.; Ciavola, P. Dynamics of a nearshore bar system in the northern Adriatic: A video-based morphological classification. Geomorphology 2011, 126, 201–216. [Google Scholar] [CrossRef]
- Ruessink, B.; Pape, L.; Turner, I. Daily to interannual cross-shore sandbar migration: Observations from a multiple sandbar system. Cont. Shelf Res. 2009, 29, 1663–1677. [Google Scholar] [CrossRef]
- Almeida, L.P.; de Oliveira, I.E.; Lyra, R.; Dazzi, R.L.S.; Martins, V.G.; da Fontoura Klein, A.H. Coastal Analyst System from Space Imagery Engine (CASSIE): Shoreline management module. Environ. Model. Softw. 2021, 140, 105033. [Google Scholar] [CrossRef]
- Do, A.T.; Vries, S.d.; Stive, M.J. The estimation and evaluation of shoreline locations, shoreline-change rates, and coastal volume changes derived from Landsat images, 2018 The estimation and evaluation of shoreline locations, shoreline-change rates, and coastal volume changes derived from Landsat images. J. Coast. Res. 2019, 35, 56–71. [Google Scholar]
- Pardo-Pascual, J.E.; Sánchez-García, E.; Almonacid-Caballer, J.; Palomar-Vázquez, J.M.; Priego De Los Santos, E.; Fernández-Sarría, A.; Balaguer-Beser, Á. Assessing the accuracy of automatically extracted shorelines on microtidal beaches from Landsat 7, Landsat 8 and Sentinel-2 imagery. Remote Sens. 2018, 10, 326. [Google Scholar] [CrossRef]
- García-Rubio, G.; Huntley, D.; Russell, P. Evaluating shoreline identification using optical satellite images. Mar. Geol. 2015, 359, 96–105. [Google Scholar] [CrossRef]
- Fisher, A.; Flood, N.; Danaher, T. Comparing Landsat water index methods for automated water classification in eastern Australia. Remote Sens. Environ. 2016, 175, 167–182. [Google Scholar] [CrossRef]



| Orbit altitude reference | 615 km |
| Lifetime | 5 years |
| Revisit time | 29 days |
| Relook time | 7 days |
| HSI-VNIR | HSI-SWIR | PAN | |
|---|---|---|---|
| Swath (km) | 30 | 30 | 30 |
| Spatial resolution (m) | 30 | 30 | 5 |
| Spatial pixels | 1000 | 1000 | 6000 |
| Spectral range (nm) | 400–1010 | 920–2500 | 400–700 |
| Spectral bands | 66 | 176 | 1 |
| Spectral Sampling Interval, SSI (nm) | 7.2–11 | 6.5–11 | - |
| Spectral Resolution (nm) | 9–13 | 9–14.5 | - |
| Absolute Radiometric Accuracy | (Stability ) | (Stability ) | - |
| PRISMA | Ground Truth (GT) | |||
|---|---|---|---|---|
| Beach | Overpass | Overpass | Mission | Resolution (Meters) |
| Poetto | 2020/09/10 10:18:13 | 2020/09/10 10:20:01 | Sentinel S2 | 10 |
| 2020/10/09 10:17:51 | 2020/10/09 10:00:41 | Landsat L8 | 15 | |
| 2021/02/14 10:22:50 | 2021/02/14 10:00:26 | Landsat L8 | 15 | |
| 2021/05/12 10:21:40 | 2021/05/12 10:06:05 | Landsat L8 | 15 | |
| 2021/05/29 10:15:00 | 2021/05/29 09:07:07 | Landsat L7 | 15 | |
| PortBeach & Ostia | 2020/08/06 10:14:13 | 2020/08/06 10:16:25 | Pleiades PH1A | 0.5 |
| Kolymvari | 2020/11/15 09:18:18 | 2020/11/15 09:02:26 | Pleiades PH1B | 0.5 |
| Beach | Date | ♯ of Pairs | RMSE [m] |
|---|---|---|---|
| Poetto | 10 September 2020 | 17 | 3.1 |
| 9 October 2020 | 7 | 3.3 | |
| 15 October 2020 | 8 | 3.2 | |
| 14 February 2021 | 31 | 5.8 | |
| 12 May 2021 | 19 | 5.3 | |
| 29 May 2021 | 5 | 5.7 | |
| PortBeach & Ostia | 6 August 2020 | 18 | 2.3 |
| Kolymvari | 15 November 2020 | 20 | 3.7 |
| Beach | RMSE [m] | Bias [m] |
|---|---|---|
| Poetto | 6.4 | +5.36 |
| PortBeach & Ostia | 1.20 | −0.23 |
| Kolymvari | 1.98 | −0.07 |
| Beach | RMSE [m] | Bias [m] |
|---|---|---|
| Poetto | 6.94 | +2.65 |
| PortBeach & Ostia | 5.85 | +0.81 |
| Kolymvari | 12.25 | −10.03 |
| Beach | RMSE [m] | Bias [m] | |
|---|---|---|---|
| Poetto | 5.99 | −2.61 | |
| PortBeach & Ostia | 3.19 | +2.28 | |
| Kolymvari | 13.02 | −0.12 | |
| Poetto | 9.99 | +9.45 | |
| PortBeach & Ostia | 15.95 | +15.65 | |
| Kolymvary | 19.69 | +14.35 |
| Foam | No Foam | |||
|---|---|---|---|---|
| RMSE [m] | Bias [m] | RMSE [m] | Bias [m] | |
| 7.07 | +1.94 | 6.98 | +2.06 | |
| 6.05 | −2.08 | 5.77 | −2.46 | |
| Method | Mission | Spatial Res. [m] | Spectral Res. | RMSE [m] | GT |
|---|---|---|---|---|---|
| Method I: profiles | PRISMA | 30 | hyper | 6.98 | digitised |
| Method II: k-means | PRISMA | 30 | hyper | 5.77 | digitised |
| [65] | L5-7-8 + S2 | 30 | multi | 8.8 | in situ |
| [61] | L5-7-8 + S2 | 10–30 | multi | 7.3–12.8 | in situ + video |
| [66] | L5-7-8 | 30 | multi | 1.5–36.5 | in situ |
| [22] | EO-1 | 30 | hyper | 10.5–12 | digitised |
| [47] | L5-7-8 + S2 | 10–30 | multi | 9.5–21.9 | in situ |
| [67] | L7-8 + S2 | 10–30 | multi | 3.1–5.5 | in situ + video |
| [68] | SPOT5 | 10 | multi | 5.6 | in situ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Souto-Ceccon, P.; Simarro, G.; Ciavola, P.; Taramelli, A.; Armaroli, C. Shoreline Detection from PRISMA Hyperspectral Remotely-Sensed Images. Remote Sens. 2023, 15, 2117. https://doi.org/10.3390/rs15082117
Souto-Ceccon P, Simarro G, Ciavola P, Taramelli A, Armaroli C. Shoreline Detection from PRISMA Hyperspectral Remotely-Sensed Images. Remote Sensing. 2023; 15(8):2117. https://doi.org/10.3390/rs15082117
Chicago/Turabian StyleSouto-Ceccon, Paola, Gonzalo Simarro, Paolo Ciavola, Andrea Taramelli, and Clara Armaroli. 2023. "Shoreline Detection from PRISMA Hyperspectral Remotely-Sensed Images" Remote Sensing 15, no. 8: 2117. https://doi.org/10.3390/rs15082117
APA StyleSouto-Ceccon, P., Simarro, G., Ciavola, P., Taramelli, A., & Armaroli, C. (2023). Shoreline Detection from PRISMA Hyperspectral Remotely-Sensed Images. Remote Sensing, 15(8), 2117. https://doi.org/10.3390/rs15082117









