Precise Ambiguity Performance Evaluation for Spaceborne SAR with Diverse Waveforms
Abstract
1. Introduction
2. Important Review for Ambiguity Evaluation
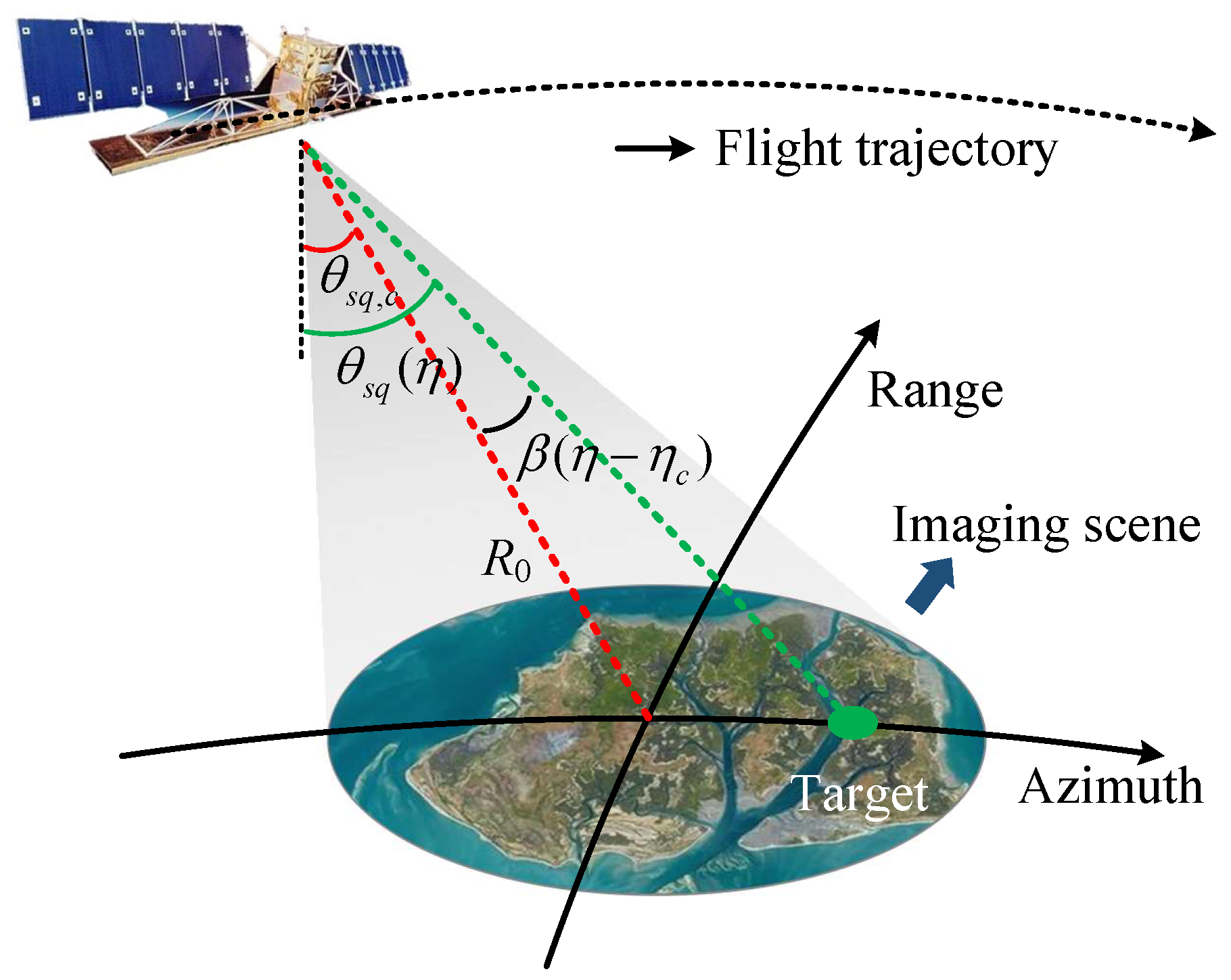
3. Signal Model
4. Proposed RASR and AASR Evaluation Method
4.1. RASR and AASR without Waveform Diversity
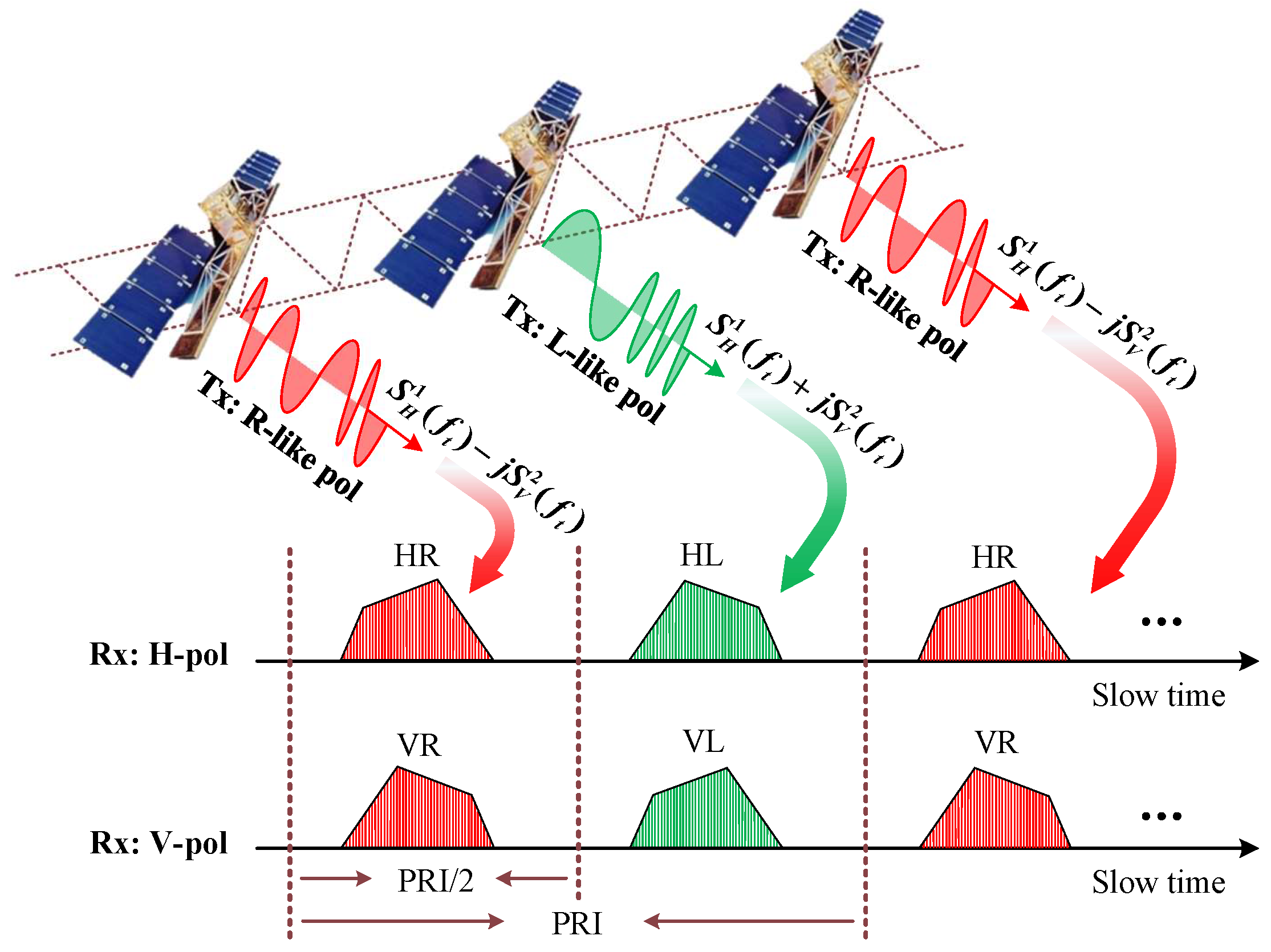
4.2. RASR and AASR with Waveform Diversity
4.2.1. Single Polarization SAR with Waveform Diversity
4.2.2. Quad-Pol SAR with Waveform Diversity
5. Simulation and Analysis
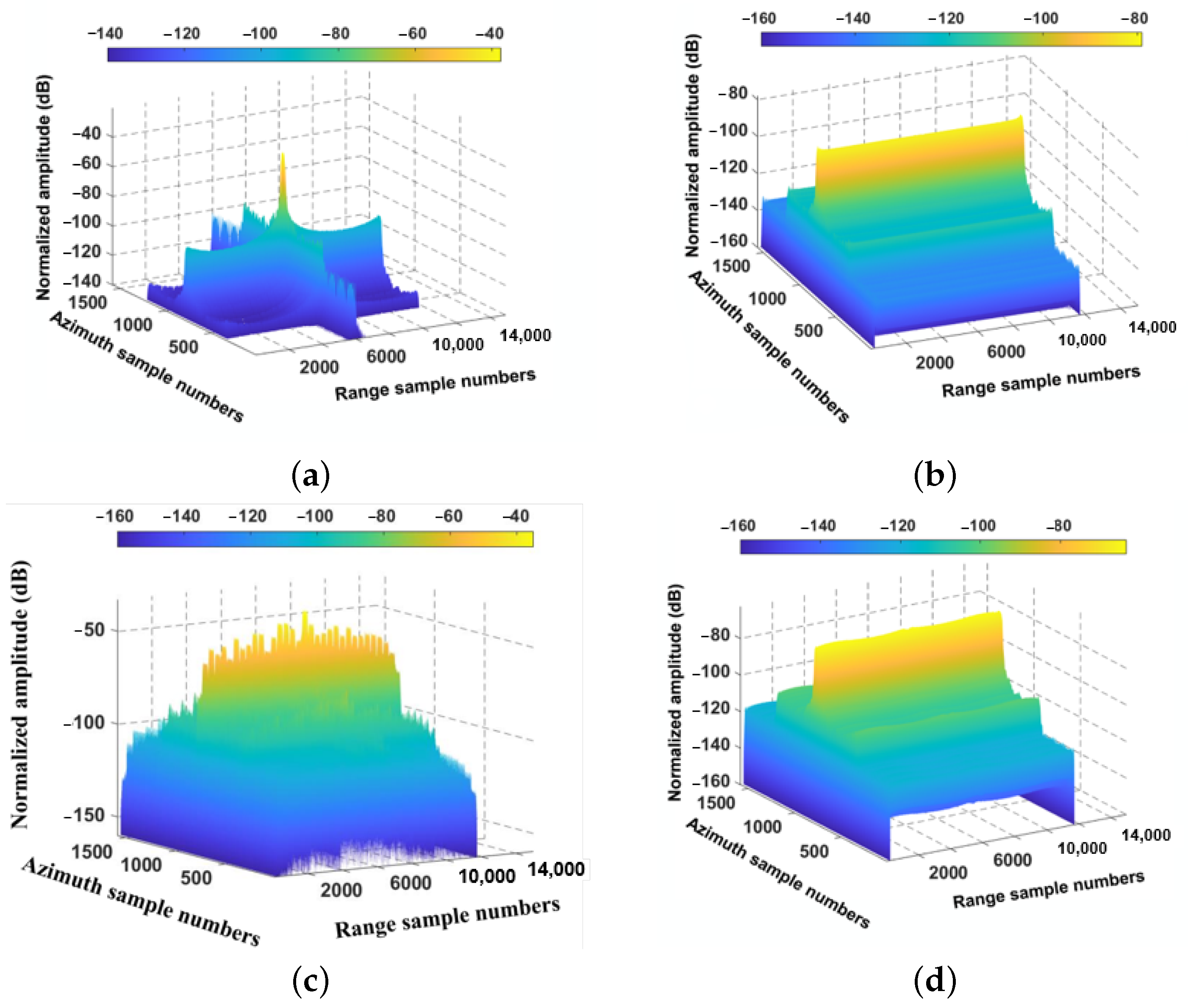
5.1. Point Target Simulation
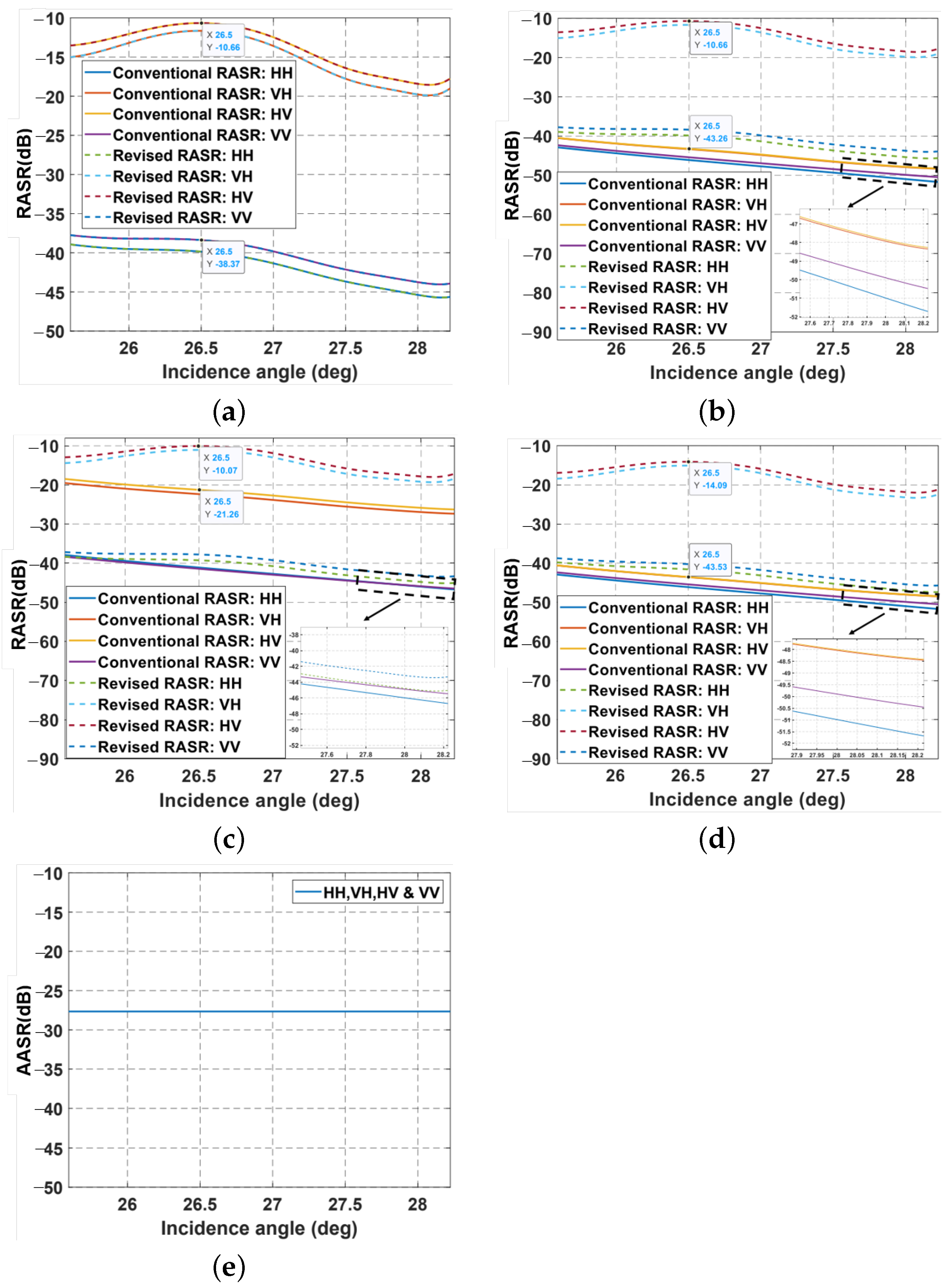
5.2. AASR and RASR
5.3. Distributed Scene Simulations
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| SAR | Synthetic Aperture Radar |
| PRF | Pulse Repetition Frequency |
| AASR | Azimuth Ambiguity-to-Signal Ratio |
| RASR | Range Ambiguity-to-Signal Ratio |
| Quad-Pol | Quadrature-Polarimetric |
| POSP | Principle Of Stationary Phase |
| OFDM | Orthogonal Frequency Division Multiplexing |
References
- Curlander, J.C.; Mcdonough, R.N. Synthetic Aperture Radar: Systems and Signal Processing; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Cumming, I.G.; Wong, F.H.C. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Deng, Y.; Yu, W.; Wang, W.; Robert, W. Forthcoming Spaceborne SAR Development. J. Radars 2020, 9, 1–33. [Google Scholar]
- Krieger, G. MIMO-SAR: Opportunities and Pitfalls. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2628–2645. [Google Scholar] [CrossRef]
- Jin, G.; Deng, Y.; Wang, R.; Wang, W.; Wang, P.; Long, Y.; Zhang, Z.M.; Zhang, Y. An Advanced Nonlinear Frequency Modulation Waveform for Radar Imaging With Low Sidelobe. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6155–6168. [Google Scholar] [CrossRef]
- Villano, M.; Krieger, G.; Moreira, A. New Insights Into Ambiguities in Quad-Pol SAR. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3287–3308. [Google Scholar] [CrossRef]
- Ze, Y.U.; Liu, M. Suppressing Azimuth Ambiguity in Spaceborne SAR Images Based on Compressed Sensing. Sci. China Inf. Sci. 2012, 55, 1830–1837. [Google Scholar]
- Wang, N.; Wang, G.H. Range Ambiguity Resolving of HPRF Radar Based on Hybrid Filter. Sci. China Inf. Sci. 2011, 54, 1534–1546. [Google Scholar] [CrossRef]
- Long, Y.; Zhao, F.; Zheng, M.; Jin, G.; Zhang, H.; Wang, R. A Novel Azimuth Ambiguity Suppression Method for Spaceborne Dual-Channel SAR-GMTI. IEEE Geosci. Remote Sens. Lett. 2021, 18, 87–91. [Google Scholar] [CrossRef]
- Ryu, J.; Yi, D.W.; Kim, S.Y.; Yoon, G. Suppression of Range Ambiguity in Spaceborne SAR With Elevation Beam Pattern Mask Design. IEEE Geosci. Remote Sens. Lett. 2021, 19, 4008605. [Google Scholar] [CrossRef]
- Chen, J.; Wang, K.; Yang, W.; Liu, W. Accurate Reconstruction and Suppression for Azimuth Ambiguities in Spaceborne Stripmap SAR Images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 102–106. [Google Scholar] [CrossRef]
- Jin, G.; Deng, Y.; Wang, R.; Wang, W.; Zhang, Y.; Long, Y.; Liang, D. Mitigating Range Ambiguities With Advanced Nonlinear Frequency Modulation Waveform. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1230–1234. [Google Scholar] [CrossRef]
- Jin, G.; Deng, Y.; Wang, W.; Zhang, H.; Long, Y.; Zhang, Y.; Wang, R. On the SAR Imaging Performance Analysis of Alternate Transmitting Mode Based on Waveform Diversity: Theory and Simulation. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1553–1557. [Google Scholar] [CrossRef]
- Jin, G.; Zhu, D.; Yan, H.; Mao, X.; Deng, Y.; Wang, W.; Wang, R. New Insights Into SAR Alternate Transmitting Mode Based on Waveform Diversity. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5209209. [Google Scholar] [CrossRef]
- Krieger, G.; Gebert, N.; Moreira, A. Multidimensional Waveform Encoding: A New Digital Beamforming Technique for Synthetic Aperture Radar Remote Sensing. IEEE Trans. Geosci. Remote Sens. 2008, 46, 31–46. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, Y.; Liao, G.; Cheung So, H. Resolving Range Ambiguity via Multiple-Input Multiple-Output Radar with Element-Pulse Coding. IEEE Trans. Signal Process. 2020, 68, 2770–2783. [Google Scholar] [CrossRef]
- Jin, G.; Deng, Y.; Wang, W.; Wang, R.; Zhang, Y.; Long, Y. Segmented Phase Code Waveforms: A Novel Radar Waveform for Spaceborne MIMO-SAR. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5764–5779. [Google Scholar] [CrossRef]
- Jin, G.; Wang, W.; Deng, Y.; Yan, H.; Wang, R. A Novel Range-Azimuth Joint Modulation Scheme for Range Ambiguity Suppression. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5207210. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, W.; Deng, Y.; Yu, W.; Zhang, Z.; Zhao, P.; Wang, R. Quadratically Constrained Ambiguity Suppression Algorithm for APC/Multichannel SAR Systems With Nonuniform Spatial Sampling. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1319–1330. [Google Scholar] [CrossRef]
- Bordoni, F.; Younis, M.; Krieger, G. Ambiguity Suppression by Azimuth Phase Coding in Multichannel SAR Systems. IEEE Trans. Geosci. Remote Sens. 2012, 50, 617–629. [Google Scholar] [CrossRef]
- Callaghan, G.D.; Longstaff, I.D. Wide-swath Space-borne SAR and Range Ambiguity. In Proceedings of the Radar 97 (Conf. Publ. No. 449), Syracuse, NY, USA, 13–15 May 1997; pp. 248–252. [Google Scholar] [CrossRef]
- Mittermayer, J.; Martinez, J.M. Analysis of Range Ambiguity Suppression in SAR by Up and Down Chirp Modulation for Point and Distributed Targets. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2003), Toulouse, France, 21–25 July 2003; Volume 6, pp. 4077–4079. [Google Scholar]
- Riche, V.; Meric, S.; Baudais, J.; Pottier, E. Investigations on OFDM Signal for Range Ambiguity Suppression in SAR Configuration. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4194–4197. [Google Scholar] [CrossRef]
- Wang, W. Mitigating Range Ambiguities in High-PRF SAR With OFDM Waveform Diversity. IEEE Geosci. Remote Sens. Lett. 2013, 10, 101–105. [Google Scholar] [CrossRef]
- Jin, G.; Aubry, A.; De Maio, A.; Wang, R.; Wang, W. Quasi-Orthogonal Waveforms for Ambiguity Suppression in Spaceborne Quad-Pol SAR. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5204617. [Google Scholar] [CrossRef]
- Kim, S.Y.; Myung, N.H.; Kang, M.J. Antenna Mask Design for SAR Performance Optimization. IEEE Geosci. Remote Sens. Lett. 2009, 6, 443–447. [Google Scholar] [CrossRef]
- Kang, M.S.; Won, Y.J.; Lim, B.G.; Kim, K.T. Efficient Synthesis of Antenna Pattern Using Improved PSO for Spaceborne SAR Performance and Imaging in Presence of Element Failure. IEEE Sens. J. 2018, 18, 6576–6587. [Google Scholar] [CrossRef]
- Kang, M.S.; Baek, J.M. SAR Image Reconstruction via Incremental Imaging with Compressive Sensing. IEEE Trans. Aerosp. Electron. Syst. 2023, 1–14. [Google Scholar] [CrossRef]
- Li, F.K.; Johnson, W.T.K. Ambiguities in Spacebornene Synthetic Aperture Radar Systems. IEEE Trans. Aerosp. Electron. Syst. 1983, 19, 389–397. [Google Scholar] [CrossRef]
- Jin, G.; Liu, K.; Liu, D.; Liang, D.; Zhang, H.; Ou, N.; Zhang, Y.; Deng, Y.; Li, C.; Wang, R. An Advanced Phase Synchronization Scheme for LT-1. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1735–1746. [Google Scholar] [CrossRef]
- Bayma, R.W. Aperture Size and Ambiguity Constraints for A Synthetic Aperture Radar. In Proceedings of the IEEE 1975 International Radar Conference, Arlington, VA, USA, 21–23 April 1975; Volume 21, pp. 499–504. [Google Scholar]
- Ulaby, F.; Dobson, M.C.; Álvarez-Pérez, J.L. Handbook of Radar Scattering Statistics for Terrain; Artech House: Dedham, MA, USA, 1989. [Google Scholar]






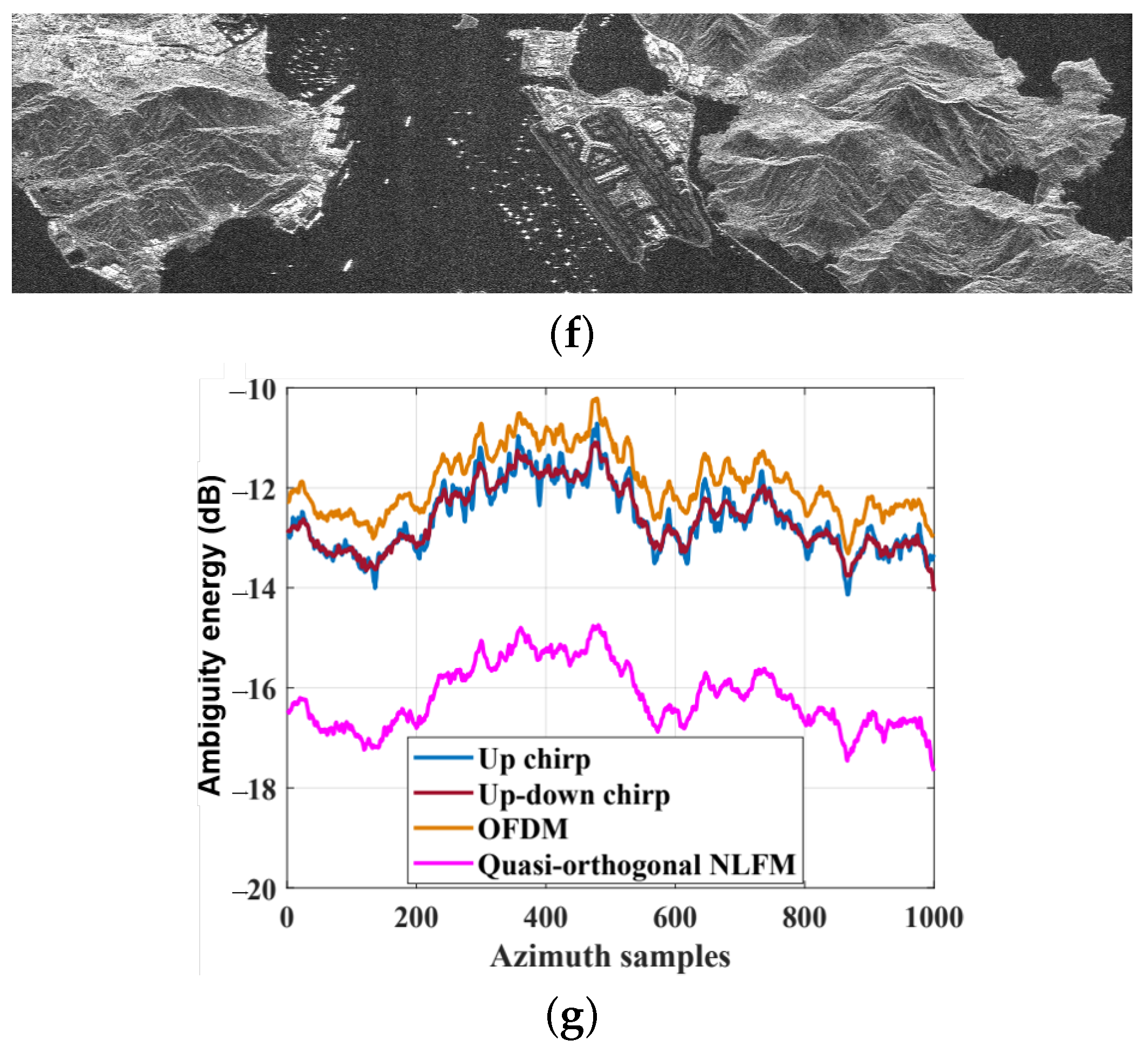

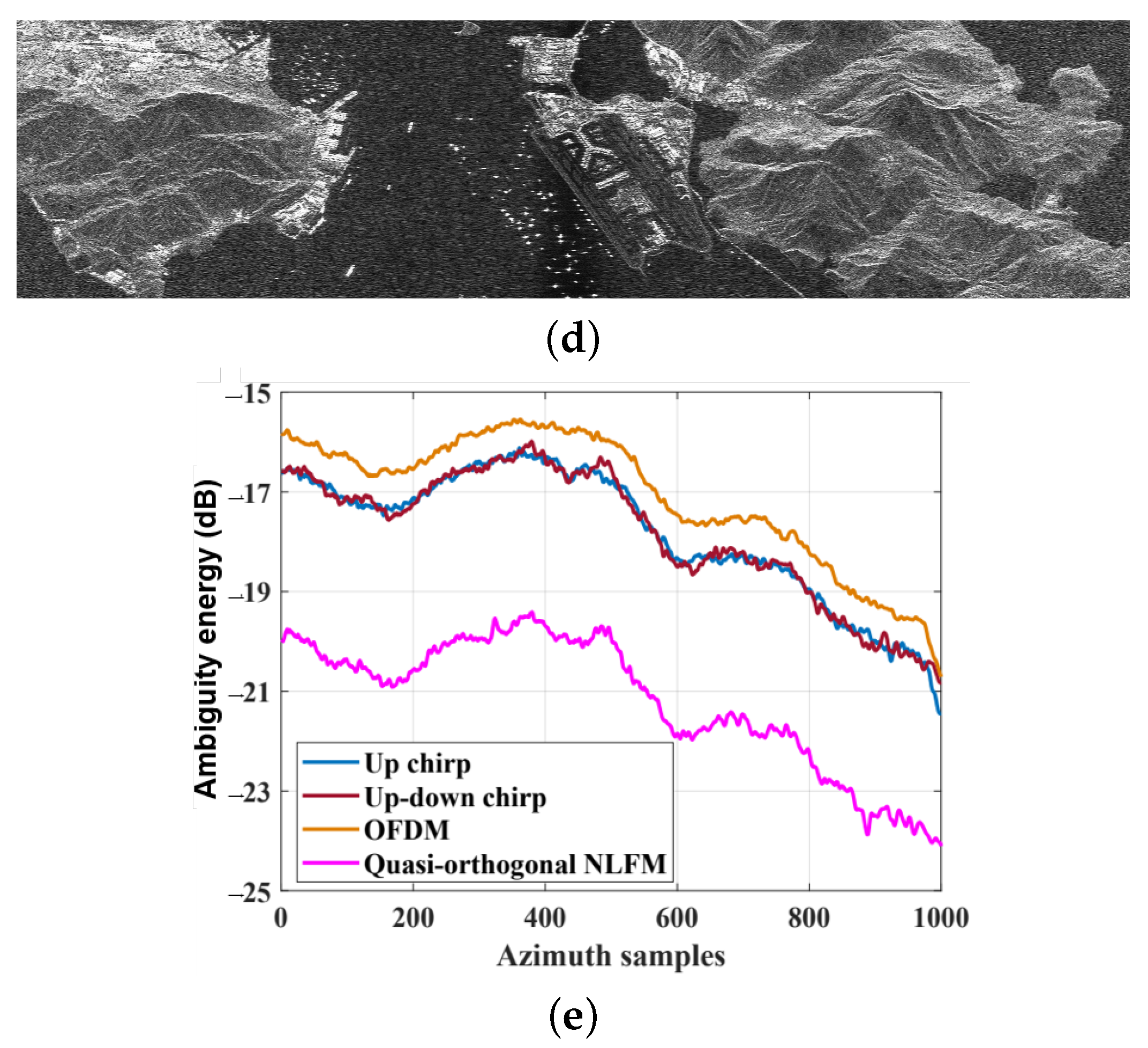
| Parameters | Value |
|---|---|
| Orbit height | 607 Km |
| Look angle access range | 25.6–28.2 deg |
| SAR pulse width | 80 s |
| Bandwidth | 60 MHz |
| PRF | 3320 Hz |
| Antenna type | Planar |
| Processed Doppler bandwidth | 1380 Hz |
| Backscatter model | Soil and Rock [32] |
| Quad-Pol Mode | Ambiguity | Tx Scheme | Ambiguity Energy | |
|---|---|---|---|---|
| Revised | Conventional | |||
| Conventional | Range | Up chirp waveform | 0 | 0 |
| Up-down chirp waveform [22] | 0 | |||
| OFDM chirp waveforms [24] | ||||
| quasi-orthogonal NLFM waveforms [25] | ||||
| Hybrid | Azimuth | Up chirp waveforms | 0 | 0 |
| Up-down chirp waveforms [22] | 0 | |||
| OFDM chirp waveforms [24] | ||||
| quasi-orthogonal NLFM waveforms [25] | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, G.; Wang, Y.; Yang, H.; Song, C.; Huang, J.; Wang, W.; Deng, Y.; Zhu, D. Precise Ambiguity Performance Evaluation for Spaceborne SAR with Diverse Waveforms. Remote Sens. 2023, 15, 1895. https://doi.org/10.3390/rs15071895
Jin G, Wang Y, Yang H, Song C, Huang J, Wang W, Deng Y, Zhu D. Precise Ambiguity Performance Evaluation for Spaceborne SAR with Diverse Waveforms. Remote Sensing. 2023; 15(7):1895. https://doi.org/10.3390/rs15071895
Chicago/Turabian StyleJin, Guodong, Yu Wang, Hui Yang, Chen Song, Jingkai Huang, Wei Wang, Yunkai Deng, and Daiyin Zhu. 2023. "Precise Ambiguity Performance Evaluation for Spaceborne SAR with Diverse Waveforms" Remote Sensing 15, no. 7: 1895. https://doi.org/10.3390/rs15071895
APA StyleJin, G., Wang, Y., Yang, H., Song, C., Huang, J., Wang, W., Deng, Y., & Zhu, D. (2023). Precise Ambiguity Performance Evaluation for Spaceborne SAR with Diverse Waveforms. Remote Sensing, 15(7), 1895. https://doi.org/10.3390/rs15071895







