Abstract
The deep learning method has achieved great success in hyperspectral image classification, but the lack of labeled training samples still restricts the development and application of deep learning methods. In order to deal with the problem of small samples in hyperspectral image classification, a novel small sample classification method based on rotation-invariant uniform local binary pattern (RULBP) features and a graph-based masked autoencoder is proposed in this paper. Firstly, the RULBP features of hyperspectral images are extracted, and then the k-nearest neighbor method is utilized to construct the graph. Furthermore, self-supervised learning is conducted on the constructed graph so that the model can learn to extract features more suitable for small sample classification. Since the self-supervised training mainly adopts the masked autoencoder method, only unlabeled samples are needed to complete the training. After training, only a small number of samples are used to fine-tune the graph convolutional network, so as to complete the classification of all nodes in the graph. A large number of classification experiments on three commonly used hyperspectral image datasets show that the proposed method could achieve higher classification accuracy with fewer labeled samples.
1. Introduction
Hyperspectral remote sensing images containing numerous bands could provide rich spectral and spatial information for ground objects, which makes it possible to distinguish ground objects more precisely [1,2]. Using the rich information provided by hyperspectral images (HSIs) to achieve ground object classification has been one of the research focuses in the field of hyperspectral remote sensing. Up to now, hyperspectral remote sensing technology has been widely used in precision agriculture, disaster investigation, resource management, geological exploration, archaeological analysis, urban planning, military and national defense, and many other fields [3,4,5,6]. However, the application and development of HSI classification technology has been restricted by the high-dimensional, nonlinear data characteristics of HSIs and the lack of labeled samples [7,8,9].
The early explorations on HSI classification are mainly carried out from the aspect of extracting manually designed features, which can be divided into three categories: spectral feature extraction, spatial feature extraction, and spatial–spectral feature extraction. Existing studies show that utilizing the spectral and spatial information in HSIs can effectively improve the accuracy of target classification and recognition. However, most of the early explorations are based on hand-designed features, which actually causes a lack of robustness and stability.
In recent years, the deep learning method could automatically carry out end-to-end feature learning from data, which makes it better adapted to HSI classification tasks [10,11]. The deep learning models, such as one-dimensional convolutional neural network (CNN) [12], stack autoencoder [13,14], and deep belief network [15], which can use one-dimensional spectral features, are first introduced into HSI classification tasks. Then, in order to use spatial information, 2D-CNNs treat different bands of HSIs as feature maps for end-to-end training [16,17,18,19]. Furthermore, in order to make good use of the three-dimensional spatial–spectral structure, the 3D-CNN directly takes the hyperspectral data cube as a whole and then uses the three-dimensional convolution operation to mine its three-dimensional spatial–spectral features [20,21,22,23]. The exploration of the above deep learning methods has promoted the development of HSI classification methods, but these methods often require a certain number of labeled training samples to ensure the classification effect, and the sparsity of labeled samples in HSIs leads to the problem of small samples [24,25]. To deal with the problem of small samples, researchers first explored the semi-supervised learning method to use a large number of unlabeled samples to improve the classification accuracy in the case of small samples [26]. For example, Liu et al. design a semi-supervised convolutional neural network for HSI classification using ladder networks [27], and Zhan et al. design a semi-supervised classification model for HSIs based on the generative adversarial network [28]. To further reduce the dependence of training on labeled samples, the latest machine learning methods, such as self-supervised learning [29] and meta-learning [30], are used to train the deep learning models’ learning to extract features more suitable for small samples. At the same time, some researchers convert HSIs into graph structures—that is, pixel points and their feature descriptions are regarded as nodes and attributes of graphs—and then use graph models to complete classification. For example, Zuo et al. propose using the graph inductive learning method for sample classification of HSIs [31]. Hong et al. design a graph convolutional network for HSI classification [32]. Zhao et al. design a graph transformer network with the graph attention mechanism for HSI classification [33]. This work is mainly inspired by the graph convolution network and the latest generative self-supervised method. First, the k-nearest neighbor method is used to convert the entire HSI into a graph, and then the graph convolution network is used to conduct generative self-supervised learning on the constructed graph so that the model can automatically learn the features more suitable for subsequent small sample classification tasks. Finally, a small number of labeled samples are used to fine-tune the graph convolution network to complete the final classification. In summary, the contributions of this paper can be summarized as follows:
- A graph-based self-supervised learning method with the rotation-invariant uniform local binary pattern (RULBP) features is proposed to deal with the small sample problem of HSI classification. The goal of training is to reconstruct the features with masking. Therefore, the training process does not need to use any label information.
- The RULBP features of the HSI are used to calculate the k-nearest neighbor when constructing the graph so that the deep model could better use the spatial–spectral information of HSIs.
- A large number of classification experiments on three hyperspectral datasets verify the effectiveness of the proposed method for small sample classification.
2. Related Work
2.1. Early Research
Aiming at the problem of HSI classification, early researchers focused on spectral features of HSIs and designed many spectral feature extraction methods, such as principal component analysis (PCA) [34,35], manifold learning [36], spectral shape feature [37,38], etc. The spectral feature extraction method combined with support vector machine (SVM), random forest (RF), and other classifiers could improve the classification accuracy to some extent. However, the wide existence of the phenomenon of the same object and different spectrum in remote sensing images makes it very limited to classify HSIs only by using spectral features [39,40]. Adjacent samples in HSIs have a high probability of belonging to the same category, so researchers have conducted a lot of exploration to improve the classification accuracy of HSIs using spatial information. There are many ways to use the spatial information of HSIs. For example, spatial neighborhood information can be comprehensively considered in the feature extraction stage. Such representative methods include extended morphological profiles [41], Gabor texture features [42], local binary pattern texture features [43], etc. In the classification stage, the spatial neighborhood information of samples can also be comprehensively considered. This kind of method usually takes the spatial neighborhood information of samples as a constraint item of classifier optimization so as to improve the classification accuracy by using spatial information [44,45]. Of course, after classification, spatial neighborhood information can also be used to post-process the classification results. For example, guided filtering can be used to post-process the classification results to remove isolated classification noise so as to improve the classification accuracy of HSIs [46,47]. The above spatial–spectral classification methods could significantly improve the classification effect of HSIs, but the disadvantage is that the classification effect needs strong expert experience, that is, the feature extraction rules or post-processing strategies need to be designed manually, which undoubtedly reduces the practicability of HSI classification technology [48].
2.2. Deep Learning-Based HSI Classification
Recently, HSI classification using deep learning models has become one of the research hotspots in the field of remote sensing. From the perspective of processing the data structure, the existing methods can be roughly divided into three types: raster-based methods, sequence-based methods, and graph structure-based methods. The 2D-CNN and 3D-CNN models are two representative methods of the first class. The 2D-CNN model can directly perform convolution operation on HSIs with raster structure and extract rich spatial information from each spectral band. For example, Zhang et al. design a novel diverse region-based 2D-CNN method for HSI classification. By aggregating spatial information in diverse neighborhoods, the performance of HSI classification can be effectively improved [49]. Gao et al. train the designed 2D-CNN model based on episode, further improving the accuracy and robustness of classification results [50]. In contrast, The 3D-CNN model regards the input HSI data as a complete cube and directly applies 3D convolution to extract the spatial–spectral features. For example, Xu et al. design a novel multiscale octave 3D-CNN model and Zhong et al. design a deep residual 3D-CNN model, achieving better classification results [51,52]. At the same time, some researchers try to treat HSIs along the spectral dimension as sequence data and then use the recurrent neural network model to complete classification [18,53,54]. To further improve the classification accuracy of HSIs, channel attention, spatial attention, and self-attention mechanisms are gradually widely used in the design of HSI deep learning classification models [55,56,57]. More recently, with the breakthrough performance of graph convolutional network (GCN) in computer vision, HSI classification methods based on GCN have begun to appear and receive a lot of attention. For example, Hong et al. take the lead in exploring the performance of GCN in HSI classification [32]. Liu et al. design a semi-supervised learning method based on the GCN model [58]. Zhao et al. introduce an attention mechanism to further improve the classification performance [33]. However, the above GCN-based methods all utilize labeled samples for supervised learning and conduct auxiliary semi-supervised training based on the graph relation structure, and there is a lack of research on the application of GCN-based self-supervised learning to HSI classification. At the same time, the classification performance still has great room for improvement. Among the existing research, the study closest to the proposed method is the work of Zuo et al. [59]. However, compared with this work, the proposed method has three advantages. First of all, Zuo et al. follow the method of supervised learning for model training, and the proposed method can utilize a large number of unlabeled samples for self-supervised training and make accurate classification and prediction based on the extracted features. Second, an advanced generative self-supervised method, namely a partial masked strategy, is applied in the proposed method, and its related hyperparameters are fully discussed. Thirdly, the proposed method can achieve better classification performance.
3. Methodology
In this section, the workflow of the proposed method is first described, and then the proposed method is introduced in detail in three parts: RULBP feature extraction, graph construction, and self-supervised learning.
3.1. Workflow
To further improve the accuracy of small sample classification of HSIs, a novel graph-based self-supervised learning method is proposed in this paper. Figure 1 shows the workflow of the proposed method, which includes two stages: self-supervised training and inference. For a given HSI, the RULBP features are first extracted to make full use of the spatial and spectral information in the image and effectively reduce band redundancy. Then, the K-neighbors algorithm is used to construct the graph based on the extracted RULBP features, and the original HSI with grid structure is converted into the graph structure data. Next, a certain proportion of nodes are masked randomly, and the whole masked graph is fed to the encoder to learn the encoded node representations. During the representations’ decoding, the randomly selected nodes are remasked, and the decoder learns to reconstruct the original node features using the masked representations. The loss is calculated on the original node features and the reconstructed node features. Actually, the proposed method is a generative self-supervised learning method, which can achieve efficient feature learning without any labeled samples. During the inference stage, only the encoder is used for fine-tuning and prediction. Specifically, all parameters of the encoder are frozen and the encoder is only responsible for generating the learned representations. Then, a simple linear classifier is established and trained on a small number of labeled samples without a mask. Finally, the trained classifier is used for inference and evaluation.
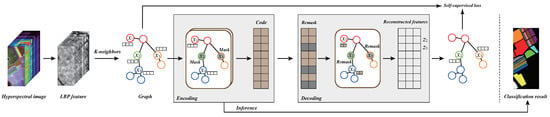
Figure 1.
Workflow of the proposed method.
Briefly speaking, the proposed method has three advantages. First, extracting the RULBP features can make full use of the spatial and spectral information in the HSI. Second, constructing the graph structure can effectively utilize the relation information between pixels and improve the data efficiency. Third, the self-supervised learning mode combined with the dual-mask strategy can perform semantic feature learning without labeled samples, significantly reducing the dependence of the deep model on supervised annotation information.
3.2. RULBP Feature Extraction
To further improve the accuracy of the HSI small sample classification, the RULBP features are adopted in the proposed method. As an algorithm used to describe the local texture features of input images, the LBP has the advantages of simple calculation, rotation invariance, and gray invariance. Specifically, the rotation-invariant local binary mode (RULBP) code of each pixel in the input HSI is calculated as follows.
In Equation (1), R denotes the neighborhood radius of the center pixel, and P denotes the number of pixels sampled in the neighborhood. denotes the gray value of the center pixel, while denote the gray value of the pixels in the neighborhood. The symbol U represents the number of hops from 0 to 1 or from 1 to 0 in the binary code. Referring to the relevant research [31], the values of R and P are set to 1 and 8, respectively. Therefore, according to Equation (1), there are 10 RULBP codes for each pixel, which can effectively improve the stability of LBP feature extraction.
Figure 2 gives the schematic of generating RULBP features. For the input HSI, the PCA features are first generated to preserve the main spectral features while reducing band redundancy. Next, each principal component is treated as a gray image and used to generate the RULBP codes. The RULBP feature of each pixel is determined by the frequency statistics of the RULBP codes in its neighborhood. As mentioned above, each pixel has 10 RULBP codes, so after RULBP feature extraction, each principal component can actually generate a feature map with 10 dimensions. Finally, the RULBP features of all principal components are connected with the original principal components to form the final feature matrix for graph construction. For example, an input HSI with 30 principal components will eventually generate a 330-dimension (330 = 30 × 10 + 30) RULBP feature.
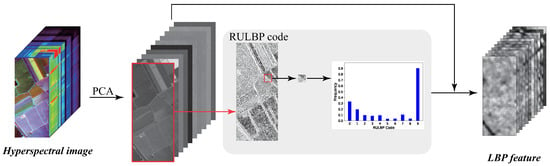
Figure 2.
Schematic of generating the RULBP features.
3.3. Graph Construction by K-Neighbors
Undoubtedly, constructing the graph structure based on the extracted RULBP features is a very important step in the proposed method, because the effect of the constructed graph has a direct impact on the expression quality of the relations between pixels. Figure 3 shows the adopted graph construction method in our work. After RULBP feature extraction, the original HSI is organized into a matrix . Specifically, the symbol N denotes the number of samples and C denotes the dimension of vectors. In this matrix, the distance between samples can be denoted as
where p is an optional parameter, and and are samples at different locations. Furthermore, a symmetric distance matrix can be generated by calculating the distance values of all sample pairs, which can be denoted as . In this matrix, the distance between the ith pixel and the jth pixel can be denoted as at row i and column j. For each pixel, the K-Neighbors algorithm selects the K pixels closest to it as the neighbor nodes. After establishing the neighbor nodes of all pixels, the graph construction process is completed. Consequently, the input HSI with the grid structure is converted to the graph where each pixel has K neighbor node.
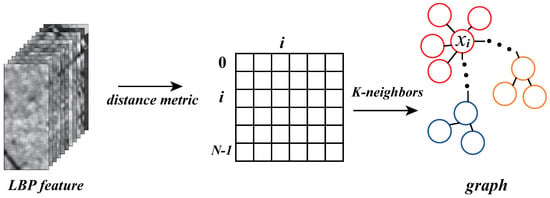
Figure 3.
Schematic of graph construction by K-Neighbors.
3.4. Graph-Based Self-Supervised Learning
The proposed method, actually a generative self-supervised learning method, can utilize a large number of unlabeled samples for deep feature learning. The whole process of graph-based self-supervised training is shown in Figure 1. For clarity, several mathematical symbols and corresponding meanings are given first. Given a graph constructed on the extracted RULBP features, it can be denoted as , where is the node set, is the input node feature matrix. is the adjacency matrix and is the number of nodes. In addition, the graph encoder and decoder can be denoted as and , and the encoded node representations can be denoted as . Therefore, the whole workflow of graph-based self-supervised learning can be denoted as
where denotes the reconstructed graph. In the proposed method, it is actually the reconstructed features.
To perform the self-supervised training with masking, a subset of nodes is first sampled randomly. Then, the features of these sampled nodes are masked with a learnable vector . Therefore, the node feature in the masked feature matrix can be denoted as follows.
It is known to all that in a graph, the connection relations are the important information to enhance the features of the nodes. Therefore, to avoid the occurrence of some extreme cases—for example, all the neighbors of a node being masked—a uniform random sampling strategy is adopted in the proposed method. In addition, referring to existing research, setting a relatively large mask ratio is better to reduce redundancy information and effectively improve the robustness of the deep model.
To further prompt the encoder to learn robust and compressed features, the generated representations are also masked, as shown in Figure 1. Specifically, the representations of the masked node are remasked again with another mask which can be denoted as . Therefore, the masked representations can be denoted as follows.
According to Equation (5), the graph decoder has to utilize the features of neighboring unmasked nodes to reconstruct the input feature of masked nodes. Actually, the above two mask strategies promote the model to utilize the connection relations in graph structure to achieve reconstruction from the two levels of nodes and deep representation, respectively, which can effectively enhance the learning of the semantic relations between pixels.
Finally, the loss between the original graph and the constructed graph is calculated as
which is actually the scaled cosine error (SCE). The scaling factor is used to reweight the contribution of samples to parameters updating. When , the corresponding losses of the predictions with high confidence are usually smaller than 1 and decay faster to zero.
4. Experimental Results
4.1. HSI Datasets
To compare the classification performance of different methods, three widely used HSIs are used for experiments. The three HSIs contain University of Pavia (UP), Indian Pines (IP), and Salinas (SA), and the details are listed in Table 1. As we can see, the three HSIs possess completely different resolutions, spectral ranges, and observation regions, providing different data environments to comprehensively evaluate the classification performance of different models. In the process of self-supervised learning, all samples are regarded as unlabeled samples for graph construction and feature learning, and in the process of fine-tuning, only a few labeled samples are used for retraining the model. Specifically, in the experiments, 20 samples per class are used for retraining (fine-tuning), another 20 samples per class are used as the validation set, and all the remaining samples are used as the test set to evaluate the classification performance of the proposed method.

Table 1.
HSI datasets. Ground Sample Distance (GSD) (m), Spatial size (pixel), Spectral range (nm), Airborne Visible Infrared Imaging Spectrometer (AVIRIS), Reflective Optics System Imaging Spectrometer (ROSIS).
4.2. Experimental Settings
The hardware environment includes a computer equipped with an AMD Ryzen 9 5900HX CPU and an Nvidia RTX 3080 GPU. The software environment is developed on Python and libraries such as Pytorch, sklearn, and numpy. The hyperparameters are described in the order of the workflow. For the UP, IP, and SA dataset, the 15, 30, and 30 principal components are first extracted, which can be used to generate the RULBP features with the dimensions of 165, 330, and 330, respectively. During graph construction, the number of neighbors of each nodes is set to 200. The standard GAT model [60] is used as the encoder network and the decoder network, which means the model has a symmetrical structure. Specifically, the network layer is set to 2 and the number of hidden units is set to 512. The first layer consists of eight attention heads followed by an exponential linear unit, while the second layer consists of a single attention head followed by a softmax activation and is used for classification. During self-supervised training, the Adam optimizer with , , and is used for network updating. The initial learning rate is set to 0.0001 and the cosine learning rate decay is adopted. The scaling factor is 3. The maximum number of epochs of self-supervised training is set to 1500, and the early stop strategy is adopted. Specifically, the validation set is used to evaluate performance, and if there is no further improvement after 20 epochs, the self-supervised training process will be stopped. The epochs of fine-tuning are set to 300, and the batchsize is set to 32, ensuring that the model can get full training. In addition, the mask ratio is set to 50%. More details and analysis about the hyperparameter settings are given in Section 5, and the overall accuracy (OA), average accuracy (AA), and kappa coefficient are used as evaluation criteria. All experiments will run 10 times and the average ± deviation will be taken as results to display.
4.3. Results and Comparison
In this section, the effectiveness and performance of the proposed method will be comprehensively verified by comparing with several influential and advanced hyperspectral image classification methods. Since the goal of the proposed method is to improve the small sample classification performance of hyperspectral images, we focus on selecting specialized small sample classification methods for comparison. First, three influential few-shot learning methods are selected, including Deep Few-Shot Learning (DFSL) [30], Relation Network of Few-Shot learning (RN-FSC) [25], and Graph Information Aggregation Cross-Domain Few-Shot Learning (Gia-CFSL) [61]. Among them, Gia-CFSL is one of the latest and state-of-the-art few-shot learning methods. In addition, a transfer learning method, Cross-Domain Pretrained Model (CDPM) [62], is also selected. The four methods above all conduct the model’s pre-training based on supervised learning on source data with sufficient labels and concentrate on improving the classification performance on the target data with few labels. Second, because the proposed method belongs to the self-supervised learning method and requires no labels in the procedure of feature learning, two similar unsupervised learning methods are further selected for comparison, including Unsupervised Meta Learning With Multi-view Constraints (UML) [10] and Unsupervised Spectrum Motion Feature Learning (SMF-UL) [63]. The settings of all comparative methods refer to their original literature, including the combination of source data, and the analysis results of accuracy with different methods on three hyperspectral datasets (the test set illustrated in Section 4.1) are shown in Table 2, Table 3 and Table 4.

Table 2.
The analysis results of accuracy with different methods on the UP data (%) (20 training samples in each class).

Table 3.
The analysis results of accuracy with different methods on the IP data (%) (20 training samples in each class).

Table 4.
The analysis results of accuracy with different methods on the SA data (%) (20 training samples in each class).
As we can observe, although supervised learning methods have a strong supervision for the pre-training with the sufficient labels in the feature learning, their performance usually cannot compete with unsupervised learning methods. This is mainly because unsupervised learning methods get rid of the restriction of labels by constructing specific learning tasks, so that the models can acquire robust feature extraction capabilities by being pre-trained on numerous unlabeled samples. Among supervised learning methods, the latest advanced method, Gia-CFSL, obtains the highest accuracy results, which mainly benefits from the joint training with abundant labels in the source data and few labels in the target data. By contrast, unsupervised learning methods do not require any labels in the pre-training of models and merely require few labels of target data to fine-tune the final classifier. Therefore, unsupervised learning methods usually can obtain more robust feature extraction capabilities in the pre-training, which is important for the superior classification performance. The performance of several unsupervised learning methods naturally surpasses the supervised learning methods. Among them, UML trains the deep relation network by constructing the unsupervised meta-learning tasks with multiview constraints, SMF-UL trains the spectrum motion network by constructing the unsupervised spectrum motion feature learning task, and both can better learn the discriminative feature contained in the hyperspectral data for small sample classification. Different from them, the proposed method, RULBP-MGCN, belongs to the generative self-supervised learning and pre-trains the model by reconstructing the graph-based features with masking, which can lead the graph convolutional network to better capture long-distance and large-range information relevancy by operating convolution on graph nodes. Furthermore, the RULBP features of hyperspectral data are used to calculate the k-nearest neighbor when constructing the graph so that the deep model can better use the spatial–spectral information. Therefore, the experimental results show that the RULBP-MGCN can obtain the highest classification accuracy in three HSI datasets among all comparative methods, which effectively verifies the superior performance of our method, RULBP-MGCN, in small samples classification.
An interesting and noteworthy result is that the proposed method improves the classification accuracy of the IP dataset much more than the other two datasets. Specifically, for the UP, SA, and IP datasets, the overall classification accuracy of the proposed method exceeds that of the second place by 0.45%, 1.22%, and 6.97%, respectively. As can be seen from Table 1, the IP dataset has a larger ground sampling distance (GSD), which means that the obtained HSI has a lower ground resolution, resulting in the increase in mixed pixels. In this case, the extraction and utilization of spatial information is particularly important, especially for the long-distance semantic information, since the discriminability of the spectral characteristic curve decreases with the decrease of ground resolution [4,5,49]. As mentioned above, the application of the masked strategy can improve the perception of the designed model of the semantic information in the long-distance space of whole HSIs, and the connection between nodes in the graph structure contains the relation between the long-distance pixels in non-Euclidean space. Therefore, compared with other methods, the proposed method has a superior capability of capturing the long-distance semantic information, which we believe should be the main reason why the proposed method performs particularly well on the IP datasets with a greater GSD.
Furthermore, to distinctly display the classification effect, we produce the classification maps of different methods for qualitative comparison, as shown in Figure 4, Figure 5 and Figure 6. As we can observe, compared with the large area misclassification and noises caused by the relatively low accuracy of other methods, our method can effectively reduce the noises and produce a classification map more close to the ground truth under the condition of a small sample. Simultaneously, the graph convolutional network’s capacity of capturing long-distance and large-range information relevancy enables the classification maps to have better homogeneity and continuity in the area of the identical ground objects, for instance, the Bare Soil area in UP data, the Oats area in IP data, the Grape area in SA data, etc.
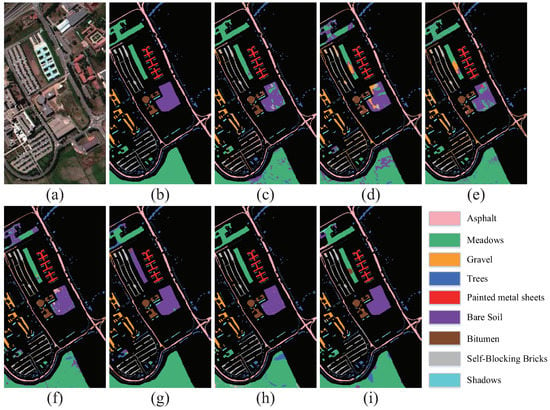
Figure 4.
The classification maps of different methods on the UP data: (a) False-color image. (b) Ground-truth map. (c) DFSL. (d) RN-FSC. (e) CDPM. (f) Gia-CFSL. (g) UML. (h) SMF-UL. (i) RULBP-MGCN.
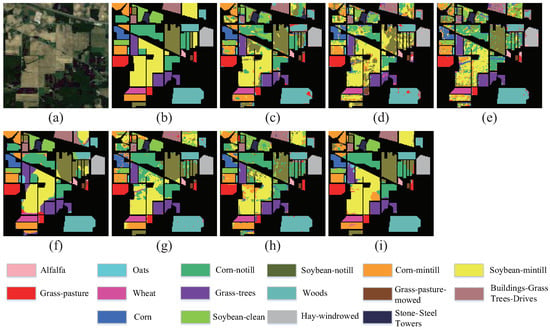
Figure 5.
The classification maps of different methods on the IP data: (a) False-color image. (b) Ground-truth map. (c) DFSL. (d) RN-FSC. (e) CDPM. (f) Gia-CFSL. (g) UML. (h) SMF-UL. (i) RULBP-MGCN.

Figure 6.
The classification maps of different methods on the SA data: (a) False-color image. (b) Ground-truth map. (c) DFSL. (d) RN-FSC. (e) CDPM. (f) Gia-CFSL. (g) UML. (h) SMF-UL. (i) RULBP-MGCN.
4.4. Influence of Labeled Training Samples
Because the pre-training of RULBP-MGCN does not require any labels, the fine-tuning of the linear classifier by labeled samples will determine the final classification performance of RULBP-MGCN. The comparison experiments of the last section have effectively demonstrated the superior performance of the proposed method under the condition of small samples. This section will further explore the performance of RULBP-MGCN varying with the number of labeled training samples, so we expand the size of training samples step by step when fine-tuning the liner classifier, and the results are shown in Figure 7. As we can observe, RULBP-MGCN can not only achieve excellent performance in small sample classification, but also obtain the stable improvement of performance in three hyperspectral datasets with the size of training samples expanding. This also shows its wide applicability in practice.
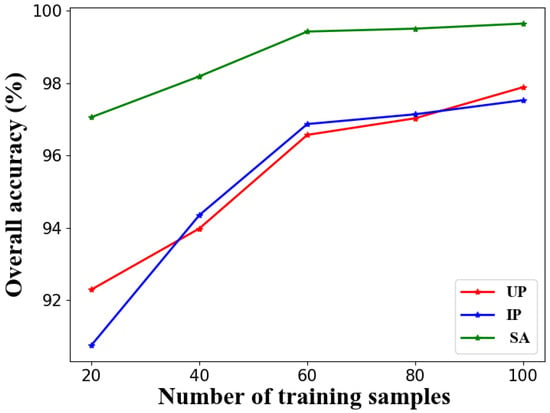
Figure 7.
The performance of RULBP-MGCN varying with the number of labeled training samples.
5. Analysis and Discussion
In this section, the influence of several important hyperparameters on the classification results of different HSI datasets is explored and analyzed in detail. In addition, the execution time of the proposed method is compared and analyzed with other methods.
5.1. Influence of Different Feature Extraction Methods
In the proposed method, the feature extraction of HSIs is the first key step. Obviously, the effect of feature extraction determines the quality and level of information contained in the subsequent constructed graph. Therefore, this section explores the influence of different feature extraction techniques on the classification accuracy of the proposed method. Table 5 lists the results. Specifically, the PCA method retains the first 30 principal components, and the feature extraction processes of EMP and LBP are carried out according to Section 3.2. It can be seen that the classification performance with the PCA method, which retains the main spectral features as the basic information of graph construction, is significantly worse than that of other methods. In addition, the extraction of EMP and LBP features in HSIs for graph construction can significantly improve the classification accuracy, since the spatial structure information has been retained and utilized to a certain extent. Obviously, in the proposed method, conducting graph construction and self-supervised learning based on the RULBP features of HSIs can achieve the best classification performance.

Table 5.
Influence of different feature extraction methods on classification accuracy.
5.2. Influence of Dimension of RULBP Features
The introduction of RULBP features can effectively utilize the spatial texture information in HSIs. As shown in Figure 2, the RULBP features are extracted from each principal component, which means that the number of principal components directly determines the dimension of RULBP features. To explore the influence of the dimension of RULBP features on classification results, the number of principal components is set as 1, 15, 30, and 45, which will generate the RULBP features with 11, 165, 330, and 495 dimensions, respectively. Table 6 shows the statistics results on the three HSI datasets. It can be seen that with the increase in dimension, the classification accuracy of the three datasets presents a trend of first rising and then decreasing, indicating that too large or too small a dimension value will lead to the decline in classification performance. For the UP dataset, the optimal value of dimension is 165, while the optimal value corresponding to the other two datasets is 330. As listed in Table 1, the number of bands in the SA and IP datasets is about twice that in the UP dataset, which can explain the above results from the perspective of the number of bands.

Table 6.
Influence of the dimension of RULBP features on classification accuracy.
5.3. Influence of Number of Neighbors
The number of neighbors in the constructed graph will directly impact the performance and computational complexity of the graph convolutional network. Therefore, this section further explores the influence of the number of neighbors, so we adjust the number of neighbors when constructing the graph to pre-train the model, and the final classification performance is shown in Figure 8. As we can observe, the performance of RULBP-MGCN can be improved on the three hyperspectral datasets when increasing the number of neighbors from 50 to 200 step by step. Therefore, within a reasonable range, the increase in the number of neighbors enables the model to capture more subtle dependency between the graph nodes. However, an excess of number of neighbors will lead to unnecessary and redundant dependency and higher computational complexity, which causes a performance degradation of the model. Thus, we finally determine the optimal number of neighbors to be 200 for all hyperspectral data.
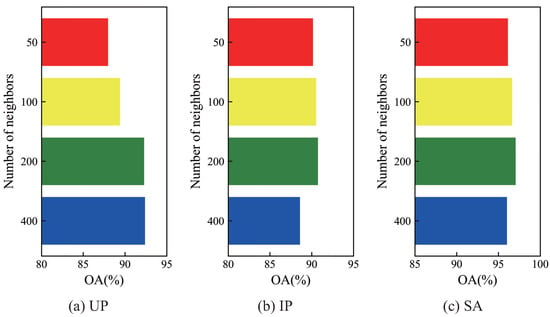
Figure 8.
Influence of the number of neighbors on classification accuracy.
5.4. Influence of Mask Ratio
The mask ratio is one of the most important hyperparameters for generative self-supervised learning based on reconstruction. Currently, a lower mask ratio (<0.5) has been verified to be more effective in the NLP field [64,65]. Because language usually has higher semantic content and is information-dense, a high mask ratio may lead the model to produce sophisticated language understanding when reconstructing the input. By contrast, images of nature always have high a redundancy of spatial information, which means that the model is capable of recovering the original spatial semantics even with fewer image patches. Thus, a higher mask ratio (>0.75) has been verified to be more effective in the CV field [66]. In this section, we adjust the mask ratio step by step to pre-train the model, and the final classification performance is shown in Figure 9. As we can observe, the optimal mask ratio is 0.5 for all three hyperspectral datasets for the RULBP-MGCN, and the higher and lower mask ratios both cause a slight performance degradation of the model. This is mainly because hyperspectral data not only have abundant spatial semantic information, but also contain complex spectral information, which means that a high mask ratio effective for the nature images will fail. This is also shows the unique characteristics of the graph-based generative self-supervised learning task for the hyperspectral data.
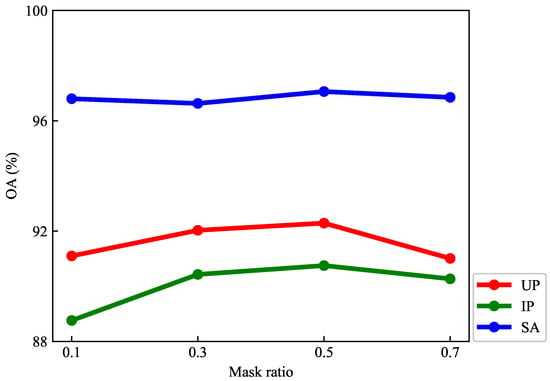
Figure 9.
Influence of the mask ratio on classification accuracy.
5.5. Execution Efficiency
Finally, the implementation efficiency of the proposed method is compared and analyzed, and the results are shown in Table 7. For the first three methods, the pre-training phase is the task-based meta-training. In this stage, a large number of source labeled samples are used for model training, so the required execution time is longer. In contrast, the proposed method can organize the HSIs to be classified into the graph structure and utilize the efficient graph convolution operation for faster model training. This advantage is also reflected in the classification phase. For the first three methods, the training phase refers to fine-tuning the deep models after pre-training using the target labeled samples, while in this stage, the proposed method utilizes the extracted features to train a simple linear network as a classifier. The DFSL+SVM method uses a support vector machine as a classifier, so the required fine-tuning time is the shortest, and the training time required by the proposed method is still acceptable in this phase. On the whole, the proposed method has the shortest execution time and better classification performance, indicating that its practical application space is larger.

Table 7.
Efficiency analysis of different methods.
6. Conclusions
To improve the classification accuracy of HSIs in the case of a small sample, a graph-based self-supervised learning method with the RULBP features is proposed in this paper. First, the RULBP features of HSIs are extracted from the principal components to make full use of the spatial and spectral information. Then, the simple and effective K-nearest neighbor method is used for graph construction to convert the HSIs with grid structure into graph structure. Next, the mask strategy is adopted to conduct the self-supervised training based on the constructed graph to learn the deep features more suitable for small sample classification. Extensive experiments have been conducted on three public datasets, and the results demonstrate that the proposed method can achieve better classification results than the existing advanced methods. Specifically, the classification accuracy of the UP and SA datasets is improved by 0.45% and 1.22%, respectively. For the IP datasets with lower ground resolution, the improved performance brought by the proposed method is better, and the classification accuracy is improved by at least 6.97%.
Although the accuracy of HSI small sample classification is improved effectively, the proposed method is still trained in a single domain. Therefore, in future work, the domain adaptation and meta learning techniques will be introduced to further improve the generalization ability of the model between different datasets.
Author Contributions
Methodology, B.L. and W.L.; investigation, P.H., Q.H. and K.G.; resources, B.L. and K.G.; writing—original draft preparation, B.L.; writing—review and editing, W.L.; visualization, Q.H., K.G. and H.L.; supervision, W.L., B.L. and H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Joint Funds of the National Natural Science Foundation of China (No. U21A20109), the National Natural Science Foundation of China (No. 41901285, 42277478), and the Natural Science Foundation of Henan Province (No. 222300420387).
Data Availability Statement
Publicly available datasets were analyzed in this study, which can be found here: https://www.ehu.eus/ccwintco/index.php?title=Hyperspectral_Remote_Sensing_Scenes (accessed on 8 January 2023).
Acknowledgments
The authors would like to thank all the professionals for kindly providing the codes associated with the experiments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, J.; Zhang, H.; Zhang, L.; Huang, X.; Zhang, L. Joint Collaborative Representation With Multitask Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5923–5936. [Google Scholar] [CrossRef]
- Liu, B.; Yu, X.; Zhang, P.; Yu, A.; Fu, Q.; Wei, X. Supervised Deep Feature Extraction for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1909–1921. [Google Scholar] [CrossRef]
- Transon, J.; D’Andrimont, R.; Maugnard, A.; Defourny, P. Survey of Hyperspectral Earth Observation Applications from Space in the Sentinel-2 Context. Remote Sens. 2018, 10, 157. [Google Scholar] [CrossRef]
- Paoletti, M.; Haut, J.; Plaza, J.; Plaza, A. Deep learning classifiers for hyperspectral imaging: A review. ISPRS J. Photogramm. Remote Sens. 2019, 158, 279–317. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Du, B. Deep Learning for Remote Sensing Data: A Technical Tutorial on the State of the Art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Guan, R.; Li, Z.; Li, T.; Li, X.; Yang, J.; Chen, W. Classification of Heterogeneous Mining Areas Based on ResCapsNet and Gaofen-5 Imagery. Remote Sens. 2022, 14, 3216. [Google Scholar] [CrossRef]
- Shi, C.; Sun, J.; Wang, T.; Wang, L. Hyperspectral Image Classification Based on a 3D Octave Convolution and 3D Multiscale Spatial Attention Network. Remote Sens. 2023, 15, 257. [Google Scholar] [CrossRef]
- Zhao, L.; Tan, K.; Wang, X.; Ding, J.; Liu, Z.; Ma, H.; Han, B. Hyperspectral Feature Selection for SOM Prediction Using Deep Reinforcement Learning and Multiple Subset Evaluation Strategies. Remote Sens. 2023, 15, 127. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, T.; Xie, B.; Mei, S. Hyperspectral Image Super-Resolution Classification with a Small Training Set Using Spectral Variation Extended Endmember Library. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 3001–3004. [Google Scholar] [CrossRef]
- Gao, K.; Liu, B.; Yu, X.; Yu, A. Unsupervised Meta Learning With Multiview Constraints for Hyperspectral Image Small Sample set Classification. IEEE Trans. Image Process. 2022, 31, 3449–3462. [Google Scholar] [CrossRef]
- Tang, C.; Liu, X.; Zhu, E.; Wang, L.; Zomaya, A.Y. Hyperspectral Band Selection via Spatial-Spectral Weighted Region-wise Multiple Graph Fusion-Based Spectral Clustering. In Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence, IJCAI 2021, Montreal, QC, Canada, 19–27 August 2021; pp. 3038–3044. [Google Scholar] [CrossRef]
- Shafaey, M.A.; Melgani, F.; Salem, M.A.M.; Al-Berry, M.N.; Ebied, H.M.; El-Dahshan, E.S.A.; Tolba, M.F. Pixel-Wise Classification of Hyperspectral Images With 1D Convolutional SVM Networks. IEEE Access 2022, 10, 133174–133185. [Google Scholar] [CrossRef]
- Özdemir, A.O.B.; Gedik, B.E.; Çetin, C.Y.Y. Hyperspectral classification using stacked autoencoders with deep learning. In Proceedings of the 2014 6th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lausanne, Switzerland, 24–27 June 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Li, J. Active learning for hyperspectral image classification with a stacked autoencoders based neural network. In Proceedings of the 2015 7th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Tokyo, Japan, 2–5 June 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Zhong, P.; Gong, Z.; Li, S.; Schönlieb, C.B. Learning to Diversify Deep Belief Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3516–3530. [Google Scholar] [CrossRef]
- Lee, H.; Kwon, H. Going Deeper With Contextual CNN for Hyperspectral Image Classification. IEEE Trans. Image Process. 2017, 26, 4843–4855. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Xu, M.; Zhou, J.; Jia, S. Unsupervised Spatial-Spectral CNN-Based Feature Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Liang, L.; Zhang, S.; Li, J. Multiscale DenseNet Meets With Bi-RNN for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 5401–5415. [Google Scholar] [CrossRef]
- Huang, L.; Chen, Y. Dual-Path Siamese CNN for Hyperspectral Image Classification With Limited Training Samples. IEEE Geosci. Remote Sens. Lett. 2021, 18, 518–522. [Google Scholar] [CrossRef]
- Ahmad, M.; Khan, A.M.; Mazzara, M.; Distefano, S.; Ali, M.; Sarfraz, M.S. A Fast and Compact 3-D CNN for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Ghaderizadeh, S.; Abbasi-Moghadam, D.; Sharifi, A.; Zhao, N.; Tariq, A. Hyperspectral Image Classification Using a Hybrid 3D-2D Convolutional Neural Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7570–7588. [Google Scholar] [CrossRef]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN Feature Hierarchy for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2020, 17, 277–281. [Google Scholar] [CrossRef]
- Yu, C.; Han, R.; Song, M.; Liu, C.; Chang, C.I. A Simplified 2D-3D CNN Architecture for Hyperspectral Image Classification Based on Spatial–Spectral Fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2485–2501. [Google Scholar] [CrossRef]
- Gao, K.; Yu, X.; Tan, X.; Liu, B.; Sun, Y. Small sample classification for hyperspectral imagery using temporal convolution and attention mechanism. Remote Sens. Lett. 2021, 12, 510–519. [Google Scholar] [CrossRef]
- Gao, K.; Liu, B.; Yu, X.; Qin, J.; Zhang, P.; Tan, X. Deep Relation Network for Hyperspectral Image Few-Shot Classification. Remote Sens. 2020, 12, 923. [Google Scholar] [CrossRef]
- Jia, S.; Jiang, S.; Lin, Z.; Li, N.; Xu, M.; Yu, S. A survey: Deep learning for hyperspectral image classification with few labeled samples. Neurocomputing 2021, 448, 179–204. [Google Scholar] [CrossRef]
- Liu, B.; Yu, X.; Zhang, P.; Tan, X.; Yu, A.; Xue, Z. A semi-supervised convolutional neural network for hyperspectral image classification. Remote Sens. Lett. 2017, 8, 839–848. [Google Scholar] [CrossRef]
- Zhan, Y.; Hu, D.; Wang, Y.; Yu, X. Semisupervised Hyperspectral Image Classification Based on Generative Adversarial Networks. IEEE Geosci. Remote Sens. Lett. 2018, 15, 212–216. [Google Scholar] [CrossRef]
- Liu, B.; Yu, A.; Yu, X.; Wang, R.; Gao, K.; Guo, W. Deep Multiview Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 7758–7772. [Google Scholar] [CrossRef]
- Liu, B.; Yu, X.; Yu, A.; Zhang, P.; Wan, G.; Wang, R. Deep Few-Shot Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2290–2304. [Google Scholar] [CrossRef]
- Zuo, X.; Yu, X.; Liu, B.; Zhang, P.; Tan, X.; Wei, X. Graph inductive learning method for small sample classification of hyperspectral remote sensing images. Eur. J. Remote Sens. 2020, 53, 349–357. [Google Scholar] [CrossRef]
- Hong, D.; Gao, L.; Yao, J.; Zhang, B.; Plaza, A.; Chanussot, J. Graph Convolutional Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5966–5978. [Google Scholar] [CrossRef]
- Zhao, X.; Niu, J.; Liu, C.; Ding, Y.; Hong, D. Hyperspectral Image Classification Based on Graph Transformer Network and Graph Attention Mechanism. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Kang, X.; Xiang, X.; Li, S.; Benediktsson, J.A. PCA-Based Edge-Preserving Features for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7140–7151. [Google Scholar] [CrossRef]
- Zhou, L.; Ma, X.; Wang, X.; Hao, S.; Ye, Y.; Zhao, K. Shallow-to-Deep Spatial-Spectral Feature Enhancement for Hyperspectral Image Classification. Remote Sens. 2023, 15, 261. [Google Scholar] [CrossRef]
- Li, F.; Xu, L.; Wong, A.; Clausi, D.A. Feature Extraction for Hyperspectral Imagery via Ensemble Localized Manifold Learning. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2486–2490. [Google Scholar] [CrossRef]
- Park, S.; Lee, H.J.; Ro, Y.M. Adversarially Robust Hyperspectral Image Classification via Random Spectral Sampling and Spectral Shape Encoding. IEEE Access 2021, 9, 66791–66804. [Google Scholar] [CrossRef]
- Hu, X.; Wang, X.; Zhong, Y.; Zhao, J.; Luo, C.; Wei, L. SPNet: A Spectral Patching Network for End-To-End Hyperspectral Image Classification. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 963–966. [Google Scholar] [CrossRef]
- Liu, B.; Gao, K.; Yu, A.; Ding, L.; Qiu, C.; Li, J. ES2FL: Ensemble Self-Supervised Feature Learning for Small Sample Classification of Hyperspectral Images. Remote Sens. 2022, 14, 4236. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, B.; Yu, X.; Yu, A.; Gao, K.; Ding, L. From Video to Hyperspectral: Hyperspectral Image-Level Feature Extraction with Transfer Learning. Remote Sens. 2022, 14, 5118. [Google Scholar] [CrossRef]
- Fauvel, M.; Benediktsson, J.A.; Chanussot, J.; Sveinsson, J.R. Spectral and Spatial Classification of Hyperspectral Data Using SVMs and Morphological Profiles. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3804–3814. [Google Scholar] [CrossRef]
- Huang, K.K.; Ren, C.X.; Liu, H.; Lai, Z.R.; Yu, Y.F.; Dai, D.Q. Hyperspectral Image Classification via Discriminant Gabor Ensemble Filter. IEEE Trans. Cybern. 2022, 52, 8352–8365. [Google Scholar] [CrossRef]
- Li, W.; Chen, C.; Su, H.; Du, Q. Local Binary Patterns and Extreme Learning Machine for Hyperspectral Imagery Classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3681–3693. [Google Scholar] [CrossRef]
- Khodadadzadeh, M.; Li, J.; Plaza, A.; Ghassemian, H.; Bioucas-Dias, J.M.; Li, X. Spectral–Spatial Classification of Hyperspectral Data Using Local and Global Probabilities for Mixed Pixel Characterization. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6298–6314. [Google Scholar] [CrossRef]
- Khodadadzadeh, M.; Rajabi, R.; Ghassemian, H. A novel approach for spectral-spatial classification of hyperspectral data based on SVM-MRF method. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 1890–1893. [Google Scholar] [CrossRef]
- Zhang, W.; Du, P.; Lin, C.; Fu, P.; Wang, X.; Bai, X.; Zheng, H.; Xia, J.; Samat, A. An Improved Feature Set for Hyperspectral Image Classification: Harmonic Analysis Optimized by Multiscale Guided Filter. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3903–3916. [Google Scholar] [CrossRef]
- Dundar, T.; Ince, T. Sparse Representation-Based Hyperspectral Image Classification Using Multiscale Superpixels and Guided Filter. IEEE Geosci. Remote Sens. Lett. 2019, 16, 246–250. [Google Scholar] [CrossRef]
- Liu, B.; Yu, X. Patch-Free Bilateral Network for Hyperspectral Image Classification Using Limited Samples. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 10794–10807. [Google Scholar] [CrossRef]
- Zhang, M.; Li, W.; Du, Q. Diverse Region-Based CNN for Hyperspectral Image Classification. IEEE Trans. Image Process. 2018, 27, 2623–2634. [Google Scholar] [CrossRef] [PubMed]
- Gao, K.; Liu, B.; Yu, X.; Zhang, P.; Tan, X.; Sun, Y. Small sample classification of hyperspectral image using model-agnostic meta-learning algorithm and convolutional neural network. Int. J. Remote Sens. 2021, 42, 3090–3122. [Google Scholar] [CrossRef]
- Xu, Q.; Xiao, Y.; Wang, D.; Luo, B. CSA-MSO3DCNN: Multiscale Octave 3D CNN with Channel and Spatial Attention for Hyperspectral Image Classification. Remote Sens. 2020, 12, 188. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–Spatial Residual Network for Hyperspectral Image Classification: A 3-D Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Ma, A.; Filippi, A.M.; Wang, Z.; Yin, Z.; Huo, D.; Li, X.; Güneralp, B. Fast Sequential Feature Extraction for Recurrent Neural Network-Based Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5920–5937. [Google Scholar] [CrossRef]
- Hang, R.; Liu, Q.; Hong, D.; Ghamisi, P. Cascaded Recurrent Neural Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5384–5394. [Google Scholar] [CrossRef]
- Yu, C.; Han, R.; Song, M.; Liu, C.; Chang, C.I. Feedback Attention-Based Dense CNN for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Haut, J.M.; Paoletti, M.E.; Plaza, J.; Plaza, A.; Li, J. Visual Attention-Driven Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8065–8080. [Google Scholar] [CrossRef]
- Bai, J.; Wen, Z.; Xiao, Z.; Ye, F.; Zhu, Y.; Alazab, M.; Jiao, L. Hyperspectral Image Classification Based on Multibranch Attention Transformer Networks. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Tan, X.; Gao, K.; Liu, B.; Fu, Y.; Kang, L. Deep global-local transformer network combined with extended morphological profiles for hyperspectral image classification. J. Appl. Remote Sens. 2021, 15, 038509. [Google Scholar] [CrossRef]
- Xibing, Z.U.O.; Bing, L.I.U.; Xuchu, Y.U.; Pengqiang, Z.H.A.N.G.; Kuiliang, G.A.O.; Enze, Z.H.U. Graph convolutional network method for small sample classification of hyperspectral images. Acta Geod. Et Cartogr. Sin. 2021, 50, 1358. [Google Scholar] [CrossRef]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph Attention Networks. CoRR 2018, 1050, 10-48550. [Google Scholar]
- Zhang, Y.; Li, W.; Zhang, M.; Wang, S.; Tao, R.; Du, Q. Graph Information Aggregation Cross-Domain Few-Shot Learning for Hyperspectral Image Classification. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–14. [Google Scholar] [CrossRef]
- Lee, H.; Eum, S.; Kwon, H. Exploring Cross-Domain Pretrained Model for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, B.; Yu, X.; Yu, A.; Gao, K.; Ding, L. Perceiving Spectral Variation: Unsupervised Spectrum Motion Feature Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Devlin, J.; Chang, M.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, NAACL-HLT 2019, Minneapolis, MN, USA, 2–7 June 2019; (Long and Short Papers). Burstein, J., Doran, C., Solorio, T., Eds.; Association for Computational Linguistics: Toronto, ON, Canada, 2019; Volume 1, pp. 4171–4186. [Google Scholar] [CrossRef]
- Brown, T.B.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language Models are Few-Shot Learners. In Proceedings of the Advances in Neural Information Processing Systems 33: Annual Conference on Neural Information Processing Systems 2020, NeurIPS 2020, Virtual, 6–12 December 2020; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M., Lin, H., Eds.; NeurIPS: New Orleans, LA, USA, 2020. [Google Scholar]
- He, K.; Chen, X.; Xie, S.; Li, Y.; Dollár, P.; Girshick, R.B. Masked Autoencoders Are Scalable Vision Learners. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, CVPR 2022, New Orleans, LA, USA, 18–24 June 2022; pp. 15979–15988. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).