A Sorting Method of SAR Emitter Signal Sorting Based on Self-Supervised Clustering
Abstract
1. Introduction
2. Related Works
2.1. Radar Signal Sorting Methods
2.2. Self-Supervised Learning
2.3. Self-Organizing Map Network
3. Signal Model and Data Preprocessing
3.1. Model of the Received Signal
3.2. Data Preprocessing
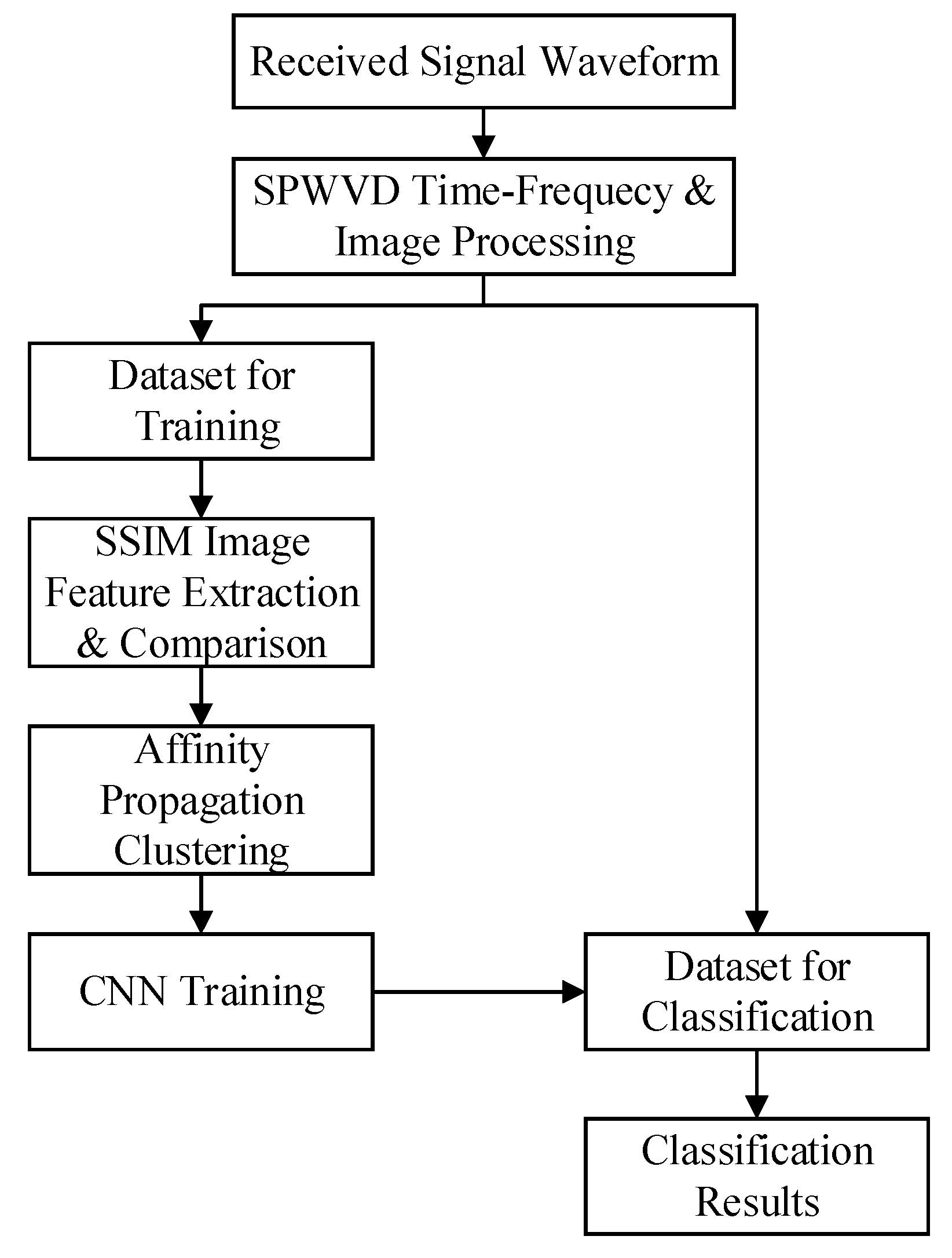
4. Self-Supervised Clustering Method Based on Pulse Time-Frequency Image Features
4.1. Overview of the Proposed Method
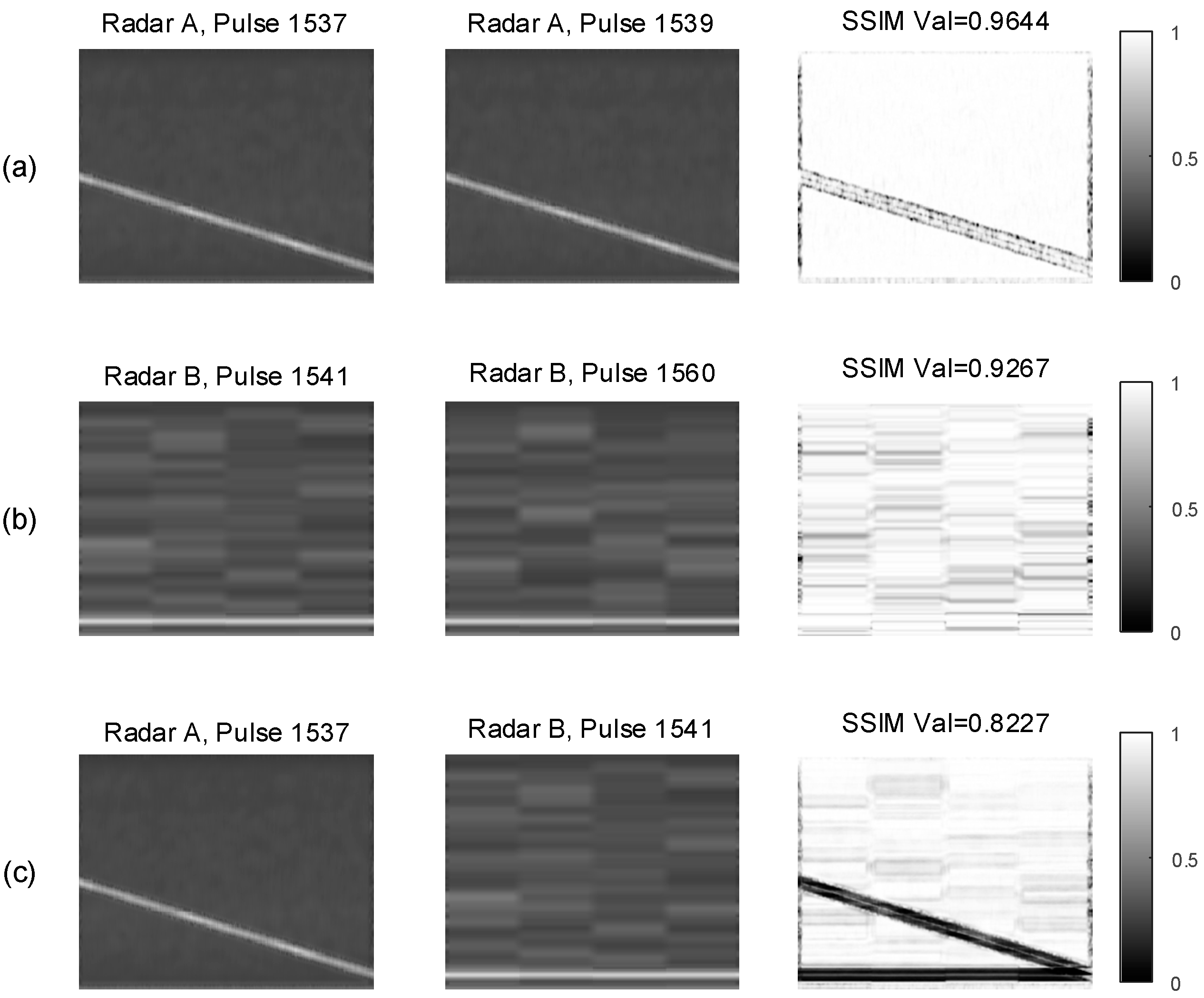
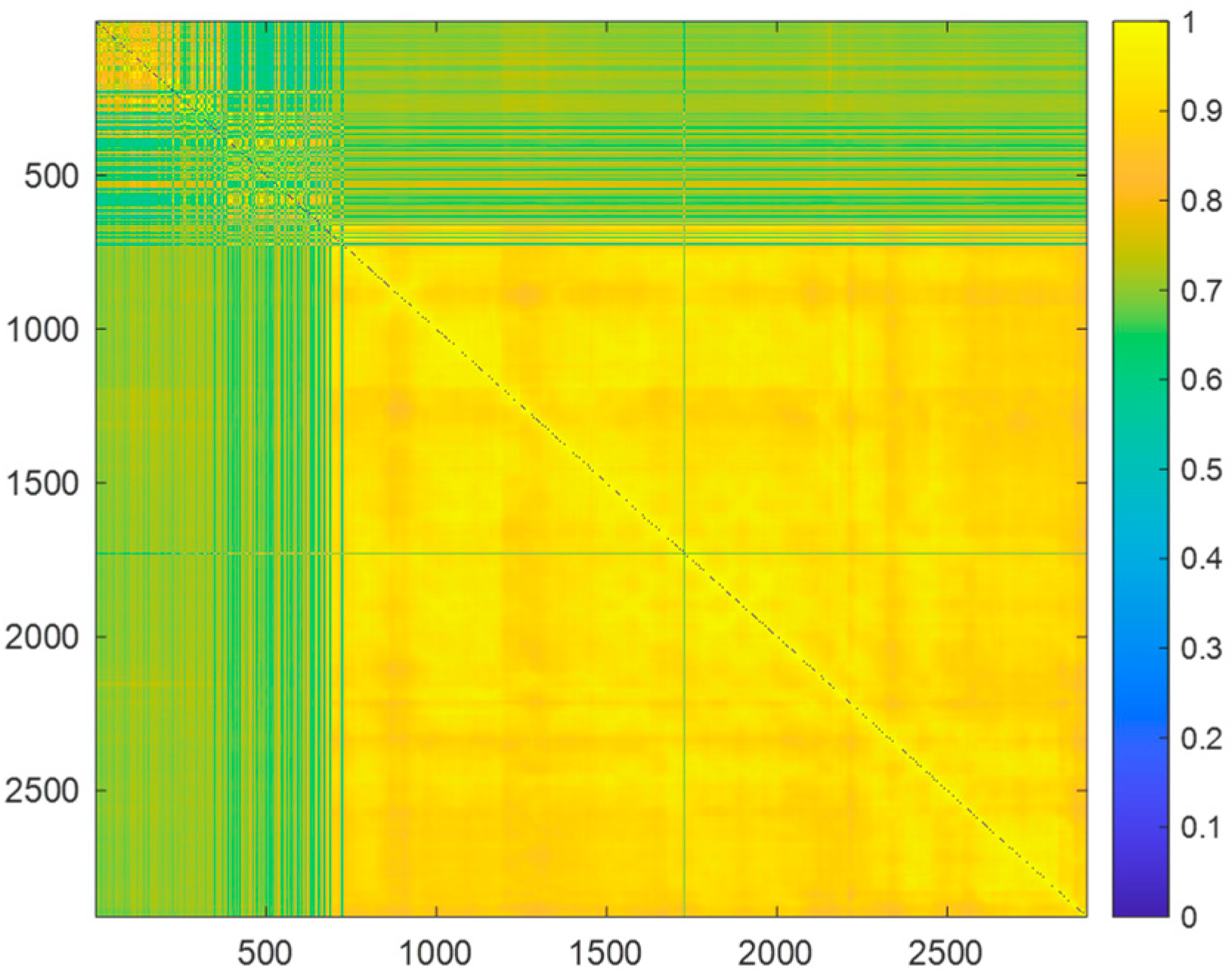
4.2. Construction of the Similarity Matrix
4.3. Affinity Propagation Clustering of the Similarity Matrix
4.4. Network Structure of the Constructed CNN
4.5. Data Augmentation
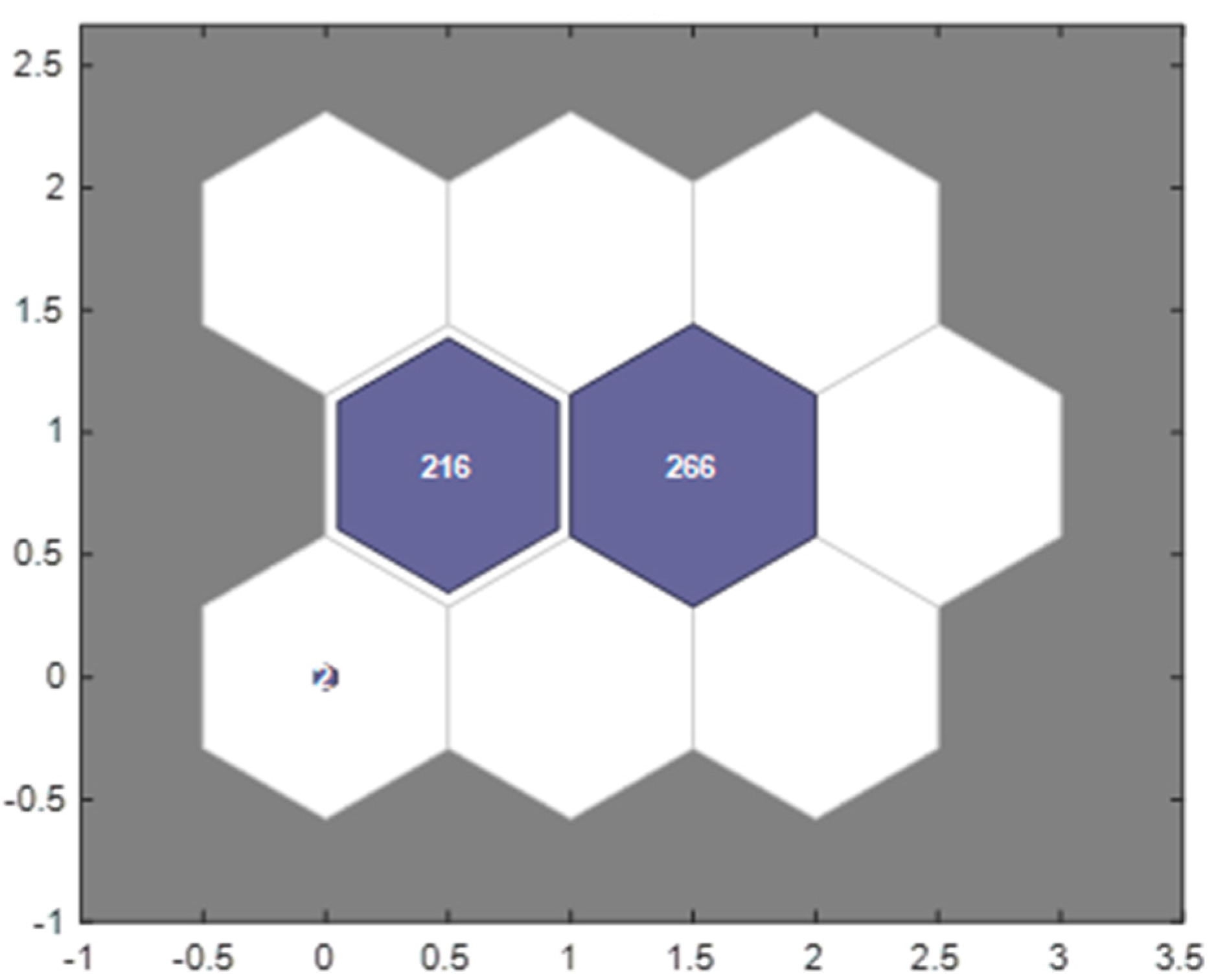
4.6. Refined Sorting Using the SOM Network
- Select clusters of subject pulses;
- Randomly select 50% of the pulses as the training set and the rest as the test set, and construct the SOM network;
- Train the SOM network with the pulse width, carrier frequency, and bandwidth of each pulse in the cluster as input;
- Clustering the pulse clusters using the SOM network;
- Merge the similar clustering centers, store the clustering centers with fewer numbers within the category and distant from other centers, set them as new pulse clusters, and repeat steps 3~5.
5. Simulations and Analyses
5.1. Dataset Description
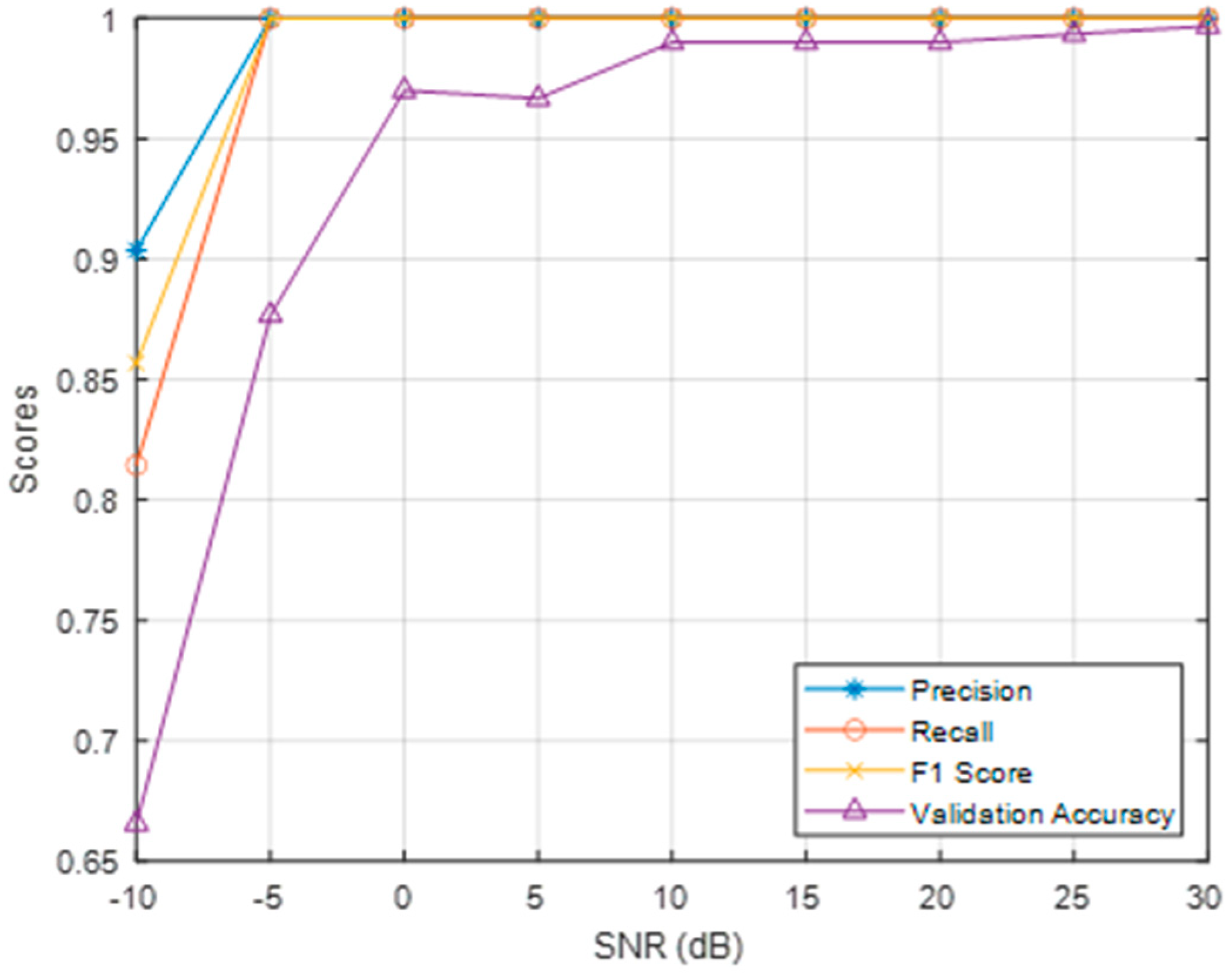
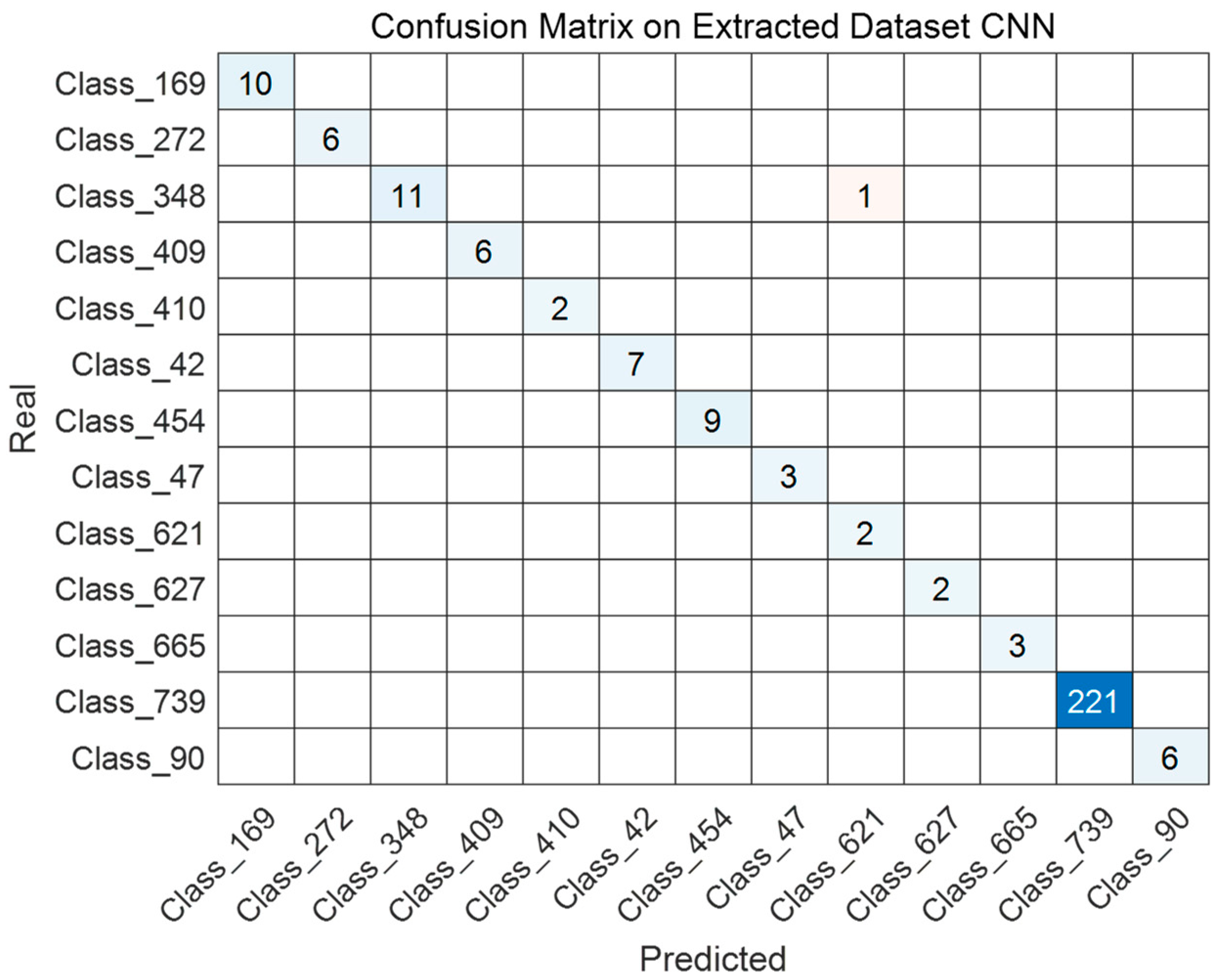
5.2. Performance Testing of the Proposed Sorting Method
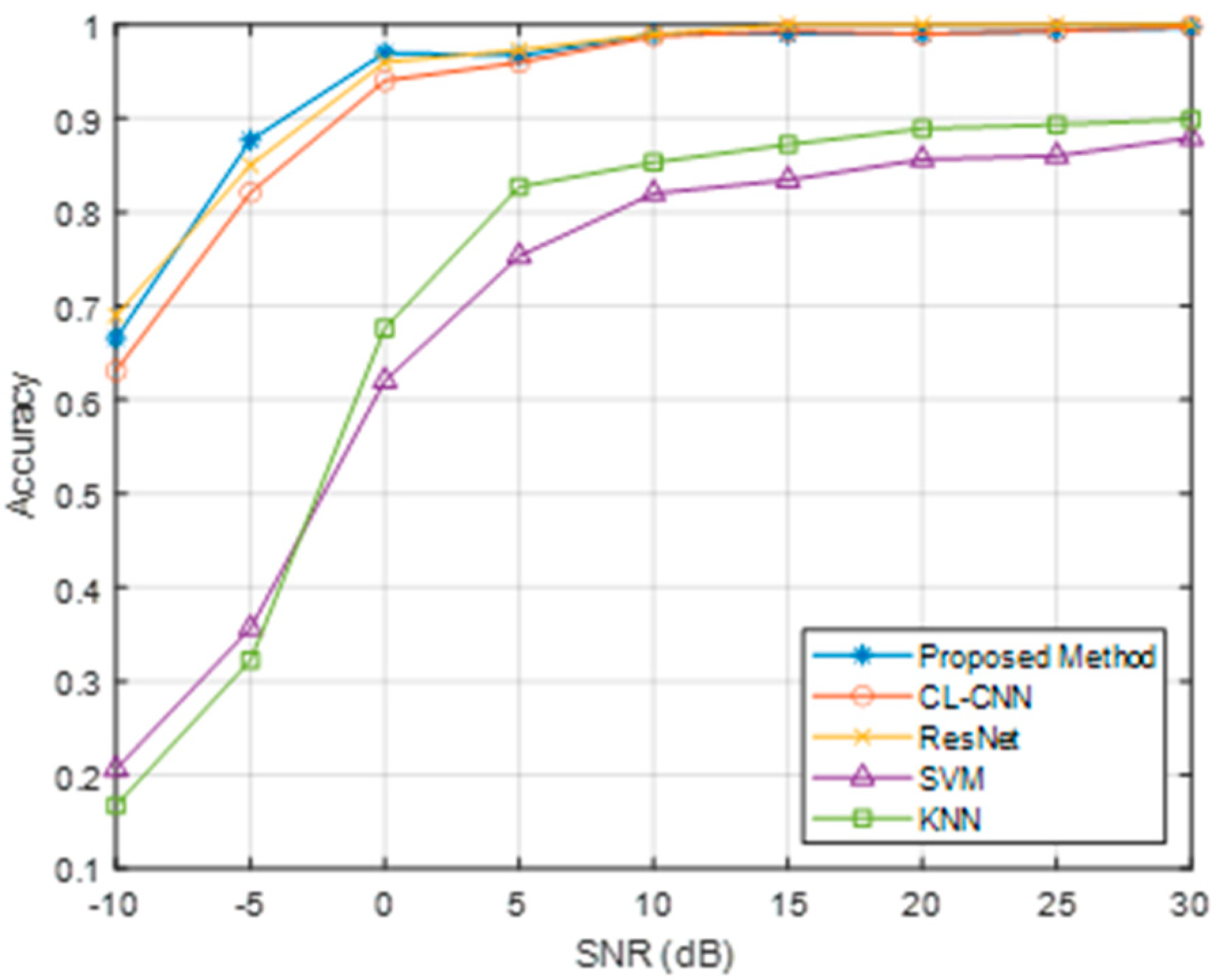
5.3. Performance Comparison
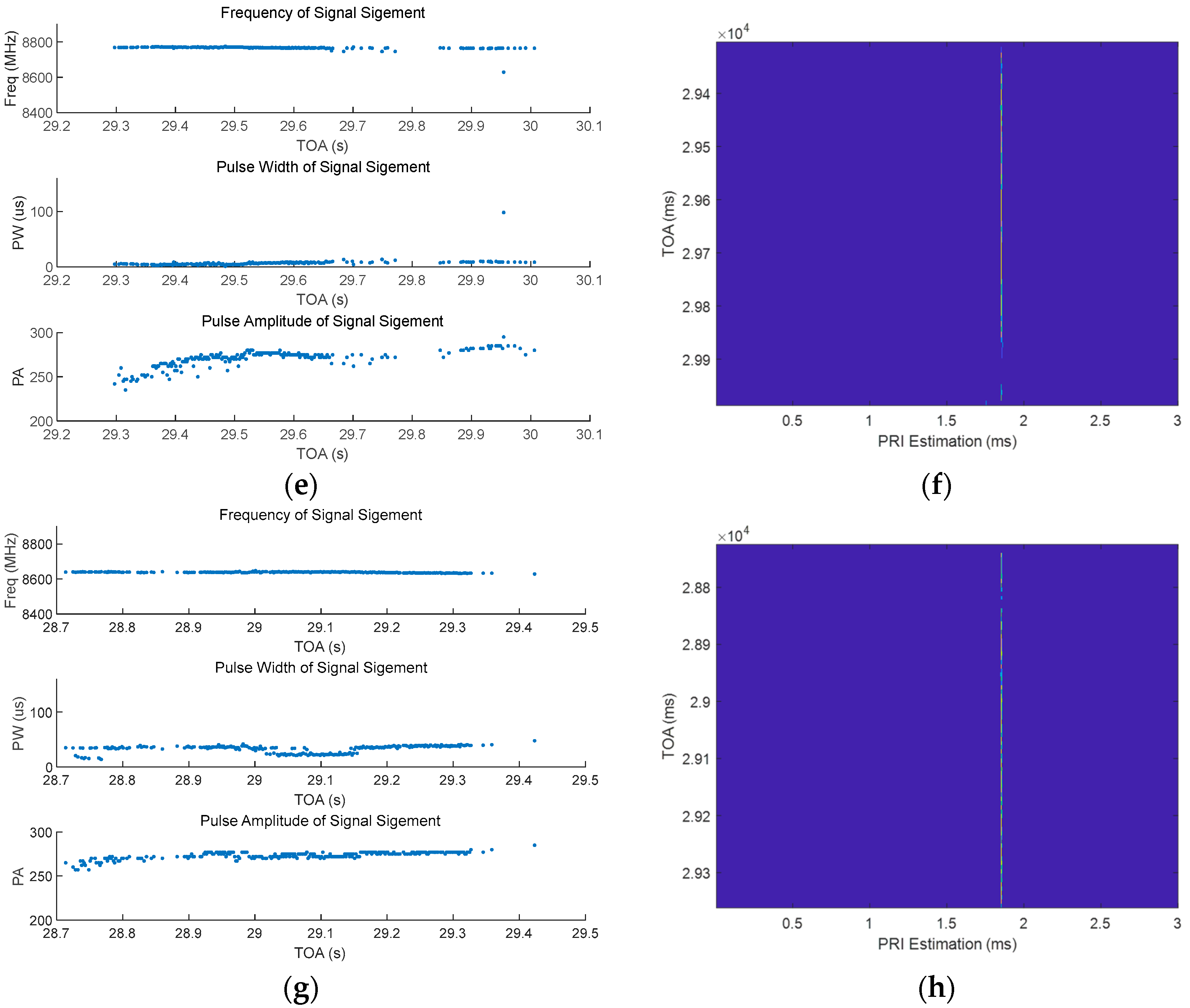
6. Validation Based on Measured Data
6.1. Dataset Description
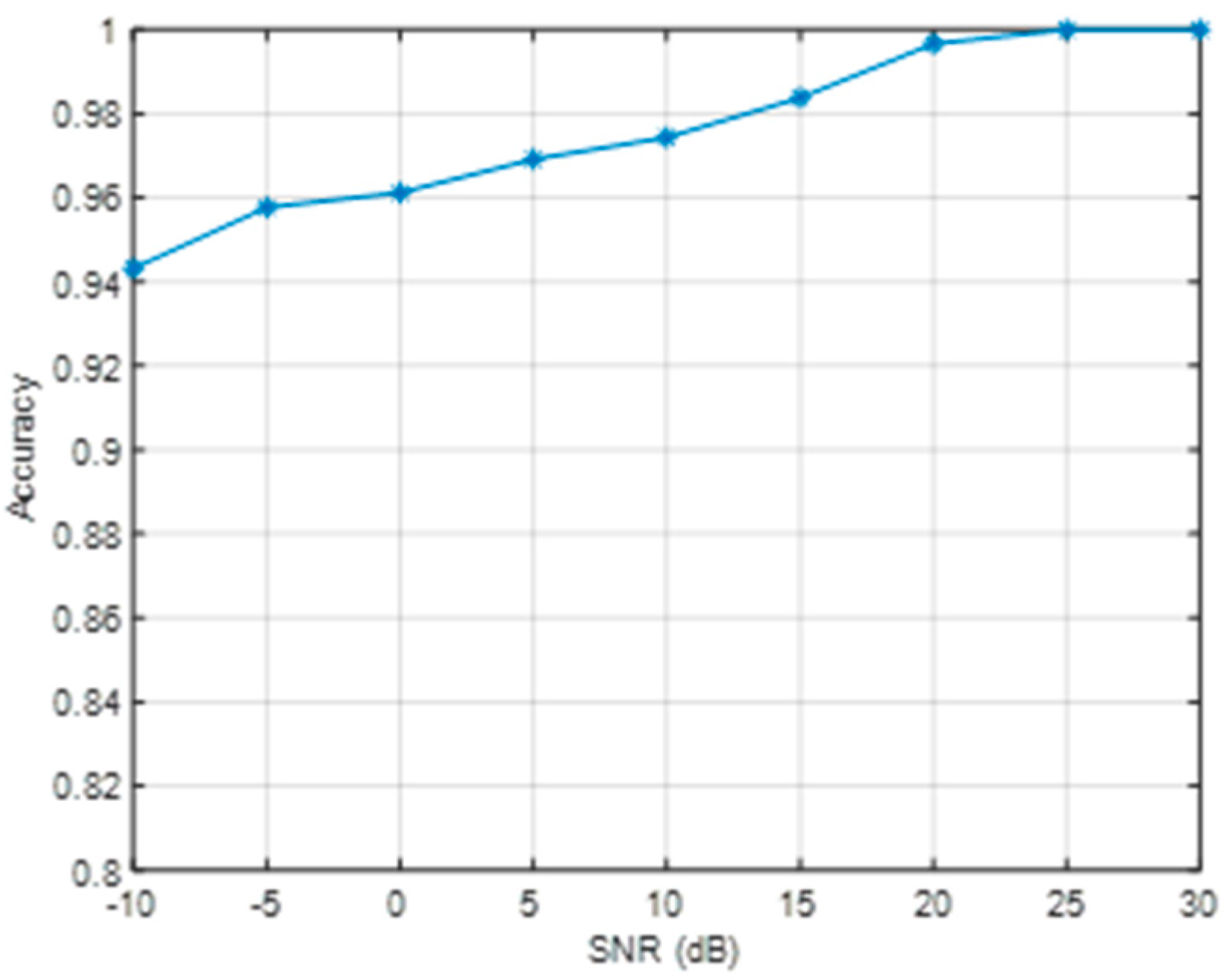
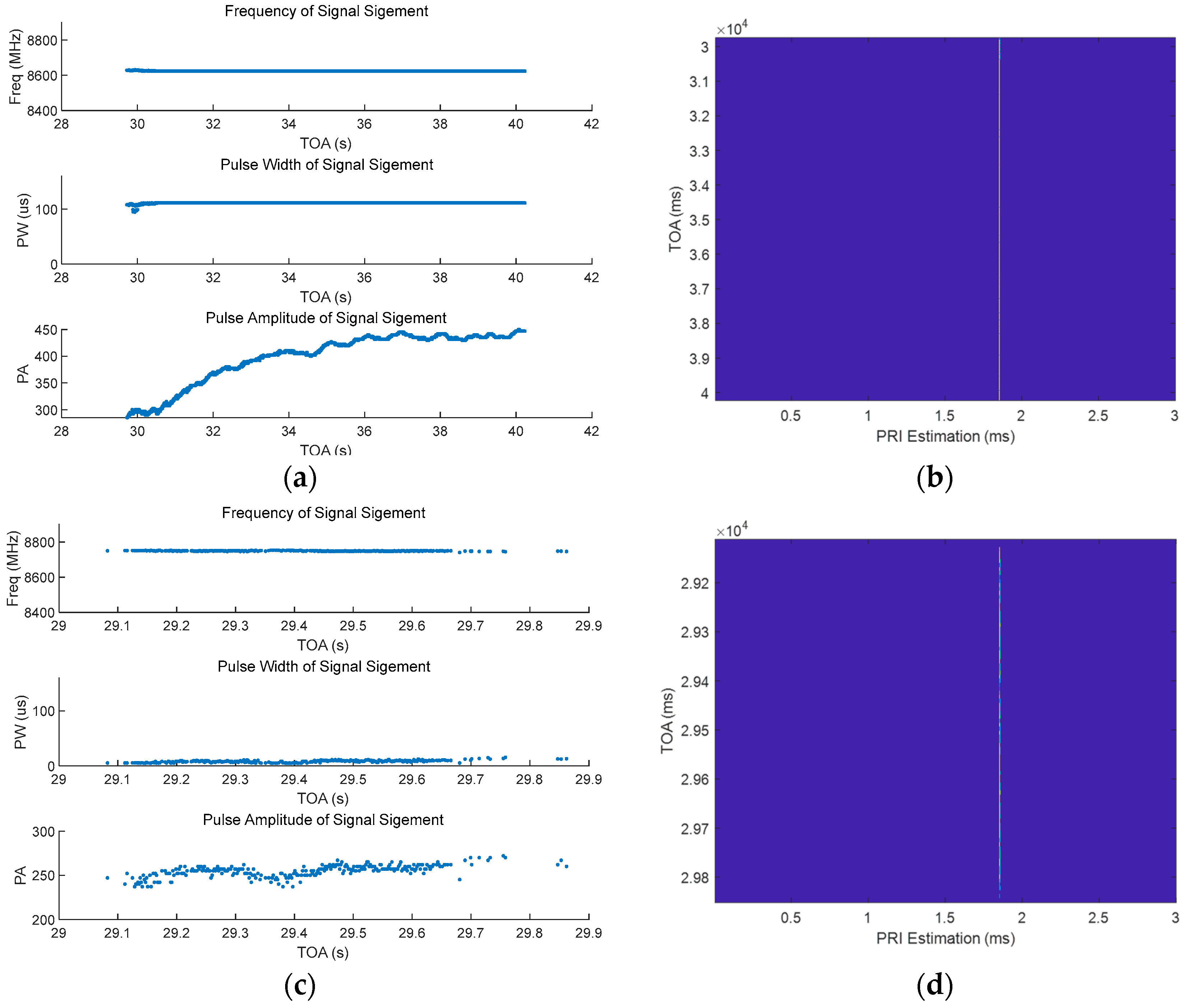
6.2. Performance Testing of the Proposed Sorting Method Using Measured Data
6.3. Performance Comparison
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gupta, M.; Hareesh, G.; Mahla, A.K. Electronic warfare: Issues and challenges for emitter classification. Def. Sci. J. 2011, 61, 228. [Google Scholar] [CrossRef]
- Qu, Z.; Mao, X.; Deng, Z. Radar signal intra-pulse modulation recognition based on convolutional neural network. IEEE Access 2018, 6, 43874–43884. [Google Scholar] [CrossRef]
- Yuan, S.; Li, P.; Wu, B.; Li, X.; Wang, J. Semi-supervised classification for intra-pulse modulation of radar emitter signals using convolutional neural network. Remote Sens. 2022, 14, 2059. [Google Scholar] [CrossRef]
- Villano, M.; Krieger, G.; Moreira, A. Nadir echo removal in synthetic aperture radar via waveform diversity and dual-focus postprocessing. IEEE Geosci. Remote Sens. Lett. 2018, 15, 719–723. [Google Scholar] [CrossRef]
- Villano, M.; Krieger, G.; Moreira, A. Waveform-Encoded SAR: A Novel Concept for Nadir Echo and Range Ambiguity Suppression. In Proceedings of the EUSAR 2018, 12th European Conference on Synthetic Aperture Radar, Aachen, Germany, 4–7 June 2018. [Google Scholar]
- Mittermayer, J.; Martinez, J.M. Analysis of Range Ambiguity Suppression in SAR by up and down Chirp Modulation for Point and Distributed Targets. In Proceedings of the IGARSS 2003, 2003 IEEE International Geoscience and Remote Sensing Symposium, Proceedings (IEEE Cat, No.03CH37477), Toulouse, France, 21–25 July 2003; Volume 6, pp. 4077–4079. [Google Scholar]
- Jeon, S.-Y.; Kraus, T.; Steinbrecher, U.; Villano, M.; Krieger, G. A TerraSAR-X Experiment for Validation of Nadir Echo Suppression through Waveform Encoding and Dual-Focus Postprocessing. In Proceedings of the European Conference on Synthetic Aperture Radar (EUSAR) 2021, Leipzig, Germany, 29 March–1 April 2021. [Google Scholar]
- Wang, R.; Chen, J.; Wang, X.; Sun, B. High-Performance Anti-Retransmission Deception Jamming Utilizing Range Direction Multiple Input and Multiple Output (MIMO) Synthetic Aperture Radar (SAR). Sensors 2017, 17, 123. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Wang, Y.; Jin, G.; Wang, Y.; Dong, Q.; Wang, B.; Zhou, L.; Lu, P.; Wu, Y. A Novel Jamming Method against SAR Using Nonlinear Frequency Modulation Waveform with Very High Sidelobes. Remote Sens. 2022, 14, 5370. [Google Scholar] [CrossRef]
- Kersten, P.; Lee, J.-S.; Ainsworth, T. Unsupervised Classification of Polarimetric Synthetic Aperture Radar Images Using Fuzzy Clustering and EM Clustering. IEEE Trans. Geosci. Remote Sens. 2005, 43, 519–527. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, Y.; Si, W. Synthetic Algorithm for Deinterleaving Radar Signals in a Complex Environment. IET Radar Sonar Navig. 2020, 14, 1918–1928. [Google Scholar] [CrossRef]
- Cheng, W.; Zhang, Q.; Dong, J.; Wang, C.; Liu, X.; Fang, G. An Enhanced Algorithm for Deinterleaving Mixed Radar Signals. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 3927–3940. [Google Scholar] [CrossRef]
- Su, S.; Fu, X.; Zhao, C.; Yang, J.; Xie, M.; Gao, Z. Unsupervised K-Means Combined with SOFM Structure Adaptive Radar Signal Sorting Algorithm. In Proceedings of the 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 11–13 December 2019. [Google Scholar] [CrossRef]
- Chen, X.; Liu, D.; Wang, X.; Chen, Y.; Cheng, S. Improved DBSCAN Radar Signal Sorting Algorithm Based on Rough Set. In Proceedings of the 2021 2nd International Conference on Big Data and Informatization Education (ICBDIE), Hangzhou, China, 2–4 April 2021. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, H.; Gan, L. A Multi-Station Signal Sorting Method Based on TDOA Grid Clustering. In Proceedings of the 2021 IEEE 6th International Conference on Signal and Image Processing (ICSIP), Nanjing, China, 22–24 October 2021. [Google Scholar] [CrossRef]
- Mottier, M.; Chardon, G.; Pascal, F. Deinterleaving and Clustering Unknown RADAR Pulses. In Proceedings of the 2021 IEEE Radar Conference (RadarConf21), Atlanta, GA, USA, 7–14 May 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, G.; Chen, S.; Hu, X.; Yuan, J. Radar Emitter Sorting and Recognition Based on Time-Frequency Image Union Feature. In Proceedings of the 2019 IEEE 4th International Conference on Signal and Image Processing (ICSIP), Wuxi, China, 19–21 July 2019. [Google Scholar] [CrossRef]
- Kong, S.-H.; Kim, M.; Hoang, L.M.; Kim, E. Automatic LPI radar waveform recognition using CNN. IEEE Access 2018, 6, 4207–4219. [Google Scholar] [CrossRef]
- Tang, Q.; Huang, H.-H.; Chen, Z. A Novel Approach for Automatic Recognition of LPI Radar Waveforms Based on CNN and Attention Mechanisms. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022. [Google Scholar] [CrossRef]
- Quan, D.; Tang, Z.; Wang, X.; Zhai, W.; Qu, C. LPI Radar Signal Recognition Based on Dual-Channel CNN and Feature Fusion. Symmetry 2022, 14, 570. [Google Scholar] [CrossRef]
- Nishiguchi, K.; Kobayashi, M. Improved Algorithm for Estimating Pulse Repetition Intervals. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 407–421. [Google Scholar] [CrossRef]
- Feng, X.; Hu, X.; Liu, Y. Radar Signal Sorting Algorithm of K-Means Clustering Based on Data Field. In Proceedings of the 2017 3rd IEEE International Conference on Computer and Communications (ICCC), Chengdu, China, 13–16 December 2017; pp. 2262–2266. [Google Scholar] [CrossRef]
- Cao, S.; Wang, S.; Zhang, Y. Density-Based Fuzzy C-Means Multi-Center Re-Clustering Radar Signal Sorting Algorithm. In Proceedings of the 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, 17–20 December 2018; pp. 891–896. [Google Scholar] [CrossRef]
- Zhang, S.; Pan, J.; Han, Z.; Qiu, R. Recognition of Radar Emitter Signal Images Using Encoding Signal Methods. In Proceedings of the 2021 International Conference on Neural Networks, Information and Communication Engineering, Qingdao, China, 15 October 2021. [Google Scholar] [CrossRef]
- Li, P. Research on Radar Signal Recognition Based on Automatic Machine Learning. Neural Comput. Appl. 2019, 32, 1959–1969. [Google Scholar] [CrossRef]
- Sun, J.; Xu, G.; Ren, W.; Yan, Z. Radar Emitter Classification Based on Unidimensional Convolutional Neural Network. IET Radar Sonar Navig. 2018, 12, 862–867. [Google Scholar] [CrossRef]
- Wang, X.; Huang, G.; Zhou, Z.; Gao, J. Radar Emitter Recognition Based on the Short Time Fourier Transform and Convolutional Neural Networks. In Proceedings of the 2017 10th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Shanghai, China, 14–16 October 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Zhang, M.; Diao, M.; Guo, L. Convolutional Neural Networks for Automatic Cognitive Radio Waveform Recognition. IEEE Access 2017, 5, 11074–11082. [Google Scholar] [CrossRef]
- Akyon, F.C.; Alp, Y.K.; Gok, G.; Arikan, O. Classification of Intra-Pulse Modulation of Radar Signals by Feature Fusion Based Convolutional Neural Networks. In Proceedings of the 2018 26th European Signal Processing Conference (EUSIPCO), Rome, Italy, 3–7 September 2018; pp. 2290–2294. [Google Scholar] [CrossRef]
- Wan, J.; Yu, X.; Guo, Q. LPI Radar Waveform Recognition Based on CNN and TPOT. Symmetry 2019, 11, 725. [Google Scholar] [CrossRef]
- Devlin, J.; Chang, M.-W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Gidaris, S.; Singh, P.; Komodakis, N. Unsupervised representation learning by predicting image rotations. arXiv 2018, arXiv:1803.07728. [Google Scholar]
- Hou, S.; Shi, H.; Cao, X.; Zhang, X.; Jiao, L. Hyperspectral Imagery Classification Based on Contrastive Learning. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Jing, L.; Tian, Y. Self-Supervised Visual Feature Learning with Deep Neural Networks: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 4037–4058. [Google Scholar] [CrossRef]
- Kohonen, T. Self-Organized Formation of Topologically Correct Feature Maps. Biol. Cybern. 1982, 43, 59–69. [Google Scholar] [CrossRef]
- Amitrano, D.; Di Martino, G.; Iodice, A.; Riccio, D.; Ruello, G. Urban Area Mapping Using Multitemporal SAR Images in Combination with Self-Organizing Map Clustering and Object-Based Image Analysis. Remote Sens. 2023, 15, 122. [Google Scholar] [CrossRef]
- Cavur, M.; Moraga, J.; Duzgun, H.S.; Soydan, H.; Jin, G. Displacement Analysis of Geothermal Field Based on PSInSAR And SOM Clustering Algorithms A Case Study of Brady Field, Nevada—USA. Remote Sens. 2021, 13, 349. [Google Scholar] [CrossRef]
- Ohno, S.; Kidera, S.; Kirimoto, T. Efficient SOM-Based ATR Method for SAR Imagery With Azimuth Angular Variations. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1901–1905. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Lim, J.S. Two-Dimensional Signal and Image Processing; Prentice-Hall: Englewood Cliffs, NJ, USA, 1990. [Google Scholar]
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Frey, B.J.; Dueck, D. Clustering by Passing Messages Between Data Points. Science 2007, 315, 972–976. [Google Scholar] [CrossRef]







| Radars | Intra-Pulse Modulation Type | Carrier Frequency (MHz) | Bandwidth (MHz) | Pulse Width (μs) | PRI (μs) |
|---|---|---|---|---|---|
| A | constant frequency | 7500 | - | 1000 | 1.73 |
| B | LFM | 1275 | 80 | 33 | 2.64 |
| C | LFM | 4600 | 20 | 20 | 2.52 |
| D | VFM | 2400 | 50 | 65 | 3.1 |
| E | OFDM-LFM | 5300 | 45 | 40 | 1.62 |
| Parameter Name | Parameter Value |
|---|---|
| Solver | SGDM |
| Mini Batch Size | 100 |
| Max Epochs | 20 |
| Initial Learning Rate | 0.001 |
| Learning Rate Decay Period | 10 |
| Learning Rate Decay Factor | 0.1 |
| Shuffle | Every epoch |
| Methods | Radar A | Radar B | Radar C | Radar D | Radar E |
|---|---|---|---|---|---|
| Proposed Method | 0.8690 | 0.8923 | 0.8347 | 0.9037 | 0.8437 |
| CL-CNN | 0.8237 | 0.8813 | 0.7323 | 0.8567 | 0.7667 |
| ResNet | 0.8317 | 0.8917 | 0.8377 | 0.8793 | 0.8217 |
| SVM | 0.3413 | 0.3633 | 0.3323 | 0.4713 | 0.2617 |
| KNN | 0.3533 | 0.3123 | 0.3217 | 0.4327 | 0.2413 |
| Radars | Intra-Pulse Modulation Type | Carrier Frequency (MHz) | Bandwidth (MHz) | Pulse Width (μs) | PRI (μs) |
|---|---|---|---|---|---|
| F | LFM | 8620 | 150 | 111 | 1.852 |
| G | LFM | 8650 | 110 | 45 | 1.793 |
| Methods | Radar F | Radar G |
|---|---|---|
| Proposed Method | 0.8620 | 0.8733 |
| CL-CNN | 0.8012 | 0.8567 |
| ResNet | 0.8318 | 0.8913 |
| SVM | 0.3117 | 0.3260 |
| KNN | 0.3018 | 0.3113 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, D.; Qiao, G.; Zhang, C.; Tian, R.; Zhang, S. A Sorting Method of SAR Emitter Signal Sorting Based on Self-Supervised Clustering. Remote Sens. 2023, 15, 1867. https://doi.org/10.3390/rs15071867
Dai D, Qiao G, Zhang C, Tian R, Zhang S. A Sorting Method of SAR Emitter Signal Sorting Based on Self-Supervised Clustering. Remote Sensing. 2023; 15(7):1867. https://doi.org/10.3390/rs15071867
Chicago/Turabian StyleDai, Dahai, Guanyu Qiao, Caikun Zhang, Runkun Tian, and Shunjie Zhang. 2023. "A Sorting Method of SAR Emitter Signal Sorting Based on Self-Supervised Clustering" Remote Sensing 15, no. 7: 1867. https://doi.org/10.3390/rs15071867
APA StyleDai, D., Qiao, G., Zhang, C., Tian, R., & Zhang, S. (2023). A Sorting Method of SAR Emitter Signal Sorting Based on Self-Supervised Clustering. Remote Sensing, 15(7), 1867. https://doi.org/10.3390/rs15071867





