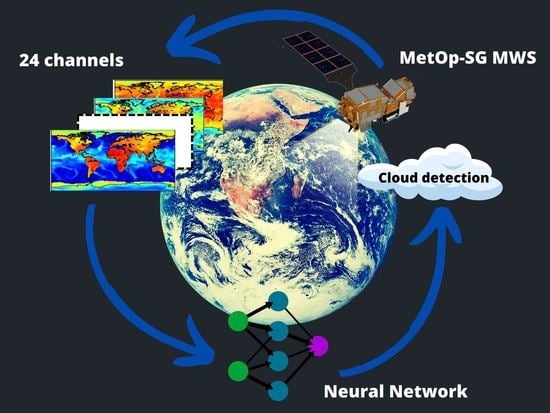
A Cloud Detection Neural Network Approach for the Next Generation Microwave Sounder Aboard EPS MetOp-SG A1
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset Used
2.1.1. Satellite Observed Dataset
2.1.2. Satellite Synthetic Dataset
2.2. Data Preparation
2.3. Evaluation Metrics
- The overall accuracy is calculated as the sum of the hits (correct classification) from each of the classes divided by the sum of the total points for the classification.
- The precision is the ratio of true positives to all positives predicted by the model. The more false positives the model predicts, the lower the precision.
- The recall is the ratio of true positives to all positives in the data set. It measures the ability of the model to detect positive samples.
- The F1 score is a single metric that combines precision and recall. The higher the F1 score, the better the performance of the model.
- The Fβ score is the weighted harmonic mean of precision and recall and reaches its optimal (worst) value at 1 (0).
- The area under the receiver operating characteristic curve (AUC-ROC) is a performance measurement for the classification problems. ROC is a probability curve and AUC represents the degree or measure of separability [67]. It provides a measure of the model skill to distinguish different classes. The higher the AUC, the better the model predicts 0 and 1 classes correctly. It is defined as the ratio of TPR against FPR
- The Jaccard index is a measure of similarity between two sets and is related to recall and precision.
- The Matthews correlation coefficient [68] is regarded as a balanced correlation coefficient that returns a value between −1 and +1, where +1 represents a perfect prediction, 0 an average random prediction and −1 an inverse prediction
2.4. Neural Network Configuration
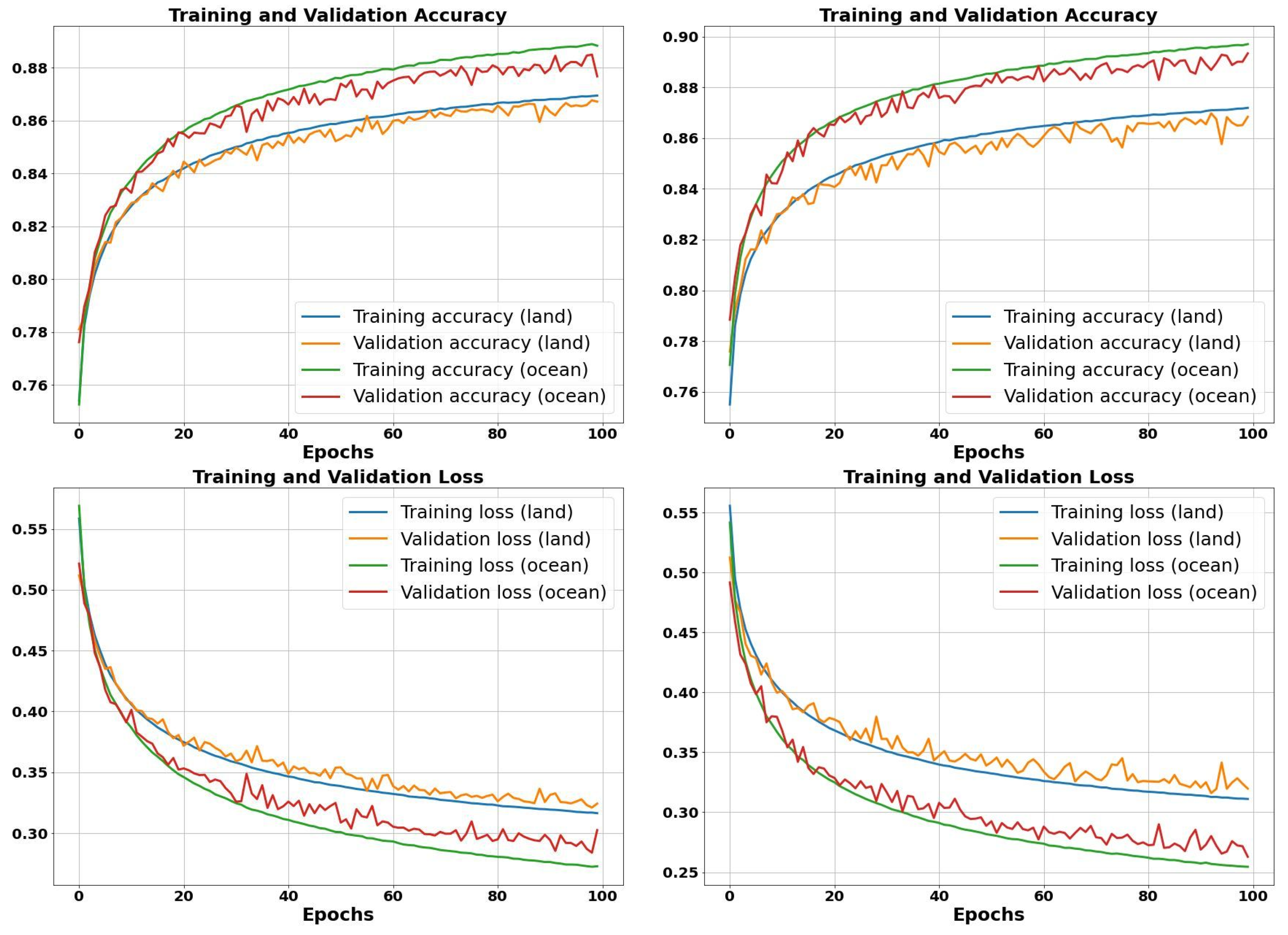
2.5. Neural Network Model Training Process
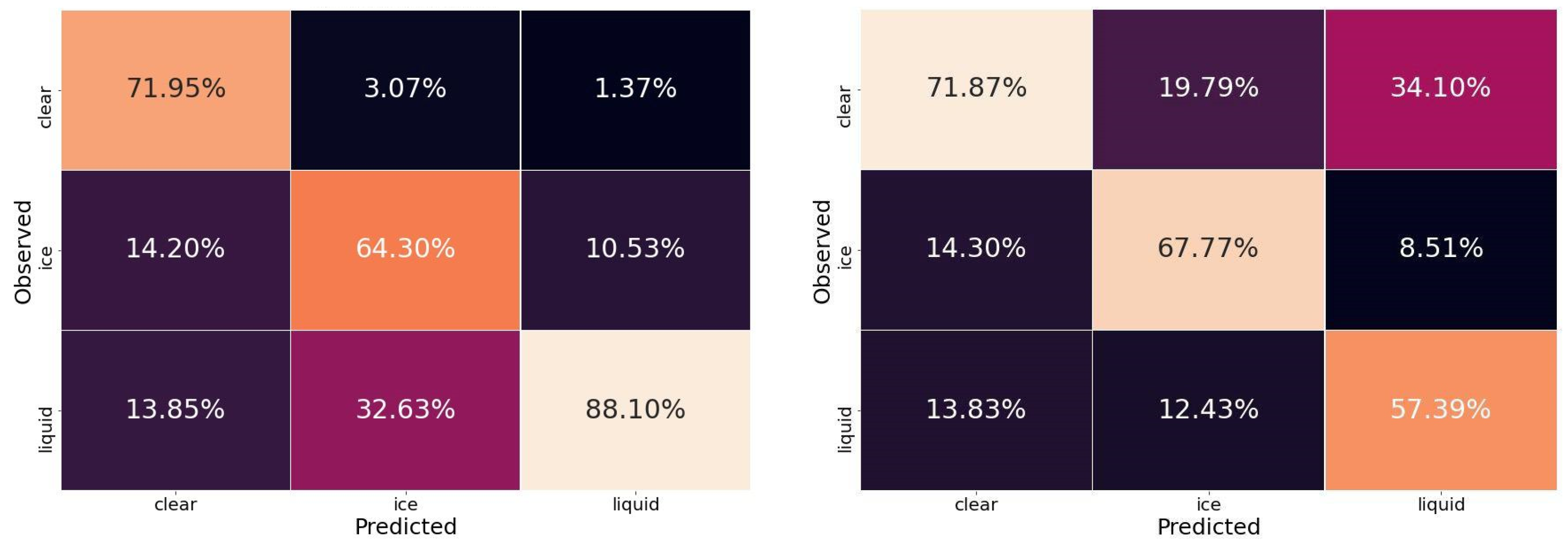
3. Results and Discussion
3.1. Evaluation with MWS and AMSU-A/MHS Synthetic Datasets
3.2. Detection Performance Using Observed Dataset
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, Y.; Sun, W.; Chi, Y.; Yan, X.; Fan, H.; Yang, X.; Ma, Z.; Wang, Q.; Zhao, C. Machine learning-based retrieval of day and night cloud macrophysical parameters over East Asia using Himawari-8 data. Remote Sens. Environ. 2022, 273, 112971. [Google Scholar] [CrossRef]
- Letu, H.; Yang, K.; Nakajima, T.Y.; Ishimoto, H.; Nagao, T.M.; Riedi, J.; Baran, A.J.; Ma, R.; Wang, T.; Shang, H.; et al. High-resolution retrieval of cloud microphysical properties and surface solar radiation using Himawari-8/AHI next-generation geostationary satellite. Remote Sens. Environ. 2020, 239, 111583. [Google Scholar] [CrossRef]
- Sreerekha, T.R.; Buehler, S.A.; O’Keeffe, U.; Doherty, A.A.; Emde, C.; John, V.O. A strong ice cloud event as seen by a microwave satellite sensor: Simulations and observations. J. Quant. Spectrosc. Radiat. Transf. 2008, 109, 1705–1718. [Google Scholar] [CrossRef]
- Bennartz, R.; Bauer, P. Sensitivity of microwave radiances at 85–183 GHz to precipitating ice particles. Radio Sci. 2003, 38, 40–41. [Google Scholar] [CrossRef]
- Romano, F.; Cimini, D.; Rizzi, R.; Cuomo, V. Multilayered cloud parameters retrievals from combined infrared and microwave satellite observations. J. Geophys. Res. 2007, 112, D08210. [Google Scholar] [CrossRef]
- Geer, A.; Lonitz, K.; Weston, P.; Kazumori, M.; Okamoto, K.; Zhu, Y.; Liu, E.; Collard, A.; Bell, W.; Migliorini, S.; et al. All sky satellite data assimilation at operational weather forecasting centres. Q. J. R. Meteorol. Soc. 2018, 144, 1191–1217. [Google Scholar] [CrossRef]
- Barlakas, V.; Galligani, V.S.; Geer, A.J.; Eriksson, P. On the accuracy of RTTOV-SCATT for radiative transfer at all-sky microwave and submillimeter frequencies. J. Quant. Spectrosc. Radiat. Transf. 2022, 283, 108137. [Google Scholar] [CrossRef]
- Qin, Z.; Zou, X.; Weng, F. Evaluating Added Benefits of Assimilating GOES Imager Radiance Data in GSI for Coastal QPFs. Mon. Weather Rev. 2013, 141, 75–92. [Google Scholar] [CrossRef]
- Zou, X.; Qin, Z.; Weng, F. Impacts from assimilation of one data stream of AMSU-A and MHS radiances on quantitative precipitation forecasts. Q. J. R. Meteorol. Soc. 2017, 143, 731–743. [Google Scholar] [CrossRef]
- Geer, A.; Bauer, P. Observation errors in all-sky assimilation. Q. J. R. Meteorol. Soc. 2011, 137, 2024–2037. [Google Scholar] [CrossRef]
- Weng, F.; Zou, X.; Qin, Z. Uncertainty of AMSU-A derived temperature trends in relationship with clouds and precipitation over ocean. Clim. Dyn. 2014, 43, 1439–1448. [Google Scholar] [CrossRef]
- Ackerman, S.A.; Strabala, K.I.; Menzel, W.P.; Frey, R.A.; Moeller, C.C.; Gumley, L.E. Discriminating clear sky from clouds with MODIS. J. Geophys. Res. 1998, 103, 32141–32157. [Google Scholar] [CrossRef]
- Ackerman, S.A.; Holz, R.E.; Frey, R.; Eloranta, E.W.; Maddux, B.C.; McGill, M. Cloud Detection with MODIS. Part II: Validation. J. Atmos. Ocean. Technol. 2008, 25, 1073–1086. [Google Scholar] [CrossRef]
- Derrien, M.; Le Gleau, H. MSG/SEVIRI cloud mask and type from SAFNWC. Int. J. Remote Sens. 2005, 26, 4707–4732. [Google Scholar] [CrossRef]
- Ricciardelli, E.; Romano, F.; Cuomo, V. Physical and statistical approaches for cloud identification using meteosat second generation-spinning enhanced visible and infrared imager data. Remote Sens. Environ. 2008, 112, 2741–2760. [Google Scholar] [CrossRef]
- Saponaro, G.; Kolmonen, P.; Karhunen, J.; Tamminen, J.; de Leeuw, G. A neural network algorithm for cloud fraction estimation using NASA-Aura OMI VIS radiance measurements. Atmos. Meas. Technol. 2013, 6, 2301–2309. [Google Scholar] [CrossRef]
- Jeppesen, J.H.; Jacobsen, R.H.; Inceoglu, F.; Toftegaard, T.S. A cloud detection algorithm for satellite imagery based on deep learning. Remote Sens. Environ. 2019, 229, 247–259. [Google Scholar] [CrossRef]
- Sun, L.; Yang, X.; Jia, S.; Jia, C.; Wang, Q.; Liu, X.; Wei, J.; Zhou, X. Satellite data cloud detection using deep learning supported by hyperspectral data. Int. J. Remote Sens. 2020, 41, 1349–1371. [Google Scholar] [CrossRef]
- Schroder, M.; Bennartz, R.; Schuller, L.; Preusker, R.; Albert, P.; Fischer, J. Generating cloudmasks in spatial high-resolution observations of clouds using texture and radiance information. Int. J. Remote Sens. 2002, 23, 4247–4261. [Google Scholar] [CrossRef]
- English, S.J.; Renshaw, R.J.; Dibben, P.C.; Eyre, J.R. The AAPP module for identifying precipitation, ice cloud, liquid water and surface type on the AMSU-A grid. In Proceedings of the 9th International TOVS Study Conference, Igls, Austria, 20–26 February 1997; pp. 20–26. [Google Scholar]
- Geer, A.J.; Bauer, P.; English, S.J. Assimilating AMSU-A Temperature Sounding Channels in the Presence of Cloud and Precipitation; European Centre for Medium-Range Weather Forecasts: Reaing, UK, 2012. [Google Scholar]
- Lawrence, H.; Bormann, N.; Lu, Q.; Geer, A.; English, S. An Evaluation of FY-3C MWHS-2 at ECMWF, EUMETSAT/ECMWF Fellowship Programme Research Report, 2015, Volume 37. Available online: https://www.ecmwf.int/node/10668 (accessed on 18 February 2023).
- Weston, P.; Geer, A.J.; Bormann, N. Investigations into the Assimilation of AMSU-A in the Presence of Cloud and Precipitation; EUMETSAT/ECMWF Technical Report 2019; European Centre for Medium-Range Weather Forecasts: Reading, UK; Volume 50, p. 42. [CrossRef]
- Qin, Z.; Zou, X. Development and initial assessment of a new land indexfor microwave humidity sounder cloud detection. J. Meteorol. Res. 2016, 30, 12–37. [Google Scholar] [CrossRef]
- Aires, F.; Marquisseau, F.; Prigent, C.; Sèze, G. A Land and Ocean Microwave Cloud Classification Algorithm Derived from AMSU-A and -B, Trained Using MSG-SEVIRI Infrared and Visible Observations. Mon. Weather Rev. 2011, 139, 2347–2366. [Google Scholar] [CrossRef]
- Lindskog, M.; Dybbroe, A.; Randriamampianina, R. Use of Microwave Radiances from Metop-C and Fengyun-3 C/D Satellites for a Northern European Limited-area Data Assimilation System. Adv. Atmos. Sci. 2021, 38, 1415–1428. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, E.; Mahajan, R.; Thomas, C.; Groff, D.; Van Delst, P.; Collard, A.; Kleist, D.; Treadon, R.; Derber, J.C. All-Sky Microwave Radiance Assimilation in NCEP’s GSI Analysis System. Mon. Weather Rev. 2016, 144, 4709–4735. [Google Scholar] [CrossRef]
- Derber, J.C.; Wu, W.S. The use of TOVS Cloud-Cleared Radiances in the NCEP SSI Analysis System. Mon. Weather Rev. 1998, 126, 2287–2299. [Google Scholar] [CrossRef]
- Wu, Z.; Li, J.; Qin, Z. Development and Evaluation of a New Method for AMSU-A Cloud Detection over Land. Remote Sens. 2021, 13, 3646. [Google Scholar] [CrossRef]
- Wu, J.; Qin, Z.; Li, J.; Wu, Z. Development and Evaluation of AMSU-A Cloud Detection over the Tibetan Plateau. Remote Sens. 2022, 14, 2116. [Google Scholar] [CrossRef]
- Qin, Z.; Wu, Z.; Li, J. Impact of the One-Stream Cloud Detection Method on the Assimilation of AMSU-A Data in GRAPES. Remote Sens. 2020, 12, 3842. [Google Scholar] [CrossRef]
- Hutchison, K.D.; Roskovensky, J.K.; Jackson, J.M.; Heidinger, A.K.; Kopp, T.J.; Pavolonis, M.J.; Frey, R.R. Automated cloud detection and classification of data collected by the Visible Infrared Imager Radiometer Suite (VIIRS). Int. J. Remote Sens. 2005, 26, 4681–4706. [Google Scholar] [CrossRef]
- Han, H.J.; Li, J.; Goldberg, M.; Wang, P.; Li, J.; Li, Z.; Sohn, B.-J.; Li, J. Microwave sounder cloud detection using a collocated high-resolution imager and its impact on radiance assimilation in tropical cyclone forecasts. Mon. Weather Rev. 2016, 144, 3937–3959. [Google Scholar] [CrossRef]
- Muth, C.; Webb, W.A.; Atwood, W.; Lee, P. Advanced technology microwave sounder on the national polar-orbiting operational environmental satellite system. In Proceedings of the IEEE International Conference on Geoscience and Remote Sensing Symposium, Seoul, Republic of Korea, 29 July 2005; pp. 99–102. [Google Scholar] [CrossRef]
- Buehler, S.A.; Kuvatov, M.; Sreerekha, T.R.; John, V.O.; Rydberg, B.; Eriksson, P.; Notholt, J. A cloud filtering method for microwave upper tropospheric humidity measurements. Atmos. Chem. Phys. 2007, 7, 5531–5542. [Google Scholar] [CrossRef]
- Yaping, Z.; Jianwen, L.; Zhoujie, C. Detection of deep convective clouds using AMSU-B and GOES-9 data. In Proceedings of the China-Japan Joint Microwave Conference, Shanghai, China, 10–12 September 2008; pp. 278–281. [Google Scholar] [CrossRef]
- Hong, G.; Heygster, G.; Miao, J.; Kunzi, K. Detection of tropicaldeep convective clouds from AMSU-B water vapor channels measurements. J. Geophys. Res. 2005, 110, D05205. [Google Scholar] [CrossRef]
- Greenwald, T.J.; Christopher, S. Effect of Cold Clouds on Satellite Measurements Near 183 GHz. J. Geophys. Res. 2002, 107, 4170. [Google Scholar] [CrossRef]
- Werner, F.; Livesey, N.J.; Schwartz, M.J.; Read, W.G.; Santee, M.L.; Wind, G. Improved cloud detection for the Aura Microwave Limb Sounder (MLS): Training an artificial neural network on colocated MLS and Aqua MODIS data. Atmos. Meas. Technol. 2021, 14, 7749–7773. [Google Scholar] [CrossRef]
- Chen, N.; Li, W.; Gatebe, C.; Tanikawa, T.; Hori, M.; Shimada, R.; Aoki, T.; Stamnes, K. New neural network cloud mask algorithm based on radiative transfer simulations. Remote Sens. Environ. 2018, 219, 62–71. [Google Scholar] [CrossRef]
- Heidinger, A.K.; Evan, A.; Foster, M.; Walther, A. A naive bayesian cloud-detection scheme derived from CALIPSO and applied within PATMOS-X. J. Appl. Meteorol. Climatol. 2012, 51, 1129–1144. [Google Scholar] [CrossRef]
- Karlsson, K.-G.; Johansson, E.; Devasthale, A. Advancing the uncertainty characterisation of cloud masking in passive satellite imagery: Probabilistic formulations for NOAA AVHRR data. Remote Sens. Environ. 2015, 158, 126–139. [Google Scholar] [CrossRef]
- Thampi, B.V.; Wong, T.; Lukashin, C.; Loeb, N.G. Determination of CERES TOA fluxes using machine learning algorithms. Part I: Classification and retrieval of CERES cloudy and clear scenes. J. Atmos. Ocean. Technol. 2017, 34, 2329–2345. [Google Scholar] [CrossRef]
- Zhang, C.W.; Zhuge, X.; Yu, F. Development of a high spatiotemporal resolution cloud-type classification approach using Himawari-8 and CloudSat. Int. J. Remote Sens. 2019, 40, 6464–6481. [Google Scholar] [CrossRef]
- Wang, C.; Platnick, S.; Meyer, K.; Zhang, Z.; Zhou, Y. A machine-learning-based cloud detection and thermodynamic-phase classification algorithm using passive spectral observations. Atmos. Meas. Technol. 2020, 13, 2257–2277. [Google Scholar] [CrossRef]
- Ishida, H.; Oishi, Y.; Morita, K.; Moriwaki, K.; Nakajima, T.Y. Development of a support vector machine based cloud detection method for MODIS with the adjustability to various conditions. Remote Sens. Environ. 2018, 205, 390–407. [Google Scholar] [CrossRef]
- Hughes, M.J.; Hayes, D.J. Automated detection of cloud and cloud shadow in single-date Landsat imagery using neural networks and spatial post-processing. Remote Sens. 2014, 6, 4907–4926. [Google Scholar] [CrossRef]
- Kox, S.; Bugliaro, L.; Ostler, A. Retrieval of cirrus cloud optical thickness and top altitude from geostationary remote sensing. Atmos. Meas. Technol. 2014, 7, 3233–3246. [Google Scholar] [CrossRef]
- Strandgren, J.; Bugliaro, L.; Sehnke, F.; Schröder, L. Cirrus cloud retrieval with MSG/SEVIRI using artificial neural networks. Atmos. Meas. Technol. 2017, 10, 3547–3573. [Google Scholar] [CrossRef]
- Atkinson, N.; Bormann, N.; Karbou, F.; Randriamampianina, R.; Simmer, C. Micro Wave Sounder (MWS) Science Plan EUMETSAT, Eumetsat Allee 1, 64295 Darmstadt (Germany). Available online: https://www.eumetsat.int/media/43204 (accessed on 23 June 2022).
- Lee, Y.-K.; Liu, Q.; Grassotti, C.; Liang, X.; Zhou, Y.; Fang, M. Preliminary Development and Testing of an EPS-SG Microwave Sounder Proxy Data Generator Using the NOAA Microwave Integrated Retrieval System. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3151–3161. [Google Scholar] [CrossRef]
- Ferraro, R.R.; Weng, F.; Grody, N.C.; Zhao, L.; Meng, H.; Kongoli, C.; Pellegrino, P.; Qiu, S.; Dean, C. NOAA Operational Hydrological Products Derived from the Advanced Microwave Sounding Unit. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1036–1049. [Google Scholar] [CrossRef]
- Weng, F.; LZhao, L.; Ferraro, R.R.; Poe, G.; Li, X.; Grody, N.C. Advanced microwave sounding unit cloud and precipitation algorithms. Radio Sci. 2003, 38, 8068. [Google Scholar] [CrossRef]
- Liu, G.; Seo, E.-K. Detecting snowfall over land by satellite high-frequency microwave observations: The lack of scattering signature and a statistical approach. J. Geophys. Res. Atmos. 2013, 118, 1376–1387. [Google Scholar] [CrossRef]
- Weng, F.; Grody, N.C. Retrieval of ice cloud parameters using a microwave imaging radiometer. J. Atmos. Sci. 2000, 57, 1069–1081. [Google Scholar] [CrossRef]
- Heidinger, A.; Walther, A.; Botambekov, D.; Straka, W.; Wanzong, S. The Clouds from AVHRR Extended User’s Guide. Available online: https://cimss.ssec.wisc.edu/clavr/clavr_page_files/clavrx_users_guide_v5.4.1.pdf (accessed on 30 November 2022).
- Saunders, R.; Hocking, J.; Turner, E.; Rayer, P.; Rundle, D.; Brunel, P.; Vidot, J.; Roquet, P.; Matricardi, M.; Geer, A.; et al. An update on the RTTOV fast radiative transfer model (currently at version 12). Geosci. Model Dev. 2018, 11, 2717–2737. [Google Scholar] [CrossRef]
- Geer, A.J.; Bauer, P.; Lonitz, K.; Barlakas, V.; Eriksson, P.; Mendrok, J.; Doherty, A.; Hocking, J.; Chambon, P. Bulk hydrometeor optical properties for microwave and sub-mm radiative transfer in RTTOV-SCATT v13.0. Geosci. Model Dev. Discuss. 2021, 1–45. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Wang, D.; Prigent, C.; Kilic, L.; Fox, S.; Harlow, C.; Jimenez, C.; Aires, F.; Grassotti, C.; Karbou, F. Surface Emissivity at Microwaves to Millimeter Waves over Polar Regions: Parameterization and Evaluation with Aircraft Experiments. J. Atmos. Ocean. Technol. 2017, 34, 1039–1059. [Google Scholar] [CrossRef]
- Liu, Q.; Weng, F.; Stephen JEnglish, S.J. An Improved Fast Microwave Water Emissivity Model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1238–1250. [Google Scholar] [CrossRef]
- Eriksson, P.; Ekelund, R.; Mendrok, J.; Brath, M.; Lemke, O.; Buehler, S.A. A general database of hydrometeor single scattering properties at microwave and sub-millimetre wavelengths. Earth Syst. Sci. Data 2018, 10, 1301–1326. [Google Scholar] [CrossRef]
- Geer, A.J.; Bauer, P.; O’Dell, C.W. A revised cloud overlap scheme for fast microwave radiative transfer in rain and cloud. J. Appl. Meteorol. Clim. 2009, 48, 2257–2270. [Google Scholar] [CrossRef]
- Geer, A.; Bormann, N.; Lonitz, K.; Weston, P.; Forbes, R.; English, S. Recent Progress in All-Sky Radiance Assimilation, ECMWF Newsletter No.161, Autumn 2019. Available online: https://www.ecmwf.int/en/newsletter/161/meteorology/recent-progress-all-sky-radiance-assimilation (accessed on 26 January 2022).
- Harris, B.A.; Kelly, G. A satellite radiance-bias correction scheme for data assimilation. Q. J. R. Meteorol. Soc. 2001, 127, 1453–1468. [Google Scholar] [CrossRef]
- Kallner, A. Formulas. In Laboratory Statistics, 2nd ed.; Kallner, A., Ed.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 1–140. ISBN 978-0-12-814348-3. [Google Scholar]
- Bradley, A. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997, 30, 1145–1159. [Google Scholar] [CrossRef]
- Jurman, G.; Riccadonna, S.; Furlanello, C. A comparison of MCC and CEN error measures in multi-class prediction. PLoS ONE 2012, 7, 41882. [Google Scholar] [CrossRef]
- Thrampoulidis, C.; Oymak, S.; Soltanolkotabi, M. Theoretical Insights into Multiclass Classification: A High-dimensional Asymptotic View. arXiv 2020, arXiv:abs/2011.07729. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Agarap, A.F. Deep learning using rectified linear units (relu). arXiv 2018, arXiv:1803.08375. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization.CoRR. arXiv 2015, arXiv:abs/1412.6980. [Google Scholar]
- Hancock, J.T.; Khoshgoftaar, T.M. Survey on categorical data for neural networks. J. Big Data 2020, 7, 28. [Google Scholar] [CrossRef]
- Russell, G. Congalton, A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Sun, H.; Wolf, W.; King, T.; Barnet, C.; Goldberg, M. Co-Location algorithms for satellite observations. In Proceedings of the 14th Conference on Satellite Meteorology and Oceanography, Atlanta, GA, USA, 27 January–3 February 2006. [Google Scholar]
- Li, C.; Mao, J.; Lau, A.K.; Yuan, Z.; Wang, M.; Liu, X. Application of MODIS satellite products to the air pollution research in Beijing. Sci. China Ser. D Earth Sci. 2005, 48, 209–219. [Google Scholar]
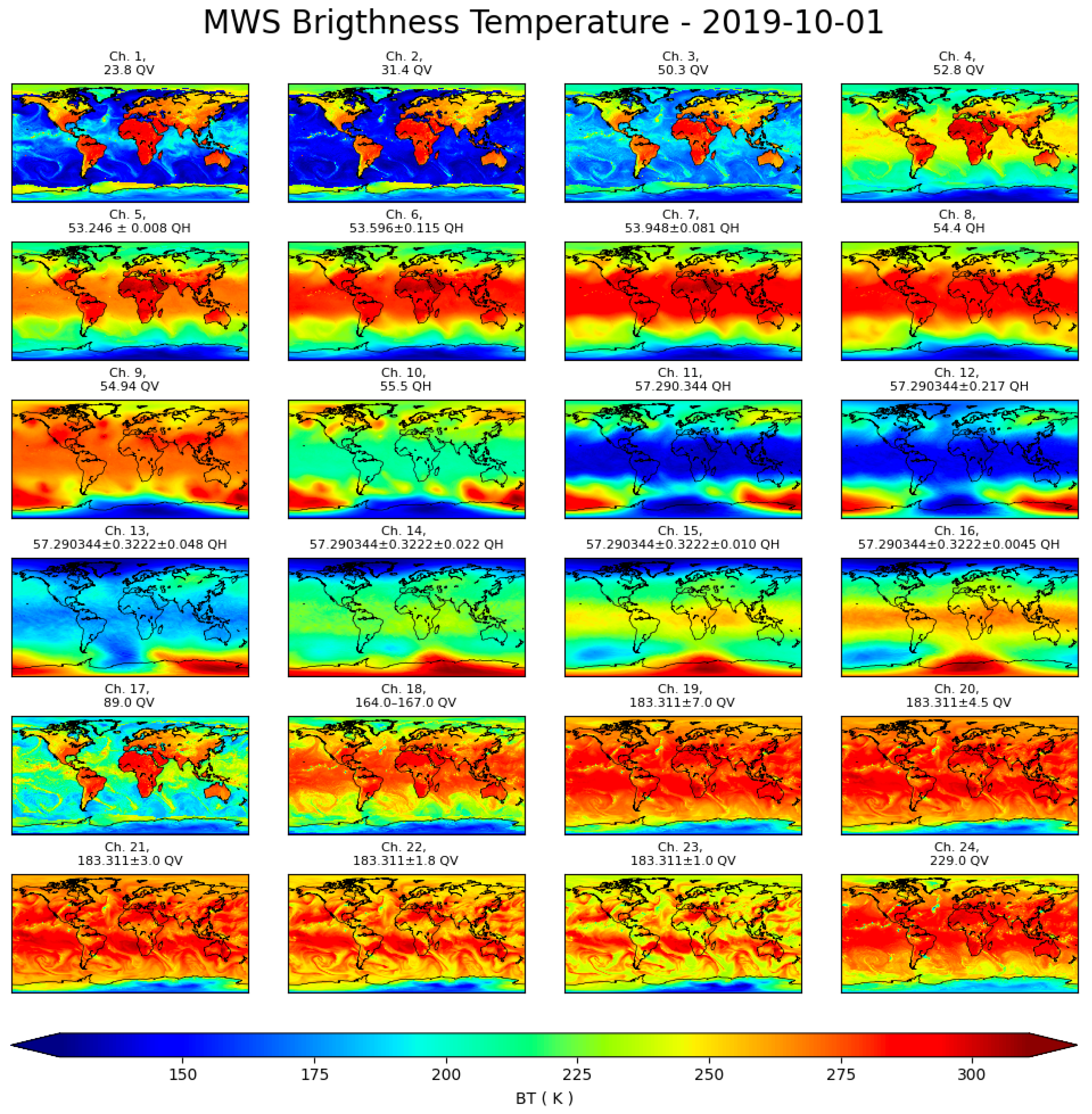






| Channel | Frequency (GHz) | Noise Equivalent (K) | Polarization | Resolution at Nadir (km) |
|---|---|---|---|---|
| 1 | 23.8 | 0.25 | QV | 40 |
| 2 | 31.4 | 0.35 | QV | 40 |
| 3 | 50.3 | 0.50 | QV | 20 |
| 4 | 52.8 | 0.35 | QV | 20 |
| 5 | 53.246 ± 0.008 | 0.40 | QH | 20 |
| 6 | 53.596 ± 0.115 | 0.40 | QH | 20 |
| 7 | 53.948 ± 0.081 | 0.40 | QH | 20 |
| 8 | 54.4 | 0.35 | QH | 20 |
| 9 | 54.94 | 0.35 | QV | 20 |
| 10 | 55.5 | 0.40 | QH | 20 |
| 11 | 57.290344 | 0.40 | QH | 20 |
| 12 | 57.290344 ± 0.217 | 0.55 | QH | 20 |
| 13 | 57.290344 ± 0.3222 ± 0.048 | 0.60 | QH | 20 |
| 14 | 57.290344 ± 0.3222 ± 0.022 | 0.90 | QH | 20 |
| 15 | 57.290344 ± 0.3222 ± 0.010 | 1.20 | QH | 20 |
| 16 | 57.290344 ± 0.3222 ± 0.0045 | 2.00 | QH | 20 |
| 17 | 89.0 | 0.25 | QV | 17 |
| 18 | 164.0–167.0 | 0.50 | QV | 17 |
| 19 | 183.311 ± 7.0 | 0.40 | QV | 17 |
| 20 | 183.311 ± 4.5 | 0.40 | QV | 17 |
| 21 | 183.311 ± 3.0 | 0.60 | QV | 17 |
| 22 | 183.311 ± 1.8 | 0.60 | QV | 17 |
| 23 | 183.311 ± 1.0 | 0.75 | QV | 17 |
| 24 | 229.0 | 0.70 | QV | 17 |
| Channel | Frequency (GHz) | Noise Equivalent (K) | Polarization | Resolution at Nadir (km) |
|---|---|---|---|---|
| AMSU-A | ||||
| 1 | 23.8 | 0.30 | QV | 48 |
| 2 | 31.4 | 0.30 | QV | 48 |
| 3 | 50.3 | 0.40 | QV | 48 |
| 4 | 52.8 | 0.25 | QV | 48 |
| 5 | 53.596 ± 0.115 | 0.25 | QH | 48 |
| 6 | 54.4 | 0.25 | QH | 48 |
| 7 | 54.94 | 0.25 | QV | 48 |
| 8 | 55.5 | 0.25 | QH | 48 |
| 9 | 57.290 | 0.25 | QH | 48 |
| 10 | 57.290 ± 0.217 | 0.40 | QH | 48 |
| 11 | 57.290 ± 0.3222 ± 0.048 | 0.40 | QH | 48 |
| 12 | 57.290 ± 0.3222 ± 0.022 | 0.60 | QH | 48 |
| 13 | 57.290 ± 0.3222 ± 0.010 | 0.80 | QH | 48 |
| 14 | 57.290 ± 0.3222 ± 0.0045 | 1.20 | QH | 48 |
| 15 | 89.0 | 0.50 | QV | 48 |
| MHS | ||||
| 1 | 89.0 | 0.22 | QV | 16 |
| 2 | 157.0 | 0.34 | QV | 16 |
| 3 | 183.311 ± 1.00 | 0.51 | QH | 16 |
| 4 | 183.311 ± 3.00 | 0.40 | QH | 16 |
| 5 | 190.311 | 0.46 | QV | 16 |
| Ocean (N: 184,657) | Land (N: 134,382) | |||||
|---|---|---|---|---|---|---|
| Jaccard index | 77.84% | 76.96% | ||||
| MCC | 81.39% | 80.56% | ||||
| F-beta score | 87.18% | 86.82% | ||||
| Accuracy | 92% | 87% | ||||
| Classes | Clear (35,549) | Ice (15,466) | Liquid (133,642) | Clear (49,250) | Ice (34,438) | Liquid (50,694) |
| Precision | 0.83 | 0.86 | 0.95 | 0.84 | 0.89 | 0.88 |
| Recall | 0.79 | 0.84 | 0.96 | 0.78 | 0.88 | 0.94 |
| F1 score | 0.81 | 0.85 | 0.96 | 0.81 | 0.89 | 0.91 |
| ROC (AUC) | 0.88 | 0.91 | 0.92 | 0.85 | 0.91 | 0.94 |
| Ocean (N: 184,657) | Land (N: 134,382) | |||||
|---|---|---|---|---|---|---|
| Jaccard index | 78.24% | 74.19% | ||||
| MCC | 81.42% | 77.45% | ||||
| F-beta score | 87.71% | 85.11% | ||||
| Accuracy | 88% | 85% | ||||
| Classes | Clear (35,549) | Ice (15,466) | Liquid (133,642) | Clear (49,250) | Ice (34,438) | Liquid (50,694) |
| Precision | 0.85 | 0.91 | 0.87 | 0.81 | 0.84 | 0.91 |
| Recall | 0.82 | 0.88 | 0.93 | 0.82 | 0.86 | 0.87 |
| F1 score | 0.83 | 0.89 | 0.90 | 0.82 | 0.85 | 0.89 |
| ROC (AUC) | 0.87 | 0.92 | 0.93 | 0.86 | 0.90 | 0.91 |
| Orbit Number | Start Datetime |
|---|---|
| 19375 | 1 August 2022 18:58:23 |
| 18066 | 1 May 2022 15:40:19 |
| 18935 | 1 July 2022 19:40:19 |
| 17634 | 1 April 2022 05:58:23 |
| 19370 | 1 August 2022 10:37:19 |
| 18926 | 1 July 2022 04:31:24 |
| 19369 | 1 August 2022 08:55:19 |
| 17638 | 1 April 2022 12:43:19 |
| Ocean (N: 9333) | Land (N: 4135) | |||||
|---|---|---|---|---|---|---|
| Jaccard index | 56.64% | 46.54% | ||||
| MCC | 60% | 46.84% | ||||
| F-beta score | 74.2% | 68% | ||||
| Accuracy | 72% | 67% | ||||
| Classes | Clear (2729) | Ice (2658) | Liquid (3946) | Clear (1267) | Ice (1710) | Liquid (1138) |
| Precision | 0.64 | 0.77 | 0.84 | 0.75 | 0.71 | 0.52 |
| Recall | 0.94 | 0.55 | 0.81 | 0.49 | 0.69 | 0.74 |
| F1 score | 0.76 | 0.64 | 0.73 | 0.59 | 0.70 | 0.61 |
| ROC (AUC) | 0.83 | 0.74 | 0.79 | 0.71 | 0.75 | 0.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Larosa, S.; Cimini, D.; Gallucci, D.; Di Paola, F.; Nilo, S.T.; Ricciardelli, E.; Ripepi, E.; Romano, F. A Cloud Detection Neural Network Approach for the Next Generation Microwave Sounder Aboard EPS MetOp-SG A1. Remote Sens. 2023, 15, 1798. https://doi.org/10.3390/rs15071798
Larosa S, Cimini D, Gallucci D, Di Paola F, Nilo ST, Ricciardelli E, Ripepi E, Romano F. A Cloud Detection Neural Network Approach for the Next Generation Microwave Sounder Aboard EPS MetOp-SG A1. Remote Sensing. 2023; 15(7):1798. https://doi.org/10.3390/rs15071798
Chicago/Turabian StyleLarosa, Salvatore, Domenico Cimini, Donatello Gallucci, Francesco Di Paola, Saverio Teodosio Nilo, Elisabetta Ricciardelli, Ermann Ripepi, and Filomena Romano. 2023. "A Cloud Detection Neural Network Approach for the Next Generation Microwave Sounder Aboard EPS MetOp-SG A1" Remote Sensing 15, no. 7: 1798. https://doi.org/10.3390/rs15071798
APA StyleLarosa, S., Cimini, D., Gallucci, D., Di Paola, F., Nilo, S. T., Ricciardelli, E., Ripepi, E., & Romano, F. (2023). A Cloud Detection Neural Network Approach for the Next Generation Microwave Sounder Aboard EPS MetOp-SG A1. Remote Sensing, 15(7), 1798. https://doi.org/10.3390/rs15071798