A Distributed Approach for Time-Dependent Observation Scheduling Problem in the Agile Earth Observation Satellite Constellation

Abstract

The increasing number of agile earth observation satellites (AEOSs) in orbit have advanced maneuverable capabilities, enabling the AEOS constellation to provide richer observation services. Therefore, observation scheduling in the AEOS constellation is crucial for improving the performance of satellite remote sensing systems. This paper focuses on the problem of distributed observation scheduling in the AEOS constellation, where a period of transition time is required between two consecutive observations, and this constraint depends on the start time of observations. We define a new fitness function that not only maximizes the profit sum but also considers system load balancing. Based on the fundamental idea of a distributed performance impact (PI) algorithm, we develop a PI-based distributed scheduling method (PIDSM) that runs concurrently on all AEOSs via local inter-satellite link (ISL)-based communications. The PIDSM iterates between two phases: target inclusion and consensus and target removal. The first phase aims to select the optimal task for each AEOS, while the second phase reaches a consensus over all AEOSs and removes targets that may decrease overall fitness. Experimental results demonstrate that the PIDSM can schedule more targets, reduce communication overhead, and achieve higher fitness values than existing algorithms. Sensitivity analyses further validate the effectiveness of the PIDSM.

1. Introduction

Earth observation satellites (EOSs) aim to collect images of ground targets using remote sensing cameras. Since EOSs have the advantages of a high resolution and large areas of coverage, they have been applied to the domains of resource exploration, disaster alteration, and climate analysis in the past 20 years [1,2]. The number of orbiting EOSs is continuously increasing and a group of EOSs share the same orbital planes so as to constitute a constellation. Therefore, the observation scheduling in constellation is important for the satellite remote sensing systems.

The conventional EOS (CEOS) can move only in the roll axis, while the Agile EOS (AEOS) can adjust the attitude in three axes (roll, pitch, and yaw). Thus, AEOSs have better maneuverability than CEOSs. Moreover, the differences in observations for CEOSs and AEOSs are shown in Figure 1. We can see that a CEOS observes a target within an observation time window (OTW), which is identical to its corresponding visible time window (VTW). In this way, the observation scheduling of CEOSs is equivalent to the VTW selection problem [3]. By contrast, since an AEOS can look forward and back along the pitch axis, the VTW for the AEOS is usually longer than the corresponding OTW. Consequently, AEOSs can observe more targets than CEOSs during a time interval, but the complexity of the AEOS schedule problem is increased greatly compared with that of the CEOS. In addition, the increasing satellite number in the AEOS constellation brings significant challenges for scheduling.

The observation task is associated with a profit that indicates the importance and value obtained by completing this task. The objective of scheduling AEOSs is often to maximize the profit sum of scheduled targets, while satisfying all operational constraints. Among them, the transition time constraint requires that there must be enough period of time for an AEOS to rotate the camera when executing two consecutive observations. Generally, such a transition time is time-dependent, since it is determined by the angular variation which is changed over time. The time-dependent transition constraint increases the complexity for scheduling. To simplify the problem, some researchers [4] relate the transition time only with task sequence instead of angular variation. The onboard resource constraints, such as energy and data storage capabilities, are considered [5,6].

There are mainly two scheduling approaches for the AEOS observation schedule: centralized and distributed methods. In the former, a centralized server generates a schedule plan for each AEOS. A few studies [7,8,9] used the exact algorithm to obtain an optimal solution. For example, by introducing a deterministic mixed integer liner programming (MILP) model, Valicka et al. [8] provided the optimality guarantees. Cho et al. [9] obtained the optimal schedule solution using a MILP solver for a constellation of AEOSs. However, due to the complexity of the considered modeling, these exact algorithms are only suitable for solving small instances. To tackle this issue, a number of heuristic and metaheuristic approaches are developed for the AEOS schedule problem [10,11,12,13,14,15,16,17,18,19,20]. Specifically, Nag et al. [10] presented the dynamic programming approach for AEOSs in Cubesat constellations based on MILP modeling. He et al. [11] used an edge computing framework where a central node and several edge nodes are included. Owing to the simplicity and efficiency, various evolutionary algorithms are applied extensively for scheduling AEOSs [3,13,14,15,16,17,18,19,20]. Du et al. [13] used the travelling salesman problem to model the AEOS scheduling problem and propose a kind of ant colony optimization. Cui et al. [14] aimed to maximize the profit sum but minimize the total task transition time in the emergence of AEOS scheduling. To obtain high-quality scheduling solutions quickly, some scholars have employed reinforcement learning methods [21,22,23,24,25]. He et al. [21] proposed a general reinforcement learning-based approach that can efficiently handle unknown data and generate good solutions in a short time. Wei et al. [22] addressed the multi-objective AEOS scheduling problem. Wang et al. [23] proposed neural networks with an ‘encoder–decoder’ structure that significantly reduce the inference time. Zhao et al. [24] presented a two-phase neural combinatorial optimization method with reinforcement learning for AEOS scheduling. Chen et al. [25] proposed a non-iterative heuristic construction neural network method, which demonstrated excellent performance. On the other hand, a series of articles addressed the time-dependent transition time constraint of AEOS scheduling. Liu et al. [26] presented an adaptive large neighborhood search algorithm for scheduling an observation task for a single AEOS. The proposed method in [26] was extended to cases with multiple AEOSs [27]. Peng et al. [28,29] presented the concept of minimal transition time and based on this idea, an effective local search algorithm was developed.

Most of the centralized schedule plans are generated on the ground and are uploaded to the satellite, thus neglecting dynamic and unpredictable events, such as the arrival of new task or the required change of users. To overcome those problems, the onboard distributed AEOS scheduling approaches have received increasing attention [30]. In a distributed framework, an AEOS creates a local schedule after exchanging information with neighbor satellites via inter-satellite links (ISLs). Then, the global schedule result can be obtained by integrating all these local schedules using coordination and communication mechanisms. Specifically, Philliops and Parra [31] proposed a market-based method to allocate observation tasks to a set of satellites, though the satellites were managed by different mission centers. Si-wei et al. [32] proposed an extended contract net protocol (ECNP) to solve dynamic task assignments for multiple satellites. Li et al. [30] developed an online schedule for distributed AEOS systems according to the idea of the well-known consensus-based bundle algorithm (CBBA). Herein, CBBA selects tasks using the auction approach and the conflict is resolved by the consensus procedure [33]. Conflict-free assignment can be achieved in the CBBA by iterating between the bundle construction phase and the conflict resolution phase. The performance impact (PI) algorithm is another important distributed task allocation approach [34,35]. It aims to directly optimize the overall objective using the same two-phase architecture as the CBBA by introducing a key concept called the significance of a task to measure its contribution to the global objective value. In other words, the PI algorithm considers not only the cost of a task assignment but also the impact of that assignment on the overall objective. Compared with the CBBA, the PI can solve more time-critical task allocation problems and find a task assignment with a lower time cost.

Although the time-dependent transition time constraint is important for realistic AEOS observation scheduling, there is no distributed scheduling method taking it into consideration. On the other hand, as far as we know, implementation of the PI algorithm for AEOS observation scheduling has not been reported. Inspired by these points, this paper intends to propose a PI-based distributed scheduling method (PIDSM) for solving the problem of time-dependent observation scheduling in the AEOS constellation. To facilitate our understanding, we propose a mathematical model of the considered problem. The global fitness (or objective) function is designed to not only maximize the profit sum but also account for system load balancing. Moreover, we compute the non-conflict VTWs for each non-scheduled target to guarantee that each AEOS can observe one target at a time. The main contributions of this paper are twofold:

(1) We are the first to apply the decentralized PI framework for solving the AEOS observation schedule problem with time-dependent transition constraints. The proposed PIDSM is concurrently run on all AEOSs via ISL-based local communications. It iterates between two phases, namely, target inclusion and consensus and target removal. The first phase aims to select the optimal task for each AEOS. The second reaches consensus based on the significance value across all AEOSs, and then removes the targets that may decrease the overall fitness.

(2) Compared with other distribution algorithms, i.e., CBBA [30], CNP [36], and ECNP [32], our PIDSM can successfully schedule more targets with less communication overhead and higher global fitness values. Moreover, the sensitivity analysis demonstrates that variations in the number, distribution density, and observation time of targets have minimal impact on the performance of the PIDSM.

The rest of this paper is organized as follows. Section 2 illustrates the studied problem and presents the corresponding mathematical model. Section 3 proposes heuristics methods to compute the global fitness value of a solution. Section 4 proposes a PIDSM consisting of two phases. Experiments are conducted in Section 5 and we discuss the whole algorithm in Section 6. This paper is concluded in Section 7.

2. Problem Description and Modelling

In this section, we introduce the observing schedule problem in the AEOS constellation and propose the corresponding mathematical model. As shown in Figure 2, the AEOS constellation consists of Z_o adjacent orbital planes with Z_s satellites in each orbital plane, i.e., it contains N_s = Z_o × Z_s satellites. Each AEOS in the constellation is connected to four adjacent satellites through ISLs, two of which are the closest in the same orbital plane, and two are the closest in adjacent orbital planes. Although all satellites move at high speed, their ISL-based connections always exist. For example, as illustrated in Figure 2, AEOS s₅ connects not only s₂ and s₈ (in the same plane), but also the closest hetero-orbiting satellites s₄ and s₆. In this paper, AEOS s is called a neighbor of c if it is connected by an ISL.

A group of AEOSs in the constellation, denoted by S = {s₁, s₂,…, s_m}, m ≤ N_s, is equipped with cameras to observe a set of ground spot targets denoted by G = {g₁, g₂,…, g_n}. The geographic positions, observation times d_g, and profits ϕ_g for each target g ∈ G are given by users in advance. We use an m × m matrix H to describe the ISL connections among AEOSs, where H[s, c] = 1 represents that satellites s and c can exchange messages via ISL, and otherwise H[s, c] = 0. Some useful notations are summarized in

Table 1. Notations.

S	Set of involved AEOSs
G	Set of ground target
H	Matrix to describe the ISLs connections among AEOSs
R	Set of orbits during the scheduling horizon
s	Satellite index
g	Target index
dg	Observation duration of target g
ϕg	Profit of target g
Wsgk = [stsgk, etsgk]	Visible time window of satellite s and target g during orbit k ∈ R
Ψsg(t) = <γsg[t], πsg[t], ψsg[t]>	Look angle of s on three axes in time t
Wsg = {Wsgk|k ∈ R}	Set of VTWs for AEOS s and target g
as = <gs1, gs2,…., gs|as|>	Target sequence assigned for satellite s
Γs	Observable targets of as for satellite s
a	Candidate schedule solution
tg	Start-observing time of target g
transA(tg, th)	Transition time between observation targets tg and th
F(as)	Partial fitness value for satellite s
ϒ(a)	Global fitness value for solution a
qsi(as⊖g)	Significance represents the variation of F(as) after removing g from as
qc*(ac⊕g)	Marginal significance represents the maximal variation of F(as) after adding g into as
Zs	Information stored in satellite s keeps the target assignment
Qs	Information stored in satellite s records the significance values of all targets
Us	Timestamp list for satellite s

.

During the scheduling horizon, an AEOS s may circle the earth several times and a target can be observed by s in different orbits. Herein, an orbit is referred to the time period that the satellite flies through the sunshine area while circling the Earth one time. Let R be the set of all orbits of AEOSs in S. According to the satellite movement parameters and camera parameters, in an orbit k ∈ R, a target g ∈ G is visible for a satellite s ∈ S during a visible time window (VTW) denoted by W_sg^k = [st_sg^k, et_sg^k], where st_sg^k (respectively, et_sg^k) is the start (respectively, end) time. Moreover, for each time t ∈ W_sg^k, the look angle of s on three axes (roll, pitch, and yaw) is provided as Ψ_sg(t) = <γ_sg[t], π_sg[t], ψ_sg[t]>. All VTWs of AEOS s regarded with target g can be denoted by W_sg = {W_sg^k|k ∈ R}. Note that each target g can be observed at most once by one satellite during one VTW of {W_sg|s ∈ S}.

Owing to the finite camera resources and visible constraints, only a set of targets can be observed in the specific horizon. The AEOS observation schedule aims to assign targets for different AEOSs in S such that the objective function is somehow optimized while satisfying the VTW limitations and transition time constraints. Firstly, based on the work [29], we make certain assumptions to simplify the scheduling problem.

Assumption: 

(1) Each satellite has enough onboard power and memory in every orbit, and hence, we do not consider the power and memory constraints; (2) each target is a spot one, which can be observed by AEOS with one pass; (3) we focus on the semiagile satellite AS-01 whose look angles are unchanged when observing a target.

We intend to schedule a target sequence a_s = <g_s1, g_s2,…., g_s|as|> for each AEOS s ∈ S such that targets in a_s are observed sequentially by s. All these target allocations constitute a candidate solution a = [a₁, a₂,…, a_m] for the AEOS constellation observing schedule.

For target g ∈ a_s, let t_g be the time that s begins to observe g within the VTW W_sg^k = [st_sg^k, et_sg^k] in an orbit k ∈ R, and the end time of observation is t_g + d_g. The following VTW condition must be satisfied:

$$t_g\ge s{t}_{sg}^k$$

(1)

$$t_g+d_g\le e{t}_{sg}^k$$

(2)

Note that there may be cases where an AEOS s cannot observe a task g in a_s due to conflicting VTMs (see Section 3.1). For completeness, we assume the start-observing or start time of this assigned but unobserved target is 0, i.e., t_g = 0. Then, let Γ_s ⊆ a_s be the sequence of observable targets by s (Γ_s can be obtained by Algorithm CGF in Section 3.3).

Based on the characteristics of AS-01 satellite [29], the look angle of AEOS s should be adjusted as Ψ_sg(t_g) before observing target g at the time t_g, and this angle remains unchanged during the subsequent observation. Therefore, if AEOS s intends to observe two consecutive targets g and h in the same orbit, a transition time denoted as trans(t_g, t_h) is required between the observation of g and h. In other words, the following transition time constraint must be satisfied:

$$t_g+d_g+trans(t_g,t_h)\le t_h$$

(3)

The transition time trans(t_g, t_h) is calculated based on Δ = |γ_sg[t_g] − γ_sh[t_h]| + |π_sg[t_g] − π_sh[t_h]| + |ψ_sg[t_g] − ψ_sh[t_h]|, which is the total look angle change of transition movement associated with g and h.

$$trans(t_g,t_h)=\left\{\begin{array}{cc}transA(\Delta ),& \mathrm{if} g \mathrm{and} h \mathrm{are} \mathrm{in} \mathrm{the} \mathrm{same} \mathrm{orbit}\\ \hfill 0,& \mathrm{otherwise}\end{array}\right.$$

(4)

where transA(Δ) is the following piecewise linear function [29]:

$$transA(\Delta )=\left\{\begin{array}{c}11.66,\Delta \le 10\\ 5+\frac{\Delta }{1.5},10<\Delta \le 30\\ 10+\frac{\Delta }{2},30<\Delta \le 60\\ 16+\frac{\Delta }{2.5},60<\Delta \le 90\\ 22+\frac{\Delta }{3},90<\Delta \end{array}\right.$$

(5)

The look angle of an AEOS during VTW varies over time, as it is influenced by the satellite parameters and the relative positions of the satellite and target. Thus, according to (4) and (5), the transition time trans(t_g, t_h) is dependent on time, and hence the AEOS observation schedule considered in this paper is time-dependent.

Given a target allocation a_s for AEOS s, we define the (partial) fitness value F(a_s) as follows:

$$F(a_s)={\displaystyle {\sum }_{g\in {\Gamma }_s}{\varphi }_g-\frac{1}{{\mathrm{e}}^{\tau }}-\frac{{\displaystyle {\sum }_{g\in {\Gamma }_s}{d}_g}}{\mathrm{Ave}(s)\times \left|{\Gamma }_s\right|}}$$

(6)

where Γ_s collects all observable targets in a_s, and τ = 1/(|Γ_s| + 1), |Γ_s| is the number of targets in Γ_s, and Ave(s) = Σ_k∈RΣ_g∈G(et_sg^k − st_sg^k)/n is the average sum of VTM length for each satellite. The proposed fitness Function (6) considers three factors: task execution benefits, satellite task load, and satellite observation capabilities towards the targets.

Clearly, the higher the profit sum of the observable targets, the bigger the fitness value F(a_s). To enforce the system load balance, when two satellites observe the same set of targets, the one with the longer average VTW is assigned a higher fitness value according to equation (6). The global fitness value for the solution a = [a₁, a₂,…, a_m] is defined as ϒ(a) = Σ_s∈SF(a_s).

Let x_skg be the decision variable such that x_skg = 1 if target g is observed by AEOS s in the orbit k ∈ R and x_skg = 0 otherwise. Another variable y_skgh = 1 if satellite s selects target h after observing g in the orbit k, and y_skgh = 0 otherwise. In addition, let l_sk and e_sk be the dummy source and sink targets in orbit k associated with s, respectively. It is assumed that the observations of s in orbit k is start from l_sk but end with e_sk.

The mathematical model of the observation scheduling of the AEOS constellation can be expressed as follows:

$$J=\mathrm{Max}\hspace{0.33em}{\displaystyle {\sum }_{s\in S}\{{\displaystyle {\sum }_{k\in R}{\displaystyle {\sum }_{g\in G}\{x_{skg}{\varphi }_g-\frac{x_{skg}{d}_g}{\mathrm{Ave}(s)}\}-\frac{1}{e^{{\displaystyle {\sum }_{k\in R}{\displaystyle {\sum }_{g\in G}{x}_{skg}}+1}}}\}}}}$$

(7)

$$\mathrm{s}.\mathrm{t}. {\displaystyle {\sum }_{s\in S}{\displaystyle {\sum }_{k\in R}{x}_{skg}\le 1,\forall g\in G}}$$

(8)

$${\displaystyle {\sum }_{h\in G\cup \left\{e_{sk}\right\}\backslash \left\{g\right\}}{y}_{skgh}}={\displaystyle {\sum }_{h\in G\cup \left\{l_{sk}\right\}\backslash \left\{g\right\}}{y}_{skhg}}=x_{skg},\forall s\in S,\forall k\in R,\forall g\in G$$

(9)

$${\displaystyle {\sum }_{g\in G\cup \left\{l_{sk}\right\}}{y}_{skg{e}_{sk}}}={\displaystyle {\sum }_{g\in G\cup \left\{e_{sk}\right\}}{y}_{sk{l}_{k}g}}=1,\forall s\in S,\forall k\in R$$

(10)

$$s{t}_{sg}^k\ast x_{skg}\hspace{0.33em}\le t_g,\forall s\in S,\forall k\in R,\forall g\in G$$

(11)

$$t_g+d_g\le e{t}_{sg}^k+K(1-x_{skg}),\forall s\in S,\forall k\in R,\forall g\in G$$

(12)

$$\hspace{0.33em}{t}_g+d_g+trans(t_g,\hspace{0.33em}{t}_h)-\hspace{0.33em}{t}_h\le K(1-y_{skgh}),\forall s\in S,\forall k\in R,\forall g\in G$$

(13)

$$x_{skg}\in \{0, 1\},\hspace{0.33em}{y}_{skgh}\in \{0, 1\},\forall s\in S,\forall k\in R,\forall g,h\in G$$

(14)

$$t_g\ge 0,\forall g\in G$$

(15)

where K is an integer that is large enough. Equation (7) implies that the objective function is to maximize the global fitness value. Equation (8) implies that each target is observed at most once. Equations (9) and (10) together imply that each scheduled task (including the dummy source and sink ones) has a predecessor and a successor task in the assigned orbit. Equations (11) and (12) are the VTW constraints that each scheduled observation must satisfy. Equation (13) is the time-dependent transition time constraint. Equations (14) and (15) state the domains of involved variables.

3. Heuristics Method to Calculate the Global Fitness of a Solution

This section computes the global fitness value ϒ(a) of a schedule solution a = [a₁, a₂, …, a_m]. First, after a set of targets are observed by an AEOS s ∈ S, and we obtain the no-conflict VTMs that are visible for a new target. Then, by using these no-conflict VTMs, we further compute the start time of each observed target in the sequence a_s.

3.1. Computation of Non-Conflict VTWs

We denote a_s = <g_s1, g_s2, …, g_s|as|> for convenience and assume that at some time point, AEOS s has tried to observe a set of targets b_s = <g_s1, g_s2,…, g_u>, where u < |a_s|, and the start-observing time of each target in b_s is known (owing to the conflicts of VTWs, the start time of some target in bs may be zero.). For a new target h ∈ a_s\b_s, its VTWs set W_sh may be overlapped with the scheduled duration {[t_g′, t_g′ + d_g′] | g′ ∈ b_s and t_g′ ≠ 0}, resulting in a VTW conflict. For example, consider b_s = {g₁} and target g₂. As illustrated in Figure 3, there are four possible situations regarding the overlap between the scheduled duration [t_g1, t_g1 + d_g1] and a VTW W_sg2^k = [ϖ, φ] ∈ W_sg2. Especially, note that in Figure 3c, the VTW [ϖ, φ] becomes infeasible for g₂ because s observes g₁ during that time interval.

Since AEOS s can observe, at most, one target at a time, at least one non-conflict VTW is required before observing a new target. Motivated by the analysis in Figure 3, we develop Algorithm 1, namely compute non-conflict VTWs (CNV), to compute a non-conflict VTW for a new target h ∉ b_s.

Algorithm 1: Compute non-conflict VTWs (CNV).

Input: AEOS s, observed target sequence bs, tg (∀g∈bs), h ∉ bs, and Wsh; Output: The non-conflict VTW set Vsh(bs); Let Ω = Wsh; for each g ∈ bs    for each VTW [ϖ, φ] ∈ Ω      if tg ≤ ϖ, tg + dg < ϕ and tg + dg > ϖ //see Figure 3a         Set ϖ = tg + dg;      else if tg > ϖ, tg + dg ≥ ϕ and tg < ϕ //see Figure 3b         Set ϕ = tg;       else if tg ≤ ϖ and tg + dg > ϕ //see Figure 3c           Delete [ϖ, φ] from Ω;      else if tg > ϖ and tg + dg < φ          //see Figure 3d          Divide [ϖ, φ] into two segments [ϖ, tg] and [tg + dg, φ];      end    end end for each [ϖ, φ] ∈ Ω    if ϕ − ϖ < dh      Delete [ϖ, ϕ] from Ω;    end End Output Vsh(bs) = Ω;

In Algorithm CNV, we begin by setting Ω = W_sh. For each visited target g ∈ b_s, we “prune” the overlapped part between every VTW [ϖ, φ] ∈ Ω and the time interval [t_g, t_g + d_g], based on four different situations illustrated by Figure 3 (Lines 2~14). Next, in Lines 15~19, we delete the VTWs from Ω that have a length shorter than d_h and finally output the non-conflict VTWs V_sh(b_s) = Ω.

3.2. Computation of the Start Time of Observation

According to Algorithm CNV, given the start time t_gu of the last target g_u in b_s and a target h ∉ a_s\b_s, the feasible non-conflict VTWs V_sh(b_s) can be obtained. Based on the idea of dichotomy, we develop Algorithm 2, namely compute start-observing time (CST), to compute the start time t_h of the observation for h such that the VTW Constraints (11) and (12), as well as the transition time Constraint (13), are satisfied.

Algorithm 2: Compute start-observing time (CST).

Input: AEOS s, tgu, h ∈ as\bs, and Vsh(bs); Output: th; Let Flag = False and th = 0; for each VTW [ϖ, φ] ∈ Vsh(bs)   if trans(tgu, −φ − dh) + tgu + dgu ≤ −φ − dh     Set x = −φ − dh, y = ϖ;     Set x′ = (x + y)/2;     Set Flag = True;     break;   end end while(Flag)   if trans(tgu, x′) + tgu + dgu ≤ x′     x = x′;     x′ = (x′ + y)/2;   else     y = x′;     x′ = (x + y)/2;   end   if–x − x′ ≤ 0.1;     break;   end end if Flag = True    Set th = x; end Output th;

In Algorithm CST, the Boolean variable Flag = True represents that we can find the start time t_h within one non-conflict VTW in V_sh(b_s) while satisfying the Constraints (11)–(13). Initially, we set Flagalsease and t_h = 0. This algorithm first tries to find a VTW [ϖ, φ] ∈ V_sh(b_s) so that

trans(t_gu, −φ − d_h) + t_gu + d_gu ≤ −φ − d_h

Satisfying the above inequity implies that the VTW and transition-time constraint are met if we set t_h = −φ − d_h. In this case, let Flag = True and we execute a loop (Lines 10~21) to further find a sufficiently small number x ∈ [ϖ, −φ − d_h] which satisfies the constraint trans(t_gu, x) + t_gu + d_gu ≤ x based on the dichotomy theory. Finally, if Flag = True, let t_h = x, otherwise t_h = 0.

3.3. Computation of Global Fitness Value

Based on the proposed Algorithms CNV and CST, we can calculate the partial fitness F(a_s) as well as the global fitness ϒ(a) by Algorithm 3 which is called compute global fitness (CGF).

Algorithm 3: Compute global fitness (CGF).

Input: A candidate solution a = [a1, a2,…, am]; Output: the global fitness value ϒ(a); for eachs ∈ S    Denote as = <g1, g2, …, g|as|>;    tg1 = min{sts, g1k, k ∈ R};    Set Γs = {g1};    Set gl = g1;    Set i = 2;    while(i ≤ |as|)       g′ = gi;       According to Algorithm CNV, obtain non-conflict VTW set Vsg′(Γs);       Let V1 = {[ϖ, φ] ∈ Vsg′(Γs)|ϖ ≥ tgl + dgl };       Let s, gl, g′, and V1 be the inputs of Algorithm CST, obtain tg′;       if tg′ > 0         Γs := Γs ∪ {g′};         gl = g′;       end       i = i + 1;    end    F(as) = Σg∈Γsϕg − 1/eτ − (Σg∈Γsdg)/Ave(s), where τ = 1/(|Γs| + 1); End Output ϒ(a) = Σs∈SF(as);    F(as) = Σg∈Γsϕg − 1/eτ− (Σg∈Γsdg)/Ave(s), where τ = 1/(|Γs| + 1); End Output ϒ(a) = Σs∈SF(as);

In Algorithm CGF, for each AEOS s, we use Γ_sto collect all observable targets in a_s and initially set Γ_s = {g₁} and t_g1 = min_k∈R{st_{s, g1}^k}. Then, a loop (Lines 7~19) is executed to compute the start time for the observation of remaining targets in a_s, where g_l ∈ Γ_s is the current target and g′ is the target to be analyzed. In particular, each iteration can be divided into the following steps:

Step 1: We use Algorithm CNV to obtain the non-conflict VTW set V_sg′(Γ_s) of g′ under the known observations of targets in Γ_s.

Step 2: Let V₁ = {[ϖ, φ] ∈ V_sg′(Γ_s)|ϖ ≥ t_gl + d_gl} be the feasible VTWs in V_sg′(Γ_s) which begins after the observation of g_l, and we further use Algorithm CST to obtain the start-observing time t_g′ of g′.

Step 3: If t_g′ > 0, we add g′ into Γ_s and update g_l = g′, otherwise if t_g′ = 0, it indicates that g′ cannot be observed by s and we continue analyzing the next target.

After all targets in a_s have been analyzed, we compute the partial fitness F(a_s) according to (6), and the global fitness value ϒ(a) = Σ_s∈SF(a_s) is finally outputted.

4. Distribution Method for Observation Scheduling in the AEOS Constellation

Based on the decentralized PI algorithm, this section proposes a PIDSM for solving the problem of time-dependent observation tasks in the AEOS constellation. Such an algorithm can be deployed and executed concurrently in all AEOSs. By exchanging information with the neighbor satellites through ISLs, each AEOS s ∈ S iteratively adds or removes some targets in or from its currently ordered sequence such that the global fitness is somehow optimized, while the constraints defined in Section II are met.

4.1. The Decentralized Framework of PI

We start by introducing the “significance value” (respectively, the “marginal significance value”) of a target with regard to the assigned (resp. non-assigned) satellite in the PI framework.

(1) Significance: Assume g ∈ a_s, the significance value q_si(a_s$\ominus$g) represents the variation of F(a_s) after removing g from a_s, it can be formulated as follows:

$$q_s({\mathbf{a}}_s\ominus g)=F({\mathbf{a}}_s)-F({\mathbf{a}}_s\ominus g)$$

(16)

where a_s$\ominus$g is the sequence after removing g from a_s. For completeness, we set q_s(a_s$\ominus$g) = 0 for g ∉ a_s.

(2) Marginal significance: Assume g ∉ a_s, the marginal significance q_c*(a_c⊕g) represents the maximal variation of F(a_s) and after adding g into a_s, it can be formulated as follows:

$$q_s^{\ast }({\mathbf{a}}_s\oplus g)=\underset{k\in \{1,2,\dots ,|a_s|+1\}}{\max }\{F({\mathbf{a}}_s{\oplus }_{k}g)-F({\mathbf{a}}_s)\}$$

(17)

where a_s⊕_k g is the target sequence after inserting g into the k-th position of a_s. If g ∈ a_s, let q_s*(a_s⊕g) toward minus infinity, i.e., q_s*(a_c⊕g) → −∞.

The basic idea of PI framework is as follows [34]: each AEOS s transmits the significance value q_s(a_s$\ominus$g) of target g ∈ a_s to its neighbor satellite c through ISLs. Then, satellite c compares the received q_s(a_s$\ominus$g) with the marginal significance value q_c*(a_c⊕g) computed based on its sequence a_c. If the criterion in (18) is satisfied (see Proposition 1 later), target g is deleted from a_s but added into some proper position of a_c such that the global fitness value ϒ(a) is increased. Similarly, the significance of target g is further transmitted to other satellites and this value is continuously updated. The above process is repeated until (18) is no longer satisfied or ϒ(a) cannot be increased by exchanging targets between satellites. Note that the convergence of PI algorithm is naturally guaranteed since the global fitness ϒ(a) is increased whenever the target assignment is changed.

To facilitate the understanding of the PI procedure, the following conclusion reveals how global fitness is increased by exchanging targets between satellites.

Proposition 1.

Given the global fitness value ϒ(a) of a solution a, two AEOSs s and c with H(s, c) = 1, and a target g ∈ a_s\a_c. Then, if (18) is satisfied, the global fitness value would be increased after removing g from a_s but inserting it into the proper position of a_c.

$$q_c^{\ast }({\mathbf{a}}_c\oplus g)>q_s({\mathbf{a}}_s\ominus g)$$

(18)

Proof: 

Let p_c = argmax_{k ∈{1,2,..|ac|+1}}{F(a_c⊕_kg) − F(a_c)}. Suppose we remove g from a_s and add it into the p_c-th position of a_c, resulting in a new solution denoted as a′. By (16) and (17), we can calculate the fitness of a′ as ϒ(a′) = ϒ(a) + q_c*(a_c⊕g) − q_s(a_s$\ominus$g). Therefore, the inequality ϒ(a′) > ϒ(a) holds and the global fitness value increases only when q_c*(_c⊕g) > q_s(_s$\ominus$ g). □

Specifically, we use F_s and F_c to denote the partial fitness value of s and c, respectively. According to whether q_c*(a_c⊕g) and q_s(a_s⊖g) is greater or less than zero, there are four cases:

Case 1. q_s(a_s$\ominus$g) < 0 and q_c*(a_c⊕g) > 0. Naturally (18) holds, then F_s and F_c are both increased. In this way, the global fitness value ϒ(a′) is increased.

Case 2. q_s(a_s$\ominus$g) ≥ 0 and q_c*(a_c⊕g) > 0. Then, the satisfaction of (18) implies that the reduction of F_s is less that the increase of F_c. Hence, ϒ(a′) is increased.

Case 3. q_s(a_s$\ominus$g) ≥ 0 and q_c*(a_c⊕g) ≤ 0. Then, (18) never holds.

Case 4. q_s(a_s$\ominus$g) < 0 and q_c*(a_c⊕g) ≤ 0. Then, we have |q_c*(a_c⊕g)| < |q_s(a_s$\ominus$g)|. That means, the increase of F_s is greater than the decrease of F_c, and hence ϒ(a′) is increased correspondingly.

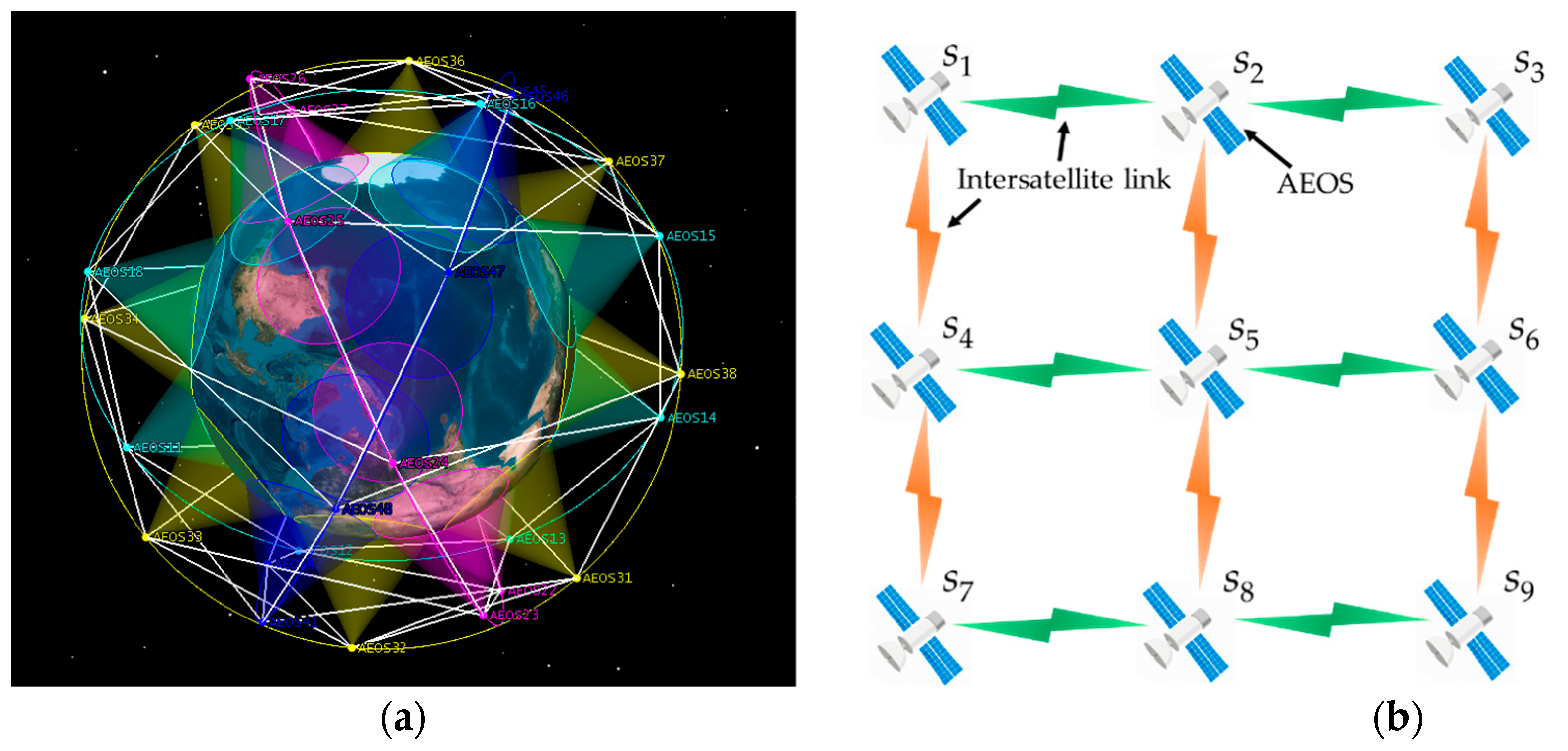
The significance value of a target can be broadcasted among AEOSs by using ISLs. According to Proposition 1, based on the received significance value, an AEOS can determine whether to remove or insert a target from or into its current target sequence so as to increase the global fitness value. However, the sparse ISL communication topology makes it difficult to deliver a target’s significance value to all satellites, leading to the possibility of the system getting trapped in a local optimum [34]. For example, consider a set of AEOSs S = {s₁, s₂, s₃} and four targets G = {g₁, g₂, g₃, g₄}. There are ISLs between s₁ and s₂ as well as between s₂ and s₃. As illustrated in Figure 4, the current schedule solution is a₁ = {g₁}, a₂ = {g₂, g₃}, and a₃ = {g₄}. We now assume that i) q_s2*(a_s2⊕g₁) ≤ q_s1(a_s1$\ominus$g₁), and ii) the global fitness will be increased if target g₁ is removed from a₁ to a₃. However, since q_s2*(a_s2⊕g₁) ≤ q_s1(a_s1$\ominus$g₁), g₁ cannot be added into a_s2 by Proposition 1, and further g₁ cannot be added into a_s3, leading to a local optimum.

To deliver the target significance value to all satellites, PI algorithm framework introduces three message lists Z_s, Q_s, and u_s stored on each satellite s, which are defined as follows:

Z_s = [Z_s1, Z_s2, …, Z_sn]^T is a vector that keeps track of which target is assigned to which satellite. The entry Z_sg = c implies that s thinks that target g is scheduled to satellite c, and if s deems g to be unassigned, Z_sg towards infinity, i.e., Z_sg → ∞.

Q_s = [Q_s1, Q_s2, …, Q_sn]^T is a vector recording the significance values of all targets. If Z_sg → ∞, we set Q_sg → ∞.

u_s = [u_s1, u_s2…, u_sm]^T is a vector where the entry u_sc records the time when (s thinks that) satellite c has received the latest message from other satellites. Once a message is passed, the timestamp u_sc is updated as follows:

$$u_{sc}=\left\{\begin{array}{ll}{\mathsf{\tau }}_r,& \mathrm{if} H(s,c)=1\\ \underset{h\in S:H(s,h)=1}{\max }{u}_{hc},& \hfill otherwise\end{array}\right.$$

(19)

where τ_r is the time that s receives the message from c. Apparently, if c is the neighbor of s, or H[s, c] = 1, we have u_sc = τ_r; otherwise, u_sc is equal to maximal timestamp u_hc where H[s, h] = 1.

The timestamp list u_s records the latest message exchange time, and the lists Q_s and Z_s together represent a schedule solution. These three lists can be continuously updated through local communication with other satellites. In particular, suppose Z_sg = c ∈ S. Then, AEOS s believes that at least at time u_sc, target g is scheduled to satellite c and the significance value of g with regard to c is Q_sg. Initially, we set a_s = ∅, Z_sg → ∞, and Q_sg = 0 for each AEOS s and every target g.

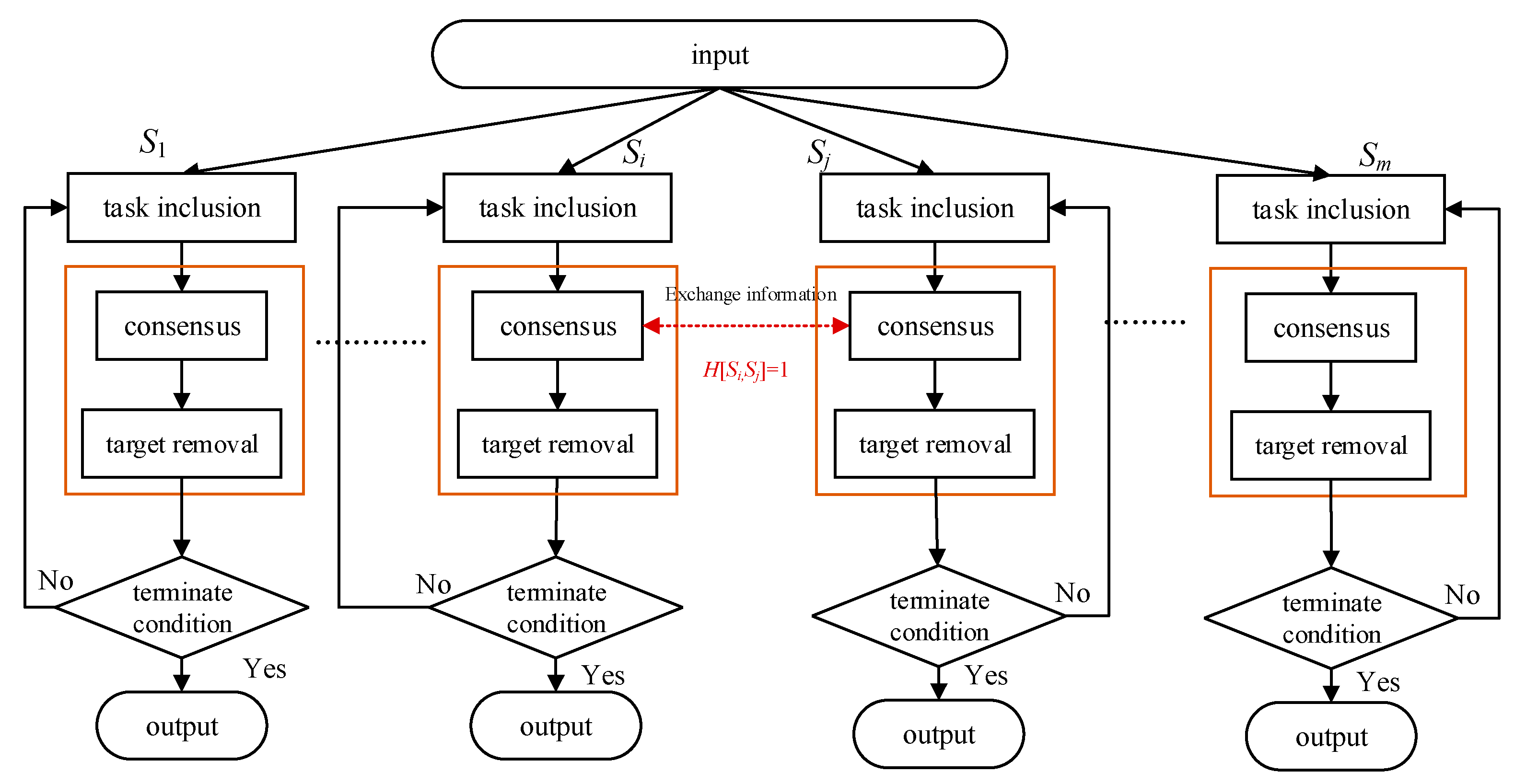
Generally, as shown in Figure 5, the decentralized PI framework contains two phases: target inclusion and consensus and target removal; they are both running concurrently on each satellite. Specifically, the task inclusion phase determines whether to add a target to its current target sequence, and different significance values may result for a specific target at the end of this phase. Thus, the second phase is required, which has two parts: (i) consensus, where a consensus significance value list is reached among all satellites, and (ii) task removal, where each satellite removes the problematic targets from its current sequence. Note that only the consensus part exchanges messages among satellites using ISLs, but the other procedures are performed independently. The above two phases are executed iteratively. When no change can be made to the obtained sequences for a period of time, the PI algorithm running on each satellite ends.

Generally, as shown in Figure 5, the decentralized PI framework contains two phases: target inclusion and consensus and target removal; they are both running concurrently on each satellite. Specifically, the task inclusion phase determines whether to add a target to its current target sequence, and different significance values may result for a specific target at the end of this phase. Thus, the second phase is required, which has two parts: (i) consensus, where a consensus significance value list is reached among all satellites, and (ii) task removal, where each satellite removes the problematic targets from its current sequence. Note that only the consensus part exchanges messages among satellites using ISLs, but the other procedures are performed independently. The above two phases are executed iteratively. When no change can be made to the obtained sequences for a period of time, the PI algorithm running on each satellite ends.

4.2. Target Inclusion Phase

In this phase, each AEOS s adds some target g ∈ G\a_s into its sequence a_s by comparing Q_sg with g’s marginal significance q_s*(a_s⊕g) computed based on its sequence a_s. Specifically, we first determine whether the following Inequality (20) is satisfied or not.

$$\underset{g\in G}{\max }\{q_s^{*}({\mathbf{a}}_s\oplus \mathrm{g})-Q_{sg}\}>0$$

(20)

If (20) holds, we select target g′ = argmax_g∈G{q_s*(a_s⊕g) − Q_sg} whose removal leads to the maximum increase in ϒ(a) and let p_f = argmax_{p∈{1, 2,.., |as|+1}}{F(a_s⊕_pg′) − F(a_s)} be the position of a_s to insert. Then, we add g′ into the p_f-position of a_s and update Z_sg′ such that Z_sg′ = s. Meanwhile, we update the marginal significance q_s*(a_s⊕g) for each target g ∈ G\a_s. We repeat the above process until (20) is not met.

At the end of this phase, we update the significance list Q_s by setting Q_sg = q_s(a_s$\ominus$g) for each target g. The whole target inclusion phase can be expressed in the following Algorithm 4.

Algorithm 4: Task inclusion phase running on each satellite.

Input: AEOS s, target sequence as, Qs and Zs; Output: New sequence as, updated lists Qs and Zs; while (1)    for each g ∈ G      Set qs*(as⊕g) = 0;      if g ∈ as         qs*(as⊕g) = −∞;      else         for each p ∈ {1, 2,.., |as|+1}           Compute F(as⊕pg);           if F(as⊕pg) − F(as) > qs*(as⊕g);              Let qs*(as⊕g) = F(as⊕pg) − F(as);           end         end      end    end //compute the marginal significance values of all targets    if maxg∈G{qs*(as⊕g) − Qsg} > 0      Let g′ = argmaxg∈G{qs*(as⊕g) − Qsg};      Let pf = argmaxp∈{1, 2,.., |as|+1}{F(as⊕pg′) − F(as)};      Insert g′ into the pf-position of as;      Let Zsg′ = s;    else      break;    end end Update Qs such that Qsg = qs(as⊖g); Output as, Qs, Zs

4.3. Consensus and Target Removal Phase

Algorithm 4 is executed independently on each satellite, which can lead to a target being allocated to more than one satellite or the significance value of a target being different on different satellites, resulting in conflicts. Thus, the second phase is required to ensure that each target g is scheduled at most once and a consensus significance value for each target is reached among all satellites. This phase includes two steps: consensus and task removal.

Consensus: By (16), the significance value of target g is dependent on the target order of the sequence that g is assigned, thus the strong synergies exist between targets. According to the basic idea of PI algorithm, the significance list is broadcasted among satellites through a series of local ISL-based communication, and the significance value of every target is gradually increased. If we just aim to find the biggest target significance value during communication, the significance of some targets may converge to a nonexisting value (in the sense of not being assigned to any satellite). To avoid such a problem, we use the heuristic rules called winning bids proposed in the work [33] to reach the consensus of the significance list. This method is discussed in detail as follows.

By using ISLs, AEOS s sends the message lists Q_s, Z_s and u_s to its neighbor c with H[s, c] = 1 and receives the corresponding lists Q_c, Z_c, and u_c. Then, s updates the stored messages Z_sg and Q_sg for each target g according to the rules given in Table 2. There are three actions in Table 2 and the default is the Leave action.

• Update: Z_sg = Z_cg, Q_sg = Q_ci;
• Leave: no change made on Z_sg and Q_sg;
• Reset: Z_sg → ∞, Q_sg → 0.

The first two columns of Table 2 record target g’s observers that are believed by the sender c and receiver s, respectively. The third column outlines the action taken on Q_sg and Z_sg with respect to receiver s. Note that once a piece of message is passed, timestamp u_i is updated according to (19) to obtain the latest time information.

Table 2. Consensus rules.

Sender c Thinks Zcg Is	Receiver s Thinks Zsg Is	Receiver’s Action
c	s	if Qcg > Qsg: Update
	c	Update
	k∉{c, s}	if uck > usk or Qcg > Qsg: Update
	none	Update
s	s	Leave
	c	Reset
	k∉{c, s}	if uck > usk: Reset
	none	Leave
k∉{c, s}	s	if uck > usk and Qcg > Qsg: Update
	c	if uck > usk: Update
		otherwise: Reset
	k	if uck > usk: Update
	β∉{c, s, g}	if uck > usk and ucβ > usβ: Update
		if uck > usk and Qcg > Qsg: Update
		if ucβ > usβ and usk > uck: Reset
	none	if uck > usk: Update
none	s	Leave
	c	Update
	k∉{c, s}	if uck > usk: Update
	none	Leave

Table 2. Consensus rules.

Sender c Thinks Zcg Is	Receiver s Thinks Zsg Is	Receiver’s Action
c	s	if Qcg > Qsg: Update
	c	Update
	k∉{c, s}	if uck > usk or Qcg > Qsg: Update
	none	Update
s	s	Leave
	c	Reset
	k∉{c, s}	if uck > usk: Reset
	none	Leave
k∉{c, s}	s	if uck > usk and Qcg > Qsg: Update
	c	if uck > usk: Update
		otherwise: Reset
	k	if uck > usk: Update
	β∉{c, s, g}	if uck > usk and ucβ > usβ: Update
		if uck > usk and Qcg > Qsg: Update
		if ucβ > usβ and usk > uck: Reset
	none	if uck > usk: Update
none	s	Leave
	c	Update
	k∉{c, s}	if uck > usk: Update
	none	Leave

Target removal: Only the local message lists Q_s and Z_s are updated during the above consensus procedure, but the target sequence a_s is not affected. Thus, it is possible that Z_sg ≠ s for some s ∈ S and g ∈ a_s when the consensus is completed. That means that s believes that it does not observe a target which is however included in its sequence a_s Then, the second step, namely, target removal, is needed to remove these problematic targets De = {g ∈ a_s | Z_sg ≠ s} from a_s. The removal criterion is given as follows:

$$\underset{g\in De}{\max }\{Q_{sg}-w_{sg}\}>0$$

(21)

where w_sg = F(a_s) − F(a_s⊖g) is the significance value of target g computed based on the current sequence a_s.

If (21) is satisfied, we remove from a_s and De the target g_k = argmax_g∈De(Q_sg − w_sg) which is associated with the largest objective increase and set Q_sgk = 0. Repeat this process until De becomes empty or (21) is no longer met. Finally, if De ≠ ∅ but (21) is not satisfied, i.e., there are some targets retained in De, we reset the observer of each remaining target g in De as s, i.e., Z_sg = s, and update the significance list Q_sg = w_sg. The consensus and target removal phase can be expressed in Algorithm 5.

Algorithm 5: Consensus and target removal phase running on each satellite.

Input: AEOS s, target sequence as, Qs and Zs; Output: New sequence as, and updated lists Qs and Zs; Send Qs, Zs and us to satellite c with H(s, c) = 1; Receive Qc, Zc and ucfrom c with H(c, h) = 1; According to rules in Table 2 to update Qs, Zs and us; Let De = {g ∈ as|Zsg ≠ s}; while maxg∈De(Qsg − wsg) > 0   gk = argmaxg∈De(Qsg − wsg);   Remove gk from as and De;   Reset Qsgk = 0; end Let Qsg = wsg ∀g ∈ as; if De ≠ ∅ Let Zsg = s, ∀g ∈ De; End Output as, Qs, Zs;

4.4. Convergence Analysis

The proposed PIDSM is essentially working on the iterative optimization principle with each satellite aiming to increase the global fitness at each iteration, and thereby the convergence is guaranteed. In particular, the significance values of all targets are exchanged among satellites via local ISL communication, and the global fitness value is increased by recursively adding/removing a target into/from the target sequence of some satellites according to Proposition 1. Meanwhile, the first phase adds as many targets as possible into the target sequence of a satellite, while the second phase ensures that a consensus significance values list can be reached for all satellites at each iteration. When no changes can be made in the obtained solution after executing the first and second phases for a period of time, the whole algorithm is converged.

Formally, the entire procedure of the PIDSM running on AEOS s is expressed in detail as follows.

Step 1: Running Algorithm 4 to include targets. First, add targets to a_s according to Criterion (20) and update the related information Z_s. When no target can be scheduled to a_s, recalculate Q_sg for each target g in a_i.

Step 2: Sending the information lists Q_s, Z_i, and u_s stored on satellite s to its neighbor c with H[s, c] = 1.

Step 3: Receiving the information lists Q_c, Z_c, and u_c from satellite c with H[s, c] = 1.

Step 4: Conducting the consensus procedure. Based on the received message Q_c, Z_c, and u_c from each neighbor c, update the message Q_s and Z_s stored on satellite s itself.

Step 5: Removing the problematic targets. According to Criterion (21), remove tasks in De = {g ∈ a_s | Z_sg ≠ s} from a_i and De until De = ∅ or that criterion is not satisfied. Then, update Q_s and place each remaining target g in De back in a_s by setting Z_sg = s.

Step 6: Repeat steps 1–7 until no further changes are made to the scheduled solution for a specified period of time.

5. Simulation Results

A series of experiments are conducted in this section to evaluate the performance of the proposed PIDSM scheduling approach.

5.1. Experimental Setup

As shown in

Table 3. Satellite constellations used in the simulation.

Constellation	Altitude (km)	Inclination (deg)	Planes	Satellites
A	6000	60	2	6
B	5000	53.8	3	9
C	3000	60	4	16
D	2800	70	4	20
E	2500	65	4	32
F	2000	60	5	40

, we develop six Walker Delta constellations A–F with different orbital elements. A number of targets are generated randomly around the world according to two distributions: low and high density. The average distances between targets are around 10 km and 100 km in the high-density and low-density cases, respectively. Moreover, the observation time for each target is generated randomly between the long-term [200 s, 300 s] or short-term [40 s, 60 s], while the profit of each target takes a random integer value from 1 to 10.

We assume that the scenario begins from the time of [1 October 2022 00:00:00UTCG] and the horizon is set as 6 h. The VTWs between satellites and targets as well as the look angle on the three axes can be obtained directly from the software STK. The experiments are conducted on three types of texting instances: small, medium, and large, as shown in

Table 4. Parameter size for each instance type.

Instance Type	Constellations	Task Number	Distribution Density	Observation Time	Combination Number
small	A, B	3, 5	low, high	long-term, short-term	2 × 2 × 2 × 2 = 16
medium	C, D	30, 50	low, high	long-term, short-term	2 × 2 × 2 × 2 = 16
large	E, F	100, 200	low, high	long-term, short-term	2 × 2 × 2 × 2 = 16

. There are 3 × 16 = 48 combinations in total and we generate 10 texting cases for each combination.

We compare the proposed PI-based distribute schedule approach, namely the PIDSM, with the existing algorithms, and the performance metrics are defined as follows:

• δ: The average proportion of successfully assigned targets;
• φ: The average communication times, which implies the communication burden between satellites;
• The relative percentage value (RPV):

RPV = ϒ_a/ϒ_best

(22)

where ϒ_a is the fitness of an algorithm for a test instance, and ϒ_best is the best fitness value obtained by all algorithms for the same instance.

To reduce randomness, each algorithm is independently run 10 times for each testing instance, then δ, φ, best RPV (bRPV), and average RPV (aRPV) are used to evaluate each algorithm. All algorithms are coded in MATLAB 2021a and run on a PC with an Intel Core i9-9900K CPU @3.60 GHz and 32 GB of RAM in the 64-bit Windows 10 operating system.

5.2. Comparison with State-of-the-Art Distribute Algorithms

We compare the proposed PIDSM with the existing distribution algorithms CBBA [30], CNP [36], and ECNP [32] based on the performance metrics in Section 5.1. The statistics results of comparison for small-type, medium-type, and large-type instances are shown in

Table 5. The comparison results for small-type instances.

	CBBA				CNP				ECNP				PIDSM
	δ	φ	bRPV	aRPV	δ	φ	bRPV	aRPV	δ	φ	bRPV	aRPV	δ	φ	bRPV	aRPV
{A, 3, high, long}	66.70%	216	0.847	0.847	100%	21	100%	0.983	100%	45	1	0.997	100%	8.7	1	1
{A, 3, high, short}	33.30%	216	0.486	0.486	100%	21	100%	0.971	100%	45	1	0.975	100%	8.9	0.997	0.997
{A, 3, low, long}	66.70%	216	0.847	0.847	100%	21	100%	0.983	100%	45	1	0.994	100%	8	1	1
{A, 3, low, short}	66.70%	216	0.771	0.771	100%	21	100%	0.972	100%	45	1	0.990	100%	8	1	1
{A, 5, high, long}	40%	216	0.492	0.492	88%	35	0.983	0.929	100%	75	1	0.995	100%	7	1	1
{A, 5, high, short}	80%	216	0.854	0.854	86%	35	100%	0.852	98%	75	1	0.982	98%	11.1	1	1
{A, 5, low, long}	60%	216	0.745	0.745	100%	35	0.981	0.971	98%	75	0.981	0.967	98%	7	1	1
{A, 5, low, short}	20%	216	0.429	0.429	100%	35	0.963	0.926	98%	75	1	0.952	98%	7	1	1
{B, 3, high, long}	66.70%	432	0.731	0.731	100%	30	100%	0.917	100%	63.5	1	0.932	100%	8	0.998	0.998
{B, 3, high, short}	66.70%	432	0.783	0.783	100%	30	100%	0.971	100%	63.3	1	0.990	100%	8	0.996	0.996
{B, 3, low, long}	100%	432	1	1	97%	30	100%	0.941	100%	63.4	1	0.982	100%	10.2	1	1
{B, 3, low, short}	33.30%	432	0.478	0.478	90%	30	0.946	0.860	100%	63.3	0.947	0.940	100%	10.2	1	1
{B, 5, high, long}	40%	432	0.492	0.492	100%	50	0.983	0.971	100%	105.5	1	0.992	100%	12	1	1
{B, 5, high, short}	20%	432	0.277	0.277	100%	50	0.979	0.961	100%	105.6	1	0.989	100%	8.9	1	1
{B, 5, low, long}	20%	432	0.239	0.239	94%	50	0.983	0.896	100%	105.6	0.983	0.982	100%	6	1	1
{B, 5, low, short}	20%	432	0.236	0.236	90%	50	0.980	0.851	100%	105.9	0.980	0.975	100%	6	1	1

,

Table 6. The comparison results for medium-type instances.

	CBBA				CNP				ECNP				PIDSM
	δ	φ	bRPV	aRPV	δ	φ	bRPV	aRPV	δ	φ	bRPV	aRPV	δ	φ	bRPV	aRPV
{C, 30, high, long}	0%	512	0	0	85%	300	0.966	0.918	89.7%	645.6	0.996	0.991	90%	39	1	1
{C, 30, high, short}	3.3%	1024	0.053	0.053	83%	300	0.938	0.870	87.3%	645.4	1	0.982	90%	37.2	0.999	0.999
{C, 30, low, long}	0%	512	0	0	100%	300	0.982	0.974	100%	645.7	0.996	0.994	100%	52.4	1	1
{C, 30, low, short}	6.7%	1152	0.101	0.101	99%	300	0.977	0.958	100%	645.7	0.996	0.992	100%	39.8	1	1
{C, 50, high, long}	6%	1024	0.086	0.086	96%	500	0.961	0.934	98.6%	1074.7	0.995	0.988	100%	56.2	1	1
{C, 50, high, short}	12%	1152	0.217	0.217	92%	500	0.949	0.903	97.6%	1077.1	0.992	0.983	99.2%	57	1	0.997
{C, 50, low, long}	16%	1024	0.240	0.240	93%	500	0.971	0.938	95.6%	1075.1	0.987	0.973	98%	66.6	1	0.999
{C, 50, low, short}	6%	1024	0.114	0.114	92%	500	0.960	0.926	95.2%	1075.7	0.981	0.973	96.8%	83.5	1	0.993
{D, 30, high, long}	3.3%	1440	0.043	0.043	100%	300	0.978	0.975	100%	647.4	0.997	0.994	100%	54.8	1	0.999
{D, 30, high, short}	13.3%	1600	0.231	0.231	100%	300	0.981	0.965	100%	649	0.993	0.987	100%	45.4	1	0.997
{D, 30, low, long}	6.7%	1440	0.087	0.087	99%	300	0.982	0.957	100%	648.1	0.996	0.993	100%	38.1	1	0.997
{D, 30, low, short}	13.3%	1280	0.226	0.226	99%	300	0.971	0.947	100%	648.7	0.995	0.991	100%	42.9	1	1
{D, 50, high, long}	34%	1600	0.503	0.503	98%	500	0.986	0.951	100%	1080.5	0.994	0.991	100%	38.7	1	1
{D, 50, high, short}	12%	1600	0.183	0.183	96%	500	0.964	0.947	100%	1078.3	0.992	0.989	100%	81.8	1	0.996
{D, 50, low, long}	6%	1440	0.087	0.087	98%	500	0.976	0.953	100%	1080.6	0.991	0.989	100%	43.5	1	0.999
{D, 50, low, short}	0%	720	0	0	97%	500	0.981	0.935	100%	1079.8	0.993	0.991	100%	78.2	1	0.999

and

Table 7. The comparison results for large-type instances.

	CBBA				CNP				ECNP				PIDSM
	δ	φ	bRPV	aRPV	δ	φ	bRPV	aRPV	δ	φ	bRPV	aRPV	δ	φ	bRPV	aRPV
{E, 100, high, long}	3.0%	3328	0.046	0.046	96%	1000	0.975	0.952	98.8%	2175	0.997	0.994	98.8%	179.6	1	0.998
{E, 100, high, short}	2.0%	3072	0.031	0.031	95%	1000	0.944	0.922	98.8%	2174	0.998	0.994	99.0%	597.4	1	1
{E, 100, low, long}	2.0%	3072	0.030	0.030	95%	1000	0.963	0.944	97.7%	2174	0.996	0.993	98.0%	167.2	1	0.999
{E, 100, low, short}	5.0%	2816	0.085	0.085	94%	1000	0.952	0.928	97.7%	2176	0.995	0.991	97.1%	223.8	1	0.997
{E, 200, high, long}	0.5%	3328	0.008	0.008	97%	2000	0.967	0.950	99.3%	4352	0.995	0.993	99.5%	323.5	1	0.998
{E, 200, high, short}	7.0%	3072	0.118	0.118	95%	2000	0.949	0.929	99.3%	4354	0.996	0.993	99.5%	418.3	1	0.999
{E, 200, low, long}	1.0%	3072	0.016	0.016	92%	2000	0.937	0.918	98.4%	4350	0.995	0.992	98.7%	196.2	1	0.998
{E, 200, low, short}	2.5%	3328	0.041	0.041	89%	2000	0.909	0.866	97.2%	4353	0.989	0.984	98.5%	338.7	1	0.999
{F, 100, high, long}	3.0%	7200	0.047	0.047	94%	1000	0.950	0.934	98.0%	2181	0.993	0.992	98.0%	2477.2	1	0.999
{F, 100, high, short}	1.0%	4480	0.014	0.014	94%	1000	0.943	0.924	98.0%	2180	0.981	0.980	98.2%	6902.3	1	0.988
{F, 100, low, long}	6.0%	4800	0.092	0.092	93%	1000	0.940	0.910	98.9%	2180	0.995	0.991	99.0%	2007.6	1	0.999
{F,100, low, short}	5.0%	6080	0.074	0.074	91%	1000	0.928	0.885	99.0%	2179	0.990	0.988	99.0%	5549.8	1	0.998
{F, 200, high, long}	1.0%	4480	0.016	0.016	92%	2000	0.952	0.929	95.0%	4361	0.990	0.989	95.5%	11096.6	1	0.999
{F, 200, high, short}	1.5%	4480	0.026	0.026	90%	2000	0.946	0.925	94.7%	4359	0.996	0.993	94.6%	8609.3	1	0.996
{F, 200, low, long}	1.5%	4800	0.023	0.023	89%	2000	0.910	0.891	97.7%	4359	0.995	0.990	98.0%	4067.6	1	0.999
{F, 200, low, short}	4.5%	4480	0.072	0.072	88%	2000	0.860	0.838	96.5%	4358	0.955	0.953	97.2%	12125.2	1	0.967

, respectively.

The performance of all algorithms varies markedly in terms of δ, φ, bRPV, and aRPV; the optimal values are given in bold. From Table 5, Table 6 and Table 7, we can conclude the following:

(1) The PIDSM enables the AEOS constellation to successfully observe almost all targets with δ ≥ 95% for each instance. It demonstrates that the proposed PIDSM has outstanding performances in the time-dependent observing schedule problem. Moreover, except in some isolated cases, the ECNP has a similar δ to the PIDSM. The CNP can observe fewer targets than the ECNP and the PIDSM and CBBA obtain the worst δ.

(2) The PIDSM terminates after the least communication times in small-sized and medium-sized instances. In particular, although the ECNP requires marginally more communication times than the CNP for the same instance, the ECNP always obtains a better solution because it uses adaptive bidding with swarm intelligence to improve the solution quality, but the CNP does not. In a small-type (respectively, medium-type) instance, the communication times of the CNP is three (respectively, six) times than of the PIDSM. Moreover, in the large-type instance, the value of φ for the PIDSM increases with the growth of the satellite number. For example, in the F-constellation, the PIDSM’s φ is greater than that of the CNP.

(3) The PIDSM obtains the best aRPV and bRPV in almost all kinds of instances. With significantly higher communication times, the ECNP has a slightly inferior performance. The CNP is worse than both the PIDSM and the ECNP, and exhibits the largest fluctuations. The CBBA performed the worst among all methods.

In summary, compared with other competitors, the PIDSM can observe more targets with the least communication burden in most instances. In addition, the fitness value of the PIDSM is always better than that of the CBBA, CNP, and ECNP.

The variations for each algorithm on different instances are further illustrated in Figure 6. Compared with the CBBA, CNP, and ECNP, the proposed PIDSM exhibits more stability and better performance in solving the time-dependent AEOS constellation observing schedule problem with different scales.

6. Discussion

6.1. Instance Parameters

The instance parameters, such as target number, target distribution density, and target observation time, may affect the performance of various algorithms. This section discusses the sensitivity of these parameters. Since CBBA obtains the worst allocation according to Table 5, Table 6 and Table 7, we only compare the CNP, ECNP, and PIDSM for the sake of clarity, and bRPV is used as the merit.

Table 8. Comparison results of different target numbers.

Target Number	CNP		ECNP		PIDSM
	bRPV	aRPV	bRPV	aRPV	bRPV	aRPV
10	0.9881	0.9740	1	0.9961	0.9995	0.9953
20	0.9774	0.9651	0.9948	0.9932	1	1
50	0.9374	0.9173	0.9885	0.9770	1	0.9832
100	0.9525	0.9280	0.9876	0.9762	1	0.9868
200	0.8601	0.8394	0.9541	0.9369	1	0.9923
500	0.8101	0.8224	0.9541	0.9269	1	0.9866

,

Table 9. Comparison results of different target distribution densities.

Target Distribution Density	CNP		ECNP		PIDSM
	bRPV	aRPV	bRPV	aRPV	bRPV	aRPV
1	0.9367	0.8884	0.9966	0.9866	1	0.9881
5	0.9328	0.8907	0.9868	0.9750	1	0.9947
10	0.9655	0.9244	0.9979	0.9766	1	0.9914
50	0.9024	0.8600	0.9903	0.9711	1	0.9961
100	0.9030	0.8615	0.9822	0.9552	1	0.9816
200	0.9422	0.9186	0.9962	0.9874	1	0.9945
500	0.9492	0.9109	0.9957	0.9862	1	0.9973
1000	0.9412	0.9238	1	0.9936	0.9988	0.9928

and

Table 10. Comparison results of different target observation durations.

Target Observation Duration	CNP		ECNP		PIDSM
	bRPV	aRPV	bRPV	aRPV	bRPV	aRPV
[8, 12]	0.9596	0.9388	0.9959	0.9869	1	0.9988
[40, 60]	0.9707	0.9381	0.9874	0.9732	1	0.9986
[80, 120]	0.9705	0.9374	0.9940	0.9802	1	0.9985
[180, 220]	0.9550	0.9177	0.9853	0.9788	1	0.9905
[480, 520]	0.9422	0.9094	0.9875	0.9796	1	0.9883

show the sensitivity analysis results of the target number, distribution density, and observation time, respectively, on the performance of the algorithms. The optimal values for each instance parameter given in bold.

The impact of target number: We consider six instance combinations whose target number belongs to {10, 20, 50, 100, 200, 500}, but all have a C-constellation, low-density distribution, and long-term observation duration. For each combination, test instances are generated randomly, and the CNP, ECNP, and PIDSM are implemented 10 times independently for each instance to eliminate data randomness. As shown in Table 8, the PIDSM outperforms the CNP and ECNP in almost all instances, and only for the instance with a target number of 10, the ECNP achieves a marginal lead. As shown in Figure 7, when the target number does not exceed 20, all three algorithms achieve the best RPV. As the target number grows gradually, the RPV of the CNP drops more sharply than the ECNP and PIDSM. Compared with the CNP and ECNP, the variation of the target number has the least impact on the performance of the PIDSM. This demonstrates that the PIDSM is more suitable for solving satellite observation schedule problems with a large number of targets.

The impact of target distribution density: We consider eight combinations with 100 targets, a C-constellation, and a long-term observation duration. The target distribution density is represented by the average shortest distances between targets, and the values for these eight combinations are 1 km, 5 km, 10 km, 50 km, 100 km, 200 km, 500 km, and 1000 km, respectively. Similarly, test instances are randomly generated and each algorithm is repeated 10 times. Table 9 shows that the ECNP obtains the best results in the instance with a target density of 1000 km, while the PIDSM achieves the optimal results in all other cases. The variance plot of the comparison results is shown in Figure 8. We can see that the CNP, ECNP, and PIDSM obtain the worst RPVs in the instances with a target density of 50 km, 5 km, and 10 km, respectively. However, after these worst cases, their RPVs improve as the average distances among targets increase. Especially in the case with 500 km density, the CNP, ECNP, and PIDSM all achieve the peak of their RPV. Meanwhile, the fluctuations of the PIDSM are significantly smaller than those of the CNP and ECNP, which verifies the stable performance of the PIDSM.

The impact of target observation duration: We consider six combinations with 50 targets, a C-constellation, and low-density target distribution, but their observation duration ranges between [8 s, 12 s], [40 s, 60 s], [80 s, 120 s], [180 s, 220 s], and [480 s, 520 s], respectively. The experimental instances are still randomly generated, and each algorithm is repeated 10 times for each instance. As shown in Table 10, the PIDSM outperforms the CNP and ECNP in all instances. Moreover, the variance plot in Figure 9 illustrates that the PIDSM achieves its best RPV when the target duration ranges between [8 s, 12 s], [40 s, 60 s], and [80 s, 120 s]. After that, the value of RPV for the PIDSM decreases slightly when the target observation duration becomes large. By contrast, the RPV values of the ECNP and CNP are more sensitive to an increase in observation time. Thus, the variation of the target observation duration has the least impact on the performance of the PIDSM.

6.2. Validation of the Reassignment

In this section, we aim to validate the ability of the proposed PIDSM algorithm to handle unexpected new targets by reassigning them. We utilize the 12 combinations obtained from Table 4, each with a low target distribution density and short-term observation time, and then generate 10 testing cases for each combination. After obtaining the initial assignment results of each testing instance using the PIDSM, we add five random targets to each testing instance and execute the PIDSM again to obtain new assignments. Subsequently, we conduct an overall assignment with both original and random targets to verify the quality of the reassignment solution.

Figure 10a presents the analysis of running time. It can be observed that compared to the overall assignment, the PIDSM’s reassignment time increases less with an increase in instance size. This is because our proposed PIDSM algorithm can make full use of the consensus results of the original assignments, significantly reducing the number of iterations required for the consensus after adding new targets. Furthermore, it is worth noting that the sum of the original assignment and the reassignment time of our algorithm is equal to the time taken for the overall assignment. This demonstrates the high efficiency of our algorithm in the reassignment, without introducing any additional computational burden when handling dynamic new targets.

Figure 10b presents the fitness value analysis, which shows that the solutions obtained through reassignment have almost the same fitness values as those obtained through the overall assignment for all testing instances. This demonstrates that our proposed PIDSM algorithm can handle dynamic new targets without sacrificing the quality of the solutions.

6.3. Runtime Analysis

We conducted a further runtime analysis of our proposed PIDSM. We obtained the required 12 combinations from Table 4 and randomly generated 10 testing instances for each combination, with the target distribution density and observation time randomly selected. The proposed PIDSM was then run on each testing instance, and the running time was recorded.

Figure 11 displays the statistical analysis results, indicating a significant increase in the running time of the PIDSM as the size of the testing instance increases, similar to the trend of communication times shown in Figure 6b. This demonstrates the advantage of our algorithm in dealing with small and medium-sized problems, particularly for small-sized problems where we can obtain a good task assignment solution in only 0.04 s. There are also some differences between Figure 6b and Figure 11. For example, in the {E × 200} combination, there is a significant difference in running time compared to the {E × 100} combination, while the difference in communication times is not significant. This is because our proposed algorithm enables satellites to communicate with each other about all tasks at once, so the increase in the number of tasks has a limited impact on communication times. However, the calculation of fitness value is more closely related to the number of tasks, and more tasks require a longer time to calculate the fitness value, ultimately resulting in an increase in the running time.

7. Conclusions

This paper addresses the problem of time-dependent observation scheduling for the AEOS constellation, where the transition time required between two consecutive observations is determined by angular change over time. This time-dependent characteristic increases the complexity of the scheduling problem.

To facilitate our understanding, we propose a mathematical model of the studied problem and a new fitness function that maximizes the profit sum while also considering system load balancing. We also compute non-conflict VTWs for each non-scheduled target to ensure that each AEOS can observe one target at a time. Using the basic idea of a distributed PI algorithm, we develop the PIDSM to solve the scheduling problem. The PIDSM iterates between two phases: the first selects the optimal task for each AEOS, while the second achieves consensus over all AEOSs and removes targets that may decrease the overall fitness. Each AEOS can run the PIDSM concurrently, and useful information is exchanged between AEOSs via ISLs during the PIDSM procedure. The convergence of the PIDSM is naturally guaranteed since the global fitness is increased whenever the schedule solution is changed at the end of each iteration. Compared with the existing distribution algorithms, CBBA [30], CNP [36], and ECNP [32], the PIDSM performs better for almost all experimental instances. Sensitivity analyses further validate the effectiveness of the PIDSM. In future work, we intend to reduce the communication overhead of the PI-based distributed scheduling approach.