Learning Sparse Geometric Features for Building Segmentation from Low-Resolution Remote-Sensing Images
Abstract
1. Introduction
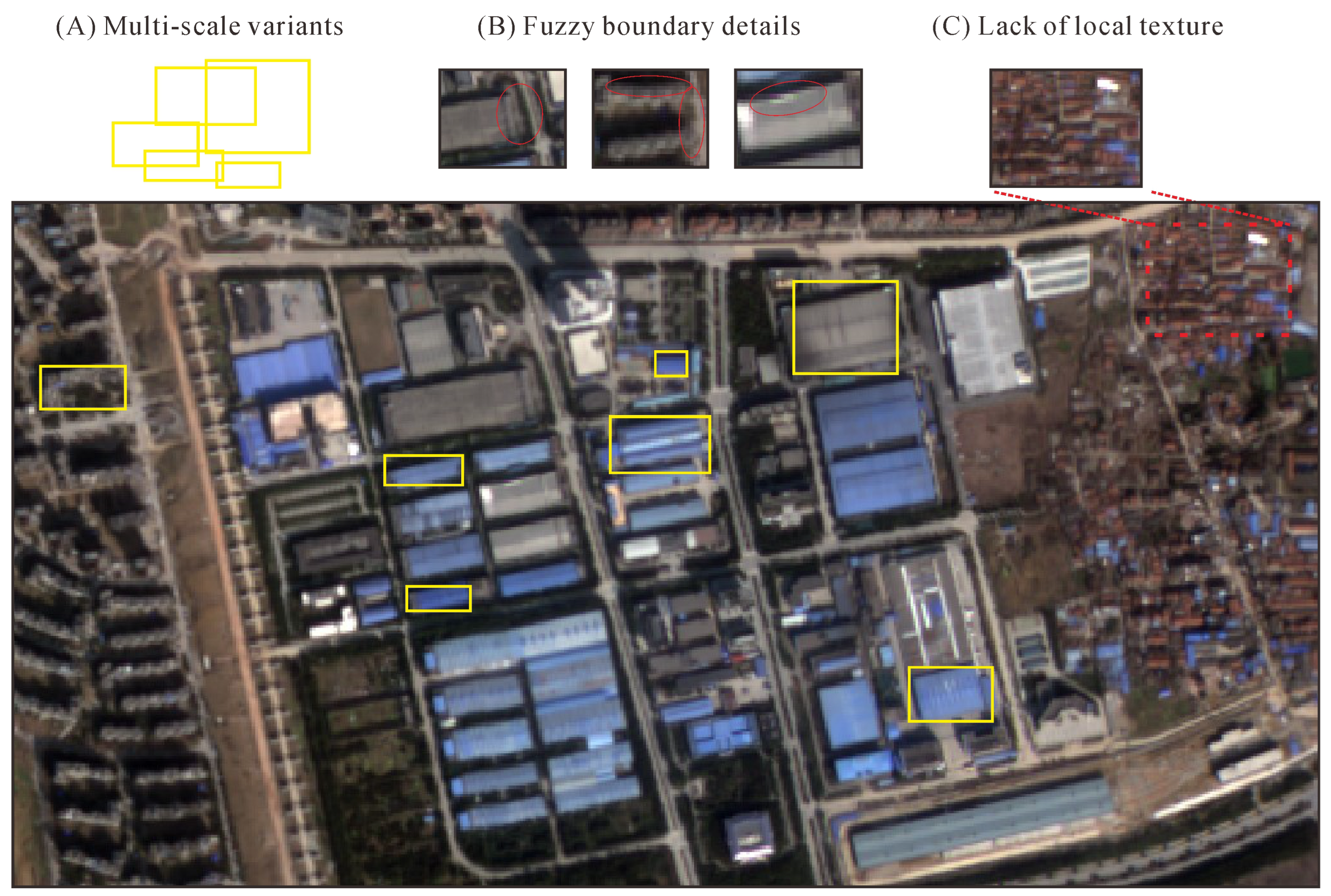
- There exists a large-scale variation of buildings in LR images (Figure 1A). This issue poses a multi-scale problem and makes it more difficult to locate and segment. This is a common issue in building segmentation.
- The boundary details of buildings (i.e., edges and corners on buildings) are fuzzier in LR images. As shown in Figure 1B, the boundaries of buildings are fuzzier and even blend into the background, which causes difficulties for models to delineate boundaries accurately.
- LR remote-sensing images always lack local textures due to low contrast in low resolution (Figure 1C). As a result, it is difficult to capture sufficient context information from a small patch of the image (e.g., the sliding window with a fixed size in a convolutional layer).
- The proposed model aims to achieve higher accuracy than the existing methods for building extraction from LR images.
- The proposed model is intended to outperform other SS methods when utilized as the SS module within the super resolution then semantic segmentation (SR-then-SS) framework.
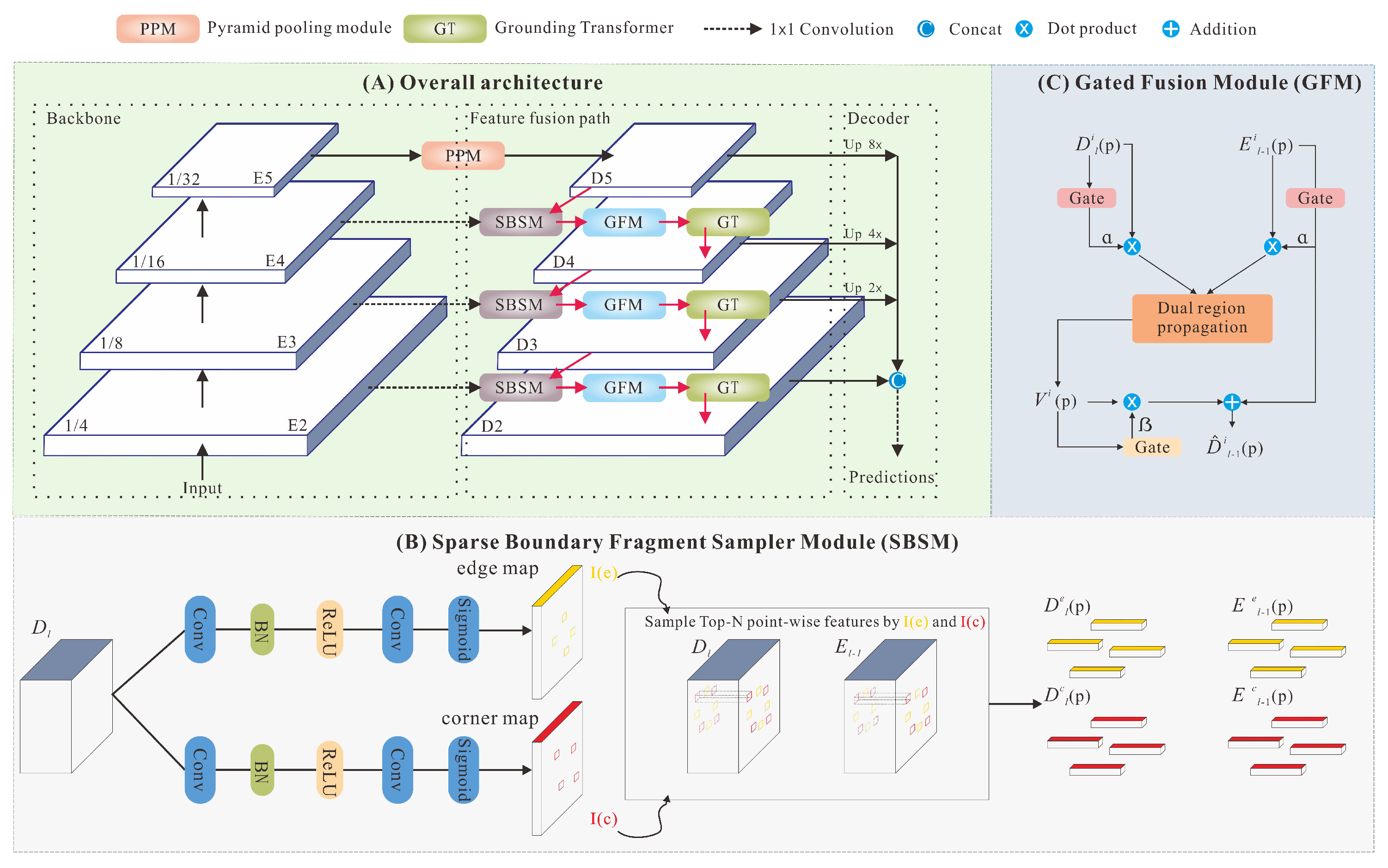
- A sparse geometry feature attention network (SGFANet) is proposed for extracting buildings from LR remote-sensing imagery accurately, where feature pyramid networks are adopted to solve multi-scale problems.
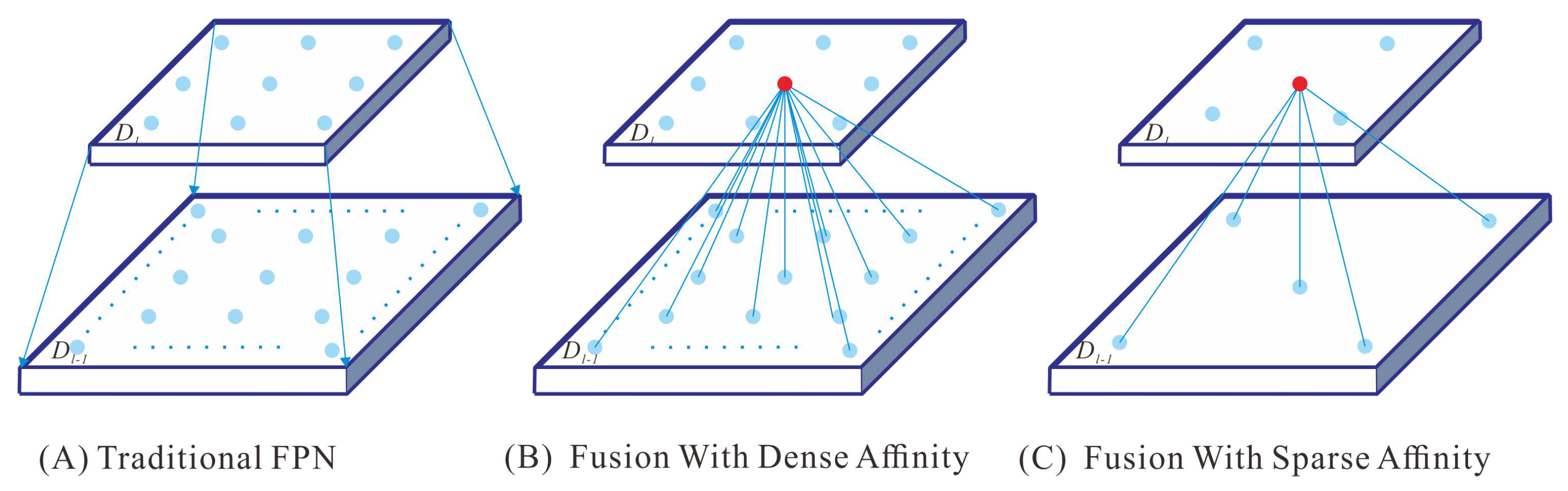
- To circumvent the effect of fuzzy boundary details on buildings in LR images, we propose the sparse boundary fragment sampler module (SBSM) and the gated fusion module (GFM) for point-wise affinity learning. The former makes the model more focused on the salient boundary fragment, and the latter is used to suppress the inferior multi-scale contexts.
- To mitigate the lack of local texture in LR images, we convert the top-down propagation from local to non-local by introducing the grounding transformer (GT). The GT leverages the global attention of images to compensate for the local texture.
2. Related Work
2.1. Deep Learning for Building Segmentation
2.2. Multi-Level Feature Fusion
2.3. Issues in Current Research
3. Sparse Geometry Feature Attention Network
3.1. Overview
3.2. Learning Sparse Geometry Features
3.2.1. Sparse Boundary Fragment Sampler Module
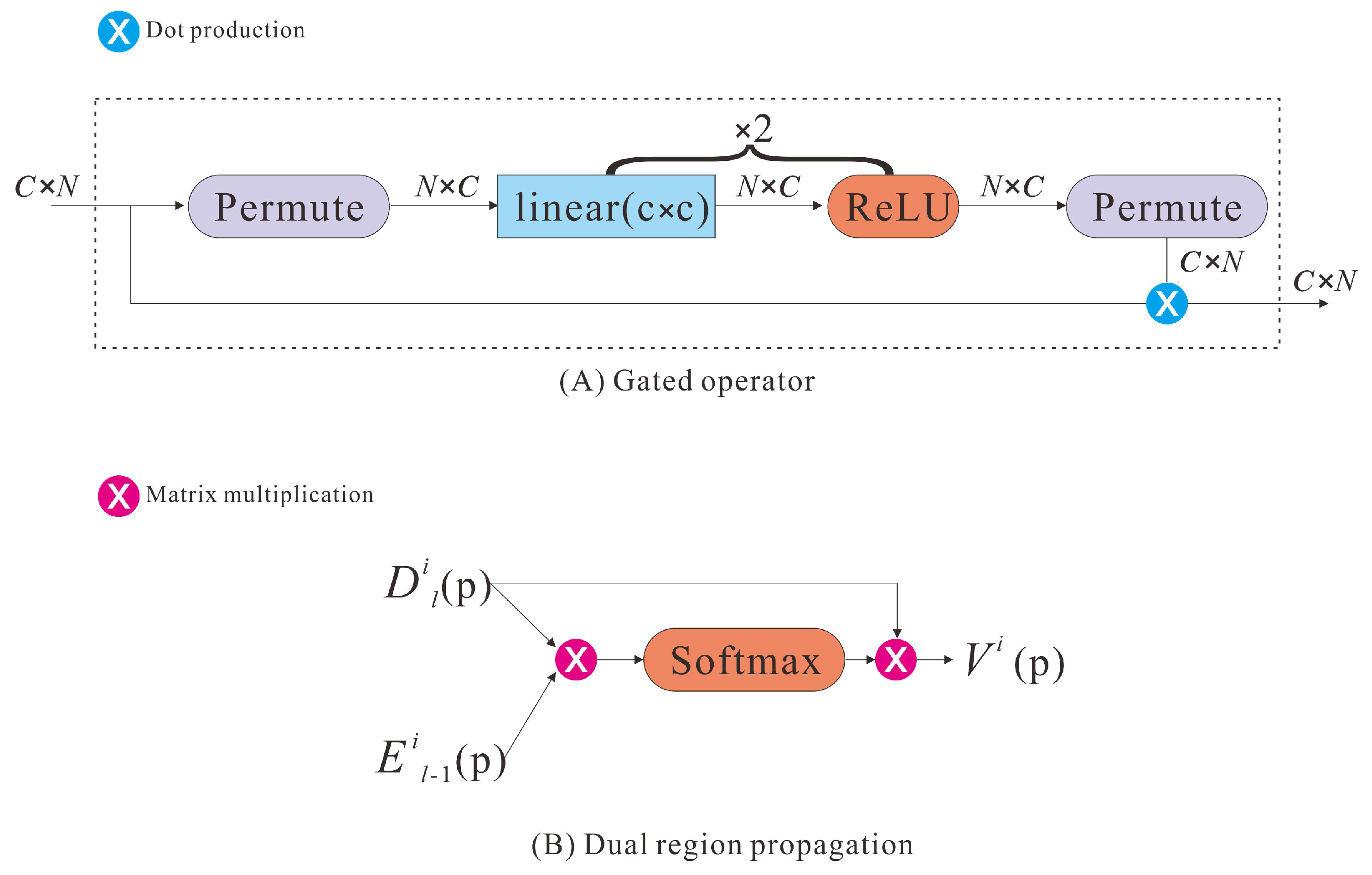
3.2.2. Gated Fusion Module
3.3. From Local to Non-Local Features
| Algorithm 1: The top-down procedure in SGFANet. |
|
3.4. Decoder and Loss Function
4. Experiments
4.1. Definition of LR and HR Images in This Paper
4.2. Datasets
4.3. Implementation Details
4.4. Accuracy Assessment
4.5. Results of SGFANet
- DeepLabV3+ [49] achieved SOTA results in the PASCAL VOC dataset. It is also a common baseline method in the semantic segmentation field.
- Unet++ [38] is the SOTA architecture among variants of the Unet. Its multi-scale architecture makes it effective in capturing various sized targets and is, therefore, often applied in building extraction.
- CBR-Net [34] achieved SOTA results in the WHU building dataset. It is also the most recent SOTA algorithm.
- PFNet [37] achieved SOTA results in the iSAID dataset. It is not dedicated to extracting buildings; however, it uses a sampling strategy similar to ours. The greatest difference is that it samples mainly to tackle the imbalance between the foreground and background pixels, while we are more refined, targeting only the building boundary and corner pixels.
- EPUNet [40] is a dense boundary propagation method. Compared with ICTNet, it introduces building boundaries as supervision. Compared with our method, it propagates the boundary contexts densely (i.e., without any context filtering).
- ASLNet [27] is a shape-learning method that applies the adversarial loss as a boundary regularizer. It is designed to extract a more regularized building shape.
4.5.1. Comparison with State-of-the-Art Methods
4.5.2. Comparison with Dense Boundary Propagation Methods
4.5.3. Comparison with Shape Learning Methods
4.6. Super Resolution and then Semantic Segmentation
4.6.1. Framework Architecture
4.6.2. Results
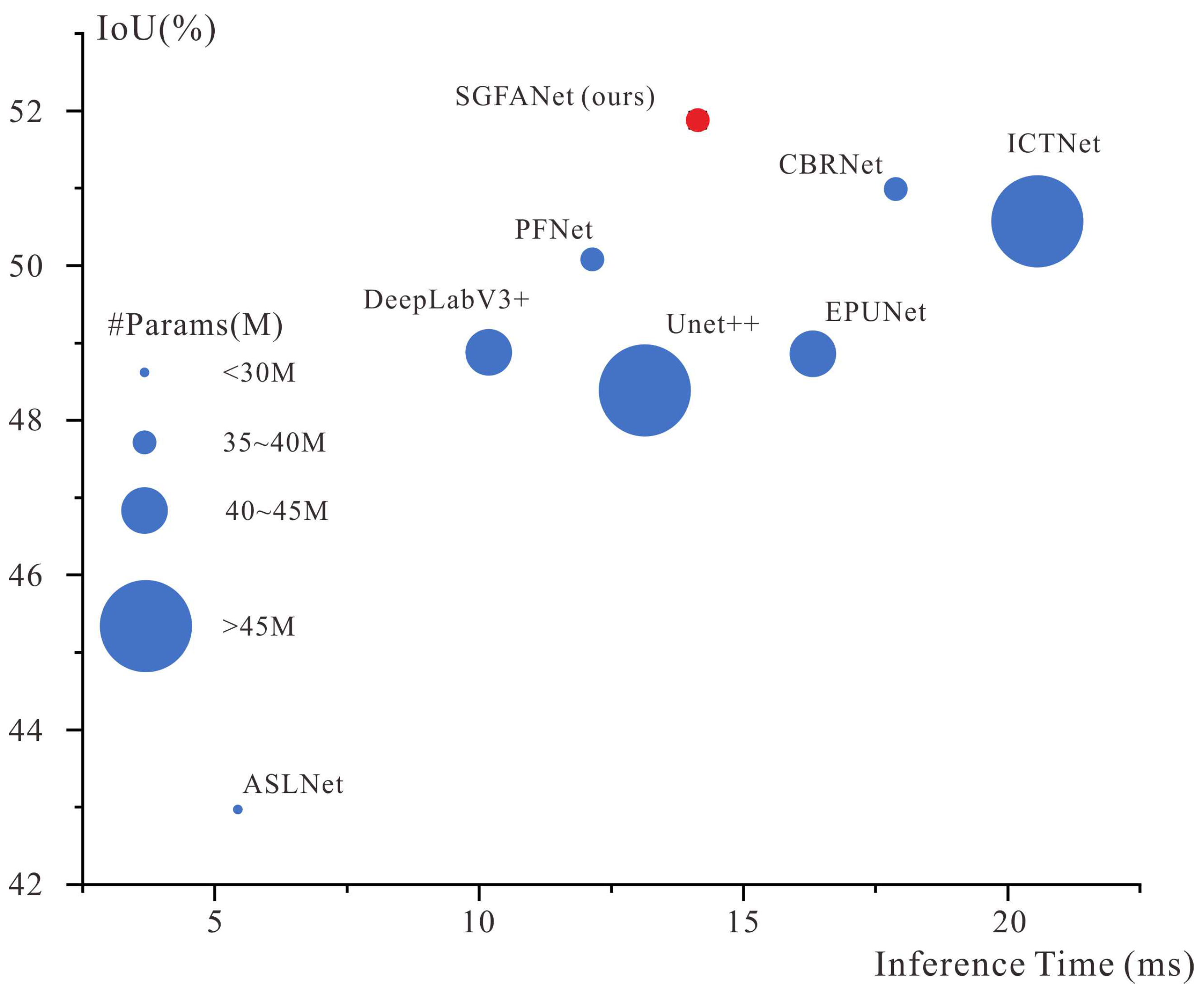
4.7. Model Efficiency
4.8. Sampling of Edge and Corner Points
4.9. Ablation Study
5. Pilot Application: Dynamic Building Change of the Xiong’an New Area in China
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wong, C.H.H.; Cai, M.; Ren, C.; Huang, Y.; Liao, C.; Yin, S. Modelling building energy use at urban scale: A review on their account for the urban environment. Build. Environ. 2021, 205, 108235. [Google Scholar] [CrossRef]
- Ma, R.; Li, X.; Chen, J. An elastic urban morpho-blocks (EUM) modeling method for urban building morphological analysis and feature clustering. Build. Environ. 2021, 192, 107646. [Google Scholar] [CrossRef]
- Chen, J.; Tang, H.; Ge, J.; Pan, Y. Rapid Assessment of Building Damage Using Multi-Source Data: A Case Study of April 2015 Nepal Earthquake. Remote Sens. 2022, 14, 1358. [Google Scholar] [CrossRef]
- Li, J.; Huang, X.; Tu, L.; Zhang, T.; Wang, L. A review of building detection from very high resolution optical remote sensing images. GISci. Remote Sens. 2022, 59, 1199–1225. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, L.; Wu, Y.; Wu, G.; Guo, Z.; Waslander, S.L. Aerial imagery for roof segmentation: A large-scale dataset towards automatic mapping of buildings. ISPRS J. Photogramm. Remote Sens. 2019, 147, 42–55. [Google Scholar] [CrossRef]
- Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. Can semantic labeling methods generalize to any city? The inria aerial image labeling benchmark. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), IEEE, Fort Worth, TX, USA, 23–28 July 2017; pp. 3226–3229. [Google Scholar]
- Ji, S.; Wei, S.; Lu, M. Fully convolutional networks for multisource building extraction from an open aerial and satellite imagery data set. IEEE Trans. Geosci. Remote Sens. 2018, 57, 574–586. [Google Scholar] [CrossRef]
- Jing, W.; Lin, J.; Lu, H.; Chen, G.; Song, H. Learning holistic and discriminative features via an efficient external memory module for building extraction in remote sensing images. Build. Environ. 2022, 222, 109332. [Google Scholar] [CrossRef]
- Zhu, Y.; Liang, Z.; Yan, J.; Chen, G.; Wang, X. ED-Net: Automatic building extraction from high-resolution aerial images with boundary information. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 4595–4606. [Google Scholar] [CrossRef]
- Lee, K.; Kim, J.H.; Lee, H.; Park, J.; Choi, J.P.; Hwang, J.Y. Boundary-Oriented Binary Building Segmentation Model With Two Scheme Learning for Aerial Images. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5604517. [Google Scholar] [CrossRef]
- Nauata, N.; Furukawa, Y. Vectorizing world buildings: Planar graph reconstruction by primitive detection and relationship inference. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 711–726. [Google Scholar]
- Girard, N.; Smirnov, D.; Solomon, J.; Tarabalka, Y. Polygonal building extraction by frame field learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 22–25 June 2021; pp. 5891–5900. [Google Scholar]
- Zhu, Y.; Huang, B.; Gao, J.; Huang, E.; Chen, H. Adaptive Polygon Generation Algorithm for Automatic Building Extraction. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–14. [Google Scholar] [CrossRef]
- Li, W.; Zhao, W.; Zhong, H.; He, C.; Lin, D. Joint semantic–geometric learning for polygonal building segmentation. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 2–9 February 2021; Volume 35, pp. 1958–1965. [Google Scholar]
- Zhang, L.; Dong, R.; Yuan, S.; Li, W.; Zheng, J.; Fu, H. Making low-resolution satellite images reborn: A deep learning approach for super-resolution building extraction. Remote Sens. 2021, 13, 2872. [Google Scholar] [CrossRef]
- He, Y.; Wang, D.; Lai, N.; Zhang, W.; Meng, C.; Burke, M.; Lobell, D.; Ermon, S. Spatial-Temporal Super-Resolution of Satellite Imagery via Conditional Pixel Synthesis. Adv. Neural Inf. Process. Syst. 2021, 34, 27903–27915. [Google Scholar]
- Kang, X.; Li, J.; Duan, P.; Ma, F.; Li, S. Multilayer Degradation Representation-Guided Blind Super-Resolution for Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5534612. [Google Scholar] [CrossRef]
- Xu, P.; Tang, H.; Ge, J.; Feng, L. ESPC_NASUnet: An End-to-End Super-Resolution Semantic Segmentation Network for Mapping Buildings From Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5421–5435. [Google Scholar] [CrossRef]
- Zhang, T.; Tang, H.; Ding, Y.; Li, P.; Ji, C.; Xu, P. FSRSS-Net: High-resolution mapping of buildings from middle-resolution satellite images using a super-resolution semantic segmentation network. Remote Sens. 2021, 13, 2290. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, H.; Tang, J.; Wang, M.; Hua, X.; Sun, Q. Feature pyramid transformer. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 323–339. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2012; Volume 25. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Yang, G.; Zhang, Q.; Zhang, G. EANet: Edge-aware network for the extraction of buildings from aerial images. Remote Sens. 2020, 12, 2161. [Google Scholar] [CrossRef]
- Huang, W.; Liu, Z.; Tang, H.; Ge, J. Sequentially Delineation of Rooftops with Holes from VHR Aerial Images Using a Convolutional Recurrent Neural Network. Remote Sens. 2021, 13, 4271. [Google Scholar] [CrossRef]
- Liu, Z.; Tang, H.; Huang, W. Building Outline Delineation From VHR Remote Sensing Images Using the Convolutional Recurrent Neural Network Embedded With Line Segment Information. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4705713. [Google Scholar] [CrossRef]
- Zorzi, S.; Bittner, K.; Fraundorfer, F. Machine-learned regularization and polygonization of building segmentation masks. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), IEEE, Milan, Italy, 10–15 January 2021; pp. 3098–3105. [Google Scholar]
- Ding, L.; Tang, H.; Liu, Y.; Shi, Y.; Zhu, X.X.; Bruzzone, L. Adversarial shape learning for building extraction in VHR remote sensing images. IEEE Trans. Image Process. 2021, 31, 678–690. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid scene parsing network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2881–2890. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Wei, S.; Ji, S.; Lu, M. Toward automatic building footprint delineation from aerial images using CNN and regularization. IEEE Trans. Geosci. Remote Sens. 2019, 58, 2178–2189. [Google Scholar] [CrossRef]
- Chatterjee, B.; Poullis, C. On building classification from remote sensor imagery using deep neural networks and the relation between classification and reconstruction accuracy using border localization as proxy. In Proceedings of the 2019 16th Conference on Computer and Robot Vision (CRV), IEEE, Kingston, ON, Canada, 29–31 May 2019; pp. 41–48. [Google Scholar]
- Liu, P.; Liu, X.; Liu, M.; Shi, Q.; Yang, J.; Xu, X.; Zhang, Y. Building footprint extraction from high-resolution images via spatial residual inception convolutional neural network. Remote Sens. 2019, 11, 830. [Google Scholar] [CrossRef]
- Wen, X.; Li, X.; Zhang, C.; Han, W.; Li, E.; Liu, W.; Zhang, L. ME-Net: A multi-scale erosion network for crisp building edge detection from very high resolution remote sensing imagery. Remote Sens. 2021, 13, 3826. [Google Scholar] [CrossRef]
- Guo, H.; Du, B.; Zhang, L.; Su, X. A coarse-to-fine boundary refinement network for building footprint extraction from remote sensing imagery. ISPRS J. Photogramm. Remote Sens. 2022, 183, 240–252. [Google Scholar] [CrossRef]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Li, X.; You, A.; Zhu, Z.; Zhao, H.; Yang, M.; Yang, K.; Tan, S.; Tong, Y. Semantic flow for fast and accurate scene parsing. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 775–793. [Google Scholar]
- Li, X.; He, H.; Li, X.; Li, D.; Cheng, G.; Shi, J.; Weng, L.; Tong, Y.; Lin, Z. Pointflow: Flowing semantics through points for aerial image segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 4217–4226. [Google Scholar]
- Zhou, Z.; Siddiquee, M.M.R.; Tajbakhsh, N.; Liang, J. Unet++: Redesigning skip connections to exploit multiscale features in image segmentation. IEEE Trans. Med. Imaging 2019, 39, 1856–1867. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Zhao, H.; Han, L.; Tong, Y.; Tan, S.; Yang, K. Gated fully fusion for semantic segmentation. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 11418–11425. [Google Scholar]
- Guo, H.; Shi, Q.; Marinoni, A.; Du, B.; Zhang, L. Deep building footprint update network: A semi-supervised method for updating existing building footprint from bi-temporal remote sensing images. Remote Sens. Environ. 2021, 264, 112589. [Google Scholar] [CrossRef]
- Akiva, P.; Purri, M.; Leotta, M. Self-supervised material and texture representation learning for remote sensing tasks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8203–8215. [Google Scholar]
- Su, H.; Jampani, V.; Sun, D.; Gallo, O.; Learned-Miller, E.; Kautz, J. Pixel-adaptive convolutional neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019; pp. 11166–11175. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Azulay, A.; Weiss, Y. Why do deep convolutional networks generalize so poorly to small image transformations? J. Mach. Learn. Res. 2019, 20, 1–25. [Google Scholar]
- Gulati, A.; Qin, J.; Chiu, C.C.; Parmar, N.; Zhang, Y.; Yu, J.; Han, W.; Wang, S.; Zhang, Z.; Wu, Y.; et al. Conformer: Convolution-augmented Transformer for Speech Recognition. In Proceedings of the Interspeech 2020, Shanghai, China, 25–29 October 2020; pp. 5036–5040. [Google Scholar] [CrossRef]
- Ma, L.; Liu, Y.; Zhang, X.; Ye, Y.; Yin, G.; Johnson, B.A. Deep learning in remote sensing applications: A meta-analysis and review. ISPRS J. Photogramm. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
- Shi, Y.; Li, Q.; Zhu, X.X. Building segmentation through a gated graph convolutional neural network with deep structured feature embedding. ISPRS J. Photogramm. Remote Sens. 2020, 159, 184–197. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. Decoupled weight decay regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Li, Q.; Zorzi, S.; Shi, Y.; Fraundorfer, F.; Zhu, X.X. RegGAN: An End-to-End Network for Building Footprint Generation with Boundary Regularization. Remote Sens. 2022, 14, 1835. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2014; Volume 27. [Google Scholar]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1874–1883. [Google Scholar]
- Weng, Y.; Zhou, T.; Li, Y.; Qiu, X. Nas-unet: Neural architecture search for medical image segmentation. IEEE Access 2019, 7, 44247–44257. [Google Scholar] [CrossRef]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2011; Volume 24. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Young, S.R.; Rose, D.C.; Karnowski, T.P.; Lim, S.H.; Patton, R.M. Optimizing deep learning hyper-parameters through an evolutionary algorithm. In Proceedings of the Workshop on Machine Learning in High-Performance Computing Environments, Austin, TX, USA, 15 November 2015; pp. 1–5. [Google Scholar]
- Zou, Y.; Zhao, W. Making a new area in Xiong’an: Incentives and challenges of China’s “Millennium Plan”. Geoforum 2018, 88, 45–48. [Google Scholar] [CrossRef]
- Zheng, H.; Gong, M.; Liu, T.; Jiang, F.; Zhan, T.; Lu, D.; Zhang, M. HFA-Net: High frequency attention siamese network for building change detection in VHR remote sensing images. Pattern Recognit. 2022, 129, 108717. [Google Scholar] [CrossRef]
- Marconcini, M.; Metz-Marconcini, A.; Üreyen, S.; Palacios-Lopez, D.; Hanke, W.; Bachofer, F.; Zeidler, J.; Esch, T.; Gorelick, N.; Kakarla, A.; et al. Outlining where humans live, the World Settlement Footprint 2015. Sci. Data 2020, 7, 242. [Google Scholar] [CrossRef]
- Xu, L.; Herold, M.; Tsendbazar, N.E.; Masiliūnas, D.; Li, L.; Lesiv, M.; Fritz, S.; Verbesselt, J. Time series analysis for global land cover change monitoring: A comparison across sensors. Remote Sens. Environ. 2022, 271, 112905. [Google Scholar] [CrossRef]
- Gong, P.; Li, X.; Wang, J.; Bai, Y.; Chen, B.; Hu, T.; Liu, X.; Xu, B.; Yang, J.; Zhang, W.; et al. Annual maps of global artificial impervious area (GAIA) between 1985 and 2018. Remote Sens. Environ. 2020, 236, 111510. [Google Scholar] [CrossRef]
- Li, X.; Gong, P.; Liang, L. A 30-year (1984–2013) record of annual urban dynamics of Beijing City derived from Landsat data. Remote Sens. Environ. 2015, 166, 78–90. [Google Scholar] [CrossRef]


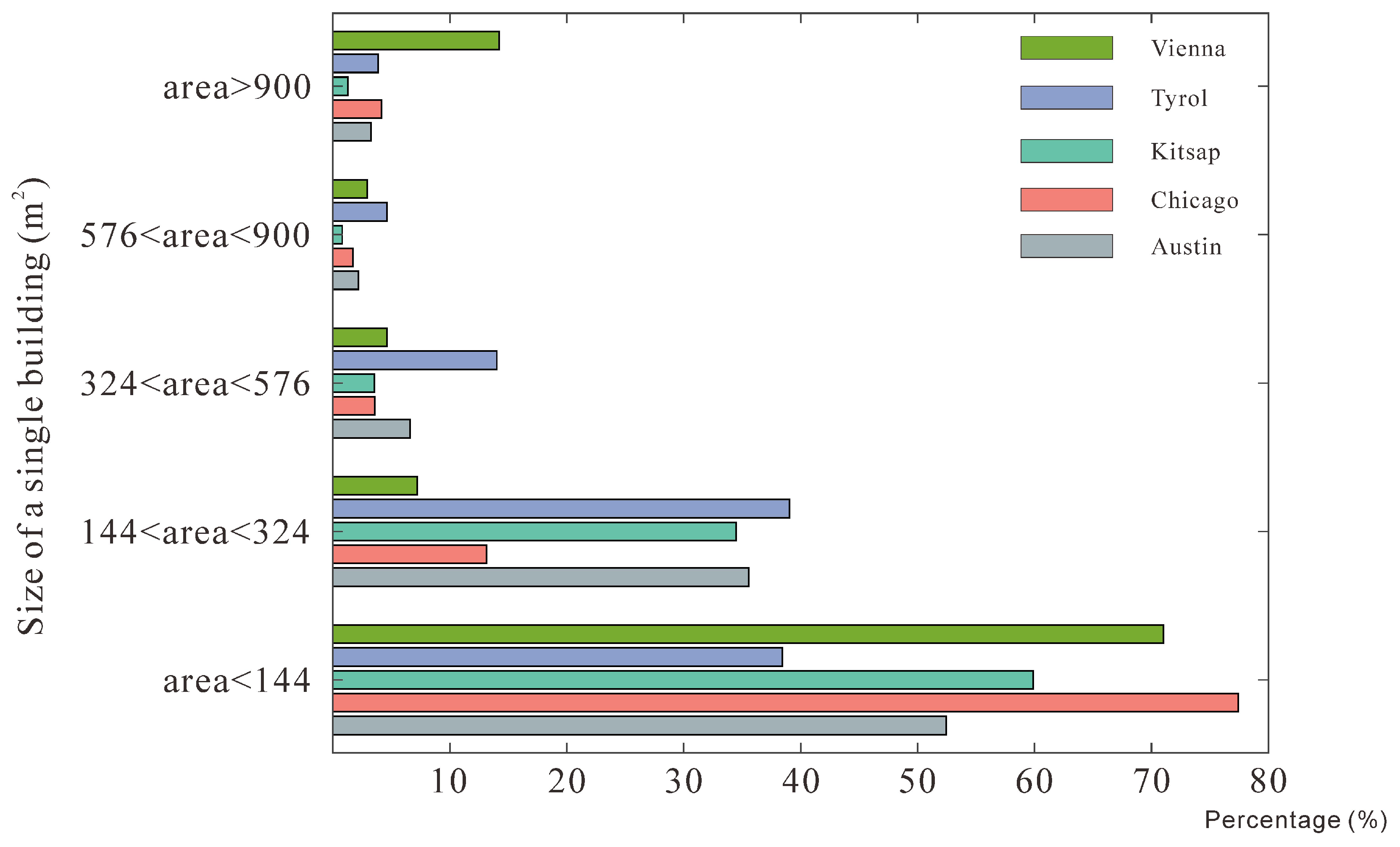
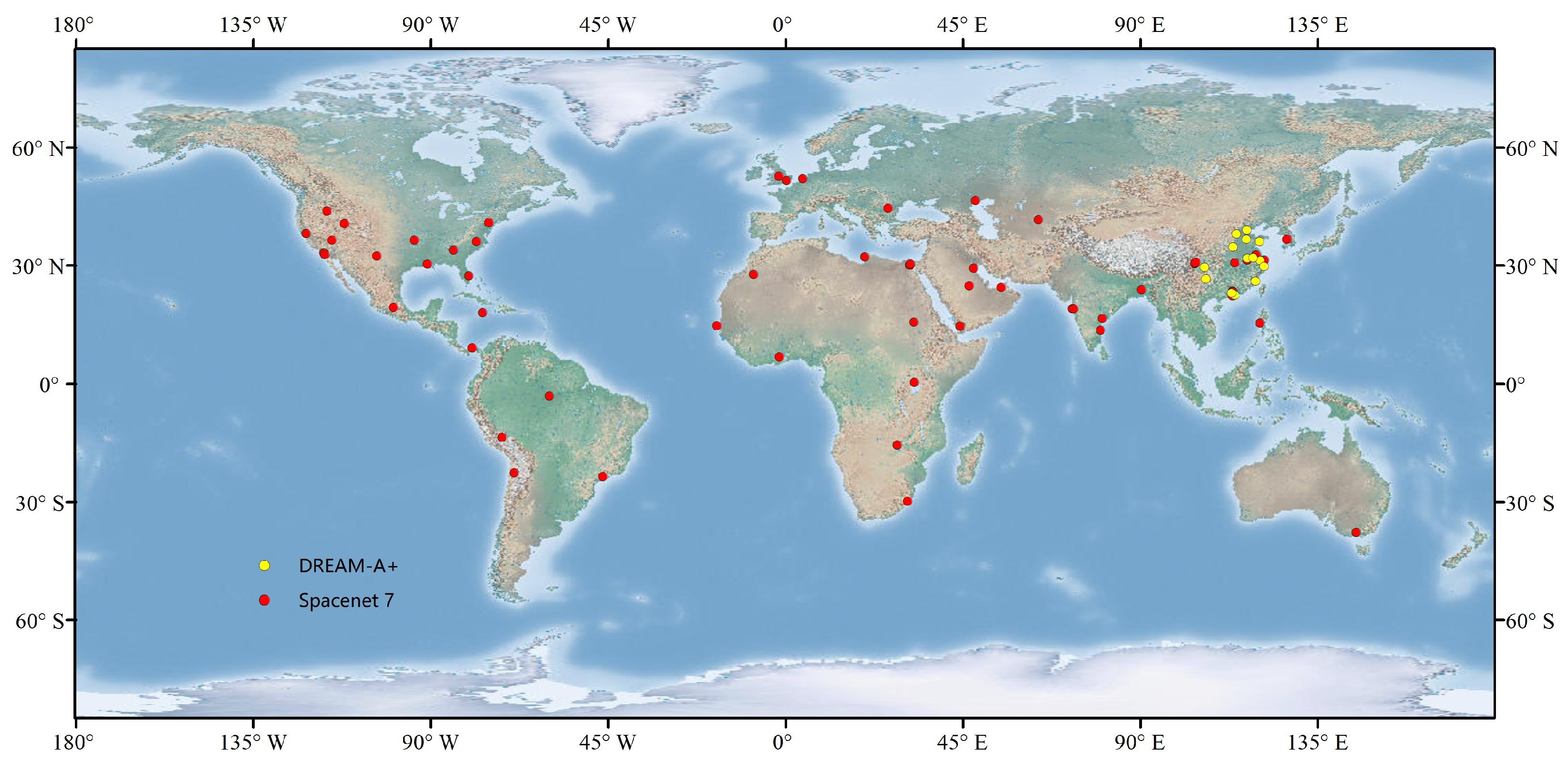








| Train | Validation | Test | |
|---|---|---|---|
| DREAM-A+ dataset | 1950 | 780 | 1169 |
| Spacenet7 dataset | 6571 | 2628 | 3941 |
| Sentinel-2 dataset | 15,274 | 6109 | 9164 |
| IoU (%) | OA (%) | F1 (%) | b-F1 (3PX) | |
|---|---|---|---|---|
| DeepLabV3+ | 45.09 | 89.29 | 62.15 | 63.70 |
| Unet++ | 46.12 | 89.32 | 63.13 | 65.87 |
| ICTNet | 46.69 | 89.32 | 63.66 | 66.89 |
| CBR-Net | 47.80 | 89.85 | 64.68 | 66.73 |
| PFNet | 47.26 | 89.72 | 64.19 | 64.92 |
| EPUNet | 45.84 | 89.14 | 62.87 | 65.45 |
| ASLNet | 40.47 | 88.79 | 58.29 | 60.18 |
| SGFANet | 48.46 | 90.06 | 65.28 | 66.94 |
| SR Module | IoU (%) | OA (%) | F1 (%) | |
|---|---|---|---|---|
| DeepLabV3+ | ESPCN | 31.07 | 82.90 | 47.41 |
| Unet++ | ESPCN | 32.04 | 83.57 | 48.53 |
| ICTNet | ESPCN | 32.19 | 82.75 | 48.71 |
| CBR-Net | ESPCN | 32.72 | 83.09 | 49.53 |
| PFNet | ESPCN | 29.44 | 84.11 | 45.49 |
| EPUNet | ESPCN | 31.83 | 83.07 | 48.29 |
| ASLNet | ESPCN | 28.12 | 82.56 | 43.90 |
| SGFANet (ours) | ESPCN | 33.11 | 84.00 | 49.75 |
| ESPC_NASUnet | ESPCN | 30.37 | 82.51 | 46.59 |
| FSRSS-Net | - | 27.28 | 83.66 | 42.87 |
| IoU (%) | OA (%) | F1 (%) | Time (h) | |
|---|---|---|---|---|
| SGFANet-S1 (192, 8) | 51.94 | 78.80 | 68.54 | 36 |
| SGFANet-S2 (128, 16) | 51.72 | 78.52 | 68.04 | 36 |
| SGFANet-S3 (128, 32) | 51.88 | 78.70 | 68.32 | 19 |
| +PPM | +SBSM | +GFM | +GT | IoU (%) | OA (%) | F1 (%) | Description |
|---|---|---|---|---|---|---|---|
| - | - | - | - | 48.44 | 78.07 | 62.91 | The baseline of the ablation studies |
| ✓ | - | - | - | 48.70 | 78.35 | 65.50 | Add PPM to the top layer in the top-down procedure, the propagation is feature-wise |
| ✓ | - | - | ✓ | 49.68 | 78.68 | 66.38 | Append GT and PPM into the top-down procedure, the propagation is feature-wise |
| ✓ | ✓ | - | ✓ | 50.31 | 78.69 | 66.94 | Append GT and PPM into the top-down procedure, the propagation is point-wise realized by the SBSM |
| ✓ | ✓ | ✓ | - | 51.21 | 79.13 | 67.74 | Append GFM and PPM into the top-down procedure, the further contexts filtering is included in the point-wise propagation |
| ✓ | ✓ | ✓ | ✓ | 51.88 | 78.70 | 68.32 | Our method |
| IoU | b-F1 (3px) | b-F1 (9px) | b-F1 (12px) | |
|---|---|---|---|---|
| baseline + PPM | 48.70 | 55.37 | 77.19 | 79.65 |
| +GT | 49.68 | 55.63 | 76.83 | 79.29 |
| +GT + SBSM | 50.31 | 56.33 | 77.73 | 80.18 |
| +GT + SBSM + GFM | 51.88 | 60.44 | 81.13 | 83.38 |
| Resolution | Correlation Coefficients | |
|---|---|---|
| Dynamic World | 10 m | 0.7702 |
| GAIA | 30 m | 0.6864 |
| MCD12Q1 | 500 m | 0.4907 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Tang, H. Learning Sparse Geometric Features for Building Segmentation from Low-Resolution Remote-Sensing Images. Remote Sens. 2023, 15, 1741. https://doi.org/10.3390/rs15071741
Liu Z, Tang H. Learning Sparse Geometric Features for Building Segmentation from Low-Resolution Remote-Sensing Images. Remote Sensing. 2023; 15(7):1741. https://doi.org/10.3390/rs15071741
Chicago/Turabian StyleLiu, Zeping, and Hong Tang. 2023. "Learning Sparse Geometric Features for Building Segmentation from Low-Resolution Remote-Sensing Images" Remote Sensing 15, no. 7: 1741. https://doi.org/10.3390/rs15071741
APA StyleLiu, Z., & Tang, H. (2023). Learning Sparse Geometric Features for Building Segmentation from Low-Resolution Remote-Sensing Images. Remote Sensing, 15(7), 1741. https://doi.org/10.3390/rs15071741







