A Modified NLCS Algorithm for High-Speed Bistatic Forward-Looking SAR Focusing with Spaceborne Illuminator
Abstract
1. Introduction
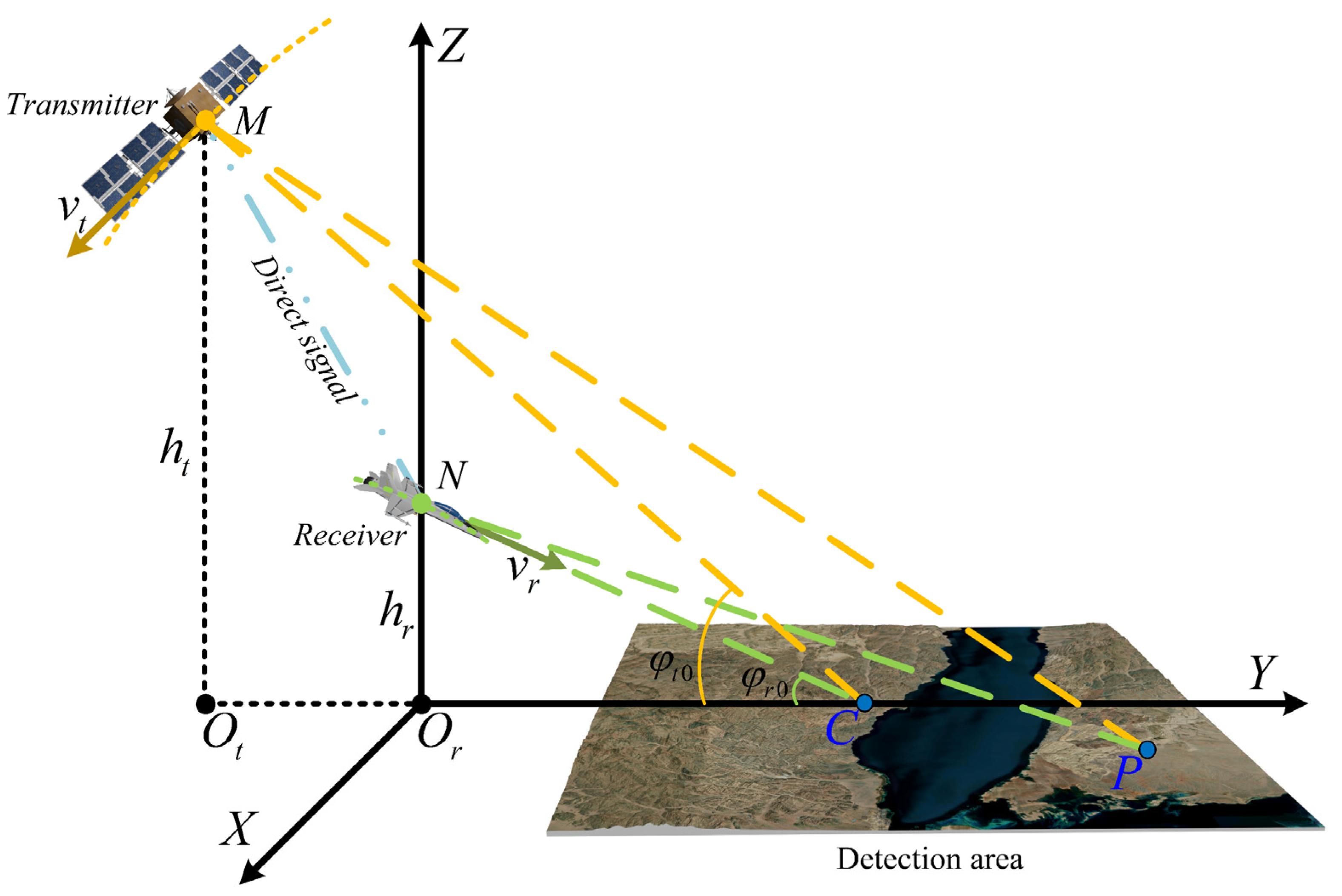
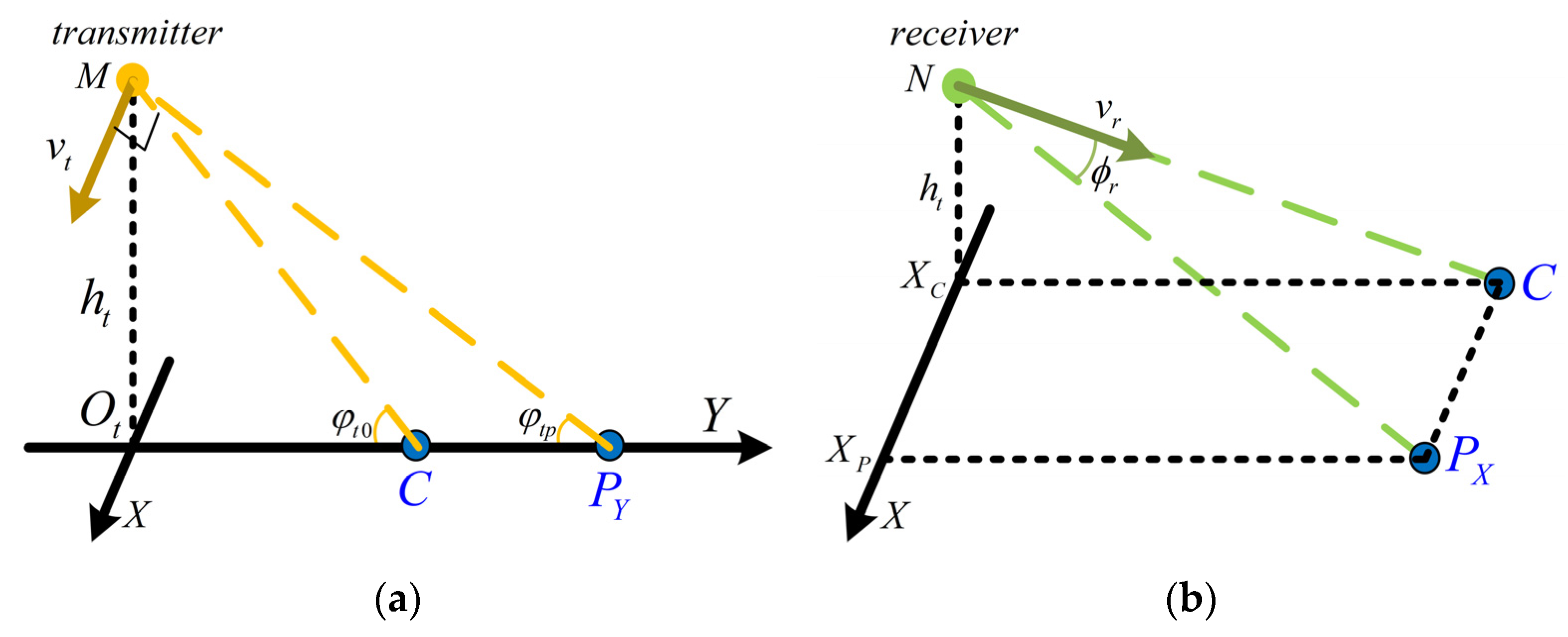
2. HS-BFSAR Signal Model and Range Doppler Spectrum
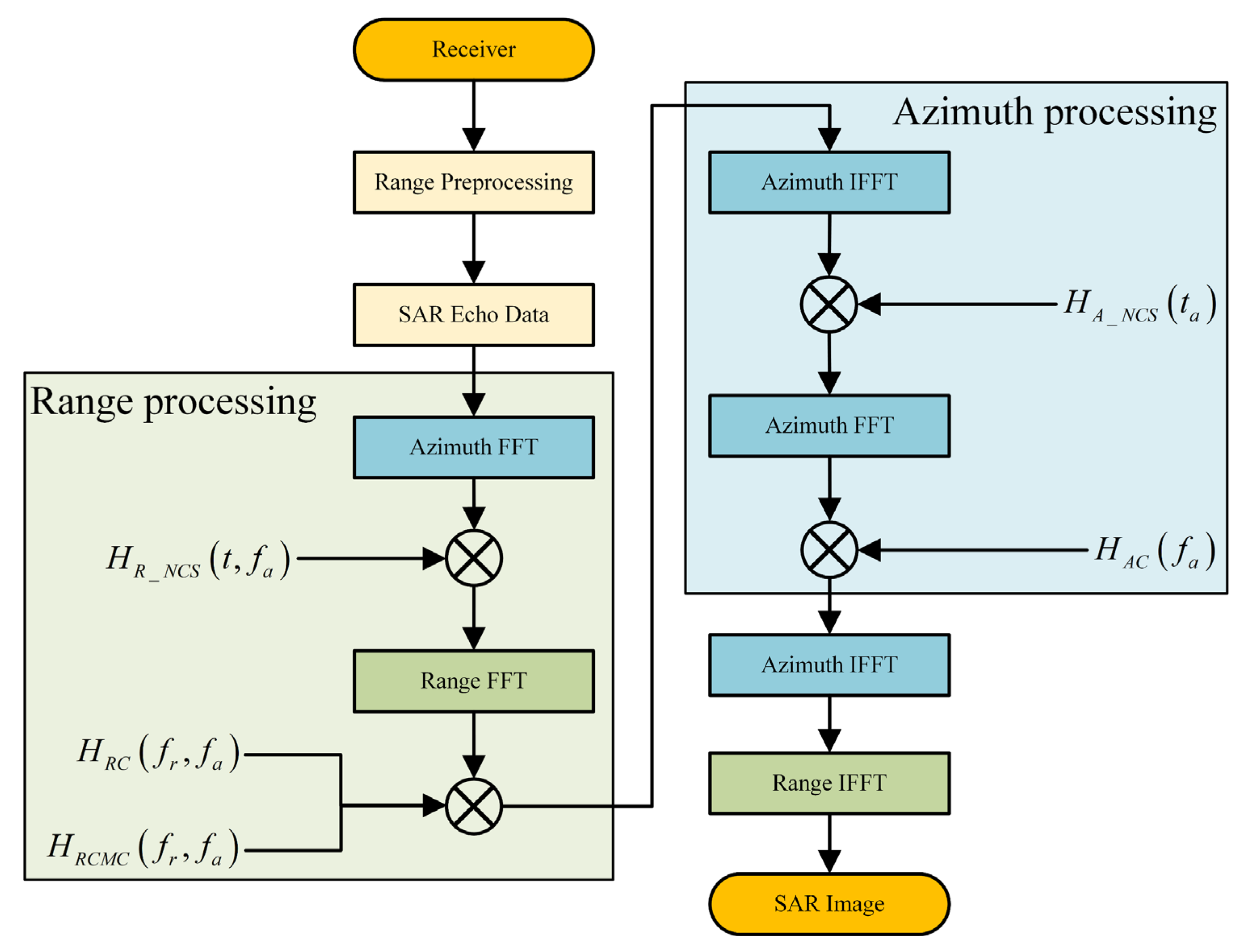
3. Range Preprocessing and Range NLCS
3.1. Range Preprocessing in Echo Recording
3.2. RCMC and Range Compression Using NLCS
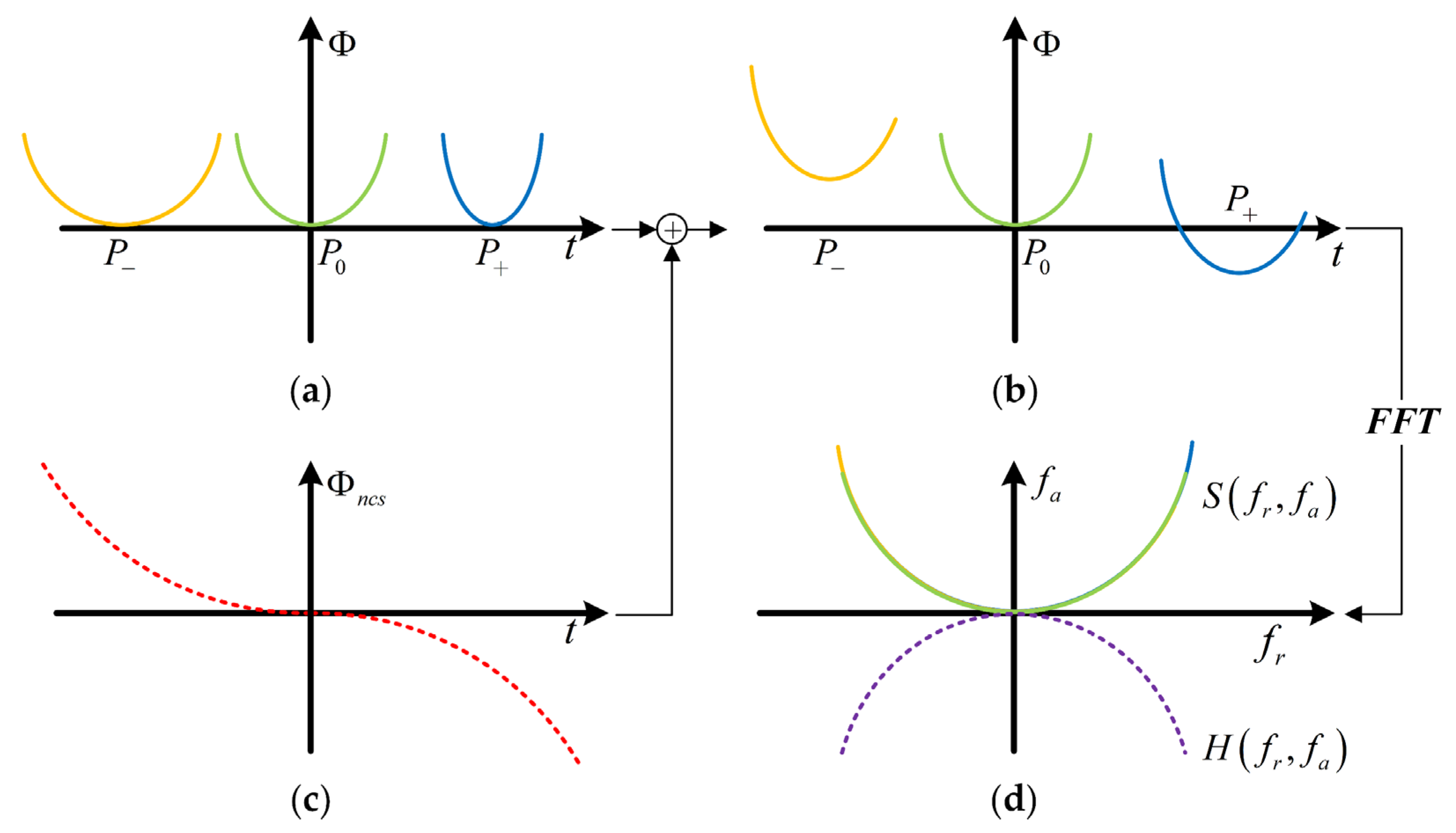
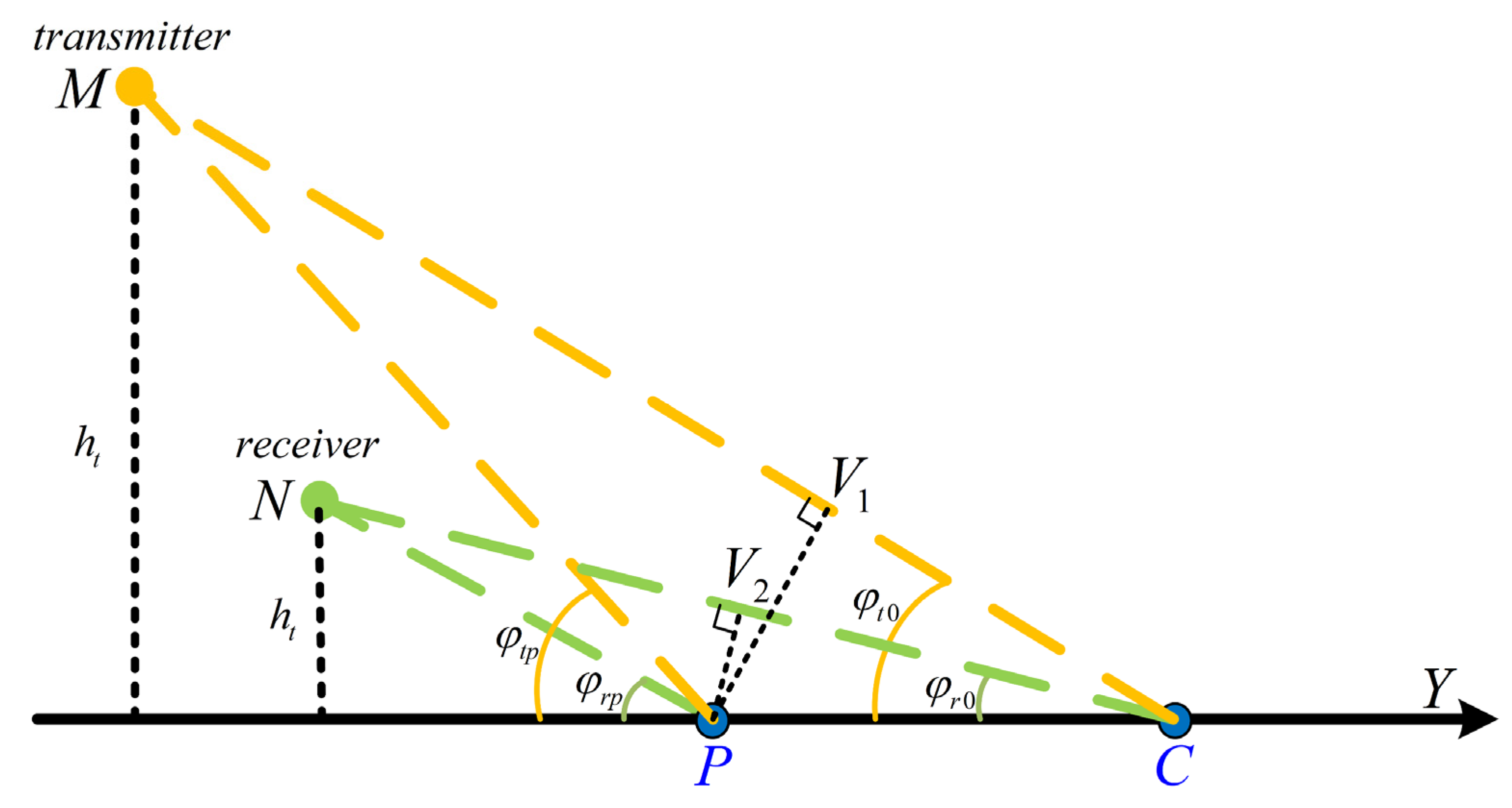
4. Azimuth Compression via Modified NLCS
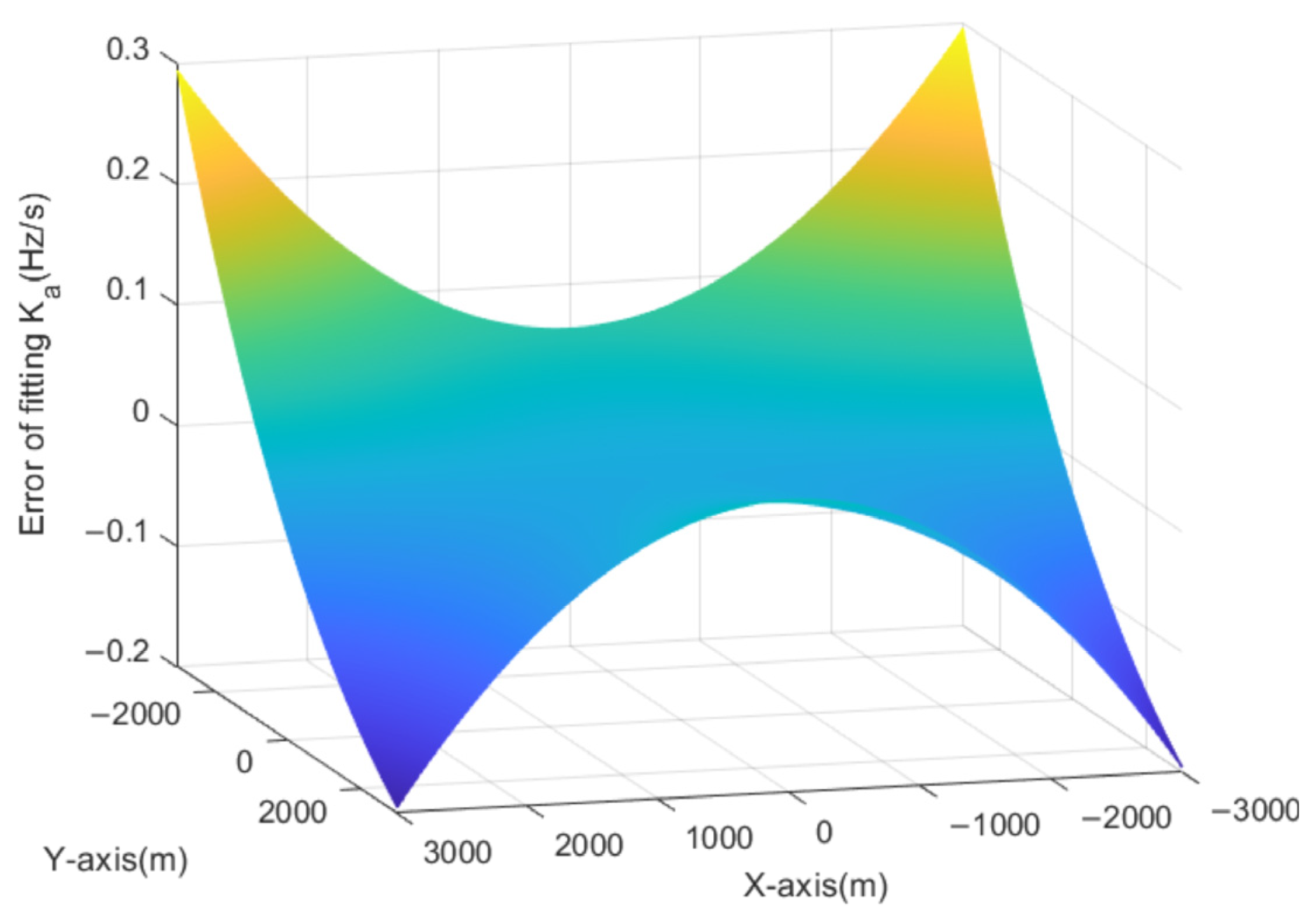
4.1. Analysis of Azimuth FM Rate
4.2. Azimuth FM Rate Equalizing by Modified NLCS
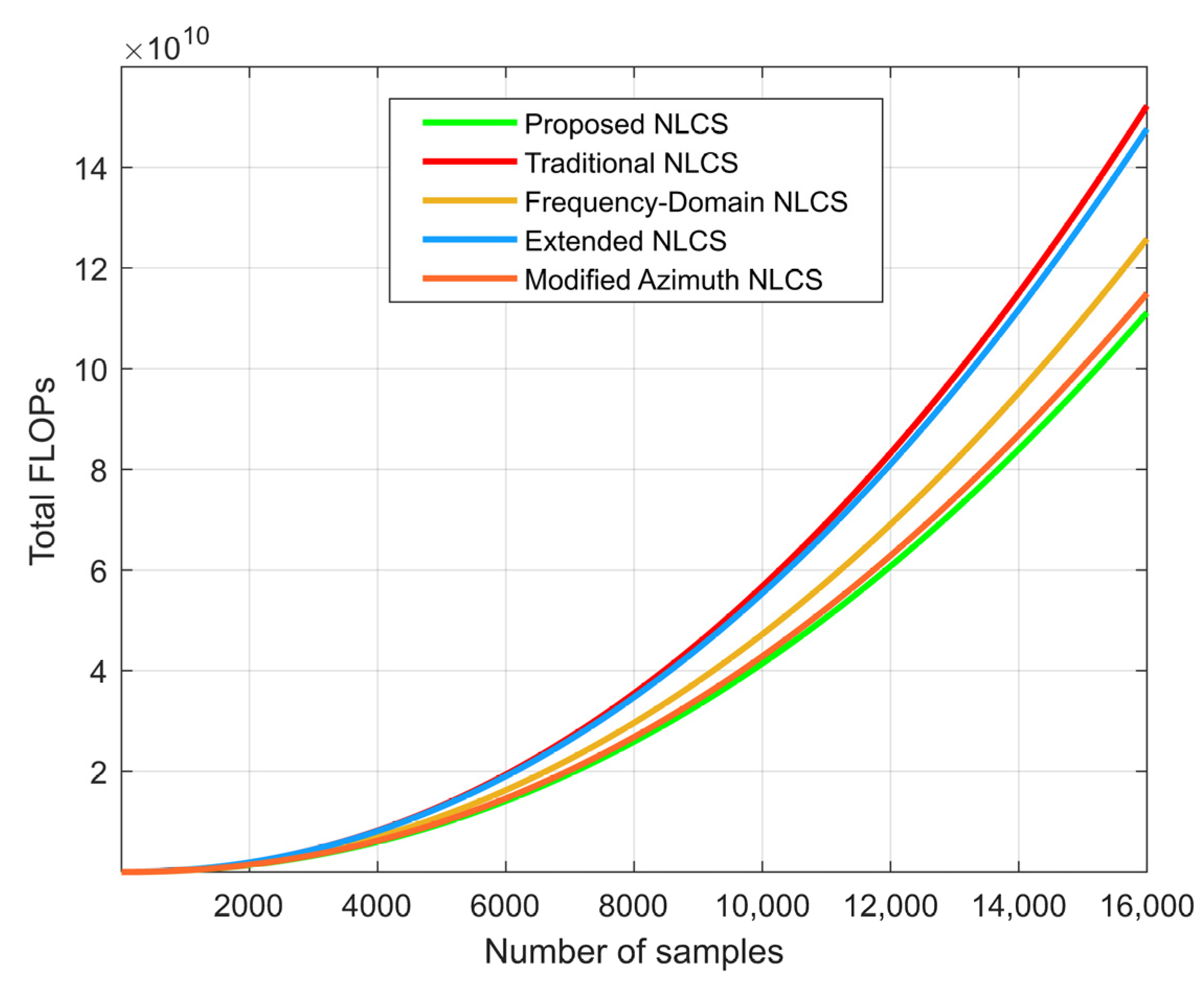
4.3. Computing Burden of Proposed Algorithm
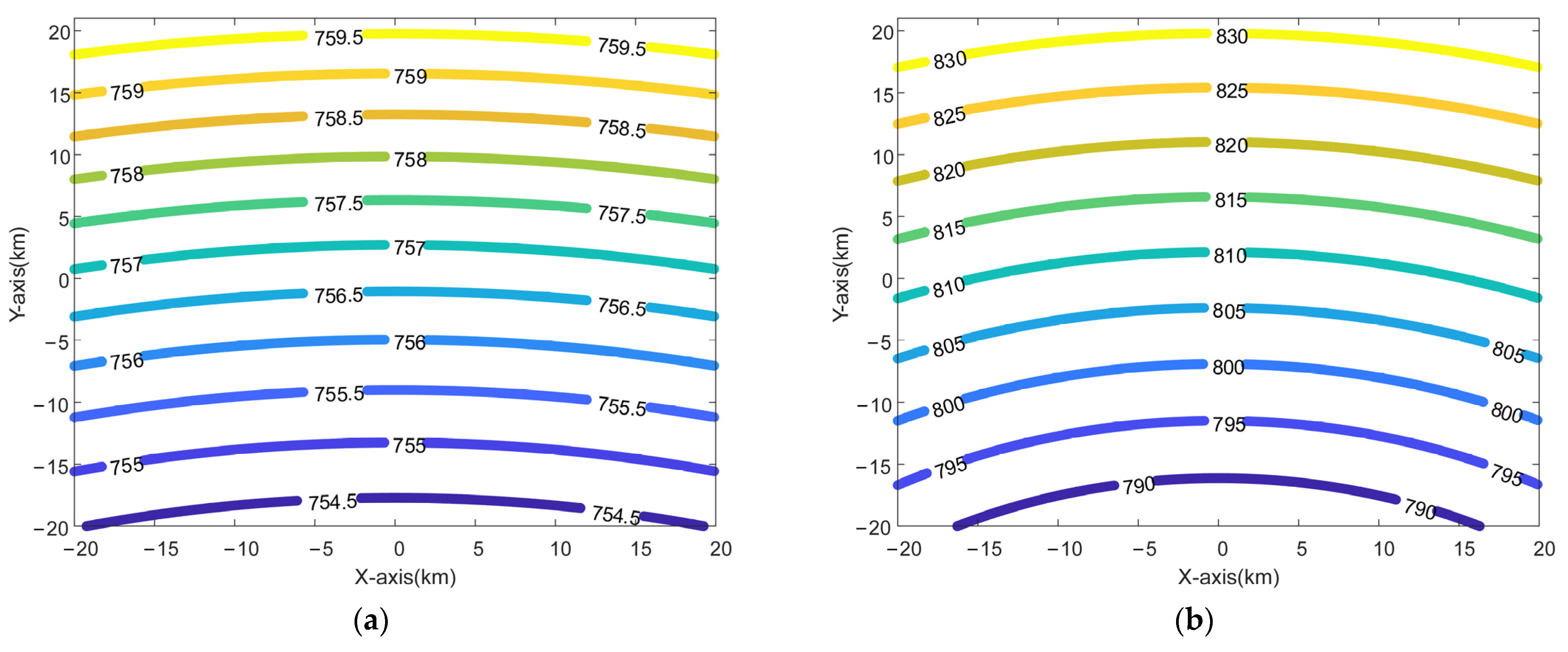
5. Simulation Results and Discussion
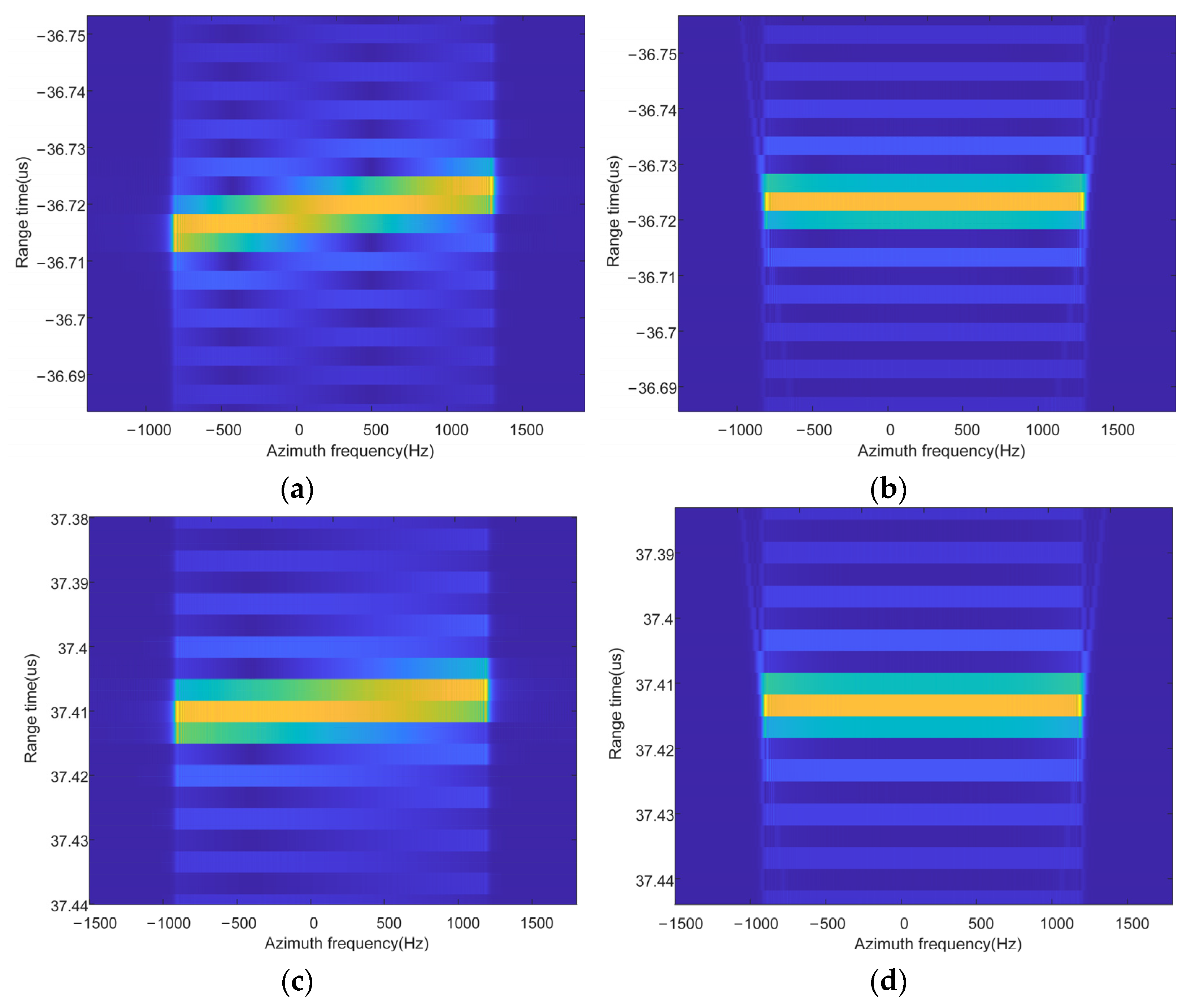
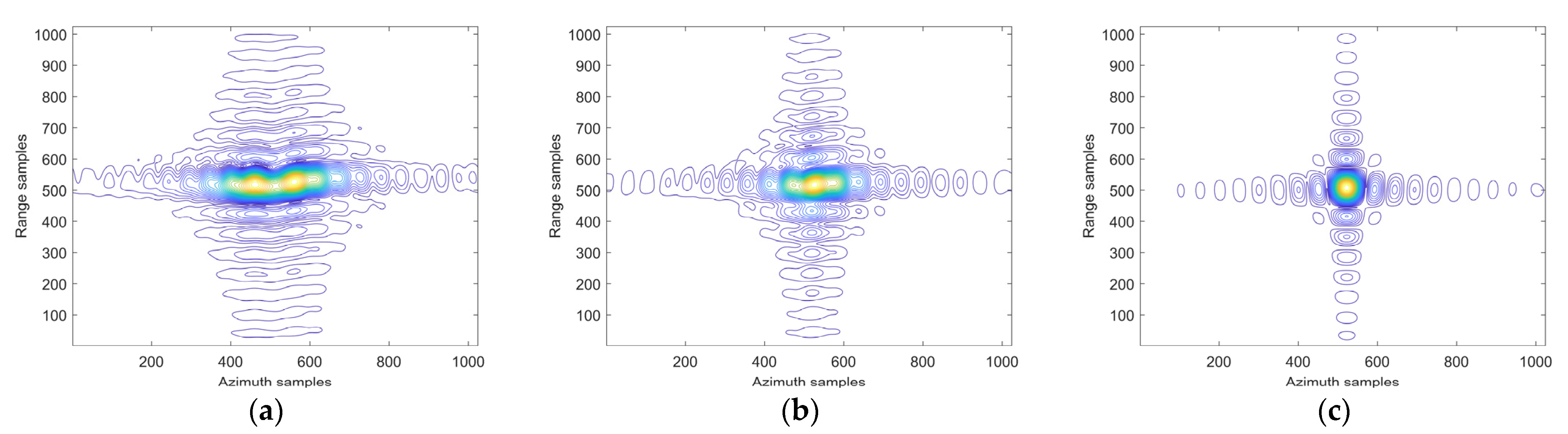
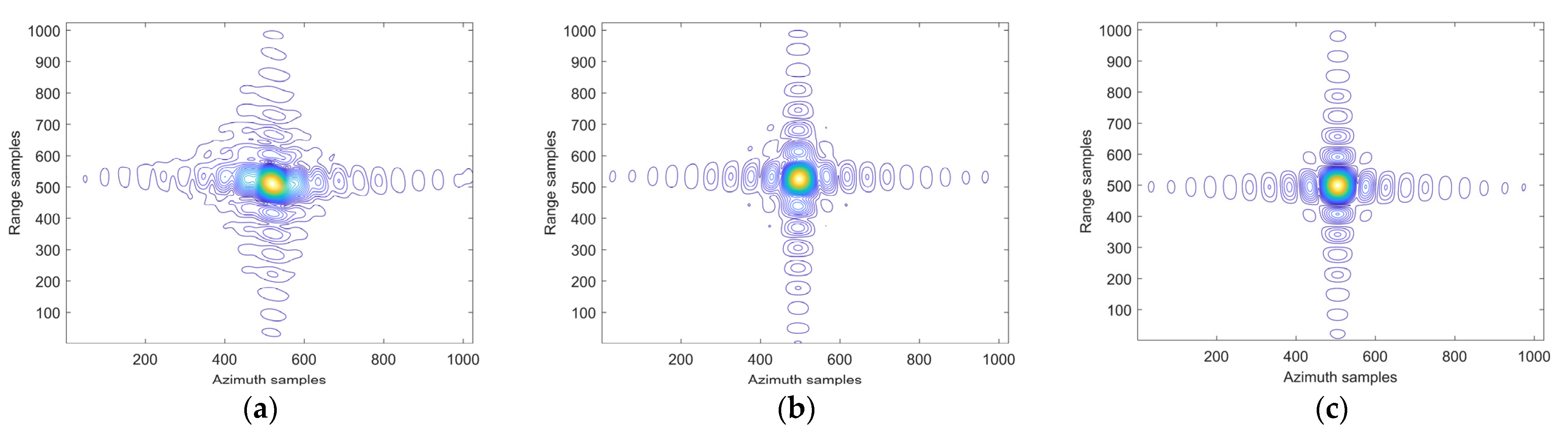
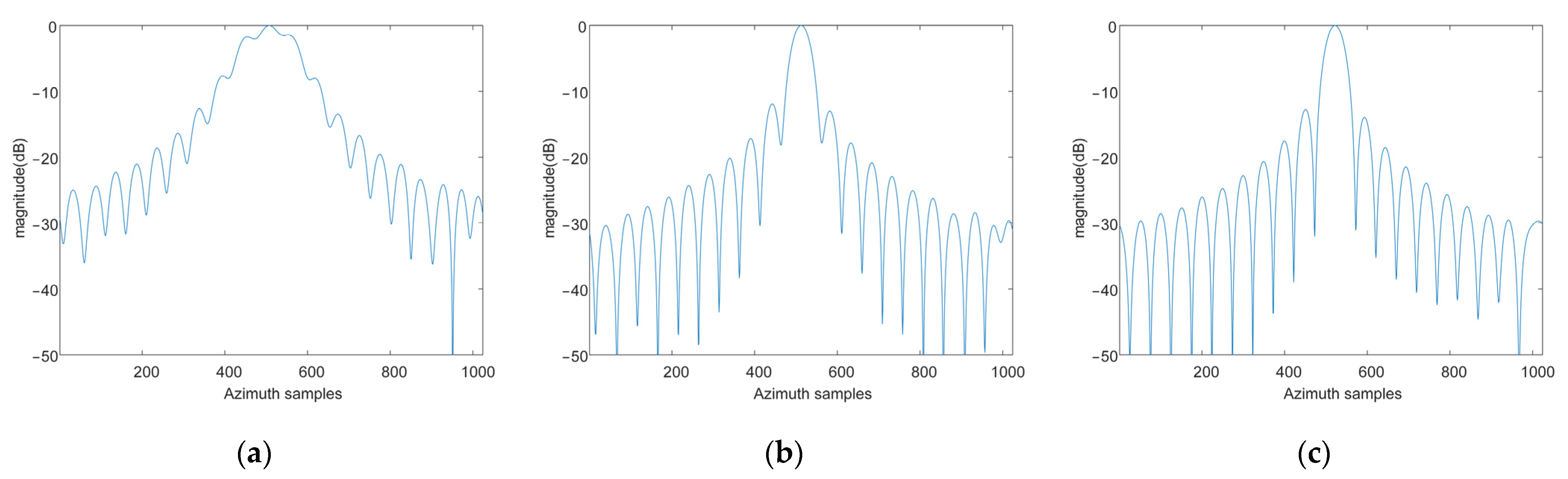
5.1. Results of Point Simulation
5.2. Results of Scene Simulation
5.3. Discussion of the Proposed Algorithm
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation. Artech House 2005, 1, 108–110. [Google Scholar]
- Balzter, H.; Cole, B.; Thiel, C.; Schmullius, C. Mapping CORINE Land Cover from Sentinel-1A SAR and SRTM Digital Elevation Model Data Using Random Forests. Remote Sens. 2015, 7, 14876–14898. [Google Scholar] [CrossRef]
- Chaabani, C.; Chini, M.; Abdelfattah, R.; Hostache, R.; Chokmani, K. Flood Mapping in a Complex Environment Using Bistatic TanDEM-X/TerraSAR-X InSAR Coherence. Remote Sens. 2018, 10, 1873. [Google Scholar] [CrossRef]
- Cruz, H.; Véstias, M.; Monteiro, J.; Neto, H.; Duarte, R.P. A Review of Synthetic-Aperture Radar Image Formation Algorithms and Implementations: A Computational Perspective. Remote Sens. 2022, 14, 1258. [Google Scholar] [CrossRef]
- Elfadaly, A.; Abouarab, M.A.R.; El Shabrawy, R.R.M.; Mostafa, W.; Wilson, P.; Morhange, C.; Silverstein, J.; Lasaponara, R. Discovering Potential Settlement Areas around Archaeological Tells Using the Integration between Historic Topographic Maps, Optical, and Radar Data in the Northern Nile Delta, Egypt. Remote Sens. 2019, 11, 3039. [Google Scholar] [CrossRef]
- Nile River in Black and White. Available online: https://www.jpl.nasa.gov/images/pia16179-nile-river-in-black-and-white (accessed on 17 November 2022).
- Curlander, J.C.; Mcdonough, R.N. Synthetic Aperture Radar: Systems and Signal Processing; Wiley: Hoboken, NJ, USA, 1991. [Google Scholar]
- Hua, Z.; Liu, X. An Effective Focusing Approach for Azimuth Invariant Bistatic SAR Processing. Signal Process. 2010, 90, 395–404. [Google Scholar] [CrossRef]
- Cardillo, G.P. On the Use of the Gradient to Determine Bistatic SAR Resolution. In Proceedings of the International Symposium on Antennas and Propagation Society, Merging Technologies for the 90’s, Dallas, TX, USA, 7–11 May 1990; IEEE: Dallas, TX, USA, 1990; pp. 1032–1035. [Google Scholar]
- Jin, Y.-Q.; Xu, F. Bistatic SAR: Simulation, Processing, and Interpretation. In Polarimetric Scattering and SAR Information Retrieval; Wiley: Hoboken, NJ, USA, 2013; pp. 123–165. [Google Scholar]
- Maslikowski, L.; Samczynski, P.; Baczyk, M.; Krysik, P.; Kulpa, K. Passive Bistatic SAR Imaging—Challenges and Limitations. IEEE Aerosp. Electron. Syst. Mag. 2014, 29, 23–29. [Google Scholar] [CrossRef]
- Moreira, A.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.; Younis, M.; Lopez-Dekker, P.; Huber, S.; Villano, M.; Pardini, M.; Eineder, M.; et al. Tandem-L: A Highly Innovative Bistatic SAR Mission for Global Observation of Dynamic Processes on the Earth’s Surface. IEEE Geosci. Remote Sens. Mag. 2015, 3, 8–23. [Google Scholar] [CrossRef]
- Wang, R.; Deng, Y. Bistatic SAR System and Signal Processing Technology; Springer: Berlin/Heildelberg, Germany, 2018. [Google Scholar]
- Summerfield, J.; Kasilingam, D.; Gatesman, A. Bistatic SAR Point Spread Function Analysis for Close Proximity Geometries. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5236715. [Google Scholar] [CrossRef]
- Wu, J.; Yang, J.; Huang, Y.; Yang, H.; Wang, H. Bistatic Forward-Looking SAR: Theory and Challenges. In Proceedings of the Radar Conference, 2009 IEEE, Rome, Italy, 30 September–2 October 2009. [Google Scholar]
- Walterscheid, I.; Espeter, T.; Klare, J.; Brenner, A.R.; Ender, J.H.G. Potential and Limitations of Forward-Looking Bistatic SAR. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 July 2010. [Google Scholar]
- Mei, H.; Meng, Z.; Liu, M.; Li, Y.; Quan, Y.; Zhu, S.; Xing, M. Thorough Understanding Property of Bistatic Forward-Looking High-Speed Maneuvering Platform SAR. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1826–1845. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, J.; Li, Z.; Miao, Y.; Huang, Y.; Yang, J. PFA for Bistatic Forward-Looking SAR Mounted on High-Speed Maneuvering Platforms. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6018–6036. [Google Scholar] [CrossRef]
- Song, X.; Li, Y.; Zhang, T.; Li, L.; Gu, T. Focusing High-Maneuverability Bistatic Forward-Looking SAR Using Extended Azimuth Nonlinear Chirp Scaling Algorithm. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Espeter, T.; Walterscheid, I.; Klare, J.; Brenner, A.R.; Ender, J.H.G. Bistatic Forward-Looking SAR: Results of a Spaceborne–Airborne Experiment. IEEE Geosci. Remote Sens. Lett. 2011, 8, 765–768. [Google Scholar] [CrossRef]
- Qi, C.D.; Shi, X.M.; Bian, M.M.; Xue, Y.J. Focusing Forward-looking Bistatic SAR Data with Chirp Scaling. Electron. Lett. 2014, 50, 206–207. [Google Scholar] [CrossRef]
- Mei, H.; Li, Y.; Xing, M.; Quan, Y.; Wu, C. A Frequency-Domain Imaging Algorithm for Translational Variant Bistatic Forward-Looking SAR. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1502–1515. [Google Scholar] [CrossRef]
- Ding, J. Focusing High Maneuvering Bistatic Forward-Looking SAR With Stationary Transmitter Using Extended Keystone Transform and Modified Frequency Nonlinear Chirp Scaling. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 17. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, J.; Song, Y.; Yang, J.; Li, Z.; Huang, Y. Bistatic-Range-Doppler-Aperture Wavenumber Algorithm for Forward-Looking Spotlight SAR With Stationary Transmitter and Maneuvering Receiver. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2080–2094. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, T.; Mei, H.; Quan, Y.; Xing, M. Focusing Translational-Variant Bistatic Forward-Looking SAR Data Using the Modified Omega-K Algorithm. IEEE Trans. Geosci. Remote Sens. 2021, 8, 1–16. [Google Scholar] [CrossRef]
- Li, Y.; Xu, G.; Zhou, S.; Xing, M.; Song, X. A Novel CFFBP Algorithm With Noninterpolation Image Merging for Bistatic Forward-Looking SAR Focusing. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5225916. [Google Scholar] [CrossRef]
- Sun, H.; Sun, Z.; Chen, T.; Miao, Y.; Wu, J.; Yang, J. An Efficient Backprojection Algorithm Based on Wavenumber-Domain Spectral Splicing for Monostatic and Bistatic SAR Configurations. Remote Sens. 2022, 14, 1885. [Google Scholar] [CrossRef]
- Loffeld, O.; Nies, H.; Peters, V.; Knedlik, S. Models and Useful Relations for Bistatic SAR Processing. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2031–2038. [Google Scholar] [CrossRef]
- Neo, Y.L.; Wong, F.; Cumming, I.G. A Two-Dimensional Spectrum for Bistatic SAR Processing Using Series Reversion. IEEE Geosci. Remote Sens. Lett. 2007, 4, 93–96. [Google Scholar] [CrossRef]
- Qiu, X.; Hu, D.; Ding, C. Some Reflections on Bistatic SAR of Forward-Looking Configuration. IEEE Geosci. Remote Sens. Lett. 2008, 5, 735–739. [Google Scholar] [CrossRef]
- Wu, J.; Yang, J.; Huang, Y.; Yang, H.; Kong, L. A Frequency-Domain Imaging Algorithm for Translational Invariant Bistatic Forward-Looking SAR. IEICE Trans. Commun. 2013, E96.B, 605–612. [Google Scholar] [CrossRef]
- Ma, C.; Gu, H.; Su, W.; Zhang, X.; Li, C. Focusing One-Stationary Bistatic Forward-Looking Synthetic Aperture Radar with Squint Minimisation Method. IET Radar Sonar Navig. 2015, 9, 927–932. [Google Scholar] [CrossRef]
- Meng, Z.; Li, Y.; Xing, M.; Bao, Z. Imaging Method for the Extended Scene of Missile-Borne Bistatic Forward-Looking SAR. J. Xidian Univ. 2016, 3, 31–37. [Google Scholar] [CrossRef]
- Wu, J.; Yang, J.; Huang, Y.; Yang, H. Focusing Bistatic Forward-Looking SAR Using Chirp Scaling Algorithm. In Proceedings of the 2011 IEEE RadarCon (RADAR), Kansas City, MI, USA, 23–27 May 2011; IEEE: Kansas City, MO, USA, 2011; pp. 1036–1039. [Google Scholar]
- Zhang, X.; Gu, H.; Su, W. Squint-minimised Chirp Scaling Algorithm for Bistatic Forward-looking SAR Imaging. IET Radar Sonar Navig. 2020, 14, 290–298. [Google Scholar] [CrossRef]
- Neo, Y.L.; Wong, F.H.; Cumming, I.G. A Comparison of Point Target Spectra Derived for Bistatic SAR Processing. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2481–2492. [Google Scholar] [CrossRef]
- Pu, W.; Li., W.; Lv, Y.; Wang, Z. An Extended Omega-K Algorithm with Integrated Motion Compensation for Bistatic Forward-Looking SAR. In Proceedings of the 2015 IEEE Radar Conference (RadarCon), Arlington, VA, USA, 10–15 May 2015; IEEE: Arlington, VA, USA, 2015; pp. 1291–1295. [Google Scholar]
- Wu, J.; Pu, W.; Huang, Y.; Yang, J.; Yang, H. Bistatic Forward-Looking SAR Focusing Using ω-k Based on Spectrum Modeling and Optimization. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4500–4512. [Google Scholar] [CrossRef]
- Wong, F.W.; Yeo, T.S. New Applications of Nonlinear Chirp Scaling in SAR Data Processing. IEEE Trans. Geosci. Remote Sens. 2001, 39, 946–953. [Google Scholar] [CrossRef]
- Wong, F.H.; Cumming, I.G.; Neo, Y.L. Focusing Bistatic SAR Data Using the Nonlinear Chirp Scaling Algorithm. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2493–2505. [Google Scholar] [CrossRef]
- Qiu, X.; Hu, D.; Ding, C. An Improved NLCS Algorithm With Capability Analysis for One-Stationary BiSAR. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3179–3186. [Google Scholar] [CrossRef]
- Zeng, T.; Wang, R.; Li, F.; Long, T. A Modified Nonlinear Chirp Scaling Algorithm for Spaceborne/Stationary Bistatic SAR Based on Series Reversion. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3108–3118. [Google Scholar] [CrossRef]
- Wu, J.; Sun, Z.; Li, Z.; Huang, Y.; Yang, J.; Liu, Z. Focusing Translational Variant Bistatic Forward-Looking SAR Using Keystone Transform and Extended Nonlinear Chirp Scaling. Remote Sens. 2016, 8, 840. [Google Scholar] [CrossRef]
- Li, Z.; Wu, J.; Sun, Z.; Huang, Y.; Yang, H.; Yang, J. An Adaptive NLCS Technique for Large-Size Moving Target Imaging with Bistatic Forward-Looking SAR. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; IEEE: Fort Worth, TX, USA, 2017; pp. 2369–2372. [Google Scholar]
- Wu, J.; Huang, Y.; Yang, J.; Li, W.; Yang, H. First Result of Bistatic Forward-Looking SAR with Stationary Transmitter. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; IEEE: Vancouver, BC, Canada, 2011; pp. 1223–1226. [Google Scholar]
- Yang, J.; Huang, Y.; Yang, H.; Wu, J.; Li, W.; Li, Z.; Yang, X. A First Experiment of Airborne Bistatic Forward-Looking SAR-Preliminary Results. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium-IGARSS, Melbourne, Australia, 21–26 July 2013; IEEE: Melbourne, Australia, 2013; pp. 4202–4204. [Google Scholar]
- Zhang, Q.; Wu, J.; Yang, J.; Huang, Y.; Yang, H.; Yang, X. Non-Stop-and-Go Echo Model for Hypersonic-Vehicle-Borne Bistatic Forward-Looking Sar. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; IEEE: Valencia, Spain, 2018; pp. 545–548. [Google Scholar]
- Xi, Z.; Duan, C.; Zuo, W.; Li, C.; Huo, T.; Li, D.; Wen, H. Focus Improvement of Spaceborne-Missile Bistatic SAR Data Using the Modified NLCS Algorithm Based on the Method of Series Reversion. Remote Sens. 2022, 14, 5770. [Google Scholar] [CrossRef]
- Rodriguez-Cassola, M.; Baumgartner, S.V.; Krieger, G.; Moreira, A. Bistatic TerraSAR-X/F-SAR Spaceborne–Airborne SAR Experiment: Description, Data Processing, and Results. IEEE Trans. Geosci. Remote Sens. 2010, 48, 781–794. [Google Scholar] [CrossRef]
- Hong, F.; Wang, R.; Zhang, Z.; Lu, P.; Balz, T. Integrated Time and Phase Synchronization Strategy for a Multichannel Spaceborne-Stationary Bistatic SAR System. Remote Sens. 2016, 8, 628. [Google Scholar] [CrossRef]
- Fu, J.; Xing, M.; Sun, G. Time-Frequency Reversion-Based Spectrum Analysis Method and Its Applications in Radar Imaging. Remote Sens. 2021, 13, 600. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, M.; Ai, G.; Wang, P.; Lv, K. Focusing of Bistatic SAR With Curved Trajectory Based on Extended Azimuth Nonlinear Chirp Scaling. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4160–4179. [Google Scholar] [CrossRef]
- Li, C.; Zhang, H.; Deng, Y. Focus Improvement of Airborne High-Squint Bistatic SAR Data Using Modified Azimuth NLCS Algorithm Based on Lagrange Inversion Theorem. Remote Sens. 2021, 13, 1916. [Google Scholar] [CrossRef]
- Fawad; Rahman, M.; Khan, M.J.; Adeel Asghar, M.; Amin, Y.; Badnava, S.; Mirjavadi, S.S. Image Local Features Description Through Polynomial Approximation. IEEE Access 2019, 7, 183692–183705. [Google Scholar] [CrossRef]











| Parameter | Transmitter | Receiver |
|---|---|---|
| Height | 750 km | 10 km |
| Velocity | 7000 m/s | 1000 m/s |
| Max detection range | 757 km | 51 km |
| Carrier band | C | |
| Pulse repetition frequency | 2000 Hz | |
| Range bandwidth | 150 MHz | |
| Synthetic aperture time | 2 s | |
| Method | Targets | Range | Azimuth | ||
|---|---|---|---|---|---|
| PSLR (dB) | ISLR (dB) | PSLR (dB) | ISLR (dB) | ||
| Conventional method | P1 | −12.56 | −9.82 | N/A | N/A |
| P3 | −13.23 | −10.25 | −13.24 | −9.86 | |
| P5 | −12.15 | −9.64 | N/A | N/A | |
| Reference method | P1 | −12.99 | −9.76 | −6.96 | −7.04 |
| P3 | −13.23 | −10.25 | −13.24 | −9.86 | |
| P5 | −12.25 | −9.79 | −11.34 | −8.62 | |
| Proposed method | P1 | −13.21 | −10.12 | −13.21 | −9.74 |
| P3 | −13.23 | −10.25 | −13.24 | −9.86 | |
| P5 | −13.23 | −10.25 | −13.23 | −9.86 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Li, Y.; Song, X.; Wang, X. A Modified NLCS Algorithm for High-Speed Bistatic Forward-Looking SAR Focusing with Spaceborne Illuminator. Remote Sens. 2023, 15, 1699. https://doi.org/10.3390/rs15061699
Liu Y, Li Y, Song X, Wang X. A Modified NLCS Algorithm for High-Speed Bistatic Forward-Looking SAR Focusing with Spaceborne Illuminator. Remote Sensing. 2023; 15(6):1699. https://doi.org/10.3390/rs15061699
Chicago/Turabian StyleLiu, Yuzhou, Yachao Li, Xuan Song, and Xuanqi Wang. 2023. "A Modified NLCS Algorithm for High-Speed Bistatic Forward-Looking SAR Focusing with Spaceborne Illuminator" Remote Sensing 15, no. 6: 1699. https://doi.org/10.3390/rs15061699
APA StyleLiu, Y., Li, Y., Song, X., & Wang, X. (2023). A Modified NLCS Algorithm for High-Speed Bistatic Forward-Looking SAR Focusing with Spaceborne Illuminator. Remote Sensing, 15(6), 1699. https://doi.org/10.3390/rs15061699






