MFGFNet: A Multi-Scale Remote Sensing Change Detection Network Using the Global Filter in the Frequency Domain
Abstract
1. Introduction
- We designed a new deep learning network, MFGFNet, which introduces a series of computer vision technologies, such as global filter, multi-scale feature fusion, etc., into remote sensing change detection. Most of the previous networks cannot obtain enough boundary information of change targets from the pictures, and it is difficult to distinguish the differences and similar information at different scales, which leads to unsatisfactory accuracy of change detection and poor practical results. In this network, potential links between remote sensing images at different times are captured and areas of change are accurately identified. At the same time, our method innovatively uses the global filter in the frequency domain, which enhances the effect of change detection (CD) from a new perspective.
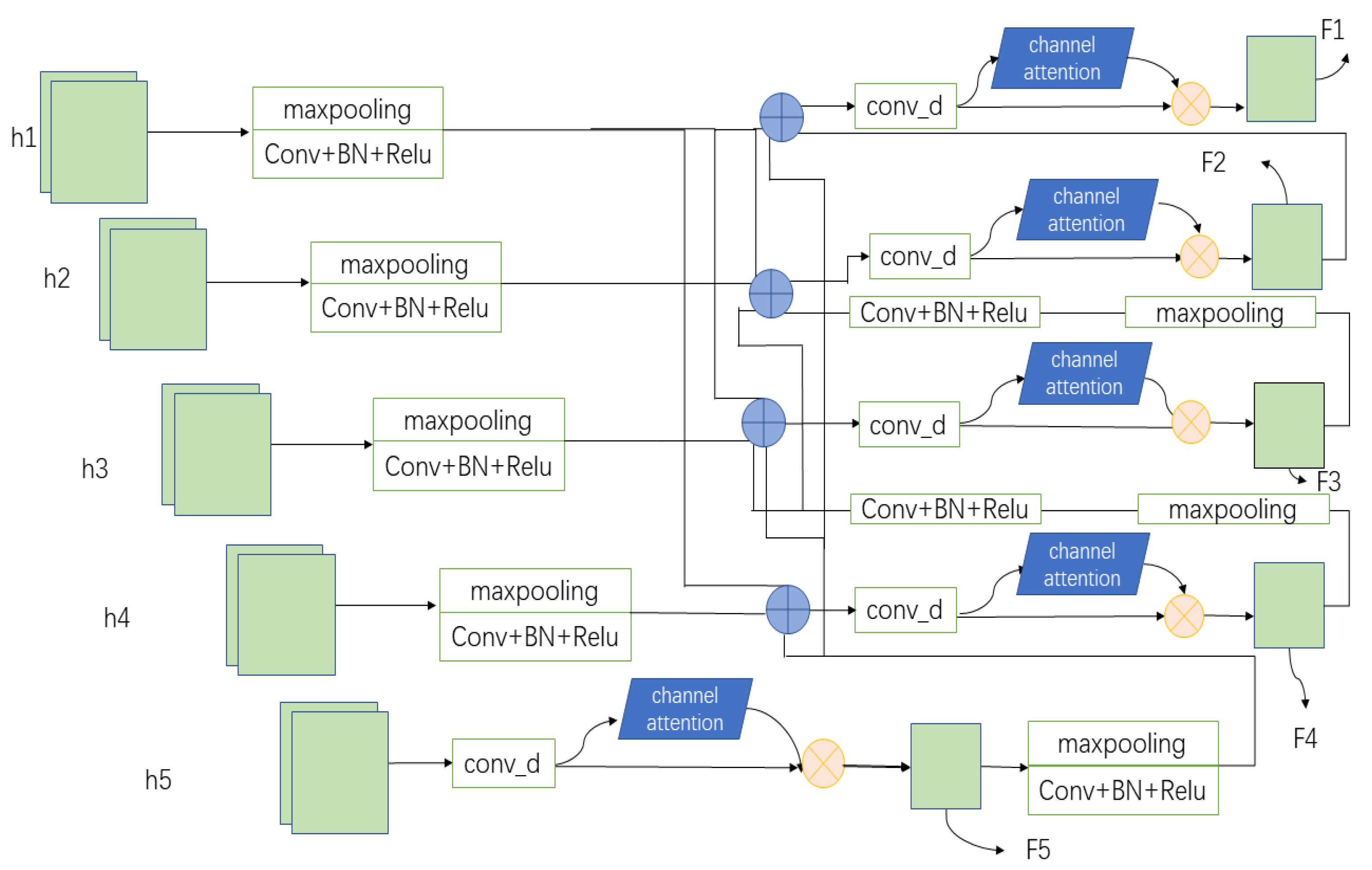
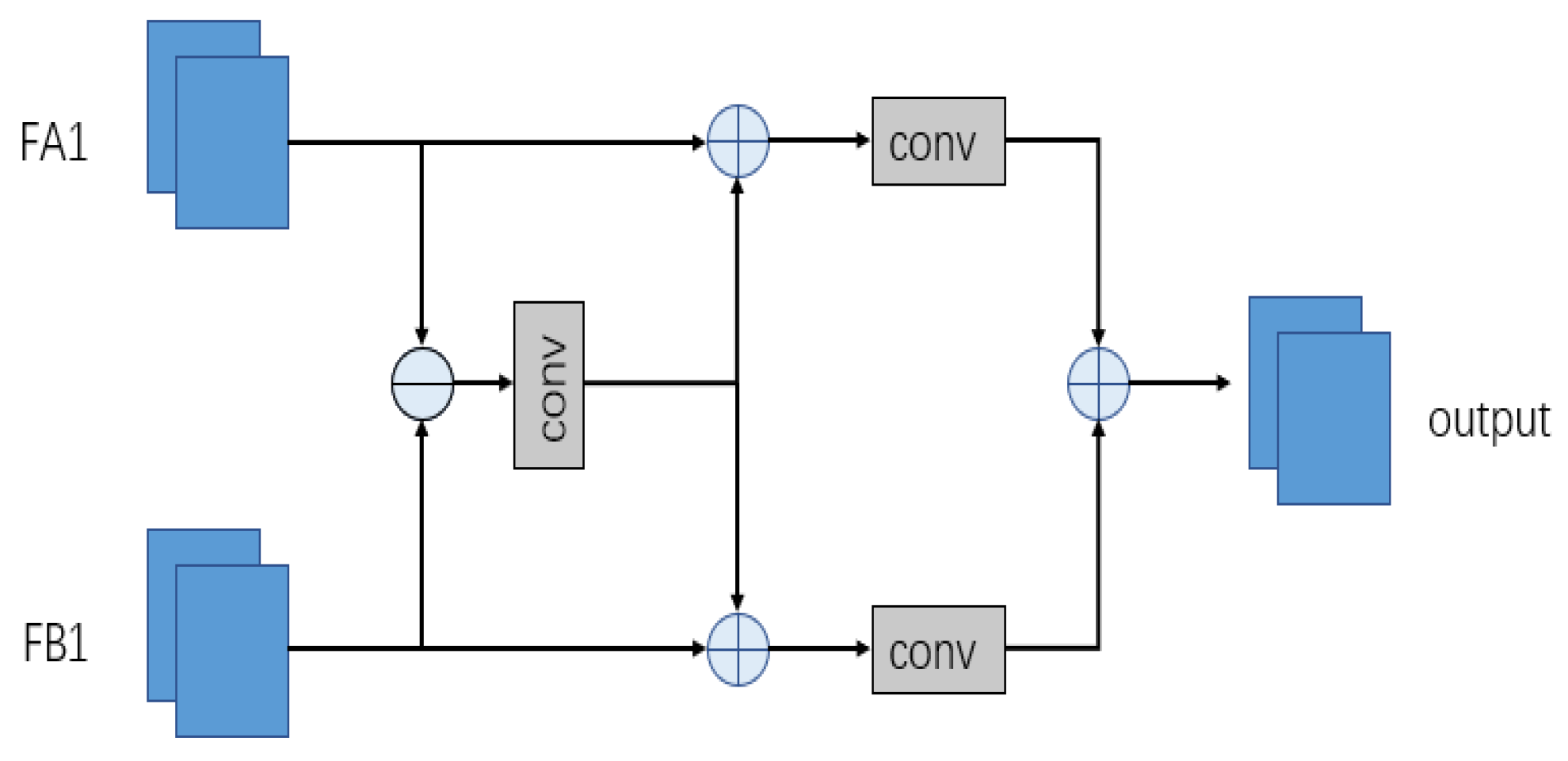
- In order to better extract comprehensive information and help the network to find regions of interest in images with large regional coverage, the muti-scale combination module (MSCB) and feature fusion module (FFM) are proposed. Since change detection data usually include change targets of different sizes, a multi-scale processing approach can be effective, bringing different perceptual fields and, thus, taking care of global and local feature information. As a necessary component of deep learning-based dual-temporal change detection, FFM fuses dual-temporal images and obtains the fused change results. These two modules can better serve for change detection.
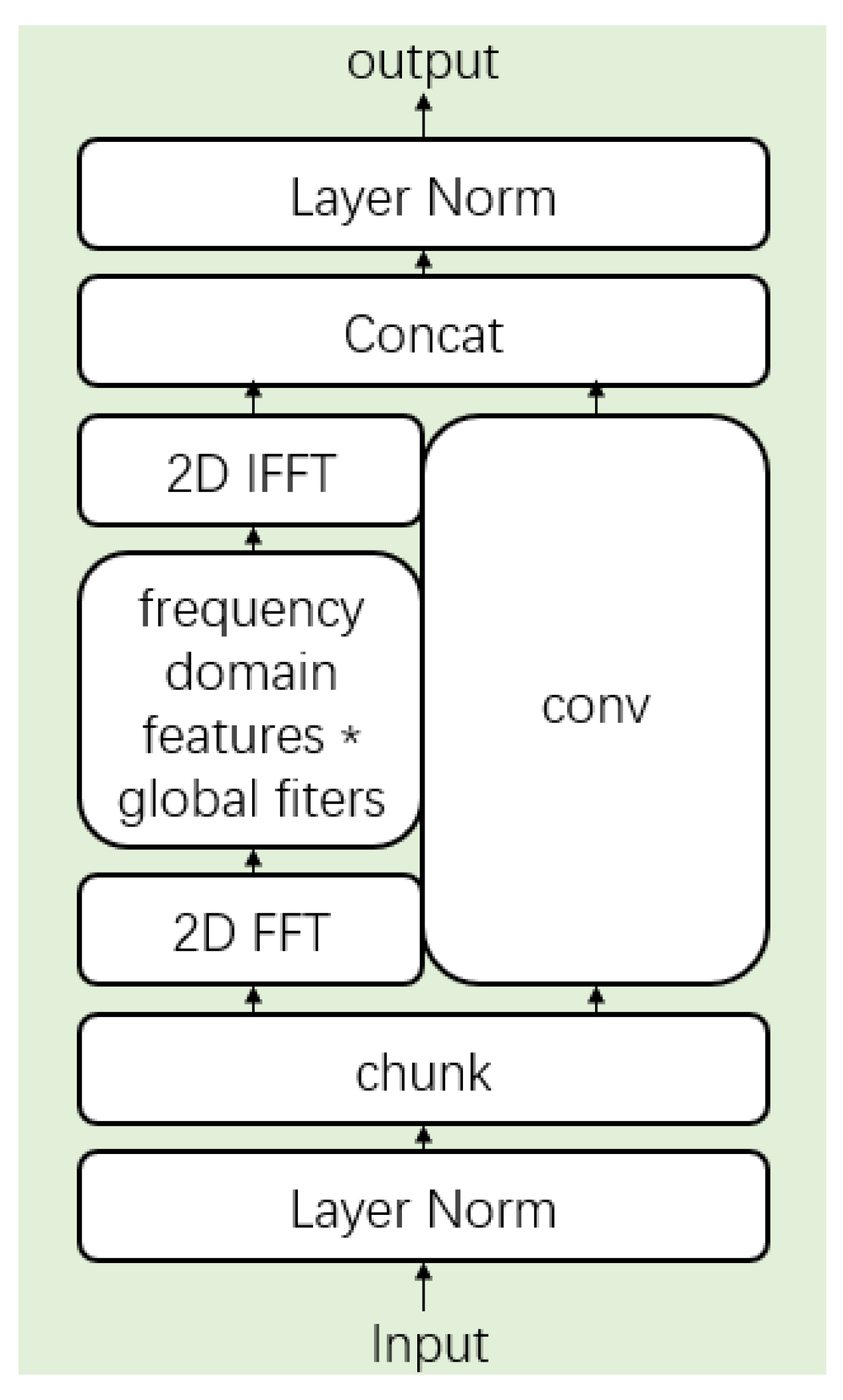
- We use the GF, which can simulate the interaction between different spatial locations, navigating changes and non-changes at the pixel level in the same area. Therefore, our excellent combination of CNN and GF models can better improve the change detection model. Moreover, the global filter (GF) can avoid the huge computational complexity of the Transformer and use 2D Fourier transform and inverse 2D Fourier transform to process the image, which is an effective alternative to the Transformer. Through comparison and experiments with many baseline models, we verify the excellent ability of MFGFNet and confirm the effect of our network on three datasets, LEVIR-CD, SYSU, and CDD.
2. Materials and Methods
2.1. Related Work
2.1.1. Traditional CNN-Based Method
2.1.2. Frequency Domain Learning
2.2. Framework Overview
2.3. Multi-Scale Combination Module
2.4. Feature Fusion Module
2.5. Global Filter
3. Experiments and Results
3.1. Dataset
3.1.1. LEVIR-CD Dataset
3.1.2. SYSU Dataset
3.1.3. CDD Dataset
3.2. Implementation Details
3.3. Evaluation Criteria
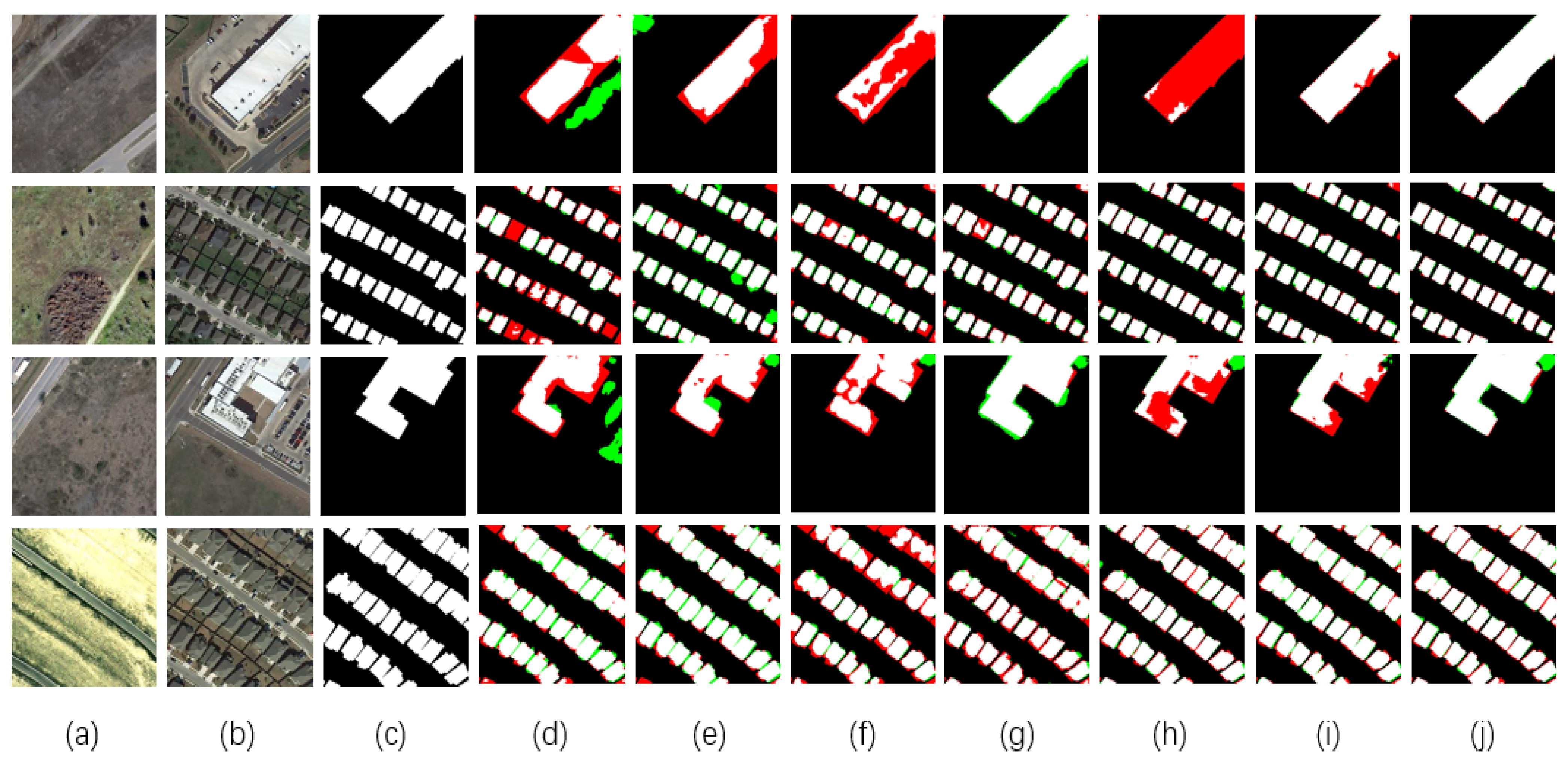
3.4. Comparison and Analysis
3.4.1. Results for LEVIR-CD
3.4.2. Results for SYSU
3.4.3. Results for CDD
3.5. Ablation Study
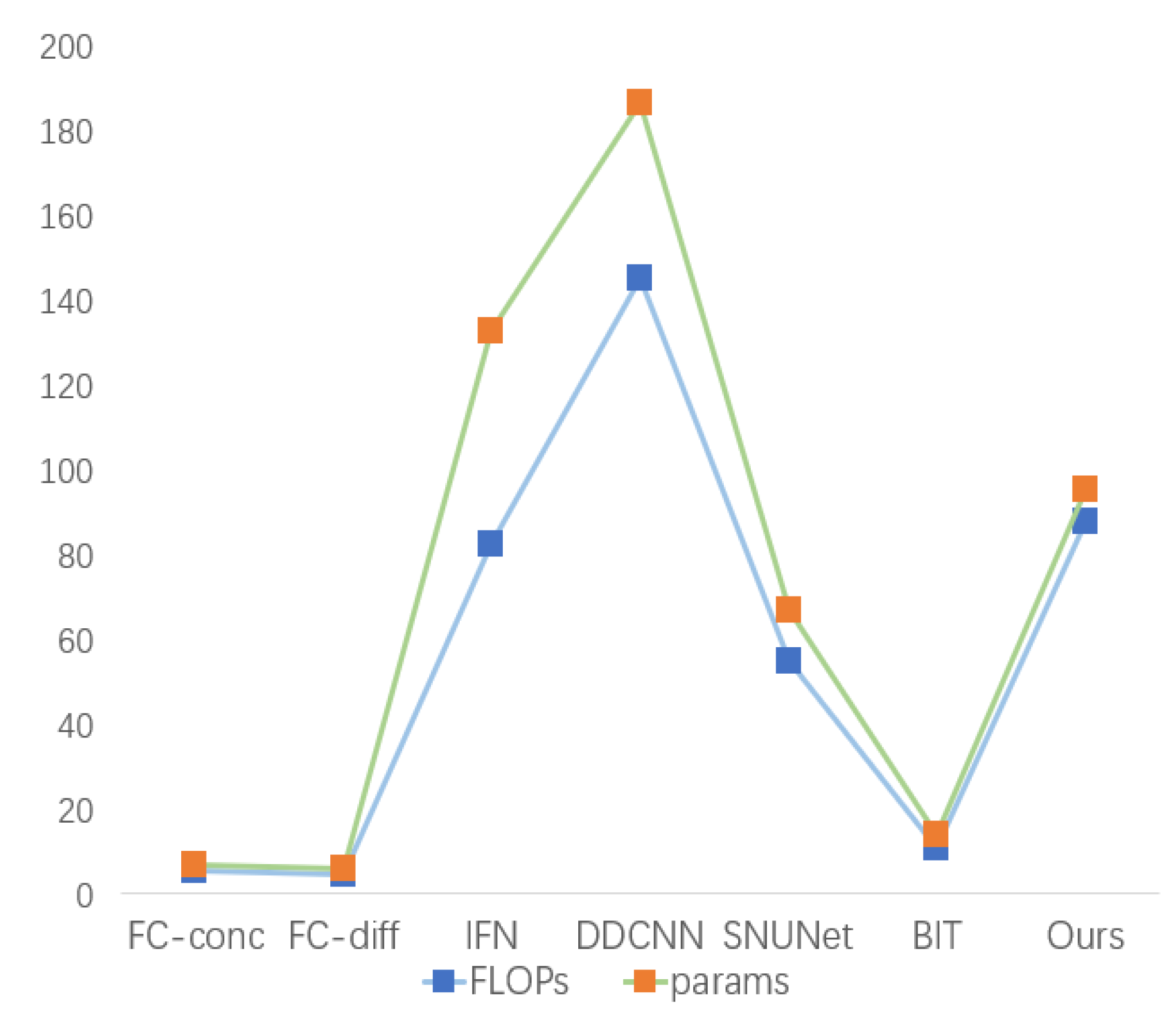
3.6. Parameter Comparison
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lu, D.; Mausel, P.; Brondízio, E.; Moran, E. Change detection techniques. Int. J. Remote Sens. 2004, 25, 2365–2401. [Google Scholar] [CrossRef]
- Hussain, M.; Chen, D.; Cheng, A.; Wei, H.; Stanley, D. Change detection from remotely sensed images: From pixel-based to object-based approaches. ISPRS J. Photogramm. Remote Sens. 1998, 80, 91–106. [Google Scholar] [CrossRef]
- Chen, H.; Shi, Z. A spatial-temporal attention-based method and a new dataset for remote sensing image change detection. Remote Sens. 2020, 12, 1662. [Google Scholar] [CrossRef]
- Ji, S.; Wei, S.; Lu, M. Fully convolutional networks for multisource building extraction from an open aerial and satellite imagery data set. IEEE Trans. Geosci. Remote Sens. 2019, 57, 574–586. [Google Scholar] [CrossRef]
- Peng, D.; Zhang, Y.; Guan, H. End-to-end change detection for high resolution satellite images using improved UNet++. Remote Sens. 2019, 11, 1382. [Google Scholar] [CrossRef]
- Daudt, R.C.; Le Saux, B.; Boulch, A. Fully convolutional Siamese networks for change detection. In Proceedings of the 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 4063–4067. [Google Scholar] [CrossRef]
- Yu, X.; Fan, J.; Chen, J.; Zhang, P.; Zhou, Y.; Han, L. NestNet: A multiscale convolutional neural network for remote sensing image change detection. Int. J. Remote Sens. 2021, 42, 4898–4921. [Google Scholar] [CrossRef]
- Shi, Q.; Liu, M.; Li, S.; Liu, X.; Wang, F.; Zhang, L. A deeply supervised attention metric-based network and an open aerial image dataset for remote sensing change detection. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5604816. [Google Scholar] [CrossRef]
- Chen, J.; Yuan, Z.; Peng, J.; Chen, L.; Huang, H.; Zhu, J.; Liu, Y.; Li, H. DASNet: Dual attentive fully convolutional Siamese networks for change detection in high-resolution satellite images. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 1194–1206. [Google Scholar] [CrossRef]
- Li, Z.; Yan, C.; Sun, Y.; Xin, Q. A Densely Attentive Refinement Network for Change Detection Based on Very-High-Resolution Bitemporal Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–18. [Google Scholar] [CrossRef]
- Lei, T.; Wang, J.; Ning, H.; Wang, X.; Xue, D.; Wang, Q.; Nandi, A.K. Difference Enhancement and Spatial–Spectral Nonlocal Network for Change Detection in VHR Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Basavaraju, K.S.; Sravya, N.; Lal, S.; Nalini, J.; Reddy, C.S.; Dell’Acqua, F. UCDNet: A Deep Learning Model for Urban Change Detection From Bi-Temporal Multispectral Sentinel-2 Satellite Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–10. [Google Scholar] [CrossRef]
- Yang, Y.; Gu, H.; Han, Y.; Li, H. An End-to-End Deep Learning Change Detection Framework for Remote Sensing Images. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020. [Google Scholar]
- Zhu, X.; Su, W.; Lu, L.; Li, B.; Wang, X.; Dai, J. Deformable DETR: Deformable transformers for end-to-end object detection. arXiv 2020, arXiv:2010.04159. [Google Scholar]
- Zheng, S.; Lu, J.; Zhao, H.; Zhu, X.; Luo, Z.; Wang, Y.; Fu, Y.; Feng, J.; Xiang, T.; Torr, P.H.S.; et al. Rethinking semantic segmentation from a sequence-to-sequence perspective with transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 6881–6890. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16×16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Pang, L.; Sun, J.; Chi, Y.; Yang, Y.; Zhang, F.; Zhang, L. CD-TransUNet: A Hybrid Transformer Network for the Change Detection of Urban Buildings Using L-Band SAR Images. Sustainability 2022, 14, 9847. [Google Scholar] [CrossRef]
- Li, Q.; Zhong, R.; Du, X.; Du, Y. TransUNetCD: A Hybrid Transformer Network for Change Detection in Optical Remote-Sensing Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–19. [Google Scholar] [CrossRef]
- Wang, W.; Tan, X.; Zhang, P.; Wang, X. A CBAM Based Multiscale Transformer Fusion Approach for Remote Sensing Image Change Detection. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2022, 15, 6817–6825. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted Windows. arXiv 2021, arXiv:2103.14030. [Google Scholar]
- Zhang, C.; Wang, L.; Cheng, S.; Li, Y. SwinSUNet: Pure Transformer Network for Remote Sensing Image Change Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Rao, Y.; Zhao, W.; Zhu, Z.; Lu, J.; Zhou, J. Global filter networks for image classification. Adv. Neural Inf. Process. Syst. 2021, 34, 980–993. [Google Scholar]
- Fang, S.; Li, K.; Shao, J.; Li, Z. SNUNet-CD: A densely connected Siamese network for change detection of VHR images. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Peng, X.; Zhong, R.; Li, Z.; Li, Q. Optical remote sensing image change detection based on attention mechanism and image difference. IEEE Trans. Geosci. Remote Sens. 2021, 59, 7296–7307. [Google Scholar] [CrossRef]
- Zhang, C.; Yue, P.; Tapete, D.; Jiang, L.; Shangguan, B.; Huang, L.; Liu, G. A deeply supervised image fusion network for change detection in high resolution bi-temporal remote sensing images. ISPRS J. Photogramm. Remote Sens. 2020, 166, 183–200. [Google Scholar] [CrossRef]
- Chen, H.; Qi, Z.; Shi, Z. Remote sensing image change detection with transformers. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–14. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, Y.; Wang, B.; Xu, X.; He, N.; Jin, S.; Jin, S. EGDE-Net: A building change detection method for high-resolution remote sensing imagery based on edge guidance and differential enhancement. ISPRS J. Photogram. Remote Sens. 2022, 191, 203–222. [Google Scholar] [CrossRef]
- Song, X.; Hua, Z.; Li, J. Remote Sensing Image Change Detection Transformer Network Based on Dual-Feature Mixed Attention. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Khusni, U.; Dewangkoro, H.I.; Arymurthy, A.M. Urban area change detection with combining CNN and RNN from Sentinel-2 multispectral remote sensing data. In Proceedings of the International Conference on Computer and Informatics Engineering (IC2IE), Depok, Indonesia, 15–16 September 2020; pp. 171–175. [Google Scholar]
- Papadomanolaki, M.; Verma, S.; Vakalopoulou, M.; Gupta, S.; Karantzalos, K. Detecting urban changes with recurrent neural networks from multitemporal Sentinel-2 data. In Proceedings of the 2019 IEEE International Geoscience and Remote Sensing Symposium(IGARSS), Yokohama, Japan, 28 July–2 August 2019; pp. 214–217. [Google Scholar]
- Lei, T.; Zhang, Y.; Lv, Z.; Li, S.; Liu, S.; Nandi, A.K. Landslide inventory mapping from bitemporal images using deep convolutional neural networks. IEEE Geosci. Remote Sens. Lett. 2019, 16, 982–986. [Google Scholar] [CrossRef]
- Daudt, R.C.; Le Saux, B.; Boulch, A.; Gousseau, Y. Urban change detection for multispectral earth observation using convolutional neural networks. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018; pp. 2115–2118. [Google Scholar]
- Yang, X.; Hu, L.; Zhang, Y.; Li, Y. MRA-SNet: Siamese networks of multiscale residual and attention for change detection in high resolution remote sensing images. Remote Sens. 2021, 13, 4528. [Google Scholar] [CrossRef]
- Cheng, G.; Wang, G.; Han, J. ISNet: Towards Improving Separability for Remote Sensing Image Change Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–11. [Google Scholar] [CrossRef]
- Ding, L.; Guo, H.; Liu, S.; Mou, L.; Zhang, J.; Bruzzone, L. Bi-Temporal Semantic Reasoning for the Semantic Change Detection in HR Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Xu, J.; Luo, C.; Chen, X.; Wei, S.; Luo, Y. Remote sensing change detection based on multidirectional adaptive feature fusion and perceptual similarity. Remote Sens. 2021, 13, 3053. [Google Scholar] [CrossRef]
- Bai, B.; Fu, W.; Lu, T.; Li, S. Edge-Guided Recurrent Convolutional Neural Network for Multitemporal Remote Sensing Image Building Change Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Lei, T.; Xue, D.; Ning, H.; Yang, S.; Lv, Z.; Nandi, A.K. Local and Global Feature Learning With Kernel Scale-Adaptive Attention Network for VHR Remote Sensing Change Detection. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2022, 15, 7308–7322. [Google Scholar] [CrossRef]
- Xu, K.; Qin, M.; Sun, F.; Wang, Y.; Chen, Y.-K.; Ren, F. Learning in the Frequency Domain. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 1737–1746. [Google Scholar] [CrossRef]
- Zheng, S.; Wu, Z.; Xu, Y.; Wei, Z.; Plaza, A. Learning Orientation Information From Frequency-Domain for Oriented Object Detection in Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Sevim, N.; Ozan Özyedek, E.; Şahinuç, F.; Koç, A. Fast-FNet: Accelerating Transformer Encoder Models via Efficient Fourier Layers. arXiv 2022, arXiv:2209.12816. [Google Scholar]
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Wu, E. Squeeze-and-excitation networks. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2011–2023. [Google Scholar] [CrossRef]
- Rao, Y.; Zhao, W.; Tang, Y.; Zhou, J.; Lim, S.; Lu, J. Hornet: Efficient high-order spatial interactions with recursive gated convolutions. arXiv 2022, arXiv:2207.14284. [Google Scholar]
- Bourdis, N.; Marraud, D.; Sahbi, H. Constrained optical flow for aerial image change detection. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 4176–4179. [Google Scholar] [CrossRef]
- Daudt, R.C.; Le Saux, B.; Boulch, A.; Gousseau, Y. Multitask learning for large-scale semantic change detection. Comput. Vis. Image Underst. 2019, 187, 102783. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, L.; Du, B. Kernel Slow Feature Analysis for Scene Change Detection. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2367–2384. [Google Scholar] [CrossRef]
- Shen, L.; Lu, Y.; Chen, H.; Wei, H.; Xie, D.; Yue, J.; Chen, R.; Lv, S.; Jiang, B. S2Looking: A satellite side-Looking dataset for building change detection. Remote Sens. 2021, 13, 5094. [Google Scholar] [CrossRef]
- Lebedev, M.A.; Vizilter, Y.V.; Vygolov, O.V.; Knyaz, V.A.; Rubis, A.Y. Change detection in remote sensing images using conditional adversarial networks. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 2, 565–571. [Google Scholar] [CrossRef]





| Method | Pre | Rec | F1 | OA | IOU |
|---|---|---|---|---|---|
| FC-Conc | 0.8063 | 0.7677 | 0.7865 | 0.9787 | 0.6482 |
| FC-Diff | 0.8222 | 0.6929 | 0.7520 | 0.9767 | 0.6026 |
| IFN | 0.9154 | 0.6128 | 0.7354 | 0.9775 | 0.5816 |
| DDCNN | 0.8542 | 0.8031 | 0.8279 | 0.9830 | 0.7063 |
| SNUNet | 0.9040 | 0.8742 | 0.8889 | 0.9888 | 0.8000 |
| BIT | 0.9130 | 0.8651 | 0.8884 | 0.9889 | 0.7992 |
| Ours | 0.9155 | 0.9014 | 0.9084 | 0.9907 | 0.8322 |
| Method | Pre | Rec | F1 | OA | IOU |
|---|---|---|---|---|---|
| FC-Conc | 0.7300 | 0.7680 | 0.7485 | 0.8783 | 0.5981 |
| FC-Diff | 0.8769 | 0.5133 | 0.6476 | 0.8682 | 0.4788 |
| IFN | 0.8777 | 0.5697 | 0.6909 | 0.8798 | 0.5278 |
| DDCNN | 0.7209 | 0.8230 | 0.7686 | 0.8831 | 0.6241 |
| SNUNet | 0.7865 | 0.7647 | 0.7754 | 0.8955 | 0.6333 |
| BIT | 0.7874 | 0.7653 | 0.7762 | 0.8959 | 0.6343 |
| Ours | 0.8232 | 0.7936 | 0.8081 | 0.9111 | 0.6780 |
| Method | Pre | Rec | F1 | OA | IOU |
|---|---|---|---|---|---|
| FC-Conc | 0.8668 | 0.6004 | 0.7094 | 0.9419 | 0.5497 |
| FC-Diff | 0.8920 | 0.4501 | 0.5983 | 0.9286 | 0.4269 |
| IFN | 0.9108 | 0.8889 | 0.8997 | 0.9766 | 0.8177 |
| DDCNN | 0.9008 | 0.8297 | 0.8638 | 0.9662 | 0.7602 |
| SNUNet | 0.9543 | 0.9420 | 0.9481 | 0.9878 | 0.9014 |
| BIT | 0.9512 | 0.8673 | 0.9073 | 0.9791 | 0.8303 |
| Ours | 0.9564 | 0.9494 | 0.9529 | 0.9889 | 0.9101 |
| FFM | MSCB | GF | Pre | Rec | F1 | OA | IOU |
|---|---|---|---|---|---|---|---|
| √ | × | × | 0.8917 | 0.8512 | 0.8710 | 0.9871 | 0.7715 |
| √ | √ | × | 0.9003 | 0.8878 | 0.8940 | 0.9892 | 0.8083 |
| √ | × | √ | 0.9131 | 0.8773 | 0.8949 | 0.9895 | 0.8098 |
| √ | √ | √ | 0.9155 | 0.9014 | 0.9084 | 0.9907 | 0.8322 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, S.; Zhong, R.; Li, Q.; Dong, Y. MFGFNet: A Multi-Scale Remote Sensing Change Detection Network Using the Global Filter in the Frequency Domain. Remote Sens. 2023, 15, 1682. https://doi.org/10.3390/rs15061682
Yuan S, Zhong R, Li Q, Dong Y. MFGFNet: A Multi-Scale Remote Sensing Change Detection Network Using the Global Filter in the Frequency Domain. Remote Sensing. 2023; 15(6):1682. https://doi.org/10.3390/rs15061682
Chicago/Turabian StyleYuan, Shiying, Ruofei Zhong, Qingyang Li, and Yaxin Dong. 2023. "MFGFNet: A Multi-Scale Remote Sensing Change Detection Network Using the Global Filter in the Frequency Domain" Remote Sensing 15, no. 6: 1682. https://doi.org/10.3390/rs15061682
APA StyleYuan, S., Zhong, R., Li, Q., & Dong, Y. (2023). MFGFNet: A Multi-Scale Remote Sensing Change Detection Network Using the Global Filter in the Frequency Domain. Remote Sensing, 15(6), 1682. https://doi.org/10.3390/rs15061682







