Hyperspectral Anomaly Detection Based on Regularized Background Abundance Tensor Decomposition

Abstract

The low spatial resolution of hyperspectral images means that existing mixed pixels rely heavily on spectral information, making it difficult to differentiate between the target of interest and the background. The endmember extraction method is powerful in enhancing spatial structure information for hyperspectral anomaly detection, whereas most approaches are based on matrix representation, which inevitably destroys the spatial or spectral information. In this paper, we treated the hyperspectral image as a third-order tensor and proposed a novel anomaly detection method based on a low-rank linear mixing model of the scene background. The obtained abundance maps possessed more distinctive features than the raw data, which was beneficial for identifying anomalies in the background. Specifically, the low-rank tensor background was approximated as the mode-3 product of an abundance tensor and endmember matrix. Due to the distinctive features of the background’s abundance maps, we characterized them by tensor regularization and imposed low rankness through CP decomposition, smoothness, and sparsity. In addition, we utilized the ${\ell }_{1,1,2}$-norm to characterize the tube-wise sparsity of the anomaly, since it accounted for a small portion of the scene. The experimental results obtained using five real datasets demonstrated the outstanding performance of our proposed method.

1. Introduction

In contrast to multispectral sensors, hyperspectral sensors enable hundreds of narrow and contiguous bands to be obtained in order to characterize each pixel in a real scene. They have attracted great attention from researchers in signal and image processing, as hyperspectral images (HSIs) contain valuable spatial and spectral information. Over the past few decades, hyperspectral images have been applied in various areas [1], such as data fusion, unmixing, classification, and target detection [2,3,4,5,6,7].

Anomaly detection (AD) aims to detect points of interest, such as natural materials, man-made targets, and other interferers, and to label each pixel as a target or background. AD is one of the most important research fields in HSI processing [8]. Specifically, it is assumed that the spectral signatures of an anomaly are different from those of their surrounding neighbors, which makes it feasible to distinguish anomalies from the background. AD is, in essence, an unsupervised classification problem without prior knowledge of the anomaly or background, leading to an incredibly challenging detection task.

To date, a large number of AD methods have been proposed for HSIs, grouped into three main categories: deep-learning-based, statistics-based, and geometric-modeling-based methods. Deep-learning-based AD algorithms usually use deep neural networks to mine deep features of spectra in HSIs. Since no prior information can be exploited in AD, many researchers train the deep model in an unsupervised way for AD tasks [9,10,11]. However, the deep model for off-the-shelf HSIs still takes a lot of time to train while exhibiting limited generalization ability. Reed–Xiaoli (RX) [12], a benchmark statistics-based method, assumes that the background follows a Gaussian distribution and accomplishes AD via the generalized likelihood ratio test (GLRT). Specifically, the Mahalanobis distance between the pixel being tested and the surrounding background is calculated to determine whether the pixel is an anomaly. Many RX-based methods have been developed [13,14,15,16,17,18]. For example, global RX (GRX) [13] and local RX (LRX) [14] are two typical versions of this method, and they estimate the background statistical variables using the entire image and the surrounding neighbors, respectively. The above methods suffer the limitation of relying on the assumption that the background obeys a single distribution, which is difficult to satisfy in real hyperspectral scenes. Hence, the kernel-RX algorithm [15,16] was developed, which employs a kernel function and maps the data into a higher-dimensional feature space to characterize non-Gaussian distributions. Geometric-modeling-based methods [19,20,21,22,23,24,25,26,27,28] are another category of AD methods. Representation-based methods [19,20,21] have been successfully applied to AD because they do not need a specific distribution assumption, but they fail to capitalize on the high spectral correlation of HSIs. Thus, robust principal component analysis (RPCA) was proposed, which assumes that the background is represented by a single subspace and aims to recover low-rank background and separate a sparse anomaly from an observed HSI [22,23]. Nevertheless, the low-rank representation (LRR)-based model assumed that the data lay in multiple subspaces since most pixels were mixed pixels, which necessitated the exploration of other methods for HSI AD [24,25]. An accurate background dictionary construction for LRR is still a challenging task. Linear mixing model (LMM)-based methods [29] have attracted considerable attention in the AD field due to their explicit physical descriptions obtained through background modeling and their ability to enhance the spatial structure [26,27,28]. Here, the background mixed pixels can be linearly represented by pure material signatures, which is normally accomplished by non-negative matrix factorization (NMF) [30], and they can be approximately written as the product of two non-negative matrices: an endmember matrix and an abundance matrix. Initially, Qu et al. [26] applied spectral unmixing to model original HSI data and regarded the obtained abundance maps as the input for LRR. To enhance the HSI spatial structure smoothness, more recently, the authors of [28] proposed an enhanced total variation (ETV) model with an endmember background dictionary (EBD) by applying ETV to the row vectors of the representation coefficient matrix. The abovementioned methods both achieved promising performance with respect to background modeling using the LMM, though they were matrix-based methods that reshaped the 3D HSI into a 2D matrix and could not avoid destroying the spatial or spectral structure of the HSI.

Since an HSI is essentially a cube, the aforementioned matrix-based background modeling methods failed to explore the intrinsic multidimensional structure of HSIs [31]. In comparison, HSI processing based on tensor decomposition can simultaneously preserve the spatial and spectral structural information [32,33]. Recent developments in tensor-based AD methods have heightened the need for inner-structure preservation [34] and the exploration of tensor physical characteristics [35,36,37]. The spectral signatures of the background pixels in the homogeneous regions have a high correlation, resulting in the background having a strong spatial linear correlation and therefore a low-rank characteristic. Conventional low-rank tensor decomposition [38] includes prior-based tensor approximation, canonical polyadic (CP) decomposition, and Tucker decomposition. Recently, several new tensor decomposition models [39,40,41] were proposed to capture the low-rank structural information in a tensoral manner. Li et al. [35] proposed a prior-based tensor approximation (PTA) method for hyperspectral AD, assuming the low rankness of the spectra and piecewise-smoothness in the spatial domain. Note that PTA actually operates on matrices and not tensors, as the hyperspectral cube is unfolded in 2D structures. Thus, these tensor-based approaches do not allow one to preserve the inner structure of the data. Song et al. [36] proposed an AD algorithm based on endmember extraction and LRR, whereas the physical meaning of the abundance maps underlying the LMM were not exploited.

In this paper, motivated by the fact that abundance maps possess more distinctive features than raw data, contributing to an accurate separation of anomalies from the background, we propose an abundance tensor regularization procedure with low rankness and smoothness based on sparse unmixing (ATLSS) for hyperspectral AD. With the proper modeling of the physical conditions, an observed third-order tensor HSI can be decomposed into a background tensor, an anomaly tensor, and Gaussian noise. Based on the LMM, the background tensor is approximated as a mode-3 product of an abundance tensor and an endmember matrix to enhance the spatial structure information for the existing mixed pixels. Peng [42] also demonstrated that abundance maps inherit the spatial structure of the original HSI, and it is rational to characterize this property on abundance maps. The spectral signatures of the background pixels in the homogeneous regions have a high correlation, which yields a spatial linear correlation and, therefore, a low-rank property. In [31,43], the authors imposed low rankness on the abundance tensor to effectively capture the HSI’s low-dimensional structure. In our paper, the abundance tensor is characterized by tensor regularization with low rankness through CP decomposition. Moreover, each pixel contains limited materials, and neighboring pixels are constituted by similar materials, which display sparsity and spatial smoothness properties. The anomaly part accounts for a small portion of the whole scene, and each tube-wise fiber (i.e., the spectral bands of each pixel) contains few non-zero values, which indicates the tube-wise sparsity of the anomaly tensor. In a real observed HSI, the spectra are usually corrupted with noise caused by the precision limits of the imaging spectrometer and errors in analog-to-digital conversion. This issue was dealt with by modeling the noise as Gaussian random variables [44,45,46]. Here, Gaussian noise was modeled separately to the anomalies to suppress the noise confusion in the anomalies.

The main contributions of this paper can be summarized as follows:

(1)

The low spatial resolution of HSIs means that existing mixed pixels rely heavily on spectral information, which makes it difficult to differentiate the target of interest and the background. Therefore, in view of the LMM, we proposed a completely blind tensor-based model where the background is decomposed using the mode-3 product of the abundance tensor and endmember matrix, with the spatial structure and spectral information preserved. Moreover, the obtained abundance tensor of the background provides more robust structural information, which is essential for AD performance improvement.

(2)

Considering the distinctive features of the background’s abundance maps, we characterized them by tensor regularization and imposed low rankness, smoothness, and sparsity. Specifically, the ${\ell }_1$-norm was introduced to enforce sparseness, and the total variation (TV) regularizer was adopted to encourage spatial smoothness. Moreover, the typically high correlation between abundance vectors implies the low-rank structure of abundance maps. In contrast to the rigorous low-rank constraint, soft low-rank regularization was imposed on the background in order to leverage its spatial homogeneity. Its strictness was controlled by scalar parameters. In addition, for the anomaly part of HSI AD, the ${\ell }_{1,1,2}$-norm was utilized to characterize the tube-wise sparsity, since the anomalies accounted for a small portion of the scene. Gaussian noise was also incorporated into the model to suppress the noise confusion in the anomalies.

The experimental results obtained using five different datasets, with extensive metrics and illustrations, demonstrated that the proposed method significantly outperformed the other competing methods.

The remainder of this article is organized as follows. The third paragraph of Section 2 introduces the problem formulation and proposed method. In Section 3, we evaluate the performance of the proposed method and compare it with some traditional and state-of-the-art AD methods using five real hyperspectral datasets. Finally, the conclusion and future works are presented in Section 4.

2. Problem Formulation and Proposed Method

In this section, we first introduce HSI AD based on the background LMM. The proposed ATLSS algorithm is then illustrated. In addition, the overall flowchart of the proposed ATLSS algorithm for hyperspectral AD is shown in Figure 1.

2.1. Tensor Notation and Definition

This subsection introduces some mathematical notation and preliminaries related to tensors, and our proposed method is clearly described. We use lowercase bold symbols for vectors, e.g., $\mathrm{x}$, and capital letters for matrices, e.g., $\mathrm{X}$. The paper denotes third-order tensors using bold Euler script letters, e.g., $\mathcal{X}$. The scalar is written as x.

Definition 1.

The dimension of a tensor is called the mode, and $\mathcal{X}\in {\mathbb{R}}^{I_1\times I_2\times \cdots \times I_N}$ has N modes. Slices are two-dimensional sections of a tensor and are defined by fixing all but two indices. For a third-order tensor $\mathcal{Y}\in {\mathbb{R}}^{I_1\times I_2\times I_3}$, and ${\mathcal{Y}}_{:,:,k}$ is the k-th frontal slice.

Definition 2

(the mode-n unfolding and folding of a tensor). The “unfold” operation along mode-n on an N-mode tensor $\mathcal{X}\in {\mathbb{R}}^{I_1\times I_2\times \cdots \times I_N}$ is defined as ${unfold}_n\left(\mathcal{X}\right)={\mathcal{X}}_{\left(n\right)}\in$${\mathbb{R}}^{I_n\times (I_1\cdots I_{n-1}{I}_{n+1}\cdots I_N)}$. Its inverse operation is mode-n folding, denoted as $\mathcal{X}={fold}_n\left({\mathcal{X}}_{\left(n\right)}\right)$.

Definition 3

(rank-one tensors). An N-way tensor $\mathcal{X}\in {\mathbb{R}}^{I_1\times I_2\times \cdots \times I_N}$ is a rank-one tensor if it can be written as the outer product of N vectors.

Definition 4

(mode-n product). The mode-n product of tensor $\mathcal{X}\in {\mathbb{R}}^{I_1\times I_2\times \cdots \times I_N}$ and a matrix $\mathrm{U}\in {\mathbb{R}}^{\mathrm{J}\times {\mathrm{I}}_{\mathrm{n}}}$ is defined as:

$${\left(\mathcal{X}{\times }_n\mathrm{U}\right)}_{I_1\cdots I_{n-1}J{I}_{n+1}\cdots I_N}=\sum _{i_n=1}^{I_n}{\mathrm{x}}_{I_1{I}_2\cdots I_N}{\mathrm{u}}_{J{I}_n}$$

(1)

In contrast, the n-mode product can be further computed by matrix multiplication.

$$\mathcal{Y}=\mathcal{X}{\times }_n\mathrm{U}⟺{\mathrm{Y}=\mathrm{U}\mathrm{X}}_{\left(n\right)}$$

(2)

Definition 5

(CP decomposition). CP decomposition factorizes an n-order tensor $\mathcal{X}\in {\mathbb{R}}^{I_1\times I_2\times \cdots \times I_N}$ into a sum of component rank-one tensors as:

$$\mathcal{X}\approx 〚\lambda ;{\mathrm{B}}^{\left(1\right)},{\mathrm{B}}^{\left(2\right)},\cdots ,{\mathrm{B}}^{\left(N\right)}〛\equiv \sum _{r=1}^R{\lambda }_r{\mathrm{b}}_r^{\left(1\right)}\circ {\mathrm{b}}_r^{\left(2\right)}\circ \cdots {\mathrm{b}}_r^{\left(N\right)}$$

(3)

where $\lambda \in {\mathbb{R}}^R$ is the weight vector and ${\mathrm{B}}^{\left(n\right)}=[{\mathrm{b}}_1^{\left(n\right)}\cdots {\mathrm{b}}_R^{\left(n\right)}]\in {\mathbb{R}}^{I_n\times R}$$\forall n=\{1,\cdots ,N\}$ is the n-th factor matrix. R is the rank of tensor $\mathcal{X}$, and we denote $\mathrm{rank}\left(\mathcal{X}\right)=R$.

2.2. HSI AD Based on Background LMM

Since an HSI cube can be naturally treated as a third-order tensor, we used a tensor-based representation to avoid spatial and spectral information loss. In such an AD application, an HSI tensor can be decomposed into so-called background and anomaly tensors [47]. However, in real-world applications, the scenes are usually corrupted by noise [45]; hence, in this paper, noise was also added into the model to suppress its confusion with the estimated anomaly term, and the model is expressed as follows:

$$\mathcal{Y}=\mathcal{B}+\mathcal{E}+\mathcal{N}$$

(4)

where $\mathcal{Y}\in {\mathbb{R}}^{H\times W\times D}$ is the observed HSI and $\mathcal{B}\in {\mathbb{R}}^{H\times W\times D}$, $\mathcal{E}\in {\mathbb{R}}^{H\times W\times D}$, and $\mathcal{N}\in {\mathbb{R}}^{H\times W\times D}$ are the background, anomaly, and noise, respectively. H, W, and D represent the height, width, and number of bands of each tensor, respectively. The purpose of AD is to reconstruct an accurate background image to more accurately separate the anomalies from the background and noise, yielding superior performance.

There are typically several mixed pixels in natural HSI scenes, implying that more than one material constitutes each mixed pixel. This refers to an explicit physical interpretation under the assumption of the LMM; that is, the spectrum of each pixel of a low-rank background can be linearly combined with a few pure spectral endmembers. NMF is an ideal solution for the LMM, as it decomposes the original data into the product of two low-dimensional non-negative matrices. Alternatively, under tensor notation, the tensor background approximates the mode-3 product of a non-negative abundance tensor and a non-negative endmember matrix. Mathematically, Equation (4), inspired by NMF, takes the following form:

$$\begin{array}{lll}\hfill \mathcal{Y}=\mathcal{X}{\times }_3\mathrm{A}+\mathcal{E}+\mathcal{N}& & \\ \hfill \mathrm{s}.\mathrm{t}.\mathcal{X}\ge 0,\mathrm{A}\ge 0\end{array}$$

(5)

where $\mathcal{X}\in {\mathbb{R}}^{H\times W\times R}$ is the third-order abundance tensor, $\mathrm{A}\in {\mathbb{R}}^{\mathrm{D}\times \mathrm{R}}$ is the endmember matrix, and R is the number of endmembers. The third-order abundance tensor is obtained by reshaping each abundance vector into a frontal slice matrix ${\mathcal{X}}_{:,:,r}$$\forall r\in \{1,\cdots ,R\}$ of dimensions $H\times W$ and then stacking them along the mode-3 direction. The newly formed abundance tensor implements the underlying inner low-rank structure information for thorough characterization.

2.3. Proposed Method

An HSI usually consists of a few materials, so it lies in low-rank subspaces. Moreover, a similar substance is distributed in the adjacent region, which gives the HSI a locally smooth property. Compared to the background, anomalies are distributed randomly; thus, anomalies are often assumed to be sparse. Therefore, in this paper, we modeled the problem based on the assumption that the observed HSI was a superposition of a low-rank background, sparse anomalies, and a noise term.

The LMM assumes that each mixed pixel in the background linearly consists of a few endmembers, indicating that many zero entries are contained in the abundance tensor, which can be represented by a sparse property. Remarkably, the ${\ell }_0$-norm can directly minimize non-zero components, but this leads to an NP-hard problem. The ${\ell }_1$-norm, therefore, is introduced to promote the sparsity of the abundance tensor, where the sparsity prior narrows the solution space and achieves accurate abundance tensor estimation. The anomaly pixels occupy a small proportion of the scene, indicating that the anomaly matrix has a column-sparse property and is characterized by the ${\ell }_{2,1}$-norm [48]. Here, we have $\parallel {\mathcal{E}}_{\left(3\right)}{\parallel }_{2,1}={\parallel \mathcal{E}\parallel }_{1,1,2}$; therefore, due to the physical meaning and the definition of the ${\ell }_{1,1,2}$-norm in [49], it is reasonable to assume that the tensor anomaly has tube-wise sparsity. In addition, an HSI is usually corrupted by noise, which is assumed to be identically and independently distributed Gaussian random variables [44]; therefore, the noise was modeled as ${\parallel \mathcal{N}\parallel }_F^2$ to suppress it from being confused with the anomaly. In general, the background model based on the LMM can be rewritten as follows:

$$\begin{array}{ll}\hfill \underset{\mathcal{X},\mathrm{A},\mathcal{E},\mathcal{N}}{min}\frac{1}{2}{\parallel \mathcal{N}\parallel }_F^2+{\lambda }_1{\parallel \mathcal{X}\parallel }_1+\beta {\parallel \mathcal{E}\parallel }_{1,1,2}& \\ \hfill \mathrm{s}.\mathrm{t}.\mathcal{Y}=\mathcal{X}\times {}_3\mathrm{A}+\mathcal{E}+\mathcal{N},\mathcal{X}\ge 0,\mathrm{A}\ge 0\end{array}$$

(6)

where ${\parallel ·\parallel }_1$ and ${\parallel ·\parallel }_F^2$ denote the ${\ell }_1$-norm and ${\ell }_2$-norm, respectively, and ${\lambda }_1$ and $\beta$ are the trade-off parameters that control the sparsity of the abundance tensor and tube-wise sparsity of the anomaly, respectively.

In addition to the single-pixel sparsity, the spatial correlation between the neighboring pixels also deserves to be exploited. It supposes that there is a high correlation among the spectra of the pixels lying in homogeneous regions. For this, we imposed a soft low-rank property on the abundance tensor $\mathcal{X}$ of the background tensor $\mathcal{B}$ in order to model the aforementioned high correlation property of homogeneous regions.

Assuming that $K_{\mathcal{X}}$ designates the rank of the abundance tensor, the loss function for HSI AD could be written as:

$$\begin{array}{l}\underset{\mathcal{X},\mathrm{A},\mathcal{E},\mathcal{N}}{min}\frac{1}{2}{\parallel \mathcal{N}\parallel }_F^2+{\lambda }_1{\parallel \mathcal{X}\parallel }_1+\beta {\parallel \mathcal{E}\parallel }_{1,1,2}\hfill \\ \mathrm{s}.\mathrm{t}.rank\left(\mathcal{X}\right)=K_{\mathcal{X}},\mathcal{Y}=\mathcal{X}{\times }_3\mathrm{A}+\mathcal{E}+\mathcal{N},\mathcal{X}\ge 0,\mathrm{A}\ge 0.\hfill \end{array}$$

(7)

However, the rank of $\mathcal{X}$ in (7) is a non-convex problem in that the optimization is also difficult. Referring to [50], we introduced $\mathcal{Q}$, which was assumed to be low-rank and represents a low-rank prior. Then, CP decomposition was employed to measure the low rankness of $\mathcal{Q}$ via the summation of the $K_{\mathcal{X}}$ rank-one components. Consequently, the CP decomposition of $\mathcal{Q}$ could be written as:

$$\begin{array}{l}\hfill \mathcal{Q}=〚{\mathrm{Z}}^{\left(1\right)},{\mathrm{Z}}^{\left(2\right)},{\mathrm{Z}}^{\left(3\right)}〛=\sum _{\mathrm{i}=1}^{{\mathrm{K}}_{\mathcal{X}}}{\mathrm{z}}_{\mathrm{i}}^{\left(1\right)}\circ {\mathrm{z}}_{\mathrm{i}}^{\left(2\right)}\circ {\mathrm{z}}_{\mathrm{i}}^{\left(3\right)}\end{array}$$

(8)

where ${\mathrm{Z}}^{\left(1\right)}=〚{\mathrm{z}}_1^{\left(1\right)}\cdots {\mathrm{z}}_{{\mathrm{K}}_{\mathcal{X}}}^{\left(1\right)}〛\in {\mathbb{R}}^{\mathrm{H}\times {\mathrm{K}}_{\mathcal{X}}}$, ${\mathrm{Z}}^{\left(2\right)}=〚{\mathrm{z}}_1^{\left(2\right)}\cdots {\mathrm{z}}_{{\mathrm{K}}_{\mathcal{X}}}^{\left(2\right)}〛\in {\mathbb{R}}^{\mathrm{W}\times {\mathrm{K}}_{\mathcal{X}}}$, and ${\mathrm{Z}}^{\left(3\right)}=〚{\mathrm{z}}_1^{\left(3\right)}\cdots {\mathrm{z}}_{{\mathrm{K}}_{\mathcal{X}}}^{\left(3\right)}〛\in {\mathbb{R}}^{\mathrm{D}\times {\mathrm{K}}_{\mathcal{X}}}$ are the factor matrices.

Subsequently, we introduced a new regularization term controlled by a low-rank tensor $\mathcal{Q}$ to enforce a non-strict constraint on $K_{\mathcal{X}}$, as shown in (9). A very large $K_{\mathcal{X}}$ value would lead to the mixing of anomalies into the background, which would undermine the low-rank characterization of the background by the regularization term. Therefore, the parameter ${\lambda }_3$ aimed to modify the strictness of the low-rank constraint on $\mathcal{X}$. Thus, not only was the non-convex issue addressed, but the small-scale details that were necessary for the background could also be preserved. The function based on (7) was approximately rewritten as:

$$\begin{array}{ll}\hfill & \underset{\mathcal{X},\mathrm{A},\mathcal{E},\mathcal{Q},\mathcal{N}}{min}\frac{1}{2}{\parallel \mathcal{N}\parallel }_F^2+{\lambda }_1{\parallel \mathcal{X}\parallel }_1+\frac{{\lambda }_3}{2}{\parallel \mathcal{X}-\mathcal{Q}\parallel }_F^2+\beta {\parallel \mathcal{E}\parallel }_{1,1,2}\\ \hfill & \mathrm{s}.\mathrm{t}.rank\left(\mathcal{Q}\right)=K_{\mathcal{X}},\mathcal{Y}=\mathcal{X}{\times }_3\mathrm{A}+\mathcal{E}+\mathcal{N},\mathcal{X}\ge 0,\mathrm{A}\ge 0\end{array}$$

(9)

where the rank is controlled by $K_{\mathcal{X}}$. Then, the model of (9) could be rewritten as:

$$\begin{array}{l}\underset{\mathcal{X},\mathrm{A},\mathcal{E},{\mathrm{Z}}^{\left(1\right)},{\mathrm{Z}}^{\left(2\right)},{\mathrm{Z}}^{\left(3\right)},\mathcal{N}}{min}\frac{1}{2}{\parallel \mathcal{N}\parallel }_F^2+{\lambda }_1{\parallel \mathcal{X}\parallel }_1+\frac{{\lambda }_3}{2}\parallel \mathcal{X}-〚{\mathrm{Z}}^{\left(1\right)},{\mathrm{Z}}^{\left(2\right)},{\mathrm{Z}}^{\left(3\right)}{〛\parallel }_F^2+\beta {\parallel \mathcal{E}\parallel }_{1,1,2}\\ \mathrm{s}.\mathrm{t}.\mathcal{Y}=\mathcal{X}{\times }_3\mathrm{A}+\mathcal{E}+\mathcal{N},\mathcal{X}\ge 0,\mathrm{A}\ge 0.\end{array}$$

(10)

Notably, pixels with spatial homogeneity are more likely to contain the same materials, which indicates the fractional abundance of the adjacent pixels that tend to be similar. Here, the spatial context information of the abundance tensor was characterized by the TV regularizer [51] by encouraging a piecewise smoothness structure with the distinct edges preserved. The spatial TV norm of the abundance tensor $\mathcal{X}$ is defined as [52]:

$${\parallel \mathcal{X}\parallel }_{TV}={\parallel \mathcal{H}\mathcal{X}\parallel }_1={∥{\mathcal{H}}_h\mathcal{X}∥}_1+{∥{\mathcal{H}}_v\mathcal{X}∥}_1.$$

(11)

Let ${\mathcal{X}}_{h,w,r}{|}_{\forall h=\{1,\dots ,H\},w=\{1,\dots ,W\},r=\{1,\dots ,R\}}$ indicate the intensity of the voxel $(h,w,r)$ and ${\mathcal{H}}_h$ and ${\mathcal{H}}_v$ be the two horizontal and vertical differential operators in the spatial domain, respectively. Then, we have:

$$\left\{\begin{array}{c}{\mathcal{H}}_h{\mathcal{X}}_{h,w,r}={\mathcal{X}}_{h,w+1,r}-{\mathcal{X}}_{h,w,r}\\ {\mathcal{H}}_v{\mathcal{X}}_{h,w,r}={\mathcal{X}}_{h+1,w,r}-{\mathcal{X}}_{h,w,r}\end{array}\right.$$

(12)

The TV-based cost function corresponding to (10) could be modeled as:

$$\begin{array}{ll}\hfill & \underset{\mathcal{X},\mathrm{A},\mathcal{E},\mathcal{N}}{min}\frac{1}{2}{\parallel \mathcal{N}\parallel }_F^2+{\lambda }_1{\parallel \mathcal{X}\parallel }_1+{\lambda }_2{\parallel \mathcal{X}\parallel }_{TV}+\beta {\parallel \mathcal{E}\parallel }_{1,1,2}\\ \hfill & \mathrm{s}.\mathrm{t}.rank\left(\mathcal{X}\right)=K_{\mathcal{X}},\mathcal{Y}=\mathcal{X}{\times }_3\mathrm{A}+\mathcal{E}+\mathcal{N},\mathcal{X}\ge 0,\mathrm{A}\ge 0\end{array}$$

(13)

where ${\parallel ·\parallel }_{TV}$ is the TV norm and ${\lambda }_2$ is a parameter to adjust the strength of the piecewise smoothness.

Similarly to $\left(7\right)$ and $\left(8\right)$, this could be further rewritten as:

$$\begin{array}{ll}\hfill & \underset{\mathcal{X},\mathrm{A},\mathcal{E},{\mathrm{Z}}^{\left(1\right)},{\mathrm{Z}}^{\left(2\right)},{\mathrm{Z}}^{\left(3\right)},\mathcal{N}}{min}\frac{1}{2}{\parallel \mathcal{N}\parallel }_F^2+{\lambda }_1{\parallel \mathcal{X}\parallel }_1+{\lambda }_2{\parallel \mathcal{X}\parallel }_{TV}+\frac{{\lambda }_3}{2}\parallel \mathcal{X}-〚{\mathrm{Z}}^{\left(1\right)},{\mathrm{Z}}^{\left(2\right)},{\mathrm{Z}}^{\left(3\right)}{〛\parallel }_F^2+\beta {\parallel \mathcal{E}\parallel }_{1,1,2}\\ \hfill & \mathrm{s}.\mathrm{t}.\mathcal{Y}=\mathcal{X}{\times }_3\mathrm{A}+\mathcal{E}+\mathcal{N},\mathcal{X}\ge 0,\mathrm{A}\ge 0.\end{array}$$

(14)

2.4. Optimization Procedure

The optimization problem in (14) could be solved by ADMM. We needed to introduce three auxiliary variables, ${\mathcal{V}}_1,{\mathcal{V}}_2$, and ${\mathcal{V}}_3$, and then transform it into the following equivalent problem:

$$\begin{array}{l}\hfill \underset{\mathcal{X},\mathrm{A},\mathcal{E},{\mathrm{Z}}^{\left(1\right)},{\mathrm{Z}}^{\left(2\right)},{\mathrm{Z}}^{\left(3\right)},\mathcal{N}}{min}\frac{1}{2}{\parallel \mathcal{N}\parallel }_F^2+{\lambda }_1\parallel {\mathcal{V}}_3{\parallel }_1+{\lambda }_2\parallel {\mathcal{V}}_2{\parallel }_1+\frac{{\lambda }_3}{2}\parallel \mathcal{X}-〚{\mathrm{Z}}^{\left(1\right)},{\mathrm{Z}}^{\left(2\right)},{\mathrm{Z}}^{\left(3\right)}〛\parallel {}_F^2+\beta {\parallel \mathcal{E}\parallel }_{1,1,2}\\ \hfill \mathrm{s}.\mathrm{t}.\mathrm{A}\ge 0,\mathcal{X}\ge 0,\mathcal{X}={\mathcal{V}}_1,{\mathcal{HV}}_1={\mathcal{V}}_2,\mathcal{X}={\mathcal{V}}_3,\mathcal{Y}=\mathcal{X}\times {}_3\mathrm{A}+\mathcal{E}+\mathcal{N}.\end{array}$$

(15)

The problem in (15) could be solved by ALM [53] to minimize the following augmented Lagrangian function:

$$\begin{array}{ll}\hfill & \mathcal{L}\left(\mathcal{X},\mathrm{A},\mathcal{Q},\mathcal{N},\mathcal{E},{\mathcal{V}}_1,{\mathcal{V}}_2,{\mathcal{V}}_3,{\mathcal{D}}_1,{\mathcal{D}}_2,{\mathcal{D}}_3,{\mathcal{D}}_4\right)\\ \hfill & =\frac{1}{2}{\parallel \mathcal{N}\parallel }_F^2+{\lambda }_1{∥{\mathcal{V}}_3∥}_1+{\lambda }_2{∥{\mathcal{V}}_2∥}_1+\frac{{\lambda }_3}{2}{\parallel \mathcal{X}-\mathcal{Q}\parallel }_F^2+{\beta \parallel \mathcal{E}\parallel }_{1,1,2}+\frac{\mu }{2}({∥\mathcal{X}-{\mathcal{V}}_1+{\mathcal{D}}_1∥}_F^2+\\ \hfill & {∥\mathcal{H}{\mathcal{V}}_1-{\mathcal{V}}_2+{\mathcal{D}}_2∥}_F^2+\left.∥\mathcal{X}-{\mathcal{V}}_3+{\mathcal{D}}_3∥{}_F^2+∥\mathcal{Y}-\mathcal{X}\times {}_3\mathrm{A}-\mathcal{E}-\mathcal{N}+{\mathcal{D}}_4{\parallel }_{\mathrm{F}}^2\right)\mathrm{s}.\mathrm{t}.\mathrm{A}\ge 0,\mathcal{X}\ge 0\end{array}$$

(16)

where ${\mathcal{D}}_1$, ${\mathcal{D}}_2$, ${\mathcal{D}}_3$, and ${\mathcal{D}}_4$ are the Lagrange multipliers, and $\mu$ is the penalty parameter. The above problem could be solved by updating one variable while fixing the others. Specifically, in the $t+1$-th iteration, where the problem could be divided into several subproblems, the variables were updated as follows:

Update $\mathcal{X}$:

$$\begin{array}{l}\hfill {\mathcal{X}}^{(t+1)}=\underset{\mathcal{X}}{argmin}\frac{{\lambda }_3}{2}{∥\mathcal{X}-Q^{\left(t\right)}∥}_F^2+\frac{\mu }{2}({∥\mathcal{X}-{\mathcal{V}}_1^{\left(t\right)}+{\mathcal{D}}_1^{\left(t\right)}∥}_F^2+{∥\mathcal{X}-{\mathcal{V}}_3^{\left(t\right)}+{\mathcal{D}}_3^{\left(t\right)}∥}_F^2\\ \hfill +{∥\mathcal{Y}-\mathcal{X}\times {}_3{\mathrm{A}}^{\left(t\right)}-{\mathcal{E}}^{\left(t\right)}-{\mathcal{N}}^{\left(t\right)}+{\mathcal{D}}_4^{\left(t\right)}∥}_F^2)\mathrm{s}.\mathrm{t}.\mathcal{X}\ge 0\end{array}$$

(17)

which could be transformed into the following linear system:

$$\begin{array}{l}{\mathcal{X}}^{(t+1)}=\mathcal{X}·\ast \left[\right(\mu \times (\mathcal{Y}-{\mathcal{E}}^{\left(t\right)}-{\mathcal{N}}^{\left(t\right)}+{\mathcal{D}}_4^{\left(t\right)}){\times }_3{\mathrm{A}}^{{\left(t\right)}^T}+{\lambda }_3{Q}^{\left(t\right)}\\ +\mu ({\mathcal{V}}_1^{\left(t\right)}-{\mathcal{D}}_1^{\left(t\right)}+{\mathcal{V}}_3^{\left(t\right)}-{\mathcal{D}}_3^{\left(t\right)})·(\mu \times \mathcal{X}{\times }_3\left({\mathrm{A}}^{{\left(t\right)}^T}{\mathrm{A}}^{\left(t\right)}\right)+({\lambda }_3+2\mu )\mathcal{X})].\end{array}$$

(18)

Update $\mathrm{A}$:

$$\begin{array}{l}\hfill {\mathrm{A}}^{(t+1)}=\underset{\mathrm{A}}{argmin}{∥\mathcal{Y}-{\mathcal{X}}^{(t+1)}\times {}_3{\mathrm{A}}^{\left(t\right)}-{\mathcal{E}}^{\left(t\right)}-{\mathcal{N}}^{\left(t\right)}+{\mathcal{D}}_4^{\left(t\right)}∥}_F^2\mathrm{s}.\mathrm{t}.\mathrm{A}\ge 0.\end{array}$$

(19)

Similarly to (18), we obtained the following solution:

$$\begin{array}{l}\hfill {\mathrm{A}}^{(t+1)}=\mathrm{A}\ast \left(\mathcal{Y}-{\mathcal{E}}^{\left(\mathrm{t}\right)}-{\mathcal{N}}^{\left(\mathrm{t}\right)}+{\mathcal{D}}_4^{\left(\mathrm{t}\right)}\right){\mathcal{X}}^{{\langle \mathrm{t}+1)}^{\mathrm{T}}}·/\mathrm{A}{\mathcal{X}}^{(\mathrm{t}+1)}{\mathcal{X}}^{{(\mathrm{t}+1)}^{\mathrm{T}}}.\end{array}$$

(20)

Update $\mathcal{B}$:

We combined (18) and (20) and computed the result as follows:

$$\begin{array}{l}\hfill {\mathcal{B}}^{(t+1)}={\mathcal{X}}^{(t+1)}\times {}_3{\mathrm{A}}^{(t+1)}.\end{array}$$

(21)

Update $\mathcal{Q}$:

$$\begin{array}{l}\hfill {\mathcal{Q}}^{(t+1)}=\underset{\mathcal{Q}}{argmin}\frac{{\lambda }_3}{2}{∥{\mathcal{X}}^{(t+1)}-\mathcal{Q}∥}_F^2.\end{array}$$

(22)

By substituting (13) into (14), the optimization problem became:

$$\begin{array}{l}\hfill \left({\mathrm{Z}}^{\left(1\right)},{\mathrm{Z}}^{\left(2\right)},{\mathrm{Z}}^{\left(3\right)}\right)=\underset{{\mathrm{Z}}^{\left(1\right)},{\mathrm{Z}}^{\left(2\right)},{\mathrm{Z}}^{\left(3\right)}}{argmin}\frac{{\lambda }_3}{2}{∥\mathcal{X}-〚{\mathrm{Z}}^{\left(1\right)},{\mathrm{Z}}^{\left(2\right)},{\mathrm{Z}}^{\left(3\right)}〛∥}_F^2\end{array}$$

(23)

where CP decomposition was solved by an alternating least-squares (ALS) [54] algorithm. Consequently, each factor matrix was calculated through a linear least-squares approach by fixing the other two matrices.

Update $\mathcal{N}$

$$\begin{array}{l}\hfill {\mathcal{N}}^{(t+1)}=\underset{\mathcal{N}}{argmin}\frac{1}{2}{∥{\mathcal{N}}^{\left(t\right)}∥}_F^2+\frac{\mu }{2}{\parallel \mathcal{Y}-{\mathcal{X}}^{(t+1)}\times {}_3{\mathrm{A}}^{(t+1)}-{\mathcal{E}}^{\left(t\right)}-{\mathcal{N}}^{\left(t\right)}+{\mathcal{D}}_4^{(t+1)}\parallel }_F^2\end{array}$$

(24)

for which the solution is:

$$\begin{array}{l}\hfill {\mathcal{N}}^{(t+1)}=\frac{\mu \left(\mathcal{Y}-{\mathcal{X}}^{(t+1)}\times {}_3{\mathrm{A}}^{(t+1)}-{\mathcal{E}}^{\left(t\right)}+{\mathcal{D}}_4^{\left(t\right)}\right)}{(\mu +1)}.\end{array}$$

(25)

Update ${\mathcal{V}}_1$:

$$\begin{array}{l}\hfill {\mathcal{V}}_1^{(t+1)}=\underset{{\mathcal{V}}_1}{argmin}{∥{\mathcal{X}}^{(t+1)}-{\mathcal{V}}_1^{\left(t\right)}+{\mathcal{D}}_1^{\left(t\right)}∥}_F^2+{∥\mathcal{H}{\mathcal{V}}_1^{\left(t\right)}-{\mathcal{V}}_2^{\left(t\right)}+{\mathcal{D}}_2^{\left(t\right)}∥}_F^2.\end{array}$$

(26)

Next, we solved the subproblem of ${\mathcal{V}}_1$:

$$\begin{array}{l}\hfill \left({\mathcal{H}}^T\mathcal{H}+\mathcal{I}\right){\mathcal{V}}_1^{(t+1)}=\left({\mathcal{X}}^{(t+1)}+{\mathcal{D}}_1^{\left(t\right)}\right)+{\mathcal{H}}^{\ast }\left({\mathcal{V}}_2^{\left(t\right)}-{\mathcal{D}}_2^{\left(t\right)}\right).\end{array}$$

(27)

where $\mathcal{I}$ is the identity tensor; $\mathcal{H}$ is a convolution, as defined in (12), that operates in the spatial domain; and ${\mathcal{H}}^T$ indicates the adjoint operator of $\mathcal{H}$. Therefore, ${\mathcal{V}}_1$ could be quickly computed by:

$$\begin{array}{l}\hfill {\mathcal{V}}_1^{(t+1)}=ifft\left(\frac{{\mathcal{X}}^{(t+1)}+{\mathcal{D}}_1^{\left(t\right)}+{\mathcal{H}}^T\left({\mathcal{V}}_2^{\left(t\right)}-{\mathcal{D}}_2^{\left(t\right)}\right)}{1+fft{\left({\mathcal{H}}_h\right)}^{T}fft\left({\mathcal{H}}_h\right)+fft{\left({\mathcal{H}}_v\right)}^{T}fft\left({\mathcal{H}}_v\right)}\right)\end{array}$$

(28)

where $fft$ and $ifft$ denote the fast Fourier transform [55] and its inverse, respectively.

Update ${\mathcal{V}}_2$ and ${\mathcal{V}}_3$:

$$\begin{array}{l}\hfill {\mathcal{V}}_2^{(t+1)}=\underset{{\mathcal{V}}_2}{argmin}{\lambda }_2{∥{\mathcal{V}}_2^{\left(t\right)}∥}_1+\frac{\mu }{2}{∥\mathcal{H}{\mathcal{V}}_1^{(t+1)}-{\mathcal{V}}_2^{\left(t\right)}+{\mathcal{D}}_2^{\left(t\right)}∥}_F^2\end{array}$$

(29)

which could be solved by a soft-thresholding function. The update rule for ${\mathcal{V}}_3$ was similar to that of ${\mathcal{V}}_2$.

Update $\mathcal{E}$:

$$\begin{array}{l}\hfill {\mathcal{E}}^{(t+1)}=\underset{\epsilon }{argmin}\frac{\mu }{2}{∥\mathcal{Y}-{\mathcal{X}}^{(t+1)}\times {}_3{\mathrm{A}}^{(t+1)}-\mathcal{E}-{\mathcal{N}}^{(t+1)}+{\mathcal{D}}_4^{\left(t\right)}∥}_F^2+\beta {\parallel \mathcal{E}\parallel }_{1,1,2}.\end{array}$$

(30)

Given ${\mathcal{F}}^{\left(t\right)}=\mathcal{Y}-{\mathcal{X}}^{(t+1)}\times {}_3{\mathrm{A}}^{(t+1)}-{\mathcal{N}}^{(t+1)}+{\mathcal{D}}_4^{\left(t\right)}$, the closed solution of (30) could be calculated as:

$$\begin{array}{l}\hfill {\mathcal{E}}^{(t+1)}(h,w,:)=max\left(1-\frac{\beta }{{\mu }^{\left(t\right)}{∥{\mathcal{F}}^{\left(t\right)}(h,w,:)∥}_F},0\right)\ast {\mathcal{F}}^{\left(t\right)}(h,w,:)\end{array}$$

(31)

where $h\in \{1,\cdots ,H\}$ and $w\in \{1,\cdots ,W\}$.

Update ${\mathcal{D}}_1$, ${\mathcal{D}}_2$, ${\mathcal{D}}_3$, ${\mathcal{D}}_4$, and $\mu$:

$$\begin{array}{l}\hfill {\mathcal{D}}_1^{(t+1)}={\mathcal{D}}_1^{\left(t\right)}+{\mathcal{X}}^{(t+1)}-{\mathcal{V}}_1^{(t+1)},\end{array}$$

(32)

$$\begin{array}{l}\hfill {\mathcal{D}}_2^{(t+1)}={\mathcal{D}}_2^{\left(t\right)}+\mathcal{H}{\mathcal{V}}_1^{(t+1)}-{\mathcal{V}}_2^{(t+1)},\end{array}$$

(33)

$$\begin{array}{l}\hfill {\mathcal{D}}_3^{(t+1)}={\mathcal{D}}_3^{\left(t\right)}+{\mathcal{X}}^{(t+1)}-{\mathcal{V}}_3^{(t+1)},\end{array}$$

(34)

$$\begin{array}{l}\hfill {\mathcal{D}}_4^{(t+1)}=\mathcal{Y}-{\mathcal{X}}^{\langle t+1)}\times {}_3{\mathrm{A}}^{(t+1)}-{\mathcal{E}}^{(t+1)}-{\mathcal{N}}^{(t+1)}+{\mathcal{D}}_4^{\left(t\right)},\end{array}$$

(35)

$$\begin{array}{l}\hfill {\mu }^{(t+1)}=min\left(\rho {\mu }^{\left(t\right)},{\mu }_{max}\right).\end{array}$$

(36)

Finally, according to the anomaly $\mathcal{E}$, the AD maps $\mathrm{T}$ could be obtained by ${\mathrm{T}}_{h,w}=\parallel {\mathcal{E}}_{h,w,:}{{\parallel }_F|}_{\forall h=\{1,\cdots ,H\},w=\{1,\cdots ,W\}}$. Then, we arrived at an augmented Lagrangian alternating direction method to solve the proposed ATLSS model.

2.5. Initialization and Termination Conditions

In the proposed ATLSS solver, the input terms were the observed HSI, the basis matrix $\mathrm{A}$, the abundance matrix $\mathcal{X}$, and the number of endmembers R. It is worth noting that the initialization of $\mathrm{A}$, $\mathcal{X}$, and R influenced the AD results of the proposed method. Hence, we initialized the background $\mathcal{B}$ by the RX algorithm. Then, HySime [56] was employed to estimate the number of background endmembers R. Afterward, NMF [57] and the related update rules were utilized to iterate over $\mathrm{A}$ and $\mathcal{X}$, respectively. The CP rank K was determined by the algorithm referred to in [50] to provide an accurate rank estimation for the proposed method. In general, the iterative process continued until a maximum number of 100 iterations or a residual error was satisfied.

2.6. Computational Complexity Analysis

Each iteration’s computational cost consisted of updating all the relevant factors. The time complexity of CP decomposition (update $\mathcal{Q}$) is $\mathcal{O}(T_{max}{R}^2(W^2{D}^2+H^2{D}^2+H^2{W}^2\left)\right)$; the time complexity of FFT (update ${\mathcal{V}}_1$) is $\mathcal{O}(HWRlog(HW\left)\right)$; the time complexity of the soft threshold operator (update ${\mathcal{V}}_2$, ${\mathcal{V}}_3$) is $\mathcal{O}\left(HWR\right)$; the time complexity of other matrix multiplication operations (update $\mathcal{X}$, $\mathrm{A}$, $\mathcal{B}$, ${\mathrm{Z}}^{\left(1\right)},{\mathrm{Z}}^{\left(2\right)},{\mathrm{Z}}^{\left(3\right)}$, $\mathcal{N}$, $\mathcal{E}$, ${\mathcal{D}}_1,{\mathcal{D}}_2,{\mathcal{D}}_3$, and ${\mathcal{D}}_4$) is $\mathcal{O}(HWR+DR+H{K}_{\mathcal{X}}+4HWD)=\mathcal{O}\left(HW(D+R)\right)$. Thus, the time complexity of the proposed method is $\mathcal{O}(R^2(W^2{D}^2+H^2{D}^2+H^2{W}^2)+HWRlog\left(HW\right)+HW(D+2R))$.

3. Experimental Results and Discussion

In this section, the proposed ATLSS algorithm is applied to five real HSI datasets for AD, and a detailed description of the experiments is provided below. All the experimental algorithms were performed in MATLAB 2016b on a computer with a 64-bit quad-core Intel Xeon 2.40 GHz CPU and 32.0 GB of RAM in Windows 7.

3.1. Experimental Datasets

(1)

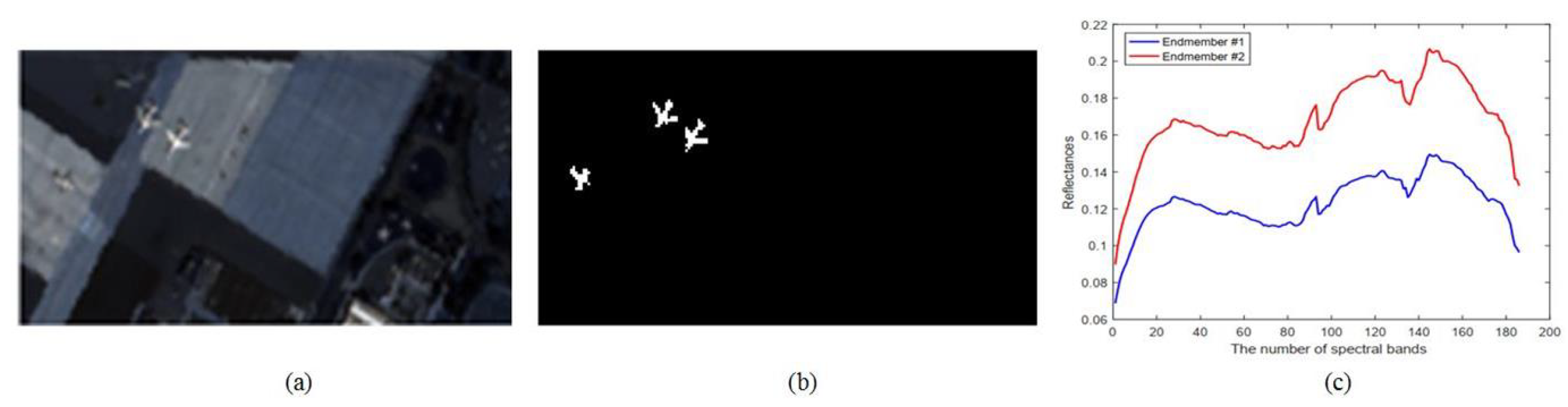
AVIRIS airplane data: The AVIRIS airplane dataset was collected by AVIRIS in San Diego. One hundred and eighty-nine bands were retained, while the water absorption regions; low-SNR bands; and bad bands (1–6, 33–35, 97, 107–113, 153–166, 221–224) were removed. In Figure 1b, the subimage is named the AVIRIS−1 dataset, and it is located in the top-left corner of the AVIRIS image with a size of $150\times 150\times 186$. The anomaly contained in the image was three airplanes, and the ground truth is shown in Figure 1c. AVIRIS−2 was located in the center of San Diego, as shown in Figure 2, and it contained 120 anomaly pixels with a size $100\times 200\times 186$.

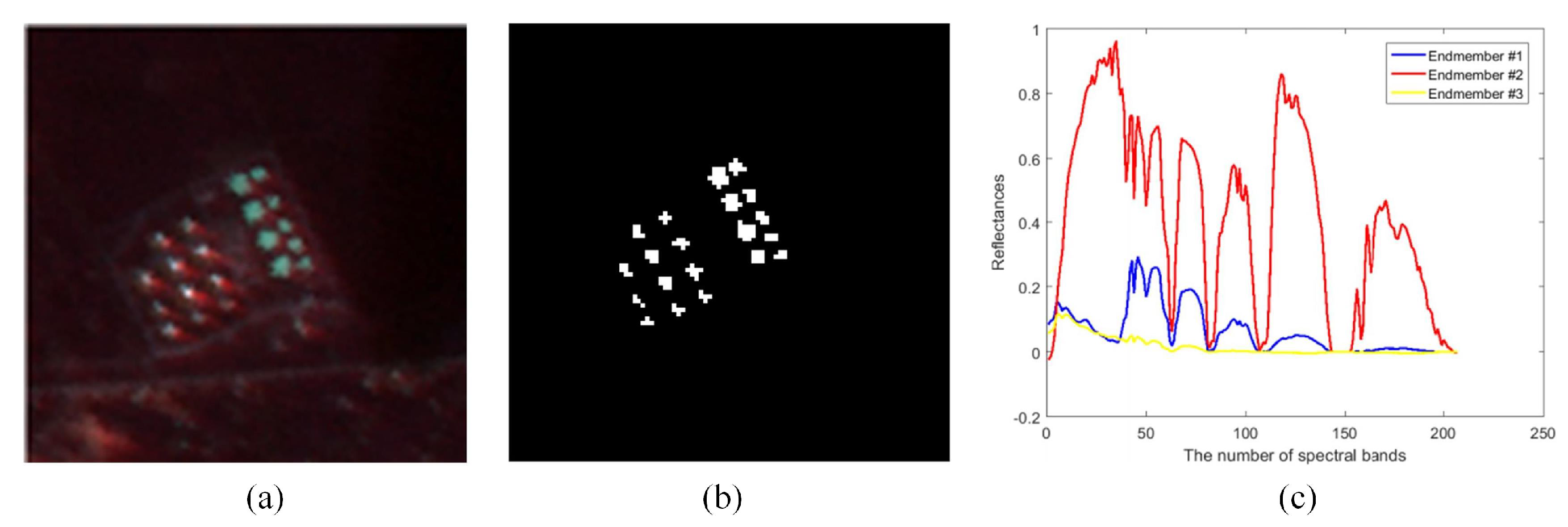
(2)

HYDICE data: The real data were collected by the hyperspectral digital imagery collection experiment (HYDICE) sensor, and the original image had a size of $307\times 307\times 210$. After removing the low-SNR and water-vapor absorption bands, 162 bands remained. An $80\times 100$ subspace was cropped from the top right of the whole image, and the cars and roofs in the image scene were considered anomalies. The false-color image and the corresponding ground truth are shown in Figure 3.

(3)

Urban (ABU) data: The Urban dataset was collected with AVIRIS sensors and contained five images of five different scenes. In this paper, we selected the Urban−1 and Urban−2 images, captured at different locations on the Texas coast, to perform the experiment. The spatial size of the Urban−1 dataset was $100\times 100$, the number of spectral bands was 204, and its false-color image and the ground truth are presented in Figure 4a,b. For the Urban−2 dataset, with a size of $100\times 100\times 207$, Figure 5a,b shows the corresponding false-color image and ground truth.

3.2. Evaluation Metrics and Parameter Settings

The AD performance of the proposed ATLSS method is demonstrated in this section.

Table 1. Formulations of the ATLSS model and its different degradation models.

Model Name	Formulation
Dm-1	$\underset{\mathcal{X},\mathrm{A},\mathcal{E},\mathcal{N}}{min}\frac{1}{2}{\parallel \mathcal{N}\parallel }_F^2+{\lambda }_1{\parallel \mathcal{X}\parallel }_1+\beta {\parallel \mathcal{E}\parallel }_{1,1,2}$
	$\mathrm{s}.\mathrm{t}.\mathcal{Y}=\mathcal{X}\times {}_3\mathrm{A}+\mathcal{E}+\mathcal{N},\mathcal{X}\ge 0,\mathrm{A}\ge 0$
Dm-2	$\underset{\mathcal{X},\mathrm{A},\mathcal{E},\mathcal{N}}{min}\frac{1}{2}{\parallel \mathcal{N}\parallel }_F^2+{\lambda }_1{\parallel \mathcal{X}\parallel }_1+\beta {\parallel \mathcal{E}\parallel }_{1,1,2}$
	$\mathrm{s}.\mathrm{t}.rank\left(\mathcal{X}\right)=K_{\mathcal{X}},\mathcal{Y}=\mathcal{X}\times {}_3\mathrm{A}+\mathcal{E}+\mathcal{N},\mathcal{X}\ge 0,\mathrm{A}\ge 0$
Dm-3	$\underset{\mathcal{X},\mathrm{A},\mathcal{E},\mathcal{N}}{min}\frac{1}{2}{\parallel \mathcal{N}\parallel }_F^2+{\lambda }_1{\parallel \mathcal{X}\parallel }_{TV}+\beta {\parallel \mathcal{E}\parallel }_{1,1,2}$
	$\mathrm{s}.\mathrm{t}.\mathcal{Y}=\mathcal{X}\times {}_3\mathrm{A}+\mathcal{E}+\mathcal{N},\mathcal{X}\ge 0,\mathrm{A}\ge 0$
Dm-4	$\underset{\mathcal{X},\mathrm{A},\mathcal{E},\mathcal{N}}{min}\frac{1}{2}{\parallel \mathcal{N}\parallel }_F^2+{\lambda }_1{\parallel \mathcal{X}\parallel }_{TV}+\beta {\parallel \mathcal{E}\parallel }_{1,1,2}$
	$\mathrm{s}.\mathrm{t}.rank\left(\mathcal{X}\right)=K_{\mathcal{X}},\mathcal{Y}=\mathcal{X}\times {}_3\mathrm{A}+\mathcal{E}+\mathcal{N},\mathcal{X}\ge 0,\mathrm{A}\ge 0$
ATLSS	$\underset{\mathcal{X},\mathrm{A},\mathcal{E},\mathcal{N}}{min}\frac{1}{2}{\parallel \mathcal{N}\parallel }_F^2+{\lambda }_1{\parallel \mathcal{X}\parallel }_1+{\lambda }_2{\parallel \mathcal{X}\parallel }_{TV}+\beta {\parallel \mathcal{E}\parallel }_{1,1,2}$
	$\mathrm{s}.\mathrm{t}.rank\left(\mathcal{X}\right)=K_{\mathcal{X}},\mathcal{Y}=\mathcal{X}\times {}_3\mathrm{A}+\mathcal{E}+\mathcal{N},\mathcal{X}\ge 0,\mathrm{A}\ge 0$

shows the formulations of ATLSS and its four degradation models (Dm), annotated as Dm-1, Dm-2, Dm-3, and Dm-4, based on the linear spectral unmixing method. In addition, we chose to compare our models with RX [12], RPCA [22], LRASR [24], GTVLRR [25], GVAE [9], PTA [35], TRPCA [49], and LRTDTV [34]. RXD is a statistics-based method in the HSI AD field, and it is the baseline in almost all reference articles. The methods listed above are based on matrix modeling. PTA is a tensor-based method, but it is based on matrix operations. GVAE is a deep learning method. TRPCA and the proposed ATLSS algorithm are based on tensor modeling. We classified the RX, RPCA, LRASR, GTVLRR, and PTA methods as matrix-based operations, and TRPCA, LRTDTV, Dm-1, Dm-2, Dm-3, Dm-4, LRTDTV, and ATLSS as tensor-based operations.

To evaluate the detector more effectively, the 3D ROC curve [58] was employed, which introduces the threshold $\tau$ in addition to the parameters $P_d$ and $P_f$ used in the 2D ROC curve [59] to specify a third dimension $(P_d,P_f,\tau )$. In addition, the 2D ROC curves $(P_d,P_f)$ and $(P_f,\tau )$ were used to measure the AD result; an efficient detector would have a performance with a larger $(P_d,P_f)(\to 1)$ value but a smaller $(P_f,\tau )(\to 0)$ value, and it is desired that the curves of $(P_d,P_f)$ and $(P_f,\tau )$ are close to the upper-left and lower-left corners of the coordinate axis, respectively. In addition, box and whisker plots were used to evaluate the separability between the anomaly and background. The boxes in the box and whisker plot reflect the distribution range of the detection values of the anomaly and background; that is, a larger gap between the anomaly and background boxes indicates better discrimination by the detector.

In the proposed ATLSS method, the number of endmembers R was first estimated in the initialization phase using the HySime algorithm, whereas the most significant task was to search for the best set of parameters $\left({\lambda }_1,{\lambda }_2,{\lambda }_3,\beta \right)$, which needed to be carefully identified. Moreover, ${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$, and $\beta$ ranged within the set $\{5·{10}^{-1},1·{10}^{-1},5·{10}^{-2},1·{10}^{-2},5·{10}^{-3},1·{10}^{-3},5·{10}^{-4},1·{10}^{-4}\}$, respectively, while $\mu$ was selected from $\{0.01,0.001\}$. Here, we carefully determined the optimal parameters for the five datasets and for all the algorithms. To demonstrate the contribution of the different parameters to AD, we took the example of the AVIRIS−2 airplane data while changing the parameters ${\lambda }_1,{\lambda }_2,{\lambda }_3$, and $\beta$ to illustrate the tuning procedure in detail. Specifically, we fixed ${\lambda }_2$, ${\lambda }_3$, and $\beta$ and traversed ${\lambda }_1$ until a favorable result was observed; then, we alternated the other parameters. We applied ATLSS with different parameter settings to the AVIRIS airplane datasets (including AVIRIS−1 and AVIRIS−2), HYDICE dataset, and Urban (ABU) datasets (including Urban−1 and Urban−2) in turn to obtain detection results under the optimal parameter combination.

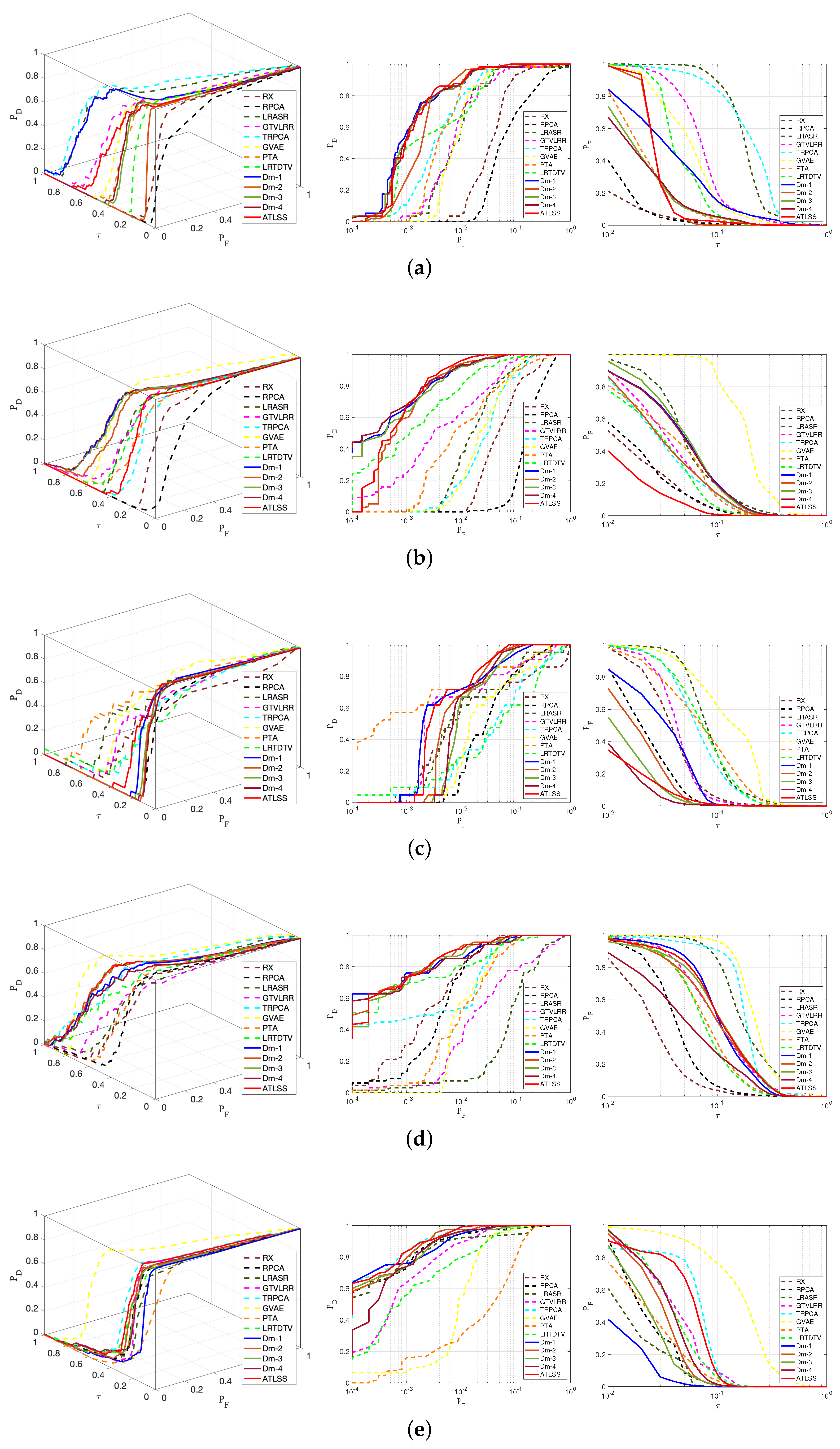
3.3. Detection Performance

We investigated the contribution of the regularization terms, including sparsity regularization, TV regularization, and CP regularization, in the proposed ATLSS method with regard to the accuracy of AD. We referred again to Table 1 for the ATLSS, Dm-1, Dm-2, Dm-3, and Dm-4 models. Furthermore, we compared the performance of ATLSS, including Dm-1, Dm-2, Dm-3, and Dm-4, with that of RX, RPCA, LRASR, GTVLRR, TRPCA, GVAE, PTA, and LRTDTV. The 2D plots of the algorithm detection results comparison for the five datasets are shown sequentially in Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10.

Table 2. The AUC values obtained by different AD algorithms for the five real datasets.

Datasets	AUC Values of $({\mathit{P}}_{\mathit{d}},{\mathit{P}}_{\mathit{f}})/({\mathit{P}}_{\mathit{f}},\mathit{\tau })$
	Matrix-Based Operations					Deep Learning
	RX	RPCA	LRASR	GTVLRR	PTA	GVAE
AVIRIS−1	$0.9551/0.0118$	$0.8935/0.0129$	$0.9716/0.1968$	$0.9822/0.0893$	$0.9890/0.2227$	$0.9860/0.0718$
AVIRIS−2	$0.9213/0.0266$	$0.7969/0.0262$	$0.9672/0.0711$	$0.9816/0.0518$	$0.9609/0.0514$	$0.9616/0.2009$
HYDICE	$0.8511/0.0470$	$0.9436/0.0277$	$0.9311/0.0989$	$0.9393/0.0488$	$0.9829/0.0935$	$0.9311/0.1549$
ABU Urban−1	$0.9934/0.0329$	$0.9916/0.0496$	$0.8666/0.2096$	$0.9093/0.1261$	$0.9852/0.1869$	$0.9778/0.0925$
ABU Urban−2	$0.9946/0.0611$	$0.9960/0.0283$	$0.9867/0.0211$	$0.9967/0.0487$	$0.9992/0.0672$	$0.9828/0.1976$
Tensor-Based Operations
TRPCA	LRTDTV	Dm-1	Dm-2	Dm-3	Dm-4	ATLSS
$0.9801/0.0304$	$0.9843/0.0472$	$0.9950/0.0649$	$0.9954/0.0293$	$0.9945/0.0290$	$0.9949/0.0295$	0.9967/0.0328
$0.9549/0.0478$	$0.9890/0.0736$	$0.9967/0.0655$	$0.9970/0.0490$	$0.9966/0.0660$	$0.9969/0.0644$	0.9982/0.0159
$0.9600/0.0817$	$0.9725/0.0887$	$0.9829/0.0388$	$0.9847/0.0222$	$0.9812/0.0177$	$0.9830/0.0126$	0.9893/0.0152
$0.9823/0.2450$	$0.9870/0.0868$	$0.9940/0.1214$	0.9960/0.1226	$0.9921/0.0783$	$0.9956/0.1293$	0.9962/0.1291
$0.9456/0.0325$	$0.9904/0.0459$	$0.9976/0.0126$	$0.9989/0.0346$	$0.9973/0.0275$	$0.9981/0.0405$	0.9992/0.0611

shows the AUC values of $(P_d,P_f)/(P_f,\tau )$ obtained by different AD algorithms on the five real datasets. Each algorithm ran ten times on each dataset to avoid randomness, and the average AUC values were used. Figure 11 and Figure 12 show the corresponding performance curves and box and whisker plots of the different methods under comparison for the five real datasets. We also took the AVIRIS−2 dataset as an example to illustrate the superior performance of the proposed method in detail.

For Dm-1, when the parameter settings were ${\lambda }_1=0.01$ and $\beta =0.1$, all five datasets achieved very good results.

3.3.1. AVIRIS−2

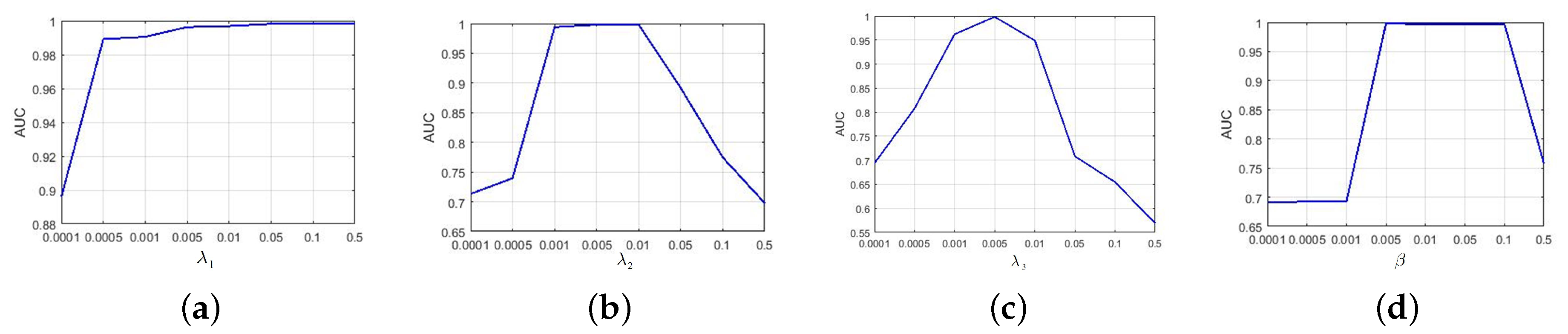
For the AVIRIS−2 dataset, the estimated number of endmembers for the background was two, as shown in Figure 2c, and the estimated rank was $K=18$. In the following two paragraphs, we study (1.a) the effects of the regularization terms and (1.b) the comparison of different anomaly detectors.

(1.a) Effects of the Regularization Terms: After a large number of parameter traversals, the trade-off parameters referenced in the ATLSS algorithm and Dm-2 both achieved their optimal performance, i.e., ${\lambda }_1=0.5$, ${\lambda }_2=0.005$, ${\lambda }_3=0.005$, and $\beta =0.005$ for ATLSS and ${\lambda }_1=0.1$, ${\lambda }_3=0.5$, and $\beta =0.001$ for Dm-2. Figure 13 shows the detection accuracy of ATLSS on the AVIRIS−2 dataset when one parameter varied within a predefined parameter range and the other three trade-off parameters were fixed. In Figure 13a, it can be observed that when ${\lambda }_1$ increased from $0.0001$ to $0.5$, the curve showed an upward trend, and the highest detection result was obtained at ${\lambda }_1=0.5$, which indicated a positive effect on controlling the sparsity of the abundance tensor. Table 2 and Figure 7 provide the certification based on quantitative analysis and visual qualitative analysis. The peak of the curve in Figure 13b was located at ${\lambda }_2=0.005$ when ${\lambda }_2$ was in the interval $[0.0001,0.005]$. The increasing curve implied that TV had a positive effect on suppressing noise, while ${\lambda }_2>0.005$ imposed a smoothness constraint on the abundance tensor, leading to a dramatic decline in the detection results. ${\lambda }_3$ was imposed on $\mathcal{Q}$ to control its low rankness, and Figure 13c reveals that setting ${\lambda }_3=0.005$ balanced the low-rank regularization with the most important information but captured small-scale details. The curve first steadily increased and then fell as it deviated from the optimal parameter value, implying that parameter values that were too large led to strict low rankness in $\mathcal{X}$ and thus resulted in a significant residual loss in the reconstructed abundance tensor. In Figure 13d, one can clearly see that the curve was stable when $\beta \in [0.005,0.1]$ and exhibited superior performance. Outside this interval, the detection result was sensitive to changes in the parameter, with the detection performance declining in a straight downward trend. When $\beta$ was set to $0.005$, the best performance was achieved.

(1.b) Comparison with Different Anomaly Detectors:Table 2 demonstrates the AUC values of $(P_d,P_f)$ and $(P_f,\tau )$ for the different methods under comparison on the five datasets. In Table 2, the anomaly detection accuracy $(P_d,P_f)$ of ATLSS, which obtained the highest score among all the methods under comparison when $\tau =0.087$, is illustrated by the ROC curve in the upper left corner, which also shows the efficiency of the model. The $(P_f,\tau )$ score was lower than the others, and the $(P_f,\tau )$ ROC curve is closest to the lower-left corner, as shown in Figure 11b. ATLSS performed well on the AVIRIS−2 dataset and achieved optimal AD accuracy and a low false-alarm rate. The proposed ATLSS model and the generation Dm-1, Dm-2, Dm-3, and Dm-4 methods better separated the anomaly and background, as shown in Figure 12b. The 2D plots of the detection results are presented in Figure 7i, showing the low-rank structure imposed by the regularization constraint (i.e., CP decomposition on the introduced low-rank prior term), which granted the abundance tensor adequate flexibility to model fine-scale spatial details with most of its spatial distribution preserved. The exploration of the background tensor enabled the suppression of the background more efficiently. Moreover, TV regularization, which smoothed the estimated abundance map, effectively suppressed Gaussian noise. When compared with the generation Dm-1, Dm-2, Dm-3, and Dm-4 methods, ATLSS demonstrated better background suppression, as shown in Figure 7, and the best AD performance, as shown in Table 2. In Figure 11b, in addition to the curves of $(P_d,P_f)$ and $(P_f,\tau )$, the 3D ROC curve also comprehensively shows the performance of the proposed ATLSS method.

The methods assumed that the background and the anomaly had a low-rank and sparse property and performed better than the RX method in terms of the AUC value and false-alarm rate, which can be observed from Table 2 and Figure 11b. The 2D plots in Figure 7 also reveal that the background and Gaussian noise were both effectively suppressed; moreover, the anomaly airplanes were more clearly detected by ATLSS compared to RX. The GTVLRR, PTA, Dm-2, Dm-3, Dm-4, LRTDTV, and ATLSS, utilized TV regularization to smooth away the noise signature while strengthening the outlines of the airplanes. One can observe that GTVLRR performed well in comparison to the other methods. However, the proposed ATLSS method based on tensor decomposition was outstanding compared to the other methods in terms of $(P_d,P_f)/(P_f,\tau )$ and the power of the anomaly and background separation.

Table 3. The computational time (seconds) of different AD algorithms for the AVIRIS−2 dataset.

Method	Matrix-Based Operations						Deep Learning		Tensor-Based Operations
	RX	RPCA	LRASR	GTVLRR	PTA	GVAE	TRPCA	LRTDTV	Dm-1	Dm-2	Dm-3	Dm-4	ATLSS
Time(s)	$3.577$	$15.457$	$26.399$	$241.099$	$241.099$	$80\times 2000+25.56$	$234.465$	$23.709$	$70.494$	$149.949$	$138.588$	$194.204$	$200.732$

shows the computational times of the ten algorithms for the AVIRIS−2 dataset. We observed that the running time of ATLSS was longer than that of Dm-1, Dm-2, Dm-3, and Dm-4, having been increased by the added regular terms, but the AD performance improved. The execution time of ATLSS was shorter than that of GTVLRR and TRPCA, while it was higher than that of LRTDTV. The detection result of ATLSS was superior to that of LRTDTV. Compared to RX, RPCA, LRASR, and PTA, the time cost of ATLSS was much higher, because the former are based on matrix operations. As shown in Table 2, the deep learning method GVAE had a training time/test time of $80\times 2000/25.56$, presenting not only high time demands but also a far inferior experimental performance compared to our proposed ATLSS model.

3.3.2. AVIRIS−1

For the AVIRIS−1 dataset, the estimated number of endmembers for the background was three, as shown in Figure 1d, and the estimated rank was $K=46$. The best performance was achieved when we set the four parameters as $(0.1,0.1,0.1,0.001)$.

When comparing Dm-1, Dm-2, Dm-3, Dm-4, and ATLSS, we observed that the anomaly included three planes, which are clearly identified in Figure 6. The ATLSS’s best performance was achieved when we set the four parameters as $(0.1,0.1,0.1,0.001)$. In Table 2 and Figure 11a, one can observe that the value of $(P_d,P_f)$ was the largest for ATLSS, and the curve is in the upper-left corner. The $(P_f,\tau )$ value of ATLSS was also relatively low. The superior performance of ATLSS demonstrated that it imposed low-rank tensor regularization and TV regularization on the abundance tensor, efficiently suppressing the background and smoothing away the noise. Among all the compared methods, as shown in Table 2, the best detection result was also achieved by ATLSS. One can observed that even though RX had the lowest false-alarm rate, the AD accuracy and the separation of the anomaly and background shown in Figure 11a and Figure 12a demonstrated that its performance was not very good. Notably, our proposed method was superior to the tensor-based PTA method on the AVIRIS−2 dataset for all measurements. Figure 11a shows that the ROC curve of ATLSS was closer to the top left than those of all the other methods, and Table 2 further proves the remarkable performance of ATLSS.

3.3.3. HYDICE

For the Urban data, the estimated number of endmembers was $R=4$, as shown in Figure 3d, and the estimated CP rank was $K=67$.

Compared to Dm-1, Dm-2, Dm-3, and Dm-4, as shown in Table 2, the ATLSS method showed a competitive performance when we set the parameters as $(0.1,0.1,0.01,0.1)$; the AD AUC value was the highest; and the false-alarm rate was the lowest. ATLSS was also powerful in separating anomalies and the background, as shown in Figure 12c. In Figure 8i, the anomaly was accurately detected; furthermore, the background and the noise were both well-suppressed, which is a benefit of tensor low-rank regularization and TV smoothness for the background abundance tensor. Compared with PTA, the $(P_d,P_f)/(P_f,\tau )$ values of ATLSS, as shown in Table 2, accounted for the fact that abundance maps possess more distinctive features than raw data, which is beneficial for identifying anomalies within a background and achieving outstanding performance. The qualitative and quantitative results are presented in Table 2 and Figure 11c, as well as in Figure 12c. These results were obtained by background low-rank decomposition, which enabled more accurate background reconstruction.

3.3.4. Urban (ABU-1)

For the ABU Urban−1 dataset, the number of estimation endmembers was two, as shown in Figure 4c, and the estimated CP rank was $K=25$.

In contrast with Dm-1, Dm-2, Dm-3, and Dm-4, the ATLSS background model imposed a CP regularization constraint and TV regularization on the abundance tensor, and an excellent AD performance was achieved when the parameters were $(0.1,0.05,0.5,0.001)$, as shown in Table 2. A higher detection result would lead to a few anomaly pixels being regarded as background pixels, resulting in a lower false-alarm rate. Thus, as shown in Table 2 and Figure 11d, the $(P_d,P_f)$ values of Dm-1, Dm-2, Dm-3, Dm-4, and ATLSS increased gradually, while the $(P_f,\tau )$ values in Table 2 also increased. Furthermore, one can observe that the $(P_f,\tau )$ of RX was the lowest and the $(P_d,P_f)$ the highest among all the compared methods. However, Figure 12d shows that ATLSS and the generation methods achieved superior separation between the anomaly and background. In general, the evaluation metrics mentioned above validated that the proposed ATLSS method outperformed the other methods in both qualitative and quantitative aspects.

3.3.5. Urban (ABU-2)

For the ABU Urban−2 dataset, the number of estimation endmembers was three, as shown in Figure 5c, and the estimated CP rank was $K=25$.

We obtained the best performance when we set the parameters as $(0.1,0.05,0.1,0.5)$. As shown in Table 2, the detection result $(P_d,P_f)$ of ATLSS was higher than those of Dm-1, Dm-2, Dm-3, and Dm-4. In contrast, the $(P_f,\tau )$ value of ATLSS was slightly higher than those of the other four generative methods. This model suffered from a much higher detection result, which caused a few anomaly pixels to be detected as background pixels. However, its efficient separation between the anomaly and background is shown in Figure 6e, demonstrating that it is still a competitive AD method. For the Urban (ABU-2) dataset, the results of the tensor-based PTA and ATLSS methods were evenly matched, as shown in Table 2 and Figure 11 and Figure 12. However, it is worth noting that the $(P_f,\tau )$ value of ATLSS was lower than that of PTA, which demonstrated that the abundance maps possessed more distinctive features than the original data and enabled the more accurate identification of the anomaly and the background; hence, the model achieved outstanding performance.

We performed the proposed ATLSS method and extensive comparison experiments using the five datasets and summarize the advantages of the proposed method as follows:

(1)

Effectiveness: The proposed ATLSS method decomposed the background into an abundance tensor and endmember matrix. The structural characteristics of the abundance tensor were fully explored, i.e., the local spatial continuity and the high abundance vector correlations, which contributed to reconstructing a more accurate abundance tensor for the background. The proposed ATLSS model performed excellently compared to its degradation models Dm-1, Dm-2, Dm-3, and Dm-4.

(2)

Performance: Eight comparison algorithms were presented to sufficiently demonstrate the performance of the proposed method. Compared to RX, ATLSS had a more accurate AD performance thanks to the low-rank and sparse assumptions. The deep learning method GVAE had a high training time while achieving a moderate performance when compared with ATLSS. Compared to the tensor-based methods PTA, TRPCA, and LRTDTV, the proposed ATLSS method exploited the abundance tensor’s physical meaning, which provided more distinctive features than the raw data, achieving outstanding AD performance.

4. Conclusions

In this paper, we proposed a novel tensor-based method for hyperspectral AD that was powerful in enhancing spatial structure information, such that the spatial and spectral information was preserved. Seeing as the low spatial resolution of HSIs makes existing mixed pixels rely heavily on spectral information, the background was decomposed into the mode-3 product of an abundance tensor and an endmember matrix to enhance the spatial structure information and the differentiation between the target and background. For the background part, considering the distinctive features of the background’s abundance maps, we characterized them by tensor regularization and imposed low rankness, smoothness, and sparsity. In addition, for the anomaly part, we utilized the ${\ell }_{1,1,2}$-norm to characterize the tube-wise sparsity, since the anomalies account for a small portion of the scene. Additionally, Gaussian noise was also incorporated into the model to suppress noise confusion with the anomalies. The experimental results obtained using the five datasets demonstrated that the proposed method had an excellent AD performance compared to the other methods.