Multi-Scale and Multi-Stream Fusion Network for Pansharpening
Abstract
1. Introduction
- Some DL-based methods combine all the input data together, but, in this way, they lose the possibility to independently analyze the inputs of the fusion process that are represented by the MS and PAN images;
- Most fusion models process the source images separately and neglect their spectral/spatial correlations;
- The use of the fixed-scale information of the input images limits the pansharpening performance.
- Multi-scale and multi-stream strategies. We combined the multi-scale and multi-stream strategies to build a hybrid network structure for pansharpening extracting both shallow and deep features at different scales;
- Multi-stream fusion network. On the basis of multi-scale and multi-stream strategies, we introduced a multi-stream fusion network, which separately leverages spectral and spatial information in the MS and PAN images. Simultaneously, we considered the pansharpening problem as a super-resolution task that concatenates the PAN and MS images to further extract spatial details;
- Multi-scale information injection. We make full use of the multi-scale information of the input (MS and PAN) images by exploiting downsampling and upsampling operations. At each scale, the information of the original MS image is injected through a multi-scale loss.
2. Related Works
2.1. Traditional Pansharpening
2.2. Deep Learning-Based Pansharpening
3. Proposed Method
3.1. Problem Formulation
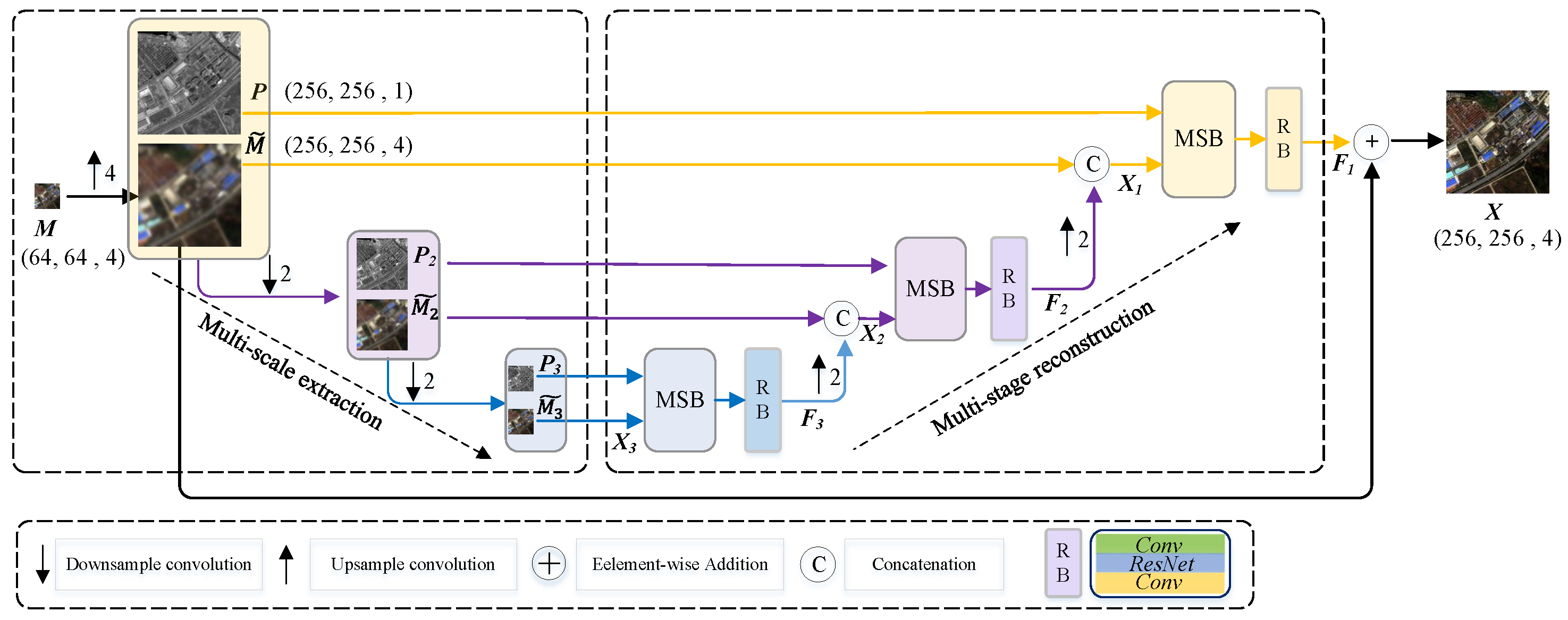
3.2. Network Architecture
3.2.1. Multi-Scale Feature Extraction
3.2.2. Multi-Stream Feature Fusion
3.2.3. Multi-Stage Image Reconstruction
3.3. Loss Function
4. Experiment and Evaluations
4.1. Datasets and Metrics
4.2. Implementation Details
4.3. Results and Discussion
4.3.1. Assessment at Reduced Resolution
4.3.2. Full Resolution Assessment
4.3.3. Parameter Numbers vs. Model Performance
4.4. Ablation Studies
4.4.1. Ablation Study about Different Scales
4.4.2. Ablation Study about Different Streams
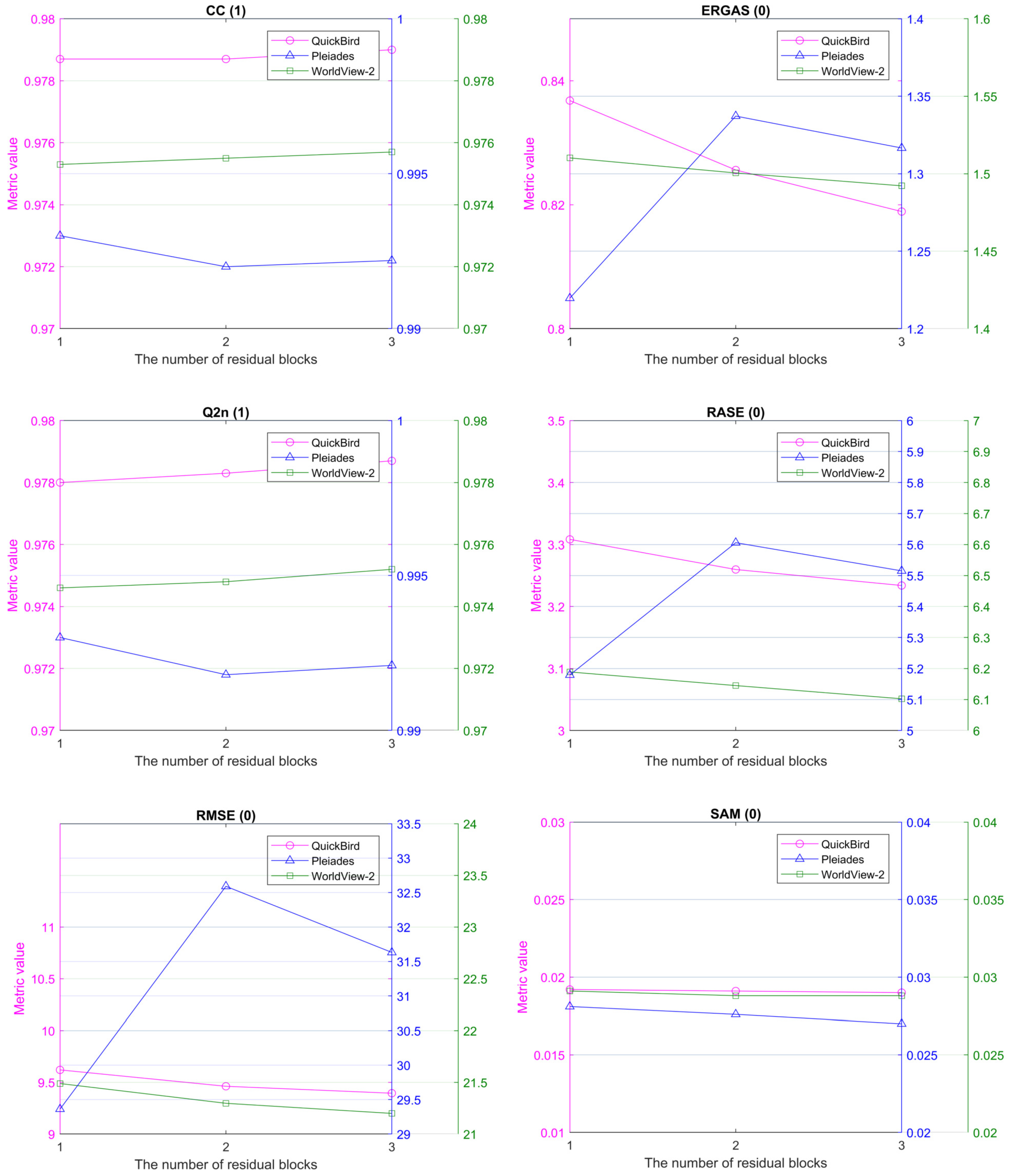
4.4.3. Ablation Study about Different numbers of Residual Blocks
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Souza, C., Jr.; Firestone, L.; Silva, L.M.; Roberts, D. Mapping forest degradation in the Eastern Amazon from SPOT 4 through spectral mixture models. Remote Sens. Environ. 2003, 87, 494–506. [Google Scholar] [CrossRef]
- Yang, B.; Kim, M.; Madden, M. Assessing optimal image fusion methods for very high spatial resolution satellite images to support coastal monitoring. GISci. Remote Sens. 2012, 49, 687–710. [Google Scholar] [CrossRef]
- Shalaby, A.; Tateishi, R. Remote sensing and GIS for mapping and monitoring land cover and land-use changes in the Northwestern coastal zone of Egypt. Appl. Geogr. 2007, 27, 28–41. [Google Scholar] [CrossRef]
- Wu, C.; Du, B.; Cui, X.; Zhang, L. A post-classification change detection method based on iterative slow feature analysis and Bayesian soft fusion. Remote Sens. Environ. 2017, 199, 241–255. [Google Scholar] [CrossRef]
- Kumar, U.; Milesi, C.; Nemani, R.R.; Basu, S. Multi-sensor multi-resolution image fusion for improved vegetation and urban area classification. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40, 51–58. [Google Scholar] [CrossRef]
- Vivone, G.; Alparone, L.; Chanussot, J.; Dalla Mura, M.; Garzelli, A.; Licciardi, G.A.; Restaino, R.; Wald, L. A critical comparison among pansharpening algorithms. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2565–2586. [Google Scholar] [CrossRef]
- Meng, X.; Shen, H.; Li, H.; Zhang, L.; Fu, R. Review of the pansharpening methods for remote sensing images based on the idea of meta-analysis: Practical discussion and challenges. Inf. Fusion 2019, 46, 102–113. [Google Scholar] [CrossRef]
- Yilmaz, C.S.; Yilmaz, V.; Gungor, O. A theoretical and practical survey of image fusion methods for multispectral pansharpening. Inf. Fusion 2022, 79, 1–43. [Google Scholar] [CrossRef]
- Rahmani, S.; Strait, M.; Merkurjev, D.; Moeller, M.; Wittman, T. An adaptive IHS pan-sharpening method. IEEE Geosci. Remote Sens. Lett. 2010, 7, 746–750. [Google Scholar] [CrossRef]
- Kwarteng, P.; Chavez, A. Extracting spectral contrast in Landsat Thematic Mapper image data using selective principal component analysis. Photogramm. Eng. Remote Sens. 1989, 55, 339–348. [Google Scholar]
- Laben, C.A.; Brower, B.V. Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pan-Sharpening. U.S. Patent 6,011,875, 4 January 2000. pp. 1–9. [Google Scholar]
- Aiazzi, B.; Baronti, S.; Selva, M. Improving component substitution pansharpening through multivariate regression of MS + Pan data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3230–3239. [Google Scholar] [CrossRef]
- Garzelli, A.; Nencini, F.; Capobianco, L. Optimal MMSE pan sharpening of very high resolution multispectral images. IEEE Trans. Geosci. Remote Sens. 2007, 46, 228–236. [Google Scholar] [CrossRef]
- Vivone, G. Robust band-dependent spatial-detail approaches for panchromatic sharpening. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6421–6433. [Google Scholar] [CrossRef]
- Choi, J.; Yu, K.; Kim, Y. A new adaptive component-substitution-based satellite image fusion by using partial replacement. IEEE Trans. Geosci. Remote Sens. 2010, 49, 295–309. [Google Scholar] [CrossRef]
- Kang, X.; Li, S.; Benediktsson, J.A. Pansharpening with matting model. IEEE Trans. Geosci. Remote Sens. 2013, 52, 5088–5099. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. MTF-tailored multiscale fusion of high-resolution MS and Pan imagery. Photogramm. Eng. Remote Sens. 2006, 72, 591–596. [Google Scholar] [CrossRef]
- Shah, V.P.; Younan, N.H.; King, R.L. An efficient pan-sharpening method via a combined adaptive PCA approach and contourlets. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1323–1335. [Google Scholar] [CrossRef]
- Choi, M.; Kim, R.Y.; Nam, M.R.; Kim, H.O. Fusion of multispectral and panchromatic satellite images using the curvelet transform. IEEE Geosci. Remote Sens. Lett. 2005, 2, 136–140. [Google Scholar] [CrossRef]
- Restaino, R.; Vivone, G.; Dalla Mura, M.; Chanussot, J. Fusion of multispectral and panchromatic images based on morphological operators. IEEE Trans. Image Process. 2016, 25, 2882–2895. [Google Scholar] [CrossRef]
- Vivone, G.; Restaino, R.; Dalla Mura, M.; Licciardi, G.; Chanussot, J. Contrast and error-based fusion schemes for multispectral image pansharpening. IEEE Geosci. Remote Sens. Lett. 2013, 11, 930–934. [Google Scholar] [CrossRef]
- Alparone, L.; Baronti, S.; Aiazzi, B.; Garzelli, A. Spatial methods for multispectral pansharpening: Multiresolution analysis demystified. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2563–2576. [Google Scholar] [CrossRef]
- Vivone, G.; Dalla Mura, M.; Garzelli, A.; Restaino, R.; Scarpa, G.; Ulfarsson, M.O.; Alparone, L.; Chanussot, J. A New Benchmark Based on Recent Advances in Multispectral Pansharpening: Revisiting pansharpening with classical and emerging pansharpening methods. IEEE Geosci. Remote Sens. Mag. 2020, 9, 53–81. [Google Scholar] [CrossRef]
- Restaino, R.; Vivone, G.; Addesso, P.; Chanussot, J. A pansharpening approach based on multiple linear regression estimation of injection coefficients. IEEE Geosci. Remote Sens. Lett. 2019, 17, 102–106. [Google Scholar] [CrossRef]
- Vivone, G.; Restaino, R.; Chanussot, J. A regression-based high-pass modulation pansharpening approach. IEEE Trans. Geosci. Remote Sens. 2017, 56, 984–996. [Google Scholar] [CrossRef]
- Vivone, G.; Marano, S.; Chanussot, J. Pansharpening: Context-based generalized Laplacian pyramids by robust regression. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6152–6167. [Google Scholar] [CrossRef]
- Vivone, G.; Restaino, R.; Chanussot, J. Full scale regression-based injection coefficients for panchromatic sharpening. IEEE Trans. Image Process. 2018, 27, 3418–3431. [Google Scholar] [CrossRef]
- Vivone, G.; Simões, M.; Dalla Mura, M.; Restaino, R.; Bioucas-Dias, J.M.; Licciardi, G.A.; Chanussot, J. Pansharpening based on semiblind deconvolution. IEEE Trans. Geosci. Remote Sens. 2014, 53, 1997–2010. [Google Scholar] [CrossRef]
- Vivone, G.; Addesso, P.; Restaino, R.; Dalla Mura, M.; Chanussot, J. Pansharpening based on deconvolution for multiband filter estimation. IEEE Trans. Geosci. Remote Sens. 2018, 57, 540–553. [Google Scholar] [CrossRef]
- Deng, L.J.; Vivone, G.; Guo, W.; Dalla Mura, M.; Chanussot, J. A variational pansharpening approach based on reproducible kernel Hilbert space and heaviside function. IEEE Trans. Image Process. 2018, 27, 4330–4344. [Google Scholar] [CrossRef]
- Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O. A new pansharpening algorithm based on total variation. IEEE Geosci. Remote Sens. Lett. 2013, 11, 318–322. [Google Scholar] [CrossRef]
- Duran, J.; Buades, A.; Coll, B.; Sbert, C. A nonlocal variational model for pansharpening image fusion. SIAM J. Imaging Sci. 2014, 7, 761–796. [Google Scholar] [CrossRef]
- Chen, C.; Li, Y.; Liu, W.; Huang, J. SIRF: Simultaneous satellite image registration and fusion in a unified framework. IEEE Trans. Image Process. 2015, 24, 4213–4224. [Google Scholar] [CrossRef]
- Liu, P.; Xiao, L.; Li, T. A variational pan-sharpening method based on spatial fractional-order geometry and spectral–spatial low-rank priors. IEEE Trans. Geosci. Remote Sens. 2017, 56, 1788–1802. [Google Scholar] [CrossRef]
- Khademi, G.; Ghassemian, H. Incorporating an adaptive image prior model into Bayesian fusion of multispectral and panchromatic images. IEEE Geosci. Remote Sens. Lett. 2018, 15, 917–921. [Google Scholar] [CrossRef]
- Deng, L.J.; Feng, M.; Tai, X.C. The fusion of panchromatic and multispectral remote sensing images via tensor-based sparse modeling and hyper-Laplacian prior. Inf. Fusion 2019, 52, 76–89. [Google Scholar] [CrossRef]
- Fu, X.; Lin, Z.; Huang, Y.; Ding, X. A variational pan-sharpening with local gradient constraints. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019; pp. 10265–10274. [Google Scholar]
- Lotfi, M.; Ghassemian, H. A new variational model in texture space for pansharpening. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1269–1273. [Google Scholar] [CrossRef]
- Tian, X.; Chen, Y.; Yang, C.; Gao, X.; Ma, J. A variational pansharpening method based on gradient sparse representation. IEEE Signal Process. Lett. 2020, 27, 1180–1184. [Google Scholar] [CrossRef]
- Deng, L.J.; Vivone, G.; Paoletti, M.E.; Scarpa, G.; He, J.; Zhang, Y.; Chanussot, J.; Plaza, A. Machine Learning in Pansharpening: A benchmark, from shallow to deep networks. IEEE Geosci. Remote Sens. Mag. 2022, 10, 279–315. [Google Scholar] [CrossRef]
- Masi, G.; Cozzolino, D.; Verdoliva, L.; Scarpa, G. Pansharpening by convolutional neural networks. Remote Sens. 2016, 8, 594. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 184–199. [Google Scholar]
- Yang, J.; Fu, X.; Hu, Y.; Huang, Y.; Ding, X.; Paisley, J. PanNet: A deep network architecture for pan-sharpening. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 5449–5457. [Google Scholar]
- Scarpa, G.; Vitale, S.; Cozzolino, D. Target-adaptive CNN-based pansharpening. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5443–5457. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Q.; Wang, Y. Remote sensing image fusion based on two-stream fusion network. Inf. Fusion 2020, 55, 1–15. [Google Scholar] [CrossRef]
- Xu, H.; Ma, J.; Shao, Z.; Zhang, H.; Jiang, J.; Guo, X. SDPNet: A Deep Network for Pan-Sharpening With Enhanced Information Representation. IEEE Trans. Geosci. Remote Sens. 2020, 59, 4120–4134. [Google Scholar] [CrossRef]
- Liu, Q.; Zhou, H.; Xu, Q.; Liu, X.; Wang, Y. PSGAN: A generative adversarial network for remote sensing image pan-sharpening. IEEE Trans. Geosci. Remote Sens. 2020, 59, 10227–10242. [Google Scholar] [CrossRef]
- Shao, Z.; Lu, Z.; Ran, M.; Fang, L.; Zhou, J.; Zhang, Y. Residual encoder–decoder conditional generative adversarial network for pansharpening. IEEE Geosci. Remote Sens. Lett. 2019, 17, 1573–1577. [Google Scholar] [CrossRef]
- Deng, L.J.; Vivone, G.; Jin, C.; Chanussot, J. Detail Injection-Based Deep Convolutional Neural Networks for Pansharpening. IEEE Trans. Geosci. Remote Sens. 2020, 59, 6995–7010. [Google Scholar] [CrossRef]
- Chen, L.; Lai, Z.; Vivone, G.; Jeon, G.; Chanussot, J.; Yang, X. ArbRPN: A Bidirectional Recurrent Pansharpening Network for Multispectral Images With Arbitrary Numbers of Bands. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5406418. [Google Scholar] [CrossRef]
- Wang, Y.; Deng, L.J.; Zhang, T.J.; Wu, X. SSconv: Explicit spectral-to-spatial convolution for pansharpening. In Proceedings of the 29th ACM International Conference on Multimedia, Virtual Event, 20–24 October 2021; pp. 4472–4480. [Google Scholar]
- Yuan, Q.; Wei, Y.; Meng, X.; Shen, H.; Zhang, L. A Multiscale and Multidepth Convolutional Neural Network for Remote Sensing Imagery Pan-Sharpening. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 978–989. [Google Scholar] [CrossRef]
- Wei, J.; Xu, Y.; Cai, W.; Wu, Z.; Chanussot, J.; Wei, Z. A Two-Stream Multiscale Deep Learning Architecture for Pan-Sharpening. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5455–5465. [Google Scholar] [CrossRef]
- Huang, W.; Fei, X.; Feng, J.; Wang, H.; Liu, Y.; Huang, Y. Pan-sharpening via multi-scale and multiple deep neural networks. SIgnal Process. Image Commun. 2020, 85, 115850. [Google Scholar] [CrossRef]
- Li, W.; Liang, X.; Dong, M. MDECNN: A multiscale perception dense encoding convolutional neural network for multispectral pan-sharpening. Remote Sens. 2021, 13, 535. [Google Scholar] [CrossRef]
- Hu, J.; Hu, P.; Kang, X.; Zhang, H.; Fan, S. Pan-Sharpening via Multiscale Dynamic Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2231–2244. [Google Scholar] [CrossRef]
- Wang, W.; Zhou, Z.; Liu, H.; Xie, G. Msdrn: Pansharpening of multispectral images via multi-scale deep residual network. Remote Sens. 2021, 13, 1200. [Google Scholar] [CrossRef]
- Fu, X.; Wang, W.; Huang, Y.; Ding, X.; Paisley, J. Deep Multiscale Detail Networks for Multiband Spectral Image Sharpening. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 2090–2104. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.; Liu, L.; Wang, J.; Zhang, E.; Zhu, X.; Zhang, Y.; Feng, J.; Jiao, L. PSMD-Net: A Novel Pan-Sharpening Method Based on a Multiscale Dense Network. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4957–4971. [Google Scholar] [CrossRef]
- Dong, M.; Li, W.; Liang, X.; Zhang, X. MDCNN: Multispectral pansharpening based on a multiscale dilated convolutional neural network. J. Appl. Remote Sens. 2021, 15, 036516. [Google Scholar] [CrossRef]
- Lai, Z.; Chen, L.; Jeon, G.; Liu, Z.; Zhong, R.; Yang, X. Real-time and effective pan-sharpening for remote sensing using multi-scale fusion network. J.-Real-Time Image Process. 2021, 18, 1635–1651. [Google Scholar] [CrossRef]
- Zhou, M.; Huang, J.; Fu, X.; Zhao, F.; Hong, D. Effective Pan-Sharpening by Multiscale Invertible Neural Network and Heterogeneous Task Distilling. IEEE Trans. Geosci. Remote Sens. 2022, 60, 14. [Google Scholar] [CrossRef]
- Lei, D.; Huang, J.; Zhang, L.; Li, W. MHANet: A Multiscale Hierarchical Pansharpening Method With Adaptive Optimization. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5411015. [Google Scholar] [CrossRef]
- Tu, W.; Yang, Y.; Huang, S.; Wan, W.; Gan, L.; Lu, H. MMDN: Multi-Scale and Multi-Distillation Dilated Network for Pansharpening. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5410514. [Google Scholar] [CrossRef]
- Liang, Y.; Zhang, P.; Mei, Y.; Wang, T. PMACNet: Parallel Multiscale Attention Constraint Network for Pan-Sharpening. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5512805. [Google Scholar] [CrossRef]
- Huang, W.; Ju, M.; Chen, Q.; Jin, B.; Song, W. Detail-Injection-Based Multiscale Asymmetric Residual Network for Pansharpening. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5512505. [Google Scholar] [CrossRef]
- Jin, C.; Deng, L.J.; Huang, T.Z.; Vivone, G. Laplacian pyramid networks: A new approach for multispectral pansharpening. Inf. Fusion 2022, 78, 158–170. [Google Scholar] [CrossRef]
- Chi, Y.; Li, J.; Fan, H. Pyramid-attention based multi-scale feature fusion network for multispectral pan-sharpening. Appl. Intell. 2022, 52, 5353–5365. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, K.; Sun, J. Multiscale Spatial–Spectral Interaction Transformer for Pan-Sharpening. Remote Sens. 2022, 14, 1736. [Google Scholar] [CrossRef]
- Zhang, E.; Fu, Y.; Wang, J.; Liu, L.; Yu, K.; Peng, J. MSAC-Net: 3D Multi-Scale Attention Convolutional Network for Multi-Spectral Imagery Pansharpening. Remote Sens. 2022, 14, 2761. [Google Scholar] [CrossRef]
- Qu, Y.; Baghbaderani, R.K.; Qi, H.; Kwan, C. Unsupervised pansharpening based on self-attention mechanism. IEEE Trans. Geosci. Remote Sens. 2020, 59, 3192–3208. [Google Scholar] [CrossRef]
- Uezato, T.; Hong, D.; Yokoya, N.; He, W. Guided deep decoder: Unsupervised image pair fusion. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 87–102. [Google Scholar]
- Wu, Z.C.; Huang, T.Z.; Deng, L.J.; Hu, J.F.; Vivone, G. VO+Net: An adaptive approach using variational optimization and deep learning for panchromatic sharpening. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5401016. [Google Scholar] [CrossRef]
- Wu, Z.C.; Huang, T.Z.; Deng, L.J.; Vivone, G.; Miao, J.Q.; Hu, J.F.; Zhao, X.L. A new variational approach based on proximal deep injection and gradient intensity similarity for spatio-spectral image fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 6277–6290. [Google Scholar] [CrossRef]
- Xiao, J.L.; Huang, T.Z.; Deng, L.J.; Wu, Z.C.; Vivone, G. A New Context-Aware Details Injection Fidelity with Adaptive Coefficients Estimation for Variational Pansharpening. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Zhao, H.; Gallo, O.; Frosio, I.; Kautz, J. Loss functions for image restoration with neural networks. IEEE Trans. Comput. Imaging 2016, 3, 47–57. [Google Scholar] [CrossRef]
- Wald, L.; Ranchin, T.; Mangolini, M. Fusion of satellite images of different spatial resolutions: Assessing the quality of resulting images. Photogramm. Eng. Remote Sens. 1997, 63, 691–699. [Google Scholar]
- Wald, L. Quality of high resolution synthesised images: Is there a simple criterion? In Proceedings of the Third Conference “Fusion of Earth Data: Merging Point Measurements, Raster Maps and Remotely Sensed Images”. SEE/URISCA, Antipolis, France, 26–28 January 2000; pp. 99–103. [Google Scholar]
- Alparone, L.; Baronti, S.; Garzelli, A.; Nencini, F. A global quality measurement of pan-sharpened multispectral imagery. IEEE Geosci. Remote Sens. Lett. 2004, 1, 313–317. [Google Scholar] [CrossRef]
- Yuhas, R.H.; Goetz, A.F.; Boardman, J.W. Discrimination among semi-arid landscape endmembers using the spectral angle mapper (SAM) algorithm. In Proceedings of the Summaries 3rd Annual JPL Airborne Geoscience Workshop, Pasadena, CA, USA, 1–5 June 1992; Volume 1, pp. 147–149. [Google Scholar]
- Choi, M. A new intensity-hue-saturation fusion approach to image fusion with a tradeoff parameter. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1672–1682. [Google Scholar] [CrossRef]
- Alparone, L.; Aiazzi, B.; Baronti, S.; Garzelli, A.; Nencini, F.; Selva, M. Multispectral and panchromatic data fusion assessment without reference. Photogramm. Eng. Remote Sens. 2008, 74, 193–200. [Google Scholar] [CrossRef]
- Arienzo, A.; Vivone, G.; Garzelli, A.; Alparone, L.; Chanussot, J. Full-Resolution Quality Assessment of Pansharpening: Theoretical and Hands-On Approaches. IEEE Geosci. Remote Sens. Mag. 2022, 10, 168–201. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32, 1–12. [Google Scholar]
- Otazu, X.; González-Audícana, M.; Fors, O.; Núñez, J. Introduction of sensor spectral response into image fusion methods. Application to wavelet-based methods. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2376–2385. [Google Scholar] [CrossRef]
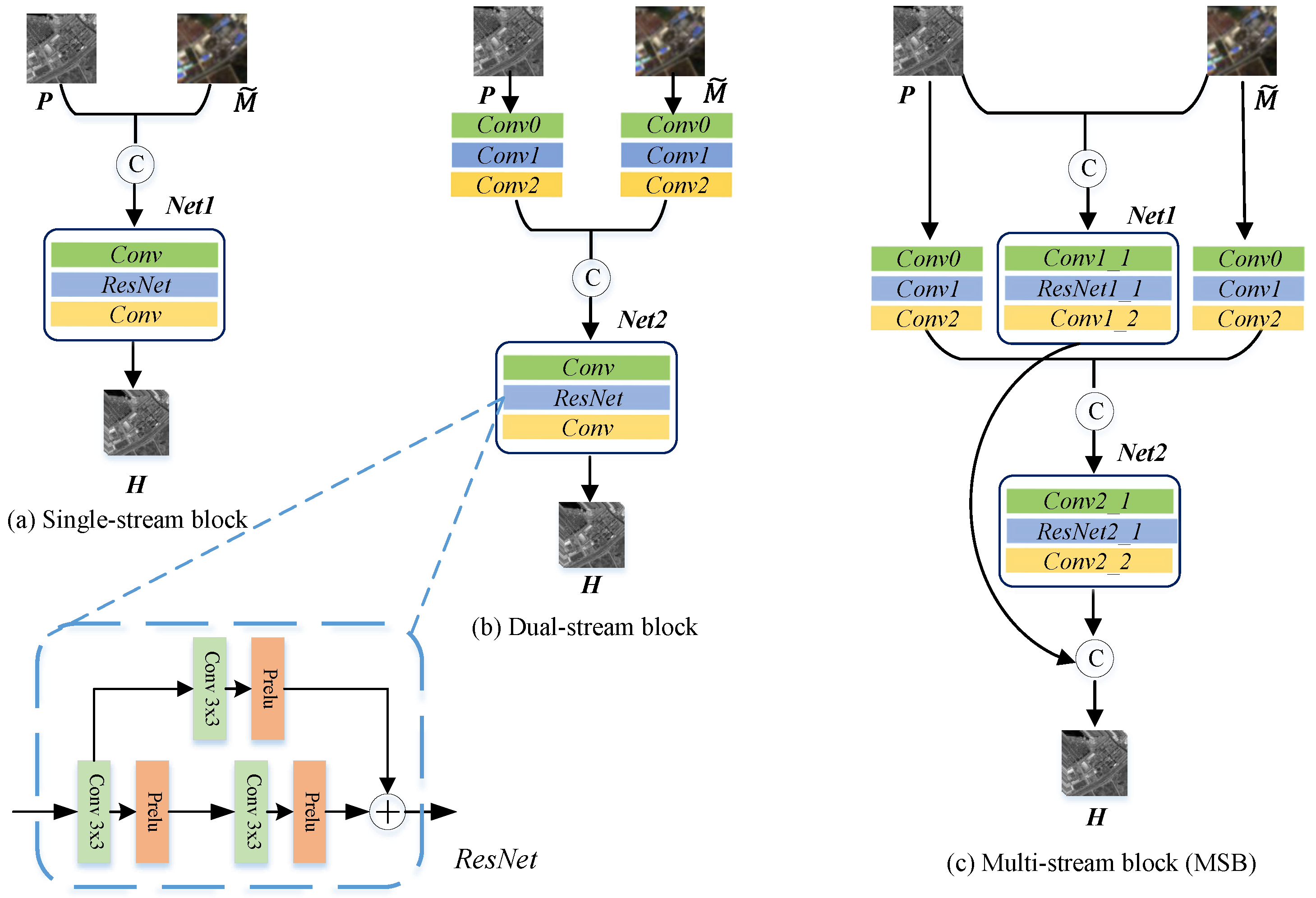









| Layer Name | Kernel Size | Stride | Padding | Input Channels | Output Channels |
|---|---|---|---|---|---|
| Conv0 | 3 × 3 | 1 | 1 | 1 (PAN) or # MS bands (MS) | 32 |
| Conv1 | 3 × 3 | 1 | 1 | 32 | 64 |
| Conv2 | 3 × 3 | 1 | 1 | 64 | 32 |
| Conv1_1 | 3 × 3 | 1 | 1 | 1 + # MS bands | 32 |
| ResNet1_1 | 3 × 3 | 1 | 1 | 32 | 32 |
| Conv1_2 | 3 × 3 | 1 | 1 | 32 | # MS bands |
| Conv2_1 | 3 × 3 | 1 | 1 | 64 | 32 |
| ResNet2_1 | 3 × 3 | 1 | 1 | 32 | 32 |
| Conv2_2 | 3 × 3 | 1 | 1 | 32 | # MS bands |
| Conv(RB) | 3 × 3 | 1 | 1 | 2 × # MS bands | 32 |
| ResNet(RB) | 3 × 3 | 1 | 1 | 32 | 32 |
| Conv(RB) | 3 × 3 | 1 | 1 | 32 | # MS bands |
| Methods | CC (1) | ERGAS (0) | (1) | RASE (0) | RMSE (0) | SAM (0) | (0) | (0) | QNR (1) |
|---|---|---|---|---|---|---|---|---|---|
| Inter23 | 0.8746 ± 0.0607 | 2.2640 ± 0.7606 | 0.8599 ± 0.0728 | 9.2008 ± 3.3102 | 26.4504 ± 11.4306 | 0.0388 ± 0.0158 | 0.0021 ± 0.0013 | 0.0699 ± 0.0303 | 0.9282 ± 0.0301 |
| AWLP | 0.9375 ± 0.0308 | 1.5913 ± 0.5495 | 0.9346 ± 0.0322 | 6.5544 ± 2.4926 | 19.1237 ± 10.1874 | 0.0304 ± 0.0106 | 0.0547 ± 0.0344 | 0.0971 ± 0.0699 | 0.8558 ± 0.0931 |
| BDSD | 0.9279 ± 0.0373 | 1.8970 ± 0.7729 | 0.9211 ± 0.0407 | 7.5889 ± 3.2623 | 22.0196 ± 12.5966 | 0.0374 ± 0.0146 | 0.0178 ± 0.0105 | 0.0436 ± 0.0326 | 0.9394 ± 0.0330 |
| GSA | 0.9321 ± 0.0382 | 1.8597 ± 0.7802 | 0.9234 ± 0.0434 | 7.3530 ± 3.0796 | 21.1029 ± 11.3929 | 0.0359 ± 0.0136 | 0.0417 ± 0.0272 | 0.0974 ± 0.0726 | 0.8666 ± 0.0884 |
| MMP | 0.9385 ± 0.0326 | 1.4731 ± 0.5839 | 0.9344 ± 0.0367 | 5.8352 ± 2.4399 | 16.9974 ± 9.7580 | 0.0302 ± 0.0112 | 0.0209 ± 0.0142 | 0.0451 ± 0.0404 | 0.9354 ± 0.0481 |
| MGH | 0.9380 ± 0.0312 | 1.6173 ± 0.5230 | 0.9358 ± 0.0316 | 6.2571 ± 2.1460 | 18.2318 ± 9.0696 | 0.0297 ± 0.0095 | 0.0637 ± 0.0359 | 0.1064 ± 0.0709 | 0.8391 ± 0.0944 |
| SIRF | 0.8252 ± 0.1064 | 2.4460 ± 0.9231 | 0.8007 ± 0.1247 | 9.6182 ± 3.8658 | 28.3468 ± 16.3364 | 0.0511 ± 0.0314 | 0.0668 ± 0.0451 | 0.0706 ± 0.0674 | 0.8687 ± 0.0893 |
| PNN | 0.9654 ± 0.0175 | 1.0973 ± 0.3758 | 0.9646 ± 0.01782 | 4.3596 ± 1.6335 | 12.6981 ± 6.3785 | 0.0243 ± 0.0086 | 0.0250 ± 0.0269 | 0.0527 ± 0.0614 | 0.9252 ± 0.0808 |
| PanNet | 0.9715 ± 0.0125 | 0.9736 ± 0.2891 | 0.9712 ± 0.0127 | 3.8504 ± 1.2341 | 11.2352 ± 5.0074 | 0.0222 ± 0.0071 | 0.0181 ± 0.0188 | 0.0208 ±0.0220 | 0.9619 ± 0.0384 |
| PSGAN | 0.9691 ± 0.0156 | 1.0041 ± 0.3031 | 0.9686 ± 0.0158 | 4.0294 ± 1.3248 | 11.7302 ± 5.0467 | 0.0230 ± 0.0073 | 0.0424 ± 0.0488 | 0.0545 ± 0.0609 | 0.9082 ± 0.0953 |
| ResTFNet- | 0.9762 ± 0.0108 | 0.8729 ± 0.2616 | 0.9758 ± 0.0111 | 3.4346 ± 1.1012 | 10.0058 ± 4.4144 | 0.0203 ± 0.0064 | 0.0226 ± 0.0224 | 0.0335 ± 0.0469 | 0.9456 ± 0.0646 |
| TACNN | 0.9602 ± 0.0203 | 1.1075 ± 0.2862 | 0.9589 ± 0.0217 | 4.2747 ± 1.1669 | 12.3099 ± 4.3565 | 0.0254 ± 0.0076 | 0.0228 ± 0.0273 | 0.0406 ± 0.0471 | 0.9387 ± 0.0667 |
| MUCNN | 0.9700 ± 0.0145 | 1.0255 ± 0.3683 | 0.9693 ± 0.0150 | 4.0755 ± 1.5800 | 11.9330 ± 6.5289 | 0.0226 ± 0.0078 | 0.0206 ± 0.0256 | 0.0291 ± 0.0411 | 0.9520 ± 0.0619 |
| MMFN (ours) | 0.9783 ± 0.0099 | 0.8368 ± 0.2575 | 0.9778 ± 0.0102 | 3.3083 ± 1.0834 | 9.6204 ± 4.3155 | 0.0192 ± 0.0061 | 0.0203 ± 0.0172 | 0.0273 ± 0.0314 | 0.9535 ± 0.0455 |
| Methods | CC (1) | ERGAS (0) | (1) | RASE (0) | RMSE (0) | SAM (0) | (0) | (0) | QNR (1) |
|---|---|---|---|---|---|---|---|---|---|
| Inter23 | 0.9247 ± 0.0344 | 4.0650 ± 1.0726 | 0.9178 ± 0.0403 | 16.4545 ± 3.3143 | 93.9909 ± 23.9316 | 0.0554 ± 0.0154 | 0.0007 ± 0.0006 | 0.0871 ± 0.0366 | 0.9122 ± 0.0368 |
| AWLP | 0.9402 ± 0.0240 | 4.0773 ± 0.8803 | 0.9376 ± 0.0244 | 18.6537 ± 4.3317 | 106.7633 ± 29.1444 | 0.0666 ± 0.0289 | 0.0354 ± 0.0182 | 0.0863 ± 0.0405 | 0.8821 ± 0.0538 |
| BDSD | 0.9154 ± 0.0340 | 5.0235 ± 1.6217 | 0.9069 ± 0.0397 | 20.0637 ± 4.1547 | 113.9981 ± 26.7171 | 0.0777 ± 0.0241 | 0.0133 ± 0.0072 | 0.0628 ± 0.0153 | 0.9247 ± 0.0158 |
| GSA | 0.9282 ± 0.0344 | 4.8284 ± 1.7408 | 0.9173 ± 0.0444 | 19.6190 ± 4.6651 | 111.9132 ± 31.0864 | 0.0705 ± 0.0239 | 0.0610 ± 0.0269 | 0.1637 ± 0.0505 | 0.7864 ± 0.0671 |
| MMP | 0.9363 ± 0.0310 | 3.7855 ± 1.1154 | 0.9353 ± 0.0322 | 15.2021 ± 3.1425 | 86.6501 ± 21.4939 | 0.0601 ± 0.0208 | 0.0077 ± 0.0031 | 0.0243 ± 0.0298 | 0.9682 ± 0.0296 |
| MGH | 0.9382 ± 0.0238 | 4.2363 ± 1.3904 | 0.9338 ± 0.0250 | 17.2398 ± 3.7794 | 97.8060 ± 22.3985 | 0.0531 ± 0.0146 | 0.0409 ± 0.0205 | 0.0958 ± 0.0396 | 0.8680 ± 0.0545 |
| SIRF | 0.9499 ± 0.0271 | 3.1350 ± 0.4913 | 0.9474 ± 0.0305 | 12.5454 ± 1.7723 | 71.7516 ± 14.5913 | 0.0595 ± 0.0156 | 0.0195 ± 0.0146 | 0.0874 ± 0.0442 | 0.8964 ± 0.0536 |
| PNN | 0.9824 ± 0.0082 | 1.9860 ± 0.5974 | 0.9821 ±0.0084 | 8.2626 ± 2.0612 | 47.1546 ± 13.7918 | 0.0406 ± 0.0120 | 0.0286 ± 0.0170 | 0.0734 ± 0.0330 | 0.9006 ± 0.0465 |
| PanNet | 0.9876 ± 0.0076 | 1.6766 ± 0.7228 | 0.9873 ± 0.0081 | 7.0452 ± 2.5112 | 39.6260 ± 12.8293 | 0.0357 ± 0.0112 | 0.0167 ± 0.0143 | 0.0289 ± 0.0154 | 0.9551 ± 0.0283 |
| PSGAN | 0.9922 ± 0.0039 | 1.2959 ± 0.3253 | 0.9921 ± 0.0040 | 5.4914 ± 1.1744 | 31.1803 ± 7.3758 | 0.0305 ± 0.0086 | 0.0258 ± 0.0208 | 0.0736 ± 0.0258 | 0.9029 ± 0.0424 |
| ResTFNet- | 0.9923 ± 0.0040 | 1.2974 ± 0.3251 | 0.9922 ± 0.0040 | 5.5191 ± 1.1801 | 31.4281 ± 7.8812 | 0.0302 ± 0.0085 | 0.0194 ± 0.0159 | 0.0514 ± 0.0153 | 0.9304 ± 0.0284 |
| TACNN | 0.9871 ± 0.0055 | 1.7147 ± 0.3856 | 0.9870 ± 0.0056 | 7.4884 ± 1.4363 | 42.7377 ± 10.0400 | 0.0417 ± 0.0110 | 0.0195 ± 0.0158 | 0.0587 ± 0.0244 | 0.9233 ± 0.0377 |
| MUCNN | 0.9896 ± 0.0053 | 1.5371 ± 0.5308 | 0.9893 ± 0.0056 | 6.5236 ± 1.9152 | 37.2740 ± 12.6312 | 0.0338 ± 0.0100 | 0.0165 ±0.0157 | 0.0229 ±0.0169 | 0.9611 ± 0.0311 |
| MMFN (ours) | 0.9930 ± 0.0037 | 1.2197 ± 0.3277 | 0.9930 ± 0.0037 | 5.1791 ± 1.1225 | 29.3613 ± 6.9001 | 0.0281 ± 0.0080 | 0.0173 ± 0.0123 | 0.0223 ± 0.0096 | 0.9609 ± 0.0189 |
| Methods | CC (1) | ERGAS (0) | (1) | RASE (0) | RMSE (0) | SAM (0) | (0) | (0) | QNR (1) |
|---|---|---|---|---|---|---|---|---|---|
| Inter23 | 0.8729 ± 0.0602 | 4.0245 ± 1.9083 | 0.8588 ± 0.0711 | 15.4794 ± 7.7455 | 53.3841 ± 25.8446 | 0.0515 ± 0.0231 | 0.0035 ± 0.0050 | 0.0545 ± 0.0333 | 0.9423 ± 0.0370 |
| AWLP | 0.9307 ± 0.0428 | 2.9811 ± 1.8452 | 0.9283 ± 0.0442 | 12.8921 ± 7.0297 | 43.5665 ± 17.8291 | 0.0484 ± 0.0201 | 0.0640 ± 0.0653 | 0.0833 ± 0.0845 | 0.8629 ± 0.1236 |
| BDSD | 0.9248 ± 0.0503 | 3.2997 ± 2.2302 | 0.9213 ± 0.0517 | 12.9515 ± 8.2815 | 43.3519 ± 20.5032 | 0.0566 ± 0.0269 | 0.0347 ± 0.0342 | 0.0456 ± 0.0426 | 0.9224 ± 0.0657 |
| GSA | 0.9301 ± 0.0542 | 3.2834 ± 2.6487 | 0.9239 ± 0.0585 | 12.8705 ± 9.4822 | 42.4991 ± 22.8362 | 0.0559 ± 0.0303 | 0.0621 ± 0.0602 | 0.1165 ± 0.1015 | 0.8335 ± 0.1330 |
| MMP | 0.9393 ± 0.0437 | 2.6916 ± 1.8941 | 0.9331 ± 0.0486 | 10.8338 ± 6.9976 | 36.3995 ± 17.6618 | 0.0467 ± 0.0235 | 0.0269 ± 0.0139 | 0.0386 ± 0.0275 | 0.9357 ± 0.0353 |
| MGH | 0.9359 ± 0.0417 | 3.0157 ± 2.0017 | 0.9340 ± 0.0425 | 11.9062 ± 7.2632 | 39.9244 ± 17.5511 | 0.0451 ± 0.0197 | 0.0689 ± 0.0614 | 0.0900 ± 0.0818 | 0.8519 ± 0.1187 |
| SIRF | 0.8431 ± 0.1578 | 4.7626 ± 1.8849 | 0.8091 ± 0.1624 | 18.5698 ± 9.0005 | 62.0451 ± 22.7993 | 0.1146 ± 0.0784 | 0.1013 ± 0.0823 | 0.0873 ± 0.0801 | 0.8263 ± 0.1377 |
| PNN | 0.9659 ± 0.0267 | 1.8580 ± 0.9584 | 0.9649 ± 0.0278 | 7.5961 ± 3.7324 | 26.0741 ± 11.5782 | 0.0360 ± 0.0181 | 0.0340 ± 0.0597 | 0.0534 ± 0.0649 | 0.9178 ± 0.1024 |
| PanNet | 0.9704 ± 0.0257 | 1.6760 ± 0.7625 | 0.9696 ± 0.0267 | 6.8436 ± 2.9796 | 23.6430 ± 10.0350 | 0.0330 ± 0.0151 | 0.0395 ± 0.0539 | 0.0547 ± 0.0720 | 0.9115 ± 0.1105 |
| PSGAN | 0.9703 ± 0.0275 | 1.6735 ± 0.7520 | 0.9694 ± 0.0286 | 6.7857 ± 2.9530 | 23.4621 ± 10.2050 | 0.0322 ± 0.0146 | 0.0454 ± 0.0716 | 0.0533 ± 0.0743 | 0.9084 ± 0.1205 |
| ResTFNet- | 0.9722 ± 0.0262 | 1.5961 ± 0.7276 | 0.9716 ± 0.0272 | 6.5399 ± 2.8571 | 22.6806 ± 10.0196 | 0.0309 ± 0.0141 | 0.0376 ± 0.0693 | 0.0411 ± 0.0667 | 0.9271 ± 0.1133 |
| TACNN | 0.9562 ± 0.0333 | 2.2537 ± 0.9703 | 0.9537 ± 0.0379 | 9.1814 ± 3.4089 | 30.9212 ± 9.9047 | 0.0440 ± 0.0172 | 0.0344 ± 0.0442 | 0.0379 ± 0.0464 | 0.9309 ± 0.0800 |
| MUCNN | 0.9694 ±0.0256 | 1.7244 ± 0.8290 | 0.9685 ± 0.0268 | 7.0707 ± 3.2251 | 24.4422 ±10.7436 | 0.0332 ± 0.0156 | 0.0305 ± 0.0548 | 0.0354 ± 0.0576 | 0.9381 ± 0.0963 |
| MMFN (ours) | 0.9753 ± 0.0226 | 1.5102 ± 0.6750 | 0.9746 ± 0.0237 | 6.1888 ± 2.6461 | 21.4883 ± 9.4222 | 0.0291 ± 0.0132 | 0.0332 ± 0.0716 | 0.0348 ± 0.0675 | 0.9379 ± 0.1137 |
| Methods | Scale (Time) | # Parameters | |
|---|---|---|---|
| RR (s) | FR (s) | ||
| PNN | 0.14 | 1.67 | 80,420 |
| PanNet | 0.26 | 3.84 | 21,384 |
| PsGan | 1.11 | 13.77 | 2,367,716 |
| ResTFNet- | 0.85 | 12.00 | 2,362,869 |
| TACNN | 0.15 | 1.72 | 80,420 |
| MUCNN | 0.51 | 7.21 | 1,362,832 |
| MMFN (ours) | 0.62 | 8.97 | 328,142 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jian, L.; Wu, S.; Chen, L.; Vivone, G.; Rayhana, R.; Zhang, D. Multi-Scale and Multi-Stream Fusion Network for Pansharpening. Remote Sens. 2023, 15, 1666. https://doi.org/10.3390/rs15061666
Jian L, Wu S, Chen L, Vivone G, Rayhana R, Zhang D. Multi-Scale and Multi-Stream Fusion Network for Pansharpening. Remote Sensing. 2023; 15(6):1666. https://doi.org/10.3390/rs15061666
Chicago/Turabian StyleJian, Lihua, Shaowu Wu, Lihui Chen, Gemine Vivone, Rakiba Rayhana, and Di Zhang. 2023. "Multi-Scale and Multi-Stream Fusion Network for Pansharpening" Remote Sensing 15, no. 6: 1666. https://doi.org/10.3390/rs15061666
APA StyleJian, L., Wu, S., Chen, L., Vivone, G., Rayhana, R., & Zhang, D. (2023). Multi-Scale and Multi-Stream Fusion Network for Pansharpening. Remote Sensing, 15(6), 1666. https://doi.org/10.3390/rs15061666







