PMPF: Point-Cloud Multiple-Pixel Fusion-Based 3D Object Detection for Autonomous Driving

Abstract

Today, multi-sensor fusion detection frameworks in autonomous driving, especially sequence-based data-level fusion frameworks, face high latency and coupling issues and generally perform worse than LiDAR-only detectors. On this basis, we propose PMPF, point-cloud multiple-pixel fusion, for 3D object detection. PMPF projects the point cloud data onto the image plane, where the region pixels are processed to correspond with the points and decorated to the point cloud data, such that the fused point cloud data can be applied to LiDAR-only detectors with autoencoders. PMPF is a plug-and-play, decoupled multi-sensor fusion detection framework with low latency. Extensive experiments on the KITTI 3D object detection benchmark show that PMPF vastly improves upon most of the LiDAR-only detectors, e.g., PointPillars, SECOND, CIA-SSD, SE-SSD four state-of-the-art one-stage detectors, and PointRCNN, PV-RCNN, Part-A² three two-stage detectors.

1. Introduction

With the increasing advancement of on-board sensors, utilizing multiple sensors to ensure the reliability and performance of autonomous driving has become a current research hotspot [1,2,3]. Environmental perception is a prerequisite for autonomous driving, and LiDAR (light detection and ranging) and cameras provide richer environmental information than radar, and IMU (inertial measurement unit). On the basis of mature 2D detection, LiDAR-based 3D detection becomes an essential task to guarantee the safety of autonomous driving in challenging environments. LiDAR point clouds and camera images complement one another well, but there are also common challenges faced in the fusion methods of point clouds and images.

Firstly, point clouds and images have different modalities. The image typically provides regular, dense lattice data that accurately records the texture information of the environment in its relative 2D coordinate system, but mono images cannot record absolute geometric information, which is essential in autonomous driving [4,5]; furthermore, camera data are affected by lighting conditions, meaning the collected data lack robustness in dark or complicated environments [6]. Unlike image data, which provide accurate geometric information about the environment, LiDAR point clouds are discrete, are disordered and have sparse data distributions in three-dimensional space; moreover, they are unable to record rich texture information.

Secondly, LiDAR-only detectors continue to lead the KITTI 3D object detection benchmark [7,8] rather than fusion modules. In order to fuse these two types of multimodal data, researchers have proposed different kinds of methods for environment perception; however, none of the current fusion models improve on the benchmark. Vora et al. attribute this to viewpoint misalignment [9], that is, a large number of SOTA (state-of-the-art) methods are based on bird’s-eye view (BEV), such as PointPillars [10] or STD [11], whereas images are represented in range view and their conversion to BEV is difficult.

In their recent work, PointPainting [9], Vora et al. propose a sequential fusion method using each point cloud with its corresponding image semantic segmentation label. This method avoids the problem of feature blurring in point-wise fusion, and the decorated data can be directly applied in most point cloud algorithms. However, this method suffers from the coupling issue between the fusion and detection stages, and the semantic segmentation network in the fusion stage requires additional time and space costs, which limits the achievement of real-time detection [12].

To solve the problems above, we propose PMPF, point-cloud multiple-pixel fusion for 3D object detection, a more direct and efficient fusion method. We project each point cloud onto the picture plane and connect the region pixels to point clouds; considering the mismatch of the point cloud corresponding to the region pixels, we conduct a region-matching module using K-means to reject mismatching data and ensure the accuracy of data fusion. The point cloud data fused by PMPF can be easily applied to any LiDAR detection model and can be competent for 3D object detection tasks including BEV and front view. Compared to the currently prevalent methods, PMPF avoids the extra neural network algorithm overhead in the fusion stage and does not require reconstruction of the LiDAR detection algorithm, avoiding the feature-blurring problem.

We conducted various experiments on the SOTA LiDAR-only detector to verify the effectiveness of the PMPF method, including the following one-stage algorithms: PointPillars [10], SECOND [13], CIA-SSD [14], SE-SSD [15] and two-stage algorithms: PointRCNN [16], PV-RCNN [17], and Part-A² [18]. The PMPF steadily improved in all of the above models, especially in PMPF-PV-RCNN, and the mAP improved to 63.62% for the KITTI 3D object detection benchmark.

PMPF proposes a simple and straightforward method of fusing point cloud data with rich image contextual texture information, which can be explained after extensive experiments. The contributions of our works are as follows:

• General—PMPF is a plug-and-play method and achieves many significant enhancements using the SOTA LiDAR-only detectors.
• Accurate—Several methods that use PMPF to fuse data, such as PV-RCNN and CIA-SSD, have improved mAP in all categories in the KITTI test set and can effectively reduce false detection rates.
• Robust—PMPF ensures the correct detection of key targets based on low-quality images.
• Fast—PMPF has low latency in the pre-fusion phase and can be directly applied to real-time detectors without sacrificing real-time performance.

2. Related Works

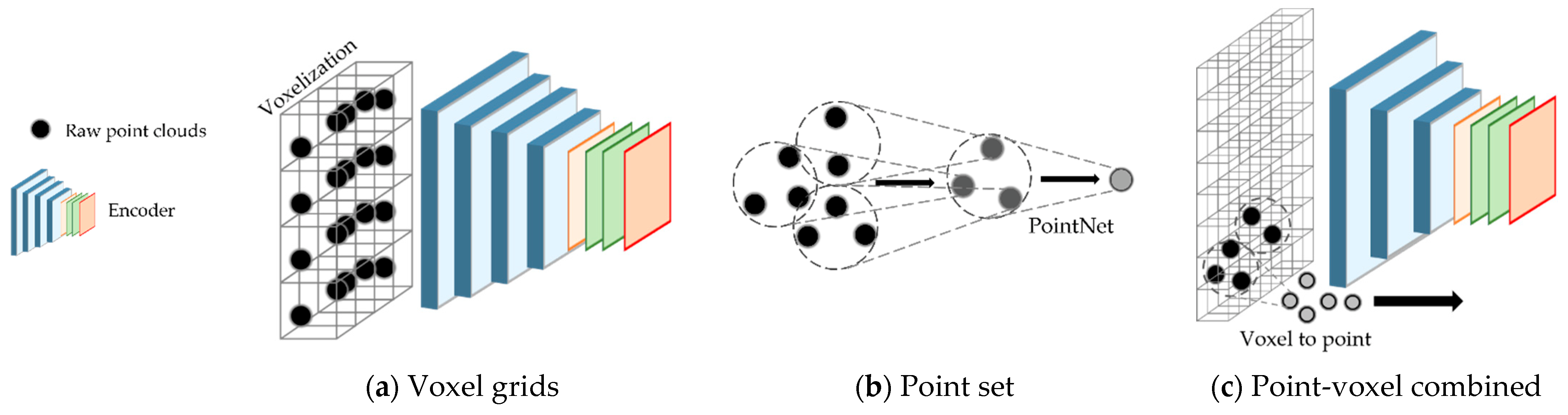
2.1. LiDAR-Only 3D Object Detector

Qi et al. [19] proposed PointNet, a pioneer in end-to-end deep learning using raw point cloud data directly, which uses MLP layers and maximum pooling layers for point cloud feature extraction. On this basis, Qi et al. [20] proposed PointNet++, a layered network based on PointNet [19], which can be used to better extract local features of point clouds and achieve better performance in 3D object detection and part segmentation.

Zhou et al. [21] proposed VoxelNet, which divides the point cloud data into fixed resolution voxels and encodes the features within each voxel, and then uses an RPN network to produce detection results. However, this representation loses the spatial resolution and fine-grained 3D geometric features of the point cloud data, and attempts to use denser voxels to increase the resolution result in a cubic multiplication of computational complexity. Yan et al. [13] proposed SECOND to improve the efficiency of VoxelNet [21] by employing a sparse convolutional network [22]. Zhang et al. [23] proposed a one-stage detection network based on height and channel attention. Ge et al. [24] proposed the first anchor-free one-stage model to achieve efficient 3D object detection.

Lang et al. [10] proposed PointPillars, which extracts longitudinal Pillars features via PointNet [19] and encodes them as pseudo-images composed of Pillars to apply a 2D detector for 3D prediction. Shi et al. [16] proposed the PointRCNN framework, which usually directly segments the point cloud to obtain the foreground points, and then fuses the semantic features; the PointVoxel-RCNN (PV-RCNN) [17] proposed by uses 3D sparse networks and PointNet [19] to learn point cloud features, and Shi et al. also proposes the key-point-to-grid ROI module to optimize voxel information. Shi et al. [18] proposed the Part-A² network, which consists of a part-aware phase and part-aggregation phase. The part-aware phase consists of a UNet-like [25] network that performs sparse convolution and sparse deconvolution on the point cloud to learn the features of the point cloud and generate coarse region recommendations.

2.2. LiDAR-Camera Fusion-Based 3D Object Detector

Despite the challenges of image-point cloud data fusion, research has been conducted for 3D object detection. We categorized previous methods into the following four representative classes: frustum-based fusion [26,27,28,29,30], point-based fusion [9,31,32], multi-view-based fusion [33,34,35,36,37,38,39,40,41,42,43] and voxel-based fusion [21,44,45,46].

Frustum-based fusion is a sequential, result-level fusion method that leverages the outputs of image detectors to refine the search space for 3D detection in order to reduce computation. F-PointNet [26], proposed by Charles et al., is the pioneering work in frustum-based fusion. F-PointNet [26] projects 2D bounding boxes, which are generated from image detectors, into the point cloud space to form corresponding 3D frustum region proposals, which are fed into PointNet [19] for 3D object detection. Wang et al. proposed F-ConvNet [27], an improvement based on F-PointNet [26], to achieve end-to-end 3D detection. Du et al. [28] achieved performance improvement by refining the stage from 2D bounding boxes to point cloud space, filtering out unnecessary points in the background before feeding them into the 3D detector. Shin et al. [29] also employ the same idea but use a neural network to optimize the frustum space for the 3D proposal. The above methods perform well when there is only one target in the subspace, but suffer from problems in detecting small targets, such as pedestrians in crowded sceneries. Therefore, Yang et al. proposed IPOD [30], which uses image semantic segmentation results to filter background points, refines the search space to each point, and uses PointNet++ [20] for 3D-bounding boxes regression, which yields significant performance benefits in complex multi-object scenes and scenes where targets are occluded. In general, the Frustum-based fusion method relies on the results of 2D data to limit the search space of 3D detectors, significantly reducing the computational cost; however, the main disadvantage is also apparent, with its performance heavily dependent on 2D detectors.

Point-based fusion is a feature-level fusion model that combines high-dimensional image information point-wise and applies the fused data for 3D object detection. PointPainting [9] proposed by Vora et al. achieves better performance than LiDAR-only 3D detectors (PointPillars [10]) by fusing the semantic segmentation encoding of the image with the point clouds point-wise and then feeding the decorated point cloud into the 3D detector. The fusion-based method solves the resolution mismatch between dense image and sparse point clouds to a certain extent: the semantic segmentation results in a combination of contextual information. Imad et al. [31] utilized a pre-trained image semantic segmentation model for the object detection of point clouds represented at BEV by transfer learning, but this approach still suffers from the quality of the semantic segmentation model. Huang et al. [32] fused deep semantic features with geometric features to improve the performance of 3D detectors. However, the image and LiDAR detectors are highly coupled and the use of semantic segmentation networks in the fusion stage leads to an increase in training costs and the overall computational cost [12], unlike IPOD [30] which limits the 3D search space by using semantic segmentation results.

The multi-view-based model is a feature-level fusion model which generates 3D region proposals from a bird’s-eye view and performs the regression of 3D bounding boxes. One of the most important pioneering works is MV3D [33] proposed by Chen. MV3D [33] pixelates the point cloud in BEV, extracts feature and generates 3D proposals; it then projects the 3D proposals into range-view, fuses them with the high-dimensional features of the image in the ROI pooling stage and then performs 3D bounding box regression. The drawback of this method is that some small targets may be completely obscured in the BEV. Ku et al. improved on MV3D [33] by proposing AVOD [34], which performs a 3D proposal stage by fusing feature maps of images from VGG-16 [47] and point cloud data, and uses an autoencoder (AE) structure to achieve feature space dimensionality reduction and decrease computational cost. Lu et al. [35] applied an encoder–decoder-based proposal network to ensure that small targets are not lost in BEV. The fusion stage of the above methods occurs at the point of ROI pooling, which results in the loss of reliable geometric coding. Yuan et al. [36] achieved building instance extraction using the feature fusion model with high-resolution images and radar data as input. Zheng et al. [37] proposed a 3D detector based on a cascaded feature fusion model. Liu et al. [38] proposed a feature fusion model using an attention module to guide LiDAR and camera data. Wang et al. [39,40] proposed KDA3D and MCF3D for 3D object detection using multiple attention mechanism and multi-stage complementary fusion, respectively. Pang et al. [41] proposed a Camera-LiDAR Object Candidates Fusion method. Liang et al. proposed ContFuse [42] for point-wise fusion using continuous convolutional fusion layers [48] and preserved fine geometric information by fusing multi-scale image and point cloud features in multiple stages of the network through continuous convolutional layers. The problem with this method is that the texture information of the image data may not be fully utilized when the point cloud data are sparse. Based on these problems, Liang et al. [43] proposed a multi-task fusion-based method that further improves point-wise fusion. The method combines the result-level fusion, depth completion task, road estimation task and continuous convolutional fusion layers to achieve better overall performance of the model.

Voxel-based fusion is achieved by fusing vowelized point clouds with image features, which has the advantage that voxels can be convolved using standard 3D convolution. V.A. Sindaqi et al. [44] proposed MVX-Net, which projects voxels onto the image plane and fuses them with texture information at a later stage of VoxelNet [21]. MVX-Net achieved significant performance improvement compared to VoxelNet [21]. It is worth mentioning that the idea of fusing vowelized point clouds with image data was proposed by S. Song et al. [45] in 2014. They used a support vector machine (SVM) pair to accomplish the classification task. Song et al. [46] then built on this by using a 3D convolutional network for classification. Voxel-based fusion methods still have the disadvantage of being vowelized, with fine geometric information becoming lost due to voxelization, and the computational cost of 3D convolution increases dramatically due to voxel refinement.

3. Method

The PMPF architecture provides corresponding point clouds and images as input data and facilitates the detection of 3D targets. The idea of this paper is to manipulate point clouds and images directly from the data level, avoiding complex tasks such as semantic segmentation in the pre-fusion stage. The method consists of the following two main stages: (1) Fusion—LiDAR points are fused with the corresponding multi-pixels by PMPF (Section 3.1); (2) input of the fused data to a 3D detector for 3D object detection and localization (Section 3.2).

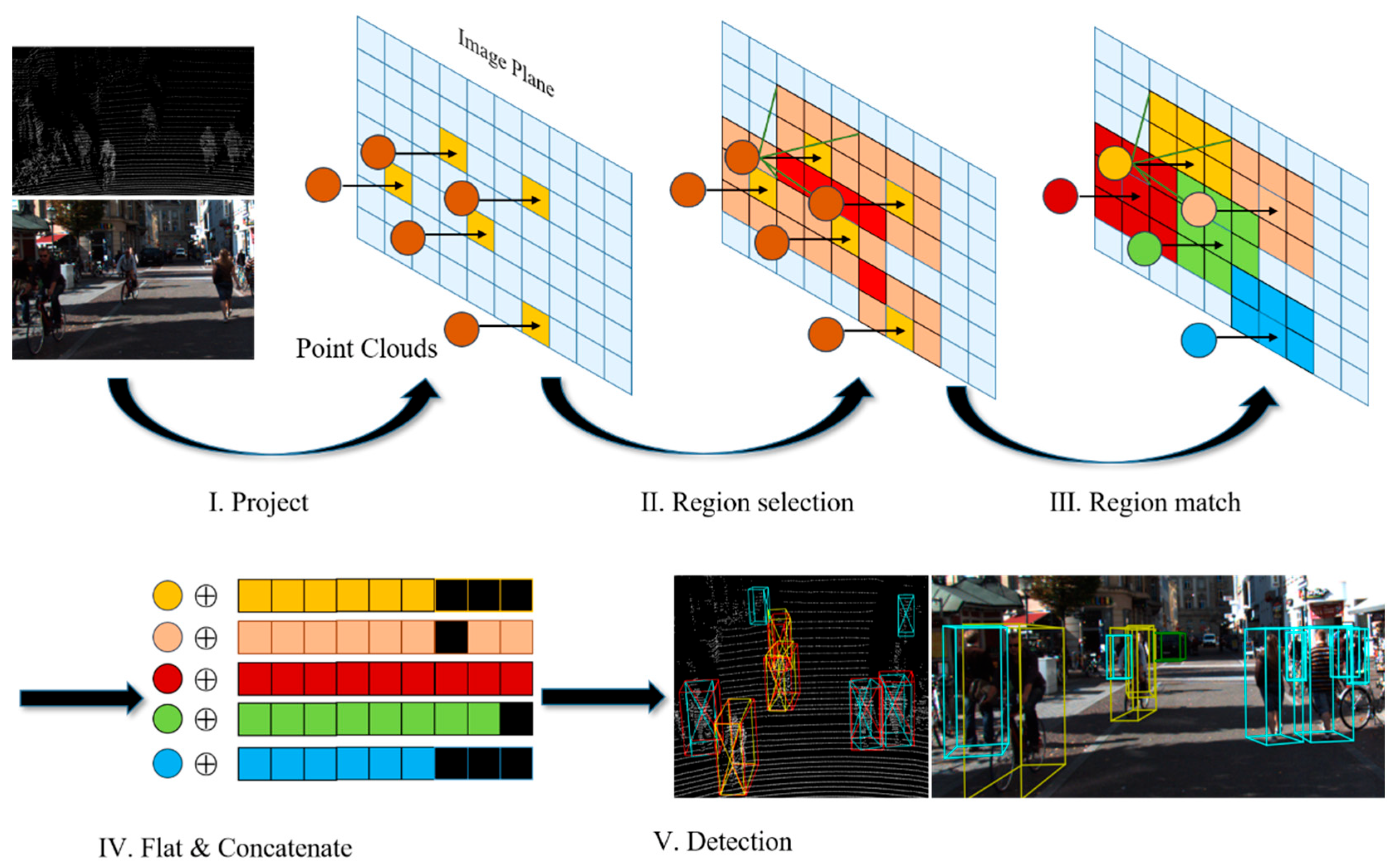
3.1. PMPF Method

The central idea of PMPF is to fuse the contextual information of the image pixels with the point cloud, which alleviates the resolution mismatch between sparse point clouds and the dense image and enriches the fused point cloud with image information to improve the performance of the LiDAR detector. The process of implementing PMPF is shown in the Figure 1. (1) Project the point cloud onto the image plane to form a point-pixel pair; (2) expand the pixels into a region-by-region size to form a point-multi-pixel pair; (3) use filters to remove pixels that are irrelevant to the points for accurate matching; and (4) fuse the points with the pixels.

Algorithm 1 shows the details of the PMPF algorithm. It should be noted that the point cloud $L\in {ℝ}^{N,4}$ is cropped, i.e., all points are within the image plane after projection. In the KITTI dataset, each point in the point clouds $L\in {ℝ}^{N,4}$ is represented as (x, y, z, reflectivity), where x, y, z is the position of each point in the relative LiDAR coordinate system. The KITTI dataset provides the homogenous transformation matrix $T\in {ℝ}^{4,4}$ for every frame of data in order to transform the LiDAR coordinate system to the camera coordinate system, and $M\in {ℝ}^{3,4}$ represents the camera parameter. The function $Project\left(·\right)$, projecting the LiDAR onto the camera plane has been provided, so it is not repeated in this paper. The projection of the point gives its coordinates in the image ${\overrightarrow{l}}_{image}\in {ℝ}^2$. We round off ${\overrightarrow{l}}_{image}$ to prevent it going outside the image ranges. Finely aligned point clouds and image data must be projected correctly. Misalignment can cause the fused data to become distorted, and when misaligned data are fed into the network for training, false positives and false negatives can lead to poor network convergence, directly affecting the final detection results. When the misaligned fused data is fed into the well-trained PMPF for detection, the detector becomes confused and false detection results occur. See Section 3.1.1 and Section 3.1.2 for details of pixel region selection and matching. After obtaining the region ${\overrightarrow{i}}_{match}\in {ℝ}^{K,K,3}$ corresponding to the point, we flatten it and concatenate it with the point to generate the fused data, which we discuss in detail in Section 3.1.3.

Algorithm 1 Point Cloud-Multiply Pixels Fusion ($L$, $I$, $K$, $T$, $M$)
Inputs:
Point clouds $L\in {ℝ}^{N,4}$ with N points.
Image $I\in {ℝ}^{W,H,3}$ with W width, H height and 3 channels.
Region size $K\in ℝ$ must be odds.
Homogenous transformation matrix $T\in {ℝ}^{4,4}$.
Camera matrix $M\in {ℝ}^{3,4}$.
Output:
Fused point clouds $P\in {ℝ}^{N,4+K^2}$.
for $\overrightarrow{l}\in L$ do
${\overrightarrow{l}}_{image}=\mathrm{Project}\left(M,T,{\overrightarrow{l}}_{xyz}\right)$	$⊳{\overrightarrow{l}}_{image}\in {ℝ}^2$
${\overrightarrow{i}}_{selection}=\mathrm{Selection}\left({\overrightarrow{l}}_{image},I,K\right)$	$⊳{\overrightarrow{i}}_{selection}\in {ℝ}^{K,K,3}$
${\overrightarrow{i}}_{match}=\mathrm{Match}\left({\overrightarrow{i}}_{selection},{\overrightarrow{l}}_{image}\right)$	$⊳{\overrightarrow{i}}_{match}\in {ℝ}^{K,K,3}$
${\overrightarrow{i}}_{flat}=\mathrm{Flat}\left({\overrightarrow{i}}_{match}\right)$	$⊳{\overrightarrow{i}}_{flat}\in {ℝ}^{K^2}$
$\overrightarrow{p}=\mathrm{Concatenate}\left(\overrightarrow{l},{\overrightarrow{i}}_{flat}\right)$	$⊳\overrightarrow{p}\in {ℝ}^{4+K^2}$
end for

3.1.1. Region Selection

The image texture information corresponding to each point’s data is determined. The current common practice for adding texture information to point cloud data is called point cloud coloring. After the point cloud-image correspondence has been completed, the information of the pixel closest to each point is fused to the point data to form a colored point cloud, completing the point cloud coloring. This is an intuitive and special method of selection, i.e., a point cloud corresponds to a pixel, which is very convenient for human observation using the naked eye, but this method suffers from underutilization, wastes a large amount of image information, and discretizes the texture information in a continuous ordered arrangement, which blurs the deep semantics of the regional pixels.

In the KITTI dataset, a point of data has about 40,000 points corresponding to the image plane, and there are 370 × 1224 pixels in the image; here, the utilization of fused data for image texture information is only 8.22% with point cloud coloring as an example. In this paper, we propose a viewpoint that one point corresponds to multiple pixels information, where each projected point is the center of the region, to obtain ${\overrightarrow{i}}_{selection}\in {ℝ}^{K,K,3}$ and the $K^2$ adjacent pixels contained in a rectangular region of size (K × K) are selected as the image region. The mathematical expression for the region selection method is as follows:

$$\mathrm{Selection}\left({\overrightarrow{l}}_{image}, I, K\right)=\left[\begin{array}{ccccc}I\left[{\overrightarrow{l}}_{image}\left[0\right]-\frac{K-1}{2},{\overrightarrow{l}}_{image}\left[1\right]-\frac{K-1}{2}\right]& \cdots & I\left[{\overrightarrow{l}}_{image}\left[0\right],{\overrightarrow{l}}_{image}\left[1\right]-\frac{K-1}{2}\right]& \cdots & I\left[{\overrightarrow{l}}_{image}\left[0\right]+\frac{K-1}{2},{\overrightarrow{l}}_{image}\left[1\right]-\frac{K-1}{2}\right]\\ ⋮& & \ddots \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⋰& & ⋮\\ I\left[{\overrightarrow{l}}_{image}\left[0\right]-\frac{K-1}{2},{\overrightarrow{l}}_{image}\left[1\right]\right]& \cdots & I\left[{\overrightarrow{l}}_{image}\left[0\right],{\overrightarrow{l}}_{image}\left[1\right]\right]& \cdots & I\left[{\overrightarrow{l}}_{image}\left[0\right]+\frac{K-1}{2},{\overrightarrow{l}}_{image}\left[1\right]\right]\\ ⋮& & ⋰\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\ddots & & ⋮\\ I\left[{\overrightarrow{l}}_{image}\left[0\right]-\frac{K-1}{2},{\overrightarrow{l}}_{image}\left[1\right]+\frac{K-1}{2}\right]& \cdots & I\left[{\overrightarrow{l}}_{image}\left[0\right],{\overrightarrow{l}}_{image}\left[1\right]+\frac{K-1}{2}\right]& \cdots & I\left[{\overrightarrow{l}}_{image}\left[0\right]+\frac{K-1}{2},{\overrightarrow{l}}_{image}\left[1\right]+\frac{K-1}{2}\right]\end{array}\right].$$

(1)

When an image boundary is searched, it is processed as follows: where $I\left[w,h\right]\in {ℝ}^3$ returns the red channel value $R\in ℝ$, green channel value $G\in ℝ$ and blue channel value $B\in ℝ$ of the image coordinate at [w, h], where $W\in ℝ$, $H\in ℝ$ is the width and height of the image. It returns [0, 0, 0] when w or h exceeds the image range, i.e., there is

$$I\left[w,h\right]=\left\{\begin{array}{c}\left[R_{\left[w,h\right]},G_{\left[w,h\right]},B_{\left[w,h\right]}\right], if 0\le w\le W and 0\le h\le H,\\ \left[0,0,0\right], otherwise. \end{array}\right.$$

(2)

As shown in Figure 2, our method increases the utilization of image texture information and gives each point richer color details. However, this method of uniformly acquiring image textures may lead to a mismatch of individual points with image texture information, e.g., points at the edges of the target, whose corresponding regional pixels may represent deep semantics of other objects, affect the detection performance of the detector.

3.1.2. Region Match

As mentioned at the end of Section 3.1.1, point cloud and multi-pixel mismatches are positively correlated with the parameter K. Excessive mismatching can affect the neural network’s understanding of the data, leading to a decrease in detector performance. In KDA3D [39], Wang et al. performed conditional clustering for a 5 × 5 sized pixel region to guide the generation of a pseudo point to densify the key point clouds. Inspired by this, we use efficient K-means clustering [49,50] to eliminate mismatched pixels in the region corresponding to each point. We use the key pixel as the initial clustering center, extract the pixels similar to the clustering center as its augmentation, based on the texture information of the pixels in the region, and fill the irrelevant pixels with [0, 0, 0]. Specifically, we use the clustering condition by calculating the Euclidean distance between each pixel in the region and the $RGB\in {ℝ}^3$ vector of the initial clustering center pixel, where $D_{texture}\in ℝ$ is calculated as follows:

$$D_{texture}=\sqrt{\Delta R^2+\Delta G^2+\Delta B^2}.$$

(3)

However, pixel matching according to the texture alone is difficult due to the problem of overlapping targets in complex road scenarios; for example, when there are similar colors for the foreground and background, overlapping targets of the same kind, and different kinds of targets, K-means is unable to perform valid clustering of target edge pixels. We propose clustering conditions that take into account texture, pixel depth and pixel reflectivity at the same time to cope with situations such as those dealing with more complex target edges where (1) texture and reflectivity are similar but there is a depth difference, (2) texture and depth are similar but there is a reflectivity difference, and (3) texture is similar but there is a depth and reflectivity gap. Depth distances $D_{depth}\in ℝ$ and reflectivity distances $D_{reflectivity}\in ℝ$ are calculated as follows:

$$D_{depth}=\Delta depth,$$

(4)

$$D_{reflectivity}=\Delta reflectivity.$$

(5)

Due to the sparsity of the point cloud, the density of the projected point cloud is much smaller than that of the image, so the contextual pixels lack true depth and reflectivity. We can obtain the pseudo-depth and pseudo-reflectivity by performing interpolation, depth complementation, etc., but the time cost of this generation is unacceptable. The PMPF method pads the augmented pixels with the same pseudo-depth and pseudo-reflectivity as the key pixels in the region selection stage and, at the same time, averages the pseudo-depth and pseudo-reflectance of the reused pixels. Objectively, both interpolation and padding methods introduce errors, but we cannot quantify the depth and reflectance errors introduced by PMPF due to the lack of true values of depth and reflectance on each pixel. Roughly speaking, depth-completion introduces the smallest number of errors, while padding introduces the largest number of errors. In Section 5.4.3, it is experimentally demonstrated that after filling the region pixels with the same pseudo-depth and pseudo-reflectivity as the key points, more confusing pixels are eliminated (utilization and repetition rate are reduced) and the detector achieves higher accuracy.

In summary, after obtaining the complete information of the pixels in the augmented region, clustering is performed based on the$\left(R,G,B,depth,reflectivity\right)$information of the pixels, and the augmented pixels of the same kind as the key pixels are considered as the region-matching pixels, which are subsequently fused with the point cloud. Ultimately, we use the Euclidean distance between each pixel in the region and the $\left(R,G,B,depth,reflectivity\right)$ vector of the initial clustering center pixel as the clustering condition, as follows:

$$Distance={\beta }_1{D}_{texture}+{\beta }_2{D}_{depth}+{\beta }_3{D}_{reflectivity},$$

(6)

where ${\beta }_1$, ${\beta }_2$ and ${\beta }_3$ are the constant coefficients of the distance formula.

3.1.3. Flat and Concatenate

Once a multi-pixel match to the point cloud has been obtained, the way in which the two data are combined needs to be considered. When matching multi-pixel ${\overrightarrow{i}}_{match}\in {ℝ}^{K,K,3}$, the point cloud $l\in {ℝ}^4$, fusing the pixels as an additional channel to the point cloud is difficult. We first perform a bitwise operation on the $RGB\in {ℝ}^3$ of the pixels and then represent them flatted in ${\overrightarrow{i}}_{flat}\in {ℝ}^{K^2}$. In this way, the matched multi-pixels can be connected to the point cloud as an additional $K^2$ channel of data to form the fused data.

3.2. 3D Object Detection

In Section 3.1, the region image with contextual information corresponding to each point cloud is determined (Section 3.1.1), the mismatched pixels in the region are eliminated using K-means (Section 3.1.2), and the fused data with rich texture information are formed as flat and concatenate (Section 3.1.3). Thus, PMPF increases the dimensionality of the point clouds $\overrightarrow{p}\in {ℝ}^{4+K^2}$ while performing data fusion, which requires the object detection model to have an autoencoder to cope with the different dimensions of the input data.

An autoencoder is an encoder–decoder network that compresses the input data into potential spatial representations and then reconstructs the output using such representations, which is a typical feature extraction method. When the dimensionality of the output data is different from that of the input data, it enables data dimensionality augmentation or compression. As shown in Figure 3, some LiDAR-only detectors convert point clouds into 2D/3D regular voxel data and input them into a 2D CNNs on BEV or 3D CNNs such as VFE (voxels feature encoder) [21]. Some detectors perform feature extraction directly on the original point cloud by using PFE (points feature encoder), while other detectors combine the advantages of both representations by fusing raw point clouds and voxel features. Here, a brief 3D-object-detection process is represented as follows:

$$P=\left\{p_1,p_2,\cdots ,p_n\right\},p_i=\left[x_i,y_i,z_i\right],$$

(7)

$$F=\left\{f_1,f_2,\cdots ,f_n\right\},f_i=FE\left(Transation(p_i)\right),$$

(8)

$$c_i,t_i,{\theta }_i=Head\left(f_i\right),$$

(9)

where $P\in {ℝ}^{n, 3}$, $F\in {ℝ}^{n, m}$ are the set of point clouds and the set of feature vectors of point clouds, and $m$ is the dimension of single feature. $Transation\left(·\right)$ is the transformation function of the point clouds, $FE\left(·\right)$ stands for feature extraction method, and $Head\left(·\right)$ represents the function of detection head model. $p_i\in {ℝ}^3$, $f_i\in {ℝ}^m$, $c_i\in {ℝ}^q$, $t_i\in {ℝ}^3$, ${\theta }_i\in ℝ$ denote the ith point, the feature vector of the ith point, the classification probability, and the position, orientation of the ith candidate bounding box, respectively. $q$ is the number of detection categories.

In the present approach, we demonstrate the effectiveness of PMPF on various SOTA LiDAR-only detectors [10,13,14,15,16,17,18] with autoencoders.

4. Experimental Setup

In this section, we describe the details of the dataset and experimental setup used in the experiments of the PMPF method. The experiments were conducted using an Intel Xeon 6338 with 32 cores, 64 GB RAM, and RTX3090 with 24 GB Memory Size.

4.1. Dataset

We use the KITTI 3D object detection dataset [7,8], which provides time-synchronized LiDAR point clouds and images, and provides each set of data separately in space for its parameters. It consists of 7481 training data sets and 7518 test data sets, containing a total of 80.256 labeled objects. It has three main classifications: car, pedestrian and cyclist. Ground truth objects were only annotated if they are visible in the image, so we follow the standard practice [21,33] of only using LiDAR points that project into the image. Note that KITTI 3D object detection ultimately uses average precision (AP) to evaluate the detection performance of the detector for each classification; for cars, KITTI requires a 3D bounding box overlap of 70%, while for pedestrians and cyclists it requires a 3D bounding box overlap of 50%; it offers three different levels of difficulty with easy, moderate, and hard. According to the official KITTI’s instructions, the above difficulty is elaborated on as follows:

• Easy: Minimum bounding box height: 40 px; maximum occlusion level: fully visible; maximum truncation: 15%;
• Moderate: Minimum bounding box height: 25 px; maximum occlusion level: partly occluded; maximum truncation: 30%;
• Hard: Minimum bounding box height: 25 px; maximum occlusion level: difficult to see; maximum truncation: 50%.

4.2. PMPF Setup

Here, we provide more details on the PMPF fusion setup.

PMPF directly fuses the original point cloud data and the corresponding image data at the data level, which requires a neural network model using the fused data to be adaptive to changes in the dimensionality of the input data.

In the projection stage, we followed the projection method provided by KITTI. Each set of time-synchronized point cloud-images provided specific camera internal references, with a conversion matrix that allowed the point clouds to be converted to coordinates in the image plane. We crop point clouds that are not in the image plane after projection, including (1) point clouds towards the backside and (2) point clouds whose coordinates are outside the image plane after projection.

In the region-selection stage, we set the region size as K = 3, i.e., the point cloud corresponds to the augmented pixel region ${\overrightarrow{i}}_{match}\in {ℝ}^{3,3,3}$. For augmented pixels that are beyond the image plane, we fill in ([0, 0, 0]).

In the region-matching stage, we use the Euclidean distance of simultaneously considering $\left(R,G,B,depth,reflectivity\right)$ and key pixels as the clustering condition, where the parameters in Equation (6) are:

$$\left(\begin{array}{c}{\beta }_1\\ {\beta }_2\\ {\beta }_3\end{array}\right)=\left(\begin{array}{c}1\\ 0.5\\ 0.5\end{array}\right),$$

(10)

due to the lack of pixel semantic labeling guidance, we cannot quantify the error of region matching and obtain the optimal solution for the above parameters. However, we derived the above parameters by eliminating as many mismatches as possible in challenging scenarios. The experiments in Section 5.4.2 and Section 5.4.3 demonstrate that the above parameters are helpful for both eliminating mismatches and improving the detector accuracy.

When executing the K-means algorithm, we use Bi-K-means, i.e., the number of clusters is 2, the key pixel is set as one initial cluster center, another non-key pixel is randomly set as the second initial cluster center, and the termination condition is 20 iterations or an accuracy of less than 1.

It should be emphasized that the above parameters are derived from the KITTI 3D object detection dataset. Different operating conditions lead to different data and model run performance, and the differences regarding parameter selection are detailed in Section 5.3 and Section 5.4.

4.3. 3D Object Detection

In this paper, we apply the open source code of the following 7 different methods: PointPillars [10], SECOND [13], CIA-SSD [14], SE-SSD [15], PointRCNN [16], PV-RCNN [17], Part-A² [18]. The fusion versions of each network that use our method will be referred to as PMPF (e.g., PMPF-PointRCNN).

We used the open-source project of the above 7 methods and decorated the point cloud with 9 items of the raw matching pixels information. In the two-stage algorithm, the fused point cloud data are used as input for both the encoder and the region proposal network. No other changes were made to the public experimental configurations.

5. Result and Analysis

In Section 5.1 and Section 5.2, we present PMPF results on the KITTI datasets and compare them with the results of SOTA approaches. The parameters of the PMPF are outlined in Section 4.2. In Section 5.3, we analyzed the time delay introduced by the PMPF. In Section 5.4, we reveal the effects of each component of the PMPF on the 3D detection accuracy with ablation studies. All the detection results are evaluated by performing official KITTI 3D validation, which evaluates the performance of the models according to moderate average precision (mAP) overall and AP according to category.

5.1. Quantitative Analysis

5.1.1. KITTI Validation Set

We investigated the impact of the PMPF method on seven different LiDAR detectors.

Table 1. Applied to SOTA LiDAR-based object detectors for PMPF. All LiDAR methods show improved 3D mean accuracy precision (mAP) for car, pedestrian and cyclist on the KITTI validation set. Abbreviations: runtime (RT).

Method	RT (ms)	mAP	Car			Pedestrian			Cyclist
		Mod.	Easy	Mod.	Hard	Easy	Mod.	Hard	Easy	Mod.	Hard
PointPillars [10]	16	66.96	87.22	76.95	73.52	65.37	60.66	56.51	82.29	63.26	59.82
PMPF-PointPillars	38	69.44	86.61	76.71	75.35	70.69	66.20	60.53	82.14	65.41	58.91
SECOND [13]	38	67.12	86.85	76.64	74.41	67.79	59.84	52.38	84.92	64.89	58.59
PMPF-SECOND	60	68.44	88.18	78.21	76.88	69.36	60.35	54.23	85.52	66.76	63.38
PointRCNN [16]	100	67.01	86.75	76.06	74.30	63.29	58.32	51.59	83.68	66.67	61.92
PMPF-PointRCNN	122	72.26	88.58	78.43	77.93	63.90	58.53	51.49	87.25	74.46	68.28
PV-RCNN [17]	80	70.83	91.55	83.12	78.94	63.63	56.62	52.93	89.17	72.75	68.57
PMPF-PV-RCNN	102	73.52	89.16	83.66	78.82	66.59	61.82	56.94	90.79	75.08	70.88
Part-A2 [18]	80	69.79	89.56	79.41	78.84	65.68	60.05	55.45	85.50	69.90	65.48
PMPF- Part-A2	101	70.82	89.44	79.17	78.67	64.01	61.25	58.35	85.56	72.04	67.12
CIA-SSD [14]	31	- *	89.89	79.63	78.65	-	-	-	-	-	-
PMPF-CIA-SSD	53	-	89.66	80.95	78.90	-	-	-	-	-	-
SE-SSD [15]	31	-	93.19	86.12	83.31	-	-	-	-	-	-
PMPF-SE-SSD	53	-	94.20	85.45	83.68	-	-	-	-	-	-

* “-”: These data were not provided in the original literature. The best result is bolded in each set of comparisons.

illustrates that the PMPF method led to improvements in PointPillars [10], SECOND [13], CIA-SSD [14], SE-SSD [15], PointRCNN [16], PV-RCNN [17], and Part-A² [18]. Of the methods for which the literature provided mAP results, 38 of the 51 comparisons were improved by PMPF. Especially in difficult situations, such as when looking at pedestrians and cyclists, the PMPF method offers significant improvements. The pedestrian category gained 5.32%, 5.54% and 4.02% when using the PMPF-PointPillars detector for easy, moderate and hard difficulties of 3D average precision (AP_3D) improvement in validation split, reaching 70.69%, 66.20% and 60.53% of mAP_3D, the highest pedestrians category AP among the seven methods tested in this paper. In the PMPF-PointRCNN, the cyclist category at easy, moderate and hard difficulties obtained the largest mAP_3D gains of 3.57%, 7.79% and 6.36%, respectively, and reached the highest AP_3D of all tested methods at 90.79%, 75.08% and 70.88%. It should be noted that, as illustrated in Figure 4b, the fusion of texture information may interfere with the detector for the car category, which has more distinct geometric features. The detector does not reflect a significant performance improvement in the pedestrian category. These differences are caused by the different detectors.

Additionally, we performed a comparison with the LiDAR detector using the PointPainting [9] method on the validation set. In the PointPainting [9] profile, which provides painted PointPillars [10] in the validation set, as shown in

Table 2. Comparison with PointPainting in KITTI 3D detection validation set. The PMPF method shows an overall improvement in car and cyclist categories, a 0.41% improvement in mAP compared to PointPainting and, more importantly, a great improvement in run time (RT).

Method	RT(s)	mAP	Car			Pedestrian			Cyclist
		Mod.	Easy	Mod.	Hard	Easy	Mod.	Hard	Easy	Mod.	Hard
PointPillars [10] (base)	0.016	66.96	87.22	76.95	73.52	65.37	60.66	56.51	82.29	63.26	59.82
PointPainting [9]	0.316	69.03	86.26	76.77	70.25	71.50	66.15	61.03	79.12	64.18	60.79
PMPF-PointPillars	0.037	69.44	86.61	76.71	75.35	70.69	66.20	60.53	82.14	65.41	58.91

The best result is bolded in each column.

, five of nine comparisons were improved with PMPF. It is noteworthy that in the class of pedestrian with the sparsest point cloud, two out of the three comparisons were negative. PointPainting [9] directly fuses the semantic results of the target pixels with the point cloud data, and its strong coupling properties in classification and bounding box regression tasks give it a unique advantage in this type of task. PMPF is more straightforward and decoupled; although it lags behind PointPainting [9] in the pedestrian category; however, it is equal to or ahead of PointPainting in the moderate mAP. Additionally, because it avoids the complex semantic segmentation task, it runs three times faster than the PointPainting [9] method and can be better applied to real-time tasks.

5.1.2. KITTI Test Set

Here, we compare the PMPF method with the SOTA LiDAR detector in the KITTI 3D object detection benchmark. In this paper, we selected the best-performing radar detector in the test set, i.e., the PMPF-PV-RCNN, and compared it to the KITTI leaderboard. The leaderboard is divided into the following two categories according to modality: LiDAR + image (L+I) and LiDAR only (L). We compare the performance of the native PV-RCNN model in the test set to our method and show the Improvement; we achieved improvements in seven out of nine comparisons and improved the overall mAP by 0.81% to 63.62%. Additionally, by comparing all current fusion detectors that use LiDAR and Image data, our method achieved the highest mAP.

Based on the consistency of PMPF-PV-RCNN improvements between the validation set and test set, and the generality of the PMPF method, it is reasonable to believe that other methods in

Table 3. Results from the KITTI test set for 3D object detection. These models are LiDAR (L), image (I). Delta is due to the difference in PMPF, i.e., PMPF-PV-RCNN minus PV-RCNN.

Method	Modality	mAP	Car			Pedestrian			Cyclist
		Mod.	Easy	Mod.	Hard	Easy	Mod.	Hard	Easy	Mod.	Hard
MV3D [33]	L+I	- *	74.97	63.63	54.00	-	-	-	-	-	-
AVOD-FPN [34]	L+I	54.86	83.07	71.76	65.73	50.46	42.27	39.04	63.76	50.55	44.93
F-PointNet [1]	L+I	59.35	82.19	69.79	50.59	50.53	42.15	38.08	72.27	56.12	49.01
F-ConvNet [27]	L+I	61.61	87.36	76.39	66.59	52.16	43.38	38.80	81.98	65.07	56.54
PointPainting [9]	L+I	58.82	82.11	71.70	67.08	50.32	40.97	37.87	77.63	63.78	55.89
SECOND [13]	L	-	84.65	75.96	68.71	-	-	-	-	-	-
PointPillars [10]	L	58.29	82.58	74.31	68.99	51.45	41.92	38.89	77.10	58.65	51.92
PointRCNN [16]	L	57.94	86.96	75.64	70.70	47.98	39.37	36.01	74.96	58.82	52.53
Part-A2 [18]	L	61.78	87.81	78.49	73.51	53.10	43.35	40.06	79.17	63.52	56.93
STD [11]	L	61.25	87.95	79.71	75.09	53.29	42.47	38.35	78.69	61.59	55.30
PV-RCNN [17]	L	62.81	90.25	81.43	76.82	52.17	43.29	40.29	78.60	63.71	57.65
CIA-SSD [14]	L	-	89.59	80.28	72.87	-	-	-	-	-	-
SE-SSD [15]	L	-	91.49	82.54	77.15	-	-	-	-	-	-
PMPF-PV-RCNN	L+I	63.62	90.23	82.13	77.25	52.20	44.50	40.36	79.09	64.23	56.95

* “-”: These data were not provided in the original literature. The best result is bolded in each column.

would decidedly improve with the PMPF method. The strength, generality, robustness, and flexibility of the PMPF method suggests that it is the leading method for image–LiDAR fusion.

5.1.3. Performance Disadvantage Analysis

In Section 5.1.1 and Section 5.1.2, the PMPF method was found to not perform well in some categories, both when comparing LiDAR-only detectors or fusion models. We summarize the performance disadvantages embodied by PMPF as follows.

• In comparison with the LiDAR-only detector, performance degradation occurred mainly in the category of car with well-defined geometric features. Since PMPF makes the detector sensitive to texture information, it may reduce the serval detector’s sensitivity to targets with explicit geometric features.
• In comparison with the fusion-based model, performance disadvantage occurs mainly in the more difficult pedestrian and cyclist categories. The comparison with PointPainting [9] is discussed in detail in Section 5.2, and this section focuses on the performance disadvantage with F-ConvNet [27] in the cyclist category. F-ConvNet generates region proposals in the image, generates the frustum in space, extracts features, and enhances the model detection for small targets by performing multi-resolution frustum feature fusion. In contrast, PMPF improves the detection of targets with sparse geometric information by directly fusing multi-pixels matched with point clouds, and achieves a general accuracy improvement for small targets compared to the LiDAR-only detector; however, there is no doubt that PMPF is not as sensitive as 2D perception models for images.

To overcome the disadvantages above, we present the following solutions.

• Adaptive fusion data selection. PMPF is a sequence-based multimodal fusion model. In the pre-fusion stage, the size of the fused information is selected based on the distinctness of geometric features (point cloud density, etc.) using an adaptive mechanism (self-attention, etc.). Fewer or even no pixels are fused to dense point clouds, and more pixels are fused to sparse point clouds, which are subsequently sampled to the same scale before being fed into the detector to ensure the accurate detection of targets with various uneven densities in the scene.
• The adoption of a multi-stage fusion strategy to achieve the accurate detection of texture information by increasing the fusion of 2D–3D features in the network.

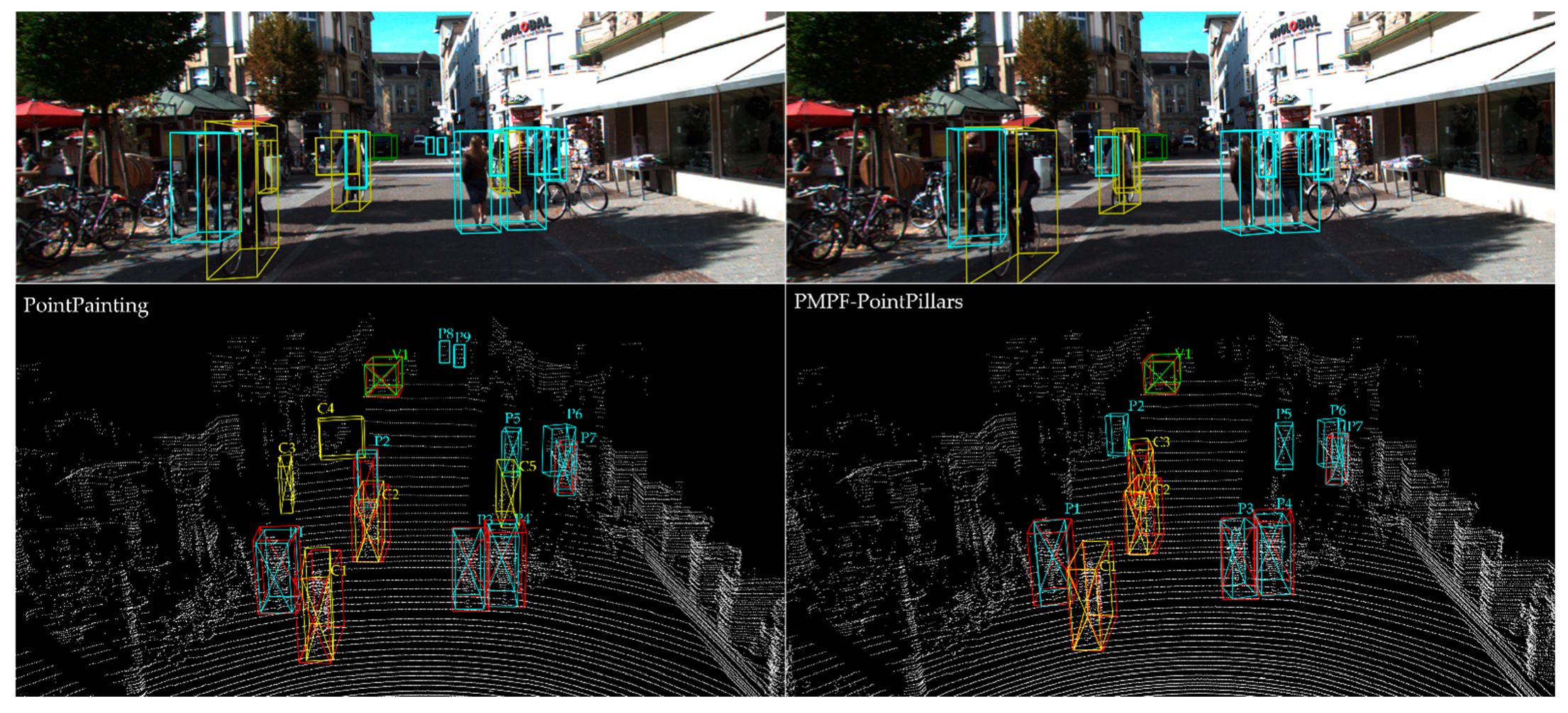
5.2. Qualitative Analysis

Here, we provide the qualitative comparison results for the well-performing LiDAR-only detectors PV-RCNN and PMPF-PV-RCNN. In Figure 5a, due to the common failure mode of the LiDAR-only detector, false positives are likely to occur for more distant targets with similar shape features, such as two cars misidentified at a distance (V1 and V3), and the PMPF-PV-RCNN method can help to address this problem by effectively avoiding false positives when pixel data are considered by the detector. In Figure 5b, the original PV-RCNN misses a cyclist, while in PMPF the cyclist(C1) is correctly identified and provides better detection and direction estimation for the vehicle.

In Figure 6, we provide a qualitative comparison from PointPainting [9] with the PMPF method for a scene that not only contains three classes of targets, but also has significant overlap and crossover in some of the targets. First, we focus on the two false positive cyclists (C3, C4) detected on the left panel as a result of PointPainting’s semantic segmentation of target false positives in the pre-fusion stage, where the two bicycles on the left side of the frame are judged to be cyclists, ultimately leading to a misjudgment by the LiDAR detector. In PMPF, the misjudgment of these two false-positive cyclists did not occur because no object classification or segmentation results were introduced to avoid the effect of false-positive information on the LiDAR detector. More importantly, we focus on the two cyclists travelling backwards and forwards in the center of the frame. As the cyclist at the rear of the image is mostly obscured and only pixels of part of the person are visible, the semantic segmentation network incorrectly judges it as a pedestrian (P2), leading PointPainting to judge the rear cyclist as a pedestrian. Similarly, the target between the two pedestrians (P3 and P4) in the middle right of the frame is visually overlapped by the bicycle in the foreground and the pedestrian in the rear; therefore, the semantic segmentation network, as before, judges it as a cyclist, while the bicycle is classified as a cyclist by the LiDAR detector (C5). Both of these false detections in PointPainting are due to typical defects in the image detector, which in turn make the LiDAR detector lose its advantage of being sensitive to geometric information. In the PMPF method, on the other hand, the LiDAR detector avoids the misidentification of targets that are easily misidentified in image detection, as there are no image classification results or semantic segmentation results, while the PMPF, which only incorporates multiple-pixels information, is able to correctly detect individual targets in complex scenes.

In addition, small targets in the distance can be focused on. Guided by the semantic segmentation results (although beyond the range of ground truth annotations), PointPainting identifies these two pedestrians (P8 and P9) as faraway, which are not detected by the LiDAR detector using PMPF, indicating that the method is currently unable to achieve the same sensitivity to pixels as image networks.

5.3. Time Latency

In Section 5.1.1, we derived the advantages of PMPF in terms of real-time performance by performing a comparison with PointPainting [9] and the time latency compared with the original detectors. In this section, we provide the details of the time latency introduced by the proposed method, as illustrated in

Table 4. Detailed time latency introduced by each component of the PMPF at different region sizes. Using PointPillars [10] as LiDAR detector.

Region Size	Projection (ms)	Region Selection (ms)	Region Match (ms)	Encoding (ms)	Total Time Latency (ms)
			Frame (Region)	(PointPillars)
K = 1	0.092	0.007	0.000 (0.000)	0.051	0.150
K = 3	0.092	0.044	20.723 (0.617)	0.662	21.521
K = 5	0.092	0.097	60.031 (1.622)	1.352	61.572

.

In the projection step, the PMPF converts the point cloud into the image coordinate system of the vehicle by performing projection to obtain the pixel coordinates corresponding to the point cloud. Projection introduces a time latency of 0.092 ms.

In the region selection step, the PMPF method obtains the texture context information corresponding to the point cloud by selecting a square region of size K. The region selection introduces a time latency of 0.044 ms (K = 3).

In the region match step, the PMPF method clusters pixels that are similar to the centroids by performing K-means to achieve the rejection of mismatched pixels. Region matching is the most time-consuming step in the PMPF method. The time complexity of K-means is O(n). PMPF requires 0.617 ms to execute K-means for a single region (K = 3). However, the time complexity of performing K-means in frame (all regions) is O(n²). The increase in the region size will rapidly increase the computational cost. In the present study, we distribute the region-matching computation to all computational cores, which leads to a time delay of 20.723 ms (K = 3).

Furthermore, since PMPF increases the dimensionality of the input data, it causes latency in the encoding phase compared to the original LiDAR detector. In PMPF-PointPainting, the input data constitute 18 dimensions as opposed to 7 dimensions of the original data, which causes a time latency of 0.662 ms (K = 3).

Overall, PMPF (K = 3) itself introduces a latency of 20.859 ms and total 21.521 ms, while encoding time latency. As shown in Table 4, for the one-stage method [10,13,14,15], PMPF can still maintain real-time performance (>20 Hz), and for the two-stage method [16,17,18], the detectors’ FPS (frames per second) rate only drops to about 2 Hz with the application of PMPF. Therefore, PMPF is low latency and generally does not affect the operational efficiency of LiDAR-only detectors.

5.4. Ablation Studies

To reveal the effect of the various components of the PMPF method on the overall model, we conducted an ablation study with the KITTI validation set. As PMPF fuses dense images with sparse point clouds, we investigated (1) the effect of the image quality (Section 5.4.1); (2) the effect of the PMPF components on the detector (Section 5.4.2); and (3) the effect of the clustering conditions and execution configuration of the K-means algorithm on the detector (Section 5.4.3). It is important to note that the PMPF method significantly improves the utilization of the fused data, and here we present the average utilization rate (AUR). The AUR measures the utilization of image texture information in the sample (reused pixels are not counted again), which is calculated as follows:

$$\mathrm{AUR}=\left({\displaystyle \sum }_{i=1}^S{\left(\frac{N\times K^2-O-R}{W\times H}\right)}_i\right)/S,$$

(11)

where S is the number of samples in the data set, N is the number of point clouds in the image range after projection, K is the region size, O is the number of out-of-bounds pixels in the matching region, R is the count of pixels being reused (for example, when a pixel is used twice, R accumulates 1), W is the image’s width, and H is image’s height.

When K > 1, there are already pixels that have been fused by multiple point clouds and appear to be duplicated, so we introduced the average reputation rate (ARR) to indicate the proportion of pixels in the dataset that have been reused. The ARR is calculated as follows:

$$\mathrm{ARR}=\left({\displaystyle \sum }_{i=1}^S{\left(\frac{R}{N\times K^2-O}\right)}_i\right)/S.$$

(12)

5.4.1. Effect of the Image Quality

This section focuses on the effect of raw image quality on PMPF. Sequence-based multimodal 3D detectors suffer from poor image and 2D detector quality. Since PMPF directly fuses the contextual texture information in the image, it avoids the problems introduced by 2D detectors, but the quality of the image used for direct fusion inevitably affects the performance of PMPF. We mainly consider the effect of low illumination and ambiguity in a dynamic environment on PMPF compared to a clear and well-illuminated image.

For comparison with PMPF, we used YOLOv5 [52] as 2D detector on both raw and low-quality images. YOLOv5 [52] was pre-trained on the coco [53] dataset and finetuned on the KITTI dataset. As shown in Figure 7, even if the input image is ambiguous or dark, PMPF still performs accurate detection of key targets in the scene, while the 2D detector fails almost completely.

In addition, we investigated whether low-quality images caused the accuracy of PMPF to fall below that of the LiDAR-only detector. As shown in Figure 8, the PMPF still maintains its detection of key targets in blurred and dark images. The false positives (P2, V4, and V5) appear after the introduction of the DARK image in PMPF, where P2 is a confusing false positive in the point cloud and is also misidentified in the baseline. This demonstrates one of the advantages that PMPF brings by fusing the raw image data. However, the appearance of more false positives than the baseline proves that the sensitivity of the 3D detector to geometric information decreases after considering pixel texture information.

As shown in

Table 5. Quantitative comparison between PMPF under different image quality scenarios and PV-RCNN on KITTI 3D object detection validation.

Method	Image Quality	Mod. mAP	Car			Pedestrian			Cyclist
			Easy	Mod.	Hard	Easy	Mod.	Hard	Easy	Mod.	Hard
PV-RCNN	-	70.83	91.55	83.12	78.94	63.06	59.45	55.02	89.48	72.46	68.86
PMPF-PV-RCNN	Raw	73.52	89.16	83.66	78.82	66.59	61.82	56.94	90.79	75.08	70.88
	Ambiguous	73.13	89.03	83.05	78.51	66.07	61.47	55.98	89.65	74.86	69.72
	Dark	70.71	88.62	81.04	75.95	63.02	59.13	54.48	89.17	71.98	68.41

The best result is bolded in each column.

, when fusing blurred images, the accuracy degradation is mainly concentrated on the hard difficulty targets in the pedestrian and cyclist categories, implying that the ambiguous image texture was not sufficient to help the LiDAR detector overcome the missed detection of small or obscured targets. When fusing dark images, the global accuracy decreases compared to the baseline (0.12%), which we attribute to the presence of more false positives. This also indicates that the LiDAR detector is less sensitive to ensemble information in the PMPF.

5.4.2. Effect of the PMPF Components

We selected the robust PMPF-SECOND model and the SOTA PMPF-PV-RCNN model for the ablation study of the PMPF components. We use the LiDAR-only detector results as a baseline. In PMPF, the image pixel information is fused with the point cloud. We investigated the effect of different kernel sizes on the detection accuracy of the LiDAR detector. At the same time, multiple point clouds correspond to areas where the images overlap. This phenomenon does not have a large impact on the AP when the K is appropriate, as long as the overlapping pixels include the correct information corresponding to the LiDAR point. When the K value is large, there will be greater overlap in the region images corresponding to multiple LiDAR points (the overlap rate exceeds the utilization rate); this leads to the question of whether a larger region selection still makes sense. In this section, we investigate the ablation of these questions.

Table 6. An ablation study result for effect of PMPF components on SECOND on KITTI 3D object detection validation set. “√” and “×” denote the results with or without the region match method.

Module (Input)	Region Size	Region Match	AUR%/ARR%	Car			Pedestrian			Cyclist
				Easy	Mod.	Hard	Easy	Mod.	Hard	Easy	Mod.	Hard
SECOND [13] (Point clouds)	-	-	-	86.85	76.64	74.41	67.79	59.84	52.38	84.92	64.89	58.59
PMPF-SECOND (Point clouds +image)	1	×	8.22/1.34	86.43	76.72	73.98	68.12	59.75	51.78	85.03	64.76	59.02
	3	×	55.27/33.86	87.93	77.96	76.59	68.95	60.55	52.26	85.34	64.98	60.35
	3	√	55.19/29.52	88.18	78.21	76.88	69.36	60.35	54.23	85.52	66.76	63.38
	5	×	85.36/144.03	85.29	74.35	72.01	67.51	57.26	49.18	83.52	63.35	56.25
	5	√	84.55/80.84	87.73	76.12	74.46	69.02	60.03	53.55	85.15	65.56	57.65

The best result is bolded in each column.

and

Table 7. An ablation study result for the effect of PMPF components on PV-RCNN on KITTI 3D object detection validation set. “√” and “×” denote the results with or without the region match method.

Module (Input)	Region Size	Region Match	AUR%/ARR%	Car			Pedestrian			Cyclist
				Easy	Mod.	Hard	Easy	Mod.	Hard	Easy	Mod.	Hard
PV-RCNN [17] (Point clouds)	-	-	-	91.55	83.12	78.94	63.06	59.45	55.02	89.48	72.46	68.86
PMPF-PV-RCNN (Point clouds +image)	1	×	8.22/1.34	87.21	81.20	75.23	64.15	59.02	55.37	87.23	71.97	68.50
	3	√	55.27/33.86	88.96	81.18	76.59	65.25	61.45	56.22	88.42	74.23	69.18
	3	√	55.19/29.52	89.16	83.66	78.82	66.59	61.82	56.94	90.79	75.08	70.88
	5	×	85.36/144.03	84.52	79.36	76.44	63.35	61.06	55.13	88.36	74.67	69.25
	5	√	84.55/80.84	87.21	79.44	76.91	66.74	61.66	55.92	89.94	74.79	69.45

The best result is bolded in each column.

shows the results of the ablation study for SECOND and PV-RCNN after using the PMPF method.

When K = 1, a point cloud is fused with one pixel, we observe a 0.43% AP improvement in hard difficulty in the cyclist category in the SECOND method, and only a weak improvement or even a decrease in the other comparisons. From a qualitative view, as shown in Figure 2, such a fusion method also makes the pixel information sparse, possibly leading to a lack of distinctive high-dimensional features of the pixels, in which case the AUR is only 8.22%. This phenomenon is even more pronounced in the PV-RCNN, especially in the car category with easy difficulty, where the maximum drop in AP reaches 4.34%.

When K = 3, the AUR increases considerably, reaching 55.27%, but we find that the utilization of pixels is lower than the number of point clouds projected in the image plane multiplied by K², which is mainly due to the following two reasons:

• Some of the projected point clouds are at the edges of the image plane, making it impossible to extend them in certain directions to obtain pixel information;
• Most of the projected point clouds are more closely aligned in the horizontal direction, resulting in multiple points repeatedly acquiring the same pixels, at which point the ARR is 33.86%.

Without region match, PMPF-SECOND (K = 3) has a stable improvement over the baseline, compared to K = 1, which leads to an improvement in all comparison terms. However, for PMPF-PV-RCNN, in contrast to baseline, both K = 1 and K = 3 lead to a performance degradation in the car category, as the target in the car category has more significant geometrical features and the added color information may cause distress to the detector, which can occur in detectors involving point-wise encoders. Compared to K = 1, there is a significant improvement in eight out of nine comparison terms, especially in challenging scenarios, with larger improvements observed in both the pedestrian and cyclist categories.

With region match, the AUR and ARR both decrease, but there is a steady improvement in PMPF-SECOND and PMPF-PV-RCNN, especially in the more geometrically sparse categories of pedestrian and cyclist, where the correct complementary texture information leads to a significant improvement over the baseline. Note that when K > 3, there are still overlapping regions after region matching, when we consider the regions to be accurate and connected to the corresponding points.

When K = 5, the AU is already over 100%, theoretically, but it is 85.36% at this point. In addition to the two reasons mentioned at K = 3, another important factor affecting the AU at this point is that a part of the projection plane does not have any projected point clouds distributed in it, which leads to a decrease in utilization. It is worth noting that at K = 5, the repetition rate has risen to 144.03%, that is, the same pixel has been used by more than two points.

Without region match, both the PMPF-SECOND and PMPF-PV-RCNN methods show degraded performance when compared to K = 3. Overall, the drop in AP is probably due to the fact that at the edges of the target, the point cloud contains more texture information from the background or other targets, resulting in more severe mismatching and thus a greater error in the final bounding box regression; therefore, it is more pronounced in the car category (which requires a 70% bounding box overlap).

With region match, a large number of texture differences are eliminated and the ARR drops rapidly to 80.84%. Reflecting this in the detectors, there is a significant performance improvement over the case without region matching, as a large amount of feature blurring is avoided.

Based on the results and analyses of this section, we suggest a general region-size selection principle: The utilization of images in the sample should be increased as much as possible according to the density of the original point cloud data to enrich the contextual texture information contained in the point cloud. There is no need to worry about the appearance of multiplexed pixels, which correctly correspond according to region matching. On this basis, caution should be taken when choosing larger region sizes, as excessive texture information may reduce the detector’s sensitivity with geometric features, and a large region will dramatically increase the computational cost of the fusion phase, thereby affecting the real-time performance. Finally, make sure the PMPF gets the best performance.

5.4.3. Effect of the Clustering Conditions and Execution Configuration of K-Means Clustering

The effectiveness of region matching was illustrated in Section 5.4.2; further, in this section, we conduct an ablation study on the specific implementation of the region-matching method, where we use the PMPF-PV-RCNN model with K = 3 and no region matching as a baseline. Experiments were conducted based on the effect of clustering conditions, the number of clusters and number of iterations of K-means on the detector. Since K-means performed on a single region is not complicated (0.6 ms on a 3 × 3 region), we distribute the point-level computation to all cores and use multi-threading to eliminate the time cost of K-means.

As shown in

Table 8. Ablation results of the clustering conditions and execution configuration of the K-means on the KITTI validation set. Abbreviations: $D_{texture}$ (D_t.), $D_{depth}$ (D_d.), $D_{reflectivity}$ (D_r.), clusters (Clu.), iteration (Iter.), run time (RT).

Dt.	Dd.	Dr.	Clu.	Iter.	RT (ms)	AUR%/ARR%	mAP Mod.	Car			Pedestrian			Cyclist
								Easy	Mod.	Hard	Easy	Mod.	Hard	Easy	Mod.	Hard
						55.27/33.86	72.29	88.96	81.18	76.59	65.25	61.45	56.22	88.42	74.23	69.18
√			2	20	20.527	55.25/30.04	72.95	89.03	82.54	77.93	66.45	61.43	56.21	88.12	74.87	69.35
√		√	2	20	20.561	55.21/29.76	72.93	88.98	82.67	78.12	66.28	61.55	56.71	88.25	74.57	69.98
√	√		2	20	20.533	55.23/29.88	73.32	88.85	83.52	78.66	66.31	61.62	56.67	90.44	74.83	70.36
√	√	√	2	20	20.723	55.19/29.52	73.52	89.16	83.66	78.82	66.59	61.82	56.94	90.79	75.08	70.88
√	√	√	4	20	22.423	30.23/11.54	71.87	88.12	82.65	77.16	65.21	60.05	55.63	86.15	72.92	69.25
√	√	√	2	40	37.589	55.08/28.47	73.44	89.54	83.35	79.12	66.76	61.76	56.73	90.63	75.21	71.10

The best result is bolded in each column.

, we are unable to determine whether much of the mismatched data is eliminated with the region-matching method without the segmentation ground truth; however, the results from 3D detection show that performing region matching does help to improve the detector performance. When more complex clustering conditions are considered, K-means can reduce the ARR, which can indicate that the clustering conditions that consider $D_{texture}$, $D_{depth}$ and $D_{reflectivity}$ can eliminate more mismatched pixels, thereby improving the performance of the detector. When the number of clusters increases, a significant decrease in both AUR and ARR can be found, which is due to the fact that over-fine classification can lead to fewer pixels of the same kind being used as the key pixels, which eventually leads to a decrease in the performance of the detector. The increase in the number of iterations improves the detector’s recognition of complex objects at the expense of real-time performance, and its mAP in the general category does not exceed that of the K-means model with 20 iterations.

To further verify the extensibility of the PMPF method, we use the PMPF method to fuse the semantic map with the point cloud. We use deeplabv3+ to generate semantic labels. As shown in

Table 9. Comparison of PMPF-PV-RCNN fusion semantic map with point cloud on the KITTI validation set. Abbreviations: run time (RT).

Module (Input)	Region Match	RT(s)	AUR%/ARR%	mAP Mod.	Car			Pedestrian			Cyclist
					Easy	Mod.	Hard	Easy	Mod.	Hard	Easy	Mod.	Hard
PMPF-PV-RCNN (Point clouds + semantic map)	×	0.22	54.25/26.68	73.81	88.95	84.05	79.36	65.89	62.04	58.03	89.73	75.36	72.02
	√	0.24	54.20/25.31	74.11	89.05	84.11	79.97	66.79	62.73	58.21	90.34	75.50	72.12

The best result is bolded in each column.

, region matching guided by semantic segmentation results can effectively reduce ARR; however, considering the exponentially increasing time cost, the method only obtains a 0.29% mAP improvement. The further decrease in ARR when using both semantic segmentation results and K-means can indicate that the error of semantic segmentation is also carried into region matching, and K-means eliminates some of the mismatches in the regions by eliminating pixels that are different from the center of clustering at the demarcation within the target range.

It should be emphasized that using semantic segmentation networks in the fusion stage is not the aim of this paper, and this part is only used as a supplement to the performance of PMPF expansion; therefore, no further qualitative results are shown or analyzed.

6. Conclusions

In this work, we present PMPF (point cloud–multiple-pixel fusion)-based 3D object detection for autonomous driving. PMPF solves the coupling problem introduced while fusing image context information in the sequence fusion model and achieves high accuracy in 3D object detection. PMPF is a plug-and-play module that can be applied to any LiDAR-only detector with autoencoder, while ensuring the operational efficiency of 3D detectors with the low latency of the PMPF model. Extensive experiments on the KITTI dataset have demonstrated the accuracy improvement of PMPF in various SOTA LiDAR-only detectors. The ablation studies demonstrate the robustness of the PMPF for different quality image inputs and illustrate the effect of the components of the PMPF on detection accuracy and run time. Although the proposed approach achieves a better detection accuracy, there are still some drawbacks in our study:

• PMPF accurately fuses all point clouds, which is computationally wasteful at background points;
• PMPF’s sensitivity to targets with significant geometric features is reduced compared to LiDAR-only detectors;
• PMPF’s detection accuracy for hard-difficulty targets is not accurate enough compared to some SOTA fusion-based methods;
• PMPF method is trained and tested on public datasets; therefore, factors such as rain, snow, dust, and illumination conduction that affect LiDAR and cameras can degrade the generalization performance of the PMPF method.

To overcome the above-mentioned drawbacks, our future research directions to improve PMPF are as follows:

• Segmenting the foreground and background and performing accurate data fusion only in the foreground without sacrificing real-time performance;
• Adaptive selection of fused image information, less or even no fusion of images in point clouds with significant geometric features, and more fusion of image information on sparse objects.
• Fusing more hierarchical multimodal data-fusion strategies, such as building a deep network of data fusion + feature fusion to enhance the performance of object detection.
• Fusing more information from sensors, such as radar, and IMU, to ensure the environment coding has greater accuracy with richer results to improve the performance of the detector;
• Enhancing the generalization performance by data augmentation or training in real data.