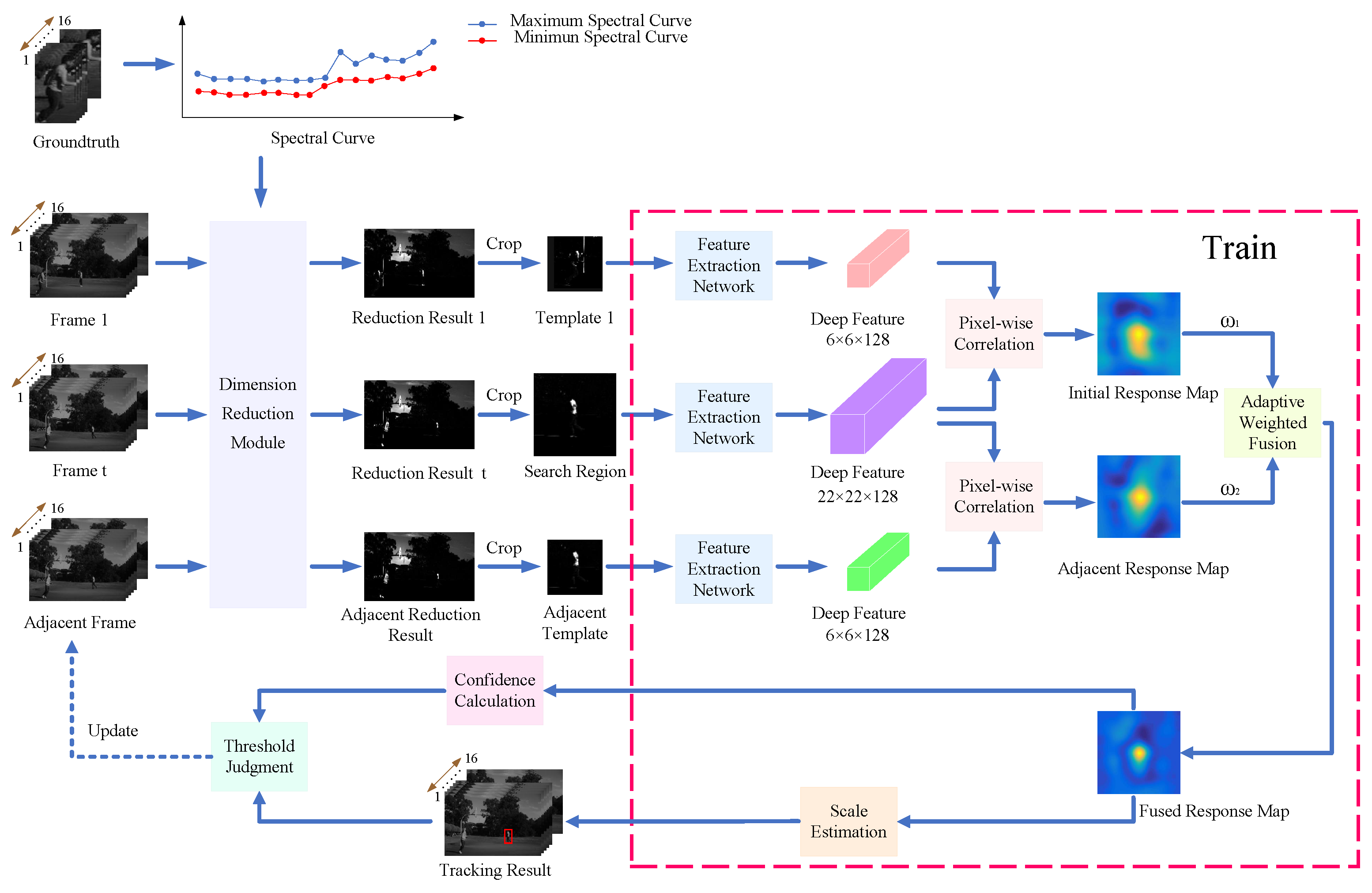
Figure 1.
The overall framework of the proposed algorithm.
Figure 1.
The overall framework of the proposed algorithm.
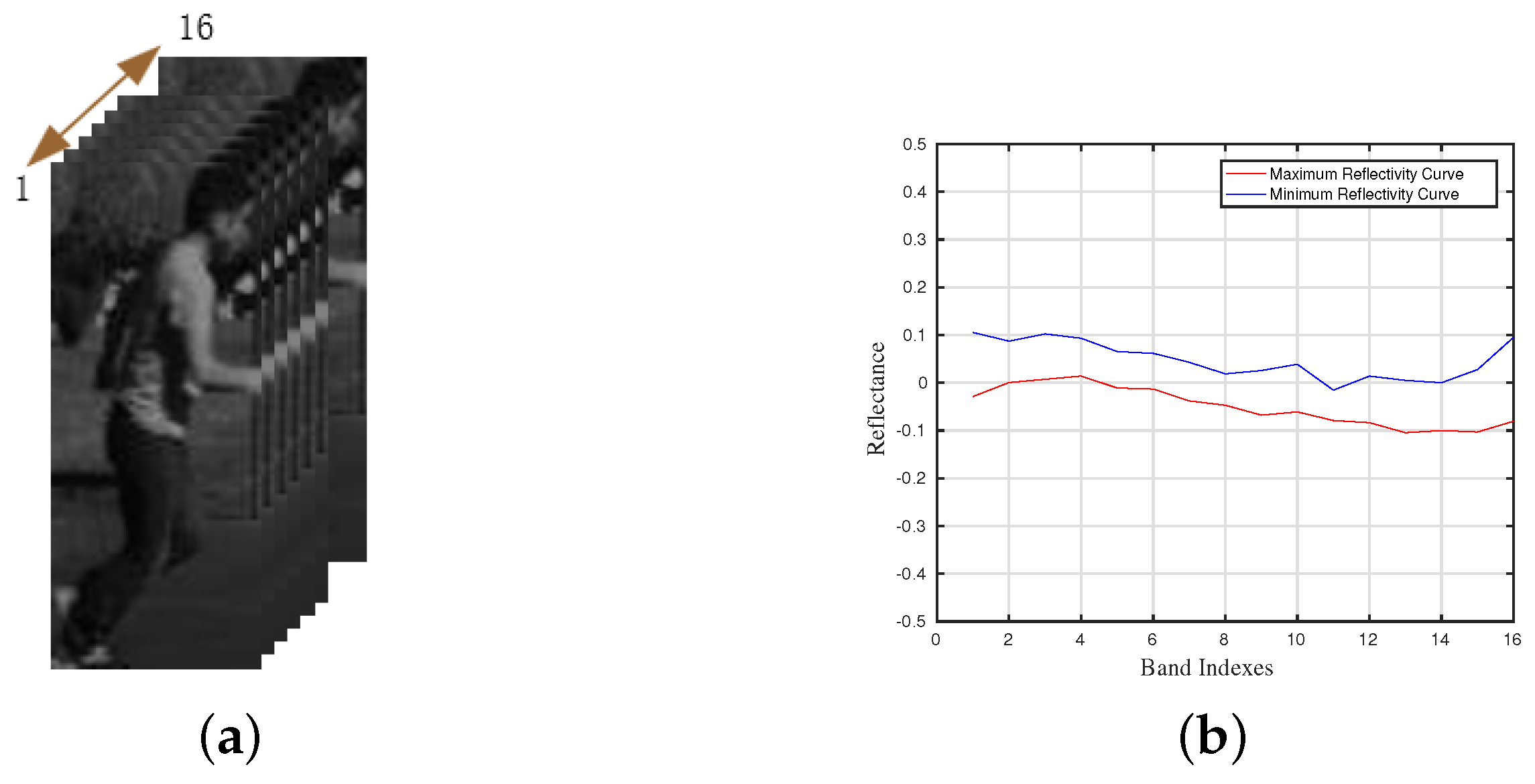
Figure 2.
The pretreatment of the proposed dimensionality reduction method. (a) The given ground truth of the first frame. (b) The extracted maximum spectral curve and minimum spectral curve from the local region in the ground truth.
Figure 2.
The pretreatment of the proposed dimensionality reduction method. (a) The given ground truth of the first frame. (b) The extracted maximum spectral curve and minimum spectral curve from the local region in the ground truth.
Figure 3.
The result of the proposed dimensionality reduction method. (a) The original hyperspectral image in the dataset. (b) The dimensionality reduction result of (a) using DRSD. (c) The dimensionality reduction result of (a) using PCA.
Figure 3.
The result of the proposed dimensionality reduction method. (a) The original hyperspectral image in the dataset. (b) The dimensionality reduction result of (a) using DRSD. (c) The dimensionality reduction result of (a) using PCA.
Figure 4.
The overall framework of SiamFC.
Figure 4.
The overall framework of SiamFC.
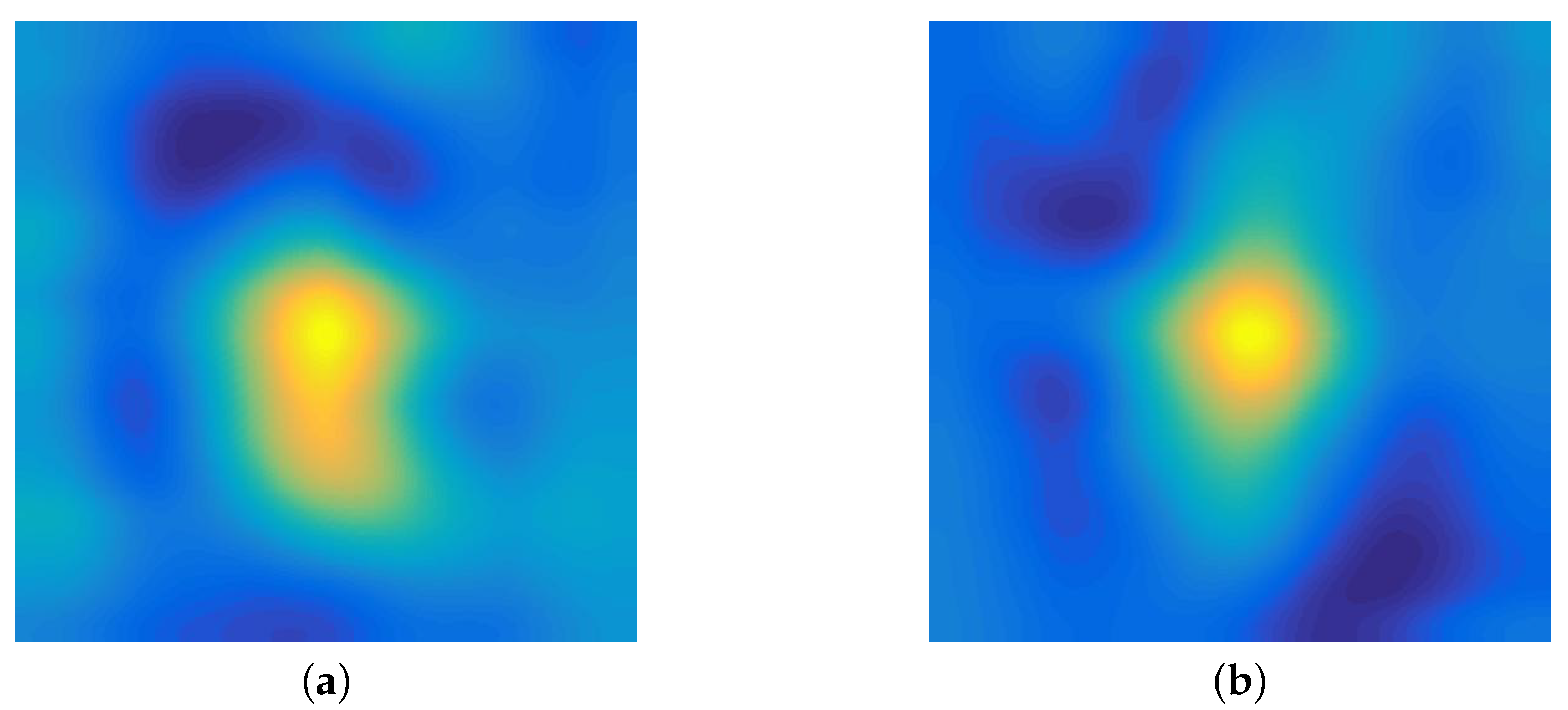
Figure 5.
A group of the initial response map and the adjacent response map in the experiments. (a) The initial response map. (b) The adjacent response map.
Figure 5.
A group of the initial response map and the adjacent response map in the experiments. (a) The initial response map. (b) The adjacent response map.
Figure 6.
The fused response map.
Figure 6.
The fused response map.
Figure 7.
Qualitative results on the coke sequence in comparative experiments.
Figure 7.
Qualitative results on the coke sequence in comparative experiments.
Figure 8.
Qualitative results on the fruit sequence in comparative experiments.
Figure 8.
Qualitative results on the fruit sequence in comparative experiments.
Figure 9.
Qualitative results on the playground sequence in comparative experiments.
Figure 9.
Qualitative results on the playground sequence in comparative experiments.
Figure 10.
Qualitative results on the rider sequence in comparative experiments.
Figure 10.
Qualitative results on the rider sequence in comparative experiments.
Figure 11.
Qualitative results on the toy sequence in comparative experiments.
Figure 11.
Qualitative results on the toy sequence in comparative experiments.
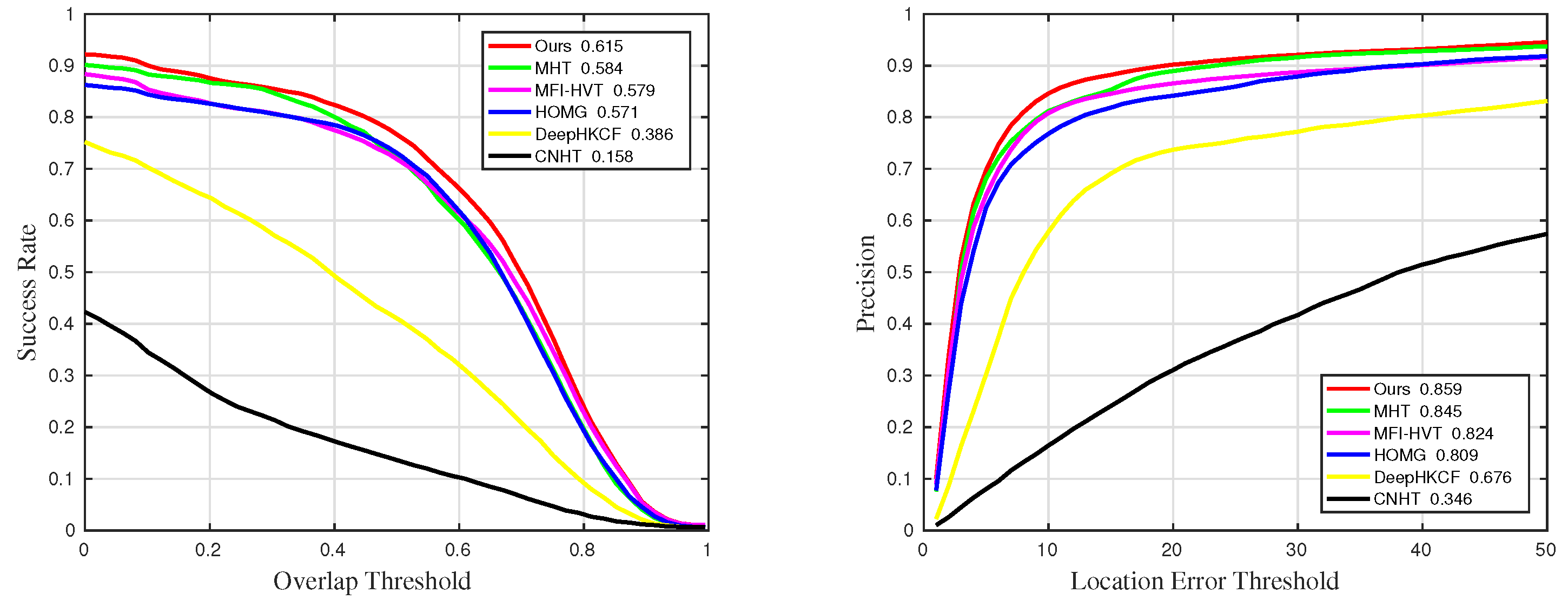
Figure 12.
Quantitative results for all sequences in comparative experiments.
Figure 12.
Quantitative results for all sequences in comparative experiments.
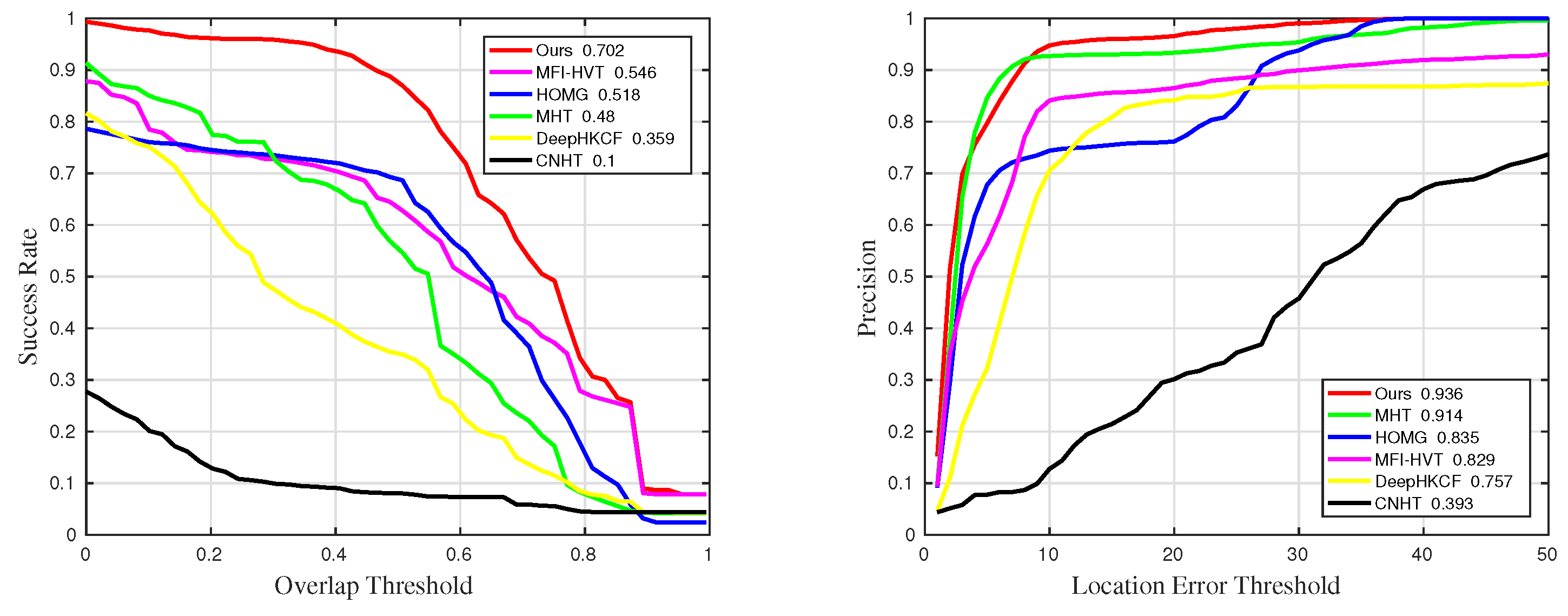
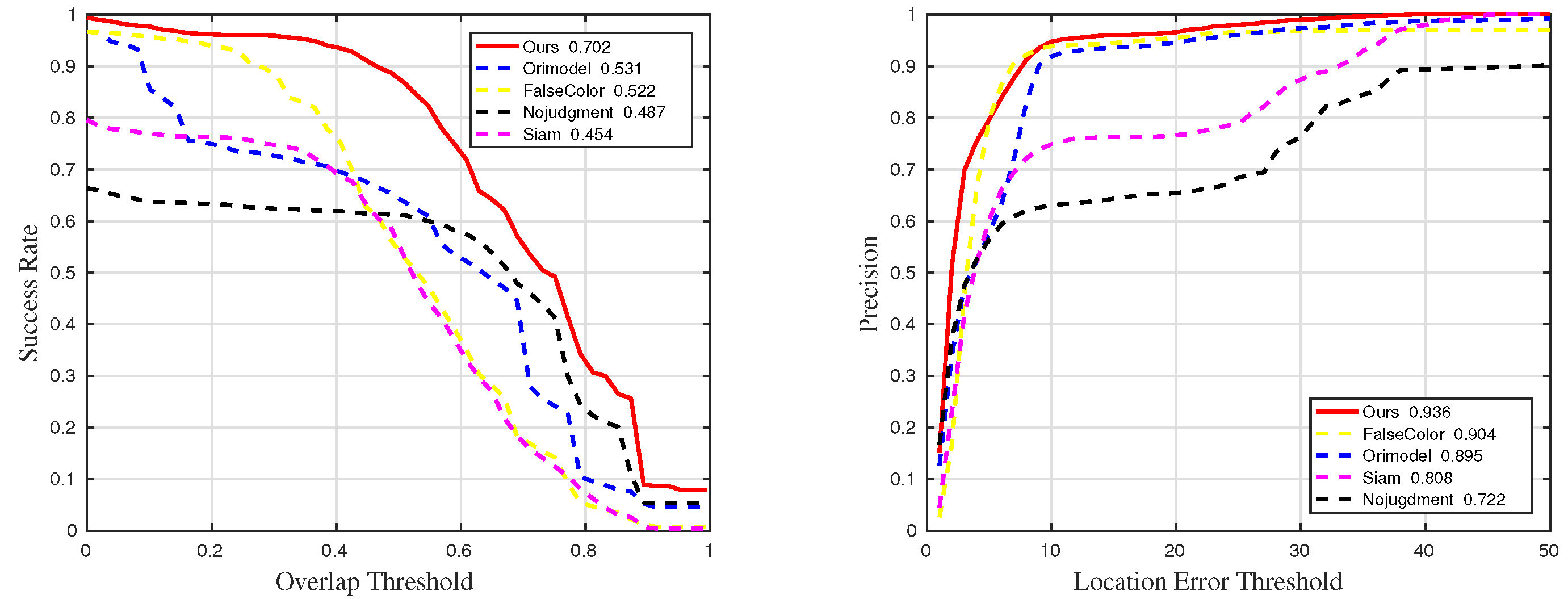
Figure 13.
Quantitative results for sequences with challenge BC in comparative experiments.
Figure 13.
Quantitative results for sequences with challenge BC in comparative experiments.
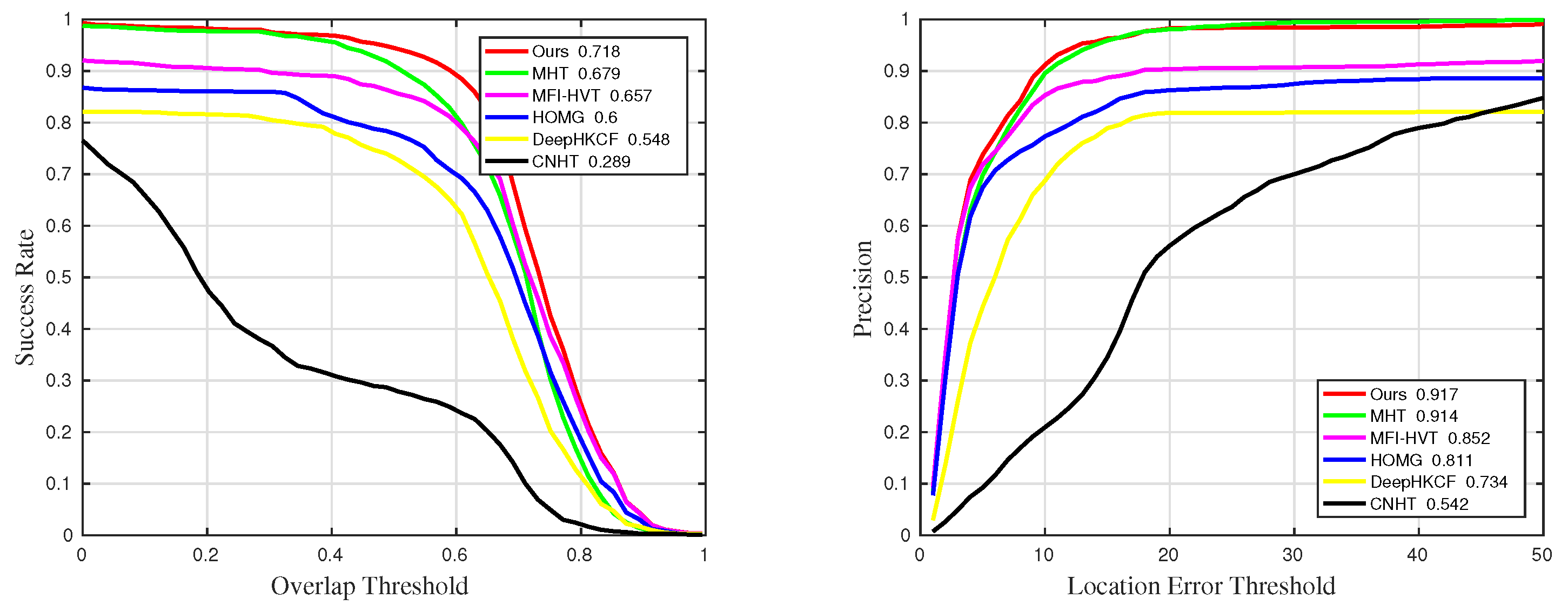
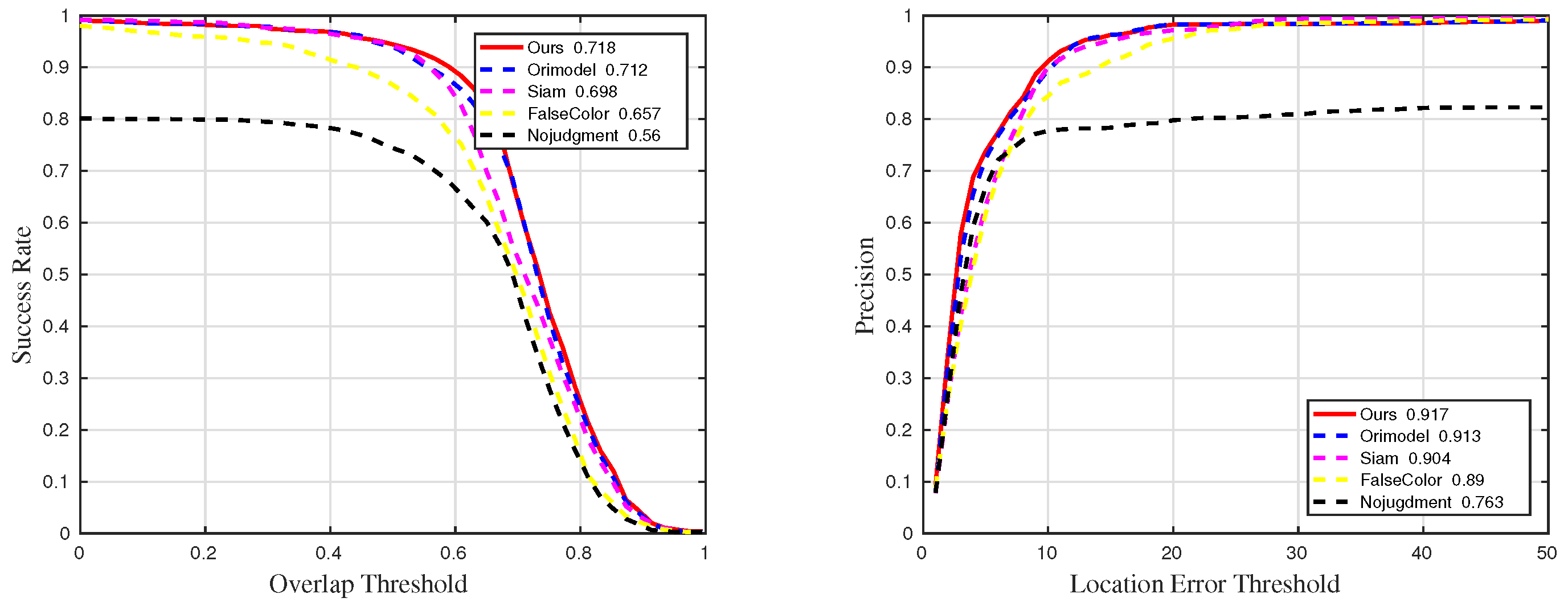
Figure 14.
Quantitative results for sequences with challenge IV in comparative experiments.
Figure 14.
Quantitative results for sequences with challenge IV in comparative experiments.
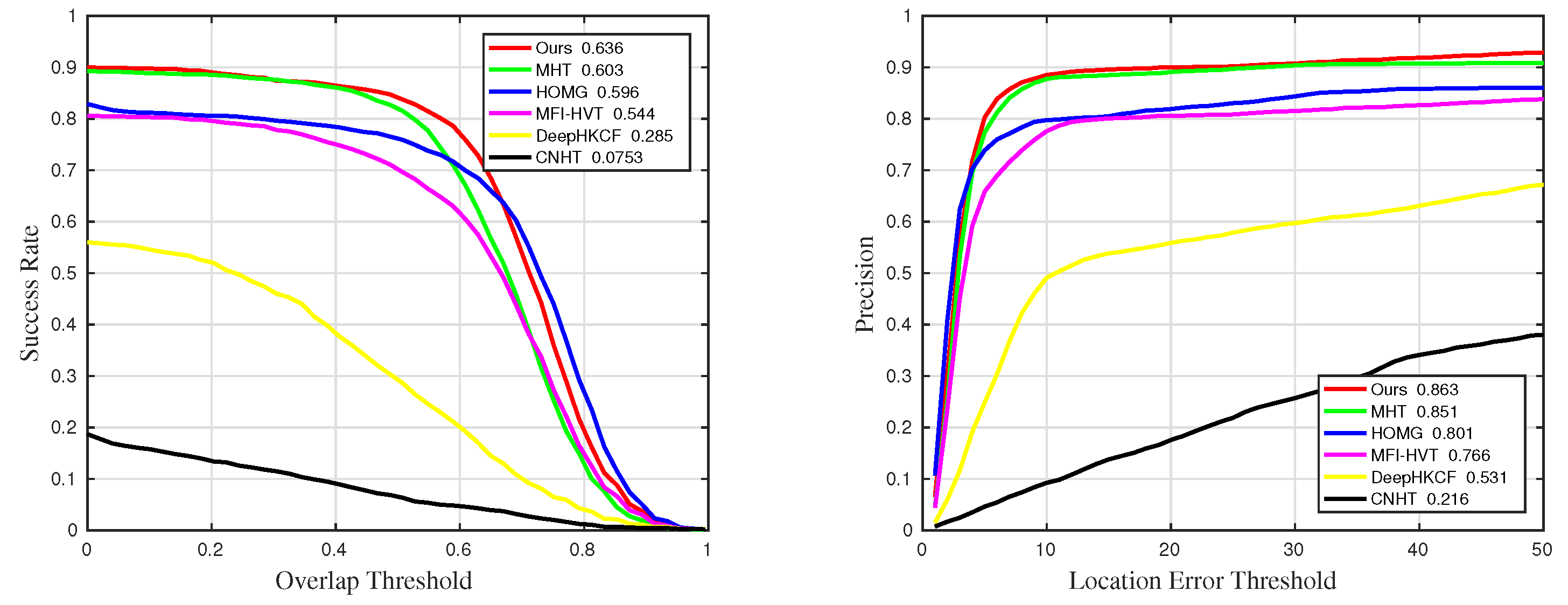
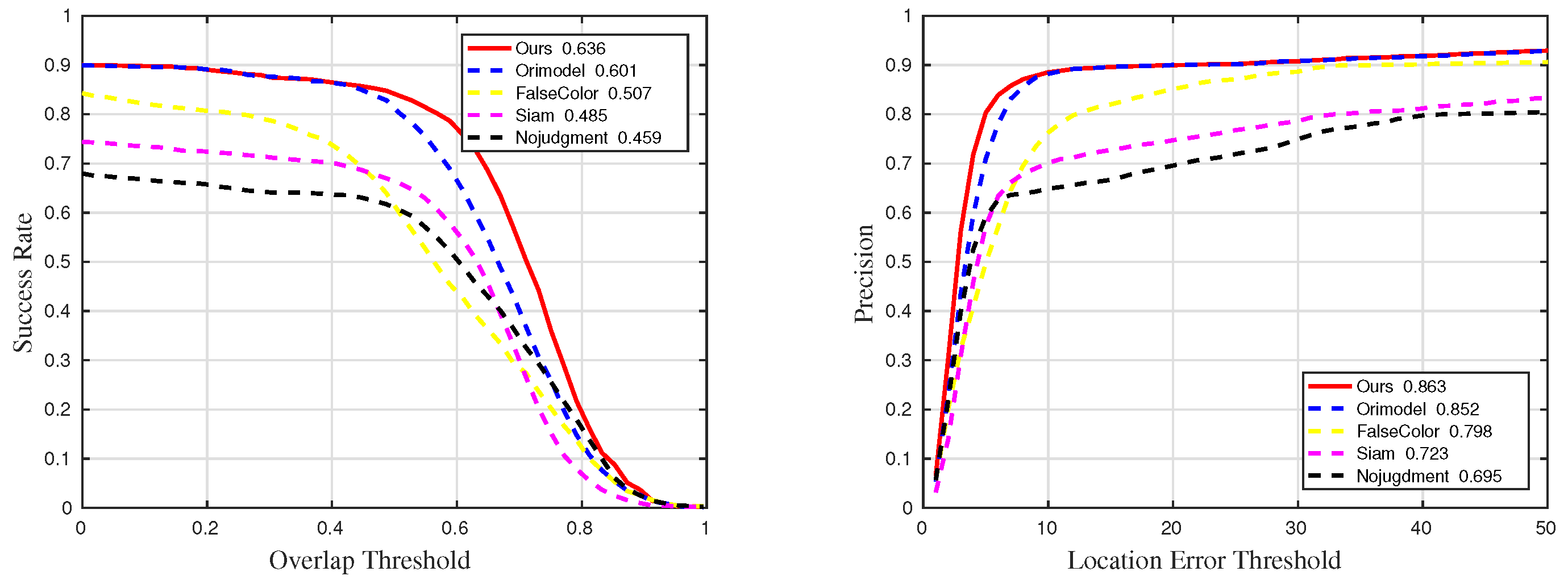
Figure 15.
Quantitative results for sequences with challenge OCC in comparative experiments.
Figure 15.
Quantitative results for sequences with challenge OCC in comparative experiments.
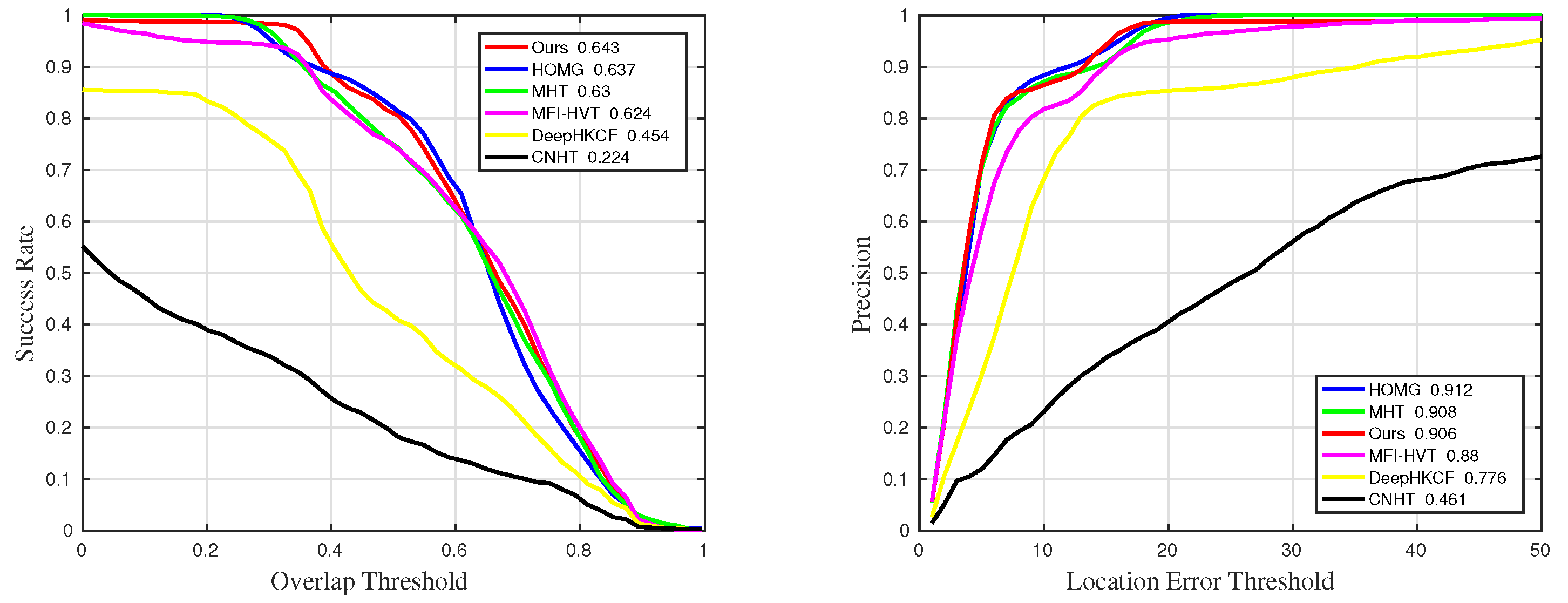
Figure 16.
Quantitative results for sequences with challenge RO in comparative experiments.
Figure 16.
Quantitative results for sequences with challenge RO in comparative experiments.
Figure 17.
Quantitative results for sequences with challenge SV in comparative experiments.
Figure 17.
Quantitative results for sequences with challenge SV in comparative experiments.
Figure 18.
Qualitative results on the coke sequence in ablation experiments.
Figure 18.
Qualitative results on the coke sequence in ablation experiments.
Figure 19.
Qualitative results on the fruit sequence in ablation experiments.
Figure 19.
Qualitative results on the fruit sequence in ablation experiments.
Figure 20.
Qualitative results on the playground sequence in ablation experiments.
Figure 20.
Qualitative results on the playground sequence in ablation experiments.
Figure 21.
Qualitative results on the rider sequence in ablation experiments.
Figure 21.
Qualitative results on the rider sequence in ablation experiments.
Figure 22.
Qualitative results on the toy sequence in ablation experiments.
Figure 22.
Qualitative results on the toy sequence in ablation experiments.
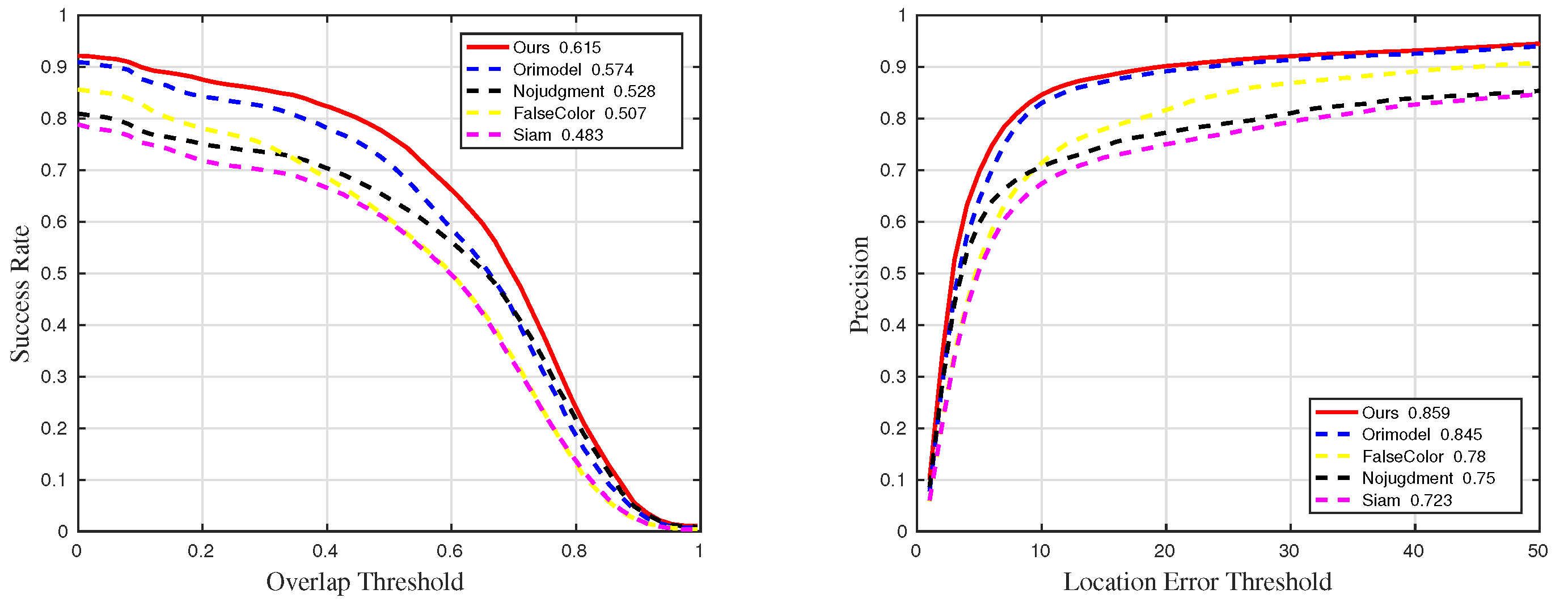
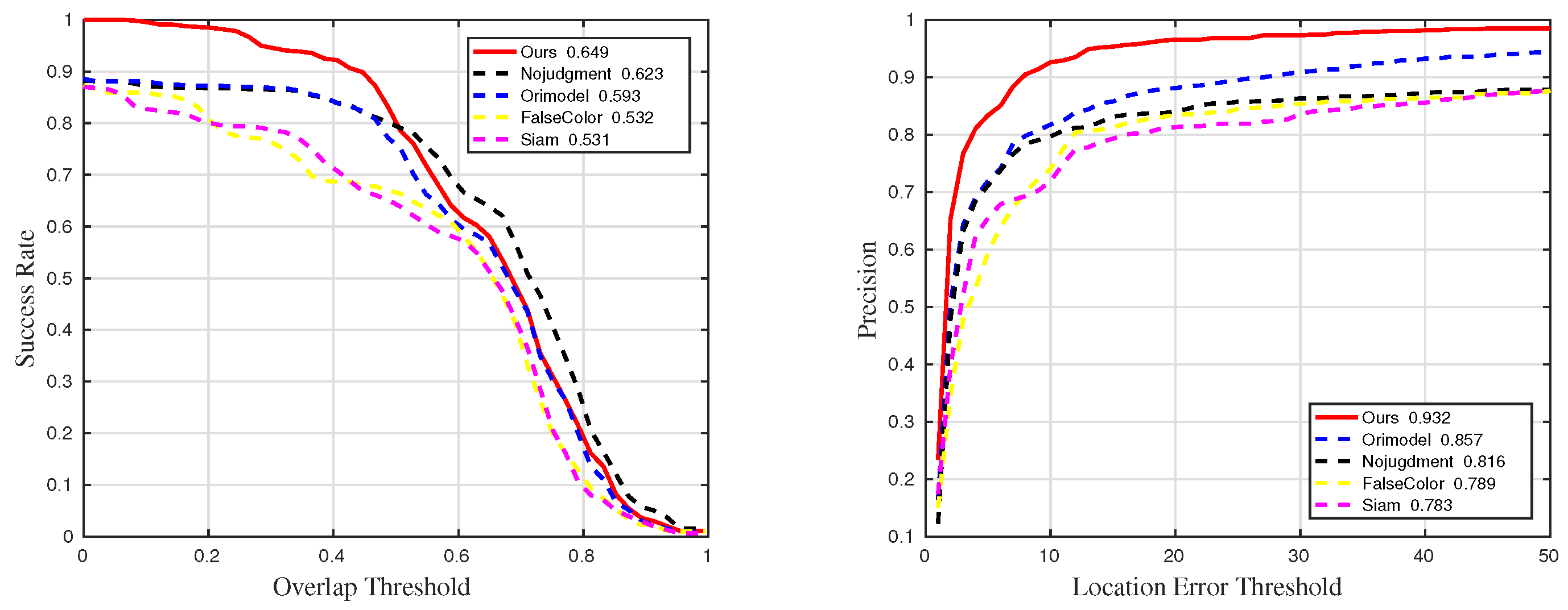
Figure 23.
Quantitative results for all sequences in ablation experiments.
Figure 23.
Quantitative results for all sequences in ablation experiments.
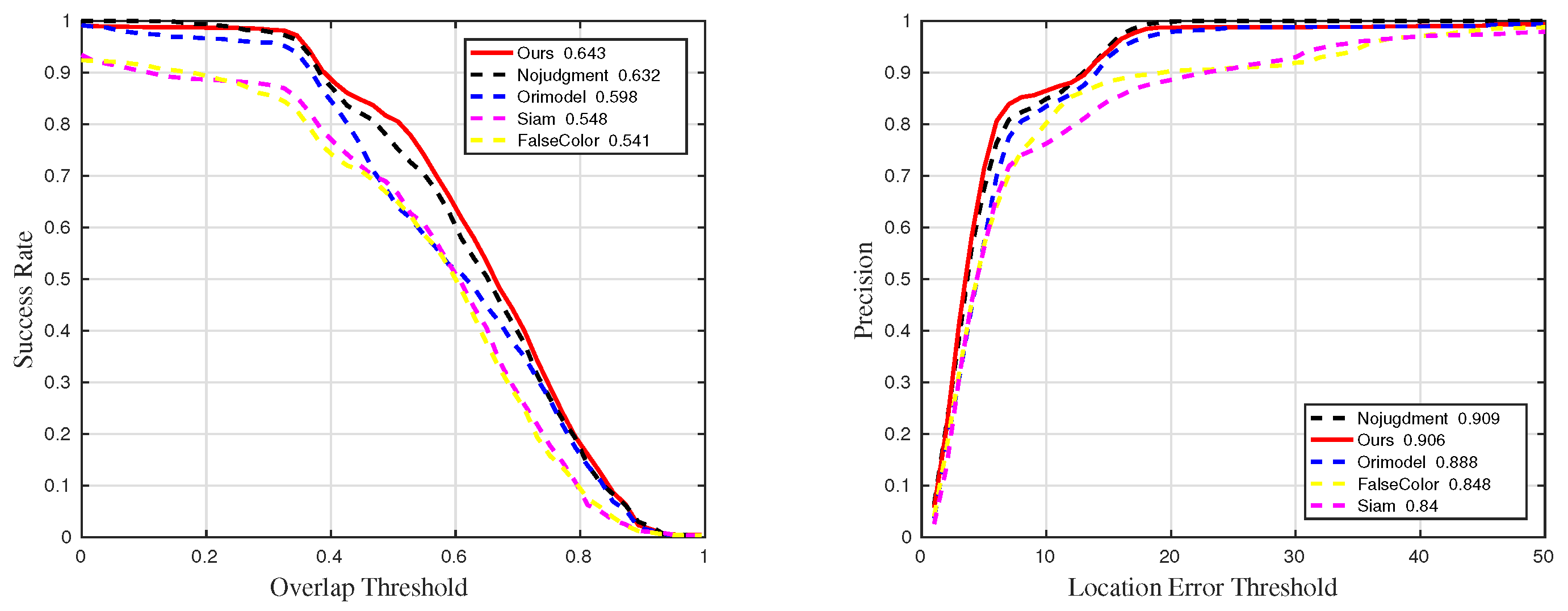
Figure 24.
Quantitative results for sequences with challenge BC in ablation experiments.
Figure 24.
Quantitative results for sequences with challenge BC in ablation experiments.
Figure 25.
Quantitative results for sequences with challenge IV in ablation experiments.
Figure 25.
Quantitative results for sequences with challenge IV in ablation experiments.
Figure 26.
Quantitative results for sequences with challenge OCC in ablation experiments.
Figure 26.
Quantitative results for sequences with challenge OCC in ablation experiments.
Figure 27.
Quantitative results for sequences with challenge RO in ablation experiments.
Figure 27.
Quantitative results for sequences with challenge RO in ablation experiments.
Figure 28.
Quantitative results for sequences with challenge SV in ablation experiments.
Figure 28.
Quantitative results for sequences with challenge SV in ablation experiments.
Figure 29.
Qualitative results of the airplane sequence in universality experiments.
Figure 29.
Qualitative results of the airplane sequence in universality experiments.
Figure 30.
Qualitative results on the boat sequence in universality experiments.
Figure 30.
Qualitative results on the boat sequence in universality experiments.
Figure 31.
Qualitative results on the camera sequence in universality experiments.
Figure 31.
Qualitative results on the camera sequence in universality experiments.
Figure 32.
Qualitative results on the doublecar sequence in universality experiments.
Figure 32.
Qualitative results on the doublecar sequence in universality experiments.
Figure 33.
Qualitative results on the girl sequence in universality experiments.
Figure 33.
Qualitative results on the girl sequence in universality experiments.
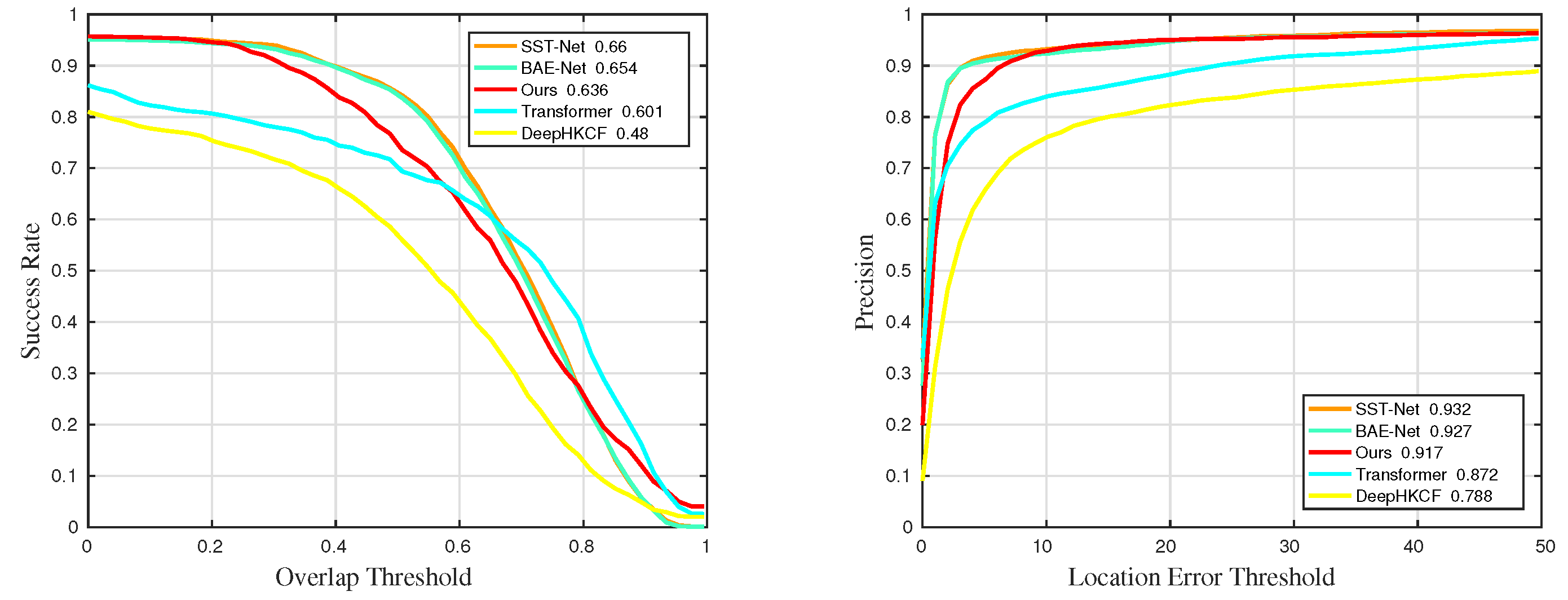
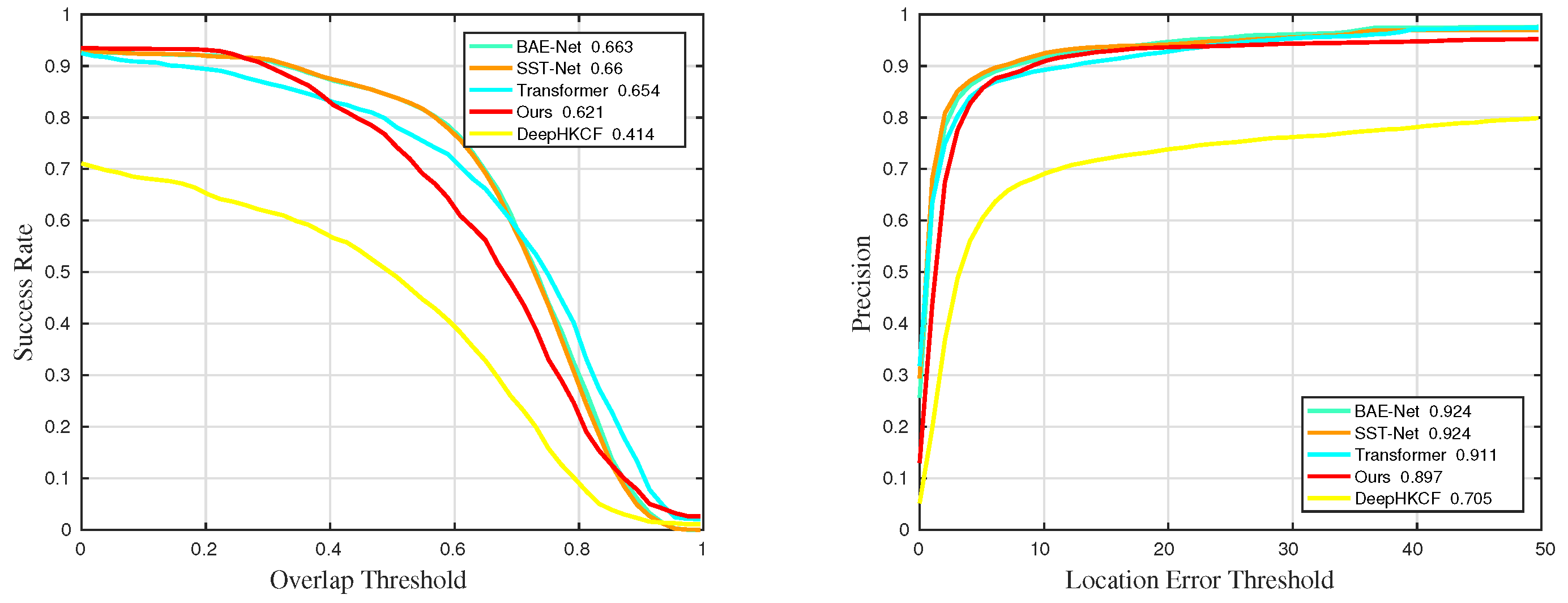
Figure 34.
Quantitative results for all sequences in universality experiments.
Figure 34.
Quantitative results for all sequences in universality experiments.
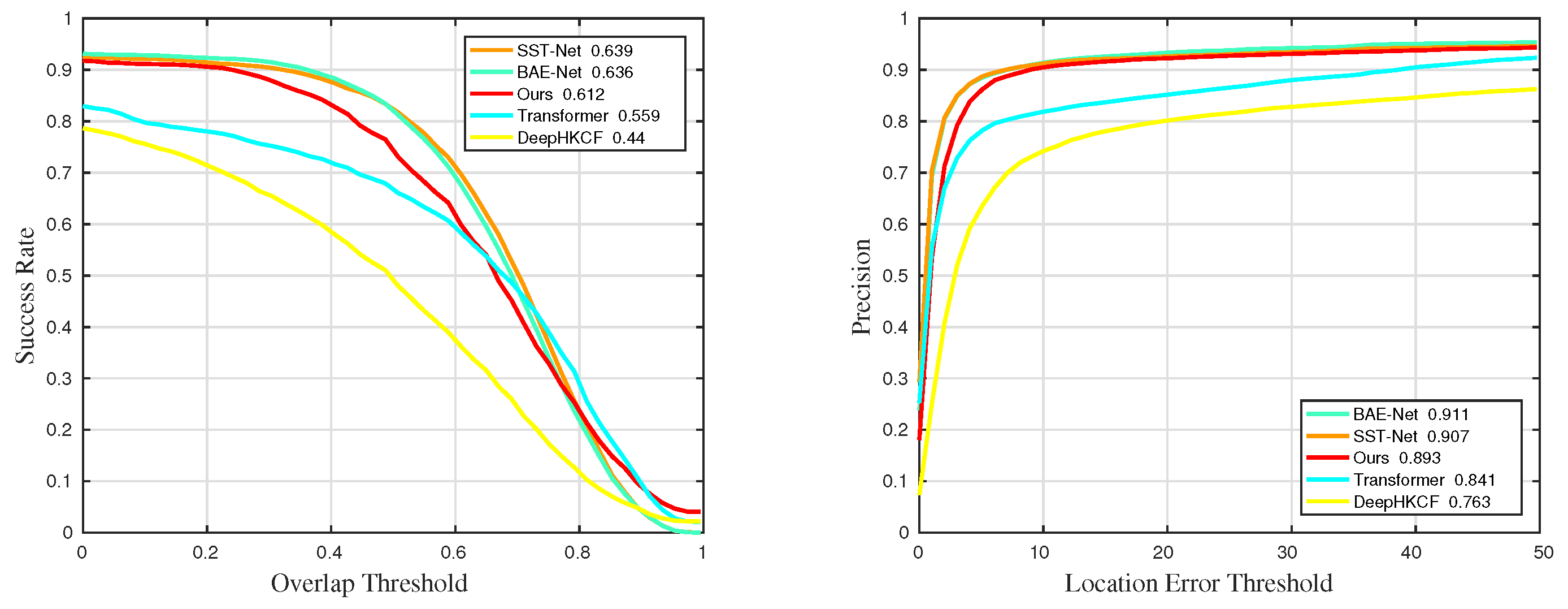
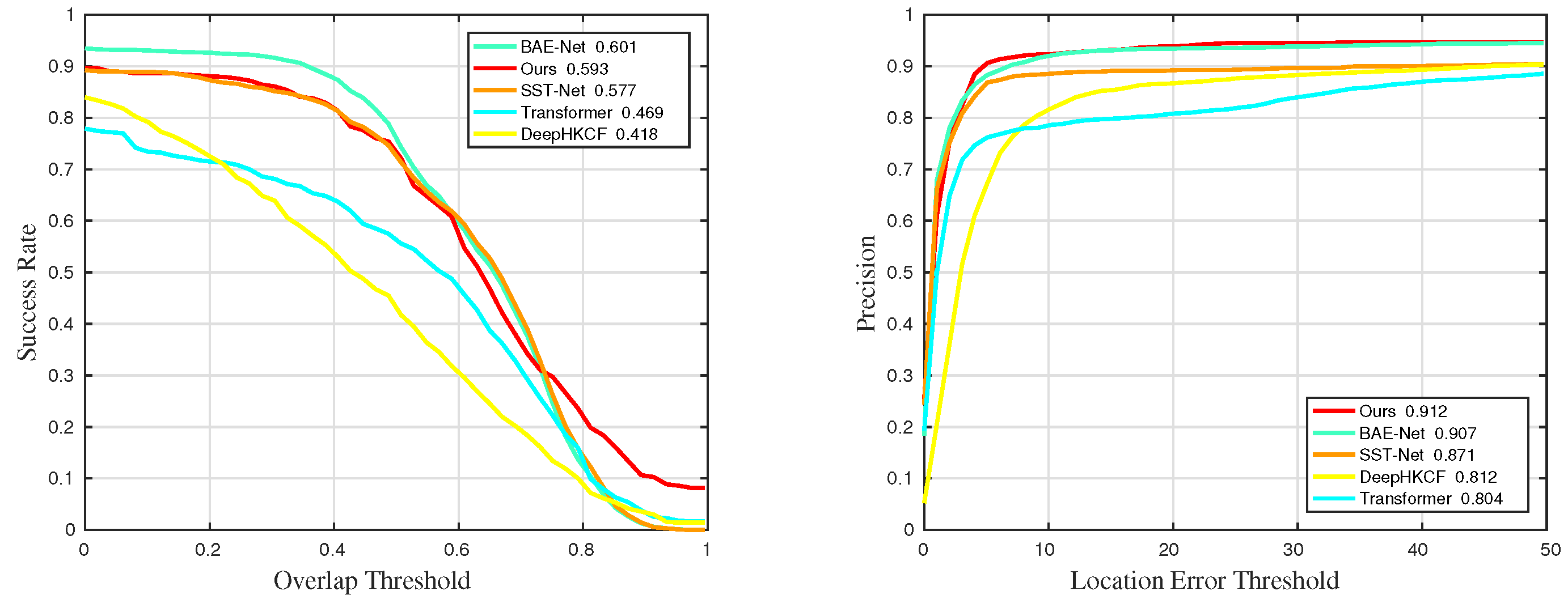
Figure 35.
Quantitative results for sequences with challenge BC in universality experiments.
Figure 35.
Quantitative results for sequences with challenge BC in universality experiments.
Figure 36.
Quantitative results for sequences with challenge LR in universality experiments.
Figure 36.
Quantitative results for sequences with challenge LR in universality experiments.
Figure 37.
Quantitative results for sequences with challenge OCC in universality experiments.
Figure 37.
Quantitative results for sequences with challenge OCC in universality experiments.
Figure 38.
Quantitative results for sequences with challenge RO in universality experiments.
Figure 38.
Quantitative results for sequences with challenge RO in universality experiments.
Figure 39.
Quantitative results for sequences with challenge SV in universality experiments.
Figure 39.
Quantitative results for sequences with challenge SV in universality experiments.
Table 1.
The details of success rate results in comparative experiments. The suffixes mean that the measurements are only counted in the sequences with the corresponding challenges. The best and the second-best results are marked in red and blue, respectively.
Table 1.
The details of success rate results in comparative experiments. The suffixes mean that the measurements are only counted in the sequences with the corresponding challenges. The best and the second-best results are marked in red and blue, respectively.
| Methods | Suc | Suc_BC | Suc_IV | Suc_OCC | Suc_RO | Suc_SV |
|---|
| Ours | 0.615 | 0.702 | 0.718 | 0.636 | 0.643 | 0.649 |
| MHT | 0.584 | 0.48 | 0.679 | 0.603 | 0.63 | 0.691 |
| MFI-HVT | 0.579 | 0.546 | 0.657 | 0.544 | 0.624 | 0.605 |
| DeepHKCF | 0.386 | 0.359 | 0.548 | 0.285 | 0.454 | 0.326 |
| HOMG | 0.571 | 0.518 | 0.6 | 0.596 | 0.637 | 0.597 |
| CNHT | 0.158 | 0.1 | 0.289 | 0.0753 | 0.224 | 0.0855 |
Table 2.
The details of precision results in comparative experiments. The suffixes mean that the measurements are only counted in the sequences with the corresponding challenges. The best and the second-best results are marked in red and blue, respectively.
Table 2.
The details of precision results in comparative experiments. The suffixes mean that the measurements are only counted in the sequences with the corresponding challenges. The best and the second-best results are marked in red and blue, respectively.
| Methods | Pre | Pre_BC | Pre_IV | Pre_OCC | Pre_RO | Pre_SV |
|---|
| Ours | 0.859 | 0.936 | 0.917 | 0.863 | 0.906 | 0.932 |
| MHT | 0.845 | 0.914 | 0.914 | 0.851 | 0.908 | 0.922 |
| MFI-HVT | 0.824 | 0.829 | 0.852 | 0.766 | 0.88 | 0.857 |
| DeepHKCF | 0.676 | 0.757 | 0.734 | 0.531 | 0.776 | 0.849 |
| HOMG | 0.809 | 0.835 | 0.811 | 0.801 | 0.912 | 0.798 |
| CNHT | 0.346 | 0.393 | 0.542 | 0.216 | 0.461 | 0.273 |
Table 3.
The details of success rate results in ablation experiments. The suffixes mean that the measurements are only counted in the sequences with the corresponding challenges. The best and the second-best results are marked in red and blue, respectively.
Table 3.
The details of success rate results in ablation experiments. The suffixes mean that the measurements are only counted in the sequences with the corresponding challenges. The best and the second-best results are marked in red and blue, respectively.
| Methods | Suc | Suc_BC | Suc_IV | Suc_OCC | Suc_RO | Suc_SV |
|---|
| Ours | 0.615 | 0.702 | 0.718 | 0.636 | 0.643 | 0.649 |
| Orimodel | 0.574 | 0.531 | 0.712 | 0.601 | 0.598 | 0.593 |
| Nojudgment | 0.528 | 0.487 | 0.56 | 0.459 | 0.632 | 0.623 |
| FalseColor | 0.507 | 0.522 | 0.657 | 0.507 | 0.541 | 0.532 |
| Siam | 0.483 | 0.454 | 0.698 | 0.485 | 0.548 | 0.531 |
Table 4.
The details of precision results in ablation experiments. The suffixes mean that the measurements are only counted in the sequences with the corresponding challenges. The best and the second-best results are marked in red and blue, respectively.
Table 4.
The details of precision results in ablation experiments. The suffixes mean that the measurements are only counted in the sequences with the corresponding challenges. The best and the second-best results are marked in red and blue, respectively.
| Methods | Pre | Pre_BC | Pre_IV | Pre_OCC | Pre_RO | Pre_SV |
|---|
| Ours | 0.859 | 0.936 | 0.917 | 0.863 | 0.906 | 0.932 |
| Orimodel | 0.845 | 0.895 | 0.913 | 0.852 | 0.888 | 0.857 |
| Nojudgment | 0.75 | 0.722 | 0.763 | 0.695 | 0.909 | 0.816 |
| FalseColor | 0.78 | 0.904 | 0.89 | 0.798 | 0.848 | 0.789 |
| Siam | 0.723 | 0.808 | 0.904 | 0.723 | 0.84 | 0.783 |
Table 5.
The details of success rate results in universality experiments. The suffixes mean that the measurements are only counted in the sequences with the corresponding challenges. The best and the second-best results are marked in red and blue, respectively.
Table 5.
The details of success rate results in universality experiments. The suffixes mean that the measurements are only counted in the sequences with the corresponding challenges. The best and the second-best results are marked in red and blue, respectively.
| Methods | Suc | Suc_BC | Suc_LR | Suc_OCC | Suc_RO | Suc_SV |
|---|
| Ours | 0.612 | 0.636 | 0.593 | 0.627 | 0.621 | 0.607 |
| BAE-Net | 0.636 | 0.654 | 0.601 | 0.599 | 0.663 | 0.639 |
| SST-Net | 0.639 | 0.66 | 0.577 | 0.611 | 0.66 | 0.637 |
| Transformer | 0.559 | 0.601 | 0.469 | 0.403 | 0.654 | 0.575 |
| DeepHKCF | 0.44 | 0.48 | 0.418 | 0.495 | 0.414 | 0.376 |
Table 6.
The details of precision results in universality experiments. The suffixes mean that the measurements are only counted in the sequences with the corresponding challenges. The best and the second-best results are marked in red and blue, respectively.
Table 6.
The details of precision results in universality experiments. The suffixes mean that the measurements are only counted in the sequences with the corresponding challenges. The best and the second-best results are marked in red and blue, respectively.
| Methods | Pre | Pre_BC | Pre_LR | Pre_OCC | Pre_RO | Pre_SV |
|---|
| Ours | 0.893 | 0.917 | 0.912 | 0.958 | 0.897 | 0.855 |
| BAE-Net | 0.911 | 0.927 | 0.907 | 0.916 | 0.924 | 0.894 |
| SST-Net | 0.907 | 0.932 | 0.871 | 0.918 | 0.924 | 0.876 |
| Transformer | 0.841 | 0.872 | 0.804 | 0.755 | 0.911 | 0.846 |
| DeepHKCF | 0.763 | 0.788 | 0.812 | 0.836 | 0.705 | 0.675 |
Table 7.
The computational speed of the algorithms using the IMEC16 dataset.
Table 7.
The computational speed of the algorithms using the IMEC16 dataset.
| Methods | Ours | MHT | MFI-HVT | DeepHKCF | HOMG | CNHT |
|---|
| FPS | 1.8 | 1.2 (CPU) | 0.85 | 1.7 | 1.4 (CPU) | 1 (CPU) |
Table 8.
The computational speed of the algorithms using the IMEC25 dataset.
Table 8.
The computational speed of the algorithms using the IMEC25 dataset.
| Methods | Ours | BAE-Net | SST-Net | Transformer | DeepHKCF |
|---|
| FPS | 0.86 | 0.48 | 0.4 | 0.8 | 0.94 |