Effect of Partially Melting Droplets on Polarimetric and Bi-Spectral Retrieval of Water Cloud Particle Size
Abstract
1. Introduction
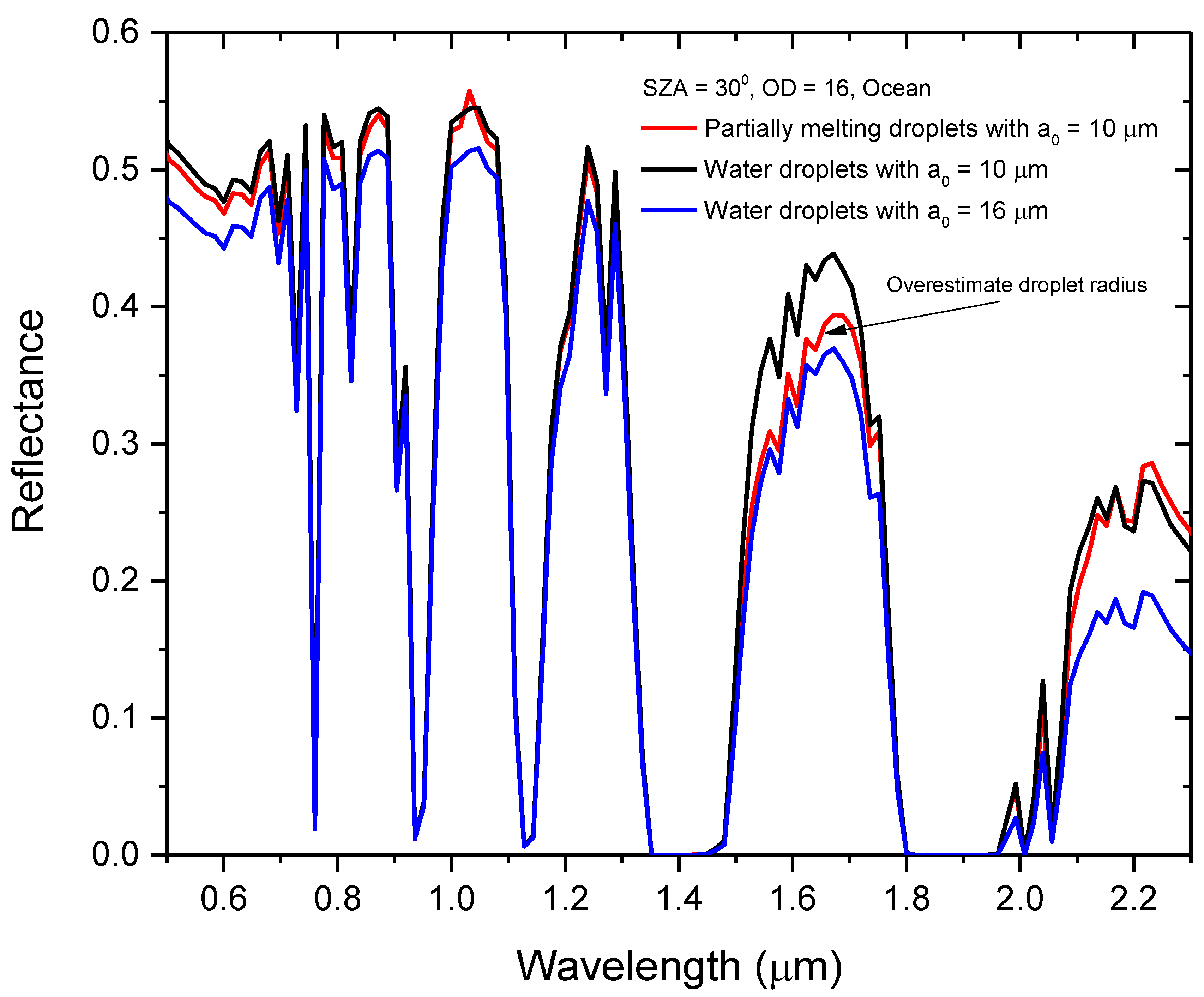
2. Algorithms and Results
3. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Randall, D.A.; Coakley, J.A.; Fairall, C.W.; Knopfli, R.A.; Lenschow, D.H. Outlook for research on marine subtropical stratocumulus clouds. Bull. Amer. Meteor. Soc. 1984, 65, 1290–1301. [Google Scholar] [CrossRef]
- Slingo, A. Sensitivity of the Earth’s radiation budget to changes in low clouds. Nature 1990, 343, 49–51. [Google Scholar] [CrossRef]
- Nakajima, T.; King, M.D. Determination of the optical thickness and effective particle radius of clouds from reflected solar radiation measurements. Part I Theory J. Atmos. Sci. 1990, 47, 1878–1893. [Google Scholar] [CrossRef]
- Rossow, W.B.; Schiffer, R.A. ISCCP cloud data products. B. Am. Meteorol. Soc. 1991, 72, 2–20. [Google Scholar] [CrossRef]
- Platnick, S.; King, M.; Ackerman, S.; Menzel, W.; Baum, B.; Riedi, J.; Frey, R. The MODIS cloud products: Algorithms and examples from terra. IEEE T. Geosci. Remote 2003, 41, 459–473. [Google Scholar] [CrossRef]
- Cao, C.; De Luccia, F.J.; Xiong, X.; Wolfe, R.; Weng, F. Early on-orbit performance of the Visible Infrared Imaging Radiometer Suite onboard the Suomi National Polar-orbiting Partnership (S-NPP) satellite. IEEE T. Geosci. Remote 2014, 52, 1142–1156. [Google Scholar] [CrossRef]
- Bessho, K.; Date, K.; Hayashi, M.; Ikeda, A.; Imai, T.; Inoue, H.; Kumagai, Y.; Miyakawa, T.; Murata, H.; Ohno, T.; et al. An introduction to Himawari-8/9–Japan’s new-generation geostationary meteorological satellites. J. Meteorol. Soc. Jpn. 2016, 94, 151–183. [Google Scholar] [CrossRef]
- Cairns, B.; Russell, E.E.; Travis, L.D. Research Scanning Polarimeter: Calibration and ground-based measurements. In Proceedings of the SPIE 3754, Polarization: Measurement, Analysis, and Remote Sensing II, Denver, CO, USA, 25 October 1999. [Google Scholar] [CrossRef]
- Bréon, F.-M.; Doutriaux-Boucher, M. A comparison of cloud droplet radii measured from space. IEEE T. Geosci. Remote 2005, 43, 1796–1805. [Google Scholar] [CrossRef]
- Alexandrov, M.D.; Cairns, B.; Emde, C.; Ackerman, A.S.; van Diedenhoven, B. Accuracy assessments of cloud droplet size retrievals from polarized reflectance measurements by the research scanning polarimeter. Remote Sens. Environ. 2012, 125, 92–111. [Google Scholar] [CrossRef]
- Alexandrov, M.D.; Cairns, B.; Wasilewski, A.P.; Ackerman, A.S.; McGille, M.J.; Yorks, J.E.; Hlavka, D.L.; Platnick, S.E.; Arnold, G.T.; van Diedenhoven, B.; et al. Liquid water cloud properties during the Polarimeter Definition Experiment (PODEX). Remote Sens. Environ. 2015, 169, 20–36. [Google Scholar] [CrossRef]
- Nakajima, T.; King, M.D.; Spinhirne, J.D.; Radke, L.F. Determination of the optical thickness and effective particle radius of clouds from reflected solar radiation measurements. Part II: Marine stratocumulus observations. J. Atmos. Sci. 1991, 48, 728–751. [Google Scholar] [CrossRef]
- Platnick, S.; Valero, F.P.J. A validation of a satellite cloud retrieval during ASTEX. J. Atmos. Sci. 1995, 52, 2985–3001. [Google Scholar] [CrossRef]
- McBride, P.J.; Schmidt, K.S.; Pilewskie, P.; Walther, A.; Heidinger, A.K.; Wolfe, D.E.; Fairall, C.W.; Lance, S. CalNex cloud properties retrieved from a ship-based spectrometer and comparisons with satellite and aircraft retrieved cloud properties. J. Geophys. Res. Atmos. 2012, 117, D21. [Google Scholar] [CrossRef]
- Liang, L.; Di Girolamo, L.; Sun, W. Bias in MODIS cloud drop effective radius for oceanic water clouds as deduced from optical thickness variability across scattering angles. J. Geophys. Res. Atmos. 2015, 120, 7661–7681. [Google Scholar] [CrossRef]
- Fu, D.; Di Girolamo, L.; Liang, L.; Zhao, G. Regional biases in MODIS marine liquid water cloud drop effective radius deduced through fusion with MISR. J. Geophys. Res. Atmos. 2019, 124, 13182–13196. [Google Scholar] [CrossRef] [PubMed]
- Fu, D.; Di Girolamo, L.; Rauber, R.M.; McFarquhar, G.M.; Nesbitt, S.W.; Loveridge, J.; Hong, Y.; van Diedenhoven, B.; Cairns, B.; Alexandrov, M.D.; et al. An evaluation of the liquid cloud droplet effective radius derived from MODIS, airborne remote sensing, and in situ measurements from CAMP2Ex. Atmos. Chem. Phys. 2022, 22, 8259–8285. [Google Scholar] [CrossRef]
- Winker, D.M.; Vaughan, M.A.; Omar, A.; Hu, Y.; Powell, K.A.; Liu, Z.; Hunt, W.H.; Young, S.A. Overview of the CALIPSO mission and CALIOP data processing algorithms. J. Atmos. Oceanic. Technol. 2009, 226, 2310–2323. [Google Scholar] [CrossRef]
- Hu, Y.; Vaughan, M.; McClain, C.; Behrenfeld, M.; Maring, H.; Anderson, D.; Sun-Mack, S.; Flittner, D.; Huang, J.; Wielicki, B.; et al. Global Statistics of Liquid Water Content and Effective Number Concentration of Water Clouds over Ocean Derived from Combined CALIPSO and MODIS Measurements. Atmos. Chem. Phys. 2007, 7, 3353–3359. [Google Scholar] [CrossRef]
- Hu, Y.; Winker, D.M.; Vaughan, M.; Lin, B.; Omar, A.; Trepte, C.; Flittner, D.; Yang, P.; Nasiri, S.L.; Baum, B.; et al. CALIPSO/CALIOP Cloud Phase Discrimination Algorithm. J. Atmos. Oceanic. Technol. 2009, 26, 2293–2309. [Google Scholar] [CrossRef]
- Hu, Y.; Lu, X.; Zhai, P.; Hostetler, C.A.; Hair, J.W.; Cairns, B.; Sun, W.; Stamnes, S.; Omar, A.; Baize, R.; et al. Liquid Phase Cloud Microphysical Property Estimates from CALIPSO Measurements. Front. Remote Sens. 2021, 2, 25. [Google Scholar] [CrossRef]
- Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann. Phys. 1908, 330, 377–445. [Google Scholar] [CrossRef]
- Sun, W.; Hu, Y.; Baize, R.R.; Omar, A. Partially melting droplets strongly enhance lidar backscatter. J. Quant. Spectrosc. Radiat. Trans. 2022, 281, 108107. [Google Scholar] [CrossRef]
- Toon, O.B.; Ackerman, T.P. Algorithms for the calculation of scattering by stratified spheres. Appl. Opt. 1981, 20, 3657–3660. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Loeb, N.G.; Fu, Q. Light scattering by coated sphere immersed in absorbing medium: A comparison between the FDTD and analytic solutions. J. Quant. Spectrosc. Radiat. Trans. 2004, 83, 483–492. [Google Scholar] [CrossRef]
- Deirmendjian, D. Electromagnetic Scattering on Spherical Polydispersions; American Elsevier Publishing Company, Inc.: New York, NY, USA, 1969. [Google Scholar]
- Sun, W.; Lukashin, C. Modeling polarized solar radiation from ocean-atmosphere system for CLARREO inter-calibration applications. Atmos. Chem. Phys. 2013, 13, 10303–10324. [Google Scholar] [CrossRef]


| At 1.6 µm | Water a0 = 10 µm | Water a0 = 16 µm | Partially melting a0 = 10 µm |
| Asymmetry factor: | 0.860 | 0.872 | 0.864 |
| 1—Single Scattering Albedo: | 1.0084 × 10−2 | 1.5509 × 10−2 | 1.5349 × 10−2 |
| At 2.1 µm | Water a0 = 10 µm | Water a0 = 16 µm | Partially melting a0 = 10 µm |
| Asymmetry factor: | 0.864 | 0.880 | 0.869 |
| 1—Single Scattering Albedo: | 3.6776 × 10−2 | 5.5580 × 10−2 | 4.4225 × 10−2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Hu, Y.; Stamnes, S.A.; Trepte, C.R.; Omar, A.H.; Baize, R.R. Effect of Partially Melting Droplets on Polarimetric and Bi-Spectral Retrieval of Water Cloud Particle Size. Remote Sens. 2023, 15, 1576. https://doi.org/10.3390/rs15061576
Sun W, Hu Y, Stamnes SA, Trepte CR, Omar AH, Baize RR. Effect of Partially Melting Droplets on Polarimetric and Bi-Spectral Retrieval of Water Cloud Particle Size. Remote Sensing. 2023; 15(6):1576. https://doi.org/10.3390/rs15061576
Chicago/Turabian StyleSun, Wenbo, Yongxiang Hu, Snorre A. Stamnes, Charles R. Trepte, Ali H. Omar, and Rosemary R. Baize. 2023. "Effect of Partially Melting Droplets on Polarimetric and Bi-Spectral Retrieval of Water Cloud Particle Size" Remote Sensing 15, no. 6: 1576. https://doi.org/10.3390/rs15061576
APA StyleSun, W., Hu, Y., Stamnes, S. A., Trepte, C. R., Omar, A. H., & Baize, R. R. (2023). Effect of Partially Melting Droplets on Polarimetric and Bi-Spectral Retrieval of Water Cloud Particle Size. Remote Sensing, 15(6), 1576. https://doi.org/10.3390/rs15061576






