End-to-End Powerline Detection Based on Images from UAVs
Abstract
1. Introduction
- (1)
- The transmission cable extends widely through the global image. The transmission wire can be roughly represented as a straight line over the entire image from a UAV flying at a low altitude and from the UAV’s perspective.
- (2)
- It can be approximated as a straight line. Due to the close proximity to the cable in the UAV image, the gravitational radian can be disregarded, allowing for a close approximation of a straight line.
2. Literature Review
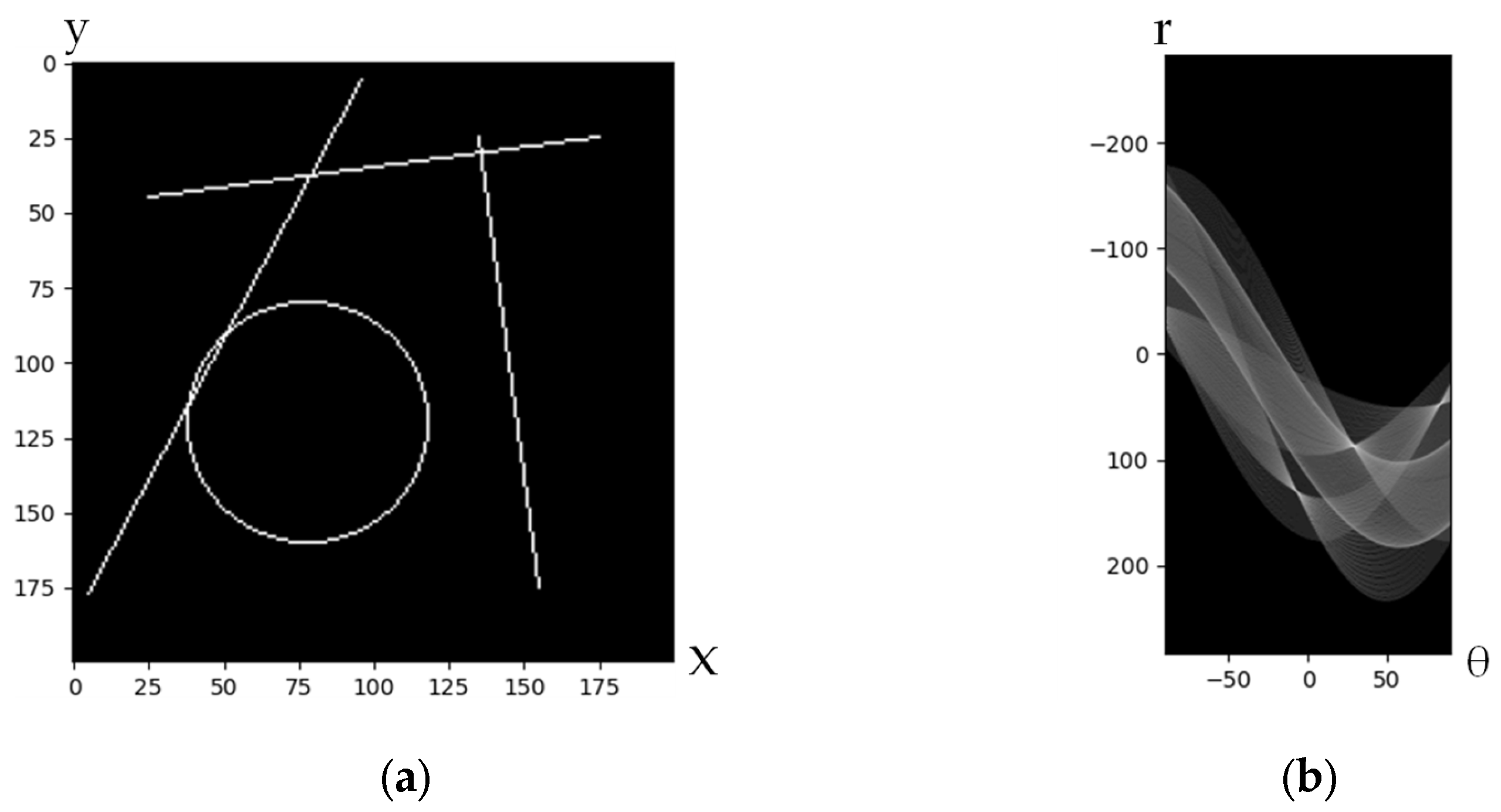
2.1. Hough Transform
2.2. Object Detection
2.3. FPN
2.4. Powerline Detection Based on Deep Learning
3. Methods
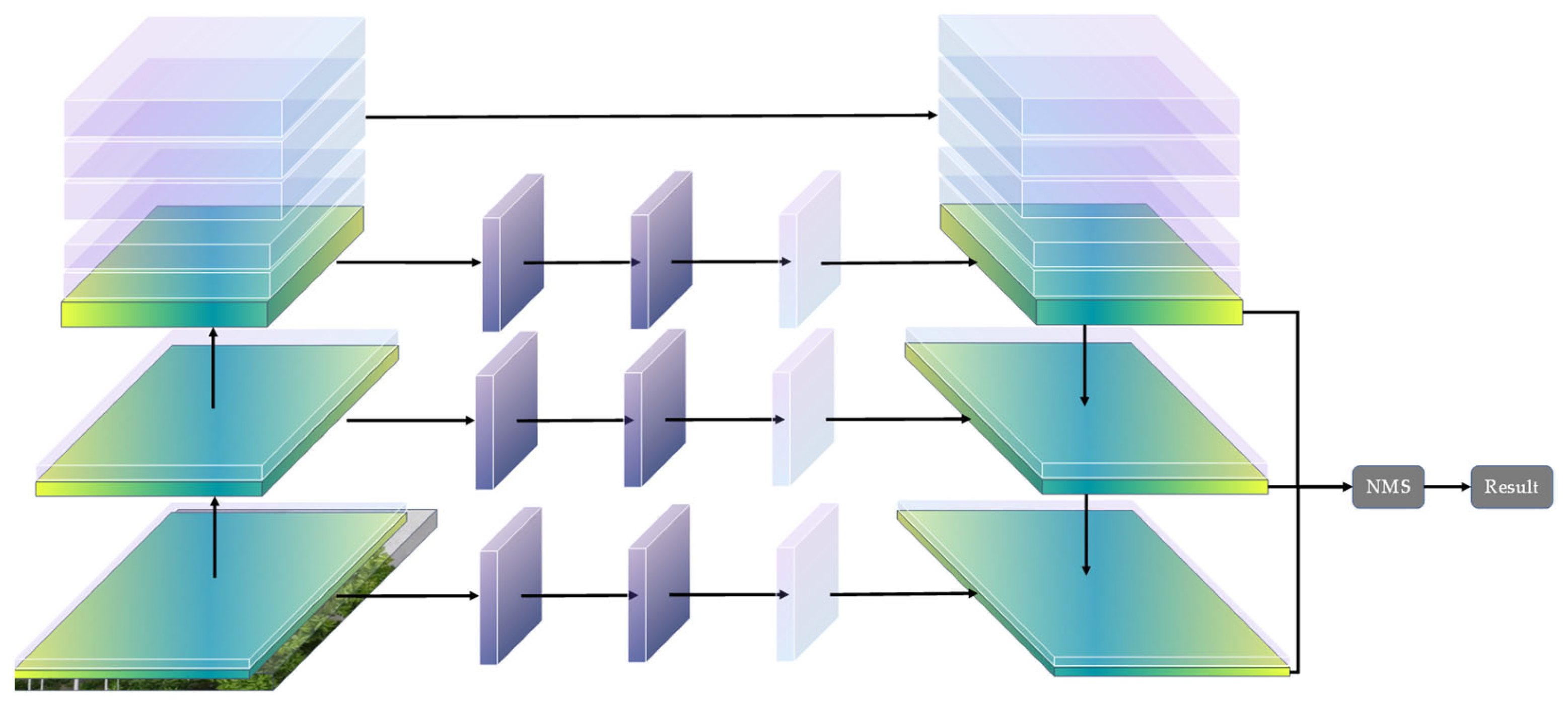
3.1. Proposed Net Architecture
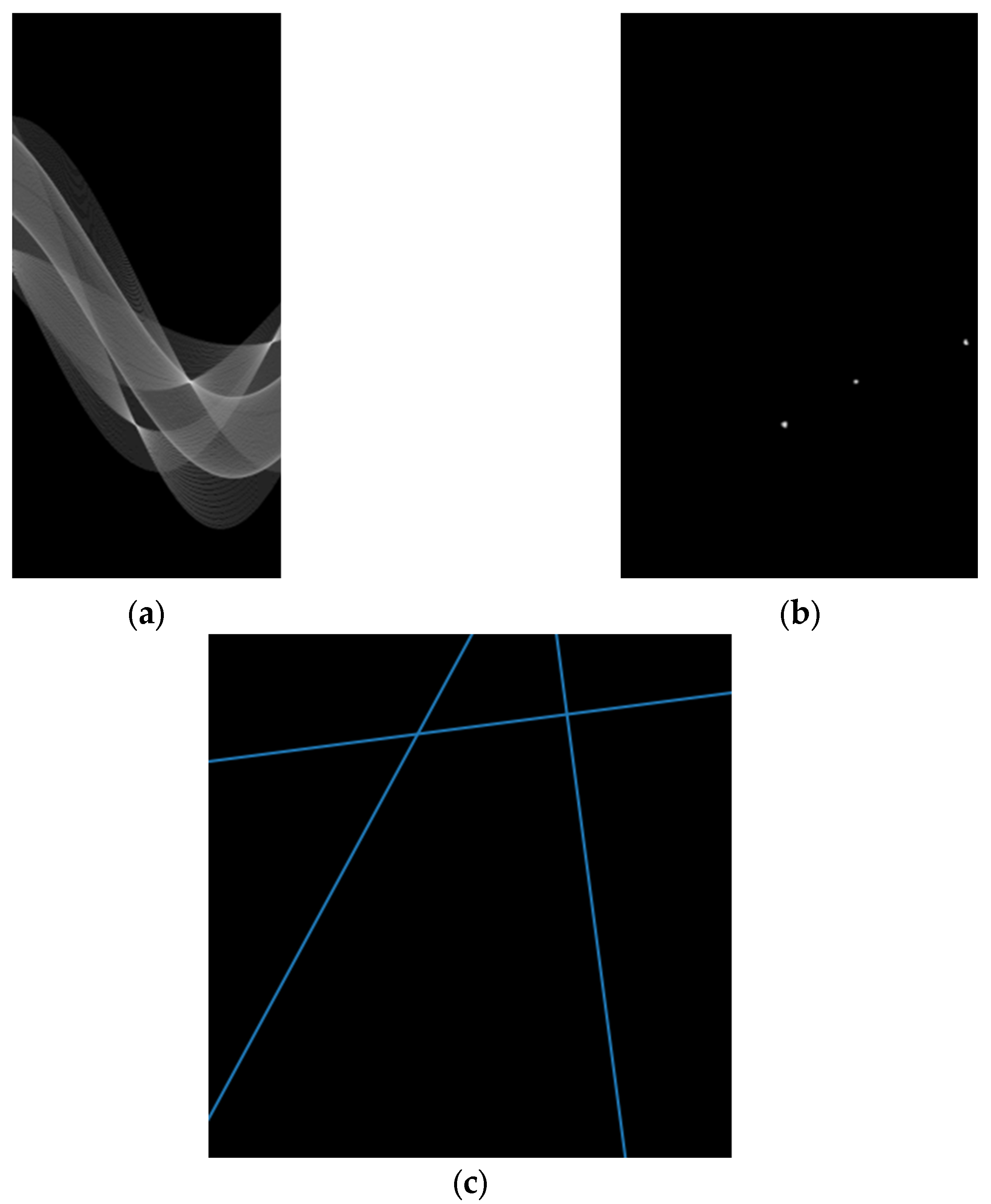
3.2. Hough FPN
3.3. Non-Maximum Suppression
| Algorithm 1 Non-Maximum Suppression |
| Input: is the list of initial detection lines contains corresponding detection scores is the NMS threshold is the midpoint of the line is the midpoint distance threshold begin While do for do if then ; ; new ; ; ifthen ; ; end end return end |
4. Results
4.1. Dataset
4.2. Implement Details
4.2.1. Experiment Environment
4.2.2. Training Detail
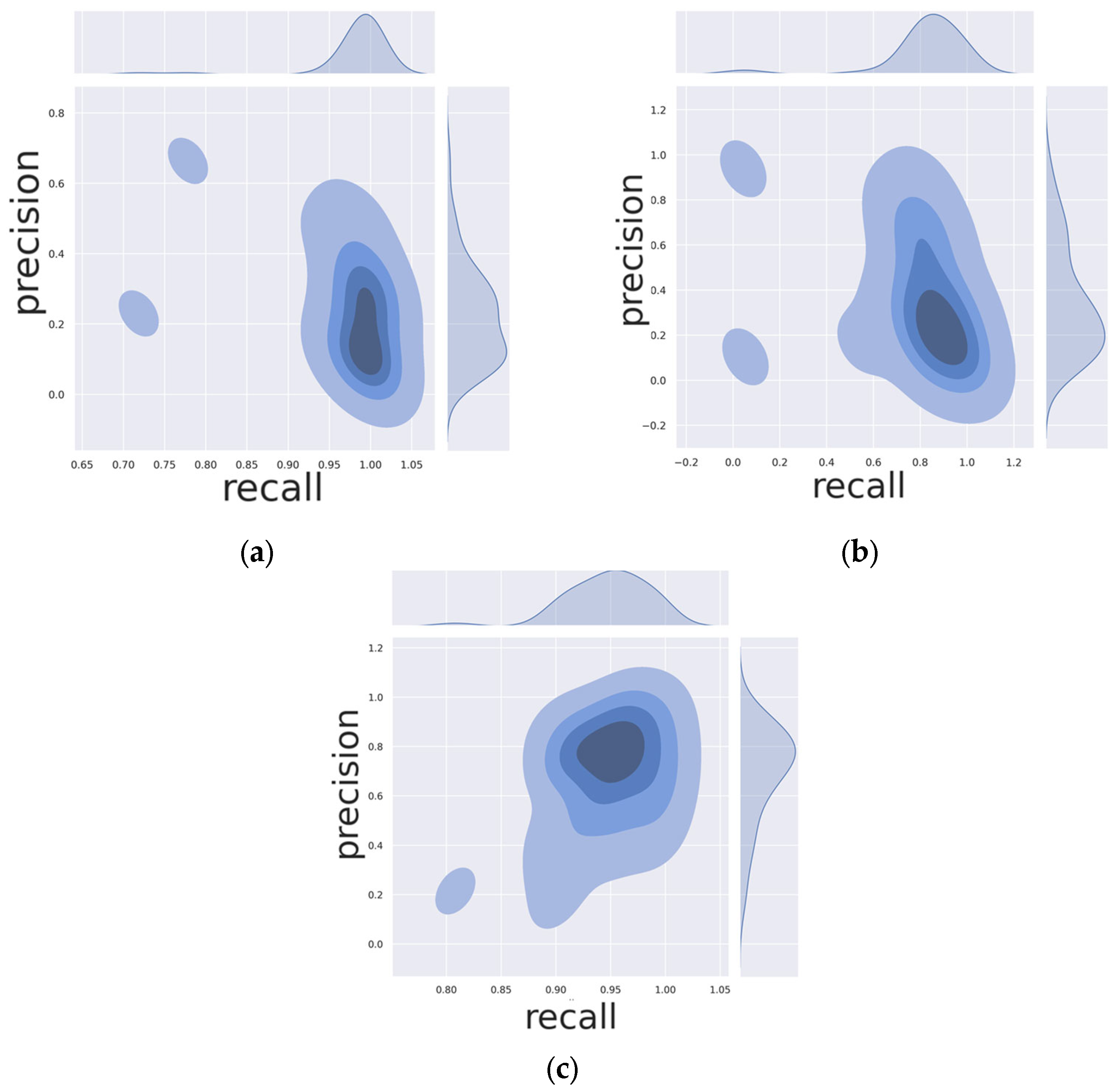
4.3. Metric
4.4. Comparison with Other Methods
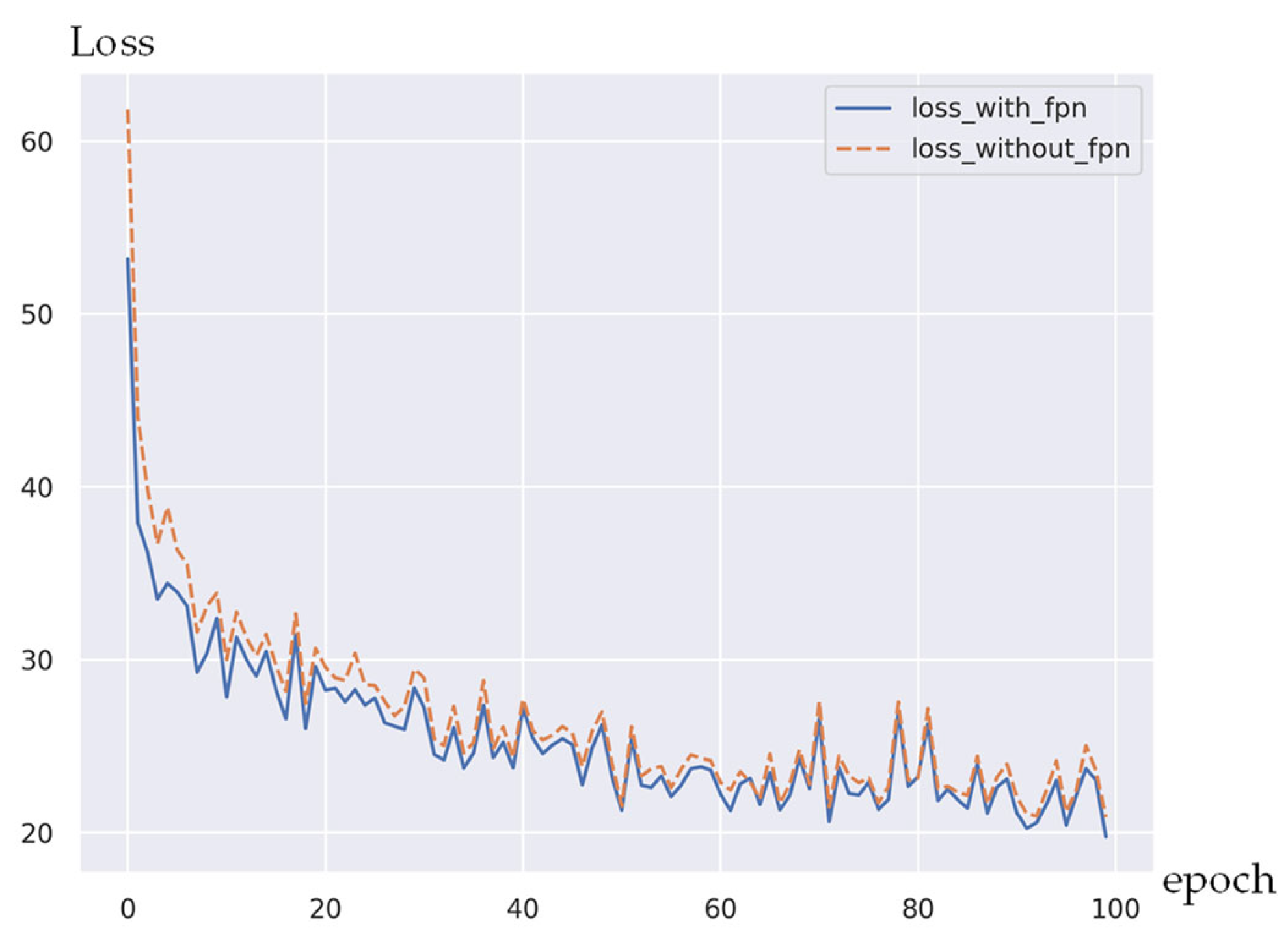
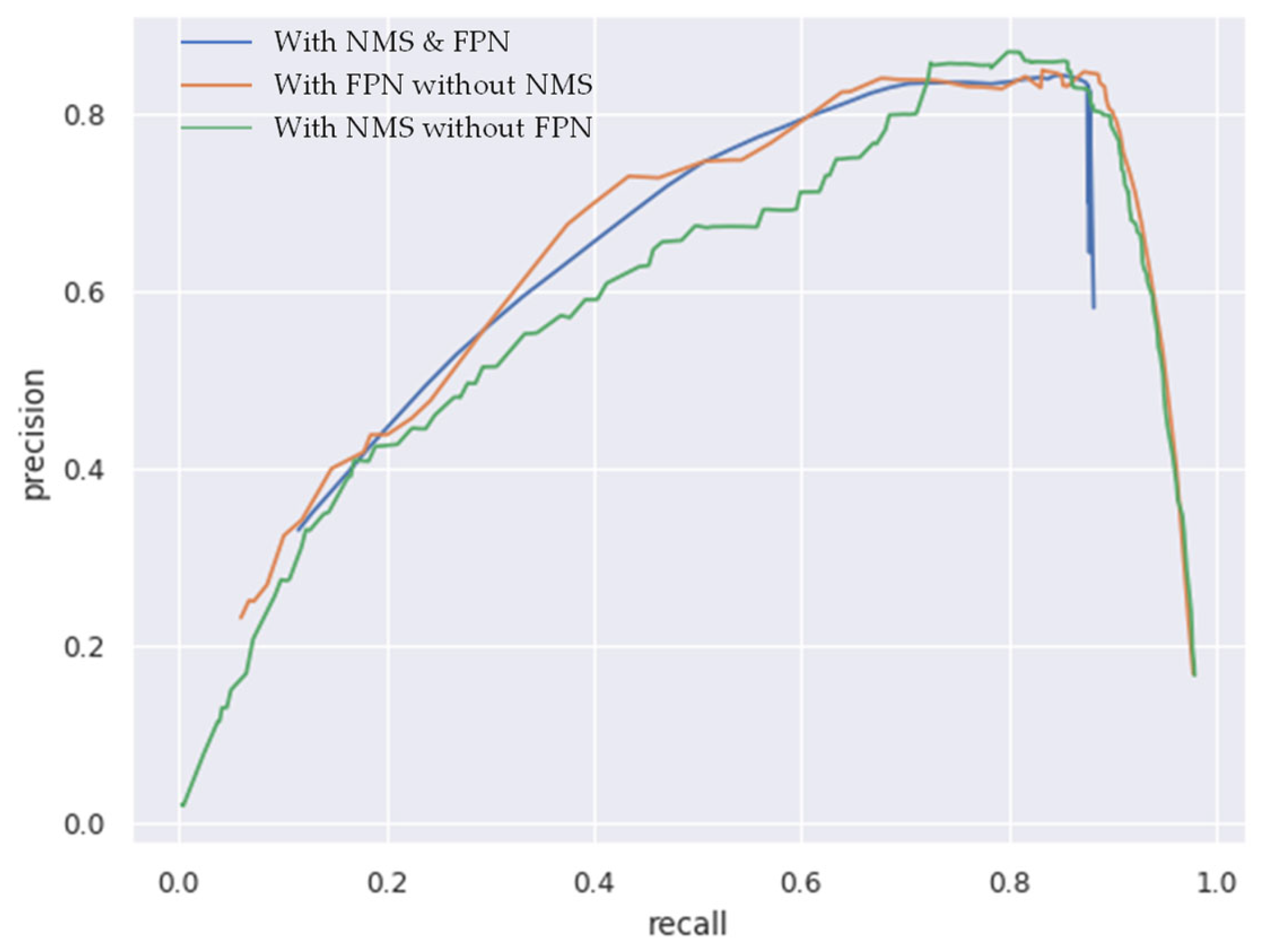
4.5. Ablation Study
5. Discussion
- Selective training for real scenarios. In order to increase the generalization capability of the model, a large number of network images are introduced in addition to the proposed dataset. In real scenarios, the model may not need to recognize multiple styles of transmission lines, and more effective obstacle rejection may be achieved with reducing the generalization capability.
- This can be accomplished with establishing negative samples. To improve the obstacle rejection effect, we design the Loss function and mark the obstacles in the dataset as negative samples.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nasseri, M.H.; Moradi, H.; Nasiri, S.M.; Hosseini, R. Power Line Detection and Tracking Using Hough Transform and Particle Filter. In Proceedings of the 2018 6th RSI International Conference on Robotics and Mechatronics (IcRoM), Tehran, Iran, 23–25 October 2018. [Google Scholar]
- Hough, P.V.C. Method and Means for Recognizing Complex Patterns. U.S. Patent 3,069,654, 18 December 1962. [Google Scholar]
- Zhang, X.; Zhang, L.; Li, D. Transmission line abnormal target detection based on machine learning yolo v3. In Proceedings of the 2019 International Conference on Advanced Mechatronic Systems (ICAMechS), Kusatsu, Japan, 26–28 August 2019; pp. 344–348. [Google Scholar]
- Bao, W.; Ren, Y.; Wang, N.; Hu, G.; Yang, X. Detection of Abnormal Vibration Dampers on Transmission Lines in UAV Remote Sensing Images with PMA-YOLO. Remote Sens. 2021, 13, 4134. [Google Scholar] [CrossRef]
- Redmon, J.; Farhadi, A. Yolov3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Zhai, Y.; Yang, X.; Wang, Q.; Zhao, Z.; Zhao, W. Hybrid knowledge R-CNN for transmission line multifitting detection. IEEE Trans. Instrum. Meas. 2021, 70, 1–12. [Google Scholar] [CrossRef]
- Vemula, S.; Frye, M. Mask R-CNN powerline detector: A deep learning approach with applications to a UAV. In Proceedings of the 2020 AIAA/IEEE 39th Digital Avionics Systems Conference (DASC), San Antonio, TX, USA, 11–15 October 2020; pp. 1–6. [Google Scholar]
- Liu, B.; Liu, H.; Yuan, J. Lane line detection based on mask R-CNN. In Proceedings of the 3rd International Conference on Mechatronics Engineering and Information Technology (ICMEIT 2019), Dalian, China, 29–30 March 2019; Atlantis Press: Paris, France, 2019; pp. 696–699. [Google Scholar]
- Duda, R.O.; Hart, P.E. Use of the Hough transformation to detect lines and curves in pictures. Commun. ACM 1972, 15, 11–15. [Google Scholar] [CrossRef]
- Illingworth, J.; Kittler, J. The adaptive Hough transform. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 5, 690–698. [Google Scholar] [CrossRef] [PubMed]
- Kiryati, N.; Eldar, Y.; Bruckstein, A.M. A probabilistic Hough transform. Pattern Recognit. 1991, 24, 303–316. [Google Scholar] [CrossRef]
- O’gorman, F.; Clowes, M.B. Finding picture edges through collinearity of feature points. IEEE Trans. Comput. 1976, 25, 449–456. [Google Scholar] [CrossRef]
- Galamhos, C.; Matas, J.; Kittler, J. Progressive probabilistic Hough transform for line detection. In Proceedings of the 1999 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (Cat. No PR00149), Fort Collins, CO, USA, 23–25 June 1999; Volume 1, pp. 554–560. [Google Scholar]
- Zhou, G.; Yuan, J.; Yen, I.L.; Bastani, F. Robust real-time UAV based power line detection and tracking. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 744–748. [Google Scholar]
- Gerke, M.; Seibold, P. Visual inspection of power lines by UAS. In Proceedings of the 2014 International Conference and Exposition on Electrical and Power Engineering (EPE), Iasi, Romania, 16–18 October 2014; pp. 1077–1082. [Google Scholar]
- Jones, D.; Golightly, I.; Roberts, J.; Usher, K. Modeling and control of a robotic power line inspection vehicle. In Proceedings of the 2006 IEEE Conference on Computer Aided Control System Design 2006 IEEE International Conference on Control Applications, 2006 IEEE International Symposium on Intelligent Control, Munich, Germany, 4–6 October 2006; pp. 632–637. [Google Scholar]
- Fernandes, L.A.F.; Oliveira, M.M. Real-time line detection through an improved Hough transform voting scheme. Pattern Recognit. 2008, 41, 299–314. [Google Scholar] [CrossRef]
- Limberger, F.A.; Oliveira, M.M. Real-time detection of planar regions in unorganized point clouds. Pattern Recognit. 2015, 48, 2043–2053. [Google Scholar] [CrossRef]
- Yacoub, S.B.; Jolion, J.M. Hierarchical line extraction. IEE Proc.-Vis. Image Signal Process. 1995, 142, 7–14. [Google Scholar] [CrossRef]
- Princen, J.; Illingworth, J.; Kittler, J. A hierarchical approach to line extraction based on the Hough transform. Comput. Vis. Graph. Image Process. 1990, 52, 57–77. [Google Scholar] [CrossRef]
- Aggarwal, N.; Karl, W.C. Line detection in images through regularized Hough transform. IEEE Trans. Image Process. 2006, 15, 582–591. [Google Scholar] [CrossRef] [PubMed]
- Min, J.; Lee, J.; Ponce, J.; Cho, M. Hyperpixel flow: Semantic correspondence with multi-layer neural features. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 3395–3404. [Google Scholar]
- Qi, C.R.; Litany, O.; He, K.; Guibas, L.J. Deep hough voting for 3d object detection in point clouds. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 9277–9286. [Google Scholar]
- Lin, Y.; Pintea, S.L.; van Gemert, J.C. Deep hough-transform line priors. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Springer International Publishing: Cham, Switzerland, 2020; pp. 323–340. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 779–788. [Google Scholar]
- Law, H.; Deng, J. Cornernet: Detecting objects as paired keypoints. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 734–750. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. Adv. Neural Inf. Process. Syst. 2015, 28. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Liew, J.H.; Zou, Y.; Zhou, D.; Feng, J. Panet: Few-shot image semantic segmentation with prototype alignment. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 9197–9206. [Google Scholar]
- Huang, K.; Wang, Y.; Zhou, Z.; Ding, T.; Gao, S.; Ma, Y. Learning to parse wireframes in images of man-made environments. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 626–635. [Google Scholar]
- Xue, N.; Bai, S.; Wang, F.; Xia, G.S.; Wu, T.; Zhang, L. Learning attraction field representation for robust line segment detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 1595–1603. [Google Scholar]
- Siranec, M.; Höger, M.; Otcenasova, A. Advanced power line diagnostics using point cloud data—Possible applications and limits. Remote Sens. 2021, 13, 1880. [Google Scholar] [CrossRef]
- Awrangjeb, M. Extraction of power line pylons and wires using airborne lidar data at different height levels. Remote Sens. 2019, 11, 1798. [Google Scholar] [CrossRef]
- Pan, C.; Cao, X.; Wu, D. Power line detection via background noise removal. In Proceedings of the 2016 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Washington, DC, USA, 7–9 December 2016; pp. 871–875. [Google Scholar]
- Benlıgıray, B.; Gerek, Ö.N. Visualization of power lines recognized in aerial images using deep learning. In Proceedings of the 2018 26th Signal Processing and Communications Applications Conference (SIU), Izmir, Turkey, 2–5 May 2018; pp. 1–4. [Google Scholar]
- Zhu, K.; Xu, C.; Wei, Y.; Cai, G. Fast-PLDN: Fast power line detection network. J. Real-Time Image Process. 2022, 19, 3–13. [Google Scholar] [CrossRef]
- Dai, Z.; Yi, J.; Zhang, H.; Wang, D.; Huang, X.; Ma, C. CODNet: A Center and Orientation Detection Network for Power Line Following Navigation. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar]
- Huang, S.; Qin, F.; Xiong, P.; Ding, N.; He, Y.; Liu, X. TP-LSD: Tri-points based line segment detector. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2020; pp. 770–785. [Google Scholar]
- Zhou, Y.; Qi, H.; Ma, Y. End-to-end wireframe parsing. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 962–971. [Google Scholar]
- Von Gioi, R.G.; Jakubowicz, J.; Morel, J.M.; Randall, G. LSD: A line segment detector. Image Process. Line 2012, 2, 35–55. [Google Scholar] [CrossRef]



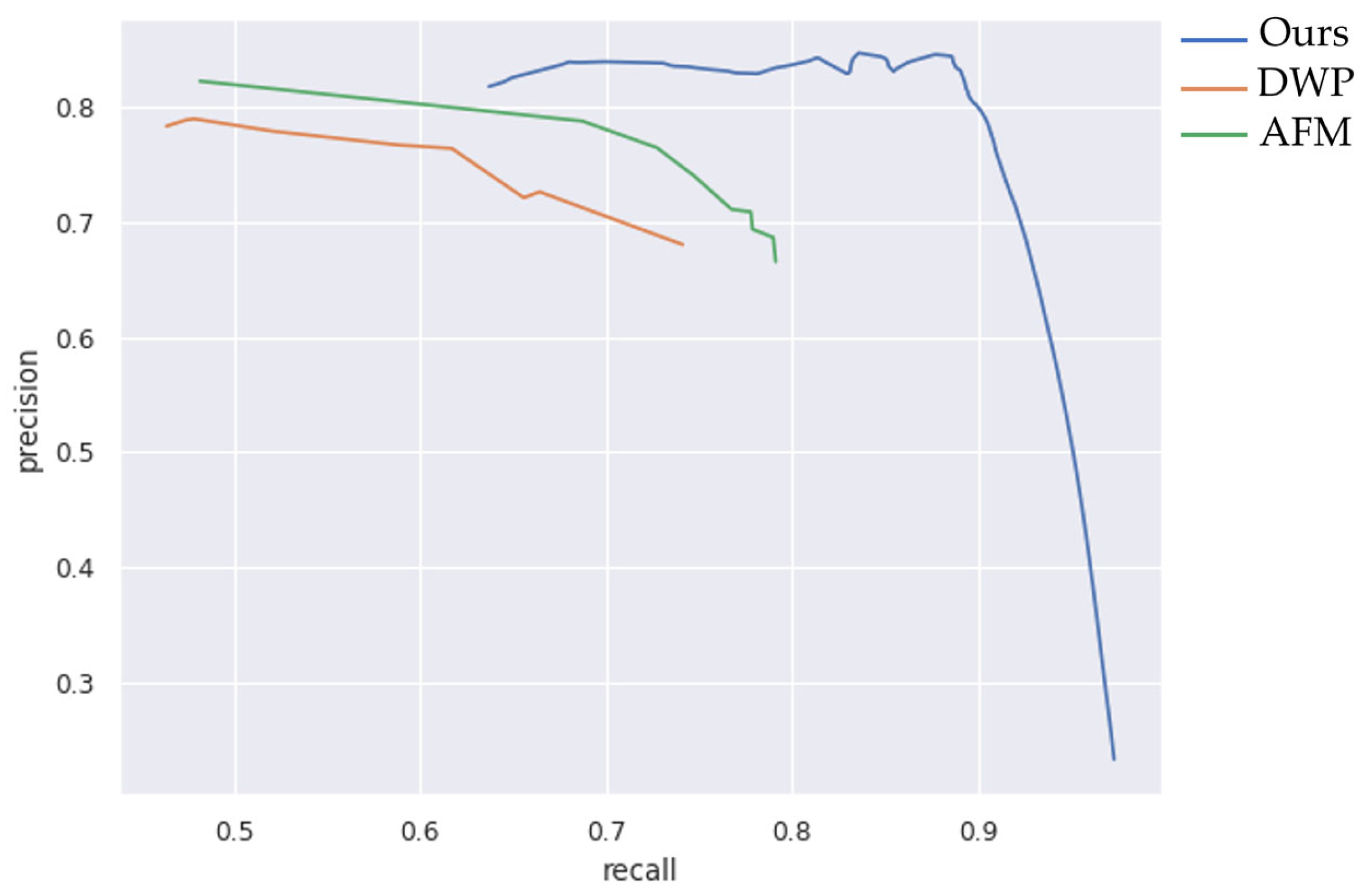




| Methods | Inputs (Image Size) | Scores | Inferences per Second | ||
|---|---|---|---|---|---|
| F-Score | Recall | Precision | |||
| LSD | 512 × 512 | 0.34 | 0.98 | 0.22 | 74.9 (cpu) |
| HoughP | 512 × 512 | 0.42 | 0.82 | 0.34 | 88.6 (cpu) |
| DWP | 320 × 320 | 0.73 | 0.75 | 0.63 | 24.8 |
| AFM | 512 × 512 | 0.70 | 0.81 | 0.65 | 6.0 |
| Ours | 512 × 512 | 0.86 | 0.85 | 0.88 | 122.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J.; He, J.; Guo, C. End-to-End Powerline Detection Based on Images from UAVs. Remote Sens. 2023, 15, 1570. https://doi.org/10.3390/rs15061570
Hu J, He J, Guo C. End-to-End Powerline Detection Based on Images from UAVs. Remote Sensing. 2023; 15(6):1570. https://doi.org/10.3390/rs15061570
Chicago/Turabian StyleHu, Jingwei, Jing He, and Chengjun Guo. 2023. "End-to-End Powerline Detection Based on Images from UAVs" Remote Sensing 15, no. 6: 1570. https://doi.org/10.3390/rs15061570
APA StyleHu, J., He, J., & Guo, C. (2023). End-to-End Powerline Detection Based on Images from UAVs. Remote Sensing, 15(6), 1570. https://doi.org/10.3390/rs15061570






