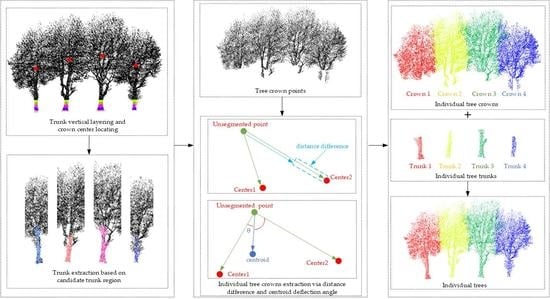
Trunk-Constrained and Tree Structure Analysis Method for Individual Tree Extraction from Scanned Outdoor Scenes
Abstract
1. Introduction
- (1)
- A comprehensive framework combining semantic segmentation with trunk-constrained and tree structure analysis is constructed for individual tree extraction. It can solve the problem whereby trees are often distributed in multiple rows, and there are overlaps between the canopies.
- (2)
- A new method for locating tree position and crown center based on the local tree trunk method is proposed. The real local tree trunks are identified by restricting the height, the number of points and the angle between the trunk and the ground, the crown centers are located by circle fitting, and complete trunks are extracted according to region growing in relation to the proposed candidate trunk region.
- (3)
- A novel individual tree extraction method based on distance difference and centroid deflection angle is proposed. Exploiting tree point classification and the effective instance segmentation strategy, the proposed method can obtain more satisfactory individual tree extraction results.
2. Materials and Methods
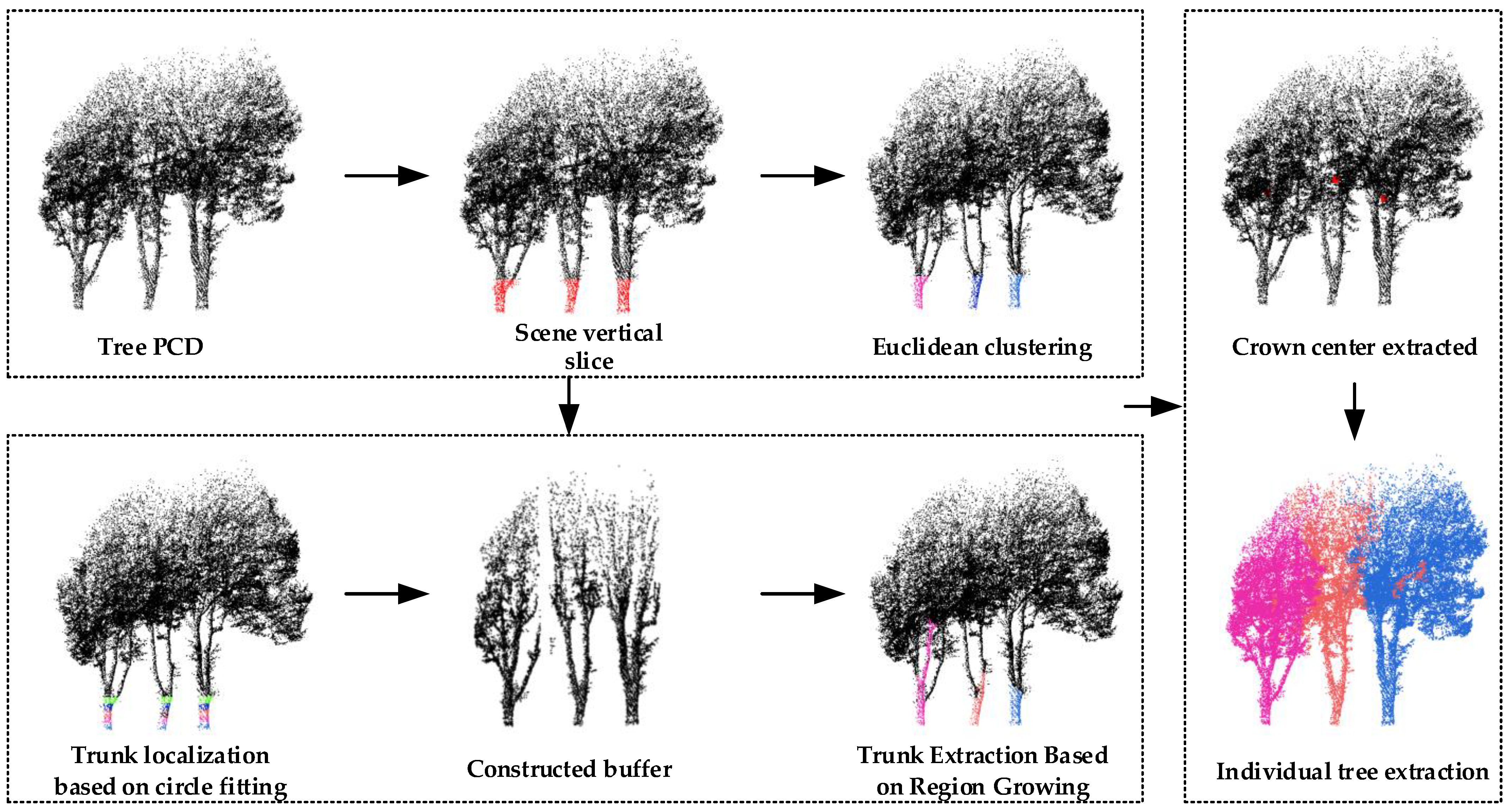
2.1. Tree Trunks Extraction
2.1.1. Local Tree Trunks Extraction
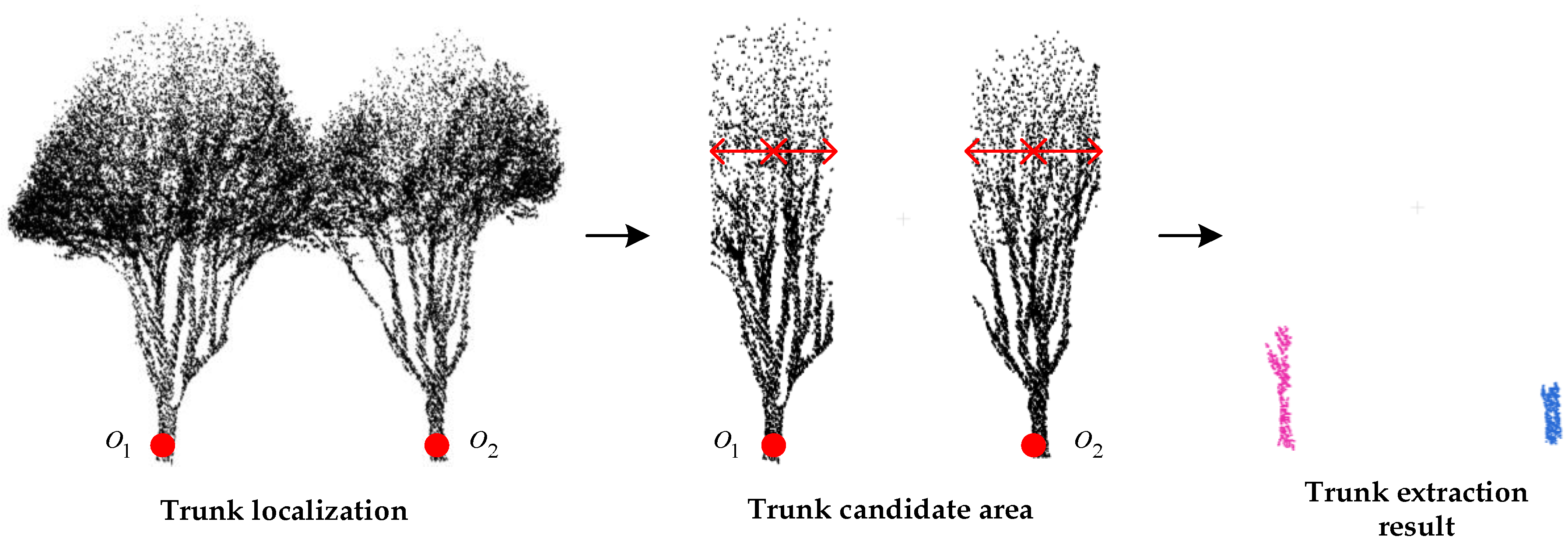
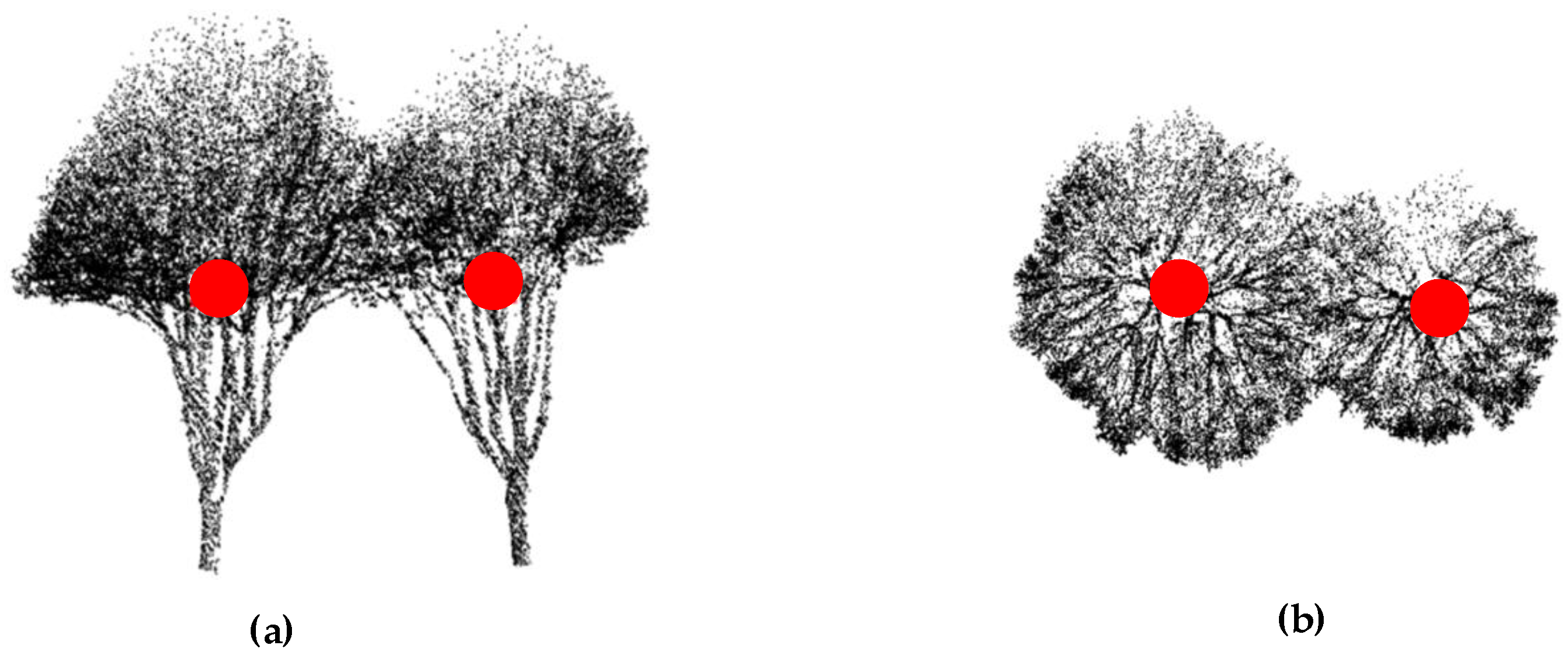
2.1.2. Tree Trunk Locating
2.1.3. Trunks Extracted by Region Growing
- (1)
- For a trunk , take as its center and expand the range of in the horizontal direction to construct the trunk candidate region. The radius of the candidate region is () times the trunk’s radius . Therefore, for all tree points , if the horizontal distance from to satisfies , then is added to the candidate region , and is calculated via Equation (9):
- (2)
- The eigenvalue and eigenvector of the point in are obtained from the PCA and represents the normal vector. The curvature is calculated by Equation (10), and the curvature is sorted in ascending order.
- (3)
- We create an empty sequence of seed points and an empty cluster , and then select the point with the smallest curvature from and place it in set .
- (4)
- Take the first seed point from and search for its neighboring points. If the angle between the normal vector of the neighborhood point and the normal vector of the seed point is less than the smooth threshold , the current point is added to the , and then we judge whether the curvature of the neighboring points is less than the curvature threshold . If it is lower, it will be added to until all neighborhood points are processed.
- (5)
- Delete the first seed point from and repeat step (4). Cluster is segmented when is empty.
- (6)
- Select the first unsegmented point from the sorted curvature data to act as the seed point, and then repeat the above steps until all the points are segmented, to derive cluster . In this way, the extraction of complete tree trunks in the trunk candidate region is obtained.
2.2. Individual Tree Extraction
2.2.1. Tree Crown Center Calculation
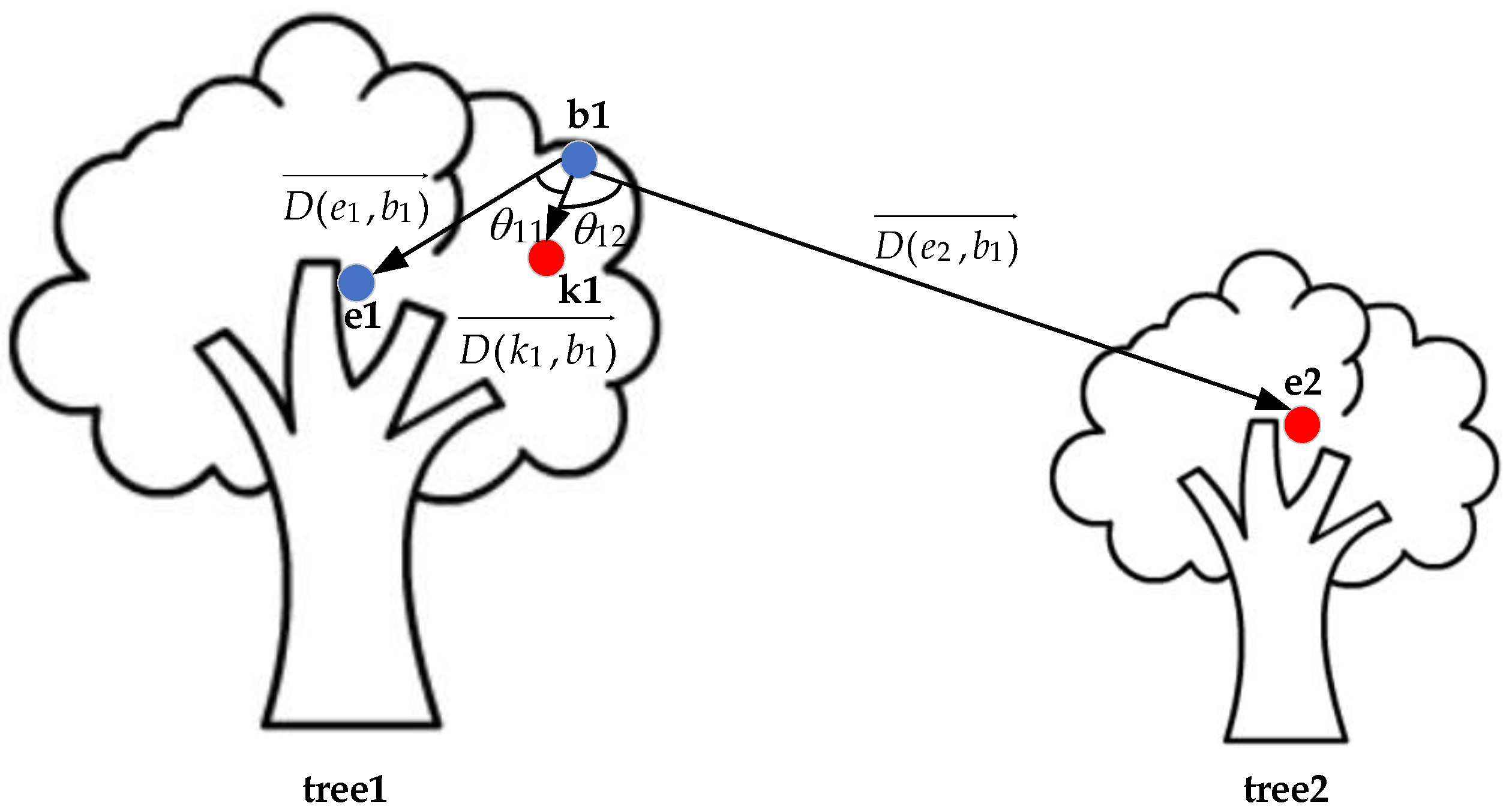
2.2.2. Individual Tree Extraction by Distance Difference and Centroid Deflection Angle
- (1)
- The set of unsegmented points is , and is the number of unsegmented points. The spatial distance from point to each crown center is achieved according to Equation (11). All distances are sorted in ascending order—the minimum distance is , the sub minimum distance is , and the corresponding crown centers are and .
- (2)
- The distance difference is . If , assign to the tree with . If , add to the remaining unsegmented point set . is the number of remaining unsegmented points. Repeat steps (1) and (2) for all points in set , and obtain the segmentation results of all core points.
- (3)
- For , the neighborhood points are obtained using the search radius . If the number of neighborhood points is less than , the point is added to the boundary point set , and then the centroids of the boundary points are calculated from the neighborhood points. The centroids set is defined as , where is the number of centroids.
- (4)
- The vector , and . The angle of and is computed according to Equations (12) and (13).Here, and are the moduli of vectors and . The radian value is converted to an angle value via Equation (13).Then the vector and the angle of and is also estimated. If , assign to the tree with , otherwise assign to the tree with , and repeat step 4) until all boundary points are segmented.
- (5)
- The intermediate point set is obtained by deleting the core points and boundary points, and the distance from to is calculated by step 1). The distance from to , and the angles between and and between and are determinedrespectively based on 4). Normalize the distance and angle using Equations (14) and (15).
3. Results
3.1. Paris-Lille-3D Dataset
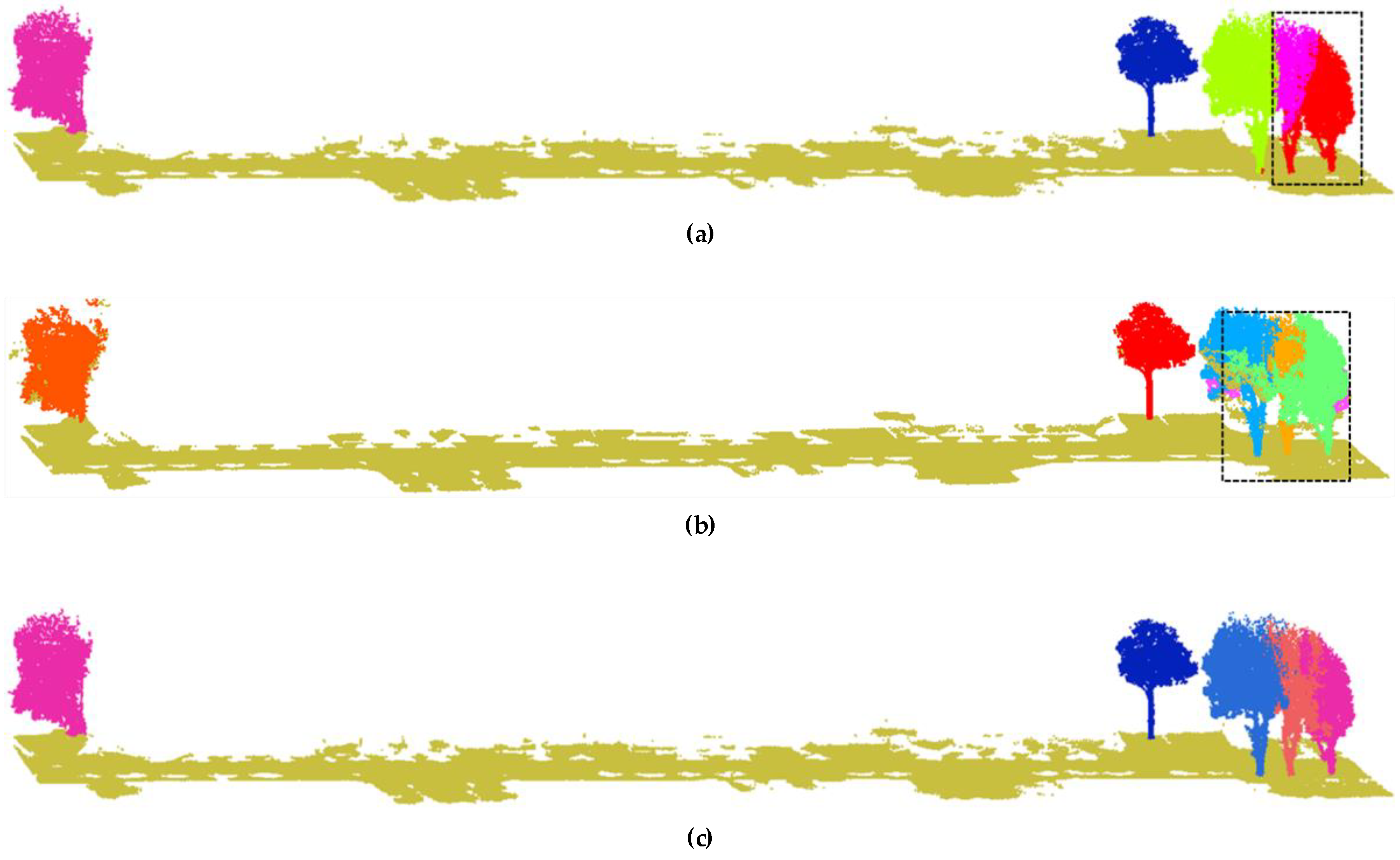
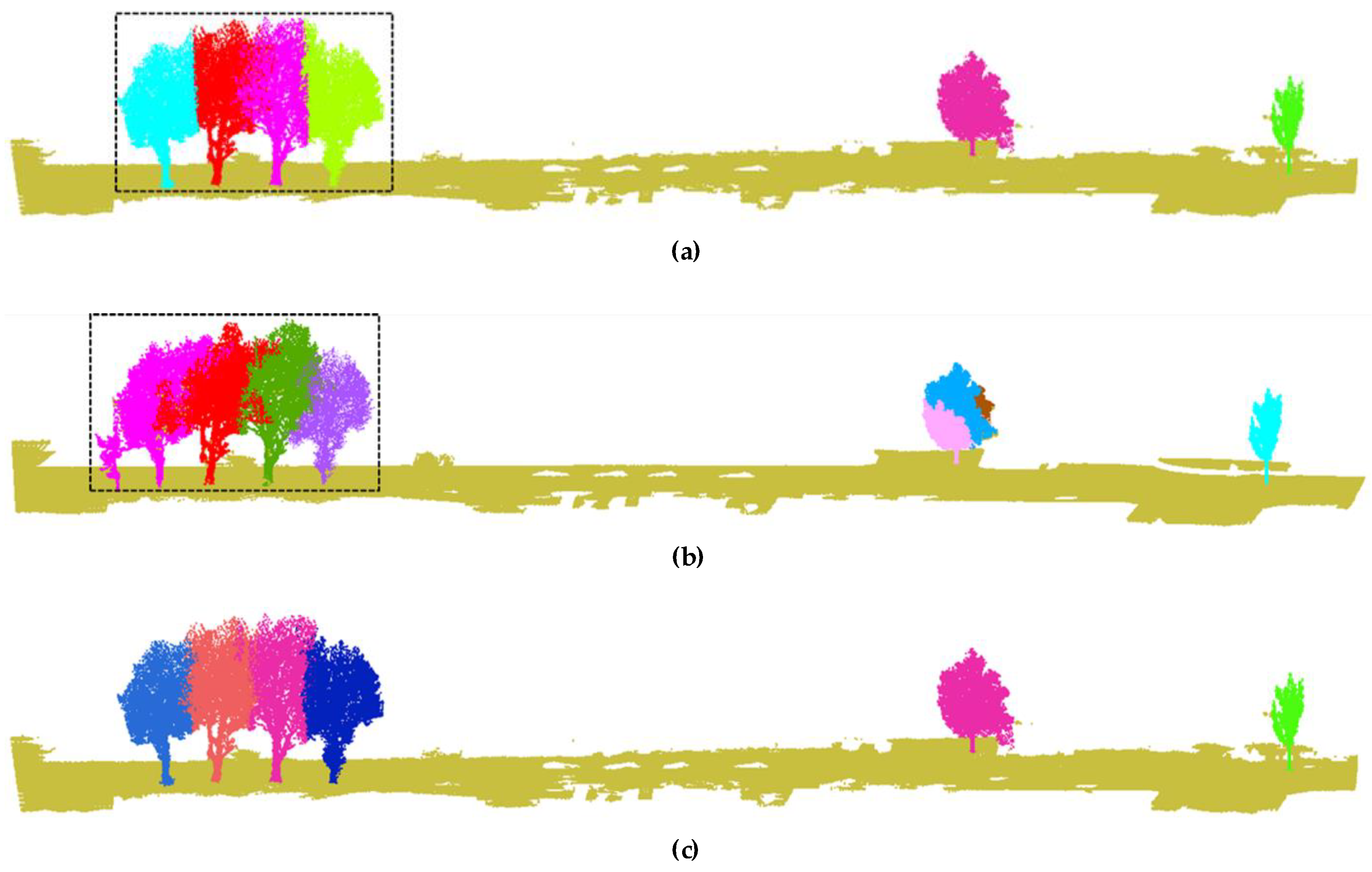
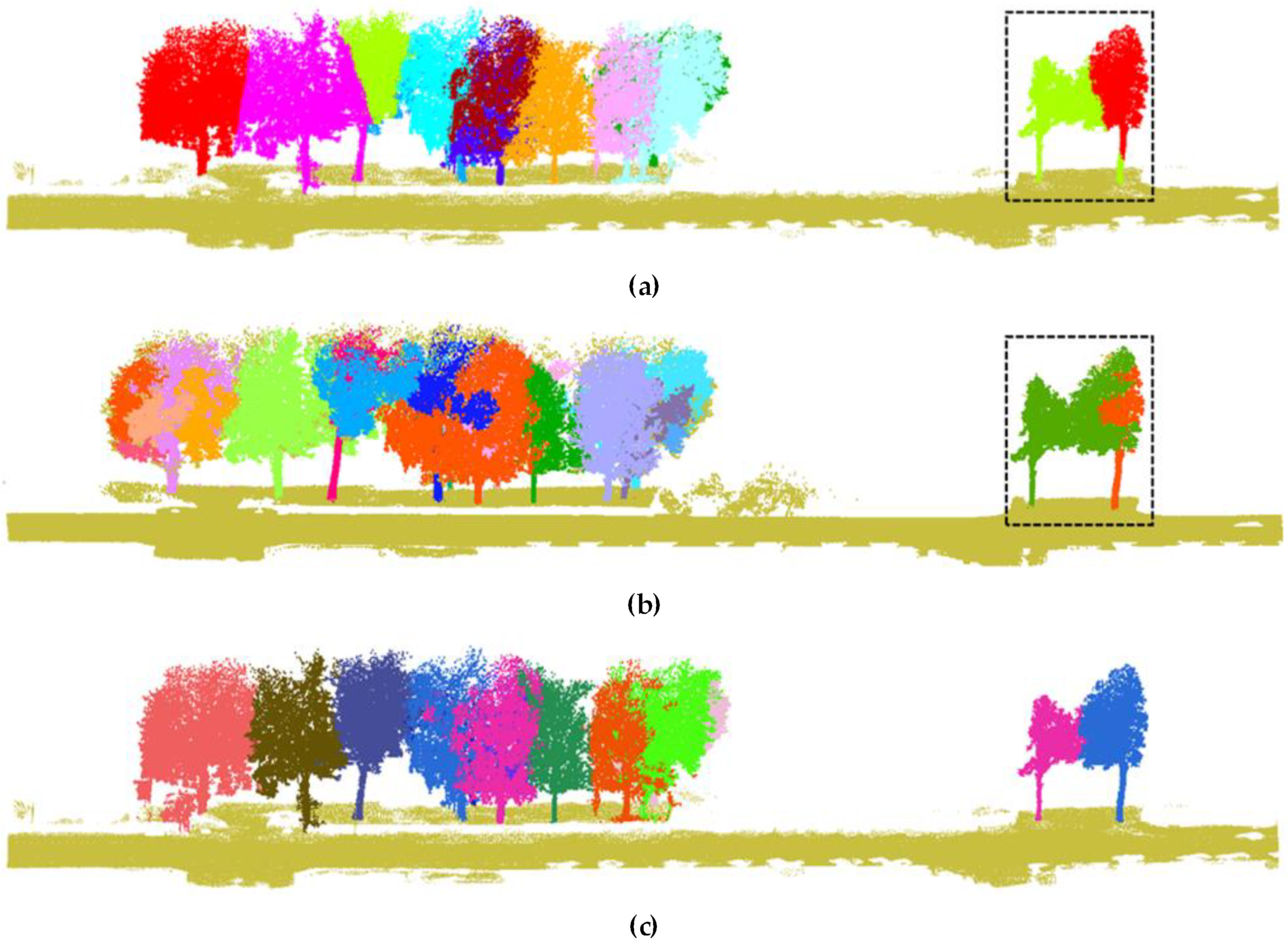
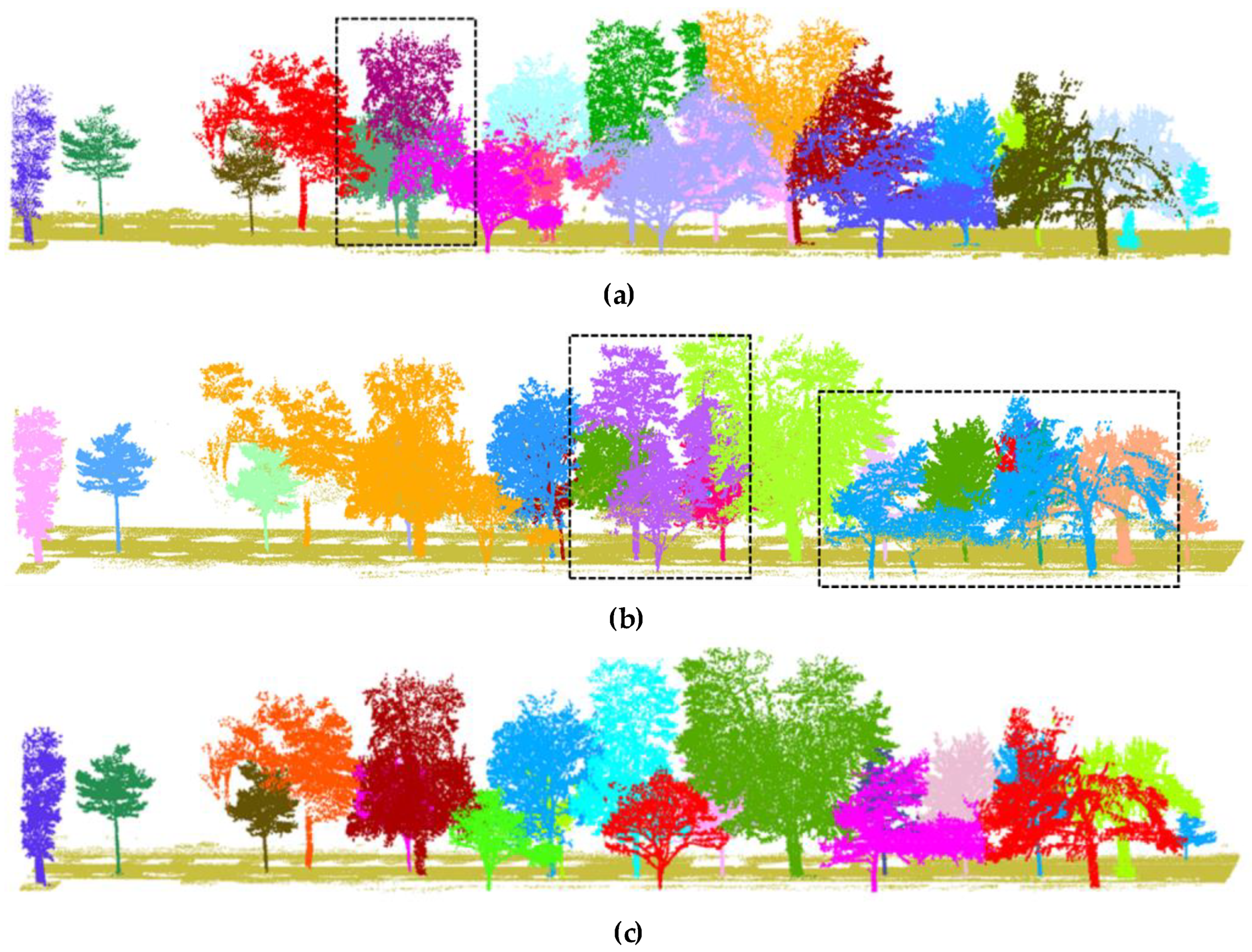
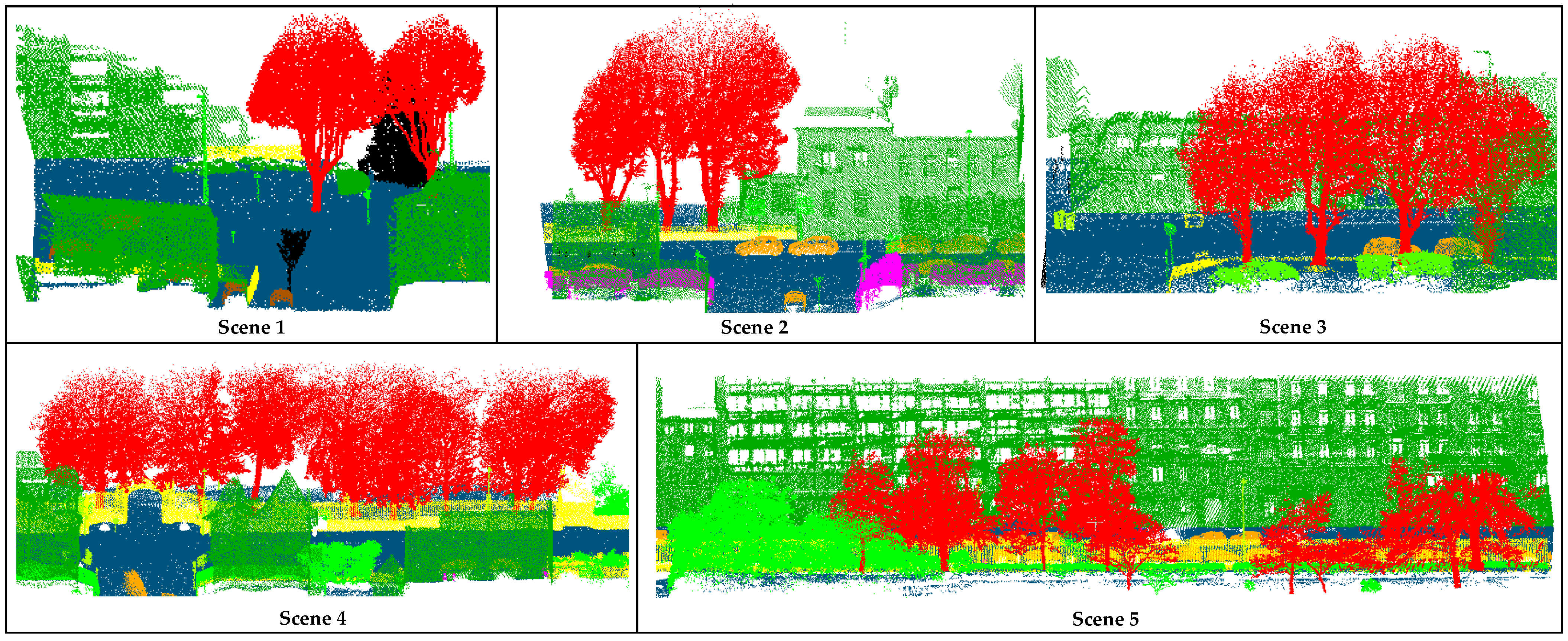
3.2. Analysis of Individual Tree Extraction Results
3.3. Comparative Analysis of Experimental Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Williams, J.; Schonlieb, C.-B.; Swinfield, T.; Lee, J.; Cai, X.; Qie, L.; Coomes, D.A. 3D Segmentation of Trees through a Flexible Multiclass Graph Cut Algorithm. IEEE Trans. Geosci. Remote Sens. 2020, 58, 754–776. [Google Scholar] [CrossRef]
- Corada, K.; Woodward, H.; Alaraj, H.; Collins, C.M.; de Nazelle, A. A systematic review of the leaf traits considered to contribute to removal of airborne particulate matter pollution in urban areas. Environ. Pollut. 2021, 269, 116104. [Google Scholar] [CrossRef]
- Liu, J.; Skidmore, A.K.; Wang, T.; Zhu, X.; Premier, J.; Heurich, M.; Beudert, B.; Jones, S. Variation of leaf angle distribution quantified by terrestrial LiDAR in natural European beech forest. ISPRS J. Photogramm. Remote Sens. 2019, 148, 208–220. [Google Scholar] [CrossRef]
- Zhao, Y.; Hu, Q.; Li, H.; Wang, S.; Ai, M. Evaluating carbon sequestration and PM2.5 removal of urban street trees using mobile laser scanning data. Remote Sens. 2018, 10, 1759. [Google Scholar] [CrossRef]
- Yadav, M.; Lohani, B. Identification of trees and their trunks from mobile laser scanning data of roadway scenes. Int. J. Remote Sens. 2019, 41, 1233–1258. [Google Scholar] [CrossRef]
- Du, S.; Lindenbergh, R.; Ledoux, H.; Stoter, J.; Nan, L. AdTree: Accurate, Detailed, and Automatic Modelling of Laser-Scanned Trees. Remote Sens. 2019, 11, 2074. [Google Scholar] [CrossRef]
- Luo, Z.; Zhang, Z.; Li, W.; Chen, Y.; Wang, C.; Nurunnabi, A.A.M.; Li, J. Detection of individual trees in UAV LiDAR point clouds using a deep learning framework based on multichannel representation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Wu, B.; Yu, B.; Yue, W.; Shu, S.; Tan, W.; Hu, C.; Huang, Y.; Wu, J.; Liu, H. A Voxel-Based Method for Automated Identification and Morphological Parameters Estimation of Individual Street Trees from Mobile Laser Scanning Data. Remote Sens. 2013, 5, 584–611. [Google Scholar] [CrossRef]
- Holopainen, M.; Vastaranta, M.; Kankare, V.; Räty, M.; Vaaja, M.; Liang, X.; Yu, X.; Hyyppä, J.; Hyyppä, H.; Viitala, R.; et al. Biomass estimation of individual trees using stem and crown diameter tls measurements. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, XXXVIII-5, 91–95. [Google Scholar] [CrossRef]
- Huo, L.; Lindberg, E.; Holmgren, J. Towards low vegetation identification: A new method for tree crown segmentation from LiDAR data based on a symmetrical structure detection algorithm (SSD). Remote Sens. Environ. 2022, 270, 112857. [Google Scholar] [CrossRef]
- Hu, T.; Wei, D.; Su, Y.; Wang, X.; Zhang, J.; Sun, X.; Liu, Y.; Guo, Q. Quantifying the shape of urban street trees and evaluating its influence on their aesthetic functions based on mobile lidar data. ISPRS J. Photogramm. Remote Sens. 2022, 184, 203–214. [Google Scholar] [CrossRef]
- Ning, X.J.; Tian, G.; Wang, Y.H. Shape classification guided method for automated extraction of urban trees from terrestrial laser scanning point clouds. Multimed. Tools Appl. 2021, 80, 33357–33375. [Google Scholar] [CrossRef]
- Kuželka, K.; Slavík, M.; Surový, P. Very High Density Point Clouds from UAV Laser Scanning for Automatic Tree Stem Detection and Direct Diameter Measurement. Remote Sens. 2020, 12, 1236. [Google Scholar] [CrossRef]
- Windrim, L.; Bryson, M. Detection, Segmentation, and Model Fitting of Individual Tree Stems from Airborne Laser Scanning of Forests Using Deep Learning. Remote Sens. 2020, 12, 1469. [Google Scholar] [CrossRef]
- Zhang, W.; Wan, P.; Wang, T.; Cai, S.; Chen, Y.; Jin, X.; Yan, G. A Novel Approach for the Detection of Standing Tree Stems from Plot-Level Terrestrial Laser Scanning Data. Remote Sens. 2019, 11, 211. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, R.; Yang, C.; Lin, Y. Urban vegetation segmentation using terrestrial LiDAR point clouds based on point non-local means network. Int. J. Appl. Earth Obs. Geoinf. 2021, 105, 102580. [Google Scholar] [CrossRef]
- Brolly, G.; Király, G.; Lehtomäki, M.; Liang, X. Voxel-Based Automatic Tree Detection and Parameter Retrieval from Terrestrial Laser Scans for Plot-Wise Forest Inventory. Remote Sens. 2021, 13, 542. [Google Scholar] [CrossRef]
- Kolendo, Ł.; Kozniewski, M.; Ksepko, M.; Chmur, S.; Neroj, B. Parameterization of the Individual Tree Detection Method Using Large Dataset from Ground Sample Plots and Airborne Laser Scanning for Stands Inventory in Coniferous Forest. Remote Sens. 2021, 13, 2753. [Google Scholar] [CrossRef]
- Gollob, C.; Ritter, T.; Wassermann, C.; Nothdurft, A. Influence of Scanner Position and Plot Size on the Accuracy of Tree Detection and Diameter Estimation Using Terrestrial Laser Scanning on Forest Inventory Plots. Remote Sens. 2019, 11, 1602. [Google Scholar] [CrossRef]
- Cabo, C.; Ordóñez, C.; López-Sánchez, C.A.; Armesto, J. Automatic dendrometry: Tree detection, tree height and diameter estimation using terrestrial laser scanning. Int. J. Appl. Earth Obs. Geoinf. 2018, 69, 164–174. [Google Scholar] [CrossRef]
- Oveland, I.; Hauglin, M.; Giannetti, F.; Kjørsvik, N.S.; Gobakken, T. Comparing Three Different Ground Based Laser Scanning Methods for Tree Stem Detection. Remote Sens. 2018, 10, 538. [Google Scholar] [CrossRef]
- Lv, Z.; Li, G.; Jin, Z.; Benediktsson, J.A.; Foody, G.M. Iterative Training Sample Expansion to Increase and Balance the Accuracy of Land Classification from VHR Imagery. IEEE Trans. Geosci. Remote Sens. 2021, 59, 139–150. [Google Scholar] [CrossRef]
- Lv, Z.; Wang, F.; Cui, G.; Benediktsson, J.A.; Lei, T.; Sun, W. Spatial–Spectral Attention Network Guided with Change Magnitude Image for Land Cover Change Detection Using Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Dong, T.; Zhang, X.; Ding, Z.; Fan, J. Multilayered tree crown extraction from LiDAR data using graphbased segmentation. Comput. Electron. Agric. 2020, 170, 105213. [Google Scholar] [CrossRef]
- Fan, W.; Yang, B.; Liang, F.; Dong, Z. Using mobile laser scanning point clouds to extract urban roadside trees for ecological benefits estimation. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 43, 211–216. [Google Scholar] [CrossRef]
- Fan, W.; Yang, B.; Dong, Z.; Liang, F.; Xiao, J.; Li, F. Confidence-guided roadside individual tree extraction for ecological benefit estimation. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102368. [Google Scholar] [CrossRef]
- Husain, A.; Vaishya, R.C. An automated approach for street trees detection using mobile laser scanner data. Remote Sens. Appl. Soc. Environ. 2020, 20, 100371. [Google Scholar] [CrossRef]
- Li, L.; Li, D.; Zhu, H.; Li, Y. A dual growing method for the automatic extraction of individual trees from mobile laser scanning data. ISPRS J. Photogramm. Remote Sens. 2016, 120, 37–52. [Google Scholar] [CrossRef]
- Luo, H.; Khoshelham, K.; Chen, C.; He, H. Individual tree extraction from urban mobile laser scanning point clouds using deep pointwise direction embedding. ISPRS J. Photogramm. Remote Sens. 2021, 175, 326–339. [Google Scholar] [CrossRef]
- Trochta, J.; Krůček, M.; Vrška, T.; Král, K. 3D Forest: An application for descriptions of three-dimensional forest structures using terrestrial LiDAR. PLoS ONE 2017, 12, e0176871. [Google Scholar] [CrossRef]
- Li, J.T.; Cheng, X.J.; Xiao, Z.H. A branch-trunk-constrained hierarchical clustering method for street trees individual extraction from mobile laser scanning point clouds. Measurement 2022, 189, 110440. [Google Scholar] [CrossRef]
- Ning, X.J.; Tian, G.; Wang, Y.H. Top-Down Approach to the Automatic Extraction of Individual Trees from Scanned Scene Point Cloud Data. Adv. Electr. Comput. Eng. 2019, 19, 11–18. [Google Scholar] [CrossRef]
- Chen, X.; Wu, H.; Lichti, D.; Han, X.; Ban, Y.; Li, P.; Deng, H. Extraction of indoor objects based on the exponential function density clustering model. Inf. Sci. 2022, 607, 1111–1135. [Google Scholar] [CrossRef]
- Yang, J.; Kang, Z.; Cheng, S.; Yang, Z.; Akwensi, P.H. An individual tree segmentation method based on watershed algorithm and three-dimensional spatial distribution analysis from airborne LiDAR point clouds. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 1055–1067. [Google Scholar] [CrossRef]
- Yan, W.; Guan, H.; Cao, L.; Yu, Y.; Li, C.; Lu, J. A self-adaptive mean shift tree-segmentation method using UAV LiDAR data. Remote Sens. 2020, 12, 515. [Google Scholar] [CrossRef]
- Dai, W.; Yang, B.; Dong, Z.; Shaker, A. A new method for 3D individual tree extraction using multispectral airborne LiDAR point clouds. ISPRS J. Photogramm. Remote Sens. 2018, 144, 400–411. [Google Scholar] [CrossRef]
- Yun, T.; Jiang, K.; Li, G.; Eichhorn, M.P.; Fan, J.; Liu, F.; Chen, B.; An, F.; Cao, L. Individual tree crown segmentation from airborne LiDAR data using a novel Gaussian filter and energy function minimization-based approach. Remote Sens. Environ. 2021, 256, 112307. [Google Scholar] [CrossRef]
- Dersch, S.; Heurich, M.; Krueger, N.; Krzystek, P. Combining graph-cut clustering with object-based stem detection for tree segmentation in highly dense airborne lidar point clouds. ISPRS J. Photogramm. Remote Sens. 2021, 172, 207–222. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, T.; Liu, J.; Li, X.; Liang, C. Hierarchical instance recognition of individual roadside trees in environmentally complex urban areas from UAV laser scanning point clouds. ISPRS Int. J. GeoInf. 2020, 9, 595. [Google Scholar] [CrossRef]
- Yang, W.; Liu, Y.; He, H.; Lin, H.; Qiu, G.; Guo, L. Airborne LiDAR and photogrammetric point cloud fusion for extraction of urban tree metrics according to street network segmentation. IEEE Access 2021, 9, 97834–97842. [Google Scholar] [CrossRef]
- Tusa, E.; Monnet, J.M.; Barré, J.B.; Mura, M.D.; Dalponte, M.; Chanussot, J. Individual Tree Segmentation Based on Mean Shift and Crown Shape Model for Temperate Forest. IEEE Geosci. Remote Sens. Lett. 2021, 18(12), 2052–2056. [Google Scholar] [CrossRef]
- Ning, X.; Ma, Y.; Hou, Y.; Lv, Z.; Jin, H.; Wang, Y. Semantic Segmentation Guided Coarse-to-Fine Detection of Individual Trees from MLS Point Clouds Based on Treetop Points Extraction and Radius Expansion. Remote Sens. 2022, 14, 4926. [Google Scholar] [CrossRef]
- Roynard, X.; Deschaud, J.E.; Goulette, F. Paris-Lille-3D: A large and high-quality ground-truth urban point cloud dataset for automatic segmentation and classification. Int. J. Robot. Res. 2018, 37, 545–557. [Google Scholar] [CrossRef]
- Xu, S.; Ye, N.; Xu, S.; Zhu, F. A supervoxel approach to the segmentation of individual trees from LiDAR point clouds. Remote Sens. Lett. 2018, 9, 515–523. [Google Scholar] [CrossRef]







| Scene | |||||
|---|---|---|---|---|---|
| Scene1 | 1.8 | 3.0 | 1800 | 0.8 | 0.2 |
| Scene2 | 1.8 | 3.0 | 1800 | 0.8 | 0.2 |
| Scene3 | 1.8 | 3.0 | 1800 | 0.8 | 0.2 |
| Scene4 | 2.0 | 3.0 | 1800 | 0.8 | 0.2 |
| Scene4 | 1.8 | 3.0 | 1800 | 0.8 | 0.2 |
| Scene5 | 2.5 | 4.0 | 10,000 | 0.7 | 0.3 |
| Scene5 | 2.5 | 2.0 | 400 | 0.9 | 0.1 |
| Scene | Method | ||||||
|---|---|---|---|---|---|---|---|
| Scene 2 | Clustering method [44] | 3 | 2 | 2 | 0.6000 | 0.6000 | 0.6000 |
| 3D Forest [30] | 5 | 0 | 2 | 0.7143 | 1 | 0.8333 | |
| Ours | 5 | 0 | 0 | 1 | 1 | 1 | |
| Scene 3 | Clustering method [44] | 6 | 0 | 0 | 1 | 1 | 1 |
| 3D Forest [30] | 5 | 1 | 3 | 0.6250 | 0.8333 | 0.7143 | |
| Ours | 6 | 0 | 0 | 1 | 1 | 1 | |
| Scene 4 | Clustering method [44] | 11 | 3 | 8 | 0.5789 | 0.7857 | 0.6666 |
| 3D Forest [30] | 5 | 9 | 9 | 0.3571 | 0.3571 | 0.3571 | |
| Ours | 13 | 1 | 0 | 1 | 0.9286 | 0.9630 | |
| Scene 5 | Clustering method [44] | 12 | 8 | 8 | 0.6000 | 0.6000 | 0.6000 |
| 3D Forest [30] | 12 | 8 | 8 | 0.6000 | 0.6000 | 0.6000 | |
| Ours | 20 | 0 | 0 | 0.6000 | 1 | 1 | |
| Average | Clustering method [44] | - | - | - | 0.6947 | 0.7464 | 0.7167 |
| 3D Forest [30] | - | - | - | 0.5741 | 0.7976 | 0.6262 | |
| Ours | - | - | - | 0.9000 | 0.9822 | 0.9908 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ning, X.; Ma, Y.; Hou, Y.; Lv, Z.; Jin, H.; Wang, Z.; Wang, Y. Trunk-Constrained and Tree Structure Analysis Method for Individual Tree Extraction from Scanned Outdoor Scenes. Remote Sens. 2023, 15, 1567. https://doi.org/10.3390/rs15061567
Ning X, Ma Y, Hou Y, Lv Z, Jin H, Wang Z, Wang Y. Trunk-Constrained and Tree Structure Analysis Method for Individual Tree Extraction from Scanned Outdoor Scenes. Remote Sensing. 2023; 15(6):1567. https://doi.org/10.3390/rs15061567
Chicago/Turabian StyleNing, Xiaojuan, Yishu Ma, Yuanyuan Hou, Zhiyong Lv, Haiyan Jin, Zengbo Wang, and Yinghui Wang. 2023. "Trunk-Constrained and Tree Structure Analysis Method for Individual Tree Extraction from Scanned Outdoor Scenes" Remote Sensing 15, no. 6: 1567. https://doi.org/10.3390/rs15061567
APA StyleNing, X., Ma, Y., Hou, Y., Lv, Z., Jin, H., Wang, Z., & Wang, Y. (2023). Trunk-Constrained and Tree Structure Analysis Method for Individual Tree Extraction from Scanned Outdoor Scenes. Remote Sensing, 15(6), 1567. https://doi.org/10.3390/rs15061567