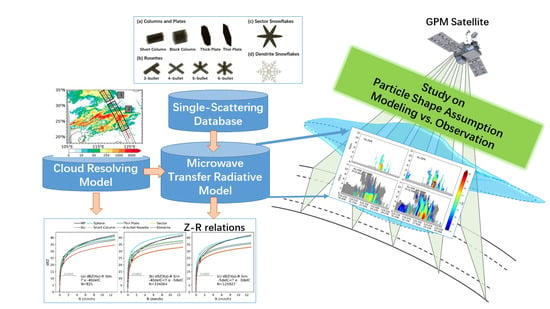
Impacts of Shape Assumptions on Z–R Relationship and Satellite Remote Sensing Clouds Based on Model Simulations and GPM Observations

Abstract

In this study, the spherical particle model and ten nonspherical particle models describing the scattering properties of snow are evaluated for potential use in precipitation estimation from spaceborne dual-frequency precipitation radar. The single scattering properties of nonspherical snow particles are computed using discrete dipole approximation (DDA), while those of spherical particles are determined using Mie theory. The precipitation profiles from WRF output are then input to a forward radiative transfer model to simulate the radar reflectivity at Ka-band and Ku-band. The results are validated with Global Precipitation Mission Dual-Frequency Precipitation Radar measurements. Greater consistency between the simulated and observed reflectivity is obtained when using the sector- and dendrite-shape assumptions. For the case in this study, when using the spherical-shape assumption, radar underestimates the error of the cloud’s top by about 300 m and underestimates the error of the cloud’s area by about 15%. As snowflake shapes change with temperature, we use the range between −40 °C and −5 °C to define three temperature layers. The relationships between reflectivity (Z) and precipitation rate (R) are fitted separately for the three layers, resulting in $\mathrm{Z}=134.59·{\mathrm{R}}^{1.184}$ (sector) and $\mathrm{Z}=127.35·{\mathrm{R}}^{1.221}$ (dendrite) below −40 °C.

1. Introduction

Precipitation is one of the most crucial processes in the global water cycle and energy balance, not only because water is a fundamental need for all life around the world but also because significant energy will be released to the atmosphere accompanied by the phase-changing process at different altitudes from the surface to the cloud top [1,2,3]. Such energy, ending up as latent heat (LH), is the primary driving source of atmospheric circulation and acts to transfer a significant proportion (about 23%, [1]) of solar energy to atmospheric kinetic energy. Therefore, knowing the vertical distribution of precipitation rates is essential to understand the thermodynamics inside storms.

To measure the vertical structure of precipitation at a global scale, a satellite precipitation radar device was sent to space in 1997. The Tropical Rainfall Measuring Mission [4,5,6] and the Global Precipitation Mission [7,8,9] are the only two in history that carried single- and dual-frequency precipitation radar (hereafter DPR) working at 13.6 GHz and 35.5 GHz to directly measure the backscattering echo from precipitating particles at a vertical resolution of 250 m and 125 m, respectively. Many formulas describing the radar reflectivity–precipitation rate (hereafter Z–R relationship) have been published to retrieve precipitation rates from the radar measurements.

A challenging task in Z–R relationship parameterization is treating solid phase particles. Traditionally, the spherical-shape assumption was used to calculate the optical properties, including the attenuation coefficient, scattering coefficient, and phase function, based on Mie theory [10,11]. However, it is known that solid particles such as cloud ice, snow, and graupels in the real atmosphere are not spherical. Instead, their shapes can be complicated both as single crystals and as aggregates. Many studies have been published to show the nonspherical effects in the microwave spectral region [12,13,14,15,16,17,18]. Some studies have applications in precipitation radar retrieval [19,20].

Will treating particles as nonspherical necessarily be better than using the sphere assumption? The answer may not be as simple as expected. Since each radar bin contains many particles with different shapes in different size distributions, the measurement of radar reflectivity is a synergetic effort that involves accounting for backscattered energy from different shapes at different scattering angles. Moreover, the shape of solid phase particles depends on temperature [21,22,23]. For example, in temperatures colder than −40 °C, simple columns, plates, or plate-like polycrystal-shaped ice dominate in the atmosphere [24,25] due to the lack of water vapor [26]. In temperatures from −40 to −20 °C, particles grow by further deposition, aggregation, and collection and show much more complicated shapes, including bullet-rosette, dendrite, and ice aggregates [24,27,28,29]. With higher temperature, the ice phase particles partly melt, starting from the periphery, especially the corner of the particles. This results in liquid–solid mixed-phase particles with particular shapes, such as the water-coated ice ball shape [30,31,32]. Therefore, the parameterization of the shape of ice phase particles in radiative transfer calculation is complicated.

There are few validation studies of radiative transfer modeling of nonspherical effects in microwave regions from real satellite observations. Kulie et al. [33] simulated the brightness temperature between 6.9 GHz and 157 GHz for precipitation observed simultaneously by CloudSat’s Cloud Profiling Radar (CPR), the Advanced Microwave Scanning Radiometer for Earth Observing System (AMSR-E), and the Microwave Humidity Sounder (MHS). They found that a few ice particle models demonstrate low bias among 25 tested, especially the long hex column, sector snowflake, 3-bullet rosette, short hex column derived from Liu [13], and aggregate derived from Hong [34]. Leinonen et al. [35] and Kulie et al. [36] compared the observed reflectivity derived from the Wakasa Bay field campaign with the simulated reflectivity under different ice particle shape assumptions through the relationship between two dual-frequency ratios: ${\mathrm{DFR}}_{\mathrm{Ku}/\mathrm{Ka}}$ and ${\mathrm{DFR}}_{\mathrm{Ka}/\mathrm{W}}$. They found that nonspherical-shape assumptions effectively interpreted the observed data. Olson et al. [19] interpreted radar observations from the ER-2 airborne High-Altitude Imaging Wind and Rain Airborne Profiler (HIWRAP) and then simulated upwelling microwave radiances for channels in which the Conical Scanning Millimeter-Wave Imaging Radiometer (CosMIR) operates. They concluded that the nonspherical crystal/aggregate snow particle model limited the discrepancies between the simulated and observed CosMIR radiances at 89 and 165.5 GHz to less than 4 K, and the discrepancies were larger than 8 K when using homogeneous ice–air spheres.

In this study, we focus on simulations and satellite validations of radar reflectivity from solid-phase precipitating particles at Ku and Ka band, and we attempt to answer the following questions: (1) What are the performances of simulations using different shape assumptions and using GPM DPR observations as a reference? (2) What are the effects of the temperature-dependent shape assumption? (3) What are the associated retrieval biases in the Z–R relationship, precipitation top height, and rain area when using different shape assumptions?

The remainder of this paper is organized as follows. Section 2 introduces basic information on the precipitation case, as well as the setting of WRF and the microwave radiative transfer model. Section 3 details the analyzed results for the case, including the verification of the simulations, the fitted Z–R relationships, and the effect of shape assumptions on detectable errors of the case. Finally, Section 4 summarizes the method and the findings of this study.

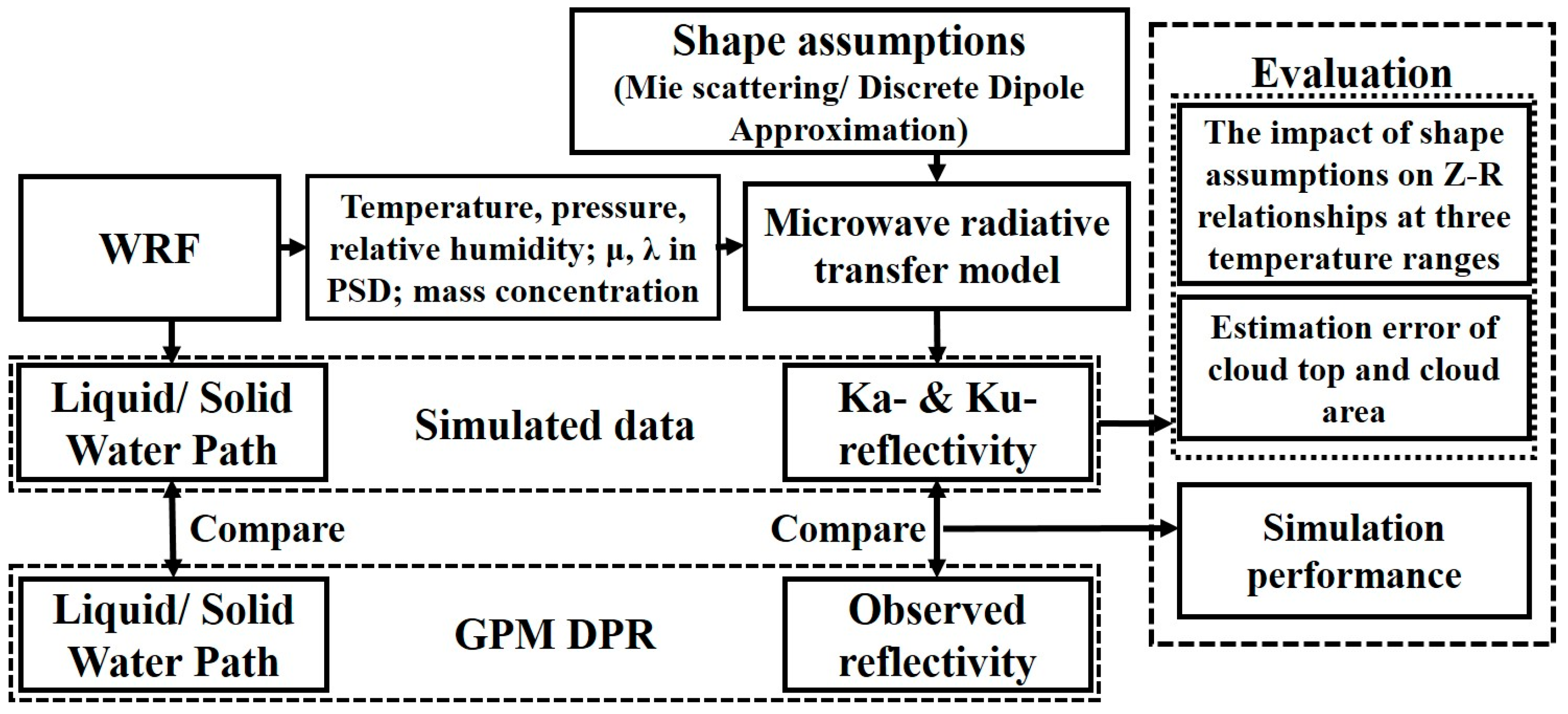
2. Data and Method

A snowfall event in East China at about 16:30 UTC on 6 January 2018 is used in this study. The flow chart of this study is shown in Figure 1. Given the lack of airborne radar observation data and the limited precision of radar observation, WRF output is utilized as an input for radiative transfer calculation, in which water content, the particle size distribution of five types of hydrometers (hereafter hydrometer profiles), and the atmospheric environment (temperature, pressure, and relative humidity) are needed. When calculating radar reflectivity for GPM DPR at Ka-band (35.5 GHz) and Ku-band (13.6 GHz), a sphere assumption, ten other nonspherical-shape assumptions, and a temperature-dependent shape assumption are considered. Then, by comparing the simulated reflectivity products and DPR observations, the accuracy of simulations and performances with different shape assumptions can be revealed. Beyond that, the associated retrieval bias in Z–R relationships, precipitation top height, and rain area are analyzed by combining the density of solid water simulated by WRF and reflectivity simulated by the radiative transfer model.

WRF V4.0 was used in this study. The model simulation used two nested domains, as shown in Figure 2. The inner and outer spatial resolutions were 4 km (convective permitting resolution) and 12 km, respectively. The cumulus parametrization scheme was turned on only for the outer domain. Other detailed simulation parameter settings are shown in

Table 1. Setting of the WRF simulation.

Domain ID	01	02
Lateral/initial data	CFSv2 $0.5°\times 0.5°$ 6 hourly
MP physics	Morrison
CU physics	Modified Tiedtke scheme	None
Boundary layer physics	Mellor–Yamada–Janjic TKE scheme
Surface layer physics	Monin–Obukhov (Janjic) scheme
Land surface physics	Unified Noah land-surface model
Longwave radiation physics	RRTMG scheme
Shortwave radiation physics	RRTMG scheme
Time step	60 s	20 s
Spatial resolution	12 km	4 km
Time range	1 January 2018–8 January 2018
Output interval	None	30 min
Feedback	False

. In the WRF output, the hydrometer profiles and the atmospheric environment were needed for radiative transfer simulations, while the hydrometer profiles are also used when analyzing Z–R relationships and cloud detection errors. To evaluate the results of the WRF simulation, the DPR products were compared with the precipitation water path (PrecipWP, includes snow, graupel, and rain), solid water path (SWP, includes snow and graupel), and liquid water path (LWP, includes rain). The reason why the water path is used instead of precipitation rate is that to compare the difference between solid and liquid water, only the water path distinguishes the phase among DPR products.

The radar simulator used in this study is the University of Science and Technology of China (USTC) Space-Borne Equivalent Radar Simulator (USERS) [37], which simulates the radiative transfer process of five hydrometers (cloud water, cloud ice, rain, snow, graupel) separately. To that end, it makes full use of the outputs of WRF that are given according to the type of hydrometer. During the simulation, all liquid water drops are assumed to be spherical, and their optical properties are calculated based on Mie theory. Solid-phase precipitating particles are assumed to have eleven shapes [13], including sphere, four of the five column/plate shapes designed in the model, four rosettes with different bullets, sector, and dendrite, as shown in Figure 3. Aggregations are also simulated. However, the simulated reflectivity is not closer to the observation than that under a single crystals shape assumption, and it is similar to that which short column performs (shown in Supplementary Materials). Considering aggregations may be a collection of different single crystals, we consider single crystals first. The optical characteristics of these shape assumptions were simulated using discrete dipole approximation (DDA) [38] and called using a lookup table mode in USERS.

In this study, the two parameters are set in WRF microphysical schemes as:

$$\mathrm{N}\left(D\right)={\mathrm{N}}_0{D}^{\mu }{\mathrm{e}}^{-\mathsf{\lambda }D}.$$

(1)

where D is the diameter, ${\mathrm{N}}_0$ (unit: 1/${\mathrm{m}}^4$), $\mathsf{\mu }$ and $\mathsf{\lambda }$ (unit: 1/m) are the intercept, spectral and slope parameter of the PSD. In Morrison microphysics scheme used in this study, $\mathsf{\mu }$ is specified and the slope parameter $\mathsf{\lambda }$ is calculated by:

$$\mathsf{\lambda }={\left[\frac{cN\Gamma \left(\mathsf{\mu }+\mathrm{d}+1\right)}{q\Gamma \left(\mathsf{\mu }+1\right)}\right]}^{1/d}.$$

(2)

Here, number density N (unit: 1/kg) and q (unit: kg/kg) are obtained from WRF directly, and $\mathrm{c}=\mathsf{\rho }\frac{\pi }{6}$ (kg/${\mathrm{m}}^3$) and d are two parameters.

In the assumed mass–diameter relationship $\mathrm{m}=\mathrm{c}{D}^d$, $\mathsf{\rho }\mathrm{s}$ (the density of the particles) are set to be 977, 977, 500, 100, and 900 $\mathrm{kg}/{\mathrm{m}}^3$ for cloud water, rain, cloud ice, snow, and graupe, respectively. The coefficients c and d are determined to be associated. Therefore, the mass-weighted diameter Dm = (μ + 2)/λ is determined.

To illustrate the accuracy of simulated radar reflectivity, it is compared with the GPM DPR product. Only the pixels identified as precipitation pixels by the DPR retrieval algorithm (in which the precipitation rate product of DPR is not the default value) are considered in this study, which means the signals are free from surface clutter and nonprecipitation noise. After excluding the influence of noise, the spatiotemporal assimilation of data needs to be considered. WRF simulated the atmospheric conditions at 16:30 UTC on 6 January 2018, while DPR observed the region from 16:24 UTC to 16:29 UTC (5100–5400 scan) during the day. However, this time difference is a tiny gap compared to the time scale of a mesoscale cloud system. Though any method will cause differences between simulated and observed signals (Sun and Fu, 2021), spatial assimilation is needed before comparing them. In the vertical direction, the linear interpolation method is used to interpolate the simulated radar reflectivity to the vertical resolution of DPR; this method uses 176 layers from the ground (0 km) to 22 km. In the horizontal direction, the closest simulated profile is used to present the DPR profile. Considering that, in reality, the solid particles in a cloud system exist in various shapes, we assume that the proportion of simple-shaped solid particles in the total solid particles is a function of temperature, and this proportion increases when temperature decreases.

Hydrometer profiles and simulated radar reflectivity are used to fit Z–R relationships for eleven shapes of snowflakes, which are later exploited to illustrate the effects of using theoretical Z–R relationships in the snowfall retrieval algorithm. The fundamental reason for the effect on the Z–R relationship of rain types and weather conditions is the difference in microphysical characteristics and microphysical processes, such as the phases of particles at different temperature layers [39]. Thus, in this study, −40 °C and −5 °C are used to distinguish three temperature layers in order to minimize the effect of these issues. This temperature-dependent approach differs from the DPR retrieval algorithm, which uses radar reflectivity as an index [4]. However, from a physical point of view, it is temperature and precipitation rate (R) that determine radar reflectivity, which means that using temperature as the index is more appropriate than using reflectivity.

3. Results

A single case at 16:30 UTC on 6 January 2018, in East China, was used in this study.

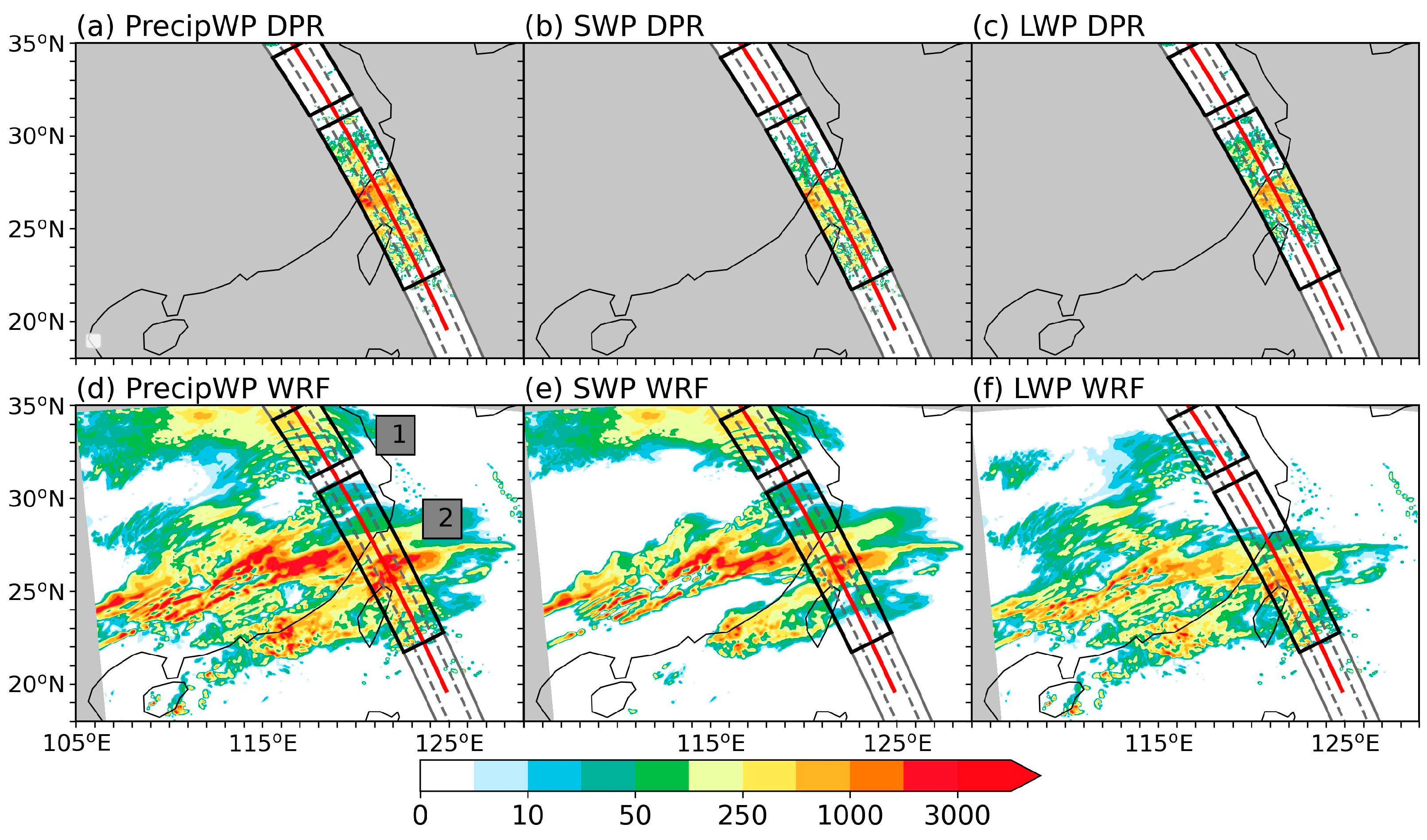
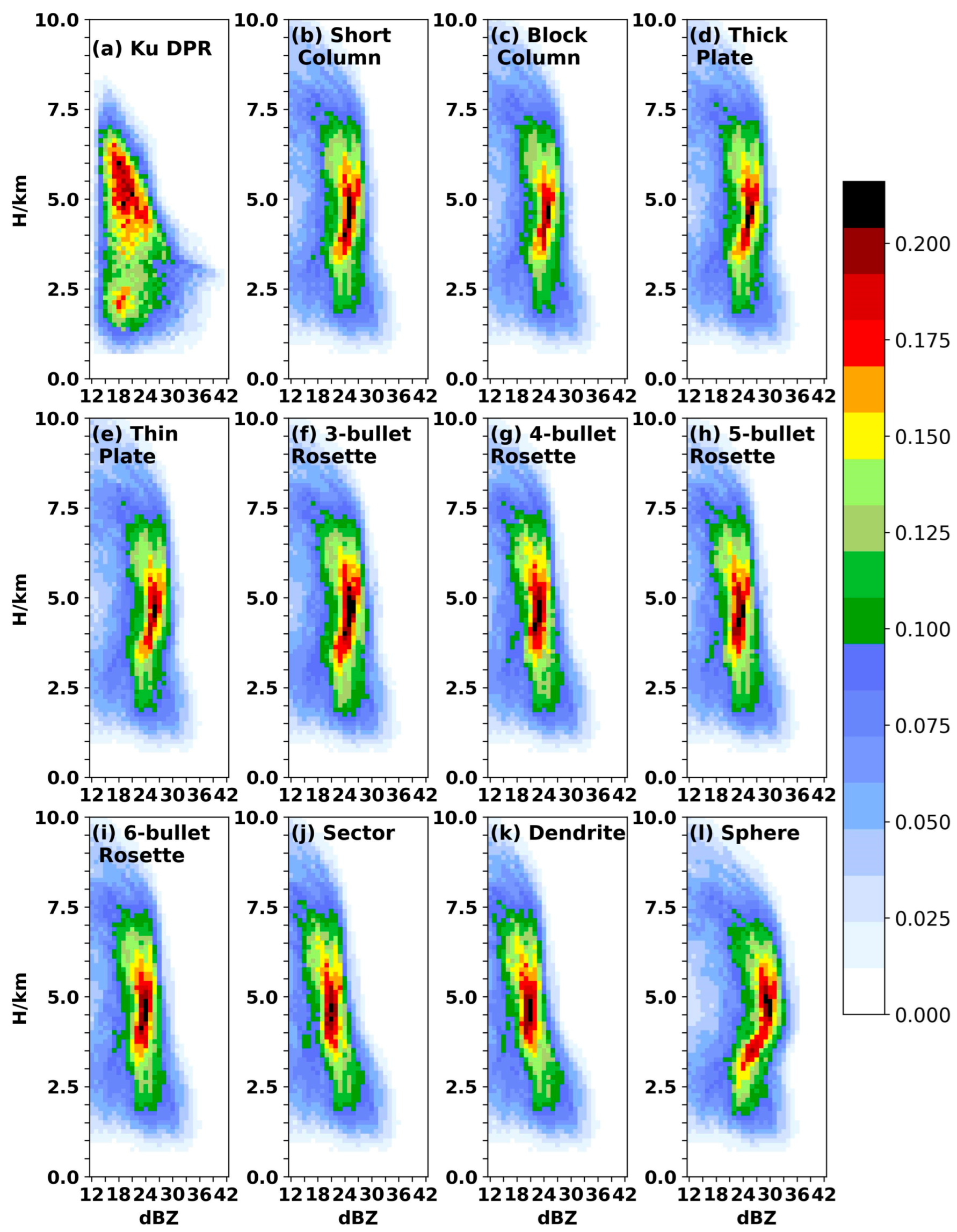
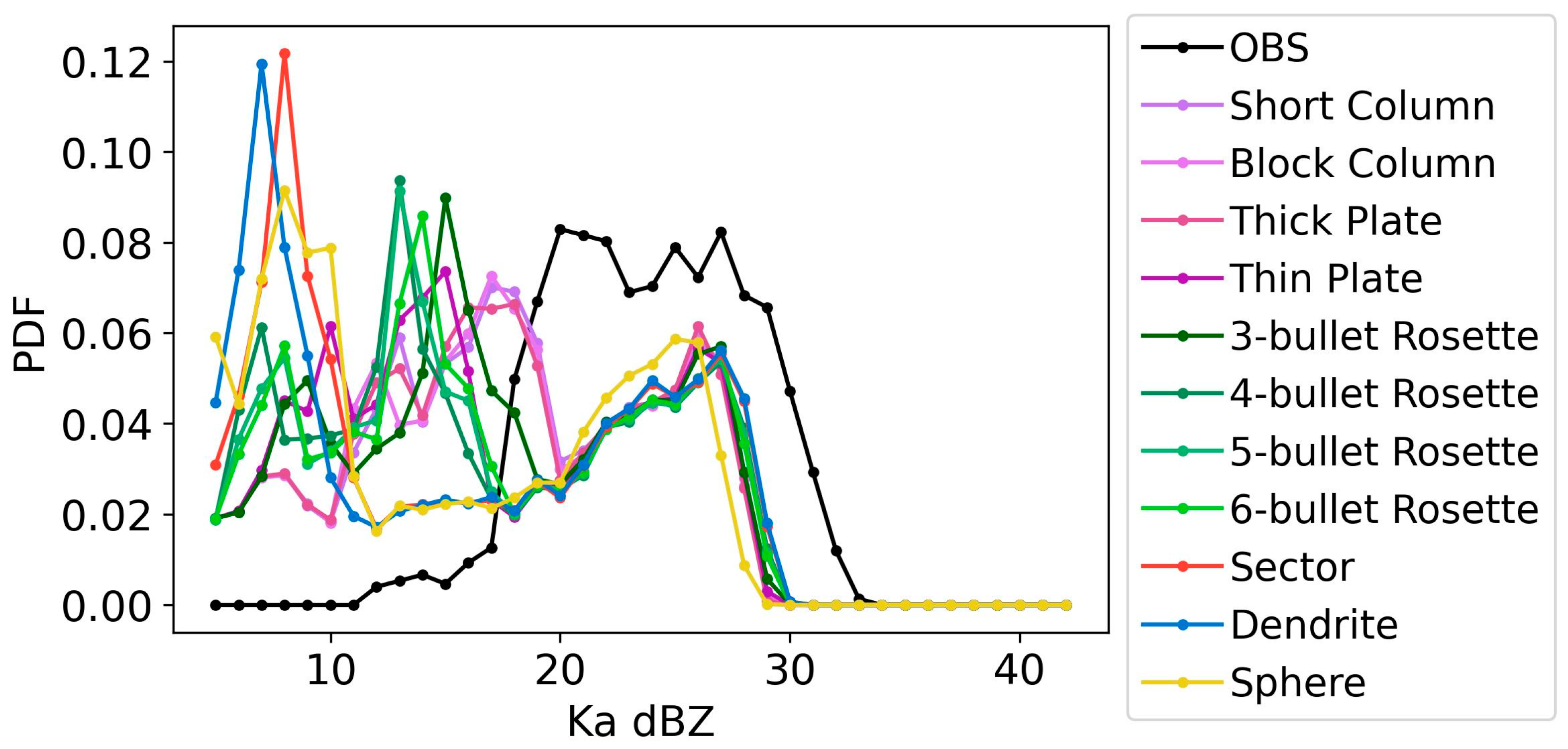
3.1. Correctness of Simulation

Figure 4d shows that WRF simulated two cloud systems, which we labeled cloud system 1 at (116E, 35N) and cloud system 2 at (121E, 26N). Cloud system 1 does not exist in the DPR product, which is mainly a snowfall system. However, the simulated position, horizontal distribution, LWP, and SWP for cloud system 2 are very consistent with the DPR observed values. Therefore, we focus on cloud system 2 when analyzing the consistency between simulated radar reflectivity and observed radar reflectivity (after spatiotemporal assimilation, only the data in the black box are used). Ground-based observations (dataset named Weather of Now at 17:00 UTC is used, which represents the weather phenomenon in the past one hour, as shown in Supplementary Materials Figure S1) illustrate that there was a large area of snow and rain near the simulated moment in this area. Note that the minima of detectable radar reflectivity are 5 dBZ (Ka, but about 17 dBZ in the inner swath) and 12 dBZ (Ku), which means weak precipitation is unobservable. Slight snowfall may be ignored in the DPR retrieval algorithm (mentioned later), so, understandably, LWP and SWP in the DPR product are slightly smaller than the simulation results of WRF. Furthermore, there are some differences between WRF simulation and reality due to the selection of boundary conditions and parameterization schemes, but this is not the focus of this experiment.

Figure 5 shows cross-sections of radar reflectivity along the red line in Figure 4. Similar cross-sections of reflectivity along the north gray dashed line are shown in the Supplementary Materials (Figure S2). It can be easily determined from Figure 5b that WRF simulates the shape of cloud system 2 well, although the height is slightly overestimated; the magnitude of simulated radar reflectivity and that of observed radar reflectivity is quite consistent. As mentioned before, cloud system 1 is dominated by snowfall, and cloud system 2 by snow at high altitudes and rain at low altitudes. Therefore, to compare the effects of shape assumption on radar reflectivity simulation, attention should be paid to the upper level of cloud system 2 and to cloud system 1. Comparing Figure 5b,f to Figure 5a,e, it is obvious that when using the spherical-shape assumption, the simulated radar reflectivity at Ka-band is close to the observed radar reflectivity, while the simulation and the observation are pretty different at Ku-band. When using the simple-shape assumptions (Figure 5d,h) for simulation, the situation is just the opposite. This means that the snow and cloud ice particles in the precipitation cloud are neither spheres nor simple shapes. However, when using the complex-shape assumption (Figure 5c,g), the simulated radar signal is similar to the observed signal in both Ku-band and Ka-band, which means snow and cloud ice particles in the real world are likely to exist in complex shapes. There is a significant feature of bright-band at about 4 km height observed by GPM DPR, as shown in Figure 5a,e. This is a strong indicator of a melting layer and the stratiform precipitation type (Houze 1997). It was found that different shape assumptions resulted in different simulation performances of this feature. The dendrite assumption led to a good simulation of clear bright-band, while simulations with the sphere assumption captured this characteristic but with a relatively weaker signature. In contrast, the short column assumption completely missed bright-band in the simulation.

The contoured frequency by altitude diagrams (CFADs) of Ka-band reflectivity observations and those of simulated reflectivity show that, compared to simple-shape assumptions (Figure 6b–i), the complex-shape assumptions (Figure 6j,k) or sphere assumption (Figure 6l) being the CFADs of reflectivity simulation closer to those of observations. More specifically, the maximum reflectivity of CFAD (Figure 6a) changes with height as follows: the maximum reflectivity value increases smoothly from ~6 km to ~3 km, and increases sharply between ~3 km and ~2.5 km, then decreases slightly toward lower levels. A similar trend can be seen in the CFADs of reflectivity simulation under the sphere assumption and complex-shape assumptions. Nevertheless, such a trend cannot be seen in simulation under the simple-shape assumption.

As for CFADs in Ku-band (Figure 7), CFADs of reflectivity simulation are also closer to the observation under complex-shape assumptions than others, as the maximum dBZ in the high altitude (3–6 km) appears at a lower value (~21 dBZ). For the radar reflectivity simulation under nonspherical-shape assumptions, the maximum value of CFAD appears at ~25 dBZ (simple shapes) or even higher (the spherical-shape assumption, ~30 dBZ).

The dynamic and thermodynamic have a great impact on the precipitation profile and thus on the reflectivity profile. Therefore, a classification methodology is required. Reflectivity at low altitude is considered a great indicator as the higher the reflectivity, the greater the precipitation, and more vigorous convection also often relates to greater precipitation. Then, in order to avoid the interference of surface echo, reflectivity at the height of 2 km (hereafter dBZ (2 km)) was used. Figure 8a,b show that simulated profiles significantly differ from the observed reflectivity profile when dBZ (2 km) is lower than 20 dBZ. The number of effectively observed reflectivity grids (the grids where dBZ (2 km) has an exact value) is far less than the simulation when dBZ (2 km) is small, so it is too arbitrary to conclude directly that the simulation was incorrect. For example, the number of effective dBZ (2 km) falling in the range of 5–17 dBZ with the DPR product is 53, which is far less than that of simulated reflectivity (the number of effective dBZ (2 km) falling in the range of 5–17 dBZ), which revealed about 1398–1909, so we hypothesize that the neglect of slight precipitation by the DPR retrieval algorithm or the difference between the minimum detectable signals in the inner and outer swaths (17 dBZ and 5 dBZ) is responsible for the difference. Nevertheless, the numbers of observed data points within other classes are nearly the same, and the number of simulated data points is comparable to that of observed data points (shown in the Supplementary Materials Table S1). In these classes, almost all simulated reflectivity is also smaller than the observed reflectivity at high altitudes, while they are equivalent at low altitudes (rainfall grids). This means that the USERS may underestimate the reflectivity on snow and cloud ice at Ka-band; otherwise, the actual snowflake shape is not among the eleven shapes assumed by the USERS. No matter what, when the dBZ (2 km) is large, the simulated reflectivity under the spherical shape or two complex-shape assumptions (sector and dendrite) shows the same phenomenon of a steep increase from high altitudes to low altitudes. This similarity indicates that these three shapes may be close to the real shapes of snowflakes.

Figure 9 shows that the probability distribution functions (PDFs) of simulated reflectivity shifted to the smaller end comparing to those of GPM-observed reflectivity. This is due to the limited detection sensitivity of GPM DPR. It illustrates that our guess about the effect of the DPR retrieval algorithm neglecting slight precipitation, mentioned in the previous paragraph, is probably right. This conclusion is consistent with that of previous studies comparing DPR-retrieved snowfall with other satellite or ground-based observation data [7,40,41,42]. Beyond that, in the radar reflectivity simulation, under all shape assumptions, the peak values of PDFs between 20 and 30 dBZ were well displayed; the sources of these signals were primarily liquid precipitation, which indicated that the USERS simulation of liquid water was more accurate than that of solid water.

In the real atmosphere, solid water cannot exist in just one shape, so a mixture of simple shapes (here, only short column is used) and complex shapes (dendrite) was considered in this study. Considering that the snowflakes are primarily of simple shape at high altitude and are of complex shape at low altitude because of condensation and collision effects during falling, the percentage of snowflakes in the short column to the total reflectivity (C) was assumed to be a function of temperature:

$$\mathrm{C}=100.0\ast {\left(\frac{\mathrm{T}}{40}\right)}^2$$

(3)

Here, T is the temperature (unit: °C) from the WRF simulation. However, when T is lower than −40 °C, C is set to 1. Figure 10 shows the cross-section of C along the red line in Figure 4.

Figure 11 shows that the correlation coefficient (R) between the observed and simulated reflectivity of cloud system 2 under any shape assumption is between 0.310 and 0.42, close to the correlation coefficient of the WRF-simulated precipitation rate and DPR precipitation rate product [43]. When comparing R under eleven single-shape assumptions (relative to aggregate-shape assumptions), we found that complex-shape assumptions performed better than any other shape assumption at both Ku-band and Ka-band. The spherical-shape assumption was acceptable in Ka-band simulation but performed worse at Ku-band than simple-shape assumptions. When considering the mixed-shape assumption, R was 0.412 in Ka-band, which was slightly higher than that under any simple-shape assumptions (short column: 0.206, dendrite: 0.411, as the mixed shape is a mixture of short column and dendrite), and R was 0.358 in Ku-band, which was superior to all simple-shape assumptions, although slightly lower than two complex-shape assumptions (short column: 0.300, dendrite: 0.357). This is because the bright-band was clearly shown in the Ka-band reflectivity cross-section when simulated under the mixed-shape assumption (see Supplementary Materials Figure S3), just like the signal under complex-shape assumptions. In addition, the reflectivity for each band in the upper atmosphere was closer to the measured one. Other temperature-dependent functions were tested, including the third, fourth, fifth, and sixth power functions of temperature, and the best denominators of temperature (40.0 for the square function), which exhibited the best fitting effects, were found for each function. However, the correlation coefficients calculated under these mixed-shape assumptions were similar to those of the square function, only ranging from 0.409 to 0.412 (Ka-band) and from 0.352 to 0.358 (Ku-band).

In this case, the simulations of reflectivity in both Ka-band and Ku-band were consistent with DPR observations and thus could be used in the following study. In addition, we found: (1) The snow shape assumption greatly influenced radar reflectivity. (2) The difference between the simulation of reflectivity and observation was significant when using simple-shape assumptions; sector and dendrite provided a more reasonable scheme for studying snow’s real shape and for radiative transfer process calculation. (3) In a real atmosphere, there were likely to be more snowflakes with simple shapes at the upper altitude and more with complex shapes at the lower altitude; the mixed-shape assumption depending on temperature provided a new perspective for studying snowflake shapes.

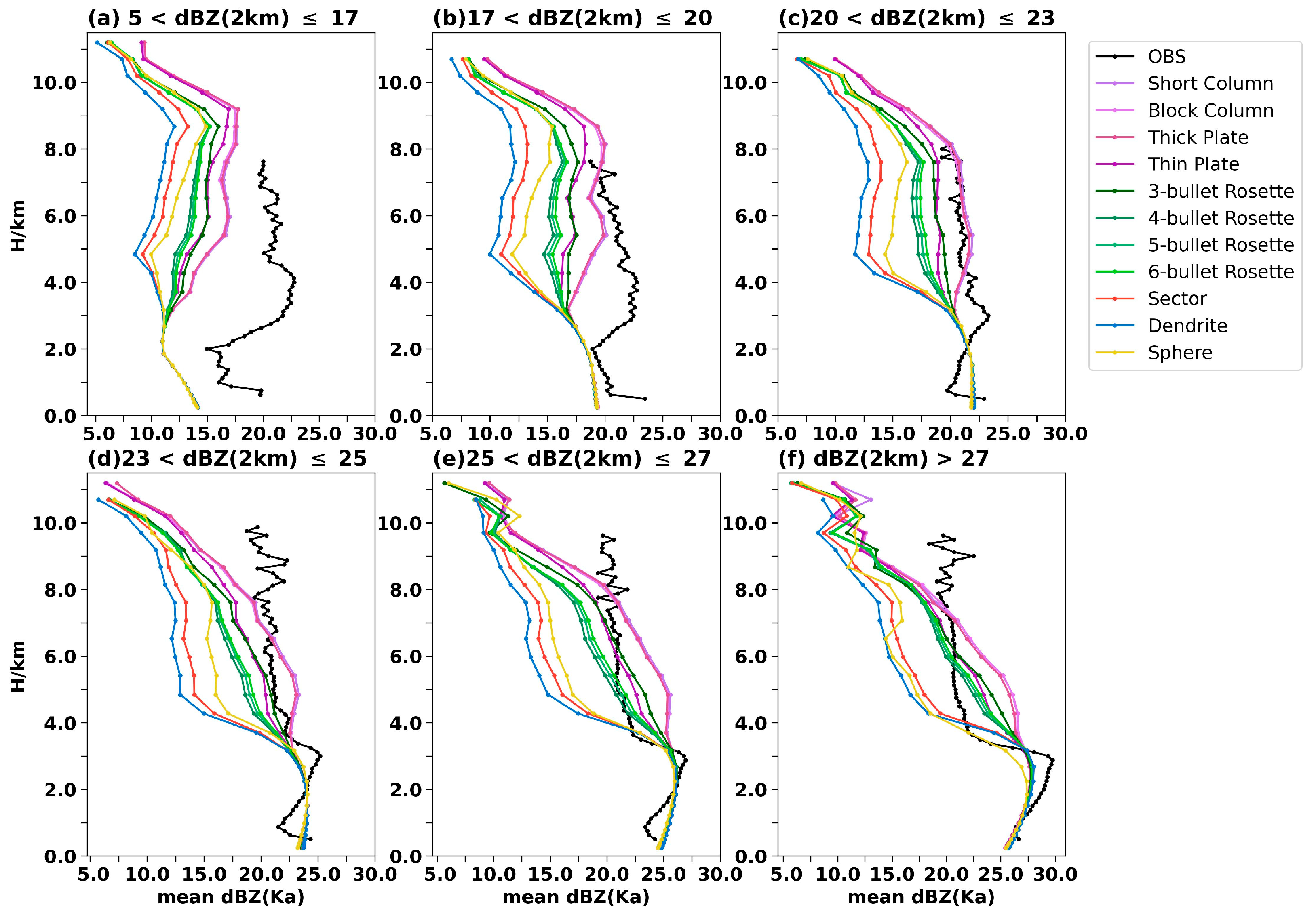
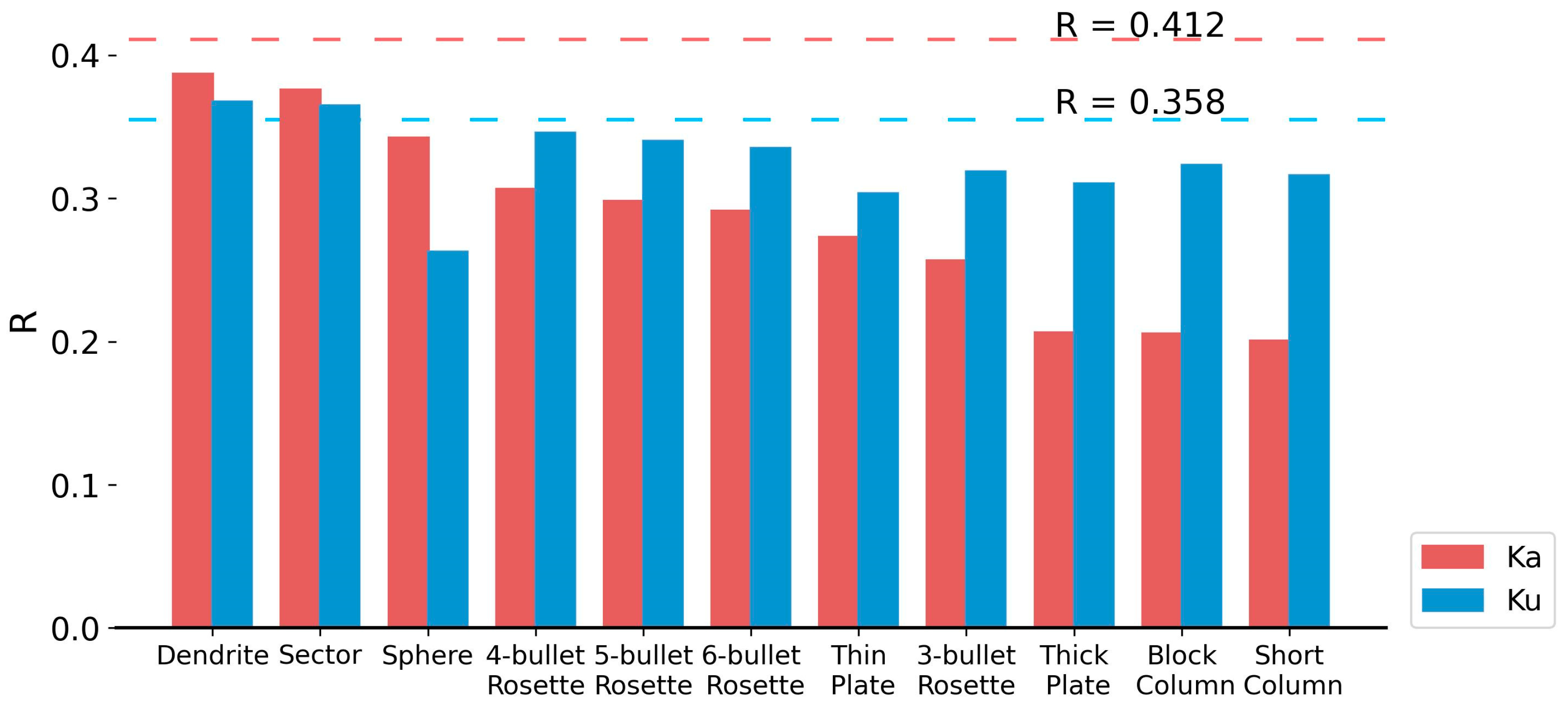
3.2. The Impact of Shape Assumptions on Z–R Relationships in Three Temperature Ranges

The Z–R relationship is the basis of precipitation retrieval from radar measurements. The shape assumption has significant impacts on this relationship and thus can lead to different retrieval bias, which has not previously been quantified. In this section, Z–R relationship is fitted from the model simulations with multiple shape assumptions and compared to selected relationships in literature. In addition, the associated retrieval error and bias are investigated to evaluate the impacts in different temperature layers.

The relationship between Z in Ku-band and the rain rate (R in mm/h), $\mathrm{Z}=\mathrm{a}·R^{\mathrm{b}}$ is often used to calculate R from Z directly in active radar retrieval algorithms [16,19,44]. Marshall and Palmer fitted the parameters a and b using observations [45], but the Z–R relationship is only for precipitation between 1 and 23 mm/h because of the limited instrument detection accuracy. Some researchers derived Z–R relationships based on the Rayleigh assumption [46,47], but that introduces errors into the estimation of reflectivity since both of the sizes and and the real shapes of snowflakes differ from that under sphere shape assumption. Therefore, it is necessary to study Z–R relationships for snowflakes with different shapes. Note that R is the short form for precipitation rate in this study, as there is also rainfall in this case.

As it is common to use dBZ as the unit of reflectivity (Z) in observation, and because we wanted to connect reflectivity observation and precipitation directly, hereafter, dBZ is used:

$$\mathrm{dBZ}=10\lg \mathrm{Z}$$

(4)

Moreover, the dBZ–R relationship is fitted:

$$\mathrm{dBZ}=10\lg \left(\mathrm{Z}\right)=10\lg \left(\mathrm{a}·{\mathrm{R}}^{\mathrm{b}}\right)=\mathrm{A}+\mathrm{B}·\lg \mathrm{R},$$

(5)

Here, A and B are two parameters to be fitted. MSE is used for the regression score:

$$\mathrm{MSE}=\frac{{{\displaystyle \sum }}_{\mathrm{i}}{\left({\mathrm{dBZ}}_{\mathrm{i}}-{\widehat{\mathrm{dBZ}}}_{\mathrm{i}}\right)}^2}{\mathrm{N}}$$

(6)

Here, N is the data volume, and the superscript indicates the fitting value. The MSEs for Ku-band reflectivity of snowflakes with six shapes in three temperature layers are reported in

Table 2. Mean squared error (MSE) for Ku-band reflectivity of snowflakes with six shapes in three temperature layers.

Temperature	Sphere	Short Column	Thin Plate	6-Bullet Rosette	Sector	Dendrite
T ≤ −40 °C	0.18	0.04	0.03	0.12	0.03	0.05
−40 < T ≤ −5 °C	4.14	0.88	0.74	0.78	0.27	0.28
−5 < T ≤ 0 °C	22.72	11.19	12.82	8.07	4.53	4.25

. The fitting effects are good for the particles in the atmosphere under −5 °C, as most MSEs are less than 1. However, MSEs for the reflectivity of spherical snowflakes existing between −40 °C and −5 °C are relatively high (>5), which results from the dispersion of the fitted data points and leads to bias that stems from using a fixed Z–R relationship in the retrieval algorithm. The MSEs are usually high for the particles existing between −5 °C and 0 °C because within this region, the scattering properties vary as precipitation particles tend to exist as a mixture of solid and liquid. Furthermore, the reflectivity partly results from cloud water, which implies strong effects from the microphysical properties of cloud water.

Figure 12 shows dBZ–R relationships for snowflakes with six shapes in three temperature layers, and the fitted parameters are listed in

Table 3. Parameters in dBZ–R relationships ($\mathrm{dBZ}=\mathrm{A}+\mathrm{B}·\lg \mathrm{R}$) of snowflakes with six shapes in three temperature layers.

Parameters	Temperature/°C	Sphere	Short Column	Thin Plate	6-Bullet Rosette	Sector	Dendrite
A	T ≤ −40	24.43	24.68	25.96	23.08	21.29	21.05
	−40 < T ≤ −5	29.88	26.43	27.33	25.03	22.41	22.07
	−5 < T ≤ 0	28.07	24.10	24.76	23.74	21.88	21.60
B	T ≤ −40	14.51	11.95	11.72	13.68	11.84	12.21
	−40 < T ≤ −5	11.85	9.61	9.48	10.06	9.74	9.67
	−5 < T ≤ 0	11.57	10.21	10.39	10.65	10.27	10.17

. The shape assumptions and temperature stratification clearly affected the fitting results of the dBZ–R relationships, so it was necessary to consider them in the radar retrieval algorithm.

Next, we compared the fitted relationships with $\mathrm{Z}=190·{\mathrm{R}}^{1.72}$ derived by Marshell and Palmer (hereafter MP relationship, [46]), and $\mathrm{Z}=366·{\mathrm{R}}^{1.42}$ derived by Atlas and Ulbrich (hereafter AU relationship, [47]), which are $\mathrm{dBZ}=22.79+17.2·\lg \mathrm{R}$ and $\mathrm{dBZ}=25.36+14.2·\lg \mathrm{R}$ (Figure 12). Below −40 °C, dBZ–R relationships of spherical snowfall and small (precipitation) snowfall in simple shapes were close to the theoretical relationships; between −40 °C and −5 °C, dBZ–R relationships of snowfall in complex shapes were close to theoretical relationships; above −5 °C, when snowfall was small (<1 mm/h), dBZ–R relationships of snowflakes in complex shapes were closer to theoretical relationships, but when snowfall was large (>6 mm/h), dBZ–R relationships of spherical snowflakes were closer. Despite all this, when theoretical dBZ–R relationships (MP or AU) were used in the retrieval algorithm, the following deviations arose: (1) The method underestimated snowfall of simple-shaped snowflakes when R was large and overestimated snowfall of simple-shaped snowflakes from −40 °C to −5 °C when R was small. (2) The method significantly underestimated snowfall of sector/dendrite-shaped snowflakes when R was large (>1 mm/h). (3) As for snowfall of spherical snowflakes, snowfall from −40 °C to −5 °C and light snowfalls (<9 mm/h) above −5 °C were significantly overestimated, but large snowfalls (>9 mm/h) above −5 °C were underestimated.

Table 3 shows that for the two shapes, sector and dendrite, that made our reflectivity simulation the most consistent with the observation in this experiment, the dBZ–R relationships below −40 °C were $\mathrm{dBZ}=21.29+11.84·\lg \mathrm{R}$ and $\mathrm{dBZ}=21.05+12.21·\lg \mathrm{R}$, which were $\mathrm{Z}=134.59·{\mathrm{R}}^{1.184}$ (sector) and $\mathrm{Z}=127.35·{\mathrm{R}}^{1.221}$ (dendrite), respectively.

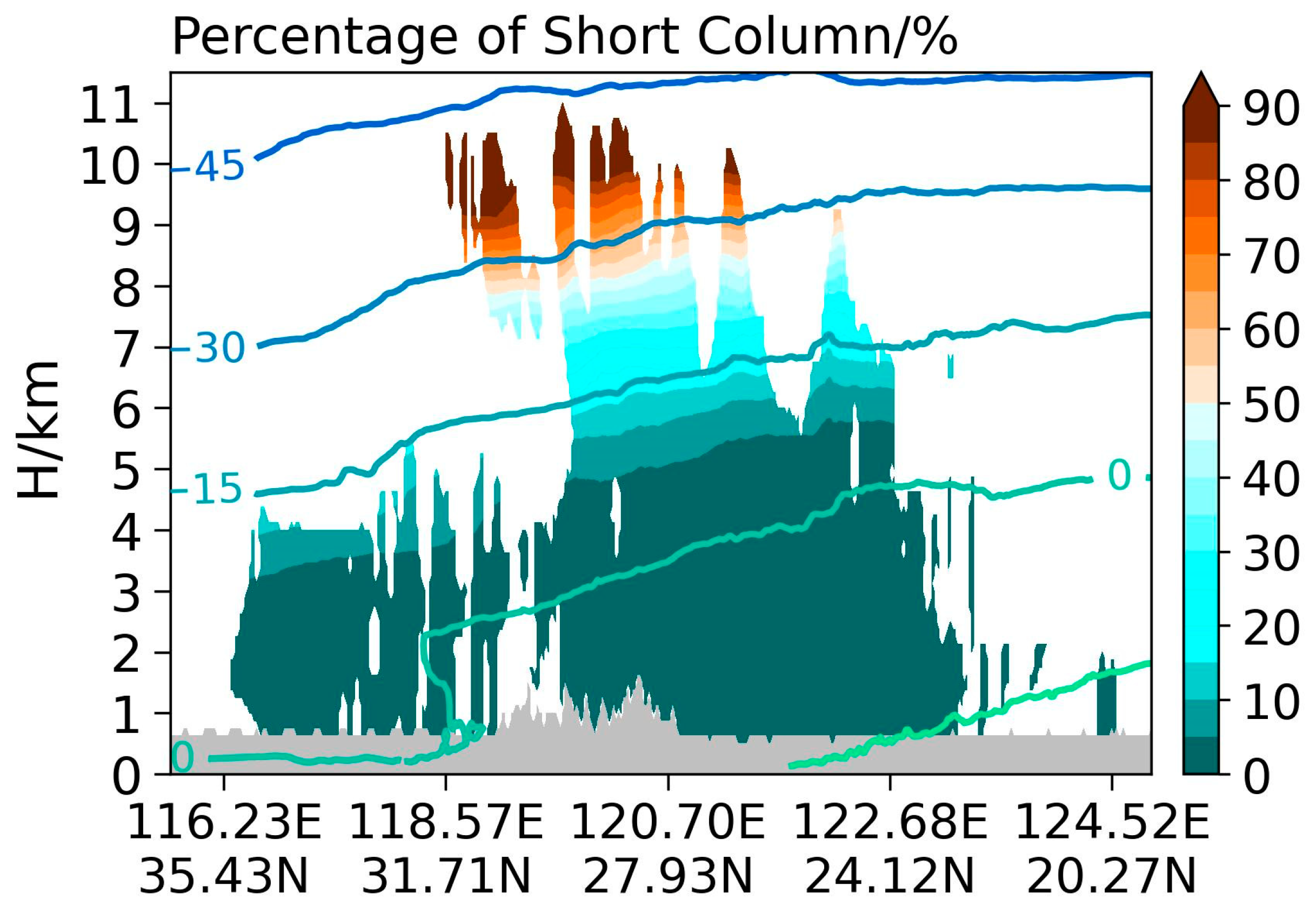
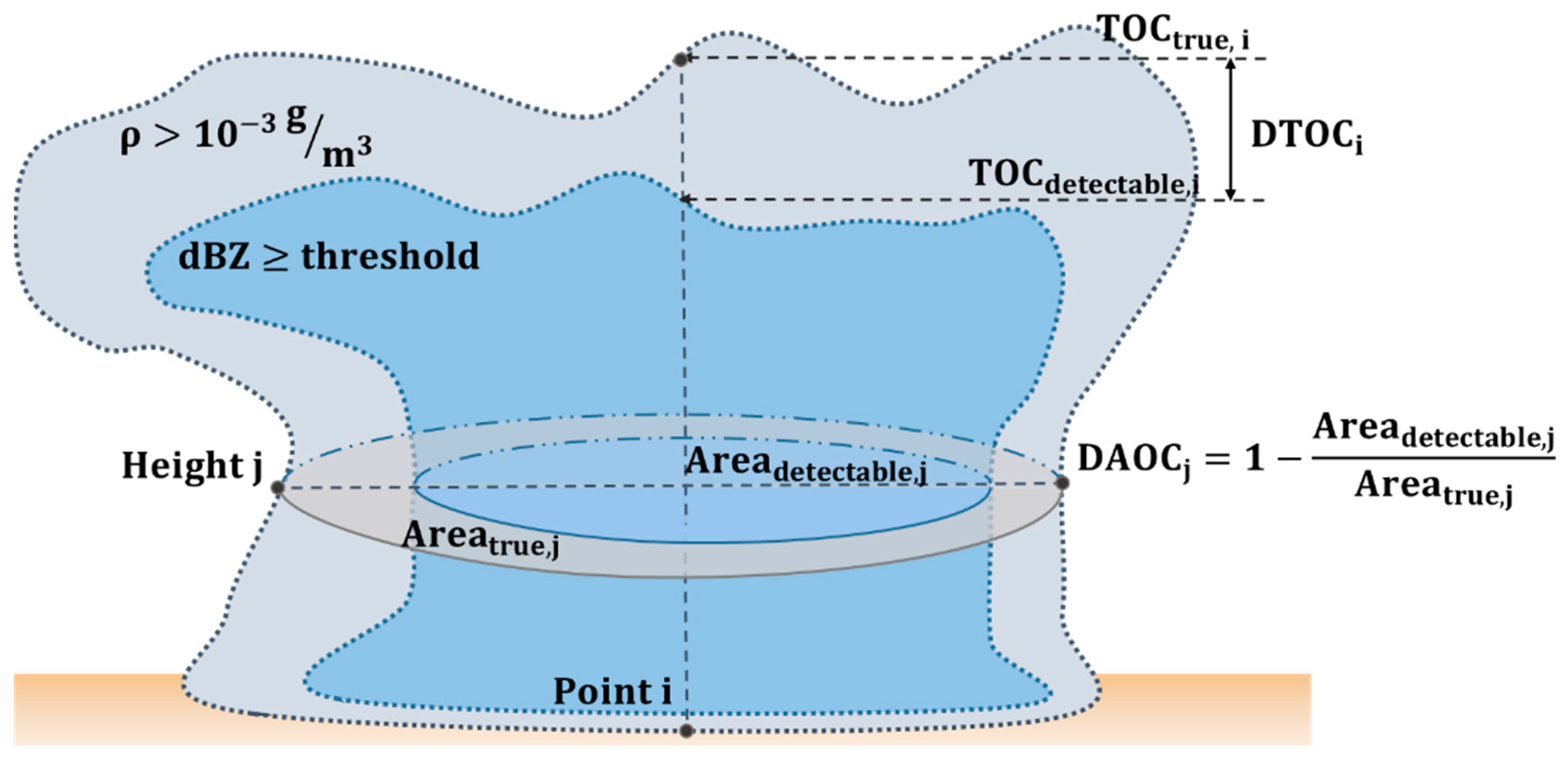
3.3. Estimation Error of Cloud Top and Cloud Area

On the one hand, the detection sensitivity of radar affects the detectable three-dimensional structure of the cloud. On the other hand, the detection capabilities are different for snowflakes in different shapes, so the estimation of detection error based on the spherical-shape assumption differs from reality. In this study, the difference of top of cloud (DTOC) and the difference in area of cloud (DAOC) are two indexes expressing cloud system detection accuracy. As shown in Figure 13, the real cloud boundary refers to where the total density of hydrometers equals 0.001 g/m³, and the detectable cloud boundary is determined according to the radar detection threshold. $DTO{C}_i$ is defined as the difference between the real cloud top and the detectable cloud top in grid $i$ in the horizontal direction. $DAO{C}_j$ is defined as the ratio of AOC detection error (the area where precipitation exists but is undetectable) and real AOC at height $j$. In addition, the DTOC and DAOC are illustrated for DPR deployed on GPM and FY3E, whose minimum detectable signals are assumed to be 5 dBZ and 10.4 dBZ at Ka-band, and 12 dBZ and 14.0 dBZ at Ku-band, respectively.

Figure 14 shows that the detected TOC and AOC error would be close to zero if the detection threshold of Ka-band and Ku-band could be limited to −15 dBZ. However, the real threshold was larger than this value; thus, the DTOCs of DPR for snowflakes in dendrite shape exceeded 1750 m (Ka, use the minimum detectable signal of the whole swath hereafter) and 1250 m (Ku), and the DAOCs were about 60% for two bands at the height of 2 km or 8 km. Moreover, the curves of DAOC variation with detection thresholds at the height of 8 km were different from those at 2 km, showing a steep increase at ~5 dBZ (Figure 14c,d). This is because cloud system 1 was a low snowfall cloud whose reflectivity was always at a low value, so if the detection threshold was higher than ~5 dBZ, the radar would ignore cloud system 1. In addition, the DTOC of cloud system 2 with snowflakes of simple shapes was smaller than that with snowflakes of complex shapes (Figure 14a,b), which further confirmed that the cloud top detected by radar was mainly composed of simple-shaped snowflakes. Typically, the detection error (DTOC and DAOC) for the cloud system with spherical snowflakes was lower than for sector or dendrite snowflakes but higher than for simple particle-shaped snowflakes (short column, thin plate). However, the previous retrieval algorithm considers the real nonspherical particles as spherical particles, which means that it will overestimate the detection ability of solid precipitation with complex shapes and underestimate the detection ability of solid precipitation with simple shapes. Under DPR’s detection threshold, the DTOC (DAOC) of complex-shape solid precipitation was 200–400 m (15%), larger than that of spherical solid precipitation.

It was easily determined that large DTOC values often appeared at the edge of the cloud system (Figure 15a,b,e). By comparing the DTOC of Ka-band and Ku-band for DPR (Figure 15a,b), we found that Ka-band was better than Ku-band at detecting cloud tops, while for designed thresholds of FYPR, the detection capabilities of these two bands were similar. However, it should be mentioned that the channels of DPR (13.6 GHz/35.5 GHz) were slightly different from those of FYPR (13.35/35.55 GHz), and the detection thresholds of DPR in the actual use stage were lower than in the test stage; thus, the actual detection capability of FYPR may have been higher than its design value. Furthermore, Figure 15c–f show that, compared to the dendrite assumption, the spherical-shape assumption often underestimated DTOC (as we found in Figure 14), but it did not uniformly underestimate DTOC horizontally. Specifically, it underestimated DTOC in the main part of the cloud and overestimated DTOC in areas with low water paths. The reflectivity of dendrite snowflakes is lower than that of spherical snowflakes. Therefore, for cloud system 1, nearly all the reflectivity was under the threshold, which made it inconsequential in the DTOC calculation. For cloud system 2, the reflectivity at high altitudes was lower, which made the DTOC larger.

4. Discussion

In addition, we hypothesize that the actual detection threshold of DPR may be higher than 5 dBZ or that the DPR retrieval algorithm ignores small snowfall. In summary, the shape assumption of snowflakes is very important in the radar radiative transfer process simulation. Using an inappropriate shape assumption affects the simulation of the Z–R relationship, thus affecting precipitation retrieval and estimation of detection error.

In this study, to focus on a case study in detail, only one snow case in East China was used. It remains necessary to conduct simulation research on different regions to develop a Z–R relationship that can be applied to the active radar retrieval algorithm, in addition to carefully considering shape assumptions in the vertical stratification.

As suggested by one anonymous reviewer, the mass-weighted diameter, Dm (fourth over third moment of the distribution), and the particle number concentration in particle size distribution (PSD) are very important factors affecting the Ku/Ka radar reflectivity of snow and deserve further in-depth study. It is worth noting that, in this study, we only focused on the impacts of particle shape assumption. The two parameters just mentioned were fixed for different shape assumptions. Further studies on the relative importance of the above three aspects (mass-weighted diameter, particle number concentration, and particle shape assumption) will be valuable for fully understanding the impacts of particle microphysical properties on radar reflectivity.

It is challenging to directly compare a storm instantaneously observed using a low-orbit satellite, such as GPM, to a simulated one, generated by a CRM or MWRT model. Both simulation errors by the CRM and the radiative transfer calculations may lead to significant discrepancies. In terms of this study, the horizontal pattern, size, and location of the simulated storms showed good consistency with the satellite observation (Figure 1). In the vertical cross-section (Figure 5), the GPM-observed convection cores between 120.70E and 122.68E were well simulated by the model using dendrite assumption in terms of location, bright-band, detectable height, etc. Therefore, although there is great uncertainty in the model, this case is valuable for informing future model sensitivity studies.

Furthermore, the dual-frequency ratio (DFR) is an important parameter when considering the mixing ratio, particle size, or mass densities.

5. Conclusions

The combination of WRF and a radiative transfer model such as the USERS is an effective way to test and verify the radiative transfer model and radar retrieval algorithm. This study used a precipitation case in East China at 16:30 UTC on 6 January 2018. This article has discussed the following issues: (1) The effect of shape assumptions (including a temperature-dependent shape assumption) on the performance of simulations. (2) The associated bias in retrieval results when using theoretical Z–R relationships. (3) The detectable errors of precipitation top height, and the rain area. Here are the main conclusions:

• Compared with the simple-shape assumptions, our complex-shape assumptions (sector and dendrite) performed better in both Ka-band and Ku-band reflectivity simulations. This was shown by the higher correlation coefficients between the simulated and observed reflectivity and smaller differences between their reflectivity profiles. Therefore, snowflakes in the real atmosphere might be closer to sector and dendrite than sphere. The Z–R relationships for these shape assumptions under −40 °C are $\mathrm{Z}=134.59·{\mathrm{R}}^{1.184}$ (sector) and $\mathrm{Z}=127.35·{\mathrm{R}}^{1.221}$ (dendrite). However, snowflakes tend to exist in simple shapes when temperature is low and in complex shapes when temperature is high. The temperature-dependent assumption performs well, especially at Ka-band, but the operational method still needs further study.
• In most conditions, the theoretical Z–R relationships (MP/AU relationships) differed from the fitted Z–R relationships of snowflakes, regardless of their shape. Furthermore, the differences led to estimation errors that stemmed from using a theoretical relationship in the retrieval algorithm. The errors were to underestimate large snowfalls with simple-shaped snowflakes below −40 °C or with complex shapes, and to overestimate snowfalls with spherical snowflakes or small snowfalls with simple-shaped snowflakes below −40 °C.
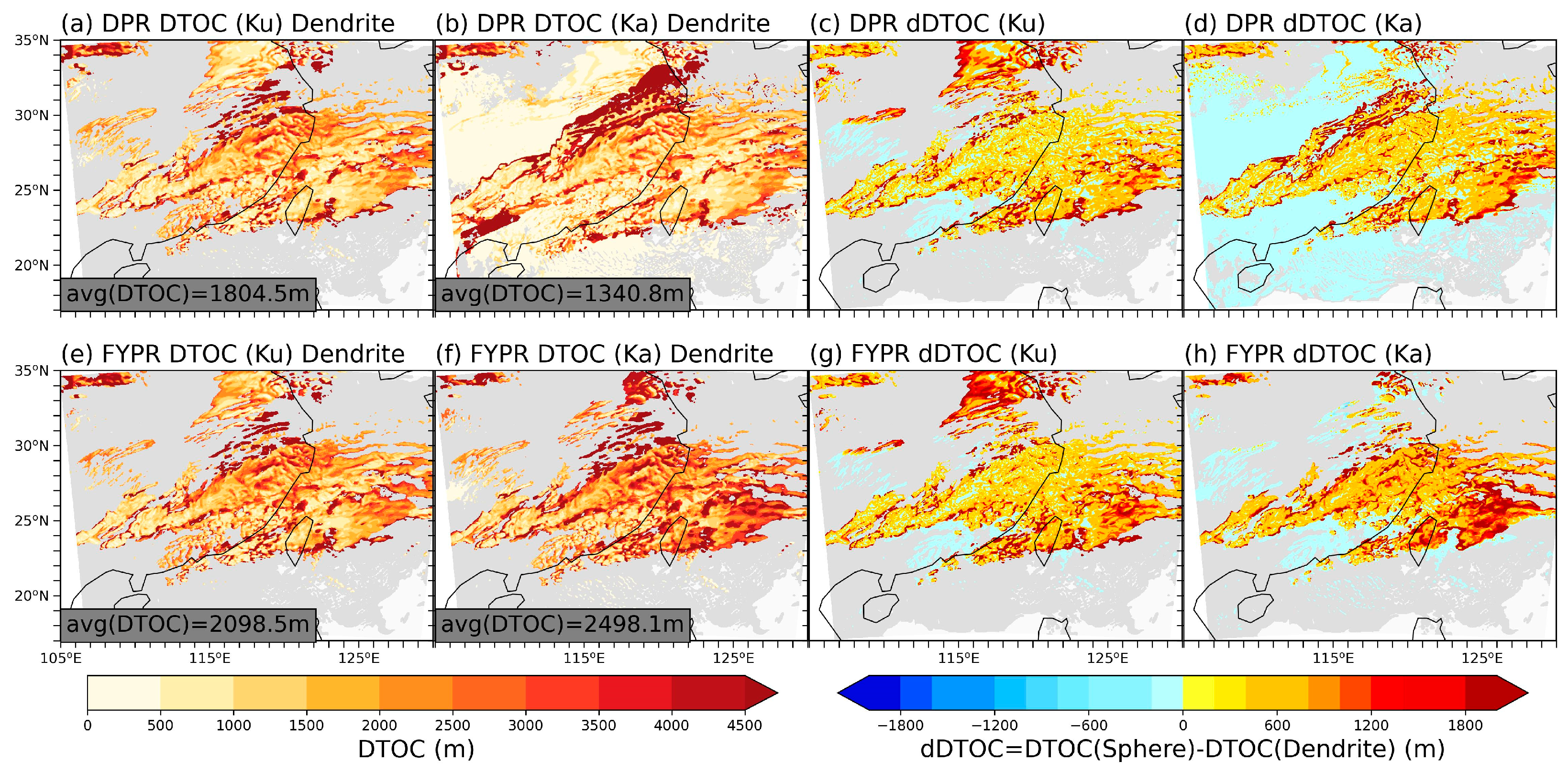
• Under the existing detection sensitivity, the DTOCs of DPR for this case were 1804.5 m (Ka) and 1340.8 m (Ku), and the DAOCs reached 50% and 20% at heights of 8 km and 2 km for Ka-band. If the detection threshold of spaceborne dual frequency radar could reach 5 dBZ (Ku)/0 dBZ (Ka), its detection capability for snowfall in eastern China would be greatly improved.
• An inappropriate shape assumption affected the estimation of detection error: the DTOC of a complex-shape assumption was 200–400 m larger than that of the spherical-shape assumption, while the DAOC was ~15% larger.