Automated Detection of Glacier Surges from Sentinel-1 Surface Velocity Time Series—An Example from Svalbard

Abstract

Even though surge-type glaciers make up only a small percentage of all glaciers, related research contributes considerably to the general understanding of glacier flow mechanisms. Recent studies based on remote sensing techniques aimed to disentangle underlying processes related to glacier surges. They have proven the possibilities yielded by combining high performance computing and earth observation. In addition, modelling approaches to surges have seen increasing popularity, yet large spatial and temporal data about timing of surge incites are missing. We aimed to develop an algorithm that not only detects surge type glaciers but also determines the timing of a surge onset, while being computationally inexpensive, transferable, and expandable in time and space. The algorithm is based on time series analyses of glacier surface velocity derived from Sentinel-1 data. After seasonal and trend decomposition, outlier detection is performed by the General Studentized Extreme Deviate Test, an iterative algorithm well suited for outlier detection in univariate time series. To determine surges, cluster analysis is performed to identify outlier clusters, which are linked to glacier surges. We demonstrate the viability on the Svalbard archipelago for the period 2015 to 2021 where we have identified 18 glacier surges and the timing of their active phase.

1. Introduction

Surge-type glaciers are glaciers that undergo semi-periodic cycles between long phases of slow ice flow and comparably short phases of fast ice flow, which are not triggered externally [1]. Even though only a small percentage of all glaciers worldwide are known to be surge-type glaciers, they have been researched extensively in order to gain further understanding of glacier flow and flow instabilities [2,3,4]. Glacier surges also impose natural hazards to affected regions [5]. Due to high velocities and mass transfer from an upper reservoir area, at which ice masses build up during the slow moving periods, to lower areas, where they are prone to melting, a glacier’s terminus can advance significantly over a short period [6]. Hence, on one hand, surges can bias the link to climate and the climatic interpretation regarding a glaciers mass balance or area [7]. On the other hand, in mountainous regions, housing steep valley systems such as the Karakoram, glacier surges imply a substantial threat to local communities due to glacier lake outburst floods as a result of termini advancing across trunk valley rivers [8]. In a recent study by Ke et al. [9], 74 glacier surges in the Karakorum in the period 2000–2020 were identified. One of these surges which was accompanied by a terminus advance which led to the build-up of a moraine dammed lake, is the surge of the Shishper glacier in the Hunza valley. Over a span of 19 months from 2018 to 2019, the glacier advanced more than 1 km and subsequently dammed a large proglacial lake. After damming up a lake of over 100 m of depth, it eventually collapsed. The outburst flood damaged critical parts of the local infrastructure several kilometres downstream [10]. Most of the currently known surge type glaciers are found in clusters which lie within a climatic envelope also referred to as the ‘Arctic Ring’. It includes regions as the Arctic, Sub-Arctica, and High Arctic Canada. Western Central Asia is the only region comprising surge type clusters outside the Arctic Ring [3]. Since most of the glaciers in these regions are hardly accessible without substantial expenses, remote sensing plays a vital role in studying their behaviour. Studies using remote sensing techniques to distinguish surge-type glaciers from others are oftentimes either based on morphological and more qualitative attributes of a surge, or quantitative approaches such as elevation or velocity changes [11,12,13,14,15]. Due to snow or cloud coverage, no visible terminus advance during a surge or missing illumination by the sun in arctic winters, the usage of radar satellite imagery and a quantitative approach may be advantageous over optical image sources [12,13]. Observing surface velocity of glaciers using repeat satellite imagery has become a regular tool in cryospheric research [16]. The Sentinel-1 mission was designed for continuous monitoring purposes with a high repetition rate and near global coverage. The commitment for successor satellites enables the built-up of cloud and weather independent time series of glacier flow using offset tracking techniques. In this study we present an approach to detect glacier surges based on the analysis of monthly composites of surface velocity time series derived from Sentinel-1 synthetic aperture radar (SAR) imagery. The approach in this paper is computationally inexpensive and independent of the data origin. The algorithm can handle large data sets and detect different anomalies in flow behaviour and yields the potential to be added to existing processing chains. The manuscript comprises a review of surge mechanisms, a brief outlook of recent studies about their quantitative detection, a description of our database and methodology applied, as well as the achieved results and their discussion.

2. About Glacier Surges

A wide spectrum of glacier types, ranging from valley glaciers to ice-streams, are known to be surge type [17]. Glacier surges are defined as a quasi-periodic oscillation between long periods of ten to hundreds of years of slow flow or quiescence and comparably short periods of rapid flow that are 10–100 times faster than during the quiescent phase. These active or surge phases can last from months to years. Originally defined, glacier surges are not directly triggered by external events, but driven by internally oscillating conditions at the bed of the glacier [1,18,19]. During an active surge, high basal water pressure and extreme basal sliding are known to be common characteristics. However, many questions regarding why some glaciers do surge, whereas others do not, are yet to be answered [5].

Surging glaciers follow a systematic change in morphology and behaviour during a surge cycle [20]. As a result of increased ice flow and mass transport, surges can result in advancing termini, which imposes the potential of catastrophic hazards in mountainous regions [21]. In polythermal glaciers, the bed may switch from a cold to a warm regime during the active surge cycle, whereas the bed of a temperate glacier remains warm throughout. These two cases led to a two-fold classification of surge-type glaciers, the “Svalbard-Type” and the “Alaskan-Type” having two distinctly different mechanisms leading to a surge: the thermal switch for Svalbard-Type and the hydrological switch for Alaskan-Type glaciers [2,20]. On land-terminating glaciers, surges often begin in their upper regions followed by a downwards propagation of the surge front. The surge front describes the boundary between the fast-flowing ice and slower ice masses in front of it. It may thus be understood as a kinematic wave of fast-moving ice. This leads to a compression zone which forms a steep bulge propagating down valley, called the surge front [22]. Some tidewater glaciers display a surge initiation in areas of their lower tongue and propagate up-glacier from there. This pattern has been documented among others in Svalbard and Iceland [23,24].

Svalbard glaciers are often referred to as thermally controlled soft-bed surge mechanisms, where the trigger of the surge is linked to a change of the glacier’s bed from a cold to a temperate state [19,20]. During the quiescence phase or phase of low flow, ice mass is being build up in the upper regions of a glacier, the reservoir area. After surpassing a critical threshold when entering the active phase of the surge, the accumulated mass is being transported down-valley. This oftentimes rapid relocation of mass is accompanied by high surface velocities typical for surge-type glaciers [25]. If till is present below the bed, it may be thawed during melt processes when the regime switches to a temperate state. Through rising pore water pressure, the shear strength of the till is reduced, which further destabilizes the glacier initiating a surge [26]. In comparison, Svalbard-type glaciers undergo a less sudden change in surface velocity when entering their active surge phase [27]. The other switch mechanism referred to as the hydrological switch explains a process, where an effective subglacial conduit system switches to an ineffectively linked cavity system that weakens basal friction and ultimately leads to the incitement of a surge [28]. In the recent past, it has been suggested that these two underlying processes may be understood as two ends of a spectrum, where internal triggers are not mutually exclusive but may accompany one another to a certain extent. Recently, more work aiming towards a unifying theory of glacier surges has been published. One of these is a study by Benn et al. [28] which includes both mechanisms based on coupled mass and enthalpy budgets. The enthalpy balance theory draws several elements of prior models and tries to explain the full spectrum of glacier dynamic behaviour within a coherent framework. Nonetheless, there is certainly a wide range of surge-types that are driven by one or another mechanism or to certain degrees by both. While Benn et al. [28] propose a model to unify oscillatory flow behaviour in adoption of a system-based view, Thøgersen et al. [4] suggest a rate-and-state friction framework on a process-based view. The concept explains a surge cycle through cycles of velocity-strengthening-weakening transitions and a characteristic length scale for the transient evolution of basal shear stress. Their model describes three stages of a surge cycle. An initiation phase equivalent to the quiescent phase, the surge phase, and a termination phase. During the initiation phase, due to mass gain, basal shear stress is increased, while the flow velocity is restrained by strengthening friction. If a shear stress threshold is surpassed due to an increase of water supply, basal friction is weakened resulting in increased flow velocity. During the surge, friction is low, velocities are high, while driving stress gradually decreases. At surge termination, due to low driving stress velocity decreases and friction strengthening returns following basal slip rates. Even though this strongly simplified view ignores details of cavity formation, as well as spatial propagation and influences of valley side friction, the rate and state friction model describes a surge initiation and propagation entirely through the evolution of friction on hard glacier beds [29]. The model aims to identify threshold shear stresses which friction flips from velocity strengthening to velocity weakening. It also explains if such friction instability occurs at scales above a certain size, it can propagate over the entirety of a glacier accompanied typical surge related morphological features such as a bulge at the surge front. Although Thøgersen et al. [4] note that mass build up is common throughout all surge-type glaciers, they underline the role of meltwater supply in weakening friction by reducing the glacier sole’s ability to adhere to the bed surface. Even though these two approaches differ in perspective, Terleth et al. [29] state that they are not mutually exclusive, but seem to complement each other. Despite the fact that fundamental descriptions of transient basal drag could explain the translation of high enthalpy conditions to basal slip, the mechanics are governed by the conditions they occur in. Enthalpy concepts offer a wider systematic framework to describe and monitoring the force of flow acceleration by conditions at the glacier bed through a single measure.

Still, internal processes are clearly not independent of external conditions, and glaciers show a variety of surging behaviours, sometimes making the distinction between surge-type and non-surge-type glaciers difficult [20,22]. This difficulty is also reflected in the literature. For example, while Jiskoot et al. [2] estimated 13% of all glaciers on Svalbard to be surge-type, Lefauconnier et al. [30] estimated a value of 90% [2]. To this day, there are still unanswered questions on what drives glaciers to surge and why some glaciers surge while others do not. This is partially due to the limited number of observations and quantitative measurements of surges, especially regarding the timing of the surge [3]. Due to a steady increase in power of modern computational systems, global scale studies based on satellite microwave remote sensing have become possible. A recent publication by Leclerq et al. [31] demonstrated the potential of Sentinel-1 data to derive global coverage of surge activity. Their approach is based on comparing backscatter intensity changes, since a strong in- or decrease in surface roughness can be attributed to crevassing linked to surges. Leclerq et al. [31] were able to detect 69 surge type glaciers in their 2018 to 2019 observation period, many of which were previously undocumented. However, the time component of glacier surges are often times not available in large scale studies, but crucial to many modern-day approaches in resolving unanswered questions about surge probability, distribution, and behaviour. Further measurements and detection allowing large-scale comparison could fill gaps in knowledge existent up to this day [32]. However, with extending both spatial and temporal coverage, automatization and computational inexpensive data handling become a factor. Additionally, automated approaches open up the possibility of being integrated into existing processing chains. The approach presented aims to detect the velocity increase that is attributed to all types of glacier surges. Yet, it is not limited to it. The analysis of detrended time series potentially unravels other events out of the “norm” regarding glacier flow. With minor adjustments, the data handling would allow for multiannual or intra annual velocity trend or change analysis, e.g., the detection of velocity increases due to frontal ice shelf disintegration of tidewater glaciers.

In the presented study, we aim to analyse the sometimes sudden but always significant change in surface velocity by time-series analysis based on Sentinel-1 imagery ranging from 2015 to 2021. The change in surface velocity, as it can be observed during the acceleration time of a glacier surge, can be detected as a statistical outlier when applying time series analyses. The underlying goal was to develop an algorithm that is capable of handling large-scale data sets while being computationally efficient, transferable to any other velocity data source, and being scalable in space and time. In this paper, we demonstrate the feasibility of our approach on the Svalbard archipelago.

3. Study Region

Located between 75° and 82°N, with contrasting atmospheric and oceanic regimes, close to the fluctuating Arctic sea-ice edge, Svalbard is one of the fastest warming regions on Earth [33]. The Arctic archipelago of Svalbard in the North Atlantic is at roughly 57% glacierized and houses a variety of glacier types such as cirque and valley glaciers, as well as ice fields and ice caps. More than 1000 individual glaciers are estimated to be larger than 1 km², and over 500 are longer than 5 km. Most glaciers are classified as polythermal, terminating on land and in the sea [34]. Roughly 15% of all glaciers by number and 60% by area are tidewater glaciers (see Figure 1) [35]. Since the 1920s, the end of the little ice age, the surface mass balance of the archipelago is negative. Since then, summer temperatures in particular have been rising significantly [36].

Surge-type glaciers cover ~50% of the glacierized area of Svalbard [2]. The duration of the active phase of a surge cycle for Svalbard glaciers is significantly longer than for other surge-type glaciers elsewhere. In Svalbard, active phases may last several years. In comparison, 1–2 years is typical for northwest North America, Iceland, and the Pamir Mountains. The velocities during protracted active phases on Svalbard are considerably lower than in other regions for which data is available. Ergo, mass transferred from the reservoir to a receiving area is done more slowly but covers for a longer period of time. The slowdown after the active surge phases can also last for several years. Svalbard’s surge glaciers are assumed to have comparably long quiescent phases of 50–500 years, based on the few ice masses for which evidence is available [24].

4. Data & Methods

This analysis is based on the global and publicly available Sentinel-1 RETREAT data set, which is an ongoing data set consisting of different velocity products covering all 12 major glacierized regions outside Antarctica and Greenland. The velocity information is derived from both archived and new Sentinel-1 SAR acquisitions by applying intensity offset tracking. The data is then post processed by filtering and correction of co-registration errors. (accessible at: http://retreat.geographie.uni-erlangen.de, accessed on 22 December 2022) [37]. Data is available as scene pair-velocity fields, as well as monthly and yearly velocity mosaics. For mosaics, if the number of measurements per pixel is greater than two, the median of the x and y displacement per pixel is calculated. Measurements that have an absolute difference to the median of more than two times the standard deviation of all measurements in at least one of the two displacement directions are removed. If only one measurement per pixel is present, it is kept [37]. This removes a considerable amount of noise during the time where only Sentinel-1A was operational, or in case of missing acquisitions due to other reasons, while ensuring the equidistant spacing of all data frames. In this study, we used velocity data extracted from monthly mosaics. Since the repeat pass frequency of the satellite system varied over the observation period, but was never less than one per month, this approach makes data handling significantly less work intensive. For almost all regions on Svalbard, a monthly mosaic is comprised of at least two velocity measurements. The spatial resolution of the mosaics is 200 m and they cover the entire Svalbard archipelago. The temporal coverage ranges from September 2015 to September 2021. Thus, the velocity data was extracted for 73 timesteps in total for each glacier on the archipelago.

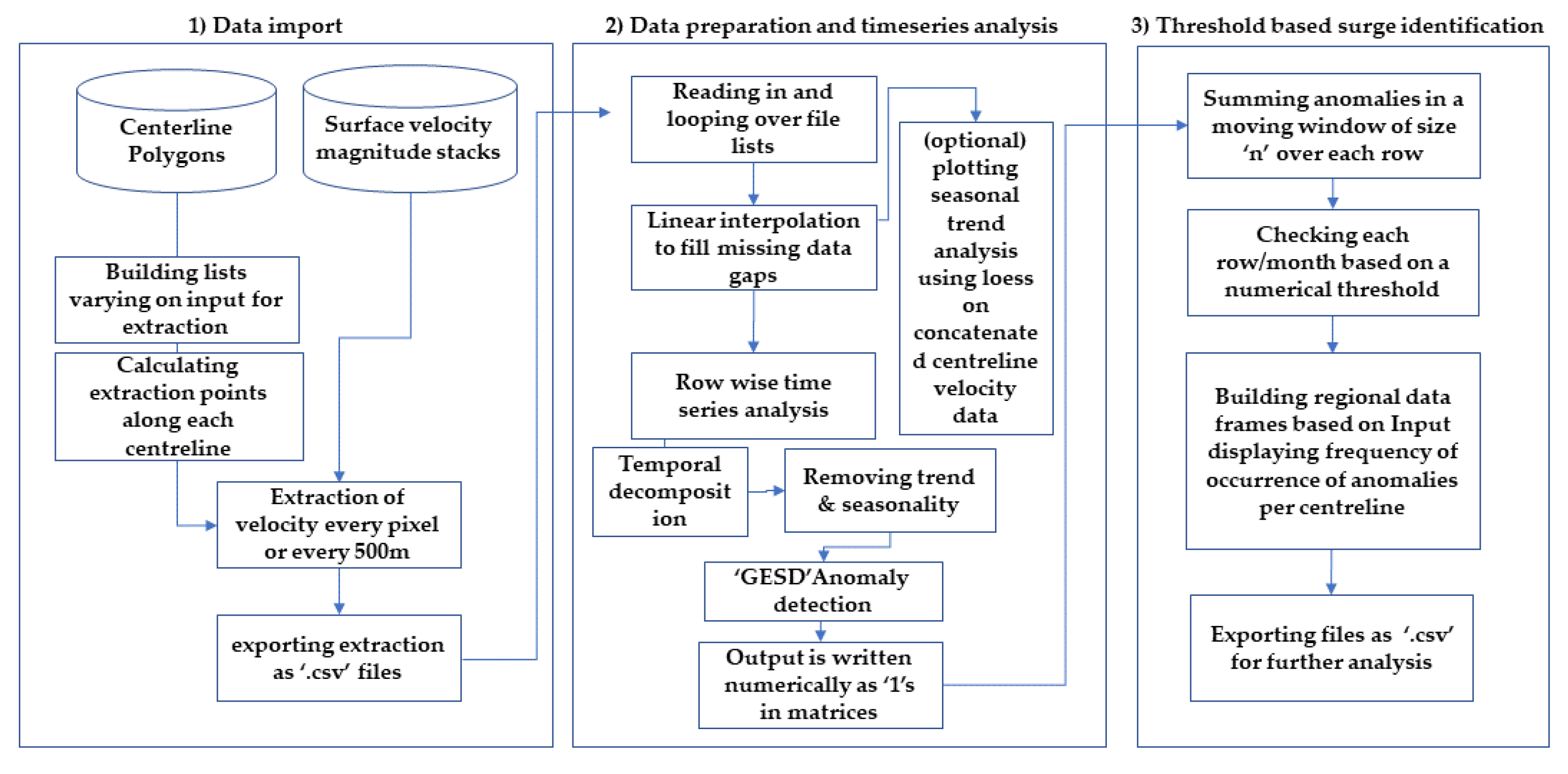
4.1. Extraction and Processing of Velocity Data for Time Series Analysis

To extract the velocity data from the monthly velocity mosaics, centrelines from Nuth et al. [34] were used. If a single glacier or glacier system had multiple centrelines, they were all used to identify if a surge incited at the glacier’s terminus or in one of its accumulation areas. Centrelines with a length below 5 km were removed from the processing chain. The methods described in the following were exclusively carried out in the open-source programming language R. The workflow consists of three major steps: (1) data import and preparation for the time series analysis, (2) the time series analysis itself and (3) a threshold-based cluster analysis to identify possible surges (see Figure 2).

First the velocity magnitude values are extracted along the flow lines every 200 m or every 500 m with a circular buffer with r = 250 m and merged into a matrix, one per flowline where each extraction per timestep is iteratively appended row wise. This results in a matrix where rows store all extractions per timestep and a column always the same extraction point per centreline for all timesteps. If the data was extracted with a buffer, the mean of the included velocity pixels was calculated. Reasoning for two extraction methods was to test if averaging closes potential data gaps, if a pixel value is missing, thus removing potential noise in the data or bias by outliers in the data.

After extraction, the ‘na.approx’ function, which is part of the ‘zoo’ R-Package [38] is used to interpolate missing values for each extraction period. We used linear interpolation between known values. The resulting time series per extraction point (columns) were analysed applying the Generalized Extreme Studentized Deviate Test (GESD). The GESD is advantageous over the original Extreme Studentized Deviate Test (ESD) since it controls type and error, both under the hypothesis of no outliers and under the alternative hypotheses of 1, …, n outliers [39]. Thus, the GESD performs better in outlier detection in univariate data sets with varying patterns [40]. Performing the time-series analysis per extraction point has several upsides. It reduces the computational time due to the iterative nature of the algorithm and it allows for a universal parameterisation and comparability between glaciers and removes most of the potential bias induced by interpolation, since gaps in the velocity data are interpolated row-wisely. The GESD algorithm for outlier detection is implemented in the “anomalize” R-package [41], which has been used in this study. The GESD performs most accurately when seasonality and trend are removed from the time series [39]. Detrending was performed with the build in ‘stl’-function, which is a seasonal decomposition of time series using LOESS (Locally Estimated Scatterplot Smoothing) [42]. The seasonal components are found by LOESS-smoothing seasonal sub-series with a length of 12 months. After removing the seasonal signal, the remainder is smoothed to find the trend. The overall level is subsequently removed from the seasonal component and added to the trend component. This process is iteratively repeated until the remainder component is built. It is the result of adding the residuals from the seasonal plus the trend fit [43].

Figure 3 visualizes the detrending process as well as the outlier detection on the remainder. In the observed band during late 2017 and the beginning of 2018, comparably low surface velocity before the start of the surge, as well as the sudden increase in velocity can be seen. It becomes apparent that the periodical cycle of high velocities during the summer months influences the removal of the seasonal component due to the strong summer to winter variation in flow, due to the negative shift and the subsequent removal of the seasonal component (3b). This may bias the detection of the surge onset (3d), since it negatively shifts the remainder curve during summer, which can be observed in summer of 2017 in Figure 3. However, the cluster analysis, which is applied on the remainder later, is set to deal with falsely detected outliers, as a set of multiple anomalies has to be detected at the same timestep.

It also becomes evident that the anomaly detection captures the surge onset well by comparing the first set of consecutively detected anomalies in late 2016 throughout 2017. The overall magnitude of surface velocity is roughly in the order of two and more where anomalies are being marked as such. When determined as an outlier, the data points are written into a matrix corresponding to the number of time steps and extraction points. From there on, a row-wise (per time step of extraction) cluster analysis of anomalies is performed, which calculates the sum $y_i$ within a one-dimensional moving window of the size n. This step may be expressed as:

$$y_i=\sum _{x_m\in W_i^{H,J}}{x}_m$$

(1)

where $x_m$ is the row-wise input vector, $W_i^{H,J}$, H and J are non-negative integers 0 and 1, the latter representing an outlier at the position i. The moving window sum calculates the sum of the values of each window $W_i^{H,J}$ and writes the result $y_i$ into a separate data frame. The window size for this study was set to 10, which equals the distance from each extraction point to the next, times ten in length. In this study, we extracted data every 500 m, thus a window size of ten is equal to 5 km of glacier length, which is the lower boundary of glacier length that we analysed in this study. If the sum meets the threshold value of nine, which has been set for all glaciers, the month is marked as anomalous. If four and more consecutive months meet the criteria, a glacier is classified as surging. Since the definition varies slightly in studies, a surge is defined here as an increase in surface velocity in the order of magnitude of at least twice the de-trended mean.

4.2. Sensitivity Studies

The GESD outlier detection and the cluster analysis allow for more or less degrees of freedom. In order to detect the correct onset of the surge but still be able to distinguish stronger seasonal fluctuations of large tidewater glaciers from surges, we conducted the following sensitivity studies. To quantitively compare the onset and duration of the active surge as determined by the algorithm, we compared two case studies with our findings, namely studies by Haga et al. [13] and Benn et al. [44] (see Figure 1). Haga et al. [13] examined the surge of Negribreen by using a combination of data sources, including the European Remote Sensing satellites (ERS), RADARSAT-1, Landsat 8, Sentinel-1, and Sentinel-2. They found a frontal collapse of the glacier in late summer 2016, after which high surface velocities were no longer restricted to the frontal zone. High velocities were observed during 2017, reaching their maximum of 25 ± 0.8 m/d during summer 2017, followed by a gradual deceleration in all parts of the glacier. It should be noted that the active phase of the Negribreen surge started before the observation period. The iterative nature of the algorithm, however, proves to also perform under given timing of a surge. Additionally, both studies are based on a quantitative analysis of surface velocity as derived from different remote sensing platforms.

We compared data frames that resemble the onset and length of an active surge to the data frames build by the algorithm, presented in this study. Therefore, we build an equispaced data frame where the length of the surge detected in the study of is represented in a data frame where a “1” also represents the length of a surge and then compared to the lengths determined by the differing parameterisations shown in

Table 1. Correlation matrix of Negribreen with each pixel and no buffer extracted compared to Haga et al. [13]. The cluster threshold marks the number of anomalies within the moving window (of the size nine) at any position per time step. Bold numbers indicate the highest correlation coefficient for each parameterization.

Cluster Threshold	a 0.05/20%	a 0.05/40%	a 0.05/80%	a 0.05/100%	a 0.1/20%	a 0.1/40%	a 0.1/80%	a 0.1/100%	a 0.2/20%	a 0.2/40%
5	0.45	0.31	0.31	0.18	0.41	0.26	0.25	0.07	0.38	0.21
6	0.51	0.45	0.45	0.40	0.49	0.41	0.41	0.33	0.49	0.31
7	0.56	0.52	0.52	0.50	0.53	0.50	0.50	0.50	0.49	0.45
8	0.56	0.53	0.53	0.51	0.56	0.58	0.58	0.54	0.56	0.54
9	0.65	0.58	0.58	0.58	0.65	0.56	0.56	0.56	0.62	0.56
Cluster Threshold	a 0.2/ 80%	a 0.2/100%	a 0.4/20%	a 0.4/40%	a 0.4/80%	a 0.4/100%	a 0.8/20%	a 0.8/40%	a 0.8/80%	a 0.8/100%
5	0.18	−0.01	0.36	0.21	0.20	0.15	0.37	0.23	0.17	0.17
6	0.28	0.19	0.49	0.28	0.24	0.07	0.48	0.27	0.18	0.18
7	0.45	0.43	0.49	0.41	0.38	0.35	0.49	0.35	0.31	0.19
8	0.52	0.50	0.53	0.52	0.50	0.50	0.56	0.46	0.43	0.40
9	0.56	0.53	0.59	0.53	0.53	0.51	0.59	0.52	0.52	0.50

,

Table 2. Correlation matrix of Negribreen. Extraction every 500 m and a 250 m circular buffer compared to Haga et al. [13]. The cluster threshold marks the number of anomalies within the moving window (of the size nine) at any position per time step.

Cluster threshold	a 0.05/20%	a 0.05/40%	a 0.05/80%	a 0.05/100%	a 0.1/20%	a 0.1/40%	a 0.1/80%	a 0.1/100%	a 0.2/20%	a 0.2/40%
5	0.49	0.4	0.4	0.27	0.48	0.38	0.38	0.3	0.44	0.36
6	0.63	0.54	0.54	0.38	0.61	0.5	0.5	0.32	0.58	0.48
7	0.65	0.63	0.63	0.6	0.65	0.6	0.6	0.52	0.66	0.58
8	0.68	0.71	0.71	0.71	0.68	0.68	0.68	0.65	0.73	0.65
9	0.76	0.74	0.74	0.74	0.76	0.74	0.74	0.74	0.76	0.74
Cluster threshold	a 0.2/80%	a 0.2/100%	a 0.4/20%	a 0.4/40%	a 0.4/80%	a 0.4/100%	a 0.8/20%	a 0.8/40%	a 0.8/80%	a 0.8/100%
5	0.36	0.27	0.41	0.34	0.34	0.16	0.42	0.29	0.29	0.11
6	0.48	0.26	0.58	0.44	0.44	0.18	0.56	0.4	0.34	0.13
7	0.58	0.46	0.66	0.54	0.54	0.41	0.63	0.51	0.48	0.26
8	0.65	0.63	0.73	0.6	0.58	0.54	0.73	0.56	0.56	0.41
9	0.74	0.74	0.76	0.65	0.65	0.65	0.72	0.6	0.6	0.56

and

Table 3. Correlation matrix of Strongbreen with velocity extraction every 500 m with a 250 m buffer compared to Benn et al. [44]. The cluster threshold marks the amount of anomalies within the moving window (of the size nine) at any position per time step.

Cluster threshold	a 0.05/20%	a 0.05/40%	a 0.05/80%	a 0.05/100%	a 0.1/20%	a 0.1/40%	a 0.1/80%	a 0.1/100%	a 0.2/20%	a 0.2/40%
5	0.93	0.90	0.90	0.87	0.93	0.90	0.87	0.85	0.93	0.87
6	0.93	0.90	0.90	0.90	0.93	0.90	0.90	0.90	0.93	0.90
7	0.89	0.86	0.90	0.90	0.89	0.90	0.93	0.93	0.89	0.86
8	0.89	0.89	0.89	0.89	0.89	0.86	0.86	0.86	0.89	0.90
9	0.86	0.93	0.93	0.93	0.86	0.93	0.93	0.93	0.86	0.89
Cluster threshold	a 0.2/80%	a 0.2/100%	a 0.4/20%	a 0.4/40%	a 0.4/80%	a 0.4/100%	a 0.8/20%	a 0.8/40%	a 0.8/80%	a 0.8/100%
5	0.85	0.82	0.93	0.87	0.85	0.77	0.93	0.87	0.82	0.67
6	0.90	0.90	0.93	0.87	0.87	0.87	0.93	0.87	0.87	0.85
7	0.90	0.90	0.93	0.86	0.90	0.90	0.93	0.90	0.90	0.90
8	0.90	0.90	0.89	0.90	0.90	0.90	0.89	0.90	0.93	0.93
9	0.89	0.89	0.86	0.89	0.89	0.89	0.86	0.86	0.86	0.86

. Alpha (a) controls the width of the “normal” range. The lower ‘a’ is set, the more conservative the classification becomes. Higher values of ‘a’ are less prone to incorrect classifications of “normal” observations [36]. An incorrect classification of “normal” refers to, e.g., stronger than usual seasonal fluctuations at a glacier’s terminus which statistically lie outside the norm but do not represent an outlier connected to a surge. Alpha may thus be understood as the width of an enveloping function on the remainder curve, where data points outside the envelop are classified as an outlier (see Figure 4).

Normal refers here to a data point which has not been classified as an outlier after being season and trend decomposed. The percentage stands for the maximum of anomalies per time series allowed to be detected. Table 1, Table 2 and Table 3 show Pearson correlation coefficients.

Table 1 shows the correlation between Haga et al. [13] findings and this study. It becomes apparent that the cluster threshold size of nine yields the best fit, while a ‘stricter’ parameterisation of the time series analysis also performs better. The combinations of a = 0.05 and a = 0.1 with a maximum amount of 20% anomalies per extraction point showed the best correlation. In Table 2, we compare the results of Negribreen again to Haga et al. [13] findings regarding surge duration, with less points extracted but with a buffer around each point that extracts the mean value of all values found in its radius. The extraction points were now set at every 500 m with a buffer of $r$ = 250 m. The highest correlation coefficients yet again are found for the largest cluster sizes. Multiple equally good performing settings can be found in the cluster size class of nine. Additionally, it may be stated that a smaller alpha positively impacts the results.

Benn et al. [44] analysed the mass and enthalpy evolution during a surge of Morsnevbreen/Strongbreen. As part of their study, they also measured the surface velocity evolution of Morsnevbreen based on TerraSAR-X data from 2013 to 2015 and Sentinel-1 velocity data from 2016 to 2018. They determined the surge initiation during summer 2016, which displayed high velocities up until the beginning of 2018 to which we compared our findings to. Strongbreen/Morsnevbreen was still in the quiescence phase at the end of 2015 and the active surge as well as the deceleration are within the observation period of this study. Thus, we chose Strongbreen/Morsnevbreen to be the second glacier for our sensitivity analysis. Compared to the distribution of high and low correlation coefficients to Negribreen, the picture appears heterogenous at first.

Noticeably the coefficients are higher throughout all parameter combinations. An explanation for that is the fact that the velocity increase was distinct as well as entirely observable in our study period. Both factors amount to a more robust classification of outliers. An indication that the strictest parameterisation a = 0.05 with 20% maximum allowance for outliers per time series (first column in Table 3) has been found is the smaller threshold settings correlate better than larger ones, which means the size of the moving window does not attribute to better performance.

The overall strictest but best fitting parameterisation has thus been determined to be a = 0.05 and 40% maximum anomalies and a cluster threshold of 9. It is the best fitting combination that is the least prone to wrongful detection of outliers. It is also the parameterisation applied in this study for all glaciers alike.

To conclude, two criteria were the focus of the sensitivity study: (1) to determine the most optimal setting for detecting the onset of the active surge with the GESD, and (2) to differentiate between a surge and velocity fluctuations not being linked to surges. The latter could be solved by classifying a surge if four or more months were consecutively determined to be anomalous in regard to their surface velocity.

5. Results

The algorithm presented in this study identified 18 active phases of glacier surges between September 2015 and September 2021. In Figure 5, we plot all detected anomalies that represent the acceleration phase of a glacier surge in a Gantt chart. More than four consecutive blue marked months represent onset and thus the beginning of the acceleration period of an active surge cycle of each glacier.

It becomes evident that surge type glaciers on Svalbard undergo different patterns in terms of their active surge phases. It could also be demonstrated that surges throughout the archipelago incite at all seasons throughout the year, which is an expectable behaviour for thermally controlled surge-type glaciers. Four or more consecutive months displaying anomalous flow, labelled dark blue in Figure 5, mark the beginning of the active phase of a surge, where velocities have been increasing strongly. While some glaciers undergo comparably distinct and steady velocity increases, most others such as Strongbreen, Sonklarbreen, Tunabreen, or Recherchebreen show increases in velocity only over periods of 9–11 months, followed by years of deceleration before entering the quiescence phase. Figure 5 also reveals that some glaciers do show more irregular flow patterns, such as Orsabreen, Penckbreen or Stonebreen, where multiple months are classified as irregular. Figure 6 displays the distribution of the detected surges on Svalbard. Active surges were observable in all parts of the Archipelago, however it can be observed that most glaciers are marine terminating and comprised of the larger glaciers.

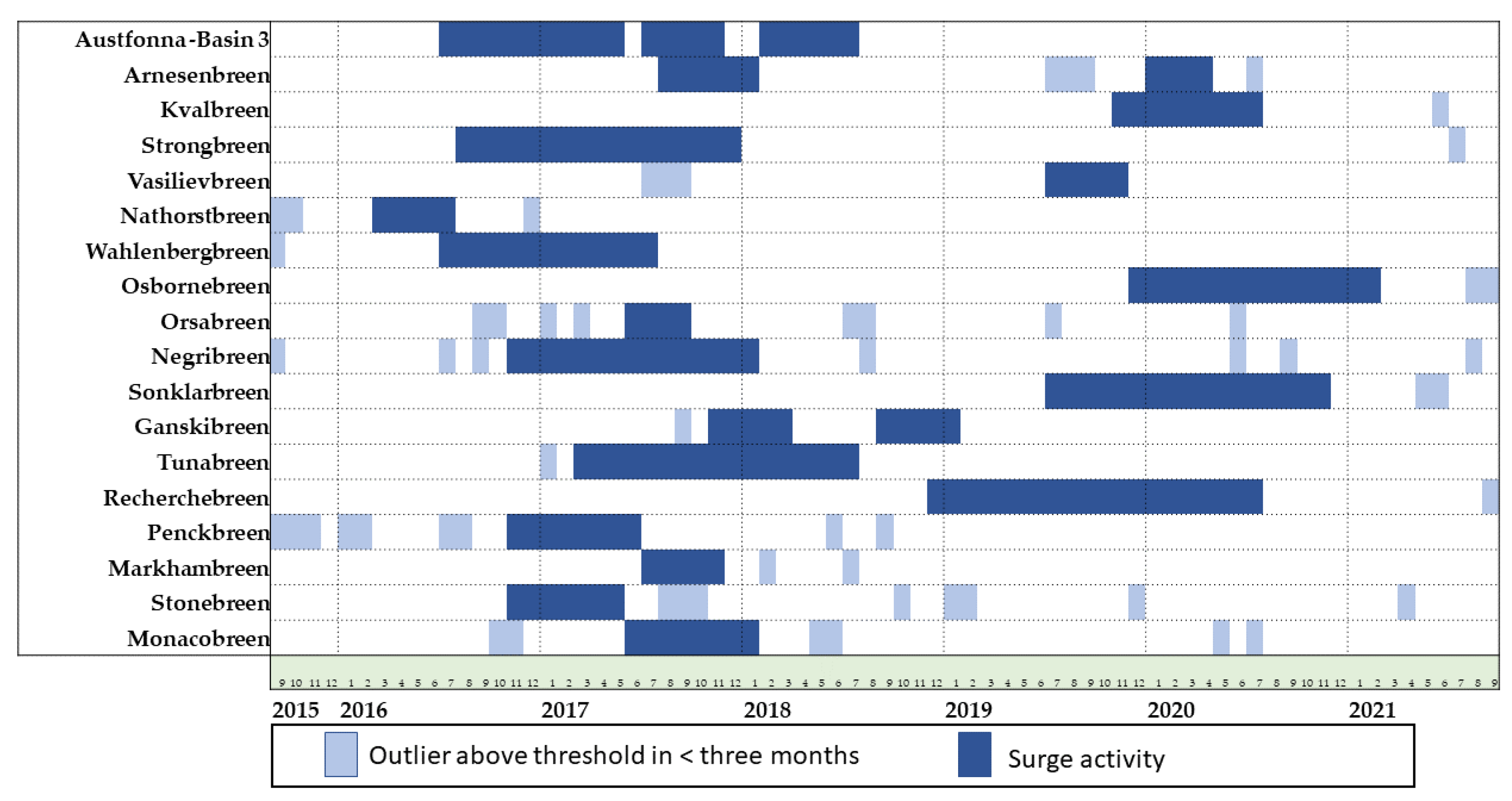
6. Discussion

The algorithm presented in this study has proven to perform well, considering the already large intra-annual velocity fluctuations that many marine-terminating glaciers on Svalbard undergo. We were not only able to detect surges, but also, and maybe more importantly, the timing of strong acceleration attributed to active cycles. Even though the Gantt chart might seem noisy at a first glance (as, e.g., for Negribreen), most of the detected fluctuations (light blue in Figure 5) are linked to the beginning of a surge and not found in others during the same period. Similar patterns are observable after peak velocities have been surpassed. Nonetheless, it should be stated at this point that some tidewater terminating glaciers undergo unregular fluctuations which are not entirely removed by seasonal detrending and are thus also detected as outliers. Furthermore, for an interpretation of the exact timing of the onset of a surge, it should be taken into consideration that strong seasonal fluctuations, especially of larger tidewater glaciers, may bias the determination of the exact surge onset by one to two months. Even though it is common for a glacier to slow down before entering the active phase, the slowdown can bias the identified seasonality which subsequently is being removed from the entirety of the time series. As a result, an acceleration attributed to the surge onset might be superimposed by the removal of the seasonality, especially in summer months and if the surge onset is closer to the glaciers terminus, where velocity fluctuations are the largest. A mismatch in terms of exact onset is possible here. This potentially becomes more problematic if the onset of the active phase is before the observation period, since the quiescence phase before the onset is not captured. Nonetheless, the algorithm proves to be able to detect anomalous flow behaviour, linked to glacier surges not only shown by the sensitivity studies but also in comparison to some other recently published work. A study by [31] offers the opportunity to compare our region-wide results with an approach that uses the same satellite system, but based on the analysis of backscatter intensity changes linked to changes in surface morphology during surges. They were able to determine 14 surging glaciers on Svalbard by comparing imagery from 2018 to 2019. Out of these 14 glaciers, 12 were detected by the approach presented in this study, further validating the presented findings. One of them being Svalisbreen, did not undergo a strong velocity increase during our observation period, hence the algorithm did not mark any month outside May 2018 as anomalous, similar to Brasvellbreen, a large southern tidewater glacier of Austfonna. We do see some irregularities in surface velocities in 2018, but some data points are missing. This may have led to not classifying the velocity increase accordingly. The timing or possibility of surge appearance of other detected surges presented in this paper is also in line with the findings of previous studies on Svalbard (see

Table 4. Comparison of findings in this study to other recent studies. If direct measurements were taken, the timing of the corresponding study is given. Leclercq et al. [31] measured the backscatter intensity change from 2018–2019, and increases and decreases linked to surge activity that most likely represent the same surges found here. If a surge was detected in their study, it is denoted as “surged in recent past”, since a direct derivation regarding the timing is not possible. If no recent study was found, the likeliness or documentation of a past surge is taken as criteria.

Glacier	This Study	Other Studies	Source
Austfonna Basin 3	May 2016–Aug. 2018	surged in recent past	Leclercq et al. [31]
Arnesenbreen	Aug. 2017–Jan. 2018 & Jan. 2020–April 2020	surged in recent past	Leclercq et al. [31]
Kvalbreen	Nov. 2019–July 2020	possible surge type	Leclercq et al. [31], Benn et al. [44], Farnsworth et al. [45]
Strongbreen	July 2016–Dec. 2017	July 2016–End of 2017	Leclercq et al. [31], Benn et al. [44]
Vasilievbreen	July 2019–Nov. 2019	documented surge type	Farnsworth et al. [45]
Wahlenbergbreen	July 2016–Aug. 2017	surged in recent past	Leclercq et al. [31]
Osbornebreen	Dec. 2019–Feb. 2021	documented surge type	Farnsworth et al. [45]
Orsabreen	May–Aug. 2017	documented surge type	Farnsworth et al. [45]
Negribreen	Nov. 2016–Feb. 2018	Dec. 2016–March 2018	Haga et al. [13], Leclercq et al. [31], Herzfeld et al. [46]
Sonklarbreen	Jun. 2019–Nov. 2020	2019–2020	Leclercq et al. [31], Andreassen et al. [47]
Ganskibreen	Nov. 2017–March 2018 Sep. 2018–Jan. 2019	2017–2018	Leclercq et al. [31], Andreassen et al. [47]
Tunabreen	March 2017–Aug. 2018	surged in recent past	Leclercq et al. [31]
Recherchebreen	Dec. 2018–Aug. 2020	surged in recent past	Leclercq et al. [31]
Penckbreen	Nov. 2016–Jun. 2017	Sep. 2016–April 2017	Leclercq et al. [31], Strozzi et al. [48]
Markhambreen	Jul. 2017–Dec. 2017	possible surge type	Farnsworth et al. [45]
Stonebreen	Nov. 2017–May 2018	surged in recent past	Leclercq et al. [31]
Monacobreen	May 2017–Feb 2018	2017–2018	Banerjee et al. [11], Leclercq et al. [31]

).

Concerning the differing length of the detected surges, it should be noted that a longer surge propagation downwards or upwards of the glacier increases the measured temporal length of a surge. This is due to the cluster analysis that looks for an anomaly cluster row-wise or monthly and marks a month as anomalous if one cluster is above the threshold. If a surge bulge now propagates the flow line from a reservoir far up downwards, a longer surge duration is determined. Thus, for further analysis, the glacier length has to be considered. Nathorstbreen’s detected surge in the summer months of 2016 appears to be wrongfully classified as such, since a set of surges from its major tributary glaciers has been reported from 2009 to 2014 with maximum velocities reaching 25 m/day in 2009 [49]. The anomalous flow detected by our algorithm thus does mark the beginning of a surge, but dynamic adjustments of the glacier close to its terminus where surface velocities were exceeding ~4–5 m/day during summer 2016. This speed up could be linked to high summer temperatures leading to increasing velocities at the unstable terminus which has advanced ~12 km during its surge prior our observation period. Another potential misclassification in this study is Stonebreen. In this study, the beginning of the glacier’s surge was determined as late summer 2016, with maximum velocities surpassing 6.5 m/day. A study by Strozzi et al. [48] revealed summer velocity peaks in both 2013 and 2014 at around 6 m/day. While Strozzi et al. [48] categorize the observed process at Stonebreen not as a classical surge but rather compare its flow behaviour and speed ups similar to a surge, Leclercq et al. [31] list it as surge-type in their recent study from 2021. Given that example, it should be noted that this approach does not exclusively determine surges per se, but anomalous flow. Dynamical adjustments by large tidewater glaciers to either large calving events or frontal collapses followed by subsequent strong multi-annual ice-flow acceleration are also detected. This does not necessarily have negative implications on the quality of the detection but should be kept in mind when analysing large amounts of data in regions where glaciers are marine terminating.

7. Conclusions

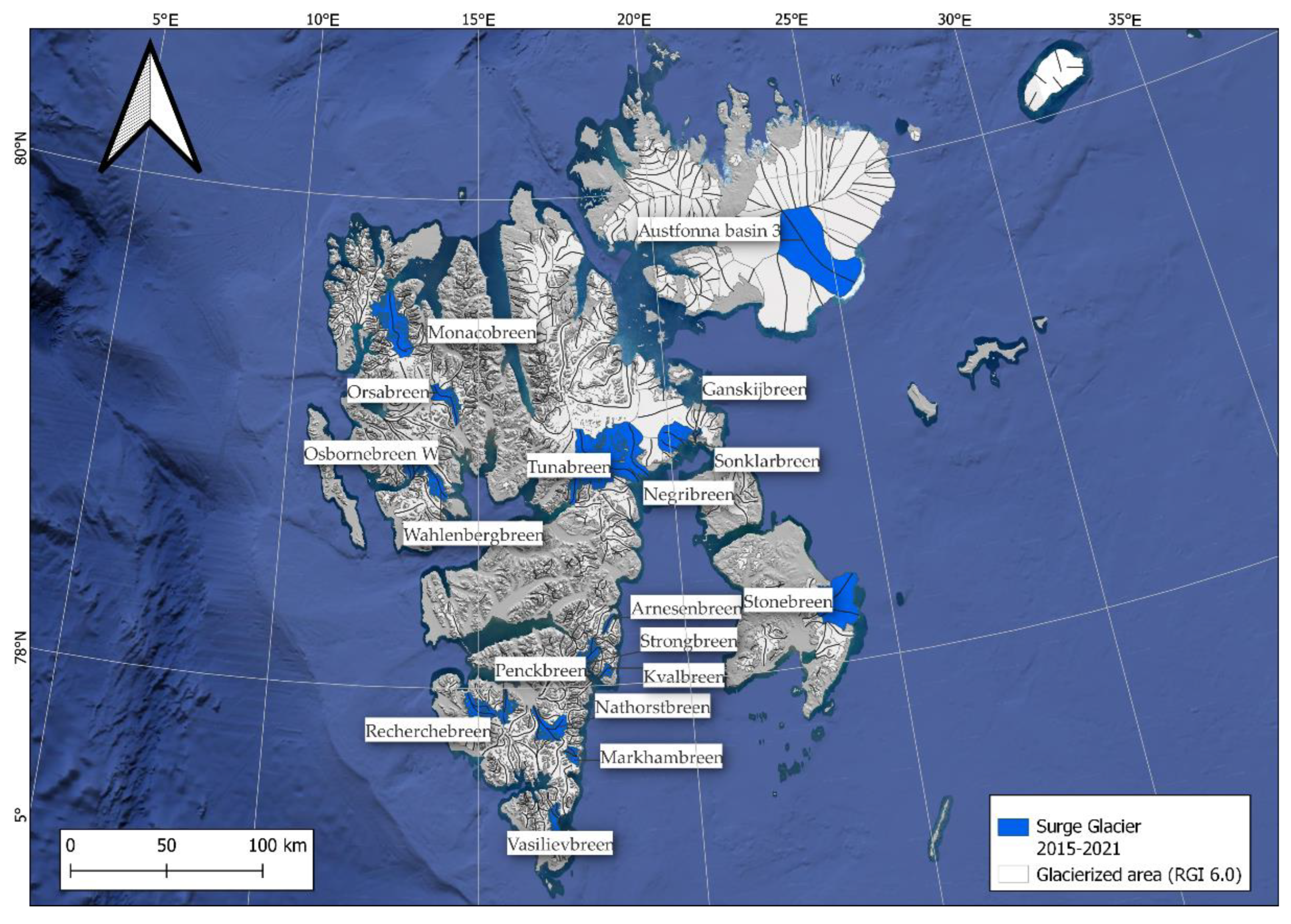
We presented an approach to detect glacier surges based on a time-series analysis of surface velocity data which could be able to close knowledge gaps about the timing of surges on regional scales. By applying the GESD, implemented in an algorithm well suited to determine outliers in extracted point data with seasonality and trend, we found a time efficient way of treating large amounts of data. To ensure the determined set of outliers is found within a given part of the glacier and not randomly distributed along it, we applied a cluster analysis within a moving window on our dataset. By doing so, at least 4.5 km of 5 km have to be categorized as anomalous before a month is being marked as such. The threshold (four consecutive months) was set to deal mainly with strong seasonal fluctuations of large tidewater glaciers. Transferring the algorithm to other regions with no marine or lake terminating glaciers similar to Pamir or Karakoram might need a re-evaluation of this threshold. Datasets like these are crucial for further understanding underlying and controlling processes of glacier surges and potentially filling existing knowledge gaps. We demonstrated our methods on Svalbard, where we successfully determined the onset of 18 individual surges between 2015 and 2021. The misclassification of Stonebreen as surge type has also shown unusual high velocity increases can be attributed to, e.g., dynamic responses to the frontal destabilisation of tidewater glaciers. This however may be seen as an opportunity to observe different kinds of events linked to velocity increases outside the norm. To increase the overall accuracy of surge determination based on remote sensing data, a combinational approach of, e.g., elevation changes or different methods based on the same sensors might yield the opportunity of unprecedented accuracy in the detection of surges in both spatial and temporal resolution. Moreover, the method presented here is not limited to a single source of data. Application on data of other sensors such as ITS_LIVE, time-series of ERS/ENVISAT data would greatly enhance the temporal resolution and/or coverage. The analysis of sub-monthly, long-lasting time-series would add an additional layer of information vital to the understanding of why and where surges incite. Building longer time-series based on missions such as ITS_LIVE would enable to observe multiple surge cycles, potentially answering questions of how and if climate change affects surge cycles, ultimately adding important information to the overall understanding of what drives surges to what extent. The data analysis is not exclusive to the identification of glacier surges. Simultaneously, trend analysis for whole regions can be performed to find patterns of decreasing or increasing ice flow over given periods of time. With minor adjustments, the observation periods could then be split in hydrological years, and shifts in the seasonal flow behaviour could be analysed.

With today’s ever-increasing amount of remote sensing data, new approaches for time-series analysis yield great prospects in the detection of surge type glaciers. The presented algorithm offers a unique opportunity in analysing data from different satellite systems, further expanding its applicability and transferability to other regions, time domains, and in an unprecedented temporal resolution. In times of high-performance computing, ever increasing knowledge about surge-type glaciers and increasing identification of such, a general trend towards open access publications and data distribution, validation, and comparison of results on a global scale offers an extraordinary opportunity to understand the dynamics and underlying physical components behind glacier surges. The approach developed here demonstrates the potential opportunities presented by openly accessible, continuous data sets. Thinking further, fully automated processes of anomaly detection by an implementation of algorithms such as or similar to the one presented here, can lead to the development of near real time, global scale early warning systems, reducing the hazards imposed by surges and other extreme events in glaciated regions.