DEM Generation from GF-7 Satellite Stereo Imagery Assisted by Space-Borne LiDAR and Its Application to Active Tectonics
Abstract
1. Introduction
2. Study Site and Materials
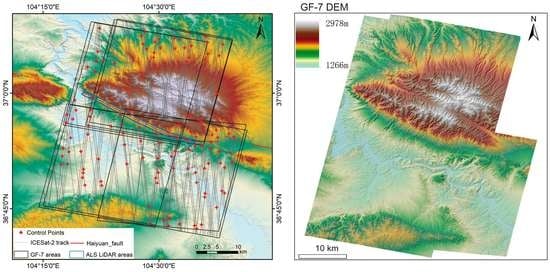
2.1. Study Site
2.2. GF-7 Data
2.3. ICESat-2/ATLAS Data
2.4. Airborne LiDAR Data
2.5. Ancillary Data
3. Methods
3.1. Extraction of GCPs from ICESat-2/ATLAS Data
3.2. Extraction of DEMs from GF-7 Stereo Images
- Block adjustment without GCPs. This method was essential for selecting some tie points in the GF-7 images and calculating the object space coordinates for each pair of GF-7 stereo pixels, utilizing the space-forward intersection. The final object space coordinate of the tie point was the average coordinate of the tie points between each pair of GF-7 stereo pixels. These tie points were utilized as the virtual GCPs in the block adjustment process.
- Block adjustment with the aid of geographic information system (GIS) data. This method utilized the existing GIS data (such as digital orthophoto maps (DOM) and DEMs) to assist the block adjustment of stereo images. First, a large number of cognominal points were obtained through the automatic registration of the GF-7 satellite images and the existing DOM. Second, the DOM and DEM were used to obtain these cognominal points’ horizontal and elevation coordinates, respectively. Finally, these cognominal points were taken as the control points. In addition to the basic geographic information data (the DOM and DEM), public geographic information data can also be utilized. The most commonly used public geographic information data are Google Earth images and SRTM DEM [21,22,23].
- Block adjustment with GCPs. This method used high-precision GCPs to constrain the elevation values of the forward intersection of the GF-7 stereo images. The most commonly used GCPs can be obtained from space-borne LiDAR data, such as ICESat-1/GLAS and ICESat-2/ATLAS.
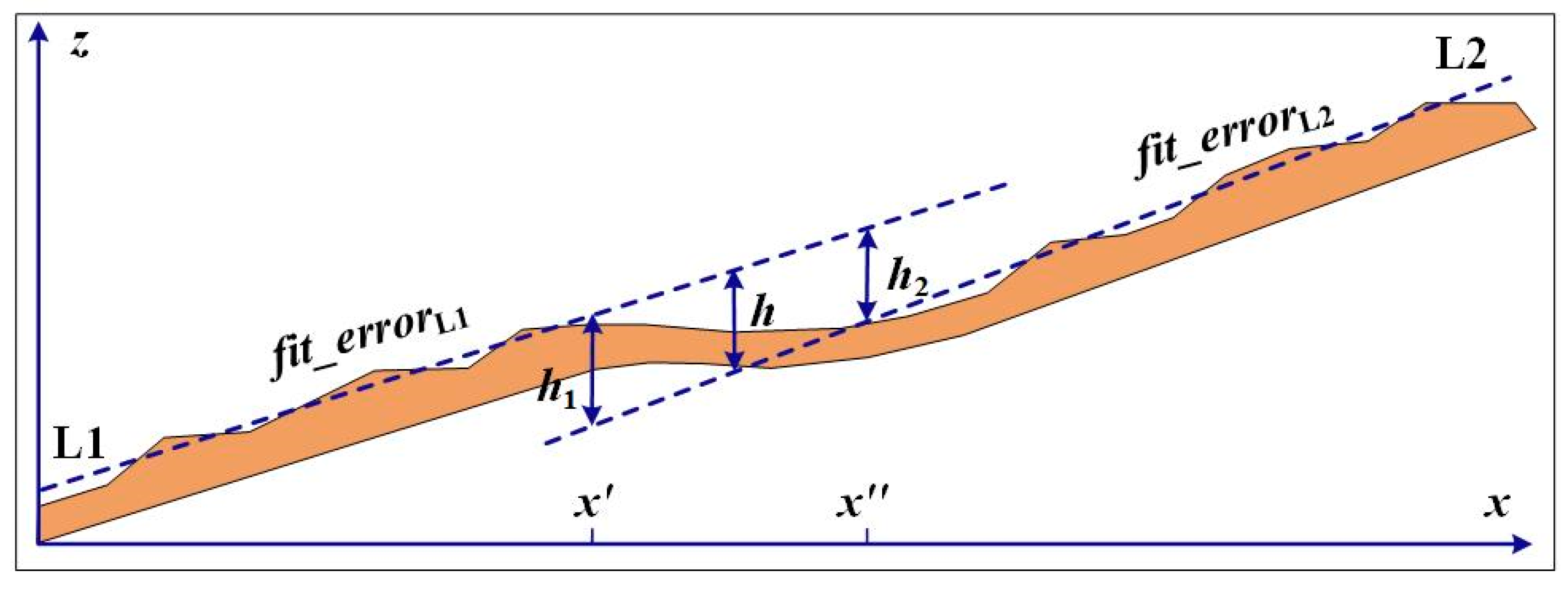
3.3. Measurement of the Horizontal and Vertical Offsets
3.4. Validation of Accuracy
4. Results and Discussion
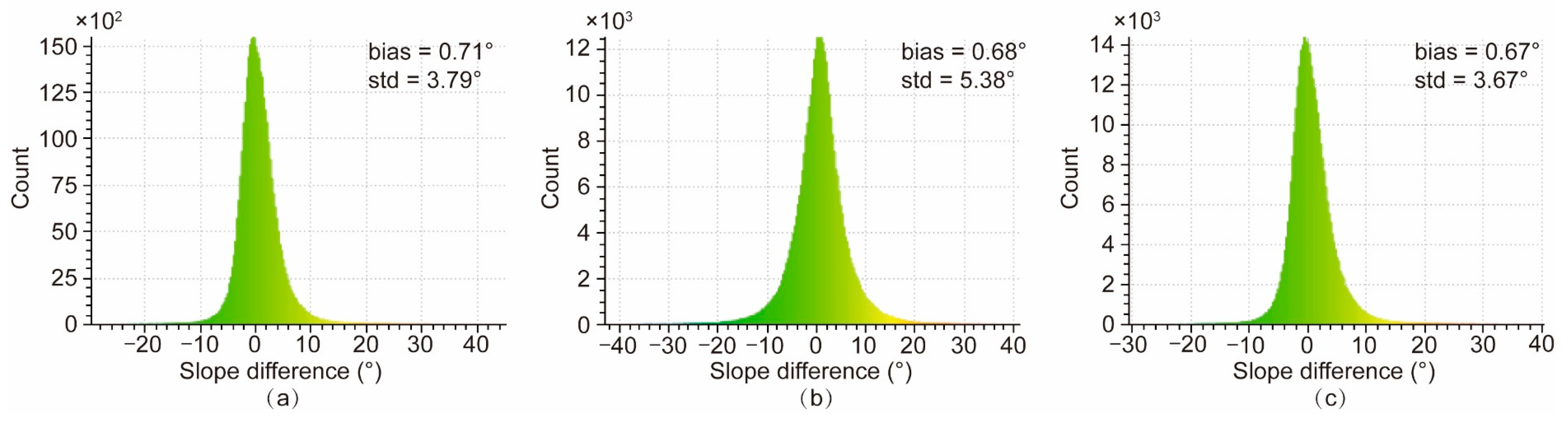
4.1. Validation of the Accuracy and a Comparison of the GF-7 DEMs
4.2. Observations of the Offset Based on GF-7 DEM
4.3. Comparison of the Measurements of the Vertical Offsets
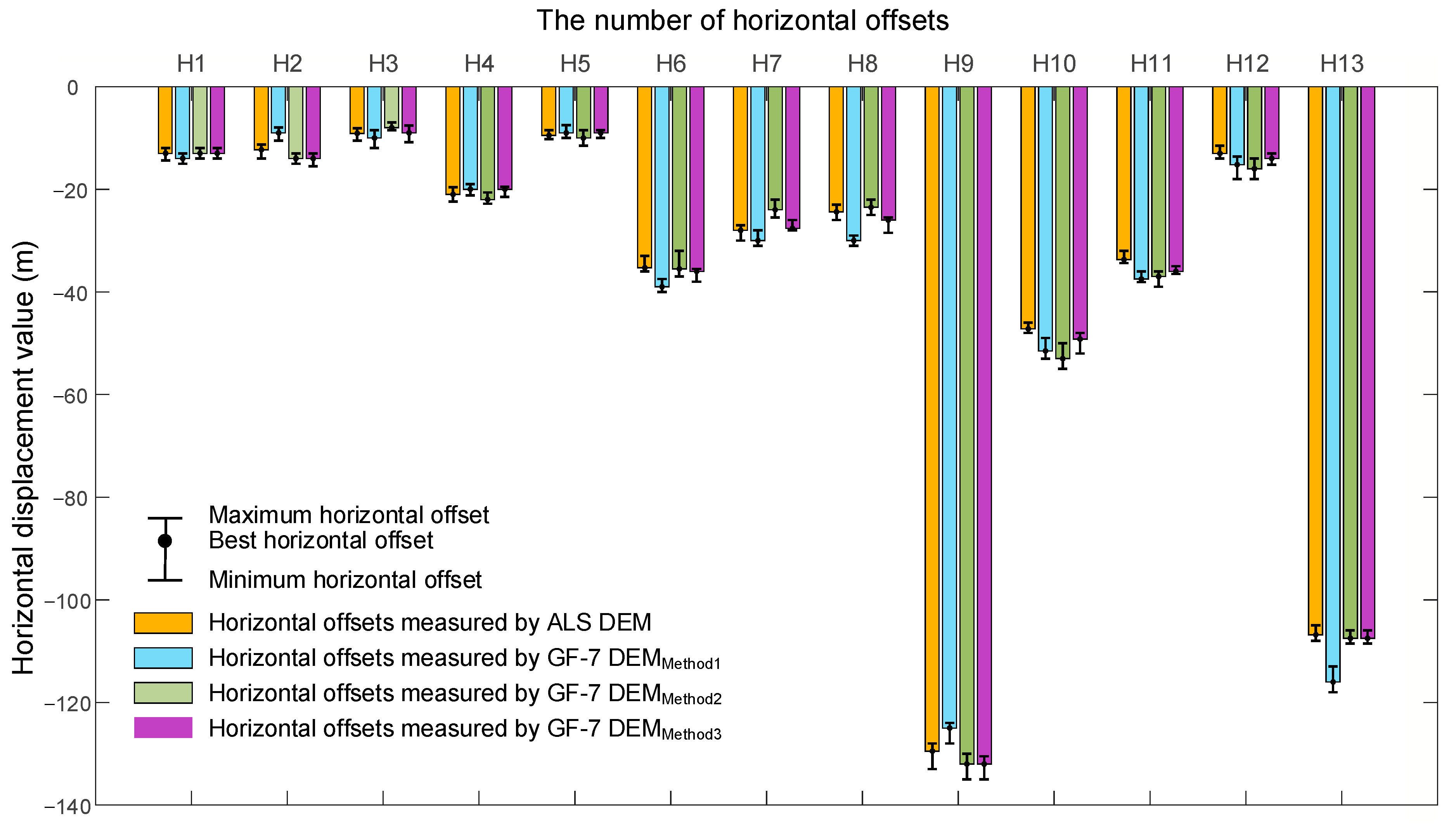
4.4. Comparison of the Measurements of the Horizontal Offset
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Deng, Q.; Chen, L.; Ran, Y. Quantitative Studies and Applications of Active Tectonics. Earth Sci. Front. 2004, 11, 383–392. [Google Scholar] [CrossRef]
- Ren, Z.; Zielke, O.; Yu, J. Active tectonics in 4D high-resolution. J. Struct. Geol. 2018, 117, 264–271. [Google Scholar] [CrossRef]
- Liu, J.; Chen, T.; Zhang, P.; Zhang, H.; Zheng, W.; Ren, Z.; Liang, S.; Sheng, C.; Gan, W. Illuminating the Active Haiyuan Fault, China by Airborne Light Detection and Ranging. Chin. Sci. Bull. 2013, 58, 41–45. [Google Scholar] [CrossRef]
- Chen, T.; Zhang, P.; Liu, J.; Li, C.; Ren, Z.; Hudnut, K. Quantitative study of tectonic geomorphology along Haiyuan fault based on airborne LiDAR. Chin. Sci. Bull. 2014, 59, 2396–2409. [Google Scholar] [CrossRef]
- Ren, Z.; Zhang, Z.; Chen, T.; Yan, S.; Yin, J.; Zhang, P.; Zheng, W.; Zhang, H.; Li, C. Clustering of offsets on the Haiyuan fault and their relationship to paleoearthquakes. Bulletin 2016, 128, 3–18. [Google Scholar] [CrossRef]
- Wang, S.; Ren, Z.; Wu, C.; Lei, Q.; Gong, W.; Ou, Q.; Zhang, H.; Ren, G.; Li, C. DEM generation from Worldview-2 stereo imagery and vertical accuracy assessment for its application in active tectonics. Geomorphology 2019, 336, 107–118. [Google Scholar] [CrossRef]
- Nissen, E.; Maruyama, T.; Arrowsmith, J.R.; Elliott, J.R.; Krishnan, A.K.; Oskin, M.E.; Saripalli, S. Coseismic fault zone deformation revealed with differential lidar: Examples from Japanese M-w similar to 7 intraplate earthquakes. Earth Planet. Sci. Lett. 2014, 405, 244–256. [Google Scholar] [CrossRef]
- Liu, J.; Ren, Z.; Zhang, H.; Li, C.; Zhang, Z.; Zheng, W.; Li, X.; Liu, C. Slip Rates Along the Laohushan Fault and Spatial Variation in Slip Rate Along the Haiyuan Fault Zone. Tectonics 2022, 41, e2021TC006992. [Google Scholar] [CrossRef]
- Johnson, K.; Nissen, E.; Saripalli, S.; Arrowsmith, J.R.; McGarey, P.; Scharer, K.; Williams, P.; Blisniuk, K. Rapid mapping of ultrafine fault zone topography with structure from motion. Geosphere 2014, 10, 969–986. [Google Scholar] [CrossRef]
- Bekaert, D.; Handwerger, A.L.; Agram, P.; Kirschbaum, D.B. InSAR-based detection method for mapping and monitoring slow-moving landslides in remote regions with steep and mountainous terrain: An application to Nepal. Remote Sens. Environ. 2020, 249, 111893. [Google Scholar] [CrossRef]
- Zhang, Y.; Meng, X.; Dijkstra, T.; Jordan, C.; Chen, G.; Zeng, R.; Novellino, A. Forecasting the magnitude of potential landslides based on InSAR techniques. Remote Sens. Environ. 2020, 241, 111738. [Google Scholar] [CrossRef]
- Bagnardi, M.; Gonzalez, P.J.; Hooper, A. High-resolution digital elevation model from tri-stereo Pleiades-1 satellite imagery for lava flow volume estimates at Fogo Volcano. Geophys. Res. Lett. 2016, 43, 6267–6275. [Google Scholar] [CrossRef]
- Shean, D.E.; Alexandrov, O.; Moratto, Z.M.; Smith, B.E.; Joughin, I.R.; Porter, C.; Morin, P. An automated, open-source pipeline for mass production of digital elevation models (DEMs) from very-high-resolution commercial stereo satellite imagery. ISPRS J. Photogramm. Remote Sens. 2016, 116, 101–117. [Google Scholar] [CrossRef]
- Zhou, Y.; Parsons, B.; Elliott, J.R.; Barisin, I.; Walker, R.T. Assessing the ability of Pleiades stereo imagery to determine height changes in earthquakes: A case study for the El Mayor-Cucapah epicentral area. J. Geophys. Res. Solid Earth 2015, 120, 8793–8808. [Google Scholar] [CrossRef]
- Martha, T.R.; Govindharaj, K.B.; Kumar, K.V. Damage and geological assessment of the 18 September 2011 M-w 6.9 earthquake in Sikkim, India using very high resolution satellite data. Geosci. Front. 2015, 6, 793–805. [Google Scholar] [CrossRef]
- Ou, Q.; Kulikova, G.; Yu, J.; Elliott, A.; Parsons, B.; Walker, R. Magnitude of the 1920 Haiyuan Earthquake Reestimated Using Seismological and Geomorphological Methods. J. Geophys. Res. Solid Earth 2020, 125, e2019JB019244. [Google Scholar] [CrossRef]
- Bi, H.; Zheng, W.; Lei, Q.; Zeng, J.; Zhang, P.; Chen, G. Surface Slip Distribution Along the West Helanshan Fault, Northern China, and Its Implications for Fault Behavior. J. Geophys. Res. Solid Earth 2020, 125, e2020JB019983. [Google Scholar] [CrossRef]
- Liu, C.; Cui, X.; Guo, L.; Wu, L.; Tang, X.; Liu, S.; Yuan, D.; Wang, X. Satellite Laser Altimetry Data-Supported High-Accuracy Mapping of GF-7 Stereo Images. Remote Sens. 2022, 14, 5868. [Google Scholar] [CrossRef]
- Chen, J.; Tang, X.; Xue, Y.; Li, G.; Zhou, X.; Hu, L.; Zhang, S. Registration and Combined Adjustment for the Laser Altimetry Data and High-Resolution Optical Stereo Images of the GF-7 Satellite. Remote Sens. 2022, 14, 1666. [Google Scholar] [CrossRef]
- Sun, Y.; Nie, S.; Li, G.; Huang, X.; Liu, Z.; Wang, C.; Xi, X.; Yu, J. Evaluation of the performance of GaoFen-7 laser altimeter data for ground elevation retrieval over vegetated areas. Remote Sens Lett. 2022, 13, 991–1001. [Google Scholar] [CrossRef]
- Pan, X.; Jiang, T.; Yu, A.; Zhang, Y.; Yu, L. Block Adjustment of High-Resolution Satellite Images with Google Earth. J. Geomat. Sci. Technol. 2017, 34, 622–627. [Google Scholar]
- Mumtaz, R.; Palmer, P.L.; Waqar, M.M. Georeferencing of UK DMC stereo-images without ground control points by exploiting geometric distortions. Int. J. Remote Sens. 2014, 35, 2136–2169. [Google Scholar] [CrossRef]
- Zhou, P.; Tang, X.; Wang, Z.; Cao, N.; Wang, X. SRTM-assisted block adjustment for stereo pushbroom imagery. Photogramm. Rec. 2018, 33, 49–65. [Google Scholar] [CrossRef]
- Ye, J.; Qiang, Y.; Zhang, R.; Liu, X.; Deng, Y.; Zhang, J. High-Precision Digital Surface Model Extraction from Satellite Stereo Images Fused with ICESat-2 Data. Remote Sens. 2022, 14, 142. [Google Scholar] [CrossRef]
- Shang, D.; Zhang, Y.; Dai, C.; Ma, Q.; Wang, Z. Extraction Strategy for ICESat-2 Elevation Control Points Based on ATL08 Product. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5705012. [Google Scholar] [CrossRef]
- Zhang, P.; Peter, M.; Burchfiel, B.C.; Royden, L.; Wang, Y.; Deng, Q.; Song, F.; Zhang, W.; Jiao, D. Bounds on the Holocene Slip Rate of the Haiyuan Fault, North-Central China. Quat. Res. 1988, 30, 151–164. [Google Scholar] [CrossRef]
- Xie, J.; Huang, G.; Liu, R.; Zhao, C.; Dai, J.; Jin, T.; Mo, F.; Zhen, Y.; Xi, S.; Tang, H.; et al. Design and Data Processing of China’s First Spaceborne Laser Altimeter System for Earth Observation: GaoFen-7. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1034–1044. [Google Scholar] [CrossRef]
- Tang, X.; Liu, C.; Zhang, H.; Wang, X.; Li, G.; Mo, F.; Li, F. GF⁃7 Satellite Stereo Images Block Adjustment Assisted with Laser Altimetry Data. Geomat. Inf. Sci. Wuhan Univ. 2021, 46, 1423–1430. [Google Scholar] [CrossRef]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D.; et al. The ice, cloud, and land elevation satellite-2 (ICESat-2): Science requirements, concept, and implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Neumann, T.A.; Martino, A.J.; Markus, T.; Bae, S.; Bock, M.R.; Brenner, A.C.; Brunt, K.M.; Cavanaugh, J.; Fernandes, S.T.; Hancock, D.W.; et al. The ice, cloud, and land elevation Satellite-2 Mission: A global geolocated photon product derived from the advanced topographic laser altimeter system. Remote Sens. Environ. 2019, 233, 111325. [Google Scholar] [CrossRef]
- Bi, H.; Zheng, W.; Ren, Z.; Zeng, J.; Yu, J. Using an unmanned aerial vehicle for topography mapping of the fault zone based on structure from motion photogrammetry. Int. J. Remote Sens. 2017, 38, 2495–2510. [Google Scholar] [CrossRef]
- Liu, A.; Cheng, X.; Chen, Z. Performance evaluation of GEDI and ICESat-2 laser altimeter data for terrain and canopy height retrievals. Remote Sens. Environ. 2021, 264, 112571. [Google Scholar] [CrossRef]
- Grodecki, J.; Dial, G. Block Adjustment of High⁃Resolution Satellite Images Described by Rational Functions. Photogramm. Eng. Remote Sens. 2003, 69, 59–68. [Google Scholar] [CrossRef]
- Li, G.; Tang, X.; Gao, X.; Wang, H.; Wang, Y. ZY-3 Block adjustment supported by glas laser altimetry data. Photogramm. Rec. 2016, 31, 88–107. [Google Scholar] [CrossRef]
- Yang, B.; Wang, M.; Xu, W.; Li, D.; Gong, J.; Pi, Y. Large-scale block adjustment without use of ground control points based on the compensation of geometric calibration for ZY-3 images. ISPRS J. Photogramm. Remote Sens. 2017, 134, 1–14. [Google Scholar] [CrossRef]
- Zielke, O.; Arrowsmith, J.R.; Ludwig, L.G.; Akciz, S.O. Slip in the 1857 and earlier large earthquakes along the Carrizo Plain, San Andreas Fault. Science 2010, 327, 1119–1122. [Google Scholar] [CrossRef]
- Ai, M.; Bi, H.; Zheng, W.; Yin, J.; Yuan, D.; Ren, Z.; Chen, G.; Liu, J. Using unmanned aerial vehicle photogrammetry technology to obtain quantitative parameters of active tectonics. Seismol. Geol. 2018, 40, 1276–1293. [Google Scholar] [CrossRef]
- Rusinkiewicz, S.; Levoy, M. Efficient variants of the ICP algorithm. In Proceedings of the 3rd International Conference on 3-D Digital Imaging and Modeling, Quebec City, QC, Canada, 28 May–1 June 2001. [Google Scholar] [CrossRef]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D comparison of complex topography with terrestrial laser scanner: Application to the Rangitikei canyon (N-Z). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar] [CrossRef]







| Number | Sensor | Product Level | Product ID | Acquisition Time | Cloud Ratio | Coordinate System |
|---|---|---|---|---|---|---|
| 1 | Dual-line-array camera | LEVEL1A | 11181 | 4 December 2019 | 5% | WGS 84 |
| 2 | Dual-line-array camera | LEVEL1A | 11182 | 4 December 2019 | 5% | WGS 84 |
| 3 | Dual-line-array camera | LEVEL1A | 51458 | 11 February 2020 | 5% | WGS 84 |
| 4 | Dual-line-array camera | LEVEL1A | 264266 | 7 December 2020 | 1% | WGS 84 |
| Space-Borne LiDAR | ICESat-2/ATLAS |
|---|---|
| Product | ATL08 |
| Version | Version 5 |
| Vertical datum | WGS 84 ellipsoid |
| Terrain parameters | h_te_best_fit |
| Location parameters | latitude, longitude |
| Other parameters | atlas_beam_type: dummy indicating strong beams or weak beams |
| cloud_flag_atm: cloud confidence flag | |
| dem_h: the elevation of the terrain of the reference DEM | |
| h_te_skew: the skewness of the heights of the ground photons | |
| h_te_uncertainty: uncertainty of the mean terrain height for the 100 m segment | |
| n_ca_photons: the number of canopy photons within the 100 m segment | |
| n_te_photons: the number of ground photons within the 100 m segment | |
| n_toc_photons: the number of top of canopy photons within the 100 m segment | |
| night_flag: dummy indicating the data acquisition time, 0 = day, 1 = night | |
| segment_landcover: land cover surface type classification, where 60 represents bare, sparse vegetation | |
| subset_te_flag: quality flag | |
| terrain_slope: the along-track terrain slope of each 100 m segment |
| Steps | Filter Criteria |
|---|---|
| 1 | night_flag = 1 |
| 2 | atlas_beam_type = strong |
| 3 | h_te_uncertainty < 3.4028235 × 1038 |
| 4 | |h_te_best_fit−dem_h| < 50 |
| 5 | terrain_slope < 0.05 |
| 6 | |
| 7 | h_te_uncertainty < 327.6 |
| 8 | h_te_skew < 6.03 |
| 9 | Five flags of subset_te_flag greater than −1 with the middle three flags equal to 1 |
| 10 | cloud_flag_atm <= 2 |
| 11 | segment_landcover = 60 |
| 12 | The distances between ATL08 points should be larger than 500 m |
| ID | DEMMethod1 | DEMMethod2 | DEMMethod3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ΔX (m) | ΔY (m) | ΔZ (m) | ΔX (m) | ΔY (m) | ΔZ (m) | ΔX (m) | ΔY (m) | ΔZ (m) | |
| 1 | 149.77 | −201.53 | −130.55 | 4.69 | −0.21 | 5.24 | 0.50 | 1.20 | 1.16 |
| 2 | 148.46 | −200.34 | −130.39 | 0.90 | 0.18 | 6.04 | 0.40 | 2.21 | 2.55 |
| 3 | 157.04 | −201.51 | −129.07 | 3.20 | 0.63 | 1.43 | 0.40 | 0.73 | −2.20 |
| 4 | 158.32 | −199.87 | −128.46 | 0.37 | −0.38 | 1.46 | 0.18 | 1.63 | −2.50 |
| 5 | 163.89 | −204.72 | −130.49 | 7.68 | −2.97 | −2.14 | 2.42 | −3.42 | −1.01 |
| 6 | 159.40 | −202.56 | −127.09 | 2.14 | −3.10 | −0.76 | −2.03 | −0.38 | −0.26 |
| 7 | 163.83 | −200.53 | −124.44 | 2.26 | −0.81 | −0.13 | 0.06 | −0.12 | −0.75 |
| 8 | 168.24 | −198.69 | −121.77 | 3.03 | 0.42 | −0.46 | 0.45 | 3.60 | −0.53 |
| 9 | 174.50 | −201.82 | −115.70 | 2.61 | −0.33 | 2.04 | −0.02 | 0.90 | −1.24 |
| 10 | 178.16 | −202.59 | −111.41 | 2.25 | −3.15 | 1.57 | 0.13 | 0.47 | −1.72 |
| 11 | 179.35 | −200.34 | −108.97 | 1.16 | −2.41 | 1.76 | −0.67 | 0.20 | −0.55 |
| 12 | 182.20 | −204.23 | −105.27 | −0.58 | −7.23 | 1.34 | −3.45 | −4.60 | −1.84 |
| 13 | 188.54 | −197.85 | −99.99 | −0.01 | −1.92 | 1.36 | −2.13 | 0.59 | −1.46 |
| 14 | 193.19 | −196.84 | −92.74 | −1.29 | −2.35 | 1.74 | −1.07 | −0.95 | −1.10 |
| 15 | 194.25 | −197.83 | −92.07 | −1.29 | −2.53 | 1.69 | −2.35 | −0.83 | −1.26 |
| 16 | 195.00 | −195.72 | −91.87 | 0.05 | −0.09 | 1.59 | −1.59 | 0.88 | −1.03 |
| 17 | 194.57 | −192.76 | −89.07 | 1.65 | −0.99 | 2.96 | 0.19 | 0.23 | −0.82 |
| 18 | 199.60 | −192.95 | −85.52 | 0.66 | 0.14 | 0.39 | −0.33 | 0.90 | 0.76 |
| 19 | 198.63 | −193.20 | −86.36 | −0.75 | −0.04 | −0.54 | −1.03 | 0.16 | −0.17 |
| 20 | 201.13 | −191.41 | −82.87 | 5.06 | 4.16 | 1.15 | −0.27 | 0.05 | 0.49 |
| RMSE | 178.24 | 198.90 | 110.58 | 2.80 | 2.47 | 2.30 | 1.38 | 1.73 | 1.35 |
| DEM | GF-7 DEMMethod1 | GF-7 DEMMethod2 | GF-7 DEMMethod3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | Bias | RMSE | R2 | Bias | RMSE | R2 | Bias | RMSE | |
| Statistics | 0.99 | –1.80 m | 3.98 m | 1.00 | −0.98 m | 2.52 m | 1.00 | –0.81 m | 1.37 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Ren, Z.; Nie, S.; Bao, G.; Ha, G.; Bai, M.; Liang, P. DEM Generation from GF-7 Satellite Stereo Imagery Assisted by Space-Borne LiDAR and Its Application to Active Tectonics. Remote Sens. 2023, 15, 1480. https://doi.org/10.3390/rs15061480
Zhu X, Ren Z, Nie S, Bao G, Ha G, Bai M, Liang P. DEM Generation from GF-7 Satellite Stereo Imagery Assisted by Space-Borne LiDAR and Its Application to Active Tectonics. Remote Sensing. 2023; 15(6):1480. https://doi.org/10.3390/rs15061480
Chicago/Turabian StyleZhu, Xiaoxiao, Zhikun Ren, Sheng Nie, Guodong Bao, Guanghao Ha, Mingkun Bai, and Peng Liang. 2023. "DEM Generation from GF-7 Satellite Stereo Imagery Assisted by Space-Borne LiDAR and Its Application to Active Tectonics" Remote Sensing 15, no. 6: 1480. https://doi.org/10.3390/rs15061480
APA StyleZhu, X., Ren, Z., Nie, S., Bao, G., Ha, G., Bai, M., & Liang, P. (2023). DEM Generation from GF-7 Satellite Stereo Imagery Assisted by Space-Borne LiDAR and Its Application to Active Tectonics. Remote Sensing, 15(6), 1480. https://doi.org/10.3390/rs15061480