Author Contributions
Conceptualization, methodology, software, dataset and writing, M.L.P.; Italy dataset and weather forcing, J.D. and S.M.; Germany dataset, L.Z.; processing, data curation, validation, and editing, T.N.; force-restore model, A.B.; methodology and review, N.O., L.J. and M.Z. All authors have read and agreed to the published version of the manuscript.
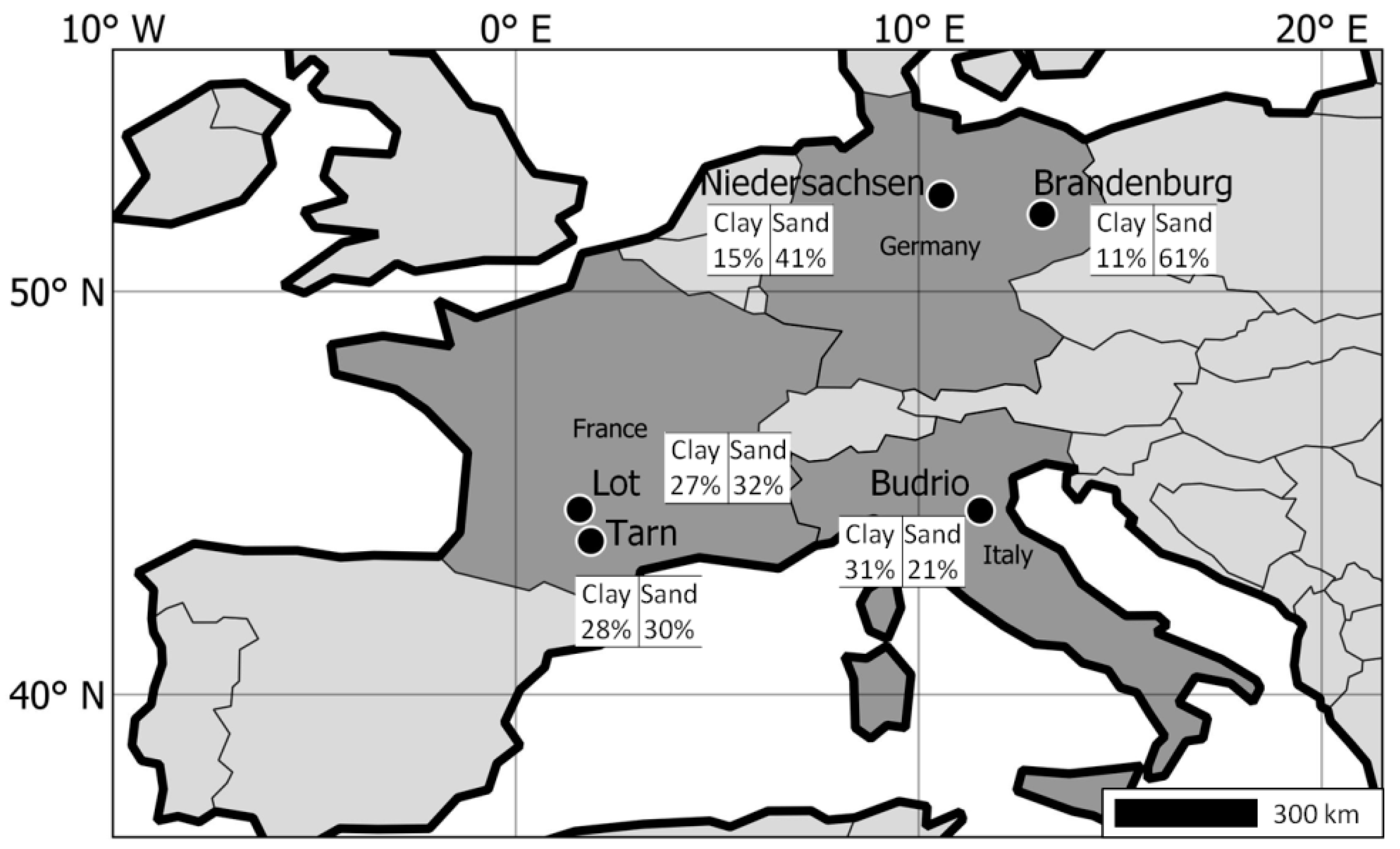
Figure 1.
Regions location and average soil texture from the dataset’s fields.
Figure 1.
Regions location and average soil texture from the dataset’s fields.
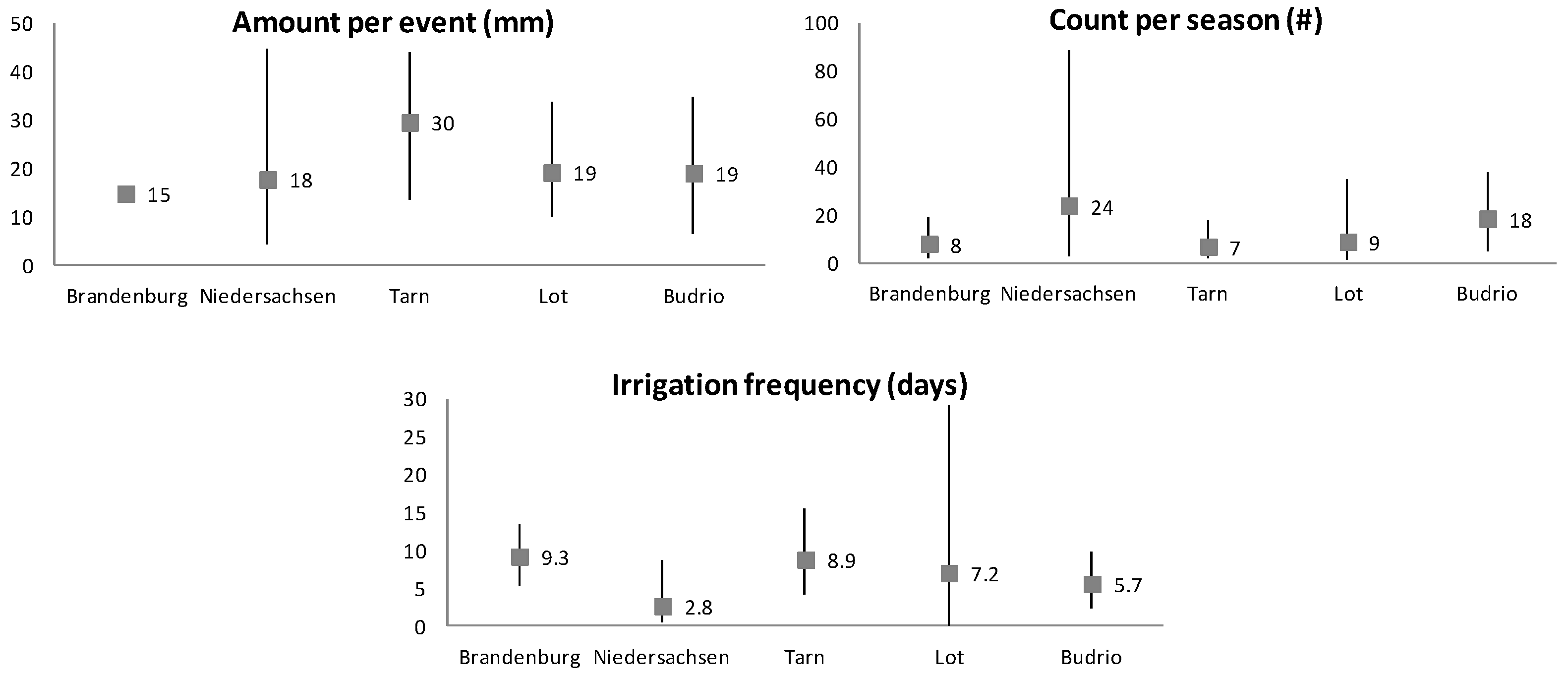
Figure 2.
Statistics of irrigation events. The bars show the minimum and maximum. The square and number show the average value.
Figure 2.
Statistics of irrigation events. The bars show the minimum and maximum. The square and number show the average value.
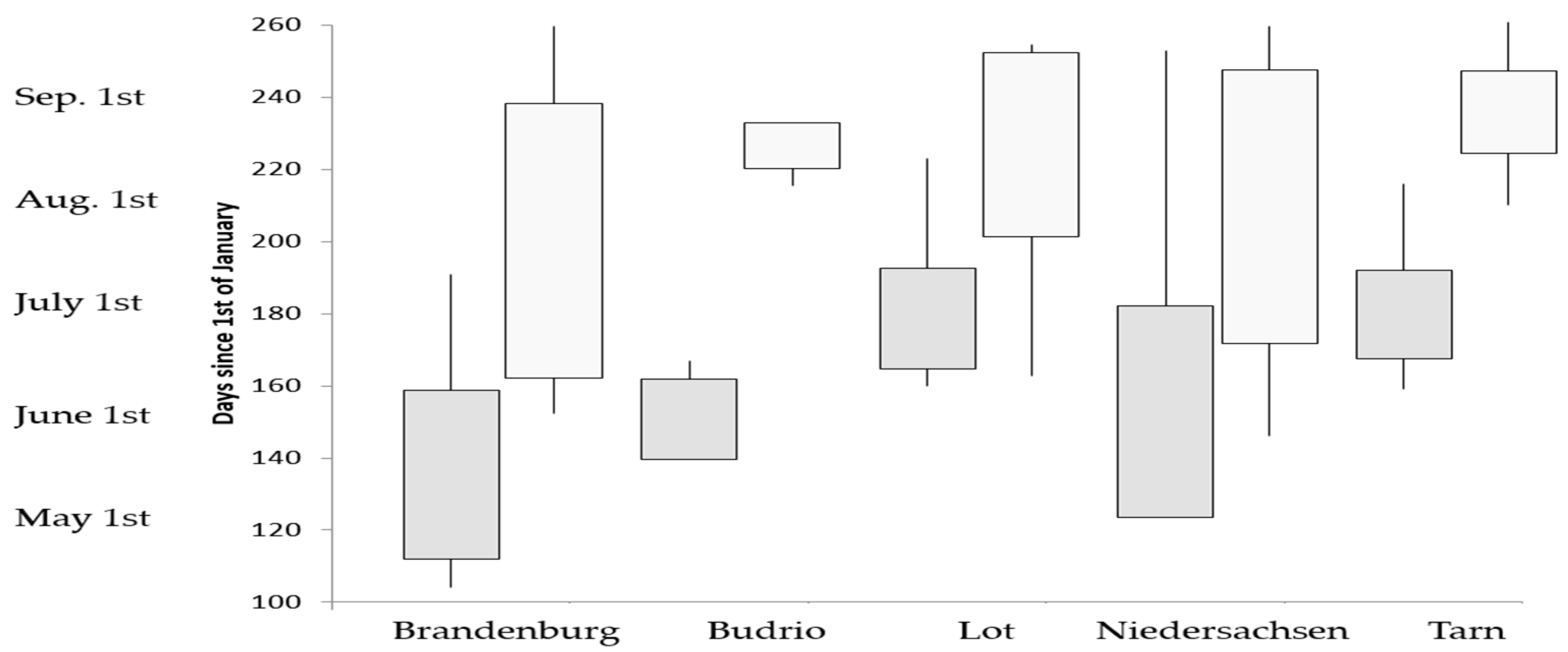
Figure 3.
Start (gray color) and end (white color) of irrigation season per region. The box shows the mean date plus or minus one standard deviation. The line indicates the extremes, i.e., the minimum and maximum date of beginning and end of the irrigation season.
Figure 3.
Start (gray color) and end (white color) of irrigation season per region. The box shows the mean date plus or minus one standard deviation. The line indicates the extremes, i.e., the minimum and maximum date of beginning and end of the irrigation season.
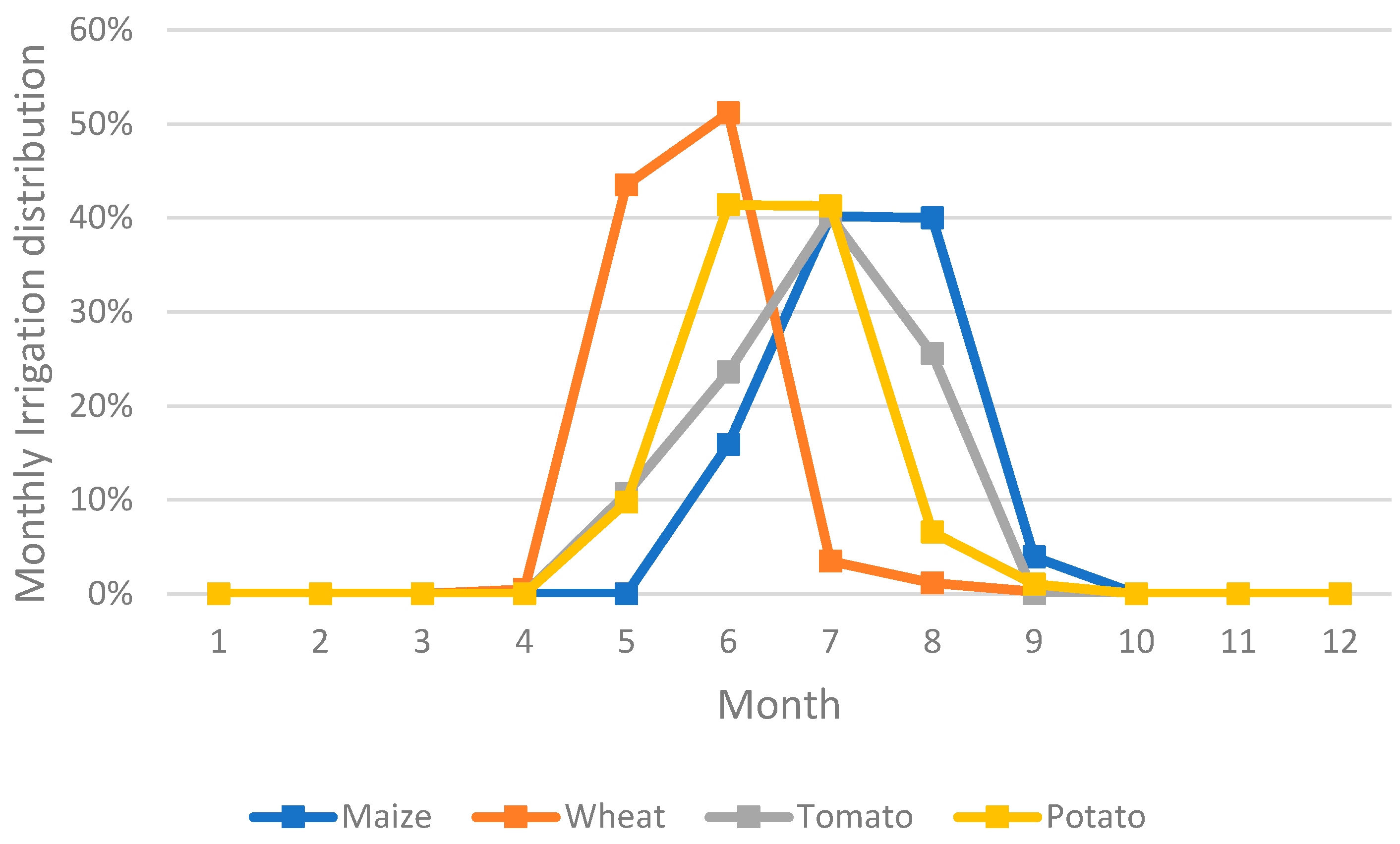
Figure 4.
Irrigation distribution of the four main crops of the dataset.
Figure 4.
Irrigation distribution of the four main crops of the dataset.
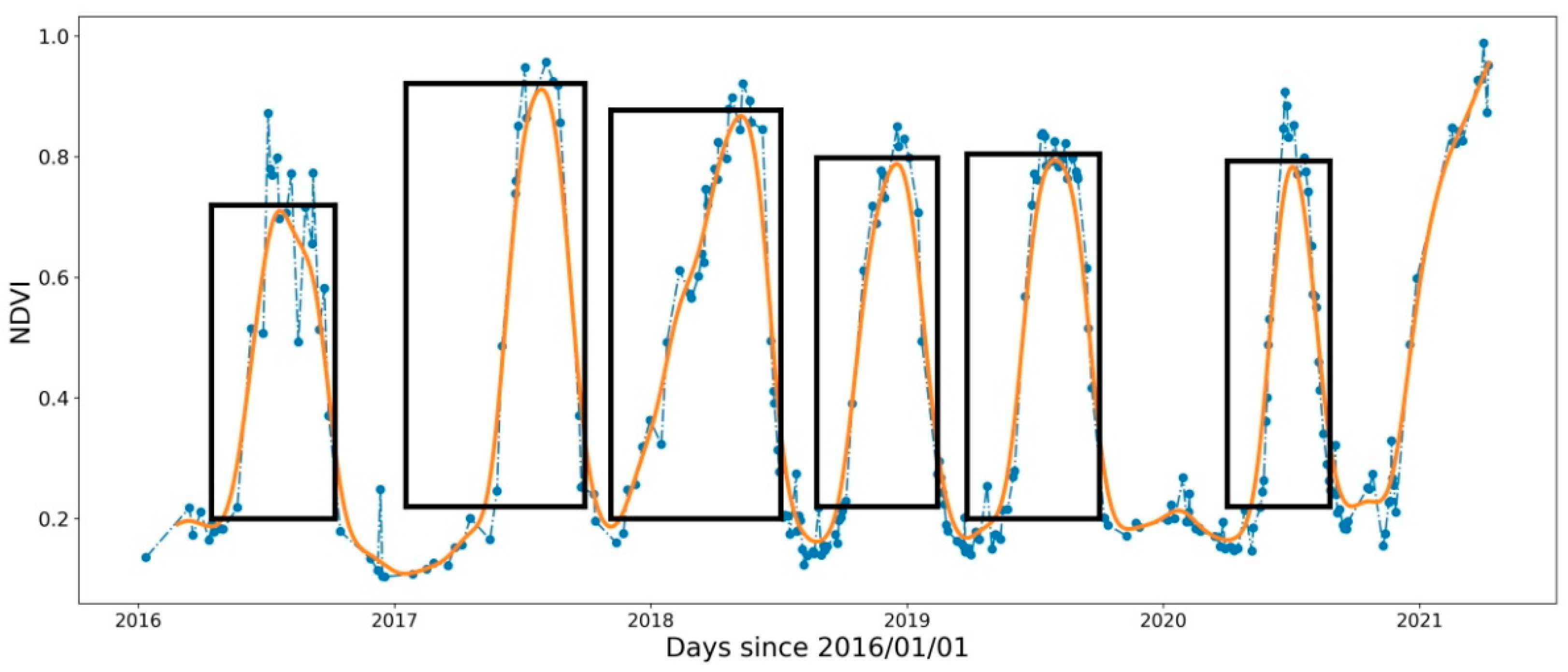
Figure 5.
Example of identification of the start and end of the crop season from Sentinel-2 NDVI time series. The dashed blue line is the original Sentinel-2 time series of NDVI. The orange line is the filtered NDVI. The black boxes are the estimated crop seasons.
Figure 5.
Example of identification of the start and end of the crop season from Sentinel-2 NDVI time series. The dashed blue line is the original Sentinel-2 time series of NDVI. The orange line is the filtered NDVI. The black boxes are the estimated crop seasons.
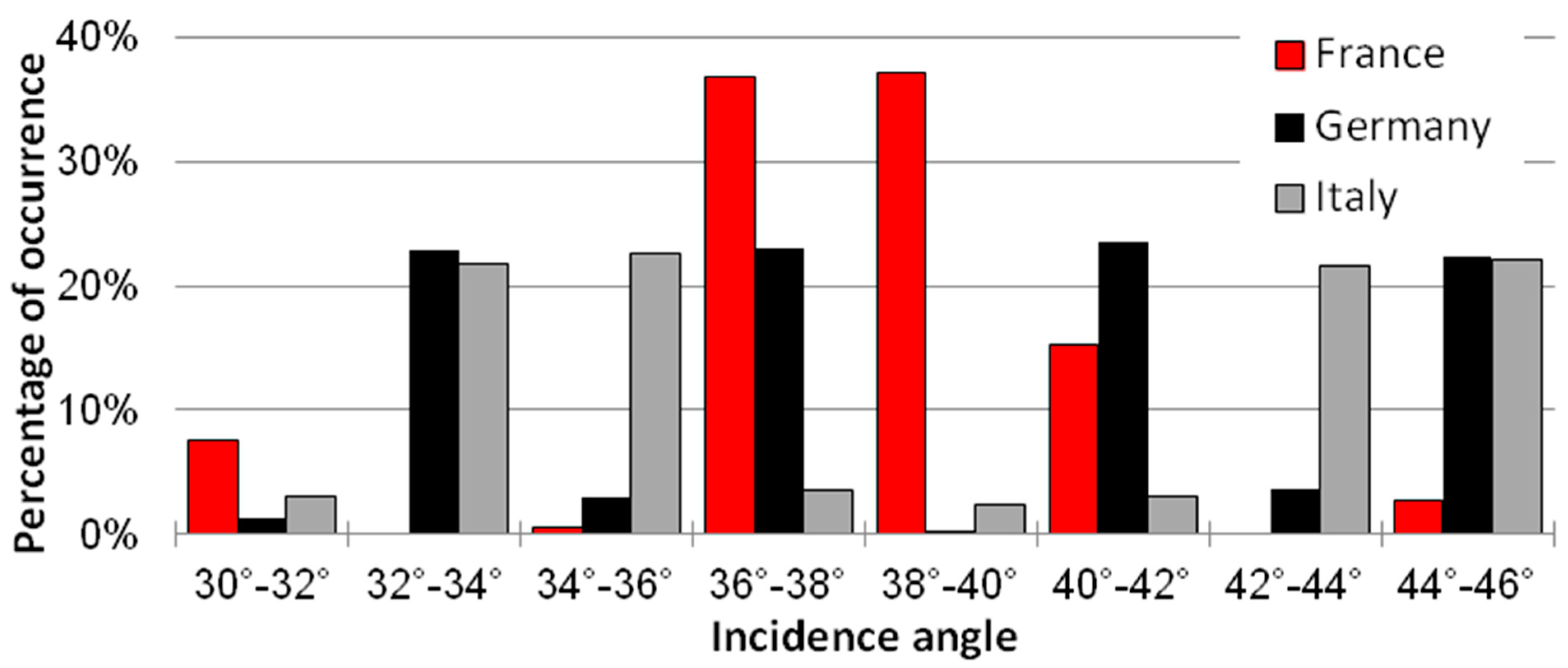
Figure 6.
Incidence angle Sentinel-1 A and B acquisitions per country studied.
Figure 6.
Incidence angle Sentinel-1 A and B acquisitions per country studied.
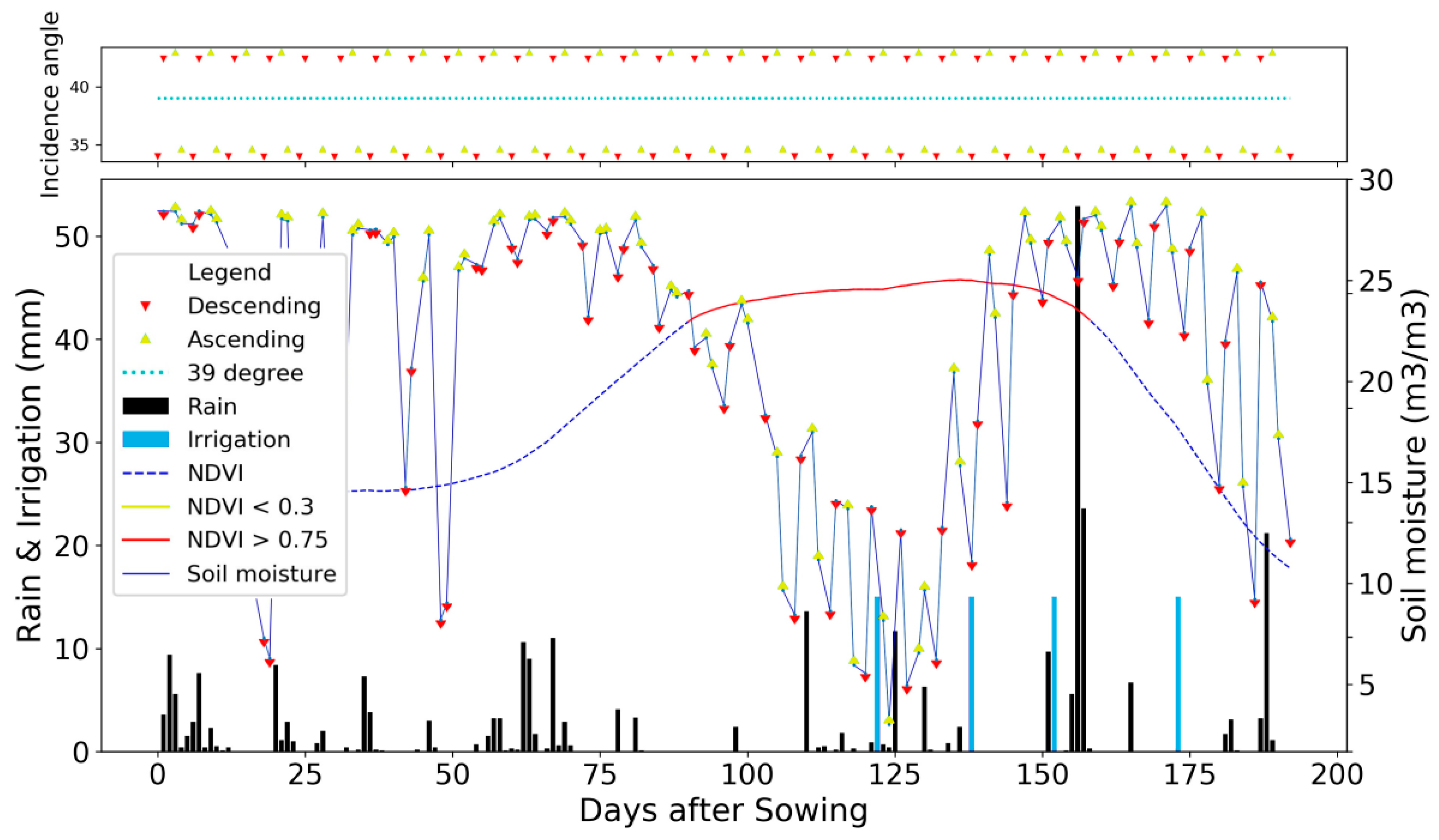
Figure 7.
Lower panel: An example of the time series used for the timing of irrigation. The main graph shows the rainfall and irrigation events as black and blue bars, respectively. The NDVI is drawn with a dark-blue dashed line when lower than 0.75 and red dashes when higher than 0.75. The S2SM product is drawn with yellow arrows (ascending orbit) and red arrows (descending orbit); Upper panel: the incidence angle of acquisition is shown.
Figure 7.
Lower panel: An example of the time series used for the timing of irrigation. The main graph shows the rainfall and irrigation events as black and blue bars, respectively. The NDVI is drawn with a dark-blue dashed line when lower than 0.75 and red dashes when higher than 0.75. The S2SM product is drawn with yellow arrows (ascending orbit) and red arrows (descending orbit); Upper panel: the incidence angle of acquisition is shown.
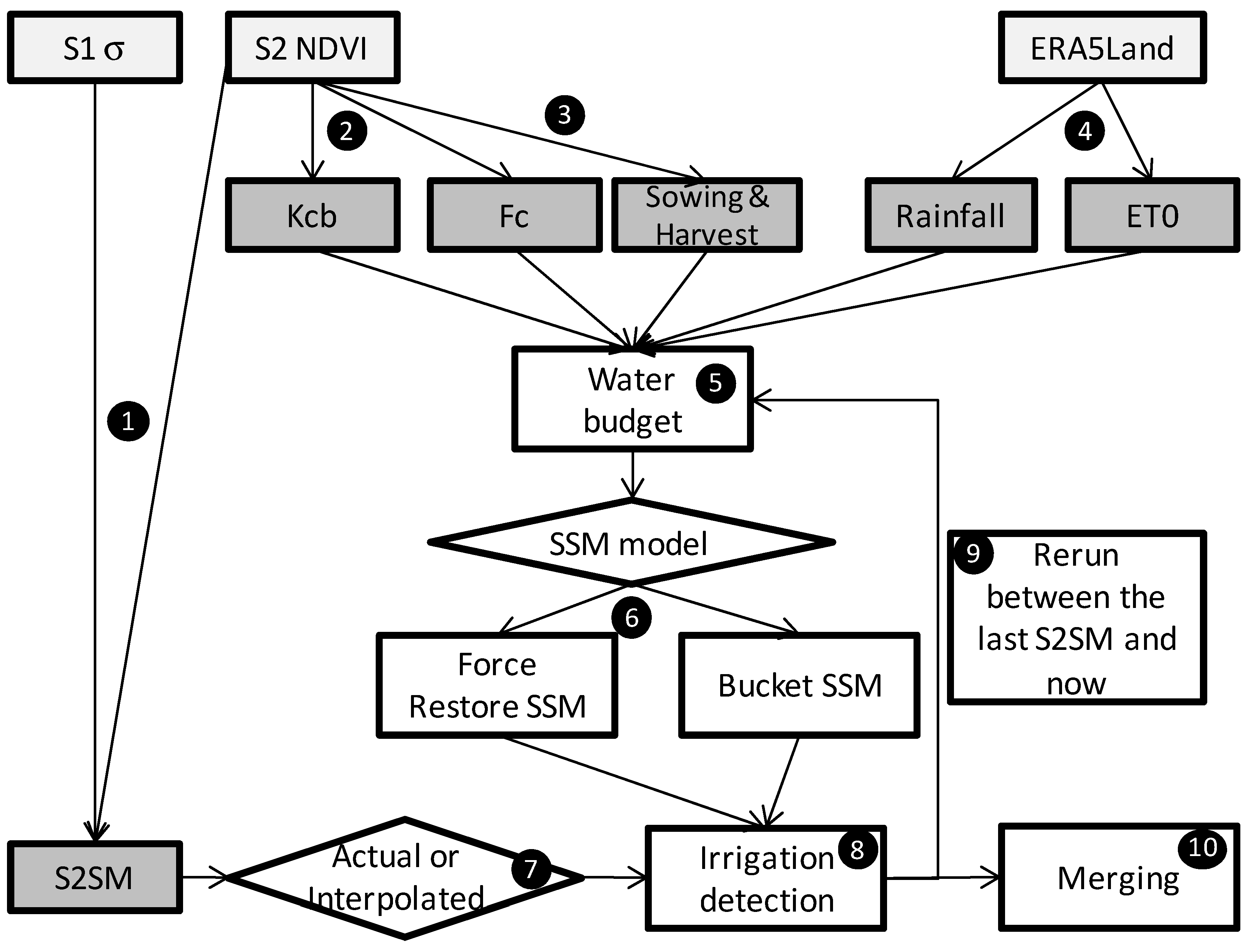
Figure 8.
The workflow of this article is based on three datasets (in light gray boxes). The steps 1 to 4 allow to obtain intermediate variables, with, on one side, the Surface Soil Moisture product obtained from satellite observations (S2SM), and, on the other side, the variables that will allow the computing of a water budget for the estimation of the surface soil moisture (basal crop coefficient (Kcb), Fraction cover (Fc), sowing and harvest date, precipitation and reference evapotranspiration (ET0)). Steps 5 to 9 are the irrigation detection steps. The two diamonds (6 and 7) indicate sub-methods for dealing with soil moisture observation and soil moisture estimation, respectively. The final step (10) consists of merging results.
Figure 8.
The workflow of this article is based on three datasets (in light gray boxes). The steps 1 to 4 allow to obtain intermediate variables, with, on one side, the Surface Soil Moisture product obtained from satellite observations (S2SM), and, on the other side, the variables that will allow the computing of a water budget for the estimation of the surface soil moisture (basal crop coefficient (Kcb), Fraction cover (Fc), sowing and harvest date, precipitation and reference evapotranspiration (ET0)). Steps 5 to 9 are the irrigation detection steps. The two diamonds (6 and 7) indicate sub-methods for dealing with soil moisture observation and soil moisture estimation, respectively. The final step (10) consists of merging results.
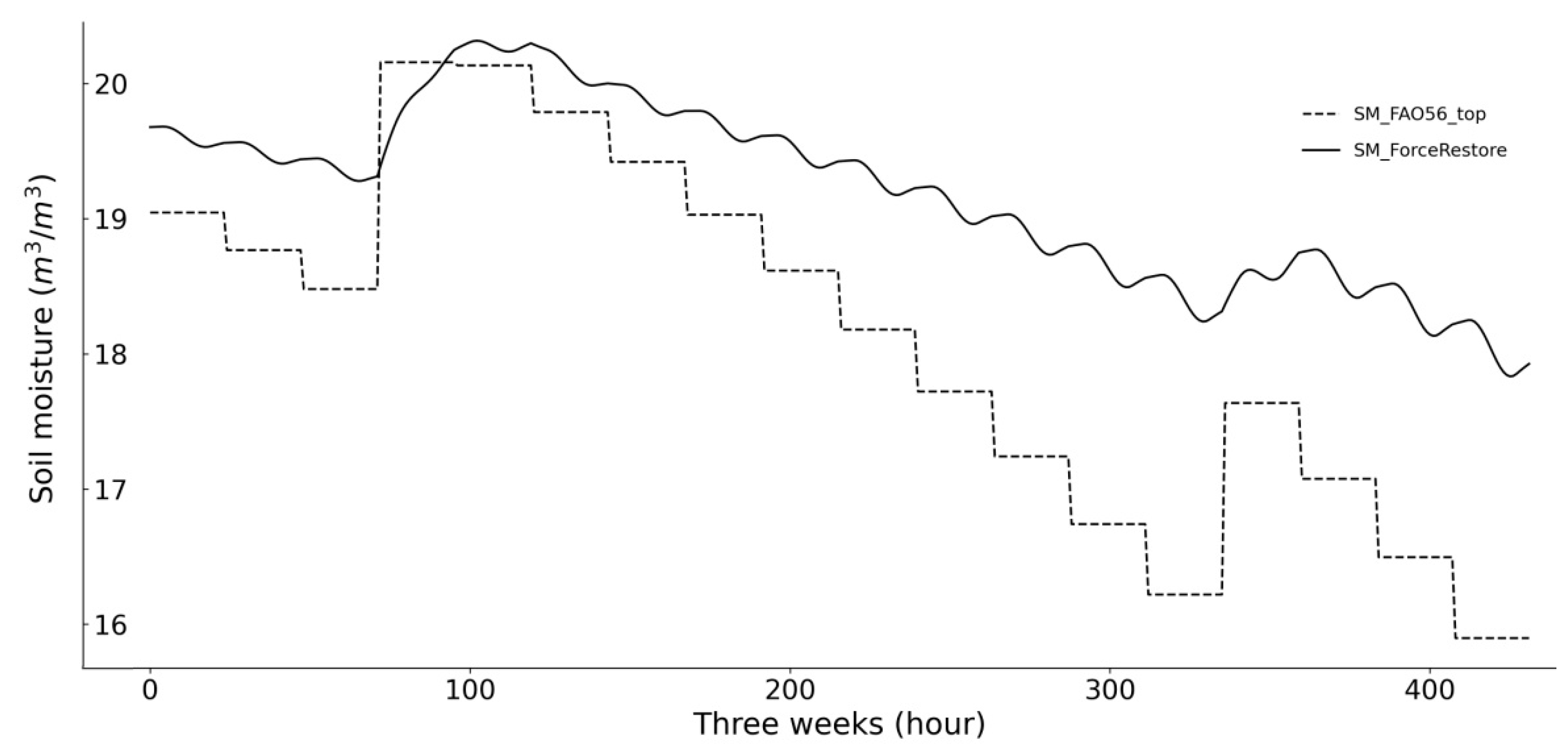
Figure 9.
Example of SSM dynamic simulated by the modified FAO-56 (dashed line) and the force-restore model (dash and point line) after a wetting event.
Figure 9.
Example of SSM dynamic simulated by the modified FAO-56 (dashed line) and the force-restore model (dash and point line) after a wetting event.
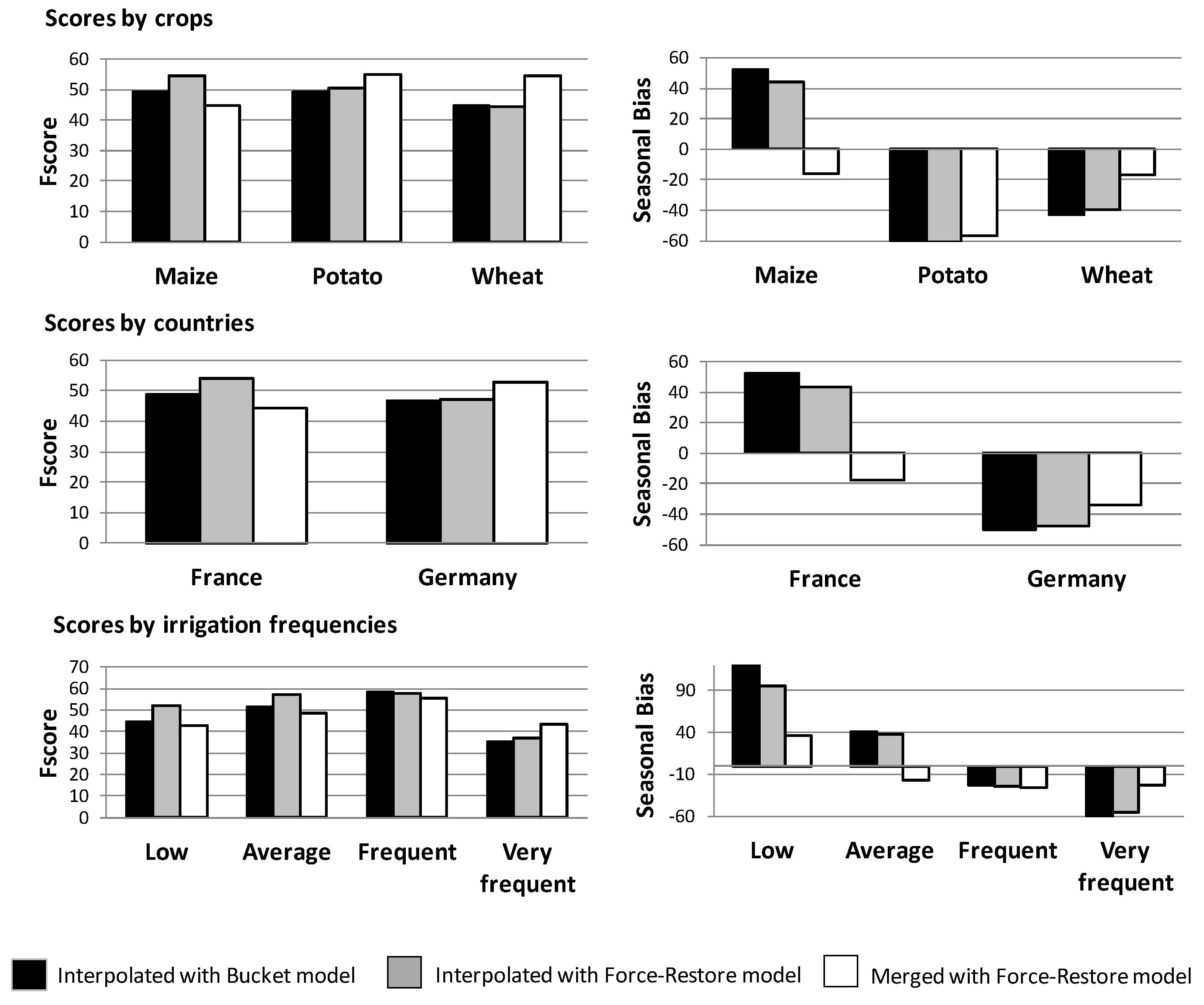
Figure 10.
Comparison of the interpolated method with all data and the original SSM model, the interpolated method with all data and the force-restore model, and the merged runs with the force restore. On the left side, the histograms show the F-scores. On the right side, the histograms show the seasonal biases. From top to bottom, the results are shown for crops, countries, and irrigation frequencies.
Figure 10.
Comparison of the interpolated method with all data and the original SSM model, the interpolated method with all data and the force-restore model, and the merged runs with the force restore. On the left side, the histograms show the F-scores. On the right side, the histograms show the seasonal biases. From top to bottom, the results are shown for crops, countries, and irrigation frequencies.
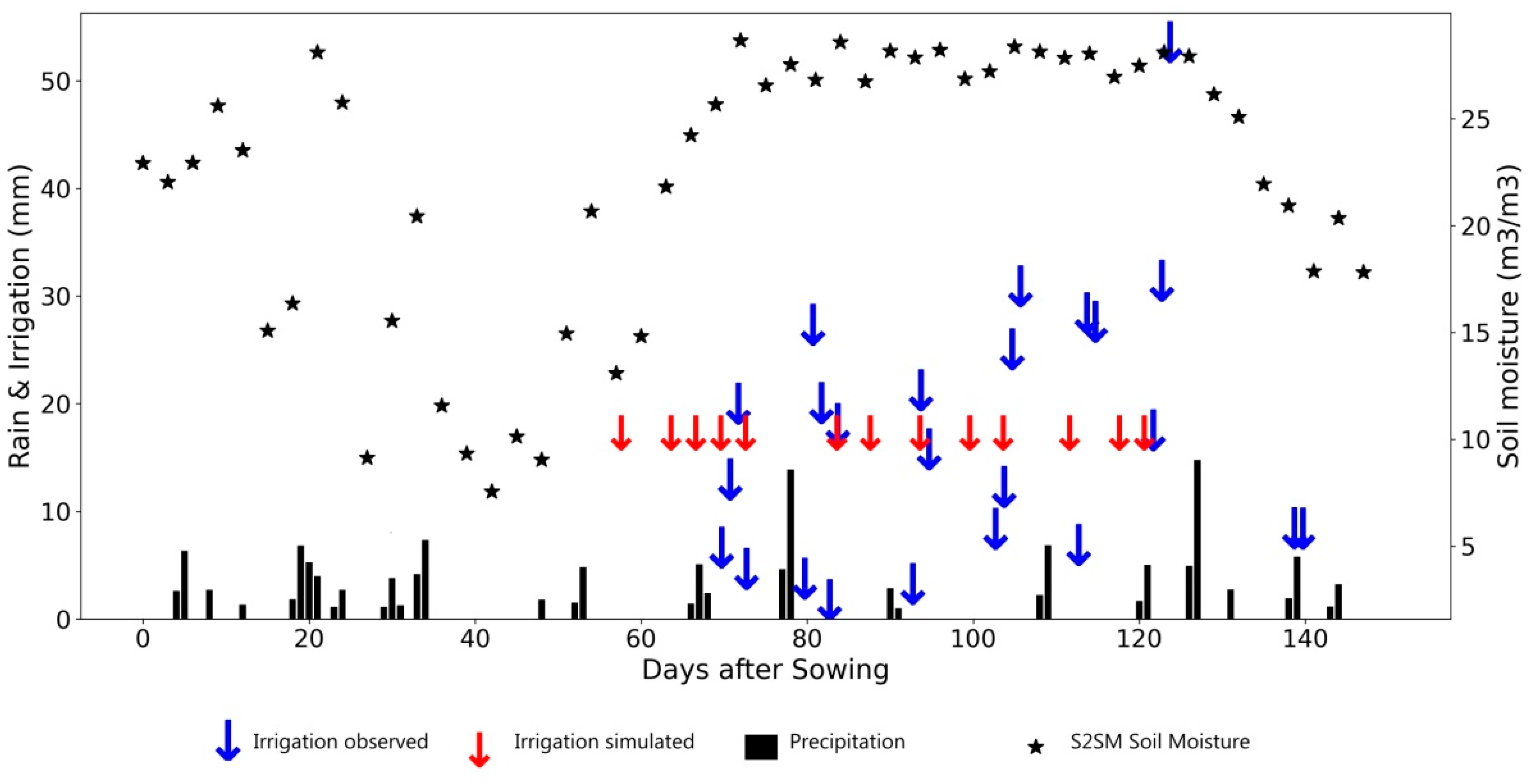
Figure 11.
Example of detection events of low frequency and average amounts of irrigation on winter rye in Brandenburg in 2017. Irrigation observations are indicated by blue arrows (Irri_obs); irrigation simulations are indicated by red arrows (Irri_simu). Actual rainfall events are shown with black bars. The interpolated S2SM product (selected every three days) is shown by stars. Vegetation (Kcb) is shown with blue dashed lines and the model predictions of soil moisture are also shown (SM_FAO, and SM_top).
Figure 11.
Example of detection events of low frequency and average amounts of irrigation on winter rye in Brandenburg in 2017. Irrigation observations are indicated by blue arrows (Irri_obs); irrigation simulations are indicated by red arrows (Irri_simu). Actual rainfall events are shown with black bars. The interpolated S2SM product (selected every three days) is shown by stars. Vegetation (Kcb) is shown with blue dashed lines and the model predictions of soil moisture are also shown (SM_FAO, and SM_top).
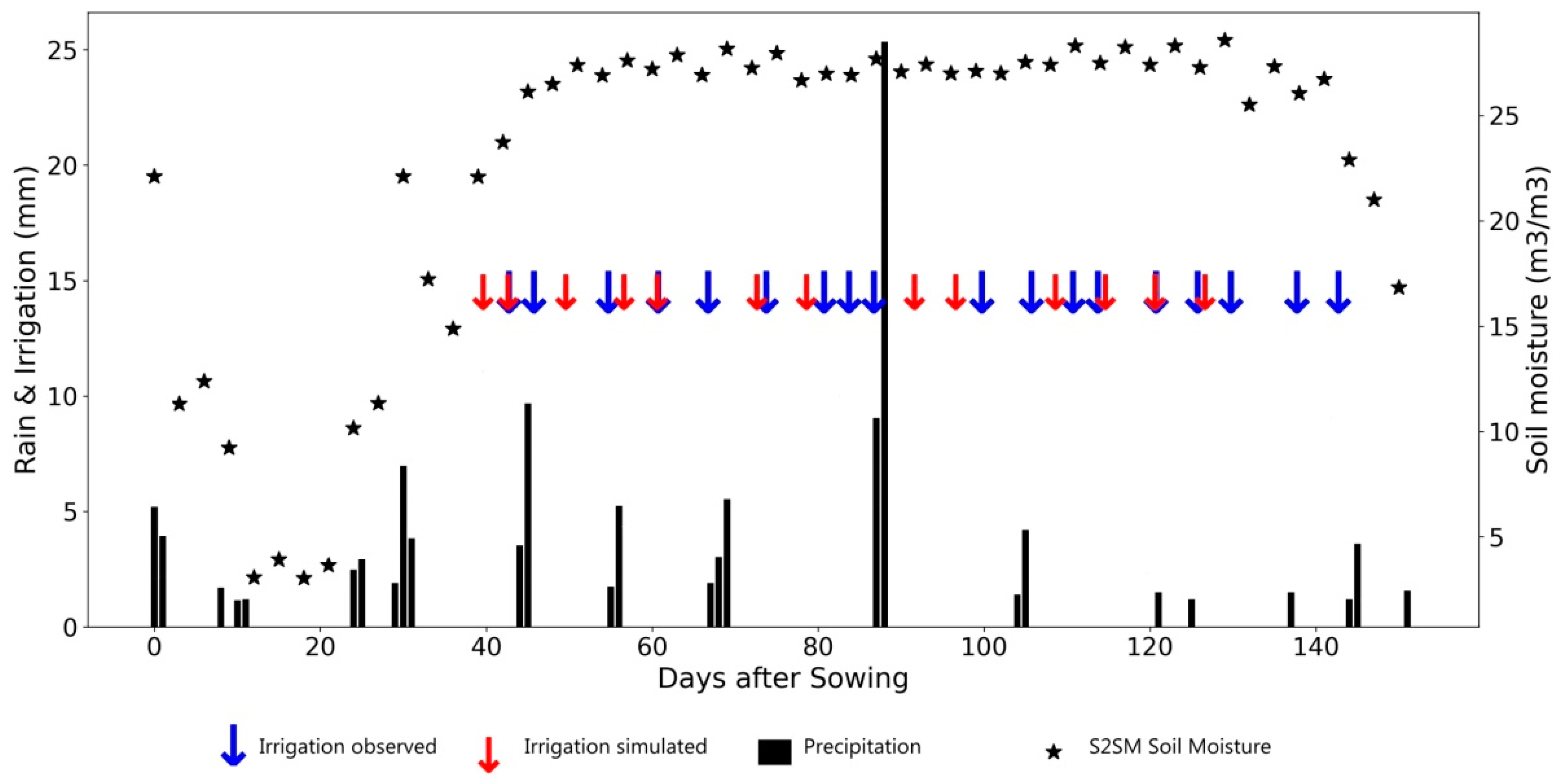
Figure 12.
Same as
Figure 12 for a potato field in Brandenburg in 2018 (high irrigation frequency and average irrigation amounts).
Figure 12.
Same as
Figure 12 for a potato field in Brandenburg in 2018 (high irrigation frequency and average irrigation amounts).
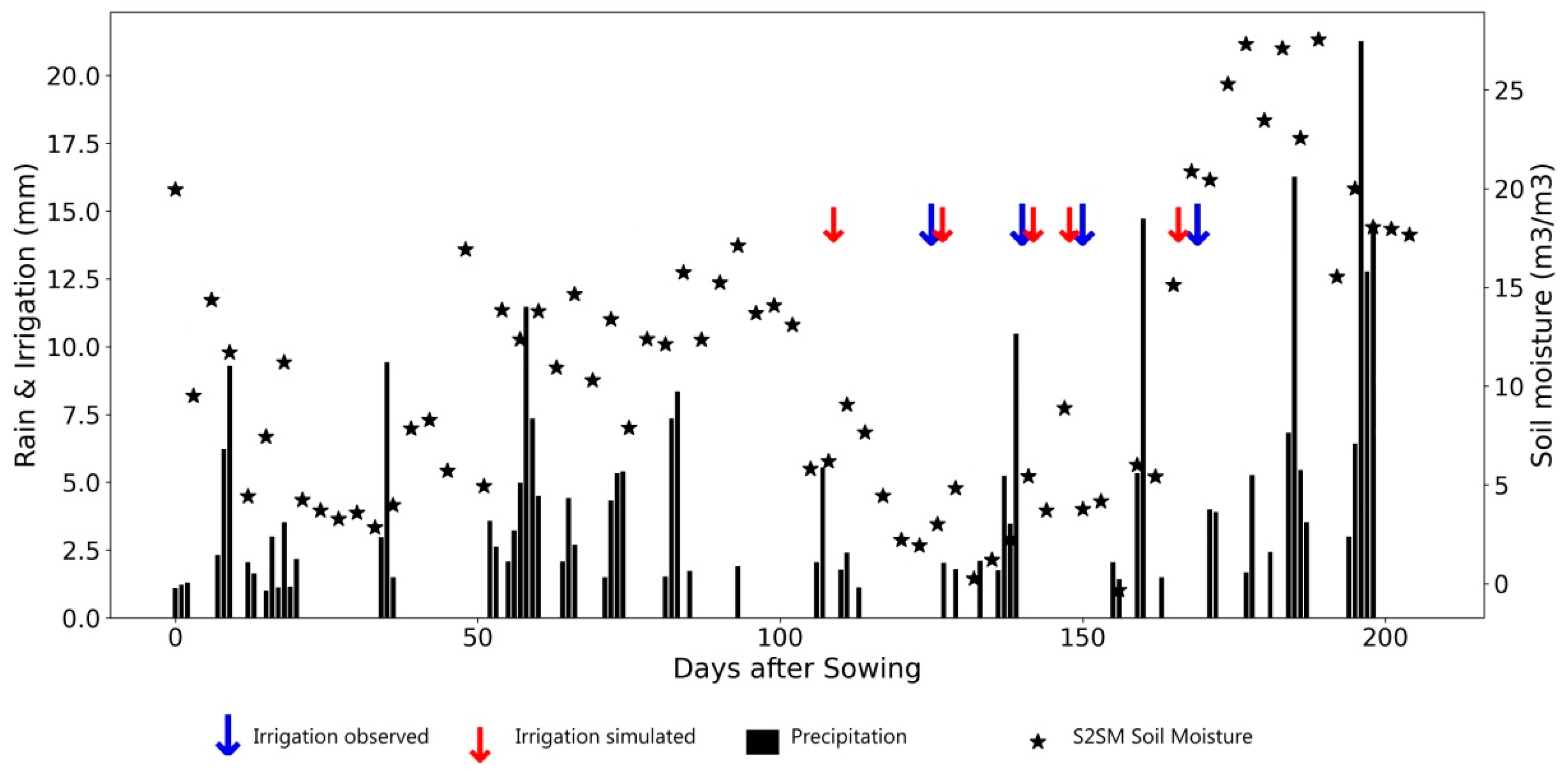
Figure 13.
Same as
Figure 12 for a potato field in Niedersachsen in 2018 (high irrigation frequency and low amounts of irrigation).
Figure 13.
Same as
Figure 12 for a potato field in Niedersachsen in 2018 (high irrigation frequency and low amounts of irrigation).
Table 1.
The number of seasons per crop and region in the dataset.
Table 1.
The number of seasons per crop and region in the dataset.
| | | Germany | France | Italy | | |
|---|
| Crop | | Brand. | Nied. | Lot | Tarn | Budrio | Total |
|---|
| Vegetables | Soybean | | | | 11 | | 11 | 16 |
| Asparragus | | | 1 | | | 1 |
| Tomato | | | | | 3 | 3 |
| Pea | 1 | | | | | 1 |
| Cereals | Triticale | | 4 | | | | 4 | 70 |
| Winter Rye | 3 | | | | | 3 |
| Winter wheat | 4 | 9 | | | | 13 |
| Maize | 2 | | | 29 | 2 | 33 |
| Maize (seed) | | | 7 | | | 7 |
| Summer barley | | 10 | | | | 10 |
| Fodder | Maize (forrage) | | | 7 | | | 7 | 13 |
| Rapeseed | 1 | 3 | | | | 4 |
| Grass | 2 | | | | | 2 |
| Tubers | Potato | 2 | 12 | | | | 14 | 24 |
| Sugar beet | | 10 | | | | 10 |
| Others | Tobacco | | | 8 | | | 8 | 10 |
| Walnut | | | 2 | | | 2 |
Table 2.
Scores (F-score, bias) of the bucket approach according to different configurations (orbit, incidence angle, crop, country, irrigation frequency), and the level of NDVI (all data, small NDVI values, high NDVI values).
Table 2.
Scores (F-score, bias) of the bucket approach according to different configurations (orbit, incidence angle, crop, country, irrigation frequency), and the level of NDVI (all data, small NDVI values, high NDVI values).
| | Fscore | Bias |
|---|
| | Configuration | All NDVI | Large NDVI | Small NDVI | All NDVI | Large NDVI | Small NDVI |
|---|
| Orbit | ASC (6PM) | 32 | 28 | 24 | −221 | −68 | −69 |
| DES (6AM) | 35 | 30 | 28 | −167 | −64 | −62 |
| Incidence angle | 37-41 | 35 | 29 | 26 | −131 | −59 | −55 |
| Other | 34 | 29 | 27 | −228 | −69 | −69 |
| Crop | Maize | 40 | 34 | 30 | −42 | −41 | −7 |
| Potato | 32 | 25 | 27 | −402 | −82 | −79 |
| Wheat | 31 | 27 | 24 | −225 | −70 | −68 |
| Country | France | 40 | 33 | 32 | −41 | −41 | −8 |
| Germany | 32 | 28 | 24 | −277 | −74 | −73 |
| Irrigation Frequency | Low | 44 | 42 | 34 | 4 | −12 | 58 |
| Average | 44 | 39 | 27 | −49 | −41 | −21 |
| Frequent | 38 | 30 | 32 | −177 | −68 | −61 |
| Very Frequent | 24 | 21 | 21 | −435 | −83 | −80 |
Table 3.
Scores (F-score, bias) of the merging of irrigations runs according to 3 merging windows (one day, two days, three days) and according to crops, country, and irrigation frequency.
Table 3.
Scores (F-score, bias) of the merging of irrigations runs according to 3 merging windows (one day, two days, three days) and according to crops, country, and irrigation frequency.
| Merging | Fscore | Bias |
|---|
| | Configuration | 1 Day | 2 Days | 3 Days | 1 Day | 2 Days | 3 Days |
|---|
| Crop | Maize | 45 | 45 | 45 | −16 | −19 | −22 |
| Potato | 55 | 53 | 45 | −57 | −60 | −68 |
| Wheat | 51 | 47 | 42 | −16 | −27 | −40 |
| Country | France | 44 | 45 | 45 | −18 | −20 | −22 |
| Germany | 53 | 49 | 44 | −34 | −42 | −53 |
| Irrigation Frequency | Low | 43 | 44 | 44 | 36 | 30 | 25 |
| Average | 49 | 49 | 49 | −17 | −20 | −24 |
| Frequent | 56 | 53 | 49 | −24 | −32 | −41 |
| Very Frequent | 43 | 40 | 33 | −53 | −58 | −67 |
Table 4.
Scores (F-score, bias) of the force-restore model according to irrigation frequency and NDVI.
Table 4.
Scores (F-score, bias) of the force-restore model according to irrigation frequency and NDVI.
| Force-Restore Model | | Fscore | | | Bias | | |
|---|
| | Configuration | All NDVI | Large NDVI | Small NDVI | All NDVI | Large NDVI | Small NDVI |
|---|
| Irrigation Frequency | Low | 50 | 51 | 29 | 29 | 17 | 118 |
| | Average | 50 | 48 | 29 | −11 | −18 | 7 |
| | Frequent | 41 | 34 | 36 | −119 | −58 | −48 |
| | Very Frequent | 26 | 22 | 24 | −337 | −80 | −74 |
Table 5.
Comparison of scores between the initial bucket soil water budget and the force-restore—FR—approach (score FR minus score Bucket), according to different configurations (Crop, Country, Irrigation frequency, Acquisition, Angle).
Table 5.
Comparison of scores between the initial bucket soil water budget and the force-restore—FR—approach (score FR minus score Bucket), according to different configurations (Crop, Country, Irrigation frequency, Acquisition, Angle).
| Crop | precision | recall | F-score | | Country | precision | recall | F-score |
| Maize | −2.9 | 13.3 | 6.6 | | France | −3.1 | 13.2 | 6.3 |
| Potato | −2.6 | 2.1 | 2.6 | | Germany | −7.1 | 3.3 | 2.4 |
| Wheat | −9.4 | 3.3 | 2.0 | | | | | |
| | | | | | Acquisition | precision | recall | F-score |
| Irrigation frequency | precision | recall | F-score | | ASC | −3.5 | 7.3 | 5.0 |
| | DES | −7.4 | 5.7 | 2.7 |
| Low | −1.9 | 15.3 | 6.1 | | | | | |
| Average | −2.3 | 11.2 | 5.8 | | Angle | precision | recall | F-score |
| Frequent | −8.0 | 4.6 | 3.1 | | 37–41 | −3.0 | 10.3 | 6.0 |
| Very | −7.4 | 2.9 | 2.3 | | Other | −7.8 | 3.8 | 2.0 |
Table 6.
Scores (F-score, bias) of the interpolated approach according to different configurations orbit, incidence angle, crop, country, irrigation frequency), and the level of NDVI (all data, small NDVI values, high NDVI values).
Table 6.
Scores (F-score, bias) of the interpolated approach according to different configurations orbit, incidence angle, crop, country, irrigation frequency), and the level of NDVI (all data, small NDVI values, high NDVI values).
| | | Fscore | | | Bias | | |
|---|
| | Configuration | All NDVI | Large NDVI | Small NDVI | All NDVI | Large NDVI | Small NDVI |
|---|
| Crop | Maize | 49 | 42 | 35 | 45 | 28 | 72 |
| | Potato | 49 | 43 | 48 | −60 | −70 | −51 |
| | Wheat | 45 | 40 | 36 | −43 | −43 | −40 |
| Country | France | 48 | 41 | 33 | 39 | 28 | 57 |
| | Germany | 47 | 42 | 40 | −50 | −54 | −45 |
| Irrigation Frequency | Low | 45 | 47 | 31 | 102 | 74 | 168 |
| | Average | 52 | 44 | 35 | 35 | 24 | 51 |
| | Frequent | 58 | 48 | 44 | −24 | −25 | −21 |
| | Very Frequent | 34 | 28 | 33 | −61 | −70 | −53 |