On-Orbit Vicarious Radiometric Calibration and Validation of ZY1-02E Thermal Infrared Sensor
Abstract
:1. Introduction
2. Materials and Methods
2.1. ZY1-02E Satellite and Thermal Infrared Camera
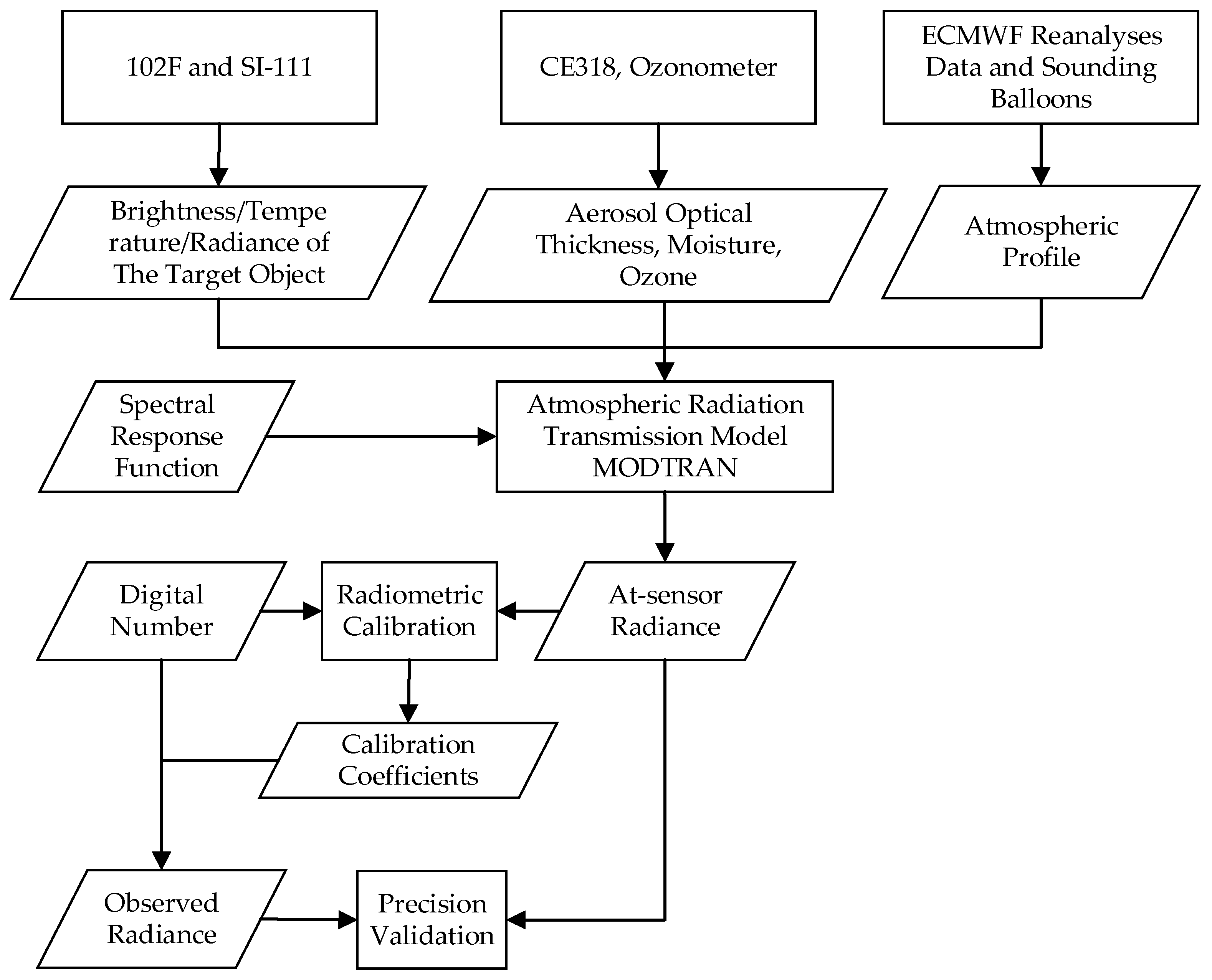
2.2. On-Orbit Vicarious Absolute Radiometric Calibration Method
2.3. Test Area
2.3.1. Ulansuhai Nur
2.3.2. Baotou Site
2.3.3. Kubuqi Desert
2.4. The Vicarious Radiometric Calibration Campaign
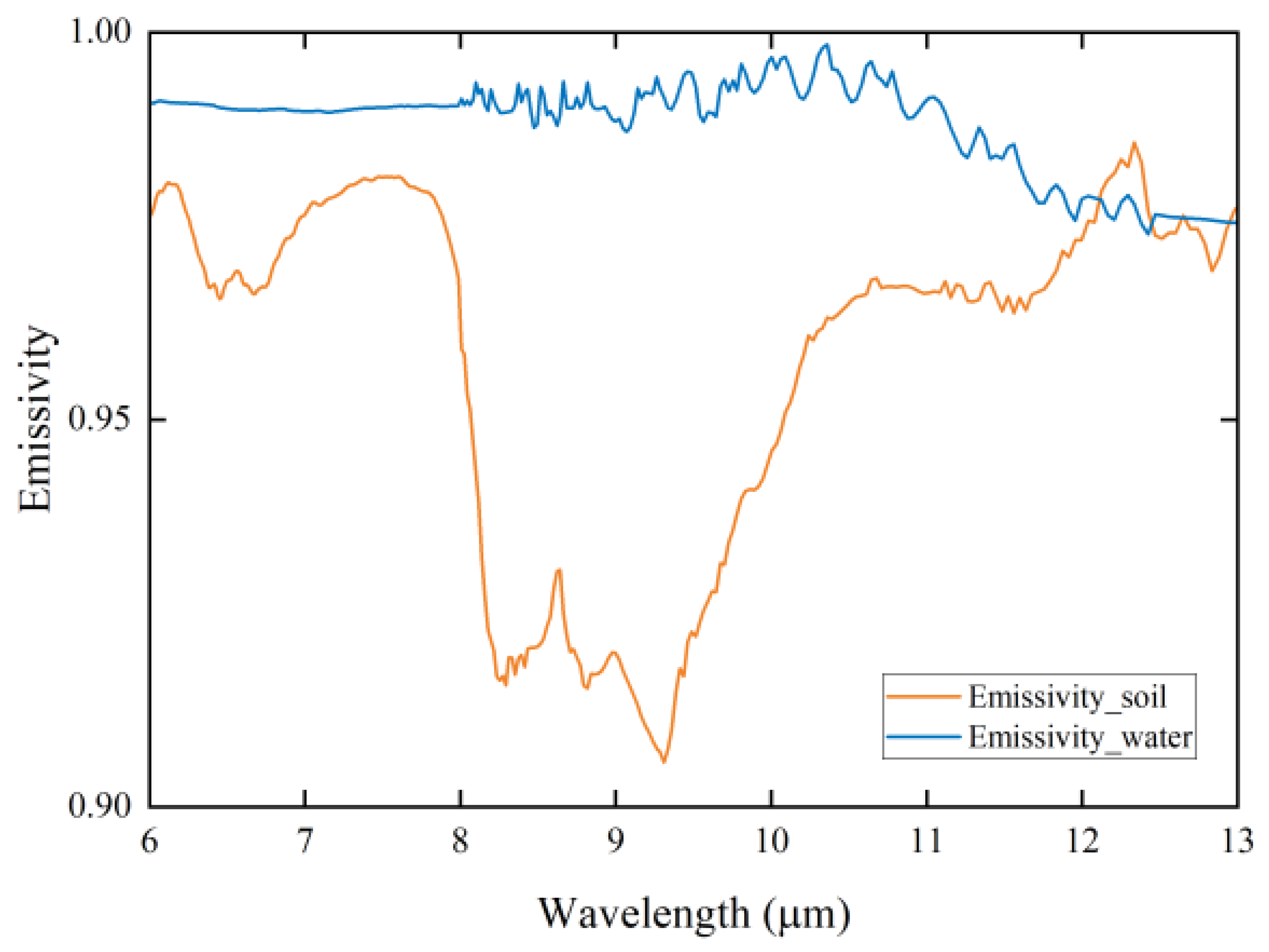
2.4.1. Acquisition of Surface Parameters
2.4.2. Acquisition of Atmospheric Parameters
3. Results
3.1. Radiative Transfer Simulations for At-Sensor Radiance
3.1.1. Thermal Infrared Radiation Transfer Equation
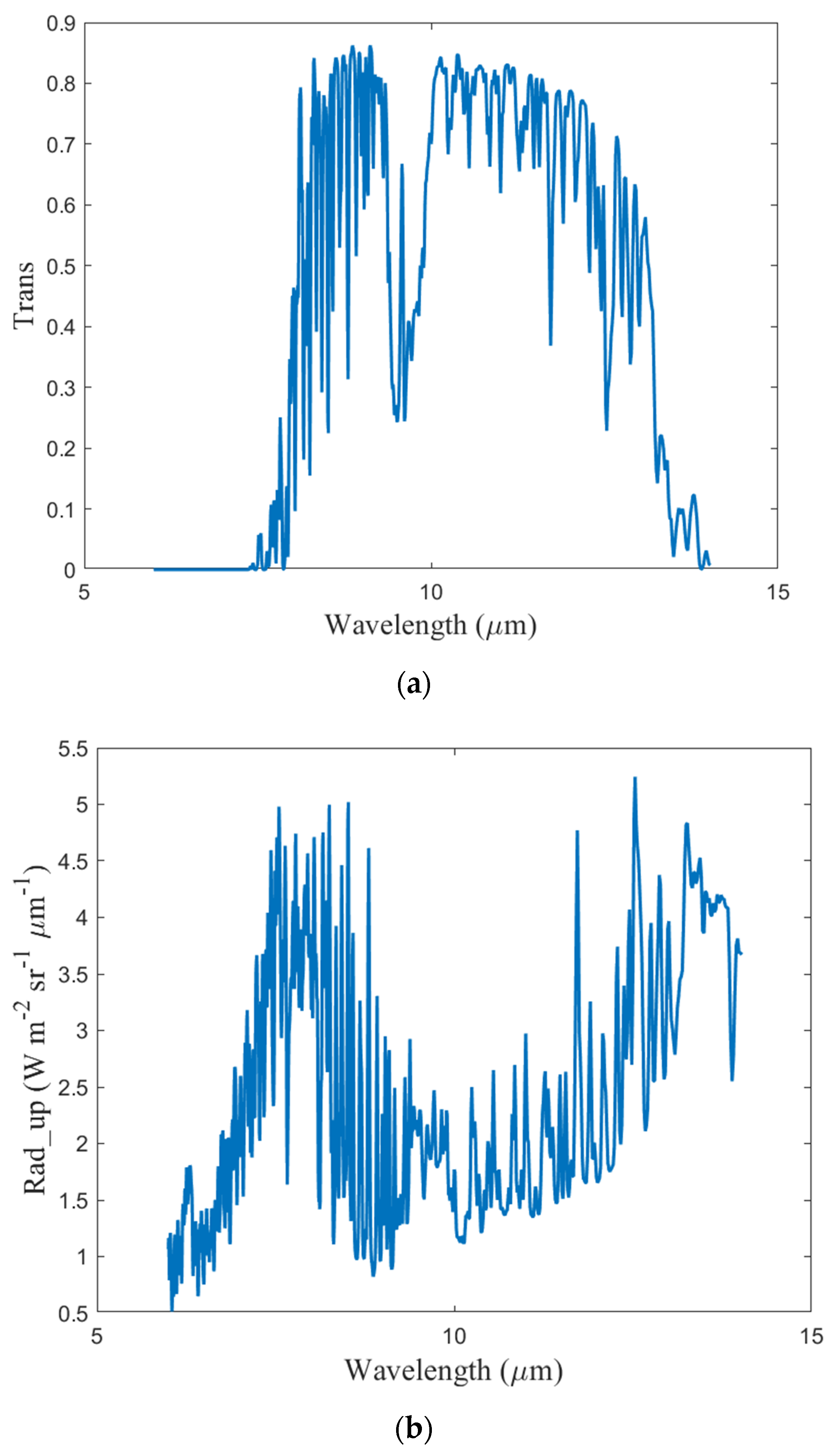
3.1.2. Acquisition of Off-Ground Radiance
3.1.3. Acquisition of Atmospheric Parameters
3.1.4. Brightness Acquisition by the On-Board Pupil
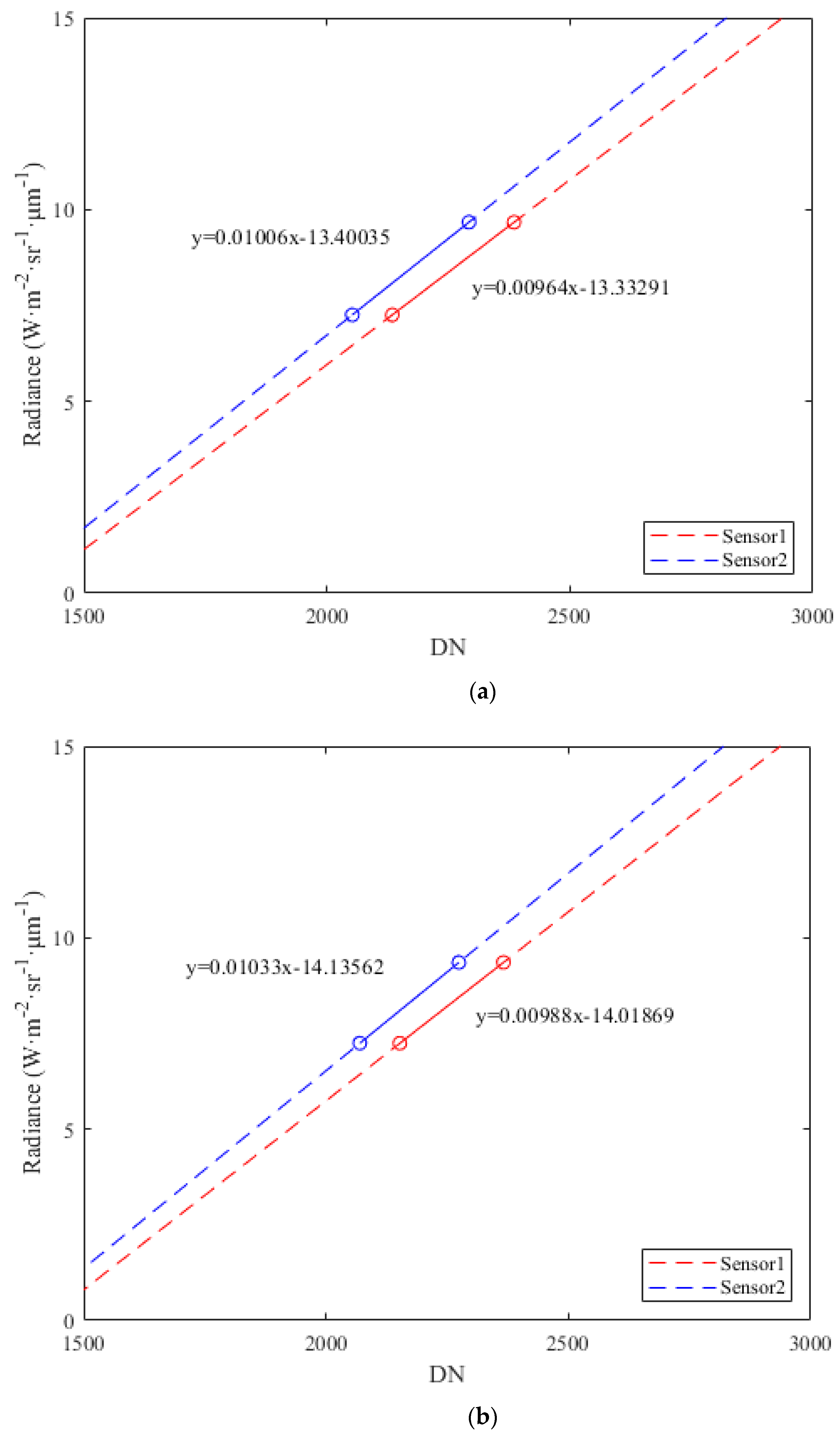
3.2. Radiometric Calibration Results
4. Discussion
- (1)
- Measurement uncertainties for off-water radiance—The 102F Fourier transform thermal infrared spectrometer used in this experiment synchronously measured water during satellite transit, measuring off-water radiance with an accuracy higher than 0.1 K.
- (2)
- Measurement uncertainties in the infrared temperature sensor—The SI-111 infrared temperature sensor was used to measure off-ground brightness temperatures for ground targets during satellite transit. A temperature–radiance lookup table was established using Planck’s law for conversion into off-ground radiance. The errors introduced in this process were ~0.2 K.
- (3)
- Measurement uncertainties for atmospheric parameters—Water vapor content in the atmosphere is one of the most important factors affecting the calculation of radiative transmission in the thermal infrared band. During on-orbit calibration of Landsat 5 TM at Lake Tahoe, Hook et al. [17] observed a brightness temperature deviation of ~0.13 K when the total water vapor content increased by 10%. In this paper, atmospheric parameters for the test area were obtained using a sounding balloon during satellite transit. Atmospheric aerosol and water vapor contents were measured by CE318, which greatly improved measurement accuracy for atmospheric parameters.
- (4)
- Errors caused by simulated atmospheric radiative transmission—MODTRAN 6.0 was used in this experiment to simulate radiative transmission. Inherent model errors were less than 2%, which meets on-orbit radiative calibration requirements. The combined error, resulting from atmospheric parameter measurements and the radiative transfer model, was ~0.2–0.3 K.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Van Der Meer, F.; Hecker, C.; Van Ruitenbeek, F.; Van der Werff, H.; De Wijkerslooth, C.; Wechsler, C. Geologic remote sensing for geothermal exploration: A review. Int. J. Appl. Earth Obs. Geoinf. 2014, 33, 255–269. [Google Scholar] [CrossRef]
- Jimenez-Munoz, J.C.; Cristobal, J.; Sobrino, J.A.; Soria, G.; Ninyerola, M.; Pons, X.; Pons, X. Revision of the single-channel algorithm for land surface temperature retrieval from landsat thermal-infrared data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 339–349. [Google Scholar] [CrossRef]
- Zhao, S.; Wang, Q.; You, D.; Yao, Y.; Zhu, L.; Sui, X. Preliminary analysis on the application of satellite infrared remote sensing techniques in environmental protection of China. J. Geo-Inf. Sci. 2015, 7, 12–17. [Google Scholar]
- Vaughan, W.W.; Johnson, D.L. Meteorological satellites—The very early years, prior to launch of tiros-1. Bull. Am. Meteorol. Soc. 1994, 75, 2295–2302. [Google Scholar] [CrossRef]
- Ninomiya, Y.; Fu, B.H. Thermal infrared multispectral remote sensing of lithology and mineralogy based on spectral properties of materials. Ore Geol. Rev. 2019, 108, 54–72. [Google Scholar] [CrossRef]
- Han, Q.J.; Liu, L.; Fu, Q.Y.; Zhang, X.W.; Wang, A.C.; Pan, Z.Q. Vicarious calibration of multiple sensors based on reanalysis data of pseudo-invariant site. Acta Opt. Sin. 2014, 34, 1128002. [Google Scholar]
- Ohring, G.; Wielicki, B.; Spencer, R.; Emery, B.; Datla, R. Satellite instrument calibration for measuring global climate change: Report of a workshop. Bull. Am. Meteorol. Soc. 2005, 86, 1303–1314. [Google Scholar] [CrossRef]
- Datla, R.U.; Rice, J.P.; Lykke, K.R.; Johnson, B.C.; Butler, J.J.; Xiong, X. Best practice guidelines for pre-launch characterization and calibration of instruments for passive optical remote sensing. J. Res. Natl. Inst. Stand. Technol. 2011, 116, 621–646. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.X.; Li, X.; Zhang, M.; Kang, Q.; Wei, W.; Zheng, X.B.; Zhang, Y. On-orbit radiometric calibration for thermal infrared band of fy3d/mersi-ⅱ satellite remote sensor based on qinghai lake radiation calibration test-site. Acta Photon. Sin. 2020, 49, 128–136. [Google Scholar]
- Barsi, J.A.; Schott, J.R.; Hook, S.J.; Raqueno, N.G.; Markham, B.L.; Radocinski, R.G. Landsat-8 thermal infrared sensor (tirs) vicarious radiometric calibration. Remote Sens. 2014, 6, 11607–11626. [Google Scholar] [CrossRef]
- Okuyama, A.; Hashimoto, T.; Nakayama, R.; Tahara, Y.; Kurino, T.; Takenaka, H.; Fukuda, S.; Nakajima, T.Y.; Higurashi, A.; Sekiguchi, M. Geostationary imager visible channel recalibration. In Proceedings of the 2009 EUMETSAT Meteorological Satellite Conference, Bath, UK, 21–25 September 2009. [Google Scholar]
- Schott, J.R.; Hook, S.J.; Barsi, J.A.; Markham, B.L.; Miller, J.; Padula, F.P.; Raqueno, N.G. Thermal infrared radiometric calibration of the entire landsat 4, 5, and 7 archive (1982–2010). Remote Sens. Environ. 2012, 122, 41–49. [Google Scholar] [CrossRef]
- Zhang, Y.; Gu, H.F.; Yu, T.; Zhang, Y.X.; Chen, L.F.; Li, X.Y.; Li, X.W.; He, L.M. Absolute radiometric calibration of cbers-02 irmss thermal band. Sci. China Ser. E 2005, 35, 70–88. [Google Scholar] [CrossRef]
- Rong, Z.G.; Qiu, K.M.; Hu, X.Q.; Zhang, Y.X. Comparison of pre-launch calibration in lab with the radiometric calibration in orbit for the fy-2 b meteorological satellite’s ir channel. J. Infrared Millim. Waves 2002, 21, 408–412. [Google Scholar]
- Han, Q.J.; Min, X.J.; Fu, Q.Y. In-flight absolute radiometric calibration for thermal infrared band of hj-1b. J. Remote Sens. 2010, 14, 1212–1225. [Google Scholar]
- Liu, L.; Gu, X.F.; Yu, T.; Li, X.Y.; Gao, H.L.; Li, J.G.; Shi, T.T. Hj-1b thermal infrared band in-flight radiometric calibration and validation. Infrared Laser Eng. 2012, 41, 1119–1125. [Google Scholar]
- Hook, S.J.; Chander, G.; Barsi, J.A.; Alley, R.E.; Abtahi, A.; Palluconi, F.D.; Markham, B.L.; Richards, R.C.; Schladow, S.G.; Helder, D.L. In-flight validation and recovery of water surface temperature with landsat-5 thermal infrared data using an automated high-altitude lake validation site at lake tahoe. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2767–2776. [Google Scholar] [CrossRef]
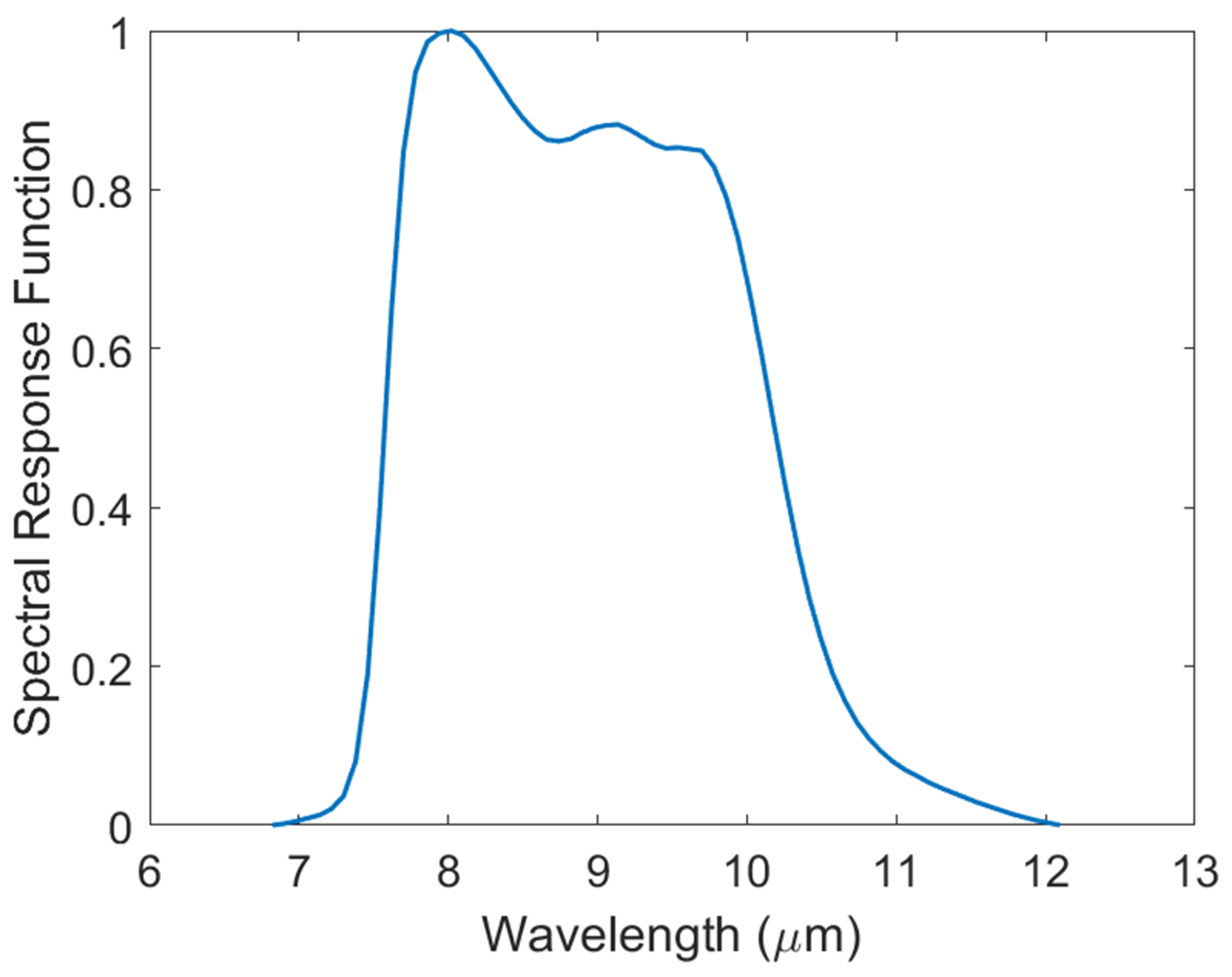








| Orbit | Classification of Track | Sun Synchronously Returns to Orbit |
| Orbital Altitude | 778.099 km | |
| Orbital Inclination | 98.5° | |
| Local Time of Descending Node | 10:30 a.m. | |
| Side Swing Ability | ±32° | |
| Return Cycle | 55 days | |
| Thermal Infrared Camera Sensor1 Sensor2 | Spectral Range | 7.7 μm–10.5 μm |
| Subsatellite Resolution | 16 m | |
| Scanning Width | 115 km | |
| Digitizing Bit | 12 bit |
| Date | Features | Sensor | DN Value | At-Sensor Radiance (W·m−2 sr−1 μm−1) |
|---|---|---|---|---|
| 10 July 2022 | Water | Sensor1 | 2134.7 | 7.2553 |
| Sensor2 | 2052.3 | |||
| Bare Soil | Sensor1 | 2385.2 | 9.6713 | |
| Sensor2 | 2292.3 | |||
| 13 July 2022 | Water | Sensor1 | 2152.4 | 7.2458 |
| Sensor2 | 2069.7 | |||
| Bare Soil | Sensor1 | 2366.1 | 9.3569 | |
| Sensor2 | 2274.1 |
| Date | Sensor | Calibration Coefficients (W·m−2 sr−1 μm−1) | |
|---|---|---|---|
| Gain | Bias | ||
| 10 July 2022 | Sensor1 | 0.009644 | 13.3329 |
| Sensor2 | 0.010064 | 13.4003 | |
| 13 July 2022 | Sensor1 | 0.009879 | 14.0186 |
| Sensor2 | 0.010331 | 14.1356 | |
| Date | Sensor | Feature | DN Value | Calculation Based on On-Orbit Calibration Coefficients | Model Simulation Based on Measured Data | Relative Radiance Deviation (%) | Equivalent Brightness Temperature Deviation ΔT (K) | ||
|---|---|---|---|---|---|---|---|---|---|
| On-Satellite Radiance (W·m−2 sr−1 μm−1) | Equivalent Brightness Temperature (K) | At-Sensor Radiance (W·m−2 sr−1 μm−1) | Equivalent Brightness Temperature (K) | ||||||
| 10 July 2022 | Sensor1 | Baotou Sand | 2354.1 | 9.3715 | 298.935 | 9.3045 | 298.354 | 0.720% | 0.581 |
| Baotou Vegetation | 2169.6 | 7.5921 | 287.778 | 7.5555 | 287.531 | 0.490% | 0.247 | ||
| Kubuqi Desert | 2270.3 | 8.5634 | 294.056 | 8.6478 | 294.58 | −0.971% | 0.523 | ||
| Sensor2 | Baotou Sand | 2260.9 | 9.3548 | 298.837 | 9.3045 | 298.354 | 0.537% | 0.483 | |
| Baotou Vegetation | 2087.9 | 7.6142 | 287.926 | 7.5555 | 287.531 | 0.781% | 0.395 | ||
| Kubuqi Desert | 2181.8 | 8.559 | 294.029 | 8.6478 | 294.58 | −1.029% | 0.550 | ||
| 13 July 2022 | Sensor1 | Baotou Sand | 2401.3 | 9.705 | 300.869 | 9.616 | 300.449 | 0.927% | 0.420 |
| Baotou Vegetation | 2167.2 | 7.3925 | 286.423 | 7.463 | 287.085 | −0.950% | 0.662 | ||
| Kubuqi Desert | 2329.8 | 8.9988 | 296.72 | 9.112 | 297.291 | −1.237% | 0.571 | ||
| Sensor2 | Baotou Sand | 2310.7 | 9.7353 | 301.043 | 9.616 | 300.449 | 1.242% | 0.594 | |
| Baotou Vegetation | 2083 | 7.3832 | 286.359 | 7.463 | 287.085 | −1.075% | 0.726 | ||
| Kubuqi Desert | 2241.3 | 9.0181 | 296.836 | 9.112 | 297.291 | −1.025% | 0.455 | ||
| Source of Uncertainty | Accuracy | TOA Radiance Uncertainty |
|---|---|---|
| Off-Water Radiance | 0.1 K | |
| SI-III Infrared Temperature Sensor | ~0.2 K | |
| Atmospheric Parameters | 10% | ~0.13 K |
| MODTRAN 6.0 Radiative Transfer | 2% | ~0.2–0.3 K |
| Overall Uncertainty | ~0.5–0.6 K |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, H.; Xie, J.; Dou, X.; Zhang, H.; Chen, W. On-Orbit Vicarious Radiometric Calibration and Validation of ZY1-02E Thermal Infrared Sensor. Remote Sens. 2023, 15, 994. https://doi.org/10.3390/rs15040994
Tang H, Xie J, Dou X, Zhang H, Chen W. On-Orbit Vicarious Radiometric Calibration and Validation of ZY1-02E Thermal Infrared Sensor. Remote Sensing. 2023; 15(4):994. https://doi.org/10.3390/rs15040994
Chicago/Turabian StyleTang, Hongzhao, Junfeng Xie, Xianhui Dou, Honggeng Zhang, and Wei Chen. 2023. "On-Orbit Vicarious Radiometric Calibration and Validation of ZY1-02E Thermal Infrared Sensor" Remote Sensing 15, no. 4: 994. https://doi.org/10.3390/rs15040994
APA StyleTang, H., Xie, J., Dou, X., Zhang, H., & Chen, W. (2023). On-Orbit Vicarious Radiometric Calibration and Validation of ZY1-02E Thermal Infrared Sensor. Remote Sensing, 15(4), 994. https://doi.org/10.3390/rs15040994








