Author Contributions
Conceptualization, X.M., Q.M. and X.Y.; Methodology, X.M., Q.M. and Z.Y.; Software, Z.Y.; Validation, X.M. and Q.M.; Investigation, Q.M.; Data curation, P.D., J.W. and C.L.; Writing—original draft, X.M. and Q.M.; Writing—review & editing, X.M., Q.M., P.D., J.W. and C.L.; Supervision, X.Y.; Funding acquisition, Q.M. All authors have read and agreed to the published version of the manuscript.
Figure 1.
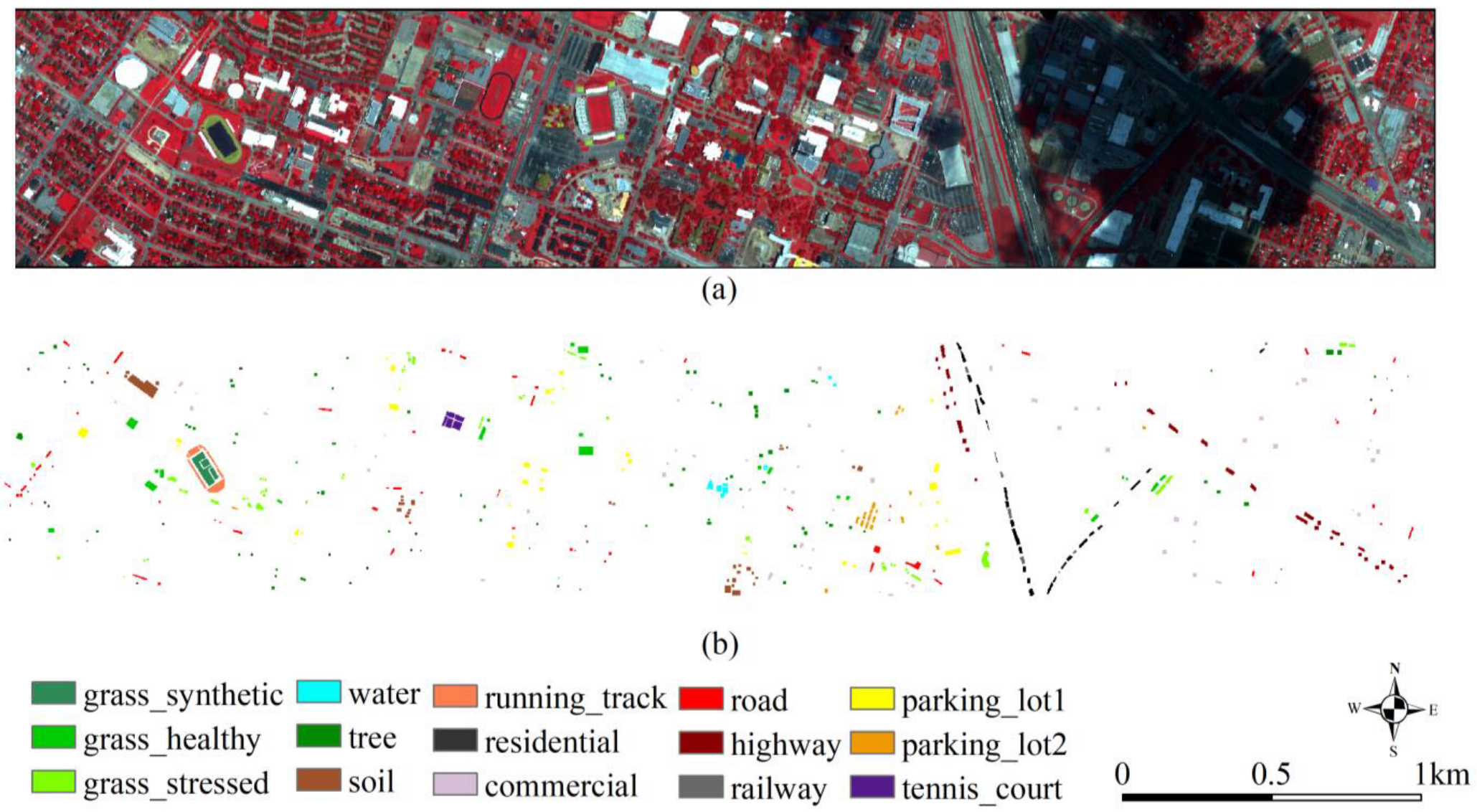
(a) The false-color image of the Houston dataset. (b) The ground truth of the Houston dataset.
Figure 1.
(a) The false-color image of the Houston dataset. (b) The ground truth of the Houston dataset.
Figure 2.
The hyperspectral image of the Surrey dataset in false-color display.
Figure 2.
The hyperspectral image of the Surrey dataset in false-color display.
Figure 3.
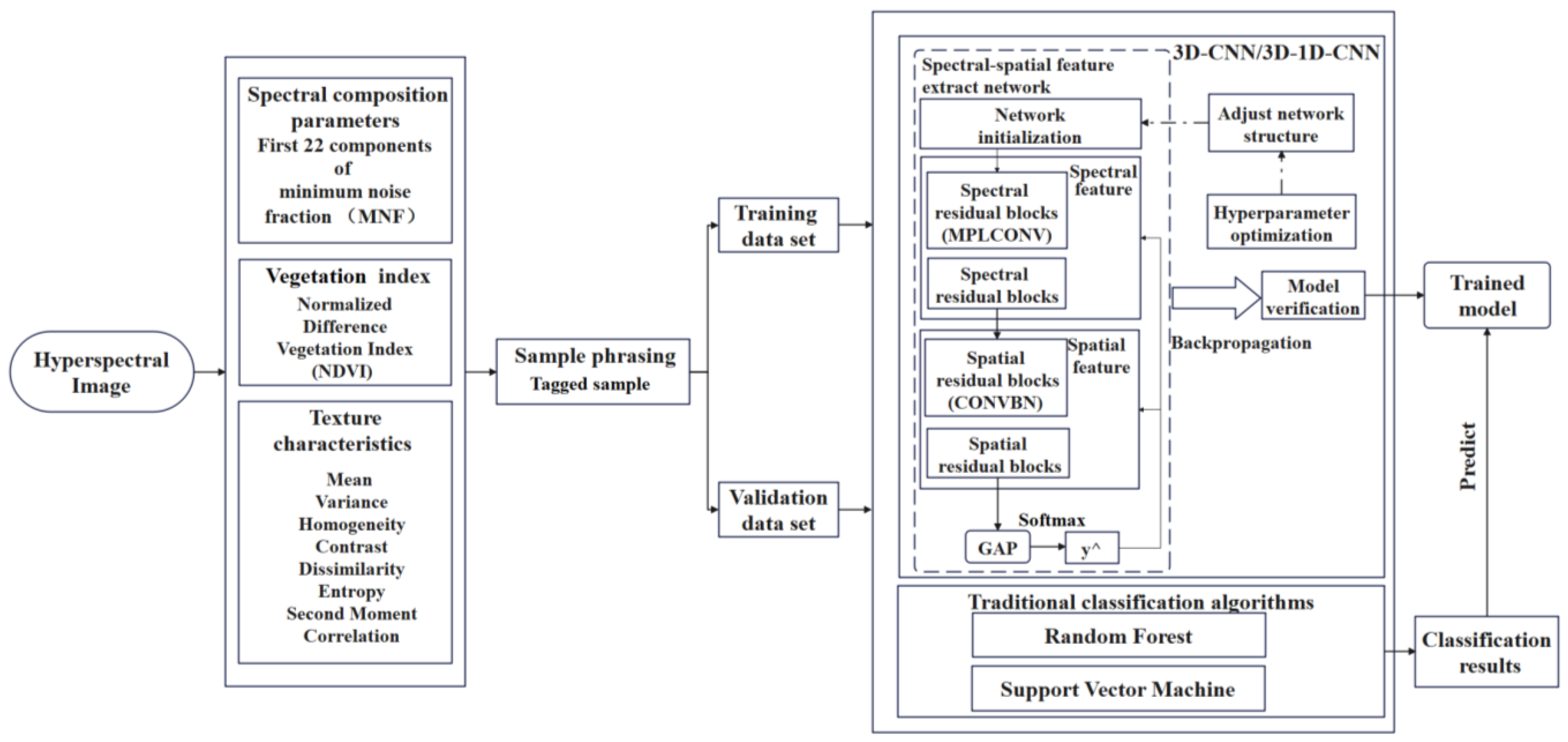
The flowchart of this research.
Figure 3.
The flowchart of this research.
Figure 4.
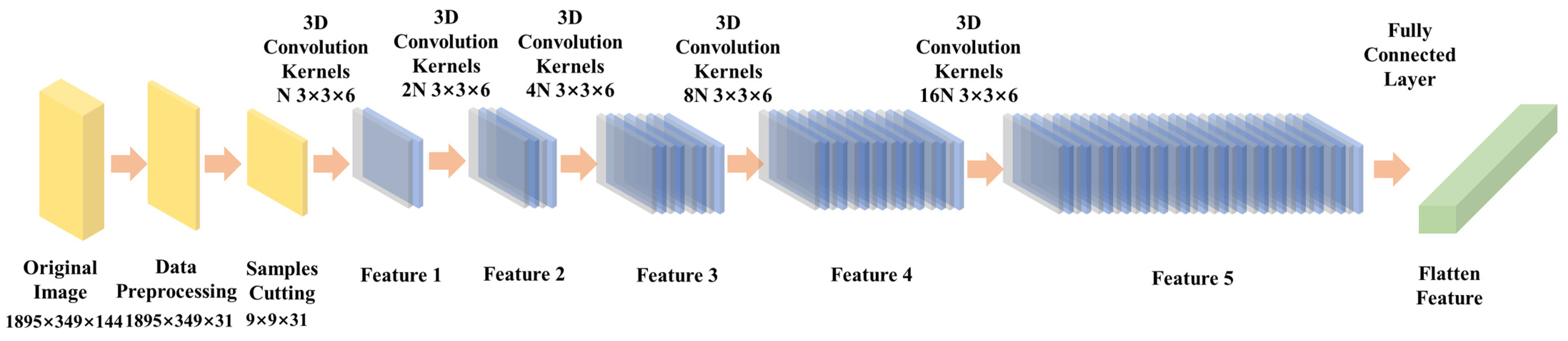
3D-CNN architecture diagram.
Figure 4.
3D-CNN architecture diagram.
Figure 5.
Schematic representation of the Random Forest principle.
Figure 5.
Schematic representation of the Random Forest principle.
Figure 6.
Schematic diagram of support vector machine principle.
Figure 6.
Schematic diagram of support vector machine principle.
Figure 7.
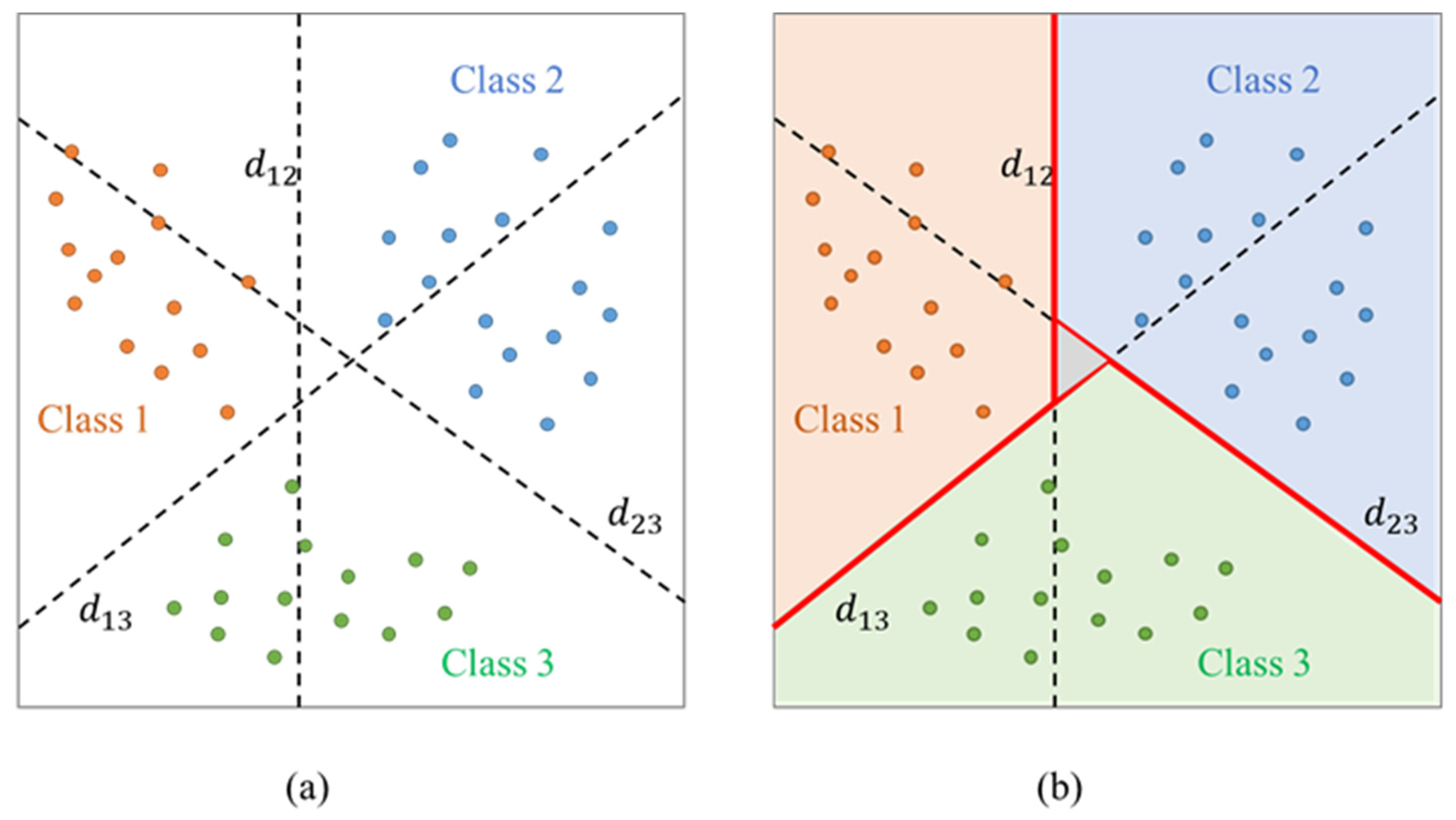
The paired classification method. (a) Decision boundary, (b) Decision boundary drawn according to the voting strategy.
Figure 7.
The paired classification method. (a) Decision boundary, (b) Decision boundary drawn according to the voting strategy.
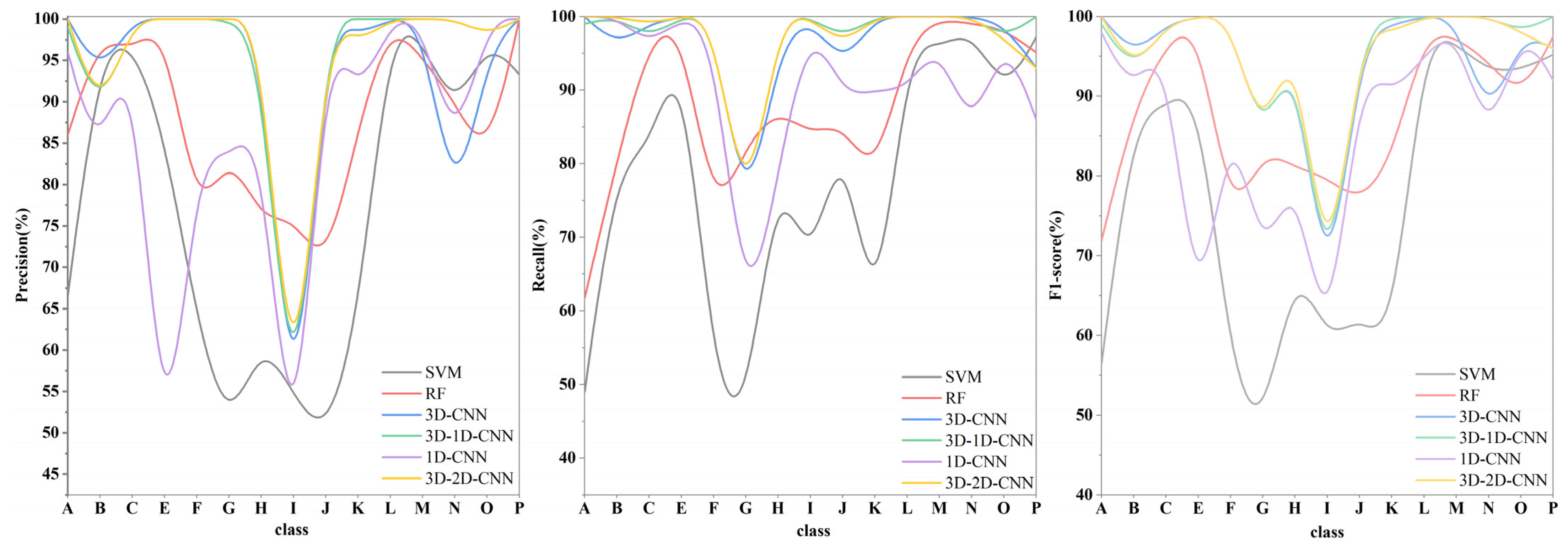
Figure 8.
Recall, Precision, and F1-score of each class in different classifiers on the Houston dataset, where A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, represent commercial, grass_healthy, grass_stressed, grass_synthetic, highway, parking_lot1, parking_lot2, railway, residential, road, running_track, soil, tennis_court, tree, water, respectively.
Figure 8.
Recall, Precision, and F1-score of each class in different classifiers on the Houston dataset, where A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, represent commercial, grass_healthy, grass_stressed, grass_synthetic, highway, parking_lot1, parking_lot2, railway, residential, road, running_track, soil, tennis_court, tree, water, respectively.
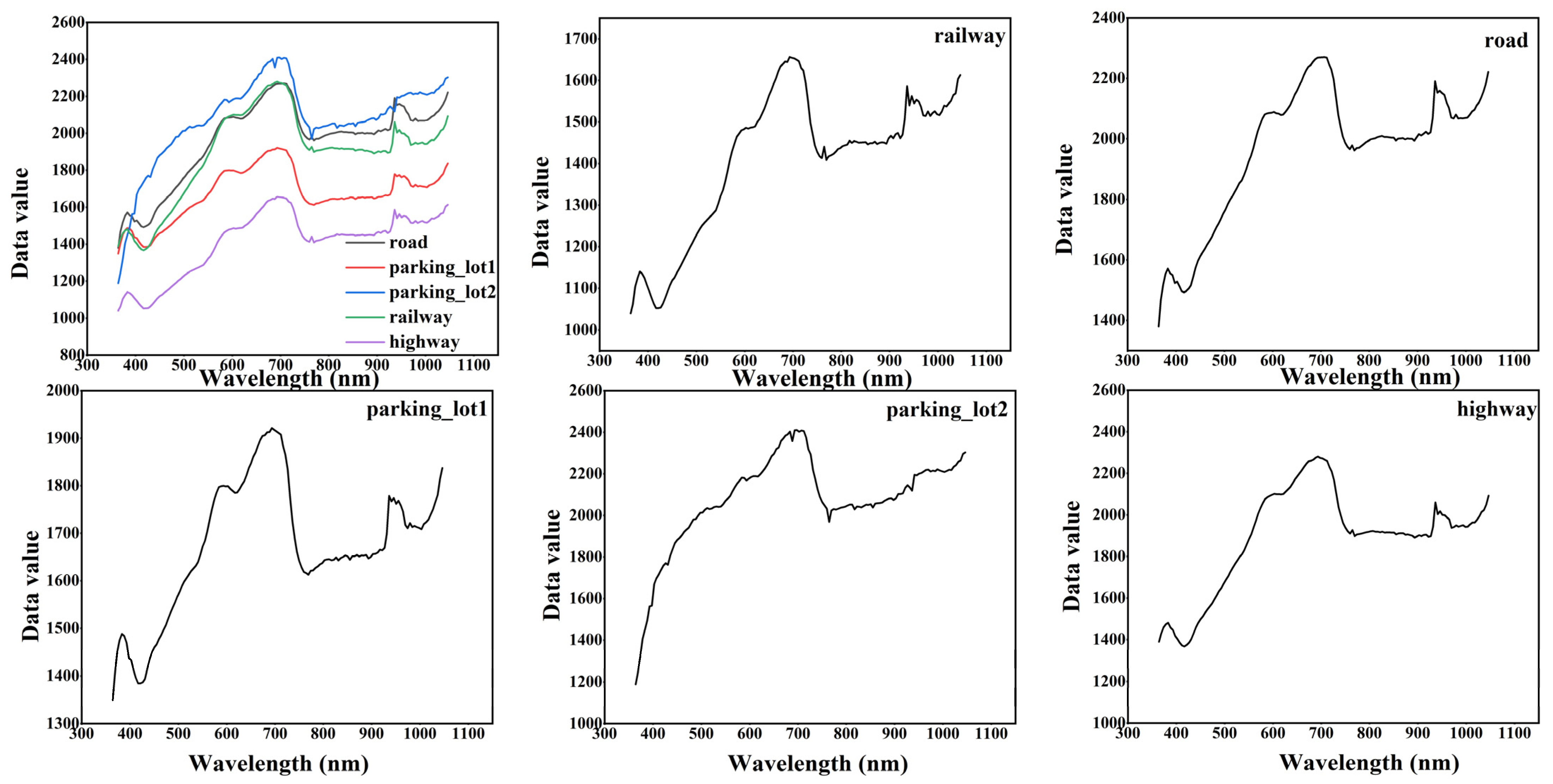
Figure 9.
Spectral curves of classes with commission and omission error on Houston dataset.
Figure 9.
Spectral curves of classes with commission and omission error on Houston dataset.
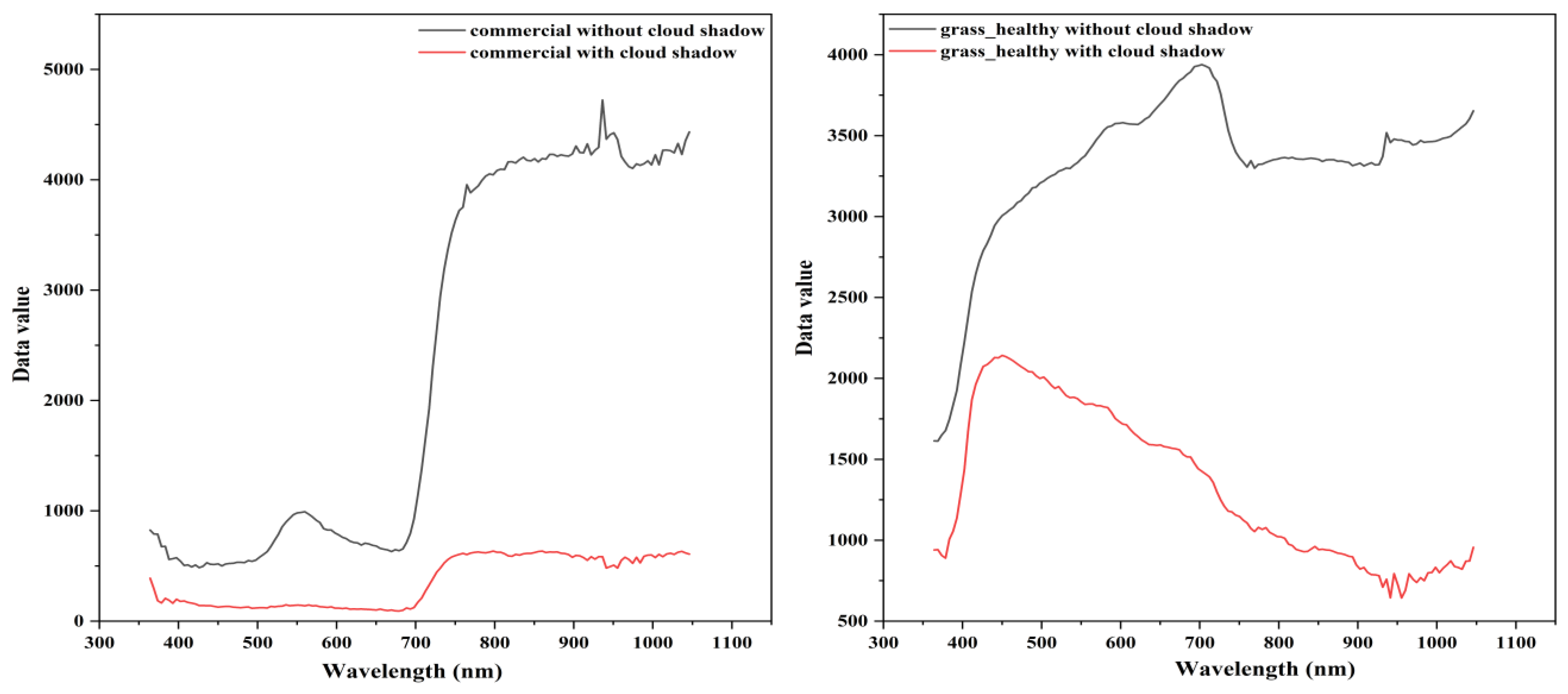
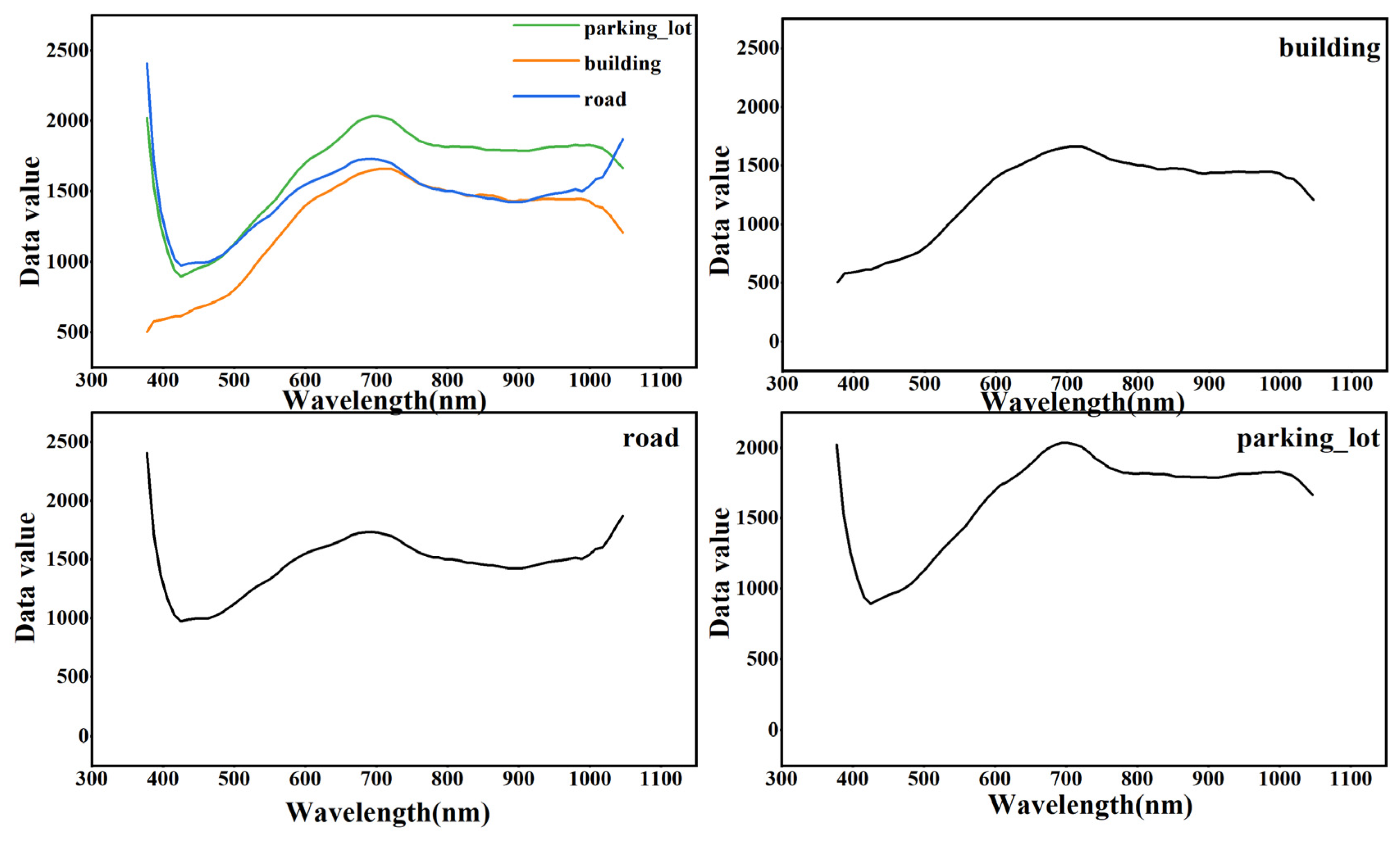
Figure 10.
Comparison of spectral curves of the same class on Houston dataset. The (left) is the spectral curves of commercial, the (right) is the spectral curves of grass_healthy.
Figure 10.
Comparison of spectral curves of the same class on Houston dataset. The (left) is the spectral curves of commercial, the (right) is the spectral curves of grass_healthy.
Figure 11.
Classification results of different methods for Houston dataset with 15 classes. (a) False color image. (b) The classification map of SVM classifier, OA = 72.36%. (c) The classification map of RF classifier, OA = 85.30%. (d) The classification map of 1D-CNN classifier, OA = 91.10%. (e) The classification map of 3D-CNN classifier, OA = 95.90%. (f) The classification map of 3D-2D-CNN classifier, OA = 96.32%. (g) The classification map of 3D-1D-CNN classifier, OA = 96.32%.
Figure 11.
Classification results of different methods for Houston dataset with 15 classes. (a) False color image. (b) The classification map of SVM classifier, OA = 72.36%. (c) The classification map of RF classifier, OA = 85.30%. (d) The classification map of 1D-CNN classifier, OA = 91.10%. (e) The classification map of 3D-CNN classifier, OA = 95.90%. (f) The classification map of 3D-2D-CNN classifier, OA = 96.32%. (g) The classification map of 3D-1D-CNN classifier, OA = 96.32%.
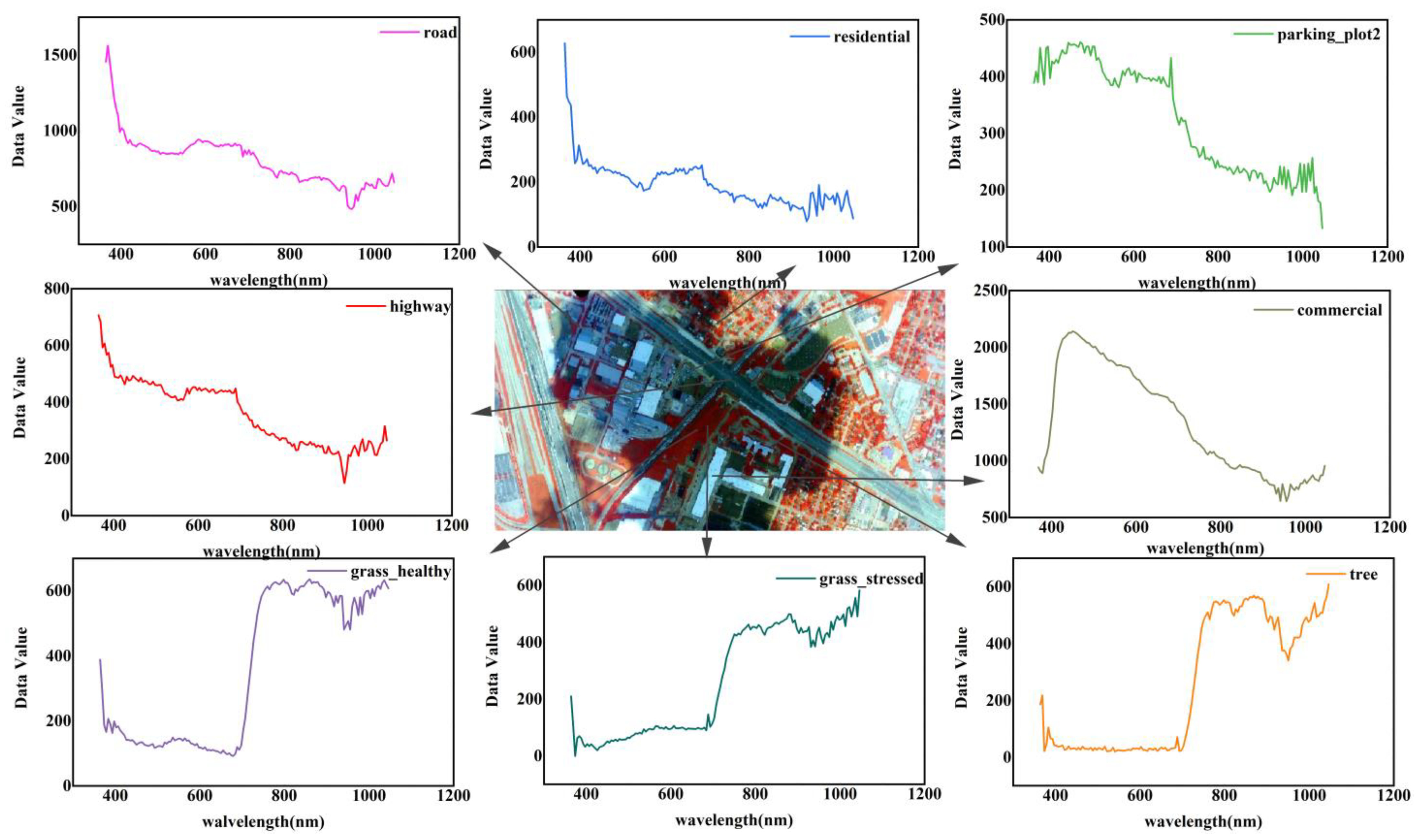
Figure 12.
Spectral curves of classes with commission and omission error on Surrey dataset.
Figure 12.
Spectral curves of classes with commission and omission error on Surrey dataset.
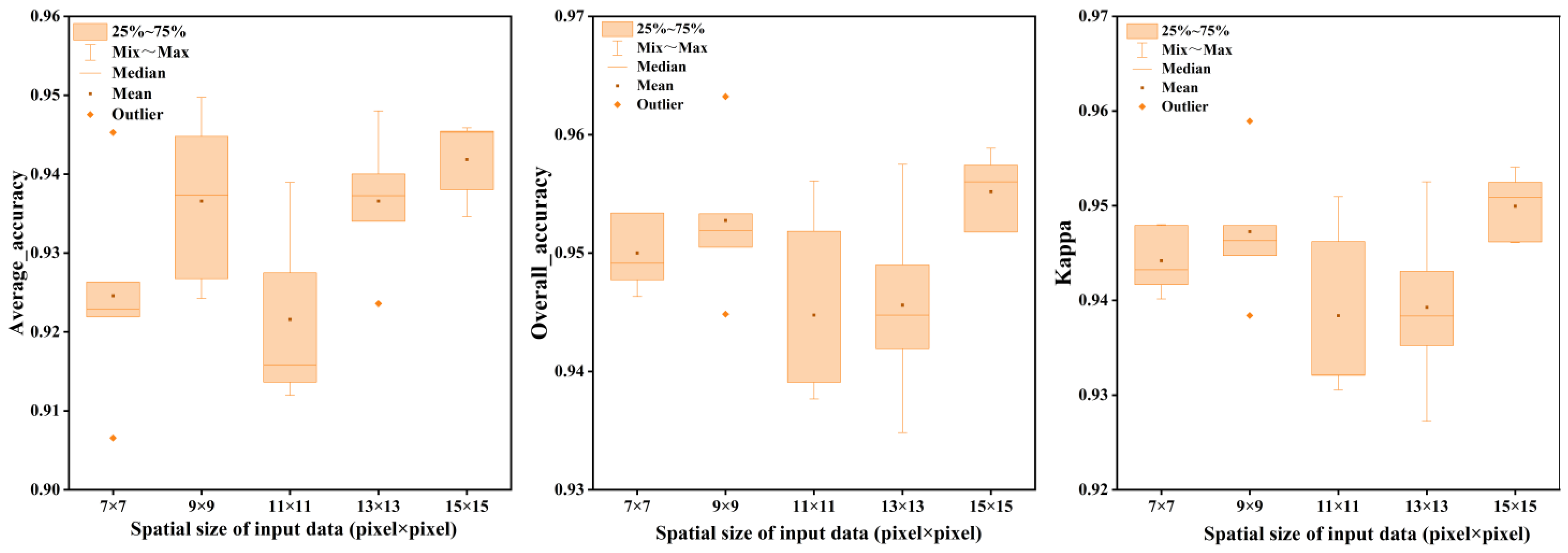
Figure 13.
Impact of different input sizes on 3D-1D-CNN for Houston dataset.
Figure 13.
Impact of different input sizes on 3D-1D-CNN for Houston dataset.
Figure 14.
Sample of road with different input sizes on the Houston dataset.
Figure 14.
Sample of road with different input sizes on the Houston dataset.
Figure 15.
Classification results in the cloud shadow area of the Houston dataset.
Figure 15.
Classification results in the cloud shadow area of the Houston dataset.
Figure 16.
Spectral curves of classes in the cloud shadow area.
Figure 16.
Spectral curves of classes in the cloud shadow area.
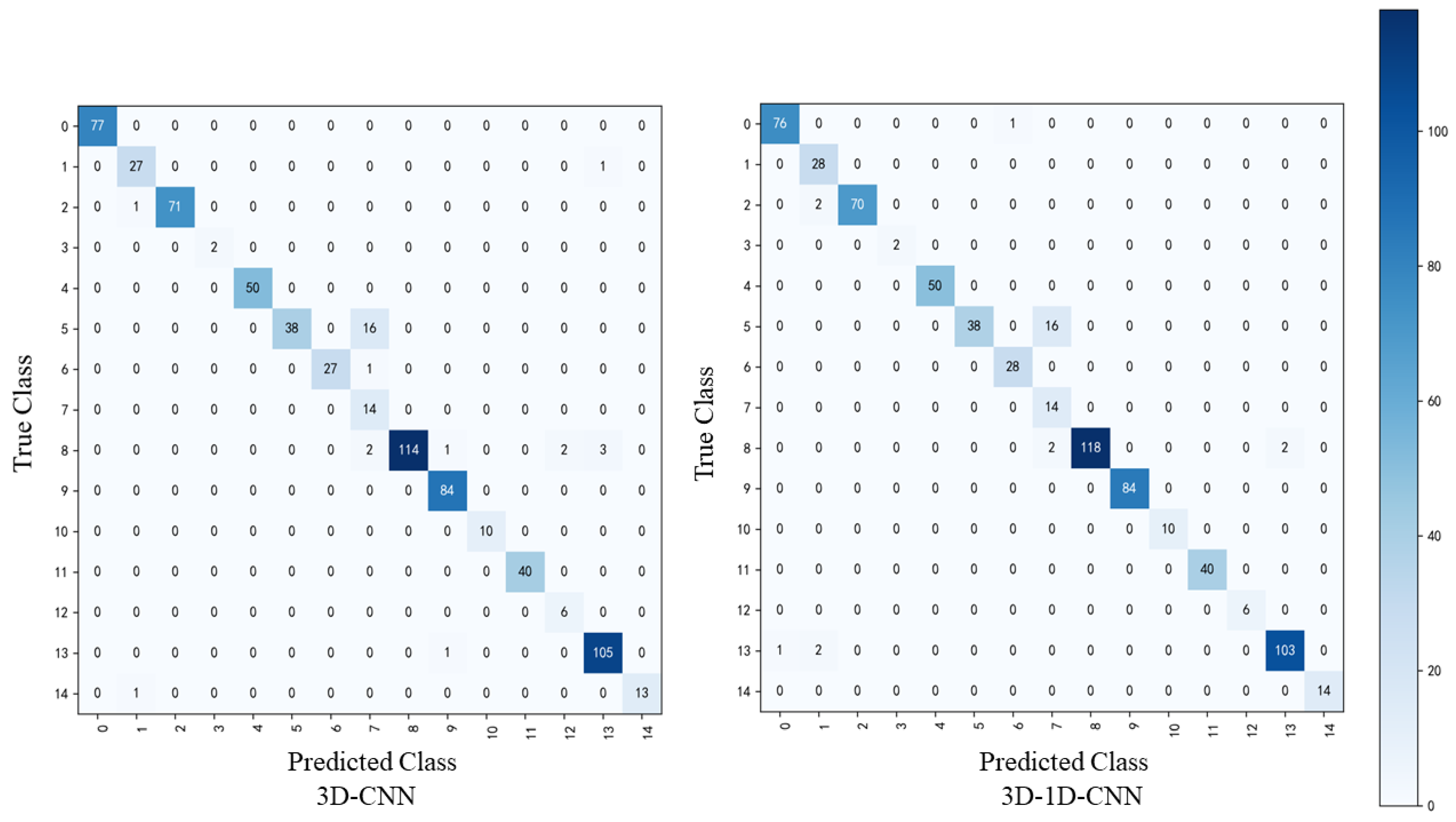
Figure 17.
Confusion matrix comparison of different models on the Houston dataset.
Figure 17.
Confusion matrix comparison of different models on the Houston dataset.
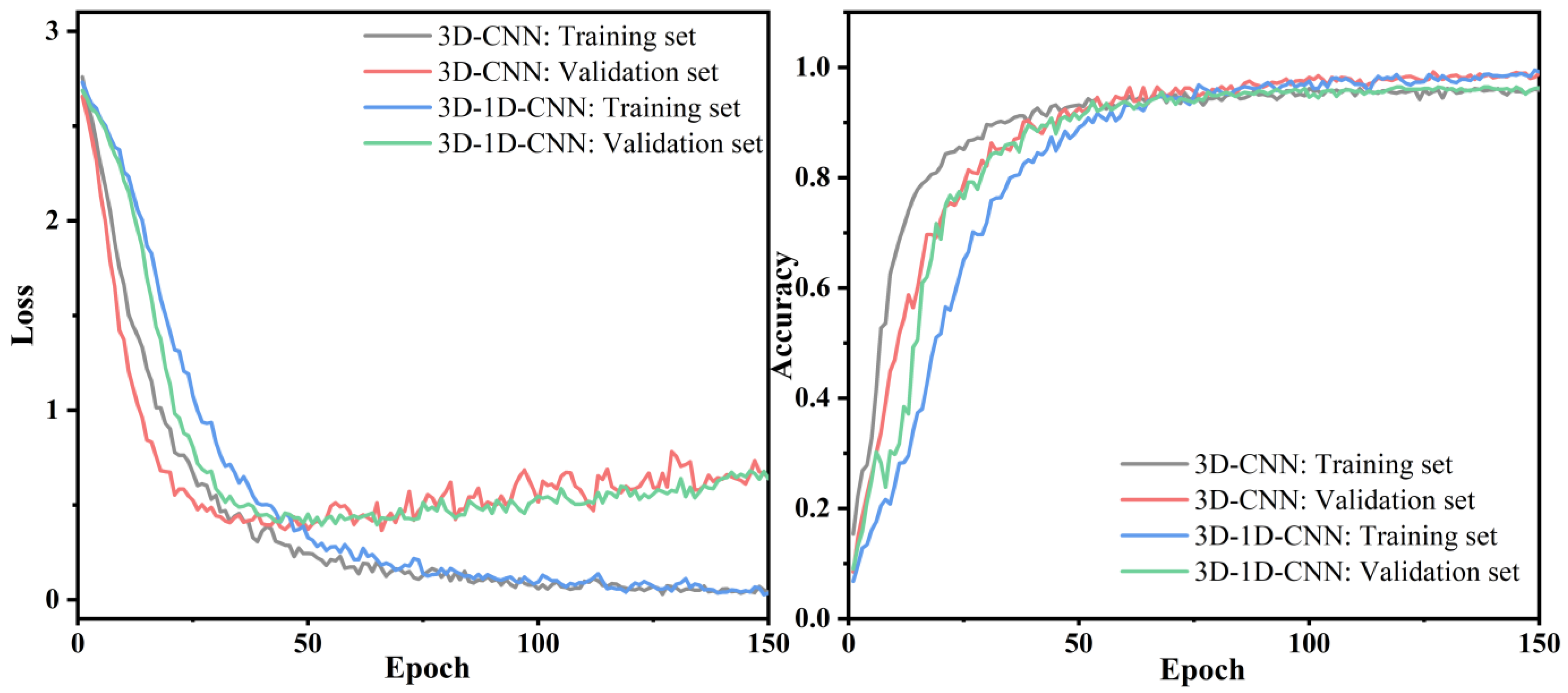
Figure 18.
Comparison of accuracy loss curves of different models on the Houston dataset.
Figure 18.
Comparison of accuracy loss curves of different models on the Houston dataset.
Table 1.
Summary of training and validation samples of Houston dataset.
Table 1.
Summary of training and validation samples of Houston dataset.
| Class | Sample |
|---|
| Train | Validation |
|---|
| commercial | 83 | 77 |
| grass_healthy | 84 | 28 |
| grass_stressed | 90 | 72 |
| grass_synthetic | 40 | 2 |
| highway | 88 | 50 |
| parking_lot1 | 88 | 54 |
| parking_lot2 | 28 | 28 |
| railway | 94 | 14 |
| residential | 91 | 122 |
| road | 98 | 84 |
| running_track | 41 | 10 |
| soil | 80 | 40 |
| tennis_court | 21 | 6 |
| tree | 77 | 106 |
| water | 10 | 14 |
| Total | 1013 | 707 |
Table 2.
Experimental dataset information.
Table 2.
Experimental dataset information.
| Dataset | Houston Dataset | Surrey Dataset |
|---|
| Sensor | CASI | CASI |
| Acquisition time | 2013/6/23 | 2013/4/30 |
| Number of Bands | 144 | 72 |
| Size | 1895 × 349 | 1655 × 988 |
| Number of Classes | 15 | 7 |
| Spatial resolution | 2.5 m | 1 m |
| Spectral resolution | 4.8 nm | 9.6 nm |
Table 3.
Variable and their respective descriptions and reference.
Table 3.
Variable and their respective descriptions and reference.
| Variable | Description | Reference |
|---|
| Spectral composition parameters | | |
| MNF22 | First 22 components of minimum noise fraction | [22] |
| Vegetation Index | | |
| Normalized Difference Vegetation Index (NDVI) | | [25] |
| Texture characteristics | | |
| Mean | | [24] |
| Variance | | [24] |
| Homogeneity | | [24] |
| Contrast | | [24] |
| Dissimilarity | | [24] |
| Entropy | | [24] |
| Second Moment | | [24] |
| Correlation | | [24] |
Table 4.
3D-CNN model structure.
Table 4.
3D-CNN model structure.
| Layer | Output Shape for 3D Data | Training Parameter Number |
|---|
| conv3d | (9, 9, 26, 4) | 220 |
| conv3d_1 | (7, 7, 21, 8) | 1736 |
| conv3d_2 | (5, 5, 16, 16) | 6928 |
| conv3d_3 | (3, 3, 11, 32) | 27,680 |
| conv3d_4 | (1, 1, 6, 64) | 110,656 |
| dropout | (1, 1, 6, 64) | 0 |
| flatten | (384) | 0 |
| dense | (128) | 49,280 |
| dropout_1 | (128) | 0 |
| dense_1 | (15) | 1935 |
Table 5.
3D-1D-CNN model structure.
Table 5.
3D-1D-CNN model structure.
| Layer | Output Shape for 3D Data | Training Parameter Number |
|---|
| conv3d | (9, 9, 26, 4) | 220 |
| conv3d_1 | (7, 7, 21, 8) | 1736 |
| conv3d_2 | (5, 5, 16, 16) | 6928 |
| conv3d_3 | (3, 3, 11, 32) | 27,680 |
| conv3d_4 | (1, 1, 6, 64) | 110,656 |
| dropout | (1, 1, 6, 64) | 0 |
| Reshape | (6, 64) | 0 |
| conv1d | (4, 48) | 9264 |
| conv1d_1 | (4, 24) | 1176 |
| flatten | (96) | 0 |
| dense | (128) | 12,416 |
| dropout_1 | (128) | 0 |
| dense_1 | (15) | 1935 |
Table 6.
Performance comparison of different classification methods on the Houston dataset.
Table 6.
Performance comparison of different classification methods on the Houston dataset.
| | SVM | RF | 1D-CNN | 3D-CNN | 3D-2D-CNN | 3D-1D-CNN |
|---|
| commercial | 0.56 | 0.72 | 0.98 | 1.00 | 1.00 | 0.99 |
| grass_healthy | 0.88 | 0.88 | 0.90 | 0.93 | 0.93 | 0.88 |
| grass_stressed | 0.89 | 0.96 | 0.98 | 1.00 | 0.99 | 1.00 |
| grass_synthetic | 0.92 | 1.00 | 0.57 | 1.00 | 1.00 | 1.00 |
| highway | 0.56 | 0.73 | 0.91 | 1.00 | 1.00 | 1.00 |
| parking_lot1 | 0.47 | 0.84 | 0.67 | 1.00 | 0.83 | 1.00 |
| parking_lot2 | 0.70 | 0.81 | 0.83 | 1.00 | 1.00 | 0.97 |
| railway | 0.59 | 0.80 | 0.54 | 0.42 | 0.62 | 0.44 |
| residential | 0.63 | 0.77 | 0.94 | 1.00 | 0.98 | 1.00 |
| road | 0.58 | 0.82 | 0.90 | 0.98 | 0.98 | 1.00 |
| running_track | 0.98 | 0.98 | 0.95 | 1.00 | 1.00 | 1.00 |
| soil | 0.97 | 0.97 | 0.99 | 1.00 | 1.00 | 1.00 |
| tennis_court | 0.93 | 0.94 | 0.83 | 0.75 | 1.00 | 1.00 |
| tree | 0.93 | 0.90 | 0.99 | 0.96 | 0.98 | 0.98 |
| water | 0.95 | 0.97 | 0.92 | 1.00 | 0.96 | 1.00 |
| AA (%) | 77.71 | 80.62 | 85.67 | 93.64 | 95.15 | 94.97 |
| OA (%) | 72.36 | 85.30 | 91.10 | 95.90 | 96.32 | 96.32 |
| Kappa × 100 | 70.01 | 84.04 | 90.08 | 95.42 | 95.89 | 95.89 |
| Training parameters | - | - | - | 198,435 | 602,743 | 172,011 |
| Training time(minute) | - | - | - | 5.77 | 7.94 | 3.58 |
Table 7.
Accuracy of each class with different classification methods for Surrey dataset.
Table 7.
Accuracy of each class with different classification methods for Surrey dataset.
| | SVM | RF | 1D-CNN | 3D-CNN | 3D-2D-CNN | 3D-1D-CNN |
|---|
| tree | 0.94 | 0.94 | 0.85 | 0.95 | 0.91 | 1.00 |
| grass | 1.00 | 0.99 | 0.97 | 0.76 | 0.97 | 1.00 |
| soil | 0.92 | 0.80 | 0.50 | 0.29 | 0.60 | 1.00 |
| water | 0.96 | 0.98 | 0.90 | 0.78 | 0.86 | 1.00 |
| parking_lot | 0.75 | 0.86 | 0.80 | 0.58 | 0.78 | 0.75 |
| road | 0.66 | 0.74 | 0.93 | 0.97 | 0.94 | 0.82 |
| building | 0.81 | 0.90 | 1.00 | 1.00 | 0.92 | 0.88 |
| OA (%) | 82.81 | 86.83 | 88.20 | 82.58 | 89.33 | 90.44 |
| Kappa × 100 | 78.96 | 83.78 | 84.95 | 78.05 | 86.29 | 87.72 |
| Training parameters | - | - | - | 199,131 | 601,711 | 172,707 |
| Training time (minute) | - | - | - | 10.16 | 11.30 | 9.46 |
Table 8.
Comparison of the performance of different hyperspectral parameters on Houston dataset (input size = 9).
Table 8.
Comparison of the performance of different hyperspectral parameters on Houston dataset (input size = 9).
| | MNF22 | MNF22 + NDVI | MNF22 + GLCM | MNF22 + GLCM + NDVI |
|---|
| commercial | 1.00 | 1.00 | 0.99 | 0.99 |
| grass_healthy | 0.89 | 0.85 | 0.79 | 0.88 |
| grass_stressed | 0.97 | 1.00 | 0.99 | 1.00 |
| grass_synthetic | 1.00 | 1.00 | 0.67 | 1.00 |
| highway | 0.96 | 0.96 | 0.91 | 1.00 |
| parking_lot1 | 0.95 | 0.86 | 0.88 | 1.00 |
| parking_lot2 | 1.00 | 1.00 | 1.00 | 0.97 |
| railway | 0.44 | 0.41 | 0.44 | 0.44 |
| residential | 1.00 | 1.00 | 0.97 | 1.00 |
| road | 0.98 | 0.99 | 0.94 | 1.00 |
| running track | 1.00 | 1.00 | 1.00 | 1.00 |
| soil | 1.00 | 1.00 | 1.00 | 1.00 |
| tennis court | 0.75 | 0.86 | 0.86 | 1.00 |
| tree | 0.93 | 0.93 | 0.98 | 0.98 |
| water | 1.00 | 1.00 | 1.00 | 1.00 |
| AA (%) | 92.44 | 92.39 | 89.33 | 94.97 |
| OA (%) | 94.48 | 93.92 | 93.07 | 96.32 |
| Kappa × 100 | 93.84 | 93.22 | 92.27 | 95.89 |