GOCE Downward Continuation to the Earth’s Surface and Improvements to Local Geoid Modeling by FFT and LSC
Abstract
1. Introduction
2. SGG Data Filtering and Reduction to a Mean Orbit
3. SGG Downward Continuation to the Earth’s Surface
3.1. Iterative Approach for Downward Continuation
3.2. Formulation of the Downward Continuation Problem
3.3. Numerical Experiments using GOCE Data
4. Geoid Estimation with GOCE and Local Gravity Data
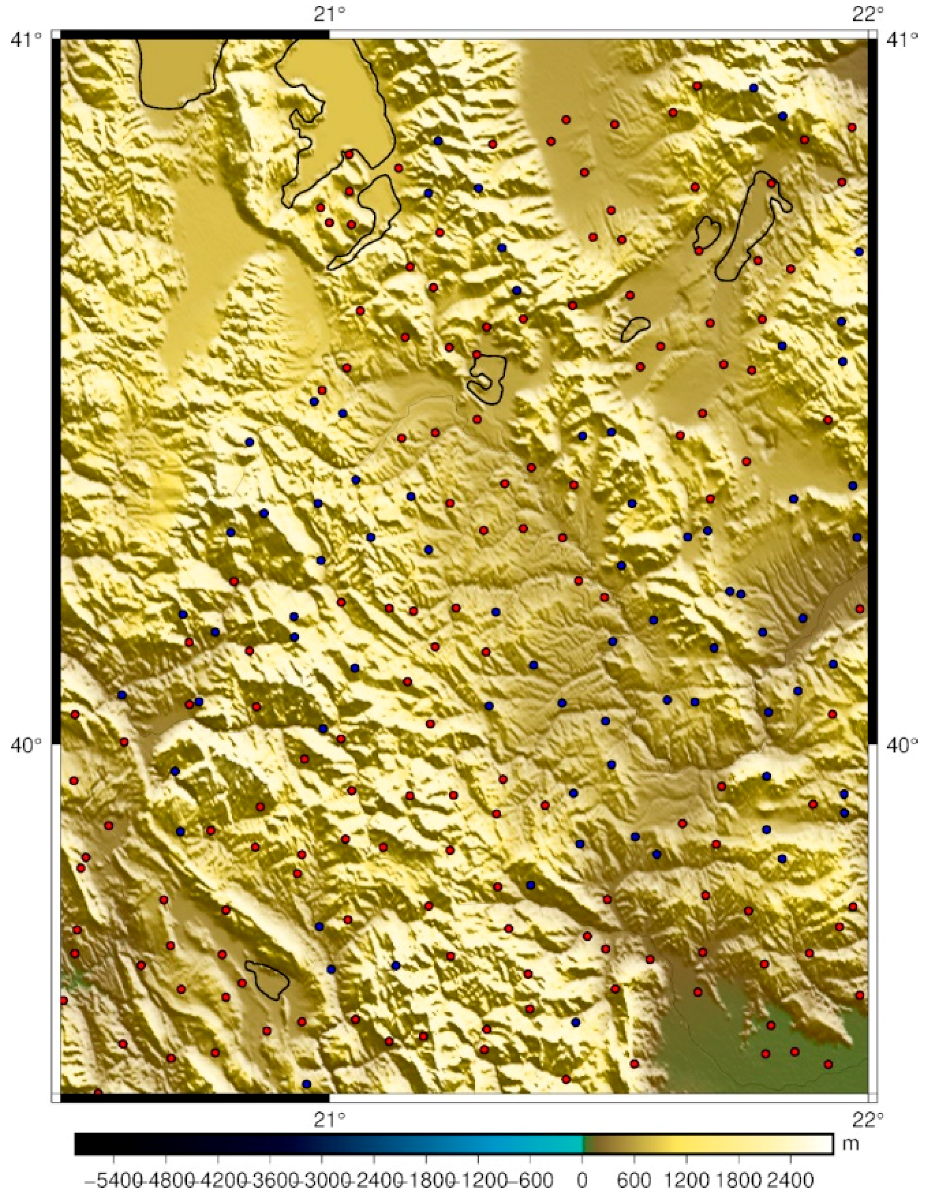
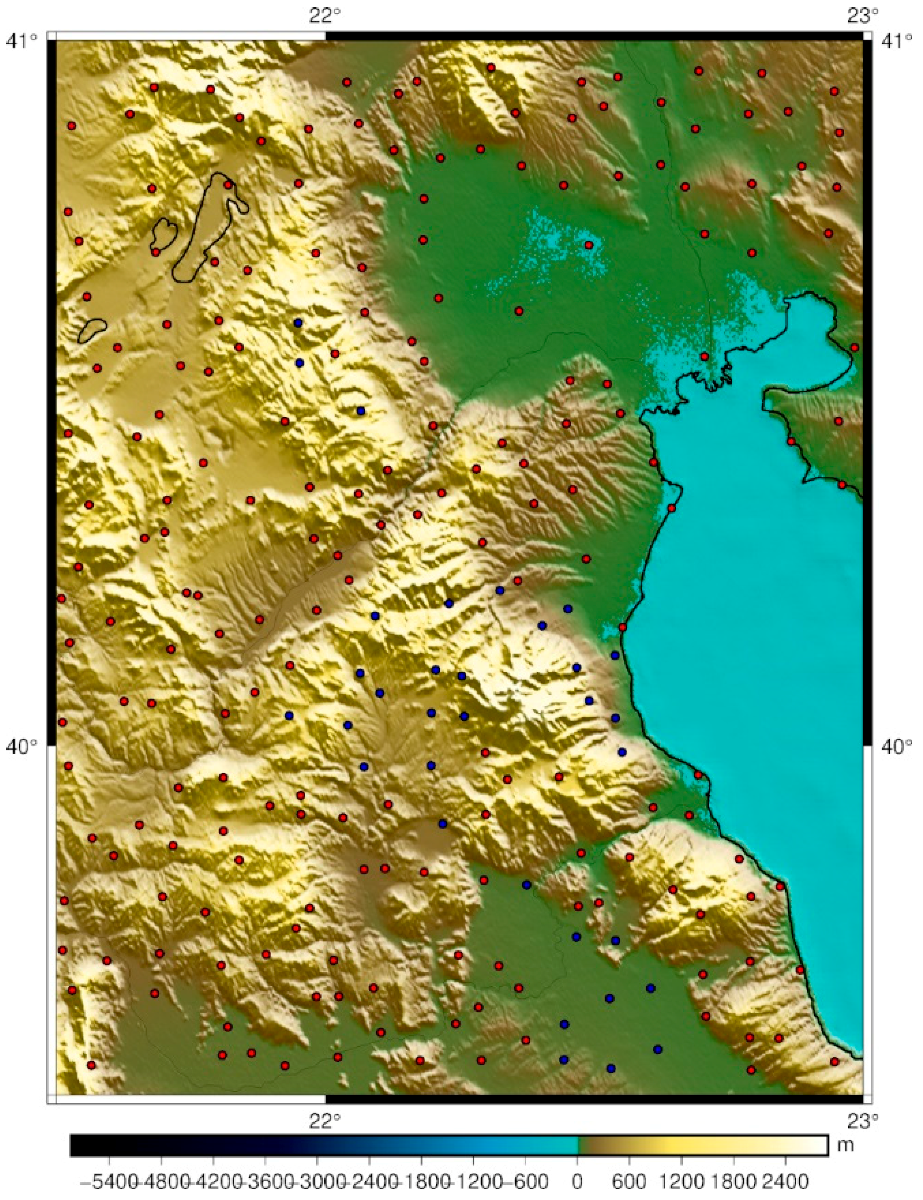
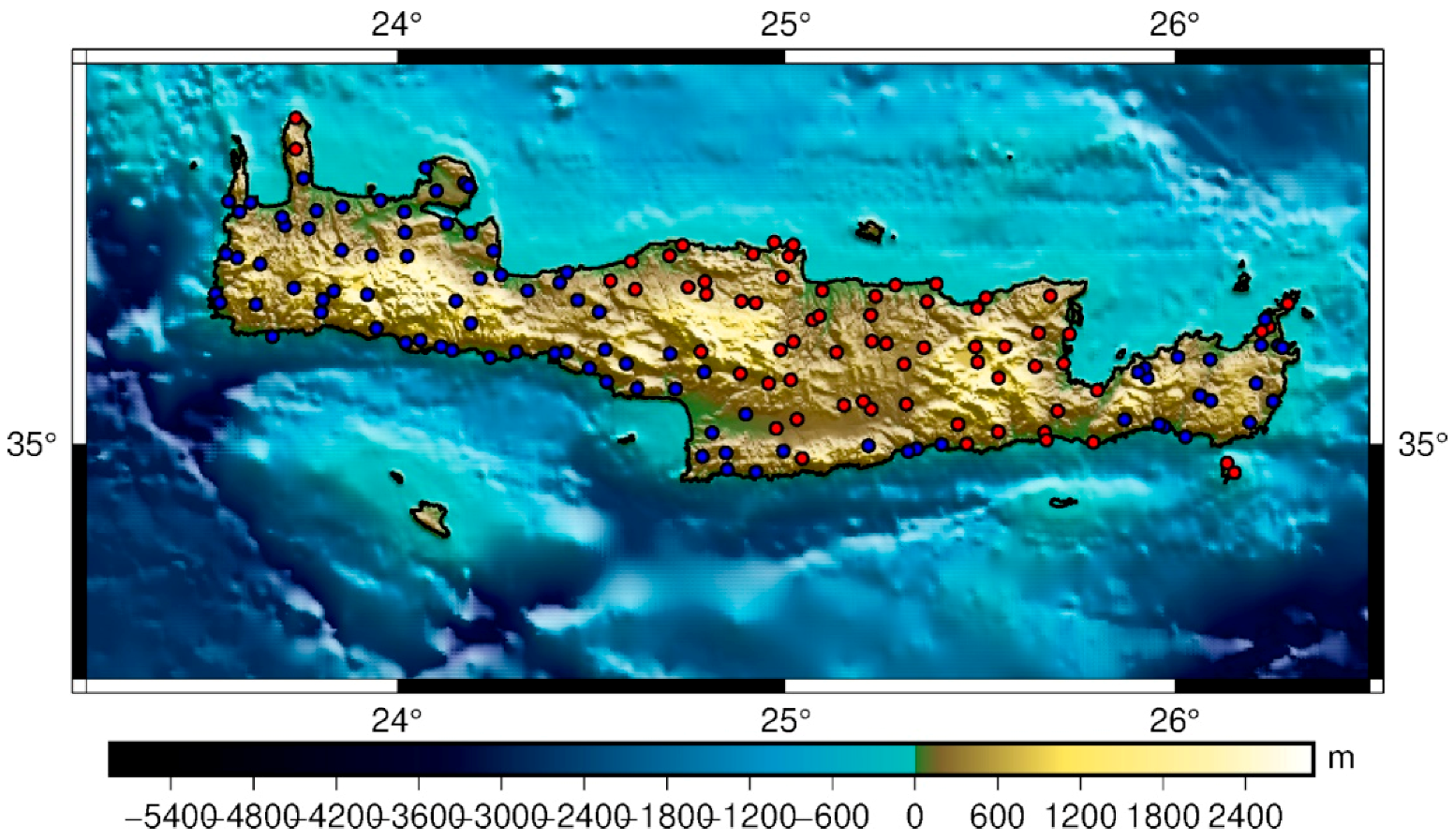
4.1. Methodology, Local Data and Gravity Reductions
4.2. Geoid Models and Validation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rummel, R.; Yi, W.; Stummer, C. GOCE Gravitational Gradiometry. J. Geod. 2011, 85, 777–790. [Google Scholar] [CrossRef]
- Rummel, R.; Gruber, T.; Flury, J.; Schlicht, A. ESA’s Gravity Field and Steady-State Ocean Circulation Explorer GOCE. ZFV—Z. Fur Geodasie Geoinf. Und Landmanag. 2009, 134, 125–130. [Google Scholar]
- Drinkwater, M.R.; Haagmans, R.; Muzi, D.; Popescu, A.; Floberghagen, R.; Kern, M.; Fehringer, M. The GOCE Gravity Mission: ESA’S First Core Earth Explorer. In Proceedings of the 3rd GOCE User Workshop, ESA SP-627, Frascati, Italy, 6–8 November 2006; European Space Agency: Noordwijk, The Netherlands, 2007; pp. 1–7. [Google Scholar]
- Tóth, G.; Földvári, L.; Tziavos, I.N.; Ádám, J. Upward/Downward Continuation of Gravity Gradients for Precise Geoid Determination. Acta Geod. Geophys. Hung. 2006, 41, 21–30. [Google Scholar] [CrossRef]
- Sinem Ince, E.; Barthelmes, F.; Reißland, S.; Elger, K.; Förste, C.; Flechtner, F.; Schuh, H. ICGEM—15 Years of Successful Collection and Distribution of Global Gravitational Models, Associated Services, and Future Plans. Earth Syst. Sci. Data 2019, 11, 647–674. [Google Scholar] [CrossRef]
- Barzaghi, R.; Carrion, D.; Vergos, G.S.; Tziavos, I.N.; Grigoriadis, V.N.; Natsiopoulos, D.A.; Bruinsma, S.; Reinquin, F.; Seoane, L.; Bonvalot, S.; et al. GEOMED2: High-Resolution Geoid of the Mediterranean. In Proceedings of the International Symposium on Advancing Geodesy in a Changing World, Kobe, Japan, 30 July–August 2017; Freymueller, J., Sánchez, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; Volume 149, pp. 43–50. [Google Scholar] [CrossRef]
- Matsuo, K.; Kuroishi, Y. Refinement of a Gravimetric Geoid Model for Japan Using GOCE and an Updated Regional Gravity Field Model. Earth Planets Sp. 2020, 72, 1–18. [Google Scholar] [CrossRef]
- Van der Meijde, M.; Pail, R.; Bingham, R.; Floberghagen, R. GOCE Data, Models, and Applications: A Review. Int. J. Appl. Earth Obs. Geoinf. 2015, 35, 4–15. [Google Scholar] [CrossRef]
- Vu, D.T.; Bruinsma, S.; Bonvalot, S.; Remy, D.; Vergos, G.S. A Quasigeoid-Derived Transformation Model Accounting for Land Subsidence in the Mekong Delta towards Height System Unification in Vietnam. Remote Sens. 2020, 12, 817. [Google Scholar] [CrossRef]
- Grigoriadis, V.N.; Vergos, G.S.; Barzaghi, R.; Carrion, D.; Koç, Ö. Collocation and FFT-Based Geoid Estimation within the Colorado 1 Cm Geoid Experiment. J. Geod. 2021, 95, 1–18. [Google Scholar] [CrossRef]
- Wang, Y.M.; Sánchez, L.; Ågren, J.; Huang, J.; Forsberg, R.; Abd-Elmotaal, H.A.; Ahlgren, K.; Barzaghi, R.; Bašić, T.; Carrion, D.; et al. Colorado Geoid Computation Experiment: Overview and Summary. J. Geod. 2021, 95, 1–21. [Google Scholar] [CrossRef]
- Marchenko, A.N.; Marchenko, D.A.; Lopushansky, A.N. Gravity Field Models Derived from the Second Degree Radial Derivatives of the GOCE Mission: A Case Study. Ann. Geophys. 2017, 59, S0649. [Google Scholar] [CrossRef]
- Marchenko, A.; Abrikosov, O. Geoid in the West Ukraine Area Derived by Means of Non-Central Multipole Analysis Technique. In Gravity and Geoid; International Association of Geodesy Symposia; Sünkel, H., Marson, I., Eds.; Springer: Berlin/Heidelberg, Germany, 1995; Volume 113, pp. 624–630. [Google Scholar]
- Vergos, G.S.; Erol, B.; Natsiopoulos, D.A.; Grigoriadis, V.N.; Işık, M.S.; Tziavos, I.N. Preliminary Results of GOCE-Based Height System Unification between Greece and Turkey over Marine and Land Areas. Acta Geod. Geophys. 2018, 53, 61–79. [Google Scholar] [CrossRef]
- Andritsanos, V.D.; Grigoriadis, V.N.; Natsiopoulos, D.A.; Vergos, G.S.; Gruber, T.; Fecher, T. GOCE Variance and Covariance Contribution to Height System Unification. In Proceedings of the International Symposium on Gravity, Geoid and Height Systems, Thessaloniki, Greece, 19–23 September 2016; Vergos, G., Pail, R., Barzaghi, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; Volume 148, pp. 157–164. [Google Scholar] [CrossRef]
- Andritsanos, V.; Grigoriadis, V.; Vergos, G.; Pagounis, V.; Tziavos, I. GOCE/GRACE GGM Evaluation over Attica and Thessaloniki, Greece and Local Geoid Modelling in Support of Height Unification. South-East. Eur. J. Earth Obs. Geomat. 2015, 4, 105–122. [Google Scholar]
- Sánchez, L. Towards a Vertical Datum Standardisation under the Umbrella of Global Geodetic Observing System. J. Geod. Sci. 2012, 2, 325–342. [Google Scholar] [CrossRef]
- Sánchez, L.; Ågren, J.; Huang, J.; Wang, Y.M.; Mäkinen, J.; Pail, R.; Barzaghi, R.; Vergos, G.S.; Ahlgren, K.; Liu, Q. Strategy for the Realisation of the International Height Reference System (IHRS). J. Geod. 2021, 95, 1–33. [Google Scholar] [CrossRef]
- Ihde, J.; Sánchez, L.; Barzaghi, R.; Drewes, H.; Foerste, C.; Gruber, T.; Liebsch, G.; Marti, U.; Pail, R.; Sideris, M. Definition and Proposed Realization of the International Height Reference System (IHRS). Surv. Geophys. 2017, 38, 549–570. [Google Scholar] [CrossRef]
- Gruber, T.; Gerlach, C.; Haagmans, R. Intercontinental Height Datum Connection with GOCE and GPS-Levelling Data. J. Geod. Sci. 2012, 2, 270–280. [Google Scholar] [CrossRef]
- Willberg, M.; Gruber, T.; Vergos, G.S. Analysis of GOCE Omission Error and Its Contribution to Vertical Datum Offsets in Greece and Its Islands. In Proceedings of the International Symposium on Gravity, Geoid and Height Systems, Thessaloniki, Greece, 19–23 September 2016; Vergos, G., Pail, R., Barzaghi, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; Volume 148, pp. 143–148. [Google Scholar] [CrossRef]
- Migliaccio, F.; Reguzzoni, M.; Gatti, A. A GOCE-Only Global Gravity Field Model by the Space-Wise Approach. Geophys. Res. Abstr. 2011, 13, EGU2011-10063-3. [Google Scholar]
- Pail, R.; Bruinsma, S.; Migliaccio, F.; Förste, C.; Goiginger, H.; Schuh, W.-D.; Höck, E.; Reguzzoni, M.; Brockmann, J.; Abrikosov, O.; et al. First GOCE Gravity Field Models Derived by Three Different Approaches. J. Geod. 2011, 85, 819–843. [Google Scholar] [CrossRef]
- Bouman, J.; Ebbing, J.; Fuchs, M.; Sebera, J.; Lieb, V.; Szwillus, W.; Haagmans, R.; Novak, P. Satellite Gravity Gradient Grids for Geophysics. Sci. Rep. 2016, 6, 1–11. [Google Scholar] [CrossRef]
- Sebera, J.; Šprlák, M.; Novák, P.; Bezděk, A.; Va’ko, M. Iterative Spherical Downward Continuation Applied to Magnetic and Gravitational Data from Satellite. Surv. Geophys. 2014, 35, 941–958. [Google Scholar] [CrossRef]
- Xiaogang, L.; Kai, W. Downward Continuation of Satellite Gravity Gradient Data Based on Poisson Integral Iteration Method. Procedia Environ. Sci. 2012, 12, 721–728. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, H.; Zhong, B.; Luo, Z. Regional Gravity Field Recovery Using the GOCE Gravity Gradient Tensor and Heterogeneous Gravimetry and Altimetry Data. J. Geophys. Res. Solid Earth 2017, 122, 6928–6952. [Google Scholar] [CrossRef]
- Lu, B.; Förste, C.; Barthelmes, F.; Petrovic, S.; Flechtner, F.; Luo, Z.; Zhong, B.; Zhou, H.; Wang, X.; Wu, T. Using Real Polar Ground Gravimetry Data to Solve the GOCE Polar Gap Problem in Satellite-Only Gravity Field Recovery. J. Geod. 2020, 94, 1–12. [Google Scholar] [CrossRef]
- Sideris, M.G. On the Use of Heterogeneous Noisy Data in Spectral Gravity Field Modeling Methods. J. Geod. 1996, 70, 470–479. [Google Scholar] [CrossRef]
- Andritsanos, V.D.; Sideris, M.G.; Tziavos, I.N. Quasi-Stationary Sea Surface Topography Estimation by the Multiple Input/Output Method. J. Geod. 2001, 75, 216–226. [Google Scholar] [CrossRef]
- Grebenitcharsky, R.; Moore, P. Application of Wavelets for Along-Track Multi-Resolution Analysis of GOCE SGG Data. Int. Assoc. Geod. Symp. 2014, 141, 41–50. [Google Scholar] [CrossRef]
- Arabelos, D.N.; Tscherning, C.C.; Veicherts, M. External Calibration of GOCE SGG Data with Terrestrial Gravity Data: A Simulation Study. In Dynamic Planet; International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- ESA. GOCE High Level Processing Facility GOCE Level 2 Product Data Handbook; ESA: Paris, France, 2014. [Google Scholar]
- Pitenis, E.; Mamagiannou, E.; Natsiopoulos, D.A.; Vergos, G.S.; Tziavos, I.N.; Grigoriadis, V.N.; Sideris, M.G. FIR, IIR and Wavelet Algorithms for the Rigorous Filtering of GOCE SGG Data to the GOCE MBW. Remote Sens. 2022, 14, 3024. [Google Scholar] [CrossRef]
- Mamagiannou, E.; Pitenis, E.; Natsiopoulos, D.A.; Vergos, G.S.; Tziavos, I.N. GeoGravGOCE: A Standalone MATLAB GUI for Processing GOCE Satellite Gradient Data. Comput. Geosci. 2022, 166, 105184. [Google Scholar] [CrossRef]
- Jan Martin, B.; Till, S.; Torsten, M.-G.; Schuh, W.-D. The Earth’s Gravity Field as Seen by the GOCE Satellite—An Improved Sixth Release Derived with the Time-Wise Approach (GO_CONS_GCF_2_TIM_R6); GFZ Data Services; ICGEM: Trieste, Italy, 2019; Volume 3, pp. 1–9. [Google Scholar] [CrossRef]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The Development and Evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. Solid Earth 2012, 117, 8916. [Google Scholar] [CrossRef]
- Gruber, T.; Rummel, R.; Koop, R. HOW to Use GOCE Level 2 Products. In Proceedings of the 3rd International GOCE User Workshop, ESA-ESRIN, Frascati, Italy, 6–8 November 2006; European Space Agency: Paris, France, 2007; Volume 2006, pp. 205–211. [Google Scholar]
- Šprlák, M. A Graphical User Interface Application for Evaluation of the Gravitational Tensor Components Generated by a Level Ellipsoid of Revolution. Comput. Geosci. 2012, 46, 77–83. [Google Scholar] [CrossRef]
- Piretzidis, D. Study and Data Process of GOCE Satellite Mission, and Approximation of the Gravity Field of the Earth in Global and Regional Scale. Ph.D. Thesis, Aristotle University of Thessaloniki, Thessaloniki, Greece, 2014. [Google Scholar]
- Tóth, G.; Földváry, L. Effect of Geopotential Model Errors on the Projection of GOCE Gradiometer Observables. In Gravity, Geoid and Space Missions; International Association of Geodesy Symposia; Jekeli, C., Bastos, L., Fernandes, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; Volume 129, pp. 72–76. [Google Scholar]
- Novák, P.; Sebera, J.; Vaľko, M.; Šprlák, M.; Zdenek, M.; Sneeuw, N.; Roth, M.; Vermerseen, B.; van der Wal, W.; Baur, O.; et al. Towards a Better Understanding of the Earth’s Interior and Geophysical Exploration Research; EGU: Munich, Germany, 2013. [Google Scholar]
- Bucha, B.; Janák, J. A MATLAB-Based Graphical User Interface Program for Computing Functionals of the Geopotential up to Ultra-High Degrees and Orders. Comput. Geosci. 2013, 56, 186–196. [Google Scholar] [CrossRef]
- Sebera, J.; Pitoňák, M.; Hamáčková, E.; Novák, P. Comparative Study of the Spherical Downward Continuation. Surv. Geophys. 2015, 36, 253–267. [Google Scholar] [CrossRef]
- Janák, J.; Mikula, K.; Šprlák, M. Downward Continuation of Satellite Gradiometry Data. In Proceedings of the 3rd International GOCE User Workshop, ESA-ESRIN, Frascati, Italy, 6–8 November 2006; European Space Agency: Paris France, 2007; pp. 109–113. [Google Scholar]
- Martinec, Z. Stability Investigations of a Discrete Downward Continuation Problem for Geoid Determination in the Canadian Rocky Mountains. J. Geod. 1996, 70, 805–828. [Google Scholar] [CrossRef]
- Novák, P.; Šprlák, M.; Pitoňák, M. On Determination of the Geoid from Measured Gradients of the Earth’s Gravity Field Potential. Earth-Sci. Rev. 2021, 221, 103773. [Google Scholar] [CrossRef]
- Huang, J.; Véronneau, M. Applications of Downward-Continuation in Gravimetric Geoid Modeling: Case Studies in Western Canada. J. Geod. 2005, 79, 135–145. [Google Scholar] [CrossRef]
- Novák, P.; Heck, B. Downward Continuation and Geoid Determination Based on Band-Limited Airborne Gravity Data. J. Geod. 2002, 76, 269–278. [Google Scholar] [CrossRef]
- Chen, M.; Yang, W. An Enhancing Precision Method for Downward Continuation of Gravity Anomalies. J. Appl. Geophys. 2022, 204, 104753. [Google Scholar] [CrossRef]
- Kusche, J. A Monte-Carlo Technique for Weight Estimation in Satellite Geodesy. J. Geod. 2003, 76, 641–652. [Google Scholar] [CrossRef]
- Mosegaard, K.; Tarantola, A. Monte Carlo Sampling of Solutions to Inverse Problems. J. Geophys. Res. 1995, 100, 12431–12447. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Grebenitcharsky, R.S.; Vergos, G.S.; Piretzidis, D.; Tziavos, I.N. GOCE Gradient Downward Continuation for Local/Regional Gravity Field Recovery. In Proceedings of the 5th International GOCE User Workshop, Paris, France, 25–28 November 2014. [Google Scholar]
- Heiskanen, W.; Moritz, H. Physical Geodesy; W. H. Freeman: San Francisco, CA, USA, 1967; 364p. [Google Scholar]
- Novák, P.; Šprlák, M.; Tenzer, R.; Pitoňák, M. Integral Formulas for Transformation of Potential Field Parameters in Geosciences. Earth-Sci. Rev. 2017, 164, 208–231. [Google Scholar] [CrossRef]
- Andritsanos, V.D.; Tziavos, I.N. Estimation of Gravity Field Parameters by a Multiple Input/Output System. Phys. Chem. Earth Part A Solid Earth Geod. 2000, 25, 39–46. [Google Scholar] [CrossRef]
- Andritsanos, V.D.; Vergos, G.S.; Tziavos, I.N.; Pavlis, E.C.; Mertikas, S.P. A High-Resolution Geoid for the Establishment of the GAVDOS Multi-Satellite Calibration Site. In Gravity, Geoid and Geodynamics 2000; Springer: Berlin/Heidelberg, Germany, 2002; Volume 123, pp. 347–354. [Google Scholar]
- Vergos, G.S.; Tziavos, I.N.; Andritsanos, V.D. On the Determination of Marine Geoid Models by Least-Squares Collocation and Spectral Methods Using Heterogeneous Data. In A Window on the Future of Geodesy; International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2005; Volume 128, pp. 332–337. [Google Scholar] [CrossRef]
- Barzaghi, R.; Maggi, A.; Tselfes, N.; Tsoulis, D.; Tziavos, I.N.; Vergos, G.S. Combination of Gravimetry, Altimetry and GOCE Data for Geoid Determination in the Mediterranean: Evaluation by Simulation. In Observing our Changing Earth; Springer: Berlin/Heidelberg, Germany, 2009; Volume 133, pp. 195–201. [Google Scholar]
- Sanso, F.; Sideris, M. On the Similarities and Differences between Systems Theory and Least-Squares Collocation in Physical Geodesy. Bolletino Di Geod. Sci. Affin. 1997, 2, 173–206. [Google Scholar]
- Barzaghi, R.; Tselfes, N.; Tziavos, I.N.; Vergos, G.S. Geoid and High Resolution Sea Surface Topography Modelling in the Mediterranean from Gravimetry, Altimetry and GOCE Data: Evaluation by Simulation. J. Geod. 2009, 83, 751–772. [Google Scholar] [CrossRef]
- Eshagh, M. On Integral Approach to Regional Gravity Field Modelling from Satellite Gradiometric Data. Acta Geophys. 2010, 59, 29–54. [Google Scholar] [CrossRef]
- Eshagh, M. Alternative Expressions for Gravity Gradients in Local North-Oriented Frame and Tensor Spherical Harmonics. Acta Geophys. 2009, 58, 215–243. [Google Scholar] [CrossRef]
- Sansò, F.; Vergos, G.; Tziavos, I.; Venuti, G.; Grigoriadis, V. Geoid and Sea Surface Topography from Satellite and Ground Data in the Mediterranean Region—A Review and New Proposals. Bull. Geod. Geomat. 2008, 67, 155–201. [Google Scholar]
- Zingerle, P.; Pail, R.; Gruber, T.; Oikonomidou, X. The Combined Global Gravity Field Model XGM2019e. J. Geod. 2020, 94, 1–12. [Google Scholar] [CrossRef]
- Tziavos, I.N.; Vergos, G.S.; Grigoriadis, V.N.; Tzanou, E.A.; Natsiopoulos, D.A. Validation of GOCE/GRACE Satellite Only and Combined Global Geopotential Models Over Greece in the Frame of the GOCESeaComb Project. In IAG 150 Years, Proceedings of the IAG Scientific Assembly, Postdam, Germany, 1–6 September 2013; Rizos, C., Willis, P., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 297–304. ISBN 978-3-319-30895-1. [Google Scholar]
- Vergos, G.S.; Grigoriadis, V.N.; Tziavos, I.N.; Kotsakis, C. Evaluation of GOCE/GRACE Global Geopotential Models over Greece with Collocated GPS/Levelling Observations and Local Gravity Data. In Gravity, Geoid and Height Systems; International Association of Geodesy Symposia; Marti, U., Ed.; Springer: Cham, Switzerland, 2014; Volume 141, pp. 85–92. [Google Scholar]
- Mallat, S.G. A Theory for Multiresolution Signal Decomposition: The Wavelet Representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Daubechies, I. Ten Lectures on Wavelets; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1992; ISBN 9780898712742. [Google Scholar]
- Balodimos, D.D. Geoidal Studies in Greece; University of Oxford: Oxford, UK, 1972. [Google Scholar]
- Arabelos, D.N. Undersuchungen Zur Gravimetrischen Geoidbestimmung Dagerstellt Am Testgebiet Griechenland, Wiss. Arb. Ph.D. Thesis, University Hannover, Hannover, Germany, 1980. [Google Scholar]
- Tziavos, I.N. Study of the Optimal Combination of Heterogeneous Data on Geoid Determination with Applications for the Area of Greece. Ph.D. Thesis, Aristotle University of Thessaloniki, Thessaloniki, Greece, 1984. [Google Scholar]
- Arabelos, D.; Tziavos, I.N. Determination of Deflections of the Vertical Using a Combination of Spherical Harmonics and Gravimetric Data for the Area of Greece. Bull. Géodésique 1983, 57, 240–256. [Google Scholar] [CrossRef]
- Tziavos, I.N.; Andritsanos, V.D. Recent Geoid Computations for the Hellenic Area. Phys. Chem. Earth Part A Solid Earth Geod. 1999, 24, 91–96. [Google Scholar] [CrossRef]
- Tziavos, I.N.; Vergos, G.S.; Grigoriadis, V.N. Investigation of Topographic Reductions and Aliasing Effects on Gravity and the Geoid over Greece Based on Various Digital Terrain Models. Surv. Geophys. 2010, 31, 23–67. [Google Scholar] [CrossRef]
- Tziavos, I.N.; Vergos, G.S.; Mertikas, S.P.; Daskalakis, A.; Grigoriadis, V.N.; Tripolitsiotis, A. The Contribution of Local Gravimetric Geoid Models to the Calibration of Satellite Altimetry Data and an Outlook of the Latest GOCE GGM Performance in Gavdos. Adv. Sp. Res. 2013, 51, 1502–1522. [Google Scholar] [CrossRef]
- Tscherning, C.C.; Forsberg, R. Geoid Determination in the Nordic Countries from Gravity and Height Data. Boll. Geod. Sci. Affin. 1987, 46, 21–43. [Google Scholar]
- Hirt, C.; Kuhn, M.; Claessens, S.; Pail, R.; Seitz, K.; Gruber, T. Study of the Earth’s Short-Scale Gravity Field Using the ERTM2160 Gravity Model. Comput. Geosci. 2014, 73, 71–80. [Google Scholar] [CrossRef]
- Rexer, M.; Hirt, C.; Bucha, B.; Holmes, S. Solution to the Spectral Filter Problem of Residual Terrain Modelling (RTM). J. Geod. 2017, 92, 675–690. [Google Scholar] [CrossRef]
- Rexer, M.; Hirt, C.; Claessens, S.; Tenzer, R. Layer-Based Modelling of the Earth’s Gravitational Potential up to 10-Km Scale in Spherical Harmonics in Spherical and Ellipsoidal Approximation. Surv. Geophys. 2016, 37, 1035–1074. [Google Scholar] [CrossRef]
- Sideris, M.G. Geoid Determination by FFT Techniques. In Geoid Determination: Theory and Methods; Lecture Notes in Earth System Sciences; Springer: Berlin/Heidelberg, Germany, 2013; Volume 110, pp. 453–516. [Google Scholar] [CrossRef]
- Sansò, F.; Sideris, M.G. The Local Modelling of the Gravity Field by Collocation. In Geoid Determination: Theory and Methods; Lecture Notes in Earth System Sciences; Springer: Berlin/Heidelberg, Germany, 2013; Volume 110, pp. 203–258. [Google Scholar] [CrossRef]
- Tscherning, C.C. Geoid Determination by 3D Least-Squares Collocation. In Geoid Determination: Theory and Methods; Lecture Notes in Earth System Sciences; Springer: Berlin/Heidelberg, Germany, 2013; Volume 110, pp. 311–336. [Google Scholar] [CrossRef]
- Grigoriadis, V.N. Geodetic and Geophysical Approximation of the Earth’s Gravity Field and Applications in the Hellenic Area. Ph.D. Thesis, Aristotle Unversity of Thessaloniki, Thessaloniki, Greece, 2009. [Google Scholar]
- Mertikas, S.P.; Daskalakis, A.; Tziavos, I.N.; Andersen, O.B.; Vergos, G.S.; Tripolitsiotis, A.; Zervakis, V.; Frantzis, X.; Partsinevelos, P. Altimetry, Bathymetry and Geoid Variations at the Gavdos Permanent Cal/Val Facility. Adv. Sp. Res. 2013, 51, 1418–1437. [Google Scholar] [CrossRef]
- Kotsakis, C.; Katsambalos, K.; Ampatzidis, D. Estimation of the Zero-Height Geopotential Level WoLVD in a Local Vertical Datum from Inversion of Co-Located GPS, Leveling and Geoid Heights: A Case Study in the Hellenic Islands. J. Geod. 2012, 86, 1–17. [Google Scholar] [CrossRef]
- Tscherning, C.C.; Rapp, R.H. Closed Covariance Expressions for Gravity Anomalies, Geoid Undulations, and Deflections of the Vertical Implied by Anomaly Degree Variance Models; Rep. No 208; Ohio State University: Columbus, OH, USA, 1974; pp. 1–89. [Google Scholar]
- Haagmans, R.; de Min, E.; von Gelderen, M. Fast Evaluation of Convolution Integrals on the Sphere Using 1D FFT, and a Comparison with Existing Methods for Stokes’ Integral. Manuscr. Geod. 1993, 18, 227–241. [Google Scholar]
- Wong, L.; Gore, R. Accuracy of Geoid Heights from Modified Stokes Kernels. Geophys. J. R. Astron. Soc. 1969, 18, 81–91. [Google Scholar] [CrossRef]
- Forsberg, R.; Tscherning, C.C. An Overview Manual for the GRAVSOFT Geodetic Gravity Field Modelling Programs 208AD; DTU: Copenhagen, Denmark, 2008; p. 68. [Google Scholar]

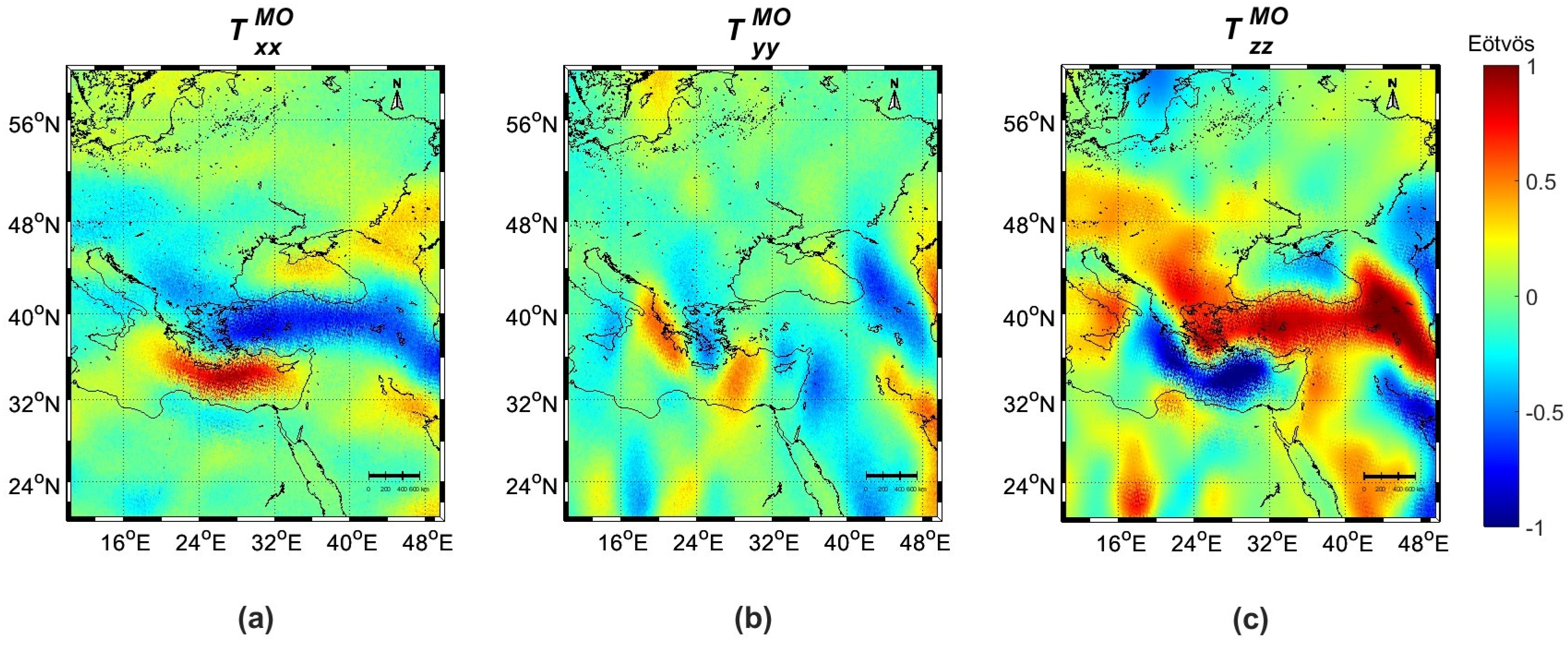
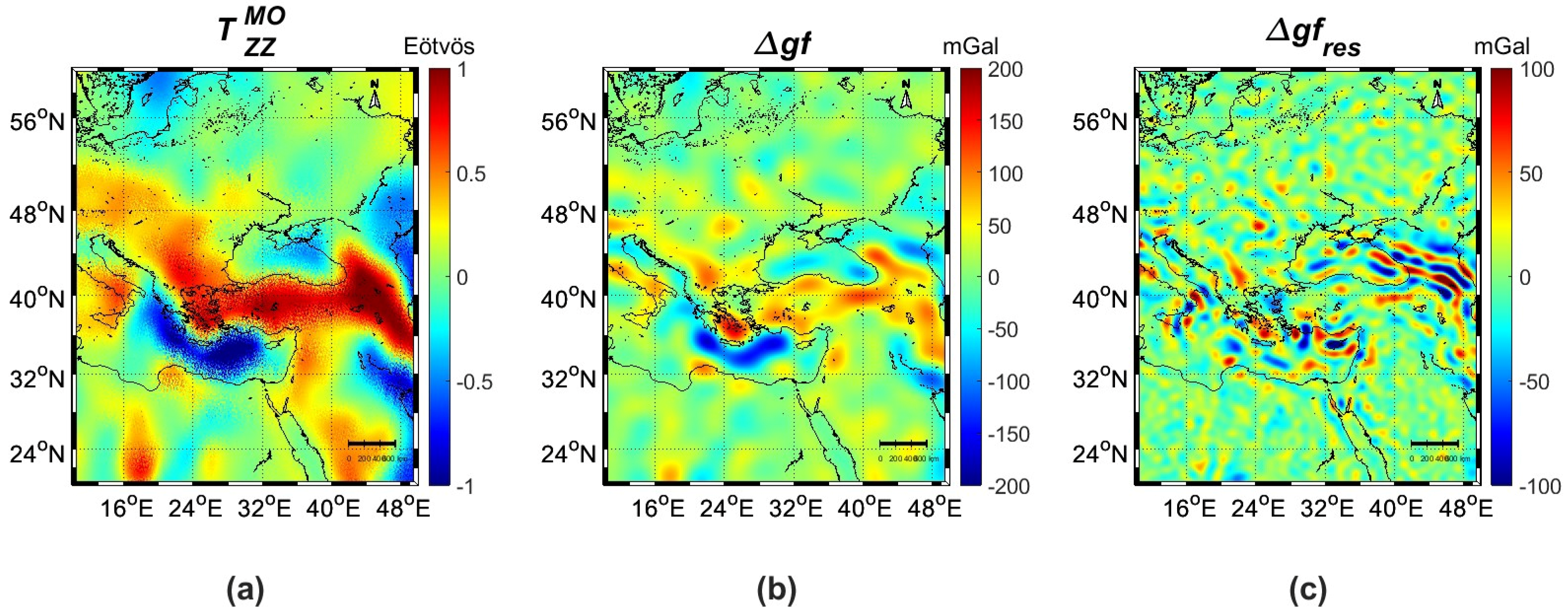
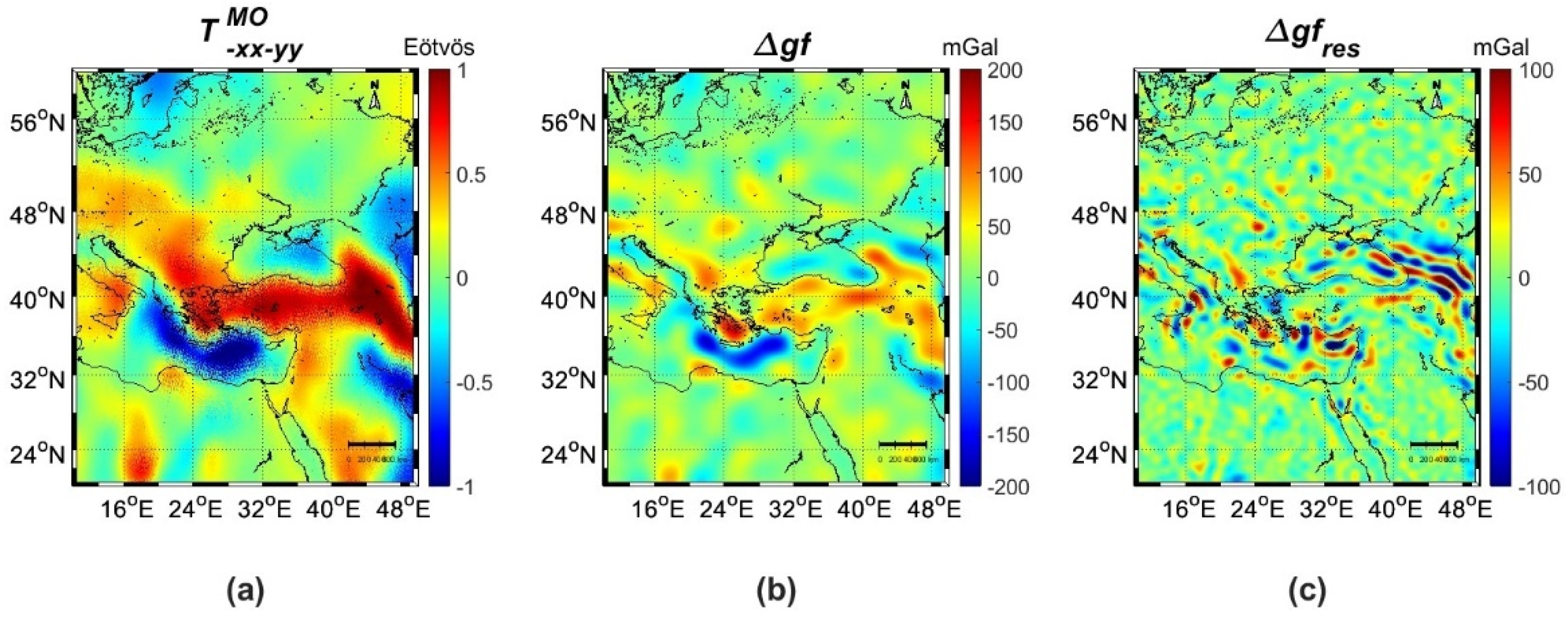
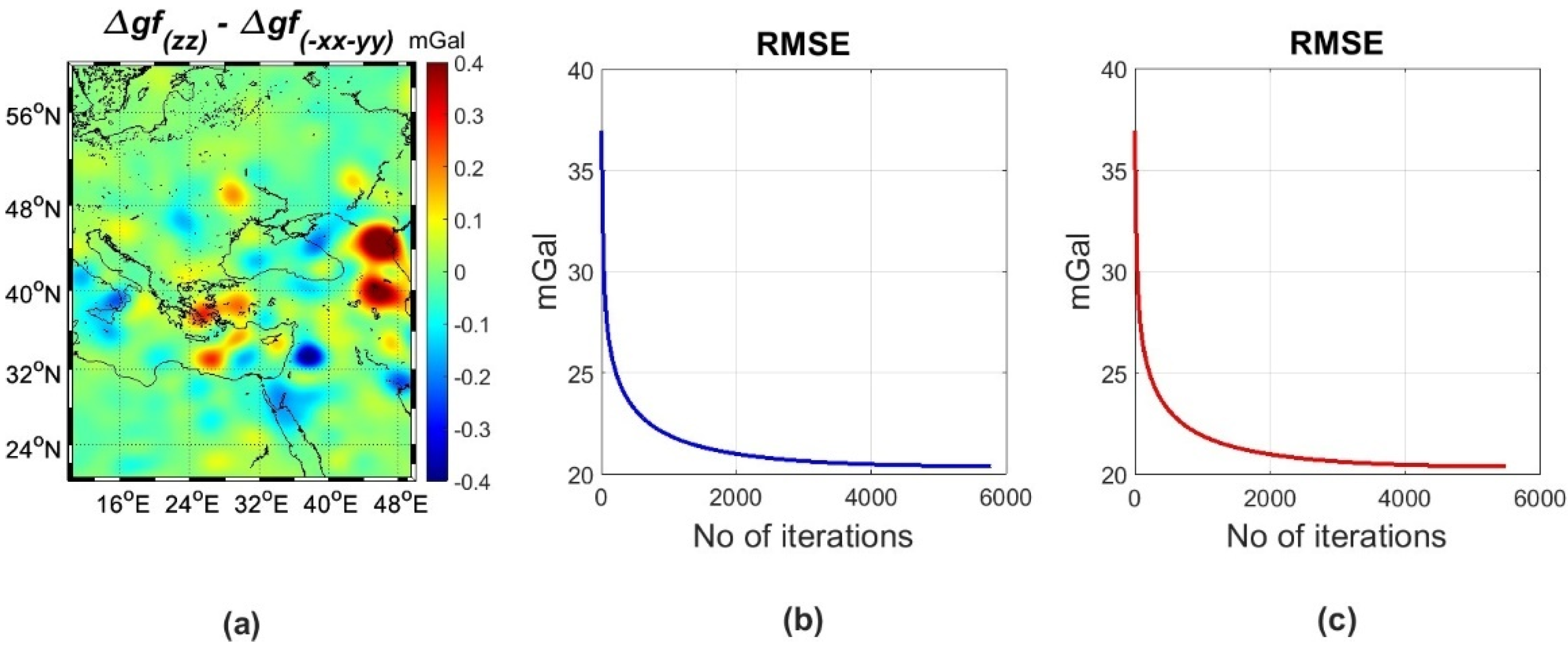
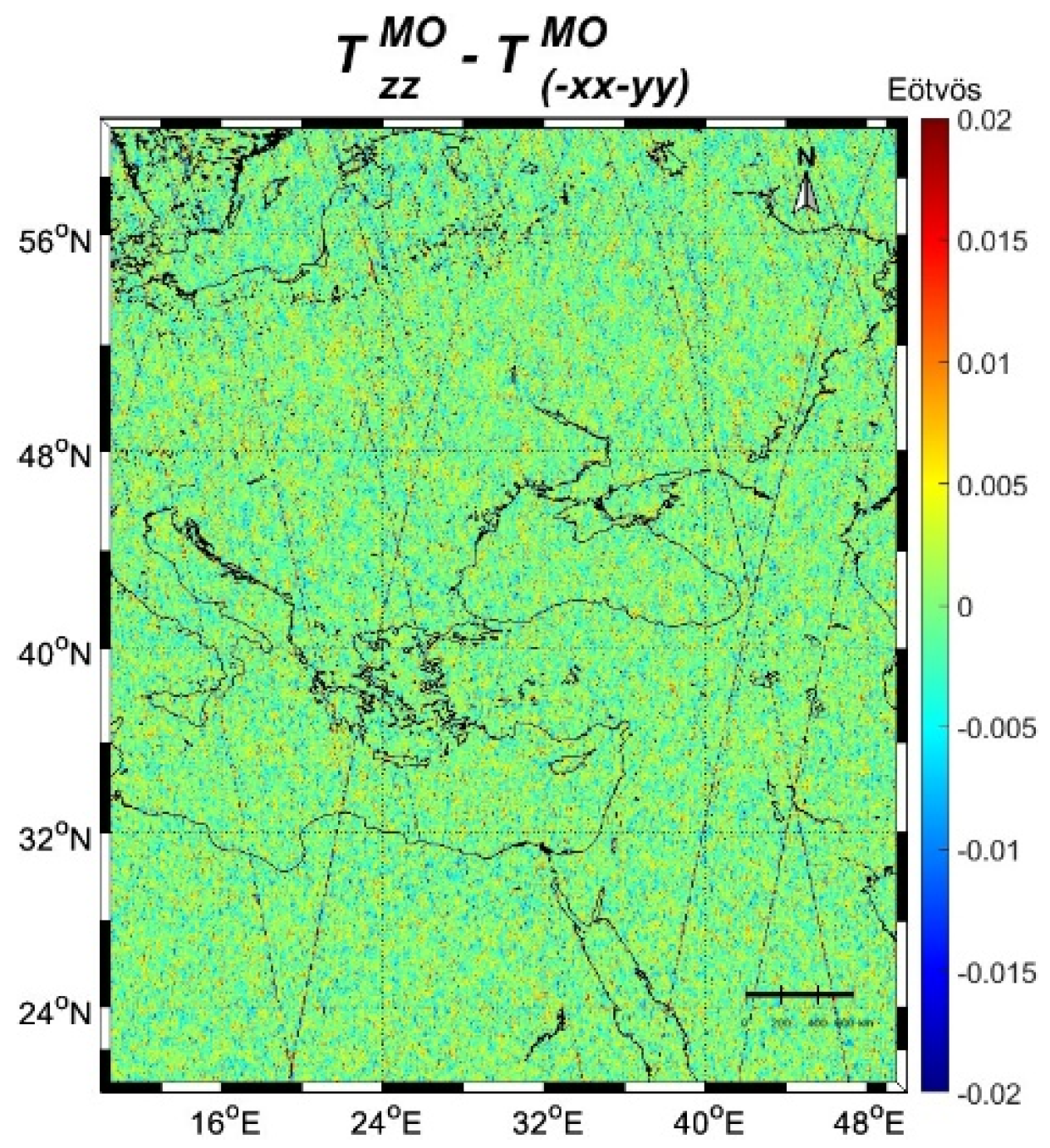

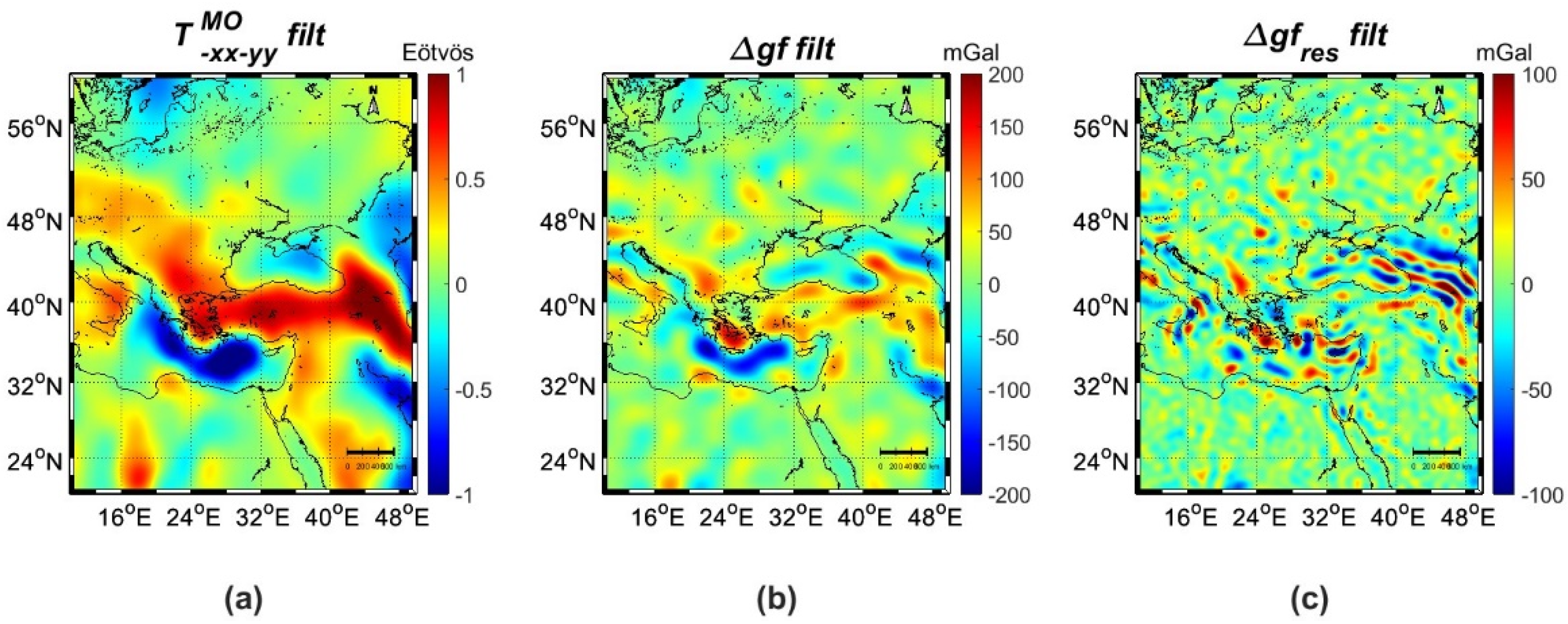
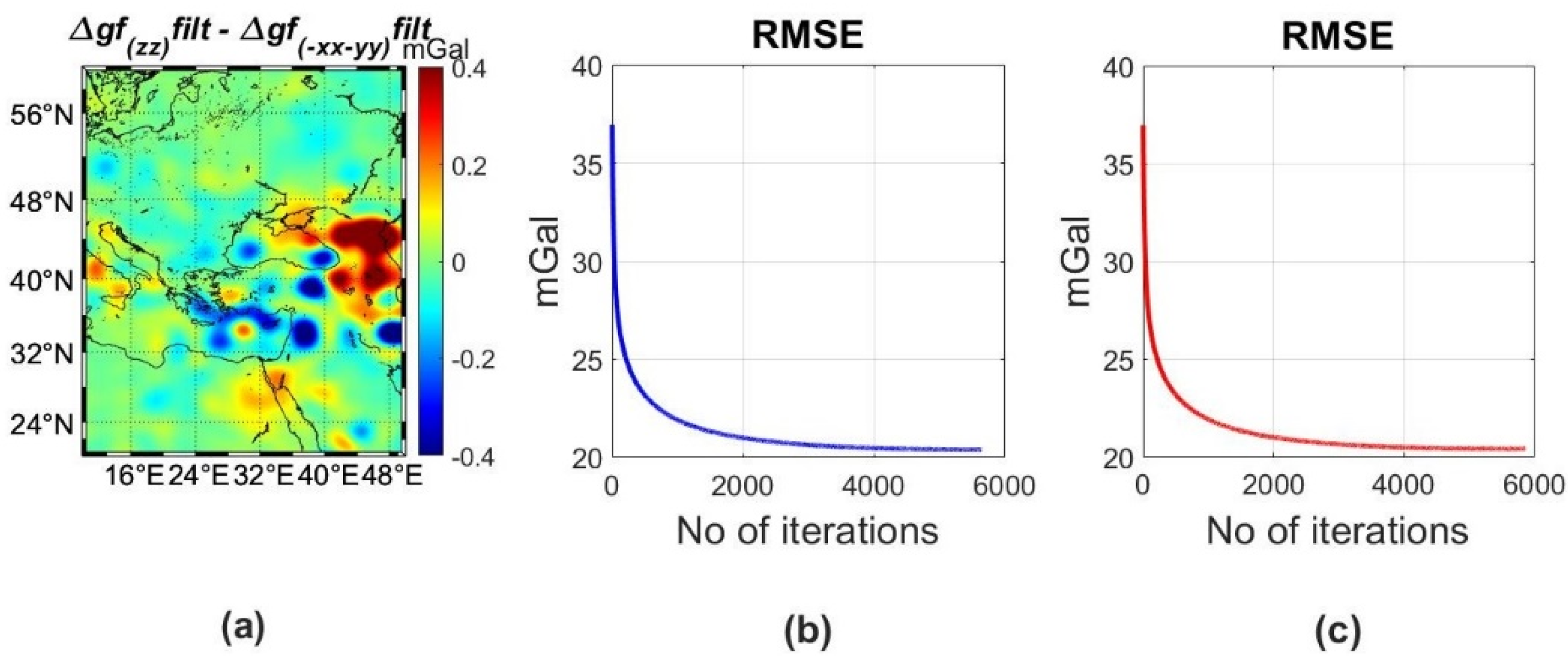

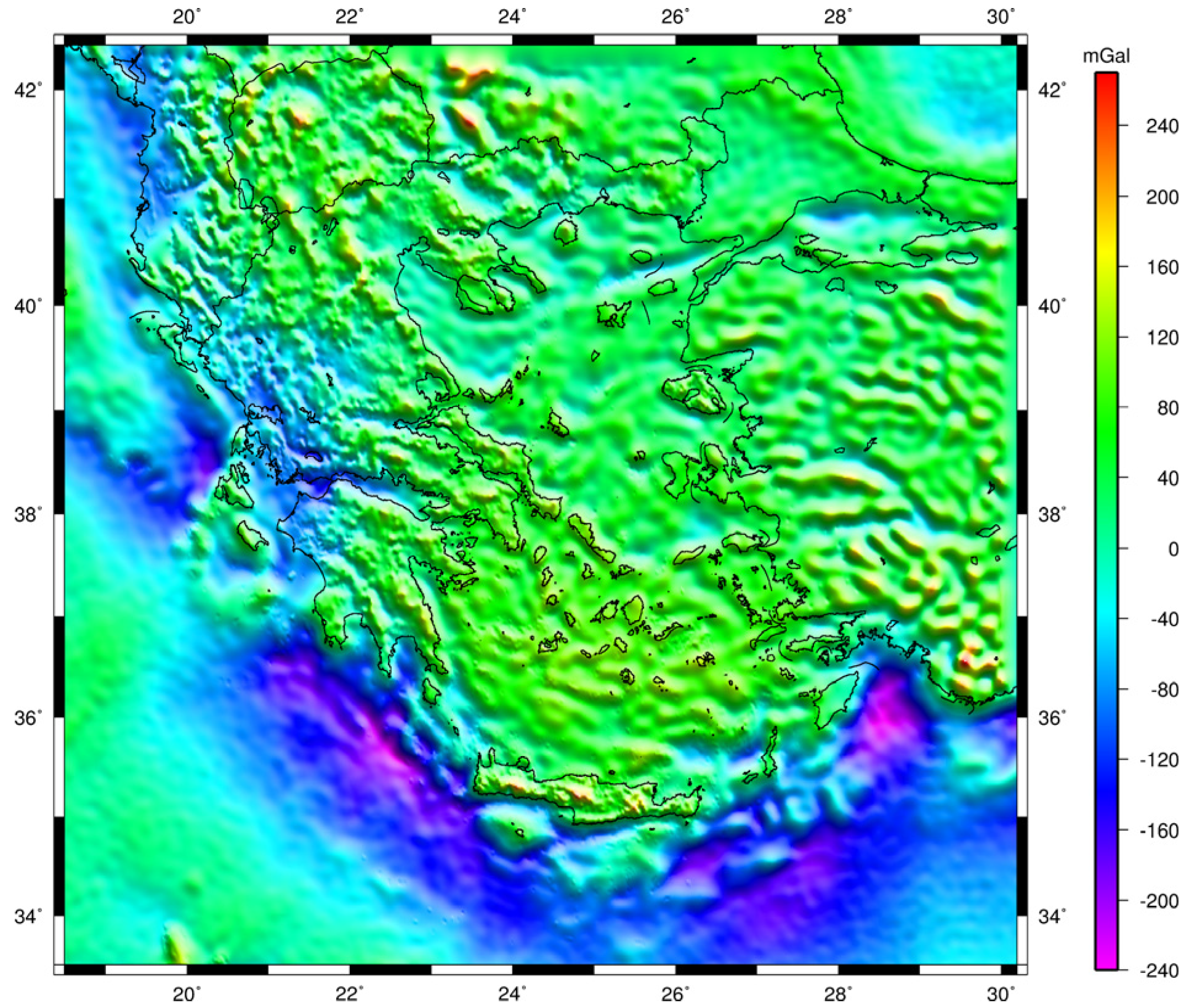
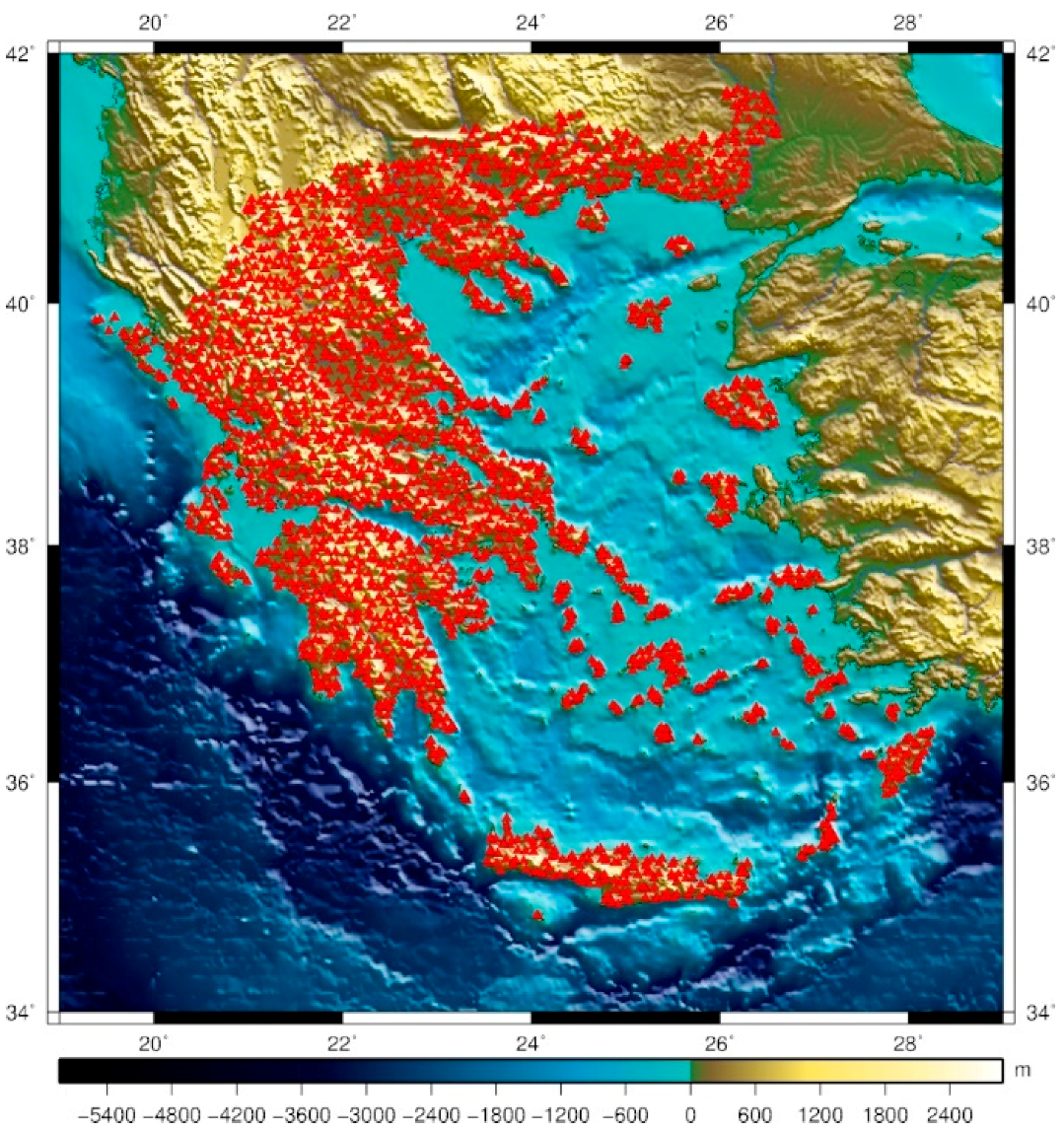
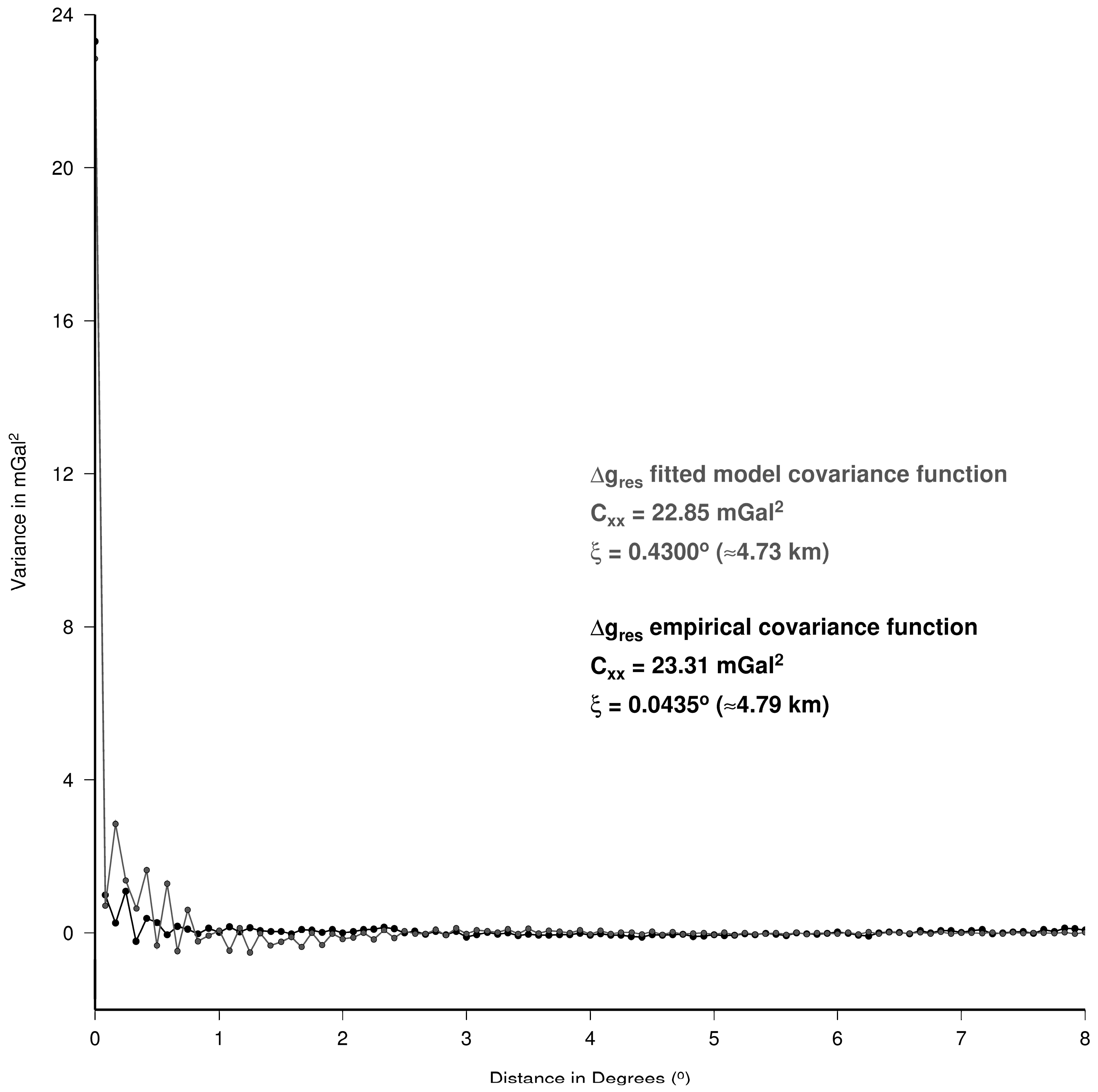
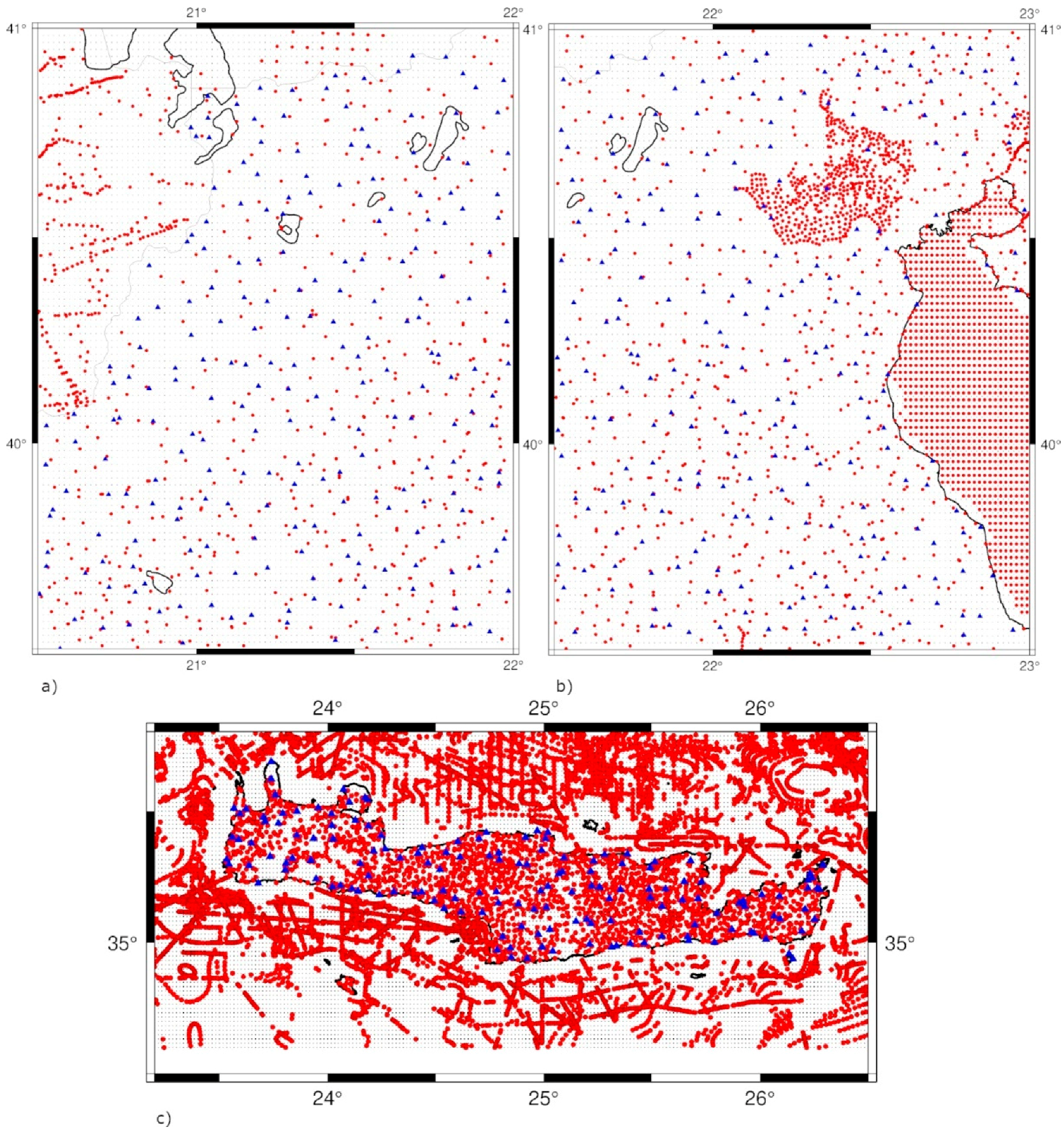
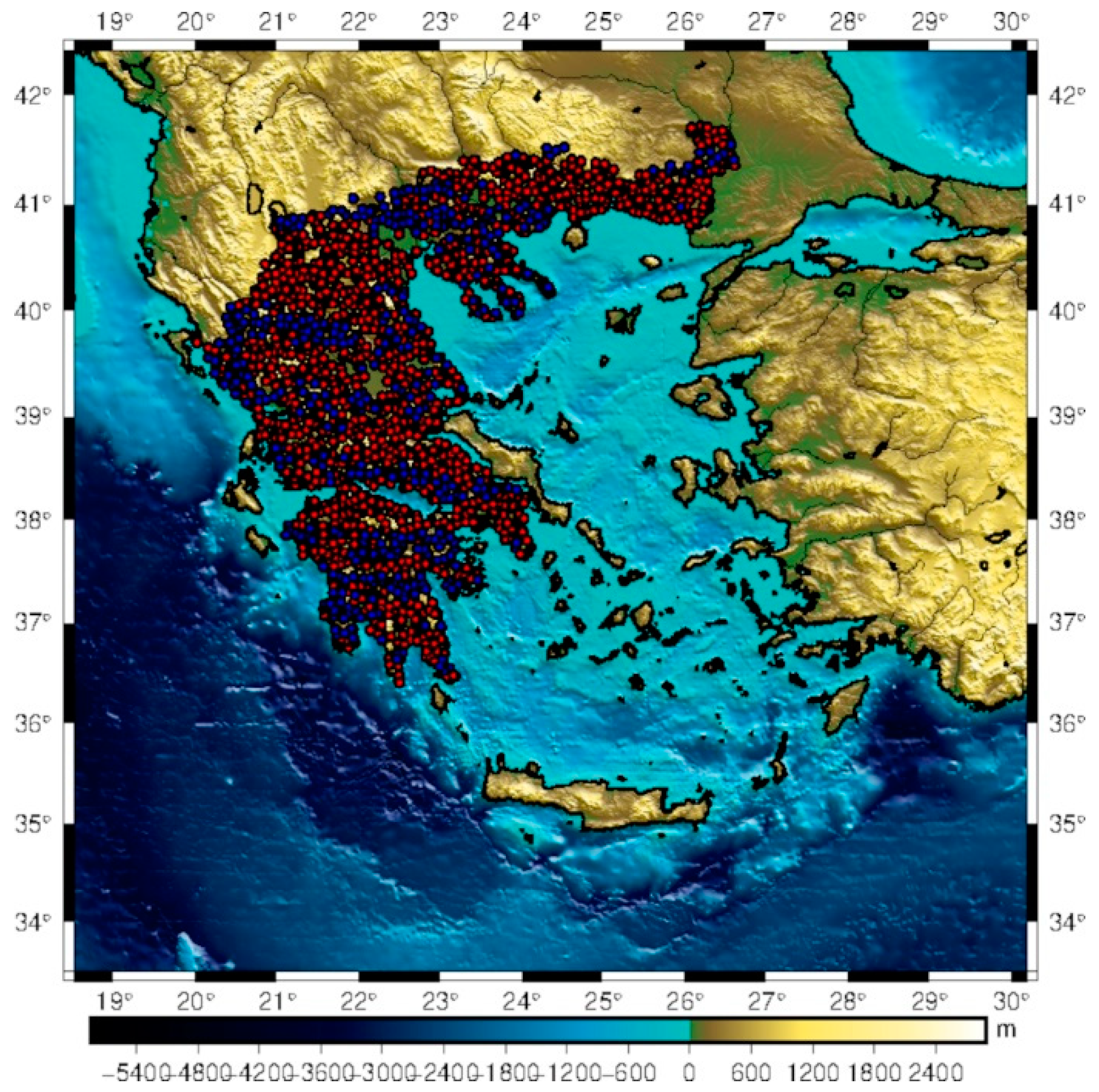
| Id | km | Min | Max | Mean | Std |
|---|---|---|---|---|---|
| (295–296) | −0.0071 | 0.0062 | 0.0000 | 0.0006 | |
| (290–291) | −0.0075 | 0.0066 | 0.0000 | 0.0006 | |
| (280–281) | −0.0082 | 0.0072 | 0.0000 | 0.0006 | |
| (270–281) | −0.0090 | 0.0080 | 0.0000 | 0.0007 | |
| (260–261) | −0.0099 | 0.0089 | 0.0000 | 0.0007 | |
| (250–251) | −0.0110 | 0.0100 | 0.0000 | 0.0008 | |
| (240–241) | −0.0122 | 0.0112 | 0.0000 | 0.0009 | |
| (230–231) | −0.0136 | 0.0127 | 0.0000 | 0.0010 | |
| (295–296) | −0.0052 | 0.0048 | 0.0000 | 0.0005 | |
| (290–291) | −0.0055 | 0.0051 | 0.0000 | 0.0006 | |
| (280–281) | −0.0062 | 0.0056 | 0.0000 | 0.0006 | |
| (270–281) | −0.0070 | 0.0062 | 0.0000 | 0.0007 | |
| (260–261) | −0.0080 | 0.0070 | 0.0000 | 0.0007 | |
| (250–251) | −0.0091 | 0.0078 | 0.0000 | 0.0008 | |
| (240–241) | −0.0105 | 0.0088 | 0.0000 | 0.0009 | |
| (230–231) | −0.0120 | 0.0099 | 0.0000 | 0.0010 | |
| (295–296) | −0.0080 | 0.0084 | 0.0000 | 0.0009 | |
| (290–291) | −0.0085 | 0.0089 | 0.0000 | 0.0009 | |
| (280–281) | −0.0093 | 0.0099 | 0.0000 | 0.0010 | |
| (270–281) | −0.0104 | 0.0113 | 0.0000 | 0.0011 | |
| (260–261) | −0.0116 | 0.0128 | 0.0000 | 0.0012 | |
| (250–251) | −0.0130 | 0.0146 | 0.0000 | 0.0013 | |
| (240–241) | −0.0147 | 0.0167 | 0.0000 | 0.0015 | |
| (230–231) | −0.0166 | 0.0191 | 0.0000 | 0.0016 |
| Orbit | Id | Min | Max | Mean | Std |
|---|---|---|---|---|---|
| Satellite Orbit | −1.1020 | 1.3058 | −0.0332 | 0.2318 | |
| −0.8545 | 0.833 | −0.0508 | 0.1807 | ||
| −1.5653 | 1.0965 | 0.0839 | 0.3223 | ||
| Mean Orbit | −1.1748 | 1.405 | −0.0341 | 0.2596 | |
| −0.9467 | 1.0361 | −0.0523 | 0.2071 | ||
| −1.7063 | 1.1531 | 0.0864 | 0.3707 |
| Min | Max | Mean | Std | Unit | |
|---|---|---|---|---|---|
| −1.807 | 1.198 | 0.088 | 0.359 | Eötvös | |
| −175.889 | 161.203 | 7.335 | 35.764 | mGal | |
| −139.008 | 148.206 | 0.196 | 20.389 | mGal | |
| −2.833 | 2.205 | 0.088 | 0.359 | Eötvös | |
| −175.888 | 161.045 | 7.336 | 35.768 | mGal | |
| Δgf − xx − yy res | −139.080 | 148.043 | 0.197 | 20.394 | mGal |
| −0.450 | 0.661 | 0.000 | 0.032 | mGal |
| Min | Max | Mean | Std | Unit | |
|---|---|---|---|---|---|
| −1.396 | 1.076 | 0.088 | 0.347 | Eötvös | |
| −190.029 | 177.306 | 6.953 | 37.617 | mGal | |
| −130.086 | 139.079 | −0.186 | 20.607 | mGal | |
| −1.394 | 1.076 | 0.088 | 0.347 | Eötvös | |
| −190.070 | 177.535 | 6.950 | 36.471 | mGal | |
| −130.636 | 138.718 | −0.189 | 20.622 | mGal | |
| −0.765 | 1.024 | 0.003 | 0.003 | mGal |
| Min | Max | Mean | Std | |
|---|---|---|---|---|
| −20.738 | 21.753 | 0.382 | 4.170 | |
| −20.960 | 22.035 | 0.386 | 4.180 |
| Min | Max | Mean | Std | |
|---|---|---|---|---|
| −236.100 | 269.930 | −22.730 | ±74.110 | |
| −236.464 | 212.762 | −22.405 | ±74.164 | |
| −178.693 | 82.077 | −2.389 | ±11.463 | |
| −20.960 | 22.035 | 0.386 | ±4.180 |
| Geoid Models | Min | Max | Mean | Std |
|---|---|---|---|---|
| a | −4.779 | 5.163 | −0.003 | ±0.999 |
| b | −4.562 | 5.238 | 0.001 | ±0.973 |
| c | −4.780 | 5.162 | −0.004 | ±1.000 |
| d | −4.568 | 5.232 | 0.000 | ±0.973 |
| e | −0.353 | 1.201 | 0.003 | ±0.109 |
| f | −1.997 | 2.489 | 0.006 | ±0.500 |
| g | −3.856 | 2.663 | 0.008 | ±0.659 |
| h | −3.851 | 2.593 | 0.008 | ±0.662 |
| i | −1.276 | 1.180 | 0.000 | ±0.307 |
| Geoid Models | Min | Max | Mean | Std | Points Improved |
|---|---|---|---|---|---|
| −0.664 | 0.402 | −0.107 | ±0.123 | ||
| −1.352 | 1.222 | −0.042 | ±0.438 | 379 | |
| 2.016 | −1.877 | 0.005 | ±0.682 | 278 | |
| 2.593 | −3.851 | 0.008 | ±0.682 | 224 | |
| 0.712 | −1.173 | −0.126 | ±0. 323 | 428 |
| Min | Max | Mean | Std | Points Improved | |
|---|---|---|---|---|---|
| −0.529 | 0.379 | −0.053 | ±0.120 | ||
| −0.620 | 0.568 | −0.059 | ±0.183 | 74 | |
| −0.688 | 0.140 | −0.198 | ±0.134 | ||
| −1.151 | 0.404 | −0.375 | ±0. 372 | 33 | |
| −0.721 | 0.088 | −0.258 | ±0.157 | ||
| −0.630 | 0.071 | −0.241 | ±0.153 | 89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Natsiopoulos, D.A.; Mamagiannou, E.G.; Pitenis, E.A.; Vergos, G.S.; Tziavos, I.N. GOCE Downward Continuation to the Earth’s Surface and Improvements to Local Geoid Modeling by FFT and LSC. Remote Sens. 2023, 15, 991. https://doi.org/10.3390/rs15040991
Natsiopoulos DA, Mamagiannou EG, Pitenis EA, Vergos GS, Tziavos IN. GOCE Downward Continuation to the Earth’s Surface and Improvements to Local Geoid Modeling by FFT and LSC. Remote Sensing. 2023; 15(4):991. https://doi.org/10.3390/rs15040991
Chicago/Turabian StyleNatsiopoulos, Dimitrios A., Elisavet G. Mamagiannou, Eleftherios A. Pitenis, Georgios S. Vergos, and Ilias N. Tziavos. 2023. "GOCE Downward Continuation to the Earth’s Surface and Improvements to Local Geoid Modeling by FFT and LSC" Remote Sensing 15, no. 4: 991. https://doi.org/10.3390/rs15040991
APA StyleNatsiopoulos, D. A., Mamagiannou, E. G., Pitenis, E. A., Vergos, G. S., & Tziavos, I. N. (2023). GOCE Downward Continuation to the Earth’s Surface and Improvements to Local Geoid Modeling by FFT and LSC. Remote Sensing, 15(4), 991. https://doi.org/10.3390/rs15040991







