Maize Ear Height and Ear–Plant Height Ratio Estimation with LiDAR Data and Vertical Leaf Area Profile
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Experimental Designs
2.2. Data Acquisition
2.2.1. TLS Data
2.2.2. DLS Data
2.2.3. In Situ Measurement Data
2.3. Point Cloud Data Voxelization
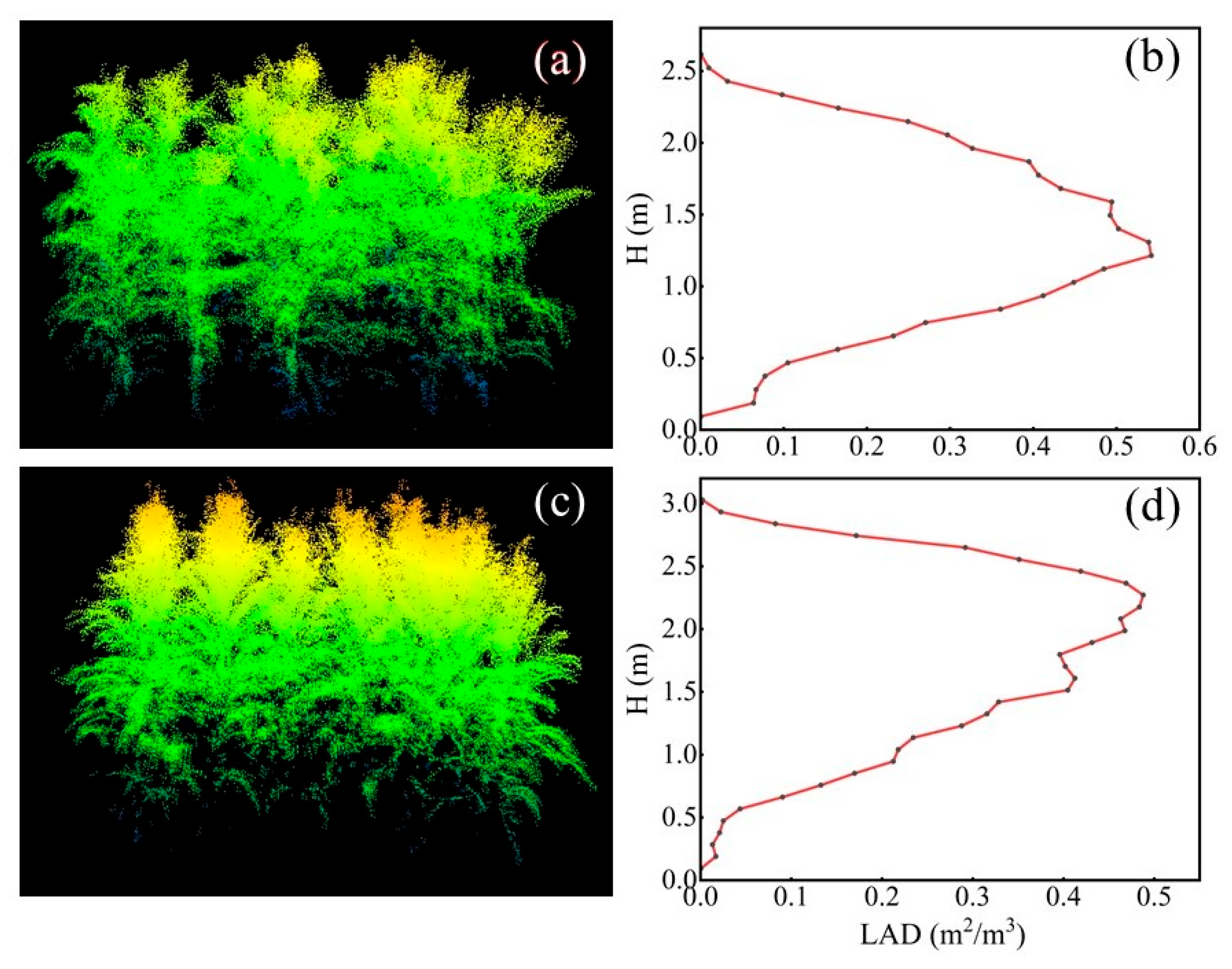
2.4. LAD Estimation Model
2.5. Estimation Model of Maize EH and ER
2.6. Accuracy Evaluation
3. Results
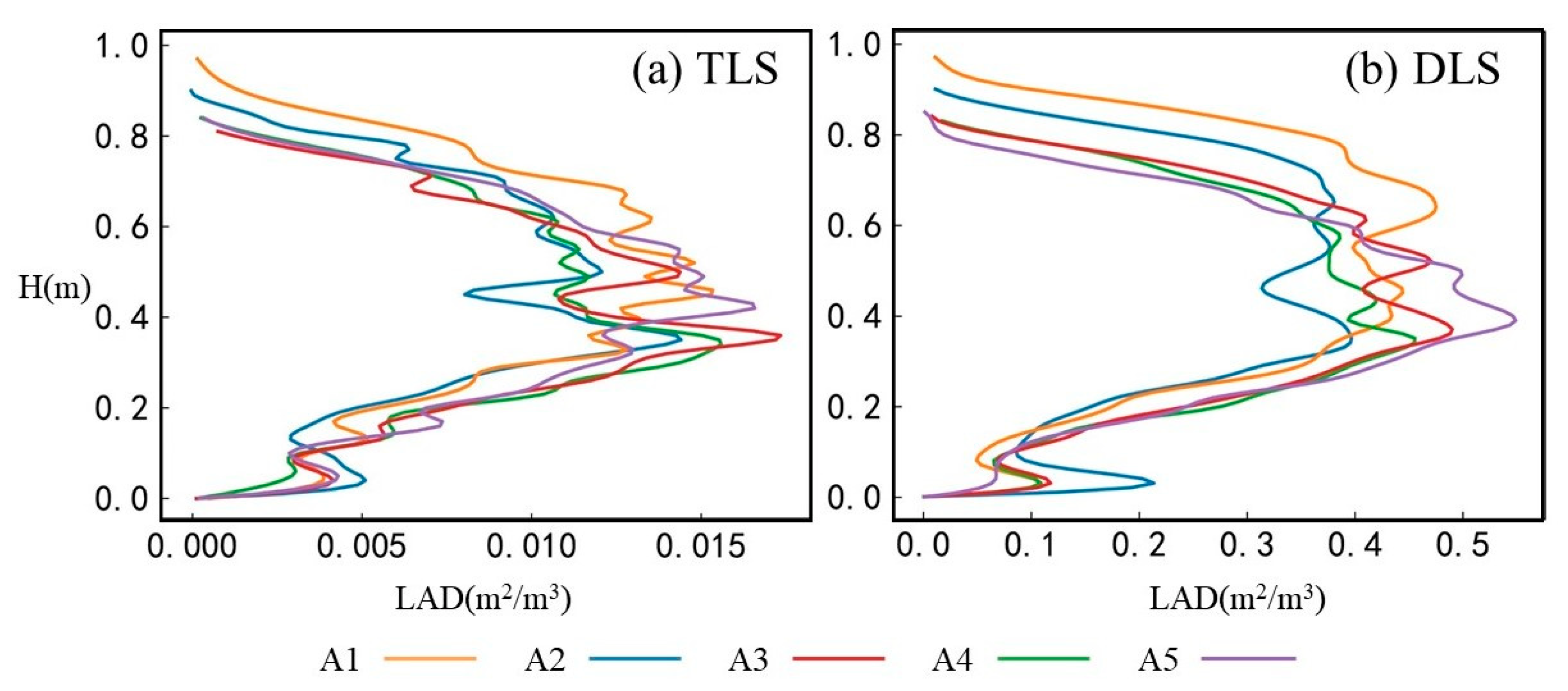
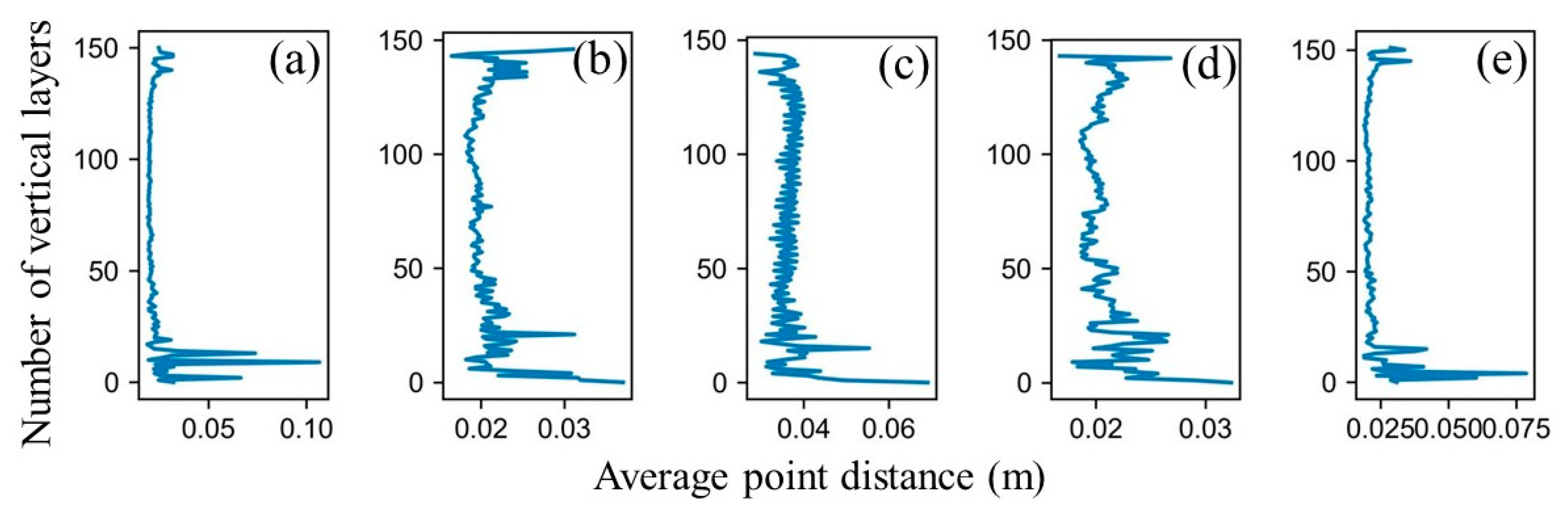
3.1. Optimal Voxel Selection for Different Platforms
Optimal Voxel Selection for TLS Platform
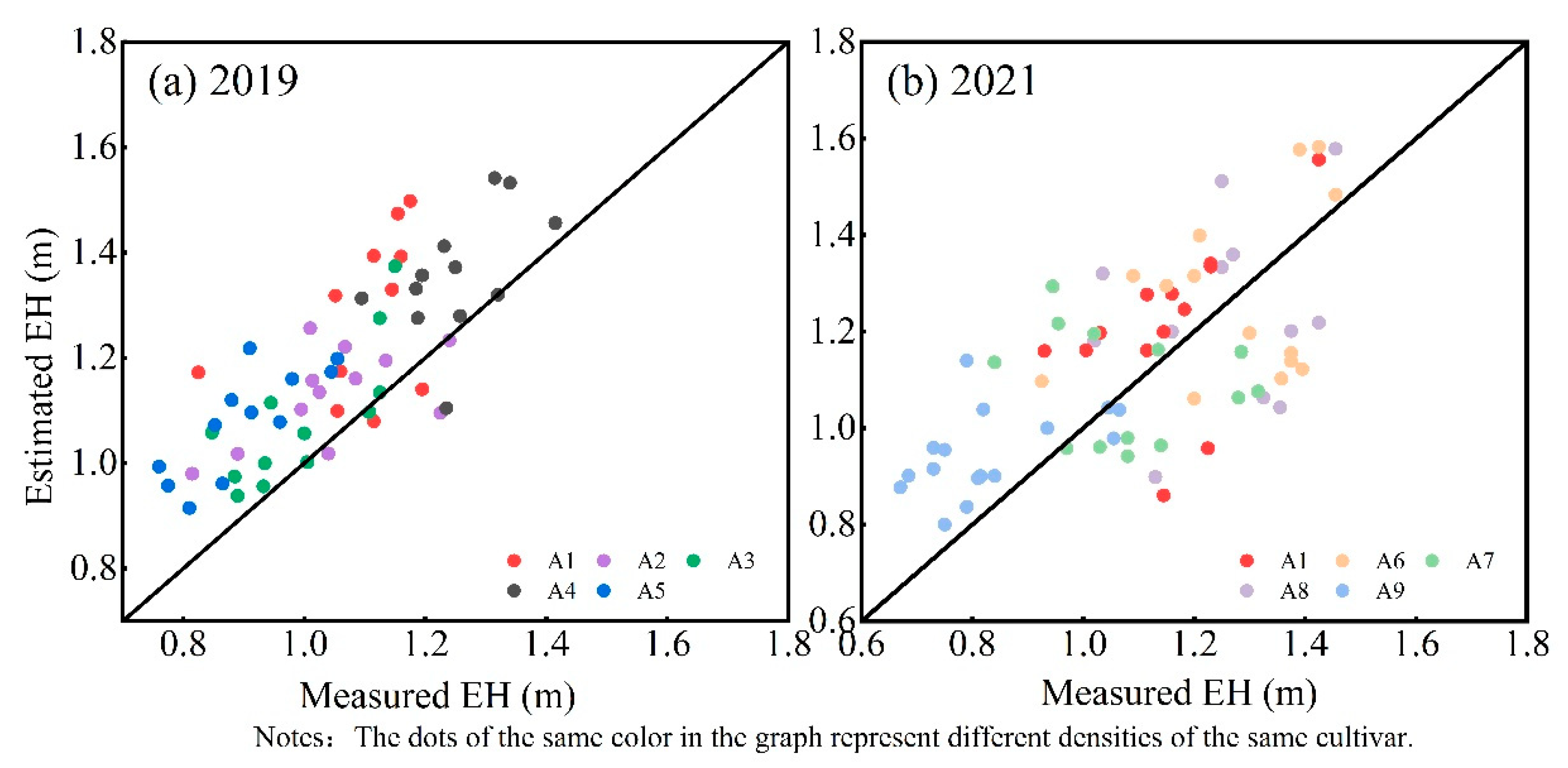
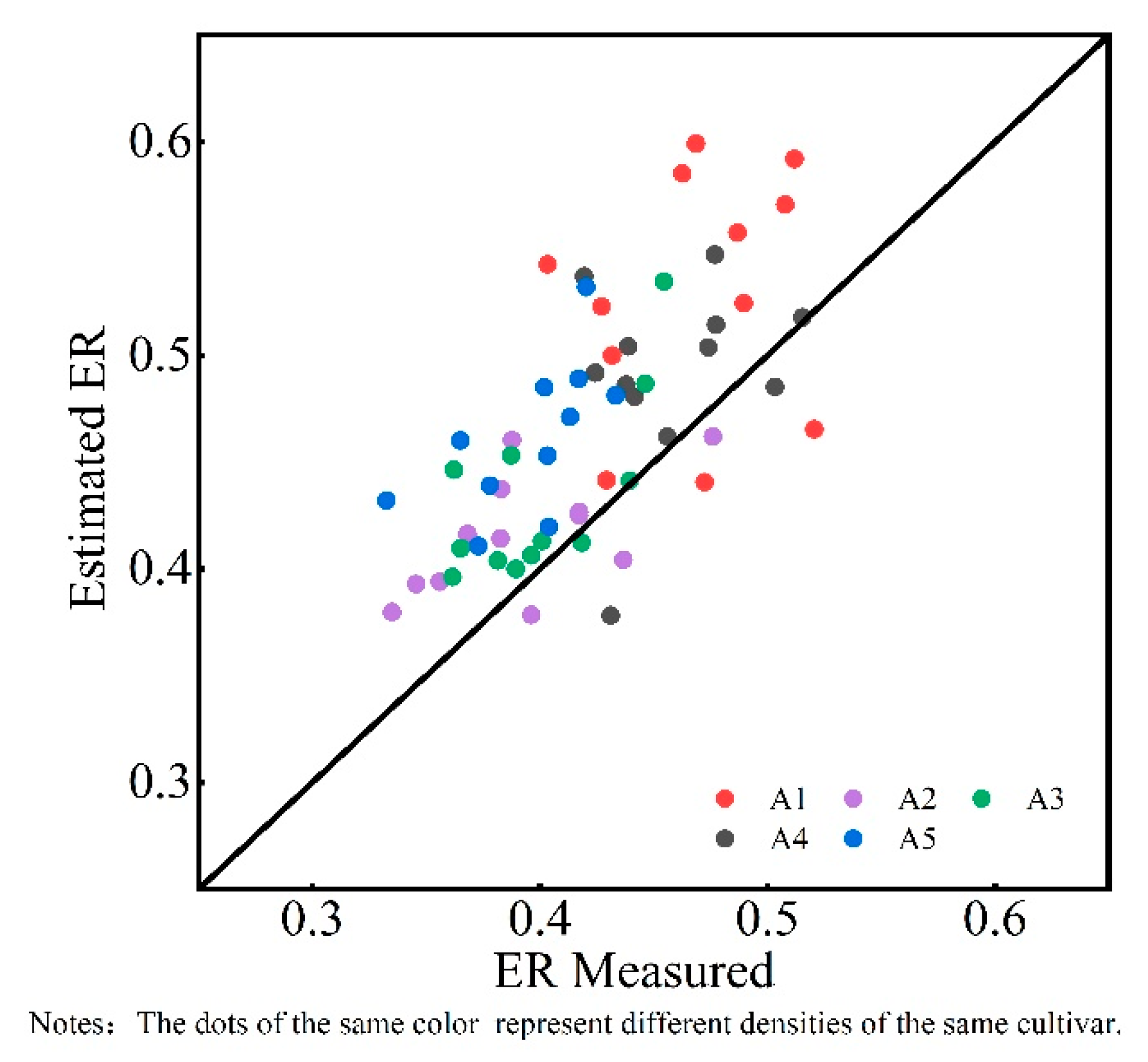
3.2. Comparison of EH and ER Estimation for Different Planting Densities
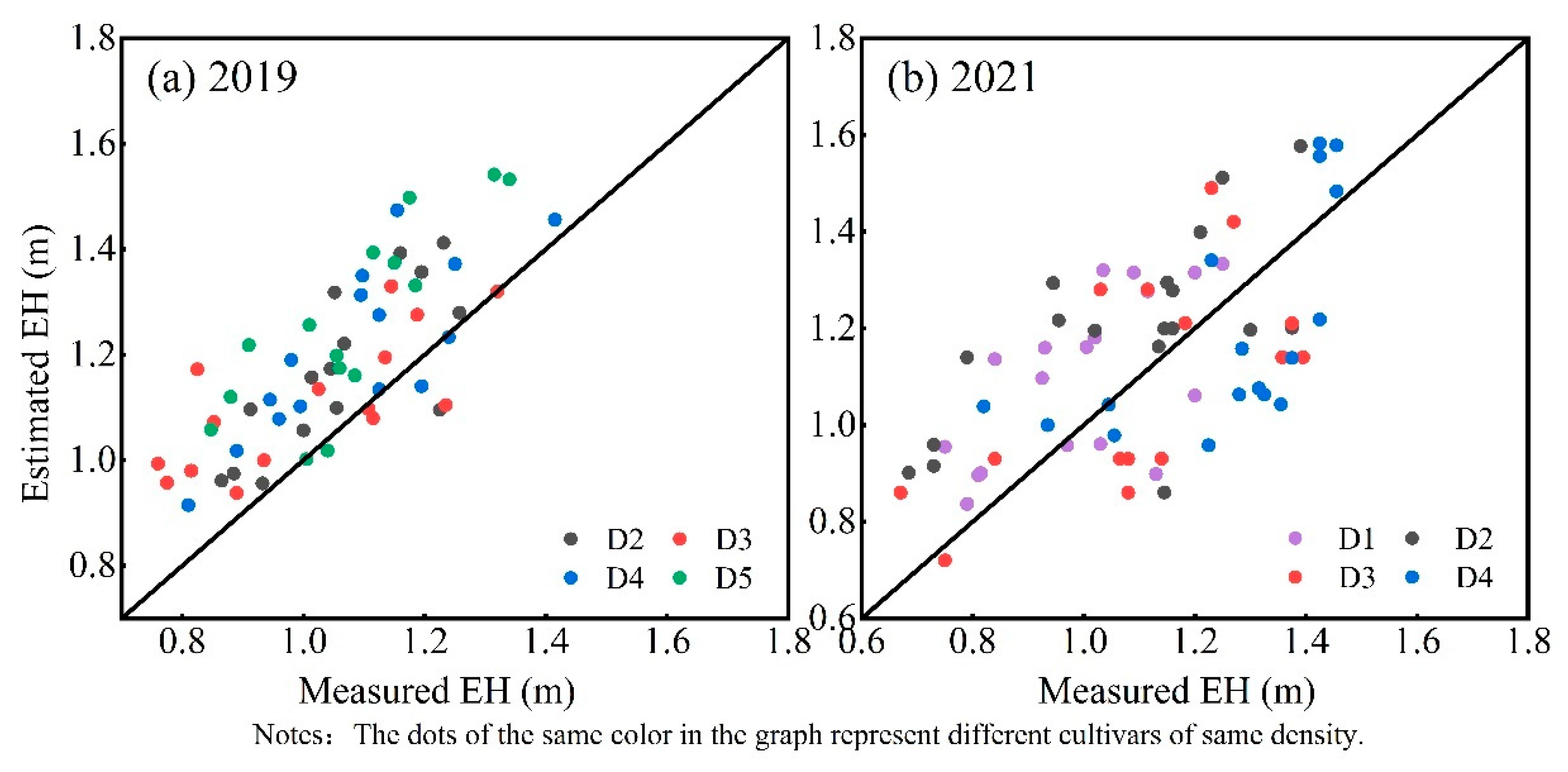
3.2.1. Comparison of EH and ER Estimation for Different Planting Densities for the TLS Platform
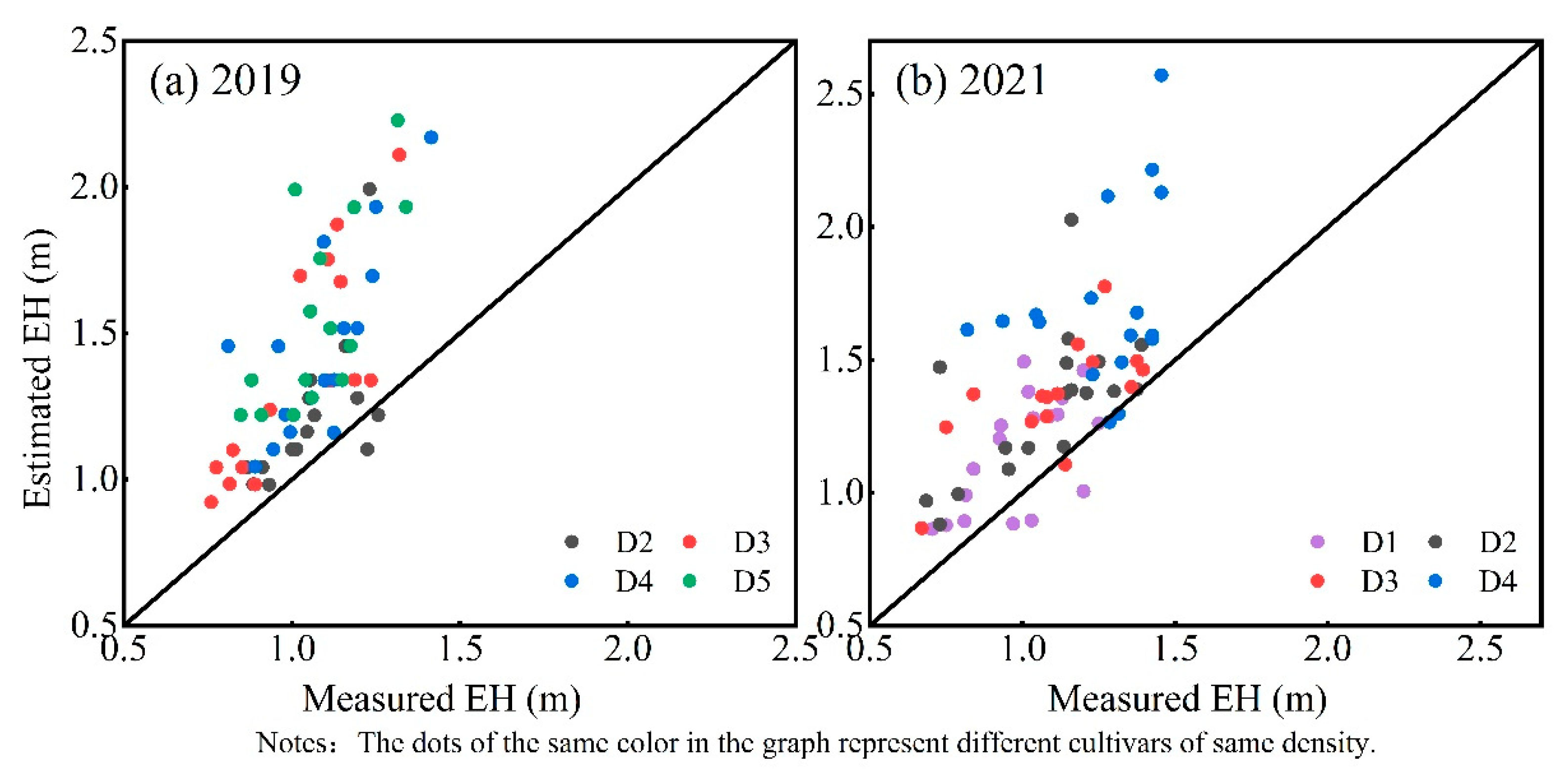
3.2.2. Comparison of EH and ER Estimation for Different Planting Densities for the DLS Platform
3.3. Comparison of EH and ER Estimation under Different Cultivars of TLS Platform
4. Discussion
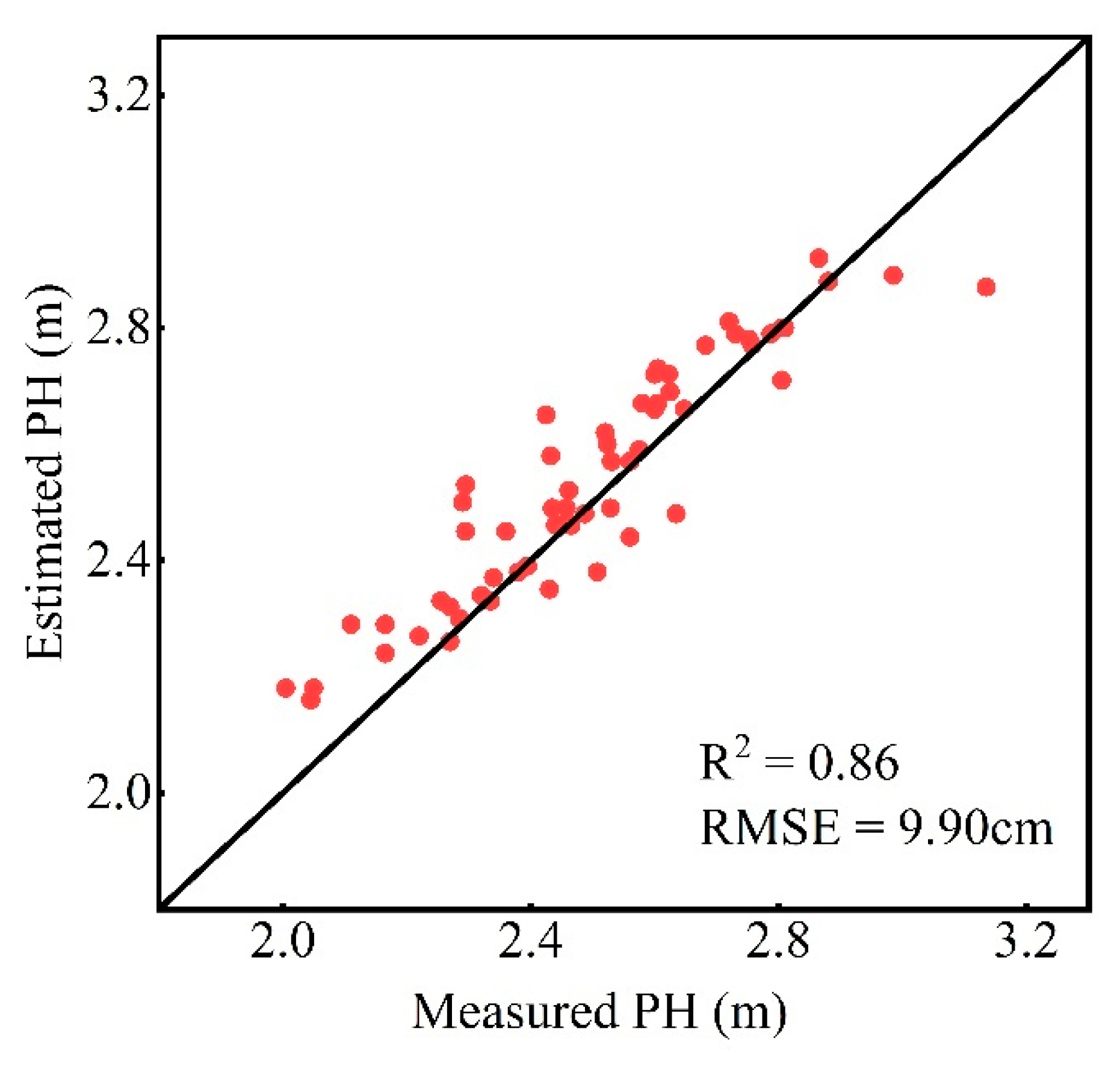
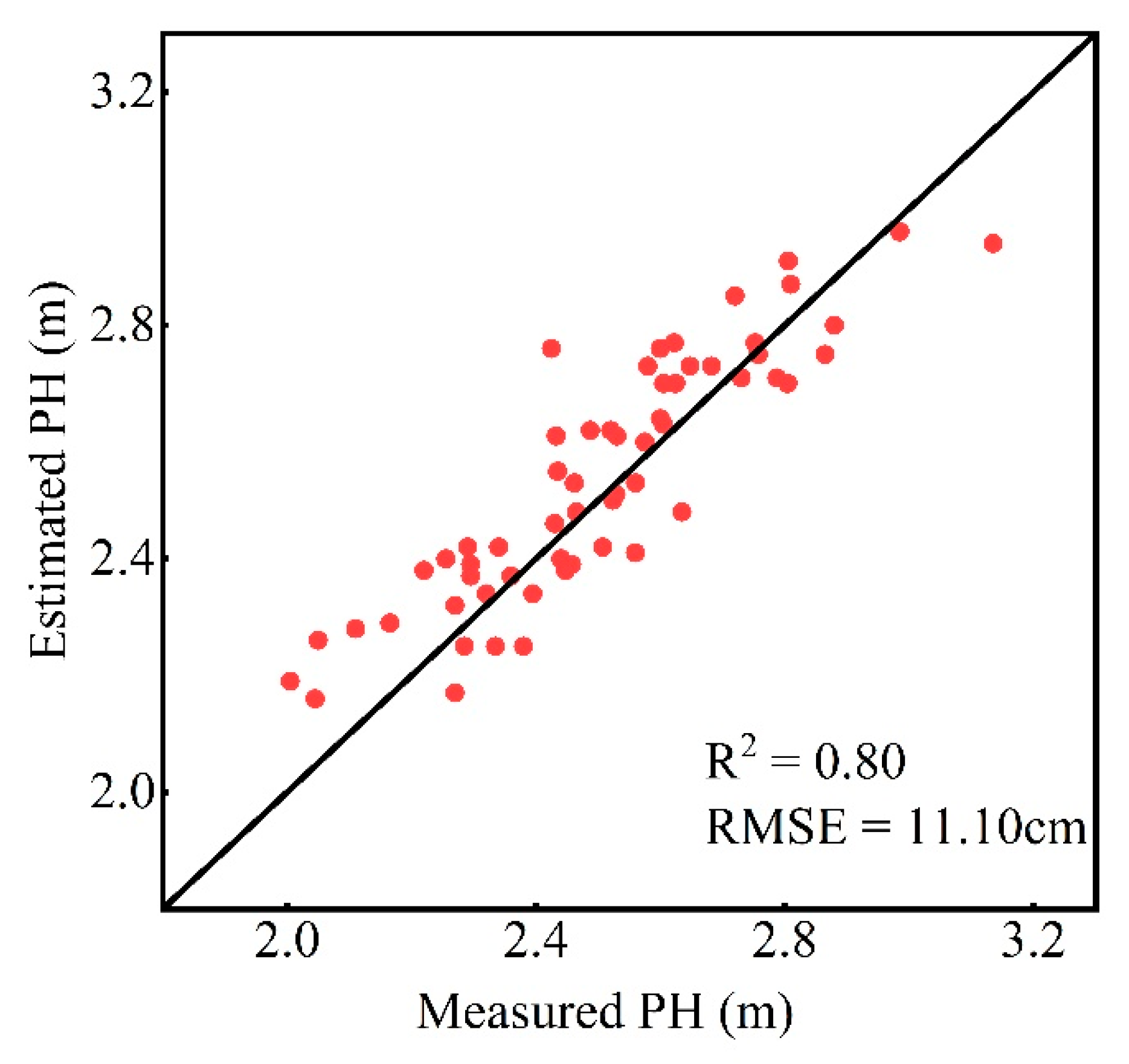
4.1. Advantages of the EH Estimation Model Compared to Similar Studies
4.2. Uncertainty in Fitting the LAD Distribution Curve
4.3. Comparison of Different Data Collection Methods
4.4. The Influence of Vertical Distribution of Point Density and Missing Point Cloud
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shu, M.; Dong, Q.; Fei, S.; Yang, X.; Zhu, J.; Meng, L.; Li, B.; Ma, Y. Improved estimation of canopy water status in maize using UAV-based digital and hyperspectral images. Comput. Electron. Agric. 2022, 197, 106982. [Google Scholar] [CrossRef]
- Andorf, C.; Beavis, W.D.; Hufford, M.; Smith, S.; Suza, W.P.; Wang, K.; Woodhouse, M.; Yu, J.; Lübberstedt, T. Technological advances in maize breeding: Past, present and future. Theor. Appl. Genet. 2019, 132, 817–849. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Liu, G.; Yang, Y.; Guo, X.; Ming, B.; Xie, R.; Liu, Y.; Wang, K.; Hou, P.; Li, S. Spatial variation of maize height morphological traits for the same cultivars at a large agroecological scale. Eur. J. Agron. 2021, 130, 126349. [Google Scholar] [CrossRef]
- Jia, Q.; Xu, Y.; Ali, S.; Sun, L.; Ding, R.; Ren, X.; Zhang, P.; Jia, Z. Strategies of supplemental irrigation and modified planting densities to improve the root growth and lodging resistance of maize (Zea mays L.) under the ridge-furrow rainfall harvesting system. Field Crops Res. 2018, 224, 48–59. [Google Scholar] [CrossRef]
- Qun, W.; Jun, X.; Chen, J.; Fan, Y.; Zhang, G.; Xie, R.; Bo, M.; Peng, H.; Wang, K.; Li, S. Key indicators affecting maize stalk lodging resistance of different growth periods under different sowing dates. J. Integr. Agric. 2020, 19, 2419–2428. [Google Scholar] [CrossRef]
- Li, J.; Xie, R.; Wang, K.; Hou, P.; Ming, B.; Zhang, G.; Liu, G.; Wu, M.; Yang, Z.; Li, S. Response of canopy structure, light interception and grain yield to plant density in maize. J. Agric. Sci. 2018, 156, 785–794. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Z.; Ding, J.; Wu, Y.; Zhou, B.; Wang, R.; Ma, J.; Wang, S.; Zhang, X.; Xia, Z. Combined linkage and association mapping reveals QTL and candidate genes for plant and ear height in maize. Front. Plant Sci. 2016, 7, 833. [Google Scholar] [CrossRef]
- Wei, H.; Zhao, Y.; Xie, Y.; Wang, H. Exploiting SPL genes to improve maize plant architecture tailored for high-density planting. J. Exp. Bot. 2018, 69, 4675–4688. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, S.; Lv, Y.; Ning, F.; Cao, Y.; Liao, S.; Wang, P.; Huang, S. Optimizing ear-plant height ratio to improve kernel number and lodging resistance in maize (Zea mays L.). Field Crops Res. 2022, 276, 108376. [Google Scholar] [CrossRef]
- Tang, L.; Ma, W.; Noor, M.A.; Li, L.; Hou, H.; Zhang, X.; Zhao, M. Density resistance evaluation of maize varieties through new “Density–Yield Model” and quantification of varietal response to gradual planting density pressure. Sci. Rep. 2018, 8, 17281. [Google Scholar] [CrossRef]
- Ku, L.; Zhang, L.; Tian, Z.; Guo, S.; Su, H.; Ren, Z.; Wang, Z.; Li, G.; Wang, X.; Zhu, Y. Dissection of the genetic architecture underlying the plant density response by mapping plant height-related traits in maize (Zea mays L.). Mol. Genet. Genom. 2015, 290, 1223–1233. [Google Scholar] [CrossRef]
- Wong, J.; Sha, H.; Al Hasan, M.; Mohler, G.; Becker, S.; Wiltse, C. Automated Corn Ear Height Prediction Using Video-Based Deep Learning. In Proceedings of the 2020 IEEE International Conference on Big Data (Big Data), Atlanta, GA, USA, 10–13 December 2020; pp. 2371–2374. [Google Scholar] [CrossRef]
- Hu, P.; Chapman, S.C.; Wang, X.; Potgieter, A.; Duan, T.; Jordan, D.; Guo, Y.; Zheng, B. Estimation of plant height using a high throughput phenotyping platform based on unmanned aerial vehicle and self-calibration: Example for sorghum breeding. Eur. J. Agron. 2018, 95, 24–32. [Google Scholar] [CrossRef]
- Duan, T.; Chapman, S.; Guo, Y.; Zheng, B. Dynamic monitoring of NDVI in wheat agronomy and breeding trials using an unmanned aerial vehicle. Field Crops Res. 2017, 210, 71–80. [Google Scholar] [CrossRef]
- Ye, M.; Cao, Z.; Yu, Z. An image-based approach for automatic detecting tasseling stage of maize using spatio-temporal saliency. In Proceedings of the MIPPR 2013: Remote Sensing Image Processing, Geographic Information Systems, and Other Applications, Wuhan, China, 26–27 October 2013; p. 89210Z. [Google Scholar] [CrossRef]
- Yu, Z.; Zhou, H.; Li, C. An image-based automatic recognition method for the flowering stage of maize. In Proceedings of the MIPPR 2017: Remote Sensing Image Processing, Geographic Information Systems, and Other Applications, Xiangyang, China, 28–29 October 2017; p. 106111O. [Google Scholar] [CrossRef]
- Brichet, N.; Fournier, C.; Turc, O.; Strauss, O.; Artzet, S.; Pradal, C.; Welcker, C.; Tardieu, F.; Cabrera-Bosquet, L. A robot-assisted imaging pipeline for tracking the growths of maize ear and silks in a high-throughput phenotyping platform. Plant Methods 2017, 13, 1–12. [Google Scholar] [CrossRef]
- Lu, J.; Cheng, D.; Geng, C.; Zhang, Z.; Xiang, Y.; Hu, T. Combining plant height, canopy coverage and vegetation index from UAV-based RGB images to estimate leaf nitrogen concentration of summer maize. Biosyst. Eng. 2021, 202, 42–54. [Google Scholar] [CrossRef]
- Niu, Q.; Feng, H.; Yang, G.; Li, C.; Yang, H.; Xu, B.; Zhao, Y. Monitoring plant height and leaf area index of maize breeding material based on UAV digital images. Trans. Chin. Soc. Agric. Eng. 2018, 34, 73–82. [Google Scholar]
- Oehme, L.H.; Reineke, A.-J.; Weiß, T.M.; Würschum, T.; He, X.; Müller, J. Remote Sensing of Maize Plant Height at Different Growth Stages Using UAV-Based Digital Surface Models (DSM). Agronomy 2022, 12, 958. [Google Scholar] [CrossRef]
- Osco, L.P.; Junior, J.M.; Ramos, A.P.M.; Furuya, D.E.G.; Santana, D.C.; Teodoro, L.P.R.; Gonçalves, W.N.; Baio, F.H.R.; Pistori, H.; Junior, C.A.d.S. Leaf nitrogen concentration and plant height prediction for maize using UAV-based multispectral imagery and machine learning techniques. Remote Sens. 2020, 12, 3237. [Google Scholar] [CrossRef]
- Jin, S.; Su, Y.; Song, S.; Xu, K.; Hu, T.; Yang, Q.; Wu, F.; Xu, G.; Ma, Q.; Guan, H. Non-destructive estimation of field maize biomass using terrestrial lidar: An evaluation from plot level to individual leaf level. Plant Methods 2020, 16, 1–19. [Google Scholar] [CrossRef]
- Su, Y.; Wu, F.; Ao, Z.; Jin, S.; Qin, F.; Liu, B.; Pang, S.; Liu, L.; Guo, Q. Evaluating maize phenotype dynamics under drought stress using terrestrial lidar. Plant Methods 2019, 15, 1–16. [Google Scholar] [CrossRef]
- Han, L.; Yang, G.; Yang, H.; Xu, B.; Li, Z.; Yang, X. Clustering field-based maize phenotyping of plant-height growth and canopy spectral dynamics using a UAV remote-sensing approach. Front. Plant Sci. 2018, 9, 1638. [Google Scholar] [CrossRef] [PubMed]
- Gao, M.; Yang, F.; Wei, H.; Liu, X. Individual Maize Location and Height Estimation in Field from UAV-Borne LiDAR and RGB Images. Remote Sens. 2022, 14, 2292. [Google Scholar] [CrossRef]
- Guo, Q.; Wu, F.; Pang, S.; Zhao, X.; Chen, L.; Liu, J.; Xue, B.; Xu, G.; Li, L.; Jing, H. Crop 3D—A LiDAR based platform for 3D high-throughput crop phenotyping. Sci. China Life Sci. 2018, 61, 328–339. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y. LiDAR: An important tool for next-generation phenotyping technology of high potential for plant phenomics? Comput. Electron. Agric. 2015, 119, 61–73. [Google Scholar] [CrossRef]
- Su, W.; Zhu, D.; Huang, J.; Guo, H. Estimation of the vertical leaf area profile of corn (Zea mays) plants using terrestrial laser scanning (TLS). Comput. Electron. Agric. 2018, 150, 5–13. [Google Scholar] [CrossRef]
- Wu, D.; Phinn, S.; Johansen, K.; Robson, A.; Muir, J.; Searle, C. Estimating changes in leaf area, leaf area density, and vertical leaf area profile for mango, avocado, and macadamia tree crowns using terrestrial laser scanning. Remote Sens. 2018, 10, 1750. [Google Scholar] [CrossRef]
- Calders, K.; Schenkels, T.; Bartholomeus, H.; Armston, J.; Verbesselt, J.; Herold, M. Monitoring spring phenology with high temporal resolution terrestrial LiDAR measurements. Agric. For. Meteorol. 2015, 203, 158–168. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, J.; Yao, X.; Deng, Y.; Hao, Z.; Lin, L.; Wu, N.; Yu, K. Effect of layer thickness and voxel size inversion on leaf area density based on the voxel-based canopy profiling method. J. For. Res. 2022, 33, 1545–1558. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, H. Estimation of LAI with the LiDAR technology: A review. Remote Sens. 2020, 12, 3457. [Google Scholar] [CrossRef]
- Zhu, X.; Skidmore, A.K.; Wang, T.; Liu, J.; Darvishzadeh, R.; Shi, Y.; Premier, J.; Heurich, M. Improving leaf area index (LAI) estimation by correcting for clumping and woody effects using terrestrial laser scanning. Agric. For. Meteorol. 2018, 263, 276–286. [Google Scholar] [CrossRef]
- Nie, S.; Wang, C.; Dong, P.; Xi, X.; Luo, S.; Zhou, H. Estimating leaf area index of maize using airborne discrete-return LiDAR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3259–3266. [Google Scholar] [CrossRef]
- Lei, L.; Qiu, C.; Li, Z.; Han, D.; Han, L.; Zhu, Y.; Wu, J.; Xu, B.; Feng, H.; Yang, H. Effect of leaf occlusion on leaf area index inversion of maize using UAV–LiDAR data. Remote Sens. 2019, 11, 1067. [Google Scholar] [CrossRef]
- Jin, S.; Su, Y.; Gao, S.; Wu, F.; Hu, T.; Liu, J.; Li, W.; Wang, D.; Chen, S.; Jiang, Y. Deep learning: Individual maize segmentation from terrestrial lidar data using faster R-CNN and regional growth algorithms. Front. Plant Sci. 2018, 9, 866. [Google Scholar] [CrossRef]
- Jin, S.; Su, Y.; Wu, F.; Pang, S.; Gao, S.; Hu, T.; Liu, J.; Guo, Q. Stem–leaf segmentation and phenotypic trait extraction of individual maize using terrestrial LiDAR data. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1336–1346. [Google Scholar] [CrossRef]
- Jin, S.; Sun, X.; Wu, F.; Su, Y.; Li, Y.; Song, S.; Xu, K.; Ma, Q.; Baret, F.; Jiang, D. Lidar sheds new light on plant phenomics for plant breeding and management: Recent advances and future prospects. ISPRS J. Photogramm. Remote Sens. 2021, 171, 202–223. [Google Scholar] [CrossRef]
- Li, Y.; Ming, B.; Fan, P.; Liu, Y.; Wang, K.; Hou, P.; Xue, J.; Li, S.; Xie, R. Quantifying contributions of leaf area and longevity to leaf area duration under increased planting density and nitrogen input regimens during maize yield improvement. Field Crops Res. 2022, 283, 108551. [Google Scholar] [CrossRef]
- Béland, M.; Baldocchi, D.D.; Widlowski, J.-L.; Fournier, R.A.; Verstraete, M.M. On seeing the wood from the leaves and the role of voxel size in determining leaf area distribution of forests with terrestrial LiDAR. Agric. For. Meteorol. 2014, 184, 82–97. [Google Scholar] [CrossRef]
- Zhen, X.; Shao, H.; Zhang, W.; Huo, W.; Batchelor, W.D.; Hou, P.; Wang, E.; Mi, G.; Miao, Y.; Li, H. Testing a bell-shaped function for estimation of fully expanded leaf area in modern maize under potential production conditions. Crop J. 2018, 6, 527–537. [Google Scholar] [CrossRef]
- Chen, F.; Liu, J.; Liu, Z.; Chen, Z.; Ren, W.; Gong, X.; Wang, L.; Cai, H.; Pan, Q.; Yuan, L. Breeding for high-yield and nitrogen use efficiency in maize: Lessons from comparison between Chinese and US cultivars. Adv. Agron. 2021, 166, 251–275. [Google Scholar] [CrossRef]
- Farrell, J.; Givargis, T. Differential GPS reference station algorithm-design and analysis. IEEE Trans. Control Syst. Technol. 2000, 8, 519–531. [Google Scholar] [CrossRef]
- Hosoi, F.; Nakai, Y.; Omasa, K. 3-D voxel-based solid modeling of a broad-leaved tree for accurate volume estimation using portable scanning lidar. ISPRS J. Photogramm. Remote Sens. 2013, 82, 41–48. [Google Scholar] [CrossRef]
- Hosoi, F.; Omasa, K. Voxel-based 3-D modeling of individual trees for estimating leaf area density using high-resolution portable scanning lidar. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3610–3618. [Google Scholar] [CrossRef]
- Jimenez-Berni, J.A.; Deery, D.M.; Rozas-Larraondo, P.; Condon, A.T.G.; Rebetzke, G.J.; James, R.A.; Bovill, W.D.; Furbank, R.T.; Sirault, X.R. High throughput determination of plant height, ground cover, and above-ground biomass in wheat with LiDAR. Front. Plant Sci. 2018, 9, 237. [Google Scholar] [CrossRef] [PubMed]
- Fan, P.; Li, Y.; Evers, J.; Ming, B.; Wang, C.; Li, S.; Xie, R. A new empirical equation to describe the vertical leaf distribution profile of maize. J. Agric. Sci. 2020, 158, 676–686. [Google Scholar] [CrossRef]
- Jia, H.; Qu, M.; Wang, G.; Walsh, M.J.; Yao, J.; Guo, H.; Liu, H. Dough-stage maize (Zea mays L.) ear recognition based on multiscale hierarchical features and multifeature fusion. Math. Probl. Eng. 2020, 2020, 9825472. [Google Scholar] [CrossRef]
- Zeng, L.; Wardlow, B.D.; Xiang, D.; Hu, S.; Li, D. A review of vegetation phenological metrics extraction using time-series, multispectral satellite data. Remote Sens. Environ. 2020, 237, 111511. [Google Scholar] [CrossRef]
- Hong, S.-H.; Wang, L.; Truong, T.-K. An improved approach to the cubic-spline interpolation. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 1468–1472. [Google Scholar] [CrossRef]
- Brede, B.; Calders, K.; Lau, A.; Raumonen, P.; Bartholomeus, H.M.; Herold, M.; Kooistra, L. Non-destructive tree volume estimation through quantitative structure modelling: Comparing UAV laser scanning with terrestrial LIDAR. Remote Sens. Environ. 2019, 233, 111355. [Google Scholar] [CrossRef]
- Zhao, X.; Su, Y.; Hu, T.; Cao, M.; Liu, X.; Yang, Q.; Guan, H.; Liu, L.; Guo, Q. Analysis of UAV lidar information loss and its influence on the estimation accuracy of structural and functional traits in a meadow steppe. Ecol. Indic. 2022, 135, 108515. [Google Scholar] [CrossRef]
- Liu, X.; Ma, Q.; Wu, X.; Hu, T.; Liu, Z.; Liu, L.; Guo, Q.; Su, Y. A novel entropy-based method to quantify forest canopy structural complexity from multiplatform lidar point clouds. Remote Sens. Environ. 2022, 282, 113280. [Google Scholar] [CrossRef]
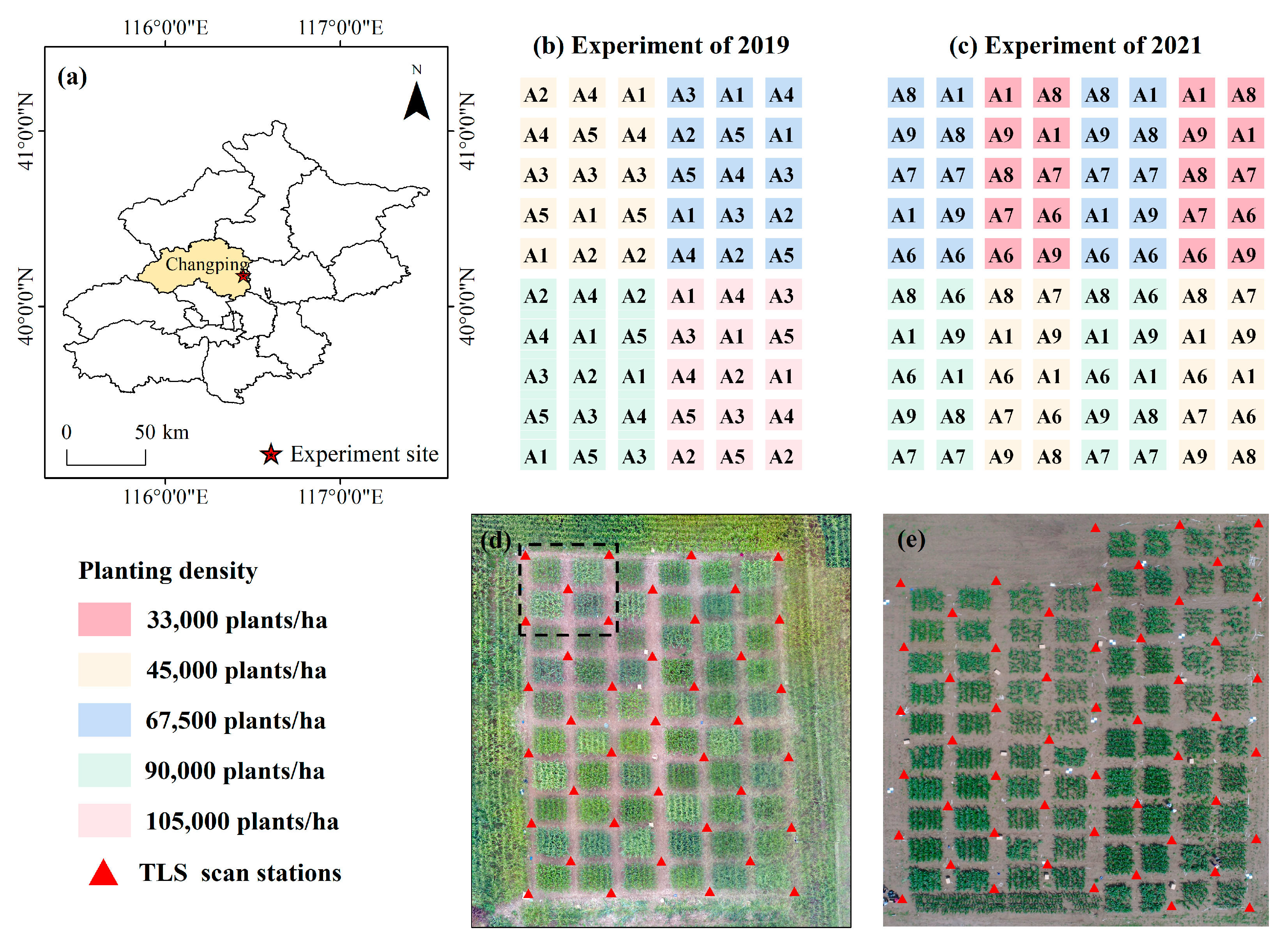
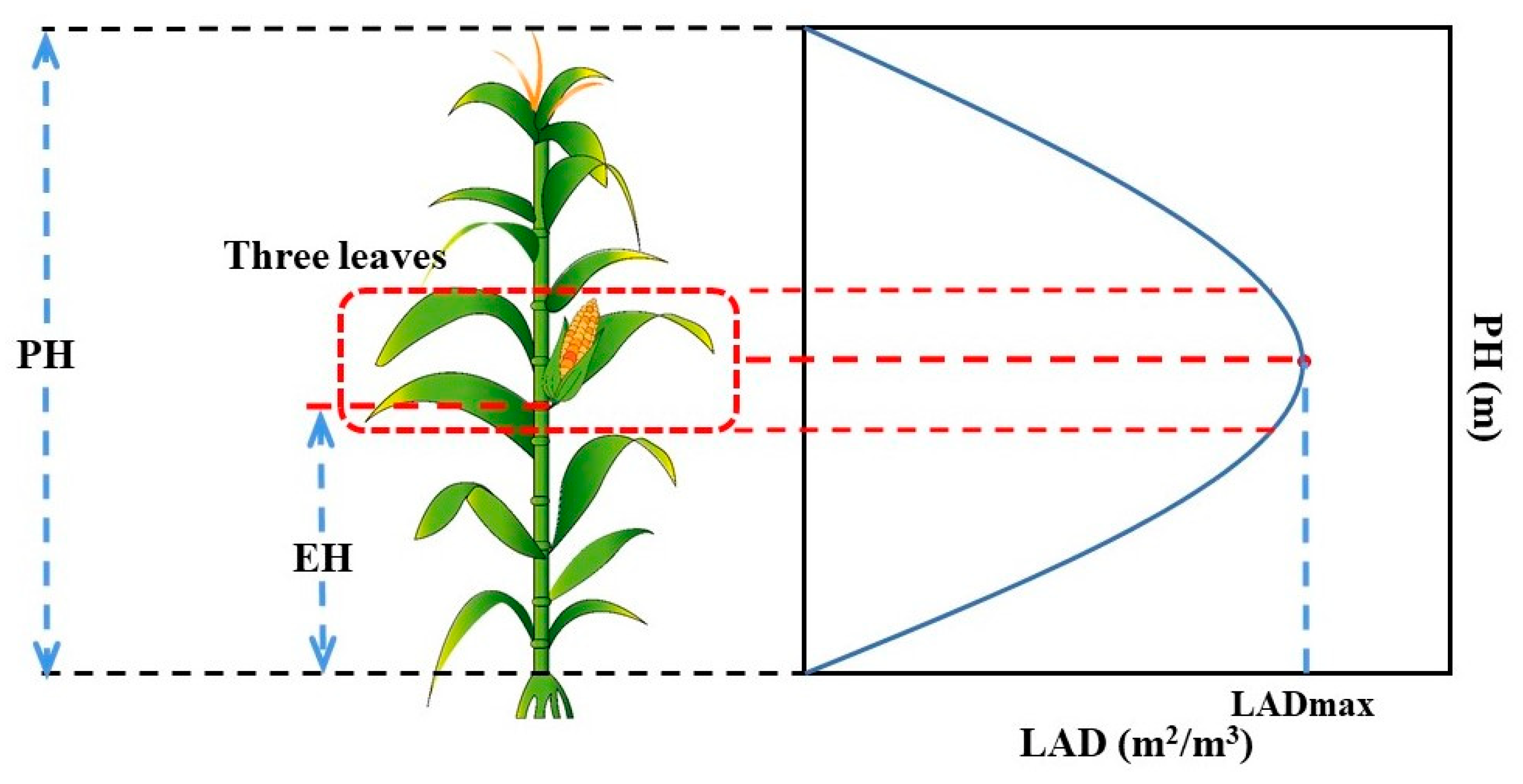


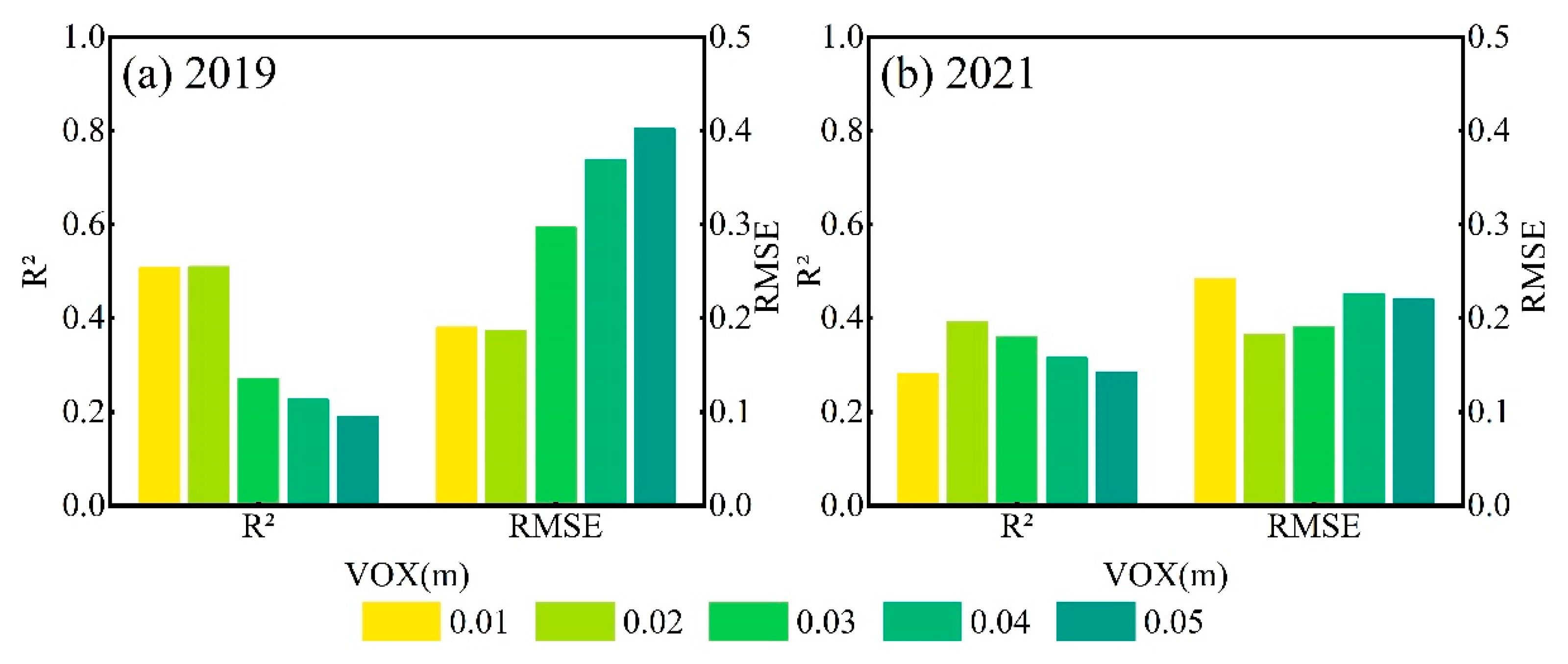
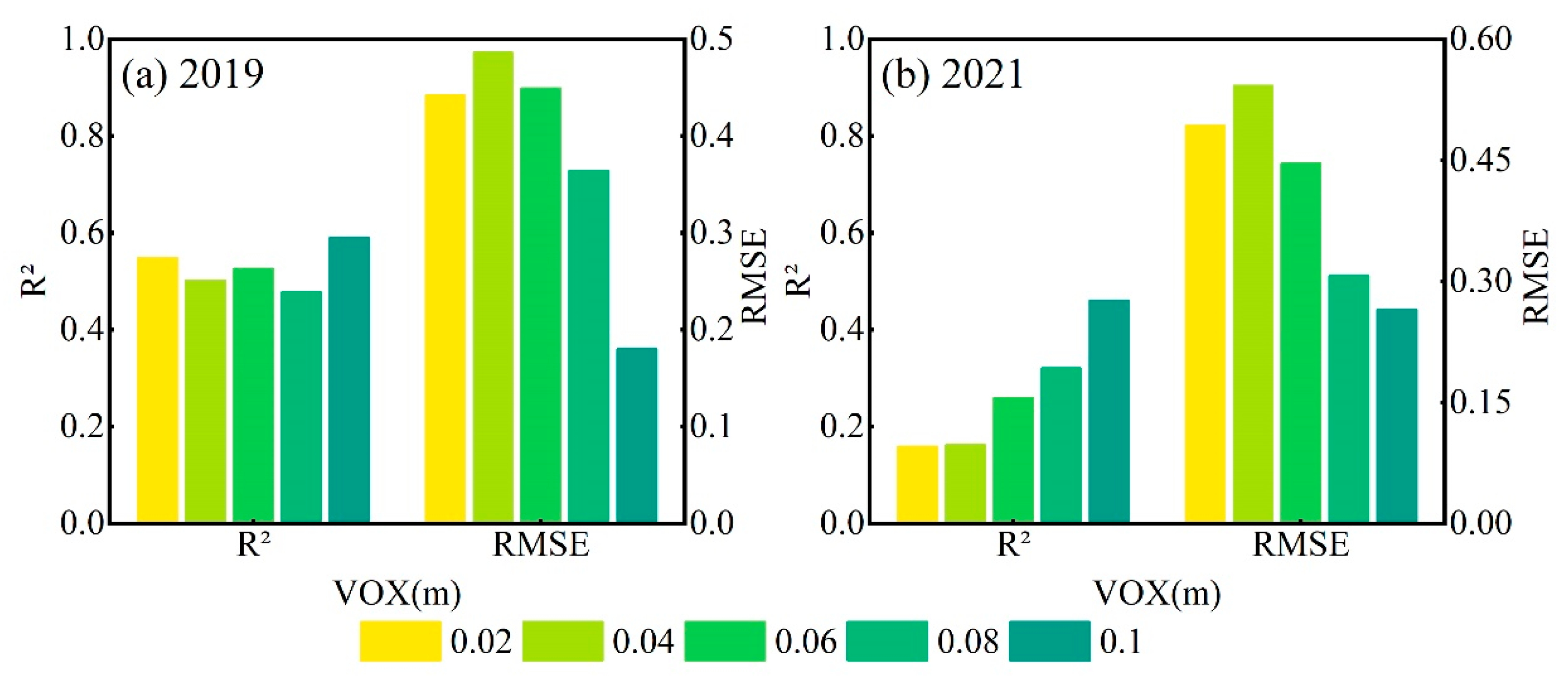
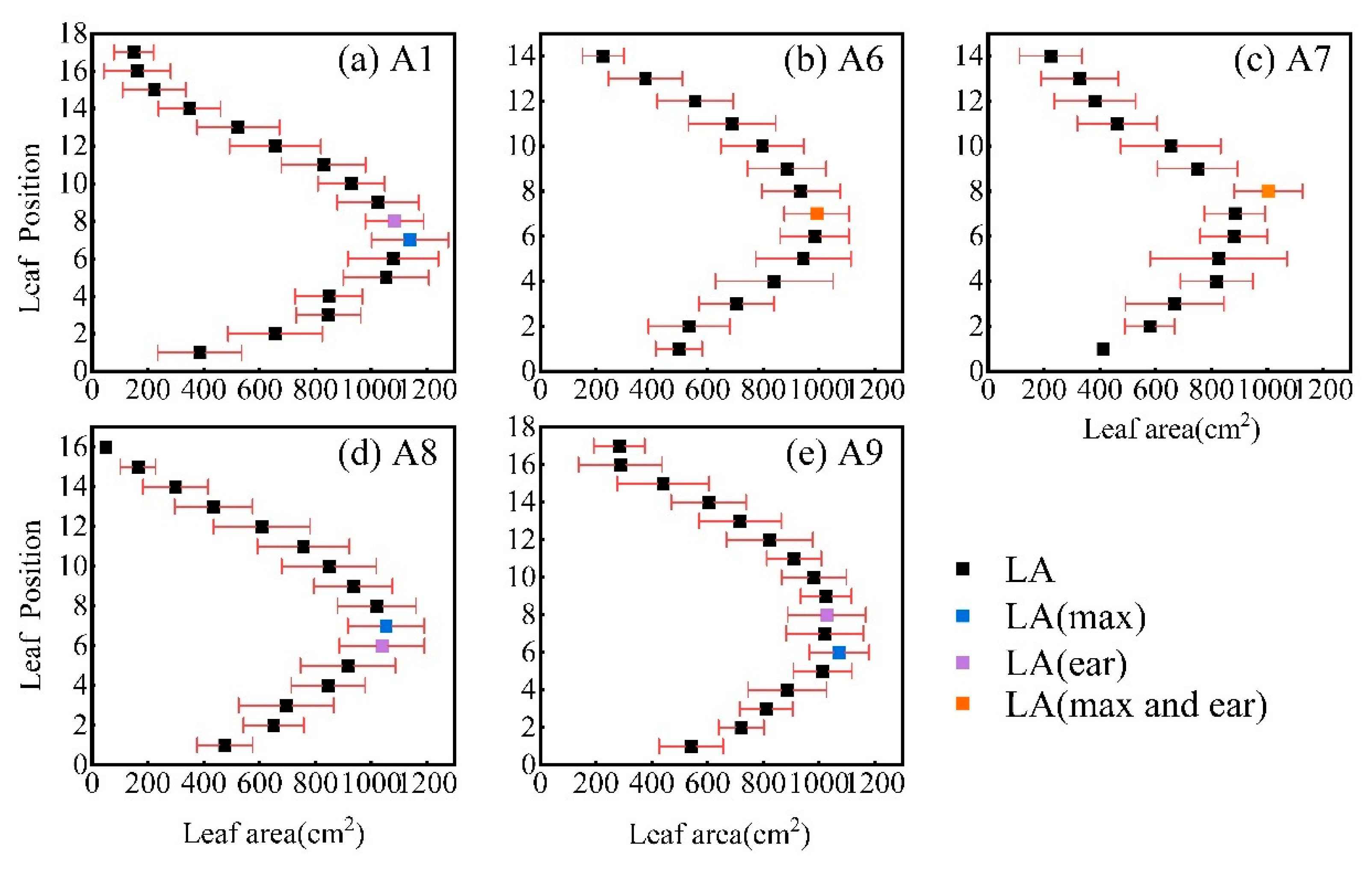
| Year | Variety | Density (Plant/ha) | Plots | Plot Length and Width (m) | Row Spacing (m) | Platform |
|---|---|---|---|---|---|---|
| 2019 | ZhengDan958 (A1), XianYu335 (A2), JingNongke728 (A3), ChengDan30 (A4), JingPin6 (A5) | 45,000 (D2), 67,500 (D3), 90,000 (D4), 105,000 (D5) | 5 cultivars * 4 densities * 3 random replicates = 60 | 3.6 × 2.5 | 0.6 (6 rows per plot) | DLS TLS |
| 2021 | ZhengDan958 (A1), JingJiu16 (A6), TianCi19 (A7), JingNuo2008 (A8), NongKeNuo336 (A9) | 33,000 (D1), 45,000 (D2), 67,500 (D3), 90,000 (D4) | 5 cultivars * 4 densities * 2 planting rows orientations * 2 random replicates = 80 | 3.6 × 2.5 | 0.6 (6 rows per plot) | DLS TLS |
| Parameters | Specification |
|---|---|
| Scanning distance | 20 m |
| Horizontal field angles | 0–360° |
| Vertical field angles | −60–90° |
| Scanning accuracy | ±1 mm |
| Scan time per station | less than 2 min and 54 s |
| Measurement speed | up to 976,000 points/s |
| Scanner height | 1.5 m |
| Parameters | Specification |
|---|---|
| Flying height | 15 m |
| Flight speed | 3 m/s |
| Scanning frequency | 550 kHz |
| Field of view angle | 330° |
| Scanning accuracy | ±10 mm |
| Scan speed | up to 200 scans/s |
| Year | Source | SS | df | MS | F | P > F |
|---|---|---|---|---|---|---|
| 2019TLS | Inter-category | 0.743 | 4 | 0.186 | 12.861 | 0.000 |
| Intra-category | 0.794 | 55 | 0.014 | — | — | |
| Total | 1.537 | 59 | — | — | ||
| 2021TLS | Inter-category | 1.066 | 4 | 0.266 | 11.448 | 0.000 |
| Intra-category | 1.466 | 63 | 0.023 | — | — | |
| Total | 2.532 | 67 | — | — | — | |
| 2019DLS | Inter-category | 0.325 | 4 | 0.081 | 3.478 | 0.026 |
| Intra-category | 0.467 | 20 | 0.023 | — | — | |
| Total | 0.791 | 24 | — | — | — | |
| 2019DLS | Inter-category | 0.935 | 4 | 0.234 | 8.847 | 0.000 |
| Intra-category | 1.163 | 44 | 0.026 | — | — | |
| Total | 2.098 | 48 | — | — | — |
| Year | D1 | D2 | D3 | D4 | D5 | Total | |
|---|---|---|---|---|---|---|---|
| 2019 | R2 | — | 0.60 | 0.55 | 0.65 | 0.68 | 0.59 |
| RMSE (cm) | — | 14.60 | 15.60 | 15.70 | 21.60 | 16.90 | |
| 2021 | R2 | 0.38 | 0.44 | 0.49 | 0.40 | — | 0.39 |
| RMSE (cm) | 17.20 | 20.80 | 15.30 | 18.50 | — | 18.40 |
| Year | D1 | D2 | D3 | D4 | D5 | Total | |
|---|---|---|---|---|---|---|---|
| 2019 | R2 | — | 0.48 | 0.35 | 0.34 | 0.64 | 0.45 |
| RMSE (cm) | — | 0.06 | 0.06 | 0.06 | 0.06 | 0.06 |
| Year | D1 | D2 | D3 | D4 | D5 | Total | |
|---|---|---|---|---|---|---|---|
| 2019 | R2 | — | 0.40 | 0.66 | 0.54 | 0.48 | 0.49 |
| RMSE (cm) | — | 25.00 | 42.50 | 43.90 | 53.70 | 42.60 | |
| 2021 | R2 | 0.37 | 0.37 | 0.46 | 0.10 | — | 0.41 |
| RMSE (cm) | 23.60 | 33.90 | 30.40 | 56.50 | — | 38.10 |
| Year | D1 | D2 | D3 | Total | |
|---|---|---|---|---|---|
| 2019 | R2 | — | 0.37 | 0.55 | 0.41 |
| RMSE (cm) | — | 0.07 | 0.08 | 0.08 |
| Cultivar | Plots with Overestimated EH/Total Number of Plots of This Cultivar (In 2019) | Plots with EH Overestimated by More than 20 cm/Total Number of Plots of This Cultivar (In 2019) | Plots with Overestimated EH/Total Number of Plots of This Cultivar (In 2021) | Plots with EH Overestimated by More than 20 cm/Total Number of Plots of This Cultivar (In 2021) |
|---|---|---|---|---|
| A1 | 83.33% | 33.33% | 84.67% | 7.67% |
| A2 | 75.00% | 8.33% | — | — |
| A3 | 83.33% | 16.67% | — | — |
| A4 | 83.33% | 16.67% | — | — |
| A5 | 100.00% | 33.33% | — | — |
| A6 | — | — | 57.1% | 7.14% |
| A7 | — | — | 38.46% | 23.08% |
| A8 | — | — | 58.33% | 16.67% |
| A9 | — | — | 81.25% | 37.50% |
| Platform | D2 | D3 | D4 | D5 | Total | |
|---|---|---|---|---|---|---|
| 2019 DLS Curve Fitting | R2 | 0.44 | 0.62 | 0.56 | 0.49 | 0.49 |
| RMSE (cm) | 22.70 | 39.10 | 39.20 | 50.60 | 39.20 | |
| 2019 TLS Curve Fitting | R2 | 0.58 | 0.48 | 0.52 | 0.71 | 0.54 |
| RMSE (cm) | 15.50 | 17.70 | 18.50 | 21.60 | 18.40 |
| Platform | D1 | D2 | D3 | D4 | Total | |
|---|---|---|---|---|---|---|
| 2021 DLS Curve Fitting | R2 | 0.44 | 0.34 | 0.46 | 0.10 | 0.41 |
| RMSE (cm) | 22.70 | 36.80 | 30.30 | 51.70 | 38.10 | |
| 2021 TLS Curve Fitting | R2 | 0.40 | 0.71 | 0.41 | 0.38 | 0.43 |
| RMSE (cm) | 17.20 | 19.10 | 18.20 | 24.00 | 18.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhang, W.; Yang, G.; Lei, L.; Han, S.; Xu, W.; Chen, R.; Zhang, C.; Yang, H. Maize Ear Height and Ear–Plant Height Ratio Estimation with LiDAR Data and Vertical Leaf Area Profile. Remote Sens. 2023, 15, 964. https://doi.org/10.3390/rs15040964
Wang H, Zhang W, Yang G, Lei L, Han S, Xu W, Chen R, Zhang C, Yang H. Maize Ear Height and Ear–Plant Height Ratio Estimation with LiDAR Data and Vertical Leaf Area Profile. Remote Sensing. 2023; 15(4):964. https://doi.org/10.3390/rs15040964
Chicago/Turabian StyleWang, Han, Wangfei Zhang, Guijun Yang, Lei Lei, Shaoyu Han, Weimeng Xu, Riqiang Chen, Chengjian Zhang, and Hao Yang. 2023. "Maize Ear Height and Ear–Plant Height Ratio Estimation with LiDAR Data and Vertical Leaf Area Profile" Remote Sensing 15, no. 4: 964. https://doi.org/10.3390/rs15040964
APA StyleWang, H., Zhang, W., Yang, G., Lei, L., Han, S., Xu, W., Chen, R., Zhang, C., & Yang, H. (2023). Maize Ear Height and Ear–Plant Height Ratio Estimation with LiDAR Data and Vertical Leaf Area Profile. Remote Sensing, 15(4), 964. https://doi.org/10.3390/rs15040964









