Learning Domain-Adaptive Landmark Detection-Based Self-Supervised Video Synchronization for Remote Sensing Panorama

Abstract

The synchronization of videos is an essential pre-processing step for multi-view reconstruction such as the image mosaic by UAV remote sensing; it is often solved with hardware solutions in motion capture studios. However, traditional synchronization setups rely on manual interventions or software solutions and only fit for a particular domain of motions. In this paper, we propose a self-supervised video synchronization algorithm that attains high accuracy in diverse scenarios without cumbersome manual intervention. At the core is a motion-based video synchronization algorithm that infers temporal offsets from the trajectories of moving objects in the videos. It is complemented by a self-supervised scene decomposition algorithm that detects common parts and their motion tracks in two or more videos, without requiring any manual positional supervision. We evaluate our approach on three different datasets, including the motion of humans, animals, and simulated objects, and use it to build the view panorama of the remote sensing field. All experiments demonstrate that the proposed location-based synchronization is more effective compared to the state-of-the-art methods, and our self-supervised inference approaches the accuracy of supervised solutions, while being much easier to adapt to a new target domain.

1. Introduction

Recently, remote sensing image mosaic technology has regained importance in the image processing and pattern recognition community; it can be used for the detection and reconnaissance of Unmanned Aerial Vehicles (UAV), e.g., UAV panoramic imaging system [1] and hyperspectral panoramic image stitching [2]. Many algorithms have been proposed for this issue [3,4]. Especially, due to the limitations of the imaging width, it is common that the ROI region cannot be contained in one view of a remote sensing image. Hence, it is necessary to capture multi-view and time-synchronized images from videos, then splice them into a panoramic image.

Accurate video synchronization aims at aligning different videos that capture the same event and share a temporal and visual overlap from multiple views; it is the de-facto industry standard for many scientific fields such as remote sensing image mosaic [3,4], human motion capture [5,6], optical flow estimation [7,8], group retrieval [9,10], dense 3D reconstructions [11,12], and spatial-temporal trajectory prediction modeling [13,14]. While recent advances allow moving from marker-based solutions to purely visual reconstruction [15], which alleviates actor instrumentation, multiple cameras are still required for millimeter-level reconstruction. For instance, monocular human pose estimation has drastically improved in recent years [16,17,18]. However, the attained error is still above 3 cm on average, with occasional large outliers. A key factor is the unavoidable ambiguities in reconstructing a 3D scene from a 2D image with the depth information largely obscured. Therefore, the most accurate deep learning approaches that are used in neuroscience [19], sports, medical surgery [20], and other life science studies [21] rely on multiple views to reduce ambiguities. These multi-view solutions involve a calibration and a synchronization step before, or integrated into, the reconstruction algorithm.

Video synchronization can be solved in hardware, by wiring cameras together and by wireless solutions such as GPS, Bluetooth, and WiFi. However, the former is cumbersome to set up and unpractical for mobile equipment, and the latter requires special, expensive cameras. When recording with consumer cameras, external synchronization signals are common, such as a light flash or clap recorded on the audio line [22]. However, these are error prone and require manual interventions. Therefore, most practical synchronization pipelines require the user to click the occurrence of common events in every camera and video that should be synchronized, which is a time-intensive post-processing step for recordings with many sessions and cameras. By contrast, this paper aims at an automated yet general algorithm that matches the performance of existing domain-specific approaches.

We propose a new approach for learning the synchronization of multi-view videos that (1) is accurate, by using a new network architecture with motion trajectories as intermediate representations; (2) adapts to a diverse set of domains, as the required trajectory tracking is learned without supervision; and (3) is convenient to use, because no external calibration signals are needed.

Existing synchronization algorithms have experimented with a diverse set of video representations, ranging from raw RGB frames [23,24] over optical flow [25,26], and detecting the position of humans using off-the-shelf networks [27,28,29,30]. The former two are general but strike a lower accuracy. The latter works well for recording human motion, whereas they do not translate well to other instances when no pre-trained detectors are available. Our solution attempts to combine the best of both, by self-supervised learning of a sparse representation of the pictured scene into the location trajectories and appearance of moving salient objects and persons. The location tracks are integrated into a new neural network architecture that works on inferred sparse localization. Its advantage is that the motion that is important for synchronization can be disentangled from the appearance, which may vary across views and time due to illumination and viewing angle. The only supervision is the time annotation of a few example videos in the target domain, as in the prior work [26].

Our method is different from the method of Lorenz et al. [31], which uses a part-based disentangling method to generate new views by transferring the appearance in a specific view. This paper proposes a landmark-generating method named style transfer module by using the correspondence between two existing views, which provides useful positional information at different times. The style transfer module in the proposed method plays an important role in extracting features by temporal modeling, which fits the usage of the subsequent temporal similarity calculating module. To summarize, our main contribution lies in three folds:

• We propose a self-supervised style transfer solution that decomposes a scene into objects and their parts to learn domain-specific object position per frame that allows to track keypoint locations, such as animal position and articulated human pose over time.
• We propose an efficient two-stage method of style transfer and matrix diagonal (STMD) which uses the keypoint locations to train a generalized similarity model that can predict the synchronized offset between two views.
• Experimentations on three different video-synchronization datasets and the application of the image mosaic of UAV remote sensing prove the superiority and generalization of the proposed method on different domains.

2. Related Work

2.1. Synchronization Algorithms

Previous video synchronized methods use a diverse set of low-level and high-level motion features to infer a correlation between videos. Wu et al. [26] compare 2D human pose features with optical flow for training their Synchronization Network (SynNet) and find that the pose feature works better. Xu et al. [32] use the 3D pose as input and match the consistency of two-view pixel correspondences across video sequences. However, this requires a precise 3D reconstruction method. In addition, some works combine visual and auditive elements to realize video synchronization [22,33]. However, additional information such as audio sources may not be always available in real videos or be disrupted by diffuse background noise.

Wang et al. [34] propose a nonlinear temporal synchronization method using graph-based search algorithm with coefficient matrices to minimize the misalignments between two moving cameras. Different from their work, the proposed method is easier to conduct since it is self-supervised and does not need pre-trained information to obtain the correspondence between videos, while [34] needs to use predefined basis trajectories to obtain the coefficient matrices. Recently, Huo et al. [35] propose a reference frame alignment method for frame extrapolation to establish nonlinear temporal correspondence between videos. The proposed method is different from [35] since it is not dependent on supervised tracking and not sensitive to the error brought by tracking noise. Therefore, our method can adapt to various domains.

Another branch of related work finds implicit temporal correspondence without explicit motion features. Purushwalkam et al. [36] propose an alignment procedure to connect patches between videos via cross-video cycle consistency. Similarly, Dwibedi et al. [37] also apply temporal cycle consistency to align videos, but they use it to learn an embedding space to obtain the nearest neighbors. Other methods use some prior temporal mapping information (e.g., an event appeared in multiple videos) to learn some correspondence between multiple video sequences, such as ranking [38], Canonical Correlation Analysis [39], and co-occurring events [38,40]. However, these methods are not fit for our domain-adaptive task as this prior mapping information cannot exist in different scenarios.

2.2. Object Detection and Tracking

Traditional object detection methods need some manual object position annotations for supervised training [41,42,43,44] or body part annotation, such as OpenPose [30], which is widespread for humans but difficult for most other animals. For the tracking of people, Tompson et al. [45] propose a position refinement model to estimate the joint offset location and improve human localization. Newell et al. [46] propose associative embedding tags to track each keypoint for individual people. Recently, Ning et al. [47] use a skeleton-based representation of human joints to incorporate single-person pose tracking (SPT) and visual object tracking (VOT) as a unified framework. In addition, there are some works [48,49,50] that realize tracking in non-human cases, such as animals, which inspires us to generalize our method to the non-human cases of video synchronization, but does not yield the fine-grained resolution up to body parts that we desire.

2.3. Self-Supervised Methods

To tackle the problem without supervision, self-supervised learning (SSL) has been proposed to train the model using auxiliary tasks [51]. For object detection, SSL has been used to replace the ImageNet pretraining [52] by the relevant task that does not need manual annotation data, such as colorization [53], Jigsaw puzzles [54], inpainting [55], tracking [56], optical flow [57], temporal clues [58], text [59], and sound [60]. However, the majority of their performances are not as good as the pretraining of ImageNet. In addition, there are some works that use SSL in object detection by improving the auto-encoder network with the attention mechanism [61,62] or proposal-based segmentation [63]; these approaches first use a spatial transform to detect bounding boxes and then pass them through the auto-encoder and synthesize the object with a background.

Different from the discussed previous work, we do not use any spatial supervision in this paper, yet derive high-level features that are better suited for synchronization than lower-level ones such as optical flow.

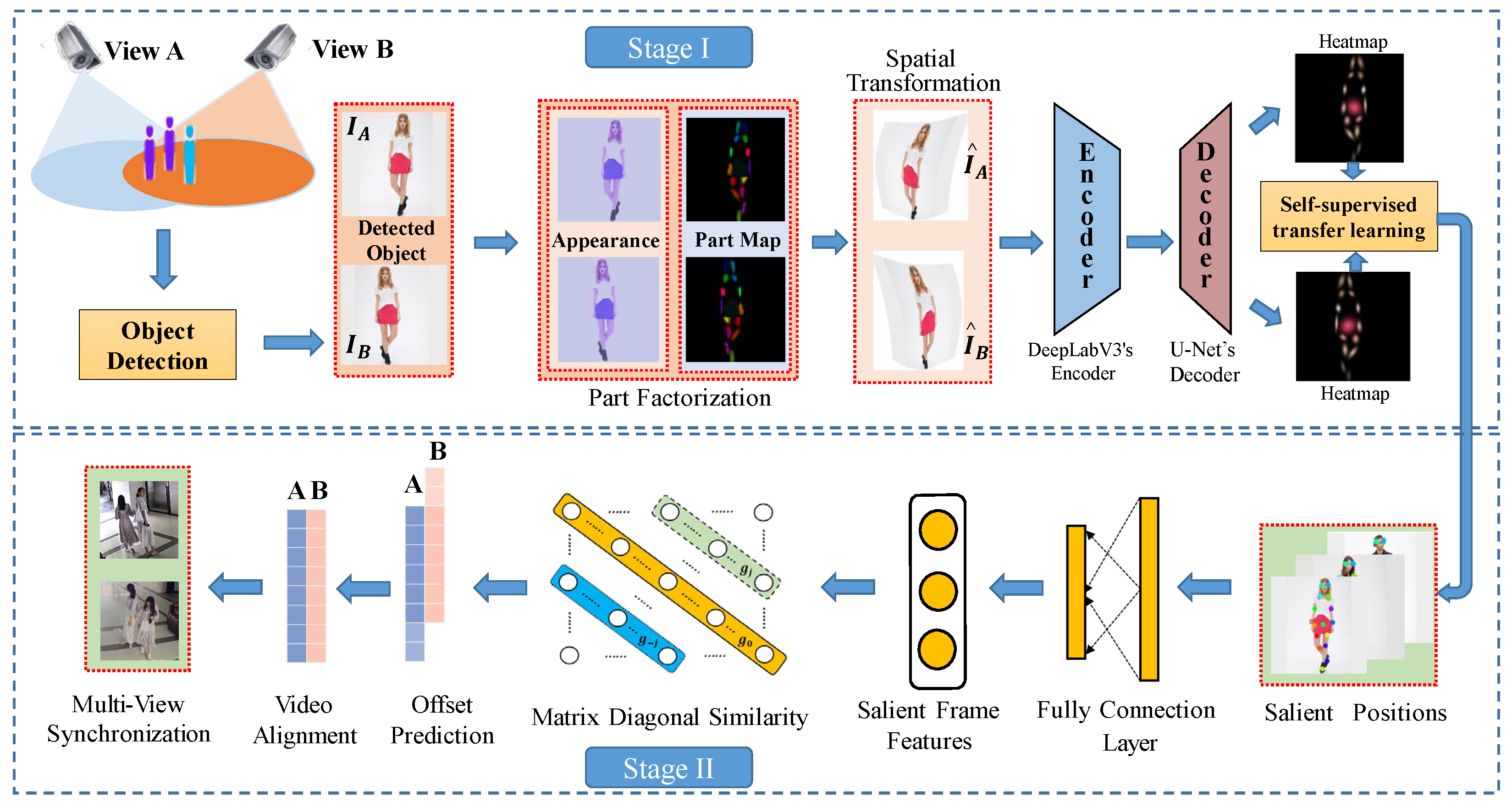
3. The Proposed Method

Generally speaking, the procedure of remote sensing panorama is summarized as five aspects: image registration, extraction of overlapping areas, radiometric normalization, seamline detection, and image blending. There are many similar aspects between panorama and video synchronization, e.g., finding internal correspondences among different overlapping views. According to the traditional procedure for remote sensing panorama, we propose a new video synchronization method as follows.

The proposed method operates in two steps as shown in Figure 1. The first stage estimates and tracks the coordinates of salient objects via a self-supervised network that is trained on the raw multi-view videos to establish correspondences. The second stage is a neural network that takes the object trajectories inferred from two videos as input, computes a similarity matrix across the two views, and predicts an offset based on these using classification into discrete classes.

3.1. Stage I: Style Transfer-Based Object Discovery and Tracking

To obtain the position of the salient objects in a video, we desire to divide each frame into an assembly of parts, defined by the 2D coordinate of the central point of each part. Many supervised approaches for the detection of objects and their parts are available. However, even though neural network architectures are sophisticated and attain high accuracy on the benchmarks, they poorly generalize to new domains. For instance, a method trained on persons will not generalize to animals, although positional and behavioral analysis is in high demand for application in neuroscience, medicine, and life sciences. Therefore, we tailor and extend the self-supervised approach from [31] to our domain before proceeding to the main goal of video synchronization.

The original idea of [31] is to disentangle pose and shape by training on pairs of images that share the same objects but have slight appearance variation and a different image constellation. A single image is turned into such a pair by adding color augmentation and spatial deformation via thin plate splines for the second example, which constructs the correspondence between two views by the style transfer of the image.

We consider the difference between two images taken from different viewpoints in a multi-view setup as a spatial image transformation $\tau :\Gamma \to \Gamma$, instead of relying on the explicit deformation that is difficult to parameterize. Therefore, we consider a pair of views as being composed of the same objects. Of course, the image transformation might have holes due to occlusions and the field of view of the two cameras will not overlap perfectly. Yet, we show that the following algorithm is robust to slight violations and works when these assumptions are approximately fulfilled.

Formally, we use a part-based factorization [31] to represent the object in an image I as Q parts:

$$\{{\phi }_i\left(I\right)\}:={({\phi }_1\left(I\right),\dots {\phi }_i\left(I\right),\dots ,{\phi }_Q\left(I\right))}^T$$

(1)

where the local part position is independent of other parts. Global image information is represented by the combinations of all individual parts $\left\{{\phi }_i\left(I\right)\right\}$. Each part consists of a 2D position ${\mathbf{u}}_i\in {\mathbb{R}}^2$, shape ${\Sigma }_i\in {\mathbb{R}}^2$, and its appearance encoding ${\mathbf{a}}_{\mathbf{i}}\in {\mathbb{R}}^{\mathbf{3}}$.

Part shape and appearance are learned by unsupervised learning as in [31], but we use multiple views instead of deformed variants of the same image. Let $I_1$ be an image from Camera 1 (Cam1) and $I_2$ be the image at the same time step in Camera 2 (Cam2), which is viewed as the geometry-transformed image of $I_1$. It is worth noting that since no explicit pose correspondence is used, the proposed ST module can also be trained with misaligned frames showing the same object in a slightly different pose (e.g., [31] trains with deformed images). Therefore, it is not necessary for the landmark generation to use extra annotations to make the images under two views aligned in the ST stage. Since the proposed subsequent MD module requires synchronized videos (cf. Section 1), we use the same synchronized footage for the ST module for simplicity here.

Color augmentation is used to create an appearance-transformed version of the two, ${\widehat{I}}_1$ and ${\widehat{I}}_2$. Thereby, $I_1$ can be reconstructed from the position in ${\widehat{I}}_1$ and the color in $I_2$. The same holds for the other direction and we select one of the two at random. This reconstruction is realized with an autoencoder consisting of the DeepLabV3’s encoder [64] and the U-Net’s [65] decoder. Specifically, there are four up-sampling layers in the U-Net decoder, each layer consists of one deconvolution layer for upsampling and two ReLU convolution layers. The encoder is independently applied to each of the two images ((${\widehat{I}}_1$, $I_2$) or (${\widehat{I}}_2$, $I_1$)) to realize semantic segmentation. The output feature maps are considered as a stack of heatmaps, one heatmap, ${\mathbf{H}}_i\in {\mathbb{R}}^{W\times H}$, where W and H are the width and height of the i’th part’s heatmap. These heatmaps are normalized to form probability maps:

$$P_i(x,y)=\frac{exp\left[{\mathbf{H}}_i(x,y)\right]}{{\sum }_{u=1}^W{\sum }_{v=1}^{H}exp\left[{\mathbf{H}}_i(u,v)\right]}$$

(2)

where $(u,v)$ and $(x,y)$ are pixel locations. The position ${\mu }_i$ of part i is then computed as the expected 2D position, i.e., the weighted sum of all pixel locations, weighted by the probability map $P_i$. The shape, ${\Sigma }_i$ is estimated as the covariance of $P_i$ around ${\mu }_i$. The appearance is estimated by creating a Gaussian map, ${\mathbf{G}}_i\in {\mathbb{R}}^{W\times H}$, with mean ${\mu }_i$ and covariance ${\Sigma }_i$ and building the expected color over this distribution, i.e., the mean color value, weighted by the Gaussian support.

To decode the entire image, appearance and pose estimated from ${\widehat{I}}_1$ and $I_2$ are mixed and converted into a color image by multiplying ${\mathbf{a}}_{\mathbf{i}}$ with ${\mathbf{G}}_{\mathbf{i}}$ and taking the maximum over all parts. This coarse image is blurry and is up-sampled to a proper image using U-Net as a form of the decoder. This chain of the network is trained on a standard reconstruction objective comprised of a photometric pixel loss and a perceptual loss using VGG:

$$L_{rec}={∥I-I_{rec}∥}_2+\beta L_{perc}(I,I_{rec})$$

(3)

where $I_{rec}$ is the reconstructed image of I and $\beta$ is the weight of perceptual loss.

In total, the first stage uses self-supervision to learn domain-specific object position per frame that allows tracking keypoint locations, such as animal position and articulated human pose over time. To this end, we rely on existing self-supervised solutions that decompose a scene into objects and their parts by finding an association between a training image and its appearance and spatially deformed twin. We utilize a similar training framework but learn the disentanglement on a pair of images from different videos picturing the same scene instead of a deformed version of the same image. This establishes correspondences across views and circumvents the use of deformation models that are difficult to tune.

3.2. Stage II: Matrix Diagonal Similarity-Based Classification Framework

After obtaining the positions of salient points, we propose to feed them into a matrix diagonal (MD) module that scores the alignment of videos.

The goal of video synchronization is to achieve temporal offset between two unaligned videos, where the video consists of many discrete images with a fixed frame rate. Therefore, the video synchronization problem is framed as a classification problem with quantified integer offset values: $\{-K,-K+1,\dots ,-1,0,1,\dots ,K\}$, where K is the half clip length and $K>0$, there are $2K+1$ class labels to formulate the possible offsets. In this way, if we find the offset between two video frames, these can be aligned by shifting with the predicted offset.

Let ${\mathbf{k}}_{c_1,i}\in {\mathbb{R}}^D$ and ${\mathbf{k}}_{c_2,j}\in {\mathbb{R}}^D$ be features of the ith frame and jth frame from Cam1 and Cam2, respectively. In our full model, the features are the positions of the parts learned in the previous section, but we also compare with other features used in related work. Each raw feature is further processed with a matching network f to the refined features ${\mathbf{e}}_{c_1,i}\in {\mathbb{R}}^{D^{\prime }}$ and ${\mathbf{e}}_{c_2,j}\in {\mathbb{R}}^{D^{\prime }}$. D and $D^{\prime }$ are the respective spatial dimension. The network f consists of two FC-layers of width $[N_1,N_2]$. To compute a similarity between these features, we arrange them in a matrix of all possible feature pairs and compute their pairwise similarity,

$$M_{m,n}=-\frac{1}{l}\left|\right|{\mathbf{e}}_{c_1,i+m}-{\mathbf{e}}_{c_2,j+n}{\left|\right|}_2^2$$

(4)

where the mean square error (MSE) is used to represent the feature distance between two frames, and the negative MSE value is used to measure the similarity between them. As shown in Figure 2, l is the length of the clip. We set the clip $C_1=\{{\mathbf{e}}_{c1,i},\dots ,{\mathbf{e}}_{c1,i+2K-1}\}$ and the clip $C_2=\{{\mathbf{e}}_{c2,j},\dots ,{\mathbf{e}}_{c2,j+2K-1}\}$ as the element of the row and the column in the matrix $\mathbf{M}$, respectively. In this way, we compute the similarity of all frames between two clips $C_1$ and $C_2$ to obtain Matrix $\mathbf{M}$.

With this similarity matrix computed, we find the offset with the highest similarity. Since all frames are recorded with the same frame rate, a temporal shift of t corresponds to matching frames in the $g_t$’th off-diagonal of $\mathbf{M}$. In the case of two synchronized clips, the minimum should appear in the main diagonal. Thus, the average similarity along diagonals of M is computed as

$$S_{C_1,C_2}=\frac{1}{l_t}\sum _{(m,n)\in g_t}{M}_{m,n}$$

(5)

where $l_t$ is the length of diagonal $g_t$. Finally, we compute the offset T between two input video clips according to the distance between the main diagonal and the diagonal that has the maximum average similarity. In this way, the two input videos can be synchronized by shifting the offset.

The feature extraction network f is trained end-to-end on a cross-entropy loss, given ground truth offset labels, we use two fully connection layers to encode the 2D coordinates of salient positions into frame features, and there is a ReLU layer between the two layers. In addition, the detected landmarks are ordered and generally consistent between two views in the output of the encoder in the style transfer (ST) stage, e.g., the same keypoint is always on the human head. Therefore, even if a given part is not identified in one of the images in some extreme cases, the MD stage includes a learned neural network and can hence rely on this ordering to avoid the remaining features being shifted, then ensures its robustness.

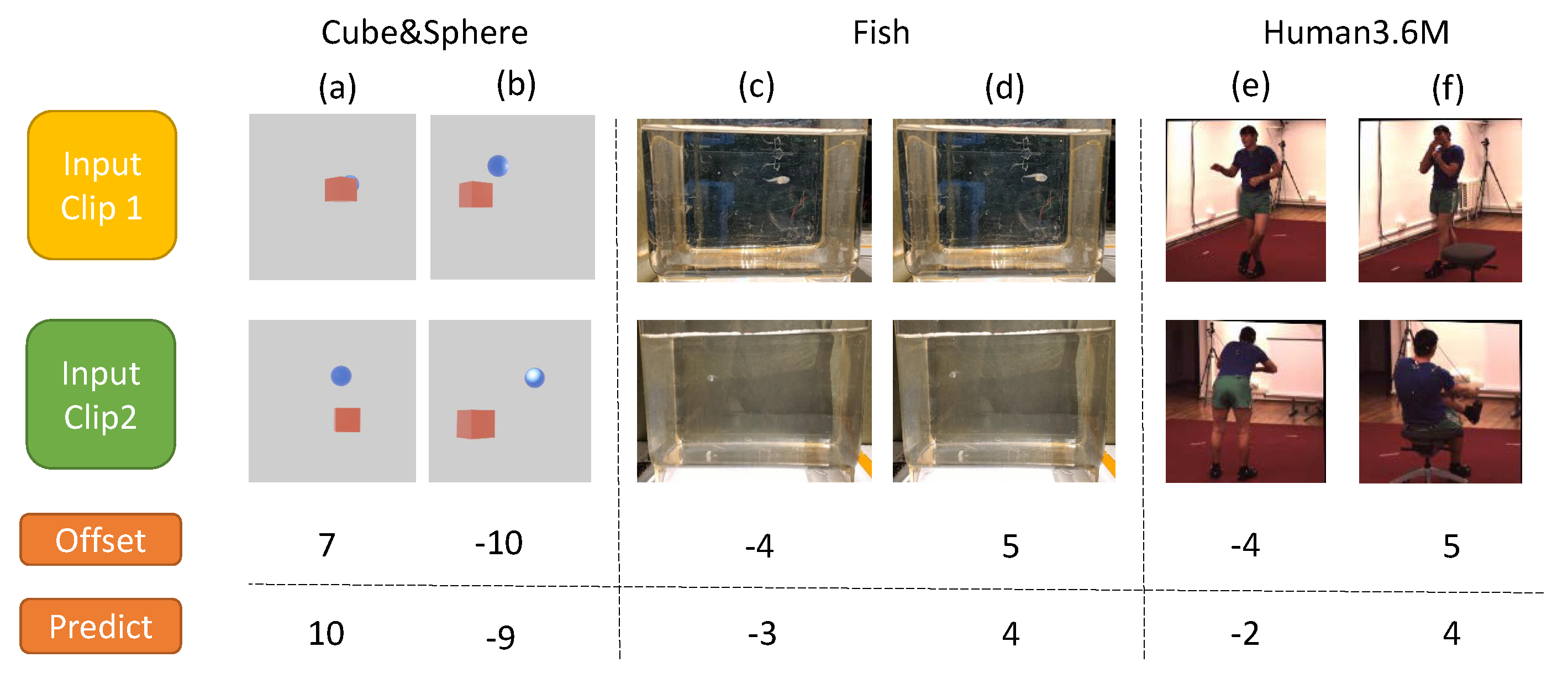
4. Experiments

In this section, we demonstrate the accuracy and generality of the proposed approach to video synchronization datasets. Besides the simulated Cube&Sphere dataset, we conduct experiments on another two datasets: One dataset is collected from two views of the Human 3.6 Million (Human3.6M) dataset [66,67], an established benchmark for 3D human pose estimation with synchronized videos. The other is a custom dataset that resembles capture setups of neuroscience laboratory animals. We refer to our full method as STMD in experiments and compare against diverse baselines. To make the experiments fair and convincing, we used the cross-validation method to evaluate and obtain average results. Specifically, to evaluate its generalization, the proposed video synchronization method will be conducted in some practical remote sensing fields, e.g., the UAV image mosaic.

4.1. Datasets

Cube&Sphere Video Synchronization Dataset. The Cube&Sphere dataset is constructed using the open-source 3D animation suite Blender. We generated 60 random 3D positions of a cube and a sphere. This scene is captured from two cameras with a view angle difference of roughly 30 degrees. Each video is 1200 frames long, with a frame rate of 24 fps. The first 960 frame pairs were used to construct the training dataset, and the last 240 were used for testing. The 3D coordinates of the virtual objects were projected onto the 2D image plane of the two cameras to form positions for a supervised baseline.

Fish Video Synchronization Dataset. We chose a pair of synchronized clips from 2 views and each consisted of 256 successive frames at 30 fps from a neuroscience experiment setup with a zebrafish (Danio rerio) in random motion, as shown in Figure 3. The first 128 frames were used for training, while the last 128 frames were used for testing. To ignore motions in the background, only the fish tank region was used as input to the algorithm.

Human3.6M Video Synchronization Dataset. We use the well-known Human3.6M dataset, which contains recordings of 11 subjects with four fully-synchronized and high-resolution progressive scan cameras at 50 Hz [66]. We use 60 sequences from two cameras of Human3.6M, which includes walking, sitting, waiting, and lying down. There are 720 frames in each camera, we use the first 540 for training and the last 180 for testing, the size of each image is 128 × 128.

4.2. Metrics

To provide a fair comparison with other methods, we use the well-known Cumulated Matching Characteristic (CMC) [26,68] to report the synchronized accuracy results. It measures the top dist-k (dk) accuracy of k-different synchronized offsets. Moreover, we complement another SynError metric to measure their time deviation between the predicted offset $R_i$ and the true offset $T_i$ at the i-th frame as [26]:

$$SynError=\left(\frac{1}{L}{\sum }_{i=1}^N\left|R_i-T_i\right|\right)\times \frac{ds}{fps}$$

(6)

where L is the length of the video clip, $ds$ is the video downsampling rate, and $fps$ is the frame rate of the video.

4.3. Experiment Setup

Our proposed STMD is implemented using Pytorch. In the style transfer stage, we use the DeepLabV3 model [64] with a ResNet-50 backbone [69] to segment the Gaussian parts from the original images, and set the learning rate at ${10}^{-3}$, the numbers of salient points are 13, 3, and 15 for Cube&Sphere, Fish, and Human3.6M dataset, respectively.

In the matrix diagonal stage, we use the cross-entropy as the loss criterion and the Adam method [70] for stochastic optimization over 50 epochs over the training set with a learning rate at ${10}^{-4}$, and the neurons of the two FC-layers $[N_1,N_2]=[240,168]$.

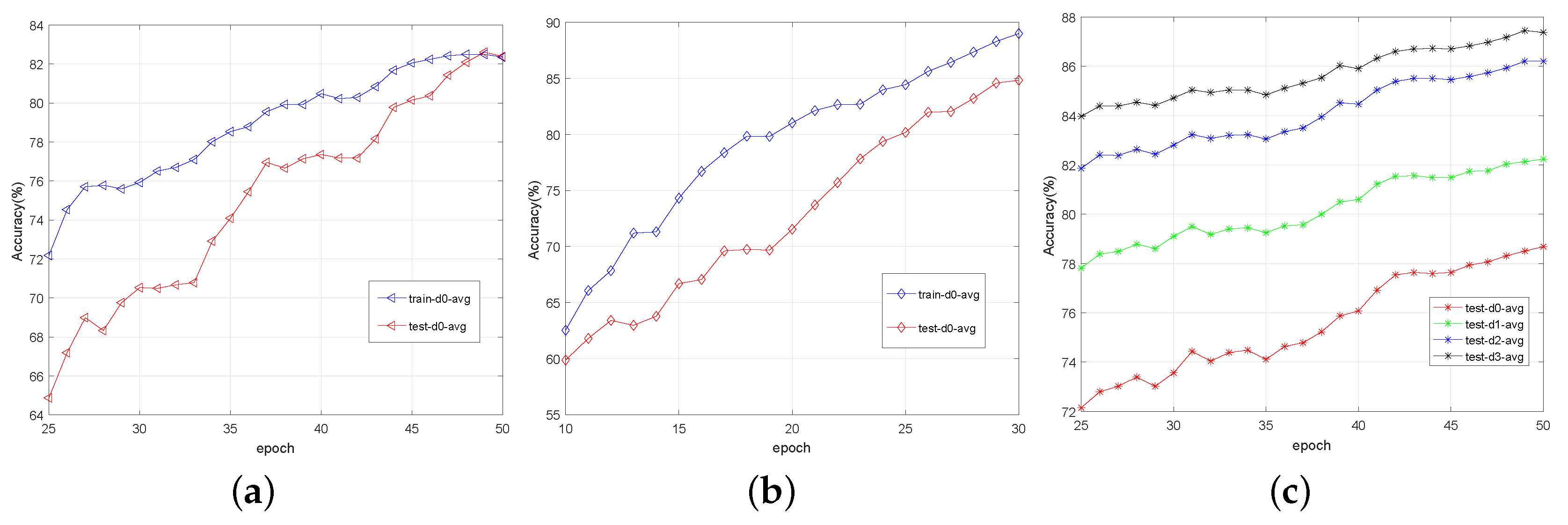
4.4. Results on Cube&Sphere Dataset

To provide a wide perspective of the performance of our proposed method, we present our results along with some start-of-the-art baselines and ablation studies on the Cube&Sphere dataset in

Table 1. Results of different methods on the Cube&Sphere dataset. “ds” represents the downsampling rate, the baselines without the “ds” label are ds = 1 by default.

Method	test-d0 (%)	test-d1 (%)	test-d2 (%)	test-d3 (%)	SynError ↓
SynNet+OpenPose [26]	10.9	31.2	50.2	68.8	0.1389
SynNet+ST	21.8	36.8	54.6	67.9	0.0782
LAMV (ds = 1) [71]	30.0	50.1	70.2	90.2	0.0638
PE [72]	34.3	67.7	72.1	79.6	0.0672
LAMV (ds = 2)	41.7	58.5	75.2	92.0	0.1061
LAMV (ds = 3)	50.1	64.5	78.9	93.1	0.1362
LAMV (ds = 4)	56.4	69.0	81.5	94.1	0.1586
TCC (ds = 1) [37]	67.1	81.8	89.6	92.9	0.0305
GTpoint+MD	77.1	99.0	99.4	99.5	0.0098
TCC (ds = 2)	80.9	88.1	91.4	92.8	0.0505
STMD+MSE	86.1	99.0	99.6	99.7	0.0059

. We reproduce the SynNet method by both the OpenPose strategy as [26] and the ST stratety, the former trains OpenPose from scratch to get keypoints according to the structure of human motion, in this case, Openpose extracts the heatmap of keypoints by human pose estimation. For the sake of illustration, we name it SynNet+OpenPose. Meanwhile, the latter uses our proposed ST module to obtain the keypoints and feed them into SynNet. In the experiment, both of them play the role of transfer, SynNet+OpenPose transfers the pre-trained human joints model on the keypoint estimation of the non-human case, while SynNet+ST uses the proposed style transfer between two camera views to generate non-human keypoints. Furthermore, we conduct the ablation study in terms of the ST and MD modules, respectively. GTpoint+MD uses the geometric central points to substitute the ST module, which are set by Blender software to handle the motion of the objects. While SynNet+ST uses SynNet after the ST module to predict the offset rather than the MD module.

From the results, we can draw the following conclusions that validate the improvements gained from our contributions.

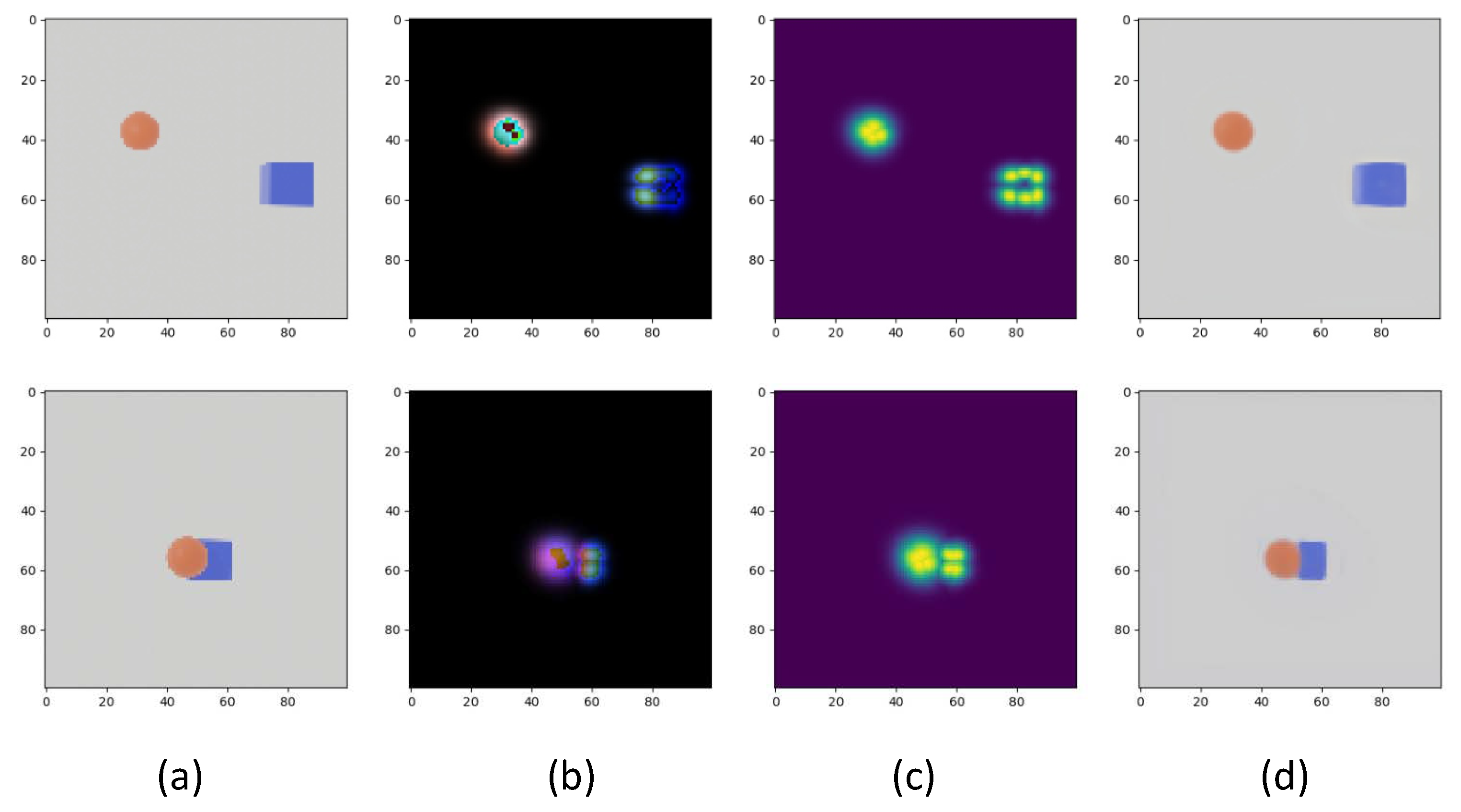
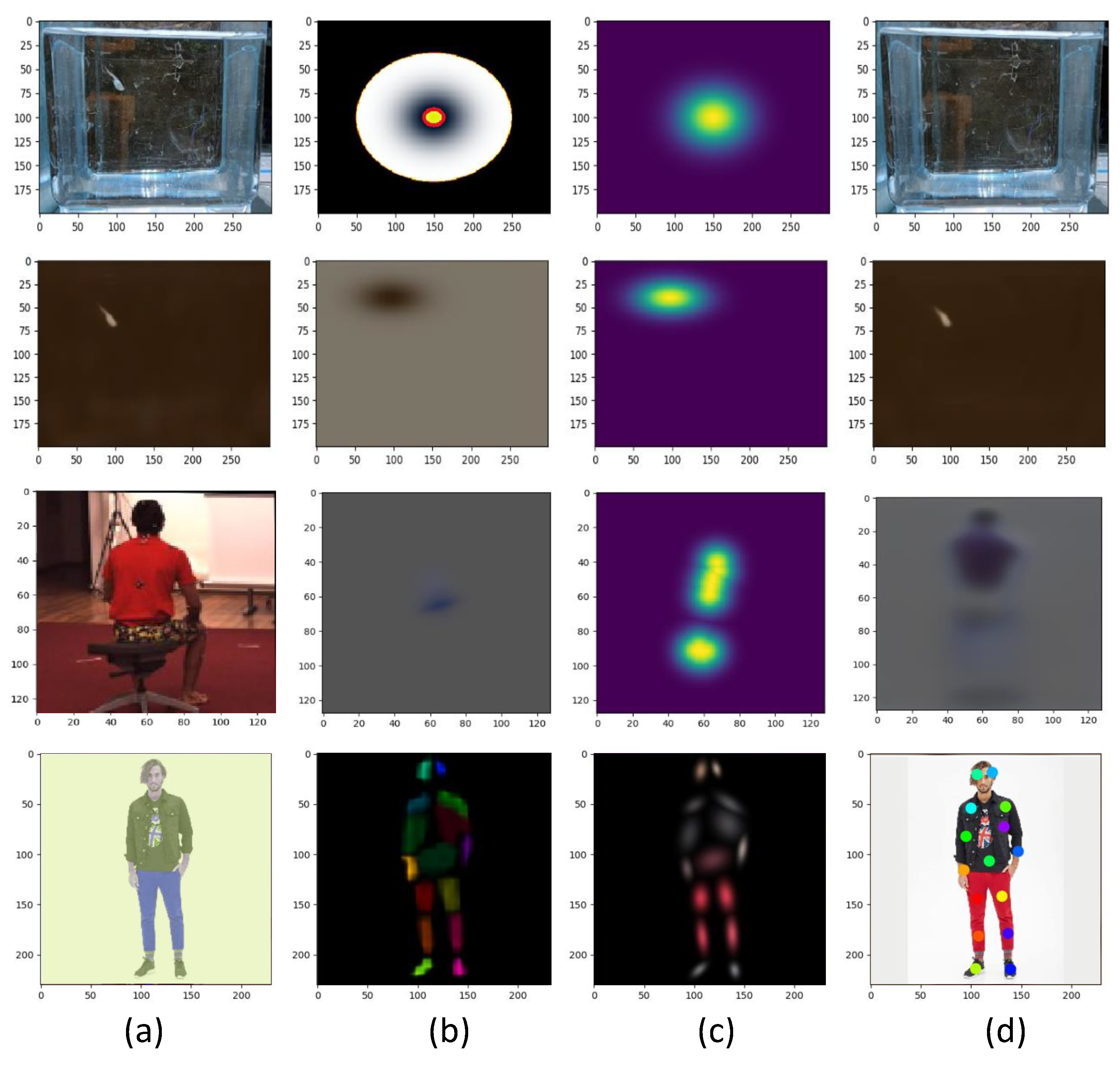
• The SynNet method [26] uses OpenPose [30], which outputs a heatmap for each human body joint. It is similar to our proposed method that disentangles the image into parts, but does not generalize to general objects since the detector is trained on humans. By contrast, our ST module precisely estimates the salient points of the non-human object that are shown in Figure 4, which showcases the better generalization of our self-supervised approach.
• To facilitate a fair comparison of the SYN network architecture and our synchronization network, we use heatmaps generated by ST as input to train SynNet. We call this combination with our self-supervised part maps (SynNet+ST). It improves the accuracy of SynNet+OpenPose by 10.9%. Moreover, our full method attains a higher offset prediction accuracy, which shows that operating on explicit 2D positions and their trajectories is better than using discretized heatmaps as input (as used in SynNet+ST).
• In addition, we also compare against the GTpoint+MD and PE methods. The former is a strong baseline that uses the ground truth 2D coordinates instead of estimated ones to compute the matrix diagonal similarity. These GT positions are the central positions of the cube and sphere in Blender, projected onto the image plane. The latter uses positional encoding (PE) [72] on the ground truth 2D positions. These are projections of the 2D point onto sinusoidal waves of different frequencies, providing a smooth and hierarchical encoding of positions. We try using the PE strategy before the coordinate feature is fed to MD to make a comparison with our absolutely coordinate feature in STMD, the proposed STMD+MSE surpasses them by a large margin, which infers that using the original absolute position generated by the ST stage is better than Blender and PE in MD stage.
• Finally, we also compare with some baselines using different downsampling rates. The results in Table 1 show that the testing accuracy is increased while the SynError is decreased, which infers that the downsampling strategy improves accuracy by sacrificing SynError. Moreover, the proposed STMD method outperforms all the downsampling cases of other baselines, and the proposed ST module can improve the MD module with the GT coordinates from Blender (GTpoint+MD) with 9.0% test-d0, which validates the superiority of our method.

4.5. Results on Fish Dataset

The Fish dataset is challenging, as the fish is small compared to the entire image, has a similar color to the fish tank glass wall, and has a smooth rather than crisp appearance. These factors pose difficulties for the style transfer module. To alleviate the impact of the changing background, we compute the background as the median pixel value over 100 frames spaced over each video. This background is subtracted from each frame. Note that the low color contrast leads to remaining artifacts. However, as the following analysis shows, the entire pipeline is robust to slight inaccuracies in object detection. We refer to background subtracted variants with the addition (Sub) to the network name.

The visualization of the results obtained by the ST model is shown in Figure 5. Without background subtractions, the localization fails (Row 1). After extracting the foreground and feeding these cleaned images to the ST stage, we obtain more precise salient points that track the fish well (Row 2). As shown in

Table 2. Results of STMD with subtraction on the Fish dataset with different epochs of ST. The number in the bracket after STMD is the training epochs of the ST stage.

Method	test-d0 (%)	test-d1 (%)	test-d2 (%)	test-d3 (%)	SynError ↓
TCC (ds = 1) [37]	16.4	25.2	34.1	45.1	0.1042
STMD (1)	18.4	33.9	38.5	47.7	0.1581
LAMV (ds = 1) [71]	21.0	35.1	49.5	64.1	0.0864
TCC (ds = 2)	28.3	36.7	47.4	58.9	0.1646
LAMV (ds = 2)	30.7	43.2	56.1	68.5	0.1512
STMD (50)	34.9	64.2	64.2	70.6	0.1248
TCC (ds = 3)	35.0	47.8	60.2	73.0	0.1785
LAMV (ds = 3)	38.4	49.8	60.8	71.9	0.2013
LAMV (ds = 4)	44.8	54.7	64.7	74.8	0.2410
TCC (ds = 4)	48.7	58.1	69.4	79.7	0.1766
STMD (100)	78.9	78.9	88.1	91.7	0.0229
STMD (150)	88.1	92.4	92.6	92.7	0.0119
STMD (190)	94.5	98.1	98.3	99.1	0.0080

, the test-d0 reaches 94.5% when ST epoch = 190. Moreover, as shown in Figure 6a, we also plot the tendency curve to illustrate the performance of MD in 190 ST epochs. To better display the result, we use the moving average result in Figure 6a, the moving window size is 25. All the curves gain a large margin as the epoch increases, which validates the robustness of our method.

4.6. Results on Human36M Dataset

The video synchronization results are shown in

Table 3. Results on the Human36M dataset; 0–3 represent the testing accuracy of the respective predicted offset, SynNet uses OpenPose [30] to extract the pose feature as [26], and “PE” denotes the variant using positional encoding to represent 2D object positions [72].

Method	test-d0 (%)	test-d1 (%)	test-d2 (%)	test-d3 (%)	SynError ↓
SynNet [26]	14.5	23.5	38.0	47.5	0.3038
PE [72]	20.9	40.5	55.7	66.0	0.2055
TCC (ds = 1) [37]	28.4	40.2	53.7	63.4	0.3154
PE (sub)	31.1	45.3	59.0	73.3	0.2000
TCC (ds = 2)	38.3	50.0	59.6	71.0	0.3400
TCC (ds = 3)	45.6	54.4	65.3	72.5	0.3801
TCC (ds = 4)	51.0	61.4	68.0	75.6	1.6402
LAMV (ds = 1) [71]	54.7	60.7	66.2	69.9	0.2226
LAMV (ds = 4)	62.9	64.9	66.6	69.7	1.1553
LAMV (ds = 2)	66.8	70.9	74.3	77.2	0.3763
LAMV (ds = 3)	67.9	70.0	72.0	73.7	0.7385
STMD	78.3	82.6	85.7	86.3	0.0963
STMD (sub)	88.2	93.1	93.3	94.4	0.0485

. The testing accuracy was computed for the best-performing snapshot computed over 50 training epochs. The best accuracy of test-d0 reached 88.2%. The proposed method scored highest, with the same order as observed for the simpler Cube&Sphere dataset.

We compared the performance of the original image and the post-procession of subtraction (Sub) for the STMD method. There was a leap in improvement from the subtraction to the proposed method, by 9.9% for the test-d0 accuracy. This result validates the visual improvements shown in Figure 5 (third vs. fourth row), leading to the ST module focusing more on the moving object rather than rich textures in the background.

In addition, we conduct experiments to monitor the training curves of the proposed model. We plot the synchronized performance with different epochs for both the ST and MD modules.

Moreover, to test the effectiveness of the ST module and observe the trend in more detail, we plotted the first 30 epochs with a moving average of window size 10. As shown in Figure 6b, both the training and testing accuracy curves keep increasing with more training epochs, which validates the effectiveness of the ST training model.

We also evaluate the training curve over 50 epochs of the MD module in Figure 6c with a moving average window size of 25. To validate the robustness of the proposed STMD method, we use the ST model without subtraction to evaluate. The test-d0 accuracy is the most important indicator in video synchronization, yet the others are auxiliary to analyze consistency. Figure 6c plots the corresponding testing results. All metrics kept increasing with the number of epochs, which validates the robust transfer ability from training to testing.

4.7. Limitations

Figure 7 shows some failure cases observed during our experiments on the three datasets. Given two unsynchronized input clips, we predict the offsets and adjust them to synchronize. From Figure 7 and others inspected, the wrong predictions mainly occurred in the hard case of large offsets or existing severe occlusions, e.g., Figure 7a. It violates the assumption that a pair of views should be composed of the same objects in Section 3.1, which is hard to predict the precise frame offset because salient features are missing. We observe that our method still predicts the correct direction of offset in all the above hard cases, which validates that the proposed STMD method can still work within a certain margin of synchronization error.

4.8. STMD Method for the UAV Remote Sensing Image Mosaic

To validate the practical performance of the proposed video synchronization method, we apply it on the remote sensing applications of reconstructing the panorama of the aerial image taken by an Unmanned Aerial Vehicle (UAV). Such UAV remote sensing image mosaic technique plays important roles in many fields such as forestry, agriculture, and soil resources. In this setting, the proposed video synchronization method can provide useful matching information of salient points among multiple views by self-supervised scene decomposition, as shown in Figure 8. The left three image sequences were collected by an UAV with minor time offsets; therefore, there were many overlapping areas among the images, which is closely related to multi-view video synchronization under the moving cameras. Hence, the salient positions between the pairwise perspective can be captured and matched by the style transfer module in our video synchronization method. Based on these common features, the images can be spliced together to a wider view. In this way, the proposed video synchronization can be used in image mosaic with a certain time range of slight offsets to obtain the panoramic aerial image, which is illustrated in Figure 8d, by self-supervised learning the correspondence among salient points effectively.

5. Conclusions

This paper presents STMD, an efficient two-stage video synchronization method that can easily be adapted to new domains by learning domain-adaptive motion features from multiple views without requiring any spatial annotation. The gains in synchronization accuracy are due to the joint contribution of this self-supervised pre-processing, and a matrix diagonal module-based network architecture is tailored to predict the temporal offset from 2D trajectories. Our experiments show the superiority of our method. It can be generalized to practical settings such as remote sensing application. It is worth mentioning that this paper treats video synchronization as a classification problem, it selects on the frame level and does not include the sub-frame level synchronization.

In future, there are three directions that can be conducted to expand the work. At first, more complicated fields such as the fish swarm scenario can be considered in the synchronization task. Furthermore, this paper mainly proposes a 2D video synchronization work, we will try to use the 3D trajectory to model the perspective and handle the occlusion problem. Finally, more precise methods can be proposed to take the synchronization of the sub-frame level into account, which makes the work more practical to the real application.