MSSF: A Novel Mutual Structure Shift Feature for Removing Incorrect Keypoint Correspondences between Images
Abstract
:1. Introduction
2. Related Work
2.1. Traditional Methods
2.2. Learning-Based Methods
3. The Proposed Method
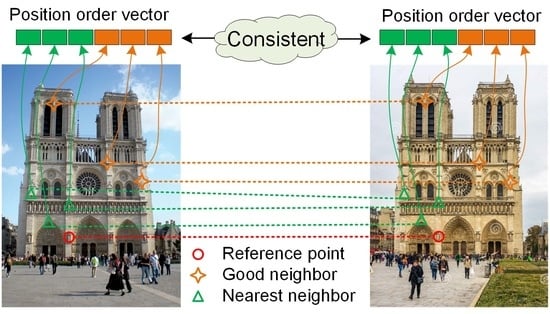
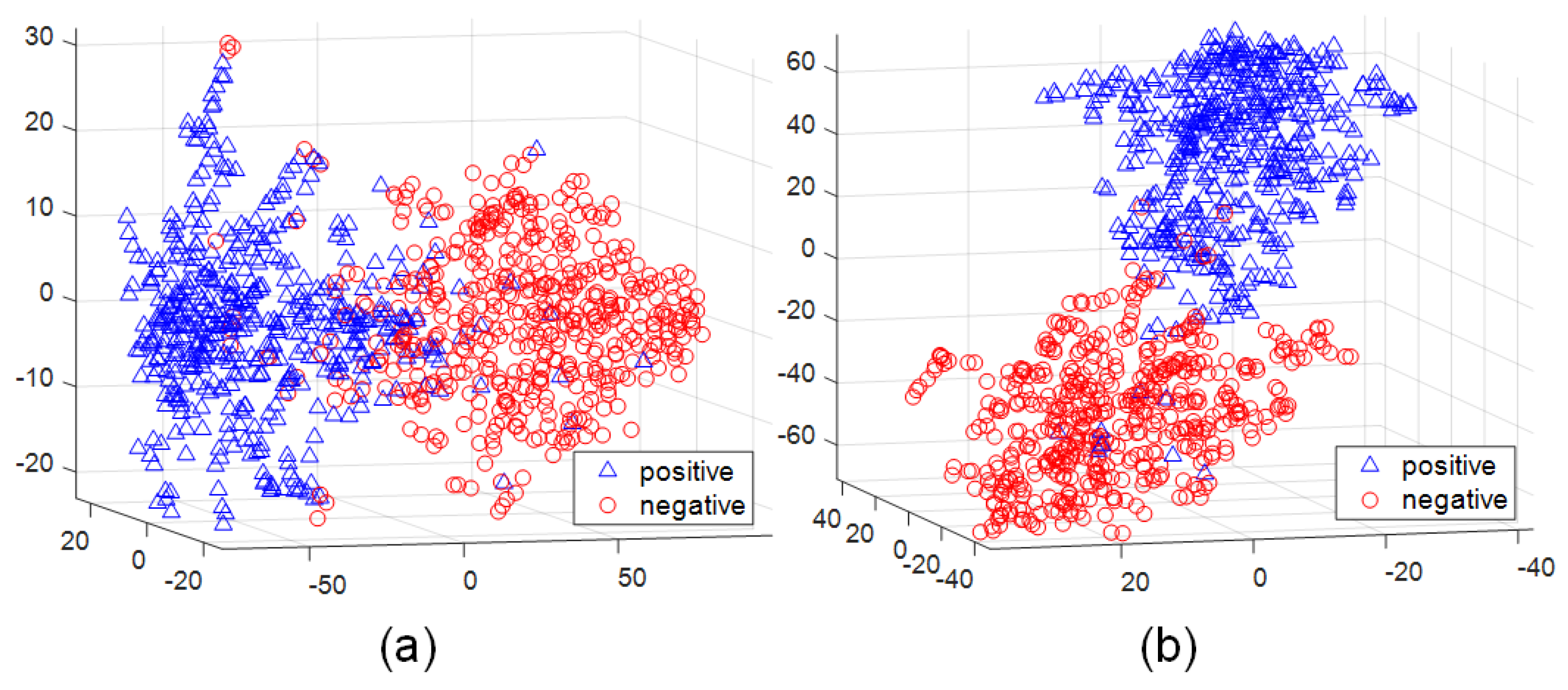
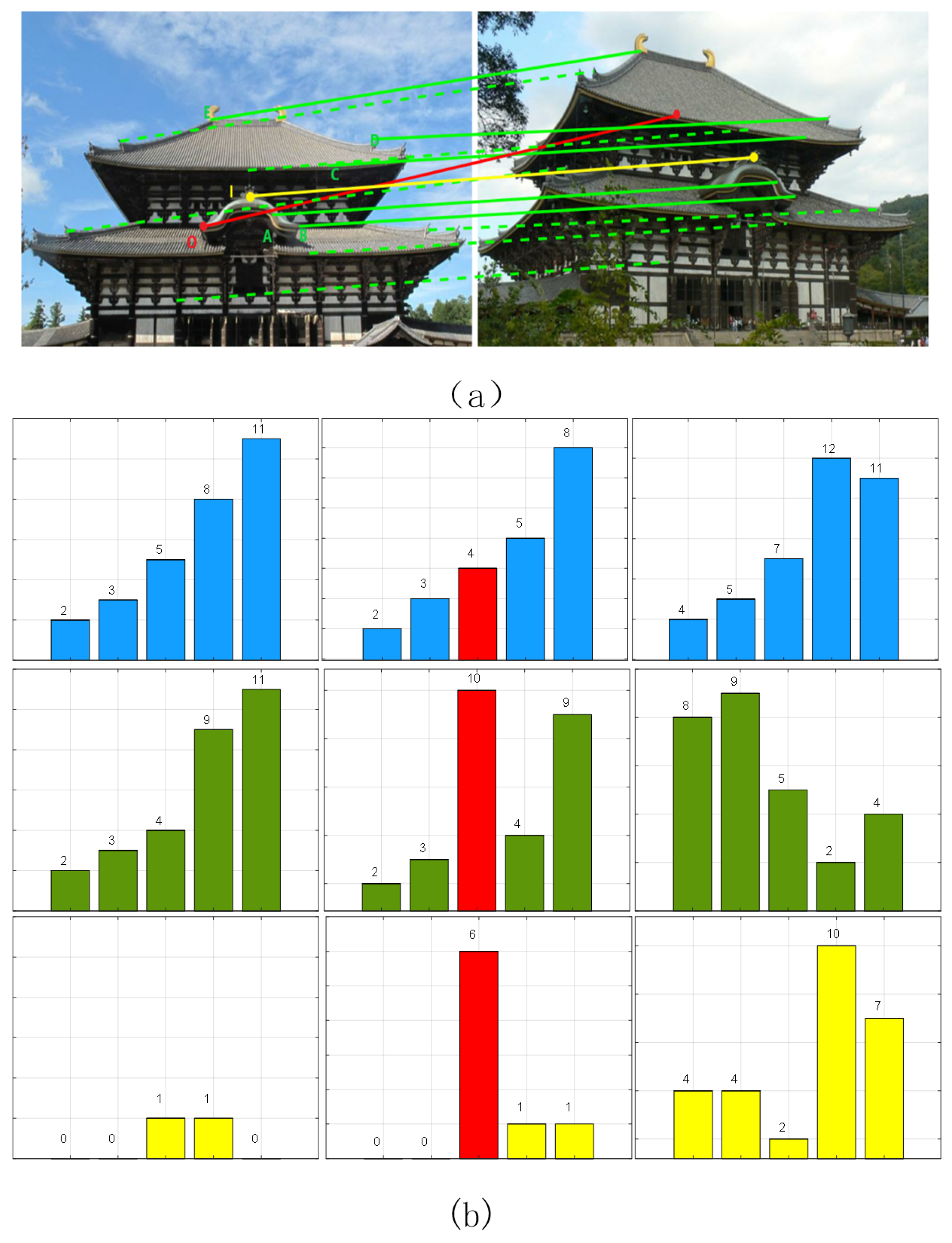
3.1. The Mutual Structure Shift Feature
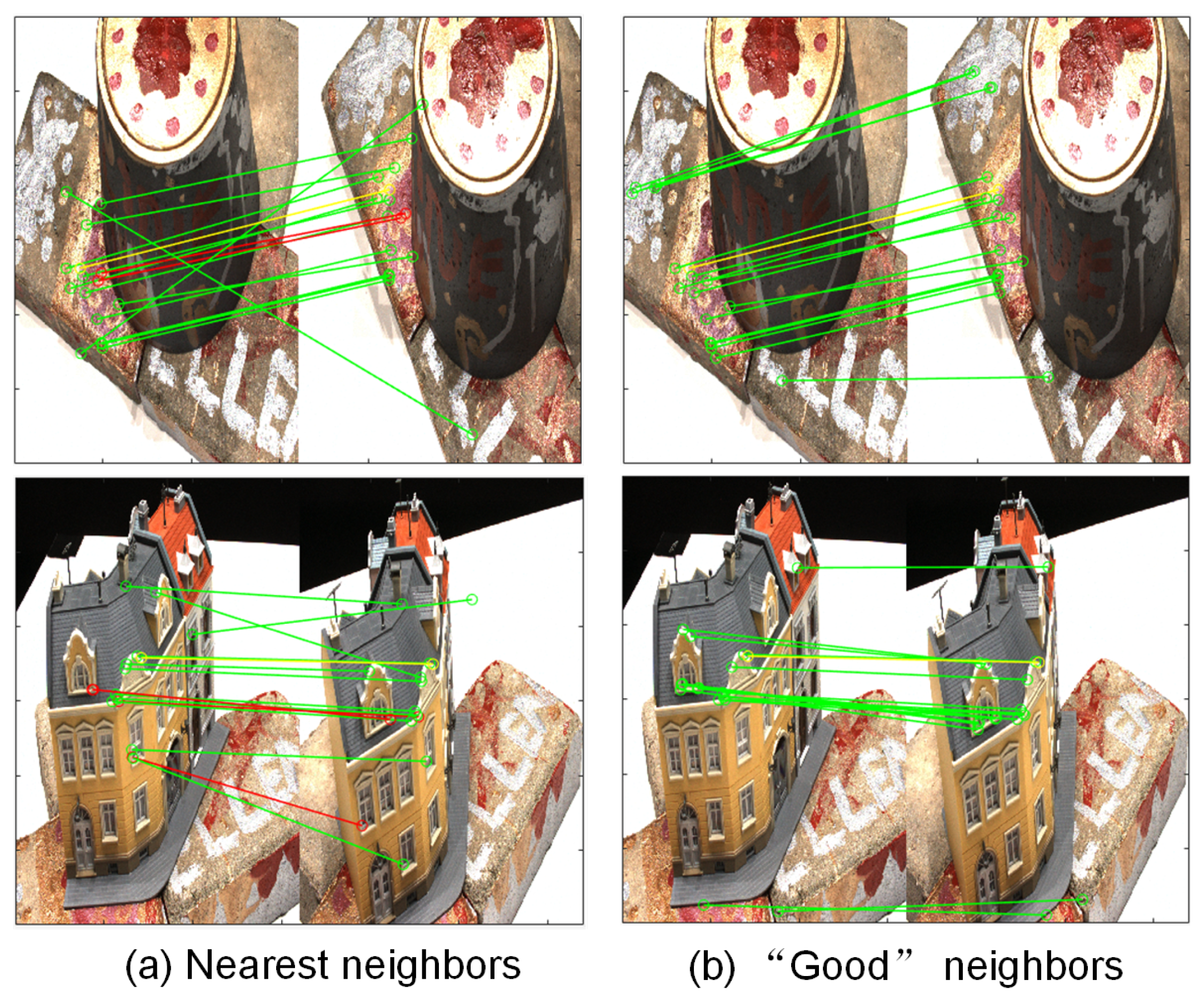
3.2. Neighbor Selection: Nearest Neighbors and “Good” Neighbors
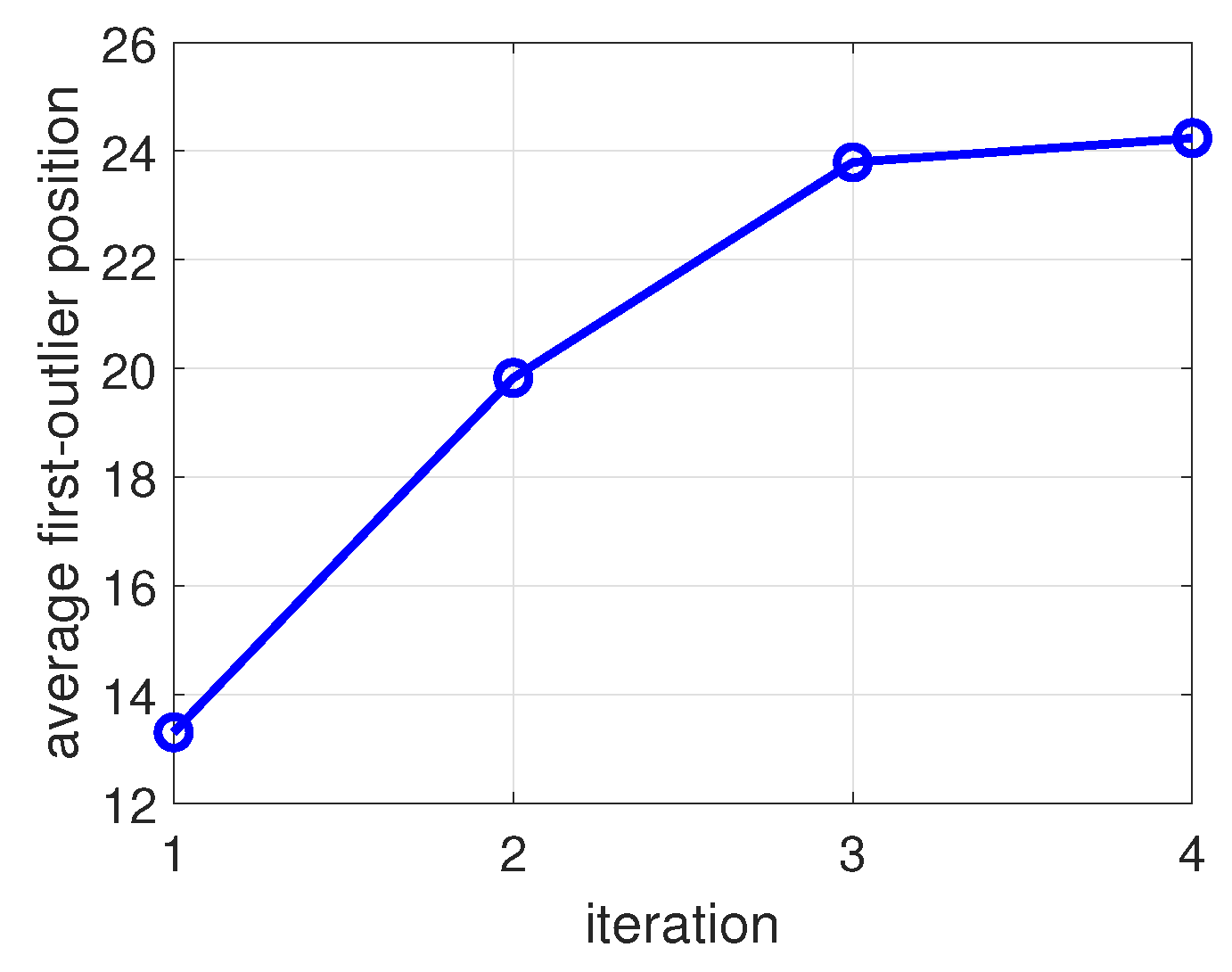
3.3. Neighbor Weighting Strategy
4. Experiments
4.1. Datasets and Settings
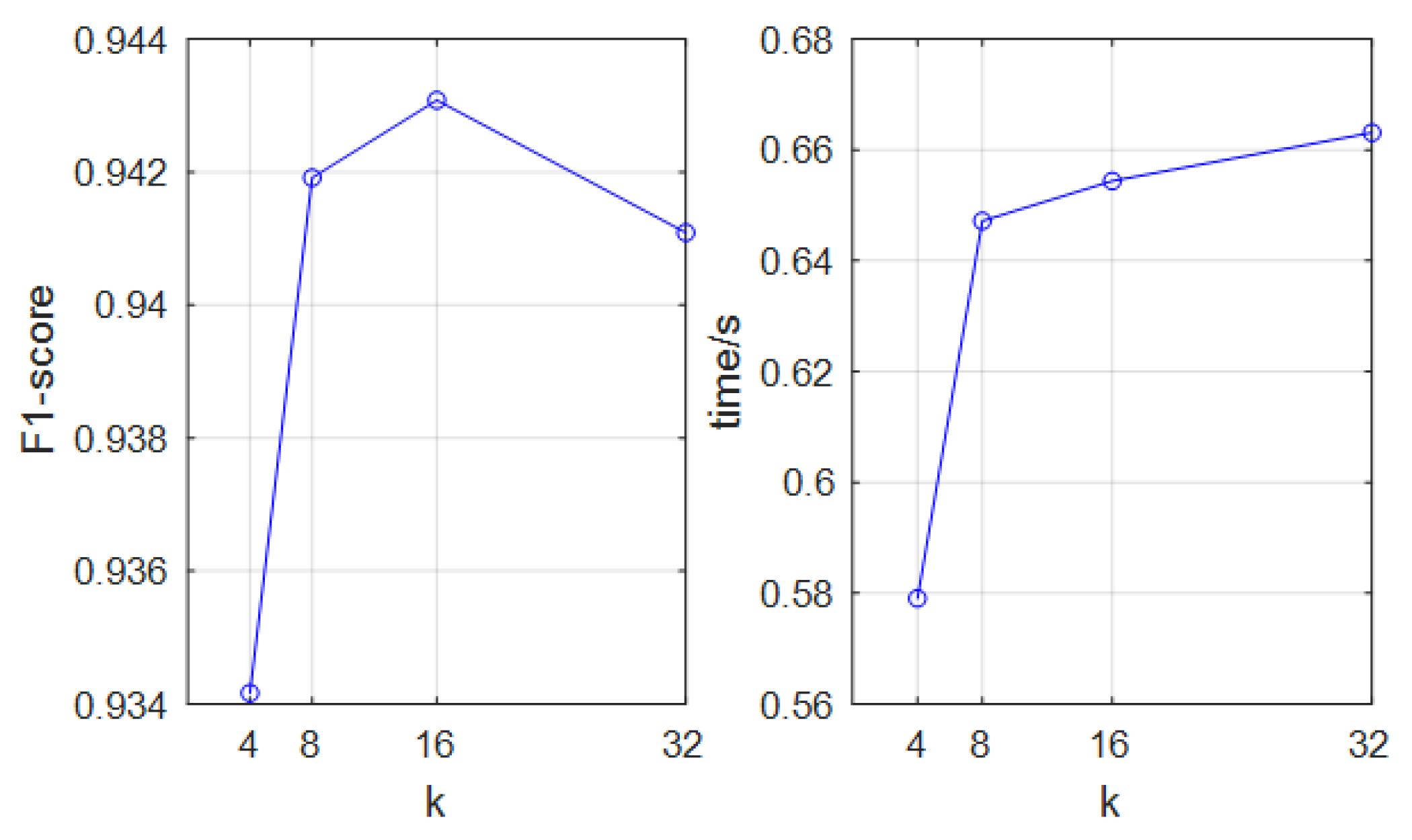
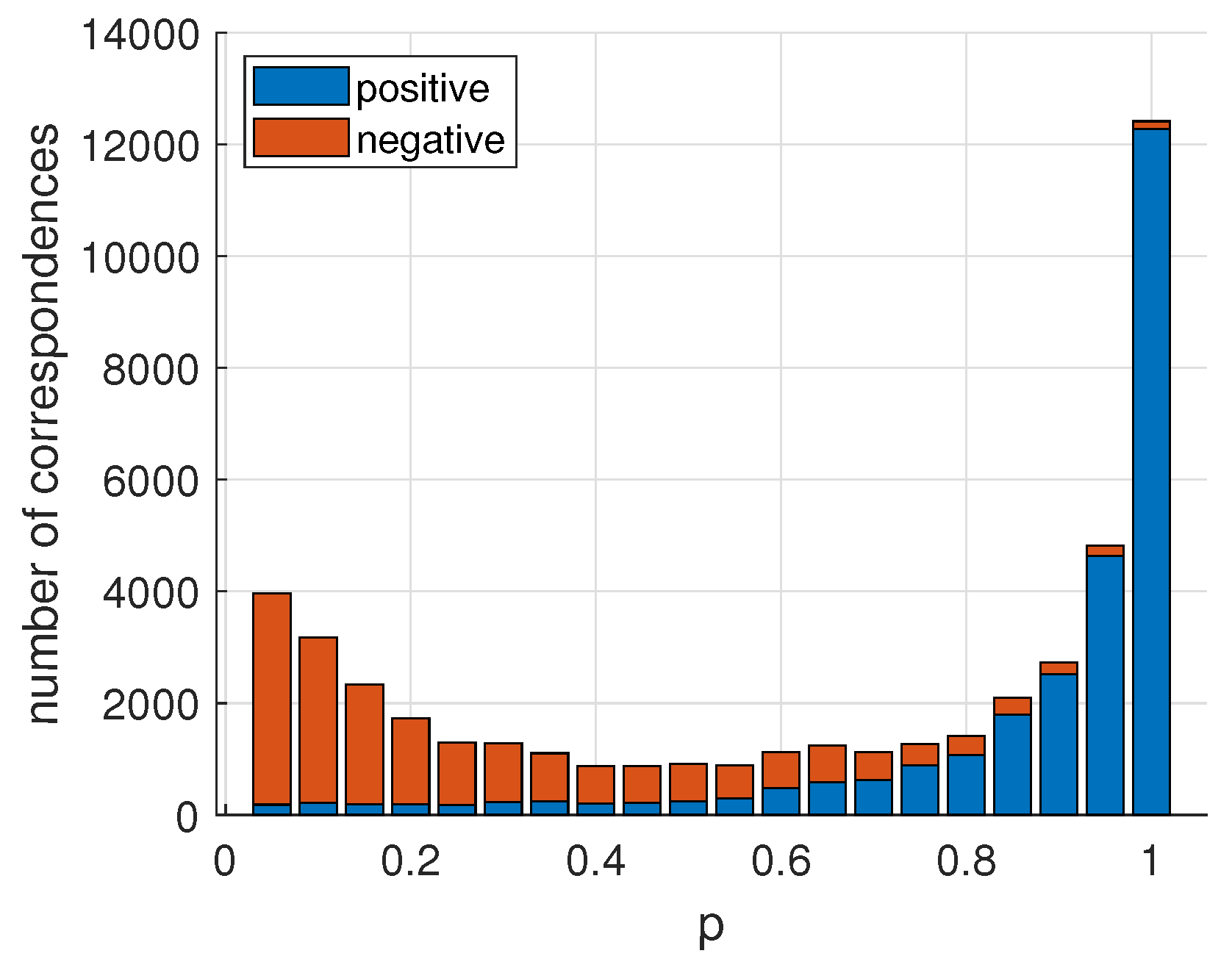
4.2. Parameter Analysis
4.3. Ablation Study
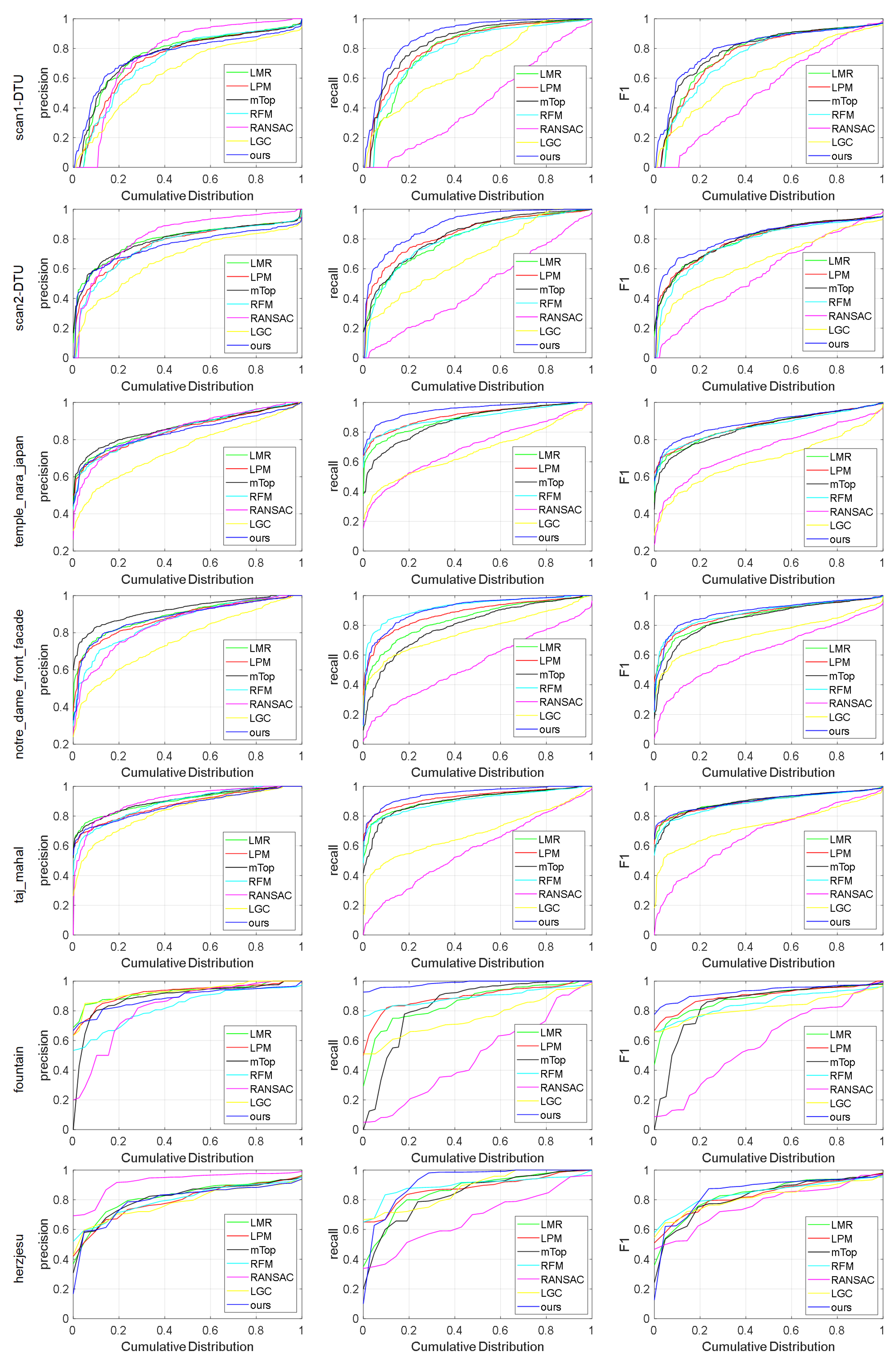
4.4. Raw Matching Quality Evaluation
4.5. Pose Estimation Evaluation
4.6. Application on UAV Images
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ma, J.; Jiang, X.; Fan, A.; Jiang, J.; Yan, J. Image Matching from Handcrafted to Deep Features: A Survey. Int. J. Comput. Vis. 2020, 129, 23–79. [Google Scholar] [CrossRef]
- Ma, X.; Xu, S.; Zhou, J.; Yang, Q.; Yang, Y.; Yang, K.; Ong, S.H. Point set registration with mixture framework and variational inference. Pattern Recognit. 2020, 104, 107345. [Google Scholar] [CrossRef]
- He, Q.; Zhou, J.; Xu, S.; Yang, Y.; Yu, R.; Liu, Y. Adaptive Hierarchical Probabilistic Model Using Structured Variational Inference for Point Set Registration. IEEE Trans. Fuzzy Syst. 2020, 28, 2784–2798. [Google Scholar] [CrossRef]
- Wang, T.; Jiang, Z.; Yan, J. Clustering-aware Multiple Graph Matching via Decayed Pairwise Matching Composition. In Proceedings of the Thirty-Fourth AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020. [Google Scholar]
- Wang, R.; Yan, J.; Yang, X. Combinatorial Learning of Robust Deep Graph Matching: An Embedding based Approach. IEEE Trans. Pattern Anal. Mach. Intell. 2020. early access. [Google Scholar] [CrossRef]
- Min, J.; Lee, J.; Ponce, J.; Cho, M. Hyperpixel flow: Semantic correspondence with multi-layer neural features. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3395–3404. [Google Scholar]
- Tang, L.; Deng, Y.; Ma, Y.; Huang, J.; Ma, J. SuperFusion: A Versatile Image Registration and Fusion Network with Semantic Awareness. IEEE CAA J. Autom. Sin. 2022, 9, 2121–2137. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Gool, L.V. SURF: Speeded Up Robust Features. In Proceedings of the European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2006; Volume 3951, pp. 404–417. [Google Scholar] [CrossRef]
- Calonder, M.; Lepetit, V.; Strecha, C.; Fua, P. BRIEF: Binary Robust Independent Elementary Features. In Proceedings of the European Conference on Computer Vision, Heraklion, Greece, 5–11 September 2010; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2010; Volume 6314, pp. 778–792. [Google Scholar] [CrossRef]
- Leutenegger, S.; Chli, M.; Siegwart, R. BRISK: Binary Robust invariant scalable keypoints. In Proceedings of the IEEE International Conference on Computer Vision, Washington, DC, USA, 20–25 June 2011; pp. 2548–2555. [Google Scholar] [CrossRef]
- Tian, Y.; Fan, B.; Wu, F. L2-Net: Deep Learning of Discriminative Patch Descriptor in Euclidean Space. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6128–6136. [Google Scholar] [CrossRef]
- Mishchuk, A.; Mishkin, D.; Radenovic, F.; Matas, J. Working hard to know your neighbor’s margins: Local descriptor learning loss. In Proceedings of the Annual Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4826–4837. [Google Scholar]
- Dusmanu, M.; Rocco, I.; Pajdla, T.; Pollefeys, M.; Sivic, J.; Torii, A.; Sattler, T. D2-Net: A Trainable CNN for Joint Description and Detection of Local Features. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Computer Vision Foundation, Long Beach, CA, USA, 15–20 June 2019; pp. 8092–8101. [Google Scholar] [CrossRef]
- Tian, Y.; Yu, X.; Fan, B.; Wu, F.; Heijnen, H.; Balntas, V. SOSNet: Second Order Similarity Regularization for Local Descriptor Learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR 2019), Long Beach, CA, USA, 16–20 June 2019; pp. 11016–11025. [Google Scholar]
- Wang, Q.; Zhou, X.; Hariharan, B.; Snavely, N. Learning Feature Descriptors Using Camera Pose Supervision. In Proceedings of the ECCV, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; Volume 12346, pp. 757–774. [Google Scholar]
- Ranftl, R.; Koltun, V. Deep fundamental matrix estimation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 284–299. [Google Scholar]
- Ma, J.; Zhao, J.; Tian, J.; Bai, X.; Tu, Z. Regularized vector field learning with sparse approximation for mismatch removal. Pattern Recognit. 2013, 46, 3519–3532. [Google Scholar] [CrossRef]
- Ma, J.; Zhao, J.; Tian, J.; Yuille, A.L.; Tu, Z. Robust point matching via vector field consensus. IEEE Trans. Image Process. 2014, 23, 1706–1721. [Google Scholar] [CrossRef]
- Ma, J.; Wu, J.; Zhao, J.; Jiang, J.; Zhou, H.; Sheng, Q.Z. Nonrigid point set registration with robust transformation learning under manifold regularization. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 3584–3597. [Google Scholar] [CrossRef]
- Liu, H.; Yan, S. Common visual pattern discovery via spatially coherent correspondences. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 1609–1616. [Google Scholar]
- Lipman, Y.; Yagev, S.; Poranne, R.; Jacobs, D.W.; Basri, R. Feature matching with bounded distortion. ACM Trans. Graph. (TOG) 2014, 33, 1–14. [Google Scholar] [CrossRef]
- Ma, J.; Zhao, J.; Jiang, J.; Zhou, H.; Guo, X. Locality preserving matching. Int. J. Comput. Vis. 2019, 127, 512–531. [Google Scholar] [CrossRef]
- Bian, J.; Lin, W.Y.; Matsushita, Y.; Yeung, S.K.; Nguyen, T.D.; Cheng, M.M. Gms: Grid-based motion statistics for fast, ultra-robust feature correspondence. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Juan, PR, USA, 17–19 June 2017; pp. 4181–4190. [Google Scholar]
- Liu, H.; Zheng, C.; Li, D.; Zhang, Z.; Lin, K.; Shen, X.; Xiong, N.N.; Wang, J. Multi-perspective social recommendation method with graph representation learning. Neurocomputing 2022, 468, 469–481. [Google Scholar] [CrossRef]
- Lhuillier, M.; Quan, L. Image Interpolation by Joint View Triangulation. In Proceedings of the 1999 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Fort Collins, CO, USA, 23–25 June 1999; pp. 2139–2145. [Google Scholar]
- Lee, I.C.; He, S.; Lai, P.L.; Yilmaz, A. BUILDING Point Grouping Using View-Geometry Relations. In Proceedings of the ASPRS 2010 Annual Conference, San Diego, CA, USA, 26–30 April 2010. [Google Scholar]
- Takimoto, R.Y.; Challella das Neves, A.; de Castro Martins, T.; Takase, F.K.; de Sales Guerra Tsuzuki, M. Automatic Epipolar Geometry Recovery Using Two Images. IFAC Proc. Vol. 2011, 44, 3980–3985. [Google Scholar] [CrossRef]
- Moo Yi, K.; Trulls, E.; Ono, Y.; Lepetit, V.; Salzmann, M.; Fua, P. Learning to find good correspondences. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2666–2674. [Google Scholar]
- Ma, J.; Jiang, X.; Jiang, J.; Zhao, J.; Guo, X. LMR: Learning a two-class classifier for mismatch removal. IEEE Trans. Image Process. 2019, 28, 4045–4059. [Google Scholar] [CrossRef]
- Zhao, C.; Cao, Z.; Li, C.; Li, X.; Yang, J. NM-Net: Mining reliable neighbors for robust feature correspondences. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 215–224. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Chum, O.; Matas, J. Matching with PROSAC-progressive sample consensus. In Proceedings of the 2005 IEEE computer society conference on computer vision and pattern recognition (CVPR’05), San Diego, CA, USA, 20–26 June 2005; Volume 1, pp. 220–226. [Google Scholar]
- Tran, Q.H.; Chin, T.J.; Carneiro, G.; Brown, M.S.; Suter, D. In defence of RANSAC for outlier rejection in deformable registration. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 274–287. [Google Scholar]
- Li, X.; Hu, Z. Rejecting mismatches by correspondence function. Int. J. Comput. Vis. 2010, 89, 1–17. [Google Scholar] [CrossRef]
- Ma, J.; Zhou, H.; Zhao, J.; Gao, Y.; Jiang, J.; Tian, J. Robust feature matching for remote sensing image registration via locally linear transforming. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6469–6481. [Google Scholar] [CrossRef]
- Lin, W.Y.; Wang, F.; Cheng, M.M.; Yeung, S.K.; Torr, P.H.; Do, M.N.; Lu, J. CODE: Coherence based decision boundaries for feature correspondence. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 34–47. [Google Scholar] [CrossRef]
- Jiang, X.; Ma, J.; Jiang, J.; Guo, X. Robust feature matching using spatial clustering with heavy outliers. IEEE Trans. Image Process. 2019, 29, 736–746. [Google Scholar] [CrossRef]
- Jiang, X.; Jiang, J.; Fan, A.; Wang, Z.; Ma, J. Multiscale locality and rank preservation for robust feature matching of remote sensing images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6462–6472. [Google Scholar] [CrossRef]
- Zhao, C.; Ge, Y.; Zhu, F.; Zhao, R.; Li, H.; Salzmann, M. Progressive Correspondence Pruning by Consensus Learning. In Proceedings of the ICCV, Montreal, BC, Canada, 11–17 October 2021; pp. 6444–6453. [Google Scholar]
- Zhang, J.; Sun, D.; Luo, Z.; Yao, A.; Chen, H.; Zhou, L.; Shen, T.; Chen, Y.; Quan, L.; Liao, H. OANet: Learning Two-View Correspondences and Geometry Using Order-Aware Network. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 3110–3122. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, L.; Lin, C.; Dong, Z.; Wang, W. Learnable Motion Coherence for Correspondence Pruning. In Proceedings of the CVPR. Computer Vision Foundation, Virtual, 19–25 June 2021; pp. 3237–3246. [Google Scholar]
- Sun, W.; Jiang, W.; Trulls, E.; Tagliasacchi, A.; Yi, K.M. ACNe: Attentive Context Normalization for Robust Permutation-Equivariant Learning. In Proceedings of the CVPR. Computer Vision Foundation, Seattle, WA, USA, 14–19 June 2020; pp. 11283–11292. [Google Scholar]
- Aanæs, H.; Jensen, R.R.; Vogiatzis, G.; Tola, E.; Dahl, A.B. Large-Scale Data for Multiple-View Stereopsis. Int. J. Comput. Vis. 2016, 120, 153–168. [Google Scholar] [CrossRef]
- Tola, E.; Lepetit, V.; Fua, P. DAISY: An Efficient Dense Descriptor Applied to Wide-Baseline Stereo. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 815–830. [Google Scholar] [CrossRef]
- Jin, Y.; Mishkin, D.; Mishchuk, A.; Matas, J.; Fua, P.; Yi, K.M.; Trulls, E. Image Matching Across Wide Baselines: From Paper to Practice. Int. J. Comput. Vis. 2021, 129, 517–547. [Google Scholar] [CrossRef]
- Schönberger, J.L.; Frahm, J. Structure-from-Motion Revisited. In Proceedings of the CVPR, Las Vegas, NV, USA, 27–30 June 2016; pp. 4104–4113. [Google Scholar]
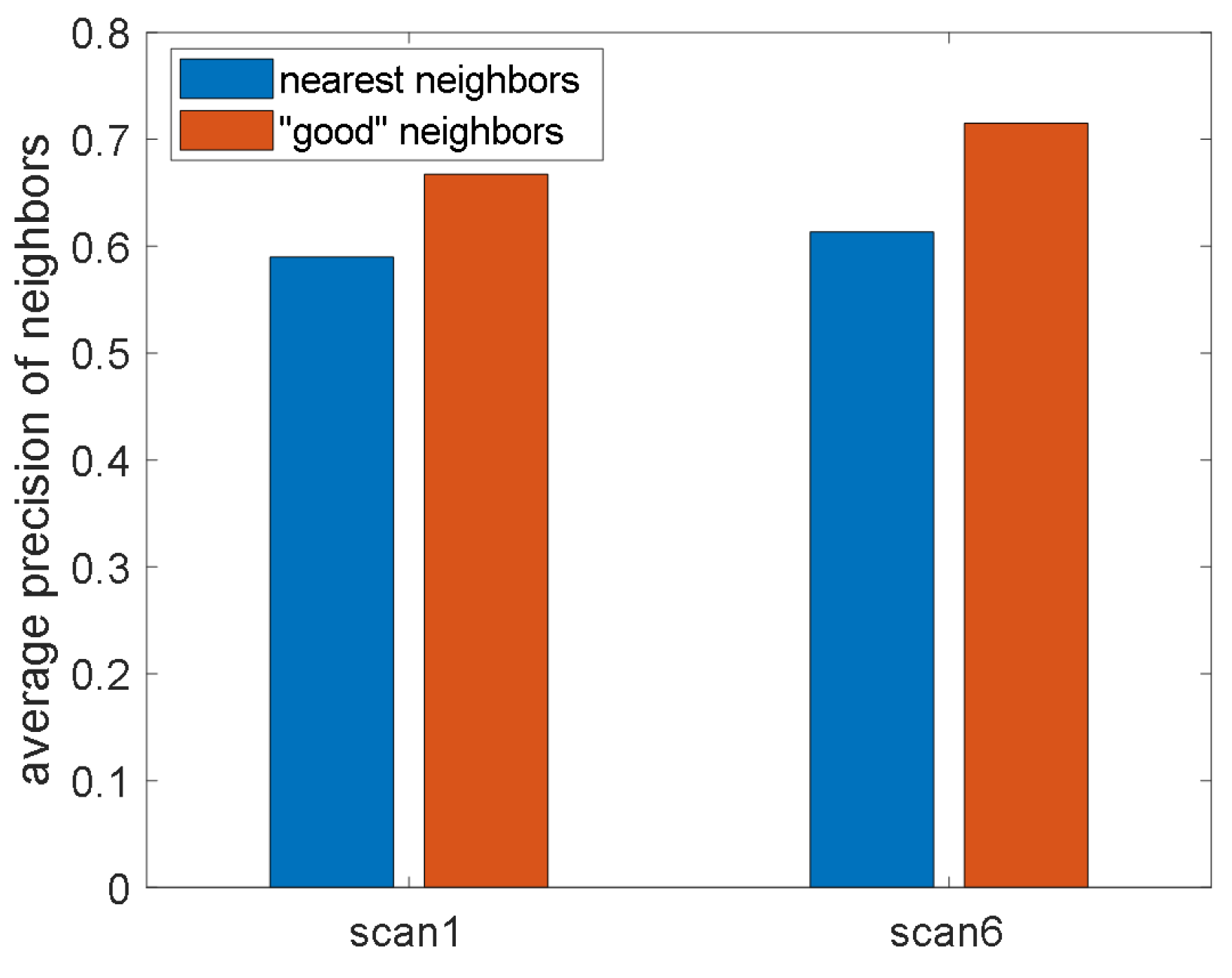
| Nearest Neighbors | “Good” Neighbors | Scan1 | Scan6 |
|---|---|---|---|
| ✔ | - | 75.43 | 80.23 |
| - | ✔ | 78.17 | 81.38 |
| ✔ | ✔ | 78.98 | 81.98 |
| Scene | Scan1 | Scan6 |
|---|---|---|
| w/o Mutual | 79.23 | 81.77 |
| w/ Mutual | 79.98 | 82.13 |
| Threshold | LMR | LPM | mTOP | RFM | RANSAC | LGC | Ours |
|---|---|---|---|---|---|---|---|
| 0.5 | 82.62 | 82.10 | 81.88 | 78.65 | 71.91 | 75.23 | 83.52 (+0.9) |
| 1 | 84.59 | 83.90 | 83.72 | 80.54 | 72.39 | 77.18 | 86.01 (+1.42) |
| 1.5 | 85.30 | 84.61 | 84.45 | 81.42 | 72.37 | 77.83 | 86.97 (+1.67) |
| 2 | 86.02 | 85.36 | 85.20 | 82.17 | 72.27 | 78.38 | 87.86 (+1.84) |
| 2.5 | 86.83 | 85.99 | 85.92 | 83.17 | 71.97 | 79.24 | 88.83 (+2.0) |
| 3 | 87.36 | 86.50 | 86.37 | 83.71 | 71.66 | 79.55 | 89.34 (+1.98) |
| 3.5 | 87.69 | 86.85 | 86.76 | 84.17 | 71.34 | 79.96 | 89.75 (+2.06) |
| 4 | 87.87 | 87.07 | 86.97 | 84.50 | 71.04 | 80.23 | 90.07 (+2.2) |
| Method | Fountain | Herzjesu |
|---|---|---|
| LMR | 72.50/70.00 | 90.91/90.91 |
| LPM | 65.00/65.00 | 86.36/86.36 |
| mTOP | 70.00/70.00 | 86.36/86.36 |
| RFM | 67.50/67.50 | 86.36/86.36 |
| RANSAC | 57.50/55.00 | 77.27/86.36 |
| LGC | 57.50/55.00 | 86.36/86.36 |
| Ours | 75.00/75.00 (+2.5/+5.0) | 95.45/95.45 (+4.54/+4.54) |
| Method | trevi_fountain | grand_place_brussels | hagia_sophia_interior | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Easy | Moderate | Hard | Easy | Moderate | Hard | Easy | Moderate | Hard | |
| LMR | 98.0/88.0 | 97.0/90.0 | 92.0/88.0 | 95.0/61.0 | 84.0/59.0 | 78.0/63.0 | 96.0/35.0 | 88.0/60.0 | 85.0/77.0 |
| LPM | 98.0/83.0 | 95.0/86.0 | 93.0/90.0 | 95.0/64.0 | 88.0/55.0 | 81.0/60.0 | 98.0/35.0 | 91.0/62.0 | 85.0/54.0 |
| mTOP | 98.0/89.0 | 95.0/87.0 | 93.0/87.0 | 93.0/61.0 | 84.0/49.0 | 78.0/55.0 | 98.0/35.0 | 91.0/60.0 | 86.0/75.0 |
| RFM | 98.0/85.0 | 87.0/81.0 | 90.0/83.0 | 93.0/56.0 | 81.0/52.0 | 76.0/64.0 | 96.0/35.0 | 89.0/59.0 | 84.0/76.0 |
| RANSAC | 96.0/81.0 | 87.0/74.0 | 82.0/80.0 | 84.0/34.0 | 72.0/42.0 | 64.0/46.0 | 87.0/27.0 | 79.0/50.0 | 55.0/56.0 |
| LGC | 92.0/77.0 | 78.0/68.0 | 76.0/73.0 | 90.0/49.0 | 76.0/47.0 | 64.0/48.0 | 94.0/30.0 | 87.0/49.0 | 64.0/56.0 |
| Ours | 100.0/92.0 (+2.0/+3.0) | 99.0/92.0 (+2.0/+2.0) | 95.0/91.0 (+2.0/+1.0) | 96.0/66.0 (+1.0/+2.0) | 91.0/63.0 (+3.0/+4.0) | 84.0/73.0 (+3.0/+9.0) | 99.0/39.0 (+1.0/+4.0) | 95.0/64.0 (+4.0/+2.0) | 90.0/82.0 (+4.0/+5.0) |
| Lib-Wide | Main-Wide | Mao-Wide | Science-Wide | |
|---|---|---|---|---|
| LMR | 82.11 | 74.47 | 94.58 | 91.44 |
| LPM | 86.08 | 76.51 | 95.36 | 93.09 |
| mTOP | 85.41 | 87.90 | 95.24 | 91.11 |
| RFM | 86.72 | 82.06 | 94.78 | 91.28 |
| RANSAC | 49.70 | 52.35 | 83.65 | 53.85 |
| LGC | 81.22 | 65.12 | 92.40 | 89.05 |
| Ours | 90.33 (+3.61) | 92.67 (+4.77) | 96.75 (+1.39) | 94.26 (+1.17) |
| Lib-Wide | Main-Wide | Mao-Wide | Science-Wide | |
|---|---|---|---|---|
| LMR | 4.87/7.74 | 13.09/18.81 | 0.12/0.90 | 0.20/0.60 |
| LPM | 3.82/4.40 | 8.30/14.22 | 0.20/1.33 | 0.15/0.52 |
| MTOP | 1.11/2.85 | 11.93/21.03 | 0.16/1.24 | 0.18/0.61 |
| RFM | 16.17/3.39 | 10.84/24.10 | 0.14/1.21 | 0.16/0.52 |
| RANSAC | 7.73/9.32 | 18.15/14.85 | 0.39/2.32 | 0.38/1.54 |
| LGC | 2.67/4.41 | 2.40/14.12 | 0.18/1.35 | 0.24/0.72 |
| Ours | 0.45/1.33 | 1.22/13.17 | 0.10/0.84 | 0.11/0.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Sun, K.; Jiang, S.; Li, K.; Tao, W. MSSF: A Novel Mutual Structure Shift Feature for Removing Incorrect Keypoint Correspondences between Images. Remote Sens. 2023, 15, 926. https://doi.org/10.3390/rs15040926
Liu J, Sun K, Jiang S, Li K, Tao W. MSSF: A Novel Mutual Structure Shift Feature for Removing Incorrect Keypoint Correspondences between Images. Remote Sensing. 2023; 15(4):926. https://doi.org/10.3390/rs15040926
Chicago/Turabian StyleLiu, Juan, Kun Sun, San Jiang, Kunqian Li, and Wenbing Tao. 2023. "MSSF: A Novel Mutual Structure Shift Feature for Removing Incorrect Keypoint Correspondences between Images" Remote Sensing 15, no. 4: 926. https://doi.org/10.3390/rs15040926
APA StyleLiu, J., Sun, K., Jiang, S., Li, K., & Tao, W. (2023). MSSF: A Novel Mutual Structure Shift Feature for Removing Incorrect Keypoint Correspondences between Images. Remote Sensing, 15(4), 926. https://doi.org/10.3390/rs15040926