Cloud Removal from Satellite Images Using a Deep Learning Model with the Cloud-Matting Method
Abstract
1. Introduction
2. Methodology
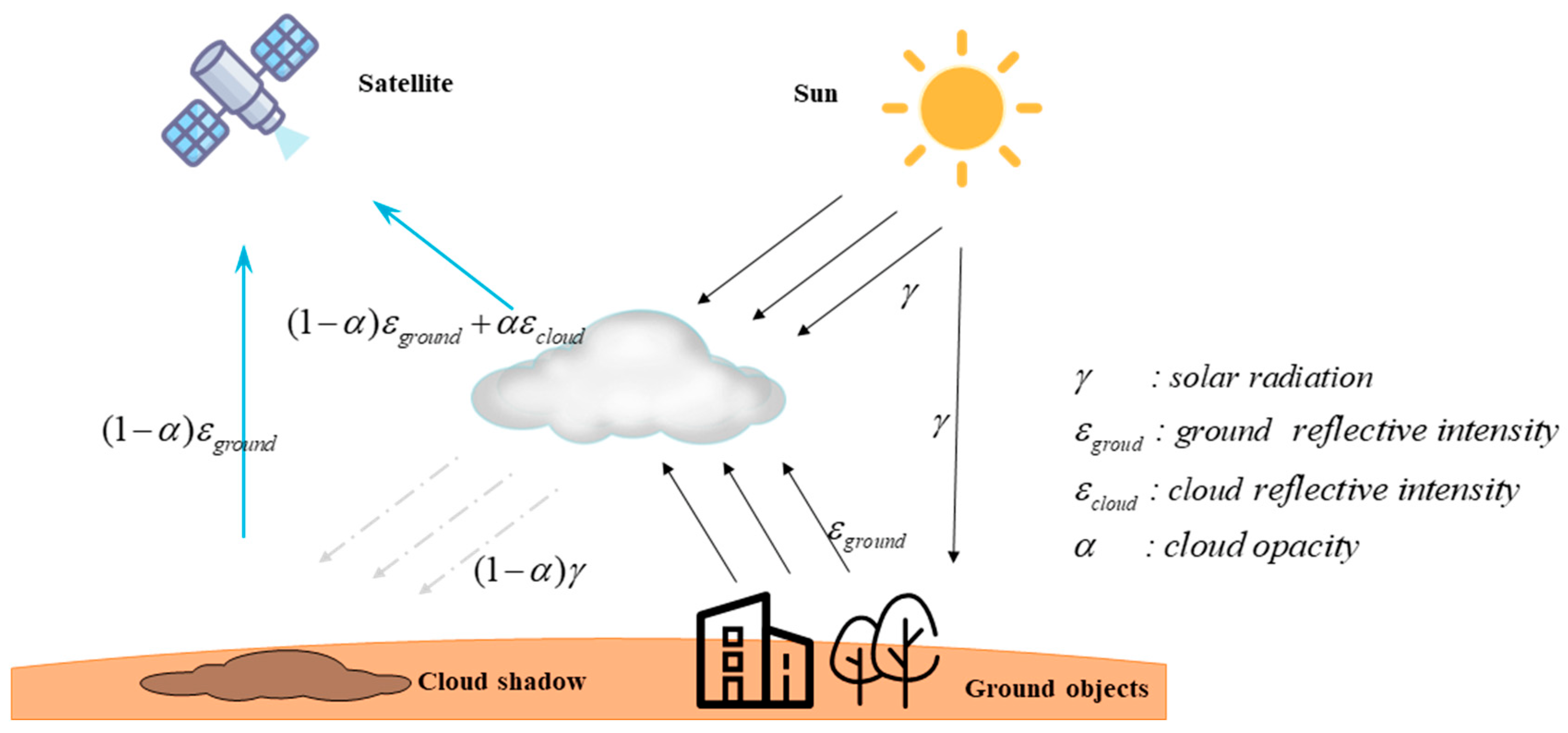
2.1. Remote Sensing Imaging Process
2.2. Model and Algorithm
2.3. Loss Function
3. Experiments
3.1. Datasets
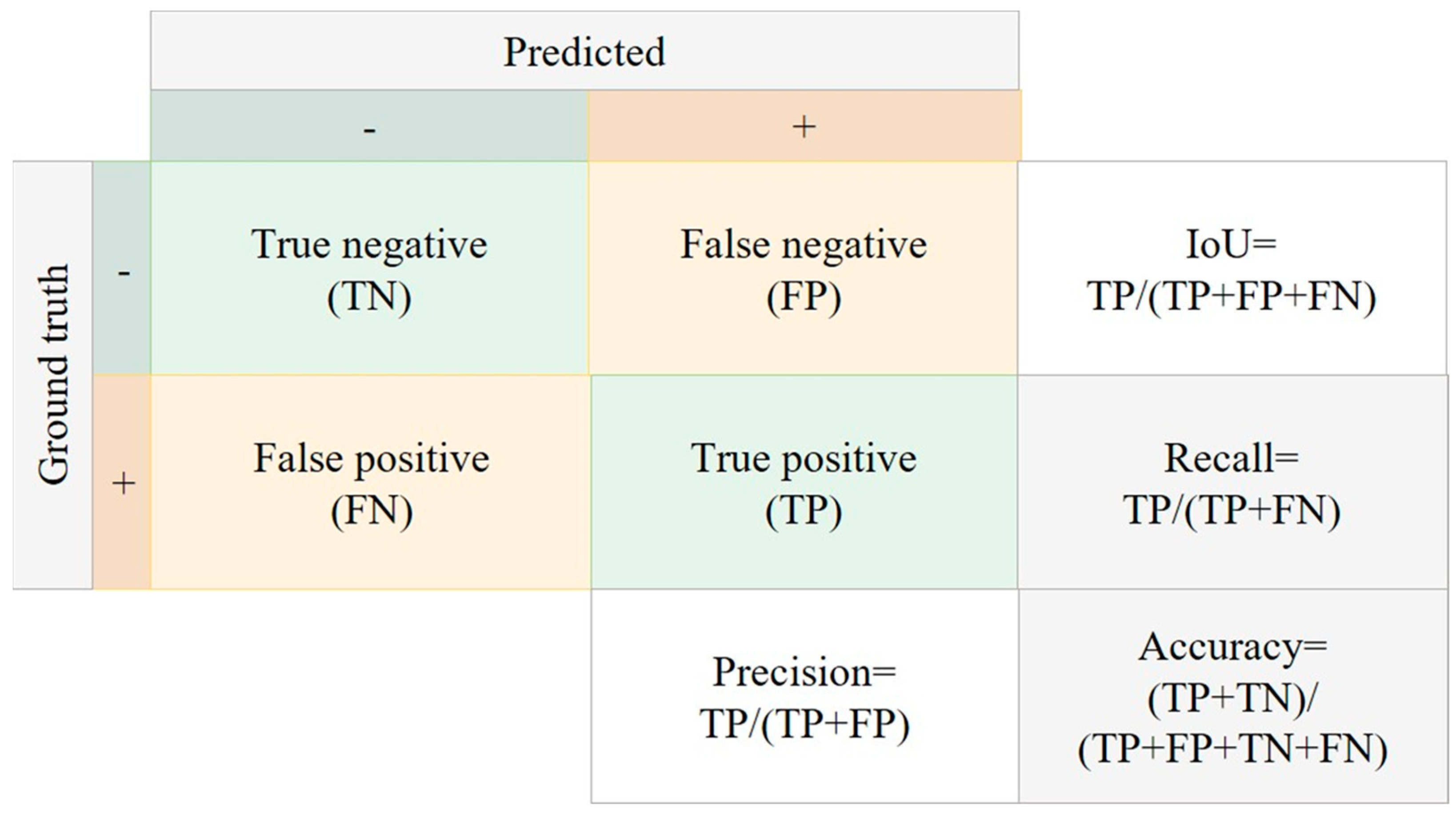
3.2. Evaluation Metrics
3.3. Implementation Details Evaluation Metrics
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ju, J.; Roy, D.P. The Availability of Cloud-Free Landsat ETM+ Data over the Conterminous United States and Globally. Remote Sens. Environ. 2008, 112, 1196–1211. [Google Scholar] [CrossRef]
- Rossow, W.B.; Schiffer, R.A. Advances in Understanding Clouds from ISCCP. Bull. Am. Meteorol. Soc. 1999, 80, 2261–2287. [Google Scholar] [CrossRef]
- Zhang, Y.; Rossow, W.B.; Lacis, A.A.; Oinas, V.; Mishchenko, M.I. Calculation of Radiative Fluxes from the Surface to Top of Atmosphere Based on ISCCP and Other Global Data Sets: Refinements of the Radiative Transfer Model and the Input Data. J. Geophys. Res. Atmos. 2004, D19, 109. [Google Scholar] [CrossRef]
- Wu, R.; Liu, G.; Zhang, R.; Wang, X.; Li, Y.; Zhang, B.; Cai, J.; Xiang, W. A Deep Learning Method for Mapping Glacial Lakes from the Combined Use of Synthetic-Aperture Radar and Optical Satellite Images. Remote Sens. 2020, 12, 4020. [Google Scholar] [CrossRef]
- Stubenrauch, C.J.C.J.; Rossow, W.B.W.B.; Kinne, S.; Ackerman, S.; Cesana, G.; Chepfer, H.; di Girolamo, L.; Getzewich, B.; Guignard, A.; Heidinger, A.; et al. Assessment of Global Cloud Datasets from Satellites: Project and Database Initiated by the GEWEX Radiation Panel. Bull. Am. Meteorol. Soc. 2013, 94, 1031–1049. [Google Scholar] [CrossRef]
- Lin, B.; Rossow, W.B. Precipitation Water Path and Rainfall Rate Estimates over Oceans Using Special Sensor Microwave Imager and International Satellite Cloud Climatology Project Data. J. Geophys. Res. Atmos. 1997, 102, 9359–9374. [Google Scholar] [CrossRef]
- Lubin, D.; Harper, D.A. Cloud Radiative Properties over the South Pole from AVHRR Infrared Data. J. Clim. 1996, 9, 3405–3418. [Google Scholar] [CrossRef]
- Hahn, C.J.; Warren, S.G.; London, J. The Effect of Moonlight on Observation of Cloud Cover at Night, and Application to Cloud Climatology. J. Clim. 1995, 8, 1429–1446. [Google Scholar] [CrossRef]
- Hagolle, O.; Huc, M.; Pascual, D.V.; Dedieu, G. A Multi-Temporal Method for Cloud Detection, Applied to FORMOSAT-2, VENμS, LANDSAT and SENTINEL-2 Images. Remote Sens. Environ. 2010, 114, 1747–1755. [Google Scholar] [CrossRef]
- Guosheng, L.; Curry, J.A.; Sheu, R.S. Classification of Clouds over the Western Equatorial Pacific Ocean Using Combined Infrared and Microwave Satellite Data. J. Geophys. Res. 1995, 100, 13811–13826. [Google Scholar] [CrossRef]
- Ackerman, S.A.; Holz, R.E.; Frey, R.; Eloranta, E.W.; Maddux, B.C.; McGill, M. Cloud Detection with MODIS. Part II: Validation. J. Atmos. Ocean. Technol. 2008, 25, 1073–1086. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Object-Based Cloud and Cloud Shadow Detection in Landsat Imagery. Remote Sens. Environ. 2012, 118, 83–94. [Google Scholar] [CrossRef]
- Scaramuzza, P.L.; Bouchard, M.A.; Dwyer, J.L. Development of the Landsat Data Continuity Mission Cloud-Cover Assessment Algorithms. IEEE Trans. Geosci. Remote Sens. 2011, 50, 1140–1154. [Google Scholar] [CrossRef]
- Zou, Z.; Li, W.; Shi, T.; Shi, Z.; Ye, J. Generative Adversarial Training for Weakly Supervised Cloud Matting. Proceedings of the IEEE Int. Conf. Comput. Vis. 2019, 2019, 201–210. [Google Scholar] [CrossRef]
- Foga, S.; Scaramuzza, P.L.; Guo, S.; Zhu, Z.; Dilley, R.D.; Beckmann, T.; Schmidt, G.L.; Dwyer, J.L.; Joseph Hughes, M.; Laue, B. Cloud Detection Algorithm Comparison and Validation for Operational Landsat Data Products. Remote Sens. Environ. 2017, 194, 379–390. [Google Scholar] [CrossRef]
- Shi, M.; Xie, F.; Zi, Y.; Yin, J. Cloud Detection of Remote Sensing Images by Deep Learning. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 701–704. [Google Scholar]
- le Goff, M.; Tourneret, J.-Y.; Wendt, H.; Ortner, M.; Spigai, M. Deep Learning for Cloud Detection. In Proceedings of the 8th International Conference of Pattern Recognition Systems (ICPRS 2017), Madrid, Spain, 11–13 July 2017; IET: Stevenage, UK, 2017; pp. 1–6. [Google Scholar]
- He, Q.; Sun, X.; Yan, Z.; Fu, K. DABNet: Deformable Contextual and Boundary-Weighted Network for Cloud Detection in Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2021, 1–16. [Google Scholar] [CrossRef]
- Jeppesen, J.H.; Jacobsen, R.H.; Inceoglu, F.; Toftegaard, T.S. A Cloud Detection Algorithm for Satellite Imagery Based on Deep Learning. Remote Sens. Environ. 2019, 229, 247–259. [Google Scholar] [CrossRef]
- Mahajan, S.; Fataniya, B. Cloud Detection Methodologies: Variants and Development—A Review. Complex Intell. Syst. 2019, 6, 251–261. [Google Scholar] [CrossRef]
- Lin, J.; Huang, T.Z.; Zhao, X.L.; Chen, Y.; Zhang, Q.; Yuan, Q. Robust thick cloud removal for multitemporal remote sensing images using coupled tensor factorization. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Pan, X.; Xie, F.; Jiang, Z.; Yin, J. Haze Removal for a Single Remote Sensing Image Based on Deformed Haze Imaging Model. IEEE Signal Process. Lett. 2015, 22, 1806–1810. [Google Scholar] [CrossRef]
- Mitchell, O.R.; Delp, E.J.; Chen, P.L. Filtering to Remove Cloud Cover in Satellite Imagery. IEEE Trans. Geosci. Electron. 1977, 15, 137–141. [Google Scholar] [CrossRef]
- Li, F.F.; Zuo, H.M.; Jia, Y.H.; Wang, Q.; Qiu, J. Hybrid Cloud Detection Algorithm Based on Intelligent Scene Recognition. J. Atmos. Ocean. Technol. 2022, 39, 837–847. [Google Scholar] [CrossRef]
- He, K.M.; SUN, J.T.X.O. Single Image Haze Removal Using Dark Channel Prior. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 2341. [Google Scholar]
- Chen, Q.; Li, D.; Tang, C.-K. KNN Matting. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2175–2188. [Google Scholar] [CrossRef]
- Levin, A.; Lischinski, D.; Weiss, Y. A closed-form solution to natural image matting. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 30, 228–242. [Google Scholar] [CrossRef]
- Mirza, M.; Osindero, S. Conditional Generative Adversarial Nets. arXiv 2014, arXiv preprint. arXiv:1411.1784. [Google Scholar]
- Isola, P.; Zhu, J.-Y.; Zhou, T.; Efros, A.A. Image-to-Image Translation with Conditional Adversarial Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Hawai, HI, USA, 20–26 June 2017; pp. 5967–5976. [Google Scholar]
- Ramjyothi, A.; Goswami, S. Cloud and Fog Removal from Satellite Images Using Generative Adversarial Networks (Gans). 2021. Available online: https://hal.science/hal-03462652 (accessed on 17 November 2022).
- Emami, H.; Aliabadi, M.M.; Dong, M.; Chinnam, R.B. Spa-gan: Spatial attention gan for image-to-image translation. IEEE Trans. Multimed. 2020, 23, 391–401. [Google Scholar] [CrossRef]
- Wen, X.; Pan, Z.; Hu, Y.; Liu, J. An effective network integrating residual learning and channel attention mechanism for thin cloud removal. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Qiu, S.; Zhu, Z.; He, B. Fmask 4.0: Improved Cloud and Cloud Shadow Detection in Landsats 4–8 and Sentinel-2 Imagery. Remote Sens. Environ. 2019, 231, 111205. [Google Scholar] [CrossRef]
- Frantz, D.; Haß, E.; Uhl, A.; Stoffels, J.; Hill, J. Improvement of the Fmask Algorithm for Sentinel-2 Images: Separating Clouds from Bright Surfaces Based on Parallax Effects. Remote Sens. Environ. 2018, 215, 471–481. [Google Scholar] [CrossRef]
- Housman, I.W.; Chastain, R.A.; Finco, M.V. An Evaluation of Forest Health Insect and Disease Survey Data and Satellite-Based Remote Sensing Forest Change Detection Methods: Case Studies in the United States. Remote Sens. 2018, 10, 1184. [Google Scholar] [CrossRef]
- Ji, T.Y.; Chu, D.; Zhao, X.L.; Hong, D. A unified framework of cloud detection and removal based on low-rank and group sparse regularizations for multitemporal multispectral images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Fattal, R. Single image dehazing. ACM Trans. Graph. (TOG) 2008, 27, 1–9. [Google Scholar] [CrossRef]
- Sun, Y.; Tang, C.-K.; Tai, Y.-W. Semantic Image Matting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 11120–11129. [Google Scholar]
- Chen, Q.; Ge, T.; Xu, Y.; Zhang, Z.; Yang, X.; Gai, K. Semantic Human Matting. In Proceedings of the 2018 ACM Multimedia Conference, Seoul, Republic of Korea, 22–26 October 2018; pp. 618–626. [Google Scholar] [CrossRef]
- Xu, N.; Price, B.; Cohen, S.; Huang, T. Deep Image Matting. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2970–2979. [Google Scholar]
- Chen, H.; Han, X.; Fan, X.; Lou, X.; Liu, H.; Huang, J.; Yao, J. Rectified cross-entropy and upper transition loss for weakly supervised whole slide image classifier. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Cham, Switzerland, 2019; pp. 351–359. [Google Scholar]
- Salehi, S.S.M.; Erdogmus, D.; Gholipour, A. Tversky Loss Function for Image Segmentation Using 3D Fully Convolutional Deep Networks. In Proceedings of the Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), Quebec City, QC, Canada, 10 September 2017; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; Volume 10541, pp. 379–387. [Google Scholar]
- Lin, T.-Y.; Goyal, P.; Girshick, R.; He, K.; Dollar, P. Focal Loss for Dense Object Detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; Volume 2017, pp. 2999–3007. [Google Scholar]
- Li, X.; Sun, X.; Meng, Y.; Liang, J.; Wu, F.; Li, J. Dice Loss for Data-Imbalanced NLP Tasks. arXiv 2020, arXiv:1911.02855. [Google Scholar]
- Wang, L.; Wang, C.; Sun, Z.; Chen, S. An Improved Dice Loss for Pneumothorax Segmentation by Mining the Information of Negative Areas. IEEE Access 2020, 8, 167939–167949. [Google Scholar] [CrossRef]
- Rhemann, C.; Rother, C.; Wang, J.; Gelautz, M.; Kohli, P.; Rott, P. A Perceptually Motivated Online Benchmark for Image Matting. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, CVPR, Miami, FL, USA, 20–25 June 2009; pp. 1826–1833. [Google Scholar]
- Shen, X.; Tao, X.; Gao, H.; Zhou, C.; Jia, J. Deep Automatic Portrait Matting. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; Volume 9905, ISBN 9783319464473. [Google Scholar]
- Irish, R.R.; Barker, J.L.; Goward, S.N.; Arvidson, T. Characterization of the Landsat-7 ETM+ Automated Cloud-Cover Assessment (ACCA) Algorithm. Photogramm. Eng. Remote Sens. 2006, 72, 1179–1188. [Google Scholar] [CrossRef]
- Hughes, M.J.; Hayes, D.J. Automated Detection of Cloud and Cloud Shadow in Single-Date Landsat Imagery Using Neural Networks and Spatial Post-Processing. Remote Sens. 2014, 6, 4907–4926. [Google Scholar] [CrossRef]
- Baetens, L.; Desjardins, C.; Hagolle, O. Validation of Copernicus Sentinel-2 Cloud Masks Obtained from MAJA, Sen2Cor, and FMask Processors Using Reference Cloud Masks Generated with a Supervised Active Learning Procedure. Remote Sens. 2019, 11, 433. [Google Scholar] [CrossRef]
- Louis, J.; Debaecker, V.; Pflug, B.; Main-Knorn, M.; Bieniarz, J.; Mueller-Wilm, U.; Cadau, E.; Gascon, F. Sentinel-2 SEN2COR: L2A Processor for Users. In Proceedings of the Living Planet Symposium 2016, Spacebooks Online, Prague, Czech Republic, 9–13 May 2016; Volume SP-740, pp. 1–8, ISBN 978-92-9221-305-3. [Google Scholar]




| Methods | Sen2cor | S2cloudless | Fmask4.0 | Ours-TNet | Label |
|---|---|---|---|---|---|
| Precision (thin cloud) | 0.6837 | 0.7712 | 0.7762 | 0.7981 | |
| Recall (thin cloud) | 0.9632 | 0.9400 | 0.9271 | 0.9445 | |
| Accuracy (thin cloud) | 0.9458 | 0.9560 | 0.9550 | 0.9596 | |
| IoU (thin cloud) | 0.6663 | 0.7351 | 0.7315 | 0.7551 | |
| Cloud content (thin cloud) | 9.4740 | 12.975 | 17.271 | 16.315 | 15.815 |
| Precision (thick cloud) | 0.6658 | 0.7172 | 0.7699 | 0.8019 | |
| Recall (thick cloud) | 0.8835 | 0.8757 | 0.8643 | 0.8665 | |
| Accuracy (thick cloud) | 0.9409 | 0.9448 | 0.9477 | 0.9596 | |
| IoU (thick cloud) | 0.6122 | 0.6509 | 0.6868 | 0.7254 | |
| Cloud content (thick cloud) | 4.4960 | 5.7000 | 13.400 | 10.810 | 12.190 |
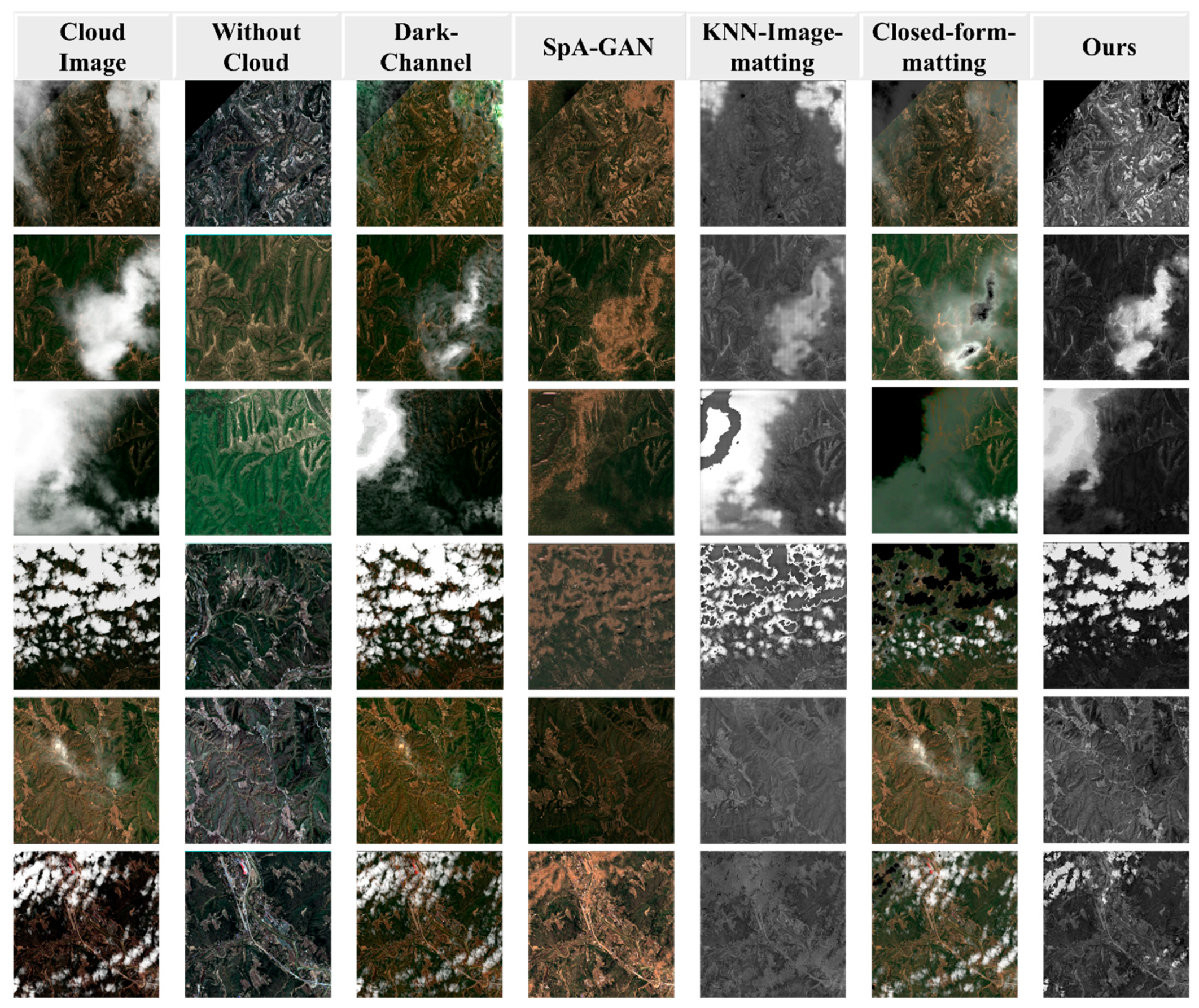
| Metrics | Dark-Channel | SpA-GAN | KNN Image Matting | Closed-Form Matting | Ours |
|---|---|---|---|---|---|
| RMSE (Image) | 0.0233 | 0.0121 | 0.0073 | 0.0065 | 0.0025 |
| 0.1234 | 0.1098 | 0.8620 | 0.1429 | 0.2121 | |
| 0.3396 | 0.3788 | 7.1633 | 1.1419 | 3.2967 | |
| SSIM (Image) | 0.8198 | 0.9959 | 0.9922 | 0.9942 | 0.9992 |
| 0.4115 | 0.8321 | 0.6153 | 0.7418 | 0.8120 | |
| 0.1542 | 0.2570 | 0.0276 | 0.1404 | 0.1040 | |
| PSNR (Image) | 32.6296 | 44.1723 | 42.6939 | 43.6871 | 51.8999 |
| 19.3394 | 26.7704 | 11.1344 | 20.0632 | 23.8369 | |
| 9.3797 | 8.4318 | −17.1023 | −1.1526 | −10.3616 | |
| RMSE (Alpha) | 0.0059 | 0.0071 | 0.0129 | 0.0159 | 0.0067 |
| 0.0803 | 0.0314 | 0.2382 | 0.1141 | 0.0263 | |
| 0.2993 | 0.0793 | 0.8259 | 0.6057 | 0.0791 | |
| SSIM (Alpha) | 0.9928 | 0.9941 | 0.9893 | 0.9953 | 0.9967 |
| 0.8171 | 0.8616 | 0.7537 | 0.8588 | 0.9810 | |
| 0.4960 | 0.6412 | 0.0000 | 0.4268 | 0.9350 | |
| PSNR (Alpha) | 44.5602 | 43.1151 | 37.7872 | 35.9338 | 43.3984 |
| 23.8009 | 30.5172 | 17.0365 | 21.1993 | 32.7192 | |
| 10.4768 | 23.1798 | 1.6613 | 4.3540 | 22.0270 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, D.; Wu, R.; Xiao, D.; Sui, B. Cloud Removal from Satellite Images Using a Deep Learning Model with the Cloud-Matting Method. Remote Sens. 2023, 15, 904. https://doi.org/10.3390/rs15040904
Ma D, Wu R, Xiao D, Sui B. Cloud Removal from Satellite Images Using a Deep Learning Model with the Cloud-Matting Method. Remote Sensing. 2023; 15(4):904. https://doi.org/10.3390/rs15040904
Chicago/Turabian StyleMa, Deying, Renzhe Wu, Dongsheng Xiao, and Baikai Sui. 2023. "Cloud Removal from Satellite Images Using a Deep Learning Model with the Cloud-Matting Method" Remote Sensing 15, no. 4: 904. https://doi.org/10.3390/rs15040904
APA StyleMa, D., Wu, R., Xiao, D., & Sui, B. (2023). Cloud Removal from Satellite Images Using a Deep Learning Model with the Cloud-Matting Method. Remote Sensing, 15(4), 904. https://doi.org/10.3390/rs15040904






