Effects of Wave-Induced Doppler Velocity on the Sea Surface Current Measurements by Ka-Band Real-Aperture Radar with Small Incidence Angle
Abstract
1. Introduction
2. Materials and Methods
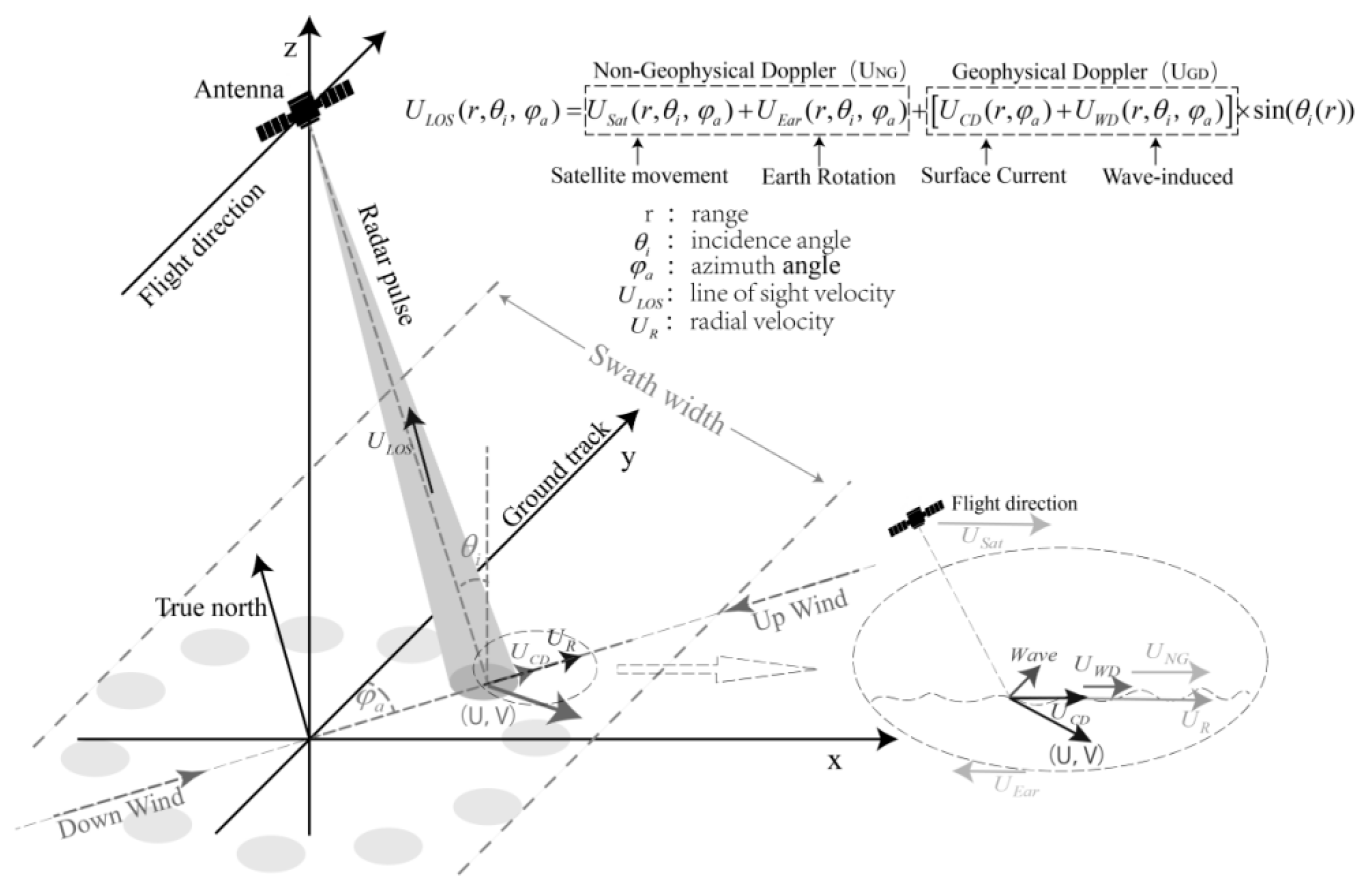
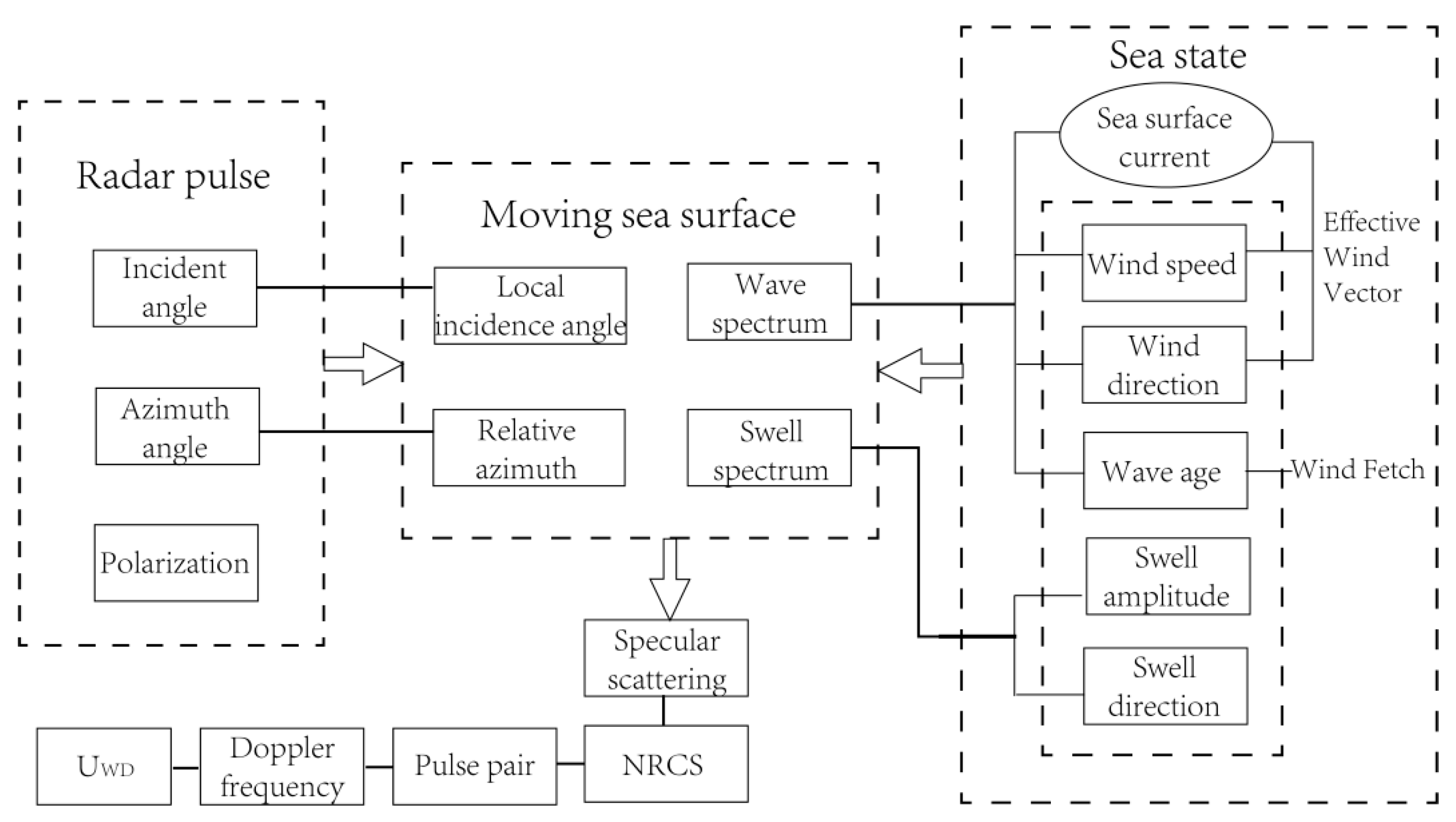
2.1. Sea Surface Motion Modeling
2.2. Sea Surface Scattering Model
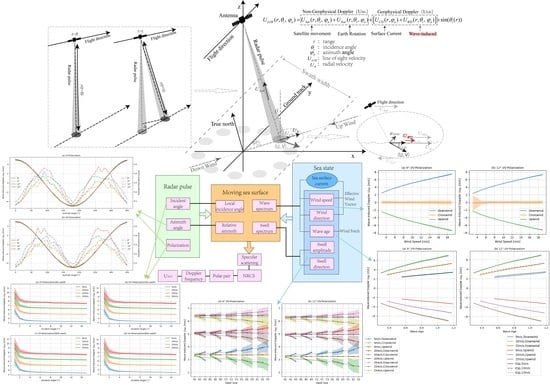
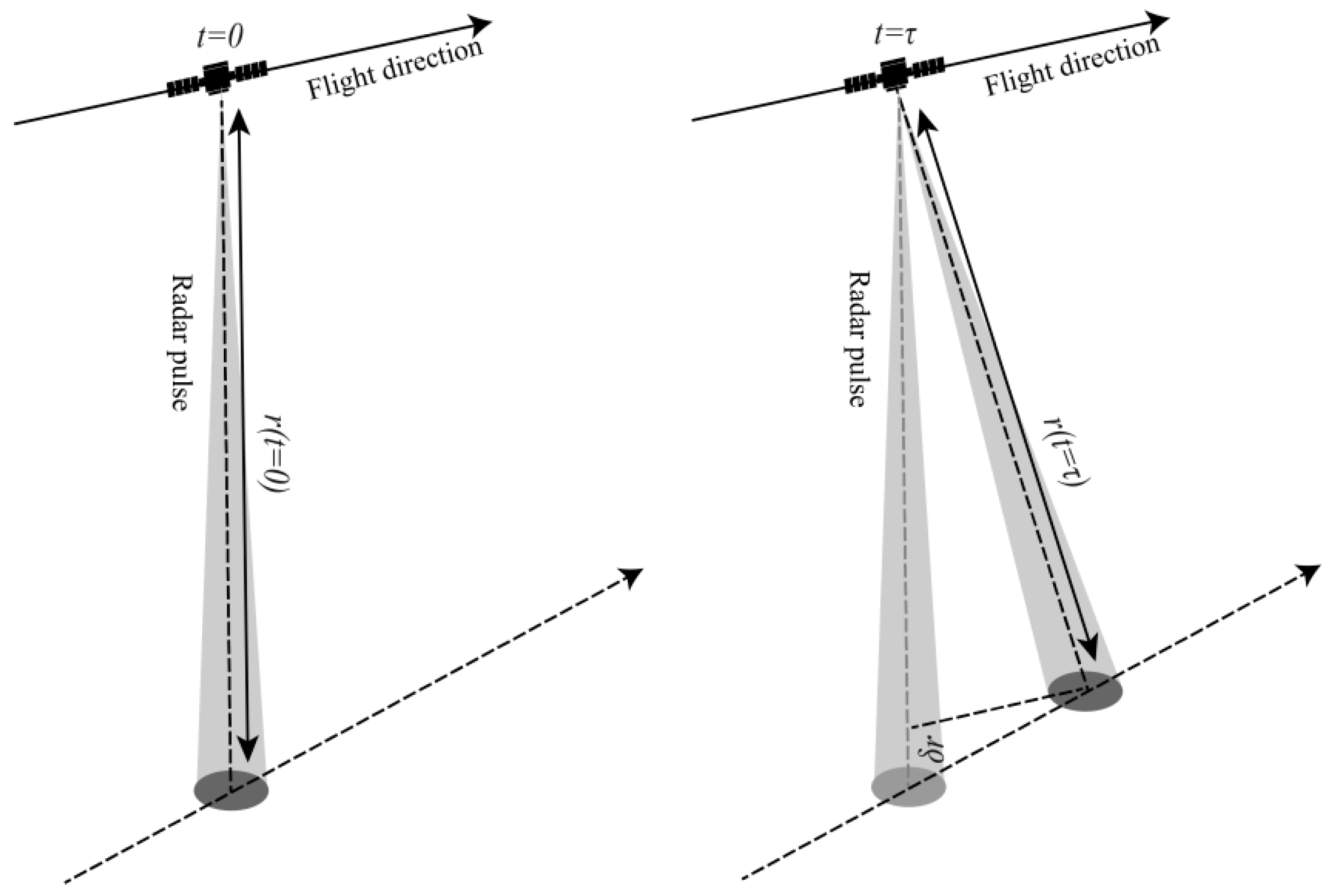
2.3. Doppler Frequency
2.4. Wave-Induced Doppler Velocity
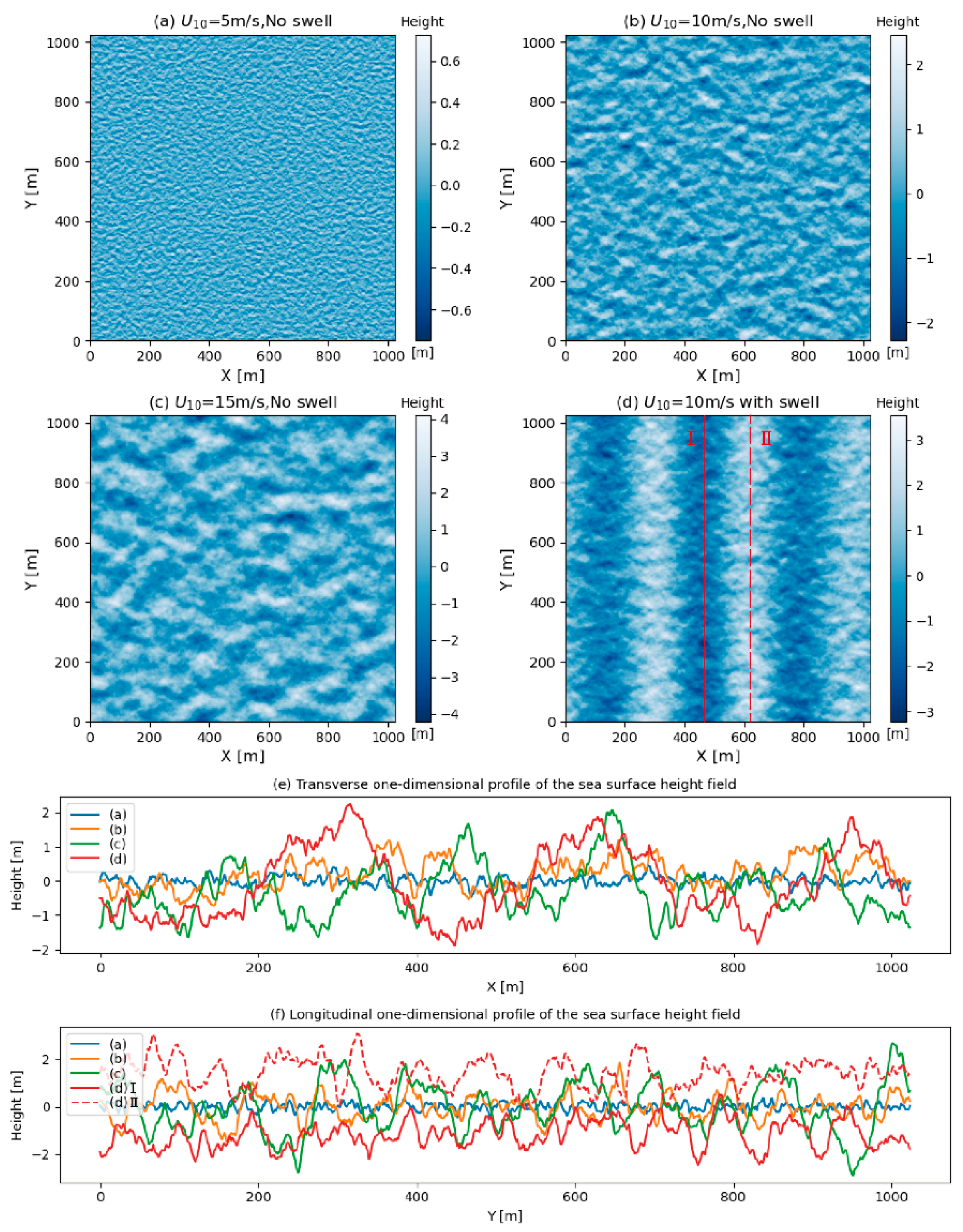
3. Simulation Experiments
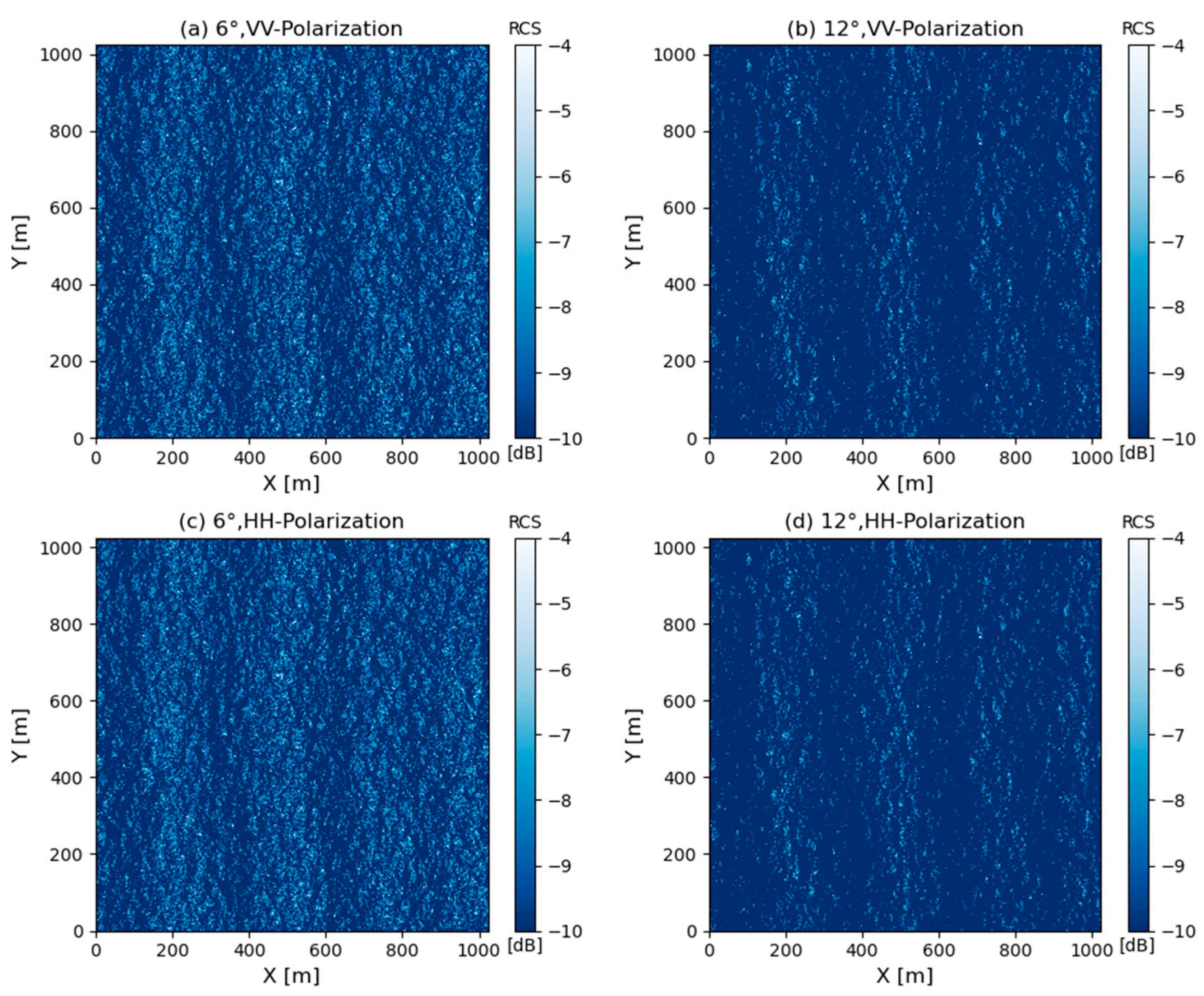
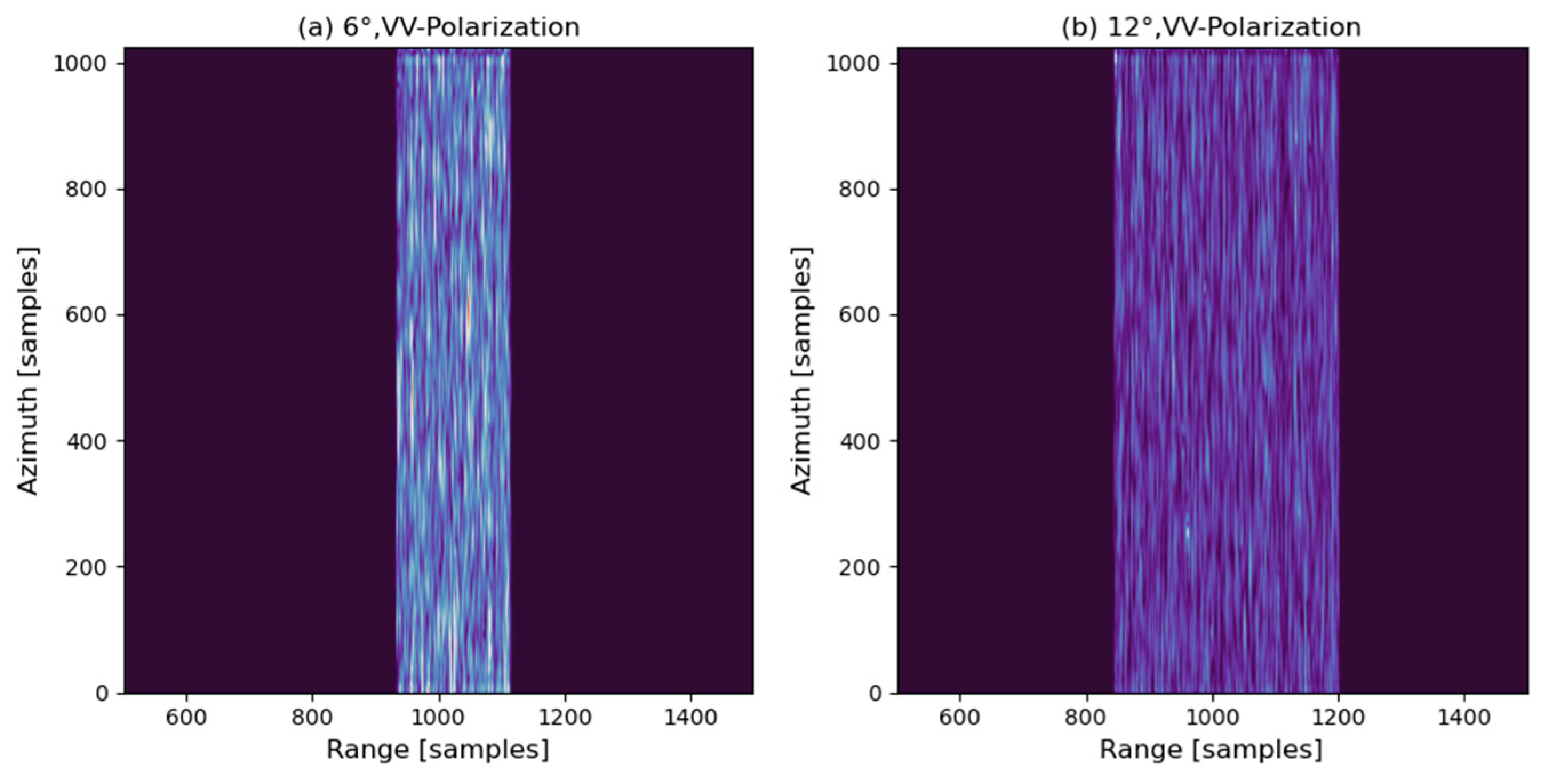
4. Results
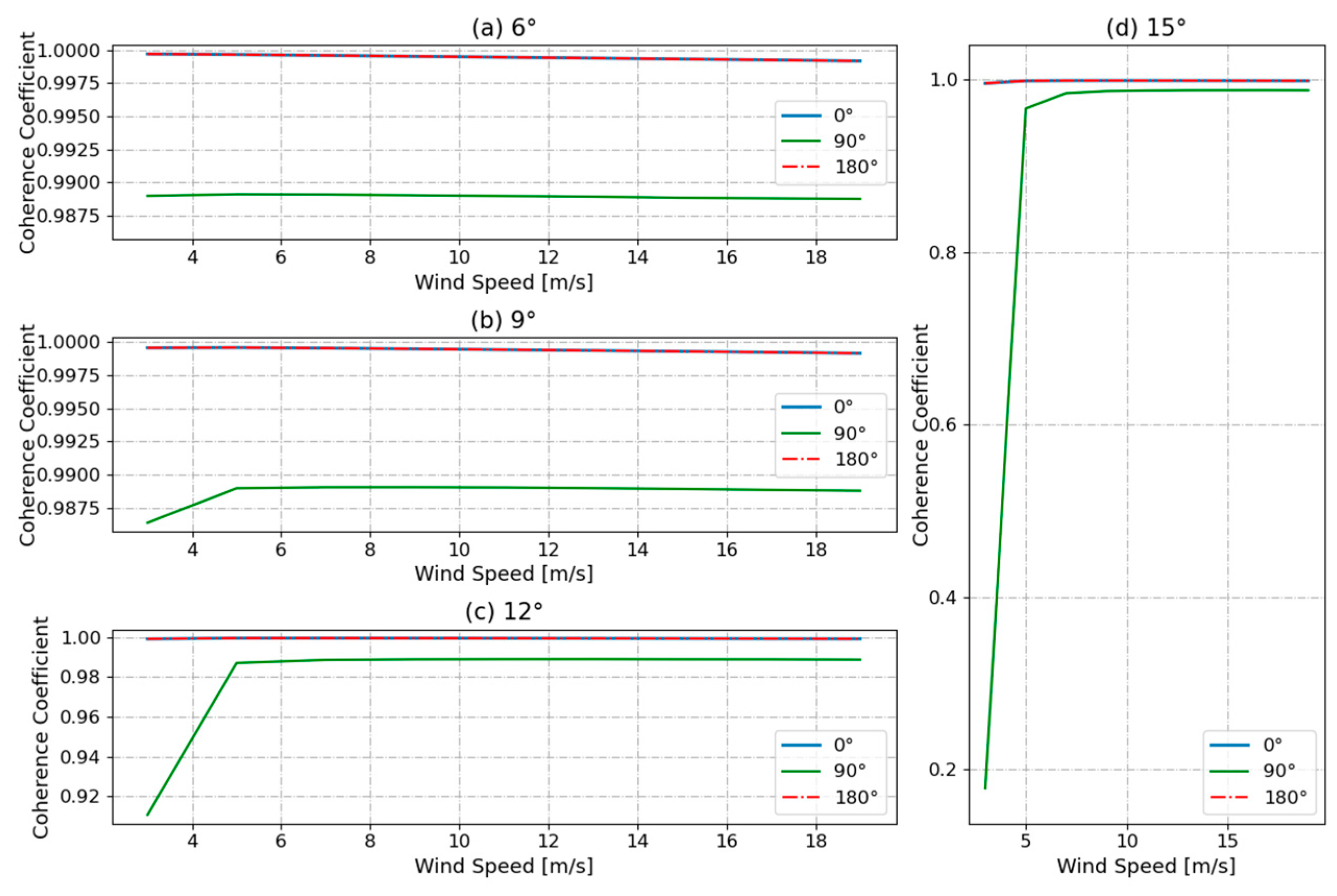
4.1. Coherence Analysis of Pulse Pairs
4.1.1. Effect of Radar Incidence and Azimuth Angles on Pulse Pair Coherence
4.1.2. Effect of Wind Speed on Pulse Pair Coherence
4.2. Effect of Radar Parameters on Wave-Induced Doppler Velocity
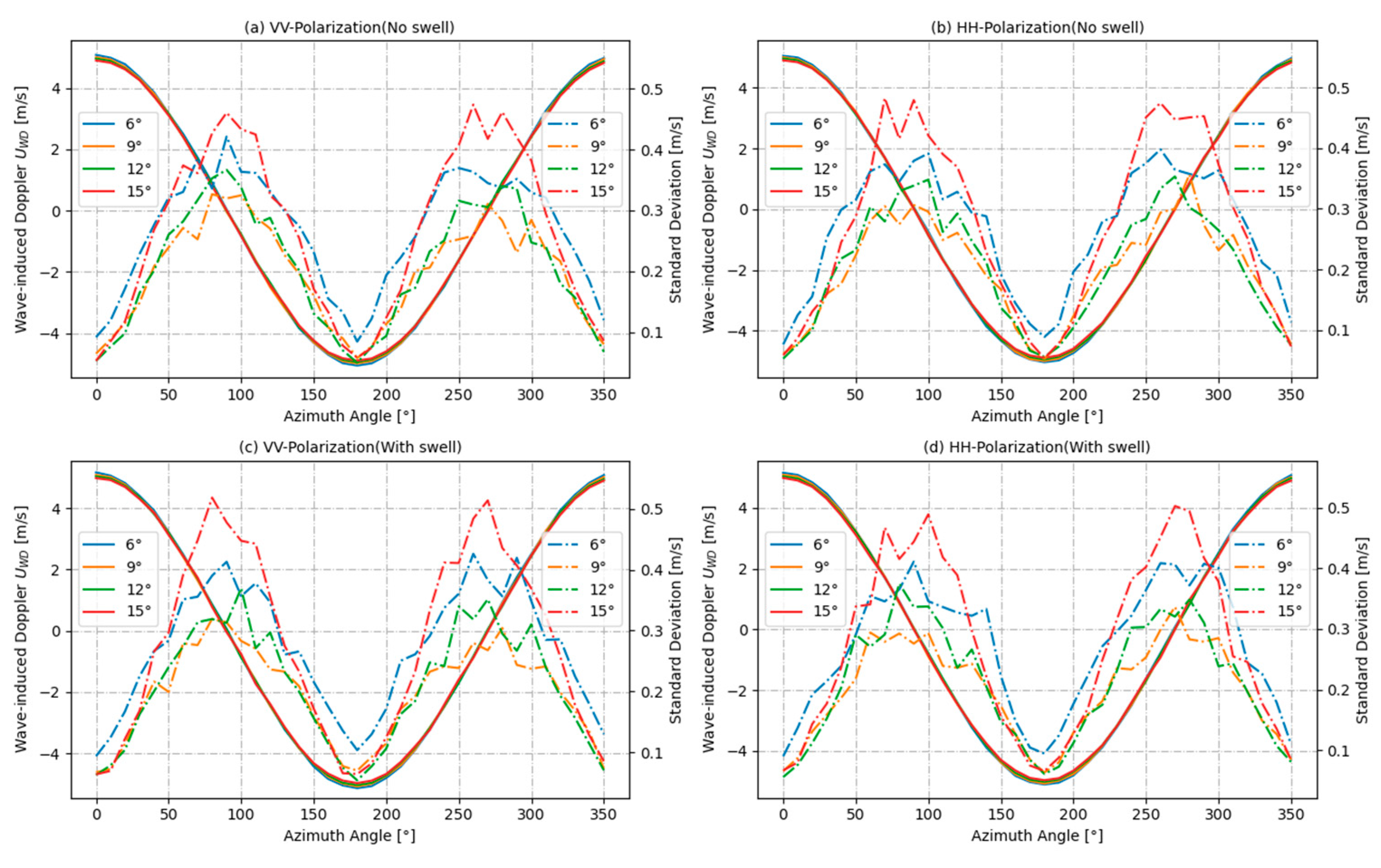
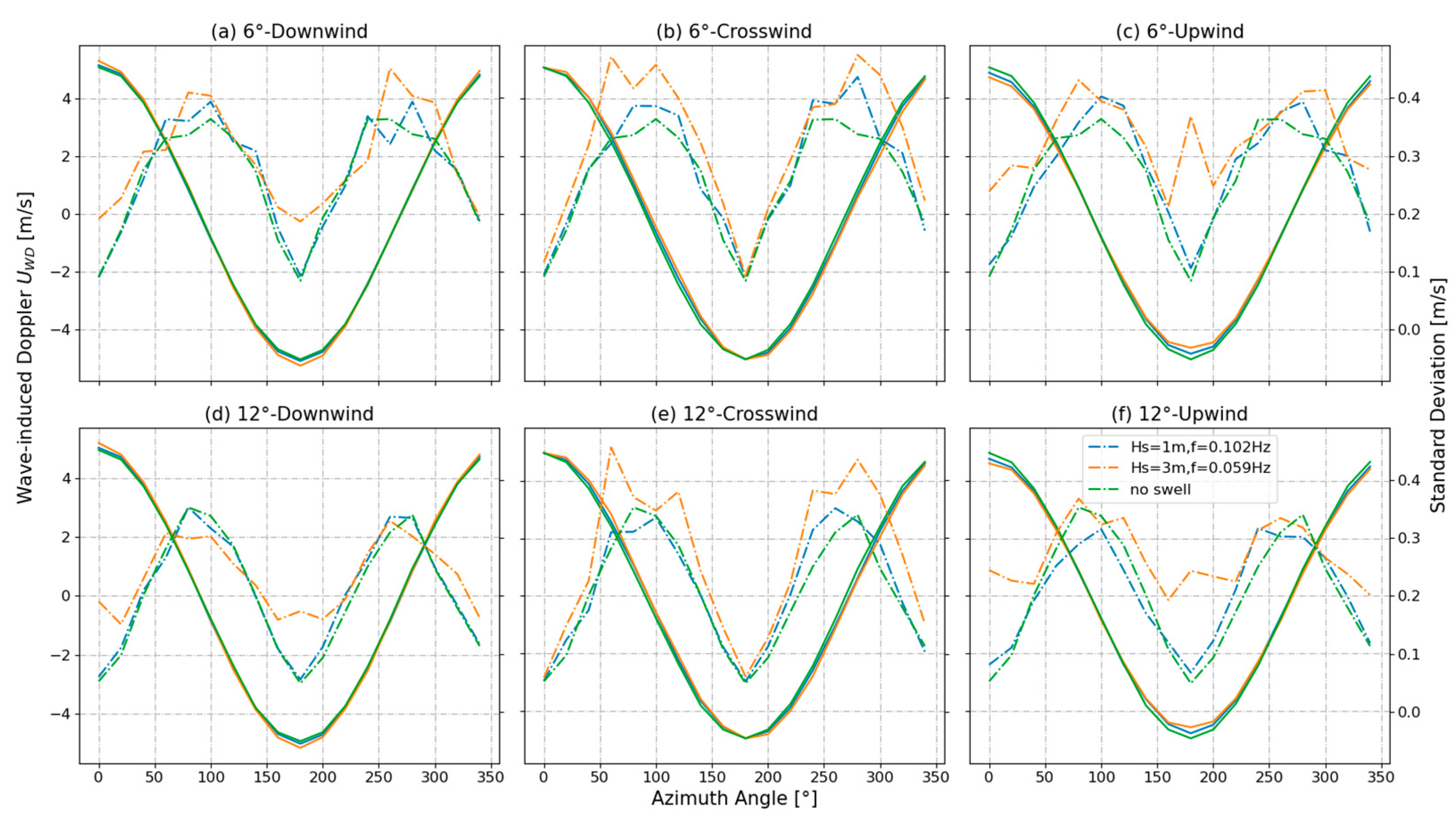
4.2.1. Effect of Radar Azimuth Angle on Wave-Induced Doppler Velocity
4.2.2. Effect of Radar Incidence Angle on Wave-Induced Doppler Velocity
4.3. Effect of Sea State on Wave-Induced Doppler Velocity
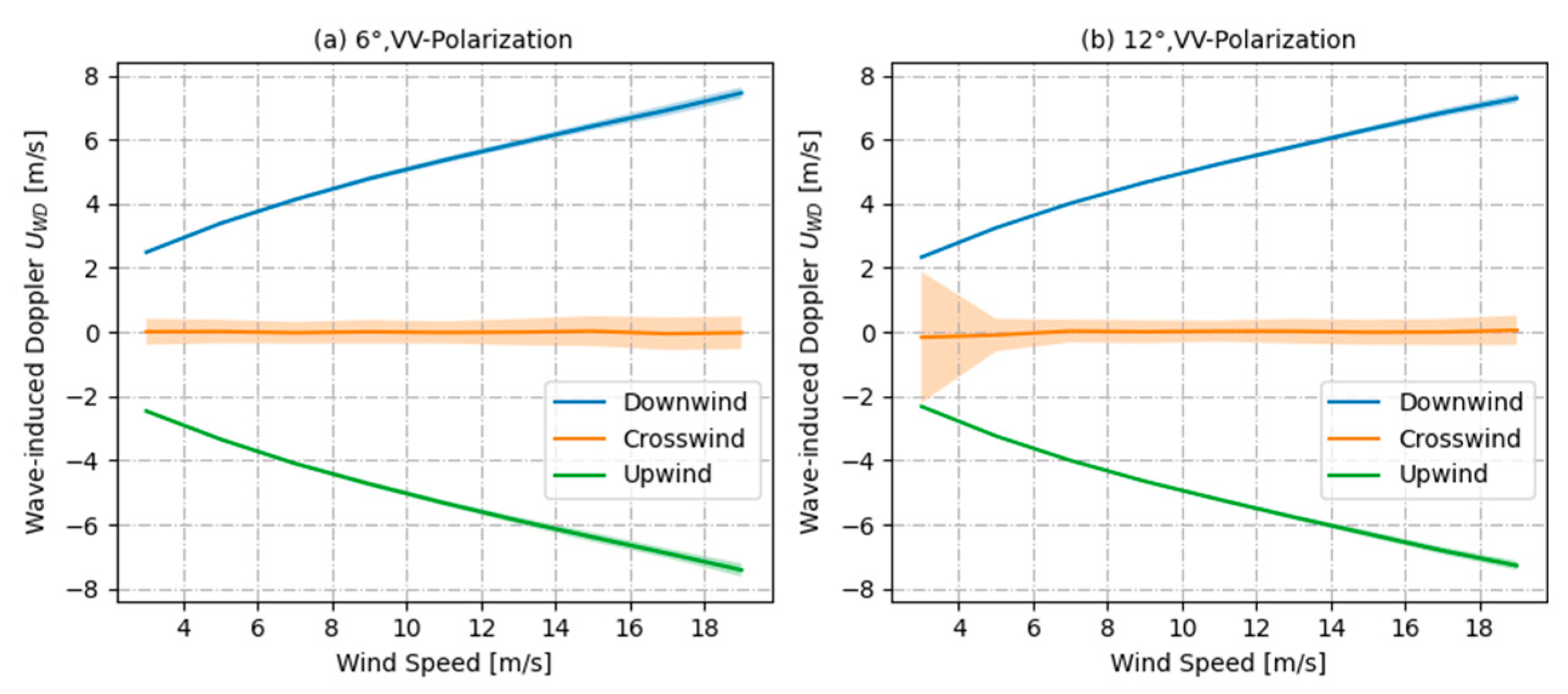
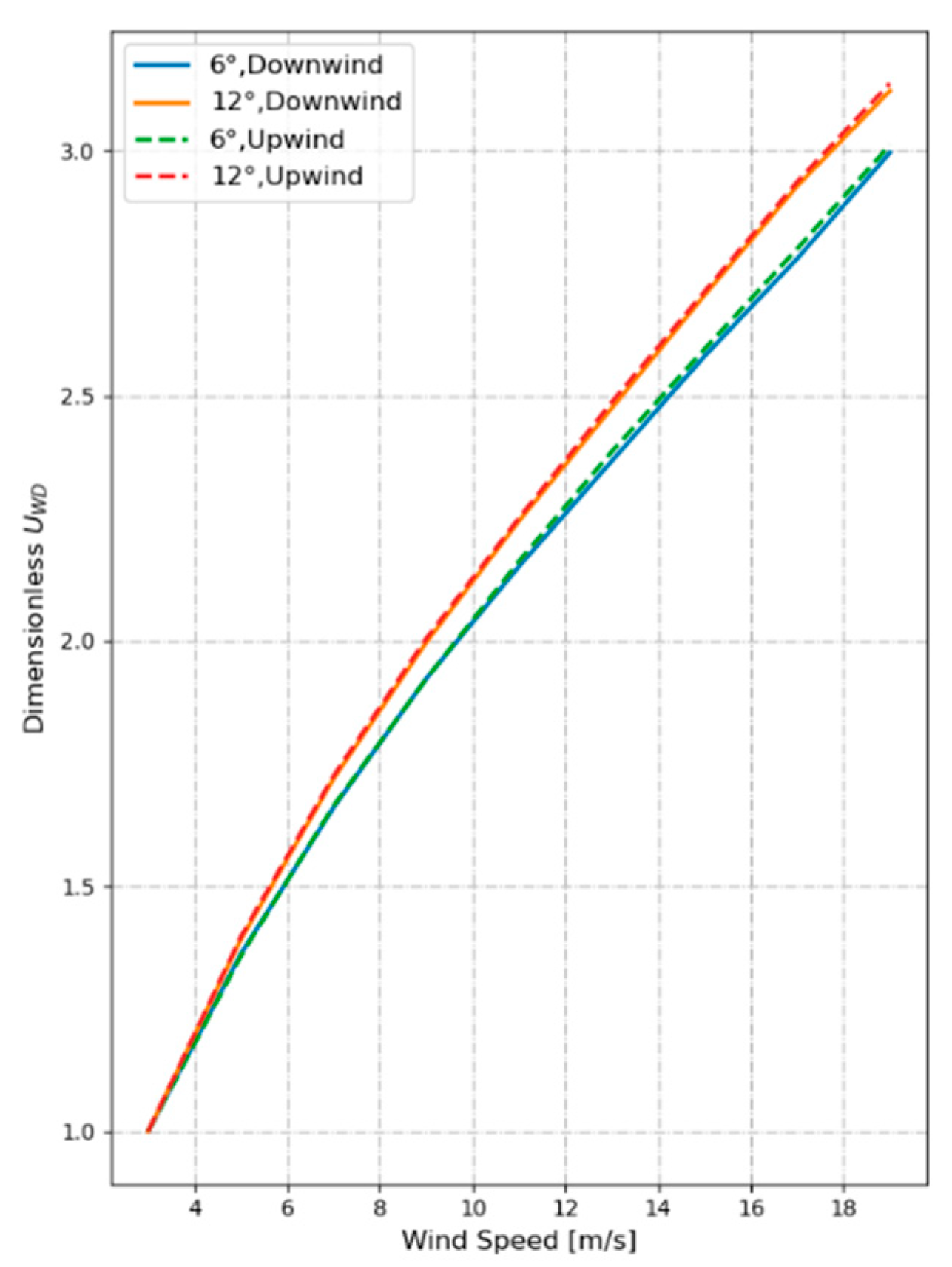
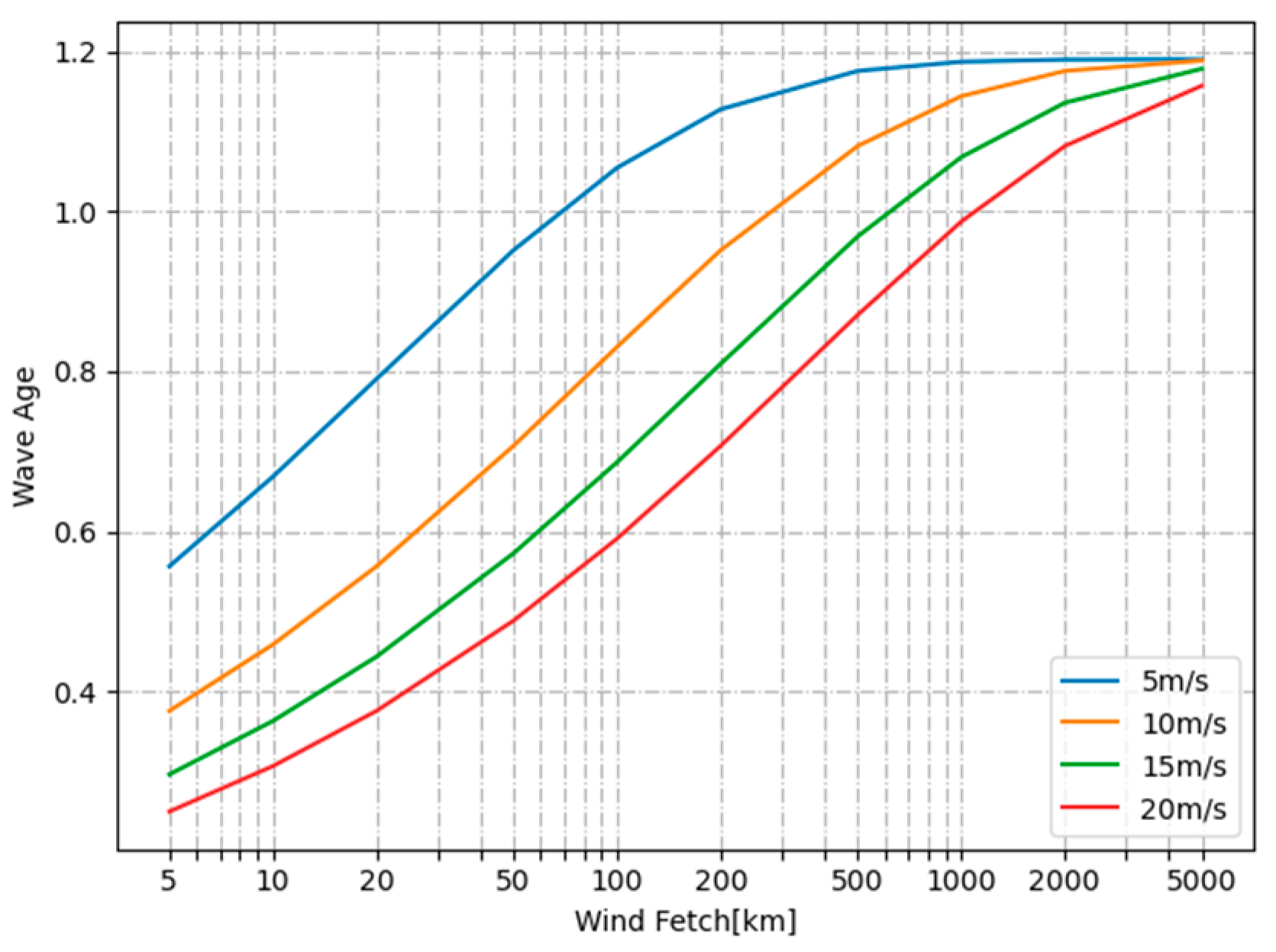
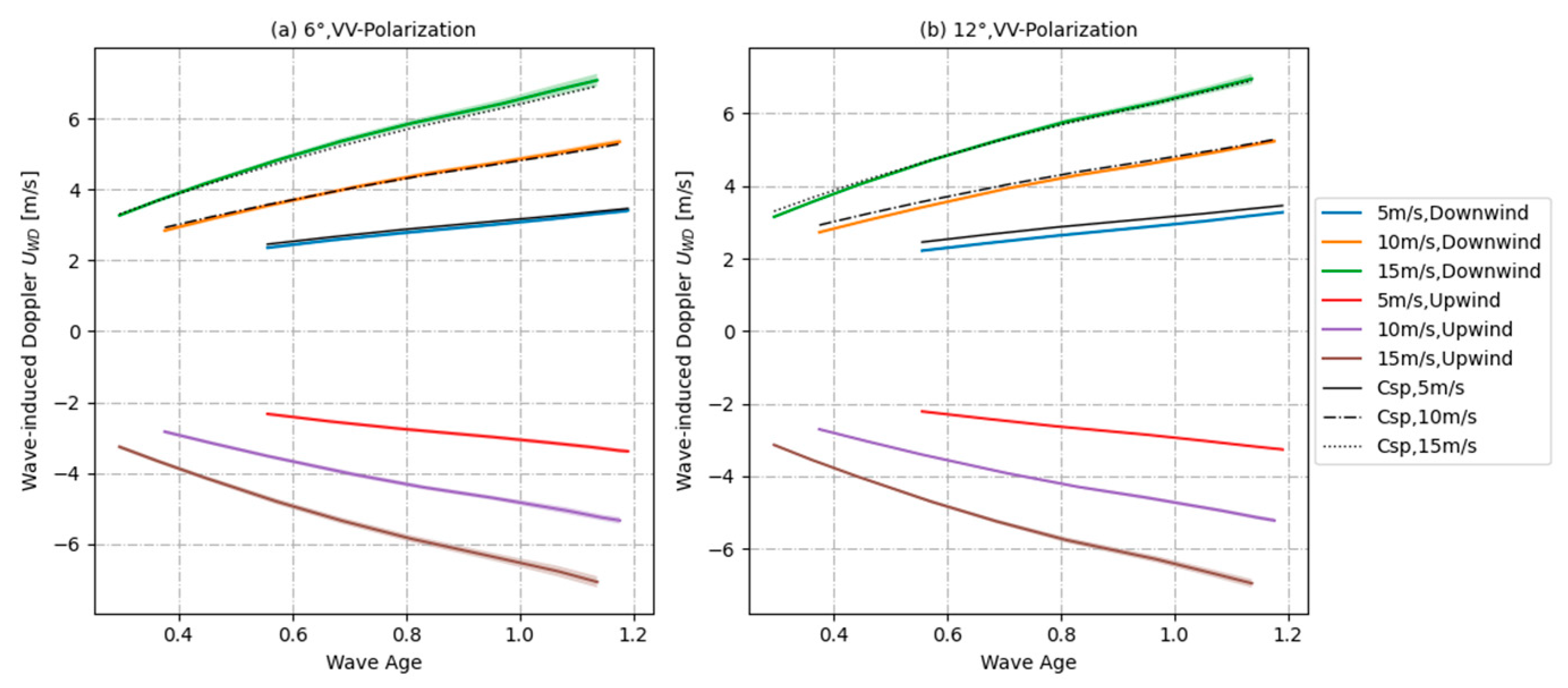
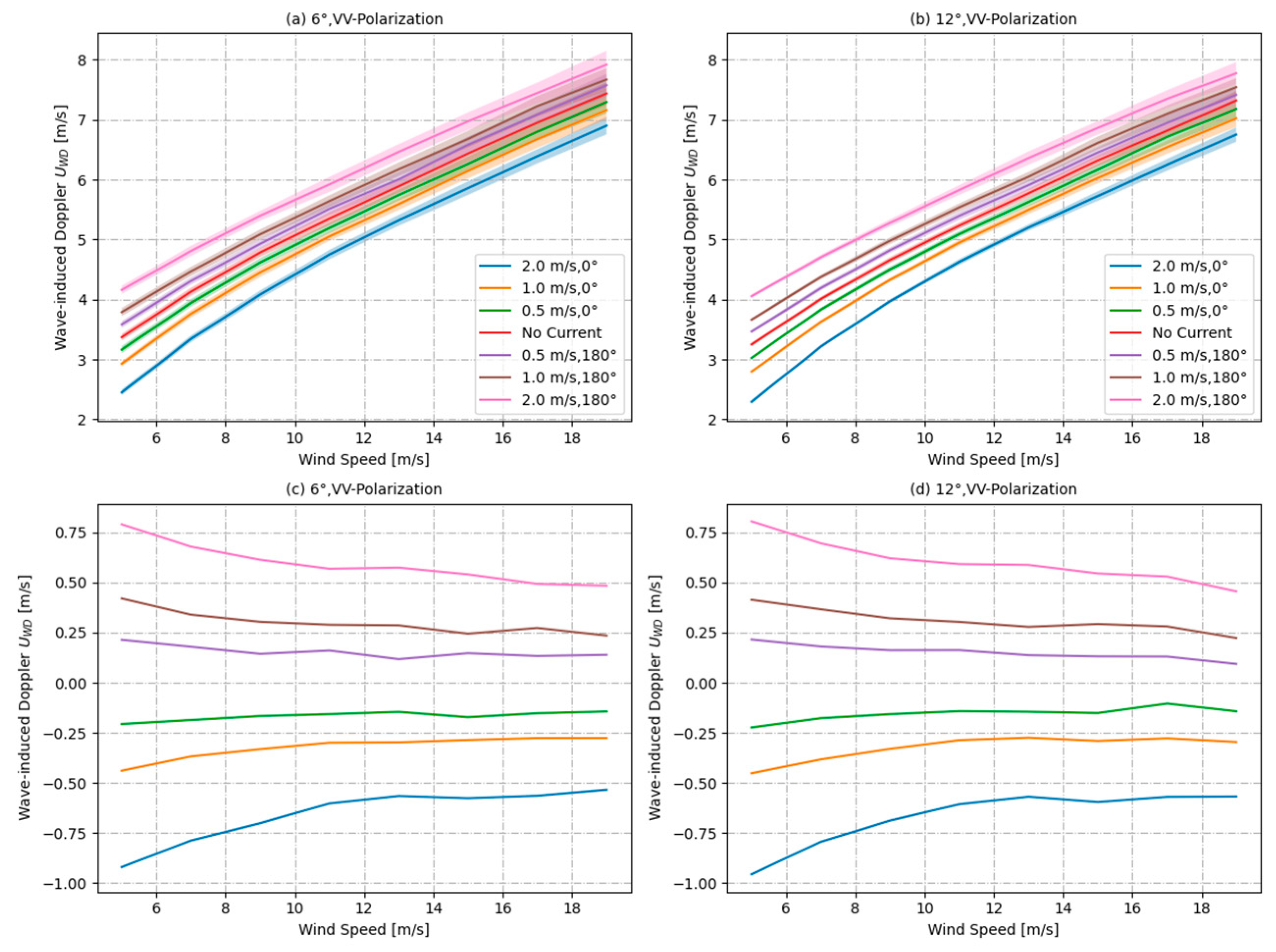
4.3.1. Contribution of Wind Speed to Wave-Induced Doppler Velocity
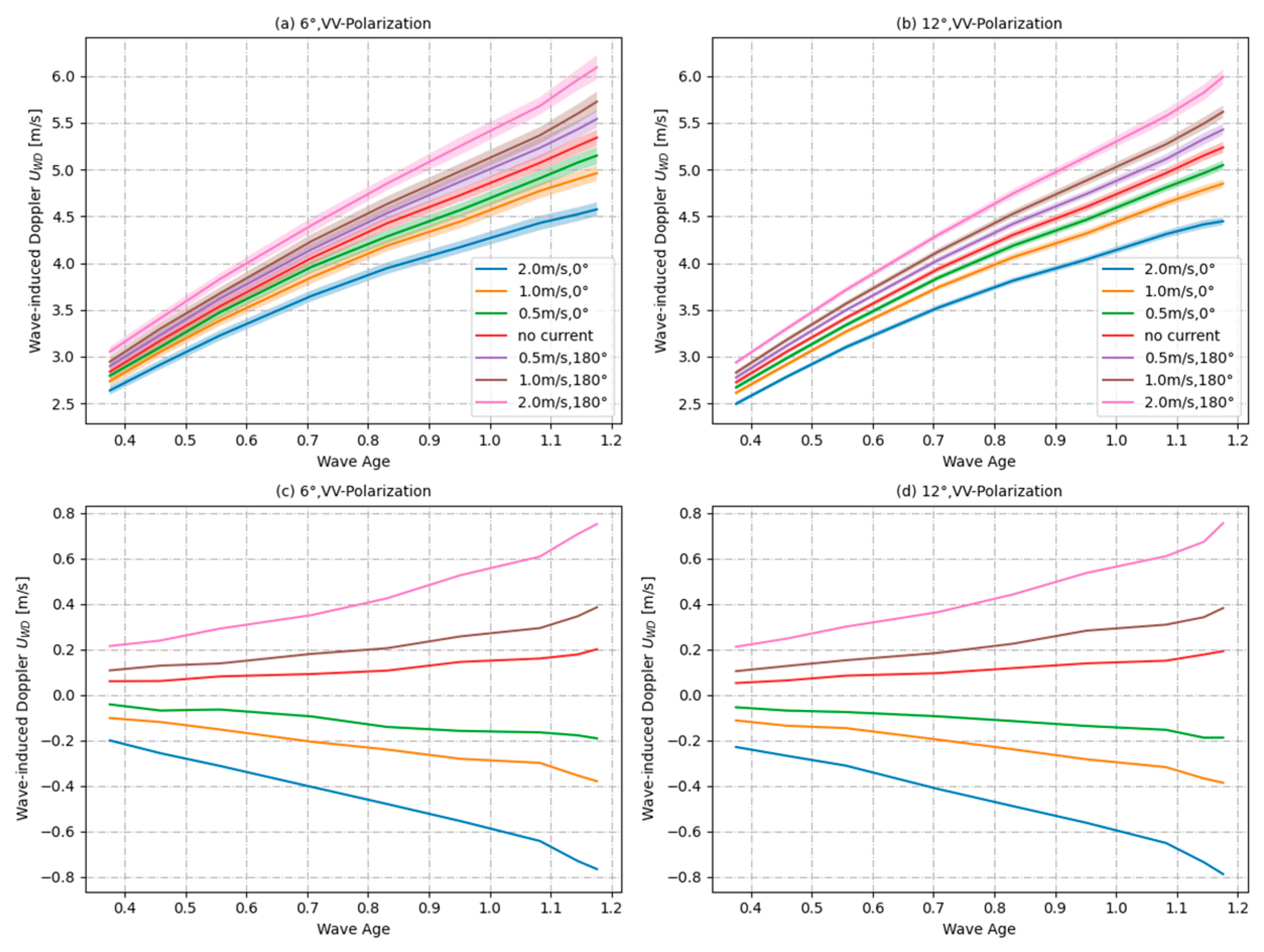
4.3.2. Contribution of Wind and Wave Development to Wave-Induced Doppler Velocity
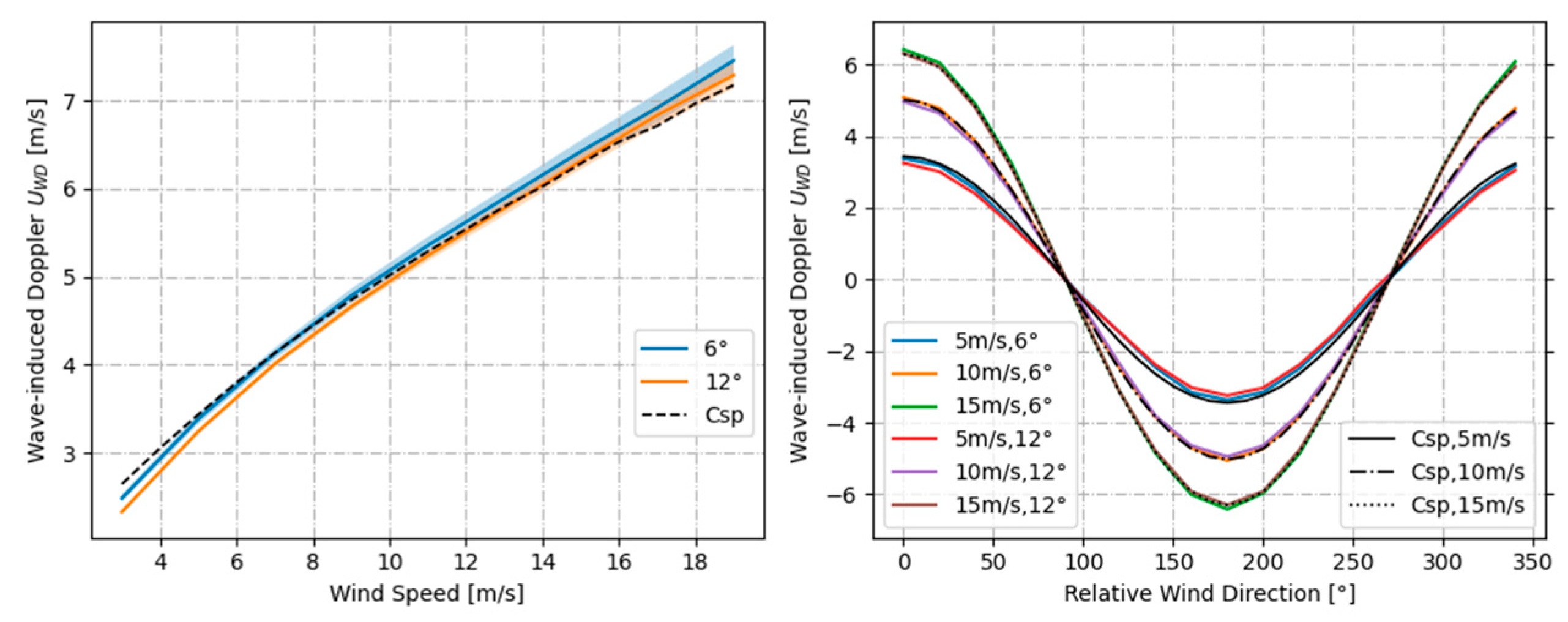
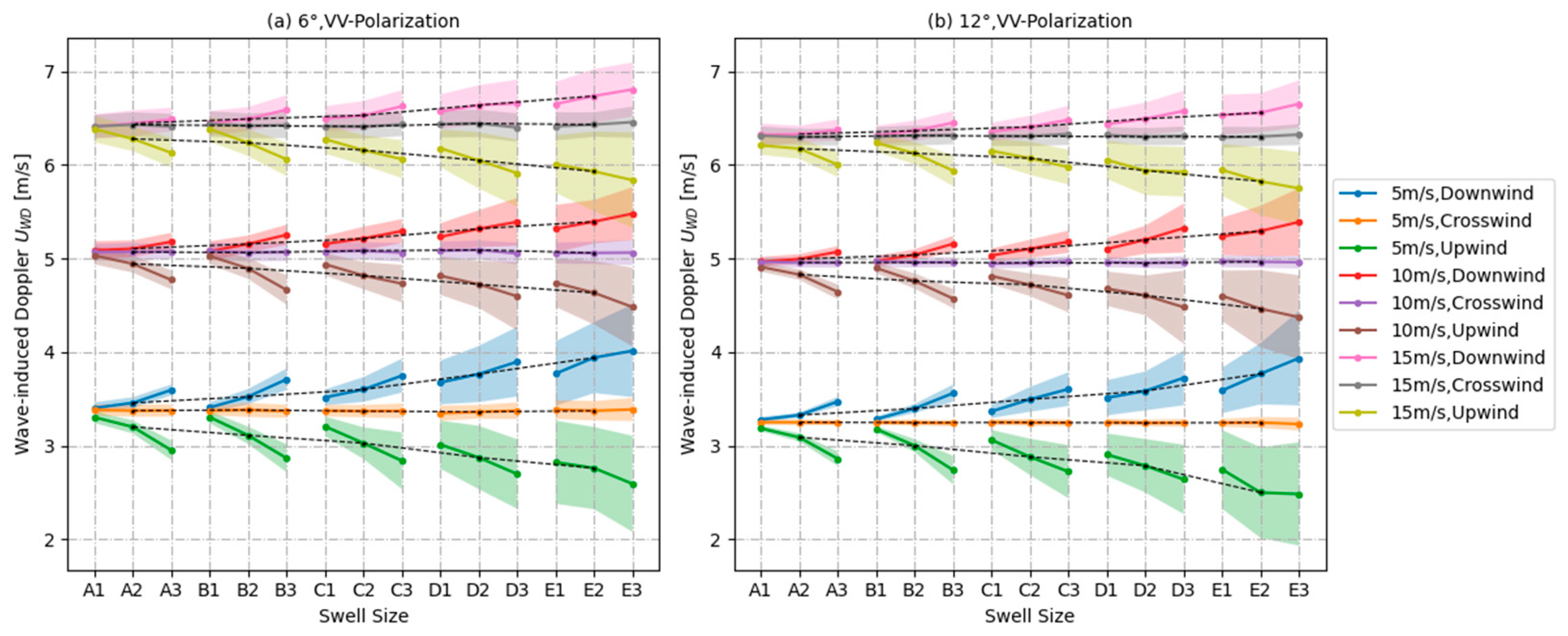
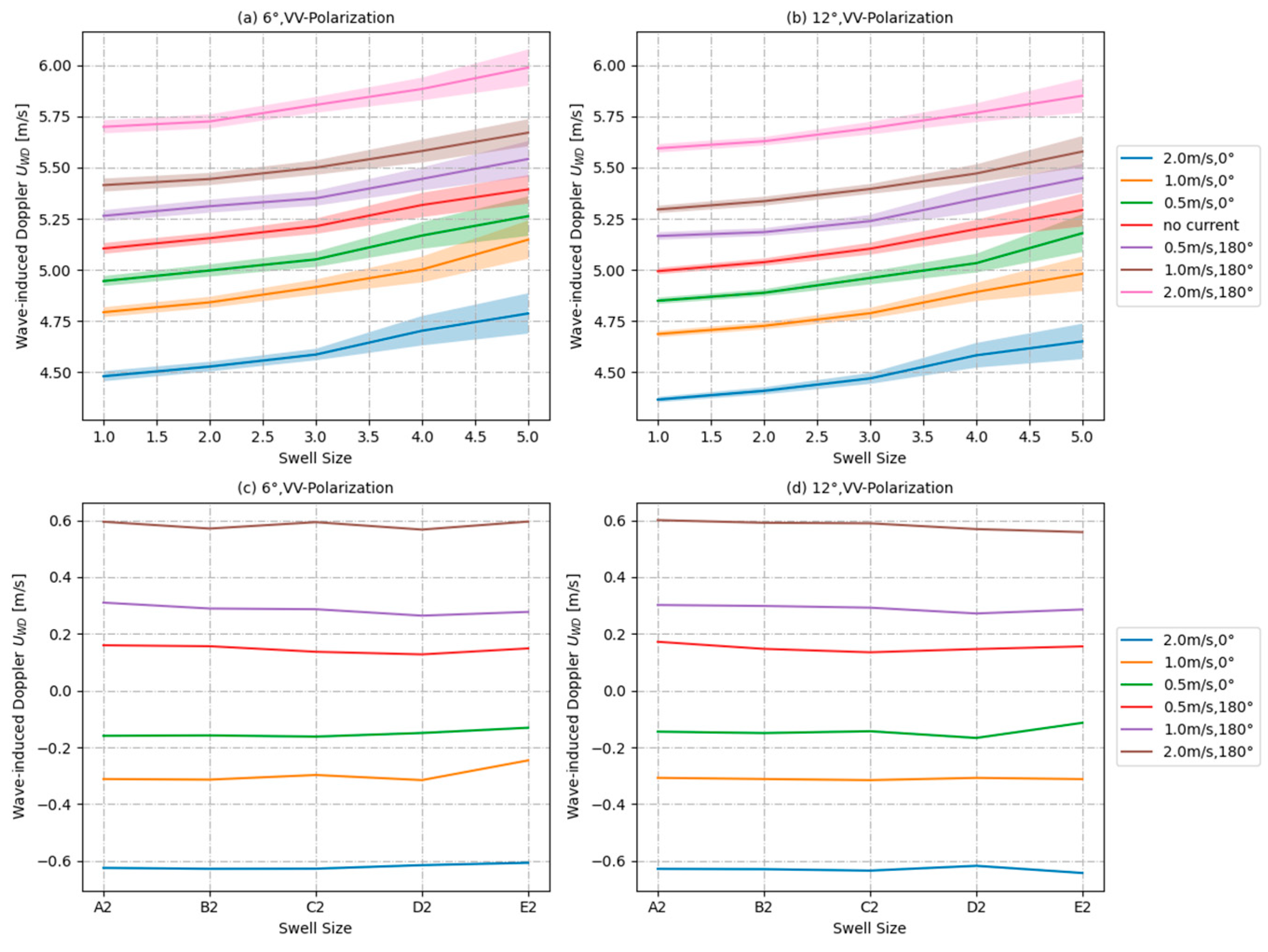
4.3.3. Combined Contribution of Wind and Swell to Wave-Induced Doppler Velocity
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Martz, H.E., Jr.; McNeil, B.J.; Amundson, S.A.; Aspnes, D.E.; Barnett, A.; Borak, T.B.; Braby, L.A.; Heimdahl, M.P.; Hyland, S.L.; Jacobson, S.H.; et al. National Academies of Sciences, Engineering, and Medicine. In Thriving on Our Changing Planet: A Decadal Strategy for Earth Observation from Space; The National Academies Press: Washington, DC, USA, 2018; Volume 700. [Google Scholar] [CrossRef]
- Rodríguez, E.; Wineteer, A.; Perkovic-Martin, D.; Gál, T.; Anderson, S.; Zuckerman, S.; Stear, J.; Yang, X. Ka-band Doppler scatterometry over a loop current Eddy. Remote Sens. 2020, 12, 2388. [Google Scholar] [CrossRef]
- Dong, C.; McWilliams, J.C.; Liu, Y.; Chen, D. Global heat and salt transports by Eddy Movement. Nat. Commun. 2014, 5, 3294. [Google Scholar] [CrossRef] [PubMed]
- Romeiser, R. Ocean applications of Interferometric SAR. In Encyclopedia of Earth Sciences Series; Springer: Amsterdam, The Netherlands, 2014; pp. 426–428. [Google Scholar] [CrossRef]
- Ardhuin, F.; Aksenov, Y.; Benetazzo, A.; Bertino, L.; Brandt, P.; Caubet, E.; Chapron, B.; Collard, F.; Cravatte, S.; Delouis, J.-M.; et al. Measuring currents, ice drift, and waves from space: The sea surface kinematics multiscale monitoring (skim) concept. Ocean Sci. 2018, 14, 337–354. [Google Scholar] [CrossRef]
- Nouguier, F.; Chapron, B.; Collard, F.; Mouche, A.A.; Rascle, N.; Ardhuin, F.; Wu, X. Sea surface kinematics from near-nadir radar measurements. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6169–6179. [Google Scholar] [CrossRef]
- Marié, L.; Collard, F.; Nouguier, F.; Pineau-Guillou, L.; Hauser, D.; Boy, F.; Méric, S.; Sutherland, P.; Peureux, C.; Monnier, G.; et al. Measuring ocean total surface current velocity with the Kuros and Karadoc Airborne near-nadir doppler radars: A multi-scale analysis in preparation for the skim mission. Ocean Sci. 2020, 16, 1399–1429. [Google Scholar] [CrossRef]
- Ardhuin, F.; Brandt, P.; Gaultier, L.; Donlon, C.; Battaglia, A.; Boy, F.; Casal, T.; Chapron, B.; Collard, F.; Cravatte, S.; et al. Skim, a candidate satellite mission exploring global ocean currents and waves. Front. Mar. Sci. 2019, 6, 209. [Google Scholar] [CrossRef]
- Rodríguez, E.; Bourassa, M.; Chelton, D.; Farrar, J.T.; Long, D.; Perkovic-Martin, D.; Samelson, R. The winds and currents mission concept. Front. Mar. Sci. 2019, 6, 438. [Google Scholar] [CrossRef]
- Du, Y.; Dong, X.; Jiang, X.; Zhang, Y.; Zhu, D.; Sun, Q.; Wang, Z.; Niu, X.; Chen, W.; Zhu, C.; et al. Ocean Surface Current Multiscale Observation Mission (OSCOM): Simultaneous measurement of ocean surface current, vector wind, and temperature. Prog. Oceanogr. 2021, 193, 102531. [Google Scholar] [CrossRef]
- Rodríguez, E.; Wineteer, A.; Perkovic-Martin, D.; Gál, T.; Stiles, B.; Niamsuwan, N.; Monje, R. Estimating ocean vector winds and currents using a Ka-band pencil-beam Doppler scatterometer. Remote Sens. 2018, 10, 576. [Google Scholar] [CrossRef]
- Chapron, B. Direct measurements of ocean surface velocity from space: Interpretation and validation. J. Geophys. Res. 2005, 110, C07008. [Google Scholar] [CrossRef]
- Fois, F.; Hoogeboom, P.; Le Chevalier, F.; Stoffelen, A. An analytical model for the description of the full-polarimetric sea surface Doppler signature. J. Geophys. Res. Oceans 2015, 120, 988–1015. [Google Scholar] [CrossRef]
- Johannessen, J.A.; Chapron, B.; Collard, F.; Kudryavtsev, V.; Mouche, A.; Akimov, D.; Dagestad, K.-F. Direct ocean surface velocity measurements from space: Improved quantitative interpretation of Envisat Asar Observations. Geophys. Res. Lett. 2008, 35, L22608. [Google Scholar] [CrossRef]
- Romeiser, R.; Thompson, D.R. Numerical Study on the along-track interferometric radar imaging mechanism of oceanic surface currents. IEEE Trans. Geosci. Remote Sens. 2000, 38, 446–458. [Google Scholar] [CrossRef]
- Johannessen, J.A.; Kudryavtsev, V.; Chapron, B. Backscatter and Doppler Signals of Surface Current in SAR Images: A Step Towards Inverse Modelling. In Proceedings of the OceanSAR 2006-Third Workshop on Coastal and Marine Applications of SAR, St. John’s, NL, Canada, 23–25 October 2006. [Google Scholar]
- Hansen, M.W.; Kudryavtsev, V.; Chapron, B.; Johannessen, J.A.; Collard, F.; Dagestad, K.-F.; Mouche, A.A. Simulation of radar backscatter and Doppler shifts of wave–current interaction in the presence of strong tidal current. Remote Sens. Environ. 2012, 120, 113–122. [Google Scholar] [CrossRef]
- Yurovsky, Y.; Kudryavtsev, V.; Grodsky, S.; Chapron, B. Sea surface ka-band Doppler measurements: Analysis and model development. Remote Sens. 2019, 11, 839. [Google Scholar] [CrossRef]
- Martin, A.C.; Gommenginger, C.; Marquez, J.; Doody, S.; Navarro, V.; Buck, C. Wind-wave-induced velocity in ATI SAR ocean surface currents: First experimental evidence from an airborne campaign. J. Geophys. Res. Oceans 2016, 121, 1640–1653. [Google Scholar] [CrossRef]
- Collard, F.; Mouche, A.; Chapron, B.; Danilo, C.; Johannessen, J. Routine high resolution observation of selected major surface currents from space. In Proceedings of the SEASAR 2008, SP-656, ESA, ESA-ESRIN, Frascati, Italy, 21–25 January 2008. [Google Scholar]
- Krug, M.; Mouche, A.; Collard, F.; Johannessen, J.A.; Chapron, B. Mapping the agulhas current from space: An assessment of asar surface current velocities. J. Geophys. Res. Oceans 2010, 115, 10026. [Google Scholar] [CrossRef]
- Mouche, A.A.; Collard, F.; Chapron, B.; Dagestad, K.-F.; Guitton, G.; Johannessen, J.A.; Kerbaol, V.; Hansen, M.W. On the use of Doppler shift for sea surface wind retrieval from SAR. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2901–2909. [Google Scholar] [CrossRef]
- Li, S.; Liu, B.; Shen, H.; Hou, Y.; Perrie, W. Wind wave effects on remote sensing of sea surface currents from SAR. J. Geophys. Res. Oceans 2020, 125. [Google Scholar] [CrossRef]
- Yurovsky, Y.Y.; Kudryavtsev, V.N.; Grodsky, S.A.; Chapron, B. Ka-band Doppler scatterometry: A strong wind case study. Remote Sens. 2022, 14, 1348. [Google Scholar] [CrossRef]
- Miao, Y.; Dong, X.; Bourassa, M.A.; Zhu, D. Effects of ocean wave directional spectra on Doppler retrievals of Ocean Surface Current. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4204812. [Google Scholar] [CrossRef]
- Bao, Q.; Lin, M.; Zhang, Y.; Dong, X.; Lang, S.; Gong, P. Ocean surface current inversion method for a Doppler scatterometer. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6505–6516. [Google Scholar] [CrossRef]
- Bourassa, M.A.; Rodriguez, E.; Chelton, D. Winds and currents mission: Ability to observe mesoscale AIR/SEA coupling. In Proceedings of the International Geoscience and Remote Sensing Symposium—IGARSS, Beijing, China, 10–15 July 2016; pp. 7392–7395. [Google Scholar] [CrossRef]
- Yan, Q.; Zhang, J.; Fan, C.; Meng, J. Analysis of ku- and ka-band sea surface backscattering characteristics at low-incidence angles based on the GPM dual-frequency precipitation radar measurements. Remote Sens. 2019, 11, 754. [Google Scholar] [CrossRef]
- Stuhlmeier, R. Gerstner’s Water Wave and Mass Transport. J. Math. Fluid Mech. 2015, 17, 761–767. [Google Scholar] [CrossRef]
- Nouguier, F.; Guérin, C.-A.; Chapron, B. “choppy wave” model for nonlinear gravity waves. J. Geophys. Res. 2009, 114, C09012. [Google Scholar] [CrossRef]
- Fournier, A.; Reeves, W.T. A simple model of ocean waves. ACM SIGGRAPH Comput. Graph. 1986, 20, 75–84. [Google Scholar] [CrossRef]
- Massel, S.R. On the geometry of Ocean Surface Waves. Oceanologia 2011, 53, 521–548. [Google Scholar] [CrossRef]
- Shahrezaei, I.H.; Kim, H.-C. A novel sar fractal roughness modeling of complex random polar media and textural synthesis based on a numerical scattering distribution function processing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7386–7409. [Google Scholar] [CrossRef]
- Donelan, A.M.; Hamilton, J.; Hui, H.W. Directional spectra of wind-generated ocean waves. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1985, 315, 509–562. [Google Scholar] [CrossRef]
- Hasselmann, K.; Barnett, T.; Bouws, E.; Carlson, H.; Cartwright, D.; Enke, K.; Ewing, J.; Gienapp, H.; Hasselmann, D.; Kruseman, P.; et al. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Deut. Hydrogr. Z. 1973, 8, 1–95. Available online: https://pure.mpg.de/pubman/item/item_3262854_4/component/file_3282032/1973_Jonswap-Hasselmann1973.pdf (accessed on 12 February 2023).
- Kahma, K.K. A study of the growth of the wave spectrum with fetch. J. Phys. Oceanogr. 1981, 11, 1503–1515. [Google Scholar] [CrossRef]
- Kitaigordskii, S.A.; Krasitskii, V.P.; Zaslavskii, M.M. On Phillips’ theory of equilibrium range in the spectra of wind-generated gravity waves. J. Phys. Oceanogr. 1975, 5, 410–420. [Google Scholar] [CrossRef]
- Phillips, O.M. Spectral and statistical properties of the equilibrium range in wind-generated gravity waves. J. Fluid Mech. 1985, 156, 505–531. [Google Scholar] [CrossRef]
- Elfouhaily, T.; Chapron, B.; Katsaros, K.; Vandemark, D. A unified directional spectrum for long and short wind-driven waves. J. Geophys. Res. Oceans 1997, 102, 15781–15796. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Introduction to Random Surface Scattering and Emission. In Microwave Remote Sensing: Active and Passive, Vol.II: Radar Remote Sensing and Surface Scattering and Emission Theory; Addision-Wesbey Publishing: London, UK, 1982; pp. 922–1033. [Google Scholar]
- Mouche, A.A.; Chapron, B.; Reul, N.; Collard, F. Predicted doppler shifts induced by ocean surface wave displacements using asymptotic electromagnetic wave scattering theories. Wave Random Complex Media 2008, 18, 185–196. [Google Scholar] [CrossRef]
- McDaniel, S.T. Small-slope predictions of microwave backscatter from the Sea Surface. Wave Random Complex Media 2001, 11, 343–360. [Google Scholar] [CrossRef]
- Nouguier, F.; Mouche, A.; Rascle, N.; Chapron, B.; Vandemark, D. Analysis of dual-frequency ocean backscatter measurements at ku- and ka-bands using near-nadir incidence GPM radar data. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1310–1314. [Google Scholar] [CrossRef]
- Boisot, O.; Pioch, S.; Fatras, C.; Caulliez, G.; Bringer, A.; Borderies, P.; Lalaurie, J.-C.; Guérin, C.-A. Ka-band backscattering from water surface at small incidence: A wind-wave tank study. J. Geophys. Res. Oceans 2015, 120, 3261–3285. [Google Scholar] [CrossRef]
- Kodis, R. A note on the theory of scattering from an irregular surface. IEEE T. Antenn. Propag. 1966, 14, 77–82. [Google Scholar] [CrossRef]
- Graber, H.C.; Thompson, D.R.; Carande, R.E. Ocean surface features and currents measured with synthetic aperture radar interferometry and HF radar. J. Geophys. Res. Oceans 1996, 101, 25813–25832. [Google Scholar] [CrossRef]
- Wineteer, A.; Perkovic-Martin, D.; Monje, R.; Rodríguez, E.; Gál, T.; Niamsuwan, N.; Nicaise, F.; Srinivasan, K.; Baldi, C.; Majurec, N.; et al. Measuring winds and currents with Ka-band Doppler scatterometry: An airborne implementation and progress towards a spaceborne mission. Remote Sens. 2020, 12, 1021. [Google Scholar] [CrossRef]
- Cox, C.; Munk, W. Measurement of the roughness of the sea surface from photographs of the sun’s glitter. J. Opt. Soc. Am. 1954, 44, 838. [Google Scholar] [CrossRef]
- Lee, J.-S.; Jansen, R.W.; Schuler, D.L.; Ainsworth, T.L.; Marmorino, G.O.; Chubb, S.R. Polarimetric analysis and modeling of multifrequency SAR signatures from Gulf Stream fronts. IEEE J. Ocean. Eng. 1998, 23, 322–333. [Google Scholar] [CrossRef]
- Bao, Q.; Dong, X.; Zhu, D.; Lang, S.; Xu, X. The feasibility of ocean surface current measurement using pencil-beam rotating scatterometer. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3441–3451. [Google Scholar] [CrossRef]
- Valenzuela, G.R. Theories for the interaction of electromagnetic and Oceanic Waves—A Review. Bound-Lay. Meteorol. 1978, 13, 61–85. [Google Scholar] [CrossRef]
- Kudryavtsev, V. A semiempirical model of the normalized radar cross-section of the sea surface 1. background model. J. Geophys. Res. 2003, 108, FET 2-1–FET 2-24. [Google Scholar] [CrossRef]
- Kudryavtsev, V. On radar imaging of current features: 1. model and comparison with observations. J. Geophys. Res. Oceans 2005, 110, 07016. [Google Scholar] [CrossRef]
- Hossan, A.; Jones, W.L. Ku- and ka-band Ocean Surface Radar backscatter model functions at low-incidence angles using full-swath GPM DPR Data. Remote Sens. 2021, 13, 1569. [Google Scholar] [CrossRef]
- Yurovsky, Y.Y.; Kudryavtsev, V.N.; Chapron, B.; Grodsky, S.A. Modulation of ka-band Doppler radar signals backscattered from the Sea Surface. IEEE Trans. Geosc. Remote Sens. 2018, 56, 2931–2948. [Google Scholar] [CrossRef]
- Mouche, A.A.; Hauser, D.; Daloze, J.-F.; Guerin, C. Dual-polarization measurements at C-band over the ocean: Results from airborne radar observations and comparison with Envisat Asar Data. IEEE Trans. Geosc. Remote Sens. 2005, 43, 753–769. [Google Scholar] [CrossRef]
- Bao, L.; Zhang, X.; Cao, C.; Wang, X.; Jia, Y.; Gao, G.; Zhang, Y.; Wan, Y.; Zhang, J. Impact of polarization basis on wind and wave parameters estimation using the azimuth cutoff from GF-3 Sar Imagery. IEEE Trans. Geosc. Remote Sens. 2022, 60, 5234716. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S. The Statistical Analysis of a Random, Moving Surface. Philos. Trans. R. Soc. A 1957, 249, 321–387. [Google Scholar] [CrossRef]
- Dobson, F.; Perrie, W.; Toulany, B. On the deep-water fetch laws for wind-generated surface gravity waves. Atmos. Ocean 1989, 27, 210–236. [Google Scholar] [CrossRef]
- Hwang, P.A. Observations of swell influence on Ocean Surface Roughness. J. Geophys. Res. Oceans 2008, 113, C12024. [Google Scholar] [CrossRef]






| Radar Parameters | Sea-State Parameters | ||
|---|---|---|---|
| Radar frequency | 35 GHz | Wind speed | 3~19 m/s |
| Polarization | VV/HH | Wind direction | 0~360° |
| PRF | 32,000 Hz | Wind fetch | 5~2000 km |
| Number of pulses | 1024 | Swell frequency | 0.051~0.140 Hz |
| Azimuth angle | 0~360° | Swell wave height | 0.3~4.5 m |
| Incidence angle | 1~15° | Swell direction | 0~360° |
| Platform altitude | 690 km | Current velocity | 0.5, 1, 2 m/s |
| Bandwidth | 200 MHz | Current direction | 0~360° |
| No. | Frequency (Hz) | Wavelength (m) | Effective Wave Height (m) | Swell Scale |
|---|---|---|---|---|
| 1 | 0.140 | ~80 | 0.3 | A1 |
| 2 | 0.5 | A2 | ||
| 3 | 0.8 | A3 | ||
| 4 | 0.102 | ~150 | 0.5 | B1 |
| 5 | 1 | B2 | ||
| 6 | 1.5 | B3 | ||
| 7 | 0.072 | ~300 | 1.5 | C1 |
| 8 | 2 | C2 | ||
| 9 | 2.5 | C3 | ||
| 10 | 0.059 | ~450 | 2.5 | D1 |
| 11 | 3 | D2 | ||
| 12 | 3.5 | D3 | ||
| 13 | 0.051 | ~600 | 3.5 | E1 |
| 14 | 4 | E2 | ||
| 15 | 4.5 | E3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Meng, J.; Fan, C.; Chen, P. Effects of Wave-Induced Doppler Velocity on the Sea Surface Current Measurements by Ka-Band Real-Aperture Radar with Small Incidence Angle. Remote Sens. 2023, 15, 1127. https://doi.org/10.3390/rs15041127
Ma X, Meng J, Fan C, Chen P. Effects of Wave-Induced Doppler Velocity on the Sea Surface Current Measurements by Ka-Band Real-Aperture Radar with Small Incidence Angle. Remote Sensing. 2023; 15(4):1127. https://doi.org/10.3390/rs15041127
Chicago/Turabian StyleMa, Xiangchao, Junmin Meng, Chenqing Fan, and Ping Chen. 2023. "Effects of Wave-Induced Doppler Velocity on the Sea Surface Current Measurements by Ka-Band Real-Aperture Radar with Small Incidence Angle" Remote Sensing 15, no. 4: 1127. https://doi.org/10.3390/rs15041127
APA StyleMa, X., Meng, J., Fan, C., & Chen, P. (2023). Effects of Wave-Induced Doppler Velocity on the Sea Surface Current Measurements by Ka-Band Real-Aperture Radar with Small Incidence Angle. Remote Sensing, 15(4), 1127. https://doi.org/10.3390/rs15041127