Relative Sea Level Trends for the Coastal Areas of Peninsular and East Malaysia Based on Remote and In Situ Observations
Abstract
1. Introduction
2. Study Area
3. Data and Methodology
3.1. Relative Sea-Level Change from Tide-Gauge Data
3.2. Absolute Sea Level Observed with Satellite Altimetry
3.3. Reference Frame and Vertical Land Motion (VLM)
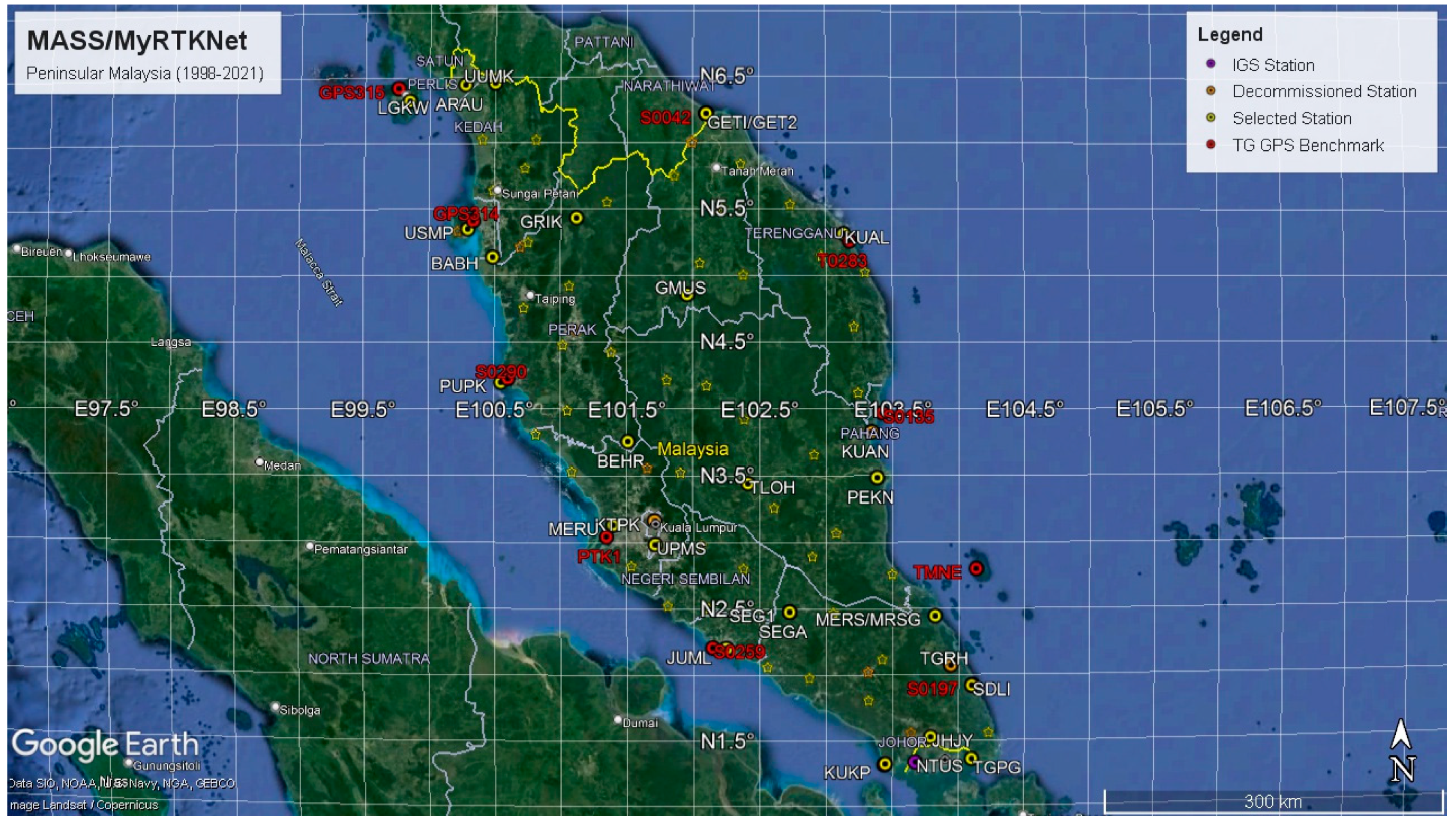
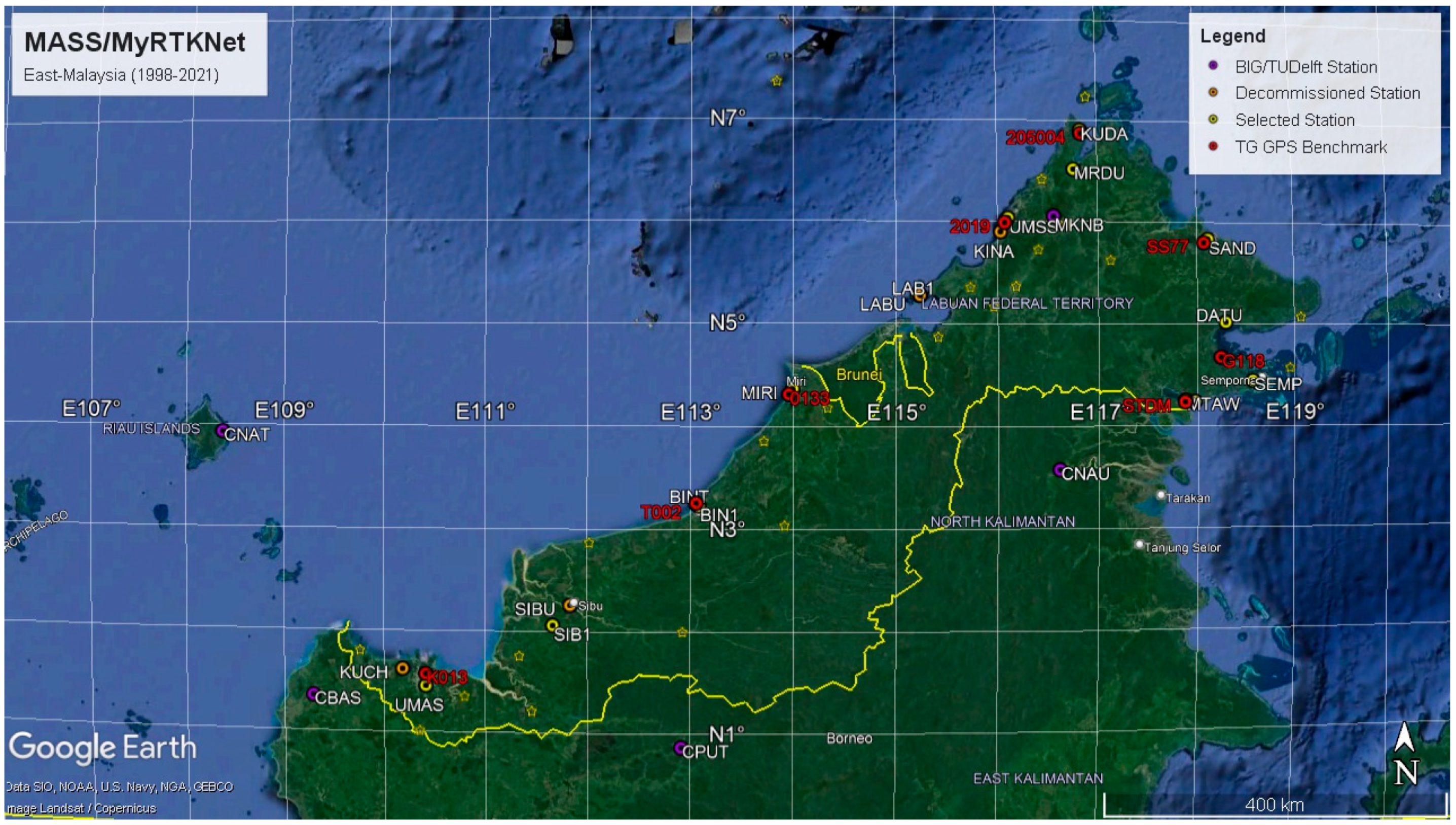
3.3.1. MASS/MyRTKNet Subset Network Selection
- Close to tide gauge (TG) stations;
- Close to (decommissioned) MASS stations (combined position time series);
- Additional inland stations (which can be used as stable reference stations);
- Early MyRTKNet stations only (2005–2007) (to construct long position time series);
- Evenly distributed throughout both Peninsular and East Malaysia.
3.3.2. GPS Data Analysis
3.3.3. GPS Velocity Estimation
Peninsular Malaysia
East Malaysia
4. Results on Relative Sea-Level Rise
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ASEAN | Association of Southeast Asian Nations |
| ASL | Absolute Sea Level |
| BIG | Geospatial Information Agency (formerly known as BAKOSURTANAL) |
| DSMM | Department Survey and Mapping Malaysia |
| EU | European Union |
| EUMETSAT | European Organisation for the Exploitation of Meteorological Satellites |
| GEODYSSEA | Geodynamics of South and South East Asia |
| GIA | Glacial Isostatic Adjustment |
| GNSS | Global Navigation Satellite System |
| GPS | Global Positioning System |
| GIPSY-OASIS | GNSS-Inferred Positioning System and Orbit Analysis Simulation Software |
| IERS | International Earth Rotation and Reference Systems Service |
| IGS | International GNSS Service |
| InaCORS | Indonesian Continuously Operating Reference Station |
| IOD | Indian Ocean Dipole |
| ITRF | International Terrestrial Reference Frame |
| JPL | Jet Propulsion Laboratory |
| LRM | Low-Resolution Mode |
| MASS | Malaysian Active GPS System |
| MSL | Mean Sea Level |
| Mw | Moment Magnitude |
| MyRTKNet | Malaysia Real-Time Kinematic GNSS Network |
| NNR | No Net Rotation |
| NOAA | National Oceanic and Atmospheric Administration |
| NWO | Dutch Research Council |
| PPP | Precise Point Positioning |
| PS InSAR | Persistent Scatterer Interferometric Synthetic Aperture Radar |
| PSMSL | Permanent Service for Mean Sea Level |
| RADS | Radar Altimeter Database System |
| RSL | Relative Sea Level |
| SALT | Satellite Altimetry |
| SLA | Sea Level Anomaly |
| TG | Tide Gauge |
| TUDelft | Delft University of Technology |
| VLM | Vertical Land Motion |
| WGS84 | World Geodetic System 1984 |
| WRMS | Weighted Root Mean Square |
| yr | year (mm/yr = mm/year) |
References
- White, N.J. Coastal and global averaged sea level rise for 1950 to 2000. Geophys. Res. Lett. 2005, 32, L01601. [Google Scholar] [CrossRef]
- Tang, K.H.D. Climate change in Malaysia: Trends, contributors, impacts, mitigation and adaptations. Sci. Total Environ. 2019, 650, 1858–1871. [Google Scholar] [CrossRef]
- Bagheri, M.; Ibrahim, Z.Z.; Akhir, M.F.; Oryani, B.; Rezania, S.; Wolf, I.D.; Pour, A.B.; Talaat, W.I.A.W. Impacts of Future Sea-Level Rise under Global Warming Assessed from Tide Gauge Records: A Case Study of the East Coast Economic Region of Peninsular Malaysia. Land 2021, 10, 1382. [Google Scholar] [CrossRef]
- Sarkar, M.S.K.; Begum, R.A.; Pereira, J.J.; Jaafar, A.H.; Saari, M.Y. Impacts of and Adaptations to Sea Level Rise in Malaysia. Asian J. Water Environ. 2014, 11, 29–36. [Google Scholar]
- Kamaruddin, A.H.; Din, A.H.M.; Pa’suya, M.F.; Omar, K.M. Long-term sea level trend from tidal data in Malaysia. In Proceedings of the 2016 7th IEEE Control and System Graduate Research Colloquium (ICSGRC), Shah Alam, Malaysia, 8 August 2016; pp. 187–192. [Google Scholar]
- Simons, W.J.F.; Naeije, M.C.; Brown, B.E.; Niemnil, S.; Pradit, S.; Thongtham, N.; Mustafar, M.A.; Towatana, P.; Darnsawasdi, R.; Yucharoen, M.; et al. Vertical motion of Phuket Island (1994–2018) due to the Sumatra-Andaman mega-thrust earthquake cycle: Impact on sea-level and consequences for coral reefs. Mar. Geol. 2019, 414, 92–102. [Google Scholar] [CrossRef]
- Kowalczyk, K.; Pajak, K.; Wieczorek, B.; Naumowicz, B. An Analysis of Vertical Crustal Movements along the European Coast from Satellite Altimetry, Tide Gauge, GNSS and Radar Interferometry. Remote Sens. 2021, 13, 2173. [Google Scholar] [CrossRef]
- Klos, A.; Kusche, J.; Fenoglio-Marc, L.; Bos, M.S.; Bogusz, J. Introducing a vertical land motion model for improving estimates of sea level rates derived from tide gauge records affected by earthquakes. GPS Solut. 2019, 23, 102. [Google Scholar] [CrossRef]
- Harvey, T.C.; Hamlington, B.D.; Frederikse, T.; Nerem, R.S.; Piecuch, C.G.; Hammond, W.C.; Blewitt, G.; Thompson, P.R.; Bekaert, D.P.S.; Landerer, F.W.; et al. Ocean mass, sterodynamic effects, and vertical land motion largely explain US coast relative sea level rise. Commun. Earth Environ. 2021, 2, 233. [Google Scholar] [CrossRef]
- Din, A.H.M.; Reba, M.N.M.; Omar, K.M.; Ses, S.; Latip, A.S.A. Monitoring Vertical Land Motion in Malaysia Using Global Positioning System (GPS). In Proceedings of the the 36th Asian Conference on Remote Sensing (ACRS), Quezon City, Philippines, 19–23 October 2015; p. 11. [Google Scholar]
- Azhari, M.; Altamimi, Z.; Azman, G.; Kadir, M.; Simons, W.J.F.; Sohaime, R.; Yunus, M.Y.; Irwan, M.J.; Asyran, C.A.; Soeb, N.; et al. Semi-kinematic geodetic reference frame based on the ITRF2014 for Malaysia. J. Geod. Sci. 2020, 10, 91–109. [Google Scholar] [CrossRef]
- Satirapod, C.; Trisirisatayawong, I.; Fleitout, L.; Garaud, J.D.; Simons, W.J.F. Vertical motions in Thailand after the 2004 Sumatra–Andaman Earthquake from GPS observations and its geophysical modelling. Adv. Space Res. 2013, 51, 1565–1571. [Google Scholar] [CrossRef]
- Vigny, C.; Simons, W.J.F.; Abu, S.; Bamphenyu, R.; Satirapod, C.; Choosakul, N.; Subarya, C.; Socquet, A.; Omar, K.; Abidin, H.Z.; et al. Insight into the 2004 Sumatra–Andaman earthquake from GPS measurements in southeast Asia. Nature 2005, 436, 201–206. [Google Scholar] [CrossRef]
- Luu, Q.H.; Tkalich, P.; Tay, T.W. Sea level trend and variability around Peninsular Malaysia. Ocean Sci. 2015, 11, 617–628. [Google Scholar] [CrossRef]
- Hamid, A.I.A.; Din, A.H.M.; Hwang, C.; Khalid, N.F.; Tugi, A.; Omar, K.M. Contemporary sea level rise rates around Malaysia: Altimeter data optimization for assessing coastal impact. J. Asian Earth Sci. 2018, 166, 247–259. [Google Scholar] [CrossRef]
- Hamid, A.I.A.; Din, A.H.M.; Khalid, N.F.; Omar, K.M. Acceleration of Sea Level Rise over Malaysian Seas from Satellite Altimeter. Int. Arch. Photogramm. 2016, 42, 277. [Google Scholar] [CrossRef]
- Din, A.H.M.; Zulkifli, N.A.; Hamden, M.H.; Aris, W.A.W. Sea level trend over Malaysian seas from multi-mission satellite altimetry and vertical land motion corrected tidal data. Adv. Space Res. 2019, 63, 3452–3472. [Google Scholar] [CrossRef]
- Cob, S.; Kadir, M.; Forsberg, R.; Simons, W.; Naeije, M.; Din, A.H.; Yacob, H.; Amat, A.; Mahdzur, D.; Ibrahim, Z.; et al. Epoch-Based Height Reference System for Sea Level Rise Impact Assessment on the Coast of Peninsular Malaysia. Remote Sens. 2022, 14, 6179. [Google Scholar] [CrossRef]
- Hamilton, W.B. Tectonics of the Indonesian Region; US Government Printing Office (USGS): Washington, DC, USA, 1979; Volume 1078. [Google Scholar] [CrossRef]
- Simons, W.J.F.; Socquet, A.; Vigny, C.; Ambrosius, B.A.C.; Haji Abu, S.; Promthong, C.; Subarya, C.; Sarsito, D.A.; Matheussen, S.; Morgan, P.; et al. A decade of GPS in Southeast Asia: Resolving Sundaland motion and boundaries. J. Geophys. Res. 2007, 112, B06420. [Google Scholar] [CrossRef]
- Satirapod, C.; Simons, W.; Promthong, C.; Yousamran, S.; Trisirisatayawong, I. Deformation of Thailand as Detected by GPS Measurements due to the December 26th, 2004 Mega-Thrust Earthquake. Surv. Rev. 2007, 39, 109–115. [Google Scholar] [CrossRef]
- Bird, P. An updated digital model of plate boundaries. Geochem. Geophys. Geosys. 2003, 4. [Google Scholar] [CrossRef]
- Argus, D.F.; Gordon, R.G.; DeMets, C. Geologically current motion of 56 plates relative to the no-net-rotation reference frame. Geochem. Geophys. Geosys. 2011, 12, 1–13. [Google Scholar] [CrossRef]
- Mustafar, M.A.; Simons, W.J.F.; Tongkul, F.; Satirapod, C.; Omar, K.M.; Visser, P.N.A.M. Quantifying deformation in North Borneo with GPS. J. Geod. 2017, 91, 1241–1259. [Google Scholar] [CrossRef]
- Naeije, M.C.; Simons, W.J.F.; Pradit, S.; Niemnil, S.; Thongtham, N.; Mustafar, M.A.; Noppradit, P. Monitoring Megathrust-Earthquake-Cycle-Induced Relative Sea-Level Changes near Phuket, South Thailand, Using (Space) Geodetic Techniques. Remote Sens. 2022, 14, 5145. [Google Scholar] [CrossRef]
- Webster, P.J.; Moore, A.M.; Loschnigg, J.P.; Leben, R.R. Coupled ocean–atmosphere dynamics in the Indian Ocean during 1997–98. Nature 1999, 401, 356–360. [Google Scholar] [CrossRef]
- Saji, N.H.; Goswami, B.N.; Vinayachandran, P.N.; Yamagata, T. A dipole mode in the tropical Indian Ocean. Nature 1999, 401, 360–363. [Google Scholar] [CrossRef]
- Wöppelmann, G.; Marcos, M. Vertical land motion as a key to understanding sea level change and variability. Rev. Geophys. 2016, 54, 64–92. [Google Scholar] [CrossRef]
- Trisirisatayawong, I.; Naeije, M.; Simons, W.; Fenoglio-Marc, L. Sea level change in the Gulf of Thailand from GPS-corrected tide gauge data and multi-satellite altimetry. Glob. Planet. Change 2011, 76, 137–151. [Google Scholar] [CrossRef]
- Scharroo, R.; Leuliette, E.; Lillibridge, J.; Byrne, D.; Naeije, M.; Mitchum, G. RADS: Consistent Multi-Mission Products. In Proceedings of the 20 Years of Progress in Radar Altimatry, Venice, Italy, 24–29 September 2012; p. 69. [Google Scholar]
- Wilson, P.; Rais, J.; Reigber, C.; Reinhart, E.; Ambrosius, B.A.C.; Le Pichon, X.; Kasser, M.; Suharto, P.; Majid, D.A.; Yaakub, D.; et al. Study provides data on active plate tectonics in southeast Asia region. Eos Trans. Am. Geophys. Union 1998, 79, 545. [Google Scholar] [CrossRef]
- Jet Propulsion Laboratory. GNSS-Inferred Positioning System and Orbit Analysis Simulation Software (GIPSY-OASIS). Available online: https://gipsy-oasis.jpl.nasa.gov (accessed on 1 November 2019).
- Rebischung, P.; Schmid, R. IGS14/igs14. In atx: A new framework for the IGS products. In Proceedings of the AGU Fall Meeting, San Francisco, CA, USA, 14 December 2016. [Google Scholar]
- Altamimi, Z.; Rebischung, P.; Métivier, L.; Collilieux, X. ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J. Geophys. Res. Solid Earth 2016, 121, 6109–6131. [Google Scholar] [CrossRef]
- Bertiger, W.; Desai, S.D.; Haines, B.; Harvey, N.; Moore, A.W.; Owen, S.; Weiss, J.P. Single receiver phase ambiguity resolution with GPS data. J. Geod. 2010, 84, 327–337. [Google Scholar] [CrossRef]
- Blewitt, G.; Lavallée, D. Effect of annual signals on geodetic velocity. J. Geophys. Res. Solid Earth 2002, 107, ETG 9-1–ETG 9-11. [Google Scholar] [CrossRef]
- Ercan, A.; Bin Mohamad, M.F.; Kavvas, M.L. The impact of climate change on sea level rise at Peninsular Malaysia and Sabah-Sarawak. Hydrol. Processes 2013, 27, 367–377. [Google Scholar] [CrossRef]
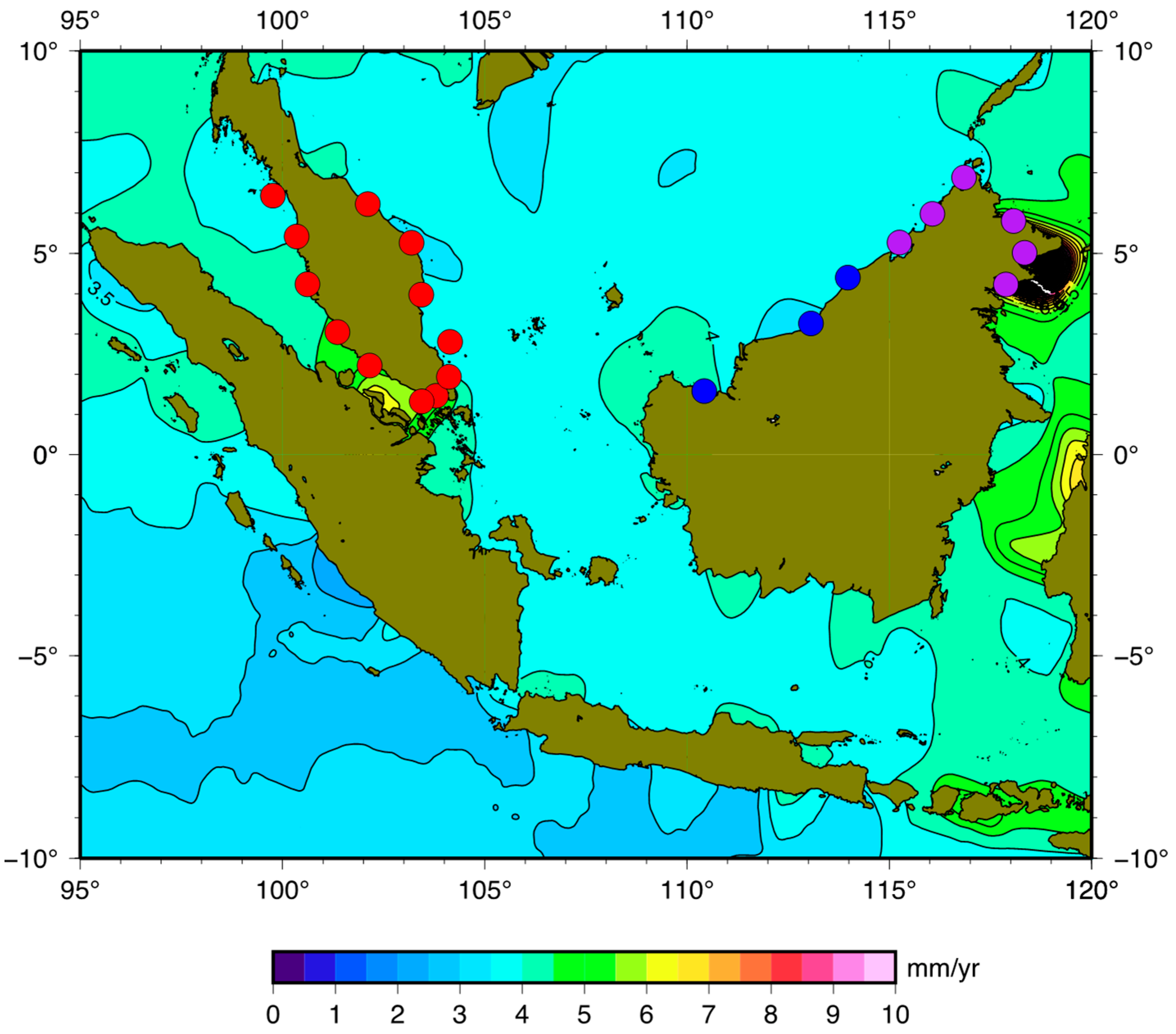
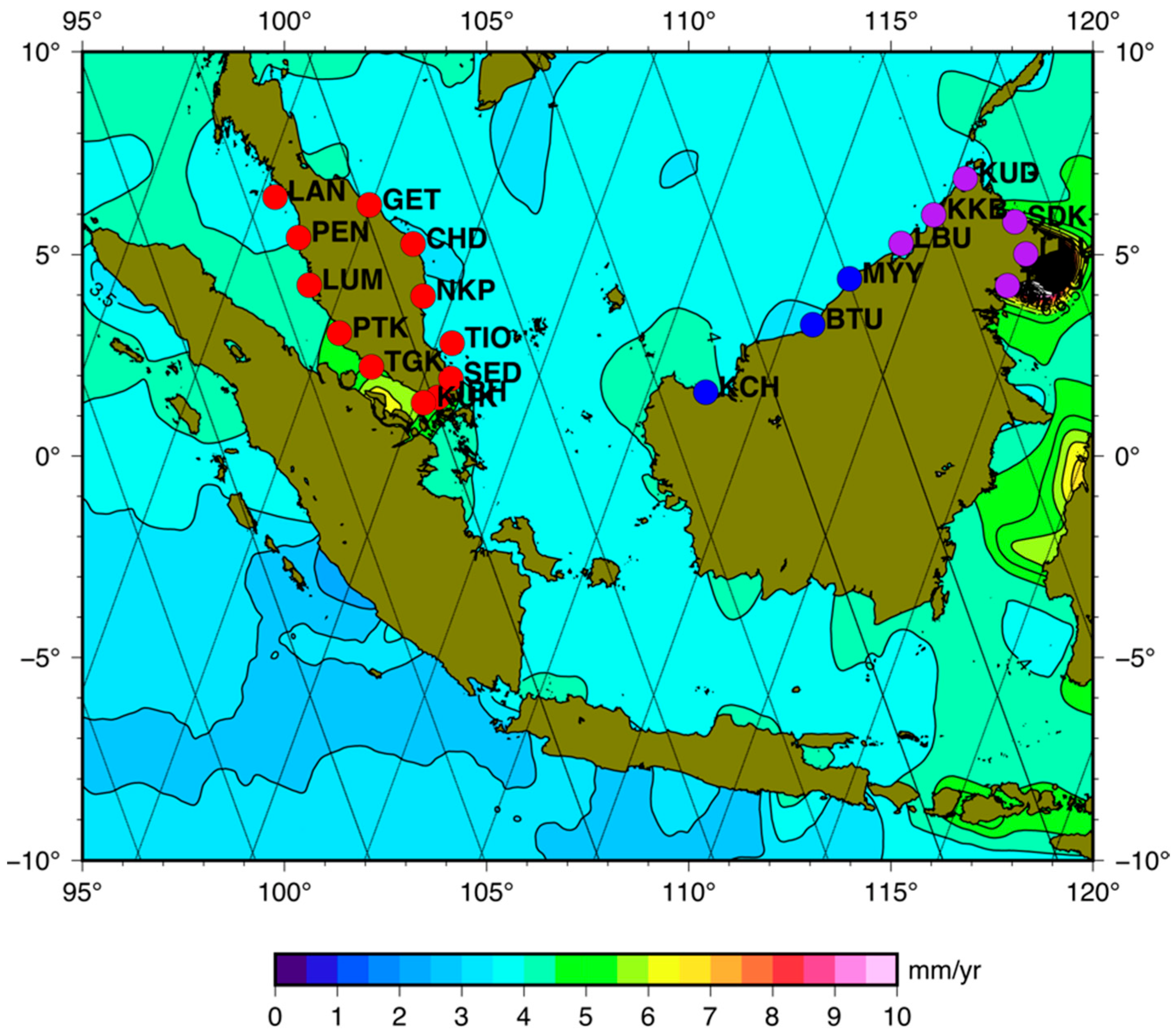


| Area | Tide Gauge | Abbr. | Lon (°E) | Lat (°N) | Period | % | ID |
|---|---|---|---|---|---|---|---|
| Peninsular | Cendering | CHD | 103.187 | 5.265 | 1985–2019 | 92.7 | 1592 |
| Geting | GET | 102.107 | 6.226 | 1986–2018 | 96.3 | 1703 | |
| Johor Bahru | JBH | 103.792 | 1.462 | 1984–2015 | 93.0 | 248 | |
| Kukup | KUK | 103.443 | 1.325 | 1986–2020 | 98.0 | 1677 | |
| Lumut | LUM | 100.613 | 4.240 | 1985–2020 | 96.7 | 1594 | |
| Pelabuhan Kelang | PTK | 101.358 | 3.050 | 1984–2020 | 91.2 | 1591 | |
| Pulau Langkawi | LAN | 99.764 | 6.431 | 1986–2020 | 97.5 | 1676 | |
| Pulau Penang | PEN | 100.347 | 5.422 | 1985–2020 | 95.4 | 1595 | |
| Pulau Tioman | TIO | 104.140 | 2.807 | 1986–2020 | 94.8 | 1678 | |
| Tanjung Gelang | NKP | 103.430 | 3.975 | 1984–2020 | 96.9 | 1589 | |
| Tanjung Keling | TGK | 102.153 | 2.215 | 1985–2020 | 96.0 | 1593 | |
| Tanjung Sedili | SED | 104.115 | 1.932 | 1986–2020 | 95.2 | 1702 | |
| Sabah | Labuan | LBU | 115.250 | 5.273 | 1996–2020 | 95.9 | 1879 |
| Lahat Datu | LDU | 118.346 | 5.019 | 1996–2020 | 97.1 | 1877 | |
| Kota Kinabalu | KKB | 116.067 | 5.983 | 1987–2020 | 92.3 | 1733 | |
| Kudat | KUD | 116.844 | 6.879 | 1996–2020 | 88.6 | 1876 | |
| Sandakan | SDK | 118.067 | 5.810 | 1986–2020 | 93.8 | 1834 | |
| Tawau | TWU | 117.883 | 4.233 | 1987–2020 | 92.9 | 1734 | |
| Sarawak | Bintulu | BTU | 113.064 | 3.262 | 1992–2019 | 85.0 | 1833 |
| Miri | MYY | 113.974 | 4.401 | 1987–2016 | 65.1 | 1819 | |
| Sejingkat | KCH | 110.422 | 1.583 | 1996–2014 | 92.8 | 1893 |
| TG Station | Trend < 2005 (mm/year) | Trend > 2005 (mm/year) | Annual (cm/days) | Semi-Annual (cm/days) | Residual SD (cm) |
|---|---|---|---|---|---|
| LAN | 2.23 ± 0.55 | 4.61 ± 0.69 | 8.91/139 | 6.60/41 | 6.06 |
| GET | 2.70 ± 0.47 | 5.56 ± 0.67 | 22.02/−1 | 3.90/29 | 5.00 |
| PEN | 2.50 ± 0.51 | 4.80 ± 0.71 | 7.97/135 | 6.72/39 | 5.97 |
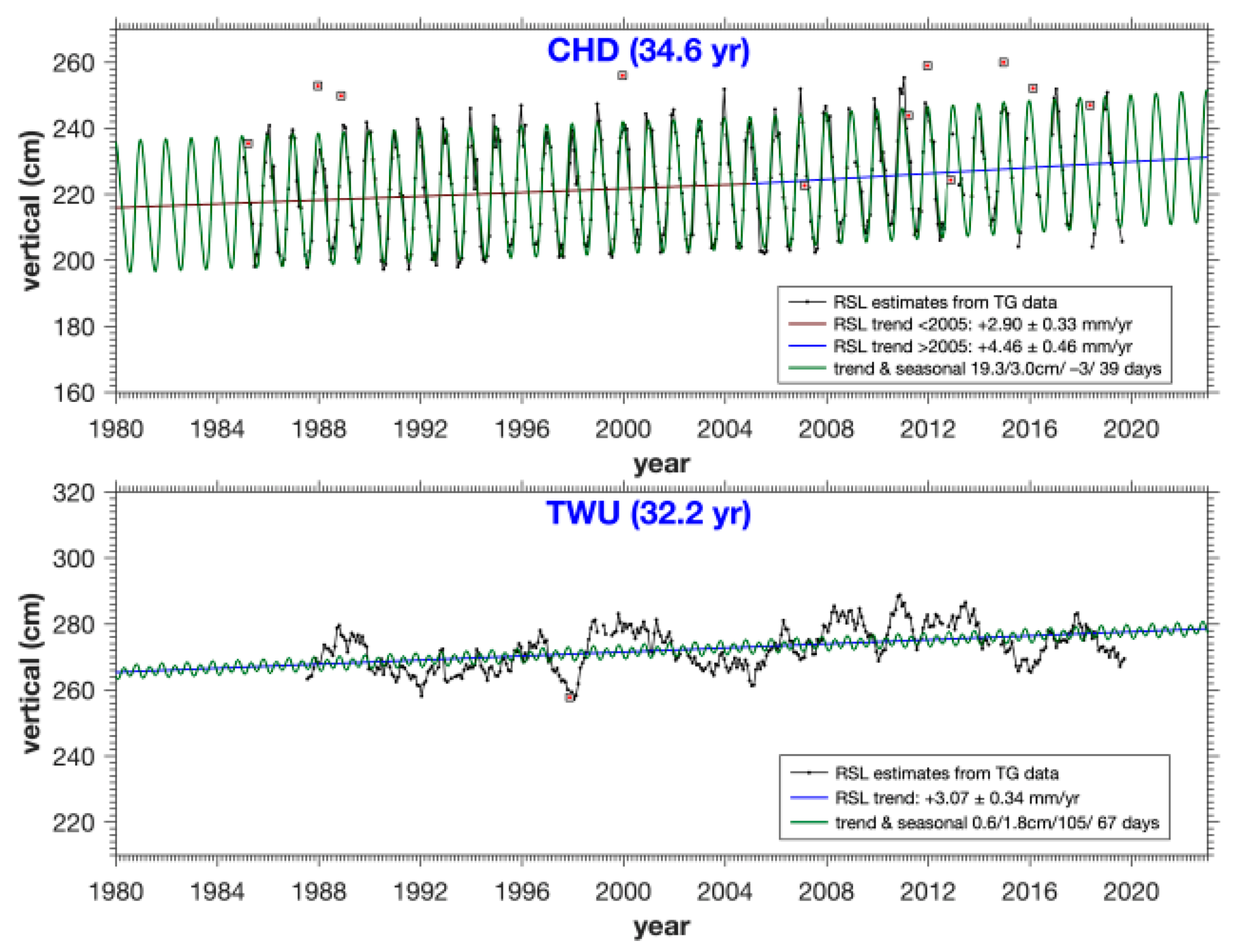
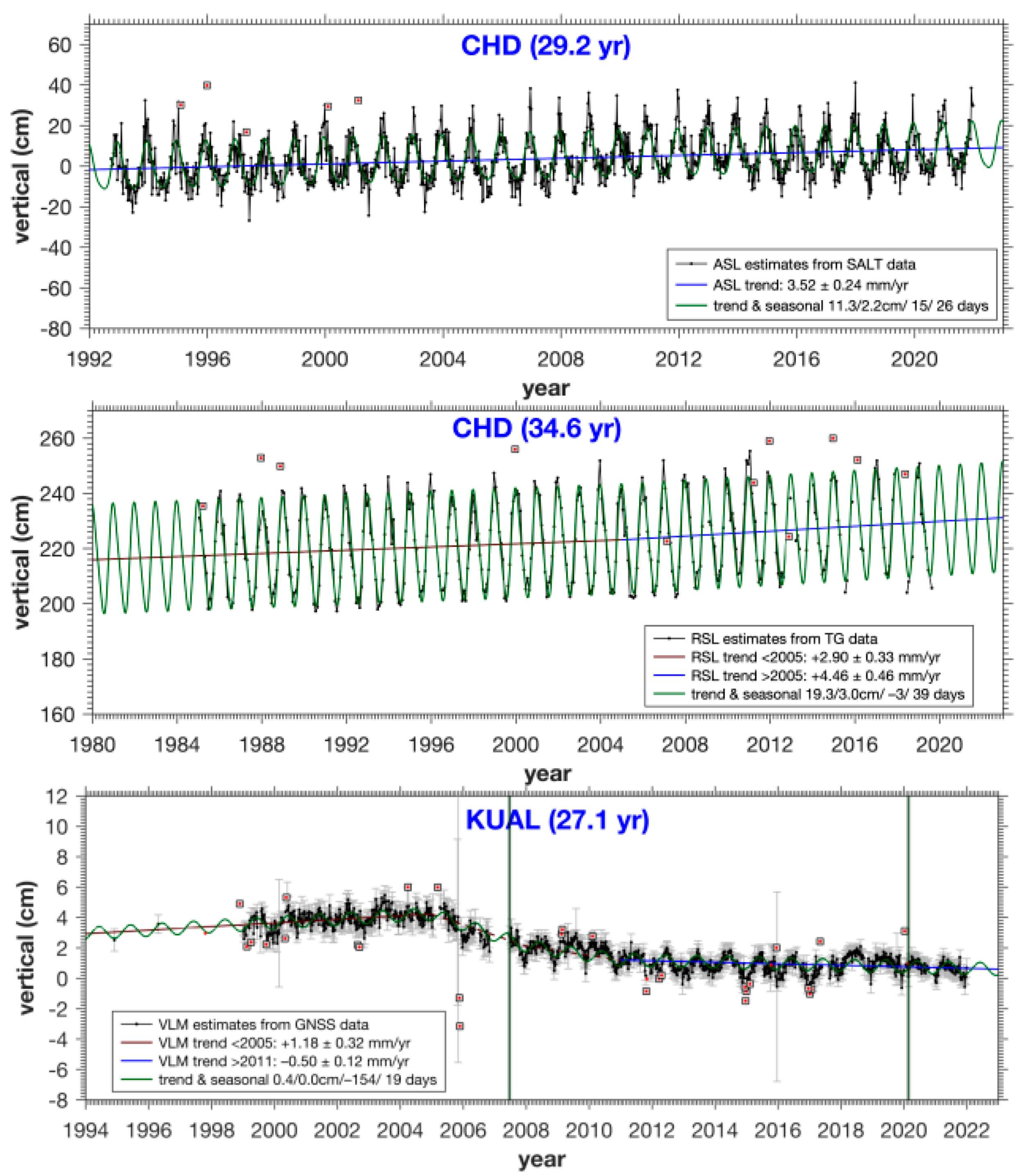
| CHD | 2.90 ± 0.33 | 4.46 ± 0.46 | 19.28/−3 | 3.01/39 | 3.90 |
| LUM | 2.27 ± 0.50 | 3.60 ± 0.66 | 6.76/127 | 6.88/37 | 5.79 |
| NKP | 2.56 ± 0.29 | 5.05 ± 0.42 | 18.68/−4 | 2.37/39 | 3.61 |
| PTK | 1.57 ± 0.50 | 3.66 ± 0.72 | 6.24/116 | 7.10/40 | 6.16 |
| TIO | 2.18 ± 0.32 | 4.26 ± 0.40 | 16.93/−1 | 2.23/37 | 3.54 |
| TGK | 1.69 ± 0.47 | 3.31 ± 0.64 | 4.98/85 | 5.52/37 | 4.73 |
| SED | 2.23 ± 0.37 | 2.55 ± 0.45 | 17.60/−2 | 2.11/22 | 3.39 |
| JBH | 2.13 ± 0.27 | 7.84 ± 0.61 | 13.65/0 | 2.22/23 | 3.34 |
| KUK | 1.87 ± 0.38 | 7.97 ± 0.48 | 5.48/46 | 4.83/35 | 4.18 |
| TG Station | Trend (mm/year) | Annual (cm/days) | Semi-Annual (cm/days) | Residual SD (cm) |
|---|---|---|---|---|
| KCH 1 | −4.98 ± 0.34 | 9.57/1 | 1.02/8 | 3.03 |
| BTU | 2.52 ± 0.28 | 8.03/35 | 2.24/32 | 3.76 |
| MYY 2 | 4.84 ± 0.31 | 7.13/48 | 2.47/37 | 4.45 |
| LBU | 2.08 ± 0.40 | 7.73/53 | 3.33/32 | 4.79 |
| KKB | 3.82 ± 0.29 | 8.16/72 | 3.53/36 | 4.76 |
| KUD | 2.46 ± 0.40 | 8.77/73 | 3.08/29 | 4.78 |
| SDK | 2.75 ± 0.36 | 6.80/46 | 1.51/27 | 4.78 |
| LDU | 1.83 ± 0.47 | 2.53/93 | 1.53/58 | 5.61 |
| TWU | 3.07 ± 0.34 | 0.60/105 | 1.78/67 | 5.52 |
| TG Station | SALT Station (km) | ASL Trend (mm/year) | Annual (cm/days) | Semi-Annual (cm/days) | Residual SD (cm) |
|---|---|---|---|---|---|
| LAN | 45 | 4.08 ± 0.28 | 7.98/143 | 7.26/37 | 8.24 |
| GET | 62 | 3.68 ± 0.26 | 18.99/−4 | 3.34/30 | 7.56 |
| PEN | 98 | 4.03 ± 0.29 | 8.57/144 | 7.16/38 | 8.53 |
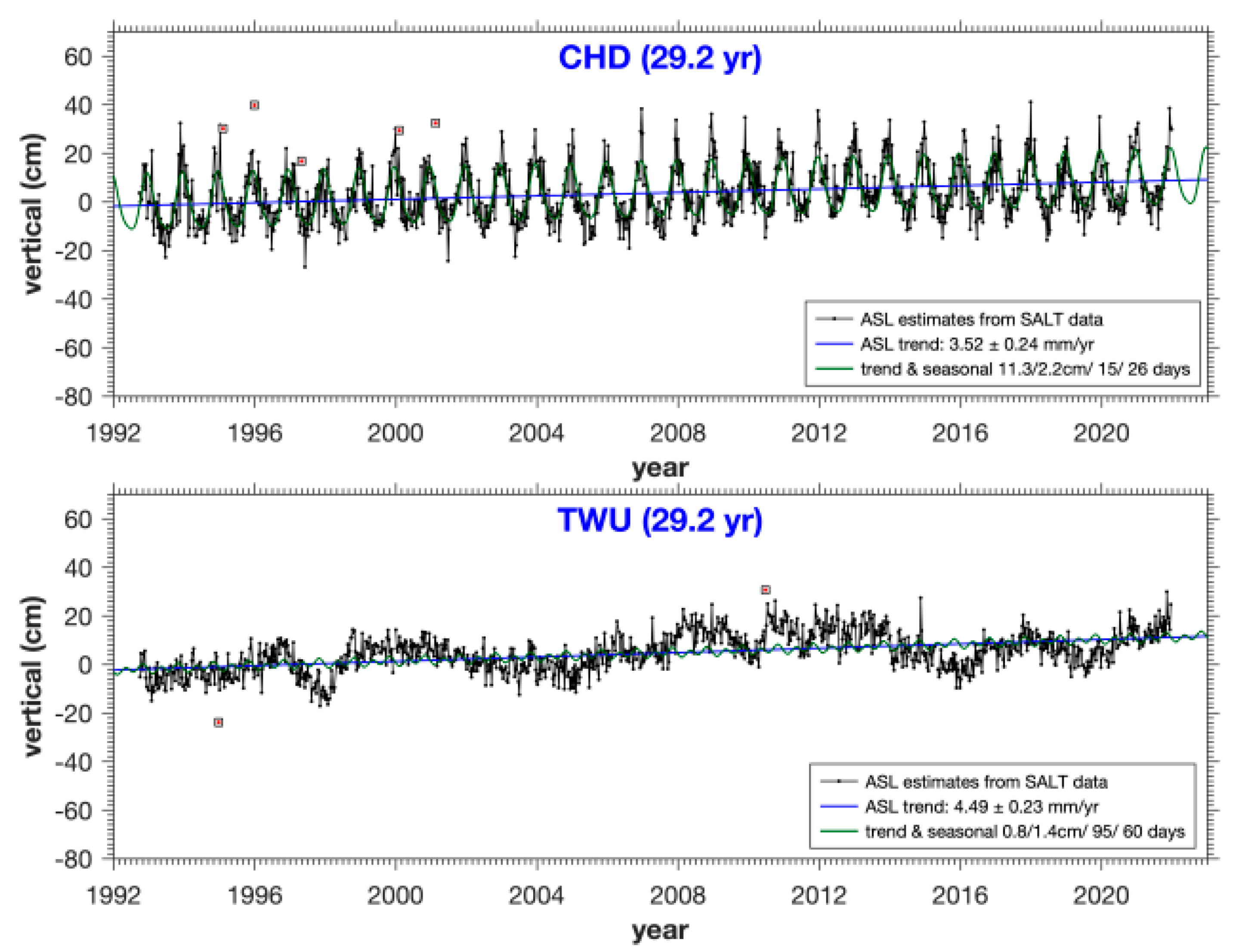
| CHD | 38 | 3.52 ± 0.24 | 11.31/15 | 2.23/26 | 7.15 |
| LUM | 34 | 4.30 ± 0.31 | 7.16/137 | 6.96/38 | 9.07 |
| NKP | 77 | 3.66 ± 0.26 | 14.40/5 | 2.58/29 | 7.72 |
| PTK | 37 | 4.73 ± 0.35 | 5.90/120 | 6.55/37 | 10.10 |
| TIO | 40 | 3.67 ± 0.27 | 15.77/2 | 2.62/30 | 8.01 |
| TGK | 4 | 4.08 ± 0.27 | 6.14/100 | 6.97/25 | 7.78 |
| SED | 16 | 4.88 ± 0.29 | 12.41/7 | 2.83/34 | 8.53 |
| JBH | 37 | 5.12 ± 0.31 | 8.91/15 | 3.37/36 | 9.19 |
| KUK | 6 | 4.73 ± 0.34 | 6.70/21 | 3.00/30 | 9.95 |
| TG Station | SALT Station (km) | Trend (mm/year) | Annual (cm/days) | Semi-Annual (cm/days) | Residual SD (cm) |
|---|---|---|---|---|---|
| KCH | 144 | 4.18 ± 0.19 | 9.97/13 | 2.70/25 | 5.67 |
| BTU | 66 | 3.43 ± 0.23 | 7.50/36 | 3.13/25 | 6.69 |
| MYY | 62 | 3.66 ± 0.18 | 7.34/45 | 3.24/26 | 5.12 |
| LBU | 144 | 3.64 ± 0.27 | 8.00/71 | 4.07/31 | 7.82 |
| KKB | 56 | 3.88 ± 0.24 | 7.91/70 | 3.86/30 | 6.91 |
| KUD | 29 | 3.92 ± 0.22 | 7.63/71 | 3.66/29 | 6.49 |
| SDK | 103 | 4.34 ± 0.20 | 5.25/85 | 1.78/42 | 5.93 |
| LDU | 39 | 4.76 ± 0.20 | 3.66/80 | 1.41/46 | 5.79 |
| TWU | 58 | 4.49 ± 0.23 | 0.83/95 | 1.45/60 | 6.71 |
| Location | Station | Position Jumps | VLM Estimate (95% CL) Absolute (IGS14) (mm/year) | Annual (cm/days) | Semi-Annual (cm/days) | Residual SD (cm) | |
|---|---|---|---|---|---|---|---|
| <2005 | >2005 | ||||||
| 1 | LGKW | 3 | - | −0.46 ± 0.13 | 0.48/−126 | 0.13/−75 | 0.37 |
| 2 | ARAU | 2 | −0.17 ± 0.36 | −1.14 ± 0.11 | 0.36/−103 | 0.09/−47 | 0.47 |
| UUMK | 3 | - | 0.45 ± 0.13 | 0.40/−110 | 0.07/−73 | 0.41 | |
| 3 | GETI + GET2 | 4 | 0.40 ± 0.33 | −2.73 ± 0.13 | 0.63/−151 | 0.08/−71 | 0.44 |
| 4 | USMP | 2 | −1.37 ± 0.41 | −0.79 ± 0.16 | 0.39/−96 | 0.11/−69 | 0.39 |
| BABH | 4 | - | −0.28 ± 0.13 | 0.39/−108 | 0.09/−57 | 0.31 | |
| 5 | GRIK | 1 | - | 0.64 ± 0.13 | 0.35/−130 | 0.08/−43 | 0.42 |
| 6 | PUPK | 3 | - | 0.79 ± 0.14 | 0.30/−109 | 0.12/−60 | 0.36 |
| 7 | GMUS | 1 | - | −0.45 ± 0.14 | 0.29/−137 | 0.02/38 | 0.39 |
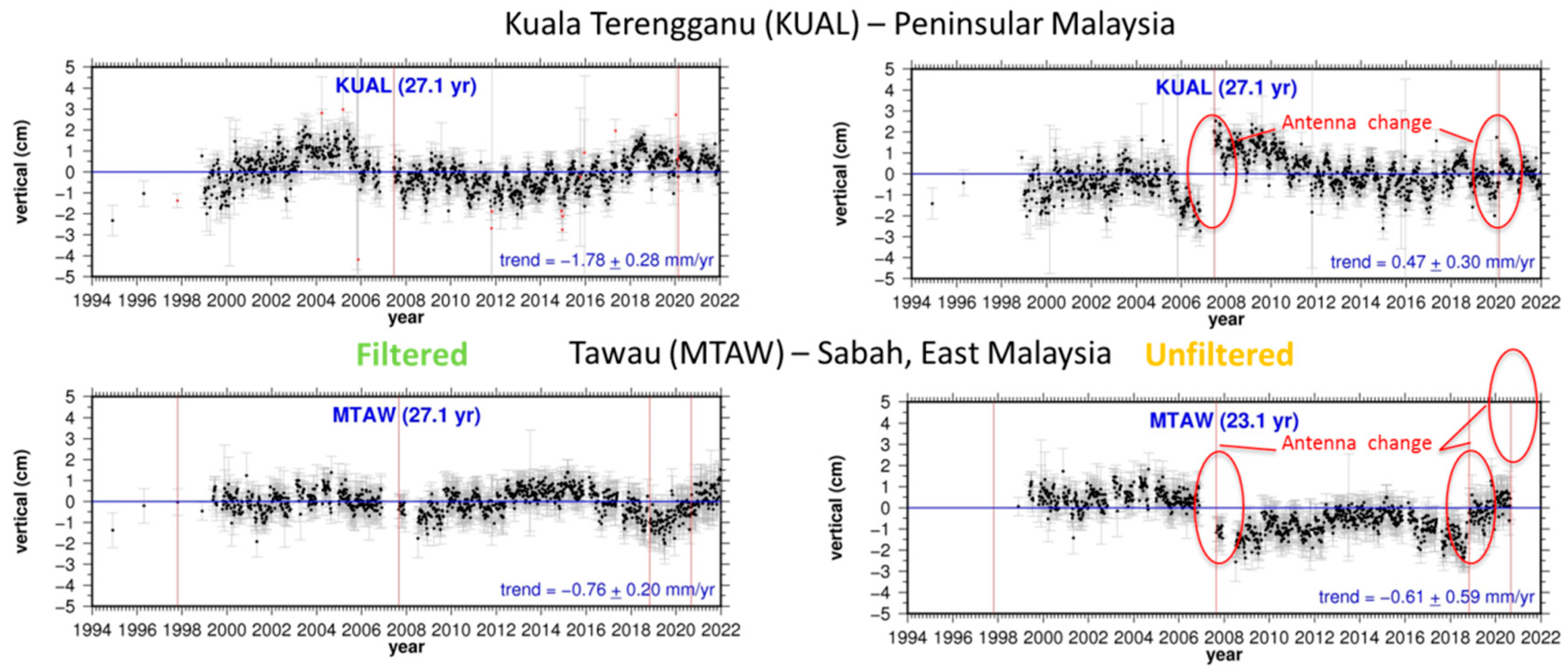
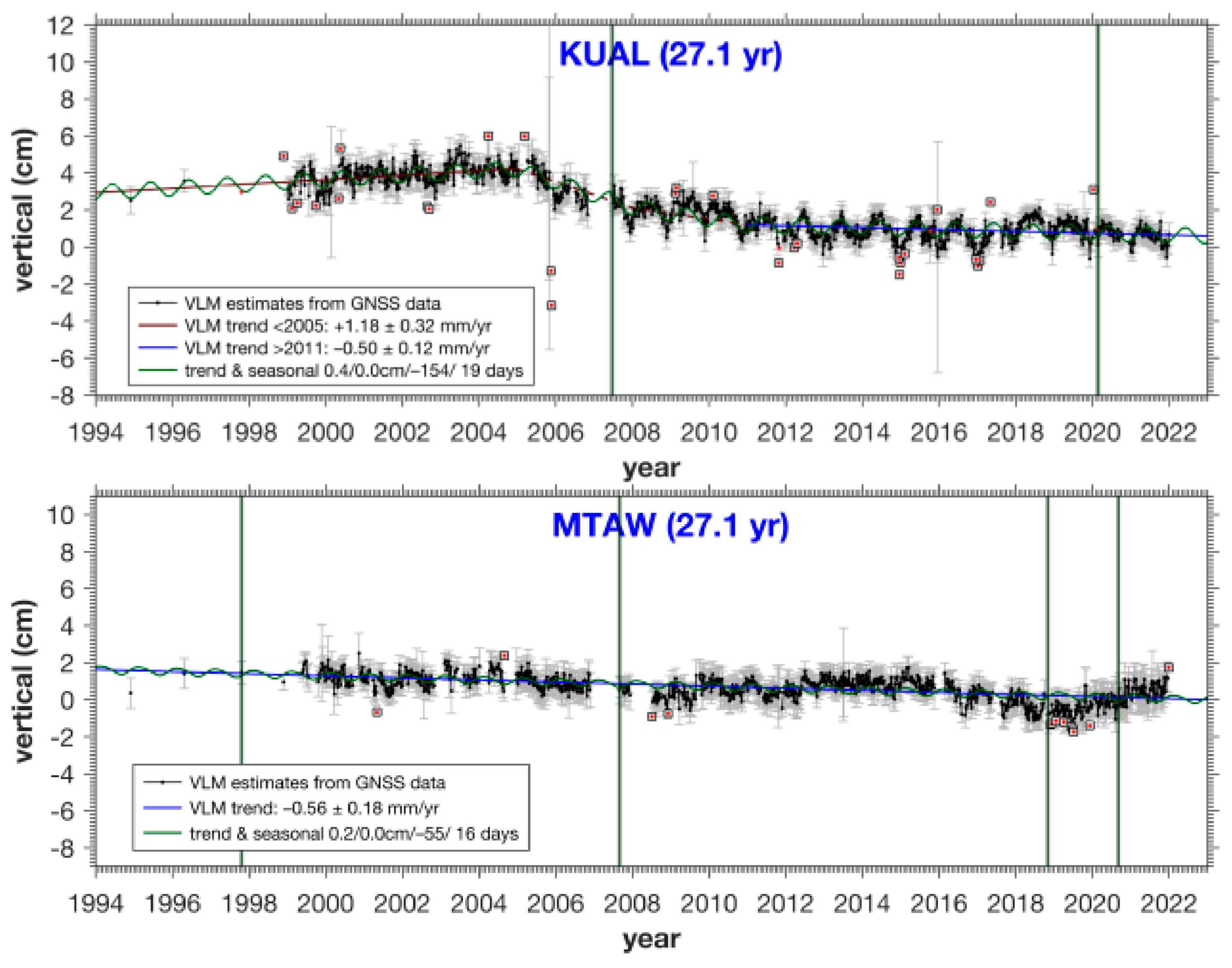
| 8 | KUAL | 3 | 1.18 ± 0.32 | −0.50 ± 0.12 | 0.41/−154 | 0.01/19 | 0.45 |
| 9 | BEHR | 5 | −0.37 ± 1.13 | −1.28 ± 0.16 | 0.34/−110 | 0.13/−51 | 0.37 |
| 10 | MERU | 1 | - | −3.29 ± 0.13 | 0.34/−77 | 0.07/64 | 0.35 |
| 11 | KTPK + UPMS | 3 | 0.85 ± 0.30 | −0.22 ± 0.13 | 0.34/−104 | 0.08/−74 | 0.32 |
| 12 | TLOH | 3 | - | −0.19 ± 0.13 | 0.26/−128 | 0.08/−85 | 0.34 |
| 13 | KUAN + PEKN | 2 | −1.06 ± 0.32 | −1.14 ± 0.13 | 0.34/−148 | 0.02/85 | 0.36 |
| 14 | JUML | 2 | - | −0.28 ± 0.13 | 0.26/−118 | 0.07/−62 | 0.32 |
| 15 | SEGA + SEG1 | 2 | 1.06 ± 0.67 | −1.54 ± 0.15 | 0.38/−105 | 0.02/4 | 0.46 |
| 16 | MERS + MRSG | 1 | - | −0.11 ± 0.14 | 0.38/−159 | 0.06/−77 | 0.34 |
| 17 | KUKP | 2 | - | −4.75 ± 0.15 | 0.25/−124 | 0.06/−40 | 0.35 |
| 18 | TGRH + SDLI | 2 | - | −0.20 ± 0.13 | 0.30/−149 | 0.11/−43 | 0.32 |
| 19 | TGPG | 1 | - | −0.55 ± 0.14 | 0.29/−139 | 0.07/−55 | 0.37 |
| 20 | UTMJ + JHJY | 4 | 1.75 ± 0.36 | −1.18 ± 0.12 | 0.34/−138 | 0.11/−88 | 0.41 |
| 21 | NTUS | 2 | 0.72 ± 0.31 | 0.05 ± 0.15 | 0.41/−147 | 0.09/−62 | 0.38 |
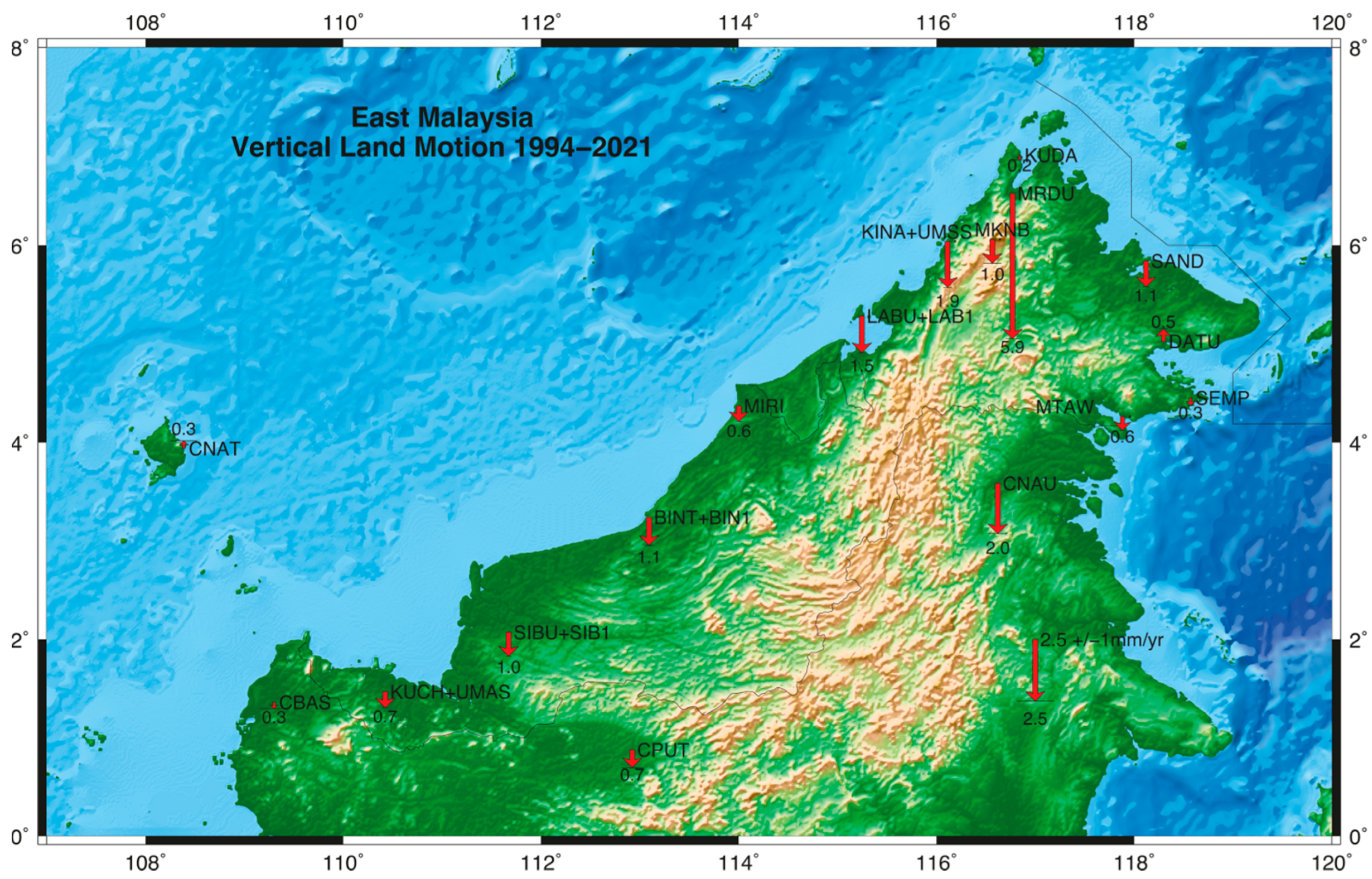
| Location | Station | Position Jumps | VLM Estimate (95% CL) Absolute (IGS14) (mm/year) 1994–2021 | Annual (cm/days) | Semi-Annual (cm/days) | Residual SD (cm) |
|---|---|---|---|---|---|---|
| 1 | KUCH + UMAS | 2 | −0.66 ± 0.16 | 0.20/−147 | 0.06/−77 | 0.36 |
| 2 | SIBU + SIB1 | 3 | −0.97 ± 0.16 | 0.12/−111 | 0.04/79 | 0.33 |
| 3 | BINT + BIN1 | 2 | −1.13 ± 0.21 | 0.23/−86 | 0.08/78 | 0.47 |
| 4 | MIRI | 2 | −0.63 ± 0.17 | 0.26/−99 | 0.04/78 | 0.38 |
| 5 | LABU + LAB1 | 3 | −1.48 ± 0.16 | 0.23/−97 | 0.03/59 | 0.36 |
| 6 | KINA + UMSS | 2 | −1.86 ± 0.22 | 0.13/−90 | 0.05/−48 | 0.52 |
| 7 | MKNB | 1 | −0.97 ± 0.48 | 0.24/−82 | 0.13/−83 | 0.41 |
| 8 | KUDA | 1 | −0.19 ± 0.24 | 0.22/−81 | 0.02/9 | 0.34 |
| 9 | MRDU | 2 | −5.88 ± 0.38 | 0.10/−130 | 0.02/−44 | 0.49 |
| 10 | SAND | 3 | −1.05 ± 0.18 | 0.23/−81 | 0.08/75 | 0.42 |
| 11 | DATU | 1 | 0.51 ± 0.22 | 0.20/−79 | 0.03/−53 | 0.29 |
| 12 | SEMP | 2 | −0.32 ± 0.21 | 0.18/−69 | 0.04/−33 | 0.28 |
| 13 | TAWA + MTAW | 4 | −0.56 ± 0.18 | 0.20/−55 | 0.03/16 | 0.48 |
| 14 | CNAT | 0 | 0.31 ± 0.71 | 0.25/−154 | 0.07/−91 | 0.35 |
| 15 | CBAS | 0 | −0.27 ± 0.72 | 0.28/−117 | 0.13/−80 | 0.51 |
| 16 | CPUT | 0 | −0.73 ± 0.58 | 0.12/−30 | 0.09/87 | 0.41 |
| 17 | CNAU | 1 | −2.04 ± 0.49 | 0.07/4 | 0.06/77 | 0.35 |
| TG Station | Nearest GNSS Station | Distance (km) | ASL (SALT) (mm/year) 1992–2020 | VLM (GNSS) (mm/year) | RSL (TG) (mm/year) | RSL (SALT−GNSS) (mm/year) | |||
|---|---|---|---|---|---|---|---|---|---|
| <2005 | >2005 | <2005 | >2005 | <2005 | >2005 | ||||
| LAN | LKGW | 15 | 4.08 ± 0.28 | - | −0.46 ± 0.13 | 2.23 ± 0.55 | 4.61 ± 0.69 | - | 4.54 ± 0.31 |
| GET | GET2 | 0 | 3.68 ± 0.24 | 0.40 ± 0.33 | −2.73 ± 0.13 | 2.70 ± 0.47 | 5.56 ± 0.67 | 3.28 ± 0.41 | 6.41 ± 0.27 |
| PEN | USMP | 8 | 4.03 ± 0.29 | −1.37 ± 0.41 | −0.79 ± 0.16 | 2.50 ± 0.51 | 4.80 ± 0.71 | 5.40 ± 0.50 | 4.82 ± 0.33 |
| CHD | KUAL | 8 | 3.52 ± 0.24 | 1.18 ± 0.32 | −0.50 ± 0.12 | 2.90 ± 0.33 | 4.46 ± 0.46 | 2.34 ± 0.40 | 4.02 ± 0.27 |
| LUM | PUPK | 7 | 4.30 ± 0.31 | - | 0.79 ± 0.14 | 2.27 ± 0.50 | 3.60 ± 0.66 | - | 3.51 ± 0.34 |
| NKP | PEKN | 54 | 3.66 ± 0.26 | −1.06 ± 0.32 | −1.14 ± 0.13 | 2.56 ± 0.29 | 5.05 ± 0.42 | 4.72 ± 0.41 | 4.80 ± 0.29 |
| PTK | MERU | 11 | 4.73 ± 0.35 | - | −3.29 ± 0.13 | 1.57 ± 0.50 | 3.66 ± 0.72 | - | 8.02 ± 0.37 |
| TIO | MRSG | 52 | 3.67 ± 0.27 | - | −0.11 ± 0.14 | 2.18 ± 0.32 | 4.26 ± 0.40 | - | 3.78 ± 0.30 |
| TGK | JUML | 11 | 4.08 ± 0.27 | - | −0.28 ± 0.13 | 1.69 ± 0.47 | 3.31 ± 0.64 | - | 4.36 ± 0.30 |
| SED | SDLI | 1 | 4.88 ± 0.29 | - | −0.20 ± 0.13 | 2.23 ± 0.37 | 2.55 ± 0.45 | - | 5.08 ± 0.32 |
| JBH | JHJY | 8 | 5.12 ± 0.31 | 1.75 ± 0.36 | −1.18 ± 0.12 | 2.13 ± 0.27 | 7.84 ± 0.61 | 3.37 ± 0.48 | 6.30 ± 0.33 |
| KUK | KUKP | 1 | 4.73 ± 0.34 | - | −4.75 ± 0.15 | 1.87 ± 0.38 | 7.97 ± 0.48 | - | 9.48 ± 0.37 |
| TG Station | Nearest GNSS Station | Distance (km) | ASL (SALT) (mm/year) 1992–2020 | VLM (GNSS) (mm/year) 1994–2021 | RSL (TG) (mm/year) 1985–2019 | RSL (SALT−GNSS) (mm/year) 1992–2021 |
| KCH | UMAS | 12 | 4.18 ± 0.19 | −0.66 ± 0.16 | −4.98 ± 0.34 | 4.84 ± 0.25 * |
| BTU | BIN1 | 4 | 3.43 ± 0.23 | −1.13 ± 0.21 | 2.52 ± 0.28 | 4.56 ± 0.31 ** |
| MYY | MIRI | 4 | 3.66 ± 0.18 | −0.63 ± 0.17 | 4.84 ± 0.31 | 4.29 ± 0.25 *** |
| LBU | LAB1 | 1 | 3.64 ± 0.27 | −1.48 ± 0.16 | 2.08 ± 0.40 | 5.12 ± 0.31 ** |
| KKB | UMSS | 8 | 3.88 ± 0.24 | −1.86 ± 0.22 | 3.82 ± 0.29 | 5.74 ± 0.33 ** |
| KUD | KUDA | 4 | 3.92 ± 0.22 | −0.19 ± 0.24 | 2.46 ± 0.40 | 4.11 ± 0.33 ** |
| SDK | SAND | 7 | 4.34 ± 0.20 | −1.05 ± 0.18 | 2.75 ± 0.36 | 5.39 ± 0.27 ** |
| LDU | DATU | 6 | 4.76 ± 0.20 | 0.51 ± 0.22 | 1.83 ± 0.47 | 4.25 ± 0.30 ** |
| TWU | MTAW | 3 | 4.49 ± 0.23 | −0.56 ± 0.18 | 3.07 ± 0.34 | 5.05 ± 0.29 ** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simons, W.; Naeije, M.; Ghazali, Z.; Rahman, W.D.; Cob, S.; Kadir, M.; Mustafar, A.; Din, A.H.; Efendi, J.; Noppradit, P. Relative Sea Level Trends for the Coastal Areas of Peninsular and East Malaysia Based on Remote and In Situ Observations. Remote Sens. 2023, 15, 1113. https://doi.org/10.3390/rs15041113
Simons W, Naeije M, Ghazali Z, Rahman WD, Cob S, Kadir M, Mustafar A, Din AH, Efendi J, Noppradit P. Relative Sea Level Trends for the Coastal Areas of Peninsular and East Malaysia Based on Remote and In Situ Observations. Remote Sensing. 2023; 15(4):1113. https://doi.org/10.3390/rs15041113
Chicago/Turabian StyleSimons, Wim, Marc Naeije, Zaki Ghazali, Wan Darani Rahman, Sanusi Cob, Majid Kadir, Asrul Mustafar, Ami Hassan Din, Joni Efendi, and Prakrit Noppradit. 2023. "Relative Sea Level Trends for the Coastal Areas of Peninsular and East Malaysia Based on Remote and In Situ Observations" Remote Sensing 15, no. 4: 1113. https://doi.org/10.3390/rs15041113
APA StyleSimons, W., Naeije, M., Ghazali, Z., Rahman, W. D., Cob, S., Kadir, M., Mustafar, A., Din, A. H., Efendi, J., & Noppradit, P. (2023). Relative Sea Level Trends for the Coastal Areas of Peninsular and East Malaysia Based on Remote and In Situ Observations. Remote Sensing, 15(4), 1113. https://doi.org/10.3390/rs15041113







